1 Introduction

We can think of the fitness of an individual organism in terms of its chances of survival and of reproducing successfully. Thus, the smaller the risk of death (in the immediate future), or the greater the chance of reproducing successfully, the greater the fitness of the organism. The average fitness of the individuals in a population can be defined as the per capita growth rate of the population (p. 9, Courchamp et al. 2008).

The concept of fitness is central to the study of Allee effects. In particular, a demographic Allee effect refers to a positive correlation between the size or density of a population and the average fitness of the individuals in it (p. 10, Courchamp et al. 2008). In other words, the greater the size or density of the population, the greater the average fitness. Alternatively, the lower the size or density of the population, the lower the average fitness.

If a population is subject to a demographic Allee effect, then this will only occur if the population is small in some sense. To be specific, if a population has a sufficiently high density over a sufficiently large range, then competition for food and other resources will be so fierce that further increases to the population will only intensify this competition and thereby reduce individual fitness. Thus, a demographic Allee effect does not hold for a population with sufficiently high density over a sufficiently large range.

There are a number of ways in which a small population may be subject to a demographic Allee effect. We give two examples. First, an increase in the size or density of a population may increase the chance of its members deriving benefits from group protection or co-operation (Courchamp et al. 1999; Boukal and Berec 2002). Second, if a population reproduces sexually, then an increase in its size or density will allow individuals to find a mate more easily and will reduce the risk of inbreeding (Courchamp et al. 1999; McCarthy 1997). Of course, competition over access to a mate or to optimal breeding sites may also be increased, but such competition may not be significant at low population size or density.

Consider a population subject to a demographic Allee effect at all sufficiently small levels (sizes or densities), and suppose it is at such a level. Suppose further that, for the particular level of the population, the average fitness of individuals in it is such that, on average, individuals cannot replace themselves (by reproduction) faster than they die. Then the per capita growth rate of the population (that is, the average fitness) will be negative, and the population will decrease. This decrease in the population will reduce average fitness, since the population is subject to a demographic Allee effect. Hence the population will continue to decrease, and in fact it will inevitably die out. Given this link between Allee effects and population extinction, Allee effects have been studied in the context of conservation biology (Burgman et al. 1993; Dennis 1989; Dobson and Lyles 1989).

Note that demographic Allee effects are one of two main types of Allee effect. The other is called a component Allee effect, which refers to a positive correlation between population size or density and any measurable component of individual fitness, such as juvenile survival or adult reproduction (p. 9, Courchamp et al. 2008). Component Allee effects may result in demographic Allee effects (p. 9, Courchamp et al. 2008). A collection of definitions of various terms relating to Allee effects may be found in chapter 1 in Courchamp et al. (2008).

The literature on the mathematical modelling of Allee effects has expanded significantly in recent years (Courchamp et al. 2008; Wang et al. 2011b; Zu and Mimura 2010; van Voorn et al. 2007; Zu et al. 2010; Terry 2009, 2010a, b, 2011). The field is currently very fertile and many interesting questions have yet to be fully addressed. In particular, although there have been a number of studies of predator–prey models in which the predator population is subject to a component Allee effect for reproduction [for example, see (Bazykin 1998; Zhou et al. 2005; Verdy 2010; Lai et al. 2010; Wang et al. 2013; Terry 2013)], there remains considerable scope for exploring this area. Therefore, our objective in this paper will be to investigate four new predator–prey models with component Allee effect for predator reproduction. We will see that this type of component Allee effect may also give rise to a demographic Allee effect for the predator.

There is an additional motivation for this work. Specifically, we seek to redress an imbalance in the modelling literature. The literature on predator–prey models with Allee effect for the prey appears, at the moment, to be more extensive than the literature on predator–prey models with Allee effect for the predator. We see this as an imbalance because, in the real world, we might expect predator populations to be more prone to Allee effects than their prey, since populations are more prone to experience an Allee effect when they are smaller, and predator populations are typically much smaller than prey populations. A selection of studies of predator–prey models with Allee effect for the prey is given here (Zhou et al. 2005; Wang et al. 2011b; Zu and Mimura 2010; van Voorn et al. 2007; Zu et al. 2010; Gonzalez-Olivares et al. 2011a; Zu 2013; Gonzalez-Olivares and Rojas-Palma 2011; Aguirre et al. 2009; Gonzalez-Olivares et al. 2011b; Sen et al. 2012).

We outline the format for the rest of this paper. In Sect. 2, we describe our four new models. Using numerical simulation results for our models, we discuss, in Sect. 3, how the customary definitions of demographic and component Allee effects, which work well for single species models, can be extended to predators in predator–prey models by assuming that the prey population is held fixed. Then, in Sect. 4, we investigate the fixed points of our models. In particular, we establish that each of our models has a fixed point that represents predator extinction, and this is always locally stable. Through numerical exploration, we also find that our models can possess multiple co-existence fixed points, and we discover a stable limit cycle in one of our models. Finally, in Sect. 5, we list a few options for extending this work. Additional results are included in a Supporting Information file—specifically, we derive conditions for a co-existence trapping region in three of our models, and show that the fourth model cannot possess a particular kind of co-existence trapping region.

2 The models

In this section, we describe four new predator–prey models with Allee effect for the predator. In each model, the predator is assumed to reproduce sexually. Letting \(N = N(t)\) and \(P = P(t)\) denote, respectively, the sizes of the prey and predator populations at time \(t \ge 0\), the first model is:

$$\begin{aligned} \left. \begin{aligned}&\frac{d\!N}{dt}=r N \left( 1 - \frac{N}{K} \right) - P\!F(N), \\&\frac{d\!P}{dt}=P \left[ c F(N) \left( \frac{P}{h + P} \right) - D(F(N)) \right] , \\&N(0) \ge 0, \quad P(0) \ge 0, \end{aligned} \quad \right\} \end{aligned}$$
(1)

where \(r, K, c\), and \(h\) are positive constants, and where:

$$\begin{aligned}&F(N) = \frac{ a N }{ 1 + b N }\quad \text {(a and b are positive constants)}, \end{aligned}$$
(2)
$$\begin{aligned}&\left. \begin{array}{l} D(F(N)) = D(F) {\text { is a continuously differentiable function of }} F \ge 0; {\text { also}},\\ \quad {\text {for }} F \ge 0, {\text { we have }} dD/dF \le 0, {\text { and }} 0 < d_1 \le D(F) \le d_2 {\text { where }} d_1, d_2\\ \quad {\text {are constants}}. \quad \end{array}\right\} \nonumber \\ \end{aligned}$$
(3)

This model is based on the following assumptions:

  1. (A1)

    The prey population grows logistically in the absence of predation, that is, when \(P = 0\).

  2. (A2)

    The average prey consumption rate per predator, namely \(F(N)\), also called the functional response of the predator or predator functional response, adopts the Holling type II form in (2).

  3. (A3)

    The average predator reproduction rate, per predator, is equal to \(c F(N) \left( \frac{P}{h + P} \right) \), a justification for which is given below.

  4. (A4)

    The average per predator death rate, namely \(D(F(N))\), is defined in (3) in such a way as to capture these ideas: (i) it is decreasing in the predator functional response \(F(N)\) because, if a predator eats more, it will be less likely to die from starvation or from the consequences of weakness brought on by hunger; and (ii) it is positive for any value of \(F(N) \ge 0\), because a predator is highly unlikely to live forever.

Assumptions (A1) and (A2) are quite typical of predator–prey models (Turchin 2003; Skalski and Gilliam 2001; Terry 2014a; Britton 2003; Brauer and Castillo-Chávez 2001). Assumption (A4) is not typical of predator–prey models. Rather, it is common to assume in such models that the per predator death rate is equal to a positive constant (Turchin 2003; Abrams and Ginzburg 2000), which represents an assumption that predators die off exponentially in the absence of prey (p. 55, Britton 2003). Whilst it is certainly sensible for the per predator death rate to be treated as strictly positive, it is debatable as to whether it should be treated as a constant, as noted in Terry (2013, 2014a) and Deng et al. (2007). The life processes of a predator are fuelled by prey consumption, and this includes, most fundamentally, staying alive. Hence it seems reasonable to choose a form for the per predator death rate that has the capacity to reflect this, such as in our choice for it in (3). For generality, however, we allow the possibility that the per predator death rate is constant in (3).

Assumption (A3) requires justification, and we give this here. As mentioned at the start of this section, the predator is assumed to reproduce sexually. Ignoring delays due to gestation or egg hatching, this allows us to write:

$$\begin{aligned}&{\text {total rate of predator reproduction at time }} t \nonumber \\&\quad ={\text {(number of sexually mature females able to find a suitable mate at time }} t \text {)} \nonumber \\&\qquad \times {\text {(average reproduction rate per sexually mature female }} \nonumber \\&\qquad \quad {\text { that is able to find a suitable mate at time }} t). \end{aligned}$$
(4)

We make two assumptions: (B1) the proportion of the predator population composed of sexually mature females is sufficiently constant over time that we can approximate it by a positive constant \(\gamma _1\); and (B2) the proportion of the predator population composed of sexually mature males is sufficiently constant over time that we can approximate it by a positive constant \(\gamma _2\). These assumptions will hold if the predator population has a stable sex distribution and stable age distribution. In view of assumptions (B1) and (B2), the numbers of sexually mature female and sexually mature male predators at time \(t\) are, respectively, \(\gamma _1 P\) and \(\gamma _2 P\).

Now the number of sexually mature females able to find a suitable mate at time \(t\) will be the total number of sexually mature females at time \(t\), which is \(\gamma _1 P\), multiplied by the proportion of such females that can find a suitable mate at time \(t\). It seems reasonable to suppose that, the more sexually mature males there are, the more likely it is that a sexually mature female will be able to find one of them. Therefore, we shall suppose that the proportion of sexually mature females able to find a mate at time \(t\) is an increasing function of the number of sexually mature males \(\gamma _2 P\), which we write as \(H(\gamma _2 P)\). Since \(H(\gamma _2 P)\) represents a proportion, we must have \(0 \le H(\gamma _2 P) \le 1\). Clearly, if there are no sexually mature males, then a sexually mature female will have zero chance of finding a suitable mate, so we must have \(H(0) = 0\). However, if there are a large number of sexually mature males, then it is arguably true that every sexually mature female will stand an excellent chance of finding a mate. Therefore, an obvious choice for \(H(\gamma _2 P)\) is \((\gamma _2 P)/(\delta + \gamma _2 P)\) where \(\delta \) is a positive constant, and we do make this choice.

Finally, we consider the rate of offspring production for a sexually mature female that has found a mate. We shall suppose that this rate of offspring production is an increasing function \(J(F(N))\) of the predator functional response (prey consumption rate) \(F(N)\), based on the following ideas: (i) a sexually mature female that has found a mate will be more successful in producing offspring when it has a higher rate of prey consumption in the recent past, because the production of offspring is fuelled by the consumption of prey; (ii) the rate of prey consumption in the recent past prior to a particular time can, for simplicity, be represented by the prey consumption rate at that particular time. It seems reasonable to assume that \(J(0) = 0\) to reflect the idea that a female will not successfully produce offspring if its prey consumption rate is zero. Arguably the simplest form for \(J(F(N))\) is a linear one, and indeed there is empirical evidence, for some arthropod predator species, that there can be a linear relationship between the birth rate per adult female (egg-laying rate) and the prey consumption rate per predator [figures 10 and 13(c), Beddington et al. 1976]. Therefore, we shall suppose that \(J(F(N)) = \gamma _3 F(N)\) for a positive constant \(\gamma _3\).

Combining our observations from the three previous paragraphs, and in particular using (4), we find:

$$\begin{aligned} {\text {total rate of predator reproduction}}&= (\gamma _1 P) H(\gamma _2 P) J(F(N)) \nonumber \\&= P \left( \gamma _1 \gamma _3 F(N) \right) \left( \frac{ \gamma _2 P }{ \delta + \gamma _2 P } \right) \!. \end{aligned}$$
(5)

Since the total rate of predator reproduction is equal to the predator population \(P\) multiplied by the per predator reproduction rate, we must have from (5) that the per predator reproduction rate is \(c F(N) \left( \frac{P}{h + P} \right) \), where \(c = \gamma _1 \gamma _3\) and \(h = \delta /\gamma _2\) are positive constants. In other words, we have established that the per predator reproduction rate (average predator reproduction rate, per predator) takes the form mentioned in assumption (A3), as required.

We have now defined and justified our first model. For ease of reference, we describe it in a single equation environment:

$$\begin{aligned} {\text {the model defined by }} (1) {\text { to }} (3). \end{aligned}$$
(6)

Our second, third, and fourth models are all simple adaptations of our first model. For our second model, we include an additional term for self-limitation in the differential equation for the predator. To be specific, we replace (1) by:

$$\begin{aligned} \left. \begin{aligned}&\frac{\textit{dN}}{dt}=r N \left( 1 - \frac{N}{K} \right) - P F(N),\\&\frac{\textit{dP}}{dt}=P \left[ c F(N) \left( \frac{P}{h + P} \right) - D(F(N)) - m P \right] , \\&N(0)\ge 0,\quad P(0)\ge 0, \end{aligned} \quad \right\} \end{aligned}$$
(7)

where \(r, K, c, h\), and \(m\) are positive constants. In the additional term, one interpretation of the parameter \(m\) is “aggression” (box 1, Abrams and Ginzburg 2000). Various other authors have considered predator–prey models with a self-limitation term for the predator (Bazykin et al. 1981; Hainzl 1988, 1992; Gourley and Kuang 2004). We may summarise our second model as follows:

$$\begin{aligned} {\text {the model defined by}}\,(7),\, (2), \,{\text {and}}\, (3). \end{aligned}$$
(8)

For our third model, we replace the Holling type II functional response in model (6) by another commonly used form for the functional response, namely the Beddington–DeAngelis form (Terry 2013; Turchin 2003; Skalski and Gilliam 2001; Zhang et al. 2008). Thus, our third model is:

$$\begin{aligned} \left. \begin{aligned}&\frac{dN}{dt} = r N \left( 1 - \frac{N}{K} \right) - P F(N,P),\\&\frac{dP}{dt} = P \left[ c F(N,P) \left( \frac{P}{h + P} \right) - D(F(N,P)) \right] , \\&N(0) \ge 0, \quad P(0) \ge 0, \end{aligned} \quad \right\} \end{aligned}$$
(9)

where \(r, K, c\), and \(h\) are positive constants, and where:

$$\begin{aligned}&F(N,P) = \frac{ a N }{ 1 + b N + q P }\quad ( a, b, \text { and } q {\text { are positive constants}}), \end{aligned}$$
(10)
$$\begin{aligned}&\left. \begin{array}{l} D(F(N,P)) = D(F) {\text { is a continuously differentiable function of }} F \ge 0; {\text { also}},\\ {\text { for }} F \ge 0, {\text { we have }} dD/dF \le 0, {\text { and }} 0 < d_1 \le D(F) \le d_2 {\text { where }} d_1, d_2\\ {\text { are constants}}. \end{array}\right\} \nonumber \\ \end{aligned}$$
(11)

We may concisely summarise our third model as follows:

$$\begin{aligned} {\text {the model defined by }} (9) {\text { to }} (11). \end{aligned}$$
(12)

Our fourth and final model involves simply combining the changes introduced in our second and third models. Thus, for our fourth model, we adapt the first model in (6) by including a self-limitation term for the predator and by replacing the functional response with a Beddington–DeAngelis form as in (10). Specifically, then, our fourth model is:

$$\begin{aligned} \left. \begin{aligned}&\frac{\textit{dN}}{\textit{dt}} = r N \left( 1 - \frac{N}{K} \right) - P F(N,P),\\&\frac{\textit{dP}}{\textit{dt}} = P \left[ c F(N,P) \left( \frac{P}{h + P} \right) - D(F(N,P)) - m P \right] , \\&N(0) \ge 0, \quad P(0) \ge 0, \end{aligned} \quad \right\} \end{aligned}$$
(13)

where \(r, K, c, h\), and \(m\) are positive constants, and where \(F(N,P)\) satisfies (10), and \(D(F(N,P))\) satisfies (11). We summarise our fourth model as follows:

$$\begin{aligned} {\text {the model defined by }} (13), (10), {\text {and}}\, (11). \end{aligned}$$
(14)

We have now defined our four models, specifically in (6), (8), (12), and (14). All of these models contain a component Allee effect for the predator birth rate, in the sense that the per capita birth rate of the predator population \(P\) is increasing in \(P\) when \(P\) is sufficiently small and \(N\) is constant (the issue of how best to define Allee effects for predators is addressed in Sect. 3 below). In all of our models, the expression for the per capita birth rate of the predator population is justified by an argument that involves this assumption: the proportions of sexually mature female and sexually mature male predators can be approximated as constants. Such an assumption may be plausible in many real-world populations, but note that stochastic effects may cause bigger fluctuations in sex ratios at lower population levels (Courchamp et al. 1999). Stochastic fluctuations in sex ratio could, in principle, either cause a component Allee effect for adult reproduction if one does not already exist, or exacerbate such an Allee effect if it is already present. Stochastic modelling studies of Allee effects have been carried out, for example, in Liebhold and Bascompte (2003), Allen et al. (2005) and Rao (2013).

Note that the parameter \(d_1\) can be interpreted in the same way in all four of our models, specifically as the minimal per predator death rate.

2.1 Our models in the context of previous studies

A predator–prey model, possessing a component Allee effect for predator reproduction but otherwise possessing some fairly general properties, has previously been proposed by us in Sect. 2 in Terry (2013). Our four models in (6), (8), (12), and (14) are all special cases of the general model in Terry (2013), although they have not specifically been studied before and can therefore be considered as new.

Verdy proposed, and numerically investigated the bifurcation structure of, two predator–prey models with Allee effect for predator reproduction in Verdy (2010). One of these models, defined by equations (33) and (36) in Verdy (2010), is generalised by our first model in (6). To be precise, by setting the death function \(D(F(N))\) in (3) equal to a constant, then model (6) reduces to the model defined by equations (33) and (36) in Verdy (2010). The model given by equations (33) and (36) in Verdy (2010) itself builds on models with Allee effect for predator reproduction that were proposed by Zhou et al. (2005) and Bazykin (1998). Finally, a hybrid predator–prey model, with component Allee effect for predator reproduction, was recently investigated numerically in the context of biological pest control in Terry (2014b).

2.2 Basic properties of solutions

Using the results in section 3 in Terry (2013), we see that, for each of our models in (6), (8), (12), and (14), the following is true:

  1. (C1)

    A unique solution exists for \(t \ge 0\).

  2. (C2)

    The solution satisfies positivity, that is, \(N(t) \ge 0\) and \(P(t) \ge 0\) for \(t \ge 0\).

  3. (C3)

    The solution satisfies strict positivity, that is, if both \(N(0) > 0\) and \(P(0) > 0\), then \(N(t) > 0\) and \(P(t) > 0\) for \(t \ge 0\). Moreover, if \(N(0) > 0\), then \(N(t) > 0\) for \(t \ge 0\), and if \(P(0) > 0\), then \(P(t) > 0\) for \(t \ge 0\).

  4. (C4)

    The solution is bounded above, that is, there exist positive constants, \(\hat{N}\) and \(\hat{P}\), such that \(N(t) \le \hat{N}\) and \(P(t) \le \hat{P}\) for \(t \ge 0\).

Property (C4) mentions upper bounds for \(N\) and \(P\) without giving explicit expressions. We use properties (C1) and (C2) to find explicit upper bounds in the following lemma:

Lemma 1

Suppose that one of the following models holds: model (6), model (8), model (12), or model (14). Then, for \(t \ge 0\), we have \(N(t) \le \hat{N} := \max \{ N(0), K \}\). Furthermore, if we define \(d_1\) according to whichever model is assumed to hold, and let \(\eta = \frac{c r K}{4} + c \hat{N} d_1\), then, for \(t \ge 0\), we have \(P(t) \le \hat{P} := \max \{ c N(0) + P(0), \frac{ \eta }{ d_1 } \}\).

Proof

First we prove the lemma for model (14). Note by properties (C1) and (C2) above that a unique solution exists for \(t \ge 0\), where this solution satisfies positivity.

We begin by establishing that \(\hat{N} := \max \{ N(0), K \}\) is an upper bound for \(N(t)\). From positivity and the equation for \(dN/dt\) in model (14), we have, for \(t \ge 0\), that \(\frac{dN}{dt} \le r N( 1 - \frac{N}{K} )\). But then, by a standard comparison argument (for example, see theorem 1.1, p. 78, Smith 1995), we have \(N(t) \le N_1(t)\) for \(t \ge 0\), where \(N_1(0) = N(0) \ge 0\) and where, for \(t \ge 0\), we have \(\frac{d N_1}{dt} = r N_1( 1 - \frac{N_1}{K} )\). Either by solving directly for \(N_1(t)\) or by a standard phase portrait argument, \(N_1(t) \equiv 0\) for \(t \ge 0\) if \(N_1(0) = N(0) = 0\), whilst \(N_1(t)\) tends monotonically to \(K\) as \(t \rightarrow \infty \) if \(N_1(0) = N(0) > 0\). Hence \(N_1(t) \le \max \{ N(0), K \} = \hat{N}\) for \(t \ge 0\). Therefore, \(N(t) \le N_1(t) \le \hat{N}\) for \(t \ge 0\), as required.

Now we bound \(P(t)\) above. Using the equations for \(dN/dt\) and \(dP/dt\) in model (14), we have, for \(t \ge 0\),

$$\begin{aligned} \frac{d}{dt} \left( c N + P \right)&= c \frac{dN}{dt} + \frac{dP}{dt} \nonumber \\&= c r N \left( 1 - \frac{N}{K} \right) + c P F(N,P) \left[ \left( \frac{P}{h + P} \right) - 1 \right] \nonumber \\&- D(F(N,P)) P - m P^{2}. \end{aligned}$$
(15)

Observe that \(c r N( 1 - \frac{N}{K} )\) is a quadratic in \(N\) and is easily seen to have a global maximum, namely \(\frac{c r K}{4}\). Also, by positivity, we have, for \(t\ge 0\), that \(P \ge 0\) and \(F(N,P) \ge 0\) and \(\left( \frac{P}{h+P} \right) - 1 \le 0\). Hence \(c P F(N,P) \left[ \left( \frac{P}{h+P} \right) - 1 \right] \le 0\) for \(t \ge 0\). By positivity and the assumptions on \(F(N,P)\) and \(D(F(N,P))\) in model (14), we have \(- D(F(N,P)) P - m P^2 \le - d_1 P\) for \(t \ge 0\), where \(d_1\) is a positive constant. Combining these observations with (15), we have, for \(t \ge 0\),

$$\begin{aligned} \frac{d}{dt} \left( c N + P \right)&\le \frac{c r K}{4} - d_1 P = \frac{c r K}{4} + d_1 c N - d_1 (c N + P) \nonumber \\&\le \frac{c r K}{4} + d_1 c \hat{N} - d_1 (c N + P). \end{aligned}$$
(16)

where, on the last step, we use the fact that we have already shown that \(N(t)\) is bounded above by \(\hat{N}\).

Using the definition of \(\eta \) in the statement of the lemma, it follows from (16) that \(c N(t) + P(t) \le Z(t)\) for \(t \ge 0\), where \(Z(0) = c N(0) + P(0) \ge 0\) and where, for \(t \ge 0\), we have \(dZ/dt = \eta - d_1 Z\). But trivially \(Z(t) \le \max \{ Z(0), \frac{ \eta }{ d_1 } \} = \max \{ c N(0) + P(0), \frac{ \eta }{ d_1 } \} = \hat{P}\). Hence \(c N(t) + P(t)\) is bounded above by \(\hat{P}\). Hence, since \(N\) satisfies positivity, it must be that \(P\) is itself bounded above by \(\hat{P}\), as required.

Thus, we have proved the lemma for model (14). Setting \(q = 0\) or \(m = 0\) in our argument gives a proof of the lemma for, respectively, model (8) or model (12). Setting both \(q = 0\) and \(m = 0\) gives a proof for model (6). \(\square \)

3 Defining an Allee effect for a predator

In this section, we use numerical simulation results to discuss how the customary definitions of demographic and component Allee effects, which work well for single-species models, can be extended to predators in predator–prey models. All of the simulation results in this work were created using MATLAB (http://www.mathworks.co.uk/products/matlab/). In simulating our models in (6), (8), (12), and (14), we used the inbuilt solver for systems of ordinary differential equations called “ode23t”. In creating each figure, we chose parameter values with the goal of demonstrating the qualitative behaviours of our models. We have not fitted our models to real-world data but this could be done in future work.

Demographic and component Allee effects have been discussed in the Introduction. In particular, the average fitness of the individuals in a population \(X\) was defined as the per capita growth rate of \(X\), and a demographic Allee effect holds if average fitness increases with \(X\) for some range of values for \(X\). Also, a component Allee effect holds for the population \(X\) if a measurable component of individual fitness increases with \(X\) for some range of values for \(X\). These definitions are sensible if average fitness, or the component being measured, are single-valued functions of \(X\). Conceptual problems may arise, however, when this is not the case. For instance, suppose, across some range of values for \(X\), say \(X \in [X_1, X_2]\), that the average fitness takes two different sets of values, where one set contains values that increase with \(X\) and the other contains values that decrease with \(X\). Does a demographic Allee effect hold for \(X \in [X_1, X_2]\)? Yes and no—it depends on which set of values for average fitness that we consider. Conceptual problems of this kind do not arise in autonomous single-species models of the form

$$\begin{aligned} \frac{d X}{d t} = X \phi (X), \end{aligned}$$
(17)

where \(\phi (X)\) is some smooth single-valued function of \(X\) that represents the per capita growth rate of \(X\) (and therefore also represents the average fitness), and where any measurable component of individual fitness of interest to us is, additionally, a single-valued function of \(X\). Examples of such models can be found in table 3.1 on page 68 of Courchamp et al. (2008).

In autonomous single-species models, as in (17), the per capita growth rate of the population changes only with the population itself. Environmental factors, including the abundance of food, influence the per capita growth rate only through constant parameter values. What would be an analogous assumption for the predator population in a predator–prey model? In order for environmental factors, including the abundance of food, to influence the per capita growth rate of the predator population only through constant parameter values, we would have to assume that the food source of the predator is constant. But this means that we would have to assume that the prey population is constant, because the food source of the predator is the prey population. Our discussion leads naturally to the following definitions for demographic and component Allee effects for predators in predator–prey models, which extend the corresponding definitions for populations governed by single-species models as in (17):

Definition 1

Suppose we are given a predator–prey model and a positive constant \(N_1\). Then the predator possesses, or is subject to, a demographic Allee effect at prey level \(N_1\), if there exist constants \(P_1\), \(P_2\), with \(0 \le P_1 < P_2\), such that the per capita growth rate of the predator population \(P\) is a strictly increasing function of \(P\) for \(P \in [P_1,P_2]\), when the prey population \(N\) is held fixed at \(N_1\).

Definition 2

Suppose we are given a predator–prey model and a positive constant \(N_1\). Suppose the predator population has a measurable component of individual fitness, which is equal to \(\psi (N,P)\) when the predator population is \(P\) and the prey population is \(N\). Then the predator possesses, or is subject to, a component Allee effect at prey level \(N_1\), for the component \(\psi (N,P)\), if there exist constants \(P_1\), \(P_2\), with \(0 \le P_1 < P_2\), such that \(\psi (N,P)\) is a strictly increasing function of \(P\) for \(P \in [P_1,P_2]\), when the prey population \(N\) is held fixed at \(N_1\).

From Definition 2, it is easy to see, for our four models in (6), (8), (12), and (14), that the predator population \(P\) possesses a component Allee effect, at any prey level \(N_1 > 0\), for per capita reproduction. After all, for any fixed prey level \(N_1 > 0\), per predator reproduction is zero when \(P = 0\) and positive for \(P > 0\). Hence, for any fixed prey level \(N_1 > 0\), per predator reproduction must be increasing for \(P \in [0, \alpha ]\) where \(\alpha > 0\) is sufficiently small.

Can our models possess, by Definition 1, a demographic Allee effect for the predator at some positive prey level \(N_1\)? To help answer this, we first make two observations on the behaviour of model (6): (i) for any fixed prey level \(N_1 > 0\), per predator reproduction is necessarily increasing for \(P \in [0, \alpha ]\) where \(\alpha > 0\) is sufficiently small; (ii) for any fixed prey level \(N_1 > 0\), the per predator death rate is constant. It follows that, for model (6), the per predator growth rate will be increasing for \(P \in [0, \alpha ]\) where \(\alpha > 0\) is sufficiently small, when the prey level is held fixed at any \(N_1 > 0\). But then, for model (6), we may immediately deduce, from Definition 1, that the predator possesses a demographic Allee effect at prey level \(N_1\), for any \(N_1 > 0\). We may deduce, in similar fashion, that models (8), (12), and (14) can also possess a demographic Allee effect at prey level \(N_1\), for any \(N_1 > 0\), provided that the per predator death rate in each model is sufficiently constant for P sufficiently small. For model (8), this occurs when the parameter \(m\) is sufficiently small; for model (12), it occurs when the death function \(D(F(N,P))\) takes values on an interval that is sufficiently narrow; and for model (14), it occurs when both the parameter \(m\) is sufficiently small and the death function \(D(F(N,P))\) takes values on an interval that is sufficiently narrow.

When, in models (8), (12), and (14), the per predator death rate is allowed to vary significantly for small values of \(P\), then we have found, from a simulation study (results not shown), that these models may not possess a demographic Allee effect for the predator at particular prey levels \(N_1 > 0\). A biological interpretation of this finding is as follows. Although an increase in the predator population ensures that female predators are more likely to find a mate and be able to reproduce, it can also increase per predator mortality by either making it more likely that there will be mortality-inducing aggressive encounters between predators [as in model (8)], or by increasing competition for prey [as in model (12)], or both [as in model (14)]. When per predator mortality is more sensitive to an increase in the predator population than per predator reproduction, then it can be possible for any increase in the predator population to lead to a reduction in the per predator growth rate (average fitness of the predators), so that a demographic Allee effect for the predator cannot hold.

In Fig. 2, we demonstrate, by simulation, how all four of our models can possess, by Definitions 1 and 2, respectively, demographic and component Allee effects for the predator. In each plot in Fig. 2, the form for the predator death function \(D(F)\) is as follows:

$$\begin{aligned} D(F) = \left\{ \begin{aligned} \begin{array}{l@{\quad }l} d_2, &{} 0 \le F \le \theta _1, \\ d_1 + (d_2 - d_1) \cos ^2 \left\{ \left( \frac{\pi }{2} \right) \left( \frac{ F - \theta _1}{\theta _2 - \theta _1 } \right) \right\} ,&{} \theta _1 \le F \le \theta _2, \\ d_{1},&{} F \ge \theta _2, \end{array} \end{aligned} \right. \end{aligned}$$
(18)

where \(\theta _1 \ge 0, \theta _2 > 0, d_2 > 0, d_1 > 0\) are all constants, with \(\theta _1 < \theta _2\) and \(d_1 < d_2\). The form for \(D(F)\) in (18) is consistent with the restrictions on it in all four of our models, and has been used in a previous study of predator–prey models Terry (2014a). A numerical example, showing the qualitative properties of \(D(F)\) in (18), is given in Fig. 1. The plots in Fig. 2 show the per predator birth rate and per predator growth rate, \((1/P) dP/dt\), for each of our four models, created by assuming that the prey population is held constant at an initial value \(N(0)\), and by choosing values for parameters and \(N(0)\) as follows:

$$\begin{aligned}&c = 0.5, \, K = 50, \, a = 0.35, \, h = 0.2, \, \theta _1 = 5, \, \theta _2 = 15 \, {\text {(all models)}} \end{aligned}$$
(19)
$$\begin{aligned}&b = 0.3, \, d_1 = 0.1, \, d_2 = 0.3, \, N(0) = 10 \, {\text {(model (6))}} \end{aligned}$$
(20)
$$\begin{aligned}&b = 0.2, \, d_1 = 0.1, \, d_2 = 0.3, \, m = 0.1, \, N(0)= 10 \, ({\text {model (8)}} ) \end{aligned}$$
(21)
$$\begin{aligned}&b = 0.3, \, q = 3, \, d_1 = 0.1, \, d_2 = 0.3, \, N(0) = 10 \, ({\text {model (12)}}) \end{aligned}$$
(22)
$$\begin{aligned}&b =0.1, \, q = 0.2, \, d_1 = 0.03, \, d_2 = 0.09, \, m = 0.1, \, N(0) = 1 \, ({\text {model (14)}}). \end{aligned}$$
(23)
Fig. 1
figure 1

Plot of the death function \(D(F)\) defined in (18). The parameter choices are: \(\theta _1 = 5, \theta _2 = 15, d_1 = 0.1, d_2 = 0.3\)

Full size image
Fig. 2
figure 2

Plots of per predator birth rate and per predator growth rate, \((1/P) {\textit{d}P}/dt\), versus predator population \(P\), where the prey population is held fixed at its initial value \(N(0)\). In each plot, the predator death function \(D(F)\) has the form stated in (18). Choices for the parameters and \(N(0)\) are stated in (19)–(23)

Full size image

From Fig. 2, and Definitions 1 and 2, we see that all four of our models possess a demographic Allee effect for the predator at the prey level being used, and a component Allee effect for per predator reproduction at the prey level being used. In particular, in all four models, the per predator birth rate and per predator growth rate are increasing in \(P\) when \(P\) is sufficiently small. By comparison, standard predator–prey models, such as the Lotka–Volterra model (p. 33, Turchin 2003), Rosenzweig–MacArthur model (p. 95, Turchin 2003), Beddington–DeAngelis model (p. 2, Haque 2011), and Bazykin model (p. 98, Turchin 2003), do not possess the types of Allee effect described in Definitions 1 and 2, which is reassuring because we would not expect them to. Thus, Definitions 1 and 2 are practical enough to identify the kinds of models that we would expect to possess an Allee effect.

Nevertheless, Definitions 1 and 2 have a limitation. By requiring that the prey population \(N\) is held constant, they ignore the dynamics of the model in question. It seems somehow dissatisfying to claim that our models possess demographic and component Allee effects based on definitions that ignore their dynamics. Moreover, in real-world ecosystems, prey populations do not conveniently hold themselves fixed when we want to study the possibility of Allee effects for their predators.

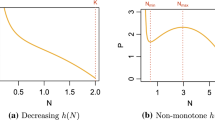
Therefore, it is natural to ask what happens if we relax the condition, in Definitions 1 and 2, that \(N\) is held constant? More precisely, how do the per predator birth rate and per predator growth rate change with \(P\) when the models are solved with given initial conditions? We investigate this issue in Fig. 3. In the left and right plots of Fig. 3a, we show, respectively, the per predator birth rate versus \(P\) and the per predator growth rate versus \(P\), when model (14) is solved for \(t \in [0,1500]\), where parameters and initial condition \(N(0)\) are chosen as in (19) and (23), and where \(r = 0.15\) and \(P(0) = 0.1\). Figure 3b was created in the same way as Fig. 3a, except that \(P(0)\) was reduced to \(0.03\). From Fig. 3a, we see that the per predator birth rate and per predator growth rate do not behave like single-valued functions of \(P\). For instance, for \(P \in [1.7,2.2]\), the per predator birth rate and per predator growth rate are both double-valued functions of \(P\), where the lower set of values is increasing in \(P\) and the upper set of values is decreasing in \(P\). Thus, we have encountered the conceptual problem described in the second paragraph of this section. This problem is not encountered in Fig. 3b, which differs from Fig. 3a only in the initial condition for \(P\). In summary, although it may seem reasonable to seek to improve Definitions 1 and 2 by accounting for the dynamics of the model in question, this can lead to conceptual problems. Whether or not Definitions 1 and 2 can be improved, or if they really need to be, is a matter that we invite the modelling community to consider.

Fig. 3
figure 3

Plots of per predator birth rate and per predator growth rate, \((1/P) {\textit{d}P}/dt\), versus predator population \(P\), created by simulating model (14). In all plots, model (14) is solved for \(t \in [0,1500]\), where parameters and initial condition \(N(0)\) are chosen as in (19) and (23), and where \(r = 0.15\). In (a), the initial condition for the predator population is \(P(0) = 0.1\). In (b), we have \(P(0) = 0.03\)

Full size image

Note that the trajectory \((N,P)\), in the case depicted in Fig. 3a, tends to a co-existence fixed point (results not shown). This is despite the fact that the bottom right plot of Fig. 2, which was created using the same model and parameters and initial conditions, shows a negative per predator growth rate for all values of \(P\). However, there is no contradiction, because the plots in Figs. 2 and 3a use different assumptions for the prey population. For the case considered in Fig. 3b, the trajectory \((N,P)\) tends to the fixed point \((K,0)\), representing predator extinction (results not shown).

4 Fixed points

In models (6), (8), (12), and (14), fixed points are found from simultaneously solving \(d\!N/dt = 0\) and \(d\!P/dt = 0\). We solve algebraically for \(N\) and \(P\). Trivially we find that \((N,P) = (0,0)\) and \((N,P) = (K,0)\) are fixed points in all four models. Co-existence fixed points, that is, fixed points such that \((N,P) = (N^{*},P^{*})\) where \(N^{*} > 0\) and \(P^{*} > 0\), can also be found, as we will see below in Sect. 4.3.

4.1 The fixed point \((0,0)\)

For each of the models in (6), (8), (12), and (14), the local stability of the fixed point \((N,P) = (0,0)\) is determined by the following argument. Letting \(d\!N/dt = \chi _1(N,P)\) and \(d\!P/dt = \chi _2(N,P)\) in whichever model is assumed to hold, we find by routine computation that:

$$\begin{aligned} {\text {when }} (N,P) = (0,0), {\text { then }} \frac{ \partial \chi _1 }{ \partial N} = r, \frac{ \partial \chi _1 }{ \partial P} = 0, \frac{ \partial \chi _2 }{ \partial N} = 0, \frac{ \partial \chi _2 }{ \partial P} = - D(0).\quad \end{aligned}$$
(24)

Here \(D\) is the death function defined in either (3) or (11), according to whichever model is assumed to hold. Whether \(D\) is defined by (3) or (11), we have \(D(0) > 0\). By (24), it is easy to see that the Jacobian matrix at the fixed point \((N,P) = (0,0)\) has determinant \(- r D(0)\), which is negative since \(D(0) > 0\). Hence \((0,0)\) is, locally, a saddle point, and is therefore locally unstable.

4.2 The fixed point \((K,0)\)

Conditions for the stability of the fixed point \((N,P) = (K,0)\) are given in the two theorems that follow.

Theorem 1

Suppose that one of the following models holds: model (6), model (8), model (12), or model (14). Suppose also that \(N(0) > 0\) and that \(\frac{ c a K }{ 1 + b K } \le d_1\), where \(d_1\) is defined according to whichever model is assumed to hold. Then \((N(t),P(t)) \rightarrow (K,0)\) as \(t \rightarrow \infty \).

Proof

First we prove the theorem for model (14). Our proof will exploit positivity [property (C2), Sect. 2.2]. We begin by bounding \(dP/dt\) above. To do this, we bound the per predator death rate below and the per predator birth rate above. In view of positivity, the per predator death rate [that is, the term \(D(F(N,P)) + m P\)] is bounded below by the parameter \(d_1\).

For model (14), the per predator birth rate is \(\left( \frac{ c a N }{ 1 + b N + q P } \right) \left( \frac{ P }{ h + P } \right) \). To bound this above, we first note, by positivity and Lemma 1, that \(P/(h + P) \le \hat{P}/(h + \hat{P})\) for \(t \ge 0\), where \(\hat{P}\) is a positive constant defined in Lemma 1. Second, note that, by positivity, we have, for \(t \ge 0\):

$$\begin{aligned} \frac{ c a N }{ 1 + b N + q P } \le \frac{ c a N }{ 1 + b N }. \end{aligned}$$
(25)

We can make this upper bound more specific. In the proof of Lemma 1, we saw that \(N(t)\) can be bounded above by a function \(N_1(t)\) which, when \(N(0) > 0\), tends to \(K\) as \(t \rightarrow \infty \). Hence, for any \(\epsilon _1 > 0\), there exists \(T_1 > 0\) such that \(N(t) \le N_1(t) < K + \epsilon _1\) for \(t \ge T_1\). Using this, and also using positivity, we have, for \(t \ge T_1\):

$$\begin{aligned} \frac{ c a N }{ 1 + b N } \le \frac{ c a (K + \epsilon _1) }{ 1 + b (K + \epsilon _1) }. \end{aligned}$$
(26)

Combining our observations from the last two paragraphs, and using positivity and the equation for \({ dP}/dt\) in model (14), we have, for \(t \ge T_1\),

$$\begin{aligned} \frac{ dP}{dt} \le P \left[ \left( \frac{ c a (K + \epsilon _1) }{ 1 + b (K + \epsilon _1) } \right) \left( \frac{ \hat{P} }{ h + \hat{P} } \right) - d_1 \right] . \end{aligned}$$
(27)

Now by assumption, \(\frac{c a K}{1 + b K} \le d_1\). Using this, we may choose \(\epsilon _1 > 0\) small enough that the large term in square brackets in (27) is a negative constant, say \(- \theta \) (where \(\theta > 0\)). Then, using (27), we have \(P(t) \le P_1(t)\) for \(t \ge T_1\) where \(P_1(T_1) = P(T_1)\) and where, for \(t \ge T_1\), we have \(\frac{d P_1}{dt} = - \theta P_1\). Since \(P\) satisfies positivity and is bounded above by Lemma 1, then \(P_1(T_1) = P(T_1)\) is non-negative and finite. Hence \(P_1(t) \rightarrow 0\) as \(t \rightarrow \infty \). But then \(P(t) \rightarrow 0\) as \(t \rightarrow \infty \), since \(0 \le P(t) \le P_1(t)\) for \(t \ge T_1\).

Finally we show that \(N(t) \rightarrow K\) as \(t \rightarrow \infty \). To that end, choose any \(\epsilon _2 > 0\). Then, reasoning as in the second paragraph in this proof, there exists \(T_2 > 0\) such that \(N(t) < K + \epsilon _2\) for \(t \ge T_2\). Now choose \(\epsilon _3 > 0\) so that \(\epsilon _3 < \max \{ \frac{r}{a}, \frac{ r \epsilon _2 }{ 2 a K } \}\). Then, since \(P(t) \rightarrow 0\) as \(t \rightarrow \infty \), we see that there exists \(T_3 > 0\) such that \(0 < P(t) < \epsilon _3\) for all \(t \ge T_3\). Using this, and using positivity, we have \(\frac{ a N P }{ 1 + b N + q P } \le a \epsilon _3 N\) for \(t \ge T_3\). Hence, by the equation for \(dN/dt\) in model (14), we have, for \(t \ge T_3\), that \(\frac{dN}{dt} \ge r N( 1 - \frac{a \epsilon _3}{ r } - \frac{N}{K} )\). Also, we know that \(N(T_3)\) is bounded (by Lemma 1) and positive [by the assumption that \(N(0) > 0\) and property (C3) in Sect. 2.2]. Then \(N(t) \ge N_2(t)\) for \(t \ge T_3\) where \(N_2(T_3) = N(T_3) > 0\) and where, for \(t \ge T_3\), we have \(\frac{dN_2}{dt} = r N_2( 1 - \frac{a \epsilon _3}{ r } - \frac{N_2}{K} )\). Since \(\epsilon _3 < \frac{r}{a}\) by assumption, then \(1 - \frac{a \epsilon _3}{ r } > 0\), so that, by solving explicitly for \(N_2(t)\) or by using a phase portrait argument, we have \(N_2(t) \rightarrow K \left( 1 - \frac{a \epsilon _3}{ r } \right) \) as \(t \rightarrow \infty \). In particular, then, \(N_2(t) > K \left( 1 - \frac{2 a \epsilon _3}{ r } \right) \) for \(t \ge T_4\), say, where \(T_4 \ge T_3\). But by our choice for \(\epsilon _3\), we have \(\epsilon _3 < \frac{ r \epsilon _2 }{ 2 a K }\), so that \(1 - \frac{2 a \epsilon _3}{ r } > 1 - \frac{\epsilon _2}{K}\). Hence \(N(t) \ge N_2(t) > K \left( 1 - \frac{\epsilon _2}{K} \right) = K - \epsilon _2\) for \(t \ge T_4\). Combining our observations, and letting \(T_5 = \max \{ T_2, T_4 \}\), we see that \(K - \epsilon _2 < N(t) < K + \epsilon _2\) for \(t \ge T_5\). Thus, \(N(t) \rightarrow K\) as \(t \rightarrow \infty \), as required.

Thus, we have proved the theorem for model (14). Setting \(q = 0\) or \(m = 0\) in our argument gives a proof of the theorem for, respectively, model (8) or model (12). Setting both \(q = 0\) and \(m = 0\) gives a proof for model (6). \(\square \)

Theorem 2

Suppose that one of the following models holds: model (6), model (8), model (12), or model (14). Suppose also that \(\frac{ c a \hat{N} }{ 1 + b \hat{N} } > d_1\), where \(d_1\) is defined according to whichever model is assumed to hold, and where \(\hat{N} = \max \{ N(0), K \}\). Then \(( \frac{ c a \hat{N} }{ 1 + b \hat{N} }) ( \frac{ P }{ h + P }) = d_1\) has a least positive solution \(P_m\). Moreover:

  1. (i)

    if \(P(0) < P_m\) and \(N(0) > 0\), then \((N(t),P(t)) \rightarrow (K,0)\) as \(t \rightarrow \infty \);

  2. (ii)

    if \(P(0) \ge P_m\), then \(\tau = (2/d_1) \left[ 1 + \ln ( P(0)/P_m ) \right] \) is a positive constant and \((N(t),P(t)) \rightarrow (K,0)\) as \(t \rightarrow \infty \) if \(0 < N(0) < 1/(c a \tau e^{r \tau })\).

Proof

First we prove the theorem for model (14). From Lemma 1, we know that \(N(t) \le \max \{ N(0), K \} = \hat{N}\) for \(t \ge 0\). Let \(\xi (P) = ( \frac{ c a \hat{N} }{ 1 + b \hat{N} }) ( \frac{ P }{ h + P }) - d_1\). Then clearly \(\xi (0) < 0\). Also, \(\xi (P)\) is continuous in \(P \ge 0\), and \(\xi (P) > 0\) for all \(P\) sufficiently large because of the assumption that \(\frac{ c a \hat{N} }{ 1 + b \hat{N} } > d_1\). Therefore, standard results ensure that there is a least positive solution \(P_m\) to \(\xi (P) = 0\). We clearly then have \(\xi (P) < 0\) for \(0 \le P < P_m\).

Now we prove part (i). By an argument similar to the derivation of (27) in the proof of Theorem 1, we find, for \(t \ge 0\), that:

$$\begin{aligned} \frac{dP}{dt} \le P \left[ \left( \frac{ c a \hat{N} }{ 1 + b \hat{N} } \right) \left( \frac{ P }{ h + P } \right) - d_1 \right] = P \xi (P). \end{aligned}$$
(28)

Then \(P(t) \le P_1(t)\) for \(t \ge 0\) where \(P_1(0) = P(0) \ge 0\) and where, for \(t \ge 0\), we have \(\frac{d P_1}{dt} = P_1 \xi (P_1)\). By assumption, \(P(0) < P_m\). Also we have seen that \(\xi (P) < 0\) for \(0 \le P < P_m\). Therefore, by a standard argument (such as a phase portrait argument), we have \(P_1(t) \rightarrow 0\) as \(t \rightarrow \infty \). But then \(P(t) \rightarrow 0\) as \(t \rightarrow \infty \), since [using positivity of \(P(t)\), which is ensured by property (C2) in Sect. 2.2] we have \(0 \le P(t) \le P_1(t)\) for \(t \ge 0\). We may argue that \(N(t) \rightarrow K\) in the same way that we did this in the proof of Theorem 1.

Next we prove part (ii). Thus, suppose \(P(0) \ge P_m\). Then, since \(P_m > 0\), it is clear that we may define the positive constant \(\tau = (2/d_1) \left[ 1 + \ln ( P(0)/P_m ) \right] \). Hence \(c a \tau e^{r \tau } > 0\), and we may (and we do) choose \(N(0)\) so that \(0 < N(0) < 1/(c a \tau e^{r \tau })\). Now by the equation for \(d\!N/dt\) in model (14), and using strict positivity [see property (C3) in Sect. 2.2], we may write \(d\!N/dt < r N\) for \(t \ge 0\). Hence \(N(t) \le N(0) e^{r t}\) for \(t \ge 0\). But then, using our choice for \(N(0)\), we have

$$\begin{aligned} N(t) < 1/(c a \tau ) \quad \text { for } 0 \le t \le \tau . \end{aligned}$$
(29)

By the equation for \({ dP}/dt\) in model (14), and using positivity, we have

$$\begin{aligned} \frac{ dP}{dt} \le \left( c a N - d_1 \right) P \quad \text { for } t \ge 0. \end{aligned}$$
(30)

By (29) and (30), and using positivity, we have

$$\begin{aligned} \frac{dP}{dt} \le \left( \frac{1}{\tau } - d_1 \right) P \quad \text { for } 0 \le t \le \tau . \end{aligned}$$
(31)

But then \(P(t) \le P(0) e^{ \left( \frac{1}{\tau } - d_1 \right) t }\) for \(0 \le t \le \tau \). Hence \(P(\tau ) \le P(0) e^{ \left( 1 - d_1 \tau \right) }\). But then we will have \(P(\tau ) < P_m\) if \(P(0) e^{ \left( 1 - d_1 \tau \right) } < P_m\), which holds if \(\tau > (1/d_1) \left[ 1 + \ln ( P(0)/P_m ) \right] \). This latter inequality holds, in view of how \(\tau \) has been defined. Hence \(P(\tau ) < P_m\). If we now apply the argument used above to prove part (i) of the theorem, with the time origin shifted from \(t = 0\) to \(t = \tau \), we may deduce that \((N(t),P(t)) \rightarrow (K,0)\) as \(t \rightarrow \infty \).

Thus, we have proved the theorem for model (14). Setting \(q = 0\) or \(m = 0\) in our argument gives a proof of the theorem for, respectively, model (8) or model (12). Setting both \(q = 0\) and \(m = 0\) gives a proof for model (6). \(\square \)

Remark 1

In models (6), (8), (12), and (14), either \(\frac{ c a K }{ 1 + b K } \le d_1\) or \(\frac{ c a K }{ 1 + b K } > d_1\). Moreover, if \(\frac{ c a K }{ 1 + b K } > d_1\), then \(\frac{ c a \hat{N} }{ 1 + b \hat{N} } > d_1\) where \(\hat{N} = \max \{ N(0), K \}\). It follows, using Theorem 1 and part (i) of Theorem 2, that the fixed point \((K,0)\) is always locally stable. Similarly, it follows, using Theorem 1 and part (i) of Theorem 2, that the predator either always dies out or there exists \(P_m > 0\) where the predator dies out if its initial population \(P(0)\) is less than \(P_m\). Thus, predator extinction will always occur if the initial predator population \(P(0)\) is sufficiently small. This is not necessarily the case when there is no component Allee effect for predator reproduction in the models. To see this for model (6), first note that, if we were to assume in our derivation of the per predator birth rate (in Sect. 2) that every sexually mature female predator can always find a mate, then this would amount to setting \(H(\gamma _2 P) \equiv 1\), with the result that the factor \(( \frac{P}{h + P})\) would be omitted from the equation for \(d\!P/dt\). This omission would cause model (6) to become a special case of model (7) in Terry (2014a), which does not permit predator extinction, regardless of how small the initial predator population is, unless the model parameters satisfy certain conditions [see section 5 in Terry (2014a)].

Remark 2

Using Theorem 1 and part (ii) of Theorem 2, the predator either always dies out or it will die out if the initial prey population \(N(0)\) is sufficiently small. Thus, survival of the predator population depends on some sort of threshold behaviour for the prey population—the predator population cannot persist unless the prey population is bigger than some critical value (corresponding, biologically, to a sufficient quantity of food to sustain the predator population). Of course, we have yet to see if the predator population can persist at all, but we will see, by results in the next section and in the Supporting Information file, that co-existence of the predator and prey is possible in models (8), (12), and (14). The idea that the extinction of a predator population can depend on some sort of threshold behaviour for a prey population has been encountered previously in a study of a discrete predator–prey model, where it was described as an indirect Allee effect (Lopez-Ruiz and Fournier-Prunaret 2005). The same idea was encountered in a hybrid predator–prey model in Terry (2013).

Remark 3

In view of Theorem 1, we see that, for models (6), (8), (12), and (14), a necessary condition for the possibility of co-existence of predator and prey is \(d_1 < \frac{ c a K }{ 1 + b K }\). A biological interpretation of this condition is that predators do not die “too quickly”. This interpretation is valid because, as noted in the paragraph immediately before Sect. 2.1, the parameter \(d_1\) represents the minimal per predator death rate.

4.3 Co-existence fixed points

Co-existence fixed points in models (6), (8), (12), and (14) are found from solving \({ dN}/dt = 0\) and \({ dP}/dt = 0\) simultaneously, where we solve algebraically for \(N > 0\) and \(P > 0\). In Sects. 4.3.1–4.3.4 below, we shall, for simplicity, discuss co-existence fixed points only for the special cases in which the predator death function \(D\), representing the per predator death rate in relation to prey consumption, is assumed to be a constant for all values of the prey consumption rate. The function \(D\) is defined in either (3) or (11), according to whichever model is assumed to hold.

We will see below that co-existence fixed points can exist in any of the four models when the predator death function \(D\) is equal to a constant for all values of the prey consumption rate, and that the maximum number of such fixed points is finite for each model. We claim that it follows that co-existence fixed points can exist in any of the four models when the predator death function \(D\) is not equal to a constant for all values of the prey consumption rate. We first prove this claim for model (14). Thus, suppose that model (14) has at least one co-existence fixed point when the predator death function \(D = D(F(N,P))\) is identically equal to a constant \(d > 0\). Since there can only be finitely many such fixed points, we can write them as \((N_1^{*},P_1^{*}),..,(N_i^{*},P_i^{*})\), where \(i\) is an integer such that \(i \ge 1\). We must have \(0 < N_j^{*}, P_j^{*}\) for \(1 \le j \le i\), since the fixed points represent co-existence. There must also be a minimum and maximum \(N_j^{*}\) for \(1 \le j \le i\), which we respectively denote by \(N_u^{*}\) and \(N_v^{*}\). Similarly, denote by \(P_u^{*}\) and \(P_v^{*}\), respectively, the minimum and maximum values for \(P_j^{*}\) such that \(1 \le j \le i\). The co-existence fixed points are found from solving \(dN/dt = 0\) and \(dP/dt = 0\) for \(N > 0\) and \(P > 0\), but they exist only where \(N_u^{*} \le N \le N_v^{*}\) and \(P_u^{*} \le P \le P_v^{*}\). Now, when \(N_u^{*} \le N \le N_v^{*}\) and \(P_u^{*} \le P \le P_v^{*}\), the functional response \(F(N,P)\) takes a continuous range of values, specifically \(F_1 \le F \le F_2\) where \(F_1 = F(N_u^{*},P_v^{*}) > 0\) and \(F_2 = F(N_v^{*},P_u^{*})\). Therefore, the fixed points would still exist if we were to redefine the death function \(D\) so that it was equal to \(d\) when the prey consumption rate \(F(N,P)\) satisfies \(0 < F_1 \le F \le F_2\) but was otherwise allowed to vary, provided it still satisfied the conditions imposed on it in model (14). Thus, we have proved our claim for model (14). The claim can be proved for models (6), (8), and (12) by a very similar argument.

4.3.1 Model (6)

When the death function \(D(F(N))\) in model (6) is equal to a constant, then model (6) becomes equivalent to the model given by equations (33) and (36) in Verdy (2010). There are at most two co-existence fixed points, which are easily found from solving a quadratic equation. These fixed points are stated, and their stability properties discussed, in Verdy (2010).

4.3.2 Model (14)

When the death function \(D(F(N,P))\) in model (14) is chosen to equal a constant \(d > 0\) [that is, when we set \(d_1 = d_2 = d > 0\) in (11)], then we find co-existence fixed points from solving, for \(N > 0\) and \(P > 0\), the following system of equations:

$$\begin{aligned} 0&= r \left( 1 - \frac{N}{K} \right) - \frac{ a P }{ 1 + b N + q P }, \end{aligned}$$
(32)
$$\begin{aligned} 0&= \left( \frac{ c a N }{ 1 + b N + q P } \right) \left( \frac{P}{h + P} \right) - d - m P. \end{aligned}$$
(33)

From (32), we see that \(P = \left( \frac{r}{a} \right) \left( 1 - \frac{N}{K} \right) \left( 1 + b N + q P \right) \). Hence, solving (32) and (33) for \(N > 0\) and \(P > 0\) requires us, more specifically, to solve for \(0 < N < K\) and \(P > 0\). Rearranging the system in (32) and (33) yields:

$$\begin{aligned}&\displaystyle P \left[ 1 - q \left( \frac{r}{a} \right) \left( 1 - \frac{N}{K} \right) \right] = \left( \frac{r}{a} \right) \left( 1 - \frac{N}{K} \right) \left( 1 + b N \right) , \end{aligned}$$
(34)
$$\begin{aligned}&\displaystyle c a N P = \left( d + m P \right) \left( h + P \right) \left( 1 + b N + q P \right) . \end{aligned}$$
(35)

In order to solve (34) and (35) for \(0 < N < K\) and \(P > 0\), we are required, more specifically, to solve for \(P > 0\), \(0 < N < K\), and \(\left[ 1 - q \left( \frac{r}{a} \right) \left( 1 - \frac{N}{K} \right) \right] > 0\), that is, we must solve for

$$\begin{aligned} P > 0\quad \text { and }\quad \max \left\{ 0, \frac{ K [ q (r/a) - 1 ] }{ q (r/a) } \right\} < N < K. \end{aligned}$$
(36)

Assuming that the restrictions in (36) hold, then the expression \(\left[ 1 - q \left( \frac{r}{a} \right) \left( 1 - \frac{N}{K} \right) \right] ^{3}\) is positive. Multiplying through by this expression in (35) is therefore a reversible act. Performing this multiplication, and then using (34), and then simplifying, we arrive at a quartic in \(N\):

$$\begin{aligned}&c r N \left( 1 - \frac{N}{K} \right) \left[ 1 - q \left( \frac{r}{a} \right) \left( 1 - \frac{N}{K} \right) \right] ^2\nonumber \\&\quad = \left[ d \!+\! \left( \frac{r}{a} \right) \left( 1 \!-\! \frac{N}{K} \right) \left( m \!-\! d q \!+\! m b N \right) \right] \left[ h \!+\! \left( \frac{r}{a} \right) \left( 1 \!-\! \frac{N}{K} \right) \left( 1 \!-\! h q + b N \right) \right] . \nonumber \\ \end{aligned}$$
(37)

In summary, we may find co-existence fixed points \((N,P)\) from carrying out the following steps:

  1. (S1)

    solve (37) for \(N\) restricted as in (36); the number of co-existence fixed points is equal to the number of values thus found for \(N\);

  2. (S2)

    if at least one value is found for \(N\) from step (S1), then the value for \(P\) corresponding to a particular value for N is found from substituting, into (34), the particular value for \(N\).

Step (S2) is trivial, and step (S1) involves solving a quartic. A quartic can have at most four positive real solutions, so there are never more than four co-existence fixed points.

Using steps (S1) and (S2), it is easy to determine by numerical methods that there are four co-existence fixed points in model (14) when parameter values are chosen as follows:

$$\begin{aligned}&c = 0.5, r = 0.15, K = 50, a = 0.35, d = d_1 = d_2 = 0.1, \nonumber \\&m = 0.2, h = 0.2, b = 0.3, q = 0.01. \end{aligned}$$
(38)

The four co-existence fixed points, together with the fixed points at \((0,0)\) and \((K,0)\), are shown as green dots in the diagram of the phase plane \((N,P)\) in Fig. 4a. Also shown are trajectories, with various initial conditions, found from numerically solving model (14) when parameters satisfy (38). Let us label the co-existence fixed points in ascending order of their \(N\) co-ordinate—we label them as \(F_1\), \(F_2\), \(F_3\), \(F_4\) with \(N\) co-ordinates \(N_1\), \(N_2\), \(N_3\), \(N_4\), respectively, where \(N_1 < N_2 < N_3 < N_4\). Then from Fig. 4a, we see that \(F_1\) and \(F_3\) are locally stable, whilst \(F_2\) is a saddle. In addition, simulations of trajectories that start sufficiently close to \(F_4\) suggest that \(F_4\) is a saddle (results not shown). In view of (38), Theorem 2 holds. Hence the constant \(P_m > 0\), defined in Theorem 2, exists. It is easily determined numerically; we show \(P = P_m\) in Fig. 4a as a red dashed line. By Theorem 2, trajectories tend to \((K,0)\) when \(N(0) > 0\) and \(P(0) < P_m\); this fact is corroborated by one of the trajectories in Fig. 4a. By Sect. 4.1, the fixed point \((0,0)\) is a saddle.

Fig. 4
figure 4

Simulation results found from solving model (14) when the per predator death function \(D(F(N,P))\) is equal to a constant \(d\). The parameter choices are stated in (38). See Sect. 4.3.2 for a description of this figure. a Phase portraits, b basins of attraction

Full size image

As in Fig. 4a, we created Fig. 4b using model (14) and the parameter choices in (38). The fixed points are shown as black dots in Fig. 4b. We also show, in Fig. 4b, the basins of attraction of the locally stable fixed points. To be specific, the red, light blue, and yellow regions are basins of attraction for, respectively, the fixed points \(F_1\), \(F_3\), and \((K,0)\). Trajectories that start on the \(P\)-axis will tend to \((0,0)\); we show the \(P\)-axis as orange to highlight this fact. The basins of attraction were found from considering a fine grid of positive initial conditions, simulating from each point of initial conditions until time \(t = 800\), and asking, at the end of the simulation, if the trajectory was within a small distance of \(F_1\), \(F_3\), or \((K,0)\). The line \(P = P_m\), which is shown as a red dashed line in Fig. 4a, is shown as a green dashed line in Fig. 4b.

From the yellow basin of attraction for \((K,0)\) in Fig. 4b, we see, in corroboration of Theorem 2, that a trajectory \((N,P)\) tends to \((K,0)\) either when \(P(0)\) is sufficiently small [and \(N(0)\) is positive] or when \(N(0)\) is sufficiently small [and \(N(0)\) is positive].

In Fig. 4b, a point \((N,P)\) in the red region of the phase plane could move to the light blue region by jumping in a south-westerly direction. Biologically, we could interpret such a jump as a mortality event that reduces both the predator and prey populations, with the event temporarily interrupting the dynamical relationship of these populations—before and after the event, the behaviour of the trajectory in the phase plane would be determined by the basins of attraction in it. Examples for such an event include: a severe storm, a flood, or an application of a fast-degrading pesticide (Ives et al. 2000; Terry 2013). If a mortality event were to re-set the predator and prey populations by moving the point \((N,P)\) in the phase plane from the red region to the light blue region, then it would increase the long-term mean of the predator and prey populations, because: (i) the trajectory would tend to the fixed point \(F_1\) in the absence of the event, whilst it would ultimately tend to the fixed point \(F_3\) in the scenario where the event happens; and (ii) the predator and prey populations are bigger at \(F_3\) than at \(F_1\). That a mortality event could ultimately increase both the predator and prey populations is counter-intuitive and represents an example of the hydra effect (Sieber and Hilker 2012). If, in Fig. 4b, a trajectory \((N,P)\) is located in either the red co-existence region or in the light blue co-existence region, then any sufficiently lethal mortality event (except for events that completely eradicate the prey population) would relocate \((N,P)\) to the yellow basin of attraction for \((K,0)\). It follows that prey resurgence (resurgence of the prey population) would be caused by the event, provided that the prey population were less than \(K\) before the event. Prey resurgence from mortality events in predator–prey models has been discussed in Terry (2013).

Finally, we give brief insight into other behaviours that model (14) can exhibit. By reducing the parameter \(c\) in (38) to equal \(0.48\), but otherwise retaining the parameter choices in (38), we have found that the number of co-existence fixed points falls to two, one of which is stable whilst the other is a saddle (results not shown). By reducing \(c\) still further to equal \(0.24\), we have found that all co-existence fixed points disappear, and \((K,0)\) attracts all trajectories with positive initial conditions.

4.3.3 Model (12)

If we set \(m = 0\) in model (14), then we obtain model (12). It follows that, if we set \(m = 0\) in the method for finding co-existence fixed points in Sect. 4.3.2, then we acquire a method for finding co-existence fixed points for model (12) when the death function \(D(F(N,P))\) is chosen to equal a constant \(d > 0\). By setting \(m = 0\) in the method described in Sect. 4.3.2, we find that (34) is unchanged, but (37) reduces to a cubic:

$$\begin{aligned} c r N \left( 1 \!-\! \frac{N}{K} \right) \left[ 1 - q \left( \frac{r}{a} \right) \left( 1 \!-\! \frac{N}{K} \right) \right] = d \left[ h + \left( \frac{r}{a} \right) \left( 1 - \frac{N}{K} \right) \left( 1 - h q + b N \right) \right] .\nonumber \\ \end{aligned}$$
(39)

In conclusion, steps (S1) and (S2) in Sect. 4.3.2, with (37) replaced by (39), can be used to find the co-existence fixed points for model (12) with constant death function \(D(F(N,P)) = d\). Finding the co-existence fixed points therefore effectively amounts to solving a cubic in \(N\). Since a cubic has at most three positive real solutions, there can be at most three co-existence fixed points.

Applying steps (S1) and (S2) in Sect. 4.3.2, with (37) replaced by (39), we find, by trivial numerical methods, that there are two co-existence fixed points in model (12) when parameter values are chosen as follows:

$$\begin{aligned}&c = 0.2, r = 0.2, K = 50, a = 0.7, d = d_1 = d_2 = 0.1,\nonumber \\&\quad h =2.2, b = 0.1, q = 2.5. \end{aligned}$$
(40)

These two co-existence fixed points, together with the fixed points at \((0,0)\) and \((K,0)\), are shown as green dots in Fig. 5a. Also shown are trajectories, with various initial conditions, found from numerically solving model (12) when parameters satisfy (40). We label the co-existence fixed points as \(F_1\) and \(F_2\), where the \(N\) co-ordinate is smaller for \(F_1\) than for \(F_2\). The fixed point \(F_2\) is a saddle, and the fixed point \(F_1\) is locally unstable and is surrounded by a stable limit cycle. The conditions of Theorem 2 hold, in view of (40). Hence the constant \(P_m > 0\), defined in Theorem 2, exists. It is easily determined numerically; we show \(P = P_m\) in Fig. 5a as a red dashed line. By Theorem 2, trajectories tend to \((K,0)\) when \(N(0) > 0\) and \(P(0) < P_m\); this fact is corroborated by a number of trajectories in Fig. 5a. By Sect. 4.1, the fixed point \((0,0)\) is a saddle.

Fig. 5
figure 5

Simulation results found from solving model (12) when the per predator death function \(D(F(N,P))\) is equal to a constant \(d\). The parameter choices are stated in (40). See Sect. 4.3.3 for a description of this figure. a Phase portraits, b basins of attraction

Full size image

As in Fig. 5a, we created Fig. 5b using model (12) and the parameter choices in (40). In Fig. 5b, the fixed points are shown as black dots and the stable limit cycle is shown as a thick black line. Also shown, as red and yellow regions, respectively, are the basins of attraction of the stable limit cycle and the fixed point \((K,0)\). The \(P\)-axis is shown as orange to signify that trajectories that start on it will tend to \((0,0)\). The basins of attraction were found from considering a fine grid of positive initial conditions, simulating from each point of initial conditions until time \(t = 800\), and asking, at the end of the simulation, if the trajectory was within a small distance of \((K,0)\) or not. If it was within a small distance of \((K,0)\), then we assumed that the initial conditions belonged to the basin of attraction for \((K,0)\); otherwise, we assumed that they belonged to the basin of attraction of the stable limit cycle. The line \(P = P_m\), which is shown as a red dashed line in Fig. 5a, is shown as a green dashed line in Fig. 5b.

It is illuminating to interpret Fig. 5b in terms of its implications for biological pest control or “biocontrol”. To this end, suppose that the prey species is a pest, such as a crop pest, living in a region in the absence of predators, as could happen if the prey species were an invasive or exotic pest (Pimentel 1993; Pimentel et al. 2000). If we were to introduce \(P_i\) predators as a biocontrol program with the aim of reducing the long-term mean population of the prey, then, by Fig. 5b, the program would fail (in the sense that the predator would simply die out, offering no long-term control of the prey) if \(P_i\) were sufficiently small or sufficiently large, or if the prey population were sufficiently small at the time of the introduction. Whilst the model used to create Fig. 5b may be too simple to shed light on many specific real-world biocontrol programs, our conclusions from Fig. 5b on the apparent ease with which a biocontrol program would fail are consistent with the lack of success attained in many real-world programs (Orr 2009). This lack of success is demonstrated in the following excerpt from Roderick and Navajas (2003):

“Recent estimates indicate that in the biological control of arthropods only 34 % of all introductions have resulted in establishment, only 47 % of which provided control of the targeted pest, giving an overall success rate of 16 %.”

Finally, we note that by reducing the parameter \(c\) in (40) to equal \(0.11\), but otherwise retaining the parameter choices in (40), we have found, for model (12), that the co-existence fixed points in Fig. 5b disappear, and that \((K,0)\) attracts all trajectories with positive initial conditions (results not shown).

4.3.4 Model (8)

Setting \(q = 0\) in the method for finding co-existence fixed points in Sect. 4.3.2 yields a method for finding co-existence fixed points for model (8) when the death function \(D(F(N))\) is chosen to equal a constant \(d > 0\). By setting \(q = 0\) in the method in Sect. 4.3.2, we find that (34) simplifies to

$$\begin{aligned} P = \left( \frac{r}{a} \right) \left( 1 - \frac{N}{K} \right) \left( 1 + b N \right) , \end{aligned}$$
(41)

and that (37) remains a quartic but is slightly simpler:

$$\begin{aligned} c r N \left( 1 - \frac{N}{K} \right) = \left[ d + m \left( \frac{r}{a} \right) \left( 1 - \frac{N}{K} \right) \left( 1 + b N \right) \right] \left[ h + \left( \frac{r}{a} \right) \left( 1 - \frac{N}{K} \right) \left( 1 + b N \right) \right] .\nonumber \\ \end{aligned}$$
(42)

We may conclude that steps (S1) and (S2) in Sect. 4.3.2 can be used to find the co-existence fixed points for model (8), with constant death function \(D(F(N)) = d\), if the following changes are made: (i) in step (S1), (37) is replaced by (42); and (ii) in step (S2), (34) is replaced by (41). Thus, finding the co-existence fixed points for model (8), with constant death function \(D(F(N))\), amounts to solving a quartic in \(N\), so that there can be at most four co-existence fixed points.

The results in Fig. 4 and in the final paragraph of Sect. 4.3.2 are not changed qualitatively, and are almost identical quantitatively, when the value of the parameter \(q\) is changed from \(0.01\) to \(0\). Therefore, since model (8) is obtained from setting \(q = 0\) in model (14), we see that the discussion of the results for model (14) in Sect. 4.3.2 applies also to model (8) when parameters and initial conditions are chosen as in Sect. 4.3.2 except for setting \(q = 0\).

5 Summary; future work

We have presented four predator–prey models with component Allee effect for predator reproduction. Using numerical simulation results for our models, we have described how the customary definitions of component and demographic Allee effects, which work well for single species models, can be extended to predators in predator–prey models by assuming that the prey population is held fixed. We have then explored our four models, analytically and numerically. We have found that each of our models has a fixed point that represents predator extinction, which is always locally stable. We have proved that the predator will always die out either if the initial predator population is sufficiently small or if the initial prey population is sufficiently small. Through numerical simulations, we have explored co-existence fixed points. We have also demonstrated, by simulation, the existence of a stable limit cycle in one of our models. We have punctuated our results with comments on their real-world implications; in particular, we have mentioned the possibility of prey resurgence from mortality events, and the possibility of failure in a biological pest control program. Additional results are included in a Supporting Information file; specifically, in this file, we derive analytical conditions for a co-existence trapping region in three of our models, and show that the fourth model cannot possess a particular kind of co-existence trapping region.

We outline several avenues for future work. First, although we have commented on co-existence fixed points in our models and have given some numerical results on them, we have not analytically derived and classified them. Thus, there is certainly scope for extending our discussion of co-existence fixed points. Second, we have not analytically investigated the existence of closed orbits in our models. This could be done in future work, perhaps combining the Poincaré–Bendixson theorem with the fact that we have established conditions for co-existence trapping regions in three of our models in the Supporting Information file. Third, our models could be extended by incorporating an Allee effect for the prey. As far as we are aware, there have only been a few studies that consider predator–prey models with Allee effect for both predator and prey—for example, see Terry (2013) and Wang et al. (2011a). Finally, our models could be extended by the inclusion of a third trophic level. For instance, we are not aware of any studies of predator–prey-vegetation models with Allee effect for the predator; it may be fruitful to derive and explore such models.

6 Supporting information file

Additional results are included in a Supporting Information file. In this file, we prove that models (8), (12), and (14) can possess a co-existence trapping region, and that model (6) cannot possess a particular kind of co-existence trapping region. Also, using numerical simulation results, we corroborate our proof that model (12) can possess a co-existence trapping region.