Bifurcation and Dynamic Analyses of Non-monotonic Predator–Prey System with Constant Releasing Rate of Predators

Abstract

In this paper, we systematical study the rich dynamics and complex bifurcations of a non-monotonic predator–prey system with a constant releasing rate for the predator. We prove that the system can have at most three positive equilibria, and can undergo a sequence of bifurcations, including transcritical, saddle-node, Hopf, degenerate Hopf, double limit cycle, saddle-node homoclinic bifurcation (or homoclinic loop with a saddle-node), cusp bifurcation of codimension 2, and Bogdanov–Takens bifurcation of codimension 2 and 3. And the system can generate very rich dynamics, such as the existence of a semi-stable limit cycle, multiple coexistent periodic orbits, homoclinic loops, etc. Moreover, our results show that the dynamical behaviors highly rely on the constant releasing rate of predators and the initial conditions. That is, there exists a critical value of the constant releasing rate of predators such that (i) when the constant releasing rate is greater than the critical value, the prey goes to extinction for all admissible initial populations of both species; (ii) when the constant releasing rate is less than the critical value, the prey can always coexist with the predator. Numerical simulations are presented to verify the main results.

1 Introduction

It is well known that the predator–prey systems are used for analyzing the interactions between two species. Based on different biological backgrounds, various kinds of response functions (i.e., Holling type I to IV functional responses) are proposed to describe the interactions between the predator and the prey. Many existing studies have extensively investigated the rich dynamic behaviors and complex bifurcations of the predator–prey systems with the different functional responses [1,2,3,4,5]. Particularly, in the study [3], Ruan and Xiao deeply investigated the global dynamics and bifurcations of the predator–prey system with group defense (i.e., the Holling type IV functional response), including the saddle-node bifurcation, Hopf bifurcation and Bogdanov–Takens bifurcation of codimension 2. Group defense is usually characterized as the ability of preys to better defend or hide themselves from predators when they are more numerous [6]. There are many good examples in population ecology: Small herds of musk ox (2 to 6 animals) are attacked but with rare success and no successful attacks have been observed in larger herds [7]; Large swarms of insects are able to escape from the identification of their predators [8]. Group defense has become an important focus of research and analyzed mathematically in detail [3, 5].

Considering the integrated pest management (IPM) [9], the predator–prey systems are extended to many novel models, particularly to different kinds of dynamical systems. Usually, there can be three kinds of control strategies: constant releasing of predators, pulse or state-dependent impulsive control [10, 11], and piecewise interventions [12,13,14]. This can induce lots of novel dynamical behaviors, such as sliding equilibrium, sliding dynamics, sliding bifurcation, and the order-k periodic solutions [15, 16]. In this study, considering the releasing of the natural enemy to control the growth of pests, we extend the predator–prey system with group defense (i.e., the Holling type IV functional response) in [3] to the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx(t)}{dt}=rx\left[ 1-\frac{x}{K}\right] -\frac{\beta x y}{1+\omega x^{2}},\\ &{}\frac{dy(t)}{dt}=\frac{\eta \beta x y}{1+\omega x^{2}}-\delta y+\tau , \end{aligned} \end{array}\right. } \end{aligned}$$

(1.1)

where x and y represent the densities of prey and predator population, respectively. r denotes the intrinsic growth rate, K the carrying capacity of the prey species, $\delta$ the death rate of the predator species, $\eta \in (0, 1]$ the efficiency rate with which captured prey are converted to the predators, $\dfrac{\beta x}{1+\omega x^{2}}$ is the Holling type IV functional response, $\beta >0$ is the maximal growth rate of the predator species and $\omega >0$ is the handling time. $\tau$ represents the constant recruitment of the predator species. It is worth mentioning that $\tau$ can not only represent the constant releasing rate of the nature enemy in the IPM [14], but also an external source of effector cells such as LAK or TIL cells for treating tumors [17, 18]. Note that, when the death rate of the predator species is smaller than the intrinsic growth rate of the prey species, i.e., $\delta < r$, it would be good situation for the predator (natural enemy) to control the prey (pest). However, if the death rate of the predator species is larger than the intrinsic growth rate of the prey species, i.e., $\delta > r$, then the predator (nature enemy) might not be able to successfully control the prey (pest) by itself. Therefore, the recruitment of the natural enemy can be a good choice to reverse the situation. The main purpose of this study is to analyze the impact of the constant releasing rate of predators by investigating the dynamics and complex bifurcations of the proposed model.

With the constant releasing rate, we find that, except all the dynamic behaviors and bifurcations shown in [3], we prove that the extended system can present much more novel dynamical behaviors and bifurcations, including the co-existence of three positive equilibria, the existence of double limit cycle bifurcation [19] (or called the saddle-node bifurcation of limit cycles [20]), saddle-node homoclinic bifurcation [21] (or called the homoclinic bifurcation with a saddle-node), cusp bifurcation of codimension 2 [21], and Bogdanov–Takens (cusp type) bifurcation of codimension 3 [5, 22] which is a very complex bifurcation phenomenon. For simplicity, we convert system (1.1) to a topologically equivalent non-dimensionalized system. Let

$$\begin{aligned} u=\frac{x}{K}, \ \ v=\frac{\beta }{r}y, \ \ t_{1}=rt, \end{aligned}$$

and still denote $(u,v,t_{1})$ as (x, y, t), then system (1.1) becomes the following equivalent system

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx(t)}{dt}=x(1-x)-\frac{x y}{1+a x^{2}}\doteq P(x,y), \\ &{}\frac{dy(t)}{dt}=\frac{b x y}{1+ a x^{2}}-c y+ d\doteq Q(x,y), \\ \end{aligned} \end{array}\right. } \end{aligned}$$

(1.2)

where $a \doteq K^{2} \omega >0$, $b \doteq \frac{\eta \beta K}{r}>0$, $c \doteq \frac{\delta }{r}>0$ and $d \doteq \frac{\beta \tau }{r^{2}}>0$, which are the parameters after simplification and do not have specific biological significance.

This paper is organized as follows. In Sect. 2, we analyze the existence and the stability of the equilibria, where the types for all the possible equilibria are deeply discussed. In Sect. 3, we prove all the possible bifurcations, including the transcritical, saddle-node, Hopf, degenerate Hopf of codimension 2, cusp bifurcation of codimension 2, and Bogdanov–Takens (cusp type) bifurcation of codimension 3. In Sect. 4, we numerically verify all the bifurcations through bifurcation diagrams. Finally, we make the conclusions and discussions in Sect. 5.

2 Equilibria and Their Types

In this section, we discuss the existence and the stability of the equilibria of system (1.2). By the biological implications, we only analyze the dynamics of system (1.2) in the region $\mathbf{R} ^{+}_{2}=\{(x,y)|x\ge 0, y\ge 0\}$. It is easy to verify that all solutions of system (1.2) are non-negative bounded and we first present a lemma.

Lemma 2.1

All solutions of system (1.2) starting from the first quadrant are positively bounded in $\mathbf{R} ^{+}_{2}$.

Proof

Given a sufficiently large positive number $M_{0} > \frac{b(c+1)}{c}+\frac{d}{c}$, we construct a trapezoidal area G which contains all equilibria of system (1.2), and it is surrounded by four line segments:

$$\begin{aligned}&L_{1}:=\{(x,y)|x=0, 0\le y \le M_{0} \}, \ \ L_{2}:=\{(x,y)|0 \le x \le 1, y=0 \}, \\&L_{3}:=\{(x,y)|x=1, 0\le y \le -b +M_{0} \}, \\&L_{4}:=\{(x,y)|0 \le x \le 1, y= -b x +M_{0} \}, \end{aligned}$$

where $L_{1}$ is a part of one trajectory of system (1.2). By simple calculation, we have

$$\begin{aligned} \frac{dL_{2}}{dt}\big |_{(1.2)}=d >0 \ \ \mathrm {and} \ \ \frac{dL_{3}}{dt}\big |_{(1.2)}=- \frac{ y}{1+a}<0. \end{aligned}$$

Furthermore,

$$\begin{aligned} \frac{dL_{4}}{dt}\big |_{(1.2)}=-bx^{2}+b(c+1)x+ (d-c M_{0}) \le b(c+1)+d-c M_{0}<0. \end{aligned}$$

Thus, G is a positively invariant subset of system (1.2) in $\mathbf{R} ^{+}_{2}$, and all solutions of system (1.2) in $\mathbf{R} ^{+}_{2}$ enter convex set G as t tends to $+\infty$. The proof is completed. $\square$

2.1 The Existence of Equilibria

Through some straightforward calculations, we find that, unlike the classical predator–prey systems [1, 3, 5, 23], (K, 0) and (0, 0) are not the equilibria of system (1.2) anymore when we include the constant releasing rate. Instead, $E_{0}(0,\frac{d}{c})$ is always a boundary equilibrium of system (1.2). The interior equilibria satisfy the following equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}(1-x)-\frac{ y}{1+a x^{2}} =0,\\ &{}\frac{b x y}{1+ a x^{2}}-c y+ d =0.\\ \end{aligned} \end{array}\right. } \end{aligned}$$

(2.1)

It follows from the first equation that any positive equilibrium must satisfy $0< x< 1$ and $y=(1+a x^{2})(1- x)$. Re-arranging the second equation of (2.1), we obtain when exists, the x - coordinator of the positive equilibrium is the root of

$$\begin{aligned} acx^{3}-(ac+b)x^{2}+(b+c)x+(d-c)=0. \end{aligned}$$

(2.2)

Equation (2.2) can have at most three positive roots, and we denote the three possible roots as $x_{1}$, $x_{2}$ and $x_{3}$ with $x_{1}\le x_{2} \le x_{3}$, respectively. Then, we have a detailed discussion on the existence of the positive roots of Eq. (2.2).

Let

$$\begin{aligned} F(x)\doteq acx^{3}-(ac+b)x^{2}+(b+c)x+(d-c), \end{aligned}$$

(2.3)

While F(x) passes the points $(0,d-c)$ and (1, d). Further, denoting

$$\begin{aligned} x^{*}_{1}\doteq \frac{(ac+b)-\sqrt{\Delta }}{3ac}, \ \ x^{*}_{2}\doteq \frac{ (ac+b)+\sqrt{\Delta }}{3ac}, \ \ x^{*}\doteq \frac{1}{3}+\frac{b}{3ac} \end{aligned}$$

(2.4)

with $\Delta \doteq (ac+b)^{2}-3 ac(b+c)$. Taking the derivative of Eq. (2.3) with respect to x, one yields

$$\begin{aligned} F'(x)=3acx^{2}-2(ac+b)x+(b+c). \end{aligned}$$

(2.5)

It is easy to verify that if $\Delta =(ac+b)^{2}-3 ac(b+c)< 0$ holds true, then $F'(x)> 0$ for all $x\in \mathbf{R}$, which clarifies that F(x) is increasing on the interval $(-\infty ,+\infty )$. Thus, there is a unique positive root $x_1$ for $F(x)=0$ (i.e., Eq. (2.2)) if and only if $d-c<0$, as shown in Fig. 1o. Meanwhile, there is no positive root when $\Delta < 0$ and $d-c\ge 0$.

Fig. 1

The distribution of positive roots for Eq. (2.2) on the plane of (d, c). There can be 0, 1, 2 and 3 simple positive roots in different parameter spaces, where $x^{*}_{1}$ and $x^{*}_{2}$ ($x^{*}_{1} \le x^{*}_{2}$) are the extreme points of function F(x), $x^{*}$ is a positive root of multiplicity 3 for Eq. (2.2), $c_{1}$ and $c_{2}$ are two positive roots of $\Delta =0$ (i.e., $(ac+b)^{2}-3 ac(b+c)=0$) with respect to c

When $\Delta =(ac+b)^{2}-3 ac(b+c)>0$, by solving the equation $F'(x)=0$, we get two positive real roots: $x^{*}_{1}$ and $x^{*}_{2}$, i.e., $x^{*}_{1}$ and $x^{*}_{2}$ are the extreme points of function F(x), as shown in Fig. 1b. Then, F(x) is increasing on the interval $(-\infty ,x^{*}_{1}]\cup [x^{*}_{2},+\infty )$, and decreasing on the interval $(x^{*}_{1},x^{*}_{2})$. Therefore, when $d-c \ge 0$, Eq. (2.2) has at most two positive real roots, as shown in Fig. 1g–l. More precisely, there can be three subcases: (a) there are two distinct positive real roots $x_{2}$ and $x_{3}$ with $F'(x_{2})<0$ and $F'(x_{3})>0$ when $F(x^{*}_{2})<0$; (b) there is a unique positive real root $x^{*}_{2}$ (i.e., $x_{2}=x^{*}_{2}=x_{3}$) when $F(x^{*}_{2})=0$; (c) there is no positive real root when $F(x^{*}_{2})>0$. Similarly, we can verify that Eq. (2.2) has at most three positive roots when $\Delta \ge 0$ and $d-c<0$, and omit the proof here. All the possible situations for the existence of the positive real roots are presented in Fig. 1a–t.

Note that, incorporating the condition $0<x<1$, the existence of the positive real roots for Eq. (2.2) indicates the existence of the positive equilibria for system (1.2). Consequently, system (1.2) may have at most three positive equilibria, denoted by $E_{i}(x_{i}, y_{i}), i=1,2,3$, and $y_{i}=(1 + a x^{2}_{i})(1- x_{i})$. The conditions of the existence for the positive equilibria of system (1.2) are concluded in Table 1 in details.

Table 1 The existence of positive equilibria of system (1.2)

2.2 The Stability of Equilibria When $d \ge c$

In this case, system (1.2) has a boundary equilibria $E_{0}(0,\frac{d}{c})$ and at most two positive equilibria: $E_{2}(x_{2},y_{2})$ and $E_{3}(x_{3},y_{3})$. The Jacobian matrix of system (1.2) at any equilibrium takes the following form

$$\begin{aligned} \mathbf{A} |_{E_{i}}= \begin{pmatrix} 1-2x_{i}-\frac{ y_{i}(1-a x^{2}_{i})}{(1+a x^{2}_{i})^{2}} &{}\quad -\frac{ x_{i}}{1+a x^{2}_{i}} \\ \frac{b y_{i}(1-a x^{2}_{i})}{(1+a x^{2}_{i})^{2}} &{}\quad \frac{b x_{i}}{1+a x^{2}_{i}}-c \end{pmatrix}\Bigg |_{E_{i}},\,\,\, i=0, 1, 2 ,3. \end{aligned}$$

Considering the Jacobian matrix of system (1.2) at theses equilibria, we can obtain the following results.

Theorem 2.1

When $d \ge c$, if one of the following conditions (a) $\Delta \le 0$; (b) $\Delta >0$ and $F(x^{*}_{2})>0$ (or $F(x^{*}_{2})\le 0$, $x^{*}_{2}>1$)) holds, then system (1.2) has and only has a boundary equilibrium $E_{0}(0,\frac{d}{c})$ which is globally asymptotically stable. More precisely,

(i):

if $d>c$, then $E_{0}$ is a globally asymptotically stable node;

(ii):

if $d=c$, then $E_{0}$ is a saddle-node of codimension 1.

Proof

Without loss of generality, we only prove the case for $d \ge c$ and $\Delta \le 0$. (i) From Table 1, we know that system (1.2) has no positive equilibrium if $d \ge c$ and $\Delta \le 0$. Following the Jacobian matrix, we get that the characteristic equation at $E_{0}(0,\frac{d}{c})$ is given by

$$\begin{aligned} |\mathbf{A} |_{E_{0}}-\lambda \mathbf{E} |=\lambda ^{2}+p_{E_{0}}\lambda +q_{E_{0}}=0, \end{aligned}$$

(2.6)

where

$$\begin{aligned} q_{E_{0}}\doteq d-c \ge 0,\ p_{E_{0}}\doteq c+ \frac{d}{c}-1 >0 \ \ \mathrm {and} \ \ p^{2}_{E_{0}}-4 q_{E_{0}} = \frac{1}{c^{2}} \left( c^{2}- d +c \right) ^{2} \ge 0. \end{aligned}$$

If $d>c$, then $q_{E_{0}}>0$, hence $E_{0}$ is a locally asymptotically stable node. If $d=c$, then $q_{E_{0}}=0$, which indicates that $E_{0}$ is a degenerate equilibrium.

Since all solutions of system (1.2) starting in the first quadrant are non-negative bounded and eventually end up in the invariant region G with $G= \{(x,y)|0\le x\le 1 ,0\le y\le -bx+M_{0} \}$ (see the proof in Lemma 2.1). Hence, the unique $\omega$-limit set of all the trajectories for system (1.2) is the boundary equilibrium $E_{0}$ by the Poincaré-Bendixson Theorem in [24, 25]. Thus, $E_{0}$ is a globally asymptotically stable node, as shown in Fig. 2b, c.

Fig. 2

a The convex set G. b The boundary equilibrium $E_{0}(0,\frac{d}{c})$ is a globally asymptotically stable node with $a=2.43$, $b=0.81$, $c=0.4$ and $d=0.45$. c The boundary equilibrium $E_{0}(0,\frac{d}{c})$ is a saddle-node with $a=2.43$, $b=0.81$, $c=0.4$ and $d=0.4$

(ii) To determine the type of $E_{0}$ for $d=c$, we translate $E_{0}$ to the origin by letting $u=x$ and $v=y-\frac{d}{c}$. For simplicity, still denoting (u, v) as (x, y) and rewriting system (1.2) as

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=-x^{2}- xy+ a x^{3}+ O(|x,y|^{4}),\\ &{}\frac{dy}{dt}=b x-c y+b xy- ab x^{3}+ O(|x,y|^{4}). \end{aligned} \end{array}\right. } \end{aligned}$$

(2.7)

Further, taking the transformations $u=x$ and $v=bx-cy$, and rewriting (u, v) as (x, y), system (2.7) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{dx}{dt}&{}=-\left( 1+\frac{b}{c}\right) x^{2}+ \frac{b}{c} x y + a x^{3}+ O(|x,y|^{4}),\\ \frac{dy}{dt}&{}=-c y - b \left( 1+b+\frac{b}{c}\right) x^{2}+b\left( 1+\frac{b}{c}\right) xy+ ab (1+c)x^{3}+ O(|x,y|^{4}). \end{aligned} \end{array}\right. } \end{aligned}$$

(2.8)

By the Center Manifold Theorem [24, 25] and Theorems 7.1–7.3 in [25], we conclude that $E_{0}$ is a saddle-node of codimension 1 when $d=c$. The proof is completed. $\square$

Remark 2.1

Note that, $d\ge c$ is equivalent to $\tau \ge \frac{r \delta }{\beta }$ for the original system. From Theorem 2.1, we find that there exists a critical releasing constant $\tau ^{*}>0$ for the predator such that the prey goes to extinction when $\tau \ge \tau ^{*}$, corresponding to the global stability of the boundary equilibrium. This means the predator with a constant recruitment can control the growth of preys effectively.

Theorem 2.2

If $d\ge c$, $\Delta >0$, $F(x^{*}_{2})<0$ and $x^{*}_{2}<1$, except the boundary equilibrium $E_{0}(0,\frac{d}{c})$, system (1.2) has two positive equilibria $E_{2}(x_{2},y_{2})$ and $E_{3}(x_{3},y_{3})$. Furthermore, $E_2$ is an unstable saddle while $E_3$ is an anti-saddle. Denoting $H(x)\doteq 3ax^{3}-(2a-ac)x^{2}-(b-1)x+c$, we have

(i):

if $H(x_{3})<0$, then $E_{3}$ is an unstable focus (or node);

(ii):

if $H(x_{3})=0$, then $E_{3}$ is a weak focus (or center);

(iii):

if $H(x_{3})>0$, then $E_{3}$ is a locally asymptotically stable focus (or node).

Proof

The existence of the two positive equilibria has been clarified in Table 1. The characteristic equation at $E_{2}(x_{2},y_{2})$ is given by

$$\begin{aligned} |\mathbf{A} |_{E_{2}}-\lambda \mathbf{E} |=\lambda ^{2}+p_{E_{2}}\lambda +q_{E_{2}}=0, \end{aligned}$$

(2.9)

where

$$\begin{aligned} \begin{aligned} q_{E_{2}}=\frac{x_{2}[3acx^{2}_{2}-2(ac+b)x_{2}+b+c]}{1+a x^{2}_{2}} \doteq \frac{x_{2}F'(x_{2})}{1+a x^{2}_{2}} \end{aligned} \end{aligned}$$

(2.10)

and

$$\begin{aligned} \begin{aligned} p_{E_{2}}=\frac{3ax^{3}_{2}-(2a-ac)x^{2}_{2}-(b-1)x_{2}+c}{1+a x^{2}_{2}}\doteq \frac{H(x_{2})}{1+a x^{2}_{2}}. \end{aligned} \end{aligned}$$

(2.11)

Obviously, $F'(x_{2})<0$ holds, hence we have $q_{E_{2}}<0$. This indicates that $E_{2}$ is an unstable saddle. Similarly, the characteristic equation at $E_{3}(x_{3},y_{3})$ is

$$\begin{aligned} |\mathbf{A} |_{E_{3}}-\lambda \mathbf{E} |=\lambda ^{2}+p_{E_{3}}\lambda +q_{E_{3}}=0, \end{aligned}$$

(2.12)

where

$$\begin{aligned} q_{E_{3}}= \frac{x_{3}F'(x_{3})}{1+a x^{2}_{3}}>0 \ \quad \mathrm {and} \ \quad p_{E_{3}}= \frac{H(x_{3})}{1+a x^{2}_{3}}. \end{aligned}$$

(2.13)

It follows from (2.13) that if

$$\begin{aligned} H(x_{3})=3ax^{3}_{3}-(2a-ac)x^{2}_{3}-(b-1)x_{3}+c >0, \end{aligned}$$

then $p_{E_{3}}>0$, consequently $E_{3}$ is a locally asymptotically stable focus (or node). With the similar process, we can easily prove the rest cases, here we omit them. This completes the proof. $\square$

Fig. 3

a There exist two positive equilibria $E_{2}(x_{2},y_{2})$ and $E_{3}(x_{3},y_{3})$ when $d\ge c$, $\Delta >0$, $F(x^{*}_{2})<0$ and $x^{*}_{2}<1$, where $E_{3}$ is a locally asymptotically stable node, $E_{2}$ is an unstable hyperbolic saddle with $a=24.048$, $b=4$, $c=0.4$ and $d=0.56$. b There is a unique positive equilibrium $(x^{*}_{2},y^{*}_{2})$, which is a saddle-node of codimension 1 with $a=20.363$, $b=3.681$, $c=0.4$ and $d=0.56$

Remark 2.2

When $d\ge c$, i.e., $\tau \ge \frac{r \delta }{\beta }$, from Theorem 2.2 and Fig. 3a, two equilibria $E_{0}$ and $E_{3}$ are bistable. Further, we can see that the prey will go to extinction if the initial populations lie in the left of the two stable manifolds of the equilibrium $E_{2}$, and will persist if the initial populations lie in the right of the two stable manifolds of the equilibrium $E_{2}$. This means whether the prey will go to extinction or be persistent depends on the initial populations.

Theorem 2.3

If $d\ge c$, $\Delta >0$, $F(x^{*}_{2})=0$ and $x^{*}_{2}<1$, then system (1.2) has a unique positive equilibrium $(x^{*}_{2},y^{*}_{2})$. More precisely,

(i):

if $H(x^{*}_{2})\ne 0$, then $(x^{*}_{2},y^{*}_{2})$ is a saddle-node of codimension 1;

(ii):

if $H(x^{*}_{2})=0$, then $(x^{*}_{2},y^{*}_{2})$ is a cusp of codimension 2.

Proof

• (i) According to the discussion in Table 1, when $F(x^{*}_{2})=0$, then $E_{2}(x_{2},y_{2})$ and $E_{3}(x_{3},y_{3})$ coincide into one positive equilibrium of multiplicity 2, i.e., $(x^{*}_{2},y^{*}_{2})$, where $x^{*}_{2}=\frac{2 (ac+b)+\sqrt{\Delta }}{6ac}$ and $y^{*}_{2}=(1+a(x^{*}_{2})^{2})(1-x^{*}_{2})$. The characteristic equation related to $(x^{*}_{2},y^{*}_{2})$ is

  $$\begin{aligned} |\mathbf{A} |_{(x^{*}_{2},y^{*}_{2})}-\lambda \mathbf{E} |=\lambda ^{2}+p_{(x^{*}_{2},y^{*}_{2})}\lambda +q_{(x^{*}_{2},y^{*}_{2})}=0, \end{aligned}$$

  (2.14)

  where

  $$\begin{aligned} q_{(x^{*}_{2},y^{*}_{2})}= \frac{x^{*}_{2}F'(x^{*}_{2})}{1+a (x^{*}_{2})^{2}}=0 \ \quad \mathrm {and} \ \quad p_{(x^{*}_{2},y^{*}_{2})}= \frac{H(x^{*}_{2})}{1+a (x^{*}_{2})^{2}}. \end{aligned}$$

  If $H(x^{*}_{2})\ne 0$, then $p_{(x^{*}_{2},y^{*}_{2})}\ne 0$. Thus, one of the eigenvalues of the characteristic equation (2.14) is zero while the other one is nonzero. In this case, we linearize system (1.2) at $(x^{*}_{2},y^{*}_{2})$ by making the transformation of $u=x-x^{*}_{2}$ and $v=y-y^{*}_{2}$. Rewriting (u, v) as (x, y), and expanding the right-hand side of system (1.2) in a Taylor series up to the second order around the origin, we get

  $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=a_{10}x+b_{01}y+a_{20}x^{2}+2a_{11}x y +O(|x,y|^{3}),\\ &{}\frac{dy}{dt}=c_{10}x+d_{01}y+b_{20}x^{2}+2b_{11}xy+O(|x,y|^{3}), \end{aligned} \end{array}\right. } \end{aligned}$$

  (2.15)

  where $a_{10} = -x^{*}_{2}+\frac{2a(x^{*}_{2})^{2}(1-x^{*}_{2})}{1+a (x^{*}_{2})^{2}}$, $b_{01} = -\frac{x^{*}_{2}}{1+a (x^{*}_{2})^{2}}$, $c_{10} = \frac{b y^{*}_{2}[1-a (x^{*}_{2})^{2}]}{[1+a (x^{*}_{2})^{2}]^{2}}$, $d_{01} = -c+\frac{b x^{*}_{2}}{1+a (x^{*}_{2})^{2}}$, $a_{11} = -\frac{1-a (x^{*}_{2})^{2}}{2[1+a (x^{*}_{2})^{2}]^{2}}$, $a_{20} = -1+\frac{a x^{*}_{2}y^{*}_{2}[3-a (x^{*}_{2})^{2}]}{[1+a (x^{*}_{2})^{2}]^{3}}$, $b_{11} = \frac{b[1-a (x^{*}_{2})^{2}]}{2[1+a (x^{*}_{2})^{2}]^{2}}$ and $b_{20} = -\frac{ab x^{*}_{2}y^{*}_{2}[3-a (x^{*}_{2})^{2}]}{[1+a (x^{*}_{2})^{2}]^{3}}$.

  As $b_{01} \ne 0$, we further make the following transformations

  $$\begin{aligned} u=-\frac{d_{01}x}{b_{01}(a_{10}+d_{01})}+\frac{y}{a_{10}+d_{01}} \ \ \mathrm {and} \ \ v=\frac{a_{10}x}{b_{01}(a_{10}+d_{01})}+\frac{y}{a_{10}+d_{01}}, \end{aligned}$$

  rewrite (u, v) as (x, y), when $F(x^{*}_{2})=0$ and $H(x^{*}_{2})\ne 0$ (i.e., $a_{10}d_{01}-b_{01}c_{10}=0$ and $a_{10}+d_{01}\ne 0$), then system (2.15) becomes

  $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=c_{20}x^{2}+c_{11}xy+c_{02}y^{2}+ O(|x,y|^{3}),\\ &{}\frac{dy}{dt}=(a_{10}+d_{01})y+d_{20}x^{2}+d_{11}xy+d_{02}y^{2}+ O(|x,y|^{3}), \end{aligned} \end{array}\right. } \end{aligned}$$

  (2.16)

  where $c_{20}\doteq \frac{b_{01}(b_{01}b_{20}-d_{01}a_{20})-2a_{10}(b_{01}b_{11}-d_{01}a_{11})}{a_{10}+d_{01}}$, $d_{20}\doteq \frac{b_{01}(a_{10}a_{20}+b_{01}b_{20})-2a_{10}(a_{10}a_{11}-b_{01}b_{11})}{a_{10}+d_{01}}$, $c_{11}\doteq \frac{2b_{01}(d_{01}a_{20}-b_{01}b_{20})}{a_{10}+d_{01}}+\frac{2(a_{10}-d_{01})(b_{01}b_{11}-d_{01}a_{11})}{a_{10}+d_{01}}$, $d_{11}\doteq \frac{2(a_{10}-d_{01})(a_{10}a_{11}+b_{01}b_{11})-2b_{01}(a_{10}a_{20}+b_{01}b_{20})}{a_{10}+d_{01}}$, $c_{02}\doteq \frac{b_{01}(b_{01}b_{20}-d_{01}a_{20})+2d_{01}(b_{01}b_{11}-d_{01}a_{11})}{a_{10}+d_{01}}$ and $d_{02}\doteq \frac{b_{01}(a_{10}a_{20}+b_{01}b_{20})+2d_{01}(a_{10}a_{11}+b_{01}b_{11})}{a_{10}+d_{01}}.$ Again by the Center Manifold Theorem, system (2.16) reduced to the center manifold takes the following form

  $$\begin{aligned} \frac{dx}{dt}=c_{20}x^{2}+O(x^{3}),\ c_{20}=\frac{ac (x^{*}_{2})^{2}}{(1+a (x^{*}_{2})^{2})^{2}}\left[ 3x^{*}_{2}- 1-\frac{b}{ac} \right] . \end{aligned}$$

  (2.17)

  Since $x_{1}+x_{2}+x_{3}=x_{1}+2x^{*}_{2}=1+\frac{b}{ac}$ and $x_{1}<x^{*}_{2}$, there is $x^{*}_{2} \ne \frac{1}{3}+\frac{b}{3ac}$, hence we have $c_{20}> 0$. Therefore, $(x^{*}_{2},y^{*}_{2})$ is a saddle-node of codimension 1 according to Theorems 7.1–7.3 in [25], as shown in Fig. 3b.

• (ii) By case (i), we know that if $H(x^{*}_{2})= 0$, then $p_{(x^{*}_{2},y^{*}_{2})}= 0$, consequently both eigenvalues of the characteristic equation (2.14) are zeros, which indicates that $(x^{*}_{2},y^{*}_{2})$ is a cusp of codimension at least 2. Further, we transform the linear part of system (2.15) to the Jordan canonical form. Let

  $$\begin{aligned} u=x \ \ \mathrm {and} \ \ v=a_{10}x+b_{01}y, \end{aligned}$$

  rewrite (u, v) as (x, y), then system (2.15) becomes

  $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{dx}{dt}&{}=y+\left( a_{20}-\frac{2a_{10} a_{11}}{b_{01}}\right) x^{2}+ \frac{2 a_{11}}{b_{01}}xy+ O(|x,y|^{3}),\\ \frac{dy}{dt}&{}=\left( a_{10} a_{20}-\frac{2 a^{2}_{10} a_{11}}{b_{01}}+b_{01} b_{20}-2a_{10} b_{11}\right) x^{2}\\ &{}\quad + \left( \frac{2 a_{10} a_{11}}{b_{01}}+2b_{11}\right) xy+ O(|x,y|^{3}). \end{aligned} \end{array}\right. } \end{aligned}$$

  (2.18)

  In order to find the canonical normal form of the cusp of codimension 2, we take

  $$\begin{aligned} u=x-\frac{a_{11}}{b_{01}}x^{2} \ \ \mathrm {and} \ \ v=y+\left( a_{20}-\frac{2 a_{10} a_{11}}{b_{01}}\right) x^{2}, \end{aligned}$$

  rewrite (u, v) as (x, y), then system (2.18) is rewritten as

  $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=y+O(|x,y|^{3}) ,\\ &{}\frac{dy}{dt}=E_{0}x^{2}+F_{0}xy+O(|x,y|^{3}), \end{aligned} \end{array}\right. } \end{aligned}$$

  (2.19)

  where

  $$\begin{aligned} F_{0} \doteq 2 b_{11}+2 a_{20}-\frac{2 a_{10} a_{11}}{b_{01}}=-\frac{H'(x^{*}_{2})}{1+a (x^{*}_{2})^{2}} \end{aligned}$$

  (2.20)

  and

  $$\begin{aligned} E_{0} \doteq a_{10} a_{20}-\frac{2 a^{2}_{10} a_{11}}{b_{01}}+b_{01} b_{20}-2a_{10} b_{11} =\frac{ac x^{*}_{2}}{1+a (x^{*}_{2})^{2}}\left[ 1+\frac{b}{ac}-3x^{*}_{2} \right] <0.\nonumber \\ \end{aligned}$$

  (2.21)

  It follows from Eqs. (2.20) and (2.21) that $E_{0}F_{0}\ne 0$ if $H'(x^{*}_{2})\ne 0$. By the qualitative theory of ordinary differential equations and the theory of differential manifolds [24], we know that $(x^{*}_{2},y^{*}_{2})$ is a cusp of codimension 2 if $H'(x^{*}_{2})\ne 0$, and a cusp of codimension at least 3 if $H'(x^{*}_{2})=0$. For system (1.2), we show that there can not exist a $x^{*}_{2}$ such that $H'(x^{*}_{2})=0$. Assuming the contrary and letting $H'(x^{*}_{2})=0$, then from $F(x^{*}_{2})=F'(x^{*}_{2})=0$ and $H(x^{*}_{2})=H'(x^{*}_{2})=0$, a, b, c and d can be expressed as follows

  $$\begin{aligned}&a=-\frac{2x^{*}_{2}-1}{[12(x^{*}_{2})^{2}-15x^{*}_{2}+4]x^{*}_{2}},\ \ b=-\frac{2x^{*}_{2}(x^{*}_{2}-1)(3x^{*}_{2}-1)^{2}}{[12(x^{*}_{2})^{2}-15x^{*}_{2}+4][7(x^{*}_{2})^{2}-8x^{*}_{2}+2]}, \\&c=-\frac{x^{*}_{2}(3x^{*}_{2}-1)(2x^{*}_{2}-1)}{7(x^{*}_{2})^{2}-8x^{*}_{2}+2} \ \ \mathrm {and} \ \ d=\frac{2x^{*}_{2}(3x^{*}_{2}-1)(x^{*}_{2}-1)^{2}}{12(x^{*}_{2})^2-15x^{*}_{2}+4}. \end{aligned}$$

  Further, because of $a>0$, $b>0$, $c>0$ and $d>0$, there is $x^{*}_{2}\in (\frac{1}{3},\frac{4-\sqrt{2}}{7})$. However, it is easy to verify that $d<c$ for $x^{*}_{2}\in (\frac{1}{3},\frac{4-\sqrt{2}}{7})$. This is a contradictory. Thus, $H'(x^{*}_{2})\ne 0$ and $(x^{*}_{2},y^{*}_{2})$ is a cusp of codimension 2 if $H(x^{*}_{2})=0$. Note that we can further conclude that there is no closed orbits in this case. Otherwise, there exists a closed orbit, then the closed orbit must contain some equilibria in its interior and the sum of indices of these equilibria should be one. However, $(x^{*}_{2},y^{*}_{2})$ is a unique equilibrium of system (1.2), which is a saddle-node or a cusp whose index is not one. This is a contradictory and the proof is completed. $\square$

2.3 The Stability of Equilibria When $d < c$

In this case, it is easy to verify that the boundary equilibrium $E_{0}(0,\frac{d}{c})$ is unstable while system (1.2) can have at most three positive equilibria: $E_{1}(x_{1},y_{1})$, $E_{2}(x_{2},y_{2})$ and $E_{3}(x_{3},y_{3})$. With the similar process in Sects. 2.1 and 2.2, the local stability for all possible equilibria in different scenarios can be easily obtained. We omit the detailed proof and just conclude all the cases in Table 2. Then, we focus on the cases (II)-(b) and (III)-(c)(f) in Table 2, that is, system (1.2) has a degenerate positive equilibrium, which leads to the following main results.

Table 2 Scenarios for the local stability of all possible equilibria when $d<c$

Theorem 2.4

For the case (III)(c), system (1.2) has two different positive equilibria: an elementary equilibrium $E_{1}(x_{1},y_{1})$ and a degenerate positive equilibrium $(x^{*}_{2},y^{*}_{2})$ of multiplicity 2. More precisely,

(i):

if $H(x^{*}_{2})\ne 0$, then $(x^{*}_{2},y^{*}_{2})$ is a saddle-node of codimension 1;

(ii):

if $H(x^{*}_{2})=0$, then $(x^{*}_{2},y^{*}_{2})$ is a cusp of codimension 2.

Proof

The proof is similar to Theorems 2.3. The difference is the proof of (ii), hence we omit the proof of (i) here. Making a sequence of coordinate transformations used in the proof of Theorem 2.3, we obtain the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=y+O(|x,y|^{3}) ,\\ &{}\frac{dy}{dt}=E_{0}x^{2}+F_{0}xy+O(|x,y|^{3}). \end{aligned} \end{array}\right. } \end{aligned}$$

(2.22)

Then, $(x^{*}_{2},y^{*}_{2})$ is a cusp of codimension 2 if $H'(x^{*}_{2})\ne 0$, and a cusp of codimension at least 3 if $H'(x^{*}_{2})=0$.

Next, we also show that there can not exist a $x^{*}_{2}$ such that $H'(x^{*}_{2})=0$ when $d<c$. Similarly, assuming the contrary and letting $H'(x^{*}_{2})=0$, then from $F(x^{*}_{2})=F'(x^{*}_{2})=0$ and $H(x^{*}_{2})=H'(x^{*}_{2})=0$, a, b, c and d can be expressed as follows

$$\begin{aligned}&a=-\frac{2x^{*}_{2}-1}{[12(x^{*}_{2})^{2}-15x^{*}_{2}+4]x^{*}_{2}},\ \ b=-\frac{2x^{*}_{2}(x^{*}_{2}-1)(3x^{*}_{2}-1)^{2}}{[12(x^{*}_{2})^{2}-15x^{*}_{2}+4][7(x^{*}_{2})^{2}-8x^{*}_{2}+2]}, \\&c=-\frac{x^{*}_{2}(3x^{*}_{2}-1)(2x^{*}_{2}-1)}{7(x^{*}_{2})^{2}-8x^{*}_{2}+2} \ \ \mathrm {and} \ \ d=\frac{2x^{*}_{2}(3x^{*}_{2}-1)(x^{*}_{2}-1)^{2}}{12(x^{*}_{2})^2-15x^{*}_{2}+4} \\&\,\mathrm {with} \ \ x^{*}_{2}\in \left( \frac{1}{3},\frac{4-\sqrt{2}}{7}\right) . \end{aligned}$$

From Sect. 2.1, we know that

$$\begin{aligned} x^{*}_{2}= \frac{ (ac+b)+\sqrt{\Delta }}{3ac} > \frac{1}{3}+\frac{b}{3ac}=\frac{1}{3}+\frac{2x^{*}_{2}(1-x^{*}_{2})(3x^{*}_{2}-1)}{3(2x^{*}_{2}-1)^{2}}. \end{aligned}$$

However, it is easy to verify that

$$\begin{aligned} \frac{1}{3}+\frac{2x^{*}_{2}(1-x^{*}_{2})(3x^{*}_{2}-1)}{3(2x^{*}_{2}-1)^{2}} - x^{*}_{2} \ge 0, \ \ x^{*}_{2}\in \left( \frac{1}{3},\frac{4-\sqrt{2}}{7}\right) . \end{aligned}$$

This is a contradictory. Hence, there is no $x^{*}_{2}\in (\frac{1}{3},\frac{4-\sqrt{2}}{7})$ such that $H'(x^{*}_{2})=0$ when $d<c$. Thus, $H'(x^{*}_{2})\ne 0$ and $(x^{*}_{2},y^{*}_{2})$ is a cusp of codimension 2 if $H(x^{*}_{2})=0$. The proof is completed. $\square$

Theorem 2.5

For the case (III)(f), system (1.2) has two different positive equilibria: an elementary equilibrium $E_{3}(x_{3},y_{3})$ and a degenerate positive equilibrium $(x^{*}_{1},y^{*}_{1})$ of multiplicity 2. More precisely,

(i):

if $H(x^{*}_{1})\ne 0$, then $(x^{*}_{1},y^{*}_{1})$ is a saddle-node of codimension 1;

(ii):

if $H(x^{*}_{1})=0$ and

(a):

$H'(x^{*}_{1})\ne 0$, then $(x^{*}_{1},y^{*}_{1})$ is a cusp of codimension 2;

(b):

$H'(x^{*}_{1})=0$ and $N_{0}(x^{*}_{1}) \ne 0$ with $N_{0}(x) \doteq 2802 x^{7}-9648 x^{6}+13716 x^{5}-10399 x^{4}+ 4527 x^{3}-1129 x^{2}+ 149 x-8$, then $(x^{*}_{1},y^{*}_{1})$ is a cusp of codimension 3.

Proof

The proofs of (i) and (ii)(a) are similar to Theorem 2.3, we omit the procedures for brevity. In the following, we focus on the proof of (ii)(b). Similarly, in this case, from $F(x^{*}_{1})=F'(x^{*}_{1})=0$ and $H(x^{*}_{1})=H'(x^{*}_{1})=0$, we can obtain

$$\begin{aligned}&a=-\frac{2x^{*}_{1}-1}{[12(x^{*}_{1})^{2}-15x^{*}_{1}+4]x^{*}_{1}},\ \ b=-\frac{2x^{*}_{1}(x^{*}_{1}-1)(3x^{*}_{1}-1)^{2}}{[12(x^{*}_{1})^{2}-15x^{*}_{1}+4][7(x^{*}_{1})^{2}-8x^{*}_{1}+2]},\\&c=-\frac{x^{*}_{1}(3x^{*}_{1}-1)(2x^{*}_{1}-1)}{7(x^{*}_{1})^{2}-8x^{*}_{1}+2} \ \ \mathrm {and} \ \ d=\frac{2x^{*}_{1}(3x^{*}_{1}-1)(x^{*}_{1}-1)^{2}}{12(x^{*}_{1})^2-15x^{*}_{1}+4} \\&\,\mathrm {with} \ \ x^{*}_{1}\in \left( \frac{1}{3},\frac{4-\sqrt{2}}{7}\right) . \end{aligned}$$

Substituting a, b, c and d into system (1.2) and translating the positive equilibrium $(x^{*}_{1},y^{*}_{1})$ to the origin, expanding the right-hand side of system (1.2) in a Taylor series up to the fourth order around the origin, then we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=\hat{a}_{10}x+\hat{b}_{01}y+\hat{a}_{20}x^{2}+2\hat{a}_{11}x y + \hat{a}_{30}x^3+\hat{a}_{21}x^{2}y+\hat{a}_{40}x^{4}+\hat{a}_{31}x^{3}y + O(|x,y|^{5}),\\ &{}\frac{dy}{dt}=\hat{c}_{10}x+\hat{d}_{01}y+\hat{b}_{20}x^{2}+2\hat{b}_{11}x y + \hat{b}_{30}x^3+\hat{b}_{21}x^{2}y+\hat{b}_{40}x^{4}+\hat{b}_{31}x^{3}y + O(|x,y|^{5}), \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.23)

where $\hat{a}_{10} \doteq -x^{*}_{1}+\frac{2a(x^{*}_{1})^{2}(1-x^{*}_{1})}{1+a (x^{*}_{1})^{2}}$, $\hat{b}_{01} \doteq \frac{-x^{*}_{1}}{1+a (x^{*}_{1})^{2}}$, $\hat{a}_{20} \doteq -1+\frac{a x^{*}_{1}y^{*}_{1}[3-a (x^{*}_{1})^{2}]}{[1+a (x^{*}_{1})^{2}]^{3}}$, $\hat{a}_{11} \doteq \frac{-1+a (x^{*}_{1})^{2}}{2[1+a (x^{*}_{1})^{2}]^{2}}$, $\hat{c}_{10} \doteq \frac{b y^{*}_{1}[1-a (x^{*}_{1})^{2}]}{[1+a (x^{*}_{1})^{2}]^{2}}$, $\hat{d}_{01} \doteq -c+\frac{b x^{*}_{1}}{1+a (x^{*}_{1})^{2}}$, $\hat{b}_{11} \doteq \frac{b[1-a (x^{*}_{1})^{2}]}{2[1+a (x^{*}_{1})^{2}]^{2}}$, $\hat{b}_{20} \doteq -\frac{ab x^{*}_{1}y^{*}_{1}[3-a (x^{*}_{1})^{2}]}{[1+a (x^{*}_{1})^{2}]^{3}}$, $\hat{a}_{30} \doteq \frac{a y^{*}_{1}[1+ a^{2}(x^{*}_{1})^{4}-6 a (x^{*}_{1})^{2}]}{[1+ a (x^{*}_{1})^{2}]^{4}}$, $\hat{a}_{21} \doteq \frac{a x^{*}_{1}[3- a (x^{*}_{1})^{2}]}{[1+a (x^{*}_{1})^{2}]^{3}}$, $\hat{a}_{31} \doteq \frac{a [1+ a^{2}(x^{*}_{1})^{4}-6 a (x^{*}_{1})^{2}]}{[1+a (x^{*}_{1})^{2}]^{4}}$, $\hat{a}_{40} \doteq \frac{a^{2}x^{*}_{1}y^{*}_{1}[10a (x^{*}_{1})^{2}-a^{2}(x^{*}_{1})^{4}-5]}{[1+a (x^{*}_{1})^{2}]^{5}}$, $\hat{b}_{30} \doteq -\frac{ab y^{*}_{1}[1+ a^{2}(x^{*}_{1})^{4}-6 a (x^{*}_{1})^{2}]}{[1+ a (x^{*}_{1})^{2}]^{4}}$, $\hat{b}_{21} \doteq -\frac{ab x^{*}_{1}[3- a(x^{*}_{1})^{2}]}{[1+a (x^{*}_{1})^{2}]^{3}},$ $\hat{b}_{40} \doteq -\frac{a^{2}b x^{*}_{1}y^{*}_{1}[10a (x^{*}_{1})^{2}-a^{2}(x^{*}_{1})^{4}-5]}{[1+a (x^{*}_{1})^{2}]^{5}}$ and $\hat{b}_{31} \doteq -\frac{a b [1+ a^{2}(x^{*}_{1})^{4}-6 a (x^{*}_{1})^{2}]}{[1+a (x^{*}_{1})^{2}]^{4}}$.

In order to find the canonical normal form of the cusp of codimension 3, we take $u=x \ \ \mathrm {and} \ \ v=\frac{dx}{dt},$ rewrite (u, v) as (x, y), then system (2.23) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{d x}{dt}=y,\\ &{}\frac{d y}{dt}=\hat{c}_{20} x^{2}+\hat{c}_{02}y^{2}+\hat{c}_{30}x^{3}+ \hat{c}_{21}x^{2}y +\hat{c}_{12}xy^{2} +\hat{c}_{40}x^{4}+\hat{c}_{31}x^{3}y +\hat{c}_{22} x^{2}y^{2}+ O(|x,y|^{5}), \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.24)

where $\hat{c}_{20}\doteq \hat{a}_{10} \hat{a}_{20}-\frac{2 \hat{a}^{2}_{10} \hat{a}_{11}}{\hat{b}_{01}}+\hat{b}_{01} \hat{b}_{20}-2\hat{a}_{10} \hat{b}_{11}$, $\hat{c}_{02}\doteq \frac{2 \hat{a}_{11}}{\hat{b}_{01}}$, $\hat{c}_{30}\doteq -\hat{a}_{10}\hat{b}_{21}+2\hat{a}_{11}\hat{b}_{20}-2\hat{a}_{20}\hat{b}_{11}+\hat{a}_{21} \hat{c}_{10}-\hat{a}_{30}\hat{d}_{01}+\hat{b}_{01}\hat{b}_{30}$, $\hat{c}_{21} \doteq \hat{b}_{21}+3\hat{a}_{30}-\frac{2 \hat{a}_{11}\hat{a}_{20}}{\hat{b}_{01}}-\frac{2 \hat{a}_{10}\hat{a}_{21}}{\hat{b}_{01}}+\frac{4\hat{a}_{10}\hat{a}^{2}_{11}}{\hat{b}^{2}_{01}}$, $\hat{c}_{12} \doteq \frac{2\hat{a}_{21}}{\hat{b}_{01}}-\frac{4 \hat{a}^{2}_{11}}{\hat{b}^{2}_{01}}$, $\hat{c}_{40} \doteq -\hat{a}_{10}\hat{b}_{31}+2\hat{a}_{11}\hat{b}_{30}-\hat{a}_{20}\hat{b}_{21}+\hat{a}_{21}\hat{b}_{20}-2\hat{a}_{30}\hat{b}_{11}+\hat{a}_{31}\hat{c}_{10}-\hat{a}_{40}\hat{d}_{01}+\hat{b}_{01}\hat{b}_{40}$, $\hat{c}_{31} \doteq \hat{b}_{31}+4\hat{a}_{40}-\frac{2\hat{a}_{20}\hat{a}_{21}}{\hat{b}_{01}}-\frac{2\hat{a}_{11}\hat{a}_{30}}{\hat{b}_{01}}-\frac{3\hat{a}_{10}\hat{a}_{31}}{\hat{b}_{01}} +\frac{4\hat{a}^{2}_{11}\hat{a}_{20}}{\hat{b}^{2}_{01}}+\frac{6\hat{a}_{10}\hat{a}_{11}\hat{a}_{21}}{\hat{b}^{2}_{01}}-\frac{8\hat{a}_{10}\hat{a}^{3}_{11}}{\hat{b}^{3}_{01}}$ and $\hat{c}_{22} \doteq \frac{3 \hat{a}_{31}}{\hat{b}_{01}}-\frac{6\hat{a}_{11}\hat{a}_{21}}{\hat{b}^{2}_{01}}+\frac{8 \hat{a}^{3}_{11}}{\hat{b}^{3}_{01}}$.

Next, we introduce a new time variable $\tau$ by $dt=(1-\hat{c}_{02}x)d\tau$ and rewrite $\tau$ as t, then system (2.24) can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{d x}{dt}&{}= y(1-\hat{c}_{02}x),\\ \frac{d y}{dt}&{}= (1-\hat{c}_{02}x)(\hat{c}_{20} x^{2}+\hat{c}_{02}y^{2}+\hat{c}_{30}x^{3}+ \hat{c}_{21}x^{2}y +\hat{c}_{12}xy^{2})\\ &{}\quad + (1-\hat{c}_{02}x) (\hat{c}_{40}x^{4}+\hat{c}_{31}x^{3}y +\hat{c}_{22} x^{2}y^{2})+ O(|x,y|^{5}). \end{aligned} \end{array}\right. } \end{aligned}$$

(2.25)

Let $u=x$ and $v=y(1-\hat{c}_{02}x)$, rewrite (u, v) as (x, y), then system (2.25) is transformed into

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{d x}{dt}= y,\\ &{}\frac{d y}{dt}= \hat{d}_{20}x^{2}+\hat{d}_{30}x^{3}+\hat{d}_{21}x^{2}y+\hat{d}_{12}xy^{2}+\hat{d}_{40}x^{4}+\hat{d}_{31}x^{3}y +\hat{d}_{22}x^{2}y^{2}+ O(|x,y|^{5}), \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.26)

where $\hat{d}_{20}\doteq \hat{c}_{20}$, $\hat{d}_{30}\doteq \hat{c}_{30}-2\hat{c}_{20}\hat{c}_{02}$, $\hat{d}_{21}\doteq \hat{c}_{21}$, $\hat{d}_{12}\doteq \hat{c}_{12}-\hat{c}^{2}_{02}$, $\hat{d}_{40}\doteq \hat{c}_{40}+\hat{c}_{20}\hat{c}^{2}_{02}-2\hat{c}_{30}\hat{c}_{02}$, $\hat{d}_{31} \doteq \hat{c}_{31}-\hat{c}_{02}\hat{c}_{21}$ and $\hat{d}_{22}\doteq \hat{c}_{22}-\hat{c}^{3}_{02}$. Notice that $\hat{d}_{20}=\frac{ac x^{*}_{1}}{1+a (x^{*}_{1})^{2}}\left[ 1+\frac{b}{ac}-3x^{*}_{1} \right] > 0$, making the following change of variables

$$\begin{aligned} u=x, \ \ v=\frac{1}{\sqrt{\hat{d}_{20}}}y \ \ \mathrm {and} \ \ d \tau =\sqrt{\hat{d}_{20}}dt, \end{aligned}$$

rewriting $(u,v,\tau )$ as (x, y, t), then system (2.26) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{d x}{dt}= y,\\ &{}\frac{d y}{dt}= x^{2}+\hat{e}_{30}x^{3}+\hat{e}_{21}x^{2}y+\hat{e}_{12}xy^{2}+\hat{e}_{40}x^{4} +\hat{e}_{31}x^{3}y +\hat{e}_{22}x^{2}y^{2}+ O(|x,y|^{5}), \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.27)

where $\hat{e}_{30}\doteq \frac{\hat{d}_{30}}{\hat{d}_{20}}$, $\hat{e}_{21} \doteq \frac{\hat{d}_{21}}{\sqrt{\hat{d}_{20}}}$, $\hat{e}_{12} \doteq \hat{d}_{12}$, $\hat{e}_{40} \doteq \frac{\hat{d}_{40}}{\hat{d}_{20}}$, $\hat{e}_{31} \doteq \frac{\hat{d}_{31}}{\sqrt{\hat{d}_{20}}}$ and $\hat{e}_{22} \doteq \hat{d}_{22}$.

According to Proposition 5.3 in [26], we get an equivalent system of system (2.27) in a small neighborhood of (0, 0), which is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=y,\\ &{}\frac{dy}{dt}=x^{2}+M_{1}(x^{*}_{1}) x^{3}y+ R(x,y), \end{aligned} \end{array}\right. } \end{aligned}$$

(2.28)

where

$$\begin{aligned} M_{1}(x^{*}_{1})\doteq \frac{(x^{*}_{1}-\frac{1}{2})N_{0}(x^{*}_{1})}{x^{*}_{1}(-1+3x^{*}_{1})(5x^{*}_{1}-2)^{2}(x^{*}_{1}-1)^{2}[7(x^{*}_{1})^{2}-8x^{*}_{1}+2][6(x^{*}_{1})^{2}-6x^{*}_{1}+1] \sqrt{\hat{d}_{20}}} \end{aligned}$$

and $R(x,y) \doteq y^{2} O(|x,y|^{2})+O(|x,y|^{5})$. Note that $x^{*}_{1}\in (\frac{1}{3},\frac{4-\sqrt{2}}{7})$ indicates that each factor in $M_{1}(x^{*}_{1})$ is nonzero except $N_{0}(x^{*}_{1})$. Thus, when $N_{0}(x^{*}_{1})\ne 0$, we have $M_{1}(x^{*}_{1})\ne 0$. Correspondingly, $(x^{*}_{1},y^{*}_{1})$ is a cusp of codimension 3 by the results in [19, 22, 27]. Otherwise, when $N_{0}(x^{*}_{1})=0$, then $M_{1}(x^{*}_{1})=0$ and $(x^{*}_{1},y^{*}_{1})$ may be a cusp of codimension 4, which is extremely complex and the study of exact codimension of this cusp is beyond our current scope. This is left for the future works. This completes the proof. $\square$

Next, we consider the case (II)(b) in Table 2. In this case, three equilibria $E_{1}(x_{1},y_{1})$, $E_{2}(x_{2},y_{2})$ and $E_{3}(x_{3},y_{3})$ coincide into a unique positive equilibrium $(x^{*},y^{*})$, where $x^{*}=\frac{1}{3}+\frac{b}{3ac}$ and $y^{*}=\frac{a^{2}c+ab+5ac-4b}{9ac}$. The characteristic equation related to $(x^{*},y^{*})$ is given by

$$\begin{aligned} |\mathbf{A} |_{(x^{*},y^{*})}-\lambda \mathbf{E} |=\lambda ^{2}+p_{(x^{*},y^{*})}\lambda +q_{(x^{*},y^{*})}=0, \end{aligned}$$

(2.29)

where

$$\begin{aligned} q_{(x^{*},y^{*})}=\frac{x^{*}F'(x^{*})}{1+\omega (x^{*})^{2}}=0 \ \ \mathrm {and} \ \ p_{(x^{*},y^{*})}=\frac{H(x^{*})}{1+\omega (x^{*})^{2}}. \end{aligned}$$

If $H(x^{*})\ne 0$ (i.e., $a+b\ne ac+c+\frac{2b}{ac}+3$), then $p_{(x^{*},y^{*})} \ne 0$. Thus, one of the eigenvalues is zero and the other one is nonzero. If $H(x^{*})=0$ (i.e., $a+b = ac+c+\frac{2b}{ac}+3$), then $p_{(x^{*},y^{*})} = 0$. Consequently the two eigenvalues are zeros. Then, we have the following results in terms of the type of the positive equilibrium $(x^{*},y^{*})$.

Theorem 2.6

For the case (II)(b), system (1.2) has a unique positive equilibrium $(x^{*},y^{*})$, which is a degenerate equilibrium of multiplicity 3. More precisely,

(i):

if $H(x^{*})\ne 0$, then $(x^{*},y^{*})$ is a stable degenerate node of codimension 2 provided $a+b<ac+c+\frac{2b}{ac}+3$ and unstable provided $a+b>ac+c+\frac{2b}{ac}+3$;

(ii):

if $H(x^{*})= 0$ and

(a):

$H'(x^{*})=0$ (or $H'(x^{*})\ne 0$ and $(H'(x^{*}))^{2}< 8acx^{*}[1+a(x^{*})^{2}]$), then $(x^{*},y^{*})$ is a degenerate focus (or center);

(b):

$H'(x^{*})\ne 0$ and $(H'(x^{*}))^{2}\ge 8acx^{*}[1+a(x^{*})^{2}]$, then $(x^{*},y^{*})$ is a degenerate elliptic equilibrium consisting of one hyperbolic sector and one elliptic sector.

Proof

The proof of (i) is similar to those in Theorem 2.3 and using Theorem 7.1–7.3 in [25], we can obtain the conclusion in (i). Next, we focus on the proof of (ii). Firstly, we translate the positive equilibrium $(x^{*},y^{*})$ to the origin, and expand the right-hand side of system (1.2) in a Taylor series up to the fourth order around the origin, then we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=\bar{a}_{10}x+\bar{b}_{01}y+\bar{a}_{20}x^{2}+2\bar{a}_{11}x y + \bar{a}_{30}x^{3}+ \bar{a}_{21}x^{2}y+\bar{a}_{40}x^{4}+ \bar{a}_{31}x^{3}y +O(|x,y|^{5}),\\ &{}\frac{dy}{dt}=\bar{c}_{10}x+\bar{d}_{01}y+\bar{b}_{20}x^{2}+2\bar{b}_{11}xy+ \bar{b}_{30}x^{3}+ \bar{b}_{21}x^{2}y+\bar{b}_{40}x^{4}+ \bar{b}_{31}x^{3}y +O(|x,y|^{5}), \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.30)

where $\bar{a}_{10} \doteq -x^{*}+\frac{2a(x^{*})^{2}(1-x^{*})}{1+a (x^{*})^{2}}$, $\bar{b}_{01} \doteq -\frac{x^{*}}{1+a (x^{*})^{2}}$, $\bar{a}_{20} \doteq \frac{a x^{*}y^{*}[3-a (x^{*})^{2}]}{[1+a (x^{*})^{2}]^{3}}-1$, $\bar{a}_{11} \doteq \frac{a (x^{*})^{2}-1}{2[1+a (x^{*})^{2}]^{2}}$, $\bar{a}_{21} \doteq \frac{a x^{*}[3- a (x^{*})^{2}]}{[1+a (x^{*})^{2}]^{3}}$, $\bar{a}_{30} \doteq \frac{a y^{*}[1+ a^{2}(x^{*}_{1})^{4}-6 a (x^{*})^{2}]}{[1+ a (x^{*})^{2}]^{4}}$, $\bar{c}_{10} \doteq \frac{b y^{*}[1-a (x^{*})^{2}]}{[1+a (x^{*})^{2}]^{2}}$, $\bar{d}_{01} \doteq -c+\frac{b x^{*}}{1+a (x^{*})^{2}}$, $\bar{b}_{11} \doteq \frac{b[1-a (x^{*})^{2}]}{2[1+a (x^{*})^{2}]^{2}}$, $\bar{b}_{20} \doteq -\frac{ab x^{*}y^{*}[3-a (x^{*})^{2}]}{[1+a (x^{*})^{2}]^{3}}$, $\bar{b}_{21} \doteq -\frac{ab x^{*}[3- a (x^{*})^{2}]}{[1+a (x^{*})^{2}]^{3}}$, $\bar{b}_{30} \doteq -\frac{ab y^{*}[1+ a^{2}(x^{*})^{4}-6 a (x^{*})^{2}]}{[1+ a (x^{*})^{2}]^{4}}$, $\bar{a}_{40} \doteq \frac{a^{2}x^{*}y^{*}[10a (x^{*})^{2}-a^{2}(x^{*})^{4}-5]}{[1+a (x^{*})^{2}]^{5}}$, $\bar{a}_{31} \doteq \frac{a [1+ a^{2}(x^{*})^{4}-6 a (x^{*})^{2}]}{[1+a (x^{*})^{2}]^{4}}$, $\bar{b}_{31} \doteq -\frac{a b [1+ a^{2}(x^{*})^{4}-6 a (x^{*})^{2}]}{[1+a (x^{*})^{2}]^{4}}$ and $\bar{b}_{40} \doteq -\frac{a^{2}b x^{*}y^{*}[10a (x^{*})^{2}-a^{2}(x^{*})^{4}-5]}{[1+a (x^{*})^{2}]^{5}}$. Then, we transform the linear part of system (2.30) to the Jordan canonical form. Let

$$\begin{aligned} u=x \ \ \mathrm {and} \ \ v=\bar{a}_{10}x+\bar{b}_{01}y, \end{aligned}$$

rewrite (u, v) as (x, y), then system (2.30) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{d x}{dt}=y+\bar{c}_{20}x^{2}+\bar{c}_{11}xy+\bar{c}_{30}x^{3}+\bar{c}_{21}x^{2}y+\bar{c}_{40}x^{4}+\bar{c}_{31}x^{3}y+ O(|x,y|^{5}),\\ &{}\frac{d y}{dt}=\bar{d}_{11} xy+\bar{d}_{30}x^{3}+\bar{d}_{21} x^{2}y+ \bar{d}_{40}x^{4}+\bar{d}_{31}x^{3}y+ O(|x,y|^{5}). \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.31)

where $\bar{c}_{20} \doteq \bar{a}_{20}-\frac{2\bar{a}_{10}\bar{a}_{11}}{\bar{b}_{01}}$, $\bar{c}_{11} \doteq \frac{2\bar{a}_{11}}{\bar{b}_{01}}$, $\bar{c}_{30} \doteq \bar{a}_{30}-\frac{\bar{a}_{10}\bar{a}_{21}}{\bar{b}_{01}}$, $\bar{c}_{21} \doteq \frac{\bar{a}_{21}}{\bar{b}_{01}}$, $\bar{c}_{40} \doteq \bar{a}_{40}-\frac{\bar{a}_{10}\bar{a}_{31}}{\bar{b}_{01}}$, $\bar{c}_{31} \doteq \frac{\bar{a}_{31}}{\bar{b}_{01}}$, $\bar{d}_{11} \doteq 2\bar{b}_{11}+\frac{2\bar{a}_{10}\bar{a}_{11}}{\bar{b}_{01}}$, $\bar{d}_{30} \doteq \bar{a}_{10}\bar{a}_{30}+\bar{b}_{01}\bar{b}_{30}-\frac{\bar{a}^{2}_{10}\bar{a}_{21}}{\bar{b}_{01}}-\bar{a}_{10}\bar{b}_{21}$, $\bar{d}_{21} \doteq \bar{b}_{21}+\frac{\bar{a}_{10}\bar{a}_{21}}{\bar{b}_{01}}$, $\bar{d}_{40} \doteq \bar{a}_{10}\bar{a}_{40}-\bar{a}_{10}\bar{b}_{31}+\bar{b}_{01}\bar{b}_{40}-\frac{\bar{a}^{2}_{10}\bar{a}_{31}}{\bar{b}_{01}}$ and $\bar{d}_{31} \doteq \bar{b}_{31}+\frac{\bar{a}_{10}\bar{a}_{31}}{\bar{b}_{01}}$. Further, we take $u=x$ and $v=\frac{dy}{dt}$, rewrite (u, v) as (x, y), then system (2.31) is transformed into

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{d x}{dt}=&{}y,\\ \frac{d y}{dt}=&{}\bar{e}_{11} xy+\bar{e}_{02}y^{2}+ \bar{e}_{30}x^{3}+\bar{e}_{21} x^{2}y+ \bar{e}_{12}xy^{2}+\bar{e}_{40}x^{4}+\bar{e}_{31}x^{3}y + \bar{e}_{22}x^{2}y^{2}+ O(|x,y|^{5}), \end{aligned} \end{array}\right. } \end{aligned}$$

(2.32)

where $\bar{e}_{11} \doteq 2\bar{c}_{20}+\bar{d}_{11}$, $\bar{e}_{02} \doteq \bar{c}_{11}$, $\bar{e}_{30} \doteq \bar{d}_{30}-\bar{c}_{20}\bar{d}_{11}$, $\bar{e}_{21} \doteq -\bar{c}_{11}\bar{c}_{20}+3\bar{c}_{30}+\bar{d}_{21}$, $\bar{e}_{12} \doteq 2\bar{c}_{21}-\bar{c}_{11}^{2}$, $\bar{e}_{40} \doteq \bar{c}_{11}\bar{d}_{30}-\bar{c}_{20}\bar{d}_{21}-\bar{c}_{30}\bar{d}_{11}+\bar{d}_{40}$, $\bar{e}_{31} \doteq \bar{c}_{11}^{2}\bar{c}_{20}-\bar{c}_{11}\bar{c}_{30}-2\bar{c}_{20}\bar{c}_{21}+4\bar{c}_{40}+\bar{d}_{31}$ and $\bar{e}_{22} \doteq \bar{c}_{11}^{3}-3\bar{c}_{11}\bar{c}_{21}+3\bar{c}_{31}$.

For system (2.32), there are

$$\begin{aligned} \bar{e}_{11}=2\bar{c}_{20}+\bar{d}_{11}=-\frac{H'(x^{*})}{1+a (x^{*})^{2}} \end{aligned}$$

and

$$\begin{aligned} \bar{e}_{30}=\bar{d}_{30}-\bar{c}_{20}\bar{d}_{11}=-\frac{acx^{*}}{1+a(x^{*})^{2}}. \end{aligned}$$

If $H'(x^{*})\ne 0$, then $\bar{e}_{11}\ne 0$ and system (2.32) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{d x}{dt}=&{} y,\\ \frac{d y}{dt}=&{} \bar{e}_{30}x^{3}\left( 1 + \frac{\bar{e}_{40}}{\bar{e}_{30}} x \right) +\bar{e}_{11}xy \left( 1+\frac{\bar{e}_{21}}{\bar{e}_{11}}x+\frac{\bar{e}_{31}}{\bar{e}_{11}}x^{2}\right) +y^{2}\left( \bar{e}_{02}+\bar{e}_{12}x \right) +\bar{e}_{22}x^{2}y^{2}+O(|x,y|^{5}). \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.33)

A further calculation yields

$$\begin{aligned} G_{0}\doteq \bar{e}_{11}^{2}+8\bar{e}_{30}=\frac{[H'(x^{*})]^{2}-8acx^{*}[1+a(x^{*})^{2}]}{[1+a(x^{*})^{2}]^{2}}. \end{aligned}$$

It follows from Theorems 7.1–7.3 in [25] that $(x^{*},y^{*})$ is a degenerate focus (or center) if $G_{0}< 0$ (i.e., $(H'(x^{*}))^{2}< 8acx^{*}[1+a(x^{*})^{2}]$), a degenerate elliptic equilibrium consisting of one hyperbolic sector and one elliptic sector if $G_{0}\ge 0$ (i.e., $(H'(x^{*}))^{2}\ge 8acx^{*}[1+a(x^{*})^{2}]$). If $H'(x^{*})= 0$, then $\bar{e}_{11}= 0$ and system (2.32) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{d x}{dt}=y,\\ &{}\frac{d y}{dt}= \bar{e}_{30}x^{3}\left( 1 + \frac{\bar{e}_{40}}{\bar{e}_{30}} x \right) + x^{2}y \left( \bar{e}_{21}+ \bar{e}_{31} x\right) +y^{2}\left( \bar{e}_{02}+\bar{e}_{12}x+\bar{e}_{22}x^{2}\right) +O(|x,y|^{5}). \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.34)

Therefore, $(x^{*},y^{*})$ is a degenerate focus (or center) according to Theorems 7.1–7.3 in [25]. This completes the proof. $\square$

Remark 2.3

When $d<c$, i.e., $\tau <\frac{r \delta }{\beta }$, system (1.2) can have multiple positive equilibria while the boundary equilibrium $E_{0}$ is an unstable. This means that the prey will always coexist with the predator when the constant releasing rate is small than the critical value $\frac{r \delta }{\beta }$, i.e., the predator can not eliminate the prey in spite of the constant releasing of predators.

3 Bifurcations

In this section, we investigate the bifurcations of system (1.2), including transcritical, saddle-node, Hopf, degenerate Hopf, Bogdanov–Takens and cusp bifurcations.

3.1 The Transcritical Bifurcation and Saddle-Node Bifurcation

Theorem 3.1

(i):

System (1.2) undergoes a transcritical bifurcation at $d=c$ (i.e., $\tau =\frac{r \delta }{\beta }$);

(ii):

If $d<c$, $\Delta >0$, $F(x^{*}_{1})=0$ and $H(x^{*}_{1})\ne 0$ (or $\Delta >0$, $x^{*}_{2}<1$, $F(x^{*}_{2})=0$ and $H(x^{*}_{2})\ne 0$), then $(x^{*}_{1},y^{*}_{1})$ (or $(x^{*}_{2},y^{*}_{2})$) is a saddle-node of codimension 1 and system (1.2) undergoes a saddle-node bifurcation at this point.

Proof

• (i) It follows from Table 1 and Theorem 2.1 that the positive equilibrium $E_{1}(x_{1},y_{1})$ collides with the boundary equilibrium $E_{0}(0,\frac{d}{c})$ when $d=c$ (i.e., $\tau =\frac{r \delta }{\beta }$). Let $d=d^{*}+\varepsilon$ and substitute it into system (1.2) while $\varepsilon =0$ corresponding to $d=c$, we have

  $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}= x(1-x)-\frac{x y}{1+a x^{2}},\\ &{}\frac{dy}{dt}=\frac{b x y}{1+a x^{2}}-c y+d^{*}+\varepsilon . \end{aligned} \end{array}\right. } \end{aligned}$$

  (3.1)

  Linearizing system (3.1) at $E_{0}(0,\frac{d}{c})$ and diagonalizing the linear part, then system (3.1) is transformed into

  $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=-\left( 1+\frac{b}{c}\right) x^{2}+ \frac{b}{c} x y + O(|x,y|^{3}),\\ &{}\frac{dy}{dt}=- c \varepsilon -cy-b\left( 1+b+\frac{b}{c}\right) x^{2}+b\left( 1+\frac{b}{c}\right) xy+ O(|x,y|^{3}). \end{aligned} \end{array}\right. } \end{aligned}$$

  (3.2)

  By the Liapunov–Schmidt Method introduced in [28], system (3.2) reduced to the center manifold takes the following form:

  $$\begin{aligned} \frac{dx}{dt}=-\frac{ b }{c}\varepsilon x-\left( 1+\frac{b}{c}\right) x^{2}+O(x^{3}). \end{aligned}$$

  (3.3)

  Denote the right side of system (3.3) as $G(x,\varepsilon )$, we have

  $$\begin{aligned} G(x,\varepsilon )|_{(0,0)}= & {} 0, \ G_{x}(x,\varepsilon )|_{(0,0)}=0,\ G_{\varepsilon }(x,\varepsilon )|_{(0,0)}=0, \\ G_{x \varepsilon }(x,\varepsilon )|_{(0,0)}= & {} -\frac{ b }{c}\ \ \mathrm {and} \ \ G_{x x}(x,\varepsilon )|_{(0,0)}=-2\left( 1+\frac{b}{c}\right) . \end{aligned}$$

  Therefore, system (1.2) undergoes a transcritical bifurcation, correspondingly, $TB:=\{(a, b, c, d)| d=c \}$ is the transcritical bifurcation surface of system (1.2).

• (ii) The proof is similar to those of Theorem 2.3, we omit them here. Particularly,

  $$\begin{aligned} SN_{1}:=\{(a,b,c,d)| d<c,\ \Delta >0, \ F(x^{*}_{1})=0 \ \mathrm {and} \ H(x^{*}_{1})\ne 0 \} \end{aligned}$$

  is the saddle-node bifurcation surface. Further,

  $$\begin{aligned} BT_{1}:=\{(a,b,c,d)|d<c,\ \Delta >0, \ F(x^{*}_{1})=0 \ \mathrm {and} \ H(x^{*}_{1})=0 \} \end{aligned}$$

  is called a Bogdanov–Takens bifurcation surface of system (1.2), which will be discussed in more detail in Sect. 3.3. Similarly, we have another saddle-node bifurcation surface

  $$\begin{aligned} SN_{2}:=\{(a,b,c,d)| \Delta >0, \ x^{*}_{2}<1, \ F(x^{*}_{2})=0 \ \mathrm {and} \ H(x^{*}_{2})\ne 0 \} \end{aligned}$$

  and another Bogdanov–Takens bifurcation surface

  $$\begin{aligned} BT_{2}:=\{(a,b,c,d)| \Delta >0, \ x^{*}_{2}<1, \ F(x^{*}_{2})=0 \ \mathrm {and} \ H(x^{*}_{2})=0 \}. \end{aligned}$$

  The proof is completed. $\square$

3.2 Hopf Bifurcation and Degenerate Hopf Bifurcation of Codimension 2

Based on the analyses in Sect. 2, we know that $E_{i}(x_{i},y_{i})$ $(i=1,3)$ is a weak focus or center when $H(x_{i})=0$, which indicates that a Hopf bifurcation may occur at these equilibria. Without loss of generality, in this section, we only discuss the Hopf bifurcation at $E_{1}(x_{1},y_{1})$. The necessary condition of Hopf bifurcation requires that $H(x_{1})=0$, and the properties of function H(x) is concluded as the following.

Lemma 3.1

If $H(x_{1})=0$, then $H'(x_{1})=0$ if and only if $x_{1}=\frac{(2a-ac)+\sqrt{\Delta _{*}}}{9a}$ with $\Delta _{*}=(2a-ac)^{2}+9a(b-1)>0$.

The proof is shown in “Appendix A”.

According to the formula for the third focal value (i.e., the first Liapunov number $\sigma _{1}$) at the positive equilibrium $E_{1}$ of system (1.2) in [24], we have

$$\begin{aligned} \sigma _{1} =\frac{3 \pi }{2q_{E_{1}}^{\frac{3}{2}}} \left[ \frac{2a -4ac + (ab-10a)x_{1}}{(1+a x^{2}_{1})^{2}} q_{E_{1}} - \frac{ (ac+b) x_{1}-3acx^{2}_{1}}{(1+a x^{2}_{1})^{2}} H'(x_{1}) \right] . \end{aligned}$$

Based on the properties of $H(x_{1})$, we get the following results.

Theorem 3.2

System (1.2) undergoes a Hopf bifurcation if $H(x_{1})=0$. Particularly, if $\sigma _{1} \ne 0$, then $E_{1}(x_{1},y_{1})$ is a multiple focus of multiplicity 1, and one limit cycle arises from the Hopf bifurcation in the neighborhood of $E_{1}$ as parameter varies. In more details, $E_{1}$ is stable and a stable limit cycle exists when $\sigma _{1}<0$; $E_{1}$ is unstable and an unstable limit cycle exists when $\sigma _{1}>0$.

Proof

From Sect. 2, the characteristic equation related to $E_{1}(x_{1},y_{1})$ is given by

$$\begin{aligned} |\mathbf{A} |_{E_{1}}-\lambda \mathbf{E} |=\lambda ^{2}+p_{E_{1}}\lambda +q_{E_{1}}=0. \end{aligned}$$

(3.4)

Choosing d as the bifurcation parameter, and taking $q_{E_{1}}$, $p_{E_{1}}$ and $x_{1}$ as the functions of d, we have

$$\begin{aligned} q_{E_{1}}(d)\doteq q_{E_{1}}(x_{1}(d),d)=\frac{x_{1}(d)F'(x_{1}(d))}{1+a (x_{1}(d))^{2}} \end{aligned}$$

and

$$\begin{aligned} p_{E_{1}}(d)\doteq p_{E_{1}}(x_{1}(d),d)=\frac{H(x_{1}(d))}{1+a (x_{1}(d))^{2}}. \end{aligned}$$

Let $\lambda (d) = \mu (d)+i\omega (d)$ be a complex root of the characteristic equation (3.4), and suppose that there exists a critical value $d=d^{*}$ such that $H(x_{1}(d^{*}))=0$ (i.e., $p_{E_{1}}(d^{*})=0$), that is, characteristic equation (3.4) has a pair of pure imaginary roots. Thus, there are $\mu (d^{*})=0$ and $\omega (d^{*})=\sqrt{q_{E_{1}}(d^{*})}$. Then, we obtain

$$\begin{aligned} \mu '(d)|_{d=d^{*}}=-\frac{1}{2(1+a x^{2}_{1})} \frac{\partial H(x_{1}(d))}{\partial x_{1}} \frac{\partial x_{1}(d)}{\partial d} \bigg |_{d=d^{*}}, \end{aligned}$$

(3.5)

where $\frac{\partial x_{1}(d)}{\partial d}\big |_{d=d^{*}}=-\frac{1}{F'(x_{1}(d^{*}))}<0$. From Lemma 3.1, we find that when $x_{1} \ne \frac{(2a-ac)+\sqrt{\Delta _{*}}}{9a}$, then there are

$$\begin{aligned} \frac{\partial H(x_{1}(d))}{\partial x_{1}} \bigg |_{x=x_{1}} \ne 0 \ \mathrm {and} \ \mu '(d)|_{d=d^{*}}\ne 0. \end{aligned}$$

Therefore, the transversality condition is satisfied at $d=d^{*}$ and system (1.2) undergoes a Hopf bifurcation at $d=d^{*}$ if $x_{1} \ne \frac{(2a-ac)+\sqrt{\Delta _{*}}}{9a}$.

In addition, when $x_{1}=\frac{(2a-ac)+\sqrt{\Delta _{*}}}{9a}$, we alternatively choose c as the bifurcation parameter. Suppose that there exists a critical value $c=c^{*}$ such that $H(x_{1}(c^{*}))=0$, with the analogous calculations we have $\mu '(c)|_{c=c^{*}}=-\frac{1}{2}$. Therefore, system (1.2) undergoes a Hopf bifurcation at $c=c^{*}$ when $x_{1}=\frac{(2a-ac)+\sqrt{\Delta _{*}}}{9a}$. Note that, by choosing b as the bifurcation parameter, we can get the similar result for $x_{1}=\frac{(2a-ac)+\sqrt{\Delta _{*}}}{9a}$. As a conclusion, system (1.2) undergoes a Hopf bifurcation at $H(x_{1})=0$.

Furthermore, if $\sigma _{1}<0$, then $E_{1}$ is a stable multiple focus of multiplicity 1, hence system (1.2) undergoes a supercritical Hopf bifurcation and there is a unique and stable limit cycle as parameter varies; If $\sigma _{1}>0$, $E_{1}$ is an unstable multiple focus of multiplicity 1, then system (1.2) undergoes a subcritical Hopf bifurcation and there is a unique and unstable limit cycle as parameter varies. This completes the proof. $\square$

Note that, if $\sigma _{1}=0$, then $E_{1}$ is a multiple focus of multiplicity at least 2 and system (1.2) may undergo a degenerate Hopf bifurcation. Then the nth order Liapunov number $\sigma _{n}$ should be calculated, $n=1,2,3, \dots$. And when $\sigma _{i}=0$, $i=1,2,\dots ,n-1$ and $\sigma _{n}\ne 0$, we can obtain that $E_{1}$ is a multiple focus of multiplicity n, which means system (1.2) undergoes a degenerate Hopf bifurcation of codimension n, and there exist at most n limit cycles in the neighborhood of $E_{1}$. Using the formal series method in [25, 26], when $\sigma _{1}=0$, we obtain the second Liapunov number as follows

$$\begin{aligned} \sigma _{2} =-\frac{1}{16 A^{\frac{5}{2}}_{1}}\left[ \left( \frac{5}{3}A_{2}A_{3}-A_{1}A_{4}\right) \left( 6ax_{1}+ac-2a-\frac{c}{x^{2}_{1}}\right) + \left( \frac{5}{3}A_{2}+\frac{A_{1}}{x_{1}}\right) \frac{A_{1}c}{x^{4}_{1}} \right] , \end{aligned}$$

where

$$\begin{aligned}&A_{1}\doteq \frac{(1+ax^{2}_{1})F'(x_{1})}{x_{1}},\ A_{2}\doteq 6a^{2}cx^{2}_{1}-3(a^{2}c+ab)x_{1}+ab+ac+\frac{B}{x^{2}_{1}}, \\&A_{3}\doteq 4a^{2}cx_{1}-a^{2}c-ab+\frac{ac}{x_{1}}-\frac{B}{x^{3}_{1}},\ A_{4}\doteq a^{2}c-\frac{ac}{x^{2}_{1}}+\frac{B}{x^{4}_{1}} \\&\quad \mathrm {and} \ B\doteq (ac+b)x_{1}-b-c. \end{aligned}$$

Further, if $\sigma _{1}=0$ and $\sigma _{2} \ne 0$, there can be at most two limit cycles arise from the degenerate Hopf bifurcation of codimension 2 (i.e., the Bautin bifurcation). The existence of the limit cycle is shown in Fig. 4a–c. Since the expression of $\sigma _{2}$ is complex, it is difficult to determine the sign of $\sigma _{2}$ and the codimension of the most degenerate Hopf bifurcation for system (1.2). We leave this problem as future work.

According to the above analyses, we have the following theorem.

Theorem 3.3

System (1.2) undergoes a degenerate Hopf bifurcation of codimension 2 if $H(x_{1})=0$ when $\sigma _{1}=0$ and $\sigma _{2}\ne 0$. And $E_{1}(x_{1},y_{1})$ is a multiple focus of multiplicity 2, which is stable (unstable) as $\sigma _{2}<0$ ($\sigma _{2}>0$, respectively). Moreover, there exist at most two limit cycles arising form the Hopf bifurcation in the neighborhood of $E_{1}$, one is stable and another is unstable.

Fig. 4

a A stable limit cycle created by the supercritical Hopf bifurcation with $a=5$, $b=1$, $c=0.348$ and $d=0.14$. b An unstable limit cycle created by the subcritical Hopf bifurcation with $a=16$, $b=2.8$, $c=0.5$ and $d=0.25$. c Two limit cycles created by the degenerate Hopf bifurcation of codimension 2 (i.e., the Bautin bifurcation), the inner one is unstable and the outer one is stable with $a=5$, $b=1$, $c=0.312$ and $d=0.115403$

3.3 The Bogdanov–Takens (Cusp Type) Bifurcation of Codimension 3

As we discussed above, system (1.2) may exhibit a degenerate positive equilibrium $(x^{*}_{1},y^{*}_{1})$ (or $(x^{*}_{2},y^{*}_{2})$), which is a cusp of codimension 2 (or 3) in different parameter spaces. This means that system (1.2) can admit a Bogdanov–Takens bifurcation of codimension 2 (or 3) under a small parameter perturbation. Without loss of generality, we only study the bifurcation around the cusp $(x^{*}_{1},y^{*}_{1})$, which is a cusp of codimension 2 if the parameters satisfy

$$\begin{aligned} d<c,\ \Delta >0, \ F(x^{*}_{1})=0, \ H(x^{*}_{1})=0 \ \mathrm {and} \ H'(x^{*}_{1})\ne 0, \end{aligned}$$

(3.6)

a cusp of codimension 3 if the parameters satisfy

$$\begin{aligned} d<c,\ \Delta >0, \ F(x^{*}_{1})=0, \ H(x^{*}_{1})=0, \ H'(x^{*}_{1})=0 \ \mathrm {and} \ N_{0}(x^{*}_{1})\ne 0, \end{aligned}$$

(3.7)

i.e.,

$$\begin{aligned} \begin{aligned} d<c, \ \Delta >0, (a,b)&=\left( -\frac{2x^{*}_{1}-1}{[12(x^{*}_{1})^{2}-15x^{*}_{1}+4]x^{*}_{1}}, \right. \\&\quad \left. -\frac{2x^{*}_{1}(x^{*}_{1}-1)(3x^{*}_{1}-1)^{2}}{[12(x^{*}_{1})^{2}-15x^{*}_{2}+4][7(x^{*}_{1})^{2}-8x^{*}_{1}+2]}\right) , \\ (c,d)&=\left( -\frac{x^{*}_{1}(3x^{*}_{1}-1)(2x^{*}_{1}-1)}{7(x^{*}_{1})^{2}-8x^{*}_{1}+2}, \frac{2x^{*}_{1}(3x^{*}_{1}-1)(x^{*}_{1}-1)^{2}}{12(x^{*}_{1})^2-15x^{*}_{1}+4} \right) \\&\quad \mathrm {and} \ N_{0}(x^{*}_{1})\ne 0. \end{aligned}\nonumber \\ \end{aligned}$$

(3.8)

As the Bogdanov–Takens bifurcation of codimension 2 is included in the Bogdanov–Takens bifurcation of codimension 3 [20]. Therefore, here we only provided the detailed proof for the Bogdanov–Takens bifurcation of codimension 3. Choosing b, c and d as bifurcation parameters and fix $a=a_{0}$, we will show that system (1.2) can undergo a Bogdanov–Takens bifurcation of codimension 3 in a small neighborhood of equilibrium $(x^{*}_{1},y^{*}_{1})$ as parameters (b, c, d) varies in a small neighborhood of $(b_{0},c_{0},d_{0})$, where $(a_{0},b_{0},c_{0},d_{0})$ satisfies the conditions in (3.7) (or (3.8)).

Theorem 3.4

Assume that the conditions in (3.7) are satisfied, then the degenerate equilibrium $(x^{*}_{1},y^{*}_{1})$ is a cusp of codimension 3. Choosing b, c and d as bifurcation parameters, then system (1.2) undergoes a Bogdanov–Takens (cusp type) bifurcation of codimension 3 in a small neighborhood of $(x^{*}_{1},y^{*}_{1})$ as (b, c, d) varies near $(b_{0},c_{0},d_{0})$. More precisely,

(i):

if $N_{0}(x^{*}_{1})<0$, then system (1.2) can exhibit the co-existence of a stable homoclinic loop and an unstable limit cycle, co-existence of two limit cycles (the inner one unstable and the outer stable), and the existence of a semi-stable limit cycle for different parameter spaces;

(ii):

if $N_{0}(x^{*}_{1})>0$, then system (1.2) can exhibit the co-existence of an unstable homoclinic loop and a stable limit cycle, co-existence of two limit cycles (the inner one stable and the outer unstable), and the existence of a semi-stable limit cycle for different parameter spaces.

Proof

Substituting a, b, c and d by $a_{0}$, $b_{0}-\varepsilon _{1}$, $c_{0}-\varepsilon _{2}$ and $d_{0}-\varepsilon _{3}$ into system (1.2), it becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=x(1-x)-\frac{x y}{1+a_{0} x^{2}},\\ &{}\frac{dy}{dt}=\frac{(b_{0}-\varepsilon _{1})x y}{1+a_{0} x^{2}}-(c_{0}-\varepsilon _{2}) y+(d_{0}-\varepsilon _{3}), \end{aligned} \end{array}\right. } \end{aligned}$$

(3.9)

where $\varepsilon _{1}$, $\varepsilon _{2}$ and $\varepsilon _{3}$ are very small parameters ($0<|\varepsilon _{i}| \ll 1, i=1,2,3$). Then translating the positive equilibrium $(x^{*}_{1},y^{*}_{1})$ to the origin, and expanding the right-hand side of system (3.9) in a Taylor series up to the fourth order around the origin, we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{dx}{dt}&{}=\tilde{a}_{10}x+\tilde{b}_{01}y+\tilde{a}_{20}x^{2}+2\tilde{a}_{11}x y + \tilde{a}_{30}x^3+\tilde{a}_{21}x^{2}y+\tilde{a}_{40}x^{4}+\tilde{a}_{31}x^{3}y + O(|x,y|^{5}),\\ \frac{dy}{dt}&{}= \tilde{b}_{00}+(\tilde{c}_{10}+\tilde{a}_{10}\varepsilon _{1}-\varepsilon _{1}+2 x^{*}_{1} \varepsilon _{1})x+(\tilde{d}_{01}+\tilde{b}_{01}\varepsilon _{1}+\varepsilon _{2})y+(\tilde{b}_{20}+\tilde{a}_{20}\varepsilon _{1}+\varepsilon _{1})x^{2} \\ &{}\quad +2(\tilde{b}_{11}+\tilde{a}_{11} \varepsilon _{1})x y +(\tilde{b}_{30}+\tilde{a}_{30}\varepsilon _{1})x^3+(\tilde{b}_{21}+\tilde{a}_{21} \varepsilon _{1})x^{2}y+(\tilde{b}_{40}+\tilde{a}_{40}\varepsilon _{1})x^{4} \\ &{}\quad +(\tilde{b}_{31}+\tilde{a}_{31}\varepsilon _{1})x^{3}y + O(|x,y,\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}|^{5}), \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.10)

where $\tilde{a}_{10} \doteq \frac{2a_{0}(x^{*}_{1})^{2}(1-x^{*}_{1})}{1+a_{0} (x^{*}_{1})^{2}}-x^{*}_{1}$, $\tilde{b}_{01} \doteq -\frac{x^{*}_{1}}{1+a_{0} (x^{*}_{1})^{2}}$, $\tilde{a}_{20} \doteq -1+\frac{a_{0} x^{*}_{1}y^{*}_{1}[3-a_{0} (x^{*}_{1})^{2}]}{[1+a_{0} (x^{*}_{1})^{2}]^{3}}$, $\tilde{a}_{11} \doteq -\frac{1-a_{0} (x^{*}_{2})^{2}}{2[1+a_{0} (x^{*}_{2})^{2}]^{2}}$, $\tilde{a}_{30} \doteq \frac{a_{0} y^{*}_{1}[1+ a_{0}^{2}(x^{*}_{1})^{4}-6 a_{0} (x^{*}_{1})^{2}]}{[1+ a_{0} (x^{*}_{1})^{2}]^{4}}$, $\tilde{a}_{21} \doteq \frac{a_{0} x^{*}_{1}[3- a_{0} (x^{*}_{1})^{2}]}{[1+a_{0} (x^{*}_{1})^{2}]^{3}}$, $\tilde{a}_{40} \doteq \frac{a_{0}^{2}x^{*}_{1}y^{*}_{1}[10a_{0} (x^{*}_{1})^{2}-a_{0}^{2}(x^{*}_{1})^{4}-5]}{[1+a_{0} (x^{*}_{1})^{2}]^{5}}$, $\tilde{a}_{31} \doteq \frac{a_{0} [1+ a_{0}^{2}(x^{*}_{1})^{4}-6 a_{0} (x^{*}_{1})^{2}]}{[1+a_{0} (x^{*}_{1})^{2}]^{4}}$, $\tilde{b}_{00}\doteq -\frac{\varepsilon _{1} x^{*}_{1}y^{*}_{1}}{1+a_{0}(x^{*}_{1})^{2}}+\varepsilon _{2}y^{*}_{1}-\varepsilon _{3}$, $\tilde{c}_{10} \doteq \frac{b_{0} y^{*}_{1}[1-a_{0} (x^{*}_{1})^{2}]}{[1+a_{0} (x^{*}_{1})^{2}]^{2}}$, $\tilde{d}_{01} \doteq \frac{b_{0} x^{*}_{1}}{1+a_{0} (x^{*}_{1})^{2}}$, $\tilde{b}_{20} \doteq \frac{a_{0}b_{0} x^{*}_{1}y^{*}_{1}[a_{0} (x^{*}_{1})^{2}-3]}{[1+a_{0} (x^{*}_{1})^{2}]^{3}}$, $\tilde{b}_{11} \doteq \frac{b_{0}[1-a_{0} (x^{*}_{1})^{2}]}{2[1+a_{0} (x^{*}_{1})^{2}]^{2}}$, $\tilde{b}_{30} \doteq \frac{a_{0}b_{0} y^{*}_{1}[6 a_{0} (x^{*}_{1})^{2}- a_{0}^{2}(x^{*}_{1})^{4}-1]}{[1+ a_{0} (x^{*}_{1})^{2}]^{4}}$, $\tilde{b}_{21} \doteq \frac{a_{0}b_{0} x^{*}_{1}[a_{0} (x^{*}_{1})^{2}-3]}{[1+a_{0} (x^{*}_{1})^{2}]^{3}}$, $\tilde{b}_{31} \doteq \frac{a_{0} b_{0} [6 a_{0} (x^{*}_{1})^{2}- a_{0}^{2}(x^{*}_{1})^{4}-1]}{[1+a_{0} (x^{*}_{1})^{2}]^{4}}$, $\tilde{b}_{40} \doteq -\frac{a_{0}^{2}b_{0} x^{*}_{1}y^{*}_{1}[10a_{0} (x^{*}_{1})^{2}-a_{0}^{2}(x^{*}_{1})^{4}-5]}{[1+a_{0} (x^{*}_{1})^{2}]^{5}}$, and $O(|x,y,\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}|^{5})$ is a function in variables (x, y) at least of the fifth order with respect to (x, y) and the coefficients depend smoothly on $\varepsilon _{1}$, $\varepsilon _{2}$ and $\varepsilon _{3}$. Further, let $u=x$ and $v=\frac{dx}{dt}$, rewrite (u, v) as (x, y), then system (3.10) can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{dx}{dt}&{}=y,\\ \frac{dy}{dt}&{}=\tilde{e}_{00}+\tilde{e}_{10}x+\tilde{e}_{01}y+\tilde{e}_{20}x^{2}+\tilde{e}_{11}x y +\tilde{e}_{02}y^{2}+ \tilde{e}_{30}x^3+\tilde{e}_{21}x^{2}y\\ &{}\quad +\tilde{e}_{12}xy^{2}+\tilde{e}_{40}x^{4}+\tilde{e}_{31}x^{3}y +\tilde{e}_{22}x^{2}y^{2}+ O(|x,y,\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}|^{5}), \end{aligned} \end{array}\right. } \end{aligned}$$

(3.11)

where $\tilde{e}_{00}\doteq \tilde{b}_{00}\tilde{b}_{01}$, $\tilde{e}_{10}\doteq (2x^{*}_{1}-1)\tilde{b}_{01}\varepsilon _{1}- \tilde{a}_{10}\varepsilon _{2}$, $\tilde{e}_{01}\doteq \tilde{b}_{01} \varepsilon _{1}+\varepsilon _{2}$, $\tilde{e}_{20}\doteq -2 \bar{a}_{10}\bar{b}_{11}+2 \bar{a}_{11} \bar{c}_{10}-\bar{a}_{20} \bar{d}_{01}+\bar{b}_{01} \bar{b}_{20}+ (-2\tilde{a}_{11}+4\tilde{a}_{11}x^{*}_{1}+\tilde{b}_{01})\varepsilon _{1}-\tilde{a}_{20}\varepsilon _{2}+\tilde{a}_{21}\tilde{b}_{00}$, $\tilde{e}_{11}\doteq 2 \tilde{a}_{11}\varepsilon _{1}$, $\tilde{e}_{02}\doteq \frac{2\tilde{a}_{11}}{\tilde{b}_{01}}$, $\tilde{e}_{30}\doteq -\tilde{a}_{10}\tilde{b}_{21}+2\tilde{a}_{11}\tilde{b}_{20}-2\tilde{a}_{20}\tilde{b}_{11}+\tilde{a}_{21}\tilde{c}_{10}-\tilde{a}_{30}\tilde{d}_{01}+\tilde{b}_{01}\tilde{b}_{30}+\tilde{a}_{31} \tilde{b}_{00}+(2\tilde{a}_{11}-\tilde{a}_{21}+2\tilde{a}_{21}x^{*}_{1})\varepsilon _{1}-\tilde{a}_{30}\varepsilon _{2}$, $\tilde{e}_{21}\doteq \tilde{b}_{21}+3\tilde{a}_{30}-\frac{2\tilde{a}_{20}\tilde{a}_{11}}{\tilde{b}_{01}}-\frac{2\tilde{a}_{10}\tilde{a}_{21}}{\tilde{b}_{01}}+\frac{4\tilde{a}_{10}\tilde{a}^{2}_{11}}{\tilde{b}^{2}_{01}}+ \tilde{a}_{21}\varepsilon _{1}$, $\tilde{e}_{12}\doteq \frac{2\tilde{a}_{21}}{\tilde{b}_{01}}-\frac{4\tilde{a}^{2}_{11}}{\tilde{b}^{2}_{01}}$, $\tilde{e}_{40}\doteq -\tilde{a}_{10}\tilde{b}_{31}+2\tilde{a}_{11}\tilde{b}_{30}-\tilde{a}_{20}\tilde{b}_{21}+\tilde{a}_{21}\tilde{b}_{20}-2\tilde{a}_{30}\tilde{b}_{11}+\tilde{a}_{31}\tilde{c}_{10}-\tilde{a}_{40}\tilde{d}_{01}+\tilde{b}_{01}\tilde{b}_{40}+(\tilde{a}_{21}-\tilde{a}_{31}+2\tilde{a}_{31}x^{*}_{1})\varepsilon _{1}-\tilde{a}_{40}\varepsilon _{2}$, $\tilde{e}_{31}\doteq \tilde{b}_{31}+4\tilde{a}_{40}-\frac{2\tilde{a}_{20}\tilde{a}_{21}}{\tilde{b}_{01}}-\frac{2\tilde{a}_{11}\tilde{a}_{30}}{\tilde{b}_{01}}-\frac{3\tilde{a}_{10}\tilde{a}_{31}}{\tilde{b}_{01}}+\frac{4\tilde{a}^{2}_{11}\tilde{a}_{20}}{\tilde{b}^{2}_{01}}+ \frac{6\tilde{a}_{10}\tilde{a}_{11}\tilde{a}_{21}}{\tilde{b}^{2}_{01}}-\frac{8\tilde{a}_{10}\tilde{a}^{3}_{11}}{\tilde{b}^{3}_{01}}+ \tilde{a}_{31}\varepsilon _{1}$ and $\tilde{e}_{22}\doteq \frac{3\tilde{a}_{31}}{\tilde{b}_{01}}-\frac{6\tilde{a}_{11}\tilde{a}_{21}}{\tilde{b}^{2}_{01}}+\frac{8\tilde{a}^{3}_{11}}{\tilde{b}^{3}_{01}}$.

Next, in order to find the universal unfolding of the cusp of codimension 3, we follow the procedure in [19, 29] by the following steps:

(i):

Simplifying the $y^{2}$-term in system (3.11). Making the following change of variables

$$\begin{aligned} x=u+\frac{\tilde{e}_{02}}{2}u^{2} \ \ \mathrm {and} \ \ y=v+\tilde{e}_{02} u v, \end{aligned}$$

rewrite (u, v) as (x, y), then system (3.11) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{dx}{dt}&{}=y,\\ \frac{dy}{dt}&{}=\tilde{f}_{00}+\tilde{f}_{10}x+\tilde{f}_{01}y+\tilde{f}_{20}x^{2}+\tilde{f}_{11}xy + \tilde{f}_{30}x^3+\tilde{f}_{21}x^{2}y+\tilde{f}_{12}xy^{2}\\ &{}\quad +\tilde{f}_{40}x^{4} +\tilde{f}_{31}x^{3}y + R(x,y,\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}), \end{aligned} \end{array}\right. } \end{aligned}$$

(3.12)

where $\tilde{f}_{00}\doteq \tilde{e}_{00}$, $\tilde{f}_{10}\doteq \tilde{e}_{10}-\tilde{e}_{00}\tilde{e}_{02}$, $\tilde{f}_{01}\doteq \tilde{e}_{01}$, $\tilde{f}_{20}\doteq \tilde{e}_{20}+\tilde{e}_{00}\tilde{e}^{2}_{02}-\frac{\tilde{e}_{10}\tilde{e}_{02}}{2}$, $\tilde{f}_{11}\doteq \tilde{e}_{11}$, $\tilde{f}_{30}\doteq \tilde{e}_{30}-\tilde{e}_{00}\tilde{e}^{3}_{02}+\frac{\tilde{e}_{10}\tilde{e}^{2}_{02}}{2}$, $\tilde{f}_{21}\doteq \tilde{e}_{21}+ \frac{\tilde{e}_{11}\tilde{e}_{02}}{2}$, $\tilde{f}_{12}\doteq \tilde{e}_{12}+2\tilde{e}^{2}_{02}$, $\tilde{f}_{40}\doteq \tilde{e}_{40}+\tilde{e}_{00}\tilde{e}^{4}_{02}-\frac{\tilde{e}_{10}\tilde{e}^{3}_{02}}{2}+\frac{\tilde{e}_{02}\tilde{e}_{30}}{2}+\frac{\tilde{e}_{20}\tilde{e}^{2}_{02}}{4}$, $\tilde{f}_{31}\doteq \tilde{e}_{31}+\tilde{e}_{02}\tilde{e}_{21}$ and $R(x,y,\varepsilon _{1},\varepsilon _{2},\varepsilon _{3})\doteq y^{2}O(|x,y|^{2})+O(|x,y|^{5})+O(|\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}|)(O(y^{2}) +O(|x,y|^{3}))+O(|\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}|^{2})O(|x,y|)$.

(ii):

Simplifying the $xy^{2}$-term in system (3.12). Let

$$\begin{aligned} x=u+ \frac{\tilde{f}_{12}}{6}u^{3} \ \ \mathrm {and} \ \ y=v+ \frac{\tilde{f}_{12}}{2} u^{2} v , \end{aligned}$$

rewrite (u, v) as (x, y), then system (3.12) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{dx}{dt}&{}=y,\\ \frac{dy}{dt}&{}=\tilde{g}_{00}+\tilde{g}_{10}x+\tilde{g}_{01}y+\tilde{g}_{20}x^{2}+\tilde{g}_{11}x y + \tilde{g}_{30}x^3+\tilde{g}_{21}x^{2}y +\tilde{g}_{40}x^{4}\\ &{}\quad +\tilde{g}_{31}x^{3}y+ R(x,y,\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}), \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.13)

where $\tilde{g}_{00}\doteq \tilde{f}_{00}$, $\tilde{g}_{10}\doteq \tilde{f}_{10}$, $\tilde{g}_{01}\doteq \tilde{f}_{01}$, $\tilde{g}_{20}\doteq \tilde{f}_{20}-\frac{\tilde{f}_{00}\tilde{f}_{12}}{2}$, $\tilde{g}_{11}\doteq \tilde{f}_{11}$, $\tilde{g}_{30}\doteq \tilde{f}_{30}-\frac{\tilde{f}_{10}\tilde{f}_{12}}{3}$, $\tilde{g}_{21}\doteq \tilde{f}_{21}$, $\tilde{g}_{40}\doteq \tilde{f}_{40}+\frac{\tilde{f}_{00}\tilde{f}^{2}_{12}}{4}-\frac{\tilde{f}_{20}\tilde{f}_{12}}{6}$ and $\tilde{g}_{31}\doteq \tilde{f}_{31}+\frac{\tilde{f}_{11}\tilde{f}_{12}}{6}$.

(iii):

Simplifying the $x^{3}$ and $x^{4}$-terms in system (3.13). Notice that

$$\begin{aligned} \lim _{\varepsilon _{j}\rightarrow 0}\tilde{g}_{20}= \frac{a_{0}c_{0} x^{*}_{1}}{1+a_{0} (x^{*}_{1})^{2}}\left[ 1+\frac{b_{0}}{a_{0}c_{0}}-3x^{*}_{1} \right] >0, j=1,2,3. \end{aligned}$$

Then we let

$$\begin{aligned} x=u- \frac{\tilde{g}_{30}}{4\tilde{g}_{20}}u^{2}+ \left( \frac{3\tilde{g}^{2}_{30}}{16\tilde{g}^{2}_{20}}-\frac{\tilde{g}_{40}}{5\tilde{g}_{20}} \right) u^{3}, \ \ y=v , \end{aligned}$$

and

$$\begin{aligned} d \tau =\left( 1+\frac{\tilde{g}_{30}}{2\tilde{g}_{20}}u+\frac{48\tilde{g}_{20}\tilde{g}_{40}-25\tilde{g}^{2}_{30}}{80\tilde{g}^{2}_{20}} u^{2} +\frac{48\tilde{g}_{20}\tilde{g}_{30}\tilde{g}_{40}-35\tilde{g}^{3}_{30}}{80\tilde{g}^{3}_{20}} u^{3} \right) dt, \end{aligned}$$

rewrite $(u,v,\tau )$ as (x, y, t), then we obtain the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=y,\\ &{}\frac{dy}{dt}=\tilde{h}_{00}+\tilde{h}_{10}x+\tilde{h}_{01}y+\tilde{h}_{20}x^{2}+\tilde{h}_{11}x y + \tilde{h}_{21}x^{2}y+\tilde{h}_{31}x^{3}y+ R(x,y,\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}), \end{aligned} \end{array}\right. } \end{aligned}$$

(3.14)

where $\tilde{h}_{00}\doteq \tilde{g}_{00}$, $\tilde{h}_{10}\doteq \tilde{g}_{10}-\frac{\tilde{g}_{00}\tilde{g}_{30}}{2\tilde{g}_{20}}$, $\tilde{h}_{01}\doteq \tilde{g}_{01}$, $\tilde{h}_{11}\doteq \tilde{g}_{11}-\frac{\tilde{g}_{01}\tilde{g}_{30}}{2\tilde{g}_{20}}$, $\tilde{h}_{20}\doteq \tilde{g}_{20}-\frac{3\tilde{g}_{10}\tilde{g}_{30}}{4\tilde{g}_{20}}-\frac{3\tilde{g}_{00}\tilde{g}_{40}}{5\tilde{g}_{20}}+\frac{9\tilde{g}_{00}\tilde{g}^{2}_{30}}{16\tilde{g}^{2}_{20}}$, $\tilde{h}_{21}\doteq \tilde{g}_{21}-\frac{3\tilde{g}_{11}\tilde{g}_{30}}{4\tilde{g}_{20}}-\frac{3\tilde{g}_{01}\tilde{g}_{40}}{5\tilde{g}_{20}}+\frac{9\tilde{g}_{01}\tilde{g}^{2}_{30}}{16\tilde{g}^{2}_{20}}$ and $\tilde{h}_{31}\doteq \tilde{g}_{31}+\frac{7\tilde{g}_{11}\tilde{g}^{2}_{30}}{8\tilde{g}^{2}_{20}}-\frac{\tilde{g}_{21}\tilde{g}_{30}}{\tilde{g}_{20}}-\frac{4\tilde{g}_{11}\tilde{g}_{40}}{5\tilde{g}_{20}}$.

(iv):

Simplifying the $x^{2}y$-term in system (3.14). Similarly, we let

$$\begin{aligned} x=u, \ \ y=v+ \frac{\tilde{h}_{21}}{3\tilde{h}_{20}}v^{2}+\frac{\tilde{h}^{2}_{21}}{36\tilde{h}^{2}_{20}}v^{3} \ \ \mathrm {and} \ \ d \tau = \left( 1+ \frac{\tilde{h}_{21}}{3\tilde{h}_{20}}v+\frac{\tilde{h}^{2}_{21}}{36\tilde{h}^{2}_{20}}v^{2} \right) dt, \end{aligned}$$

rewrite $(u,v,\tau )$ as (x, y, t), then system (3.14) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=y,\\ &{}\frac{dy}{dt}=\tilde{k}_{00}+\tilde{k}_{10}x+\tilde{k}_{01}y+\tilde{k}_{20}x^{2}+\tilde{k}_{11}x y +\tilde{k}_{31}x^{3}y+ R(x,y,\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}), \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.15)

where $\tilde{k}_{00}\doteq \tilde{h}_{00}$, $\tilde{k}_{10}\doteq \tilde{h}_{10}$, $\tilde{k}_{01}\doteq \tilde{h}_{01}-\frac{\tilde{h}_{00}\tilde{h}_{21}}{\tilde{h}_{20}}$, $\tilde{k}_{20}\doteq \tilde{h}_{20}$, $\tilde{k}_{11}\doteq \tilde{h}_{11}-\frac{\tilde{h}_{10}\tilde{h}_{21}}{\tilde{h}_{20}}$ and $\tilde{k}_{31}\doteq \tilde{h}_{31}$.

(v):

Changing $\tilde{k}_{20}$ to 1 and $\tilde{k}_{31}$ to sign($M_{2}$) in system (3.15). Notice that

$$\begin{aligned} \lim _{\varepsilon _{j}\rightarrow 0}\tilde{k}_{20}=\frac{a_{0}c_{0} x^{*}_{1}}{1+a_{0} (x^{*}_{1})^{2}}\left[ 1+\frac{b_{0}}{a_{0}c_{0}}-3x^{*}_{1} \right] >0 \end{aligned}$$

and

$$\begin{aligned} \lim _{\varepsilon _{j}\rightarrow 0}\tilde{k}_{31}= \frac{a_{0}c_{0} x^{*}_{1}}{1+a_{0} (x^{*}_{1})^{2}} \left[ 1+\frac{b_{0}}{a_{0}c_{0}}-3x^{*}_{1} \right] M_{2}(x^{*}_{1})\ne 0, \ j=1,2,3. \end{aligned}$$

where $M_{2}(x^{*}_{1})\doteq \frac{(x^{*}_{1}-\frac{1}{2}) N_{0}(x^{*}_{1}) }{x^{*}_{1}(-1+3x^{*}_{1})(5x^{*}_{1}-2)^{2}(x^{*}_{1}-1)^{2}[7(x^{*}_{1})^{2}-8x^{*}_{1}+2][6(x^{*}_{1})^{2}-6x^{*}_{1}+1] } \ne 0$. As it is difficult to directly determine the sign of $M_{2}(x^{*}_{1})$ (i.e., the sign of $N_{0}(x^{*}_{1})$), we make the following transformations

$$\begin{aligned} x=\frac{\tilde{k}^{\frac{1}{5}}_{20}}{\tilde{k}^{\frac{2}{5}}_{31}}u,\ \ y=\mathrm {sign}(M_{2}) \frac{\tilde{k}^{\frac{4}{5}}_{20}}{\tilde{k}^{\frac{3}{5}}_{31}}v \ \ \mathrm {and} \ \ d\tau =\mathrm {sign}(M_{2}) \frac{\tilde{k}^{\frac{3}{5}}_{20}}{\tilde{k}^{\frac{1}{5}}_{31}}dt, \end{aligned}$$

rewrite $(u,v,\tau )$ as (x, y, t), then system (3.15) can be represented as

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{dx}{dt}=y,\\ &{}\frac{dy}{dt}=\tilde{l}_{00}+\tilde{l}_{10}x+\tilde{l}_{01}y+\tilde{l}_{11}x y + x^{2} +\mathrm {sign}(M_{2})x^{3}y+ R(x,y,\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}), \end{aligned} \end{array}\right. } \end{aligned}$$

(3.16)

where $\tilde{l}_{00}\doteq \frac{\tilde{k}_{00}\tilde{k}^{\frac{4}{5}}_{31}}{\tilde{k}^{\frac{7}{5}}_{20}}$, $\tilde{l}_{10}\doteq \frac{\tilde{k}_{10}\tilde{k}^{\frac{2}{5}}_{31}}{\tilde{k}^{\frac{6}{5}}_{20}}$, $\tilde{l}_{01}\doteq \mathrm {sign}(M_{2})\frac{\tilde{k}_{01}\tilde{k}^{\frac{1}{5}}_{31}}{\tilde{k}^{\frac{3}{5}}_{20}}$ and $\tilde{l}_{11}\doteq \mathrm {sign}(M_{2})\frac{\tilde{k}_{11}}{\tilde{k}^{\frac{1}{5}}_{31}\tilde{k}^{\frac{2}{5}}_{20}}$.

(vi):

Simplifying the x-term in system (3.16). Let $x=u-\frac{\tilde{l}_{10}}{2}$ and $y=v$, rewrite (u, v) as (x, y), then system (3.16) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{dx}{dt}&{}=y,\\ \frac{dy}{dt}&{}=\mu _{1}(\varepsilon _{1},\varepsilon _{2},\varepsilon _{3})+\mu _{2}(\varepsilon _{1},\varepsilon _{2},\varepsilon _{3})y+\mu _{3}(\varepsilon _{1},\varepsilon _{2},\varepsilon _{3})x y + x^{2} +\mathrm {sign}(M_{2})x^{3}y \\ &{}\quad + R(x,y,\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}), \end{aligned} \end{array}\right. } \end{aligned}$$

(3.17)

where

$$\begin{aligned} \mu _{1}(\varepsilon _{1},\varepsilon _{2},\varepsilon _{3})\doteq & {} \tilde{l}_{00}-\frac{\tilde{l}^{2}_{10}}{4} =K^{-\frac{7}{5}}_{20}K^{\frac{4}{5}}_{31}(m_{11} \varepsilon _{1}+ m_{12}\varepsilon _{2}+ m_{13}\varepsilon _{3})+O(|\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}|^{2}), \\ \mu _{2}(\varepsilon _{1},\varepsilon _{2},\varepsilon _{3})\doteq & {} \tilde{l}_{01}-\frac{\tilde{l}_{10}\tilde{l}_{11}}{2}-\mathrm {sign}(M_{2})\frac{\tilde{l}^{3}_{10}}{8}\\= & {} \mathrm {sign}(M_{2})K^{-\frac{3}{5}}_{20}K^{\frac{1}{5}}_{31}(m_{21} \varepsilon _{1}+ m_{22}\varepsilon _{2}+ m_{23}\varepsilon _{3})+O(|\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}|^{2}), \\ \mu _{3}(\varepsilon _{1},\varepsilon _{2},\varepsilon _{3})\doteq & {} \tilde{l}_{11}+\mathrm {sign}(M_{2})\frac{3\tilde{l}^{2}_{10}}{4}\\= & {} \mathrm {sign}(M_{2})K^{-\frac{1}{5}}_{20}K^{-\frac{2}{5}}_{31}(m_{31} \varepsilon _{1}+ m_{32}\varepsilon _{2}+ m_{33}\varepsilon _{3})+O(|\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}|^{2}), \end{aligned}$$

$K_{20}=\frac{a_{0}c_{0} x^{*}_{1}}{1+a_{0} (x^{*}_{1})^{2}}\left[ 1+\frac{b_{0}}{a_{0}c_{0}}-3x^{*}_{1} \right]$, $K_{31}=M_{2}K_{20}$, and the coefficients $m_{ij}$ $(i,j=1,2,3)$ are given in “Appendix B”. By lengthy calculations, we can obtain that

$$\begin{aligned} \Bigg | \frac{\partial (\mu _{1},\mu _{2},\mu _{3})(\varepsilon _{1},\varepsilon _{2},\varepsilon _{3})}{\partial (\varepsilon _{1},\varepsilon _{2},\varepsilon _{3})} \Bigg |_{(0,0,0)} =\frac{\lambda M^{\frac{4}{5}}_{2}}{\left( \frac{a_{0}c_{0} x^{*}_{1}}{1+a_{0} (x^{*}_{1})^{2}} \right) ^{\frac{8}{5}} \left[ 1+\frac{b_{0}}{a_{0}c_{0}}-3x^{*}_{1} \right] ^{\frac{8}{5}}}\ne 0 \end{aligned}$$

where $\lambda \doteq \frac{[12(x^{*}_{1})^{2}-15x^{*}_{1}+4]^{2}[7(x^{*}_{1})^{2}-8x^{*}_{1}+2][24(x^{*}_{1})^{3}-33(x^{*}_{1})^{2}+15x^{*}_{1}-2]}{4(3x^{*}_{1}-1)^{2}(x^{*}_{1}-1)^{3}(5x^{*}_{1}-2)^{3}[6(x^{*}_{1})^{2}-6x^{*}_{1}+1]}\ne 0$. Since $x^{*}_{1}\in (\frac{1}{3},\frac{4-\sqrt{2}}{7})$, each factor in $\lambda$ is nonzero. Thus, system (3.17) with $(\mu _{1},\mu _{2},\mu _{3}) \sim (0,0,0)$ for (x, y) near (0, 0) is equivalent to system (1.2) with $(\varepsilon _{1},\varepsilon _{2},\varepsilon _{3}) \sim (0,0,0)$ for (x, y) near $(x^{*}_{1},y^{*}_{1})$. That is, the dynamics of system (1.2) in a small neighborhood of the positive equilibrium $(x^{*}_{1},y^{*}_{1})$ as (b, c, d) varying near $(b_{0},c_{0},d_{0})$ are equivalent to that of system (3.17) in a small neighborhood of (0, 0) as $(\mu _{1},\mu _{2},\mu _{3})$ varying near (0, 0, 0) according to the results in [19, 22, 29]. It is easy to verify that cases (i) and (ii) in this Theorem are true by the results in [27]. This completes the proof. $\square$

Here we carry out some numerical simulations to show that $N_{0}(x^{*}_{1})$ can be positive or negative in different parameter sets. For example, we fix $a=7.103510$, $b=31.062569$, $c=6.078025$ and $d=0.312174$, system (1.2) has a cusp of codimension 3, i.e., $(x^{*}_{1},y^{*}_{1})$=(0.3688,1.2163) with $N_{0}(x^{*}_{1})=0.000033>0$. When $a=6$, $b=2.769934$, $c=0.761079$ and $d=0.227635$, we get ($x^{*}_{1}$,$y^{*}_{1}$)=(0.365085,1.142719) and $N_{0}(x^{*}_{1})=-0.000103<0$. In this case, as bifurcation parameters (b, c, d) varies in a small neighborhood of (2.769934, 0.761079, 0.227635), system (1.2) can exhibit the co-existence of a stable homoclinic loop and an unstable limit cycle, co-existence of two limit cycles (the inner one unstable and the outer one stable), and the existence of a semi-stable limit cycle for different parameter spaces, as shown in Fig. 5a–d.

Fig. 5

The phase portraits of system (1.2). a An unstable limit cycle enclosing the stable focus $E_{1}(x_{1},y_{1})$ with $(b,c,d)=(1.2,0.3464,0.1415)$. b A stable homoclinic cycle and an unstable limit cycle enclosing the stable focus $E_{1}(x_{1},y_{1})$ when $(b,c,d)=(1.2,0.3464,0.14187)$. c Two limit cycles enclosing the stable focus $E_{1}(x_{1},y_{1})$, where the outer stable limit cycle arises from the Homoclinic bifurcation when $(b,c,d)=(1.2,0.3464,0.1421)$. d A semi-stable cycle enclosing the stable focus $E_{1}(x_{1},y_{1})$ when $(b,c,d)=(1.2,0.3464,0.142222)$

3.4 Cusp Bifurcation of Codimension 2

For case (II)(b) in Table 2, system (1.2) has a unique positive equilibrium $(x^{*},y^{*})$, which is a degenerate node of codimension 2 when $H(x^{*})\ne 0$, a degenerate focus (or center) when $H'(x^{*})=0$ (or $H'(x^{*})\ne 0$ and $(H'(x^{*}))^{2}< 8acx^{*}[1+a(x^{*})^{2}]$), or a degenerate elliptic equilibrium consisting of one hyperbolic sector and one elliptic sector when $H'(x^{*})\ne 0$ and $(H'(x^{*}))^{2}\ge 8acx^{*}[1+a(x^{*})^{2}]$. This indicates that there can exist more complicated and interesting bifurcation phenomena. Next, we choose c and d as bifurcation parameters and fix $(a,b)=(a_{*},b_{*})$ to study the cusp bifurcation of codimension 2 [21] for system (1.2). We have the following results.

Theorem 3.5

Assume that the conditions in case (i) of Theorem 2.6 are satisfied, then equilibrium $(x^{*},y^{*})$ is a degenerate node of codimension 2. Choosing c and d as bifurcation parameters, then system (1.2) undergoes a cusp bifurcation of codimension 2 in a small neighborhood of $(x^{*},y^{*})$ as (c, d) varies near $(c_{*},d_{*})$ provided that $a_{*}+\frac{2b_{*}}{c_{*}}+\frac{b^{2}_{*}}{a_{*}c^{2}_{*}}\ne 9$, where $c_{*}$ and $d_{*}$ satisfy $d_{*}<c_{*}$, $\Delta =0$, $F(x^{*})=0$ and $H(x^{*})\ne 0$.

Proof

Similarly, substituting a, b, c and d by $a_{*}$, $b_{*}$, $c_{*}-\varepsilon _{1}$ and $d_{*}-\varepsilon _{2}$ for system (1.2). Then translating the positive equilibrium $(x^{*},y^{*})$ to the origin, and expanding the right-hand side of system (1.2) in a Taylor series up to the fourth order around the origin, we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{dx}{dt}=&{}\alpha _{10}x+\alpha _{01}y+\alpha _{20}x^{2}+2\alpha _{11}x y + \alpha _{30}x^{3}+ \alpha _{21}x^{2}y+\alpha _{40}x^{4}+ \alpha _{31}x^{3}y +O(|x,y|^{5}),\\ \frac{dy}{dt}=&{}\beta _{00} +\beta _{10}x+(\beta _{01}+\varepsilon _{1})y+\beta _{20}x^{2}+2\beta _{11}xy+ \beta _{30}x^{3}+ \beta _{21}x^{2}y+\beta _{40}x^{4}\\ &{}\quad + \beta _{31}x^{3}y +O(|x,y,\varepsilon _{1},\varepsilon _{2}|^{5}), \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.18)

where $\alpha _{10} \doteq -x^{*}+\frac{2a_{*}(x^{*})^{2}(1-x^{*})}{1+a_{*} (x^{*})^{2}}$, $\alpha _{01} \doteq -\frac{x^{*}}{1+a_{*} (x^{*})^{2}}$, $\alpha _{20} \doteq -1+\frac{a_{*} x^{*}y^{*}[3-a_{*} (x^{*})^{2}]}{[1+a_{*} (x^{*})^{2}]^{3}}$, $\alpha _{11} \doteq -\frac{1-a_{*} (x^{*})^{2}}{2[1+a_{*} (x^{*})^{2}]^{2}}$, $\alpha _{30} \doteq \frac{a_{*} y^{*}[1+ a^{2}_{*}(x^{*}_{1})^{4}-6 a_{*} (x^{*})^{2}]}{[1+ a_{*} (x^{*})^{2}]^{4}}$, $\alpha _{21} \doteq \frac{a_{*} x^{*}[3- a_{*} (x^{*})^{2}]}{[1+a_{*} (x^{*})^{2}]^{3}}$, $\alpha _{40} \doteq \frac{a^{2}_{*}x^{*}y^{*}[10a_{*} (x^{*})^{2}-a^{2}_{*}(x^{*})^{4}-5]}{[1+a_{*} (x^{*})^{2}]^{5}}$, $\alpha _{31} \doteq \frac{a_{*} [1+ a^{2}_{*}(x^{*})^{4}-6 a_{*} (x^{*})^{2}]}{[1+a_{*} (x^{*})^{2}]^{4}}$, $\beta _{00} \doteq \varepsilon _{1}y^{*}-\varepsilon _{2}$, $\beta _{01} \doteq \frac{b_{*} x^{*}}{1+a_{*} (x^{*})^{2}}-c_{*}$, $\beta _{10} \doteq \frac{b_{*} y^{*}[1-a_{*} (x^{*})^{2}]}{[1+a_{*} (x^{*})^{2}]^{2}}$, $\beta _{20} \doteq \frac{a_{*}b_{*} x^{*}y^{*}_{2}[a_{*} (x^{*})^{2}-3]}{[1+a_{*} (x^{*})^{2}]^{3}}$, $\beta _{11} \doteq \frac{b_{*}[1-a_{*} (x^{*})^{2}]}{2[1+a_{*} (x^{*})^{2}]^{2}}$, $\beta _{21} \doteq \frac{a_{*}b_{*} x^{*}[a_{*} (x^{*})^{2}-3]}{[1+a_{*} (x^{*})^{2}]^{3}}$, $\beta _{30} \doteq \frac{a_{*}b_{*} y^{*}[6 a_{*} (x^{*})^{2}-a^{2}_{*}(x^{*})^{4}-1]}{[1+ a_{*} (x^{*})^{2}]^{4}}$, $\beta _{31} \doteq \frac{a_{*} b_{*} [6 a_{*} (x^{*})^{2}-a^{2}_{*}(x^{*})^{4}-1]}{[1+a_{*} (x^{*})^{2}]^{4}}$, $\beta _{40} \doteq \frac{a^{2}_{*}b_{*} x^{*}y^{*}[a^{2}_{*}(x^{*})^{4}-10a_{*} (x^{*})^{2}+5]}{[1+a_{*} (x^{*})^{2}]^{5}}$, and $O(|x,y,\varepsilon _{1},\varepsilon _{2}|^{5})$ is a function in variables (x, y) at least of the fifth order with respect to (x, y) and the coefficients depend smoothly on $\varepsilon _{1}$ and $\varepsilon _{2}$. Notice that $\alpha _{01} \ne 0$, we further make the following transformations

$$\begin{aligned} u=x \ \ \mathrm {and} \ \ v=\alpha _{10}x+\alpha _{01}y, \end{aligned}$$

rewrite (u, v) as (x, y), then system (3.18) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{dx}{dt}=&{}y+\bar{\alpha }_{20}x^{2}+\bar{\alpha }_{11}xy+\bar{\alpha }_{30}x^{3} + \bar{\alpha }_{21}x^{2}y +\bar{\alpha }_{40}x^{4}+\bar{\alpha }_{31}x^{3}y+O(|x,y|^{5}),\\ \frac{dy}{dt}=&{}\bar{\beta }_{00}+\bar{\beta }_{10}x +\bar{\beta }_{01}y+\bar{\beta }_{20}x^{2}+\bar{\beta }_{11}xy+\bar{\beta }_{30}x^{3}+\bar{\beta }_{21}x^{2}y+\bar{\beta }_{40}x^{4}+\bar{\beta }_{31}x^{3}y + O(|x,y,\varepsilon _{1},\varepsilon _{2}|^{5}), \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.19)

where $\bar{\alpha }_{20} \doteq \alpha _{20}-\frac{2\alpha _{10}\alpha _{11}}{\alpha _{01}}$, $\bar{\alpha }_{11} \doteq \frac{2\alpha _{11}}{\alpha _{01}}$, $\bar{\alpha }_{30} \doteq \alpha _{30}-\frac{\alpha _{10}\alpha _{21}}{\alpha _{01}}$, $\bar{\alpha }_{21} \doteq \frac{\alpha _{21}}{\alpha _{01}}$, $\bar{\alpha }_{40} \doteq \alpha _{40}-\frac{\alpha _{10}\alpha _{31}}{\alpha _{01}}$, $\bar{\alpha }_{31} \doteq \frac{\alpha _{31}}{\alpha _{01}}$, $\bar{\beta }_{00} \doteq \beta _{00}\alpha _{01}$, $\bar{\beta }_{10} \doteq -\alpha _{10}\varepsilon _{1}$, $\bar{\beta }_{01} \doteq \alpha _{10}+\beta _{01}+\varepsilon _{1}$, $\bar{\beta }_{20} \doteq \beta _{20}\alpha _{01}+\alpha _{10}(\alpha _{20}-2\beta _{11})- \frac{2\alpha _{11}\alpha ^{2}_{10}}{\alpha _{01}}$, $\bar{\beta }_{11} \doteq 2\beta _{11}+\frac{2\alpha _{10}\alpha _{11}}{\alpha _{01}}$, $\bar{\beta }_{30} \doteq \beta _{30}\alpha _{01}+ \alpha _{10}(\alpha _{30}-\beta _{21}) - \frac{\alpha _{21}\alpha ^{2}_{10}}{\alpha _{01}}$, $\bar{\beta }_{21} \doteq \beta _{21}+\frac{\alpha _{10}\alpha _{21}}{\alpha _{01}}$, $\bar{\beta }_{40} \doteq \beta _{40}\alpha _{01}+ \alpha _{10} (\alpha _{40}-\beta _{31}) -\frac{\alpha _{31}\alpha ^{2}_{10}}{\alpha _{01}}$ and $\bar{\beta }_{31} \doteq \beta _{31}+\frac{\alpha _{10}\alpha _{31}}{\alpha _{01}}$.

By the Liapunov–Schmidt Method in [28], system (3.19) reduced to the center manifold takes the following form:

$$\begin{aligned} \frac{dx}{dt}=\mu _{1}(\varepsilon _{1},\varepsilon _{2})+ \mu _{2}(\varepsilon _{1},\varepsilon _{2})x +\gamma _{20}x^{2}+ \gamma _{30}x^{3} +O(|x,y|^{4}), \end{aligned}$$

(3.20)

where

$$\begin{aligned} \mu _{1}(\varepsilon _{1},\varepsilon _{2})\doteq & {} -\frac{\bar{\beta }_{00}}{\bar{\beta }_{01}} =-\frac{\alpha _{01}y^{*}}{\alpha _{10}+\beta _{01}}\varepsilon _{1} +\frac{\alpha _{01}}{\alpha _{10}+\beta _{01}}\varepsilon _{2}+O(|\varepsilon _{1},\varepsilon _{2}|^{2}), \\ \mu _{2}(\varepsilon _{1},\varepsilon _{2})\doteq & {} (\bar{\alpha }_{11}-\frac{\bar{\beta }_{11}}{\bar{\beta }_{01}})\mu _{1}-\frac{\bar{\beta }_{10}}{\bar{\beta }_{01}} =\left( \frac{\alpha _{10}-\alpha _{01}\bar{\alpha }_{11}y^{*}}{\alpha _{10}+\beta _{01}}+\frac{\alpha _{01}\bar{\alpha }_{11}\bar{\beta }_{11}y^{*}}{(\alpha _{10}+\beta _{01})^{2}} \right) \varepsilon _{1}\\&+\left( \frac{\alpha _{01}\bar{\alpha }_{11}}{\alpha _{10}+\beta _{01}}-\frac{\alpha _{01}\bar{\alpha }_{11}\bar{\beta }_{11}}{(\alpha _{10}+\beta _{01})^{2}} \right) \varepsilon _{2}+O(|\varepsilon _{1},\varepsilon _{2}|^{2}) , \\ \gamma _{20}\doteq & {} \bar{\alpha }_{20}-\frac{\bar{\beta }_{20}}{\bar{\beta }_{01}}+ O(|\varepsilon _{1},\varepsilon _{2}|) \ \mathrm {and} \\ \gamma _{30}\doteq & {} \bar{\alpha }_{30}-\frac{\bar{\alpha }_{11}\bar{\beta }_{20}+\bar{\beta }_{30}}{\bar{\beta }_{01}} +\frac{\bar{\beta }_{11}\bar{\beta }_{20}}{\bar{\beta }^{2}_{01}}+ O(|\varepsilon _{1},\varepsilon _{2}|) \end{aligned}$$

with $\lim _{\varepsilon _{i}\rightarrow 0}\gamma _{20} = 0$ and $\lim _{\varepsilon _{i}\rightarrow 0}\gamma _{30} \ne 0, \ i=1,2$. Further, denote the right side of system (3.20) as $G(x,\varepsilon _{1},\varepsilon _{2})$, we can find

$$\begin{aligned} G_{x}(x,\varepsilon _{1},\varepsilon _{2})|_{(0,0,0)}=0, \ G_{xx}(x,\varepsilon _{1},\varepsilon _{2})|_{(0,0,0)}=0, \ G_{xxx}(x,\varepsilon _{1},\varepsilon _{2})|_{(0,0,0)}\ne 0 \end{aligned}$$

and

$$\begin{aligned} (G_{\varepsilon _{1}}G_{x\varepsilon _{2}}-G_{\varepsilon _{2}}G_{x\varepsilon _{1}})(x,\varepsilon _{1},\varepsilon _{2})|_{(0,0,0)}= -\frac{\alpha _{10}\alpha _{01}}{(\alpha _{10}+\beta _{01})^{2}}, \end{aligned}$$

where $\alpha _{01}\ne 0$ and $\alpha _{10}+\beta _{01}\ne 0$. When $\alpha _{10}\ne 0$, i.e., $a_{*}+\frac{2b_{*}}{c_{*}}+\frac{b^{2}_{*}}{a_{*}c^{2}_{*}}\ne 9$, system (1.2) undergoes a cusp bifurcation of codimension 2 by the results in [21]. This completes the proof. $\square$

4 Bifurcation Diagrams

Fig. 6

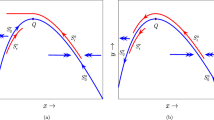
The bifurcation diagrams near the Bogdanov–Takens bifurcation points of codimension 2 for system (1.2). a An attracting Bogdanov–Takens bifurcation of codimension 2 with $H'(x^{*}_{1})>0$. b A repelling Bogdanov–Takens bifurcation of codimension 2 with $H'(x^{*}_{1})<0$. c The local amplified phase portrait of b. The parameter values are fixed as $a=5$, $b=1$ in a, and $a=6$, $b=1.2$ in b

In this section, we numerically verify all the bifurcations presented in Sect. 3 through bifurcation diagrams. In the last section, we proved the existence of the transcritical bifurcation, saddle-node bifurcation, Hopf bifurcation, degenerate Hopf bifurcation, cusp bifurcation of codimension 2 and Bogdanov–Takens (cusp type) bifurcation of codimension 3. It is worth mentioning that the Bogdanov–Takens (cusp type) bifurcation of codimension 3 for system (1.2) would have the conical structure in $\mathbf{R} ^{3}$ starting from $(\mu _{1},\mu _{2},\mu _{3})=(0,0,0)$, which consists of four types of codimension 1 bifurcation surfaces (a Hopf bifurcation surface, a homoclinic bifurcation surface, two saddle-node bifurcation surfaces, a double limit cycle bifurcation surface) and four types of codimension 2 bifurcation curves based on five bifurcation points (two Bogdanov–Takens points of codimension 2, a degenerate Hopf point of codimension 2, a degenerate homoclinic point of codimension 2 and a point which is the intersection of the Hopf bifurcation curve and homoclinic bifurcation curve, as shown in Fig. 6a–c). The detailed bifurcation phenomena can be referred to [5, 22, 30]. However, it is difficult to plot a three parameters bifurcation diagram of the Bogdanov–Takens (cusp type) bifurcation of codimension 3. In [20], Shan and Zhu give the bifurcation diagram in two parameters plane to describe all the phenomena of the Bogdanov–Takens (cusp type) bifurcation of codimension 3.

Fig. 7

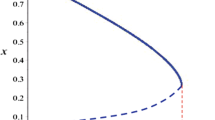
One parameter bifurcation diagrams of system (1.2) with respect to parameter d. Here, the red curves represent the unstable equilibria, red vertical lines represent the unstable limit cycles, black curves represent the stable equilibria, blue vertical lines represent the stable limit cycles. And HB is the Hopf bifurcation point, $SN_{i}$ (i = 1, 2) the saddle-node bifurcation point, NS the neutral saddle and i is the local amplified phase portrait of h. Saddle-node bifurcation occurs in a–h. The subcritical Hopf bifurcation occurs in a, b and f–i. The supercritical Hopf bifurcation in c, d. The double limit cycle bifurcation occurs in a, b and g, i. The homoclinic bifurcation occurs in b, c and f, i. The saddle-node homoclinic bifurcation occurs in a

In the following, for simplicity, instead of plotting a three parameters bifurcation diagram, in Fig. 6, by choosing (c, d) as bifurcation parameters and fixing other parameters, we have shown three subplots of two parameters bifurcation diagrams near the Bogdanov–Takens bifurcation of codimension 2, which have included all the possible bifurcations of the Bogdanov–Takens (cusp type) bifurcation of codimension 3. In Fig. 6, there are five bifurcation curves: $SN_{c_{1}}$ and $SN_{c_{2}}$ represent the first saddle bifurcation curve and the second bifurcation curve, respectively. $H_{c_{1}}$ denotes the Hopf bifurcation curve, $H_{om}$ the homoclinic bifurcation curve (or called the saddle Homoclinic bifurcation curve, i.e., a homoclinic loop with a saddle), $H_{oms}$ the saddle-node homoclinic bifurcation curve (a homoclinic loop with a saddle-node), $L_{c}$ the double limit cycle bifurcation curve, $NS_{c}$ the neutral saddle curve which is not the bifurcation curve. Further, $BT^{+}$ and $BT^{-}$ are the Bogdanov–Takens bifurcation points of codimension 2, GH the degenerate Hopf bifurcation point of codimension 2 with $\sigma _{1}=0$, $GH_{om}$ the degenerate homonlinic bifurcation point of codimension 2 with $p_{E_{2}}=0$, D a parameter value of simultaneous Hopf and homoclinic bifurcations, DL a parameter value of simultaneous double limit cycle and saddle-node bifurcations, H a parameter value of simultaneous Hopf and saddle-node bifurcations, and DH a intersection of two types homoclinic bifurcation curves $H_{om}$ and $H_{oms}$.

Furthermore, by choosing d as the bifurcation parameter, we have also presented all types of bifurcations related to Fig. 6, as shown in Fig. 7. Particularly, for the cases (a)–(b) and (g)–(h), two limit cycles appear from the double limit cycle bifurcation, the inner one disappearing via the subcritical Hopf bifurcation, the outer one disappearing via the saddle-node homoclinic bifurcation for the case (a), while the outer one disappearing via the homoclinic bifurcation for the cases (b) and (g)–(h). Especially, between the cases (g) and (h), there should be a case that the two limit cycles appear from the double limit cycle bifurcation, the inner one disappearing via the subcritical Hopf bifurcation and the outer one disappearing via the homoclinic bifurcation simultaneously corresponding to the point D in Fig. 6b, c.

Fig. 8

The existence of the double limit cycle bifurcation for system (1.2) with $(a,b,c)=(16,2.8,0.15)$. a A double limit cycle bifurcation. b The existence of two limit cycles where the red curve represents the unstable limit cycle $\Gamma _{r}$ and the blue curve represents the stable cycle $\Gamma _{b}$, $d_{H}$ is the Hopf bifurcation point with the first Liapunov number $\sigma _{1}=0.21982$. c A globally stable limit cycle when $d<d_{H}$. d Two limit cycles enclose the stable weak focus $E_{1}$ when $d\in (d_{H},d_{max})$. e Two limit cycles collide simultaneously such that there exists a unique semi-stable cycle when $d=d_{max}$. f $E_{1}$ is a globally stable focus when $d>d_{max}$

Remark 4.1

The occurrence of the saddle-node homoclinic bifurcation is accompanied by the occurrence of the saddle-node bifurcation. This means the saddle-node homoclinic bifurcation curve $H_{oms}$ is a part of the saddle-node bifurcation curve $SN_{c_{2}}$, as shown in Fig. 6a–c.

Remark 4.2

It is worth mentioning that for the double limit cycle bifurcation in cases (a)–(b) and (g)–(h), which has two limit cycles with the inner one disappearing via the Hopf bifurcation and the outer one disappearing via the homoclinic bifurcation (or the saddle-node homoclinic bifurcation). Moreover, there exists another type double limit cycle bifurcation in system (1.2), where the outer one always exists when $d<d_{H}$ by the Poincaré-Bendixson Theorem, which is different from these cases, as shown in Fig. 8a–f.

When we set $(a,b)=(3.5,2.1)$, as parameters (c, d) varies, all types of bifurcation curves and bifurcation points in Fig. 6 disappear except two saddle-node bifurcation curves $SN_{c_{1}}$ and $SN_{c_{2}}$. And two saddle-node bifurcation curves intersect, resulting in a unique equilibrium $(x^{*},y^{*})$ for system (1.2) when $(c,d)=(3.4748,2.7484)$, as shown in Fig. 9a, b. It is easy to verify that a cusp bifurcation of codimension 2 occurs in $\mathbf{R} ^{+}_{2}$, as shown in Fig. 9a–g.

Fig. 9

A cusp bifurcation of codimension 2 for system (1.2) with $(a,b)=(3.5,2.1)$, and the phase portraits in the different regions of parameters, where CP denote a cusp bifurcation point of codimension 2, i.e., the intersection of $SN_{c_{1}}$ and $SN_{c_{2}}$

5 Conclusions and Discussions

In this paper, we extended the classical predator–prey system with Holling type IV functional response by including a constant releasing rate for the predator, considering the constant releasing of the natural enemy in the IPM [12, 14]. We studied the global dynamics and bifurcations of the proposed model, discussed the impact of the constant releasing rate on the dynamics and proved that it can include much more rich dynamical behaviors and complex bifurcation phenomena which are also numerically verified by bifurcation diagrams and phase portraits.

We initially showed that the parameter d (i.e., the constant releasing rate $\tau$) can have an essential effect on the number of equilibria (at most three positive equilibria) with various types (focus, node, center, saddle-node, cusp, elliptic). Choosing parameter d (i.e., parameter $\tau$) as one of the bifurcation parameters, we proved that the proposed system can undergo a sequence of bifurcations, including transcritical, saddle-node, Hopf, degenerate Hopf, saddle-node homoclinic, cusp bifurcation of codimension 2, Bogdanov–Takens bifurcation of codimension 2 and degenerate Bogdanov–Takens (cusp type) bifurcation of codimension 3. With these bifurcations, in different parameter spaces, system (1.2) can exist a semi-stable limit cycle, two types of homoclinic loops (homoclinic loop with a saddle and homoclinic with a saddle-node), and coexist a stable limit cycle and an unstable limit cycle, or an unstable limit cycle and a stable homoclinic loop, or a stable limit cycle and an unstable homoclinic loop.

Compared with the main results for the classical predator–prey system with Holling IV functional response [3], we found that with a constant releasing rate for predators, the system can present various novel dynamical behaviors, including the co-existence of three positive equilibria, the novel and complex bifurcations. In details, we proved that there can only have the Bogdanov–Takens bifurcation of codimension 2 without the constant releasing rate (i.e., the system in [3]). In contrast, the proposed system can exhibit a Bogdanov–Takens (cusp type) bifurcation of codimension 3, which is a much more complicated bifurcation phenomenon. Also, the proposed system can present the existence of a semi-stable limit cycle as well as the co-existence of a limit cycle and a homoclinic loop. One the other hand, as mentioned above, there can be three positive equilibria while the system studied by Ruan and Xiao in [3] can only have two. Consequently, the proposed system can undergo a cusp bifurcation of codimension 2 when the three equilibria coincide into one equilibrium simultaneously. Note that, in Theorem 2.6, if $H'(x^{*})\ne 0$, then system (2.21) can be translated to

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\frac{d x}{dt}=y,\\ &{}\frac{d y}{dt}=\bar{\gamma }_{1} xy+\bar{\gamma }_{2}x^{3}+\bar{\gamma }_{3} x^{2}y+ \bar{\gamma }_{4}x^{4}+\bar{\gamma }_{5}x^{3}y+ O(|x,y|^{5}) \end{aligned} \end{array}\right. } \end{aligned}$$

in a small neighborhood of the origin (0, 0). Further, if $5\bar{\gamma }_{2}\bar{\gamma }_{3}-3\bar{\gamma }_{1}\bar{\gamma }_{4}\ne 0$, then $(x^{*},y^{*})$ is a degenerate equilibrium of codimension 3 [31, 32]. Consequently, system (1.2) can have a focus (or elliptic) type degenerate Bogdanov–Takens bifurcation of codimension 3, which can be much more complicated and interesting. This is left for the future works.

It is also worth mentioning the biological implications of our main results. Taking the constant releasing rate of predators as the release of natural enemies in the IPM, our results show that the constant releasing of natural enemies has an important role in controlling the growth of pests. There exists a critical value of the constant releasing rate such that (i) the pest goes to extinction for all admissible initial populations of both species when the constant releasing rate is greater than the critical value, i.e., the natural enemy can successfully help to eliminate the pest by the constant releasing of natural enemies; (ii) there exist multiple positive steady states and periodic orbits for the model when the constant releasing rate is less than the critical value, which indicates that the pest can always coexist with the natural enemy in the form of a steady state or a periodic orbit, i.e., the natural enemy can not control the growth of pests effectively, in spite of the predation of pests and the constant releasing of natural enemies. Those indicate that choosing a proper releasing rate of the natural enemy is essential to control the pest.

Appendices

Appendix A: Proof of Lemma 3.1

Proof

Considering the function

$$\begin{aligned} H(x)=3ax^{3}-(2a-ac)x^{2}-(b-1)x+c. \end{aligned}$$

It follows from $H(x_{1})=0$ that $x_{1}$ is a positive real root of the cubic equation $H(x)=0$. Moreover, since H(x) passes the point (0, c), and $H(+\infty )=+\infty$ and $H(-\infty )=-\infty$, the cubic equation $H(x)=0$ always has a negative real root. Hence, the cubic equation $H(x)=0$ has three real roots (a negative real root and two positive real roots), as shown in Fig. 10. Denote the roots of the cubic equation $H(x)=0$ as follows:

$$\begin{aligned} x_{01}<0, \ \ x_{02}>0 \ \ \mathrm {and} \ \ x_{03}>0, \end{aligned}$$

where $x_{1}$ is equal to one of $x_{02}$ and $x_{03}$. Especially, when $H'(x)|_{x=x_{1}}=0$, we have

$$\begin{aligned} x_{1}=x_{02}=x_{03}=\frac{(2a-ac)+\sqrt{\Delta _{*}}}{9a}, \end{aligned}$$

where $\Delta _{*}=(2a-ac)^{2}+9a(b-1)>0$. Thus, we have $H'(x_{1})= 0$ if and only if $x_{1}=\frac{(2a-ac)+\sqrt{\Delta _{*}}}{9a}$. The proof is completed. $\square$

Fig. 10

The existence of the positive real roots of the cubic equation $H(x)=0$. The Hopf bifurcation occurs when $x_{1}=x_{02}$, $x_{1}=x_{03}$ or $x_{1}=x^{2}_{*}$

Appendix B: Coefficients in the proof of Theorem 3.4

Here we provide the expressions of some coefficients that were used in the proof of Theorem 3.4.

• $m_{11}= \frac{(1-x^{*}_{1})(x^{*}_{1})^{2}}{1+a_{0}(x^{*}_{1})^{2}}$, $m_{12}=(x^{*}_{1}-1)x^{*}_{1}$, $m_{13}=\frac{x^{*}_{1}}{1+a_{0}(x^{*}_{1})^{2}}$,

• $m_{21}=\frac{[12(x^{*}_{1})^{2}-15x^{*}_{1}+4][7(x^{*}_{1})^{2}-8x^{*}_{1}+2][-24(x^{*}_{1})^{3}+33(x^{*}_{1})^{2}-15x^{*}_{1}+2]}{2(x^{*}-1)(5x^{*}_{1}-2)[6(x^{*}_{1})^{2}-6x^{*}_{1}+1](3x^{*}_{1}-1)^{2}}$,

• $m_{22}=\frac{[7(x^{*}_{1})^{2}-8x^{*}_{1}+2][24(x^{*}_{1})^{3}-33(x^{*}_{1})^{2}+15x^{*}_{1}-2]}{x^{*}_{1}[6(x^{*}_{1})^{2}-6x^{*}_{1}+1](3x^{*}_{1}-1)^{2}}$,

• $m_{23}=\frac{(2x^{*}_{1}-1)[12(x^{*}_{1})^{2}-15x^{*}_{1}+4][57(x^{*}_{1})^{3}-81 (x^{*}_{1})^{2}+33x^{*}_{1}-4]}{x^{*}_{1}(x^{*}_{1}-1)(5x^{*}_{1}-2)[6(x^{*}_{1})^{2}-6x^{*}_{1}+1](3x^{*}_{1}-1)^{2}}$,

• $m_{31}=\frac{[12 (x^{*}_{1})^{2}-15 x^{*}_{1}+4] [-15060(x^{*}_{1})^{10}+72837(x^{*}_{1})^{9}-154485(x^{*}_{1})^{8}+189370 (x^{*}_{1})^{7}-148793(x^{*}_{1})^{6}+78459(x^{*}_{1})^{5}-28182(x^{*}_{1})^{4}+6825(x^{*}_{1})^{3} -1069(x^{*}_{1})^{2}+98x^{*}_{1} -4]}{2(3x^{*}_{1}-1)^{3}(5x^{*}_{1}-2)^{2}(x^{*}_{1}-1)^{2}[6(x^{*}_{1})^{2}-6x^{*}_{1}+1]^{2}x^{*}_{1}}$,

• $m_{32}=\frac{-6108(x^{*}_{1})^{10}+32877(x^{*}_{1})^{9}-78921 (x^{*}_{1})^{8}+110363 (x^{*}_{1})^{7}-98839(x^{*}_{1})^{6}+58890(x^{*}_{1})^{5}-23540(x^{*}_{1})^{4}+6215(x^{*}_{1})^{3} -1035(x^{*}_{1})^{2}+98x^{*}_{1} -4}{(3x^{*}_{1}-1)^{3}(5x^{*}_{1}-2)(x^{*}_{1}-1)[6(x^{*}_{1})^{2}-6x^{*}_{1}+1]^{2}(x^{*}_{1})^{2}}$,

• $m_{33}= \frac{(1-2x^{*}_{2})[57(x^{*}_{1})^{3}-81(x^{*}_{1})^{2}+33 x^{*}_{1}-4][12 (x^{*}_{1})^{2}-15 x^{*}_{1}+4][73(x^{*}_{1})^{5}-180(x^{*}_{1})^{4}+166(x^{*}_{1})^{3}-71(x^{*}_{1})^{2}+14x^{*}_{1}-1]}{2(3x^{*}_{1}-1)^{3}(5x^{*}_{1}-2)^{2}(x^{*}_{1}-1)^{2}[6(x^{*}_{1})^{2}-6x^{*}_{1}+1]^{2}(x^{*}_{1})^{2}}$.