1 Introduction

The complexity of ecological dynamics has been a challenging field for mathematical and theoretical ecologists for several decades. As an elementary building block for many interesting population models, the predator–prey models have attracted considerate interest and remain to be research focus. As we know, the classical Leslie–Gower predator–prey model [1, 2] can be described as follows:

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{\textrm{d}x}{\textrm{d}t}=rx\left( 1-\frac{x}{K}\right) -p(x)y, \\ \frac{\textrm{d}y}{\textrm{d}t}=sy(1-\frac{y}{hx}), \end{array} \right. \end{aligned}$$
(1)

where x and y denote population density of prey and predator at time t, respectively, p(x) is the functional response, and other parameters r, s, K and h are all positive which have corresponding biological meanings: r and s stand for the intrinsic growth rates of prey and predator, respectively, K indicates the prey environment carrying capacity, and h represents the quality of the prey as food for the predator. The term \(\frac{y}{x}\) is the Leslie–Gower term which measures the loss in the predator population due to rarity of its favorite food. In the classical Leslie–Gower model, the carrying capacity of the predator is proportional to the number of prey, stressing the fact that there are upper limits to the rates of increase in both prey and predator, which are not recognized in the Lotka–Volterra model. There has been great interest in studying dynamics of the classical Leslie–Gower model and its variants. Hsu and Huang [3, 4] dealt with limit cycle, Hopf bifurcation, and global stability of the positive locally asymptotically stable equilibrium about system (1). Korobeinikov [5] introduced a Lyapunov function and established global stability of the unique coexisting equilibrium state of Leslie–Gower predator–prey models. Yuan and Song [6] focused on bifurcation and stability of a delayed Leslie–Gower predator–prey system. As we know, one important feature of the prey–predator relationship is the rate of prey consumption by an average consumer (predator), i.e., functional response. The effects of different functional responses (Holling type I, II, III, IV, and so on) on the dynamics of the predator–prey models have been investigated to a great extent [7]. Huang et al. [8] and Dai et al. [9] concentrated on dynamics of a Leslie–Gower predator–prey model with generalized Holling type III functional response. Tripathi et al. [10,11,12,13] dealt with rich dynamics of Leslie–Gower predator–prey models with Beddington–DeAngelis functional response. It is well–known that Allee effect [14], which reflects the relation between population size and fitness, is also a critical factor in characterizing species diversity maintenance, species evolution, species conservation and management in ecological research. Therefore, much effort has been made to study the dynamics of the predator–prey models with Allee effect [15]. For instance, Aguirre et al. [16, 17] studied system (1) with the additive Allee effect

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{\textrm{d}x}{\textrm{d}t}=rx(1-\frac{x}{K}-\frac{m}{x+b})-p(x)y, \\ \frac{\textrm{d}y}{\textrm{d}t}=sy(1-\frac{y}{hx}), \end{array} \right. \end{aligned}$$

where m and b are positive constants that indicate the severity of the Allee effect, and Aguirre [18] also focused on system (1) with the multiplicative Allee effect

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{\textrm{d}x}{\textrm{d}t}=rx(1-\frac{x}{K})(x-m)-p(x)y, \\ \frac{\textrm{d}y}{\textrm{d}t}=sy(1-\frac{y}{hx}), \end{array} \right. \end{aligned}$$

where m is the Allee threshold of viable population.

Zhu et al. [19] considered system (1) with another form of Allee effect (indicating that the intrinsic growth rate of the prey depends on the population size) and Holling Type I functional response \(p(x)=ex\),

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{\textrm{d}x}{\textrm{d}t}=x\left( \frac{rx}{x+a}-bx-c\right) -exy, \\ \frac{\textrm{d}y}{\textrm{d}t}=sy(1-\frac{y}{hx}), \end{array} \right. \end{aligned}$$
(2)

where \(a>0\) is the Allee effect constant of the prey, \(c>0\) is the mortality of the prey, \(b>0\) is the intra–specific competition intensity of the prey, and \(e>0\) represents the maximal predator per capita consumption rate. Zhu et al. [19] studied the existence and stability of equilibria, and then showed that system (2) undergoes Bogdanov–Takens bifurcation of codimension two (or three). Zu and Mimura [20] found that this type of Allee effect can increase the risk of extinction of both predator and prey by including Allee effect and Holling Type II functional response. They [20, 21] also showed that the model can undergo the heteroclinic loop bifurcation and Hopf bifurcation. In this paper, we concentrate on the dynamics of the slow–fast version of the following system with Allee effect and Holling Type II functional response \(p(x)=\frac{ex}{d+x}\),

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{\textrm{d}x}{\textrm{d}t}=x\left( \frac{rx}{x+a}-bx-c\right) -\frac{exy}{d+x}, \\ \frac{\textrm{d}y}{\textrm{d}t}=sy(1-\frac{y}{hx}). \end{array} \right. \end{aligned}$$
(3)

It is believed that ecological systems in nature usually evolve on different time scales. Therefore, considering the fact that the growth of the prey and its predator occurs on different time scales, many researchers have devoted to studying the dynamics of the fast–slow predator–prey models [22,23,24,25,26,27,28,29,30,31,32]. Wang et al. [22, 23] studied dynamics of a slow–fast predator–prey model with the generalized Holling type III functional response. Chen and Zhang [24] studied canard explosion of a slow–fast predator–prey model with the Sigmoid functional response. Atabaigi [25] analyzed dynamics of a slow–fast generalist predator–prey model with Holling type III functional response. Saha et al. [26] investigated dynamics of a slow–fast modified Leslie–type prey–generalist predator system with piecewise-smooth Holling type I functional response. Zhu and Liu [27] investigated canard cycles and relaxation oscillation in a slow–fast predator–prey model with the generalized Holling type II functional response and Allee effect. Zhao and Shen [28] focused on canards and homoclinic orbits of a slow–fast modified May–Holling–Tanner predator–prey model with weak multiple Allee effect. Shi and Wen [29] investigated canard cycles and their cyclicity of the slow–fast version of system (2). Chowdhury, Banerjee and Petrovskii [30] studied canards, relaxation oscillations, and pattern formation in a slow–fast ratio–dependent predator–prey model. Li et al. [31] concentrated on relaxation oscillation and canard explosion in a slow–fast predator–prey model with Holling type I functional response and addictive Allee effect. Wen and Shi [32] proved the existence and uniqueness of a canard cycle with cyclicity at most two in a singularly perturbed Leslie–Gower predator–prey model with prey harvesting. With these great success, one may wander what about the dynamics in the slow–fast version of system (3). Motivated by this, by assuming that prey reproduces much faster than predator, that is, \(\varepsilon =s/r \ll 1\), exploiting the transformation

$$\begin{aligned} x=\frac{r}{b}\bar{x}, y=\frac{r^2}{be}\bar{y}, t=\frac{t_1}{r}, \end{aligned}$$

and dropping the bars, we rewrite system (3) into

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{dx}{dt_1}=x\left( \frac{x}{A+x}-\alpha -x-\frac{y}{\beta +x}\right) , \\ \frac{dy}{dt_1}=\varepsilon y\left( 1-\frac{ky}{x}\right) , \end{array} \right. \end{aligned}$$
(4)

where \(A=\frac{ab}{r}\), \(\alpha =\frac{c}{r}\), \(\beta =\frac{bd}{r}\), and \(k=\frac{r}{eh}\). Note that A in system (4) corresponds to Allee effect constant a in system (3).

Obviously, system (4) is topologically equivalent to

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{dx}{dt}=x^{2}\Big (\big (x-(\alpha +x)(A+x)\big )(\beta +x)-y(A+x)\Big ), \\ \frac{dy}{dt}=\varepsilon y(A+x)(\beta +x)(x- ky). \end{array} \right. \end{aligned}$$
(5)

From the perspective of geometric singular perturbation theory (GSPT), system (5) is called the fast system. We are going to study dynamics of system (5), including canard explosion and homoclinic orbit.

2 Preliminaries

In this section, to study the dynamics of system (5), we first give some preliminary results, based on geometric singular perturbation theory [33] and the slow–fast normal form [34].

2.1 The Slow and Fast Limiting Dynamics

Introducing \(\tau =\varepsilon t\), we obtain the associated slow system of system (5)

$$\begin{aligned} \left\{ \begin{array}{lc} \varepsilon \frac{dx}{d\tau }=x^{2}\Big (\big (x-(\alpha +x)(A+x)\big )(\beta +x)-y(A+x)\Big ), \\ \frac{dy}{d\tau }=y(A+x)(\beta +x)(x- ky). \end{array} \right. \end{aligned}$$
(6)

Setting \(\varepsilon =0\) in systems (5) and (6), we arrive at the fast subsystem

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{dx}{dt}=x^{2}\Big (\big (x-(\alpha +x)(A+x)\big )(\beta +x)-y(A+x)\Big ), \\ \frac{dy}{dt}=0, \end{array} \right. \end{aligned}$$
(7)

and the slow subsystem

$$\begin{aligned} \left\{ \begin{array}{lc} 0=x^{2}\Big (\big (x-(\alpha +x)(A+x)\big )(\beta +x)-y(A+x)\Big ), \\ \frac{dy}{d\tau }= y(A+x)(\beta +x)(x- ky), \end{array} \right. \end{aligned}$$
(8)

respectively. According to GSPT, our aim is to study dynamics of system (5) by combining the limiting information of systems (7) and (8).

2.2 The Critical Manifold

It follows that the critical manifold of system (8) is given by

$$\begin{aligned} C_{0}=\{(x,y)|x=0\} \cup \{(x,y)| y=C(x)\} :=C_1\cup C_2, \end{aligned}$$
(9)

where

$$\begin{aligned} C(x)=(\beta +x)\left( \frac{x}{A+x}-\alpha -x\right) . \end{aligned}$$
(10)

To state conveniently, throughout the remainder of the paper, we always assume that

$$\begin{aligned} 0<A<1 \ \text {and} \ 0<\alpha <\left( 1-\sqrt{A}\right) ^2. \end{aligned}$$
(11)

Then we easily find that the critical manifold \(C_2\) has a unique fold point \(Q(x_{Q},y_{Q})\), where \(y_{Q}=C(x_{Q})\). Besides, one also notice that \(y=C(x)\) intersects the x–axis at two points \(E_{b1}(x_{b1},0)\) and \(E_{b2}(x_{b2},0)\), where

$$\begin{aligned} x_{b1}= & {} \frac{1}{2} \left( 1-A-\alpha -\sqrt{(1-\alpha -A)^2-4A\alpha }\right) \ \text {and} \\ x_{b2}= & {} \frac{1}{2} \left( 1-A-\alpha +\sqrt{(1-\alpha -A)^2-4A\alpha }\right) . \end{aligned}$$

Hence the critical manifold \(C_2\) can be divided into the following two parts by the point Q

$$\begin{aligned} \begin{aligned}&C_2^r\!=\!\left\{ (x,y)|y\!=\!C(x), x_{b1}<x<x_Q\right\} \ \text {and} \ C_2^a\!=\!\left\{ (x,y)|y=C(x), x_Q<x<x_{b2}\right\} . \end{aligned}\end{aligned}$$
(12)

According to GSPT, one immediately has the following results.

Lemma 1

One has,

  1. (i)

    \(C_2^r\) is normally hyperbolic repelling; and \(C_2^a\) is normally hyperbolic attracting.

  2. (ii)

    \(C_2^r\) and \(C_2^a\) perturb to nearby invariant manifolds \(C_{2,\varepsilon }^r\) and \(C_{2,\varepsilon }^a\), respectively.

2.3 Equilibria and their Dynamics

One first easily notices that the set \(\Omega =\{(x,y)|0<x<x_{b2}, y\ge 0\}\) is positively invariant and is attracting with respect to the flow of system (5). Additionally, one also has the following results by direct calculation.

Lemma 2

System (5) has two boundary equilibria \(E_{b1}\) and \(E_{b2}\) with \(0<A<1\) and \(0<\alpha <\left( 1-\sqrt{A}\right) ^2\). Furthermore, \(E_{b1}\) is a saddle and \(E_{b2}\) is an unstable node.

Next, we turn to positive equilibria of system (5). Cleary, the abscissa of positive equilibria should satisfy

$$\begin{aligned} \begin{aligned} k x^3+\big (k (\alpha +A+\beta -1)+1\big )x^2+\big (\beta k (\alpha +A-1)+A (\alpha k+1)\big )x+\alpha A\beta k=0. \end{aligned}\end{aligned}$$
(13)

Let

$$\begin{aligned}\begin{aligned} \Delta _{1}&=(k (\alpha +A+\beta -1)+1)^{2} -3k\big (\beta k (\alpha +A-1)+A (\alpha k+1)\big ),\\ \Delta _{2}&=-27k^{3}\alpha A\beta +9k\big (k (\alpha +A+\beta -1)+1\big )\big (\beta k (\alpha +A-1)+A (\alpha k+1)\big )\\&\quad +2\big (k (\alpha +A+\beta -1)+1\big )^{3}. \end{aligned}\end{aligned}$$

Now we can state the results about the number, position and dynamics of positive equilibria of system (5).

Theorem 1

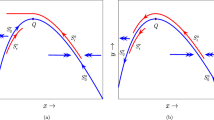
If \(0<\varepsilon \ll 1\), \(0<A<1\), and \(0<\alpha <\left( 1-\sqrt{A}\right) ^2\), \(\Delta _{2}^{2}-4\Delta _{1}^{3}<0\), and \(\sqrt{\Delta _{1}}-k (\alpha +A+\beta -1)-1>0\), then system (5) has two positive equilibria \(E_{1}(x_{1},y_{1})\) and \(E_{2}(x_{2},y_{2})\) with \(x_{b1}<x_2<x_1<x_{b2}\). Additionally, \(E_2\) is saddle, and

  1. (i)

    if \(k<\frac{x_Q}{y_Q}\), then \(x_2<x_{1}<x_Q\). Moreover, if \(k<\frac{x_Q}{y_Q}\) and k is not sufficiently close to \(\frac{x_Q}{y_Q}\), then \(E_1\) is unstable node.

  2. (ii)

    if \(k=\frac{x_Q}{y_Q}\), then \(x_2<x_{1}=x_Q\). Moreover, \(E_1\) is stable focus.

  3. (iii)

    if \(k>\frac{x_Q}{y_Q}\), then \(x_2<x_Q<x_{1}\). Moreover, if \(k>\frac{x_Q}{y_Q}\) and k is not sufficiently close to \(\frac{x_Q}{y_Q}\), then \(E_1\) is stable node.

Proof

The statements about the existence of two positive equilibria and their location follow from direct calculation. To study the dynamical behavior of the positive equilibrium (x, y), we find the Jacobian matrix of system (5) at the equilibrium (x, y)

$$\begin{aligned} J(x,y)= \begin{bmatrix} x^2 \Big ((\beta +x) (1-\alpha -A-2 x)-(A+x) (\alpha +x)+x-y\Big )&{}&{}-x^{2}\left( A+x\right) \\ \varepsilon y(\beta +x)\left( A+x\right) &{}&{}-\varepsilon ky(\beta +x)\left( A+x\right) \end{bmatrix}. \end{aligned}$$

Clearly, its trace Tr(J(x, y)) and determinant Det(J(x, y)) are given by

$$\begin{aligned} \begin{aligned} Tr(J(x,y))&=x^{2}(A+x)\left( \frac{x}{A+x}-x-\alpha +\frac{\left( A-(A+x)^2\right) (\beta +x)}{(A+x)^2}\right) \\&\quad -\varepsilon x(\beta +x) (A+x)\\&=x^2(A+x)C'(x)-\varepsilon x(\beta +x)(A+x), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} Det(J(x,y))&=\varepsilon x^2 y (\beta +x) (A+x)\Big (3 k x^2+2( k (\alpha +A+\beta -1)+1)x\\&\quad +\big (\beta k (\alpha +A-1)+A (\alpha k+1)\big )\Big )\\&=-\varepsilon x^2 y (\beta +x) (A+x)H'(x), \end{aligned} \end{aligned}$$

respectively.

Obviously, one has, for the equilibrium \(E_2\) if exists, \(Det(J(x_2,y_2))=-\varepsilon x_2^{2}y_2(\beta +x_2)\left( A+x_2\right) H'(x_2)<0\) and \(Tr^2(J(x_2,y_2))-4Det(J(x_2,y_2))>0\), which implies that \(E_2\) is saddle. While, for the equilibrium \(E_1\), \(Det(J(x_1,y_1))=-\varepsilon x_1^{2}y_1(\beta +x_1)\left( A+x_1\right) H'(x_1)>0\) and \(Tr^2(J(x_1,y_1))-4Det(J(x_1,y_1))>0\) (resp. \(Tr^2(J(x_1,y_1))-4Det(J(x_1,y_1))<0\)) for sufficiently small \(\varepsilon >0\) if \(x_1\ne x_Q\) and \(x_{1}\) is not sufficiently close to \(x_Q\) (resp. \(x_1= x_Q\)). Besides, one also has, if \(x_1<x_Q\) (resp. \(x_1>x_Q\)) and \(x_{1}\) is not sufficiently close to \(x_Q\), then \(Tr(J(x_1,y_1))>0\) (resp. \(Tr(J(x_1,y_1))<0\)) for sufficiently small \(\varepsilon >0\), and if \(x_1=x_Q\), then \(Tr(J(x_1,y_1))=-\varepsilon x_1\left( \beta +x_1\right) \left( A+x_1\right) <0\). Additionally, one also notices that if k is not sufficiently close to \(\frac{x_Q}{y_Q}\), then \(x_{1}\) is not sufficiently close to \(x_Q\). Hence, the dynamical behavior of \(E_1\) follows. \(\square \)

Remark 1

One can also determine the number, stability and topological types of positive equilibria through analyzing fast dynamics and slow dynamics along \(C_2\) (see [35, 36] for details).

Taking \(\epsilon =0.0005, A=0.4, \alpha =0.05\), and \(\beta =1.8\), here we illustrate the phase portraits and types of positive equilibria \(E_{1}\) and \(E_{2}\) in Fig. 1a–c when \(k=1.1, k=1.417692643\), and \(k=3\), respectively, which satisfy corresponding conditions given in (i), (ii), and (iii) of Theorem 1.

Fig. 1
figure 1

Illustrations of saddle \(E_{2}\) and a unstable node \(E_{1}\); b stable focus \(E_{1}\); c stable node \(E_{1}\)

Full size image

2.4 Slow–Fast Normal Form

From Theorem 1, we know that when \(k=\frac{x_Q}{y_Q}\), the fold point \(Q(x_Q,y_Q)\) is also an equilibrium point of system (5), that is, \(x_Q=x_1\), and it is easy to verify that Q is a non–degenerate canard point [34] of system (5).

Now we transform system (5) into its slow–fast normal form given in [34]. To get started, let \(T=x^{2}\left( A+x\right) t\), and then system (5) can be written as

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{dx}{dT}=-y+(\beta +x)\left( \frac{x}{A+x}-\alpha -x\right) ,\\ \frac{dy}{dT}=\varepsilon \frac{y(\beta +x)}{x}\left( 1-\frac{ky}{x}\right) . \end{array} \right. \end{aligned}$$
(14)

Then we move the point \((x_{Q},y_{Q})\) to the origin through \(X=x-x_{Q},Y=y-y_{Q}\), and system (14) becomes

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{dX}{dT}=-Y+\left( \frac{A(A-\beta )}{\left( A+x_Q\right) ^{3}}-1\right) X^{2}+\frac{A(\beta -A)}{\left( A+x_Q\right) ^{4}}X^{3}+O(X^{4}),\\ \frac{dY}{dT}=\varepsilon \left( a_{00}+a_{10}X+a_{20}X^{2} +\left( a_{01}+a_{11}X+a_{02}Y\right) Y+O(|X,Y|^{3})\right) , \end{array} \right. \end{aligned}$$
(15)

where

$$\begin{aligned}\begin{aligned}&a_{00}=\frac{y_{Q}(\beta +x_{Q})(x_{Q}-ky_{Q})}{x_{Q}^{2}}, \ a_{10}=\frac{\beta y_{Q}(2ky_{Q}-x_{Q})+kx_{Q}y_{Q}^{2}}{x_{Q}^{3}}, \\&a_{20}=\frac{\beta y_{Q}(x_{Q}-3ky_{Q})-kx_{Q}y_{Q}^{2}}{x_{Q}^{4}}, \\&a_{01}=\frac{(\beta +x_{Q})(x_{Q}-2ky_{Q})}{x_{Q}^{2}}, \ a_{11}=\frac{(2 k x_{Q} y_{Q}+4 \beta ky_{Q}-\beta x_{Q})}{x_{Q}^3}, \ a_{02}=-\frac{k(\beta +x_{Q})}{x_{Q}^2}.\\ \end{aligned} \end{aligned}$$

Further employing the transformation \(X=-\frac{(A+x_{Q}) \sqrt{y_{Q} (k y_{Q} (2 \beta +x_{Q})-\beta x_{Q})}}{x_{Q}^{3/2} (\alpha +A+\beta +3 x_{Q}-1)}X_{1}, \ Y=-\frac{y_{Q}(A+x_Q) (ky_{Q}(2 \beta +x_{Q})-\beta x_{Q})}{x_{Q}^3 (\alpha +A+\beta +3 x_{Q}-1)}Y_{1}, \ T=\frac{x_{Q}^{3/2}}{\sqrt{y_{Q}(k y_{Q} (2 \beta +x_{Q})-\beta x_{Q})}}T_{1}\), we convert system (15) into the slow–fast normal form

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{dX_{1}}{dT_{1}}=-Y_{1}h_{1}(X_{1},Y_{1},\lambda ,\varepsilon )+X_{1}^{2}h_{2}(X_{1},Y_{1},\lambda ,\varepsilon )+\varepsilon h_{3}(X_{1},Y_{1},\lambda ,\varepsilon ),\\ \frac{dY_{1}}{dT_{1}}=\varepsilon \Big (X_{1}h_{4}(X_{1},Y_{1},\lambda ,\varepsilon )-\lambda h_{5}(X_{1},Y_{1},\lambda ,\varepsilon )+Y_{1}h_{6}(X_{1},Y_{1},\lambda ,\varepsilon )\Big ), \end{array} \right. \end{aligned}$$
(16)

where

$$\begin{aligned}&\lambda =\frac{x_{Q}^{5/2}(\beta +x_{Q}) (x_{Q}-k y_{Q}) (\alpha +A+\beta +3 x_{Q}-1)}{\sqrt{y_{Q}}(A+x_{Q}) (k y_{Q} (2 \beta +x_{Q})-\beta x_{Q})^{3/2}}, \nonumber \\&h_{1}(X_{1},Y_{1},\lambda ,\varepsilon )=1, \nonumber \\ {}&h_{2}(X_{1},Y_{1},\lambda ,\varepsilon )=1+\frac{(\alpha +\beta +2x_{Q}-1) \sqrt{y_{Q} (k y_{Q} (2 \beta +x_{Q})-\beta x_{Q})}}{x_{Q}^{3/2} (\alpha +A+\beta +3 x_{Q}-1)^2}X_{1}+O(X_{1}^{2}),\nonumber \\&h_{3}(X_{1},Y_{1},\lambda ,\varepsilon )=0,\nonumber \\ {}&h_{4}(X_{1},Y_{1},\lambda ,\varepsilon )=1+\frac{\sqrt{y_{Q}}(A+x_{Q}) (k y_{Q} (3 \beta +x_{Q})-\beta x_{Q})}{x_{Q}^{5/2} (\alpha +A+\beta +3 x_{Q}-1) \sqrt{ k y_{Q}(2 \beta +x_{Q})-\beta x_{Q}}}X_{1}+O(X_{1}^{2}), \nonumber \\ {}&h_{5}(X_{1},Y_{1},\lambda ,\varepsilon )=1,\nonumber \\ {}&h_{6}(X_{1},Y_{1},\lambda ,\varepsilon )=\frac{(\beta +x_{Q}) (x_{Q}-2 k y_{Q})}{\sqrt{x_{Q}} \sqrt{y_{Q} (k y_{Q} (2 \beta +x_{Q})-\beta x_{Q})}}+O(X_{1},Y_{1}). \end{aligned}$$
(17)

Note that

$$\begin{aligned} \lambda =0\Leftrightarrow k=\frac{x_Q}{y_{Q}}. \end{aligned}$$
(18)

Therefore, we have

$$\begin{aligned} \begin{aligned}&a_{1}=\frac{\partial h_{3}}{\partial X_{1}}(0,0,0,0)=0, \ a_{2}=\frac{\partial h_{1}}{\partial X_{1}}(0,0,0,0)=0, \\&\ a_{3}=\frac{(\alpha +\beta +2 x_Q-1) \sqrt{y_Q (\beta +x_Q)}}{x_Q (\alpha +A+\beta +3x_Q-1)^2},\\&a_{4}=\frac{\sqrt{y_Q} (A+x_Q) (2 \beta +x_Q)}{x_Q^2 \sqrt{\beta +x_Q} (\alpha +A+\beta +3 x_Q-1)}, \ a_{5}=h_{6}(0,0,0,0)=-\frac{\sqrt{\beta +x_Q}}{\sqrt{y_Q}}, \end{aligned} \end{aligned}$$
(19)

and further

$$\begin{aligned} \begin{aligned} B&=-a_{2}+3a_{3}-2a_{4}-2a_{5}\\&=\frac{1}{x_Q^2 \sqrt{y_Q(\beta +x_Q)} (\alpha +A+\beta +3 x_Q-1)^2}\Bigg (18 x_Q^5+6 x_Q^4 (2 (\alpha +A-1)+5 \beta )\\&\quad +2 x_Q^3 (\alpha +A+\beta -1) (\alpha +A+7 \beta -1)+x_Q^2 \left( 2 \beta (\alpha +A+\beta -1)^2\right. \\&\left. \quad +y_Q (\alpha -8 A-5 \beta -1)\right) \\&\quad -x_Q y_Q \left( \beta (\alpha +18 A-1)+2 A (\alpha +A-1)+\beta ^2\right) -4 A \beta y_Q (\alpha +A+\beta -1)\Bigg ). \end{aligned} \end{aligned}$$
(20)

Hence the singular Hopf bifurcation curve and the maximal canard curve of the slow–fast normal form (16) are given by

$$\begin{aligned} \begin{aligned} \lambda _{H}(\sqrt{\varepsilon })&=-\frac{a_1+a_5}{2}\varepsilon +O(\varepsilon ^{\frac{3}{2}})=\frac{\sqrt{\beta +x_Q}}{2 \sqrt{y_Q}}\varepsilon +O(\varepsilon ^{\frac{3}{2}}), \end{aligned} \end{aligned}$$
(21)

and

$$\begin{aligned} \lambda _{c}(\sqrt{\varepsilon })&=-\left( \frac{a_1+a_5}{2}+\frac{1}{8}B\right) \varepsilon +O(\varepsilon ^{\frac{3}{2}})\nonumber \\&=\frac{1}{8 x_Q^2 \sqrt{y_Q(\beta +x_Q)} (\alpha +A+\beta +3x_Q-1)^2}\Big (18 x_Q^5+6 x_Q^4 (2 (\alpha +A-1)\nonumber \\&\quad +5 \beta ) +2 x_Q^3 (\alpha +A+\beta -1) (\alpha +A+7 \beta -1)\nonumber \\&\quad +x_Q^2 \left( 2 \beta (\alpha +A+\beta -1)^2+y_Q (-\alpha +8 A+5 \beta +1)\right) \nonumber \\&\quad +x_Q y_Q \left( \beta (\alpha +18 A-1)+2 A (\alpha +A-1)+\beta ^2\right) \nonumber \\&\quad +4 A \beta y_Q (\alpha +A+\beta -1)\Big )\varepsilon +O(\varepsilon ^{\frac{3}{2}}), \end{aligned}$$
(22)

respectively.

Correspondingly, the singular Hopf bifurcation curve and the maximal canard curve of system (5) can be expressed as, respectively

$$\begin{aligned} \begin{aligned} k_H(\sqrt{\varepsilon })&\!=\!\frac{x_{Q}}{y_{Q}}\!-\!\frac{A+x_Q}{2\sqrt{\beta +x_Q}(2 \beta +x_{Q})^{\frac{3}{2}} \Big (x_Qy_Q\Big )^{\frac{5}{2}} (\alpha +A+\beta +3x_Q-1)}\varepsilon \!+\!O(\varepsilon ^{\frac{3}{2}}), \end{aligned} \end{aligned}$$
(23)

and

$$\begin{aligned} \begin{aligned} k_c(\sqrt{\varepsilon })&=\frac{x_{Q}}{y_{Q}}-\frac{A+x_Q}{8\Big ((\beta +x_Q)(2 \beta +x_{Q})\Big )^{\frac{3}{2}}x_Q^{\frac{7}{2}}y_Q^{\frac{5}{2}} (\alpha +A+\beta +3x_Q-1)^{3}}\\&\quad \Bigg (18 x_Q^5+6 x_Q^4 (2 (\alpha +A-1)+5 \beta )\\&\quad +2 x_Q^3 (\alpha +A+\beta -1) (\alpha +A+7 \beta -1)\\&\quad +x_Q^2 \left( 2 \beta (\alpha +A+\beta -1)^2+y_Q (-\alpha +8 A+5 \beta +1)\right) \\&\quad +x_Q y_Q \left( \beta (\alpha +18 A-1)+2 A (\alpha +A-1)+\beta ^2\right) \\&\quad +4 A \beta y_Q (\alpha +A+\beta -1)\Bigg )\varepsilon +O(\varepsilon ^{\frac{3}{2}}). \end{aligned}\nonumber \\ \end{aligned}$$
(24)

3 Canard Cycles and Homoclinic Orbit of the Slow–Fast System (5)

In this section, we focus on canard cycles and homoclinic orbit of the slow–fast system (5). From Theorem 1, we know when \(0<A<1\), \(0<\alpha <\left( 1-\sqrt{A}\right) ^{2}\), and \(k=\frac{x_{Q}}{y_{Q}}\), the positive equilibrium \(E_1\) of system (5) coincides with Q and the other positive equilibrium \(E_2\) is saddle of system (5).

Fig. 2
figure 2

The critical manifold \(C_2\). Double arrows indicate fast flow, and single arrows indicate slow flow. a The sketch of the canard cycles for system (5). b The sketch of the homoclinic orbit for system (5)

Full size image

Theorem 2

Assume that \(0<\varepsilon \ll 1\), \(0<A<1\), and \(0<\alpha <\left( 1-\sqrt{A}\right) ^{2}\), one has,

  1. (i)

    there exists a \(k_{0}>0\) such that for \(|k-\frac{x_{Q}}{y_{Q}}|<k_{0}\), system (5) has exactly two positive equilibria \(Q^*\) and \(E_2^*\) in the small neighborhood of Q and \(E_2\), respectively, and \(Q^*\rightarrow Q\) and \(E_2^*\rightarrow E_2\) as \((\varepsilon ,k)\rightarrow (0,\frac{x_{Q}}{y_{Q}})\). Furthermore, there exists a singular Hopf bifurcation curve \(k=k_H(\sqrt{\varepsilon })\) such that \(Q^*\) is stable for \(k>k_H(\sqrt{\varepsilon })\) and unstable for \(k<k_H(\sqrt{\varepsilon })\). Additionally, the singular Hopf bifurcation is supercritical if \(B<0\) and subcritical if \(B>0\).

  2. (ii)

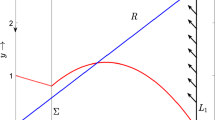
    there exists a parameterized smooth family \(s\rightarrow (k(s, \sqrt{\varepsilon }),\gamma (s, \sqrt{\varepsilon }))\) of periodic orbits bifurcated from the slow–fast cycles \(\gamma (s)\) for each \(s\in \left( 0, y_Q-y_2 \right) \) and \(\gamma (s, \sqrt{\varepsilon })\rightarrow \gamma (s)\) as \(\varepsilon \rightarrow 0\), where \(\gamma (s)\) (see Fig. 2a) is defined by

    $$\begin{aligned}\begin{aligned} \gamma (s)&=\left\{ (x,C(x))|x\in [\sigma _l(y_Q-s),\sigma _r(y_Q-s)]\right\} \cup \left\{ (x,y_Q-s)|x\right. \\&\quad \left. \in [\sigma _l(y_Q-s),\sigma _r(y_Q-s)]\right\} , \ \text {for} \ s\in \left( 0, y_Q-y_2 \right) . \end{aligned} \end{aligned}$$

    Furthermore, for \(\delta \in (0, 1)\) and \(s\in [\varepsilon ^{\delta }, y_Q-y_2-\varepsilon ^{\delta }]\), the canard explosion occurs, where

    $$\begin{aligned}\begin{aligned} \left| k(s, \sqrt{\varepsilon })-k_c(\sqrt{\varepsilon })\right| \le e^{-1/\varepsilon ^{1- \delta }}. \end{aligned} \end{aligned}$$
  3. (iii)

    there exists one homoclinic orbit to the saddle \(E_2\) for system (5) if \(k=k_c(\sqrt{\varepsilon })\).

Proof

According to Theorems 3.1 in [34], for \(0<\varepsilon \ll 1\), there exists \(\lambda _0>0\) such that for \(|\lambda |<\lambda _0\), system (5) has two positive equilibria \(Q^*\) and \(E_2^*\) in the small neighborhood of Q and \(E_2\), respectively, and \(Q^*\rightarrow Q\) and \(E_2^*\rightarrow E_2\) as \((\varepsilon ,k)\rightarrow (0,\frac{x_{Q}}{y_{Q}})\). Furthermore, there exists a singular Hopf bifurcations curve \(\lambda =\lambda _H(\sqrt{\varepsilon })\) such that \(Q^*\) is stable for \(\lambda <\lambda _H(\sqrt{\varepsilon })\) and unstable for \(\lambda >\lambda _H(\sqrt{\varepsilon })\). Now we show that \(\frac{d \lambda }{d k}<0\) for k sufficiently close to \(\frac{x_{Q}}{y_{Q}}\). It follows from \(\lambda =\frac{x_{Q}^{5/2}(\beta +x_{Q}) (x_{Q}-k y_{Q}) (\alpha +A+\beta +3 x_{Q}-1)}{\sqrt{y_{Q}}(A+x_{Q}) (k y_{Q} (2 \beta +x_{Q})-\beta x_{Q})^{3/2}}\) in (17) that

$$\begin{aligned}\begin{aligned} \frac{d \lambda }{d k}&=\frac{\sqrt{y_{Q}}x_{Q}^{5/2}(\beta +x_{Q})(\alpha +A+\beta +3 x_{Q}-1)\Big (ky_{Q}(2\beta +x_{Q})-x_{Q}(4\beta +3x_{Q})\Big )}{2(A+x_{Q})(k y_{Q} (2 \beta +x_{Q})-\beta x_{Q})^{5/2}}\\&=\frac{\sqrt{y_{Q}}x_{Q}^{5/2}(\beta +x_{Q})(\alpha +A+\beta +3 x_{Q}-1)\Big ((ky_{Q}-x_Q)(2\beta +x_{Q})-2x_{Q}(\beta +x_{Q})\Big )}{2(A+x_{Q})(k y_{Q} (2 \beta +x_{Q})-\beta x_{Q})^{5/2}}\\&<0, \end{aligned} \end{aligned}$$

for k sufficiently close to \(\frac{x_{Q}}{y_{Q}}\), which indicates that equation \(\lambda =\frac{x_{Q}^{5/2}(\beta +x_{Q}) (x_{Q}-k y_{Q}) (\alpha +A+\beta +3 x_{Q}-1)}{\sqrt{y_{Q}}(A+x_{Q}) (k y_{Q} (2 \beta +x_{Q})-\beta x_{Q})^{3/2}}\) has a unique solution \(k_H(\sqrt{\varepsilon })\) such that \(\lambda <\lambda _H(\sqrt{\varepsilon })\) (resp. \(\lambda >\lambda _H(\sqrt{\varepsilon })\)) if and only if \(k>k_H(\sqrt{\varepsilon })\) (resp. \(k<k_H(\sqrt{\varepsilon })\)). Therefore, up to now, we have established the statements (i) and (ii) by exploiting the results in [34]. Now we turn to the statement (iii), according to Theorem 3.2 in [34] (or Theorem 3.1) in [37], \(C_{2,\varepsilon }^{r}\) will connect to \(C_{2,\varepsilon }^{a}\) transversally if \(k=k_{c}(\sqrt{\varepsilon })\), which implies that one of the local stable manifold \(E_{2}^s\) and the local unstable manifolds \(E_{2}^{u,r}\) of \(E_{2}\) are connected, and hence the homoclinic orbit follows (see Fig. 2b). The proof is completed. \(\square \)

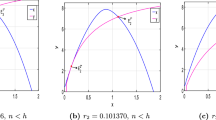
Canard cycles in Theorem 2 indicate that the prey and predator can coexist in this system under certain parameters conditions about Allee effect a, the intra–specific competition intensity b, the mortality c, etc, and the prey and predator evolve in a periodic way.

Here we exploit numerical simulations to confirm the appearance of canard explosion. We first take \(\epsilon =0.00045, A=0.4, \alpha =0.05\), and \(\beta =1.8\), and then choose \(k=1.413512, k=1.4135104\), and \(k=1.413510310114\), respectively, which yield canard cycles in Fig. 3a–c respectively.

Fig. 3
figure 3

Illustrations of canard cycles when \(\epsilon =0.00045, A=0.4, \alpha =0.05, \beta =1.8\), and a \(k=1.413512\); b \(k=1.4135104\); c \(k=1.413510310114\)

Full size image

Remark 2

In Theorem 2, the sign of B determines the properties of the singular Hopf bifurcation. Due to the complexity of B, generally we can not derive the explicit conditions on the sign of B. However, we can illustrate that \(B<0\), \(B=0\), and \(B>0\) are all possible under some suitable conditions by numerical examples. For instance, we have \(B=-1.91402<0\) for \(A=0.5, \alpha =0.03, \beta =0.5\), and \(k=5.842138\); \(B=0\) for \(A=0.5, \alpha =0.0425729, \beta =0.5\), and \(k=7.372281\); and \(B=1.5398>0\) for \(A=0.5, \alpha =0.05, \beta =0.5\), and \(k=8.780488\).

4 Discussion

In this paper, we focused on the dynamical behaviors of a fast–slow Leslie–Gower predator–prey system with Allee effect and Holling Type II functional response. To be specific, by applying geometric singular perturbation theory, we first tranform system (3) into its slow–fast system (5), through which, we find the sufficient conditions for the existence of two positive equilibria and their location, and then we further fully detected their dynamics (see Theorem 1). It is worth mentioning that it is generally hard to find the sufficient conditions to determine whether an equilibrium point is a node or focus in many predator–prey systems (for example, see Theorem 2.3 in [38]). However, we indeed find some sufficient conditions to determine when the equilibrium point \(E_1\) is node in Theorem 1. We further transformed system (5) into its slow–fast normal form, from which we determine the associated bifurcation curve and characterized its canard cycles and homoclinic orbit to the saddle \(E_2\) with slow and fast segments under explicit parameters conditions (see Theorem 2). Finally, we also included numerical simulations to to highlight the theoretical results obtained.

From the results in Theorem 2, we see that the existence of canard point Q on the critical manifold \(C_2\) is an organizing center for the complex dynamics including the birth of canard cycles and homoclinic orbit. From Fig. 2a or the proof of Theorem 2, canard cycles consist of fast and slow segments. The biological interpretation of this interesting feature is as follows: the existence of the canard cycle indicates that the prey and predator can coexist in this concrete system. When the predator density is lower than a certain level, we have a prey outbreak in a very short time. After the prey density arrives at some level which is enough to support the reproduction of the predators, the predator density begins to grow slowly and the prey density begins to decrease slowly for a long period. As the prey density continuous to decrease slowly, the predator density declines slowly due to the less food. After some time, the whole procedure continues and forms a periodic move.

As we know, many important factors [10,11,12,13, 15], such as functional response, Allee effect, fear effect, prey refuge, cooperation hunting and so on, determine rich and complex dynamics of prey–predator relationship. In the later study, we can consider the slow–fast dynamics of the predator–prey models including these factors and expect to find new dynamical behaviors.