Exact solitary solution and a three-level linearly implicit conservative finite difference method for the generalized Rosenau–Kawahara-RLW equation with generalized Novikov type perturbation

Abstract

In this paper, we study the solitary wave solution and numerical simulation for the generalized Rosenau–Kawahara-RLW equation with generalized Novikov type nonlinear perturbation, which is an extension of our recent work He and Pan (Appl Math Comput 271:323–336, 2015), He (Nonlinear Dyn 82:1177–1190, 2015). We first derive the exact solitary wave solution for the newly proposed perturbed Rosenau–Kawahara-RLW equation with power law nonlinearity and then develop a three-level linearly implicit difference scheme for solving the equation. We prove that the proposed scheme is energy-conserved, unconditionally stable and second-order convergent both in time and space variables. Finally, numerical experiments are carried out to confirm the energy conservation, the convergence rates of the scheme and effectiveness for long-time simulation.

1 Introduction

The nonlinear wave is one of the most important scientific research areas. During the past several decades, many scientists developed different mathematical models to explain the wave behavior, such as the KdV equation, the RLW equation, the Rosenau equation, the Camassa–Holm equation, the Novikov equation and etc. In the following, we give a short review of these important wave models.

The well-known KdV equation

$$\begin{aligned} u_{t}+u_{xxx}+6uu_x=0, \end{aligned}$$

(1)

was first introduced by Boussinesq [3] in 1877 and rediscovered by Diederik Korteweg and Gustav de Vries [4] in 1895. Since then, there are a lot of studies on this equation and its variational form. Here we just mention some of the recent work. Kudryashov [5] reviewed the traveling wave solutions for the KdV and the KdV-Burgers equations proposed by Wazzan  [6], Biswas [7] studied the solitary wave solution for KdV equation with power law nonlinearity and time-dependent coefficients, Wang et al. [8] investigated the solitons, shock waves for the potential KdV equation, while Ma et al. [9] studied the solitary wave solution for the generalized KdV equation. In addition to the theoretical studies, readers can refer to [10, 11] for the numerical simulations of the KdV equation and the generalized KdV equation.

The regularized long-wave (RLW) equation (also known as Benjamin-Bona-Mahony equation)

$$\begin{aligned} u_{t}+u_{x}+ \left( u^{2}\right) _{x}-u_{xxt}=0, \end{aligned}$$

(2)

was first proposed as a model for small-amplitude long wave of water in a channel by Peregrine [12, 13]. The regularized long-wave (RLW) equation and generalized regularized long-wave (GRLW) equation were well studied both theoretically and numerically in the literature. Readers can refer to [14–17] for theoretical studies and  [18–24] for numerical studies.

Since the well-known KdV equation cannot describe the wave-wave and wave-wall interactions when study of compact discrete systems, Rosenau proposed the following so-called Rosenau equation [25, 26] to overcome the shortcoming of the KdV equation:

$$\begin{aligned} u_{t}+u_{xxxxt}+u_{x}+0.5\left( u^2\right) _x=0. \end{aligned}$$

(3)

The existence and uniqueness of the solution for the Rosenau equation were theoretically proved by Park [27]. Besides the theoretical analysis, numerical studies of Eq. (3) also exist in the literature, see [28–32] and references therein.

By adding the term $-u_{xxt}$ into the Rosenau equation, one can obtain the following Rosenau-RLW equation [33–37]:

$$\begin{aligned} u_{t}-u_{xxt}+u_{xxxxt}+u_{x}+0.5\left( u^2\right) _x=0. \end{aligned}$$

(4)

The initial boundary value problem for the Rosenau-RLW equation has been well studied numerically in the past years [33–37]. For example, Pan and Zhang [33, 34] developed three-level linear implicit conservative schemes for the Rosenau-RLW equation and the generalized Rosenau-RLW equation, respectively.

For further consideration of the nonlinear wave, the viscous term $u_{xxx}$ needs to be included in the Rosenau equation, the resulting equation is usually called the Rosenau-KdV equation [38–40]:

$$\begin{aligned} u_{t}+u_{xxxxt}+u_{xxx}+u_{x}+0.5\left( u^2\right) _x=0. \end{aligned}$$

(5)

For theoretical studies, Saha [38] provided 1-soliton solution for the generalized Rosenau-KdV equation, Triki and Biswas [39] investigated the solitary wave solution and the asymptotic study of the Rosenau-KdV equation with power law nonlinearity, where the power law nonlinearity means the last term in the left-hand side of Eq. (5) is replaced by a general nonlinear term $(u^p)_x$ and p is any positive integer. For numerical investigations, Hu et al. [40] proposed a second-order conservative finite difference method for the Rosenau-KdV equation.

Moreover, the following Kawahara equation

$$\begin{aligned} u_{t}+u_{x}+uu_{x}+ u_{xxx}-u_{}=0, \end{aligned}$$

(6)

arose in the theory of shallow water waves with surface tension [41]. Equation (6) is called the modified Kawahara equation if the third nonlinear term in the left-hand side is replaced by $u^2u_x$. There is a wide range of literature on the numerical investigations and theoretical studies for the usual Kawahara equation and the modified Kawahara equation. For theoretical aspects, some periodic and solitary wave solutions for both the Kawahara equation and the modified Kawahara equation are provided in [42–44]. In addition to the theoretical studies, readers can refer to [45–47] for the numerical studies of the Kawahara equation and the modified Kawahara equation.

As one more step consideration of the nonlinear wave, Zuo [48] obtained the Rosenau–Kawahara equation by adding another viscous term $-u_{}$ to the Rosenau-KdV equation (5) and studied the solitary solution and periodic solution of the Rosenau–Kawahara equation. The Rosenau–Kawahara equation is given as follows [48]:

$$\begin{aligned} u_{t}+u_{x}+uu_x+u_{xxx}+u_{xxxxt}-u_{}=0. \end{aligned}$$

(7)

For theoretical study, Biswas [49] investigated the solitary solution and the two invariance of the following generalized Rosenau–Kawahara equation

$$\begin{aligned} u_{t}+au_{x}+bu^{m}u_{x}+cu_{xxx}+\lambda u_{xxxxt}-\mu u_{}=0,\nonumber \\ \end{aligned}$$

(8)

where $a, b, c, \mu , \alpha ,\lambda$ are real constants, m is a positive integer, which indicates the power law nonlinearity. For numerical study, the author [2] developed a three-level second-order conservative finite difference method for simulating the above generalized Rosenau–Kawahara equation (8), while Hu et al. [50] proposed a two-level nonlinear Crank-Nicolson scheme and another three-level implicit linear conservative finite difference scheme for the usual Rosenau–Kawahara equation, where both methods are proved to be second-order convergent.

By coupling the above Rosenau-RLW equation (4) and Rosenau-KdV equation (5), one can obtain the following Rosenau-KdV-RLW equation [51–55],

$$\begin{aligned} u_{t}-u_{xxt}+u_{xxxxt}+u_{xxx}+u_{x}+0.5\left( u^2\right) _x=0. \end{aligned}$$

(9)

For numerical investigation, Wongsaijai et al. [51] proposed a three-level implicit conservative finite difference method for the above Rosenau-KdV-RLW equation. Moreover, solitary waves, shock waves, conservation laws and the asymptotic behavior of the Rosenau-KdV-RLW equation with power law nonlinearity are theoretically studied by [52–55].

In addition, by coupling the above Kawahara equation (6) and Rosenau-KdV-RLW equation (9), the author and coauthor studied the exact solitary solution and developed a conservative finite difference method for the following generalized Rosenau–Kawahara-RLW equation [1],

$$\begin{aligned}&u_{t}+au_{x}+bu^{m}u_{x}+cu_{xxx}-\alpha u_{xxt}\nonumber \\&\quad +\,\lambda u_{xxxxt}-\mu u_{}=0, \end{aligned}$$

(10)

where $a, b, c, \mu$ are real constants, $\alpha ,\lambda$ are positive constants, m is a positive integer, which indicates the power law nonlinearity.

On the other hand, the following Camassa–Holm equation was first proposed by Camassa and Holm [56] for modeling the unidirectional propagation of irrotational water wave over a planar wall

$$\begin{aligned} u_{t}+2\kappa u_x-u_{xxt}+3uu_x=2u_xu_{xx}+uu_{xxx}, \end{aligned}$$

(11)

where $\kappa$ is a constant related to gravity and initial undisturbed water depth. The exact traveling wave solutions of the Camassa–Holm equation and modified Camassa–Holm equation are derived in [57–60].

More recently, the Novikov equation

$$\begin{aligned} u_{t}-u_{txx}+4u^2u_x=3uu_xu_{xx}+u^2u_{xxx}, \end{aligned}$$

(12)

has been discovered by Vladimir Novikov in a symmetry classification of nonlocal PDEs with quadratic or cubic nonlinearity [61]. Like the Camassa–Holm equation, the Novikov equation was shown to admit peakon solutions [62]. And readers can refer to [63–68] for theoretical studies of the Novikov equation.

In this paper, we consider exact solitary wave solution and numerical simulation for the following generalized Rosenau–Kawahara-RLW equation with generalized Novikov type perturbation

$$\begin{aligned}&u_{t}+au_{x}+bu^{m}u_{x}+cu_{xxx}-\alpha u_{xxt}\nonumber \\&\quad +\lambda u_{xxxxt}-\mu u_{}\nonumber \\&\quad =s\left( (m+1)u^{m-1}u_xu_{xx}+u^{m}u_{xxx}\right) , \nonumber \\&\quad x_{l}\le x \le x_{r},\quad 0\le t\le T, \end{aligned}$$

(13)

with initial condition

$$\begin{aligned} u(0,x)=u_{0}(x), \quad x_{l} \le x \le x_{r}, \end{aligned}$$

(14)

and boundary conditions

$$\begin{aligned}&u(x_l,t)=u(x_r,t)=0,\quad u_x(x_l,t)=u_x(x_r,t)=0,\nonumber \\&u_{xx}(x_l,t)=u_{xx}(x_r,t)=0, \quad 0\le t\le T, \end{aligned}$$

(15)

where $x_l$ is a large negative number, $x_r$ is a large positive number, $a, b, c, \mu , s$ are real constants, $\alpha ,\lambda$ are positive constants, m is a positive integer, which indicates the power law nonlinearity. Here we point out that the newly proposed perturbed Rosenau–Kawahara-RLW equation with power law nonlinearity (13) combines the generalized Rosenau–Kawahara-RLW equation (10) and the nonlinear terms (in general form) of the right-hand side of the Novikov equation (12). We note that when $m=1, a=2\kappa , b=3, c=0, \alpha =1, \lambda =0, \mu =0, s=1$, the above perturbed Rosenau–Kawahara-RLW equation with power law nonlinearity (13) reduced into the Camassa–Holm equation (11), and when $m=2, a=0, b=4, c=0, \alpha =1, \lambda =0, \mu =0, s=1$, the above perturbed Rosenau–Kawahara-RLW equation with power law nonlinearity (13) reduced into the Novikov equation (12).

In this work, we only discuss the solitary wave solution of Eq. (13) which will be derived in the next section. By solitary wave assumptions, the solitary solution and its derivatives have the following asymptotic values: $u\rightarrow 0$ as $x\rightarrow \pm \infty$, and $\frac{\partial ^n u}{\partial x^n}\rightarrow 0$ as $x\rightarrow \pm \infty$, for $n\ge 1$. Thus, the boundary conditions (15) are meaningful for the solitary solution of Eq. (13). In addition, we assume that the wave peak is initially located at $x=0$, and $x_l, x_r$, which are large numbers, are used to assure that the solitary wave peak is always located inside the domain $[x_l, x_r]$ during the time interval [0, T]. Similar set up are used in [40, 51].

When numerically solving differential equations, the total accuracy of a particular method is affected not only the order of accuracy of the method, but also other factors. The conservative property of the method is another factor that has the same or possibly even more impact on results. For example, one successful and active research is to construct structure-preserving schemes (or called symplectic schemes) for the ODE systems (see [69] and the references therein). Numerical experiments show that conservative difference scheme can simulate the conservative law of initial value problem better since it could avoid the nonlinear blow-up [19, 34, 70–73]. And Li et al. [70] even pointed out that in some areas, the ability to preserve some invariant properties of the original differential equation is a criterion to judge the success of a numerical simulation.

In the following, we will show that the initial boundary value problem (13)–(15) satisfies a fundamental energy conservative property. In addition, the Eq. (13) is nonlinear due to the third term in the left-hand side and the two terms in right-hand side. When considering the finite difference scheme for the Eq. (13), the usual Crank-Nicolson scheme will lead to a nonlinear scheme with heavy computation, while other standard linearized discretizations for the nonlinear term, e.g., one step Newton’s method or a second-order extrapolation method, will loss the energy conservative property. An ideal scheme should have relative less computational cost, can preserve energy, be unconditionally stable and maintain second-order accuracy.

In this paper, a three-level linearly implicit finite difference method for the initial value problem (13)–(15) will be presented. The fundamental energy conservation is preserved by the presented numerical scheme. The existence and uniqueness of the numerical solution are also proved. Moreover, numerical analysis shows that the method is second-order convergent both in time and space variables, and the method is unconditionally stable. Numerical results confirm well with the theoretical results.

The rest of the paper is organized as follows: Sect. 2 gives the exact solitary wave solution for the initial boundary value problem (13)–(15). Section 3 shows the energy conservation. Section 4 gives the detailed description of the three-level linearly implicit finite difference method, the proof for the discrete conservative property, the existence and uniqueness as well as the convergence and stability of the numerical solution. Numerical results are shown in Sect. 5. Conclusions are provided in the final section.

2 Exact solitary solution

Solitary solutions and other wave solutions are very important for the nonlinear models arose in many physics and engineering areas. Besides the references mentioned in the above section, there are a lot of related references which used different methods to find the solitons and other wave solutions for different nonlinear models. For example, [74] discussed the solitary solution for the Gear–Grimshaw model, [75] provided solitons, cnoidal waves and snoisal waves for the Whitham–Broer–Kaup system, while [76] gave the solitons and other solutions to the (3 + 1)-dimensional extended Kadomtsev–Petviashvili equation with power law nonlinearity. In addition, the fractional differential equations are also studied in the literature [77–79]. Readers can refer to [74–90] for more discussions on finding solitons and other wave solutions for different nonlinear models.

The sine-cosine method, as one of the most useful tools, uses the sine or cosine function as the wave form function to seek the traveling wave solution of a time-dependent partial differential equation, which has the advantage of reducing the nonlinear problem to a system of algebraic equations that can be easily solved by using a symbolic computation system such as Mathematica or Maple [51, 83–86].

For Eq. (13), one can obtain the exact solitary solutions by using the sine-cosine method. Firstly, we use an ansatz method to seek the following traveling wave solutions [51, 83–86]:

$$\begin{aligned} u(x,t)={\hat{u}}(\xi ),\quad \xi =x-vt, \end{aligned}$$

(16)

where v is referred as the wave velocity which is a constant to be determined later.

Under the transformation of (16), Eq. (13) can be reduced into:

$$\begin{aligned}&(a-v){\hat{u}}_{\xi }+b{\hat{u}}^m\hat{u}_{\xi }+(\alpha v+c){\hat{u}}_{\xi \xi \xi }\nonumber \\&\quad -(\lambda v+\mu )u_{\xi \xi \xi \xi \xi }\nonumber \\&\quad \quad =s\left( (m+1){\hat{u}}^{m-1}\hat{u}_{\xi }{\hat{u}}_{\xi \xi }+{\hat{u}}^{m} \hat{u}_{\xi \xi \xi }\right) . \end{aligned}$$

(17)

Using the sine-cosine method [51, 86], we may choose the solution of above reduced ODE (17) in the form

$$\begin{aligned} {{\hat{u}}}(\xi ) = \left\{ \begin{array}{ll} A\cos ^{\eta }(B\xi ), \ \ \ \ \ &{} \text {if } \, |\xi |<\frac{\pi }{2B},\\ 0,\ \ \ \ &{} \text {otherwise}, \end{array} \right. \end{aligned}$$

(18)

or in the form

$$\begin{aligned} {\hat{u}}(\xi ) = \left\{ \begin{array}{ll} A\sin ^{\eta }(B\xi ), \ \ \ \ \ &{} \text {if } \, |\xi |<\frac{\pi }{2B},\\ 0,\ \ \ \ &{} \text {otherwise}, \end{array} \right. \end{aligned}$$

(19)

where $A, B, \eta$ are parameters to be determined. Using (18), one have

$$\begin{aligned} {\hat{u}}_{\xi }&=-AB\eta \cos ^{\eta -1}(B\xi )\sin (B\xi ), \end{aligned}$$

(20)

$$\begin{aligned} {\hat{u}}_{\xi \xi }&=AB^2\eta (\eta -1)\cos ^{\eta -2}(B\xi )-AB^2\eta ^2\cos ^{\eta }(B\xi ), \end{aligned}$$

(21)

$$\begin{aligned} {\hat{u}}_{\xi \xi \xi }&=-AB^3\eta (\eta -1)(\eta -2)\cos ^{\eta -3}(B\xi )\sin (B\xi )\nonumber \\&\quad +AB^3\eta ^3\cos ^{\eta -1}(B\xi )\sin (B\xi ), \end{aligned}$$

(22)

and

$$\begin{aligned} {\hat{u}}_{\xi \xi \xi \xi \xi }&=\bigg (-AB^5\eta (\eta -1)(\eta -2)(\eta \nonumber \\&\quad \quad -\,3)(\eta -4) \cos ^{\eta -5}(B\xi )\nonumber \\&\quad \quad +2AB^5\eta (\eta -1)(\eta -2)(\eta ^2-2\eta \nonumber \\&\quad \quad +2)\cos ^{\eta -3}(B\xi )\nonumber \\&\quad \quad -AB^5\eta ^5\cos ^{\eta -1}(B\xi )\bigg )\sin (B\xi ). \end{aligned}$$

(23)

Substituting (20)–(23) into (17), one obtain

$$\begin{aligned}&(\lambda v+\mu )AB^5\eta (\eta -1)(\eta -2)(\eta -3)(\eta \nonumber \\&\qquad -4)\cos ^{\eta -5}(B\xi )\sin (B\xi )\nonumber \\&\qquad +\big (-(\alpha v+c)AB^3\eta (\eta -1)(\eta -2)\nonumber \\&\qquad -2AB^5(\lambda v+\mu )\eta (\eta -1)(\eta -2)(\eta ^2-2\eta \nonumber \\&\qquad +2)\big )\cos ^{\eta -3}(B\xi )\sin (B\xi )\nonumber \\&\qquad +\big (-AB\eta (a-v)+(\alpha v+c)AB^3\eta ^3\nonumber \\&\qquad +(\lambda v+\mu )AB^5\eta ^5\big )\cos ^{\eta -1}(B\xi )\sin (B\xi )\nonumber \\&\qquad -bA^{m+1}B\eta \cos ^{(m+1)\eta -1}(B\xi )\sin (B\xi )\nonumber \\&\quad =s\big ((m+2)A^{m+1}B^3\eta ^3\cos ^{(m+1)\eta -1}(B\xi )\nonumber \\&\qquad -A^{m+1}B^3(m+1)\eta ^2(\eta -1)\cos ^{(m+1)\eta -3}(B\xi )\nonumber \\&\qquad -A^{m+1}B^3\eta (\eta -1)(\eta \nonumber \\&\qquad -2)\cos ^{(m+1)\eta -3}(B\xi )\big )\sin (B\xi ). \end{aligned}$$

(24)

Balancing $\cos ^{\eta -5}(B\xi )$ and $\cos ^{(m+1)\eta -3}(B\xi )$, one obtain that $\eta -5=(m+1)\eta -3$, which gives $\eta =-\frac{2}{m}$. And setting the each coefficients of $\cos ^{j}(B\xi )$ ($j=\eta -3, \eta -1$) to be zero and noting that $\eta -3=(m+1)\eta -1$, one can obtain a set of equations for v, A, B as follows:

$$\begin{aligned}&(\lambda v+\mu )AB^5\eta (\eta -1)(\eta -2)(\eta -3)(\eta -4)\nonumber \\&\quad =-sA^{m+1}B^3\big ((m+1)\eta ^2(\eta -1)+\eta (\eta -1)(\eta -2)\big ),\end{aligned}$$

(25)

$$\begin{aligned}&\qquad -(\alpha v+c)AB^3\eta (\eta -1)(\eta -2)-bA^{m+1}B\eta \nonumber \\&\qquad -2AB^5(\lambda v+\mu )\eta (\eta -1)(\eta -2)(\eta ^2-2\eta +2)\nonumber \\&\quad =(2+m)sA^{m+1}B^3\eta ^3,\end{aligned}$$

(26)

$$\begin{aligned}&\qquad -AB\eta (a-v)+(\alpha v+c)AB^3\eta ^3\nonumber \\&\qquad +(\lambda v+\mu )AB^5\eta ^5=0. \end{aligned}$$

(27)

(25)–(27) give the following non-zeros solutions:

$$\begin{aligned} B^2=\frac{-B_0\pm \sqrt{B^2_0-4A_0C_0}}{2A_0}, \end{aligned}$$

(28)

where

$$\begin{aligned} A_0&=-32\lambda s c+32\alpha s\mu -16\lambda msc+16\alpha ms\mu \nonumber \\&\quad -64\alpha m^2 s\mu -32\alpha m^3s\mu +32\lambda m^3sc+64\lambda scm^2, \end{aligned}$$

(29)

$$\begin{aligned} B_0&=-8\lambda m^5sa-16\lambda m^2sa-8\mu m^5s-28bm^2\lambda c\nonumber \\&\quad -16\mu m^4s-24bm^3\lambda c+24bm^3\mu \alpha -4\mu m^3s\nonumber \\&\quad +28bm^2\mu \alpha -16\lambda sam-16\mu ms-8bm\lambda c\nonumber \\&\quad -4\lambda m^3sa+8bm\mu \alpha -16\mu m^2s-16\lambda sam^4, \end{aligned}$$

(30)

$$\begin{aligned} C_0&=2bm^3\mu +6bm^5\lambda a+7bm^4\lambda a+7bm^4\mu \nonumber \\&\quad -4c m^3s-6\alpha m^4sa-6c m^4s-2\alpha m^5sa\nonumber \\&\quad -4\alpha m^3sa-2c m^5s+6bm^5\mu +2bm^3\lambda a, \end{aligned}$$

(31)

and

$$\begin{aligned}&v=\frac{a-cB^2\eta ^2-\mu B^4\eta ^4}{1+\alpha B^2\eta ^2+\lambda B^4\eta ^4}, \end{aligned}$$

(32)

$$\begin{aligned}&A=\left( \frac{(\lambda v+\mu )B^2(\eta -2)(\eta -3)(\eta -4)}{s(2-(m+2)\eta )}\right) ^{\frac{1}{m}}. \end{aligned}$$

(33)

The results can be classified into the following four categories.

(1) $\frac{-B_0+\sqrt{B^2_0-4A_0C_0}}{2A_0}>0$ and $\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}>0$. We can obtain two periodic solutions,

$$\begin{aligned} u(x,t)={\hat{u}}(\xi )=A\cos ^{-\frac{2}{m}}\left( B\left( x-vt\right) \right) , \end{aligned}$$

(34)

where B is given by $\sqrt{\frac{-B_0+\sqrt{B^2_0-4A_0C_0}}{2A_0}}$ or

$\sqrt{\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}}$ and v, A are given by (32)–(33).

(2) $\frac{-B_0+\sqrt{B^2_0-4A_0C_0}}{2A_0}>0$ and $\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}<0$. We can obtain a periodic solution

$$\begin{aligned} u(x,t)={\hat{u}}(\xi )=A\cos ^{-\frac{2}{m}}\left( B\left( x-vt\right) \right) , \end{aligned}$$

(35)

where B is given by $\sqrt{\frac{-B_0+\sqrt{B^2_0-4A_0C_0}}{2A_0}}$ and v, A are given by (32)–(33).

In addition, we can obtain a solitary solution,

$$\begin{aligned} u(x,t)={\hat{u}}(\xi )=A\text {sech}^{\frac{2}{m}} \left( B^*\left( x-vt\right) \right) , \end{aligned}$$

(36)

where $B^*$ is given by $B^*=\sqrt{-\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}}$ and v, A are given by (32)–(33).

(3) $\frac{-B_0+\sqrt{B^2_0-4A_0C_0}}{2A_0}<0$ and $\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}>0$. We can obtain a periodic solution

$$\begin{aligned} u(x,t)={\hat{u}}(\xi )=A\cos ^{-\frac{2}{m}} \left( B\left( x-vt\right) \right) , \end{aligned}$$

(37)

where B is given by $\sqrt{\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}}$ and v, A are given by (32)–(33).

In addition, we can obtain a solitary solution,

$$\begin{aligned} u(x,t)={\hat{u}}(\xi )=A\text {sech}^{\frac{2}{m}} \left( B^*\left( x-vt\right) \right) , \end{aligned}$$

(38)

where $B^*$ is given by $B^*=\sqrt{-\frac{-B_0+\sqrt{B^2_0-4A_0C_0}}{2A_0}}$ and v, A are given by (32)–(33).

(4) $\frac{-B_0+\sqrt{B^2_0-4A_0C_0}}{2A_0}<0$ and $\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}<0$. We can obtain two solitary solutions,

$$\begin{aligned} u(x,t)={\hat{u}}(\xi )=A\text {sech}^{\frac{2}{m}} \left( B^*\left( x-vt\right) \right) , \end{aligned}$$

(39)

where $B^*$ is given by $\sqrt{-\frac{-B_0+\sqrt{B^2_0-4A_0C_0}}{2A_0}}$ or

$\sqrt{-\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}}$ and v, A are given by (32)–(33).

In this paper, we focus on the study of the solitary wave solution.

3 Conservative property

Equations (13)–(15) satisfy the following energy conservative property.

Theorem 1

Suppose $u_0\in C^{7}_{0}[x_l,x_r]$, then the solution of (13)–(15) satisfies the energy conservation law:

$$\begin{aligned} E(t)&=\int ^{x_r}_{x_l}u^2(x,t)+\alpha u^2_{x}(x,t)+\lambda u^2_{xx}(x,t)dx\nonumber \\&=\int ^{x_r}_{x_l}u^2(x,0)+\alpha u^2_{x}(x,0)+\lambda u^2_{xx}(x,0)dx\nonumber \\&=E(0), \end{aligned}$$

(40)

for any $t\in [0,T]$, where $C^{7}_{0}[x_l,x_r]$ is the set of functions which are seventh-order continuous differentiable in the interval $[x_l, x_r]$ and have compact supports inside $(x_l, x_r)$.

Proof

Multiplying (13) by 2u and integrating over the interval $[x_l, x_r]$, one get

$$\begin{aligned}&\frac{d}{dt}\int ^{x_r}_{x_l}u^2dx+a\int ^{x_r}_{x_l}2uu_xdx\nonumber \\&\quad \quad +b \int ^{x_r}_{x_l}2u^{m+1}\left( u\right) _xdx\nonumber \\&\quad \quad +c\int ^{x_r}_{x_l}2uu_{xxx}dx-\alpha \int ^{x_r}_{x_l}2uu_{xxt}dx\nonumber \\&\quad \quad +\lambda \int ^{x_r}_{x_l}2uu_{xxxxt}dx-\mu \int ^{x_r}_{x_l}2uu_{}dx\nonumber \\&\quad \quad =2s\int ^{x_r}_{x_l}\left( u^{m-1}u_xu_{xx}+(u^mu_{xx})_x\right) udx, \end{aligned}$$

(41)

where we note that $(m+1)u^{m-1}u_xu_{xx}+u^{m}u_{xxx}$ $=u^{m-1}u_xu_{xx}+(u^mu_{xx})_x$.

Using the integration by parts, one can easily obtain

$$\begin{aligned}&\int ^{x_r}_{x_l}uu_xdx=\int ^{x_r}_{x_l}udu=\frac{1}{2} \left( u^2(x_r,t)\right. \\&\quad \quad \left. -u^2(x_l,t)\right) =0,\\&\quad \int ^{x_r}_{x_l}u^{m+1}\left( u\right) _xdx=\int ^{x_r}_{x_l} u^{m+1}du\\&\quad \quad =\frac{1}{m+2}u^{m+2}\big |^{x_r}_{x_l}=0,\\&\quad \int ^{x_r}_{x_l}uu_{xxx}dx=uu_{xx}\big |^{x_r}_{x_l}-\int ^{x_r}_{x_l}u_{xx}du\\&\quad \quad =-\int ^{x_r}_{x_l}u_{xx}u_xdx\\&\quad \quad =-\int ^{x_r}_{x_l}u_xdu_x=-\frac{1}{2}u^2_x\big |^{x_r}_{x_l}=0, \\&\quad \int ^{x_r}_{x_l}uu_{xxt}dx=uu_{xt}\big |^{x_r}_{x_l} -\frac{1}{2}\frac{d}{dt}\int ^{x_r}_{x_l}u^2_{x}dx\\&\quad \quad =-\frac{1}{2}\frac{d}{dt}\int ^{x_r}_{x_l}u^2_{x}dx,\\&\quad \int ^{x_r}_{x_l}uu_{xxxxt}dx=\int ^{x_r}_{x_l}udu_{xxxt}\\&\quad \quad =uu_{xxxt}\big |^{x_r}_{x_l}-\int ^{x_r}_{x_l}u_xu_{xxxt}dx\\&\quad \quad =-u_xu_{xxt}\big |^{x_r}_{x_l}+\frac{1}{2} \frac{d}{dt}\int ^{x_r}_{x_l}u^{2}_{xx}dx\\&\quad \quad =\frac{1}{2}\frac{d}{dt}\int ^{x_r}_{x_l}u^{2}_{xx}dx,\\&\quad \int ^{x_r}_{x_l}uu_{}dx=uu_{xxxx} \big |^{x_r}_{x_l}-\int ^{x_r}_{x_l}u_{xxxx}u_xdx\\&\quad \quad =-u_xu_{xxx}\big |^{x_r}_{x_l}+\int ^{x_r}_{x_l} u_{xxx}u_{xx}dx=\frac{1}{2}u^{2}_{xx}\big |^{x_r}_{x_l}=0,\\&\quad \int ^{x_r}_{x_l}\left( u^{m-1}u_xu_{xx}+(u^mu_{xx})_x\right) udx\\&\quad \quad =\int ^{x_r}_{x_l}u^{m}u_xu_{xx}dx-\int ^{x_r}_{x_l}u^{m}u_xu_{xx}dx=0, \end{aligned}$$

where the boundary conditions (15) are used.

Thus, only the first, fifth and sixth term in the left-hand side of (41) are nonzero, all other terms are zero. This yields,

$$\begin{aligned} \frac{d}{dt}\int ^{x_r}_{x_l}u^2+\alpha u^2_{x}+\lambda u^2_{xx}dx=0. \end{aligned}$$

(42)

Therefore,

$$\begin{aligned} E(t)&=\int ^{x_r}_{x_l}u^2(x,t)+\alpha u^2_{x}(x,t)+\lambda u^2_{xx}(x,t)dx\nonumber \\&=\int ^{x_r}_{x_l}u^2(x,0)+\alpha u^2_{x}(x,0)+\lambda u^2_{xx}(x,0)dx\nonumber \\&=E(0), \end{aligned}$$

(43)

for any $t\in [0,T]$. This completes the proof.

4 Numerical method

In this section, we give a complete description of our numerical method for the problem (13)–(15). We first describe our solution domain and its grid. The solution domain is defined as $\Omega =\{(x,t) | x_l\le x\le x_r,\ 0\le t\le T\}$, which is covered by a uniform grid $\Omega _{h}=\{(x_i,t_n)|x_i=x_l+ih,\ t_n=n\tau ,\ i=0, \cdots , M,\ n=0, \cdots , N\}$, with spacing $h=\frac{x_r-x_l}{M},\ \tau =\frac{T}{N}$. We denote $U^{n}_{i}$ is the numerical approximation of $u(x_i,t_n)$ and $Z^{0}_{h}=\{U=(U_i)|U_{-1}=U_{0}=U_{1}=U_{M-1}=U_{M}=U_{M+1}=0,\ i=-1,0,1, \cdots , M-1,M, M+1\}$. For convenience, the difference operators, inner product and norms are defined as follows:

$$\begin{aligned}&\bar{U}^{n}_{i}=\frac{U^{n+1}_{i}+U^{n-1}_{i}}{2}, \quad (U^{n}_i)_{t}=\frac{U^{n+1}_i-U^{n-1}_i}{2\tau },\\&(U^{n}_{i})_{x}=\frac{U^{n}_{i+1}-U^{n}_i}{h},\quad (U^{n}_{i})_{\bar{x}}=\frac{U^{n}_{i}-U^{n}_{i-1}}{h}, \\&(U^{n}_{i})_{\hat{x}}=\frac{U^{n}_{i+1}-U^{n}_{i-1}}{2h},\quad (U^n,V^n)=h\sum ^{M-1}_{j=1}U^{n}_iV^{n}_i, \\&\parallel U^n\parallel ^2=(U^n,U^n),\quad \parallel U^n\parallel _{\infty }=\max _{1\le i \le M-1}|U^{n}_i|. \end{aligned}$$

The essential of our scheme is that the third term in the left-hand side of (13) is rewritten and discretized as

$$\begin{aligned} bu^mu_x&=\frac{b}{m+2}\left( u^mu_x+(u^{m+1})_x\right) \nonumber \\&\approx \frac{b}{m+2}\left[ (U^n_i)^{m}(\bar{U}^{n}_{i})_{\hat{x}} +((U^n_i)^{m}\bar{U}^{n}_{i})_{\hat{x}}\right] , \end{aligned}$$

and which is a second-order approximation around $(x_i=x_l+ih,t_{n}=n\tau )$. Moreover, the nonlinear terms in the right-hand side of (13) are rewritten and discretized as:

$$\begin{aligned}&s\left( (m+1)u^{m-1}u_xu_{xx}+u^{m}u_{xxx}\right) \\&\quad =s\left( u^{m-1}u_xu_{xx}+(u^mu_{xx})_x\right) \\&\quad \approx s\left( (U^n_i)^{m-1}(\bar{U}^n_i)_{\hat{x}} (U^n_i)_{x\bar{x}}\right. \\&\quad \quad \left. +\left( (U^n_i)^{m-1}\bar{U}^n_i(U^n_i)_{x \bar{x}}\right) _{\hat{x}}\right) , \end{aligned}$$

which is a second-order approximation around $(x_i=x_l+ih,t_n=n\tau$). Other terms in (13) are discretized by using the standard second-order central difference method.

The detailed numerical scheme is as follows:

$$\begin{aligned} (U^n_i)_t&+a(\bar{U}^{n}_{i})_{\hat{x}}+\frac{b}{m+2}\big [(U^n_i)^{m} (\bar{U}^{n}_{i})_{\hat{x}}\nonumber \\&+((U^n_i)^{m}\bar{U}^{n}_{i})_{\hat{x}}\big ]\nonumber \\&+c(\bar{U}^{n}_{i})_{x\bar{x}\hat{x}}-\alpha (U^{n}_i)_{x\bar{x}t} +\lambda (U^{n}_{i})_{xx\bar{x}\bar{x}t}\nonumber \\&-\mu (\bar{U}^{n}_{i})_{xx \bar{x}\bar{x}\hat{x}}\nonumber \\&=s\left( (U^n_i)^{m-1}(\bar{U}^n_i)_{\hat{x}}(U^n_i)_{x\bar{x}}\right. \nonumber \\&\left. +\left( (U^n_i)^{m-1}\bar{U}^n_i(U^n_i)_{x\bar{x}}\right) _{\hat{x}}\right) ,\nonumber \\&2\le i\le M-2,\ \ 1\le n \le N-1. \end{aligned}$$

(44)

and

$$\begin{aligned}&U^{0}_{i}=u_0(x_i), \quad 0\le i\le M, \end{aligned}$$

(45)

$$\begin{aligned}&U^{j}_{0}= U^{j}_{M}=0, \quad (U^{j}_{0})_{\hat{x}}= (U^{j}_{M})_{\hat{x}}=0,\nonumber \\&(U^{j}_{0})_{x\bar{x}}= (U^{j}_{M})_{x\bar{x}}=0, \quad 0\le j \le N. \end{aligned}$$

(46)

Obviously, the above conditions (46) will give $U^j_1=U^j_{M-1}=0$ on two internal points and $U^j_{-1}=U^j_{M+1}=0$ on two fictitious points, for any $0\le j\le N$. Thus, $U^j \in Z^{0}_{h}$, for any $0\le j\le N$. And we can see that (44) is a three-level linear implicit scheme and the coefficient matrix of linear equation of (44) is banded; thus, the resulting linear algebra equation in (44) can be solved efficiently using a linear algebra equation solver, such as the LU decomposition method.

Since the scheme is a three-level method, to start the computation, we need to give the method for computation of $U^1$. The $U^1$ is computed through the following Crank-Nicolson scheme:

$$\begin{aligned}&\frac{U^1_i-U^0_i}{\tau }+a\left( \frac{U^1_i+U^0_i}{2}\right) _{\hat{x}}+\frac{b}{m+2}\left[ \left( \frac{U^1_i+U^0_i}{2}\right) ^{m}\right. \nonumber \\&\quad \left. \times \left( \frac{U^1_i+U^0_i}{2}\right) _{\hat{x}}+\left( \left( \frac{U^1_i+U^0_i}{2}\right) ^{m}\left( \frac{U^1_i+U^0_i}{2}\right) \right) _{\hat{x}}\right] \nonumber \\&\quad +c\left( \frac{U^1_i+U^0_i}{2}\right) _{x\bar{x}\hat{x}}-\alpha \left( \frac{U^{1}_i-U^{0}_i}{\tau }\right) _{x\bar{x}}\nonumber \\&\quad +\lambda \left( \frac{U^1_i-U^0_i}{\tau }\right) _{xx\bar{x}\bar{x}}-\mu \left( \frac{U^1_i+U^0_i}{2}\right) _{xx\bar{x}\bar{x}\hat{x}}\nonumber \\&=s\left( \left( \frac{U^1_i+U^0_i}{2}\right) ^{m-1}\left( \frac{U^1_i+U^0_i}{2}\right) _{\hat{x}}\left( \frac{U^1_i+U^0_i}{2}\right) _{x\bar{x}}\right. \nonumber \\&\left. \quad +\left( \left( \frac{U^1_i+U^0_i}{2}\right) ^{m-1}\left( \frac{U^1_i+U^0_i}{2}\right) _{x\bar{x}}\right) _{\hat{x}}\right) . \end{aligned}$$

(47)

where it is a nonlinear scheme and is second-order accurate both in time and space variables.

The following Lemmas are well-known results, which are essential for existence, uniqueness, convergence, and stability of the numerical solution. In the rest part of the paper, unless otherwise indicated, C is the notation referring to a general positive constant, which may have the difference values in different contexts.

Lemma 1

For any two mesh functions $U, V\in Z^{0}_{h}$, one have

$$\begin{aligned}&(U_{\hat{x}}, V)=-(U, V_{\hat{x}}), \quad (U_{x}, V)=-(U, V_{\bar{x}}), \\&(U_{x\bar{x}}, V)=-(U_x,V_x), \end{aligned}$$

Furthermore,

$$\begin{aligned} (U, U_{xx\bar{x}\bar{x}})=\parallel U_{x\bar{x}}\parallel ^2. \end{aligned}$$

Lemma 2

For any mesh function $U\in Z^{0}_{h}$, one have

$$\begin{aligned} (U_{\hat{x}},U)=0,\quad (U_{x\bar{x}\hat{x}},U)=0,\quad (U_{xx\bar{x}\bar{x}\hat{x}},U)=0. \end{aligned}$$

Lemma 3

(Discrete Sobolev’s inequality (Lemma 1, page 110 of [91]) For any mesh function $U\in Z^{0}_{h}$, one have

$$\begin{aligned} \parallel U\parallel _{\infty }\le C\parallel U_{x}\parallel . \end{aligned}$$

4.1 Discrete conservation

Theorem 2

Suppose $u_0\in C^{7}_{0}[x_l,x_r]$, then the solution of finite difference scheme (44)–(46) satisfies $\parallel U^{n}\parallel _{\infty }\le C$ and $\parallel U^{n}_{x}\parallel _{\infty }\le C$, for any $0\le n \le N$. Moreover, the following discrete energy conservative identity is valid:

$$\begin{aligned}&E^n\triangleq \frac{\parallel U^{n+1}\parallel ^2+\parallel U^{n}\parallel ^2}{2}+\alpha \frac{\parallel U^{n+1}_{x}\parallel ^2+\parallel U^{n}_{x}\parallel ^2}{2}\nonumber \\&\qquad +\,\lambda \frac{\parallel U^{n+1}_{x\bar{x}}\parallel ^2+\parallel U^{n}_{x\bar{x}}\parallel ^2}{2}\nonumber \\&\quad =\frac{\parallel U^{1}\parallel ^2+\parallel U^{0}\parallel ^2}{2}+\alpha \frac{\parallel U^{1}_{x}\parallel ^2+\parallel U^{0}_{x}\parallel ^2}{2}\nonumber \\&\qquad +\,\lambda \frac{\parallel U^{1}_{x\bar{x}}\parallel ^2+\parallel U^{0}_{x\bar{x}}\parallel ^2}{2}\triangleq E^0, \end{aligned}$$

(48)

for any $0\le n \le N-1$, where $E^{n}$ is the discrete energy at time $t=(n+\frac{1}{2})\tau$.

Proof

Taking the conditions $U^j_{-1}=U^j_{0}=U^j_{1}=U^j_{M-1}=U^j_{M}=U^j_{M+1}=0$ ($0\le j \le N$) into account, and after computing the inner product of Eq. (44) with $\bar{U}^{n}$, i. e., $\frac{U^{n+1}+U^{n-1}}{2}$, we have

$$\begin{aligned}&\frac{\parallel U^{n+1}\parallel ^2-\parallel U^{n-1}\parallel ^2}{4\tau }+a(\bar{U}^n_{\hat{x}},\bar{U}^n)\nonumber \\&\quad +\frac{b}{m+2}\left( (U^n)^{m}(\bar{U}^{n})_{\hat{x}}+((U^n)^{m}\bar{U}^{n})_{\hat{x}},\bar{U}^{n}\right) \end{aligned}$$

(49)

$$\begin{aligned}&\quad +c(\bar{U}^{n}_{x\bar{x}\hat{x}},\bar{U}^{n})-\alpha (U^n_{x\bar{x}t},\bar{U}^{n})+\lambda (U^n_{xx\bar{x}\bar{x}t},\bar{U}^{n})\nonumber \\&\quad -\mu (\bar{U}^{n}_{xx\bar{x}\bar{x}\hat{x}},\bar{U}^{n})=s\left( (U^n)^{m-1}(\bar{U}^n)_{\hat{x}}(U^n)_{x\bar{x}},\bar{U}^{n}\right) \nonumber \\&\quad +s\left( \left( (U^n)^{m-1}\bar{U}^n(U^n)_{x\bar{x}}\right) _{\hat{x}},\bar{U}^{n}\right) . \end{aligned}$$

(50)

By using lemma 2, we get

$$\begin{aligned}&(\bar{U}^{n}_{\hat{x}},\bar{U}^{n})=0, \quad (\bar{U}^{n}_{x\bar{x}\hat{x}},\bar{U}^{n})=0,\nonumber \\&\quad (\bar{U}^{n}_{xx\bar{x}\bar{x}\hat{x}},\bar{U}^{n})=0. \end{aligned}$$

(51)

Moreover,

$$\begin{aligned}&\left( \left[ \left( U^n\right) ^{m}\left( \bar{U}^{n}\right) _{\hat{x}}+\left( \left( U^n\right) ^{m}\bar{U}^{n}\right) _{\hat{x}}\right] ,\bar{U}^{n}\right) \nonumber \\&\quad =\left( (U^n)^{m}(\bar{U}^{n})_{\hat{x}},\bar{U}^{n}\right) +\left( ((U^n)^{m}\bar{U}^{n})_{\hat{x}},\bar{U}^{n}\right) \nonumber \\&\quad =\left( (U^n)^{m}(\bar{U}^{n})_{\hat{x}},\bar{U}^{n}\right) -\left( (U^n)^{m}\bar{U}^{n},(\bar{U}^{n})_{\hat{x}}\right) \nonumber \\&\quad =0, \end{aligned}$$

(52)

and

$$\begin{aligned}&\left( (U^n)^{m-1}(\bar{U}^n)_{\hat{x}}(U^n)_{x\bar{x}},\bar{U}^{n}\right) \nonumber \\&\qquad +\left( \left( (U^n)^{m-1}\bar{U}^n(U^n)_{x\bar{x}}\right) _{\hat{x}},\bar{U}^{n}\right) \nonumber \\&\quad =\left( (U^n)^{m-1}(\bar{U}^n)_{\hat{x}}(U^n)_{x\bar{x}},\bar{U}^{n}\right) \nonumber \\&\qquad -\left( (U^n)^{m-1}\bar{U}^n(U^n)_{x\bar{x}},(\bar{U}^{n})_{\hat{x}}\right) \nonumber \\&\quad =0, \end{aligned}$$

(53)

where lemma 1 is used. $\square$

In addition,

$$\begin{aligned}&(U^n_{xx\bar{x}\bar{x}t},\bar{U}^{n})=\frac{\parallel U^{n+1}_{x\bar{x}}\parallel ^2-\parallel U^{n-1}_{x\bar{x}}\parallel ^2}{4\tau },\nonumber \\&(U^n_{x\bar{x}t},\bar{U}^{n})=-\frac{\parallel U^{n+1}_{x}\parallel ^2-\parallel U^{n-1}_{x}\parallel ^2}{4\tau }, \end{aligned}$$

(54)

where boundary conditions (45) and (46) are used.

Thus,

$$\begin{aligned}&\parallel U^{n+1}\parallel ^2-\parallel U^{n-1}\parallel ^2+\alpha \parallel U^{n+1}_{x}\parallel ^2-\nonumber \\&\alpha \parallel U^{n-1}_{x}\parallel ^2+\lambda \parallel U^{n+1}_{x\bar{x}}\parallel ^2-\lambda \parallel U^{n-1}_{x\bar{x}}\parallel ^2=0, \end{aligned}$$

(55)

for any $1\le n\le N-1$. This is equivalent to

$$\begin{aligned}&\frac{\parallel U^{n+1}\parallel ^2+\parallel U^{n}\parallel ^2}{2}+\alpha \frac{\parallel U^{n+1}_{x}\parallel ^2+\parallel U^{n}_{x}\parallel ^2}{2}\nonumber \\&\quad +\lambda \frac{\parallel U^{n+1}_{x\bar{x}}\parallel ^2+\parallel U^{n}_{x\bar{x}}\parallel ^2}{2}=\nonumber \\&\frac{\parallel U^{n}\parallel ^2+\parallel U^{n-1}\parallel ^2}{2}+\alpha \frac{\parallel U^{n}_{x}\parallel ^2+\parallel U^{n-1}_{x}\parallel ^2}{2}\nonumber \\&\quad +\lambda \frac{\parallel U^{n}_{x\bar{x}}\parallel ^2+\parallel U^{n-1}_{x\bar{x}}\parallel ^2}{2}, \end{aligned}$$

(56)

for any $1\le n\le N-1$. This further yields

$$\begin{aligned} E^n=E^0, \quad \text {for any}\ 1\le n\le N-1, \end{aligned}$$

(57)

which is actually the energy conservation law (48).

Multiplying (47) both sides by $\frac{U^1_i+U^0_i}{2}$ and using the similar techniques as above, one can obtain

$$\begin{aligned}&\parallel U^{0}\parallel ^2+\alpha \parallel U^{0}_{x}\parallel ^2+\lambda \parallel U^{0}_{x\bar{x}}\parallel ^2\nonumber \\&\quad =\parallel U^{1}\parallel ^2+\alpha \parallel U^{1}_{x}\parallel ^2+\lambda \parallel U^{1}_{x\bar{x}}\parallel ^2. \end{aligned}$$

(58)

Thus, (57) can be rewritten as

$$\begin{aligned} E^n=\parallel U^{0}\parallel ^2+\alpha \parallel U^{0}_{x}\parallel ^2+\lambda \parallel U^{0}_{x\bar{x}}\parallel ^2. \end{aligned}$$

(59)

Since $u_0\in C^7_0[x_l, x_r]$ and the initial condition (45) are used in the numerical method, the right-hand side of (59) is bounded. By assumptions, $\alpha , \lambda$ are positive constants, therefore,

$$\begin{aligned} \parallel U^{n}_{x}\parallel \le C,\ \ \parallel U^{n}_{x\bar{x}}\parallel \le C,\quad \text {for any}\ 0\le n\le N. \end{aligned}$$

(60)

By using lemma 3, we have $\parallel U^{n}\parallel _{\infty }\le C$.

In addition, through direct computation, one can verify that

$$\begin{aligned} \parallel U^{n}_{xx}\parallel = \parallel U^{n}_{x\bar{x}}\parallel , \quad \text {for any}\ 0\le n\le N. \end{aligned}$$

(61)

Thus,

$$\begin{aligned} \parallel U^{n}_{xx}\parallel \le C, \quad \text {for any}\ 0\le n\le N. \end{aligned}$$

(62)

Again by using lemma 3, we have $\parallel U^{n}_x\parallel _{\infty }\le C$. This completes the proof.

4.2 Existence and uniqueness

Theorem 3

The finite difference scheme (44)–(46) has a unique solution.

Proof

To prove the theorem, we proceed by the mathematical induction. Suppose $U^1,\cdots ,U^{n} (1\le n\le N-1)$ are solved uniquely, we now consider the Eq. (44) for $U^{n+1}$. Assume that $U^{n+1,1},U^{n+1,2}$ are two solutions of (44) and let $W^{n+1}=U^{n+1,1}-U^{n+1,2}$, then it is easy to verify that $W^{n+1}$ satisfies the following equation:

$$\begin{aligned}&\frac{1}{2\tau }W^{n+1}_i+\frac{a}{2}\left( W^{n+1}_i\right) _{\hat{x}}\nonumber \\&\qquad +\frac{b}{2(m+2)}\big [(U^n_i)^{m}\left( W^{n+1}_{i}\right) _{\hat{x}}\nonumber \\&\qquad +((U^n_i)^{m}W^{n+1}_{i})_{\hat{x}}\big ]\nonumber \\&\qquad +\frac{c}{2}\left( W^{n+1}_{i}\right) _{x\bar{x}\hat{x}}\nonumber \\&\qquad -\frac{\alpha }{2\tau }\left( W^{n+1}_{i}\right) _{x\bar{x}}+\frac{\lambda }{2\tau }(W^{n+1}_{i})_{xx\bar{x}\bar{x}}\nonumber \\&\qquad -\frac{\mu }{2}(W^{n+1}_{i})_{xx\bar{x}\bar{x}\hat{x}}\nonumber \\&\quad =\frac{s}{2}\left( (U^n_i)^{m-1}\left( W^{n+1}_i\right) _{\hat{x}}(U^n_i)_{x\bar{x}}\right. \nonumber \\&\qquad \left. +\left( (U^n_i)^{m-1}W^{n+1}_i(U^n_i)_{x\bar{x}}\right) _{\hat{x}}\right) . \end{aligned}$$

(63)

$\square$

Taking the inner product of (63) with $W^{n+1}$, we have

$$\begin{aligned}&\frac{1}{2\tau }\parallel W^{n+1}\parallel ^2+\frac{\alpha }{2\tau }\parallel W^{n+1}_{x}\parallel ^2\nonumber \\&\quad + \frac{\lambda }{2\tau }\parallel W^{n+1}_{x\bar{x}}\parallel ^2=0, \end{aligned}$$

(64)

where

$$\begin{aligned}&\left( W^{n+1}_{x\bar{x}}, W^{n+1}\right) =-\left( W^{n+1}_{x},W^{n+1}_{x}\right) ,\nonumber \\&\quad \left( W^{n+1}_{xx\bar{x}\bar{x}},W^{n+1}\right) =\parallel W^{n+1}_{x\bar{x}}\parallel ^2,\nonumber \\&\quad \left( W^{n+1}_{xx\bar{x}\bar{x}\hat{x}},W^{n+1}\right) =0,\nonumber \\&\quad \left( W^{n+1}_{x\bar{x}\hat{x}},W^{n+1}\right) =0,\quad (W^{n+1}_{\hat{x}},W^{n+1})=0,\nonumber \\&\quad \left( \left[ \left( U^n\right) ^{m}W^{n+1}_{\hat{x}}+\left( \left( U^n\right) ^{m}W^{n+1}\right) _{\hat{x}}\right] ,W^{n+1}\right) =0,\nonumber \\&\quad \left( (U^n)^{m-1}W^{n+1}_{\hat{x}}U^n_{x\bar{x}}\right. \nonumber \\&\left. \qquad \qquad +\left( (U^n)^{m-1}W^{n+1}U^n_{x\bar{x}}\right) _{\hat{x}}, W^{n+1}\right) \nonumber \\&\quad \quad =0, \end{aligned}$$

(65)

are used. The first five identities of (65) are directly from lemma 1 and 2, and the sixth one can be obtained as follows:

$$\begin{aligned}&\left( \left[ \left( U^n\right) ^{m}W^{n+1}_{\hat{x}}\right. \right. \nonumber \\&\left. \left. \qquad +\left( \left( U^n\right) ^{m}W^{n+1}\right) _{\hat{x}}\right] ,W^{n+1}\right) \nonumber \\&\quad =\left( \left( U^n\right) ^{m}W^{n+1}_{\hat{x}},W^{n+1}\right) \nonumber \\&\qquad +\left( \left( \left( U^n\right) ^{m}W^{n+1}\right) _{\hat{x}},W^{n+1}\right) \nonumber \\&\quad =\left( \left( U^n\right) ^{m}W^{n+1}_{\hat{x}},W^{n+1}\right) \nonumber \\&\qquad -\left( \left( U^n\right) ^{m}W^{n+1},W^{n+1}_{\hat{x}}\right) \nonumber \\&\quad =0. \end{aligned}$$

(66)

And the last one can be obtained through:

$$\begin{aligned}&\left( (U^n)^{m-1}W^{n+1}_{\hat{x}}U^n_{x\bar{x}}\right. \nonumber \\&\left. \qquad +\left( (U^n)^{m-1}W^{n+1}(U^n)_{x\bar{x}}\right) _{\hat{x}}, W^{n+1}\right) \nonumber \\&\quad =\left( (U^n)^{m-1}W^{n+1}_{\hat{x}}U^n_{x\bar{x}}, W^{n+1}\right) \nonumber \\&\qquad +\left( \left( (U^n)^{m-1}W^{n+1}U^n_{x\bar{x}}\right) _{\hat{x}},W^{n+1}\right) \nonumber \\&\quad =\left( (U^n)^{m-1}W^{n+1}_{\hat{x}}U^n_{x\bar{x}}, W^{n+1}\right) \nonumber \\&\qquad -\left( (U^n)^{m-1}W^{n+1}U^n_{x\bar{x}},W^{n+1}_{\hat{x}}\right) \nonumber \\&\quad =0. \end{aligned}$$

(67)

From (64) and the definition of the $\parallel \cdot \parallel$-norm, one can see that (64) has only a trivial solution. Thus, (44) determines $U^{n+1}$ uniquely. This completes the proof.

4.3 Convergence and stability

Let u(x, t) be the solution of problem (13)–(15), $U^n_i$ be the solution of the numerical schemes (44)–(46), and $u^n_i=u(x_i,t_n),\ e^n_i=u^n_i-U^n_i$, then the truncation error of the scheme (44)–(46) can be obtained as follows:

$$\begin{aligned} r^n_i&=\left( e^n_i\right) _t+a(\bar{e}^{n}_i)_{\hat{x}}+\frac{b}{m+2}\bigg [(u^n_i)^{m}(\bar{u}^{n}_{i})_{\hat{x}}\nonumber \\&\quad +\left( \left( u^n_i\right) ^{m}\bar{u}^{n}_{i}\right) _{\hat{x}}\nonumber \\&\quad -\left( U^n_i\right) ^{m}\left( \bar{U}^{n}_{i}\right) _{\hat{x}}-\left( \left( U^n_i\right) ^{m}\bar{U}^{n}_{i}\right) _{\hat{x}}\bigg ]\nonumber \\&\quad +c\left( \bar{e}^{n}_{i}\right) _{x\bar{x}\hat{x}}\nonumber \\&\quad -\alpha (e^{n}_{i})_{x\bar{x}t}+\lambda (e^n_i)_{xx\bar{x}\bar{x}t}\nonumber \\&\quad -\mu \left( \bar{e}^{n}_{i}\right) _{xx\bar{x}\bar{x}\hat{x}}\nonumber \\&\quad -s\bigg ((u^n_i)^{m-1}(\bar{u}^n_i)_{\hat{x}}(u^n_i)_{x\bar{x}}\nonumber \\&\quad +((u^n_i)^{m-1}\bar{u}^n_i(u^n_i)_{x\bar{x}})_{\hat{x}}\nonumber \\&\quad -(U^n_i)^{m-1}(\bar{U}^n_i)_{\hat{x}}(U^n_i)_{x\bar{x}}\nonumber \\&\quad -\left( (U^n_i)^{m-1}\bar{U}^n_i(U^n_i)_{x\bar{x}}\right) _{\hat{x}}\bigg ), \end{aligned}$$

(68)

where $\bar{e}^{n}=\frac{e^{n+1}+e^{n-1}}{2}$, $2\le i\le M-2$ and $1\le n \le N-1$.

Since all terms in (44) are the second-order approximations of the corresponding terms in left-hand side of (13) around $(x_i=x_l+ih, t_{n}=n\tau )$, by Taylor expansion, it can be easily obtained that $r^n_i=O(\tau ^2+h^2)$ if $h, \tau \rightarrow 0$ and $u(x,t)\in C^{7,3}(\Omega )$, where $C^{7,3}(\Omega )$ is the set of functions which are seventh-order continuous differentiable in space and third-order continuous differentiable in time. This following lemma is a well-known result.

Lemma 4

(Discrete Gronwall’s inequality). Suppose that w(k) and $\rho (k)$ are nonnegative functions while $\rho (k)$ is a non-decreasing function. If

$$\begin{aligned} w(k)\le \rho (k)+C\tau \sum ^{k-1}_{l=0}w(l), \forall \ k, \end{aligned}$$

then

$$\begin{aligned} w(k)\le \rho (k)e^{C\tau k}, \forall \ k. \end{aligned}$$

Theorem 4

Suppose $u_0\in C^{7}_{0}[x_l,x_r]$, and $u(x,t)\in C^{7,3}(\Omega )$, then the numerical solution $U^n$ of the finite difference scheme (44)–(46) converges to the solution of the problem (13)–(15) in the sense of $\parallel \cdot \parallel _{\infty }$, and the convergence rate is $O(\tau ^2+h^2)$, i.e.,

$$\begin{aligned} \parallel u^n-U^n\parallel _{\infty }\le C(\tau ^2+h^2), \quad \text {for any}\ 2\le n \le N. \end{aligned}$$

(69)

Proof

Taking the inner product of (68) with $2\bar{e}^{n}$, we have

$$\begin{aligned}&\parallel e^{n+1}\parallel ^2-\parallel e^{n-1}\parallel ^2+\alpha (\parallel e^{n+1}_{x}\parallel ^2-\parallel e^{n-1}_{x}\parallel ^2)\nonumber \\&\qquad +\lambda (\parallel e^{n+1}_{x\bar{x}}\parallel ^2-\parallel e^{n-1}_{x\bar{x}}\parallel ^2)\nonumber \\&\quad =2\tau \big [\left( r^n,2\bar{e}^{n}\right) -a\left( \bar{e}^{n}_{\hat{x}},2\bar{e}^{n}\right) \nonumber \\&\qquad -c\left( \left( \bar{e}^{n}\right) _{x\bar{x}\hat{x}},2\bar{e}^{n}\right) +\mu \left( \left( \bar{e}^{n}\right) _{xx\bar{x}\bar{x}\hat{x}},2\bar{e}^{n}\right) \nonumber \\&\qquad -\left( P,2\bar{e}^{n}\right) -\left( Q,2\bar{e}^{n}\right) +\left( R,2\bar{e}^{n}\right) +\left( S,2\bar{e}^{n}\right) \big ], \end{aligned}$$

(70)

where

$$\begin{aligned} P&=\frac{b}{m+2}\left[ \left( u^n\right) ^{m}\left( \bar{u}^n\right) _{\hat{x}}-\left( U^n\right) ^{m}\left( \bar{U}^n\right) _{\hat{x}}\right] ,\nonumber \\ Q&=\frac{b}{m+2}\left[ \left( \left( u^n\right) ^{m}\bar{u}^n\right) _{\hat{x}}-\left( \left( U^n\right) ^{m}\bar{U}^n\right) _{\hat{x}}\right] ,\nonumber \\ R&=s\left( (u^n)^{m-1}(\bar{u}^n)_{\hat{x}}(u^n)_{x\bar{x}}\right. \nonumber \\&\left. \quad -(U^n)^{m-1}(\bar{U}^n)_{\hat{x}}(U^n)_{x\bar{x}}\right) ,\nonumber \\ S&=s\left( ((u^n)^{m-1}\bar{u}^n(u^n)_{x\bar{x}})_{\hat{x}}\right. \nonumber \\&\left. \quad -\left( (U^n)^{m-1}\bar{U}^n(U^n)_{x\bar{x}}\right) _{\hat{x}}\right) . \end{aligned}$$

(71)

$\square$

By using lemma 2, we obtain

$$\begin{aligned} \left( \bar{e}^{n}_{\hat{x}},2\bar{e}^{n}\right) =0, \quad \left( (\bar{e}^{n})_{x\bar{x}\hat{x}},2\bar{e}^{n}\right)&=0, \nonumber \\ \left( (\bar{e}^{n})_{xx\bar{x}\bar{x}\hat{x}},2\bar{e}^{n}\right)&=0. \end{aligned}$$

(72)

From the notations introduced at the beginning of Sect. 3, for any $0\le n\le N$, we have the following inequality

$$\begin{aligned} \parallel e^{n}_{\hat{x}}\parallel ^2&=\sum ^{M-1}_{j=1}\left( \frac{e_{j+1}-e_{j-1}}{2h}\right) ^2h\nonumber \\&=\frac{1}{4}\sum ^{M-1}_{j=1}\left( \frac{e_{j+1}-e_{j}}{h}+\frac{e_{j}-e_{j-1}}{h}\right) ^2h\nonumber \\&\le \frac{1}{2}\sum ^{M-1}_{j=1}\left[ \left( \frac{e_{j+1}-e_{j}}{h}\right) ^2\!\!+\!\left( \frac{e_{j}-e_{j-1}}{h}\right) ^2\right] h\nonumber \\&=\parallel e^n_{x}\parallel ^2. \end{aligned}$$

Thus, for any $0\le n\le N$, we have

$$\begin{aligned} \parallel e^n_{\hat{x}}\parallel \le \parallel e^n_{x}\parallel . \end{aligned}$$

(73)

In addition, we have

$$\begin{aligned}&|(P,2\bar{e}^{n})|=\bigg |\frac{2b h}{m+2}\sum ^{M-1}_{j=1}\left[ (u^n_j)^{m}(\bar{u}^n_j)_{\hat{x}}\right. \nonumber \\&\qquad \left. - \, (U^n_j)^{m}(\bar{U}^n_j)_{\hat{x}}\right] \bar{e}^{n}_{j}\bigg |\nonumber \\&\quad =\bigg |\frac{2 b h}{m+b}\sum ^{M-1}_{j=1}\big [(u^n_j)^{m}(\bar{u}^n_j)_{\hat{x}}-(u^n_j)^{m}(\bar{U}^n_j)_{\hat{x}}\nonumber \\&\qquad +(u^n_j)^{m}(\bar{U}^n_j)_{\hat{x}}-(U^n_j)^{m}(\bar{U}^n_j)_{\hat{x}}\big ]\bar{e}^{n}_{j}\bigg |\nonumber \\&\quad =\bigg |\frac{2b h}{m+2}\sum ^{M-1}_{j=1}(u^n_j)^{m}(\bar{e}^n_j)_{\hat{x}}\bar{e}^{n}_{j}\nonumber \\&\qquad \!+\frac{2 bh}{m+2}\sum ^{M-1}_{j=1}\left[ \sum ^{m-1}_{k=0}(u^n_j)^{m-1-k}(U^n_j)^{k}\right] e^n_j(\bar{U}^n_j)_{\hat{x}}\bar{e}^{n}_{j}\bigg |\nonumber \\&\quad \le Ch\sum ^{M-1}_{j=1}\left[ |(\bar{e}^n_j)_{\hat{x}}|+|e^n_j|\right] |\bar{e}^{n}_{j}|\nonumber \\&\quad \le C(\parallel e^{n+1}_{\hat{x}}\parallel ^2+\parallel e^{n-1}_{\hat{x}}\parallel ^2+\parallel e^{n+1}\parallel ^2\nonumber \\&\qquad +\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2),\nonumber \\&\quad \le C(\parallel e^{n+1}_x\parallel ^2+\parallel e^{n-1}_x\parallel ^2+\parallel e^{n+1}\parallel ^2\nonumber \\&\qquad +\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2), \end{aligned}$$

(74)

where Theorem 2, $u(x,t)\in C^{7,3}(\Omega )$, Cauchy-Schwarz inequality and inequality (73) are used.

Similarly, we have

$$\begin{aligned} |(Q,2\bar{e}^{n})|= & {} \bigg |\frac{2bh}{m+2}\sum ^{M-1}_{j=1}\left[ \left( (u^n_j)^{m}\bar{u}^n_j\right) _{\hat{x}}\right. \nonumber \\&\left. -\left( (U^n_j)^{m}\bar{U}^n_j\right) _{\hat{x}}\right] \bar{e}^{n}_{j}\bigg |\nonumber \\= & {} \bigg |\frac{2bh}{m+2}\sum ^{M-1}_{j=1}\big [\left( (u^n_j)^{m}\bar{u}^n_j\right) _{\hat{x}}\nonumber \\&-\left( (u^n_j)^{m}\bar{U}^n_j\right) _{\hat{x}}\nonumber \\&+\left( (u^n_j)^{m}\bar{U}^n_j\right) _{\hat{x}}-\left( (U^n_j)^{m}\bar{U}^n_j\right) _{\hat{x}}\big ]\bar{e}^{n}_{j}\bigg |\nonumber \\= & {} \bigg |-\frac{2bh}{m+2}\sum ^{M-1}_{j=1}\bigg [(u^n_j)^{m}\bar{e}^n_j\nonumber \\&+\sum ^{m-1}_{k=0}(u^n_j)^{m-1-k}(U^n_j)^{k}\bar{U}^n_je^n_j\bigg ](\bar{e}^{n}_{j})_{\hat{x}}\bigg |\nonumber \\\le & {} Ch\sum ^{M-1}_{j=1}\left[ |\bar{e}^n_j|+|e^n_j|\right] |(\bar{e}^{n}_{j})_{\hat{x}}|\nonumber \\\le & {} C(\parallel e^{n+1}_{\hat{x}}\parallel ^2+\parallel e^{n-1}_{\hat{x}}\parallel ^2+\parallel e^{n+1}\parallel ^2\nonumber \\&+\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2),\nonumber \\\le & {} C(\parallel e^{n+1}_x\parallel ^2+\parallel e^{n-1}_x\parallel ^2+\parallel e^{n+1}\parallel ^2\nonumber \\&+\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2), \end{aligned}$$

(75)

where Theorem 2, $u(x,t)\in C^{7,3}(\Omega )$, Cauchy-Schwarz inequality and inequality (73) are used again.

$$\begin{aligned}&|(R,2\bar{e}^{n})|=\left| s\left( (u^n)^{m-1}\bar{u}^n_{\hat{x}}u^n_{x\bar{x}}\right. \right. \nonumber \\&\left. \left. \qquad -(U^n)^{m-1}\bar{U}^n_{\hat{x}}U^n_{x\bar{x}},2\bar{e}^{n}\right) \right| \nonumber \\&\quad =\big |s\big ((u^n)^{m-1}(\bar{u}^n)_{\hat{x}}u^n_{x\bar{x}}-(U^n)^{m-1}\bar{u}^n_{\hat{x}}u^n_{x\bar{x}}\nonumber \\&\qquad +(U^n)^{m-1}\bar{u}^n_{\hat{x}}u^n_{x\bar{x}}-(U^n)^{m-1}\bar{U}^n_{\hat{x}}u^n_{x\bar{x}}\nonumber \\&\qquad +(U^n)^{m-1}\bar{U}^n_{\hat{x}}u^n_{x\bar{x}}-(U^n)^{m-1}\bar{U}^n_{\hat{x}}U^n_{x\bar{x}},2\bar{e}^{n}\big )\big |\nonumber \\&\quad =\left| s\left( \bar{u}^n_{\hat{x}}u^n_{x\bar{x}}\left[ \sum ^{m-2}_{k=0}(u^n)^{m-2-k}(U^n)^k\right] e^n,2\bar{e}^{n}\right) \right| \nonumber \\&\qquad +\left| s\left( (U^n)^{m-1}u^n_{x\bar{x}}\bar{e}^n_{\hat{x}},2\bar{e}^{n}\right) \right| \nonumber \\&\qquad +\left| s\left( (U^n)^{m-1}\bar{U}^n_{\hat{x}}e^n_{x\bar{x}},2\bar{e}^{n}\right) \right| \nonumber \\&\quad \le C\left( \left| (e^n,2\bar{e}^{n})\right| +\left| (\bar{e}^n_{\hat{x}},2\bar{e}^{n})\right| +\left| (e^n_{x\bar{x}},2\bar{e}^{n})\right| \right) \nonumber \\&\quad \le C(\parallel e^{n}_{x\bar{x}}\parallel ^2+\parallel e^{n+1}_{\hat{x}}\parallel ^2+\parallel e^{n-1}_{\hat{x}}\parallel ^2\nonumber \\&\qquad +\parallel e^{n+1}\parallel ^2+\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2),\nonumber \\&\quad \le C(\parallel e^{n}_{x\bar{x}}\parallel ^2+\parallel e^{n+1}_x\parallel ^2+\parallel e^{n-1}_x\parallel ^2\nonumber \\&\qquad +\parallel e^{n+1}\parallel ^2+\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2), \end{aligned}$$

(76)

where theorem 2, $u(x,t)\in C^{7,3}(\Omega )$, Cauchy-Schwarz inequality and inequality (73) are used.

Similarly, we have

$$\begin{aligned}&|(S,2\bar{e}^{n})|\nonumber \\&\quad =\left| s\left( ((u^n)^{m-1}\bar{u}^nu^n_{x\bar{x}})_{\hat{x}}-((U^n)^{m-1}\bar{U}^nU^n_{x\bar{x}})_{\hat{x}},2\bar{e}^{n}\right) \right| \nonumber \\&\quad =\left| -s\left( (u^n)^{m-1}\bar{u}^nu^n_{x\bar{x}}-(U^n)^{m-1}\bar{U}^nU^n_{x\bar{x}},2\bar{e}^{n}_{\hat{x}}\right) \right| \nonumber \\&\quad =\big |-s\big ((u^n)^{m-1}\bar{u}^nu^n_{x\bar{x}}-(U^n)^{m-1}\bar{u}^nu^n_{x\bar{x}}\nonumber \\&\qquad +(U^n)^{m-1}\bar{u}^nu^n_{x\bar{x}}-(U^n)^{m-1}\bar{U}^nu^n_{x\bar{x}}\nonumber \\&\qquad +(U^n)^{m-1}\bar{U}^nu^n_{x\bar{x}}-(U^n)^{m-1}\bar{U}^nU^n_{x\bar{x}},2\bar{e}^{n}_{\hat{x}}\big )\big |\nonumber \\&\quad =\bigg |-s\big (\bar{u}^nu^n_{x\bar{x}}\left[ \sum ^{m-2}_{k=0}(u^n)^{m-2-k}(U^n)^k\right] e^n,2\bar{e}^{n}_{\hat{x}}\big )\bigg |\nonumber \\&\qquad +\bigg |-s\big ((U^n)^{m-1}u^n_{x\bar{x}}\bar{e}^n,2\bar{e}^{n}_{\hat{x}}\big )\bigg |\nonumber \\&\qquad +\bigg |-s\big ((U^n)^{m-1}\bar{U}^ne^n_{x\bar{x}},2\bar{e}^{n}_{\hat{x}}\big )\bigg |\nonumber \\&\quad \le C\left( \left| (e^n,2\bar{e}^{n}_{\hat{x}})\right| +\left| (\bar{e}^n,2\bar{e}^{n}_{\hat{x}})\right| +\left| (e^n_{x\bar{x}},2\bar{e}^{n}_{\hat{x}})\right| \right) \nonumber \\&\quad \le C(\parallel e^{n}_{x\bar{x}}\parallel ^2+\parallel e^{n+1}_{\hat{x}}\parallel ^2+\parallel e^{n-1}_{\hat{x}}\parallel ^2\nonumber \\&\qquad +\parallel e^{n+1}\parallel ^2+\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2),\nonumber \\&\quad \le C(\parallel e^{n}_{x\bar{x}}\parallel ^2+\parallel e^{n+1}_x\parallel ^2+\parallel e^{n-1}_x\parallel ^2\nonumber \\&\qquad +\parallel e^{n+1}\parallel ^2+\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2), \end{aligned}$$

(77)

where theorem 2, $u(x,t)\in C^{7,3}(\Omega )$, Cauchy-Schwarz inequality and inequality (73) are used again.

Furthermore, we have

$$\begin{aligned} (r^{n},2\bar{e}^{n})&\le 2\parallel r^n\parallel \parallel \bar{e}^{n}\parallel \nonumber \\&\le \parallel r^n\parallel ^2+\parallel \bar{e}^{n}\parallel ^2\nonumber \\&\le \parallel r^n\parallel ^2+\frac{1}{2}\left( \parallel e^{n+1}\parallel ^2+\parallel e^{n-1}\parallel ^2\right) , \end{aligned}$$

(78)

where Cauchy-Schwarz inequality are used.

Substituting (74)–(78) into (70), we get

$$\begin{aligned}&\parallel e^{n+1}\parallel ^2-\parallel e^{n-1}\parallel ^2+\alpha (\parallel e^{n+1}_{x}\parallel ^2-\parallel e^{n-1}_{x}\parallel ^2)\nonumber \\&\qquad +\lambda (\parallel e^{n+1}_{x\bar{x}}\parallel ^2-\parallel e^{n-1}_{x\bar{x}}\parallel ^2)\nonumber \\&\quad \le C\tau (\parallel e^{n+1}\parallel ^2+\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2\nonumber \\&\qquad +\parallel e^{n+1}_{x}\parallel ^2+\parallel e^{n-1}_{x}\parallel ^2\nonumber \\&\qquad +\parallel e^{n}_{x\bar{x}}\parallel ^2)+2\tau \parallel r^n\parallel ^2. \end{aligned}$$

(79)

Since $\alpha , \lambda$ are positive constants, it is easy to check that

$$\begin{aligned}&\parallel e^{n+1}\parallel ^2-\parallel e^{n-1}\parallel ^2+\alpha (\parallel e^{n+1}_{x}\parallel ^2\nonumber \\&\qquad -\parallel e^{n-1}_{x}\parallel ^2)\nonumber \\&\qquad +\lambda (\parallel e^{n+1}_{x\bar{x}}\parallel ^2-\parallel e^{n-1}_{x\bar{x}}\parallel ^2)\nonumber \\&\quad \le C\tau (\parallel e^{n+1}\parallel ^2\!+\!\parallel e^{n}\parallel ^2\!+\!\parallel e^{n-1}\parallel ^2+\parallel e^{n+1}_{x}\parallel ^2\nonumber \\&\qquad +\parallel e^{n-1}_{x}\parallel ^2+\parallel e^{n}_{x\bar{x}}\parallel ^2)+2\tau \parallel r^n\parallel ^2\nonumber \\&\quad \le C'\tau (\parallel e^{n+1}\parallel ^2+2\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2\nonumber \\&\qquad +\alpha \parallel e^{n+1}_{x}\parallel ^2+\alpha \parallel e^{n-1}_{x}\parallel ^2+2\lambda \parallel e^{n}_{x\bar{x}}\parallel ^2)\nonumber \\&\qquad +2\tau \parallel r^n\parallel ^2, \end{aligned}$$

where $C'=\max (\frac{C}{\alpha }, \frac{C}{2\lambda }, C)$ and C is the positive constant in the above inequality (79).

Replacing $C'$ in the above inequality by the general positive constant notation C, we have

$$\begin{aligned}&\parallel e^{n+1}\parallel ^2-\parallel e^{n-1}\parallel ^2+\alpha (\parallel e^{n+1}_{x}\parallel ^2-\parallel e^{n-1}_{x}\parallel ^2)\nonumber \\&\qquad +\lambda (\parallel e^{n+1}_{x\bar{x}}\parallel ^2-\parallel e^{n-1}_{x\bar{x}}\parallel ^2)\nonumber \\&\quad \le C\tau (\parallel e^{n+1}\parallel ^2+2\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2\nonumber \\&\qquad +\alpha \parallel e^{n+1}_{x}\parallel ^2+\alpha \parallel e^{n-1}_{x}\parallel ^2\nonumber \\&\qquad +2\lambda \parallel e^{n}_{x\bar{x}}\parallel ^2)+2\tau \parallel r^n\parallel ^2\nonumber \\&\quad \le C\tau (\parallel e^{n+1}\parallel ^2+2\parallel e^{n}\parallel ^2+\parallel e^{n-1}\parallel ^2\nonumber \\&\qquad +\alpha \parallel e^{n+1}_{x}\parallel ^2+2\alpha \parallel e^{n}_{x}\parallel ^2+\alpha \parallel e^{n-1}_{x}\parallel ^2\nonumber \\&\qquad +\lambda \parallel e^{n+1}_{x\bar{x}}\parallel ^2+2\lambda \parallel e^{n}_{x\bar{x}}\parallel ^2\nonumber \\&\qquad +\lambda \parallel e^{n-1}_{x\bar{x}}\parallel ^2)+2\tau \parallel r^n\parallel ^2. \end{aligned}$$

(80)

Let

$$\begin{aligned} D^n=&\parallel e^{n}\parallel ^2+\alpha \parallel e^{n}_{x}\parallel ^2+\lambda \parallel e^{n}_{x\bar{x}}\parallel ^2\nonumber \\&+\parallel e^{n-1}\parallel ^2+\alpha \parallel e^{n-1}_{x}\parallel ^2+\lambda \parallel e^{n-1}_{x\bar{x}}\parallel ^2, \end{aligned}$$

then (80) can be rewritten as follows:

$$\begin{aligned} (D^{n+1}-D^n)\le C\tau (D^{n+1}+D^n)+2\tau \parallel r^n\parallel ^2, \end{aligned}$$

which is equivalent to

$$\begin{aligned} (1-C\tau )(D^{n+1}-D^n)\le 2C\tau D^n+2\tau \parallel r^n\parallel ^2. \end{aligned}$$

(81)

If $\tau$, which is sufficiently small, satisfies $\tau <\frac{1}{3C}$ (C is the positive constant in the inequality (81)), then $1-C\tau >0$ and (81) gives

$$\begin{aligned} D^{n+1}-D^n&\le \frac{2C}{1-C\tau }\tau D^n+\frac{2\tau }{1-C\tau }\parallel r^n\parallel ^2\\&\le 3C\tau D^n+3\tau \parallel r^n\parallel ^2,\\&\le C''\left( \tau D^n+\tau \parallel r^n\parallel ^2\right) , \end{aligned}$$

where $C''=\max (3C,3)$ and we have used $\frac{2}{1-C\tau }<3$ since $\tau <\frac{1}{3C}$.

Replacing $C''$ in the above inequality by the general positive constant notation C, we have

$$\begin{aligned} D^{n+1}-D^n \le C\tau D^n+C\tau \parallel r^n\parallel ^2. \end{aligned}$$

(82)

Summing (82) from 1 to $n-1$, we get

$$\begin{aligned} D^{n}\le D^1+C\tau \sum ^{n-1}_{l=1} D^l+C\tau \sum ^{n-1}_{l=1}\parallel r^l\parallel ^2, \end{aligned}$$

(83)

where

$$\begin{aligned} \tau \sum ^{n-1}_{l=1}\parallel r^l\parallel ^2\le n\tau \max _{1\le l\le n-1}\parallel r^l\parallel ^2\le T\cdot O(\tau +h^2)^2. \end{aligned}$$

(84)

Since $e^{0}_i=0$ and the Crank-Nicolson scheme (47) is used to compute $U^1$, we have $D^1=O(\tau ^2+h^2)$ followed by a simple analysis for the scheme (47). Therefore

$$\begin{aligned} D^{n}\le O(\tau ^2+h^2)^2+C\tau \sum ^{n-1}_{l=1} D^l. \end{aligned}$$

(85)

Using lemma 4, we obtain

$$\begin{aligned} D^{n}\le O(\tau ^2+h^2)^2. \end{aligned}$$

(86)

Thus,

$$\begin{aligned} \parallel e^n\parallel \le O(\tau ^2+h^2), \quad \parallel e^n_{x} \parallel \le O(\tau ^2+h^2). \end{aligned}$$

(87)

By using lemma 3, we have

$$\begin{aligned} \parallel e^n\parallel _{\infty }\le O(\tau ^2+h^2), \end{aligned}$$

(88)

i.e.,

$$\begin{aligned} \parallel u^n-U^n\parallel _{\infty }\le C\left( \tau ^2+h^2\right) . \end{aligned}$$

(89)

This completes the proof.

Theorem 5

Suppose $u_0\in C^{7}_{0}[x_l,x_r]$, then the solution $U^n$ of the finite difference scheme (44)–(46) is unconditionally stable with the $\parallel \cdot \parallel _{\infty }$ norm.

The proof of this theorem is similar as the above theorem.

5 Numerical results

Example 1

We present the numerical results for the case $m=2, a=1, b=0.5, c=2, \alpha =1, \lambda =1, \mu =1, s=1$. From Sect. 2, we find that $\frac{-B_0+\sqrt{B^2_0-4A_0C_0}}{2A_0}>0$ and $\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}<0$, where $A_0, B_0, C_0$ are given by (29)–(31). The exact solitary solution is given by

$$\begin{aligned} u(x,t)=A\text {sech}\left( B^*\left( x-vt\right) \right) , \end{aligned}$$

(90)

where $B^*$ is given by $B^*=\sqrt{-\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}}$ and v, A are given by (32)–(33). And in the numerical computation, we set the initial condition as

$$\begin{aligned} u(x,0)=A\text {sech}\left( B^*x\right) , \end{aligned}$$

(91)

Table 1 Spatial mesh refinement analysis with $\tau =0.005, T=10$ for example 1

We first carry out the numerical convergence studies. For the spatial convergence, we set $\tau =0.005$ as the fixed time step and use 5 different spatial meshes: $h=\frac{5}{6},\frac{5}{12},\frac{5}{24},\frac{5}{48}, \frac{5}{96}$, where $\tau$ is sufficient small such that the temporal error is negligible comparing to the spatial error (Here the time step is $\tau =0.005$, while the smallest spatial size is $h=\frac{5}{96}$, thus $h^2>>\tau ^2$, therefore, the dominant errors are the spatial errors). The final time T is set to be 10, and $x_l=-200, x_r=300$. Table 1 gives the errors between numerical solutions and exact solutions. We can see that the error decreases when the spatial mesh is refined and the convergence rate is two. Thus, the method is second-order convergent in space variable, which is consistent with theoretical results in the above section. For the temporal convergence, we set $h=\frac{5}{600}$ as the fixed spatial mesh and use 4 different temporal meshes: $\tau =0.4, 0.2, 0.1, 0.05, 0.025$, where h is sufficient small such that the spatial error is negligible comparing to the temporal error (Here the smallest time step is $\tau =0.05$, while the spatial size is $h=\frac{5}{600}$, thus $h^2<<\tau ^2$, therefore, the dominant errors are the temporal errors). The final time T is set to be 10, and $x_l=-200, x_r=300$. Table 2 gives the errors between numerical solutions and exact solutions. Again, we can see that the error decreases when the temporal mesh is refined, and the convergence rate is also two. Thus, the method is second-order convergent in time variable, which is again consistent with theoretical results in the above section.

Table 2 Temporal mesh refinement analysis with $h=\frac{5}{600}, T=10$ for example 1

Table 3 Invariant of $E^{n}$ for example 1

Fig. 1

The evolution of discrete energy

Fig. 2

Numerical solutions and the corresponding errors in the $\parallel \cdot \parallel _{\infty }$ norm at different time stages. a Numerical solutions, b errors in the $\parallel \cdot \parallel _{\infty }$ norm

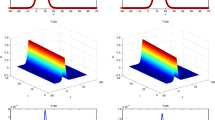
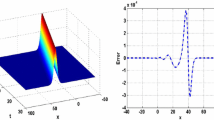
In order to show that the numerical scheme has the energy conservative property (48), we carry out another computation, where $T=100, x_{l}=-200, x_{r}=300, h=0.1, \tau =0.1$ are used. Table 3 gives the quantities of $E^{n}$ at several time stages, while Fig. 1 shows the evolution of the discrete energy. We can see that $E^{n}$ is conserved exactly (up to 9 decimals) during the time evolution of the solitary wave. In addition, we provide the numerical solutions and the corresponding errors with the $\parallel \cdot \parallel _{\infty }$ norm at several different time stages in Fig. 2 and Table 4, one can easily see that the errors are maintained in the order of $\tau ^2+h^2$ during the evolution of the solitary wave. Therefore, numerical solutions are very accurate approximations of the exact solutions.

Table 4 $\parallel e^n\parallel _{\infty }$ in terms of $h^2+\tau ^2$ for example 1

Table 5 Spatial mesh refinement analysis with $\tau =0.005, T=10$ for example 2

Example 2

We present the numerical results for the case $m=4, a=1, b=0.5, c=2, \alpha =1, \lambda =1, \mu =1, s=1$. From Sect. 2, we find that $\frac{-B_0+\sqrt{B^2_0-4A_0C_0}}{2A_0}>0$ and $\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}<0$, where $A_0, B_0, C_0$ are given by (29)–(31). The exact solitary solution is given by

$$\begin{aligned} u(x,t)=A\text {sech}^{\frac{1}{2}}\left( B^*\left( x-vt\right) \right) , \end{aligned}$$

(92)

where $B^*$ is given by $B^*=\sqrt{-\frac{-B_0-\sqrt{B^2_0-4A_0C_0}}{2A_0}}$ and v, A are given by (32)–(33). And in the numerical computation, we set the initial condition as

$$\begin{aligned} u(x,0)=A\text {sech}^{\frac{1}{2}}\left( B^*x\right) , \end{aligned}$$

(93)

Again, we carry out the spatial and temporal convergence. Tables 5 and 6 give the errors between numerical solutions and exact solutions for spatial and temporal convergence, respectively. Once again, we can see that the method is second-order convergent both in time and space variables.

Table 6 Temporal mesh refinement analysis with $h=\frac{5}{600}, T=10$ for example 2

Table 7 Invariant of $E^{n}$ for example 2

Fig. 3

The evolution of discrete energy

Table 8 $\parallel e^n\parallel _{\infty }$ in terms of $h^2+\tau ^2$ for example 2

Fig. 4

Numerical solutions and the corresponding errors in the $\parallel \cdot \parallel _{\infty }$ norm at different time stages. a Numerical solutions, b errors in the $\parallel \cdot \parallel _{\infty }$ norm

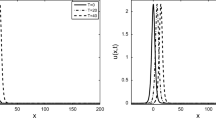
Additionally, Table 7 and Fig. 3 provide the several quantities and the evolution of $E^{n}$, while Table 8 and Fig. 4 give the numerical solutions and the corresponding errors with the $\parallel \cdot \parallel _{\infty }$ norm at several different time stages, where $T=100, x_{l}=-200, x_{r}=300, h=0.1, \tau =0.1$. Once again, we can see that $E^{n}$ is conserved exactly and the errors are maintained in the order of $\tau ^2+h^2$ during the evolution of the solitary wave. Thus, the method can be well used to study the solitary wave at long time.

6 Conclusions

In this paper, exact solitary solutions are derived through the sine-cosine method for the generalized Rosenau–Kawahara-RLW equation with generalized Novikov type nonlinear perturbation. Moreover, a three-level linearly implicit finite difference method for the initial boundary value problem of the above perturbed Rosenau–Kawahara-RLW equation with power law nonlinearity is developed. The fundamental energy conservative property is preserved by the current numerical scheme. The existence and uniqueness of the numerical solution are proved. The method is shown to be second-order convergent both in time and space variables, and the method is unconditionally stable. Numerical results confirm well with the theoretical results.