Performance of compact and non-compact structure preserving algorithms to traveling wave solutions modeled by the Kawahara equation

Abstract

The main contribution of this article is to introduce new compact fourth-order, standard fourth-order, and standard second-order finite difference schemes for solving the Kawahara equation, the fifth-order partial derivative equation. The conservation of mass only of the numerical solution obtained by the compact fourth-order finite difference scheme is proven. However, the standard fourth-order and standard second-order finite difference schemes can preserve both mass and energy. The stability is also proven by von Neumann analysis. According to analysis for numerical experiments, the order of accuracy for each scheme and the computational efficiency of the compact scheme are presented. To validate the potential of the presented methods, we also consider long-time behavior. Finally, results obtained from the compact scheme are superior than those from the non-compact schemes.

1 Introduction

In the past, Kakutani and Ono [1] investigated the type of a mathematical model for an analysis of magnet-acoustic waves in cold collision–free plasma. Consequently, Hasimoto [2, 3] derived a higher order Korteweg–de Vries equation with an additional fifth-order derivative term as the Kawahara equation. The equation was constructed to study capillary–gravity waves in an infinitely long canal over a flat bottom in long waves when the Bond number is almost one third. Moreover, many physical phenomena, such as the blowing of the wind over an ocean surface and the propagation of a shallow water wave were also studied by using the Kawahara equation. Then, Kawahara [4] numerically investigated and noticed that this type of the equation generates both oscillatory and monotone solitary wave solutions.

Using adjacent grid points, a derivative is approximated by the numerical techniques, such as finite difference, finite volume, and finite element methods, and the methods are much more effective for controlling complicated boundary conditions and geometries. With grid refinement, their sluggish convergence to the exact solution which requires many more grid points to execute a targeted accuracy level is the major difficulty of these methods. Regarding the mentioned problem, then researchers have developed compact higher order finite difference schemes because they can furnish a productive way of merging the accuracy and robustness of the numerical methods [5,6,7]. The main benefits of the developed schemes are less computational cost and robustness because of the effective completeness of the solution to the resulting multidiagonal sparse system. As of the same order of accuracy, compact schemes generally employ a fewer stencil and present more suitable resolution when compared with the finite difference schemes.

In recent years, many numerical methods have been proposed to solve for an approximated solution to varieties of nonlinear partial differential equations. Many numerical schemes inherit some physical structures from the original problem, so, in these cases, they are called structure preserving numerical schemes. Examples of physical properties which usually can be inherited are energy, mass conservation laws, and entropy increasing laws. Recently, a number of structure preserving numerical schemes were proposed. For example, Miyatake [8, 9] proposed conservative finite difference schemes for the Degasperis–Procesi equation, a completely integrable shallow water equation. In this case, the schemes preserve two invariants associated with the bi-hamiltonian form. Later, Poochinapan et al. [10] proposed the compact fourth-order and standard fourth-order finite difference schemes in order to solve the KdV equation. The schemes are unconditionally stable and preserve mass. In this paper, a class of structure preserving finite difference schemes with spatial orders of accuracy is presented for the Kawahara equation

$$ u_{t}+\beta u_{\text{xxx}}+\gamma u_{\text{xxxxx}}+\eta (u^{2})_{x}=0,~~~x\in(x_{L},x_{R}),~~t>0 $$

(1)

where the subscript t (or x respectively) denotes the differentiation with respect to time (or space) variable t (or x). The parameters β,γ, and η are constants.

Yuan et al. [11] proposed the numerical scheme of both the Kawahara and the modified Kawahara equations by using the dual-Petrov–Galerkin method and the Crank–Nicholson-leap-frog to approximate in space and in time, respectively. It was shown that the scheme is second-order accurate in time. In 2011, Ezzati et al. [12] used the multiquadric quasi-interpolation method that does not require solving any system of equations. In the same year, Bibi et al. [13] used the meshless method of lines, and numerical results were shown that utilizing multiquadric and Gaussian is better than the Crank–Nicolson differential quadrature algorithm. Besides, Suarez and Morales [14] applied Strang’s splitting method to the Kawahara and the generalized Kawahara equations; hence, the numerical solutions were shown to coincide with known analytical results. Karakoc et al. [15] proposed a septic B-spline collocation method which was proved to be unconditionally stable by the von Neumann stability analysis. Korkmaz and Dag [16] applied both the polynomial-based differential quadrature method (PDQ) and the cosine expansion-based differential quadrature method (CDQ) for the space discretization method of the Kawahara equation. Also, Bashan [17] obtained the numerical solution via the Crank–Nikolson differential quadrature method based on modified cubic B-splines (MCBC-DQM).

A finite difference approach for approximating a solution of the KdV–Kawahara equation in the past has also been considered. Sepulveda and Villagran [18] proposed the implicit finite difference scheme which was proven to be unconditionally stable. Consequently, Ceballos et al. [19] presented the second-order implicit finite difference scheme and proved its unconditional stability result. Also, Koley [20] investigated the semi-implicit scheme and the fully implicit Crank–Nicolson scheme, which were proved convergent. Results were shown that the fully implicit Crank–Nicolson scheme works far better than the semi-implicit scheme.

This paper is organized as follows. In Section 2, we briefly examine the notations of the finite differences schemes and also present the proposed finite-difference schemes. Proofs of the structure preserving for three schemes are also presented. In Section 3, some numerical results are provided. Concluding remarks and comments are presented in Section 4.

2 Finite difference schemes

This section describes a complete description of how structure preserving methods can be modeled for the Kawahara equation. To begin with, an explanation about a computational domain will be discovered. First, we introduce the solution domain to be as follows:

$$ Q=\{(x,t)| x_{L}\leq x\leq x_{R}, 0\leq t \leq T\}, $$

which is covered by a uniform grid as follows:

$$ Q_{h}=\{(x_{j},t_{n})| x_{j}=x_{L}+jh, t_{n}=n\tau, j=0,{\ldots} ,M, n=0,{\ldots} ,N\}. $$

The time domain uniformly identified by t_n = nτ is discretized, and here, τ is a time step length. In the same way, the spatial domain [x_L,x_R] is discretized by using function values on a finite set of the points $\{x_{j}\}_{j=0}^{M} \subset [x_{L},x_{R}]$, where the grid size h = (x_R − x_L)/M is the uniform distance between two points. According to values of j and n, points can be located, so difference equations are commonly written in a term of the point (j,n). The notation ${u_{j}^{n}}$ is utilized for a value of a function u at the point (x_L + jh,nτ), and the space ${Z^{0}_{h}}$ is introduced:

$$ \begin{array}{@{}rcl@{}} {Z^{0}_{h}}&=&\{u=(u_{j})| u_{-4}=u_{-3}=u_{-2}=u_{-1}=u_{0}=u_{1}=u_{M-1}=u_{M}=u_{M+1}\\ &=&u_{M+2}=u_{M+3}=u_{M+4}=0, j=-4,-3,-2,...,M+2,M+3,M+4\}. \end{array} $$

For completeness, the following notations will be used:

$$ \begin{array}{@{}rcl@{}} \bar{u}_{j}^{n}&=&\frac{u_{j}^{n+1}+u_{j}^{n-1}}{2}, \quad\qquad\quad ({u_{j}^{n}})_{\hat{t}}=\frac{u_{j}^{n+1}-u_{j}^{n-1}}{2\tau},\\ ({u_{j}^{n}})_{x}&=&\frac{u_{j+1}^{n}-{u_{j}^{n}}}{h},\quad\quad\quad\qquad({u_{j}^{n}})_{\bar{x}}=\frac{{u_{j}^{n}}-u_{j-1}^{n}}{h},\\ ({u_{j}^{n}})_{\hat{x}}&=&\frac{u_{j+1}^{n}-u_{j-1}^{n}}{2h}, \quad\quad\qquad({u_{j}^{n}})_{\ddot{x}}=\frac{u_{j+2}^{n}-u_{j-2}^{n}}{4h},\\ ||u^{n}||^{2}&=&h\sum\limits_{j=1}^{M-1}({u_{j}^{n}})^{2},\quad\quad\qquad\|u^{n}||_{\infty}=\max\limits_{1\leq j \leq M-1}|{u_{j}^{n}}|. \end{array} $$

In the view of numerical examples, let us consider the Kawahara equation with boundary conditions as follows:

$$ \begin{array}{@{}rcl@{}} u(x_{L},t)&=&u(x_{R},t)=0, u_{x}(x_{L},t)=u_{x}(x_{R},t)=0,\\ u_{\text{xx}}(x_{L},t)&=&u_{\text{xx}}(x_{R},t)=0, t>0 \end{array} $$

and the initial condition u(x,0) = u₀(x),x ∈ [x_L,x_R]. The solution and its derivatives for the solitary wave are supposed to have the following asymptotic values, $\frac {\partial ^{n}u}{\partial x^{n}}\rightarrow 0$ as $x\rightarrow \pm \infty$ for n ≥ 0. For that reason, if x_L ≪ 0 andx_R ≫ 0, the initial–boundary value problem is in agreement with the Cauchy problem of (1). Besides, the central difference approximations can be used to treat boundary conditions significantly for numerical algorithms in this paper.

2.1 Compact finite difference scheme

By setting

$$w=-\beta u_{\text{xxx}}-\gamma u_{\text{xxxxx}}-\eta (u^{2})_{x},$$

it follows that w = u_t. Substituting

$$\gamma({\partial_{x}^{7}}u)_{j}^{n}=-\beta({\partial_{x}^{5}}u)_{j}^{n}-\eta({\partial_{x}^{3}}u^{2})_{j}^{n}-({\partial_{x}^{2}}w)_{j}^{n}$$

into

$$ \begin{array}{@{}rcl@{}} {w_{j}^{n}}&=&-\beta \left[ ({u_{j}^{n}})_{\text{x}\bar{\text{x}}\hat{\text{x}}}-\frac{h^{2}}{4}({\partial_{x}^{5}}u)_{j}^{n} \right]-\gamma \left[ ({u_{j}^{n}})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}}-\frac{h^{2}}{3}({\partial_{x}^{7}}u)_{j}^{n} \right]\\ &&-\eta \left[ [({u_{j}^{n}})^{2}]_{\hat{x}}-\frac{h^{2}}{6}({\partial_{x}^{3}}u^{2})_{j}^{n} \right]+O(h^{4}), \end{array} $$

we obtain the following:

$$ \begin{array}{@{}rcl@{}} {w_{j}^{n}}&=&-\beta ({u_{j}^{n}})_{\text{x}\bar{\text{x}}\hat{\text{x}}}+\frac{\beta h^{2}}{4}({\partial_{x}^{5}}u)_{j}^{n}- \gamma ({u_{j}^{n}})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{x}}+ \frac{h^{2}}{3}\left[ -\beta({\partial_{x}^{5}}u)_{j}^{n}-\eta({\partial_{x}^{3}}u^{2})_{j}^{n}\right.\\ &&\left.- ({\partial_{x}^{2}}w)_{j}^{n}\right] -\eta [({u_{j}^{n}})^{2}]_{\hat{x}}+\frac{\eta h^{2}}{6}({\partial_{x}^{3}}u^{2})_{j}^{n} +O(h^{4}). \end{array} $$

By applying second-order accuracy for approximations, it leads to the following:

$$ \begin{array}{@{}rcl@{}} {w_{j}^{n}}&=&(\partial_{t}u)_{j}^{n}=({u_{j}^{n}})_{\hat{t}}+O(\tau^{2}), ({\partial_{x}^{5}} u)_{j}^{n}=({u_{j}^{n}})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{x}}+O(h^{2}),\\ ({\partial_{x}^{3}} u^{2})_{j}^{n}&=&[({u_{j}^{n}})^{2}]_{\text{x}\bar{\text{x}}\hat{\text{x}}}+O(h^{2}), ({\partial_{x}^{2}} w)_{j}^{n}=({w_{j}^{n}})_{{\text{x}}\bar{\text{x}}}+O(h^{2}). \end{array} $$

As a result, we obtain a compact fourth-order finite difference scheme to solve the problem (1):

$$ \begin{array}{@{}rcl@{}} ({u_{j}^{n}})_{\hat{t}}&+&\frac{h^{2}}{3}({u_{j}^{n}})_{{\text{x}}\bar{\text{x}}\hat{t}}+\beta(\bar{u}_{j}^{n})_{\text{x}\bar{\text{x}}\hat{x}}+(\gamma+\frac{\beta h^{2}}{12})(\bar{u}_{j}^{n})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}} +\eta[({u_{j}^{n}})(\bar{u}_{j}^{n})]_{\hat{x}}\\ &+&\frac{\eta h^{2}}{6}[({u_{j}^{n}})(\bar{u}_{j}^{n})]_{\text{x}\bar{\text{x}}\hat{\text{x}}}=0, \end{array} $$

(2)

where

$$ {u_{j}^{0}}=u_{0}(x_{j}), 0\leq j \leq M. $$

Since the boundary conditions are homogeneous, they give the following:

$$ {u_{0}^{n}}={u_{M}^{n}}=0,\quad({u_{0}^{n}})_{\hat{x}}=({u_{M}^{n}})_{\hat{x}}=0,\quad({u_{0}^{n}})_{x\bar{x}}=({u_{M}^{n}})_{\text{x}\bar{\text{x}}}=0,~~~1\leq n \leq N. $$

(3)

Let ${e_{i}^{n}}={v_{i}^{n}}-{u_{i}^{n}}$ where ${v_{i}^{n}}$ and ${u_{i}^{n}}$ are the solutions of (1) and (2), respectively. Thus, the truncation error of the finite difference scheme (2) can be written as follows:

$$ \begin{array}{@{}rcl@{}} {r_{j}^{n}}&=&({e_{j}^{n}})_{\hat{t}}+\frac{h^{2}}{3}({e_{j}^{n}})_{{\text{x}}\bar{\text{x}}\hat{\text{t}}}+\beta(\bar{e}_{j}^{n})_{\text{x}\bar{\text{x}}\hat{\text{x}}}+(\gamma+\frac{\beta h^{2}}{12})(\bar{e}_{j}^{n})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}}+\eta[({v_{j}^{n}})(\bar{v}_{j}^{n})]_{\hat{x}}\\ &&-\eta[({u_{j}^{n}})(\bar{u}_{j}^{n})]_{\hat{x}}+\frac{\eta h^{2}}{6}[({v_{j}^{n}})(\bar{v}_{j}^{n})]_{\text{x}\bar{\text{x}}\hat{\text{x}}}-\frac{\eta h^{2}}{6}[({u_{j}^{n}})(\bar{u}_{j}^{n})]_{\text{x}\bar{\text{x}}\hat{\text{x}}}. \end{array} $$

By applying the Taylor expansion, it is easy to see that ${r_{i}^{n}}=O(\tau ^{2}+h^{4})$ holds as $\tau , h \rightarrow 0$.

Theorem 1

The scheme (2) is unconditionally stable in the linearized sense.

Proof

The linear form of (2) is as follows:

$$ \begin{array}{@{}rcl@{}} ({u_{j}^{n}})_{\hat{t}}&+&\frac{h^{2}}{3}({u_{j}^{n}})_{{\text{x}}\bar{\text{x}}\hat{\text{t}}}+\beta(\bar{u}_{j}^{n})_{\text{x}\bar{\text{x}}\hat{\text{x}}}+(\gamma+\frac{\beta h^{2}}{12})(\bar{u}_{j}^{n})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}} +\eta[U(\bar{u}_{j}^{n})]_{\hat{x}}\\ &&+\frac{\eta h^{2}}{6}[U(\bar{u}_{j}^{n})]_{\text{x}\bar{\text{x}}\hat{\text{x}}}=0. \end{array} $$

(4)

At this time, the von Neumann stability analysis of (2) with ${u_{j}^{n}}=\xi ^{n}e^{\text {ikjh}},$ where i² = − 1 and k is a wave number, gives the following amplification factor

$$ \xi^{2}=\frac{A-i\tau B}{A+i\tau B}, $$

where

$$ A= 4h^{5}+8h^{5}\text{cos}(\text{kh}) $$

and

$$ \begin{array}{@{}rcl@{}} B&=&\left( 60\gamma-19\beta h^{2}\right)\sin(\text{kh})-\left( 48\gamma-8\beta h^{2}\right)\sin(2\text{kh})+\left( 12\gamma+\beta h^{2} \right)\sin(3\text{kh})\\ &&+2\eta h^{4} U\left( 4\sin(2\text{kh})+\sin(4\text{kh})\right). \end{array} $$

We can see that the amplification factor which is a complex number has modulus equal to one. Hence, the compact finite difference scheme is unconditionally stable. □

Theorem 2

Let uⁿ be the solution of the finite difference scheme (2). Then,

$$ Q^{n}=\frac{h}{2}\sum\limits_{j=1}^{M-1}\left( u_{j}^{n+1}+{u_{j}^{n}}\right)=Q^{n-1}=\ldots=Q^{0}. $$

(5)

Proof

By multiplying (2) by h, summing up for j from 1 to M − 1, and considering the boundary conditions (3), we get the following:

$$ \frac{h}{2\tau}\sum\limits_{j=1}^{M-1}\left( u_{j}^{n+1}-u_{j}^{n-1}\right)=0. $$

Then, this gives (5). □

In the next subsection, we present a standard forth-order finite difference scheme. Also, similar to the previous section, the stability and structure preserving properties are proven.

2.2 Standard fourth-order finite difference scheme

Now, following the relation [21,22,23,24,25]

$$ (u^{2})_{x}=\frac{2}{3}\left[\text{uu}_{x}+(u^{2})_{x}\right], $$

Equation (1) can be immediately obtained that

$$ u_{t}+\beta u_{\text{xxx}}+\gamma u_{\text{xxxxx}}+\eta\frac{2}{3}\left[\text{uu}_{x}+(u^{2})_{x}\right]=0. $$

(6)

We can easily extend a fourth-order finite difference scheme by utilizing standard fourth-order accurate central difference approximations to (6):

$$ \begin{array}{@{}rcl@{}} (\partial_{x} u )_{j}^{n} &=&\frac{-u_{j+2}^{n}+8u_{j+1}^{n}-8u_{j-1}^{n}+u_{j-2}^{n}}{12h}+O(h^{4}) \\ &=&\frac{4}{3}({u_{i}^{n}})_{\hat{x}}-\frac{1}{3}({u_{i}^{n}})_{\ddot{x}}+O(h^{4}) ,\\ ({\partial_{x}^{3}} u )_{j}^{n} \!&=&\!\frac{-u_{j+3}^{n}+8u_{j+2}^{n}-13u_{j+1}^{n}+13u_{j-1}^{n}-8u_{j-2}^{n}+u_{j-3}^{n}}{8h^{3}}+O(h^{4}) \\ \!&=&\!\frac{3}{2}({u_{i}^{n}})_{\text{x}\bar{\text{x}}\hat{\text{x}}}-\frac{1}{2}({u_{i}^{n}})_{\text{x}\bar{\text{x}}\ddot{\text{x}}}+O(h^{4}) ,\\ ({\partial_{x}^{5}} u )_{j}^{n} \!&=&\!\frac{-u_{j+4}^{n} + 9u_{j + 3}^{n} - 26u_{j+2}^{n} + 29u_{j+1}^{n} - 29u_{j-1}^{n} + 26u_{j-2}^{n} - 9u_{j - 3}^{n} + u_{j - 4}^{n}}{6h^{5}} + O(h^{4}) \\ \!&=&\!\frac{5}{3}({u_{i}^{n}})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}}-\frac{2}{3}({u_{i}^{n}})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\ddot{\text{x}}}+O(h^{4}). \end{array} $$

By using an average value $\bar {u}^{n}_{j}$, the approximation in the nonlinear term ([uu_x + (u²)_x] at the point (x_j,t_n)

$$ \text{uu}_{x}+(u^{2})_{x}=\left[ \left( \frac{4}{3} {u_{j}^{n}}(\bar{u}_{j}^{n})_{\hat{x}} -\frac{1}{3}{u_{j}^{n}}(\bar{u}_{j}^{n})_{\ddot{x}}\right) +\left( \frac{4}{3}({u_{j}^{n}}\bar{u}_{j}^{n})_{\hat{x}} -\frac{1}{3} ({u_{j}^{n}}\bar{u}_{j}^{n})_{\ddot{x}} \right) \right]+O(h^{4}). $$

With an application of central differences to spatial derivatives and second-order accurate central difference approximation in time, we propose a standard nine-point implicit difference scheme for the problem (6) as follows:

$$ \begin{array}{@{}rcl@{}} ({u_{j}^{n}})_{\hat{t}}&+&\beta\left (\frac{3}{2}(\bar{u}_{j}^{n})_{\text{x}\bar{\text{x}}\hat{\text{x}}}-\frac{1}{2}(\bar{u}_{j}^{n})_{\text{x}\bar{\text{x}}\ddot{\text{x}}}\right) +\gamma\left( \frac{5}{3}(\bar{u}_{j}^{n})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}}-\frac{2}{3}(\bar{u}_{j}^{n})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\ddot{\text{x}}}\right)\\ &&+\eta\left[ \frac{8}{9}\left( {u_{j}^{n}}(\bar{u}_{j}^{n})_{\hat{x}}+({u_{j}^{n}}\bar{u}_{j}^{n})_{\hat{x}} \right)-\frac{2}{9}\left( {u_{j}^{n}}(\bar{u}_{j}^{n})_{\ddot{x}}+({u_{j}^{n}}\bar{u}_{j}^{n})_{\ddot{x}} \right) \right] =0, \end{array} $$

(7)

where

$$ {u_{j}^{0}}=u_{0}(x_{j}),\quad 0\leq j\leq M. $$

Since the boundary conditions are homogeneous, we obtain the following:

$$ {u_{0}^{n}}={u_{M}^{n}}=0,\quad 4({u_{0}^{n}})_{\hat{x}}-({u_{0}^{n}})_{\ddot{x}}=4({u_{M}^{n}})_{\hat{x}}-({u_{M}^{n}})_{\ddot{x}}=0, $$

(8)

$$ -(u_{-1}^{n})_{\text{x}\bar{\text{x}}}+14({u_{0}^{n}})_{\text{x}\bar{\text{x}}}-({u_{1}^{n}})_{x\bar{x}}=-(u_{M-1}^{n})_{\text{x}\bar{\text{x}}}+14({u_{M}^{n}})_{\text{x}\bar{\text{x}}}-(u_{M+1}^{n})_{\text{x}\bar{\text{x}}}=0, $$

(9)

$$ 3({u_{0}^{n}})_{\text{x}\bar{\text{x}}\hat{\text{x}}}-({u_{0}^{n}})_{\text{x}\bar{\text{x}}\ddot{\text{x}}}=3({u_{M}^{n}})_{\text{x}\bar{\text{x}}\hat{\text{x}}}-({u_{M}^{n}})_{\text{x}\bar{\text{x}}\ddot{\text{x}}}=0,~~~1\leq n\leq N. $$

(10)

According to the boundary conditions, u, u_x, u_xx, and u_xxx are required by a standard fourth-order technique to be zero at the upstream and downstream boundaries since the method utilizes a nine-point finite difference scheme for the approximation of the solution u. Through the analytical technique of contrasting, (2) requires only three homogeneous boundary conditions. Then, similar to the compact fourth-order scheme, we obtain the convergent result. The truncation error of the finite difference scheme (2) can be written as follows:

$$ \begin{array}{@{}rcl@{}} {r_{j}^{n}}&=&({e_{j}^{n}})_{\hat{t}}+\beta\left (\frac{3}{2}(\bar{e}_{j}^{n})_{\text{x}\bar{\text{x}}\hat{\text{x}}}-\frac{1}{2}(\bar{e}_{j}^{n})_{\text{x}\bar{\text{x}}\ddot{\text{x}}}\right) +\gamma\left( \frac{5}{3}(\bar{e}_{j}^{n})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}}-\frac{2}{3}(\bar{e}_{j}^{n})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\ddot{\text{x}}}\right)\\ &&+\eta\left[ \frac{8}{9}\left( {v_{j}^{n}}(\bar{v}_{j}^{n})_{\hat{x}}+({v_{j}^{n}}\bar{v}_{j}^{n})_{\hat{x}} \right)-\frac{2}{9}\left( {v_{j}^{n}}(\bar{v}_{j}^{n})_{\ddot{x}}+({v_{j}^{n}}\bar{v}_{j}^{n})_{\ddot{x}} \right) \right]\\ &&-\eta\left[ \frac{8}{9}\left( {u_{j}^{n}}(\bar{u}_{j}^{n})_{\hat{x}}+({u_{j}^{n}}\bar{u}_{j}^{n})_{\hat{x}} \right)-\frac{2}{9}\left( {u_{j}^{n}}(\bar{u}_{j}^{n})_{\ddot{x}}+({u_{j}^{n}}\bar{u}_{j}^{n})_{\ddot{x}} \right) \right]. \end{array} $$

By taking the Taylor expansion, it is easy to see that ${r_{j}^{n}}=O(\tau ^{2}+h^{4})$ holds as $\tau ,h\rightarrow 0$.

Theorem 3

The scheme (7) is unconditionally stable in the linearized sense.

Proof

The linear form of (7) is a follows:

$$ \begin{array}{@{}rcl@{}} ({u_{j}^{n}})_{\hat{t}}&+&\beta\left (\frac{3}{2}(\bar{u}_{j}^{n})_{\text{x}\bar{\text{x}}\hat{\text{x}}}-\frac{1}{2}(\bar{u}_{j}^{n})_{\text{x}\bar{\text{x}}\ddot{\text{x}}}\right) +\gamma\left( \frac{5}{3}(\bar{u}_{j}^{n})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}}-\frac{2}{3}(\bar{u}_{j}^{n})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\ddot{x}}\right)\\ &&+\eta\left[ \frac{8}{9}\left( U(\bar{u}_{j}^{n})_{\hat{x}}+(U\bar{u}_{j}^{n})_{\hat{x}} \right)-\frac{2}{9}\left( U(\bar{u}_{j}^{n})_{\ddot{x}}+(U\bar{u}_{j}^{n})_{\ddot{x}} \right) \right] =0. \end{array} $$

(11)

The von Neumann stability analysis of (7) with ${u_{j}^{n}}=\xi ^{n}e^{\text {ikjh}}$ gives the following amplification factor

$$ \xi^{2}=\frac{36h^{5}-i\tau A}{36h^{5}+i\tau A}, $$

where

$$ \begin{array}{@{}rcl@{}} A\!&=&\!\left( 116\gamma - 39\beta h^{2} \right)\sin(\text{kh}) - \left( 104\gamma-24\beta h^{2} \right)\sin(2\text{kh}) + \left( 36\gamma - 3\beta h^{2} \right)\sin(3\text{kh})\\ &&-4\gamma \sin(4\text{kh})+4\eta h^{4} U\left( 8\sin(\text{kh})+7\sin(2\text{kh})-\sin(4\text{kh})\right). \end{array} $$

The amplification factor which is a complex number has its modulus equal to one; therefore, the finite difference scheme is unconditionally stable. □

Lemma 1

[25, 26] For any two mesh functions $u, v \in {Z^{0}_{h}}$, one has the following:

$$ (u_{\hat{x}}, v ) =-(u , v_{\hat{x}}), (u_{x}, v) =-(u , v_{\bar{x}}), (u_{\ddot{x}},v)=-(u,v_{\ddot{x}}). $$

Lemma 2

[25, 26] For any mesh function $u\in {Z^{0}_{h}}$, one has the following:

$$ (u_{\hat{\text{x}}}, u)=0, (u_{\text{x}\bar{\text{x}}\hat{\text{x}}}, u)=0, (u_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}}, u)=0. $$

Lemma 3

[25, 26] For any mesh function $u\in {Z^{0}_{h}}$, one has the following:

$$ (u_{\text{x}\bar{\text{x}}\ddot{\text{x}}}, u)=0,\qquad(u_{\text{xx}\bar{\text{x}}\bar{\text{x}}\ddot{x}}, u)=0. $$

Theorem 4

Let uⁿ be the solution of the finite difference scheme (7). Then,

$$ \begin{array}{@{}rcl@{}} Q^{n}&=&\frac{h}{2}\sum\limits_{j=1}^{M-1}\left( u_{j}^{n+1} +{u_{j}^{n}} \right) +\tau h \eta \sum\limits_{j=1}^{M-1} \left[ \frac{4}{9}{u_{j}^{n}}\left( u_{j}^{n+1} \right)_{\hat{x}} - \frac{1}{9}{u_{j}^{n}}\left( u_{j}^{n+1} \right)_{\ddot{x}} \right]\\ &=&Q^{n-1}=\cdots=Q^{0}. \end{array} $$

(12)

Moreover, the scheme (7) is conservative in a sense:

$$ E^{n}=\frac{1}{2}||u^{n+1}||^{2}+\frac{1}{2}||u^{n}||^{2}=E^{n-1}=\cdots=E^{0}. $$

(13)

Proof

As a result, we have the following:

$$ \frac{h}{2}\sum\limits_{j=1}^{M-1}\left( u_{j}^{n+1} - u_{j}^{n-1} \right) + \tau h \eta\sum\limits_{j=1}^{M-1} \left[\! \frac{4}{9}\left( {u_{j}^{n}}\left( u_{j}^{n+1}\right)_{\hat{x}} - u_{j}^{n-1}\left( {u_{j}^{n}}\right)_{\hat{x}}\right) - \frac{1}{9}\left( {u_{j}^{n}}\left( u_{j}^{n+1} \right)_{\ddot{x}} - u_{j}^{n-1}\left( {u_{j}^{n}} \right)_{\ddot{x}}\right)\!\right] = 0. $$

By multiplying (7) by h and summing up for j from 1 to M − 1, we have the following:

$$ \begin{array}{@{}rcl@{}} &&\tau h \sum\limits_{j=1}^{M-1} \left[ \frac{8}{9}\left( {u_{j}^{n}}\left( \bar{u}_{j}^{n} \right)_{\hat{x}}\right) - \frac{2}{9}\left( {u_{j}^{n}}\left( \bar{u}_{j}^{n} \right)_{\ddot{x}}\right) \right]\\ &=&\tau h \sum\limits_{j=1}^{M-1} \left[ \frac{4}{9}\left( {u_{j}^{n}}\left( u_{j}^{n+1}\right)_{\hat{x}}-u_{j}^{n-1}\left( {u_{j}^{n}}\right)_{\hat{x}}\right)-\frac{1}{9}\left( {u_{j}^{n}}\left( u_{j}^{n+1} \right)_{\ddot{x}}-u_{j}^{n-1}\left( {u_{j}^{n}} \right)_{\ddot{x}}\right)\right]. \end{array} $$

Equation (12) follows easily by using similar argument as of (5). We then take an inner product between (7) and $2\bar {u}^{n}$. We obtain the following:

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{2\tau}\left( ||u^{n+1}||^{2}-||u^{n-1}||^{2} \right)+\frac{3\beta}{2}(\bar{u}^{n}_{\text{x}\bar{\text{x}}\hat{\text{x}}},2\bar{u}^{n})-\frac{\beta}{2}(\bar{u}^{n}_{\text{x}\bar{\text{x}}\ddot{\text{x}}},2\bar{u}^{n}) \\ &&+\frac{5\gamma}{3}(\bar{u}^{n}_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}},2\bar{u}^{n})-\frac{2\gamma}{3}(\bar{u}^{n}_{xx\bar{x}\bar{x}\ddot{x}},2\bar{u}^{n}) +2\eta(\psi^{n}(u^{n},\bar{u}^{n}),2\bar{u}^{n})=0, \end{array} $$

where

$$ \psi^{n}(u^{n},\bar{u}^{n})=\frac{4}{9}({u_{j}^{n}}(\bar{u}_{j}^{n})_{\hat{x}}+({u_{j}^{n}}\bar{u}_{j}^{n})_{\hat{x}}) -\frac{1}{9}({u_{j}^{n}}(\bar{u}_{j}^{n})_{\ddot{x}}+({u_{j}^{n}}\bar{u}_{j}^{n})_{\ddot{x}}). $$

By considering the boundary conditions (8)–(10) and according to Lemmas 3 and 3,

$$ (\bar{u}^{n}_{\text{x}\bar{\text{x}}\hat{\text{x}}},\bar{u}^{n})=0,\quad(\bar{u}^{n}_{\text{x}\bar{\text{x}}\ddot{\text{x}}},\bar{u}^{n})=0,\quad(\bar{u}^{n}_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}},\bar{u}^{n})=0,\quad (\bar{u}^{n}_{\text{xx}\bar{\text{x}}\bar{\text{x}}\ddot{\text{x}}},\bar{u}^{n})=0. $$

Indeed, by simple direct calculations and Lemma 1,

$$ \begin{array}{@{}rcl@{}} &&(\psi^{n}(u^{n},\bar{u}^{n}),2\bar{u}^{n})\\ &=&\frac{4h}{9}\left( \sum\limits_{j=1}^{M-1}\left[u_{j}^{n}(u_{j}^{n+1})_{\hat{x}}+({u_{j}^{n}}u_{j}^{n+1})_{\hat{x}} \right]u_{j}^{n+1} + \sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(\bar{u}_{j}^{n})_{\hat{x}}+({u_{j}^{n}}\bar{u}_{j}^{n})_{\hat{x}} \right)u_{j}^{n-1}\right)\\ &&-\frac{2h}{9}\left( \sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(\bar{u}_{j}^{n})_{\ddot{x}} +({u_{j}^{n}}\bar{u}_{j}^{n})_{\ddot{x}} \right)u_{j}^{n+1} + \sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(\bar{u}_{j}^{n})_{\ddot{x}} +({u_{j}^{n}}\bar{u}_{j}^{n})_{\ddot{x}} \right)u_{j}^{n-1}\right)\\ &=&\frac{4h}{9}\left( \sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(u_{j}^{n+1})_{\hat{x}}+({u_{j}^{n}}u_{j}^{n+1})_{\hat{x}} \right)u_{j}^{n+1} + \sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(u_{j}^{n-1})_{\hat{x}}+({u_{j}^{n}}u_{j}^{n-1})_{\hat{x}} \right)u_{j}^{n-1}\right.\\ &&+\sum\limits_{j=1}^{M-1} \left( {u}_{j}^{n}{(u_{j}^{n+1})}_{\hat{x}}u_{j}^{n-1}+({u_{j}^{n}}u_{j}^{n-1})_{\hat{x}} u_{j}^{n+1} \right)\\ &&\left.+\sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(u_{j}^{n-1})_{\hat{x}}u_{j}^{n+1}+({u_{j}^{n}}u_{j}^{n+1})_{\hat{x}}u_{j}^{n-1 }\right)\right)\\ &&-\frac{h}{9}\left( \sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(u_{j}^{n+1})_{\ddot{x}}+({u_{j}^{n}}u_{j}^{n+1})_{\ddot{x}} \right)u_{j}^{n+1} + \sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(u_{j}^{n-1})_{\ddot{x}}+({u_{j}^{n}}u_{j}^{n-1})_{\ddot{x}} \right)u_{j}^{n-1}\right.\\ &&+\sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(u_{j}^{n+1})_{\ddot{x}}u_{j}^{n-1}+({u_{j}^{n}}u_{j}^{n-1})_{\ddot{x}}u_{j}^{n+1} \right)\\ &&\left.+\sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(u_{j}^{n-1})_{\ddot{x}}u_{j}^{n+1}+({u_{j}^{n}}u_{j}^{n+1})_{\ddot{x}}u_{j}^{n-1 }\right)\right)\\ &=& 0. \end{array} $$

Therefore,

$$ \frac{1}{2\tau}\left( ||u^{n+1}||^{2}-||u^{n-1}||^{2} \right)=0. $$

Then, this gives (13). □

The conservative approximation confirms that the energy would not increase in time, which allows us to also conclude that the scheme is stable.

2.3 Standard second-order finite difference scheme

The standard second-order finite difference scheme is also considered, and it will be used as a benchmark of the compact forth-order finite difference scheme since both schemes apply to the same number of nodes. That is, the system of linear equations are similar and of the same complexity. As before, we notice that (u²)_x = (2/3)[uu_x + (u²)_x] and using an implicit finite difference method, we propose a standard seven-point implicit difference scheme for the problem (1):

$$ ({u_{j}^{n}})_{\hat{t}}+\beta(\bar{u}_{j}^{n})_{\text{x}\bar{\text{x}}\hat{\text{x}}}+\gamma(\bar{u}_{j}^{n})_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}}+\frac{2\eta}{3}\left( {u_{j}^{n}}(\bar{u}_{j}^{n})_{\hat{x}}+({u_{j}^{n}}\bar{u}_{j}^{n})_{\hat{x}} \right)=0, $$

(14)

where

$$ {u_{j}^{0}}=u_{0}(x_{j}),~~~0\leq j\leq M. $$

Since the boundary conditions are homogeneous, we obtain the following:

$$ {u_{0}^{n}}={u_{M}^{n}}=0, ({u_{0}^{n}})_{\hat{x}}=({u_{M}^{n}})_{\hat{x}}=0, ({u_{0}^{n}})_{\text{x}\bar{\text{x}}}=({u_{M}^{n}})_{\text{x}\bar{\text{x}}}=0, 1\leq n \leq N. $$

(15)

Just like in two previous schemes, the order of accuracy and stability results can be proven by using a similar argument and calculations.

Theorem 5

The scheme (14) is unconditionally stable in the linearized sense.

Theorem 6

Let uⁿ be the solution of the finite difference scheme (14). Then,

$$ Q^{n}=\frac{h}{2}\sum\limits_{j=1}^{M-1}\left( u_{j}^{n+1} +{u_{j}^{n}} \right) +\frac{\tau h \eta}{3} \sum\limits_{j=1}^{M-1} ({u_{j}^{n}}(u_{j}^{n+1} )_{\hat{x}})=Q^{n-1}=\cdots=Q^{0}. $$

(16)

Moreover, the scheme (14) is conservative in a sense:

$$ E^{n}=\frac{1}{2}||u^{n+1}||^{2}+\frac{1}{2}||u^{n}||^{2}=E^{n-1}=\cdots=E^{0}. $$

(17)

Proof

As a result, we have the following:

$$ \frac{h}{2}\sum\limits_{j=1}^{M-1}(u_{j}^{n+1}-u_{j}^{n-1} )+\frac{\tau h \eta}{3}\sum\limits_{j=1}^{M-1} [ ({u_{j}^{n}}(u_{j}^{n+1})_{\hat{x}}-u_{j}^{n-1}({u_{j}^{n}})_{\hat{x}})]=0. $$

By multiplying (14) by h and summing up for j from 1 to M − 1, we have the following:

$$ \frac{\tau h}{3} \sum\limits_{j=1}^{M-1}({u_{j}^{n}})(\bar{u}_{j}^{n} )_{\hat{x}} =\frac{\tau h}{3} \sum\limits_{j=1}^{M-1} ({u_{j}^{n}}(u_{j}^{n+1})_{\hat{x}}-u_{j}^{n-1}({u_{j}^{n}})_{\hat{x}}). $$

Then, this give (16). We then take an inner product between (14) and $2\bar {u}^{n}$ to obtain the following:

$$ \begin{array}{@{}rcl@{}} \frac{1}{2\tau}\left( ||u^{n+1}||^{2}-||u^{n-1}||^{2} \right)+\beta(\bar{u}^{n}_{\text{x}\bar{\text{x}}\hat{\text{x}}},2\bar{u}^{n})\\ +\gamma(\bar{u}^{n}_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}},2\bar{u}^{n}) +\eta(\psi^{n}(u^{n},\bar{u}^{n}),2\bar{u}^{n})=0, \end{array} $$

where

$$ \psi^{n}(u^{n},\bar{u}^{n})=\frac{2}{3}({u_{j}^{n}}(\bar{u}_{j}^{n})_{\hat{x}}+({u_{j}^{n}}\bar{u}_{j}^{n})_{\hat{x}}). $$

By considering the boundary conditions (15) and according to Lemma 3,

$$ (\bar{u}^{n}_{\text{x}\bar{\text{x}}\hat{\text{x}}},\bar{u}^{n})=0, (\bar{u}^{n}_{\text{xx}\bar{\text{x}}\bar{\text{x}}\hat{\text{x}}},\bar{u}^{n})=0, $$

we have the following:

$$ \begin{array}{@{}rcl@{}} &&(\psi^{n}(u^{n},\bar{u}^{n}),2\bar{u}^{n})\\ &=&\frac{2h}{3}\left( \sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(\bar{u}_{j}^{n})_{\hat{x}}+({u_{j}^{n}}\bar{u}_{j}^{n})_{\hat{x}} \right)u_{j}^{n+1}+\sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(\bar{u}_{j}^{n})_{\hat{x}}+({u_{j}^{n}}\bar{u}_{j}^{n})_{\hat{x}} \right)u_{j}^{n-1}\right)\\ &=&\frac{h}{3}\left( \sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(u_{j}^{n+1})_{\hat{x}} + ({u_{j}^{n}}u_{j}^{n+1})_{\hat{x}} \right)u_{j}^{n+1} + \sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(u_{j}^{n-1})_{\hat{x}}+({u_{j}^{n}}u_{j}^{n-1})_{\hat{x}} \right)u_{j}^{n-1}\right.\\ &&+\sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(u_{j}^{n+1})_{\hat{x}}u_{j}^{n-1}+({u_{j}^{n}}u_{j}^{n-1})_{\hat{x}}u_{j}^{n+1} \right)\\&&\left.+\sum\limits_{j=1}^{M-1} \left( {u_{j}^{n}}(u_{j}^{n-1})_{\hat{x}}u_{j}^{n+1}+({u_{j}^{n}}u_{j}^{n+1})_{\hat{x}}u_{j}^{n-1 }\right)\right)\\ &=& 0 \end{array} $$

when Lemma 1 is used. Therefore,

$$ \frac{1}{2\tau}\left( ||u^{n+1}||^{2}-||u^{n-1}||^{2} \right)=0. $$

Then, this gives (17). □

3 Numerical experiments

The numerical methods discussed in the previous section are applied to the Kawahara equation when β = 1, γ = − 1, and η = 0.5, which has an analytical solution as follows:

$$ u(x,t)=\frac{105}{169}\text{sech}^{4}\left( \frac{1}{2\sqrt{13}}\left( x-\frac{36}{169}t \right)\right). $$

The accuracy of methods is measured by a comparison of numerical solutions with the exact solution by using discrete norms defined as follows:

$$\left\|e^{n}\right\|=\left\|u^{\text{exact}}-u^{n}\right\|=\left( h{\sum}_{j=1}^{M-1} \left| u^{\text{exact}}_{j}-{u^{n}_{j}}\right|^{2}\right)^{1/2} $$

and

$$ \left\|e^{n}\right\|_{\infty}=\left\|u^{\text{exact}}-u^{n}\right\|_{\infty}= \max_{1\le j\le M-1}\left|u^{\text{exact}}_{j}-{u^{n}_{j}} \right|. $$

The initial condition for each model is chosen in such a way that the exact solution can be explicitly computed. The performance of each of numerical models was evaluated for test cases involving different mesh size, long time behavior, and structure preserving. For simplicity, we call the Scheme I, Scheme II, and Scheme III to represent the compact fourth-order finite difference scheme, the standard fourth-order finite difference scheme, and the standard second-order finite difference scheme, respectively. Since the accuracy of the compact scheme (Scheme I) presented here is of second- and fourth-orders in time and in space, respectively, and a three-level approximation in time is used in the algorithm together with the initial condition, we need u¹ as a known condition. Therefore, we first choose a two-level scheme which is an available fourth-order accuracy method for calculation u¹. For this reason, we can determine u² by the new three-level finite difference schemes (Scheme I, Scheme II, and Scheme III). In order to show the accuracy in space of schemes proposed here, we do not allow the error in time which is absorbing accuracy in space. Therefore, we decide the temporal step by choosing τ = h². The rate of convergence from the calculations coincides with the one from theoretical results. That is, the Scheme I and Scheme II are fourth order of accuracy, but the Scheme III is second order of accuracy, as presented in Table 1. The Scheme I and Scheme II can make errors dropped to 10^− 7 by using h = 0.125 while the Scheme III can make the ones dropped to just only 10^− 4. According to the results, the Scheme I and Scheme II can increase in the speedup of the convergence rate compared to the Scheme III.

Table 1 The errors of numerical solutions and rate of convergence at t = 120 using τ = h², x_L = − 60, and x_R = 100

The numerical models generate very similar results in most cases, which compared to the exact solution. Excellent agreement between numerical and exact solutions was observed; however, only moderately good agreement was seen in the error result from the Scheme III as seen in Fig. 1. Moreover, if we use the Scheme I instead of the Scheme II, then the error of numerical results can be reduced. Regarding an observation on Figs. 2 and 3, we can see that the solitary wave performed by the Scheme III propagates slower than the wave generated by the exact solution significantly in a long time. Besides, Figs. 2 and 3 illustrate that the expanded left-tail figure exhibits fluctuation of numerical approximations on x ∈ [− 50,100]. As observed, the Scheme I offers the fit resolution of wave structure at the left tail. Next, a solution of the Kawahara equation has the following conservative properties [27]:

$$ Q(t)={\int}_{x_{L}}^{x_{R}}u(x,t)\text{dx}={\int}_{x_{L}}^{x_{R}}u_{0}(x)\text{dx}=Q(0) $$

and

$$ E(t)={\int}_{x_{L}}^{x_{R}}u^{2}(x,t)\text{dx}={\int}_{x_{L}}^{x_{R}}{u^{2}_{0}}(x)\text{dx}=E(0). $$

Then, by using discrete forms, we can approximate two conservative quantities as follows:

$$ Q^{n}= \frac{h}{2}{\sum}_{j=1}^{M-1} \left( u_{j}^{n+1}+{u_{j}^{n}}\right) \text{and} E^{n}= \frac{h}{2}{\sum}_{j=1}^{M-1}\left( \left( u_{j}^{n+1}\right)^{2} +\left( {u_{j}^{n}}\right)^{2}\right) $$

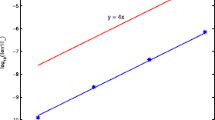
which are related to mass and energy, respectively. Figures 4 and 5 show $\log _{10}|Q^{n}-Q^{0}|$ and $\log _{10}|E^{n}-E^{0}|$ distributions for t ∈ [0,500]. Obviously, there are numerous oscillations occurring in the results. These are due to the theoretical result. That is, the Scheme I does not guarantee energy preserving, but the other two schemes do. Nevertheless, all three schemes guarantee mass preserving, but the obtained results shown Figs. 4 and 5 show that Scheme I and Scheme II give the better result which is caused by using higher order of accuracy.

Fig. 1

The distribution of absolute errors, $|u_{j}^{\text {exact}}-{u^{n}_{j}}|$, using h = 0.5,τ = h², x_L = − 60, and x_R = 100 (top) Scheme I, (middle) Scheme II, and (bottom) Scheme III

Fig. 2

The expanded left-tail oscillation of numerical solutions at t = 2000 using h = 0.5,τ = h²,x_L = − 60, and x_R = 600

Fig. 3

The long-time behavior of numerical solutions at t = 2000 using h = 0.5,τ = h²,x_L = − 60, and x_R = 600

Fig. 4

The distribution of $\log _{10}|Q^{n}-Q^{0}|$ using h = 0.5,τ = h²,x_L = − 60, and x_R = 500

Fig. 5

The distribution of $\log _{10}|E^{n}-E^{0}|$ for t ∈ [0,500] using h = 0.5,τ = h²,x_L = − 60, and x_R = 250.

Next, numerical simulations are designed to confirm the efficiency of the compact finite difference scheme. The results are reported here, and the initial condition is set to be as follows:

$$u(x,0)=\frac{105}{169}\text{sech}^{4}\left( \frac{1}{2\sqrt{13}}\left( x-\frac{36}{169}-x_{0}\right)\right),$$

where x₀ is the center of the solitary wave. We model a single solitary wave with x₀ = 2, β = 1, γ = − 1, and η = 0.5 as in [13, 15,16,17] and with the spatial step size h = 0.2 as in [15] in order to make a comparison to those given in the references. The motion of a solitary wave is simulated with the range [− 40,50], and the simalutions run up to t = 25. We decide the temporal step by choosing τ = 0.1 and τ = 0.01 as one can see in Table 2. The tests show that the error from the Scheme I is improved about 90% compared with methods in [13, 15, 16] when τ = 0.1 is used. Numerical solutions obtained by the Scheme I have 2-digit more accuracy comparing with the PDQ method [16]. Moreover, the tests show that the error from the Scheme I is improved about 50% comparing with the MCBC-DQM method [16] when τ = 0.01 and t = 25 are used. The invariants are compared with results from [13, 15,16,17] to guarantee the performance of the present methods until the final time t = 25 is reached. For observation, the invariants Qⁿ and Eⁿ whose reference values are gained as Q⁰ = 5.97369 and E⁰ = 1.27250 are listed in Table 2. The tests show that, at t = 25, the quantities Qⁿ obtained from Scheme I and Scheme II are about 1–2 digits better than that of the Scheme III and the schemes in [13, 15,16,17]. As seen, the values Eⁿ obtained from Scheme I, Scheme II, and Scheme III are conserved in our simulations with at least 5-digit correctness for values of τ = 0.1 and τ = 0.01.

Table 2 Error comparison and change in invariants

4 Concluding remarks

The calculation results for a long-time behavior with the second-order scheme (Scheme III) used in numerical experiments showed need of higher accuracy. As a result, it was replaced by the fourth-order Schemes I and II discussed in Section 2. This modification is straightforward, but special attention must be taken at the boundary of the computational domain for the Scheme II as the computational stencil is larger than the one in the Scheme III. However, the computational stencil of the Scheme I is equal to the one of the Scheme III. When compared to the standard finite difference schemes, the compact scheme normally use a fewer stencil and indicate more appropriate resolution as of the same order of accuracy. Because of the effective completeness of the solution to the resulting multidiagonal sparse system, the computational cost of the developed compact scheme is very less when compared to the standard schemes. Moreover, the numerical solutions should reproduce the properties of the original problem, which is an important factor for improving the efficiency of a numerical method. This is a considerable challenge to the computational technique community. For this reason, the numerical algorithms in the paper have been developed to preserve the structure of the original equation—i.e., conservation of mass and energy.