Convergence and stability of spectral collocation method for hyperbolic partial differential equation with piecewise continuous arguments

Abstract

This paper deals with the convergence and stability of the spectral collocation method for a hyperbolic partial differential equation with piecewise continuous arguments. Firstly, the convergence of continuous-time and discrete-time collocation methods is analyzed by means of equivalent schemes with $L^2$-norm rigorously. We obtain the order of convergence of the continuous-time collocation method is $O(h^4)$ and the discrete-time collocation method is $O(h^4+p)$, where h and p are spatial step and temporal step, respectively. Secondly, the stability of two numerical schemes is analyzed by Fourier analysis method. It is proven that the continuous-time collocation method is unconditionally stable. The stability conditions for the discrete-time collocation method are derived under which the analytic solution is asymptotically stable. Finally, some numerical experiments are carried out to demonstrate our theoretical results.

1 Introduction

In this paper we principally investigate theoretical and computational aspects of the spectral collocation method for the numerical solution of following hyperbolic partial differential equation with piecewise continuous arguments (PEPCA)

$$\begin{aligned} \begin{aligned}&u_{tt}(x,t)=a^2u_{xx}(x,t)+bu_{xx}(x,[t]), \quad {\text {in}} \quad \Omega \times J,\\&u(x,0)=v(x), \,u_t(x,0)=w(x), \quad {\text {in}} \quad \Omega ,\\&u(x,t)=0 \quad {\text {on}} \quad \partial \Omega \times J, \end{aligned} \end{aligned}$$

(1)

where $a, b \in {\mathbb {R}}$, $\Omega =[0,1]$ with smooth boundary $\partial \Omega$, $J=[0, +\infty )$ and $[\cdot ]$ denotes the greatest integer function.

Nowadays, differential equations with piecewise continuous arguments (EPCA) are used to model various different phenomena in economy (Cavalli and Naimzada 2016), competition (Kartal and Gurcan 2015), population growth (Karakoc 2017) and so on. Hence, the extensive applications of delay effects in describing the past and future status of systems show the importance of the theory of EPCA. The study of EPCA was initiated by Aftabizadeh and Wiener (1986). They found that the change of sign in the argument deviation leads to interesting periodic properties, asymptotic and oscillatory behavior of solutions. Since EPCA can hardly be solved by analytical methods or much complicated to deal with, the numerical analysis of EPCA is currently an active area of research, which although start a little late. And there has been a number of literatures on numerical methods for EPCA, see Gao (2017), Liu and Zeng (2018), Milošević (2016), Wang and Wang (2018), Wang et al. (2011) and Zhang et al. (2018). However, the numerical methods in these papers mainly focus on the EPCA in case of ordinary differential equations. Up to now there has existed some literatures about PEPCA with various numerical methods (Liang et al. 2010a, b; Wang 2017; Wang and Wen 2014; Wang and Wang 2019). Parabolic PEPCA was investigated with the $\theta$-method (Liang et al. 2010a) and Galerkin finite element method (Liang et al. 2010b). In Wang and Wen (2014), the $\theta$-method was also applied to another PEPCA of mixed type and the sufficient conditions for the numerical stability were established. In addition, Wang and Wang (2019) considered the analytical and numerical stability of PEPCA of alternately retarded and advanced type in the $\theta$-schemes and achieved the corresponding stability conditions. For more information on PEPCA, the interested readers can refer to publications (Wiener and Debnath 1992, 1997; Wiener and Heller 1986; Bereketoglu and Lafci 2017) and the references contained therein.

The spectral methods have been developed to investigate all kind of equations in the recent two decades, which are known generally as the method of weighted residuals with distinctive feature that the trial functions are used as the basis functions for a truncated series expansion of solution. The Galerkin method, collocation method and Tau method are viewed as three well-known spectral types. Compared with the existing numerical methods such as finite element method and finite difference method, spectral methods provide superior economical and accurate schemes when dealing with differential equations. The privilege of collocation methods over other spectral methods mainly reflects on solving of linear and nonlinear differential equations with accurate and efficient procedures, especially suitable for the numerical analysis of nonlinear problems. The orthogonal spline collocation method initially was proposed to investigate a m-order ordinary differential equation in De Boor and Swartz (1973) and considered to deal with various equations later. Collocation schemes based on Chebyshev polynomials (Ardabili and Talaei 2018; Babaei et al. 2020; Morgado et al. 2017; Nagy 2017), Legendre polynomials (Sharma et al. 2018; Yousefi et al. 2019), B-spline functions (Roul and Goura 2019; Singh et al. 2021) and Jacobi polynomials (Bhrawy et al. 2016a, b) have been frequently applied to approximate the solution of various types of differential equations and integral equations. Some of the recent studies on collocation methods are described as follows. Saw and Kumar (2021) proposed an efficient and accurate scheme based on Chebyshev collocation method and finite difference approximation to investigate time-fractional convection–diffusion equation and illustrated the convergence analysis. In Rahimkhani and Ordokhani (2019), 2D Bernoulli wavelets together with a fractional integral operator were applied to reduce two types of fractional partial differential equations to systems of algebraic equations which were solved by the Newton’s iterative method and the corresponding error estimate was presented in $L^2$-norm. Similarly, a nonlinear weakly singular partial integro-differential equation was investigated in Singh et al. (2018) and it was reduced to nonlinear system of algebraic equations by the operational matrix of integration of 2D Legendre wavelets. Roul et al. studied Bratu-type and Lane–Emden-type problems (Roul et al. 2019) with the optimal quartic B-spline collocation method and a class of nonlinear singular Lane-Emden type equations (Roul et al. 2019) with the optimal quintic spline function. They achieved optimal convergence of order six through imposing perturbation to the original problem while the normal quartic and quintic spline function just arrived at four order. Orthogonal polynomials were selected matching to their specific properties which construct them appropriate for the problem under investigation, like Fourier series (Arezoomandan and Soheili 2021) for periodic problems and Chebyshev and Legendre polynomials for non-periodic problems. The Chebyshev series expansion can be seen as a proper alternative to the Fourier basis in the form of cosine Fourier series especially dealing with Gibbs phenomenon at the boundaries (Rakhshan and Effati 2018). In addition, collocation methods have been successfully applied in magnetic field (Renu et al. 2021), heat transfer (Ma et al. 2017; Wang et al. 2017), radiative transfer (Li and Wei 2018), model of squeezing flow (Saadatmandi et al. 2016) and so on. For more information on collocation methods, the interested reader can refer to literatures (Hammad and El-Azab 2016; Baseri et al. 2018; Rohaninasab et al. 2018; Zaky and Ameen 2019) and the references contained therein.

In this paper, we apply Hermite piecewise-cubic polynomial to instruct the spectral collocation method, then we numerically solve Problem (1) by this spectral collocation method, which can transform the given differential equation to algebraic systems of equations with unknown coefficients. It is worthy noticing that the distinguishing advantage of collocation method over Galerkin finite element method reflects on no effort to compute integrals when setting up the corresponding algebraic system of equations. Since no integral need to be evaluated or approximated, the calculation of the coefficients determining the approximate solution is vary fast. Moreover, the operational matrices of proposed method are sparse ones, which make computation easy and quick. Also, unlike finite difference method, it yields continuous approximation to the solution with high-order accuracy. On the basis of the outstanding advantages of collocation method described above, we propose the continuous-time collocation and discrete-time collocation schemes for Problem (1) and discuss their convergence by means of equivalent schemes. We also achieve unconditional stability for continuous-time collocation scheme and some stability conditions for discrete-time collocation scheme with Fourier analysis method. The satisfactory results can be obtained only using a little number of nodes in numerical experiments, along with the comparisons with other existing numerical methods showing that the spectral collocation method possesses higher accuracy.

The rest of paper is structured as follows. Sect. 2 presents some important preliminaries which also includes reasons for locating two collocation points in per interval and bases of Hermite piecewise-cubic space. In Sect. 3, we start with the convergence analysis of continuous-time collocation scheme by means of its equivalent scheme with its corresponding inner product and obtain the corresponding convergence order. Moreover, we prove that this scheme is unconditional asymptotically stable. We analyze the convergence and stability of discrete-time collocation scheme in analogous with continuous-time one in Sect. 4. Some numerical experiments are provided to illustrate our theoretical analysis in Sect. 5 and the last section contains some conclusions.

2 Preliminaries

Definition 1

(Wiener 1993) A function u(x, t) is called a solution of Problem (1) if it satisfies the conditions:

• (i) u(x, t) is continuous in $\Omega \times J$.

• (ii) ${\partial }^ku/\partial x^k$ and ${\partial }^ku/\partial t^k (k=1, 2)$ exist and are continuous in $\Omega \times J$ with the possible exception of the points (x, n), where one-sided derivatives exist $(n=0, 1, 2, \cdots )$.

• (iii) u(x, t) satisfies $u_{tt}(x,t)=a^2u_{xx}(x,t)+bu_{xx}(x,[t])$ in $\Omega \times J$ with the possible exception of the points (x, n), and conditions $u(x,0)=v(x), u_t(x,0)=w(x)$ in $\Omega$ and $u(x,t)=0$ on $\partial \Omega \times J$.

Lemma 1

(Wiener 1993) The zero solution of Problem (1) is asymptotically stable if and only if

$$\begin{aligned} -a^2<b<0. \end{aligned}$$

(2)

As we know, a collocation method is based on the principle of approximating the analytic solution of given equation with an appropriate function belonging to a chosen finite dimensional space, usually a piecewise polynomial which satisfies the equation exactly on a set of specific points (called the set of collocation points). In this paper, we will concern with the numerical solution of Problem (1) by a kind of particular method of collocation equipped with Hermite piecewise-cubic polynomials with respect to space variable x at each time t.

Let $\delta =[x_0,x_1,\cdots ,x_N]$, where $0=x_0<x_1<\cdots <x_{N}=1$ denote the regular partitions of $\Omega _i=[x_{i-1},x_i]$ with the steps $h_i=x_i-x_{i-1}$ and $h=\underset{1\le i\le N}{\max }(x_i-x_{i-1})$. Set time-size $p=1/m \,( m\ge 1)$ and let $S_{r-1}$ be the piecewise polynomial spline space

$$\begin{aligned} S_{r-1}=\{ \nu \in C^2({\bar{\Omega }}):\nu \mid _{\Omega _i} \in P_{r-1}(\Omega _i), 1\le i \le N\}, \end{aligned}$$

(3)

where $P_{r-1}(\Omega _i)$ denotes the space of all (real) polynomials of degree no more than $r-1$ when restricted to the set $\Omega _i$. When $r=4$, the space $S_3$ is commonly known as Hermite piecewise-cubic space. The bases of the Hermite piecewise-cubic space are considered as follows

$$\begin{aligned} \begin{aligned} \phi _{i}(x)&=\left\{ \begin{aligned}&\left( 1+2\frac{x-x_i}{x_{i-1}-x_i}\right) \left( \frac{x-x_{i-1}}{x_i-x_{i-1}}\right) ^2, \quad \quad&x\in [x_{i-1},x_{i}], \\&\left( 1+2\frac{x-x_i}{x_{i+1}-x_i}\right) \left( \frac{x-x_{i+1}}{x_i-x_{i+1}}\right) ^2,&x\in [x_{i},x_{i+1}], \\&0,&{\text {elsewhere}}, \end{aligned} \right. \\ \varphi _{i}(x)&=\left\{ \begin{aligned}&(x-x_i)\left( \frac{x-x_{i-1}}{x_i-x_{i-1}}\right) ^2, \qquad \qquad \,\, \qquad&x\in [x_{i-1},x_{i}], \\&(x-x_i)\left( \frac{x-x_{i+1}}{x_i-x_{i+1}}\right) ^2,&x\in [x_{i},x_{i+1}], \\&0,&{\text {elsewhere}}, \end{aligned} \right. \\&\qquad i=1,2,\ldots ,N-1\\ \end{aligned} \end{aligned}$$

(4)

that is, $S_3={\text {span}}[\phi _0,\varphi _0,\ldots ,\phi _N,\varphi _N]$ and $\dim (S_3)=2N+2$. Therefore, we need $2N+2$ relations to specify the numerical solution of Problem (1) at each time t. It’s obvious to see that the coefficient of $\phi _0$ and $\phi _N$ are 0 from the boundary conditions in Problem (1). For convenience, let

$$\begin{aligned} S_{3}^0={\text {span}}\{\varphi _0,\phi _1, \varphi _1, \ldots , \phi _{N-1}, \varphi _{N-1}, \varphi _N\}={\text {span}}\{\Phi _1,\Phi _2, \ldots , \Phi _{2N}\}. \end{aligned}$$

(5)

The method of collocation requires that the remaining relations should be obtained by having the differential equation satisfied at 2N points. Since there are N intervals $\Omega _i$, two points are located in each interval subsequently. We choose the points in the following form

$$\begin{aligned} \xi _{i,k_1}=\frac{1}{2}(x_{i-1}+x_i)+(-1)^{k_1}\frac{h_i}{2\surd {3}}, i=1,2,\ldots ,N, k_1=1,2, \end{aligned}$$

(6)

then $x_{i-1}<\xi _{i,1}<\xi _{i,2}<x_i$.

We can denote a discrete inner product in $C(\Omega )$ and its associated norm by

$$\begin{aligned} \langle f,g \rangle _i=\frac{1}{2}\left( f(\xi _{i,1})g(\xi _{i,1})+f(\xi _{i,2})g(\xi _{i,2})\right) h_i, \quad |f|_i^2=\langle f,f \rangle _i, \end{aligned}$$

(7)

and

$$\begin{aligned} \langle f,g\rangle =\sum _{i=1}^N \langle f,g \rangle _i, \quad |f^2|=\langle f,f \rangle . \end{aligned}$$

(8)

Let $H^s(\Omega )$ be Sobolev space on $\Omega$ and $|\cdot |_s$ is the related norm. Define $H^1_0=\{\phi \in H^1(\Omega ):\phi =0 \quad {\text {on}} \quad \partial \Omega \}$. $H^1_0(\Omega )$ is the completion of $C^{\infty }_0(\Omega )$ under $L^2(\Omega )$-norm $\Vert \cdot \Vert$ and denote

$$\begin{aligned} \Vert f\Vert =\Vert f\Vert _{L^2}=(f,f)^{\frac{1}{2}}, \Vert \nabla f\Vert =\Vert \nabla f\Vert _{L^2}=(\nabla f,\nabla f)^{\frac{1}{2}}, \end{aligned}$$

(9)

where

$$\begin{aligned} \begin{aligned}&\Vert f\Vert _s=\left( \sum _{0\le |\alpha |\le s}\Vert D^{\alpha }u\Vert ^2\right) ^{\frac{1}{2}}, (f,g)=\int _{\Omega }f(x)g(x) {\text {d}}x, \\&(\nabla f,\nabla g)=\int _{\Omega }\frac{\partial f}{\partial x}\frac{\partial g}{\partial x}{\text {d}}x,\,\forall f,g\in L^2(\Omega ). \end{aligned} \end{aligned}$$

(10)

By the Gauss type integration, we have

$$\begin{aligned} \langle f,g \rangle =(f,g),\,\forall f,g\in P_{2N-1}. \end{aligned}$$

(11)

3 Continuous-time collocation method

The continuous-time approximation is a differentiable map $U(t)=U(\cdot ,t) : {\bar{J}} \rightarrow S_3$, belonging to $S_3$ for each t, such that

$$\begin{aligned} \begin{aligned}&U_{tt}(\xi _{i,k},t)=a^2U_{xx}(\xi _{i,k},t)+bU_{xx}(\xi _{i,k},[t]),i=1,\ldots ,N, k=1,2, t\in J,\\&U(\xi _{i,k},0)={\bar{v}}(\xi _{i,k}),\,U_t(\xi _{i,k},0)={\bar{w}}(\xi _{i,k}),\\&U(x_0,t)=U(x_N,t)=0, \end{aligned} \end{aligned}$$

(12)

where ${\bar{v}},{\bar{w}}$ are the $S_3$-interpolation of v and w at the nodes $\xi _{i,k}$, respectively.

It is useful to introduce a continuous time discrete Galerkin procedure, whose solution can be viewed as the solution of (12), that is

$$\begin{aligned} \langle U_{tt}(x,t)-U_{xx}(x,t)-U_{xx}(x,[t]),\chi \rangle =0, \chi \in S_3. \end{aligned}$$

(13)

According to (Douglas and Dupont 1974, Lemma 4.1), we know that the collocation method (12) and the discrete Galerkin method (13) each posses a unique solution and these solutions are identical if the processes start from the same initial values.

We write Problem (1) in weak form: Finding u: ${\bar{J}}\rightarrow H_0^1$, application of Green’s formula to the second term and third term gives

$$\begin{aligned} \begin{aligned}&(u_{tt}(x,t),\phi )+a^2( \nabla u(x,t),\nabla \phi )+b(\nabla u(x,[t]),\nabla \phi )=0, \forall \phi \in H_0^1, t>0,\\&u(0)=v, u_t(0)=w, \end{aligned} \end{aligned}$$

(14)

from (11) and (13), (14) is equivalent to the following Galerkin type scheme

$$\begin{aligned} \begin{aligned} (U_{tt}(x,t),\chi )+a^2(\nabla U(x,t),\nabla \chi )+b(\nabla U(x,[t]),\nabla \chi )=0, \forall \chi \in S_3, t>0.\\ \end{aligned} \end{aligned}$$

(15)

We introduce the Ritz projection $R: H_0^1(\Omega )\rightarrow S_3$ as the orthogonal projection with respect to the inner product $(\nabla \varphi ,\nabla \chi )$, thus

$$\begin{aligned} (\nabla R \varphi , \nabla \chi )=(\nabla \varphi , \nabla \chi ), \,\forall \chi \in S_3, \,for \,\varphi \in H_0^1. \end{aligned}$$

(16)

Lemma 2

(Thomée 1986) For $\varphi \in H^s\cap H_0^1$ and $1\le s\le r$, if

$$\begin{aligned} \Vert \varphi -\chi \Vert +h\Vert \nabla (\varphi -\chi )\Vert \le Ch^s\Vert \varphi \Vert _s, \chi \in S_{r-1} \end{aligned}$$

(17)

holds, then we have

$$\begin{aligned} \Vert R\varphi -\varphi \Vert +h\Vert \nabla (R\varphi -\varphi )\Vert \le Ch^s\Vert \varphi \Vert _s, \end{aligned}$$

(18)

where C is a positive constant.

Since we discuss the test function in Hermite piecewise-cubic space, so let $r=4$ in Lemma 2.

3.1 Convergence analysis

Theorem 1

Let u and U be the solutions of (1) and (12), respectively. For $t\in [n,n+1)(n\in Z)$, if $\Vert {\bar{v}}-v\Vert \le Ch^4\Vert v\Vert _4$ and $\Vert {\bar{w}}-w\Vert \le Ch^4\Vert w\Vert _4$, then

$$\begin{aligned} \begin{aligned}&\Vert U(t)-u(t)\Vert \\ {}&\quad \le C(t)h^4\left\{ \Vert v\Vert _4+\Vert w\Vert _4+\int _0^t\Vert u_s(s)\Vert {\text {d}}s+\int _0^t\left( \int _0^t\Vert u_{ss}(s)\Vert _4^2{\text {d}}s\right) ^{\frac{1}{2}}{\text {d}}t\right\} , \end{aligned} \end{aligned}$$

(19)

where C(t) is a function of t.

Proof

From $R(u)_{tt}=Ru_{tt}$ , (14) and (15) we have

$$\begin{aligned} \begin{aligned} (u_{tt}(t)-Ru_{tt}(t),\chi ) =&(U_{tt}(t),\chi )-((Ru)_{tt}(t),\chi )+a^2(\nabla U(t),\nabla \chi )\\&-a^2(\nabla Ru(t),\nabla \chi )+b(\nabla U([t]),\nabla \chi )-b(\nabla RU([t]),\nabla \chi ). \end{aligned} \end{aligned}$$

(20)

Denote

$$\begin{aligned} U(t)-u(t)=\left( U(t)-Ru(t)\right) +\left( Ru(t)-u(t)\right) \triangleq \mu (t)+\nu (t), \end{aligned}$$

(21)

then by (20) we get

$$\begin{aligned} (\mu _{tt}(t),\chi )+a^2(\nabla \mu (t),\nabla \chi )+b(\nabla \mu ([t]),\nabla \chi )=(-\nu _{tt}(t), \chi ). \end{aligned}$$

(22)

Now, we begin to estimate $\nu (t)$ and $\mu (t)$. For $\nu (t), t\in [n,n+1)$, by Lemma 2 we have

$$\begin{aligned} \Vert \nu (t)\Vert =\Vert Ru(t)-u(t)\Vert\le & {} Ch^4\Vert u(t)\Vert _4=Ch^4\left\| u(0)+\int _0^tu_s {\text {d}}s\right\| _4 \nonumber \\\le & {} Ch^4\left( \Vert v\Vert _4+\int _0^t\Vert u_s\Vert _4 {\text {d}}s\right) . \end{aligned}$$

(23)

To estimate $\mu (t)$, we begin with (22) by taking $\chi =a^2\mu _t(t)+b\mu _t([t])$, so

$$\begin{aligned} \begin{aligned}&(\mu _{tt}(t),a^2\mu _t(t)+b\mu _t([t]))+(a^2\nabla \mu (t)+b\nabla \mu ([t]),a^2\nabla \mu _t(t)+b\nabla \mu _t([t]))\\&\quad =-(\nu _{tt}(t),a^2\mu _t(t)+b\mu _t([t])), \end{aligned} \end{aligned}$$

(24)

further

$$\begin{aligned}{} & {} (\mu _{tt}(t),a^2\mu _t(t)+b\mu _t([t]))+\frac{1}{2}\frac{{\text {d}}}{{\text {d}}t}\left\| a^2\nabla \mu (t)+b\nabla \mu ([t])\right\| ^2\nonumber \\ {}{} & {} =-(\nu _{tt}(t),a^2\mu _t(t)+b\mu _t([t])), \end{aligned}$$

(25)

then we derive

$$\begin{aligned} (\mu _{tt}(t),a^2\mu _t(t)+b\mu _t(n))\le \Vert \nu _{tt}(t)\Vert \Vert a^2\mu _t(t)+b\mu _t(n)\Vert \end{aligned}$$

(26)

and

$$\begin{aligned} \frac{a^2}{2}\frac{{\text {d}}}{{\text {d}}t}\Vert \mu _t(t)\Vert ^2+b\frac{d}{dt}(\mu _t(t),\mu _t(n))\le \Vert \nu _{tt}(t)\Vert \Vert a^2\mu _t(t)+b\mu _t(n)\Vert . \end{aligned}$$

(27)

Integrating (27) from n to t, we get

$$\begin{aligned} \begin{aligned}&\frac{a^2}{2}\Vert \mu _t(t)\Vert ^2-\frac{a^2}{2}\Vert \mu _t(n)\Vert ^2+b(\mu _t(t),\mu _t(n))-b\Vert \mu _t(n)\Vert ^2\\ {}&\le \int _n^t\Vert \nu _{ss}(s)\Vert \Vert a^2\mu _s(s)+b\mu _s(n)\Vert {\text {d}}s, \end{aligned} \end{aligned}$$

(28)

then

$$\begin{aligned} \begin{aligned}&\frac{a^2}{2}\Vert \mu _t(t)\Vert ^2-\frac{a^2}{2}\Vert \mu _t(n)\Vert ^2-\frac{|b|\delta _1}{2}\Vert \mu _t(t)\Vert ^2-\frac{|b|}{2\delta _1}\Vert \mu _t(n)\Vert ^2-b\Vert \mu _t(n)\Vert ^2\\&\quad \le \frac{a^2\delta _2}{2}\int _n^t\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s+\frac{a^2}{2\delta _2}\int _n^t\Vert \mu _s(s)\Vert ^2{\text {d}}s+\frac{|b|\delta _3}{2}\int _n^t\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s\\&\qquad +\frac{|b|}{2\delta _3}\int _n^t\Vert \mu _s(n)\Vert ^2{\text {d}}s, \end{aligned} \end{aligned}$$

(29)

by Schwarz–Cauchy inequality

$$\begin{aligned} \begin{aligned}&b(\mu _t(t),\mu _t(n))\le |b|\Vert \mu _t(t)\Vert \Vert \mu _t(n)\Vert \le \frac{|b|\delta _1}{2}\Vert \mu _t(t)\Vert ^2+\frac{|b|}{2\delta _1}\Vert \mu _t(n)\Vert ^2, \delta _1>0,\\&\quad \Vert \nu _{ss}(s)\Vert \Vert a^2\mu _s(s)\Vert \le \frac{a^2\delta _2}{2}\Vert \nu _{ss}(s)\Vert ^2+\frac{a^2}{2\delta _2}\Vert \mu _s(s)\Vert ^2, \delta _2>0,\\&\quad \Vert \nu _{ss}(s)\Vert \Vert b\mu _s(n)\Vert \le \frac{|b|\delta _3}{2}\Vert \nu _{ss}(s)\Vert ^2+\frac{|b|}{2\delta _3}\Vert \mu _s(n)\Vert ^2, \delta _3>0. \end{aligned} \end{aligned}$$

(30)

Thus

$$\begin{aligned} \begin{aligned} \left( \frac{a^2-|b|\delta _1}{2}\right) \Vert \mu _t(t)\Vert ^2\le&\left( \frac{a^2}{2}+\frac{|b|}{2\delta _1} +|b|+\frac{|b|}{2\delta _3}(t-n)\right) \Vert \mu _t(n)\Vert ^2\\ {}&+\frac{a^2\delta _2+|b|\delta _3}{2}\int _n^t\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s+\frac{a^2}{2\delta _2}\int _n^t\Vert \mu _s(s)\Vert ^2{\text {d}}s. \end{aligned} \end{aligned}$$

(31)

Let $\alpha =(a^2-|b|\delta _1)/2$ and make $a^2-|b|\delta _1>0$ hold by $\delta _1>0$, (31) turns into

$$\begin{aligned} \begin{aligned} \Vert \mu _t(t)\Vert ^2\le&\left( \frac{a^2}{2\alpha }+\frac{|b|}{2\delta _1\alpha }+\frac{|b|}{\alpha }+\frac{|b|}{2\delta _3\alpha }(t-n)\right) \Vert \mu _t(n)\Vert ^2\\&+\frac{a^2\delta _2+|b|\delta _3}{2\alpha }\int _n^t\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s+\frac{a^2}{2\delta _2\alpha }\int _n^t\Vert \mu _s(s)\Vert ^2{\text {d}}s. \end{aligned} \end{aligned}$$

(32)

Gronwall inequality implies that

$$\begin{aligned} \begin{aligned} \Vert \mu _t(t)\Vert ^2\le&\left( \left( \frac{a^2}{2\alpha }+\frac{|b|}{2\delta _1\alpha }+\frac{|b|}{\alpha }+\frac{|b|}{2\delta _3\alpha }(t-n)\right) \Vert \mu _t(n)\Vert ^2\right. \\&\left. +\frac{a^2\delta _2+|b|\delta _3}{2\alpha }\int _n^t\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s\right) e^{\frac{a^2}{2\alpha \delta _2}(t-n)}\\ =&\left( \frac{a^2}{2\alpha }+\frac{|b|}{2\delta _1\alpha }+\frac{|b|}{\alpha }+\frac{|b|}{2\delta _3\alpha }(t-n)\right) e^{\frac{a^2}{2\alpha \delta _2}(t-n)}\Vert \mu _t(n)\Vert ^2\\ {}&+\frac{a^2\delta _2+|b|\delta _3}{2\alpha }e^{\frac{a^2}{2\alpha \delta _2}(t-n)}\int _n^t\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s. \end{aligned} \end{aligned}$$

(33)

For convenience, denoting

$$\begin{aligned} \beta =\left( \frac{a^2}{2\alpha }+\frac{|b|}{2\delta _1\alpha }+\frac{|b|}{\alpha }+\frac{|b|}{2\delta _3\alpha }\right) e^{\frac{a^2}{2\alpha \delta _2}}, \gamma =\frac{a^2\delta _2+|b|\delta _3}{2\alpha }e^{\frac{a^2}{2\alpha \delta _2}}, \end{aligned}$$

(34)

taking $t=n+1$ we obtain

$$\begin{aligned} \begin{aligned} \Vert \mu _t(n+1)\Vert ^2\le&\beta \Vert \mu _t(n)\Vert ^2+\gamma \int _n^{n+1}\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s\\ \le&\beta \left( \beta ||\mu _t(n-1)||^2+\gamma \int _{n-1}^n||\nu _{ss}(s)||^2{\text {d}}s\right) +\gamma \int _n^{n+1}\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s\\ =&\beta ^2\Vert \mu _t(n-1)\Vert ^2+\beta \gamma \int _{n-1}^n\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s+\gamma \int _n^{n+1}\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s\\ \le&\beta ^{n+1}\Vert \mu _t(0)\Vert ^2+\beta ^n\gamma \int _0^1\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s+\cdots +\beta \gamma \int _{n-1}^n\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s\\ {}&+\gamma \int _n^{n+1}\Vert \nu _{ss}(s)\Vert ^2{\text {d}}s. \end{aligned} \end{aligned}$$

(35)

Furthermore, in view of (18) we have

$$\begin{aligned} \Vert \mu _t(0)\Vert =\Vert {\bar{w}}-Rw\Vert \le \Vert {\bar{w}}-w\Vert +\Vert Rw-w\Vert \le \Vert {\bar{w}}-w\Vert +Ch^4\Vert w\Vert _4 \end{aligned}$$

(36)

and

$$\begin{aligned} \Vert \nu _{tt}(t)\Vert =\Vert Ru_{tt}(t)-u_{tt}(t)\Vert \le Ch^4\Vert u_{tt}(t)\Vert _4, \end{aligned}$$

(37)

then by (36) and (37), (35) gives

$$\begin{aligned} \Vert \mu _t(n+1)\Vert ^2\le & {} 2\beta ^{n+1}\Vert {\bar{w}}-w\Vert ^2+\beta ^{n+1}Ch^{8}\Vert w\Vert _4^2+\beta ^n\gamma Ch^{8}\int _0^1\Vert u_{ss}(s)\Vert _4^2{\text {d}}s\nonumber \\{} & {} +\cdots +\beta \gamma Ch^{8}\int _{n-1}^n\Vert u_{ss}(s)\Vert _4^2{\text {d}}s+\gamma Ch^{8}\int _n^{n+1}\Vert u_{ss}(s)\Vert _4^2{\text {d}}s, \end{aligned}$$

(38)

so

$$\begin{aligned} \begin{aligned} \Vert \mu _t(t)\Vert ^2\le&C(t)\Vert {\bar{w}}-w\Vert ^2+C(t)h^{8}\Vert w\Vert _4^2+C(t)h^{8}\sum _{i=0}^{n-1}\int _i^{i+1}\Vert u_{ss}(s)\Vert _4^2{\text {d}}s\\ {}&+C(t)h^{8}\int _n^t\Vert u_{ss}(s)\Vert _4^2{\text {d}}s, \end{aligned} \end{aligned}$$

(39)

where C(t) is a function of $t\in [n, n+1)$.

Therefore, if $\Vert {\bar{w}}-w\Vert \le Ch^4\Vert w\Vert _4$, then

$$\begin{aligned} \Vert \mu _t(t)\Vert\le & {} C(t)\Vert {\bar{w}}-w\Vert +C(t)h^4\Vert w\Vert _4\nonumber \\{} & {} +C(t)h^{4}\left( \sum _{i=0}^{n-1}\int _i^{i+1}\Vert u_{ss}(s)\Vert _4^2{\text {d}}s\quad +\int _n^t\Vert u_{ss}(s)\Vert _4^2{\text {d}}s\right) ^{\frac{1}{2}}\nonumber \\\le & {} C(t)h^4\left( \Vert w\Vert _4+\left( \int _0^{t}\Vert u_{ss}(s)\Vert _4^2{\text {d}}s\right) ^{\frac{1}{2}}\right) . \end{aligned}$$

(40)

Due to

$$\begin{aligned} \Vert \mu (t)\Vert =\left\| \theta (0)+\int _0^t\mu _s(s){\text {d}}s\right\| \le \Vert \mu (0)\Vert +\int _0^t\Vert \mu _s(s)\Vert {\text {d}}s \end{aligned}$$

(41)

and

$$\begin{aligned} \Vert \mu (0)\Vert =\Vert {\bar{v}}-Rv\Vert \le \Vert {\bar{v}}-v\Vert +\Vert Rv-v\Vert \le \Vert {\bar{v}}-v\Vert +Ch^4\Vert v\Vert _4, \end{aligned}$$

(42)

we get

$$\begin{aligned} \begin{aligned} \Vert \mu (t)\Vert&\le C(t)h^4\left( \Vert v\Vert _4+\Vert w\Vert _4\right) +C(t)h^4\int _0^t\left( \int _0^t\Vert u_{ss}(s)\Vert _4^2{\text {d}}s\right) ^{\frac{1}{2}}{\text {d}}t. \end{aligned} \end{aligned}$$

(43)

Hence

$$\begin{aligned} \begin{aligned}&\Vert U(t)-u(t)\Vert \le \Vert \mu (t)\Vert +\Vert \nu (t)\Vert \\&\quad \le C(t)h^4\left\{ \Vert v\Vert _4+\Vert w\Vert _4+\int _0^t\Vert u_s(s)\Vert _4{\text {d}}s+\int _0^t\left( \int _0^t\Vert u_{ss}(s)\Vert _4^2{\text {d}}s\right) ^{\frac{1}{2}}{\text {d}}t\right\} . \end{aligned} \end{aligned}$$

(44)

So $U(t)\rightarrow u(t)$ as $h\rightarrow 0$. The proof is completed. $\square$

3.2 Stability analysis

In this subsection, we apply Fourier analysis method to discuss the numerical stability.

Definition 2

If any solution U(x, t) of (12) satisfies

$$\begin{aligned} \lim _{t\rightarrow \infty }U(x,t)=0, x\in \Omega , \end{aligned}$$

(45)

then the zero solution of (12) is asymptotically stable.

Using the bases of space $S_3^0$, we have

$$\begin{aligned} U(\xi _{i,k_1},t)=\sum _{j=1}^{2N}\beta _j(t)\Phi _j(\xi _{i,k_1}), \end{aligned}$$

(46)

where $\beta _j(t)$ are undetermined coefficients.

Let

$$\begin{aligned} \beta _j(t)\Phi _j(\xi _{i,k_1})=\zeta _j(t)e^{{\tilde{i}}c\xi _{i,k_1}}, j=1,2,\ldots ,2N, ({\tilde{i}})^2=-1, c=1,2,\ldots ,N, \end{aligned}$$

(47)

substituting (47) into the equation in (12) yields

$$\begin{aligned} \sum _{j=1}^{2N}\zeta _j^{\prime \prime }(t)e^{{\tilde{i}}c\xi _{i,k_1}}=-a^2c^2\sum _{j=1}^{2N}\zeta _j(t)e^{{\tilde{i}}c\xi _{i,k_1}}-bc^2\sum _{j=1}^{2N}\zeta _j([t])e^{{\tilde{i}}c\xi _{i,k_1}}, \end{aligned}$$

(48)

that is

$$\begin{aligned} \zeta ^{\prime \prime }(t)=-a^2c^2\zeta (t)-bc^2\zeta ([t]), \end{aligned}$$

(49)

where $\zeta (t)=(\zeta _1(t), \zeta _2(t), \ldots , \zeta _{2N}(t))^{T}$.

For convenience, we introduce $z(t)=\zeta ^{\prime }(t)$, so (49) reduces to

$$\begin{aligned} W^{\prime }(t)=A_1W(t)+A_2W([t]), \end{aligned}$$

(50)

where

$$\begin{aligned} W(t)=\left( \begin{array}{c} \zeta (t) \\ z(t) \end{array} \right) , \begin{aligned} A_1=\left( \begin{array}{cc} O &{} I \\ -a^2c^2I &{} O \end{array} \right) , A_2=\left( \begin{array}{cc} O &{} O \\ -bc^2I &{} O \end{array} \right) . \end{aligned} \end{aligned}$$

(51)

From (50) we obtain

$$\begin{aligned} W(t)=M(t-n)W(n), t\in [n,n+1), \end{aligned}$$

(52)

where

$$\begin{aligned} M(t-n)=e^{A_1(t-n)}+(e^{A_1(t-n)}-I)A_1^{-1}A_2. \end{aligned}$$

(53)

Let $t=n+1$, (53) gives

$$\begin{aligned} W(n+1)=M(1)W(n), \end{aligned}$$

(54)

here M(1) is called as a growth matrix in Fourier analysis method, it is convenient to introduce the following lemma to verify $\max |{\lambda _{M(1)}}|<1$.

Lemma 3

(Smith 1985) The sets of eigenvalues of the matrix Q consist of all the eigenvalues of the following family of matrices

$$\begin{aligned} \begin{aligned} Q=\left( \begin{array}{ccccc} Q_{11} &{} Q_{12} &{} Q_{13} &{} \cdots &{} Q_{1n}\\ Q_{21} &{} Q_{22} &{} Q_{23} &{} \cdots &{} Q_{2n}\\ &{} \ddots &{} \ddots &{} \ddots &{} \\ Q_{(n-1)1} &{} \cdots &{} Q_{(n-1)(n-2)} &{} Q_{(n-1)(n-1)} &{} Q_{(n-1)n}\\ Q_{n1} &{} \cdots &{} Q_{n(n-2)} &{} Q_{n(n-1)} &{} Q_{nn} \end{array} \right) . \end{aligned} \end{aligned}$$

(55)

Lemma 4

(Kosmala et al. 2000) The polynomial $x^2-d_1x-d_2 (d_1, d_2\in {\mathbb {R}})$ is Schur polynomial if and only if $|d_1|<1-d_2<2$.

Theorem 2

Under the condition (2), the zero solution of (12) is asymptotically stable.

Proof

By the Taylor expansion of matrix exponential, M(1) can be written in following fashion

$$\begin{aligned} \begin{aligned} M(1)=\left( \begin{array}{cc} \frac{b}{a^2}(\cos (acI)-I)+\cos (acI)&{} (acI)^{-1}\sin (acI)\\ -(\frac{b}{a^2}+1)(acI)\sin (acI)&{} \cos (acI) \end{array} \right) . \end{aligned} \end{aligned}$$

(56)

From Lemma 3, the characteristic equation of M(1) is

$$\begin{aligned} \begin{aligned} \left|\begin{array}{cc} \lambda -\left( \frac{b}{a^2}(\cos (ac)-1)+\cos (ac)\right) &{} -(ac)^{-1}\sin (ac)\\ \left( \frac{b}{a^2}+1\right) (ac)\sin (ac)&{} \lambda -\cos (ac) \end{array} \right|=0, \end{aligned} \end{aligned}$$

(57)

where ac is the eigenvalue of acI.

Thus

$$\begin{aligned} \lambda ^2-\left( \frac{b}{a^2}\cos (ac)-\frac{b}{a^2}+2\cos (ac)\right) \lambda +1+\frac{b}{a^2}(1-\cos (ac))=0. \end{aligned}$$

(58)

It is easy to verify

$$\begin{aligned}{} & {} \frac{b}{a^2}\cos (ac)-\frac{b}{a^2}+2\cos (ac)<2+\frac{b}{a^2}(1-\cos (ac)),\\{} & {} \frac{b}{a^2}(\cos (ac)-1)+2\cos (ac)>-\frac{b}{a^2}(1-\cos (ac))-2, \end{aligned}$$

and

$$\begin{aligned} 2+\frac{b}{a^2}(1-\cos (ac))<2. \end{aligned}$$

Therefore, in view of Lemma 4 we get $\max |\lambda _{M(1)}|<1$. The proof is finished. $\square$

4 Discrete-time collocation method

Let $\{t_n\}$ be the uniform partition of [0, T] with $t_n=np$ $(n=0,1,2,\cdots )$, $U^n$ be the approximation in $S_3$ of u(t) at $t_n$ and denote ${\partial }_{tt}U^n=(U^{n+1}-2U^n+U^{n-1})/p^2$, then (1) can be written as

$$\begin{aligned} \begin{aligned}&\frac{U^{n+1}(\xi _{i,k})-2U^n(\xi _{i,k})+U^n(\xi _{i,k})}{p^2}=a^2U^n_{xx}(\xi _{i,k})+bU^{n,p}_{xx}(\xi _{i,k}),\\ {}&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad i=1,2,\ldots , N, k=1,2,\\&U^0(\xi _{i,k})={\bar{v}}(\xi _{i,k}), \frac{U^1(\xi _{i,k})-U^0(\xi _{i,k})}{p}={\bar{w}}(\xi _{i,k}), \\&U^n(x_0)=U^n(x_N)=0, \end{aligned} \end{aligned}$$

(59)

where $U^{n,p}_{xx}$ denotes a given approximation to $u_{xx}(x,[t_n]), n=1,2,3,\ldots$.

Using the similar technique as in Sect. 3.1 apply the central Euler Galerkin method to (1) gives

$$\begin{aligned} ({\partial }_{tt}U^n,\chi )+a^2(\nabla U^n, \nabla \chi )+b(\nabla U^{n,p},\nabla \chi )=0, \forall \chi \in S_3. \end{aligned}$$

(60)

Let $n=km+l, k=0,1,2,\ldots , l=1,2,\ldots , m$, then $U^{n,p}$ can be written as $U^{km}$ according to Definition 1. So (60) turns into

$$\begin{aligned} ({\partial }_{tt}U^{km+l},\chi )+a^2(\nabla U^{km+l}, \nabla \chi )+b(\nabla U^{km},\nabla \chi )=0, \forall \chi \in S_3, \end{aligned}$$

(61)

that is

$$\begin{aligned} (U^{km+l+1},\chi )= & {} 2(U^{km+l},\chi )-a^2p^2(\nabla U^{km+l}, \nabla \chi )\nonumber \\ {}{} & {} -(U^{km+l-1},\chi )-bp^2(\nabla U^{km}, \nabla \chi ). \end{aligned}$$

(62)

4.1 Convergence analysis

Theorem 3

Let $U^n$ and u be the solution of (59) and (1), respectively. If $\Vert {\bar{v}}-v\Vert \le Ch^4\Vert v\Vert _4$, then

$$\begin{aligned} \begin{aligned} \Vert U^n-u(t_n)\Vert \le&Ch^4\left( \Vert v\Vert _4+\frac{p}{6}\sum _{i=1}^{n}\int _{t_{i-1}}^{t_{i+1}}\Vert u_{ttt}\Vert _4{\text {d}}t+\sum _{i=1}^n\Vert u(t_i)\Vert _4+\int _0^{t_n}\Vert u_s\Vert _4{\text {d}}s\right) \\ {}&+Cp\left( \sum _{i=1}^{n}\frac{1}{6}\int _{t_{i-1}}^{t_{i+1}}\Vert u_{tttt}\Vert {\text {d}}t\right) , \end{aligned} \end{aligned}$$

(63)

where C is a positive constant.

Proof

Similar to (20) and (21), from (14) and (61) we have

$$\begin{aligned} ({\partial }_{tt}\mu ^{km+l}, \chi )+a^2(\nabla \mu ^{km+l}, \nabla \chi )+b(\nabla \mu ^{km}, \nabla \chi )=-(\eta ^{km+l},\chi ), \,\chi \in S_3, \end{aligned}$$

(64)

where

$$\begin{aligned} \begin{aligned} \eta ^{km+l}&=R{\partial }_{tt}u(t_{km+l})-u_{tt}(t_{km+l})\\ {}&=(R-I){\partial }_{tt}u(t_{km+l})+({\partial }_{tt}u(t_{km+l})-u_{tt}(t_{km+l}))\\ {}&\triangleq \eta _1^{km+l}+\eta _2^{km+l},\\ U^{km+l}-u(t_{km+l})&=(U^{km+l}-Ru(t_{km+l}))+(Ru(t_{km+l})-u(t_{km+l}))\\ {}&\triangleq \mu ^{km+l}+\nu ^{km+l}. \end{aligned} \end{aligned}$$

(65)

The following work mainly focuses on the estimates for $\mu ^{km+l}$ and $\nu ^{km+l}$. We notice that $\nu ^{km+l}=\nu (t_{km+l})$ is bounded as claimed in (23), so we only to estimate $\mu ^{km+l}$ as follows.

Substituting $\chi =a^2(\mu ^{km+l+1}-\mu ^{km+l})+b\mu ^{km}$ into (64), Schwarz-Cauchy inequality gives

$$\begin{aligned}&\left( a^2\left( \mu ^{km+l+1}-\mu ^{km+l}\right) ,\mu ^{km+l}-\mu ^{km+l-1}\right) \le \frac{a^2s_1}{2}\left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| ^2\nonumber \\&\quad +\frac{a^2}{2s_1}\left\| \mu ^{km+l}-\mu ^{km+l-1}\right\| ^2,\nonumber \\&\left( \mu ^{km+l+1}-\mu ^{km+l}, b\mu ^{km}\right) \le \frac{|b|s_2}{2}\left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| ^2+\frac{|b|}{2s_2}\left\| \mu ^{km}\right\| ^2,\nonumber \\&\left( \mu ^{km+l}-\mu ^{km+l-1}, b\mu ^{km}\right) \le \frac{|b|s_3}{2}\left\| \mu ^{km+l}-\mu ^{km+l-1}\right\| ^2+\frac{|b|}{2s_3}\left\| \mu ^{km}\right\| ^2,\nonumber \\&\left( a^2\nabla \left( \mu ^{km+l+1}-\mu ^{km+l}\right) ,a^2\nabla \mu ^{km+l}\right) \le \frac{a^4}{2s_4}\left\| \nabla \left( \mu ^{km+l+1}-\mu ^{km+l}\right) \right\| ^2\nonumber \\&\quad +\frac{a^4s_4}{2}\left\| \nabla \mu ^{km+l}\right\| ^2,\nonumber \\&\left( a^2\nabla \mu ^{km+l}, b\nabla \mu ^{km}\right) \le \frac{a^2|b|s_5}{2}\left\| \nabla \mu ^{km+l}\right\| ^2+\frac{a^2 |b|}{2s_5}\left\| \nabla \mu ^{km}\right\| ^2,\nonumber \\&\left( a^2\nabla \left( \mu ^{km+l+1}-\mu ^{km+l}\right) , b\nabla \mu ^{km}\right) \le \frac{a^2|b|s_6}{2}\left\| \nabla \left( \mu ^{km+l+1}-\mu ^{km+l}\right) \right\| ^2\nonumber \\&\quad +\frac{a^2|b|}{2s_6}\left\| \nabla \mu ^{km}\right\| ^2,\nonumber \\&a^2p^2\left\| \eta ^{km+l}\right\| \left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| \le \frac{a^2p^2}{2s_7}\left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| ^2\nonumber \\&\quad +\frac{a^2p^2s_7}{2}\left\| \eta ^{km+l}\right\| ^2,\nonumber \\&|b|p^2\left\| \eta ^{km+l}\right\| \left\| \mu ^{km}\right\| \le \frac{|b|p^2s_8}{2}\left\| \eta ^{km+l}\right\| ^2+\frac{|b|p^2}{2s_8}\left\| \mu ^{km}\right\| ^2,\nonumber \\&\quad \,s_i>0, i=1,2,\ldots ,8, \end{aligned}$$

(66)

then we have

$$\begin{aligned}&a^2\left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| ^2 \le \frac{a^2s_1}{2}\left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| ^2+\frac{a^2}{2s_1}\left\| \mu ^{km+l}-\mu ^{km+l-1}\right\| ^2\nonumber \\&\quad +\frac{\mid b\mid s_2}{2}\left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| ^2+\frac{|b|}{2s_2}\left\| \mu ^{km}\right\| ^2+\frac{|b|}{2s_3}\left\| \mu ^{km}\right\| ^2\nonumber \\&\quad +\frac{|b|s_3}{2}\left\| \mu ^{km+l}-\mu ^{km+l-1}\right\| ^2 +\frac{a^4}{2s_4}\left\| \nabla \left( \mu ^{km+l+1}-\mu ^{km+l}\right) \right\| ^2+\frac{a^4s_4}{2}\left\| \nabla \mu ^{km+l}\right\| ^2\nonumber \\&\quad +\frac{a^2|b|s_5}{2}\left\| \nabla \mu ^{km+l}\right\| ^2+\frac{a^2|b|}{2s_5}\left\| \nabla \mu ^{km}\right\| ^2 +\frac{a^2|b|s_6}{2}\left\| \nabla \left( \mu ^{km+l+1}-\mu ^{km+l}\right) \right\| ^2\nonumber \\&\quad +\frac{a^2|b|}{2s_6}\left\| \nabla \mu ^{km}\right\| ^2+b^2\left\| \nabla \mu ^{km}\right\| ^2+\frac{a^2p^2s_7}{2}\left\| \eta ^{km+l}\right\| ^2 +\frac{a^2p^2}{2s_7}\left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| ^2\nonumber \\&\quad +\frac{|b|p^2s_8}{2}\left\| \eta ^{km+l}\right\| ^2+\frac{|b|p^2}{2s_8}\left\| \mu ^{km}\right\| ^2, \end{aligned}$$

(67)

that is

$$\begin{aligned} \begin{aligned}&\left( a^2-\frac{a^2s_1}{2}-\frac{|b|s_2}{2}-\frac{a^2p^2}{2s_7}\right) \left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| ^2\\&\quad \le \left( \frac{a^2}{2s_1}+\frac{|b|s_3}{2}\right) \left\| \mu ^{km+l}-\mu ^{km+l-1}\right\| ^2+\left( \frac{ |b|}{2s_3}+\frac{|b|p^2}{2s_8}\right) \left\| \mu ^{km}\right\| ^2\\&\qquad +\left( \frac{a^4s_4}{2}+\frac{a^2|b|s_5}{2}\right) \left\| \nabla \mu ^{km+l}\right\| ^2+\left( \frac{a^2|b|}{2s_5}+\frac{a^2|b|}{2s_6}+b^2\right) \left\| \nabla \mu ^{km}\right\| ^2\\&\qquad +\left( \frac{a^4}{2s_4}+\frac{a^2|b|s_6}{2}\right) \left\| \nabla (\mu ^{km+l+1}-\mu ^{km+l})\right\| ^2+\left( \frac{a^2p^2s_7}{2}+\frac{|b|p^2s_8}{2}\right) \left\| \eta ^{km+l}\right\| ^2. \end{aligned} \end{aligned}$$

(68)

From (68), we notice the items $\Vert \nabla \left( \mu ^{km+l+1}-\mu ^{km+l}\right) \Vert ^2$, $\Vert \nabla \mu ^{km+l}\Vert ^2$ and $\Vert \nabla \mu ^{km}\Vert ^2$ should be estimated so that the recurrence relation between $\left\| \mu ^{km+l+1}-\mu ^{km+l}\right\|$ and $\left\| \mu ^{km+l}-\mu ^{km+l-1}\right\|$ can be obtained. Substituting $\chi =\mu ^{km+l}$ and $\chi =b\mu ^{km}$ into (64), respectively, we have

$$\begin{aligned} \begin{aligned} a^2\Vert \nabla \mu ^{km+l}\Vert ^2\le&\Vert \eta ^{km+l}\Vert \Vert \mu ^{km+l}\Vert +|b|\Vert \nabla \mu ^{km}\Vert \Vert \nabla \mu ^{km+l}\Vert +\Vert {\partial }_{tt}\mu ^{km+l}\Vert \Vert \mu ^{km+l}\Vert \end{aligned} \end{aligned}$$

(69)

and

$$\begin{aligned} \begin{aligned} b^2\Vert \nabla \mu ^{km}\Vert ^2\le&|b|\Vert \eta ^{km+l}\Vert \Vert \mu ^{km}\Vert +a^2|b|\Vert \nabla \mu ^{km+l}\Vert \Vert \nabla \mu ^{km}\Vert +|b|\Vert {\partial }_{tt}\mu ^{km+l}\Vert \Vert \mu ^{km}\Vert . \end{aligned} \end{aligned}$$

(70)

By Poincar$\acute{e}$ inequality

$$\begin{aligned} \begin{aligned}&\Vert \mu ^{km+l}\Vert \le C_2\Vert \nabla \mu ^{km+l}\Vert , C_2=C_2(\Omega ),\\&\Vert \mu ^{km}\Vert \le \tilde{C_2}\Vert \nabla \mu ^{km}\Vert , \tilde{C_2}=\tilde{C_2}(\Omega ), \end{aligned} \end{aligned}$$

(71)

we obtain the value range of $\Vert \nabla \mu ^{km+l}\Vert ^2$ in (69) and $\Vert \nabla \mu ^{km}\Vert ^2$ in (70) related to items

$$\begin{aligned} \Vert \eta ^{km+l}\Vert , \Vert \mu ^{km+l+1}-\mu ^{km+l}\Vert , \Vert \mu ^{km+l}-\mu ^{km+l-1}\Vert . \end{aligned}$$

(72)

Moreover, subtracting $a^2(\nabla \mu ^{km+l+1}, \nabla \chi )$ on both sides of (23) and taking $\chi =\mu ^{km+l+1}+\mu ^{km+l}$ and $\chi =\mu ^{km+l+1}-\mu ^{km+l}$, respectively, we derive

$$\begin{aligned}&a^2\left\| \nabla \left( \mu ^{km+l+1}-\mu ^{km+l}\right) \right\| ^2 \nonumber \\&\quad \le \left\| \eta ^{km+l}\right\| \left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| \nonumber \\&\qquad +\left\| {\partial }_{tt}\mu ^{km+l}\right\| \left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| \nonumber \\&\qquad +a^2\left\| \nabla \mu ^{km+l+1}\right\| \left\| \nabla (\mu ^{km+l+1}-\mu ^{km+l})\right\| \nonumber \\&\qquad +|b|\left\| \nabla \mu ^{km}\right\| \left\| \nabla \left( \mu ^{km+l+1}-\mu ^{km+l}\right) \right\| \end{aligned}$$

(73)

and

$$\begin{aligned}&a^2\left\| \nabla \mu ^{km+l+1}\right\| ^2-a^2\left\| \nabla \mu ^{km+l}\right\| ^2\nonumber \\&\quad \le \left\| \eta ^{km+l}\right\| \left\| \mu ^{km+l+1}+\mu ^{km+l}\right\| +\left\| {\partial }_{tt}\mu ^{km+l}\right\| \left\| \mu ^{km+l+1}+\mu ^{km+l}\right\| \nonumber \\&\qquad +a^2\left\| \nabla \mu ^{km+l+1}\right\| \left\| \nabla \left( \mu ^{km+l+1}+\mu ^{km+l}\right) \right\| \nonumber \\&\qquad +|b|\left\| \nabla \mu ^{km}\right\| \left\| \nabla (\mu ^{km+l+1}+\mu ^{km+l})\right\| , \end{aligned}$$

(74)

so the value range of item $\Vert \nabla (\mu ^{km+l+1}-\mu ^{km+l})\Vert ^2$ in (73) is related to items

$$\begin{aligned} \Vert \eta ^{km+l}\Vert , \Vert \mu ^{km+l+1}-\mu ^{km+l}\Vert , \Vert \mu ^{km+l}-\mu ^{km+l-1}\Vert . \end{aligned}$$

(75)

And we can handle (73) and (74) with corresponding Poincar$\acute{e}$ inequality like (69) and (70).

Based on the above discussion on $\Vert \nabla (\mu ^{km+l+1}-\mu ^{km+l})\Vert ^2$, $\Vert \nabla \mu ^{km+l}\Vert ^2$ and $\Vert \nabla \mu ^{km}\Vert ^2$, (68) turns into

$$\begin{aligned} \left\| \mu ^{km+l+1}-\mu ^{km+l}\right\| ^2&\le r_1\left\| \mu ^{km+l}-\mu ^{km+l-1}\right\| ^2+r_2\left\| \eta ^{km+l}\right\| ^2\nonumber \\&\le r_1\left( r_1\left\| \mu ^{km+l-1}-\mu ^{km+l-2}\right\| ^2+r_2\left\| \eta ^{km+l-1}\right\| ^2\right) \nonumber \\&\quad +r_2\left\| \eta ^{km+l}\right\| ^2\nonumber \\&=r_1^2\left\| \mu ^{km+l-1}-\mu ^{km+l-2}\right\| ^2+r_1r_2\left\| \eta ^{km+l-1}\right\| ^2\nonumber \\&\quad +r_2\left\| \eta ^{km+l}\right\| ^2\nonumber \\&\le r_1^l\left\| \mu ^{km+1}-\mu ^{km}\right\| ^2+\sum _{i=1}^{l}r_1^{l-i}r_2\left\| \eta ^{km+i}\right\| ^2\nonumber \\&\le r_1^l\left\| \mu ^{km+1}\right\| ^2+r_1^l\left\| \mu ^{km}\right\| ^2+\sum _{i=1}^{l}r_1^{l-i}r_2\left\| \eta ^{km+i}\right\| ^2, \end{aligned}$$

(76)

where $r_1, r_2>0$ and they are determined by (68)–(71), (73) and (74).

Hence, we have

$$\begin{aligned}&\left\| \mu ^{km+l+1}\right\| \le \left\| \mu ^{km+l}\right\| +r_1^l\left\| \mu ^{km+1}\right\| +r_1^l\left\| \mu ^{km}\right\| +\sum _{i=1}^{l}r_1^{l-i}r_2\left\| \eta ^{km+i}\right\| \nonumber \\&\quad \le \left\| \mu ^{km+1}\right\| +lr_1^l\left\| \mu ^{km+1}\right\| +lr_1^l\left\| \mu ^{km}\right\| +l\sum _{i=1}^{l}r_1^{l-i}r_2\left\| \eta ^{km+i}\right\| \nonumber \\&\quad =\left( 1+lr_1^l\right) \left\| \mu ^{km+1}\right\| +lr_1^l\left\| \mu ^{km}\right\| +l\sum _{i=1}^{l}r_1^{l-i}r_2\left\| \eta ^{km+i}\right\| \nonumber \\&\quad \le \left( 1+lr_1^l\right) ^2\left\| \mu ^{km}\right\| +l\left( 1+lr_1^l\right) r_1^l\left\| \mu ^{km}\right\| +l(1+lr_1^l)\sum _{i=1}^{l}r_1^{l-i}r_2\left\| \eta ^{km+i}\right\| \nonumber \\&\qquad +lr_1^l\left\| \mu ^{km}\right\| +l\sum _{i=1}^{l}r_1^{l-i}r_2\left\| \eta ^{km+i}\right\| \nonumber \\&\quad =\left( \left( 1+lr_1^l\right) ^2+l\left( 1+lr_1^l\right) r_1^l+lr_1^l\right) \left\| \mu ^{km}\right\| +l\left( 2+lr_1^l\right) \sum _{i=1}^{l}r_1^{l-i}r_2\left\| \eta ^{km+i}\right\| . \end{aligned}$$

(77)

Denote

$$\begin{aligned} \begin{aligned} K_1=&\left( 1+(m-1)r_1^{m-1}\right) ^2+(m-1)\left( 1+(m-1)r_1^{m-1}\right) r_1^{m-1}+(m-1)r_1^{m-1},\\ K_2=&(m-1)\left( 2+(m-1)r_1^{m-1}\right) , \end{aligned} \end{aligned}$$

then (77) gives

$$\begin{aligned} \left\| \mu ^{(k-1)m}\right\| \le&K_1\left\| \mu ^{km}\right\| +K_2\sum _{i=2}^mr_1^{m-i}r_2\left\| \eta ^{km+i-1}\right\| \nonumber \\ \le&K_1^2\left\| \mu ^{(k-1)m}\right\| +K_1K_2\sum _{i=2}^mr_1^{m-i}r_2\left\| \eta ^{(k-1)m+i-1}\right\| \nonumber \\&+K_2\sum _{i=2}^mr_1^{m-i}r_2\left\| \eta ^{km+i-1}\right\| \nonumber \\ \le&K_1^{k+1}\left\| \mu ^{(0)}\right\| +K_1^kK_2\sum _{i=2}^mr_1^{m-i}r_2\left\| \eta ^{i-1}\right\| \nonumber \\&+\cdots +K_2\sum _{i=2}^mr_1^{m-i}r_2\left\| \eta ^{km+i-1}\right\| , \end{aligned}$$

(78)

here $\mu ^{(0)}=\mu (0)$ is bounded as desired in (42). We notice that

$$\begin{aligned} \begin{aligned} \eta _1^i=&(R-I){\partial }_{tt}u(t_i)\\ =&(R-I)p^{-2}(u(t_{i+1})-2u(t_i)+u(t_{i-1}))\\ =&\frac{1}{6p^{2}}\left( \int _{t_{i-1}}^{t_{i}}(t-t_{i-1})^3(R-I)u_{ttt}{\text {d}}t-\int _{t_i}^{t_{i+1}}(t-t_{i+1})^3(R-I)u_{ttt}{\text {d}}t\right. \\ {}&\left. +6p^2(R-I)u(t_i)\right) , \end{aligned} \end{aligned}$$

(79)

so

$$\begin{aligned} \begin{aligned} \Vert \eta _1^i\Vert \le&\frac{1}{6p^{2}}\left( p^3\int _{t_{i-1}}^{t_{i}}\left\| (R-I)u_{ttt}\right\| {\text {d}}t+p^3\int _{t_i}^{t_{i+1}}\left\| (R-I)u_{ttt}\right\| {\text {d}}t+6p^2\left\| (R-I)u(t_i)\right\| \right) \\ \le&\frac{1}{6}\left( p\int _{t_{i-1}}^{t_{i}}Ch^4\left\| u_{ttt}\right\| _4dt+p\int _{t_i}^{t_{i+1}}Ch^4\left\| u_{ttt}\right\| _4{\text {d}}t+6Ch^4\left\| u(t_i)\right\| _4\right) \\ =&Ch^4\left( \frac{p}{6}\int _{t_{i-1}}^{t_{i+1}}\left\| u_{ttt}\right\| _4dt+\left\| u(t_i)\right\| _4\right) . \end{aligned} \end{aligned}$$

(80)

Further

$$\begin{aligned} \begin{aligned} \eta _2^i&={\partial }_{tt}u(t_i)-u_{tt}(t_i)\\&=\frac{1}{p^2}(u(t_{i+1})-2u(t_i)+u(t_{i-1})-p^2u_{tt}(t_i))\\&=\frac{1}{6p^2}\left( \int _{t_{i-1}}^{t_{i}}(t-t_{i-1})^3u_{tttt}dt-\int _{t_i}^{t_{i+1}}(t-t_{i+1})^3u_{tttt}{\text {d}}t\right) , \end{aligned} \end{aligned}$$

(81)

so

$$\begin{aligned} \begin{aligned} \Vert \eta _2^i\Vert =&\frac{1}{6p^2}\left\| \int _{t_{i-1}}^{t_{i}}(t-t_{i-1})^3u_{tttt}dt-\int _{t_i}^{t_{i+1}}(t-t_{i+1})^3u_{tttt}{\text {d}}t\right\| \\ \le&\frac{1}{6p^2}\left( p^3\int _{t_{i-1}}^{t_{i}}\Vert u_{tttt}\Vert dt+p^3\int _{t_i}^{t_{i+1}}\Vert u_{tttt}\Vert dt\right) \\ \le&\frac{p}{6}\int _{t_{i-1}}^{t_{i+1}}\Vert u_{tttt}\Vert {\text {d}}t. \end{aligned}\nonumber \\ \end{aligned}$$

(82)

Thus together with (23) we have

$$\begin{aligned} \left\| U^n-u(t_n)\right\|\le & {} \left\| \nu ^n\right\| +\left\| \mu ^n\right\| \nonumber \\\le & {} Ch^4\left( \Vert v\Vert _4+\frac{p}{6}\sum _{i=1}^{n}\int _{t_{i-1}}^{t_{i+1}}\Vert u_{ttt}\Vert _4{\text {d}}t+\sum _{i=1}^n\Vert u(t_i)\Vert _4+\int _0^{t_n}\Vert u_s\Vert _4{\text {d}}s\right) \nonumber \\{} & {} +Cp\left( \sum _{i=1}^{n}\frac{1}{6}\int _{t_{i-1}}^{t_{i+1}}\Vert u_{tttt}\Vert {\text {d}}t\right) . \end{aligned}$$

(83)

Therefore, $U^n \rightarrow u(t_n)$ as $h\rightarrow 0$ and $p \rightarrow 0$. This completes the proof. $\square$

4.2 Stability analysis

In this subsection, the stability of numerical scheme (59) is analyzed with Fourier analysis method in analogy with continuous-time collocation method.

Definition 3

If any solution $U^n$ of (59) satisfies

$$\begin{aligned} \lim _{n\rightarrow \infty }U^n=0, x\in \Omega , \end{aligned}$$

(84)

then the zero solution of (59) is asymptotically stable.

Similar with (46) and (47), we take

$$\begin{aligned} U^n(\xi _{i,k_1})=\sum _{j=1}^{2N}\beta _j^n\Phi _j(\xi _{i,k_1}), \end{aligned}$$

(85)

where $\beta _j^n$ are unknown coefficients and

$$\begin{aligned} \beta _j^n\Phi _j(\xi _{i,k_1})=\zeta _j^ne^{{\tilde{i}}c\xi _{i,k_1}}, j=1,2,\cdots , 2N, ({\tilde{i}})^2=-1, c=1,2, \cdots ,N, \end{aligned}$$

(86)

and the first part of (59) can be written as

$$\begin{aligned} \sum _{j=1}^{2N}\zeta _j^{km+l+1}=\sum _{j=1}^{2N}(2-a^2c^2p^2)\zeta _j^{km+l}-\sum _{j=1}^{2N}\zeta _j^{km+l-1}-\sum _{j=1}^{2N}bc^2\zeta _j^{km}. \end{aligned}$$

(87)

Since (87) holds for all $k\ge 1$, we derive that

$$\begin{aligned} \zeta _j^{km+l+1}=(2-a^2c^2p^2)\zeta _j^{km+l}-\zeta _j^{km+l-1}-bc^2\zeta _j^{km}. \end{aligned}$$

(88)

Let $z_j^{km+l+1}=\zeta _j^{km+l}$ and $W^{km+l+1}=(\zeta _j^{km+l+1}, z_j^{km+l+1})^T$, so (88) becomes

$$\begin{aligned} W^{km+l+1}=CW^{km+l}+DW^{km}, \end{aligned}$$

(89)

where

$$\begin{aligned} C=\left( \begin{array}{cc} 2-a^2c^2p^2&{} -1\\ 1&{}0 \end{array} \right) , D=\left( \begin{array}{cc} -bc^2p^2&{} 0\\ 0&{}0 \end{array} \right) . \end{aligned}$$

(90)

Therefore, from (89) we derive

$$\begin{aligned} W^{km+l+1}= & {} CW^{km+l}+DW^{km}\nonumber \\= & {} C^2W^{km+l-1}+(C+I)DW^{km}\nonumber \\= & {} \left( C^{l+1}+(C^{l+1}-I)(C-I)^{-1}D\right) W^{km}, \end{aligned}$$

(91)

that is

$$\begin{aligned} W^{(k+1)m} =MW^{km}, \end{aligned}$$

(92)

where $M=C^{m}+(C^{m}-I)(C-I)^{-1}D.$

Theorem 4

Under the condition (2), if

$$\begin{aligned} \begin{aligned} \frac{4}{a^2N^2}=\min \left\{ \frac{4}{a^2c^2}\right\}<p^2< \max \left\{ \frac{4}{a^2c^2}\right\} =\frac{4}{a^2} \end{aligned} \end{aligned}$$

(93)

for m is even or

$$\begin{aligned} p^2>\min \left\{ \frac{4}{a^2c^2}\right\} =\frac{4}{a^2N^2} \end{aligned}$$

(94)

for m is odd, then the zero solution of (59) is asymptotically stable.

Proof

As we know, the zero solution of (59) is asymptotically stable if and only if the eigenvalue of growth matrix satisfies $\max |\lambda _{M}|<1$, where M is defined in (92). From Lemma 3 we know the eigenvalues of C consist of the roots of the following equation

$$\begin{aligned} \lambda ^2-(2-a^2c^2p^2)\lambda +1=0. \end{aligned}$$

(95)

It is worthy noticing that neither $\lambda =0$ nor $\lambda =1$ is the root of (95). For convenience, denote

$$\begin{aligned} f(\lambda )=\lambda ^2-(2-a^2c^2p^2)\lambda +1, \end{aligned}$$

so the symmetry axis of $f(\lambda )$ is

$$\begin{aligned} {\bar{\lambda }}=\frac{2-a^2c^2p^2}{2}. \end{aligned}$$

• (i) When m is even, we can obtain $f({\bar{\lambda }})<0$ from $p^2> \min \left\{ \frac{4}{a^2c^2}\right\}$, while $f(0)=1>0$ and $f(1)=a^2c^2p^2>0$ hold. In addition, $p^2< \max \left\{ \frac{4}{a^2c^2}\right\}$ guarantees $f(-1)>0$ so the root of (95) exists in (0,1) and $(-1,0)$. Therefore, we get $0<|\lambda |<1$.

• (ii) When m is odd, from (94) we get $f({\bar{\lambda }})<0$ which implies the root of (95) lies in (0, 1). Hence, we obtain $0<\lambda <1$.

Further, we obtain the eigenvalues of $(C-I)^{-1}D$ are $\lambda _1=0$ and $\lambda _2=b/a^2$. Therefore, we have

$$\begin{aligned} \max |\lambda _{M}|= & {} \max |\left( \lambda _C)^m+((\lambda _{C})^m-1\right) \lambda _{(C-I)^{-1}D}|\nonumber \\\le & {} \max (|(\lambda _C)^m|+|(\lambda _{C})^m-1||\lambda _{(C-I)^{-1}D}|)\nonumber \\< & {} \max (|(\lambda _C)^m|+|(\lambda _{C})^m-1|)\nonumber \\= & {} \max ((\lambda _C)^m+1-(\lambda _{C})^m)=1, \end{aligned}$$

(96)

which completes the proof. $\square$

5 Numerical experiments

In this section, we present some numerical simulations based on Hermite piecewise-cubic polynomials to verify the corresponding theoretical results.

Consider the following problem

$$\begin{aligned}{} & {} u_{tt}(x,t)=9u_{xx}(x,t)-u_{xx}(x,[t]), (x,t)\in [0,1] \times (0,+\infty ),\nonumber \\{} & {} u(x,0)=\sin (\pi x), u_t(x,0)=0, x\in [0, 1],\nonumber \\{} & {} u(0,t)= u(1,t)=0, t\in (0,+\infty ). \end{aligned}$$

(97)

It is easy to check that condition (2) holds. Moreover, according to the method of separation of variables, we obtain the analytic solutions of (97) is the first component of

$$\begin{aligned} {\widetilde{u}}(x,t)=\sin (\pi x)G(t-[t])G^{[t]}(1)b_1, \end{aligned}$$

(98)

where $b_1=(1,0)^{T}$ and

$$\begin{aligned} \begin{aligned} G(t)=&\left( \begin{array}{cc} (1+ba^{-2})\cos (a\pi t)-ba^{-2} &{} {(a\pi )}^{-1}\sin (a \pi t) \\ -(ba^{-2}+1) (a\pi )\sin ( a \pi t) &{} \cos ( a \pi t) \end{array} \right) , \end{aligned} \end{aligned}$$

(99)

in fact, when t is an integer, ${\widetilde{u}}(x,t)= \sin (\pi x)(G(1))^{t}b_1$.

Since $\phi _i(0)=\phi _i(1)=0$, substituting

$$\begin{aligned} U(\xi _{i,k_1},t)=\beta _1(t)\Phi _1(\xi _{i,k_1})+\beta _2(t)\Phi _2(\xi _{i,k_1})+\cdots +\beta _{2N}(t)\Phi _{2N}(\xi _{i,k_1}) \end{aligned}$$

(100)

and

$$\begin{aligned} U^n(\xi _{i,k_1})=\beta _1^n\Phi _1(\xi _{i,k_1})+\beta _2^n\Phi _2(\xi _{i,k_1})+\cdots +\beta _{2N}^n\Phi _{2N}(\xi _{i,k_1}) \end{aligned}$$

(101)

into (12) and (59), respectively, where $\beta _i(t)$ and $\beta _i^n$ are undetermined coefficients, then we obtain the continuous-time collocation scheme

$$\begin{aligned} B_1\beta ^{''}(t)=a^2B_2\beta (t)+bB_2\beta ([t]) \end{aligned}$$

(102)

and the discrete-time collocation scheme

$$\begin{aligned} B_1\beta ^{km+l+1}=(2B_1+a^2p^2B_2)\beta ^{km+l}-B_1\beta ^{km+l-1}+bp^2B_2\beta ^{km}, \end{aligned}$$

(103)

where the coefficient matrices $B_1=(\Phi _j(\xi _{i,k_1}))$ and $B_2=(\Phi _j^{''}(\xi _{i,k_1}))$ are following almost block diagonal form with dimension 2N

$$\begin{aligned} B_1=\left( \begin{array}{ccccc} B_{1,1}&{} &{} &{} &{} \\ &{}B_{1,2}&{} &{} &{} \\ &{} &{}\ddots &{} &{} \\ &{} &{} &{}B_{1,N-1} &{} \\ &{} &{} &{} &{}B_{1,N} \end{array} \right) , B_2=\left( \begin{array}{ccccc} B_{2,1}&{} &{} &{} &{} \\ &{}B_{2,2}&{} &{} &{} \\ &{} &{}\ddots &{} &{} \\ &{} &{} &{}B_{2,N-1} &{} \\ &{} &{} &{} &{}B_{2,N} \end{array} \right) , \end{aligned}$$

(104)

here

$$\begin{aligned}{} & {} B_{1,1}=\left( \begin{array}{ccc} \Phi _1(\xi _{0,1})&{}\Phi _2(\xi _{0,1})&{}\Phi _3(\xi _{0,1}) \\ \Phi _1(\xi _{0,2})&{}\Phi _2(\xi _{0,2})&{}\Phi _3(\xi _{0,2}) \\ \end{array} \right) ,\nonumber \\{} & {} B_{1,2}=\left( \begin{array}{cccc} \Phi _2(\xi _{1,1})&{}\Phi _3(\xi _{1,1}) &{}\Phi _4(\xi _{1,1}) &{}\Phi _5(\xi _{1,1})\\ \Phi _2(\xi _{1,2})&{}\Phi _3(\xi _{1,2}) &{}\Phi _4(\xi _{1,2})&{}\Phi _5(\xi _{1,2})\\ \end{array} \right) ,\nonumber \\{} & {} B_{1,N-1}=\left( \begin{array}{cccc} \Phi _{2N-4}(\xi _{N-2,1})&{}\Phi _{2N-3}(\xi _{N-2,1})&{}\Phi _{2N-2}(\xi _{N-2,1})&{}\Phi _{2N-1}(\xi _{N-2,1}) \\ \Phi _{2N-4}(\xi _{N-2,2})&{}\Phi _{2N-3}(\xi _{N-2,2})&{}\Phi _{2N-2}(\xi _{N-2,2})&{}\Phi _{2N-1}(\xi _{N-2,2}) \\ \end{array} \right) ,\nonumber \\{} & {} B_{1,N}=\left( \begin{array}{cccc} \Phi _{2N-2}(\xi _{N-1,1}) &{}\Phi _{2N-1}(\xi _{N-1,1})&{}\Phi _{2N}(\xi _{N-1,1})\\ \Phi _{2N-2}(\xi _{N-1,2}) &{}\Phi _{2N-1}(\xi _{N-1,2})&{}\Phi _{2N}(\xi _{N-1,2})\\ \end{array} \right) ,\nonumber \\{} & {} B_{2,1}=\left( \begin{array}{ccc} \Phi ^{''}_1(\xi _{0,1})&{}\Phi ^{''}_2(\xi _{0,1})&{}\Phi ^{''}_3(\xi _{0,1}) \\ \Phi ^{''}_1(\xi _{0,2})&{}\Phi ^{''}_2(\xi _{0,2})&{}\Phi ^{''}_3(\xi _{0,2}) \\ \end{array} \right) ,\nonumber \\{} & {} B_{2,2}=\left( \begin{array}{cccc} \Phi ^{''}_2(\xi _{1,1})&{}\Phi ^{''}_3(\xi _{1,1}) &{}\Phi ^{''}_4(\xi _{1,1}) &{}\Phi ^{''}_5(\xi _{1,1})\\ \Phi ^{''}_2(\xi _{1,2})&{}\Phi ^{''}_3(\xi _{1,2}) &{}\Phi ^{''}_4(\xi _{1,2}) &{}\Phi ^{''}_5(\xi _{1,2})\\ \end{array} \right) ,\nonumber \\{} & {} B_{2,N-1}=\left( \begin{array}{cccc} \Phi ^{''}_{2N-4}(\xi _{N-2,1})&{}\Phi ^{''}_{2N-3}(\xi _{N-2,1})&{}\Phi ^{''}_{2N-2}(\xi _{N-2,1})&{}\Phi ^{''}_{2N-1}(\xi _{N-2,1}) \\ \Phi ^{''}_{2N-4}(\xi _{N-2,2})&{}\Phi ^{''}_{2N-3}(\xi _{N-2,2})&{}\Phi ^{''}_{2N-2}(\xi _{N-2,2})&{}\Phi ^{''}_{2N-1}(\xi _{N-2,2}) \\ \end{array} \right) ,\nonumber \\{} & {} B_{2,N}=\left( \begin{array}{cccc} \Phi ^{''}_{2N-2}(\xi _{N-1,1}) &{}\Phi ^{''}_{2N-1}(\xi _{N-1,1})&{}\Phi ^{''}_{2N}(\xi _{N-1,1})\\ \Phi ^{''}_{2N-2}(\xi _{N-1,2}) &{}\Phi ^{''}_{2N-1}(\xi _{N-1,2})&{}\Phi ^{''}_{2N}(\xi _{N-1,2})\\ \end{array} \right) . \end{aligned}$$

(105)

In continuous-time collocation scheme and discrete-time collocation scheme, the order of convergence is defined as

$$\begin{aligned} order=\frac{log(AE_*(h_i)/AE_*(h_{i+1}))}{log(h_i/h_{i+1})}, \end{aligned}$$

(106)

where $AE_*(h_i)$ is the error calculated in $L^{\infty }$ norm and $L^2$ norm by the following formulas when taking step-size $h_i$ and $*$ represents 2-norm or $\infty$-norm:

$$\begin{aligned} L^{\infty }=\Vert u-U\Vert _{L^{\infty }}=\max _{0\le i\le N}|u(x_i,t)-U(x_i,t)|, \end{aligned}$$

(107)

$$\begin{aligned} L^2=\Vert u-U\Vert _{L^2}=\sqrt{\int _{\Omega }(u-U)^2dx}\approx \sqrt{h\sum _{i=1}^{N-1}\left( u(x_i,t)-U(x_i,t)\right) ^2}. \end{aligned}$$

(108)

Table 1 Error estimations of continuous-time collocation scheme for Problem (97) at $t=2$

Table 2 Error estimations of continuous-time collocation scheme for Problem (97) at $t=3$

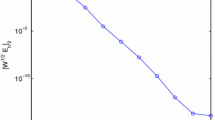
For convenience, we take spatial step $h=1/N$. Firstly, we consider the case of continuous-time collocation scheme. In Table 1 and Table 2 we list $AE_{*}$ in different norms and their order of convergence for different h, respectively. From these Tables we can see that the continuous-time collocation scheme has a good convergence, which validates the theoretical results in Theorem 1. Moreover, in Figs. 1 and 2 we plot the numerical solutions of the continuous-time collocation scheme. These two figures illustrate that the continuous-time collocation scheme can achieve unconditional stability, which coincides Theorem 2 well.

Fig. 1

The continuous-time collocation numerical solutions of Problem (97) with $N = 40$

Fig. 2

The continuous-time collocation numerical solutions of Problem (97) with $N = 70$

Fig. 3

Error curve for three methods at (1/4,2)

Fig. 4

Error curve for three methods at (1/2,3)

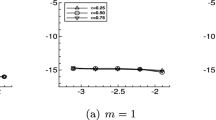
Secondly, we consider the case of the discrete-time collocation scheme. We choose the time step $p=1/N^4$ as we expect to obtain one-order accuracy in time direction and four-order accuracy in space direction, respectively. The $AE_{*}$ in two norms and their order of convergence of the discrete-time collocation scheme at $t=2$ and $t=3$ are shown in Table 3 and Table 4, which are in accordance with Theorem 3. Moreover, what are shown in Table 5 and Table 6 are comparisons of the absolute error (AE) between numerical solution and analytic solution with the discrete-time collocation scheme (DTCS), finite element method (FEM) (Liang et al. 2010b) and Crank-Nicolson method (CNM) by different spatial steps and time steps. Meanwhile, the comparison results are plotted in Figs. 3 and 4 either. It is not difficult to see that the AE of discrete-time collocation scheme is relatively smaller than those of finite element method and Crank-Nicolson method for the same step-size and the discrete-time collocation scheme can achieve same error magnitude with lower computational cost than other methods, which can reflect that the discrete-time collocation scheme possesses better accuracy. Further, Figs. 5 and 6 are presented to describe the stability of numerical solution under the discrete-time situation by different time steps. The two figures are in accordance with Theorem 4. Some detailed analysis are presented as follows.

Fig. 5

The discrete-time collocation numerical solutions of Problem (97) with $N =10$, $m=120$

Fig. 6

The discrete-time collocation numerical solutions of Problem (97) with $N =15$, $m =180$

When $N=10, m=120$ and $N=15, m=180$, then

$$\begin{aligned} \frac{4}{a^2N^2}=0.0044<p^2=0.0100< \frac{4}{a^2}=0.4444 \end{aligned}$$

and

$$\begin{aligned} p^2=0.0044>\frac{4}{a^2N^2}=0.0029, \end{aligned}$$

that is, (93) and (94) hold. So the numerical solutions of Problem (97) are asymptotically stable.

Table 3 Error estimations of discrete-time collocation scheme for Problem (97) at $t=2$

Table 4 Error estimations of discrete-time collocation scheme for Problem (97) at $t=3$

Table 5 Comparison of AE with three methods at (1/4, 2)

Table 6 Comparison of AE with three methods at (1/2, 3)

6 Conclusions

The spectral collocation method is proposed to deal with hyperbolic PEPCA in this paper. We choose Hermite piecewise-cubic function as test function, which has been verified to be effective for approximation in numerical experiments. The error estimations for both continuous-time and discrete-time collocation schemes are obtained by means of equivalent schemes. The stability analysis for the two schemes are also conducted with Fourier analysis method. We present some numerical experiments to illustrate the accuracy of schemes. The advantage of spectral collocation method is that it can achieve higher approximate accuracy with less nodes compared with FEM and CNM. In our future work, we will deal with the multidimensional and nonlinear problems.