Analysis of continuous collocation solutions for nonlinear functional equations with vanishing delays

Abstract

In this paper, we study the existence, uniqueness, and regularity of solutions for the nonlinear functional equations y(t) $=b(t,y(\theta (t))) +f(t), t\in [0,T],$ with vanishing delay $\theta (t)$. We then present a collocation method to solve this equation, and analyze the convergence properties of the piecewise polynomial collocation approximations. Several numerical experiments are used to illustrate the theoretical results.

1 Introduction

In Liu (1995), the linear q-difference equation

$$\begin{aligned} y(t)=ay(qt)+f(t),\quad t\ge 0 \end{aligned}$$

(1.1)

is discussed and the existence and uniqueness of solutions in $C[0,\infty )$ and $L^{p}(\mathbb {R^{+}})$ are analyzed. The author uses globally continuous piecewise linear polynomials to approximate the exact solution and gives error estimates.

In Brunner et al. (2010), a more complicated class of equations:

$$\begin{aligned} y(t)=b(t)y(\theta (t))+f(t),\quad t\in I:=[0,T], \end{aligned}$$

(1.2)

is discussed and some high-order numerical methods are constructed to solve these functional equations. The delay function $\theta$ is assumed to possess the following properties:

• (P1) $\theta (0)=0$, and $\theta$ is strictly increasing on I.

• (P2) $\theta (t)\le q_{1}t$ on I for some $q_{1}\in (0,1)$.

• (P3) $\theta (t)\in C^{d}(I)$ for some integer $d\ge 0$.

Here, such a delay function is referred to as a vanishing delay function, or simply, vanishing delay (cf. Iserles 1993). An important special case is the linear delay function $\theta (t)=qt$ $(0<q<1)$, which is also known as the pantograph case (Refs. Brunner et al. 2010; Fox et al. 1971; Iserles 1993, 1994, 1997; Yang et al. 2019). It is natural to extend the discussion to a more general form of nonlinear functional equations and discuss their numerical solutions.

In this paper, we focus on the following nonlinear functional equation:

$$\begin{aligned} y(t)=b(t,y(\theta (t)))+f(t),\quad t\in I, \end{aligned}$$

(1.3)

where $\theta (t)$ subjects to the properties (P1)–(P3).

The other motivation of our work is for solving a class of classical first kind nonlinear Volterra functional integral equations: Volterra (1897)

$$\begin{aligned} \int _{\theta (t)}^{t}G(t,s,y(s))\mathrm{d}s=g(t),\quad t\in I, \end{aligned}$$

(1.4)

where $\theta (t)$ is also assumed to satisfy properties (P1)–(P3).

It is easy to see that the corresponding differential version is

$$\begin{aligned}&G(t,t,y(t))-\theta '(t)G(t,\theta (t),y(\theta (t)))+\int _{\theta (t)}^{t}\frac{\partial G}{\partial t}(t,s,y(s))\mathrm{d}s=g'(t),\quad t\in I.\nonumber \\ \end{aligned}$$

(1.5)

If the kernel function G(t, s, v) has the property that $\frac{\partial G}{\partial t}(t,s,v)\equiv 0$, (t, s, v) $\in$ $I\times I\times \mathbb {R}$, then Eq. (1.5) reduces to the following form:

$$\begin{aligned} a(t,y(t))=b(t,y(\theta (t)))+f(t), \end{aligned}$$

(1.6)

where we set

$$\begin{aligned} a(t,y(t)):= & {} G(t,t,y(t)),\\ b(t,y(\theta (t))):= & {} \theta '(t)G(t,\theta (t),y(\theta (t))) \end{aligned}$$

and

$$\begin{aligned} f(t):= & {} g'(t). \end{aligned}$$

Equation (1.3) considered in this paper is a special case of the (implicit) functional equation (1.6).

The convergence analysis of the collocation method in piecewise polynomial spaces for the Volterra functional integral equation with first kind (1.4) is at present still open. However, in Xie et al. (2011), two of the authors with Brunner analyzed its linear differential form (1.5). However, as to a general nonlinear Volterra functional integral equation of the second kind (Hui et al. 2017; Yang and Brunner 2014) is not yet completely understood. Hence, to gain some insight that might eventually lead to a solution of these problems, we focus on a study of the optimal convergence orders of piecewise polynomial collocation solutions for the key special case (1.3) of (1.4).

The organization of this paper is as follows. In Sect. 2, we discuss the existence, uniqueness, and regularity of solutions to Eq. (1.3). The piecewise polynomial collocation method and the optimal error estimates for such collocation solutions are discussed in Sect. 3. Section 4 is dedicated to numerical examples to illustrate the theoretical results for these functional equations. Finally, we point out some future work in Sect. 5.

2 Existence, uniqueness, and regularity of solutions

In this section, we discuss the existence and regularity to Eq. (1.3).

Theorem 2.1

Assume that the following properties hold:

• (i) $b\in C(I\times \mathbb {R} )$.

• (ii) $|b(t,s_{1})-b(t,s_{2})|\le L|s_{1}-s_{2}|$, for some constant L, $0<L<1$, and for all $t\in I$, $s_{1},s_{2}\in \mathbb {R}$.

• (iii) $\theta (t)$ possesses the properties (P1)–(P3), with $d=0$.

Then, Eq. (1.3) has a unique solution $u\in C(I)$ for any $f\in C(I)$.

Proof

Define the operator $\mathcal {K}:C(I)\rightarrow C(I)$ as follows: for $\phi \in C(I)$

$$\begin{aligned} (\mathcal {K}\phi )(t):=b(t,\phi (\theta (t))),\quad t\in I. \end{aligned}$$

(2.1)

Then, Eq. (1.3) is equivalent to the operator equation:

$$\begin{aligned} y=\mathcal {K}y+f,\quad y\in C(I). \end{aligned}$$

From Assumption (ii), we can obtain the following estimate:

$$\begin{aligned} \Vert \mathcal {K}\phi _{1}-\mathcal {K}\phi _{2}\Vert _{\infty }\le L\max _{t\in I}|\phi _{1}(\theta (t))-\phi _{2}(\theta (t))|\le L\Vert \phi _{1}-\phi _{2}\Vert _{\infty }. \end{aligned}$$

This indicates that the operator $\mathcal {K}$ is a contraction mapping, which in turn suggests the uniqueness and existence of solution in C(I) based on the contraction mapping theory. $\square$

Next, we will make precise analysis of the regularity conditions for these solutions of Eq. (1.3).

Theorem 2.2

Assume that the following properties hold:

• (i) $f\in C^{v}(I)$ and $b\in C^{v}(I\times \mathbb {R})$ for some integer $v\ge 1$.

• (ii) $\left\| \displaystyle \frac{\partial b}{\partial y}\right\| _{\infty }<1$.

• (iii) $\theta (t)$ is subject to the hypotheses (P1)–(P3) with $d=v$ and $\Vert \theta '\Vert _{\infty }<1$.

  Then, the solution y(t) of Eq. (1.3) has the regularity property $y\in C^{v}(I)$.

Proof

By Theorem 2.1, the (unique) solution of (1.3) lies in C(I). Since $f,\;b$ and $\theta$ are in $C^1(I)$, formal differentiation leads to

$$\begin{aligned} y'(t)=\frac{\partial b}{\partial y}(t,y({\theta }(t)))\theta '(t)y'(\theta (t))+\frac{\partial b}{\partial t}(t,y({\theta }(t)))+f'(t),\quad t\in I. \end{aligned}$$

(2.2)

There, setting

$$\begin{aligned} \widetilde{y}(t):= & {} y'(t),\\ \widetilde{b}(t):= & {} \frac{\partial b}{\partial y}(t,y({\theta }(t)))\theta '(t) \end{aligned}$$

and

$$\begin{aligned} \widetilde{f}(t):=\frac{\partial b}{\partial t}(t,y({\theta }(t)))+f'(t). \end{aligned}$$

Equation (2.2) can be rewritten as

$$\begin{aligned} \widetilde{y}(t)= & {} \widetilde{b}(t)\widetilde{y}(\theta (t))+\widetilde{f}(t),\ \ \ \ t\in I. \end{aligned}$$

(2.3)

Assumption (i) and the fact that $y\in C(I)$ imply that $\tilde{f}, \; \tilde{b}\in C(I)$. It now follows from assumption (iii) and Theorem 2.2 in Brunner et al. (2010) that $\tilde{y} \in C(I)$ is the unique solution of the functional equation (2.3). Hence, the solution of (1.3) satisfies $y\in C^1(I)$.

The assertion that the solution of (1.3) has in fact the regularity $y\in C^{\nu }(I)$ for any given $\nu \ge 2$ is then readily verified along similar lines. $\square$

If $\theta (t)$ is linear on I, then assumption (iii) in Theorem 2.2 is automatically satisfied. Therefore, we have the following corollary.

Corollary 2.3

Assume that the following properties hold:

• (i) $f\in C^{v}(I)$ and $b\in C^{v}(I\times \mathbb {R})$ for some integer $v\ge 1$.

• (ii) $\displaystyle \left\| \frac{\partial b}{\partial y}\right\| _{\infty }<1$.

• (iii) $\theta (t)=qt, \ t\in I$, for some constant $0<q<1$. Then, the solution y(t) of Eq. (1.3) has the regularity property $y\in C^{v}(I)$.

3 Numerical methods

3.1 Discretization

Let $I_h:=\{t_n: 0=t_0<t_1<\cdots <t_N=T\}$ be a given mesh on the interval $I = [0, T]$, with

$$\begin{aligned} e_n:=(t_n, t_{n+1}], \;\; h_n:=t_{n+1}-t_{n},\;\; (n=0,1,\ldots N-1), \end{aligned}$$

and mesh diameter $h:= \max \{h_n: \; 0\le n \le N-1\}$.

The solution of the functional equation (1.3) will be approximated by a collocation solution $u_h$ lying in the (discontinuous) piecewise polynomial space:

$$\begin{aligned} S_{m-1}^{(-1)}(I_h):=\left\{ v: \ v|_{e_n}\in \mathbb {P}_{m-1} \; (n=0, 1, \ldots , N-1)\right\} , \end{aligned}$$

(3.1)

where $m\ge 1$ and where $\mathbb {P}_{m-1}$ denotes the space of (real) polynomials of degree not exceeding $m-1 \ge 0$. For prescribed (distinct) collocation parameters $\{ c_{i}\}$ in (0, 1], the collocation points are chosen as

$$\begin{aligned} X_h:=\left\{ t_{n,i}:=t_{n}+c_i h_n: 0< c_1<\cdots <c_m\le 1 \; (n=0,\ldots , N-1)\right\} . \end{aligned}$$

Hence, we are looking for $u_h\in S_{m-1}^{(-1)}(I_h)$ satisfying the collocation equation:

$$\begin{aligned} u_h(t)=b(t,u_h(\theta (t)))+f(t), \quad t\in X_h. \end{aligned}$$

(3.2)

We denote by $P_h$ the interpolation projection of C(I) onto $S_{m-1}^{(-1)}(I_h)$ satisfying

$$\begin{aligned} P_h y(t_{n,i}) := y(t_{n,i}),\ \ \ \ i=1,2,\ldots ,m\quad (n=0, 1,\ldots , N-1). \end{aligned}$$

Since $P_hu_h=u_h$, then (3.2) may be written in the form:

$$\begin{aligned} u_h-P_h\mathcal {K}u_h=P_hf, \end{aligned}$$

(3.3)

where the linear operator $\mathcal {K}$ has been defined in (2.1).

3.2 Existence and uniqueness of the collocation solution

Here, we give the analysis for the existence and uniqueness of the discrete collocation solution of Eq. (3.3).

Due to Theorem 2.1, from the definition of $P_h$, we have

$$\begin{aligned} P_hy(t_{n,i}):=y(t_{n,i}), i=1,2\cdot m, n=0,1\cdot N-1. \end{aligned}$$

Therefore, we get

$$\begin{aligned} |P_h b(t,s_1)-P_hb(t,s_2)|=|b(t,s_1)-b(t,s_2)|. \end{aligned}$$

According to (ii) in the Theorem 2.1, we obtain

$$\begin{aligned} |b(t,s_1)-b(t,s_2)|\le \widetilde{L}|s_1-s_2|. \end{aligned}$$

Thus, we can make the following theorem

Theorem 3.1

Assume:

• (i) f and b in the functional equation $y(t)=b(t,y(\theta (t)))+f(t), \; t \in I$, are continuous on I.

• (ii) $|P_hb(t,s_{1})-P_hb(t,s_{2})|\le \widetilde{L}|s_{1}-s_{2}|$, for some constant $\widetilde{L}$, $0<\widetilde{L}<1$, and for all $t\in I$, $s_{1},s_{2}\in \mathbb {R}$.

• (iii) $\theta (t)$ satisfies (P1)–(P2) with $d \ge 2$, and $\Vert \theta '\Vert _{\infty }<1$.

Then, the collocation solution $u_{h} \in S_{m-1}^{(-1)}(I_{h})$ of (3.3) for the functional equation (1.3) exists and is unique for all meshes.

Proof

Similar to Theorem 2.1, we can know the operator $P_h\mathcal {K}$ used in (3.3) is also a contraction mapping, which in turn suggests the uniqueness and existence of solution in $S_{m-1}^{-1}(I_h)$ based on the contraction mapping theory. $\square$

3.3 Error estimates

We now analyze the attainable global order of convergence for the collocation solution $u_{h} \in S_{m-1}^{(-1)}(I_h)$ when the exact solution y of the functional equation (1.3) is sufficiently smooth (Theorem 2.2).

Theorem 3.2

Suppose that $u_h\in S_{m-1}^{(-1)}(I_h)$ is the collocation solution to the functional equation (1.3) with respect to a uniform mesh and given collocation parameters $\{c_i\}$. Then, under the assumptions (i) and (ii) of Theorem 3.1, the resulting collocation error satisfies

$$\begin{aligned} \Vert y-u_h\Vert _{\infty }\le & {} C(\Vert (\mathcal {I}-P_h)f\Vert _{\infty }+\Vert (\mathcal {I}-P_h)\mathcal {K}y\Vert _{\infty }). \end{aligned}$$

(3.4)

If the exact solution y lies in $W^{\nu ,\infty }(I)$ with $\nu \ge m$, $b(\cdot ,\cdot )$ is smooth enough and $\theta (t)$ satisfies (P1)–(P3) with $d\ge m$, then the global order of convergence for $u_{h}$ on I is given by

$$\begin{aligned} \Vert y-u_h\Vert _{\infty }\le & {} Ch^m\Vert y\Vert _{m,\infty }, \end{aligned}$$

(3.5)

where $\Vert y\Vert _{m, \infty }:=\max \nolimits _{0\le j\le m}\Big (\sup \nolimits _{t\in I}\big |\frac{d^j}{\mathrm{d}t^j}y(t)\big |\Big )$ and the constant C does not depend on h.

Proof

It follows from Eq. (3.3) that

$$\begin{aligned} \left\{ \begin{array}{l} u_h=P_h f+P_h \mathcal {K} u_h,\\ y=f+\mathcal {K} y. \end{array} \right. \end{aligned}$$

The collocation error $y-u_h$ can be expressed in the following form:

$$\begin{aligned} y-u_h= & {} f-P_hf + \mathcal {K}y-P_h\mathcal {K}u_h\nonumber \\= & {} f-P_hf + \mathcal {K}y-P_h\mathcal {K}y + P_h\mathcal {K}y- P_h\mathcal {K}u_h\nonumber \\= & {} (I-P_h) f + (I-P_h)\mathcal {K}y + P_h\mathcal {K}y- P_h\mathcal {K}u_h. \end{aligned}$$

This leads to

$$\begin{aligned} \Vert y-u_h\Vert _{\infty }\le & {} C(\Vert (\mathcal {I}-P_h)f\Vert _{\infty }+\Vert (\mathcal {I}-P_h)\mathcal {K}y\Vert _{\infty }) + \widetilde{L}\Vert y-u_h\Vert _{\infty }. \end{aligned}$$

Then, we have

$$\begin{aligned} \Vert y-u_h\Vert _{\infty }\le & {} \frac{C}{1-\widetilde{L}}\Big (\Vert (\mathcal {I}-P_h)f\Vert _{\infty }+\Vert (\mathcal {I}-P_h)\mathcal {K}y\Vert _{\infty }\Big ). \end{aligned}$$

This is the desired result (3.4). Moreover, if $y\in W^{d,\infty }(I) \; (d \ge m)$, then the estimate

$$\begin{aligned} \Vert y-u_h\Vert _{\infty }\le & {} Ch^m\Vert y\Vert _{m,\infty } \end{aligned}$$

follows from the error estimate of the interpolation operator $P_h$. $\square$

4 Numerical examples

In this section, we illustrate the numerical results by solving four different functional equations with fixed-point nonlinear iteration on uniform meshes. All the analytic solutions y(t) are already known and we try to get the collocation solution $y_h(t)$ and evaluate the error between y and $y_h$.

First, we give an example with the linear delay $\theta (t)=qt,\ q\in (0,1)$, $t\in I$.

Example 4.1

We consider the following equation:

$$\begin{aligned} y(t)=b(t,y(\theta (t)))+f(t),\quad \quad t\in \left[ 0,\frac{\pi }{2}\right] , \end{aligned}$$

where we chose $\theta (t)=qt$, $b(t,y)=0.7t\sin (y)$, and $f(t)=e^{t}-0.7t\sin (e^{qt})$, such that the exact solution $y(t)=e^t$ with q being a given positive constant between (0, 1).

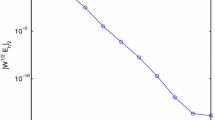
In our numerical implementation, we choose $q=0.5$ and $q=0.99$. We use the spaces $S_{0}^{(-1)}(I_h)$ ($m = 1$: piecewise constant functions) with collocation parameter $c_1=1/2$ (Gauss point); $S_{1}^{(-1)}(I_h)$ ($m = 2$: piecewise linear functions) with the collocation parameters given again by the Gauss points, $c_1=(3-\sqrt{3})/6,\; c_2=(3+\sqrt{3})/6$; and $S_{2}^{(-1)}(I_h)$ ($m = 3$: piecewise quadratic polynomials) with (Gauss points) collocation parameters $c_{1} = (5-\sqrt{15})/10,\; c_{2} = 1/2, \; c_{3} = (5+\sqrt{15})/10$. The numerical results are presented in Fig. 1. The results listed in Fig. 1 clearly exhibit the theoretical orders as described in Theorem 3.2.

Fig. 1

Numerical results for Example 4.1

In the following examples, we choose three different nonlinear vanishing delays $\theta (t)$. They all satisfy $\Vert \theta '\Vert _{\infty }\le 1$ in given domains.

Example 4.2

In this example, we solve the nonlinear functional equation (1.3) in $I=[0,\frac{\pi }{2}]$ with $\theta (t)=\beta \arctan (t),\ (0<\beta <1)$, $b(t,y)=0.7\cos (ty)$ and $f(t)=e^{t}-0.7\cos (te^{\beta \arctan (t)})$, such that exact solution $y(t)=e^t$.

Here, we choose $\beta =0.5$ and $\beta =0.99$. We also use the spaces $S_{0}^{(-1)}(I_h)$ ($m = 1$: piecewise constant functions) with collocation parameter $c_1=1/2$ (Gauss point); $S_{1}^{(-1)}(I_h)$ ($m = 2$: piecewise linear functions) with the collocation parameters given again by the Gauss points, $c_1=(3-\sqrt{3})/6,\; c_2=(3+\sqrt{3})/6$; and $S_{2}^{(-1)}(I_h)$ ($m = 3$: piecewise quadratic polynomials) with (Gauss points) collocation parameters $c_{1} = (5-\sqrt{15})/10,\; c_{2} = 1/2, \; c_{3} = (5+\sqrt{15})/10$. The numerical results are presented in Fig. 2. The results listed in Fig. 2 also clearly exhibit the theoretical orders, as described in Theorem 3.2.

Fig. 2

Numerical results for Example 4.2

Example 4.3

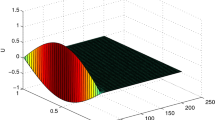
In the third example, we solve Eq. (1.3) with $I=[0,\frac{\pi }{2}]$, where $\theta (t)=\beta \sin (t)\ (0<\beta <1)$, $b(t,y)=0.7t\sin (y)$ and $f(t)=\alpha t e^{-\gamma t}-0.7t\sin (\alpha \beta \sin (t)$ $e^{-\gamma \beta \sin (t)})$, such that the exact solution is $y(t)=\alpha t e^{-\gamma t}$.

In this example, we choose $\beta =0.5, 0.9$, $\alpha =10, 100$, and $\gamma =10, 100$, respectively. The graphs of the corresponding exact solutions are shown in Fig. 3. We also use the spaces $S_{0}^{(-1)}(I_h)$ ($m = 1$: piecewise constant functions) with collocation parameter $c_1=1/2$ (Gauss point); $S_{1}^{(-1)}(I_h)$ ($m = 2$: piecewise linear functions) with the collocation parameters given again by the Gauss points, $c_1=(3-\sqrt{3})/6,\; c_2=(3+\sqrt{3})/6$; and $S_{2}^{(-1)}(I_h)$ ($m = 3$: piecewise quadratic polynomials) with (Gauss points) collocation parameters $c_{1} = (5-\sqrt{15})/10,\; c_{2} = 1/2, \; c_{3} = (5+\sqrt{15})/10$. The numerical results are presented in Fig. 4. The results listed in Fig. 4 also clearly exhibit the theoretical orders, as described in Theorem 3.2.

Fig. 3

Figures for exact solutions $u(t)=\alpha t e^{-\gamma t} \$for Example 4.3

Fig. 4

Numerical results for Example 4.3

Example 4.4

In the final example, we solve the nonlinear functional equation (1.3) in $I=[0,\frac{\pi }{2}]$ with $\theta (t)=\beta \log (1+t),\ (0<\beta <1)$, $b(t,y)=0.7\cos (ty)$ and $f(t)=e^{t}-0.7\cos (te^{\beta \log (1+t)})$, such that the exact solution $y(t)=e^{t}$.

Figure 5 shows the numerical results for $\beta =0.5$ and $\beta =0.99$, respectively. From this figure, we can see the similar phenomena as in last examples.

Fig. 5

Numerical results for Example 4.4

5 Future work

In this paper, we have studied the existence, uniqueness, and regularity of solutions for the nonlinear functional equation (1.3). We also analyze the convergence results of the piecewise polynomial collocation method for this problem. Numerical simulations are shown to verify the efficiency of our algorithm.

There are also some problems we should consider in the future:

• (I) In Theorem 3.1, we assume that the collocation method satisfies condition (ii). As we know, this condition depends on the distribution of the collocation points which will be considered in our future work.

• (II) As we have mentioned in Sect. 1, a more general equation of the classical problem (1.4) in the following form that will be considered by the authors:

  $$\begin{aligned} y(t)=b(t,y(\theta (t)))+\int _{\theta (t)}^{t}\frac{\partial H}{\partial t}(t,s,y(s))\mathrm{d}s+f(t),\quad t\in I. \end{aligned}$$

  In a sequel to the present paper, we will extend our analysis of the numerical analysis with uniform meshes $I_h$, to the above functional integral equations.