1 Introduction

Fredholm integro-differential equations (FIDEs) serve as mathematical models in many fields of science and engineering. FIDEs arise in fluid dynamics, physics, electro dynamics of complex medium, economics, biological models, epidemic models, many models of population growth, neural network modeling, oscillation theory, astronomy, chemistry, heat and mass transfer, theory of elasticity (Amiraliyev et al. 2020; Emamzadeh and Kajani 2010; Jerri 1999). In general, it is usually quite difficult to obtain exact solution of FIDEs. Because of this reason we need suitable discretization methods with high accuracy for solving FIDEs.

In this work, we deal with a singularly perturbed nonlinear Fredholm integro-differential equation (SPNFIDE) as follows:

$$\begin{aligned}&\displaystyle \varepsilon u^{\prime }(t)+f(t,u(t)) +\lambda {\displaystyle \int \limits _{0}^{T}} K(t,s,u(s))\mathrm{d}s=0,\ t\in I=(0,T], \end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle u(0)=A, \end{aligned}$$
(2)

where \(0<\varepsilon<<1\) is the perturbation parameter, A is given constant, \(\lambda \) is a real parameter, \(f(t,u)((t,u)\in {\overline{I}}\times R)\) and \(K(t,s,u(s))((t,s,u)\in {\overline{I}}\times {\overline{I}}\times R)\) are sufficiently smooth functions, \({\overline{I}}=[0,T]\). Furthermore,

$$\begin{aligned} \frac{\partial f}{\partial u}\ge \alpha >0. \end{aligned}$$

Under these assumptions, there exist a unique solution u to problem (1)–(2). Besides, the existence and uniqueness studies of the solutions of nonlinear FIDEs can be found in Jerri (1999), O’Regan and Meehan (1998) and reference therein.

Singularly perturbed problems involve a small perturbation parameter, \(\varepsilon \) multiplied with the highest-order derivative terms. Such problems arise in applications of mathematics to problems in numerous fields of sciences and engineering. Theory of plates, semi-conductor device models, fluid mechanics, in fluid flow at high Reynolds number, quantum mechanics, reaction–diffusion processes, elasticity, etc. are among these. Due to the presence of boundary layers, the solution of these types of problems vary suddenly in boundary layers when \(\varepsilon \) approaches zero. In regions outside the layers, the solution behaviors regularly and varies slowly (Cakir and Arslan 2021; Cimen and Cakir 2017; Doolan et al. 1980; Farell et al. 2000; Miller et al. 2012; Nayfeh 1993; O’Malley 1991; Roos et al. 2008).

In the last decades, there has received much attention in the numerical solution of integral equations. In literature, there are many different numerical models to solve such equations. Ebrahimi and Rashidina (Ebrahimi and Rashidinia 2015) presented a collocation method for solving linear and nonlinear Fredholm and Volterra integral equations, using the globally defined B-spline and auxiliary basis functions. Wang et al. Wang et al. (2019) studied on numerical solution of integro-differential equations of high-order Fredholm by the simplified reproducing kernel method. Maleknejad and Attary Maleknejad and Attary (2011) given Cattani’s method based on the collocation approach for solving linear FIDEs. Emamzadeh and Kajani Emamzadeh and Kajani (2010) proposed a numerical approach to solve the nonlinear Fredholm integral equations of the second kind. Najafi Najafi (2020) introduced Nyström-quasilinearization method for solving nonlinear weakly singular Fredholm integral equations. Asgari et al. Asgari et al. (2019) studied on an iterative method to solve one- and two-dimensional linear Fredholm integral equations.

The above-mentioned articles, related to Fredholm integral equations were only concerned with the regular cases (i.e., when the boundary layers are absent). Studies on singularly perturbed Fredholm integro-differential equations (SPFIDEs) have attracted attention in recent years (Amiraliyev et al. 2018, 2020; Cimen and Cakir 2021; Durmaz and Amiraliyev 2021). However, although there are many studies on linear SPFIDEs in the literature, we could not find any studies on nonlinear SPFIDEs. These gaps in the literature are the motivation for our study. In addition, methods such as Reproducing kernel method, Fourier spectral method and Barycentric interpolation collocation method presented for the solution of the nonlinear singularly perturbed problems have recently attracted attention (Han and Wang 2022; Han et al. 2022; Liu et al. 2018).

In this article, we try to develop an efficient fitted difference scheme on Shishkin mesh for the numerical solution of the problem (1)–(2). The difference scheme is constructed by the method of integral identities with the use of appropriate interpolating quadrature rules with remainder terms in integral form.

The outline of the paper is organized as follows. In Sect. 2, we indicate the asymptotic behavior of the exact solution and its derivative. In Sect. 3, we construct the finite difference method and describe a special piecewise uniform mesh. Convergence and error analysis of the difference discretization are presented in Sect. 4. Some numerical examples are given in Sect. 5, which demonstrate the efficiency and the proposed method.

Throughout the paper, C denotes a generic positive constant. Some specific, fixed constants of this kind are indicated by subscripting C. For any continuous function g(t),  we use \(\left\| g\right\| _{\infty }\) for the continuous maximum norm on the corresponding interval.

2 Bound of the exact solution and its derivative

In this section, we give bound of the exact solution and its derivative, which are needed in later sections for the analysis of appropriate numerical solution.

Lemma 1

Suppose that the following assumptions are fulfilled

$$\begin{aligned}&\frac{\partial ^{m}f}{ \partial t^{m}},\frac{\partial ^{n}f}{\partial u^{n}}\in C^{1}({\overline{I}}\times R),\frac{\partial ^{m}K}{\partial t^{m}}, \frac{\partial ^{n}K}{\partial s^{n}},\frac{\partial ^{k}K}{\nonumber }\\&\quad {\partial u^{k}}\in C^{1}({\overline{I}} \times {\overline{I}}\times R); m,n,k=0,1 \end{aligned}$$
(3)

and

$$\begin{aligned} \left| \lambda \right| <\frac{\alpha }{\underset{0\le t\le T}{\max } {\displaystyle \int \limits _{0}^{T}} \left| G(t,s)\right| ds}. \end{aligned}$$

Then, the solution u(t) of the problem (1)–(2) satisfies the estimates

$$\begin{aligned} \left\| u\right\| _{\infty }\le C_{0,} \end{aligned}$$
(4)

and

$$\begin{aligned} \left| u^{\prime }(t)\right| \le C\left\{ 1+\frac{1}{\varepsilon }e^{-\frac{\alpha t}{\varepsilon }}\right\} ,0\le t\le T, \end{aligned}$$
(5)

where

$$\begin{aligned} C_{0}= & {} \frac{\left| A\right| +\alpha ^{-1}\left\| q\right\| _{\infty }}{1-\alpha ^{-1}\left| \lambda \right| \underset{0\le t\le T}{\max } {\displaystyle \int \limits _{0}^{T}} \left| G(t,s)\right| \mathrm{d}s}, \\ G(t,s)= & {} \frac{\partial }{\partial u}K(t,s,\gamma u),0<\gamma <1, \\ q(t)= & {} -f(t,0)-\lambda {\displaystyle \int \limits _{0}^{T}} K(t,s,0)\mathrm{d}s. \end{aligned}$$

Proof

We first prove (4). Applying the mean value theorem to the functions in (1), we have

$$\begin{aligned} \varepsilon u^{\prime }(t)+p(t)u(t)+\lambda {\displaystyle \int \limits _{0}^{T}} G(t,s)u(s)\mathrm{d}s=q(t),t\in I, \end{aligned}$$
(6)

where

$$\begin{aligned} p(t)=\frac{\partial }{\partial u}f(t,\theta u),0<\theta <1. \end{aligned}$$

From the Eq. (6), we can write the following form:

$$\begin{aligned} \left| u(t)\right|\le & {} \left| u(0)\right| e^{-\frac{1}{\varepsilon } {\displaystyle \int \limits _{0}^{t}} p(\eta )\mathrm{d}\eta }+\frac{1}{\varepsilon } {\displaystyle \int \limits _{0}^{t}} \left| q(\tau )\right| e^{-\frac{1}{\varepsilon } {\displaystyle \int \limits _{\tau }^{t}} p(\eta )\mathrm{d}\eta }\mathrm{d}\tau \\&+\frac{\left| \lambda \right| }{\varepsilon } {\displaystyle \int \limits _{0}^{t}} \left[ {\displaystyle \int \limits _{0}^{T}} \left| G(t,s)\right| \left| u(s)\right| \mathrm{d}s\right] e^{-\frac{1}{\varepsilon } {\displaystyle \int \limits _{\tau }^{t}} p(\eta )\mathrm{d}\eta }\mathrm{d}\tau \\\le & {} \left| A\right| e^{-\frac{\alpha t}{\varepsilon }}+\frac{\left\| q\right\| _{\infty }}{\varepsilon } {\displaystyle \int \limits _{0}^{T}} e^{-\frac{\alpha (t-\tau )}{\varepsilon }}\mathrm{d}\tau \\&+\frac{\left| \lambda \right| }{\varepsilon } {\displaystyle \int \limits _{0}^{t}} \left[ {\displaystyle \int \limits _{0}^{T}} \left| G(t,s)\right| \left| u(s)\right| \mathrm{d}s\right] e^{-\frac{\alpha (t-\tau )}{\varepsilon }}\mathrm{d}\tau . \end{aligned}$$

From here, we take

$$\begin{aligned}&\left\| u\right\| _{\infty }\le \left| A\right| +\alpha ^{-1}\left\| q\right\| _{\infty }\left( 1-e^{-\frac{\alpha t}{\varepsilon }}\right) \\&\quad +\alpha ^{-1}\left| \lambda \right| \left( 1-e^{-\frac{\alpha t}{\varepsilon }}\right) \left\| u\right\| _{\infty }\underset{0\le t\le T}{\max } {\displaystyle \int \limits _{0}^{T}} \left| G(t,s)\right| \mathrm{d}s, \end{aligned}$$

which proves (6).

To prove (5), differentiating Eq. (1) we have

$$\begin{aligned} \varepsilon u^{\prime \prime }(t)+b(t)u^{\prime }(t)=F(t), \end{aligned}$$
(7)

where

$$\begin{aligned} b(t)=\frac{\partial }{\partial u}f(t,u), \end{aligned}$$

and

$$\begin{aligned} F(t)=-\frac{\partial }{\partial t}f(t,u)-\lambda {\displaystyle \int \limits _{0}^{T}} \frac{\partial }{\partial t}K(t,s,u(s))\mathrm{d}s. \end{aligned}$$

From the relations (3) and (4), we have

$$\begin{aligned} \left| F(t)\right| \le C. \end{aligned}$$
(8)

Using (1), we can obtain

$$\begin{aligned} \left| u^{\prime }(0)\right| \le \frac{\left| f(0,A)\right| }{\varepsilon }+\frac{\left| \lambda \right| }{\varepsilon } {\displaystyle \int \limits _{0}^{T}} \left| K(0,s,u(s))\right| \mathrm{d}s\le \frac{C}{\varepsilon }. \end{aligned}$$
(9)

It follows from (7) that

$$\begin{aligned}&\left| u^{\prime }(t)\right| \le \frac{C}{\varepsilon }e^{-\frac{\alpha t}{\varepsilon }}+\frac{\left\| F\right\| _{\infty }}{\varepsilon } {\displaystyle \int \limits _{0}^{T}} e^{-\frac{\alpha (t-\tau )}{\varepsilon }}\mathrm{d}\tau \\&\quad \le \frac{C}{\varepsilon }e^{-\frac{\alpha t}{\varepsilon }}+\alpha ^{-1}\left\| F\right\| _{\infty }\left( 1-e^{-\frac{\alpha t}{\varepsilon }}\right) . \end{aligned}$$

Thus we arrive at (5). \(\square \)

3 Discretization and Mesh

To give an approximation of the (1)–(2), we integrate (1) over \((t_{i-1},t_{i})\):

$$\begin{aligned}&\varepsilon u_{{\overline{t}},i}+h_{i}^{-1} {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} f(t,u)\mathrm{d}t+h_{i}^{-1}\lambda \nonumber \\&\quad {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left[ {\displaystyle \int \limits _{0}^{T}} K(t,s,u)\mathrm{d}s\right] \mathrm{d}t=0, \end{aligned}$$
(10)

where \(u_{{\overline{t}},i}=(u_{i}-u_{i-1})/h_{i}\), \(u_{i}=u(t_{i})\) and \(h_{i}=t_{i}-t_{i-1}\) for \(1\le i\le N\).

If integration by parts is applied to identity (10), we then obtain the relation

$$\begin{aligned} \varepsilon u_{{\overline{t}},i}+f(t_{i},u_{i})+\lambda {\displaystyle \int \limits _{0}^{T}} K(t_{i},s,u(s))\mathrm{d}s+R_{i}^{(1)} +R_{i}^{(2)}=0, \end{aligned}$$
(11)

where the remainder terms are

$$\begin{aligned} R_{i}^{(1)}=-h_{i}^{-1} {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left( \xi -t_{i-1}\right) \frac{\mathrm{d}}{\mathrm{d}\xi }f\left( \xi ,u(\xi )\right) \mathrm{d}\xi , \end{aligned}$$
(12)

and

$$\begin{aligned} {R_{i}^{(2)}=-\lambda h_{i}^{-1} {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left( \xi -t_{i-1}\right) \frac{\mathrm{d}}{\mathrm{d}\xi }\left( {\displaystyle \int \limits _{0}^{T}} K\left( \xi ,s,u(s)\right) \mathrm{d}s\right) \mathrm{d}\xi .} \end{aligned}$$
(13)

For integral term involving kernel function, using the composite right-side rectangle rule, we obtain the relation as follows:

$$\begin{aligned} \lambda {\displaystyle \int \limits _{0}^{T}} K(t_{i},s,u(s))\mathrm{d}s=\lambda {\displaystyle \sum \limits _{j=1}^{N}} h_{i}K(t_{i},s_{j},u_{j})+R_{i}^{(3)}, \end{aligned}$$
(14)

with

$$\begin{aligned} R_{i}^{(3)}=\lambda {\displaystyle \sum \limits _{j=1}^{N}} {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left( t_{j-1}-\xi \right) \frac{\mathrm{d}}{\mathrm{d}\xi }K(t_{i},\xi ,u(\xi ))\mathrm{d}\xi . \end{aligned}$$
(15)

By the relations (10), (11) and (14) for \(u(t_{i})\), we get the following exact relation:

$$\begin{aligned} \varepsilon u_{{\overline{t}},i}+f(t_{i},u_{i})+\lambda {\displaystyle \sum \limits _{j=1}^{N}}&h_{i}K(t_{i},s_{j},u_{j})+R_{i}=0,i=1,2,\ldots ,N, \end{aligned}$$
(16)
$$\begin{aligned}&\quad u_{0}=A, \end{aligned}$$
(17)

where the remainder term \(R_{i}\) is defined by

$$\begin{aligned} R_{i}=R_{i}^{(1)}+R_{i}^{(2)}+R_{i}^{(3)}. \end{aligned}$$
(18)

Neglecting \(R_{i}\) in (16), we may suggest the following difference scheme for approximating (1)–(2):

$$\begin{aligned} \varepsilon y_{{\overline{t}},i}+f(t_{i},y_{i})+\lambda {\displaystyle \sum \limits _{j=1}^{N}}&h_{i}K(t_{i},s_{j},y_{j})=0,i=1,2,\ldots ,N, \end{aligned}$$
(19)
$$\begin{aligned}&\quad y_{0}=A. \end{aligned}$$
(20)

The difference scheme (19)–(20) to be \(\varepsilon \)-uniformly convergent in what follows we will use the fitted piecewise uniform mesh (Shishkin type mesh). For the even number N, Shishkin-type mesh divides each of the interval \(\left[ 0,\sigma \right] \) and \(\left[ \sigma ,T\right] \) into N/2 equidistant subintervals. The transition point \(\sigma \) which separates of fine and coarse portions of the mesh is defined by

$$\begin{aligned} \sigma =\min \left\{ \frac{T}{2},\alpha ^{-1}\varepsilon \ln N\right\} . \end{aligned}$$

We denote the stepsizes in there subintervals as follows:

$$\begin{aligned}&h=\frac{2\sigma }{N},H=\frac{2(l-\sigma )}{N}, \\&\quad h\le lN^{-1},lN^{-1}\le H\le 2lN^{-1},h+H=2lN^{-1}. \end{aligned}$$

The mesh points of \(\omega _{N}\) are being defined by

$$\begin{aligned} \omega _{N}=\left\{ { \begin{array}{l} t_{i}=ih,i=1,2,\ldots ,N/2,\\ t_{i}=\sigma +\left( i-\frac{N}{2}\right) H,i=N/2+1,\ldots ,N. \end{array} }\right. \end{aligned}$$

and \({\overline{\omega }}_{N}=\omega _{N}\cup \left\{ t_{0}=0\right\} .\)

4 Uniform error estimates

To investigate the convergence of the method, note that \(z_{i}=y_{i}-u_{i}\) \((0\le i\le N)\) is the solution of the following discrete problem:

$$\begin{aligned}&\varepsilon z_{{\overline{t}},i}+\left[ f(t_{i},y_{i})-f(t_{i},u_{i})\right] \nonumber \\&\quad +\lambda {\displaystyle \sum \limits _{j=1}^{N}} h_{i}\left[ K(t_{i},s_{j},y_{j})-K(t_{i},s_{j},u_{j})\right] =R_{i},1\le i \le N, \end{aligned}$$
(21)
$$\begin{aligned}&\quad z_{0}=0. \end{aligned}$$
(22)

Lemma 2

Under the conditions of Lemma 1, for the remainder term \(R_{i}\) of the scheme (19)–(20), the estimate

$$\begin{aligned} \left\| R\right\| _{\infty ,\omega _{N}}\le CN^{-1}\ln N \end{aligned}$$
(23)

holds.

Proof

We first consider the relation (12). Taking into account (4) and (5) in (12), then we have the inequality

$$\begin{aligned} \left| R_{i}^{(1)}\right|\le & {} h_{i}^{-1} {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left( \xi -t_{i-1}\right) \left[ \left| \frac{\partial }{\partial \xi }f\left( \xi ,u(\xi )\right) \right| +\left| \frac{\partial }{\partial u}f\left( \xi ,u(\xi )\right) \right| \left| u^{\prime }(\xi )\right| \right] \mathrm{d}\xi \nonumber \\\le & {} h_{i}^{-1} {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left( \xi -t_{i-1}\right) \left| 1+u^{\prime }(\xi )\right| \mathrm{d}\xi \nonumber \\\le & {} C\left\{ h_{i}+ {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left| u^{\prime }(\xi )\right| \mathrm{d}\xi \right\} ,\ i=1,2,\ldots ,N. \end{aligned}$$
(24)

Next we analyze the relation (13). Taking into account (4) in (13), we get the inequality

$$\begin{aligned} \left| R_{i}^{(2)}\right|\le & {} \left| \lambda \right| h_{i}^{-1} {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left( \xi -t_{i-1}\right) \left| \frac{\mathrm{d}}{\mathrm{d}\xi } {\displaystyle \int \limits _{0}^{T}} K\left( \xi ,s,u(s)\right) \mathrm{d}s\right| \mathrm{d}\xi \nonumber \\\le & {} \left| \lambda \right| h_{i}^{-1} {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left( \xi -t_{i-1}\right) {\displaystyle \int \limits _{0}^{T}} \left| \frac{\partial }{\partial \xi }K\left( \xi ,s,u(s)\right) \right| \mathrm{d}s\mathrm{d}\xi \nonumber \\\le & {} Ch_{i},i=1,2,\ldots ,N. \end{aligned}$$
(25)

Finally, we denote the relation (15). By (4) and (5) in (15), we can write the following inequality:

$$\begin{aligned} \left| R_{i}^{(3)}\right|\le & {} \left| \lambda \right| {\displaystyle \sum \limits _{j=1}^{N}} {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left( t_{j-1}-\xi \right) \left| \frac{\partial }{\partial \xi }K(t_{i},\xi ,u(\xi ))+\frac{\partial }{\partial u}K(t_{i},\xi ,u(\xi ))u^{\prime } (\xi )\right| \mathrm{d}\xi \nonumber \\\le & {} C {\displaystyle \sum \limits _{j=1}^{N}} {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left( t_{j-1}-\xi \right) \left| 1+u^{\prime }(\xi )\right| \mathrm{d}\xi \nonumber \\\le & {} C\underset{1\le j\le N}{\max }h_{j} {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left| 1+u^{\prime }(\xi )\right| \mathrm{d}\xi ,\ i=1,2,\ldots ,N. \end{aligned}$$
(26)

Thus, substituting the inequalities (24), (25) and (26) in (18), we obtain

$$\begin{aligned} \left| R_{i}\right| \le C\left\{ h_{i}+ {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left| u^{\prime }(\xi )\right| \mathrm{d}\xi \right\} ,\ i=1,2,\ldots ,N. \end{aligned}$$
(27)

In the first case, we consider that \(\sigma =\frac{T}{2},\) \(\frac{T}{2} <\alpha ^{-1}\varepsilon \ln N\) and \(h=H=TN^{-1}\). From (27) we take

$$\begin{aligned} \left| R_{i}\right| \le C {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left( 1+\varepsilon ^{-1}\right) \mathrm{d}t=Ch\left( 1+\varepsilon ^{-1}\right) \end{aligned}$$
$$\begin{aligned} \le C\frac{T}{N}\left( 1+\frac{2}{T}\alpha ^{-1}\ln N\right) . \end{aligned}$$
(28)

It follows from (28) that

$$\begin{aligned} \left| R_{i}\right| \le CN^{-1}\ln N,i=1,\ldots ,N. \end{aligned}$$
(29)

In the second case, we consider \(\sigma =\alpha ^{-1}\varepsilon \ln N\), and so \(\alpha ^{-1}\varepsilon \ln N<\frac{T}{2}.\) We estimate \(R_{i}\) on \(\left[ 0,\sigma \right] \) and \(\left[ \sigma ,T\right] \), separately. In the boundary layers \(\left[ 0,\sigma \right] \), inequality (27) reduces to

$$\begin{aligned} \left| R_{i}\right| \le C\left( 1+\varepsilon ^{-1}\right) h \le C(2\alpha ^{-1}\varepsilon N^{-1}\ln N+2\alpha ^{-1}N^{-1}\ln N). \end{aligned}$$

Hence,

$$\begin{aligned} \left| R_{i}\right| \le CN^{-1}\ln N,\ \text { for }i=1,\ldots ,\frac{N}{2}. \end{aligned}$$
(30)

We now estimate the remainder term \(R_{i}\) in the region \(\left[ \sigma ,T\right] \). From (27), we take

$$\begin{aligned} \left| R_{i}\right| \le C\left\{ H+ {\displaystyle \int \limits _{t_{i-1}}^{t_{i}}} \left| u^{\prime }(t)\right| \mathrm{d}t\right\} . \end{aligned}$$

Taking into account (5) here, we have

$$\begin{aligned} \left| R_{i}\right| \le C\left\{ H+\alpha ^{-1}\left( e^{-\frac{\alpha t_{i-1}}{\varepsilon }}-e^{-\frac{\alpha t_{i}}{\varepsilon }}\right) \right\} . \end{aligned}$$
(31)

Since

$$\begin{aligned} t_{i}=\alpha ^{-1}\varepsilon \ln N+\left( i-\frac{N}{2}\right) H, \end{aligned}$$

we obtain

$$\begin{aligned} e^{-\frac{\alpha t_{i}}{\varepsilon }}=e^{-\frac{\alpha }{\varepsilon }\left[ \alpha ^{-1}\varepsilon \ln N+\left( i-\frac{N}{2}\right) H\right] } =N^{-1}e^{-\frac{\alpha }{\varepsilon }\left( i-\frac{N}{2}\right) H}\le N^{-1} \end{aligned}$$
(32)

and

$$\begin{aligned} e^{-\frac{\alpha t_{i-1}}{\varepsilon }}=e^{-\frac{\alpha }{\varepsilon }\left[ \alpha ^{-1}\varepsilon \ln N+\left( i-1-\frac{N}{2}\right) H\right] } =N^{-1}e^{-\frac{\alpha }{\varepsilon }\left( i-1-\frac{N}{2}\right) H}\le N^{-1}. \end{aligned}$$
(33)

Substituting (32) and (33) into (31), we have

$$\begin{aligned} \left| R_{i}\right| \le C\left\{ 2TN^{-1}+\alpha ^{-1}N^{-1}\right\} . \end{aligned}$$

Hence, it follows that

$$\begin{aligned} \left| R_{i}\right| \le CN^{-1},\text { for }\ i=\frac{N}{2}+1,\ldots ,N. \end{aligned}$$
(34)

Combining the estimates (29), (30) and (34), we arrive at (23). \(\square \)

Lemma 3

If we assume the condition

$$\begin{aligned} \left| \lambda \right| <\frac{\alpha }{\underset{1\le i\le N}{\max } {\displaystyle \sum \nolimits _{j=1}^{N}} h_{i}\left| G_{ij}\right| }, \end{aligned}$$

then for the solution of the difference problem (21)–(22) the following estimate holds:

$$\begin{aligned} \left\| z\right\| _{\infty }\le \alpha ^{-1}\left( 1-\alpha ^{-1}\left| \lambda \right| \underset{1\le i\le N}{\max } {\displaystyle \sum \limits _{j=1}^{N}} h_{i}\left| G_{ij}\right| \right) ^{-1}\left\| R\right\| _{\infty }. \end{aligned}$$
(35)

Proof

Applying the mean value theorem to function in (21), we get

$$\begin{aligned} \varepsilon z_{{\overline{t}},i}+a_{i}z_{i}+\lambda {\displaystyle \sum \limits _{j=1}^{N}} h_{i}G_{ij}=R_{i},1\le i\le N, \end{aligned}$$

where

$$\begin{aligned} a_{i}=\frac{\partial }{\partial u}f(t_{i},u_{i}+\theta z_{i}) \end{aligned}$$

and

$$\begin{aligned} G_{ij}=\frac{\partial }{\partial u}K(t_{i},s_{j},u_{j}+\theta z_{j}),{ \ \ }0<\theta <1. \end{aligned}$$

According to maximum principle for the operator \(\varepsilon z_{\overline{t},i}+a_{i}z_{i}\), we can write

$$\begin{aligned} \left\| z\right\| _{\infty }\le \alpha ^{-1}\left\| R\right\| _{\infty }+\alpha ^{-1}\left| \lambda \right| \left\| z\right\| _{\infty }\underset{1\le i\le N}{\max } {\displaystyle \sum \limits _{j=1}^{N}} h_{i}\left| G_{ij}\right| , \end{aligned}$$

which immediately lead to (35). \(\square \)

Finally, we obtain the main results for this work.

Theorem 1

Under the conditions of Lemma 1, the solution of (1 )–(2) and the solution (13)–(14) satisfy the estimate

$$\begin{aligned} \left\| y-u\right\| _{\infty ,{\overline{\omega }}_{N}}\le CN^{-1}\ln N. \end{aligned}$$
(36)

Proof

Combining the previous lemmas, we immediately arrive at (36). \(\square \)

Table 1 The resulting errors \(e^{\varepsilon ,N}\) and \({e^{N}}\), convergence rates \(p^{N}\) for test problem
Full size table

5 Algorithm and numerical results

5.1 Algorithm

In this section, we present the following iterative technique for solving nonlinear problem (19)–(20).

$$\begin{aligned} y_{i}^{(n)}= & {} \frac{A_{i}y_{i-1}^{(n)}+B_{i}y_{i}^{(n-1)}-C_{i}-D_{i}}{\frac{\varepsilon }{h_{i}}+\frac{\partial }{\partial y}f(t_{i},y_{i} ^{(n-1)})+\lambda h_{i}\frac{\partial }{\partial y}K(t_{i},s_{i},y_{i} ^{(n-1)})},i=1,2,\ldots ,N, \\&y_{0}^{(n)}=A, \end{aligned}$$

where

$$\begin{aligned} A_{i}= & {} \frac{\varepsilon }{h_{i}},\ B_{i}=\frac{\partial }{\partial y}f(t_{i},y_{i}^{(n-1)})+\lambda h_{i}\frac{\partial }{\partial y}K(t_{i},s_{i},y_{i}^{(n-1)}), \\ C_{i}= & {} f(t_{i},y_{i}^{(n-1)})+\lambda h_{i}K(t_{i},s_{i},y_{i}^{(n-1)}), \\ D_{i}= & {} \lambda {\displaystyle \sum \limits _{j=1}^{N}} h_{i}\left[ K(t_{i},s_{j},y_{j}^{(n-1)})+\frac{\partial }{\partial y} K(t_{i},s_{j},y_{j}^{(n-1)})\times \left( y_{j}^{(n)}-y_{j}^{(n-1)}\right) \right] ,i\ne j, \\ D_{i}= & {} 0,\text { for }i=j, \end{aligned}$$

\(n=1,2,\ldots ,\) and \(y_{i}^{(0)}\) is given.

Fig. 1
figure 1

Numerical results of test problem for \(N=64\) and \(\varepsilon =2^{-4}\)

Full size image
Fig. 2
figure 2

Numerical results of test problem for \(N=256\) and various \(\varepsilon \)

Full size image
Fig. 3
figure 3

Maximum point-wise errors of log–log plot for test problem

Full size image

5.2 Numerical example

We consider SPNFIDE in the form:

$$\begin{aligned}&\varepsilon u^{\prime }(t)+2u(t)+\tanh (u(t))+\frac{1}{4}\int _{0}^{1}t^{2} \sin (u(s))\mathrm{d}s+e^{t}=0,0<t\le 1, \\&\quad u(0)=1. \end{aligned}$$

As the exact solution u(t) of this problem unknown. Therefore, we use the double-mesh principle to approximate the maximum errors on our mesh \({\overline{\omega }}_{N}\). That is, we compare the computed solutions with the solution on a mesh that is twice as fine (Doolan et al. 1980; Farell et al. 2000). The initial guess used here is taken as \(y_{i}^{(0)}=1-e^{-t_{i}}\) and the number of iterations n is chosen such that

$$\begin{aligned} \underset{i}{\max }\left| y_{i}^{(n)}-y_{i}^{(n-1)}\right| \le 10^{-5}. \end{aligned}$$

The two mesh difference is denoted by

$$\begin{aligned} e^{\varepsilon ,N}=\underset{\omega _{N}}{\max }\left| y^{\varepsilon ,N}-{\widetilde{y}}^{\varepsilon ,2N}\right| , \end{aligned}$$

where \({\widetilde{y}}^{\varepsilon ,2N}\) is the numerical which comprises points of the original mesh \(t_{i}\in \omega _{N}\) and their midpoints \(t_{i+1/2} =(t_{i}+t_{i+1})/2\), \(i=0,1,\ldots ,N-1\).

Thus, the maximum errors are taken as

$$\begin{aligned} e^{N}=\underset{\varepsilon }{\max }e^{\varepsilon ,N}. \end{aligned}$$

In addition, the orders of convergence and the \(\varepsilon \)-uniform rates of convergence are defined as

$$\begin{aligned} p^{\varepsilon ,N}=\ln (e^{\varepsilon ,N}/e^{\varepsilon ,2N})/\ln 2, p^{N}=\ln (e^{N}/e^{2N})/\ln 2. \end{aligned}$$

The resulting errors \(e^{\varepsilon ,N}\)and the orders of convergence \(p^{\varepsilon ,N}\) for particular values of \(\varepsilon \) and N, are listed in the Table 1.

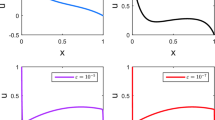
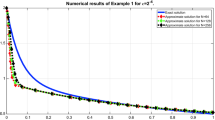
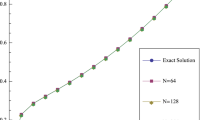
To validate the applicability of the method, one test problem is considered for numerical experimentation for different values of the perturbation parameter and mesh points. The numerical results are listed in terms of the approximate errors, the rates of convergence (see Table 1). Further, behavior of the numerical solution (see Figs. 1, 2) and the \(\varepsilon \)-uniform convergence of the method is shown by the log-log plot (see Fig. 3). From the results in the table, we observe that the maximum pointwise errors (\({e^{N}}\)) decreases monotonically and the rates of convergence (\({p^{N}}\)) increases monotonically when the number of mesh points (N) increases. From Figs. 1 and 2, we observe that the solution of the example exhibit a boundary layer \(t = 0\). And from Fig. 3, we notice that the maximum pointwise errors are bounded by \(O(N^{-1}lnN)\), which is proved in Theorem 1.

6 Conclusion

The singularly perturbed initial-value problem for a nonlinear first-order Fredholm integro-differential equation is considered. To solve this problem, a fitted difference scheme on a piecewise uniform mesh was presented. First order convergence except for a logarithmic factor, in the discrete maximum norm, independently of the perturbation parameter was obtained. The computed errors and rates of convergence were displayed in Table 1 and plotted Figs. 1, 2, 3 for the considered test problem, which supported of the theoretical results. These results showed that the presented method was effective and accuracy. We point out that the presented method in this article can be extended to other type of initial or boundary value problems such as nonlinear SPFIDEs, reaction diffusion SPFIDEs.