1 Introduction

We are interested in the numerical solution of the singularly perturbed Fredholm integro-differential equations (SPFIDEs) of the form:

$$\begin{aligned}&Lu:=\varepsilon u^{\prime \prime }(x)+a(x)u^{\prime }(x)=f(x)+\lambda \int _{0}^{l}K(x,t)u(t)\mathrm{{d}}t,\text { }x\in \varOmega , \end{aligned}$$
(1.1)
$$\begin{aligned}&u(0)=A,\text { }u(l)=B, \end{aligned}$$
(1.2)

where \(0<\varepsilon \ll 1\) is the singular perturbation parameter, A and B are given real constants, \(\lambda \) is a real parameter, \(\varOmega =\left( 0,l\right) \), and\(\ \bar{\varOmega }=\left[ 0,l\right] \). \(a(x)\ge \alpha >0,\) f(x) (\(x\in \bar{\varOmega }\)) and K(x, t) (\((x,t)\in \bar{\varOmega }\times \bar{\varOmega }\)) are given sufficiently smooth functions (their actual degree of smoothness is specified below) satisfying certain regularity conditions to be specified. The existences and the uniqueness of the solution of SPFIDEs can be found in Lange and Smith (1988), Omel’chenko and Nefedov (2002) and references therein.

Since singularly perturbed problems arise in many applications of science and engineering (such as fluid dynamics, quantum mechanics, plasticity, oceanography, meteorology, reaction–diffusion processes, and mathematical model of chemical reactions), the studies for the approximate solutions of these problems are increasing from day to day (Cakir et al. 2016a, b; Cimen and Cakir 2017; Farell et al. 2000; O’Riordan et al. 2003; Roos et al. 2008; Smith 1985).

It is well known that the usual discretization methods for solving singularly perturbed problems are unstable and do not give satisfactory results for sufficiently small values of \(\varepsilon \). Therefore, it is necessary to construct uniform numerical methods to solve such problems (Cimen and Cakir 2017; Farell et al. 2000; Roos et al. 2008).

However, singularly perturbed integral equations or integro-differential equations appear in population dynamics, polymer rheology, and mathematical model of glucose tolerance (Brunner and van der Houwen 1986; De Gaetano and Arino 2000; Jerri 1999; Lodge et al. 1978). In particular, singularly perturbed Fredholm integral equation is given by optimal control problems Nefedov and Nikitin (2007). Some asymptotic approaches for this problem have discussed in (Lange and Smith 1993; Nefedov and Nikitin 2000, 2007). In recent years, many methods have proposed by authors in Amiraliyev and Sevgin (2006), Amiraliyev and Yilmaz (2014), Bijura (2002), Kauthen (1997), Kudu et al. (2016), Ramos (2008), Salama and Bakr (2007), and Tao and Zhang (2019) for the approximate solution of the singularly perturbed Volterra integro-differential equation. However, the numerical approaches of SPFIDEs are not studied in literature so far. Motivating from these studies, our goal is to present an efficient numerical solution for the problem (1.1) and (1.2). Therefore, we first examine some properties of the exact solution of (1.1) and (1.2) in Sect. 2. In Sect. 3, we present a finite difference scheme which is constructed by the method of integral identities with the use of interpolating quadrature rules with the weight and remainder terms in integral form. We analyze the error estimates for the approximate solution and we prove the uniform convergence result for the scheme in Sect. 4. Finally, in Sect. 5, we present an example that confirms the theoretical results.

Notation Throughout the paper, C denotes a generic positive constant that is independent of both the perturbation and the mesh parameter. In addition, fixed constants of this kind are indicated by subscripting C. \(C^{n}(\bar{\varOmega })\) denotes the space of real-valued functions which are n-times continuously differentiable on \(\bar{\varOmega }\). \(C_{m}^{n}(\bar{\varOmega }\times \bar{\varOmega })\) denotes the space of two variable real-valued functions which are n-times continuously differentiable with respect to the first variable and m-times continuously differentiable with respect to the second variable on \(\bar{\varOmega }\times \bar{\varOmega }\). For any continuous function \(g\left( x\right) \) defined on the corresponding interval, we use the maximum norm \( \left\| g \right\| _{\infty } = \max _{{\left[ {0,l} \right] }} \left| {g\left( x \right) } \right| \) and \(\left\| g\right\| _{1}=\int _{0}^{l}\left| g\left( x\right) \right| \mathrm{{d}}x,\) \(\overline{K}=\max _{x\in \bar{\varOmega } }\int _{0}^{l}\left| K(x,t)\right| \mathrm{{d}}t.\)

2 Asymptotic estimates

Here, we give useful asymptotic estimates of the exact solution of the problem (1.1) and (1.2) that are needed in later sections.

Lemma 1

Assume that a,  \(f\in C(\bar{\varOmega }),\) \(K\in C_{1}^{1}(\bar{\varOmega } \times \bar{\varOmega })\) with \(a(x)\ge \alpha >0,\) and:

$$\begin{aligned} \left| \lambda \right| <\frac{\alpha }{\overline{K}l}. \end{aligned}$$

Then, the solution u of the problem (1.1)–(1.2) satisfies the inequalities:

$$\begin{aligned} \left\| u\right\| _{\infty }\le C_{0}, \end{aligned}$$
(2.1)

where

$$\begin{aligned} C_{0}=(\left| A\right| +\left| B\right| +\alpha ^{-1}\left\| f\right\| _{1})(1-\alpha ^{-1}\left| \lambda \right| \overline{K}l)^{-1}, \end{aligned}$$

and

$$\begin{aligned} \left| u^{\prime }(x)\right| \le C\left( 1+\frac{1}{\varepsilon }e^{- \frac{\alpha x}{\varepsilon }}\right) ,\text { }x\in \bar{\varOmega }. \end{aligned}$$
(2.2)

Proof

First, we prove (2.1). First of all, we consider the Green’s function of the operator:

$$\begin{aligned} \begin{array}{l} Lv:=-\varepsilon {v}^{\prime \prime }(x)-a(x){v}^{\prime }(x),\ 0<x<l, \\ v(0)=0,\text { }v(l)=0, \end{array} \end{aligned}$$

which is defined as similar to Andreev (2002):

$$\begin{aligned} G(x,s)=\frac{w(s)}{v_{1}(l)}\left\{ { \begin{array}{l} v_{1}(s)v_{2}(x),\text { }0\le s\le x\le l, \\ v_{1}(x)v_{2}(s),\text { }0\le x\le s\le l, \end{array} }\right. \end{aligned}$$
(2.3)

where the functions \(v_{1}(x)\) and \(v_{2}(x)\) are the solutions of the following initial value problems:

$$\begin{aligned}&Lv_{1}=0,\text { }v_{1}(0)=0,\text { }v_{1}^{\prime }(0)=1/\varepsilon ,\\&Lv_{2}=0,\text { }v_{2}(l)=0,\text { }v_{2}^{\prime }(l)=-1/\varepsilon \end{aligned}$$

and

$$\begin{aligned} w(s)=e^{-\frac{1}{\varepsilon }\int _{s}^{l}{a(\tau )\mathrm{{d}}\tau }}{.} \end{aligned}$$

Thus, similar to work of Amiraliyev and Cimen (2010), for the solution u of the problem (1.1) and (1.2), we can write:

$$\begin{aligned} u(x)=\left( 1-\frac{\int _{0}^{x}e^{-\frac{1}{\varepsilon }\int _{0}^{\tau }a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\tau }{\int _{0}^{l}e^{-\frac{1}{\varepsilon } \int _{0}^{\tau }a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\tau }\right) A+\frac{\int _{0}^{x}e^{- \frac{1}{\varepsilon }\int _{0}^{\tau }a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\tau }{ \int _{0}^{l}e^{-\frac{1}{\varepsilon }\int _{0}^{\tau }a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\tau }B+\int _{0}^{l}G(x,s)F(s)\mathrm{{d}}s \end{aligned}$$
(2.4)

with

$$\begin{aligned} F(x)=-f(x)-\lambda \int _{0}^{l}K(x,t)u(t)\mathrm{{d}}t. \end{aligned}$$

From (2.4), we obtain:

$$\begin{aligned} \left| u(x)\right| \le \left| A\right| +\left| B\right| +\int _{0}^{l}\left| G(x,s)\right| \left| F(s)\right| \mathrm{{d}}s \end{aligned}$$
(2.5)

and also for Green’s function known as formula (2.3) is valid \(0\le G(x,\xi )\le \alpha ^{-1}\) in Andreev (2002). Using this inequality, from (2.5), we obtain:

$$\begin{aligned} \left| u(x)\right|\le & {} \left| A\right| +\left| B\right| +\max _{x,s\in \bar{\varOmega }}\left| G(x,s)\right| \int _{0}^{l}\left| F(s)\right| \mathrm{{d}}s \\\le & {} \left| A\right| +\left| B\right| +\alpha ^{-1}\int _{0}^{l}[\left| f(s)\right| +\left| \lambda \right| \int _{0}^{l}\left| K(s,t)\right| \left| u(t)\right| \mathrm{{d}}t]\mathrm{{d}}s \\\le & {} \left| A\right| +\left| B\right| +\alpha ^{-1}\left\| f\right\| _{1}+\alpha ^{-1}\left| \lambda \right| \left\| u\right\| _{\infty }\overline{K}l. \end{aligned}$$

from which (2.1) follows immediately. Second, from (1.1), we have:

$$\begin{aligned} u^{\prime }(x)=u^{\prime }(0)e^{-\frac{1}{\varepsilon }\int _{0}^{x}a\left( \eta \right) \mathrm{{d}}\eta }+\frac{1}{\varepsilon }\int _{0}^{x}F\left( \xi \right) e^{-\frac{1}{\varepsilon }\int _{\xi }^{x}a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\xi . \end{aligned}$$
(2.6)

Integrating (2.6) over \(\left( 0,x\right) \), we get:

$$\begin{aligned} u(x)= & {} A+u^{\prime }(0)\int _{0}^{x}e^{-\frac{1}{\varepsilon }\int _{0}^{\tau }a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\tau +\frac{1}{\varepsilon }\int _{0}^{x}\mathrm{{d}}\tau \int _{0}^{\tau }F\left( \xi \right) e^{-\frac{1}{\varepsilon }\int _{\xi }^{\tau }a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\xi \\= & {} A+u^{\prime }(0)\int _{0}^{x}e^{-\frac{1}{\varepsilon }\int _{0}^{\tau }a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\tau +\frac{1}{\varepsilon }\int _{0}^{x}\mathrm{{d}}\xi F\left( \xi \right) \int _{\xi }^{x}e^{-\frac{1}{\varepsilon }\int _{\xi }^{\tau }a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\tau \end{aligned}$$

from which by setting the boundary condition \(u(l)=B\), we obtain:

$$\begin{aligned} u^{\prime }\left( 0\right) =\frac{B-A-\frac{1}{\varepsilon }\int _{0}^{l}\mathrm{{d}}\xi F\left( \xi \right) \int _{\xi }^{l}e^{-\frac{1}{\varepsilon }\int _{\xi }^{\tau }a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\tau }{\int _{0}^{l}e^{-\frac{1}{ \varepsilon }\int _{0}^{\tau }a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\tau }. \end{aligned}$$
(2.7)

Since

$$\begin{aligned} \int _{0}^{l}e^{-\frac{1}{\varepsilon }\int _{0}^{\tau }a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\tau\ge & {} \int _{0}^{l}{e^{-\frac{\left\| a\right\| _{\infty }\tau }{\varepsilon }}}\mathrm{{d}}\tau =\frac{\varepsilon }{\left\| a\right\| _{\infty }}(1-{e^{-\frac{\left\| a\right\| _{\infty }l}{\varepsilon }}} ) \\\ge & {} \frac{\varepsilon }{\left\| a\right\| _{\infty }}(1-{e} ^{-\left\| a\right\| _{\infty }l})\equiv c_{1}\varepsilon \end{aligned}$$

and

$$\begin{aligned}&\frac{1}{\varepsilon }\int _{0}^{l}{\mathrm{{d}}\xi \left| {F(\xi )}\right| \int _{\xi }^{l}{e^{-\frac{1}{\varepsilon }\int _{\xi }^{\tau }{a(\eta )\mathrm{{d}}\eta } }}}\mathrm{{d}}\tau \le \frac{1}{\varepsilon }\int _{0}^{l}{\mathrm{{d}}\xi \left| {F(\xi )} \right| \int _{\xi }^{l}{e^{-\frac{\alpha (\tau -\xi )}{\varepsilon }}}} \mathrm{{d}}\tau \\&\quad \le \frac{1}{\varepsilon }\int _{0}^{l}{\mathrm{{d}}\xi \left| {F(\xi )}\right| [\alpha ^{-1}\varepsilon (1-e^{-\frac{\alpha (l-\xi )}{\varepsilon }})]}\le \alpha ^{-1}\int _{0}^{l}{\left| {F(\xi )}\right| \mathrm{{d}}\xi } \\&\quad \le \alpha ^{-1}\left\| f\right\| _{1}+\alpha ^{-1}\left| \lambda \right| C_{0}\overline{K}l\equiv C_{1}, \end{aligned}$$

from (2.7), we are led to:

$$\begin{aligned}&\left| {{u}^{\prime }(0)}\right| \le \frac{\left| {A} \right| +\left| {B}\right| +\frac{1}{\varepsilon }\int _{0}^{l}{ \mathrm{{d}}\xi \left| {F(\xi )}\right| \int _{\xi }^{l}{e^{-\frac{1}{ \varepsilon }\int _{\xi }^{\tau }{a(\eta )\mathrm{{d}}\eta }}}}\mathrm{{d}}\tau }{\int _{0}^{l}{e^{- \frac{1}{\varepsilon }\int _{0}^{\tau }{a(\eta )\mathrm{{d}}\eta }}}\mathrm{{d}}\tau }\nonumber \\&\quad \le \frac{c_{1}^{-1}(\left| {A}\right| +\left| {B}\right| +C_{1})}{\varepsilon }\equiv \frac{C_{2}}{\varepsilon }. \end{aligned}$$
(2.8)

We see from (2.6) that:

$$\begin{aligned} \left| u^{\prime }(x)\right|\le & {} \frac{C_{2}}{\varepsilon }e^{- \frac{1}{\varepsilon }\int _{0}^{x}a\left( \eta \right) \mathrm{{d}}\eta } \\&+\frac{1}{\varepsilon }\int _{0}^{x}[\left| f\left( \xi \right) \right| +\left| \lambda \right| \int _{0}^{l}\left| K(\xi ,t)\right| \left| u(t)\right| \mathrm{{d}}t]e^{-\frac{1}{\varepsilon } \int _{\xi }^{x}a\left( \eta \right) \mathrm{{d}}\eta }\mathrm{{d}}\xi \\\le & {} \frac{C_{2}}{\varepsilon }e^{-\frac{\alpha x}{\varepsilon }}+\frac{1}{ \varepsilon }\int _{0}^{x}[\left| f\left( \xi \right) \right| +\left| \lambda \right| C_{0}\int _{0}^{l}\left| K(\xi ,t)\right| \mathrm{{d}}t]e^{-\frac{\alpha \left( x-\xi \right) }{\varepsilon }}\mathrm{{d}}\xi \\\le & {} \frac{C_{2}}{\varepsilon }e^{-\frac{\alpha x}{\varepsilon }}+\alpha ^{-1}(\left\| f\right\| _{\infty }+\left| \lambda \right| C_{0} \overline{K})(1-e^{-\frac{\alpha x}{\varepsilon }}), \end{aligned}$$

which along with (2.8) leads to (2.2). Thus, the proof of lemma completes. \(\square \)

3 Discretization and mesh

We will construct the new finite difference scheme for approximate solution of the problem (1.1) and (1.2) in this section. At first, we denote by \(\omega _{h}\) a uniform mesh on \(\varOmega \):

$$\begin{aligned} \omega _{h}=\{x_{i}=ih,\text { }i=1,2, \ldots , N-1;h=l/N\},\text {\ }\bar{\omega } _{h}=\omega _{h}\cup \left\{ x_{0}=0,\text { }x_{N}=l\right\} . \end{aligned}$$

To simplify the notation, we set \(g_{i}=g\left( x_{i}\right) \) for any function \(g\left( x\right) \), while \(y_{i}\) denotes an approximation of \( u\left( x\right) \) at \(x_{i}\). For any mesh function \(g\left( x_{i}\right) \) defined on \(\bar{\omega }_{h}\), we use:

$$\begin{aligned} g_{\bar{x},i}=\frac{g_{i}-g_{i-1}}{h},\text {\ }g_{x,i}=\frac{g_{i+1}-g_{i}}{h },\text {\ }g_{\overset{0}{x},i}=\frac{g_{i+1}-g_{i-1}}{2h},\text { }g_{ \bar{x}x,i}=\frac{g_{i+1}-2g_{i}+g_{i-1}}{h^2} \end{aligned}$$

and

$$\begin{aligned} \left\| g\right\| _{\infty }\equiv \left\| g\right\| _{\infty , \bar{\omega }_{N}}:=\underset{0\le i\le N}{\max }\left| g_{i}\right| ,\text { }\left\| g\right\| _{1,\omega _{h}}=h\sum _{i=1}^{N-1}\left| g_{i}\right| ,\text { }\widetilde{K} =\max _{0\le i\le N}{\sum _{j=1}^{N}h}\left| {K_{ij}}\right| . \end{aligned}$$

To obtain difference approximation for (1.1) and (1.2), we start with the following identity:

$$\begin{aligned}&h^{-1}\int _{x_{i-1}}^{x_{i+1}}{Lu(x)\varphi _{i}(x)\mathrm{{d}}x}\nonumber \\&\quad =h^{-1}\int _{x_{i-1}}^{x_{i+1}}[{f}\left( x\right) +\lambda \int _{0}^{l}K(x,t)u(t)\mathrm{{d}}t]{\varphi _{i}(x)\mathrm{{d}}x},\text { }1\le i\le N-1 \end{aligned}$$
(3.1)

with the basis functions:

$$\begin{aligned} \varphi _{i}(x)=\left\{ \begin{array}{cc} \varphi _{i}^{(1)}(x):=\frac{e^{\frac{a_{i}\left( x-x_{i-1}\right) }{ \varepsilon }}-1}{e^{\frac{a_{i}h}{\varepsilon }}-1}, &{} x_{i-1}<x<x_{i}, \\ \varphi _{i}^{(2)}(x):=\frac{1-e^{-\frac{a_{i}\left( x_{i+1}-x\right) }{ \varepsilon }}}{1-e^{-\frac{a_{i}h}{\varepsilon }}}, &{} x_{i}<x<x_{i+1}, \\ 0, &{} \text {otherwise,} \end{array} \right. \end{aligned}$$

where \(\varphi _{i}^{(1)}(x)\) and \(\varphi _{i}^{(2)}(x)\) are the solutions of the following problems, respectively:

$$\begin{aligned} \varepsilon \varphi _{i}^{\prime \prime }-a_{i}\varphi _{i}^{\prime }= & {} 0, \text { }x_{i-1}<x<x_{i}, \\ \varphi _{i}\left( x_{i-1}\right)= & {} 0,\text { }\varphi _{i}\left( x_{i}\right) =1, \end{aligned}$$

and

$$\begin{aligned} \varepsilon \varphi _{i}^{\prime \prime }-a_{i}\varphi _{i}^{\prime }= & {} 0, \text { }x_{i}<x<x_{i+1}, \\ \varphi _{i}\left( x_{i}\right)= & {} 1,\text { }\varphi _{i}\left( x_{i+1}\right) =0. \end{aligned}$$

If we rearrange (3.1) (except for the integral term containing kernel function), we get:

$$\begin{aligned}&\varepsilon h^{-1}\int _{x_{i-1}}^{x_{i+1}}{u}^{\prime \prime }{(x)\varphi _{i}(x)\mathrm{{d}}x+}h^{-1}\int _{x_{i-1}}^{x_{i+1}}{a(x)u}^{\prime }\left( x\right) { \varphi _{i}(x)\mathrm{{d}}x}\\&\quad =h^{-1}\int _{x_{i-1}}^{x_{i+1}}f\left( x\right) {\varphi } _{i}{(x)}\mathrm{{d}}x,\text { }1\le i\le N-1. \end{aligned}$$

Furthermore, using the integration by parts to the first integral term on the left side of this equation, we get:

$$\begin{aligned}&-\varepsilon h^{-1}\int _{x_{i-1}}^{x_{i+1}}{\varphi }_{i}^{\prime }{(x)u} ^{\prime }\left( x\right) {\mathrm{{d}}x+}a_{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}{\varphi } _{i}{(x)u}^{\prime }\left( x\right) {\mathrm{{d}}x}\nonumber \\&\quad {=f}_{i}-R_{i}^{(1)}-R_{i}^{(2)},\text { }1\le i\le N-1, \end{aligned}$$
(3.2)

where

$$\begin{aligned}&R_{i}^{(1)}=h^{-1}\int _{x_{i-1}}^{x_{i+1}}\left[ a\left( x\right) -a\left( x_{i}\right) \right] {\varphi }_{i}{(x)u}^{\prime }\left( x\right) {\mathrm{{d}}x}, \end{aligned}$$
(3.3)
$$\begin{aligned}&R_{i}^{(2)}=h^{-1}\int _{x_{i-1}}^{x_{i+1}}\left[ f\left( x_{i}\right) -f\left( x\right) \right] {\varphi }_{i}{(x)}\mathrm{{d}}x. \end{aligned}$$
(3.4)

By considering the interpolating quadrature rules (2.1) and (2.2) in Amiraliyev and Mamedov (1995) with weight functions \(\varphi _{i}(x)\) on subintervals \(\left( x_{i-1},x_{i+1}\right) \) in (3.2), we obtain the following precise relation:

$$\begin{aligned}&-\varepsilon h^{-1}\int _{x_{i-1}}^{x_{i+1}}{\varphi }_{i}^{\prime }{(x)u} ^{\prime }\left( x\right) {\mathrm{{d}}x+}a_{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}{\varphi } _{i}{(x)u}^{\prime }\left( x\right) {\mathrm{{d}}x}\nonumber \\&\quad =-\varepsilon h^{-1}u_{\bar{x},i}+a_{i}h^{-1}u_{\bar{x},i} \int _{x_{i-1}}^{x_{i}}{\varphi }_{i}^{\left( 1\right) }{(x)\mathrm{{d}}x}\nonumber \\&\qquad {+}a_{i}h^{-1}u_{x,i}\int _{x_{i}}^{x_{i+1}}{\varphi }_{i}^{\left( 2\right) }{ (x)\mathrm{{d}}x+}\varepsilon h^{-1}u_{x,i}\nonumber \\&\quad =\varepsilon u_{\bar{x}x,i}+a_{i}(\chi _{i}^{\left( 1\right) }u_{\bar{x} ,i}+\chi _{i}^{\left( 2\right) }u_{x,i}), \end{aligned}$$
(3.5)

where

$$\begin{aligned}&\chi _{i}^{\left( 1\right) }=h^{-1}\int _{x_{i-1}}^{x_{i}}{\varphi } _{i}^{\left( 1\right) }{(x)\mathrm{{d}}x=}\frac{\varepsilon }{ha_{i}}-\frac{1}{e^{\frac{ a_{i}h}{\varepsilon }}-1},\\&\chi _{i}^{\left( 2\right) }=h^{-1}\int _{x_{i}}^{x_{i+1}}{\varphi } _{i}^{\left( 2\right) }{(x)\mathrm{{d}}x=}\frac{1}{1-e^{-\frac{a_{i}h}{\varepsilon }}}- \frac{\varepsilon }{ha_{i}}, \end{aligned}$$

which, clearly, satisfy:

$$\begin{aligned} h^{-1}\int _{x_{i-1}}^{x_{i+1}}{\varphi _{i}(x)}\mathrm{{d}}x=1. \end{aligned}$$

Upon substituting

$$\begin{aligned} u_{\bar{x},i}=u_{\overset{0}{x},i}-\frac{h}{2}u_{\bar{x}x,i},\text { \ } u_{x,i}=u_{\overset{0}{x},i}+\frac{h}{2}u_{\bar{x}x,i} \end{aligned}$$

into (3.5), we get:

$$\begin{aligned} \varepsilon u_{\bar{x}x,i}+a_{i}(\chi _{i}^{\left( 1\right) }u_{\bar{x} ,i}+\chi _{i}^{\left( 2\right) }u_{x,i})=\varepsilon \theta _{i}u_{\bar{x} x,i}+a_{i}u_{\overset{0}{x},i}, \end{aligned}$$
(3.6)

where

$$\begin{aligned} \theta _{i}=1+\frac{a_{i}h}{2\varepsilon }(\chi _{i}^{\left( 2\right) }-\chi _{i}^{\left( 1\right) })=\frac{a_{i}h}{2\varepsilon }\coth \left( \frac{a_{i}h}{ 2\varepsilon }\right) . \end{aligned}$$
(3.7)

Thus:

$$\begin{aligned}&\varepsilon h^{-1}\int _{x_{i-1}}^{x_{i+1}}{u}^{\prime \prime }{(x)\varphi _{i}(x)\mathrm{{d}}x+}h^{-1}\int _{x_{i-1}}^{x_{i+1}}{a(x)u}^{\prime }\left( x\right) { \varphi _{i}(x)\mathrm{{d}}x}\nonumber \\&\quad =\varepsilon \theta _{i}u_{\bar{x}x,i}+a_{i}u_{\overset{0}{ x},i}-R_{i}^{(1)}. \end{aligned}$$
(3.8)

On the other hand, for integral term involving kernel function, we have from (3.1):

$$\begin{aligned} h^{-1}\lambda \int _{x_{i-1}}^{x_{i+1}}\mathrm{{d}}x{\varphi _{i}(x)} \int _{0}^{l}K(x,t)u(t)\mathrm{{d}}t=\lambda \int _{0}^{l}K(x_{i},t)u(t)\mathrm{{d}}t-R_{i}^{(3)} \end{aligned}$$

with remainder term:

$$\begin{aligned} R_{i}^{(3)}=h^{-1}\lambda \int _{x_{i-1}}^{x_{i+1}}\mathrm{{d}}x{\varphi _{i}(x)} \int _{x_{i-1}}^{x_{i+1}}T_{0}(\xi -x)\left( \int _{0}^{l}\frac{\partial }{ \partial \xi }K(\xi ,t)u(t)\mathrm{{d}}t\right) \mathrm{{d}}\xi \end{aligned}$$
(3.9)

and \(T_{0}(x)=1,x>0;T_{0}(x)=0,x\le 0\). Further using the composite right side rectangle rule, we obtain:

$$\begin{aligned}&\lambda \int _{0}^{l}K(x_{i},t)u(t)\mathrm{{d}}t=\lambda h\sum _{j=1}^{N}K_{ij}u_{j}-R_{i}^{(4)} \end{aligned}$$
(3.10)
$$\begin{aligned}&R_{i}^{(4)}=\lambda \sum _{j=1}^{N}\int _{x_{j-1}}^{x_{j}}(\xi -x_{j-1})\frac{ \partial }{\partial \xi }\left[ K(x_{i},\xi )u(\xi )\right] \mathrm{{d}}\xi . \end{aligned}$$
(3.11)

In the consequence, from (3.2), (3.8), and (3.10), it follows the relation:

$$\begin{aligned} \ell u_{i}:=\varepsilon \theta _{i}u_{\bar{x}x,i}+a_{i}u_{\overset{0}{x} ,i}=f_{i}+\lambda h\sum _{j=1}^{N}K_{ij}u_{j}-R_{i},\text { }1\le i\le N-1 \end{aligned}$$
(3.12)

with

$$\begin{aligned} R_{i}=R_{i}^{(1)}+R_{i}^{(2)}+R_{i}^{(3)}+R_{i}^{(4)}, \end{aligned}$$
(3.13)

where \(R_{i}^{(k)},\) (\(k=1,2,3,4\)) are determined by (3.3), (3.4), (3.9), and (3.11), respectively.

As a consequence of (3.12), we propose the following difference scheme for approximating the problem (1.1) and (1.2):

$$\begin{aligned}&\ell y_{i}:=\varepsilon \theta _{i}y_{\bar{x}x,i}+a_{i}y_{\overset{0}{x} ,i}=f_{i}+\lambda h\sum _{j=1}^{N}K_{ij}y_{j},\text { }1\le i\le N-1, \end{aligned}$$
(3.14)
$$\begin{aligned}&y_{0}=A,\text { }y_{N}=B, \end{aligned}$$
(3.15)

where \(\theta _{i}\) is given by (3.7).

4 Convergence analysis of the method

In this section, we analyze the convergence of our present method. We begin with the error function that is defined by \(z_{i}=y_{i}-u_{i},\) \(0\le i\le N.\) Thus, the error function \(z_{i}\) satisfies:

$$\begin{aligned}&\ell z_{i}:=\varepsilon \theta _{i}z_{\bar{x}x,i}+a_{i}z_{\overset{0}{x} ,i}=\lambda h\sum _{j=1}^{N}K_{ij}z_{j}+R_{i},\text { }1\le i\le N-1, \end{aligned}$$
(4.1)
$$\begin{aligned}&z_{0}=0,\text { }z_{N}=0. \end{aligned}$$
(4.2)

Lemma 2

Let \(a,f\in C^{1}(\bar{\varOmega })\) and \(K\in C_{1}^{1}(\bar{\varOmega }\times \bar{ \varOmega })\). Under the conditions of Lemma 1, the errors \({R}_{i}\) satisfy the following inequality:

$$\begin{aligned} {\left\| R\right\| _{1,\omega _{h}}\le Ch.} \end{aligned}$$
(4.3)

Proof

We estimate \({R}_{i}^{(k)},\) \((k=1,2,3,4)\) separately. For \({R}_{i}^{(1)}\), using the mean value theorem for the functions in (3.3), we get:

$$\begin{aligned} \left| {R}_{i}^{(1)}\right| \le C\int _{x_{i-1}}^{x_{i+1}}\left| {u}^{\prime }(x)\right| \left| {\varphi }_{i}{(x)}\right| {\mathrm{{d}}x.} \end{aligned}$$
(4.4)

Taking into consideration \(0<{\varphi }_{i}{(x)}\le 1\) and (2.2) in (4.4), we obtain:

$$\begin{aligned} \left\| {R}^{(1)}\right\| _{1,\omega _{h}}\le & {} Ch\sum _{i=1}^{N-1}\int _{x_{i-1}}^{x_{i+1}}\left| {u}^{\prime }(x)\right| \mathrm{{d}}x \nonumber \\\le & {} Ch\int _{0}^{l}\left| {u}^{\prime }(x)\right| v \nonumber \\\le & {} Ch\int _{0}^{l}(1+\frac{1}{\varepsilon }e^{-\frac{\alpha x}{ \varepsilon }})\mathrm{{d}}x \nonumber \\\le & {} Ch(l+\alpha ^{-1}(1-e^{-\frac{\alpha l}{\varepsilon }})). \end{aligned}$$
(4.5)

For \({R}_{i}^{(2)}\) in (3.4), we analogously have:

$$\begin{aligned} \left| {R}_{i}^{(2)}\right| \le C\int _{x_{i-1}}^{x_{i+1}}\left| {\varphi }_{i}{(x)}\right| \mathrm{{d}}x. \end{aligned}$$

Therefore:

$$\begin{aligned} \left\| {R}^{(2)}\right\| _{1,\omega _{h}}\le Ch. \end{aligned}$$
(4.6)

For \(R_{i}^{(3)}\) in (3.9), we get:

$$\begin{aligned} \left| R_{i}^{(3)}\right| \le h^{-1}\left| \lambda \right| \int _{x_{i-1}}^{x_{i+1}}\mathrm{{d}}x{\varphi _{i}(x)}\int _{x_{i-1}}^{x_{i+1}}\left( \int _{0}^{l}\left| \frac{\partial }{\partial \xi }K(\xi ,t)\right| \left| u(t)\right| \mathrm{{d}}t\right) \mathrm{{d}}\xi . \end{aligned}$$

Due to \(h^{-1}\int _{x_{i-1}}^{x_{i+1}}\mathrm{{d}}x{\varphi _{i}(x)=1}\), we have:

$$\begin{aligned} \left| R_{i}^{(3)}\right| \le \left| \lambda \right| \int _{x_{i-1}}^{x_{i+1}}\left( \int _{0}^{l}\left| \frac{\partial }{ \partial \xi }K(\xi ,t)\right| \left| u(t)\right| \mathrm{{d}}t\right) \mathrm{{d}}\xi . \end{aligned}$$

Since \(\left| \frac{\partial K(x,t)}{\partial x}\right| \le C\) and \( \left| u\right| \le C_{0}\), we have:

$$\begin{aligned} \left\| {R}^{(3)}\right\| _{1,\omega _{h}}\le & {} Ch\sum _{i=1}^{N-1}\int _{x_{i-1}}^{x_{i+1}}\left( \int _{0}^{l}\left| \frac{ \partial }{\partial \xi }K(\xi ,t)\right| \left| u(t)\right| \mathrm{{d}}t\right) \mathrm{{d}}\xi \nonumber \\\le & {} Ch\sum _{i=1}^{N-1}(x_{i+1}-x_{i-1})=2Ch^{2}(N-1)\le Ch. \end{aligned}$$
(4.7)

Finally, for \(R_{i}^{(4)}\), from (3.11), we get:

$$\begin{aligned} \left| R_{i}^{(4)}\right|\le & {} \left| \lambda \right| \sum _{j=1}^{N}\int _{x_{j-1}}^{x_{j}}(\xi -x_{j-1})\left| \frac{ \partial }{\partial \xi }\left[ K(x_{i},\xi )u(\xi )\right] \right| \mathrm{{d}}\xi \\\le & {} \left| \lambda \right| h\int _{0}^{l}\left| \frac{\partial }{\partial \xi }\left[ K(x_{i},\xi )u(\xi )\right] \right| \mathrm{{d}}\xi \\\le & {} \left| \lambda \right| h\int _{0}^{l}\left[ \left| \frac{ \partial K(x_{i},\xi )}{\partial \xi }\right| \left| u(\xi )\right| +\left| K(x_{i},\xi )\right| \left| u^{\prime }(\xi )\right| \right] \mathrm{{d}}\xi . \end{aligned}$$

Since \(\left| \frac{\partial K(x,t)}{\partial t}\right| \le C,\) \( \left| u\right| \le C_{0}\) and using (2.2), we have:

$$\begin{aligned} \left| R_{i}^{(4)}\right|\le & {} C\left| \lambda \right| h\int _{0}^{l}\left( 1+\frac{1}{\varepsilon }e^{-\frac{\alpha \xi }{\varepsilon } }\right) \mathrm{{d}}\xi \\\le & {} C\left| \lambda \right| h[l+\alpha ^{-1}(1-e^{-\frac{\alpha l }{\varepsilon }})]. \end{aligned}$$

Consequently:

$$\begin{aligned} \left\| {R}^{(4)}\right\| _{1,\omega _{h}}\le Ch. \end{aligned}$$
(4.8)

Thus, taking into account (4.5) and (4.8) in (3.13), we obtain (4.3). \(\square \)

Lemma 3

Let the error function z be the solution of the problem (4.1) and (4.2) and \(\left| \lambda \right| <\alpha /(\widetilde{K}l).\) Then, the following inequality

$$\begin{aligned} \left\| z\right\| _{\infty ,\bar{\omega }_{N}}\le C\left\| {R} \right\| _{1,\omega _{h}} \end{aligned}$$
(4.9)

holds.

Proof

Here, we will use the discrete Green’s function \(G^{h}(x_{i},\xi _{j})\) for the operator:

$$\begin{aligned}&L^{h}z_{i}:=-\varepsilon \theta _{i}z_{\bar{x}x,i}-a_{i}z_{\overset{0}{x} ,i},\ 1\le i\le N-1,\\&z_{0}=z_{N}=0. \end{aligned}$$

Namely, the \(G^{h}(x_{i},\xi _{j})\) is defined as a function of \(x_{i}\) for fixed \(\xi _{j}\) :

$$\begin{aligned}&L^{h}G^{h}(x_{i},\xi _{j})=\delta ^{h}(x_{i},\xi _{j}),\ x_{i}\in \omega _{N},\ \xi _{j}\in \omega _{N},\\&G^{h}(0,\xi _{j})=G^{h}(l,\xi _{j}),\ \xi _{j}\in \omega _{N}, \end{aligned}$$

where \(\delta ^{h}(x_{i},\xi _{j})=h^{-1}\delta _{ij}\) and \(\delta _{ij}\) is the Kronecker delta. For the solution of problem (4.1) and (4.2), the following relation can be written by using the Green’s function:

$$\begin{aligned} z_{i}=\sum \limits _{k=1}^{N-1}{hG^{h}(x_{i},\xi _{k})(\lambda h\sum _{j=1}^{N}K_{kj}z_{j}-R_{k})},\ x_{i}\in \omega _{N}. \end{aligned}$$
(4.10)

It can be shown in a manner similar to Andreev (2002) that \(0\le G^{h}(x_{i},\xi _{k})\le \alpha ^{-1}\). Thus, from (4.10), we can write the following estimate:

$$\begin{aligned} \left\| z\right\| _{\infty ,\omega _{N}}\le & {} \alpha ^{-1}\left\{ \left\| z\right\| _{\infty ,\omega _{N}}\sum \limits _{k=1}^{N-1}\left( \left| {\lambda }\right| {h}^{2}{ \sum _{j=1}^{N}}\left| {K_{kj}}\right| \right) +\left\| R\right\| _{1}\right\} \\\le & {} \alpha ^{-1}\left\{ \left\| z\right\| _{\infty ,\omega _{N}}\widetilde{K}\sum \limits _{k=1}^{N-1}\left| {\lambda }\right| h+\left\| R\right\| _{1}\right\} \\\le & {} \alpha ^{-1}\left\{ \left\| z\right\| _{\infty ,\omega _{N}}\left| {\lambda }\right| \widetilde{K}l+\left\| R\right\| _{1}\right\} , \end{aligned}$$

which implies validity of (4.9). \(\square \)

Finally, we give the main result on \(\varepsilon \)-uniform convergence of the presented method for solving the problem (1.1) and (1.2).

Theorem 1

Assume that \(a,f\in C^{1}(\bar{\varOmega })\) and \(K\in C_{1}^{1}(\bar{\varOmega } \times \bar{\varOmega })\). If u is the solution of (1.1) and (1.2) and y is the solution of (3.14) and (3.15), then the following \( \varepsilon \)-uniform estimate satisfies:

$$\begin{aligned} \left\| y-u\right\| _{\infty ,\bar{\omega }_{N}}\le Ch. \end{aligned}$$
(4.11)

Proof

Combining the previous lemmas, we immediately have (4.11). \(\square \)

5 Algorithm and numerical results

In this section, we suggest the following iterative technique for solving problem (3.14) and (3.15). In addition, we consider an example of problem (1.1) and (1.2) to demonstrate the effectiveness and accuracy of the our present method.

Table 1 The resulting errors \(e_{\varepsilon }^{N}\) and \({e^{N}}\), and convergence rates \(p^{N}\) for Example 1
Full size table
Fig. 1
figure 1

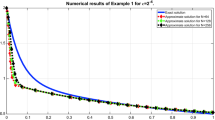
Numerical results of Example 1 for \(\varepsilon =2^{-4}\)

Full size image
Fig. 2
figure 2

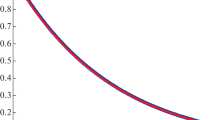
Numerical results of Example 1 for \(\varepsilon =2^{-20}\)

Full size image

At first, if we reformulate (3.14), then we can write:

$$\begin{aligned}&\varepsilon \theta _{i}y_{\bar{x}x,i}^{(n)}+a_{i}y_{\overset{0}{x} ,i}^{(n)}=f_{i}+\lambda h\sum _{j=1}^{N}K_{ij}y_{j}^{(n-1)},\text { }1\le i\le N-1, \end{aligned}$$
(5.1)
$$\begin{aligned}&y_{0}^{(n)}=A,\text { }y_{N}^{(n)}=B, \end{aligned}$$
(5.2)

\(n=1,2,\ldots \), \(y_{i}^{(0)}\) (\(1\le i\le N-1\)) are given and stopping criterion is:

$$\begin{aligned} \max _{i}\left| y_{i}^{(n)}-y_{i}^{(n-1)}\right| \le 10^{-5}. \end{aligned}$$

For the iterative error \(z_{i}^{(n)}=y_{i}^{(n)}-y_{i}\) from (3.14) and (3.15) and (5.1) and (5.2), we have:

$$\begin{aligned}&\varepsilon \theta _{i}z_{\bar{x}x,i}^{(n)}+a_{i}z_{\overset{0}{x} ,i}^{(n)}=\lambda h\sum _{j=1}^{N}K_{ij}z_{j}^{(n-1)},\text { }1\le i\le N-1,\\&z_{0}^{(n)}=0,\text { }z_{N}^{(n)}=0. \end{aligned}$$

According to maximum principle:

$$\begin{aligned} \left\| z^{(n)}\right\| _{\infty }\le & {} \left| \lambda \right| h\sum _{j=1}^{N}\left| K_{ij}\right| \left| z_{j}^{(n-1)}\right| \\\le & {} q\left\| z^{(n-1)}\right\| _{\infty } \end{aligned}$$

with

$$\begin{aligned} q=\left| \lambda \right| h\max _{0\le i\le N}{\sum _{j=1}^{N}} \left| {K_{ij}}\right| . \end{aligned}$$

For \(\left| \lambda \right| <1/\widetilde{K}\), the iterative process is evidently convergent.

Example 1

We consider the following test problem:

$$\begin{aligned}&\varepsilon u^{\prime \prime }(x)+2u^{\prime }(x)=e^{x}-\frac{1}{4} \int _{0}^{1}e^{x-t}u(t)\mathrm{{d}}t,\text { }0<x<1,\\&u(0)=0,\text { }u\left( 1\right) =1. \end{aligned}$$

The exact solution of the problem is given by:

$$\begin{aligned} u(x)=\frac{d_{1}-1}{2+\varepsilon }(1-e^{x})+d_{2}\frac{1-e^{-\frac{2x}{ \varepsilon }}}{1-e^{-\frac{2}{\varepsilon }}}, \end{aligned}$$

where

$$\begin{aligned}&d_{1}=\frac{(2+\varepsilon )(e^{-\frac{2}{\varepsilon }}-1)+(3+\varepsilon -e)(2-2e+\varepsilon (1-e^{-\frac{2}{\varepsilon }}))}{4e(2+\varepsilon )^{2}(e^{-\frac{2}{\varepsilon }}-1)-(4e+\varepsilon e-2e^{2})+(2+\varepsilon e)e^{-\frac{2}{\varepsilon }}},\\&d_{2}=1+\frac{(d_{1}-1)(e-1)}{2+\varepsilon }. \end{aligned}$$

We define the exact error \(e_{\varepsilon }^{N}\) and the computed parameter-uniform maximum pointwise error \(e^{N}\) as follows:

$$\begin{aligned} e_{\varepsilon }^{N}=\left\| {y-u}\right\| _{\infty ,\bar{\omega }},\ e^{N}=\max _{\varepsilon }e_{\varepsilon }^{N}, \end{aligned}$$

where y is the numerical approximation to u for various values of \( \varepsilon \) and N. We also define the computed parameter-uniform rate of convergence to be:

$$\begin{aligned} p^{N}=\log _{2}\left( {e^{N}/e^{2N}}\right) . \end{aligned}$$

The values of \(\varepsilon \) for which we solve the test problem are \( \varepsilon =2^{-4i}\), \(i=0,1,\ldots ,6\). Furthermore, the resulting errors and the corresponding numbers \(p^{N}\) obtained by taking \(y_{i}^{(0)}=x_{i}^{2}\) for the test problem are listed in Table 1.

6 Conclusion

We presented a new approach to solve the singularly perturbed problem for a convection–diffusion Fredholm integro-differential equation. The approach was based on an exponentially fitted difference scheme on a uniform mesh. As a consequence, we proved that our method is the first order convergent with respect to the perturbation parameter in the discrete maximum norm. Moreover, after only a few iterations, the computational errors and the rates of convergence for the test problem were presented for different values of the perturbation parameter \(\varepsilon \) and N in Table 1. Also, the graphs of the numerical solution of the test problem for different values of perturbation parameter were plotted in Figs. 1 and 2. When the numerical results in both Table 1 and Figs. 1 and 2 were examined, the results showed that the presented method was effective and accuracy. We point out that the presented method in this paper can be extended to other type of boundary-value problems such as nonlinear SPFIDEs and reaction diffusion SPFIDEs.