Numerical scheme for singularly perturbed Fredholm integro-differential equations with non-local boundary conditions

Abstract

This paper solves a class of Fredholm integro-differential equations involving a small parameter with integral boundary conditions numerically. The solution to the problem possesses boundary layers at both end boundaries. A central difference scheme is used for approximating the derivatives. In contrast, the trapezoidal rule is used for the integral term, provided an appropriately adapted mesh is considered, namely Shishkin and Bakhvalov–Shishkin meshes. The proposed numerical method presents a uniform second-order convergence rate regardless of the perturbation parameter. Furthermore, using a post-processing technique, we have significantly improved the convergence from second to fourth order. The effectiveness of the proposed approach is validated through some numerical examples.

1 Introduction

In many scientific domains, including engineering, biology, physics, chemistry, potential theory, electrostatics, finance, theory of elasticity, fluid dynamics, astronomy, economics, heat-mass transfer and other subjects, Fredholm integro-differential equations (FIDEs) are fundamental (see, e.g., Brunner 2018; Jalilian and Tahernezhad 2020; Saadatmandi and Dehghan 2010). However, obtaining precise solutions to these problems is highly challenging. As a result, numerical methods play a significant role in solving these problems, as in Brunner (2018), Chen et al. (2019), Chen et al. (2020), Jalilian and Tahernezhad (2020), Saadatmandi and Dehghan (2010). As an example, we show the convection-diffusion parabolic partial integro-differential equation Fahim and Araghi (2018); Siddiqi and Arshed (2013) given by:

$$\begin{aligned}{} & {} u_{t}(s,t)+cu_{s}(s,t)-d u_{ss}(s,t)\\ {}{} & {} \quad =\Bigg (\displaystyle \int _{0}^tK(q-t)u(s,q)dq\Bigg )+f(s,t), ~s\in [a,~b], ~t>0, \end{aligned}$$

with $u(s,0)=g(s),~~s\in (a,b)$ and $y(a,t)=g_1(t),~y(b,t)=g_2(t),~ t>0,$ where the integral term is known as memory term and g(s), $g_1(t),~g_2(t)$ are known functions.

Suppose the most excellent derivative term in a differential equations (DEs) is multiplied by a tiny parameter $\varepsilon \in (0,1)$. In that case, this parameter is said to be a singular perturbation parameter and the DEs is called a singularly perturbed differential equations (SPDEs). Due to the presence of the perturbation parameter, layers occur on the boundaries, named boundary layers. These SPDEs have a lot of applications in biology, ecology, physical sciences and other areas. For example, the one-dimensional groundwater flow and solute transport problem is governed by the following equation:

$$\begin{aligned} y_{t}(s,t)=\varepsilon z_{ss}(s,t)-\upsilon y_{x}(s,t)-\lambda y(s,t), ~s>0, ~t>0. \end{aligned}$$

It explains how water and solutes flow through the unsaturated zone (De Marsily 1986), where the time is t, the horizontal distance is s and both quantities are positive and measured to the right of the soil’s center.

Furthermore, polymer rheology, population dynamics and mathematical models of glucose tolerance all use singularly perturbed integro-differential equations (SPIDEs). For more applications of SPIDEs, we can cite Lodge et al. Lodge et al. (1978), De Gaetano and Arino De Gaetano and Arino (2000), Brunner and van der Houwen Brunner and van der (1986) and Jerri Jerri (1999). Mainly, Nefedov and Nikitin’s Nefedov and Nikitin (2007) optimum control issues use the singularly perturbed Fredholm integral equations (SPFIDEs). There have been some asymptotic solutions to this issue mentioned in Lange and Smith (1993), Nefedov and Nikitin (2000, 2007)) For instance, in Grimmer and Liu (1994) a class of singularly perturbed partial integro-differential equations in viscoelasticity is given as

$$\begin{aligned} \rho u_{tt}^{\rho }(t,x)=\varepsilon u_{xx}^{\rho }(t,x)+\displaystyle \int _{-\infty }^{t}a(t-s)u_{ss}^{\rho }(s,x)ds+\rho g(t,x)+f(x). \end{aligned}$$

However, the theory and approximate numerical solutions of SPIDEs are still at an initial stage. In recent years, various numerical methods have been proposed for first-order SPIDEs without non-local conditions on uniform and non-uniform meshes, as in Amiraliyev et al. (2018), Amiraliyev and Sevgin (2006), Cakır and Gunes (2022), De Bonis et al. (2021), De Bonis et al. (2023), Durmaz et al. (2022), Kudu et al. (2016), Mennouni (2020). In Cimen and Cakir (2021), Durmaz and Amiraliyev (2021), Durmaz et al. (2022), Durmaz et al. (2022), Durmaz et al. (2022), second-order SPIDEs without non-local boundary conditions on Shishkin meshes are discussed. In Sekar (2022), Sekar and Tamilselvan (2019), Sekar et al. (2021), Sekar and Tamilselvan (2019) various problems on singularly perturbed delay differential equations with integral boundary conditions are considered. To our knowledge, numerical methods for first-order SPFIDEs with initial and boundary conditions (IBCs) on Shishkin meshes have been discussed only in Durmaz et al. (2022). Motivated by the above research, we present an effective numerical approach for second-order SPIDEs with IBCs on Shishkin-type meshes(Shishkin and Bakhvalov-Shishkin meshes). The main aim of this article is to solve numerically a singularly perturbed Fredholm integro-differential equation with integral boundary conditions given by

$$\begin{aligned} \begin{array}{ll} Lu:=L_{1}u+L_{2} u =f(x),~x\in \Omega =(0,1),\\ \mathcal {K}u(0):=u(0)-\varepsilon \int \nolimits _0^1g_1(x)u(x)dx=l,\\ \mathcal {K}u(1):=u(1)-\varepsilon \int \nolimits _0^1g_2(x)u(x)dx=r, \end{array} \end{aligned}$$

(1.1)

where $L_{1}u= -\varepsilon u''+a(x)u$, $L_{2} u= -\lambda \displaystyle \int \nolimits _{0}^{1} K(x,s)u(s)ds$ and $\gamma >K(x,s)\in L^{2}[0,1]$. It is assumed that $a(x){\ge }\beta> \lambda \gamma >0,$ where ${\lambda }$ is a positive constant and $\int _0^1g_i(x)dx<1,i=1,2$, $g_i(x)$ are non negative sufficiently smooth functions satisfying appropriate regularity constraints.

The task will be addressed using a central difference scheme for approximating the second-order derivative and the composite trapezoidal rule for approximating an integral part, considering Shiskin-type meshes. The proposed method provides an optimal second-order rate of convergence $\left( CN^{-2}\right)$, but lately, using the extrapolation technique, a fourth order rate of convergence $\left( CN^{-4}\right)$ will be obtained.

The article is organized as follows: In Sect. 2, we present some issues concerning the exact solution. Section 3 constructs the Shishkin-type mesh and the computational analysis. Section 4 introduces the Richardson extrapolation, its application and the corresponding convergence analysis. Section 5 presents some numerical examples with graphs and tables to show the performance of the proposed method. Finally, Sect. 6 summarizes the article’s conclusions.

Along this work, we consider C to be any positive constant independent of $\varepsilon$. The standard supremum norm, $||\mathfrak {f}||_{\mathfrak {D}}=\displaystyle \sup _{y\in \mathfrak {D}}|\mathfrak {f}(y)|$, on a given domain $\mathfrak {D}$, will be used along the paper. If the domain is clear, we use only $||\mathfrak {f}||$.

2 Stability and bounds on the derivatives of the continuous solution

Theorem 2.1

Let $\Xi (x)$ be any function such that $\mathcal {K}\Xi (0)\ge 0$, $\mathcal {K}\Xi (1)\ge 0$ and $L\Xi (x)\ge 0,~ \forall x\in \Omega$, where $\mathcal {K}$ and the differential operator L are defined in (1.1). Then, it holds that $\Xi (x)\ge 0$, $\forall x\in \overline{\Omega }=[0,1].$

Proof

Consider the function $t(x)=1+x$, which is non negative for $x \in \overline{\Omega }$. Let denote

$$\begin{aligned} \mu =\max \Big \{\frac{-\Xi (x)}{t(x)}:x\in \overline{\Omega }\Big \}. \end{aligned}$$

There exists $x_0\in \overline{\Omega }$ such that $\Xi (x_0)+\mu t(x_0)=0$ and thus $\Xi (x)+\mu t(x)\ge 0,\forall x\in \overline{\Omega }$. As a result, the function $(\Xi +\mu t)$ attains its minimum at $x=x_0$. We proceed by contradiction. If we assume that the conclusion is false, then it is $\mu >0$. Now, consider two cases:

Case (i): $x_0=0$ or $x_0=1$;

Note that $\mathcal {K}(\Xi +\mu t)(x_0)= \mathcal {K}\Xi (x_0)+\mu \mathcal {K}t(x_0) >0$. On the other hand, it is

$$\begin{aligned} \mathcal {K}(\Xi +\mu t)(x_0)= & {} (\Xi +\mu t)(x_0)-\varepsilon \int \limits _0^1 g_1(x)(\Xi +\mu t)(x)dx,\\= & {} -\varepsilon \int \limits _0^1 g_1(x)(\Xi +\mu t)(x)dx \le 0, \end{aligned}$$

which is a contradiction.

Case (ii): $x_0\in \Omega .$

According to the hypothesis, it is $L\Xi (x_0)\ge 0$. On the other hand, it is

$$\begin{aligned} {L_1}(\Xi +\mu t)(x_0)= & {} -\varepsilon (\Xi +\mu t)''(x_0)+a(x_0)(\Xi +\mu t)(x_0),\\= & {} -\varepsilon (\Xi +\mu t)''(x_0)\le 0,\\ {L_2}(\Xi +\mu t)(x_0)= & {} -\lambda \int _0^1 K(x,s) (\Xi +\mu t)(s)ds\le 0, \end{aligned}$$

and thus, we arrive at a contradiction.

Theorem 2.2

(Stability Result)

Let u(x) be the solution of problem (1.1). Then, the following bounds of the solution and its derivatives hold:

• (i) $||u|| \le C \max _{x\in \Omega } \Big \{\mathcal {K}u(0),\mathcal {K}u(1),Lu(x)\Big \}.$

• (ii) $||u^{(k)}|| \le C (1+\varepsilon ^{-k/2}), ~\text{ for }~k=1,2,3,4.$

Proof

Proof is available in Miller et al. (1996, Chapter 6, p. 46).

Lemma 2.3

Let consider the decomposition of the solution u(x) of problem (1.1) in the form $u=v+w_{L}+w_{R}$, where v is smooth and $w_{L}, w_{R}$ are singular components. Then, it holds for $k=0,1,2,3,4$ that

• (i) $|v^{(k)}(x)| \le C (1+\varepsilon ^{-(k-2)/2})$.

• (ii) $|w^{(k)}_{L}(x)| \le C \varepsilon ^{-k/2} e^{-x\sqrt{\beta /\varepsilon } }$.

• (iii) $|w^{(k)}_{R}(x)| \le C \varepsilon ^{-k/2} e^{-(1-x)\sqrt{\beta /\varepsilon } }.$

Proof

(i) The proof is available in Miller et al. (1996, Chapter 6, p 48).

(ii) Consider $\psi ^{\pm }(x) =C e^{-x\sqrt{\beta /\varepsilon } }\pm w_{L}(x),$ then

$$\begin{aligned} \mathcal {K}\psi ^{\pm }(0)= & {} C\pm w_L(0)-\varepsilon \int _0^1 g_1(x) (C e^{-x\sqrt{\beta /\varepsilon } }\pm w_{L}(x)) dx,\\= & {} C(1-\varepsilon \int _{0}^1 g_1(x) e^{-x\sqrt{\beta /\varepsilon } } dx)\pm \mathcal {K} w_L(0)\ge 0.\\ \mathcal {K}\psi ^{\pm }(1)= & {} C\pm w_L(1)-\varepsilon \int _0^1 g_2(x) (C e^{-x\sqrt{\beta /\varepsilon } }\pm w_{L}(x)) dx,\\= & {} C(1-\varepsilon \int _{0}^1 g_2(x) e^{-x\sqrt{\beta /\varepsilon } } dx)\pm \mathcal {K} w_L(1)\ge 0.\\ L\psi ^{\pm }(x)= & {} Ce^{-x\sqrt{\beta /\varepsilon } }\Big [\varepsilon (-\beta /\varepsilon )+a(x)\Big ] - \lambda \displaystyle \int _{0}^{1}CK(x,s)e^{-s\sqrt{\beta /\varepsilon }}ds \pm Lw_{L}(x),\\\ge & {} C e^{-x\sqrt{\beta /\varepsilon } }\Big [a(x)-\beta - \lambda \gamma \Big ] \ge 0. \end{aligned}$$

By Theorem 2.1 we have that $\psi ^{\pm }(x)\ge 0$ and thus

$$\begin{aligned} |w_{L}(x)|\le Ce^{-x\sqrt{\beta /\varepsilon } }. \end{aligned}$$

For the derivative bounds of regular component, the proof is the same as in Miller et al. (1996), resulting in

$$\begin{aligned} |w^{(k)}_{L}(x)|\le Ce^{-x\sqrt{\beta /\varepsilon } }\varepsilon ^{-k/2}. \end{aligned}$$

(iii) It can be proven similarly as in the previous case that

$$\begin{aligned} |w^{(k)}_{R}(x)| \le C \varepsilon ^{-k/2} e^{-(1-x)\sqrt{\beta /\varepsilon } }. \end{aligned}$$

3 Non-uniform meshes and analysis

3.1 Non-uniform meshes

3.2 Shishkin mesh (S-mesh)

The transition parameter $\sigma$ is defined as

$$\begin{aligned} \sigma =\min \Big \{\dfrac{1}{4},\dfrac{\sigma _0\sqrt{\varepsilon }}{\beta }\log (N)\Big \}, \end{aligned}$$

where $\sigma _0>0$ is an user choice parameter and it is assumed that $\sqrt{\varepsilon }\le N^{-1}$. More details about the S-mesh can be found in Miller et al. (1996); Shishkin and Shishkina (2009). The mesh points are defined as $\mathcal {G}_{x}=\{x_1,x_2,\ldots , x_n\} \in [0, 1]$, where

$$\begin{aligned} x_i =\left\{ \begin{array}{ll} iH_1,&{}\quad \text{ for }\quad i=0,\ldots ,\frac{N}{4},\\ \sigma +\Bigg (\frac{i}{N}-\frac{1}{4}\Bigg )H_2,&{}\quad \text{ for }\quad i=\frac{N}{4}+1,\ldots , \frac{3N}{4},\\ 1-(N-i)H_1,&{}\quad \text{ for }\quad i=\frac{3N}{4}+1,\ldots , N,\\ \end{array}\right. \end{aligned}$$

with $H_1=\frac{4\sigma }{N}$, $H_2=\frac{2(1-2\sigma )}{N}$. The step sizes in the space variable are given by $h_i=x_i-x_{i-1},$ for $i=1,\ldots ,N$.

3.3 Bakhvalov–Shishkin mesh (B–S-mesh)

For a detailed construction of the B–S mesh one can refer to Liu and Yang (2022). The mesh points are

$$\begin{aligned} x_i =\left\{ \begin{array}{ll} \dfrac{\sigma _0\sqrt{\varepsilon }}{\beta }\ln \Big (\vartheta (\frac{i}{N})+1\Big ),&{}\quad \text{ for }\quad i=0,\ldots , N/4,\\ \sigma _1+\Big (\dfrac{4i}{N}-1\Big )\big (1/2-\sigma _1\big ),&{}\quad \text{ for } \quad i=\dfrac{N}{4}+1, \ldots , \dfrac{3N}{4},\\ 1+\dfrac{\sigma _0\sqrt{\varepsilon }}{\beta }\ln \Big (\vartheta \left( 1-\frac{i}{N}\right) +1\Big ),&{}\quad \text{ for } \quad i =\dfrac{3N}{4}+1, \dots , N, \end{array}\right. \end{aligned}$$

where, $\sigma _1=\min \Bigg \{\dfrac{1}{4},\dfrac{\sigma _0\sqrt{\varepsilon }}{\beta }\ln \min \{\varepsilon ^{-1},N\}\Bigg \}$ and $\vartheta =4\Big (\exp \big (-\beta \sigma _1/(\sigma _0\sqrt{\varepsilon })\big )-1\Big )$. The step sizes, in this case are denoted as in the previous case by $h_i=x_i-x_{i-1}$ for $i=1,\ldots , N$.

3.4 Numerical approach

Given a mesh function $\phi _i$, the backward, forward and center difference operators are defined as follows:

$$\begin{aligned} D^{+}_{x}\phi _{i} = \dfrac{\phi _{i+1}-\phi _{i}}{h_{i+1}}, \quad D^{-}_{x}\phi _{i} = \dfrac{\phi _{i}-\phi _{i-1}}{h_{i}}, \quad D^{0}_{x}\phi _{i} = \dfrac{\phi _{j+1}-\phi _{i-1}}{h_{i+1}+h_{i}}, \end{aligned}$$

respectively and the approximate second-order operator is given by

$$\begin{aligned} D^{+}_xD^{-}_x\phi _{i}= \dfrac{2}{h_{i}+h_{i+1}}\bigg (\dfrac{\phi _{i+1}-\phi _{i}}{h_{i+1}} - \dfrac{\phi _{i}-\phi _{i-1}}{h_{i}}\bigg ). \end{aligned}$$

where $\phi _{i}=\phi (x_i).$

We discretize problem (1.1) using the central difference scheme for the second order derivative and the trapezoidal method for the integral part.

The proposed numerical scheme is given as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \Big (L^{N}_{1}+L^{N}_{2}\Big )U_i=f_i, \text{ for }\quad i=1,\ldots , N-1,\\ \mathcal {K}^NU_{0}=U_{0}-\varepsilon \sum \limits _{i=1}^{N} \frac{g_{i-1}U{i-1}+g_iU_i}{2},\\ \mathcal {K}^NU_{N}=U_{N}-\varepsilon \sum \limits _{i=1}^{N} \frac{g_{i-1}U{i-1}+g_iU_i}{2}h_i, \end{array}\right. \end{aligned}$$

(3.1)

where,

$$\begin{aligned}{} & {} L^{N}_{1}U_i=-\varepsilon D^{+}_xD^{-}_xU_i+a_iU_i, ~~~ L^{N}_{2}U_i=-\lambda \displaystyle \sum _{j=0}^{N}\tau _j K_{i,j}U_j, \\{} & {} \tau _0=\frac{h_0}{2},~ \tau _j=\frac{h_j+h_{j+1}}{2},~~j=1,2,\ldots ,N-1,~\tau _N=\frac{h_N}{2}, \end{aligned}$$

$U_i=U(x_i)$ is the approximate solution to the exact solution of the problem (1.1), $a_i=a(x_i),~ f_i=f(x_i),~K_{i,j}=K(x_i,s_j)$ and $\left\{ x_i \right\}$ are the grid points considered.

The following result is a discrete version of Theorem 2.1 and the proof can be obtained similarly.

Theorem 3.1

Given any discrete function $\Xi (x_i)$ on a mesh $\left\{ x_i \right\} _{i=1}^N$ such that $\mathcal {K}^N\Xi (x_0)\ge 0$, $\mathcal {K}^N\Xi (x_N)\ge 0$ and $L^N\Xi (x_i)\ge 0$, where $\mathcal {K}^N$, $L^N$ are defined similarly as in Theorem 2.1, it holds that $\Xi (x_i)\ge 0$, $\forall x_i\in \overline{\Omega }^N.$

Proof

Consider $t(x_i)=1+x_i,$

Note that the function is non negative on $x_i \in \overline{\Omega }^N$. Let

$$\begin{aligned} \mu =\max \Big \{\frac{-\Xi (x_i)}{t(x_i)}:x_i\in \overline{\Omega }^N\Big \}. \end{aligned}$$

Furthermore, $\exists ~ x_k\in \overline{\Omega }^N$ such that $\Xi (x_k)+\mu t(x_k)=0$ and $\Xi (x_i)+\mu t(x_i)\ge 0,\forall x_i\in \overline{\Omega }^N$. As a result, at $x=x_k$, the function $(\Xi +\mu t)$ attains its minimum. We proceed by contradiction. If the theorem is false, then it is $\mu >0$.

Case (i): $x_k=x_0$ or $x_k=x_N$. Then

$$\begin{aligned} 0< \mathcal {K}^N(\Xi +\mu t)(x_k)=(\Xi +\mu t)(x_k)-\varepsilon \sum \limits _{i=1}^{N} \frac{g_{i-1}(\Xi +\mu t)x_{i-1}+g_i(\Xi +\mu t)x_{i}}{2}h_i\le 0. \end{aligned}$$

Case (ii): $x_k\in \Omega ^N$. In this case, we have

$$\begin{aligned} 0<{L_1}(\Xi +\mu t)(x_k)= & {} -\varepsilon D^{+}_xD^{-}_x(\Xi +\mu t)(x_k)+a(x_k)(\Xi +\mu t)(x_k)\le 0.\\ 0<{L_2}(\Xi +\mu t)(x_k)= & {} -\lambda \Big [h_1k_{i,1}(\Xi +\mu t)_1+\cdots +h_N k_{i,N}(\Xi +\mu t)_N\Big ], \\\le & {} -\lambda (\Xi +\mu t)_k\Big [h_1k_{i,1}+\cdots +h_N k_{i,N}\Big ]\le 0. \end{aligned}$$

It any case, we arrive at a contradiction.

Theorem 3.2

If $\phi _i$ is any mesh function, then

$$\begin{aligned} \Big |\phi _i\Big |\le \frac{1}{\beta } \displaystyle \max _{1\le j\le N-1}\Big \{|L^N\phi _j|, |\mathcal {K}^N\phi _0|, |\mathcal {K}^N\phi _N|\Big \}, ~\text{ for } ~ 0\le i \le N. \end{aligned}$$

Proof

One can prove this easily by using Theorem 3.1. $\square$

3.5 Error estimate for the difference schemes

Error estimates are bounds on the error of the numerical solution. The discrete maximum norm is a measure of the error that takes the maximum absolute value of the errors at the mesh points. Formally, if u is the exact solution and $U^N$ is the numerical solution on a mesh with parameter N, then the discrete maximum norm of the error is $\Vert (u-U^N)(x_i)\Vert _{\infty }=\max |u(x)-U^N(x_i)|$ for all mesh points $x_i$.

We demonstrate that the numerical solution approaches near first-order convergence when applied on a Shishkin mesh, while it achieves definitive first-order convergence on a Bakhvalov–Shishkin mesh. Additionally, we calculate error estimates using the discrete maximum norm to evaluate the solution accuracy.

Remark

Using the integral form of the truncation term and the composite trapezoidal rule on the range [0, 1],

$$\begin{aligned} \displaystyle \int _{0}^{1}F(s)ds= \sum _{i=0}^{N}h_{i}F_{i}+R_{N}, \end{aligned}$$

(3.2)

with $~\tau _{0}=\frac{h_{1}}{2}, ~~\tau _{i}=\frac{h_{i}+h_{i+1}}{2}, ~~~~~i=1,2,3,...,N-1,~~\tau _{N}=\frac{h_{N}}{2}$ and

$$\begin{aligned} R_{N}= & {} \frac{1}{2}\sum _{i=1}^{N}\displaystyle \int _{x_{i-1}}^{x_{i}}(x_{i}-\xi )(x_{i-1}-\xi )F''(\xi )d\xi . \end{aligned}$$

Similarly as in (3.2), then

$$\begin{aligned} \lambda \displaystyle \int _{0}^{1}K(x_{i},s)u(s)ds= & {} \lambda \sum _{j=0}^{N}h_{j}K_{ij}u_{j}+R_{i}, \end{aligned}$$

where

$$\begin{aligned} R_{i}= & {} \frac{\lambda }{2}\sum _{j=1}^{N}\displaystyle \int _{x_{j-1}}^{x_{j}}(x_{j}-\xi )(x_{j-1}-\xi )\frac{d^{2}}{d\xi ^{2}}(K(x_{i},\xi ))u(\xi )d\xi , \\|R_{i}|= & {} \Big |\frac{\lambda }{2}\sum _{j=1}^{N}\displaystyle \int _{x_{j-1}}^{x_{j}}(x_{j}-\xi )(x_{j-1}-\xi )\frac{d^{2}}{d\xi ^{2}}(K(x_{i},\xi ))u(\xi )d\xi \Big |, \\\big |R_{i}\big |\le & {} C\sum _{j=1}^{N}\displaystyle \int _{x_{j-1}}^{x_{j}}(x_{j}-\xi )(\xi -x_{j-1})(1+|u'(\xi )|+|u''(\xi )|)d\xi . \end{aligned}$$

Theorem 3.3

Given u and $U^N$, which are respectively the solutions to (1.1) and (3.1), we get the following estimate of the numerical errors (3.1)

$$\begin{aligned} \displaystyle \max _{1\le i \le N-1}\big |(u-U^N)(x_i)\big |\le \left\{ \begin{array}{ll} C\Big ((N^{-1}\ln N)^2\Big ) ~~\text{ on } \text{ a } \text{ S-mesh },\\ CN^{-2} ~~\text{ on } \text{ a } \text{ B-S-mesh }. \end{array}\right. \end{aligned}$$

Proof

The discrete solution U can be decomposed into smooth (V) and singular (W) components. The error can be written in the form

$$\begin{aligned} L^{N}(U-u)=L_{1}^{N}(U-u)+L_{2}^{N}(U-u). \end{aligned}$$

By Miller Miller et al. (1996), it is

$$\begin{aligned} L_{1}^{N}(U-u)\le C (N^{-1} \ln N)^2. \end{aligned}$$

Now, for the $L_{2}$ operator, then

$$\begin{aligned} L_{2}^{N}(U-u)=L_{2}^{N}(V-v)+L_{2}^{N}(W-w)\le C (N^{-1} \ln N)^2. \end{aligned}$$

Now, we analyzed the bounds for the smooth and singular components.

Smooth components:

$$\begin{aligned} L_{2}^{N}(V_{i}-v_{i})= & {} L_{2}^{N}(V(x_{i}))-L_{2}^{N}(v(x_{i})), \\ {}= & {} \lambda \sum _{j=0}^{N}K_{ij}V_{j}-\lambda \displaystyle \int _{0}^{1}K(x,s)v(s)ds, \\ {}= & {} \lambda \sum _{j=0}^{N}K_{ij}V_{j}-\lambda \displaystyle \int _{0}^{1}K(x_{i},s_{i})v(s_{i})ds, \\ {}\le & {} C\sum _{j=1}^{N}\displaystyle \int _{x_{j-1}}^{x_{j}}(x_{j}-\xi )(\xi -x_{j-1})(1+|v'(\xi )|+|v''(\xi )|)d\xi , \\ {}\le & {} C\sqrt{\varepsilon }(h), \\ {}\le & {} CN^{-1}(h), \\ {}\le & {} CN^{-2}. \end{aligned}$$

At the points $x_k=x_{0}$ and $x_k=x_{N}$, then

$$\begin{aligned} \mathcal {K}^{N}(V-v),(x_{k})= & {} \mathcal {K}^{N}V(x_{k})-\mathcal {K}^{N}v(x_{k}),\\= & {} l-\mathcal {K}^{N}v(x_{k}),\\ \mathcal {K}^{N}(V-v),(x_{k})= & {} \mathcal {K}^{N}V(x_{k})-\mathcal {K}^{N}v(x_{k}),\\= & {} l-\mathcal {K}^{N}v(x_{k}),\\= & {} \mathcal {K}v(x_{k})-\mathcal {K}^{N}v(x_{k}),\\= & {} v(x_{k})+\varepsilon \int \limits _{x_0}^{x_{k}}g(x)v(x)dx-v(x_{N})-\varepsilon \sum \limits _{i=1}^{N}\frac{g_{i-1}v_{i-1} +g_iv_i}{2}h_i,\\ |\mathcal {K}^{N}(V-v)(x_{N})|\le & {} C\varepsilon ((h_1^3v''(\chi _1)+\cdots +{h_2N}^3v''(\chi _{N})),\\\le & {} C\varepsilon (h_1^3+\cdots +h_{N}^3),\\\le & {} CN^{-2}, ~~~~\text {where} ~~x_{i-1}\le \chi _i\le x_i, 1\le i\le N. \end{aligned}$$

By Theorem 2.2 gives

$$\begin{aligned} |V(x_i)-v(x_i)|\le C N^{-2} \ln N. \end{aligned}$$

Singular components:

The estimate for $W_{L}-w_{L}$ is presented first. We must consider two cases, $\sigma =\frac{1}{4}$ or $\sigma =2\sqrt{\frac{\varepsilon }{\beta }}\ln N<\frac{1}{4}$ to be used in the argumentation.

Case(i): $\sigma =\frac{1}{4}.$

We have a uniform mesh in this instance and $\frac{1}{4}\le 2\sqrt{\frac{\varepsilon }{\beta }}\ln N$. It is obvious that $x_i-x_{i-1}=N^{-1}$ and $\varepsilon ^{-\frac{1}{2}}\le C\ln N$. By Miller et al. (1996), we get that

$$\begin{aligned} \\L_{2}^{N}(W_{L}(x_i)-w_{L}(x_i))= & {} L_{2}^{N}(W_L(x_{i}))-L_{2}^{N}(w_L(x_{i})), \\ {}= & {} \lambda \sum _{j=0}^{N}K_{ij}W_{L}(x_j)-\lambda \displaystyle \int _{0}^{1}K(x,s)w_L(s)ds, \\ {}= & {} \lambda \sum _{j=0}^{N}K_{ij}W_{L}(x_j)-\lambda \displaystyle \int _{0}^{1}K(x_{i},s_{i})w_L(s_{i})ds, \\ {}\le & {} C\sum _{j=1}^{N}\displaystyle \int _{x_{j-1}}^{x_{j}}(x_{j}-\xi )(\xi -x_{j-1})\left( 1+|w_L'(\xi )|+|w_L''(\xi )|\right) d\xi , \\ {}\le & {} C\sum _{j=1}^{N}\displaystyle \int _{x_{j-1}}^{x_{j}}(x_{j}-\xi )(\xi -x_{j-1})\left( \frac{1}{\varepsilon }\right) (e^{-x\sqrt{\beta /\varepsilon } })d\xi , \\ {}\le & {} C N^{-1} \frac{h^3}{\varepsilon }, \\ {}\le & {} CN^{-2}. \end{aligned}$$

At $x=x_0$ or $x=x_N$, then

$$\begin{aligned} \mathcal {K}^{N}(W_{L}-w_{L})(x_{k})= & {} \mathcal {K}^{N}W_{L}(x_{k})-\mathcal {K}^{N}w_{L}(x_{k}),\\= & {} B-\mathcal {K}^{N}w_{L}(x_{k}),\\= & {} \mathcal {K}w_{L}(x_{k})-\mathcal {K}^{N}w_{L}(x_{k}),\\ |\mathcal {K}^{N}(W_{L}-w_{L})(x_{N})|\le & {} C\varepsilon ((h_1^3w_{L}''(\chi _1)+\cdots +h_{N}^3w_{L} ''(\chi _{N})),\\\le & {} C\varepsilon ^{-1}(h_1^3+\cdots +h_{N}^3),\\\le & {} CN^{-2}. \end{aligned}$$

where $x_{i-1}\le \chi _i\le x_i$. Applying Theorem 3.2 in Miller et al. (1996) to the function $(W_L-w_L)(x_i)$ gives

$$\begin{aligned} |(W_L-w_L)(x_i)|\le C(N^{-2}\ln ^2 N). \end{aligned}$$

Case(ii): $\sigma <\frac{1}{4}.$

The resulting mesh is a piece wise uniform one, with the mesh spacing $2(1-2\sigma )/N$ in the sub interval $[\sigma , 1-\sigma ]$ and $4\sigma /N$ in each of the sub intervals $[0, \sigma ]$ and $[1-\sigma , 1].$

By Miller et al. (1996), then

$$\begin{aligned} | \mathcal {L}_1^{N}(W_{L}-w_{L})(x_i)|\le & {} C(N^{-2}\ln ^2 N), \end{aligned}$$

and

$$\begin{aligned} \\L_{2}^{N}(W_{L}(x_i)-w_{L}(x_i))= & {} L_{2}^{N}(W_L(x_{i}))-L_{2}^{N}(w_L(x_{i})), \\ {}= & {} \lambda \sum _{j=0}^{N}\tau _{j}K_{ij}W_{L}(x_j)-\lambda \displaystyle \int _{0}^{1}K(x,s)w_L(s)ds, \\ {}\le & {} C\sum _{j=1}^{N}\displaystyle \int _{x_{j-1}}^{x_{j}}(x_{j}-\xi )(\xi -x_{j-1})(1+|w_L'(\xi )|+|w_L''(\xi )|)d\xi , \\L_{2}^{N}(W_L(x_{i})-w_L(x_{i}))\le & {} CN^{-2}. \end{aligned}$$

At $x=x_0$ or $x= x_N,$ then

$$\begin{aligned} |\mathcal {K}^{N}(W_{L}-w_{L})(x_{k})|\le & {} \varepsilon |C(h_1^3w''(\chi _1)+\cdots +h_N^3w''(\chi _{N}))|,\\\le & {} C(h_1^3+\cdots + h_{N}^3),\\\le & {} CN^{-2}, \end{aligned}$$

where $x_{i-1}\le \chi _i\le x_i$. Applying Lemma 4.2 in Miller et al. (1996) to the function $(W_L-w_L)(x_i)$ gives

$$\begin{aligned} |(W_{L}-w_{L})(x_i)|\le C(N^{-2}\ln ^2 N). \end{aligned}$$

The error estimates for $W_{R}$ are established using a similar procedure. Therefore,

$$\begin{aligned} |U(x_i)-u(x_i)|=|V(x_i)-v(x_i)|+|W(x_i)-w(x_i)|\le C N^{-2} \ln ^2 N. \end{aligned}$$

$\square$

4 Post-process technique

We use the Richardson extrapolation approach to improve the accuracy of the proposed scheme. The discrete problem (3.1) is first solved on the Shishkin type mesh $\mathbb {G}^{2N}$, which is created by dividing each Shishkin mesh named $\mathbb {G}^{N}$ by a specified transition parameter. Consequently, the appropriate S-mesh nodes are $\mathbb {G}^{2N}=\{\widetilde{x}_i \in [0, 1]: 0=\widetilde{x}_0<\widetilde{x}_1<\dots<\widetilde{x}_{2N-1}<\widetilde{x}_{2N}=1\}$ given by

$$\begin{aligned} \widetilde{x}_i =\left\{ \begin{array}{ll} iH_1,&{}\quad \text{ for }\quad 0\le i \le \frac{N}{2},\\ \sigma +\Bigg (\frac{i}{N}-\frac{1}{4}\Bigg )H_2,&{}\quad \text{ for }\quad \frac{N}{2}+1\le i \le \frac{3N}{2},\\ 1-(N-i)H_1,&{}\quad \text{ for }\quad \frac{3N}{2}+1\le i \le 2N,\\ \end{array}\right. \end{aligned}$$

and the grid points in the B–S-mesh are given by

$$\begin{aligned} \widetilde{x}_i =\left\{ \begin{array}{ll} \dfrac{\sigma _0\sqrt{\varepsilon }}{\beta }\ln \Bigg (\vartheta \left( \frac{i}{N}\right) +1\Bigg ),&{}\quad \text{ for }\quad 0\le i \le N/2,\\ \sigma _1+\Bigg (\dfrac{4i}{N}-1\Bigg )\big (1/2-\sigma _1\big ),&{}\quad \text{ for } \quad \dfrac{N}{2}+1\le i \le \dfrac{3N}{2},\\ 1+\dfrac{\sigma _0\sqrt{\varepsilon }}{\beta }\ln \Big (\vartheta \left( 1-\frac{i}{N}\right) +1\Big ),&{}\quad \text{ for } \quad \dfrac{3N}{2}+1\le i \le 2N. \end{array}\right. \end{aligned}$$

Now, from Theorem 3.3, the error is

$$\begin{aligned} \left. \begin{array}{ll} (u-U^N)x_i&{}= C\Big ((N^{-1}\ln N)^2\Big )+ o\Big ((N^{-1}\ln N)^2\Big ),\\ &{}=C\left( \frac{N^{-1}\sigma }{\rho _0\sqrt{\varepsilon }}\right) ^2+o\Big ((N^{-1}\ln N)^2 \Big ), \end{array}\right. \end{aligned}$$

(4.1)

for $x_i\in \mathbb {G}^N$. Let $\widetilde{U}(\widetilde{x}_i)$ represent the discrete solution on the mesh $\mathbb {G}^{2N}$ (see (3.1)). From Theorem 3.3, we get

$$\begin{aligned} \left. \begin{array}{ll} (\widetilde{U}^N-u)\widetilde{x}_i= C\Bigg ((2N)^{-2}\left( \frac{\sigma }{\rho _0\sqrt{\varepsilon }}\right) ^2 \Bigg )+o\Big ((N^{-1}\ln N)^2\Big ), \end{array}\right. \end{aligned}$$

(4.2)

for $\widetilde{x}_i, \in \mathbb {G}^{2N}$. Now, the elimination of the $o(N^{-2})$ term from (4.1) and (4.2) leads to the following approximation

$$\begin{aligned} u({x}_i)-\dfrac{1}{3}\Big (4\widetilde{U}^N-{U^N}\Big )(x_i)= o\Big ((N^{-1}\ln N)^2\Big ),~ {x}_i\in \mathbb {G}^{N}. \end{aligned}$$

(4.3)

Therefore, we use the extrapolation formula as

$$\begin{aligned} U_{exp}(x_i)=\frac{1}{3}\Big (4\widetilde{U}^N-U^N\Big )(x_i), \quad x_i\in \mathbb {G}^N. \end{aligned}$$

(4.4)

Theorem 4.1

Let $U_{exp}$ represent the result of the Richardson extrapolation method (4.4) by solving the discrete problem (3.1) on two meshes $\mathbb {G}^N$ and $\mathbb {G}^{2N}$ and u be the solution of the continuous problem (1.1). Also, assume that $\sqrt{\varepsilon } \le N^{-1}$. Then we have the following error-bound

$$\begin{aligned} \Big |U_{exp}(x_i)-u(x_i)\Big |\le \left\{ \begin{array}{ll} C\Big (N^{-4}\ln ^4N\Big ), ~~\text{ on } \text{ a } \text{ S-mesh },\\ CN^{-4} ~~\text{ on } \text{ a } \text{ B-S-mesh }, \quad \text{ for }\quad 1 \le i \le N-1. \end{array}\right. \end{aligned}$$

Proof

The error can be written in the form

$$\begin{aligned} L^{N}(U_{exp}-u)=L_{1}^{N}(U_{exp}-u)+L_{2}^{N}(U_{exp}-u). \end{aligned}$$

For the first term, we have (the complete proof of this bound available in Natividad and Stynes 2000; Shishkin and Shishkina 2016)

$$\begin{aligned} L_{1}^{N}(U_{exp}-u)\le C (N^{-1} \ln N)^4. \end{aligned}$$

Now, to get a bound for the $L_{2}$ operator, we write

$$\begin{aligned} L_{2}^{N}(U_{exp}-u)=L_{2}^{N}(V_{exp}-v)+L_{2}^{N}(W_{exp}-w)\le C (N^{-1} \ln N)^4. \end{aligned}$$

We decompose $\widetilde{U}$ on $\mathbb {G}^{2N}$ as $\widetilde{U}=\widetilde{V}+\widetilde{W}$, where $\widetilde{W}$ is layer component and $\widetilde{V}$ is smooth layer on $\mathbb {G}^{2N}.$

Smooth component:

$$\begin{aligned} L_{2}^{N}(V_{i}-v_{i})=L_{2}^{N}(V(x_{i}))-L_{2}^{N}(v(x_{i})),\quad \text{ for }~~x_i \in \mathbb {G}^N, \end{aligned}$$

from the integral form of Taylor series expansion and using derivative bounds as we have done in Theorem 3.3, we have

$$\begin{aligned}{} & {} L_{2}^{N}(V_{i}-v_{i})\le C\big (N^{-2}+N^{-4}\big ),\\{} & {} L_{2}^{N}(V_{i}-v_{i})\le CN^{-2}+O\big (N^{-4}\big ). \end{aligned}$$

From the stability result we can write

$$\begin{aligned} \big |(V_{i}-v_{i})\big |\le CN^{-2}+O\big (N^{-4}\big ) \quad \text{ for }~~x_i \in \mathbb {G}^N. \end{aligned}$$

(4.5)

Similarly we can obtain on $\mathbb {G}^{2N}$,

$$\begin{aligned} \big |(\widetilde{V}_{i}-v_{i})\big |\le C(2N)^{-2}+O\big (N^{-4}\big ) \quad \text{ for }~~\widetilde{x}_i \in \mathbb {G}^{2N}. \end{aligned}$$

(4.6)

From the extrapolation formula (4.4), we can write

$$\begin{aligned} (V_{exp}-v)(x_i)=\Big (\dfrac{1}{3}(4\widetilde{V}-V)(x_i)\Big )-v(x_i)=\dfrac{1}{3}\Big (4(\widetilde{V}-v)-(V-v)\Big )(x_i). \end{aligned}$$

From (4.5) and (4.6), we get

$$\begin{aligned} \Big |(V_{exp}-v)(x_i)\Big |=\Big |\dfrac{1}{3}\Big (4(\widetilde{V}-v)+(V-v)\Big )(x_i)\Big |\le CN^{-4}. \end{aligned}$$

Layer components:

$$\begin{aligned} L_{2}^{N}(W_{i}-w_{i})=L_{2}^{N}(W(x_{i}))-L_{2}^{N}(w(x_{i})),\quad \text{ for }~~x_i \in \mathbb {G}^N, \end{aligned}$$

from the integral form of Taylor series expansion and using derivative bounds as we have done in Theorem 3.3, we have

$$\begin{aligned}{} & {} L_{2}^{N}(V_{i}-v_{i})\le C\big (N^{-2}(\ln N)^2+N^{-4}\big ),\\{} & {} L_{2}^{N}(W_{i}-w_{i})\le CN^{-2}(\ln N)^2+O\big (N^{-4}(\ln N)^4\big ). \end{aligned}$$

From stability result we can write

$$\begin{aligned} \big |(W_{i}-w_{i})\big |\le CN^{-2}(\ln N)^2+O\big (N^{-4}(\ln N)^4\big ) \quad \text{ for }~~x_i \in \mathbb {G}^N. \end{aligned}$$

(4.7)

Similarly we can obtain on $\mathbb {G}^{2N}$,

$$\begin{aligned}{} & {} \big |(\widetilde{V}_{i}-v_{i})\big |\le C(2N)^{-2}(\ln 2N)^2+O\big (N^{-4}(\ln N)^2\big ) \quad \text{ for }~~\widetilde{x}_i \in \mathbb {G}^{2N}.\nonumber \\{} & {} \big |(\widetilde{W}_{i}-w_{i})\big |\le C(2N)^{-2}(\ln N)^2+O\big (N^{-4}(\ln N)^2\big ) \quad \text{ for }~~\widetilde{x}_i \in \mathbb {G}^{2N}. \end{aligned}$$

(4.8)

From the extrapolation formula (4.4), we can write

$$\begin{aligned} (W_{exp}-w)(x_i)=\Bigg (\dfrac{1}{3}(4\widetilde{W}-W)(x_i)\Bigg )-w(x_i) =\dfrac{1}{3}\Big (4(\widetilde{W}-w)-(W-w)\Big )(x_i). \end{aligned}$$

From (4.7) and (4.8), we get

$$\begin{aligned} \Big |(W_{exp}-w)(x_i)\Big |=\Big |\dfrac{1}{3}\Big (4(\widetilde{W}-w)+(W-w)\Big )(x_i)\Big |\le CN^{-4}(\ln N)^4. \end{aligned}$$

Hence, we get bound on S-mesh

$$\begin{aligned} \Big |U_{exp}(x_i)-u(x_i)\Big |\le CN^{-4}(\ln N)^4. \end{aligned}$$

Similarly, we can prove the bound B–S mesh

$$\begin{aligned} \Big |U_{exp}(x_i)-u(x_i)\Big |\le CN^{-4}. \end{aligned}$$

For more details about B–S mesh, one can find in Mohapatra and Govindarao (2021). $\square$

5 Computational simulations

The suggested approach is used to solve two test problems and the results are presented in this section.

Example 5.1

Consider the following problem:

$$\begin{aligned} \left\{ \begin{array}{ll} -\varepsilon u''(x)+(2-e^{-x})u(x)-0.5\displaystyle \int _0^1xu(s)ds=x\cos (x), \quad x\in (0,1),\\ u(0)-\varepsilon \displaystyle \int _0^1xu(x)dx=1,~u(1)-\varepsilon \displaystyle \int _0^1x^2u(x)dx=0. \end{array}\right. \end{aligned}$$

(5.1)

Example 5.2

Consider the following problem:

$$\begin{aligned} \left\{ \begin{array}{ll} -\varepsilon u''(x)+\left( 1+sin\left( \frac{\pi x}{2}\right) \right) u(x)-0.5\displaystyle \int _0^1e^{1-xs}u(s)ds=\sqrt{1+x}, \quad x\in (0,1),\\ u(0)-\varepsilon \displaystyle \int _0^1xu(x)dx=-1,~u(1)-\varepsilon \displaystyle \int _0^1x^2u(x)dx=1. \end{array}\right. \end{aligned}$$

(5.2)

The exact solutions to the above problems are unknown. We apply the concept of the double mesh principle to get the pointwise errors and to confirm the $\varepsilon$-uniform convergence. Let denote $\widetilde{U}^N(x_i)$, the numerical result obtained on the Shishkin-type mesh created with the fixed transition parameter. This mesh is based on the ${\widetilde{\mathbb {G}}}^{2N}$ grid.

Now, we determine both maximum element-wise errors before and after extrapolation for each $\varepsilon$ by ${E}_\varepsilon ^{N}=\max _{(x_i)\in \mathbb {G}^N} |U^{N}(x_i)-\widetilde{U}^{N}(x_i,t_n)|$ and ${E}_\varepsilon ^{N}=\max _{(x_i)\in \mathbb {G}^N} |U_{exp}^{N}(x_i)-\widetilde{U}_{exp}^{N}(x_i)|$. The corresponding order of convergence is defined by ${P}_\varepsilon ^{N}=\log _2\Bigg (\frac{{E}_ \varepsilon ^{N}}{{E}_\varepsilon ^{2N}}\Bigg )$. Here, the double mesh concept is also applied to the obtained extrapolation solution for $\widetilde{U}_{exp}^{N}(x_i)$.

Fig. 1

Plots of the approximate solutions of Example 1 on the S-mesh taking $N=64$

Fig. 2

Plots of the approximate solutions of Example 1 on the B–S-mesh taking $N=64$

Fig. 3

Error plots before extrapolation for Example 1 taking $N=64$

Fig. 4

Error plots before extrapolation for Example 1 taking $N=64$

Table 1 Values of ${E}_\varepsilon ^{N}$ and ${P}_\varepsilon ^{N}$ obtained using the proposed approach for Example 5.1

Table 2 Values of ${E}_\varepsilon ^{N}$ and ${P}_\varepsilon ^{N}$ using the proposed approach after extrapolation for Example 5.1

Table 3 Values of ${E}_\varepsilon ^{N}$ and ${P}_\varepsilon ^{N}$ using the proposed approach for Example 5.2

Table 4 Values of ${E}_\varepsilon ^{N}$ and ${P}_\varepsilon ^{N}$ using the proposed approach after extrapolation for Example 5.2

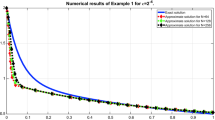
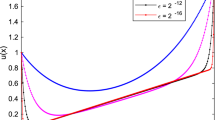
For different values of $\varepsilon$, the approximate solutions for Example 5.1 are plotted in Fig. 1 on a S-mesh. Numerical solutions of Example 5.2 are plotted in Fig. 2. These figures show that when $\varepsilon$ decreases, boundary layers are present near $x = 0$ and $x=1$. Before extrapolation, the error is plotted in Fig. 3a on a S-mesh and in Fig. 3b on a B–S mesh for Example 5.1. Similarly, after extrapolation, the errors are plotted in Fig. 4a for a S-mesh and in Fig. 4b for a B–S mesh of Example 5.1. From these figures, one can observe that the error is less on B–S mesh compared to S-mesh, as well as the use of the extrapolation approach results in a decrease in the errors.

The calculated maximum pointwise errors and the corresponding rate of convergence for Example 5.1 by using the proposed scheme are presented before extrapolation in Table 1 and after extrapolation in Table 2. Similarly, for Example 5.1, before extrapolation, the results are given in Table 3 and after extrapolation, the results are shown in Table 4. One can observe from these tables that before extrapolation, the rate of convergence is almost two (up to a logarithmic factor) on the S-mesh, but on the B–S mesh, the rate of convergence is two. Similarly, after extrapolation, the convergence rate is almost four (up to a logarithmic factor) on the S-mesh, but on the B–S mesh, the convergence rate is four. We note that the accuracy is higher on B–S meshes compared to S-meshes in both cases, before extrapolation and after extrapolation. To visualize the numerical order of convergence, the maximum pointwise errors before extrapolation are plotted in a log–log scale plot on the S-mesh in Fig. 5a and B–S-mesh in Fig. 5b. Similarly, maximum pointwise errors after extrapolation are plotted in Fig. 6 on the S-mesh and B–S mesh, respectively.

6 Conclusion

In this article, Fredholm integro-differential equations involving a small parameter with integral boundary conditions are solved numerically. The central difference scheme is used for approximating the derivative and the trapezoidal rule is used for approximating the integral part considering Shishkin-type meshes (Shishkin and Bakhvalov–Shishkin meshes). We prove that the proposed numerical scheme converges uniformly with respect to the small parameter $\varepsilon$, providing a second-order accuracy. Then, we use the post processing technique based on the extrapolation approach, providing a fourth order convergence rate. The numerical scheme has been tested in two examples, confirming the theoretical bounds.

Fig. 5

Loglog plots before extrapolation for Example 2

Fig. 6

Loglog plots after extrapolation for Example 2