1 Introduction

One of the important types of population models is the predator-prey model. Predator-prey models have appeared in many parts of ecology and biology (Kot 2001; Murray 2001). Intraguild predation (IGP) has been recognized as an important kind of interaction that occurs between species in the same community which utilizes similar resources (space or food), and thus there is competition between them. The pioneering works on intraguild predation have been done by Polis and McCormick (1987), Polis and Holt (1992), Holt and Polis (1997) which provided detailed explanations and model formulation of intraguild predation. More precisely, it was shown that IGP significantly influences the distribution, abundance and coexistence of many species. IGP differs from the pure competition in that energy is gained by the predator, which promotes its reproduction. IGP also differs from pure predation since the predator and prey are engaged in the exploitative competition. Thus, an IGP system is capable of demonstrating more complex dynamics than systems of pure competition or predation. Indeed, empirical observations indicate that IGP could lead to alternative stable states in a large number of circumstances, which can significantly affect the abundance, distribution, and evolution of many species. IGP can be seen, in turn, as a unique and extreme form of interference competition, where a dominant predator selectively kills and eats subordinate rivals to gain increased access to resources (Donadio and Buskirk 2006; Mukherjee et al. 2009; de Oliveira and Pereira 2014). For example, in Australian systems the larger and dominant dingo (Canis dingo) will kill and sometimes consume the invasive red fox, thereby reducing competition for shared prey (Cupples et al. 2011; Glen et al. 2007). There is a growing literature in modeling and analyzing IGP in recent years. Tanabe and Namba (2005) and Namba et al. (2008) observed that intraguild predation might destabilize the system and induce chaos by numerical simulations. Hsu et al. (2015) considered a three-species food web model with Lotka-Volterra type interaction between populations, classified the parameter space into three categories containing eight cases, and demonstrated extinction results for five cases and verified uniform persistence for the other three cases. On the other hand, a growing number of biological and mathematical models including IGP have also been proposed by incorporating some more realistic ecological factors. These factors include delay (Shu et al. 2015; Collera 2014), age or stage structure (Yamaguchi et al. 2007; Schellekens and Kooten 2012; Russell et al. 2009), functional response of predator (Abrams and Fung 2010; Verdy and Amarasekare 2010; Kang and Wedekin 2013; Freeze et al. 2014), refuge (Liu and Zhang 2013; Křivan 1998), additional species Kuijper et al. (2003); Holt and Huxel (2007) and spatial heterogeneity (Amarasekare 2007, 2008; Ryan and Cantrell 2015). One of the main goals in the studies above is to ascertain the mechanism of extinction and the coexistence of different species in systems with IGP. Some important predator-prey models are resource-consumer, parasite-host, plant-herbivore, susceptible-infectious interactions, etc. These models can be applied in other fields of science such as engineering and economics (Alì et al. 2012; Capone and De Luca 2012, 2014; Rosenheim et al. 1993; Torcicollo 2016).

In this paper, we consider a model of resource competition, where the consumption of each competitor can be enhanced by the presence of the other introduced in Assaneo et al. (2013). The model consists of three equations, one for the resource and two for the consumers which is characterized by a logistically growing resource population and species-specific death rates. A logistic growth function can better depict individual population growth and has become extremely popular (Hsu et al. 2015; Kang and Wedekin 2013; Holt and Polis 1997).

We now consider the general model of intraguild predation introduced in Assaneo et al. (2013), given by:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}=x(h_1(z)f_1(y)-B_1)\\ {\dot{y}}=y(h_2(z)f_2(x)-B_2)\\ {\dot{z}}=G(z)-{\tilde{B}}_1xh_1(z)f_1(y)-{\tilde{B}}_2yh_2(z)f_2(x) \end{array} \right. \end{aligned}$$
(1.1)

where two consumer species, x and y, and their resource, z are considered. G is the resource growth function in the absence of the consumers, \(h_i(z)\) indicates consumers per-capita catch rates which are modified to include consumers mutualism via functions \(f_i\). \(B_1\) and \(B_2\) are linear death rates, of the consumers which yield to \(1/{\tilde{B}}_1\) and \(1/{\tilde{B}}_2\), respectively. Actually, \({\tilde{B}}_1\) and \({\tilde{B}}_2\), respectively, show the effects of the death of x and y on specie z.

In the literature for more realistic models, the authors have presented various functional responses and different growth functions with different types of carrying capacity, see Assaneo et al. (2013), Capone et al. (2018), Capone and De Luca (2014), Jeschke et al. (2002), Kot (2001), Murray (2001), Safuan et al. (2013), Safuan et al. (2014). In this study, for the system (1.1), we consider the response functions \(h_i\) of Holling type II with

$$\begin{aligned} h_i(z)=\dfrac{A_{i}z}{Q_i+z}. \end{aligned}$$

Following Assaneo et al. (2013), we consider a classical situation, i.e., constant function \(f_1(y)=1\), while for a more feasible biological model to show facilitation, we suppose \(f_2(x)=1+cx\) and choose logistic growth as \(G(z) = rz(1- z/K)\). Similar to Assaneo et al. (2013) and Rosenzweig and MacArthur (1963), if we assume \(q_i=\frac{1}{Q_i}>1\) one may observe limit cycles in the model for some other parameters. So in this case, also for simplicity, we fix \(q_1=q_2=2>1\), equivalently \(Q_1=Q_2=1/2\), and \(r=K=1\). Moreover, we also assume that \(A_1=\frac{1}{{\tilde{B}}_1}\) and \(A_2=\frac{1}{{\tilde{B}}_2}\), equivalently \(A_1{\tilde{B}}_1=A_2{\tilde{B}}_2=1\) and by this assumption, the parameters \(A_1\) and \(A_2\) are expressed in terms of \({\tilde{B}}_1\) and \({\tilde{B}}_2\), respectively. Actually, from an ecological point of view, due to the structure of response functions, this assumption shows handling time of resource z is equal to the effect of the death of x on specie z, and also handling time of resource z is equal to the effect of the death of y on specie z. Thus, the model reduces to

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}=x\left( \dfrac{A_{1}z}{\dfrac{1}{2}+z}-B_{1}\right) \\ {\dot{y}}=y\left( \dfrac{A_{2}z(1+cx)}{\dfrac{1}{2}+z}-B_{2}\right) \\ {\dot{z}}=z(1-z)-\left( \dfrac{z}{\dfrac{1}{2}+z}\right) (x+(1+cx)y) \end{array} \right. \end{aligned}$$
(1.2)

where all the parameters are non-negative.

The plan of the paper is as follows. Section 2 is devoted to determine the equilibria of the model and investigating their stability. Bifurcation analysis of the equilibria is presented in Sect. 3. We characterize several codimension 1 and 2 bifurcations, derive parameter dependent normal forms of the obtained bifurcations and compute their corresponding normal form coefficients. In Sect. 4 and in Sect. 5, we employ the numerical continuation technique to compute several bifurcation curves. We especially compute a family of limit cycles emerging from a Hopf point. The numerical results assess the founded analytical results and reveal further dynamical behaviors of the original and modified models. We conclude the paper in Sect. 6, with a brief conclusion and give the biological implication of the obtained results.

2 Equilibria and stability

The model (1.2) has five equilibria given by

  1. 1.

    The origin i.e. \(E_0 = (0, 0, 0)\).

  2. 2.

    \(E_1 = (0, 0, 1)\).

  3. 3.

    \(E_2 =(0,\dfrac{A_2(2A_2-3B_2)}{4(A_2-B_2)^2}, \dfrac{B_2}{2(A_2-B_2)})\) when \(A_2>(3/2)B_2\).

  4. 4.

    \(E_3 = (\dfrac{A_1(2A_1-3B_1)}{4(A_1-B_1)^2},0,\dfrac{B_1}{2(A_1-B_1)})\) when \(A_1>(3/2)B_1\).

  5. 5.

    \(E^*=E_4 = (\dfrac{A_1B_2-A_2B_1}{A _2B_1c},\dfrac{A_1A_2B_1(2A_1-3B_1)c-4(A_1-B_1)^2(A_1B_2-A_2B_1)}{4A_1B_2c(A_1-B_1)^2}, \dfrac{B_1}{2(A_1-B_1)})\) when \(A_1>B_1,~A_1B_2-A_2B_1\ge 0\) and

    $$\begin{aligned} A_1A_2B_1(2A_1-3B_1)c-4(A_1-B_1)^2(A_1B_2-A_2B_1)\ge 0 . \end{aligned}$$

The equilibrium \(E_0\) is not biologically feasible and \(E_{1,2,3}\) are the boundary equilibria and \(E_4\) is an interior equilibrium.

To study stability of the equilibria, we evaluate the Jacobian matrix of the system at (x, y, z), given by

$$\begin{aligned} A=\left( \begin{array}{ccccccc} \dfrac{A_{1}z}{\dfrac{1}{2}+z}-B_{1} &{} 0 &{} x\Big (\dfrac{A_{1}}{\dfrac{1}{2}+z}-\dfrac{A_{1}z}{\Big (\dfrac{1}{2}+z\Big )^2}\Big ) \\ \dfrac{A_2cyz}{\dfrac{1}{2}+z} &{} \dfrac{A_2z(cx+1)}{\dfrac{1}{2}+z}-B_2 &{} y\Big ( \dfrac{A_2(cx+1)}{\dfrac{1}{2}+z}-\dfrac{A_2z(cx+1)}{ \Big (\dfrac{1}{2}+z\Big )^2} \Big ) \\ -\dfrac{z(cy+1)}{\dfrac{1}{2}+z} &{} -\dfrac{z(cx+1)}{\dfrac{1}{2}+z} &{} 1-2z-\dfrac{x+(cx+1)y}{\dfrac{1}{2}+z}-\dfrac{z(x+(cx+1)y)}{\Big (\dfrac{1}{2}+z\Big )^2} \end{array} \right) . \end{aligned}$$

The eigenvalues of A evaluated at \(E_0\) are \(-B_1,-B_2,1\) thus \(E_0\) is unstable. The eigenvalues at \(E_1\) are \((2/3)A_1-B_1,(2/3)A_2-B_2,-1\). Thus \(E_1\) is asymptotically stable when \((2/3)A_1<B_1,~(2/3)A_2<B_2\). It becomes unstable when \((2/3)A_1>B_1\), or \((2/3)A_2>B_2\).

The eigenvalues at \(E_2\) are given by

$$\begin{aligned}&\frac{1}{4A_2(A_2-B_2)}\\&\quad \left( A_2B_2-3B_2^2\pm \sqrt{-16A_2^4B_2+56A_2^3B_2^2-64A_2^2B_2^3+24A_2B_2^4+A_2^2B_2^2-6A_2B_2^3+9B_2^4}\right) , \\&\quad \frac{A_1B_2-A_2B_1}{A_2} \end{aligned}$$

When all of the above eigenvalues have negative real parts the equilibrium \(E_2\) is asymptotically stable, otherwise \(E_2\) is unstable.

The eigenvalues at \(E_3\) are

$$\begin{aligned}&\frac{1}{4A_1(A_1-B_1)}\\&\quad \left( A_1B_1-3B_1^2\pm \sqrt{-16A_1^4B_1+56A_1^3B_1^2-64A_1^2B_1^3+24A_1B_1^4+A_1^2B_1^2-6A_1B_1^3+9B_1^4}\right) , \\&\quad \frac{2A_1^2A_2B_1c-3A_1A_2B_1^2c-4A_1^3B_2+4A_1^2A_2B_1+8A_1^2B_1B_2-8A_1A_2B_1^2-4A_1B_1^2B_2+4A_2B_1^3}{4A_1(A_1^2-2A_1B_1+B_1^2)} \end{aligned}$$

Hence, \(E_3\) is asymptotically stable if all of the eigenvalues of A at \(E_3\) have negative real parts, otherwise \(E_3\) is unstable.

The characteristic polynomial of the Jacobian matrix at \(E^*=E_4\) is given as

$$\begin{aligned} p(r)= & {} -\dfrac{1}{2}\dfrac{1}{{A_1}^3A_2B_1B_2c(A_1-B_1)}\\\times & {} \bigg [\big (-2{A_1}^3A_2B_1B_2c(A_1-B_1)\big )r^3 \\&+ \big ({A_1}^2A_2{B_1}^2B_2c(A_1-3B_1)\big )r^2\\&+ \big ((A_1-B_1)( (-2{A_1}^3A_2B_1^2B_2c-2{A_1}^3A_2B_1{B_2}^2c+2{A_1}^2{A_2}^2{B_1}^3c+ 3{A_1}^2A_2{B_1}^3B_2c\\&+ 3{A_1}^2A_2{B_1}^2{B_2}^2c-3A_1{A_2}^2{B_1}^4c + 4{A_1}^4{B_2}^3-4{A_1}^3A_2{B_1}^2B_2-4{A_1}^3A_2B_1{B_2}^2\\&- 8{A_1}^3B_1{B_2}^3+4{A_1}^2{A_2}^2{B_1}^3+8{A_1}^2A_2{B_1}^3B_2+8{A_1}^2A_2{B_1}^2{B_2}^2+ 4{A_1}^2{B_1}^2{B_2}^3\\&- 8A_1{A_2}^2{B_1}^4-4A_1A_2{B_1}^4B_2-4A_1A_2{B_1}^3{B_2}^2+ 4{A_2}^2{B_1}^5))\big )r\\&+ B_1B_2(A_1-B_1)(A_1B_2-A_2B_1)(-2{A_1}^2A_2B_1c+3A_1A_2{B_1}^2c+4{A_1}^3B_2-4{A_1}^2A_2B_1\\&- 8{A_1}^2B_1B_2 +8A_1A_2{B_1}^2+4A_1{B_1}^2B_2-4A_2{B_1}^3) \bigg ] . \end{aligned}$$

By the Routh-Hurwitz conditions, the roots of p(r) have negative real parts if

  1. (S1)

    \((A_1-3B_1)(A_1-B_1)<0\);

  2. (S2)

    \((A_1B_2-A_2B_1)[-A_1A_2B_1(2A_1-3B_1)c+4(A_1-B_1)^2(A_1B_2-A_2B_1)]<0\);

  3. (S3)
    $$\begin{aligned}&-(A_1-B_1)[-A_1A_2B_1(2A_1-3B_1)(2A_1^3B_2^2-2A_1^2A_2B_1B_2-2A_1^2B_1B_2^2\\&\quad + 2A_1A_2B_1^2B_2+A_1^2B_1B_2+A_1^2B_2^2-A_1A_2B_1^2-3A_1B_1^2B_2-3A_1B_1B_2^2+3A_2B_1^3)c\\&\quad + 4(A_1-B_1)^2(2A_1^3B_2^2-2A_1^2A_2B_1B_2-2A_1^2B_1B_2^2+2A_1A_2B_1^2B_2+A_1^2B_2^2-A_1A_2B_1^2\\&\quad - 3A_1B_1B_2^2+3A_2B_1^3)(A_1B_2-A_2B_1)]<0 . \end{aligned}$$

Therefore we can state the following theorem.

Theorem 2.1

Consider the system (1.2) and interior equilibrium \(E^*\). Under conditions (S1)–(S3), the equilibrium \(E^*\) is asymptotically stable.

3 Bifurcations

We focus on the equilibrium \(E^*\) which represents the coexistence of predator and prey. For the sake of simplicity and following the ecological-subject paper (Assaneo et al. 2013), we consider the fixed set of parameters \(A_1 = 4\), \(A_2 = 2\), \( B_2 = 2\). Then characteristic polynomial reduces to

$$\begin{aligned} p(r)= & {} r^3 - \frac{B_1(3B_1-4)}{8(B_1-4)}r^2\nonumber \\&- \frac{({B_1}^5-3{B_1}^4c-12{B_1}^4+20{B_1}^3c+40{B_1}^3-8{B_1}^2c+32{B_1}^2 -64B_1c-384B_1+512)}{32B_1c}r\nonumber \\&- \frac{(B_1-4)({B_1}^3-3{B_1}^2c-12{B_1}^2+8B_1c+48B_1-64)}{16c} . \end{aligned}$$
(3.1)

Theorem 3.1

For the system (1.2), let \(c>0\) and the following statements hold:

  1. (i)

    If

    $$\begin{aligned} c=\frac{(B_1-4)^3}{B_1(3B_1-8)},~B_1\ne \frac{4}{3},~\frac{8}{3},~4 \end{aligned}$$

    then the characteristics polynomial (3.1) has a simple eigenvalue \(r=0\) and two other eigenvalues with non-zero real parts.

  2. (ii)

    If

    $$\begin{aligned} c= & {} \frac{(3B_1^3+12B_1^2-152B_1+288)(B_1-4)^3}{B_1(3B_1-8)(3B_1^3-136B_1+288)},\\ B_1\ne & {} \frac{4}{3},~\frac{8}{3},~4,~\frac{4\sqrt{34}}{3}\sin \left( \frac{1}{3}\tan ^{-1} \left( \frac{\sqrt{3256}}{81}\right) +\frac{\pi }{6}\right) ,\\&\frac{2\sqrt{34}}{3}\left( \sqrt{3}\cos \left( \frac{1}{3}\tan ^{-1} \left( \frac{\sqrt{3256}}{81}\right) +\frac{\pi }{6}\right) -\sin \left( \frac{1}{3}\tan ^{-1} \left( \frac{\sqrt{3256}}{81}\right) +\frac{\pi }{6}\right) \right) \end{aligned}$$

    then the characteristics polynomial (3.1) has a non-zero real root and a pair of pure conjugate imaginary eigenvalue \(r_{1,2}=\pm \mathrm{i}\omega _0\), where

    $$\begin{aligned} \omega _0=\frac{\sqrt{2B_1(3B_1-8)(3B_1^3+12B_1^2-152B_1+288)}(B_1-4)}{3B_1^3+12B_1^2-152B_1+288}. \end{aligned}$$
  3. (iii)

    If \((c,B_1)=(\frac{32}{9},\frac{4}{3})\) then the roots of the characteristics polynomial (3.1) are \(\pm \mathrm{i}\omega _0,~0\), in which \(\omega _0=\frac{\sqrt{6}}{3}\).

Regarding the above discussion with \(A_1 = 4, A_2 = 2, B_2 = 2\) and \(c>0\), we study the bifurcations of the system (1.2) at \(E^*\). For the dynamical behavior of the bifurcations, we refer to Kuznetsov (2004) and Wiggins (2003).

We obtain non-degeneracy conditions of bifurcations. We use the multilinear functions B and C as defined in Kuznetsov (2004). The left and right eigenvectors p and q are normalized such that \(<p,q>=1\). We compute all critical coefficients of the normal forms for the model reduced to the corresponding center manifold.

3.1 Fold bifurcation

If \(c={\hat{c}}\) , where

$$\begin{aligned} {\hat{c}}=\frac{(B_1-4)^3}{B_1(3B_1-8)},~B_1\ne \frac{4}{3},~\frac{8}{3},~4 \end{aligned}$$

then by Theorem 3.1, part (i), the characteristics polynomial (3.1) has a simple eigenvalue \(r=0\) and two other eigenvalues have non-zero real parts. Therefore the system (1.2) undergoes a generic fold bifurcation at \(c={\hat{c}}\). We compute the normal form of generic fold bifurcation at \(c={\hat{c}}\). If we use the translations \((x,y,z)=(X,Y,Z)+E^*\) and \(c=C+{\hat{c}}\), then system (1.2) reduces to

$$\begin{aligned} \left( \begin{array}{c} {\dot{X}} \\ {\dot{Y}} \\ {\dot{Z}} \\ \end{array} \right) =F_C\left( \begin{array}{c} X \\ Y \\ Z \\ \end{array} \right) , \end{aligned}$$
(3.2)

where the origin is an equilibrium at \(C=0\). By Kuznetsov (2004), the restriction of the vector field \(F_C\) to one-dimensional center manifold at the critical value \(C=0\), has the form

$$\begin{aligned} {\dot{u}} = bu^2+{\mathcal {O}}(u^3) \end{aligned}$$
(3.3)

where

$$\begin{aligned} b=\frac{1}{2}<p,B(q,q)> \end{aligned}$$
(3.4)

and \(Aq=0\), \(A^tp=0\) and \(<p,q>=1\). For non-degeneracy of this bifurcation of system (3.2), it is sufficient to show that the corresponding critical normal form coefficient b is non-zero. Here

$$\begin{aligned} A=\left( \begin{array}{ccc} 0 &{} 0 &{} -\frac{3B_1-8}{2} \\ 0 &{} 0 &{} 0 \\ -\frac{1}{4}B_1 &{} -1 &{} \frac{B_1(3B_1-4)}{8(B_1-4)} \\ \end{array} \right) ,~~q=\left( \begin{array}{c} -\frac{4}{B_1} \\ 1 \\ 0 \\ \end{array} \right) ,~p=\left( \begin{array}{c} 0 \\ 1 \\ 0 \\ \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} B(q,q)=\frac{(B_1-4)^3}{B_1(3B_1-8)}\left( \begin{array}{c} 0 \\ -4 \\ 2 \\ \end{array} \right) . \end{aligned}$$

Therefore

$$\begin{aligned} b=\frac{-2(B_1-4)^3}{B_1(3B_1-8)}\ne 0. \end{aligned}$$

Corollary 1

If \(c={\hat{c}}\) , where

$$\begin{aligned} {\hat{c}}=\frac{(B_1-4)^3}{B_1(3B_1-8)},~B_1\ne \frac{4}{3},~\frac{8}{3},~4, \end{aligned}$$

then equilibrium \(E^*\) of the system (1.2) undergoes a generic fold bifurcation.

3.2 Hopf bifurcation

If \(c={\tilde{c}}\), where

$$\begin{aligned} c={\tilde{c}}= & {} \frac{(3B_1^3+12B_1^2-152B_1+288)(B_1-4)^3}{B_1(3B_1-8)(3B_1^3-136B_1+288)},\\ B_1\ne & {} \frac{4}{3},~\frac{8}{3},~4,~\frac{4\sqrt{34}}{3}\sin \left( \frac{1}{3}\tan ^{-1}\left( \frac{\sqrt{3256}}{81}\right) +\frac{\pi }{6}\right) ,\\&\frac{2\sqrt{34}}{3}\left( \sqrt{3}\cos \left( \frac{1}{3}\tan ^{-1} \left( \frac{\sqrt{3256}}{81}\right) +\frac{\pi }{6}\right) -\sin \left( \frac{1}{3}\tan ^{-1}\left( \frac{\sqrt{3256}}{81}\right) +\frac{\pi }{6}\right) \right) \end{aligned}$$

then by Theorem 3.1, part (ii), the characteristics polynomial (3.1) has a non-zero real root and a pair of pure imaginary eigenvalue \(r_{1,2}=\pm \mathrm{i}\omega _0\), where

$$\begin{aligned} \omega _0=\frac{\sqrt{2B_1(3B_1-8)(3B_1^3+12B_1^2-152B_1+288)}(B_1-4)}{3B_1^3+12B_1^2-152B_1+288}. \end{aligned}$$

Therefore, the system (1.2) undergoes a Hopf bifurcation at \(c={\tilde{c}}\). We compute the normal form of Hopf bifurcation at \(c={\tilde{c}}\). If we use the translations \((x,y,z)=(X,Y,Z)+E^*\) and \(c=C+{\tilde{c}}\) then system (1.2) reduces to

$$\begin{aligned} \left( \begin{array}{c} {\dot{X}} \\ {\dot{Y}} \\ {\dot{Z}} \\ \end{array} \right) =G_C\left( \begin{array}{c} X \\ Y \\ Z \\ \end{array} \right) , \end{aligned}$$
(3.5)

where the origin is an equilibrium at \(C=0\). By Kuznetsov (2004), the restriction of the vector field \(G_C\) to center manifold in the complex domain which at the critical value \(C=0\), has the form

$$\begin{aligned} {\dot{w}} = \mathrm{i} \omega _0w+l_1(0)w|w|^2+{\mathcal {O}}(w^5),~~w\in {\mathbb {C}} \end{aligned}$$
(3.6)

where

$$\begin{aligned} l_1(0)=\frac{1}{2\omega _0} \Re [<p,C(q,q,{\bar{q}})>-2<p,B(q,A^{-1}B(q,{\bar{q}}))>+<p,B({\bar{q}},\nonumber \\(2i\omega _0I-A)^{-1}B(q,q))>] \end{aligned}$$
(3.7)

and \(Aq=\mathrm{i}\omega _0q\), \(A^tp=-\mathrm{i}\omega _0p\) and \(<p,q>=1\). If

$$\begin{aligned} l_1(0)\ne 0 \end{aligned}$$

a unique closed invariant curve for \(G_C\) emerges around the equilibrium point on the center manifold, when the bifurcation parameter crosses the critical value corresponding to the Hopf bifurcation.

For non-degeneracy of the Hopf bifurcation of system (3.5), it is sufficient to show that the corresponding critical normal form coefficient \(l_1(0)\), is non-zero. Here

$$\begin{aligned} A=\left( \begin{array}{ccc} 0 &{} 0 &{} \alpha \\ \beta &{} 0 &{} \gamma \\ \lambda &{} -1 &{} \mu \\ \end{array} \right) ,~~q=\left( \begin{array}{c} 1 \\ \frac{\gamma }{\alpha }-\frac{\beta }{\omega _0}\mathrm{i} \\ \frac{\omega _0}{\alpha }\mathrm{i} \\ \end{array} \right) ,~p=\left( \begin{array}{c} \frac{1}{2}+\frac{\omega _0 \lambda }{2\beta }\mathrm{i} \\ -\frac{\omega _0}{2\beta }\mathrm{i} \\ \frac{\omega _0^2}{2\beta } \\ \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} \alpha= & {} -\frac{(3B_1^3-136B_1+288)(3B_1-8)}{2(3B_1^3+12B_1^2-152B_1+288)}, \\ \beta= & {} -\frac{B_1^2(B_1-4)(3B_1-4)}{2(3B_1^3-136B_1+288)}, \\ \gamma= & {} -\frac{B_1(3B_1-8)(3B_1-4)}{3B_1^3+12B_1^2-152B_1+288}, \\ \lambda= & {} -\frac{2B_1(2B_1^2-19B_1+36)}{3B_1^3-136B_1+288}, \\ \mu= & {} \frac{B_1(3B_1-4)}{8(B_1-4)} . \end{aligned}$$

Therefore

$$\begin{aligned} l_1(0)= & {} \frac{1}{2\omega _0}\Re \bigg \{ \bigg (\frac{1}{2}+\frac{\omega _0 \lambda }{2\beta }\mathrm{i}\bigg ) \bigg [\big [C({\bar{q}},{\bar{q}},q)\big ]_1-2\bigg [B({\bar{q}},A^{-1}B({\bar{q}},q))\bigg ]_1 \nonumber \\&+\bigg [B(q,(-2i\omega _0I-A)^{-1}B({\bar{q}},{\bar{q}}))\big ]_1\bigg ]\nonumber \\&+ \bigg (-\frac{\omega _0}{2\beta }\mathrm{i}\bigg )\bigg [\big [C({\bar{q}},{\bar{q}},q)\big ]_2 -2\bigg [B({\bar{q}},A^{-1}B({\bar{q}},q))\bigg ]_2+\bigg [B(q,(-2i\omega _0I-A)^{-1}B({\bar{q}},{\bar{q}}))\bigg ]_2\bigg ]\nonumber \\&+\bigg (\frac{\omega _0^2}{2\beta }\bigg )\bigg [\bigg [C({\bar{q}},{\bar{q}},q)\bigg ]_3 -2\bigg [B({\bar{q}},A^{-1}B({\bar{q}},q))\bigg ]_3 +\bigg [B(q,(-2i\omega _0I-A)^{-1}B({\bar{q}},{\bar{q}}))\big ]_3\bigg ]\bigg \}\nonumber \\ \end{aligned}$$
(3.8)

where

$$\begin{aligned} \bigg [C({\bar{q}},{\bar{q}},q)\bigg ]_1= & {} \frac{3(B_1-4)^2(3B_1-8)(3B_1^3-136B_1+288)Z^3}{4(3B_1^3+12B_1^2-152B_1+288)} \bigg (\frac{\omega _0}{\alpha }\bigg )^3\mathrm{i}+(B_1-4)^3\bigg (\frac{\omega _0}{\alpha }\bigg )^2 \\ \bigg [C({\bar{q}},{\bar{q}},q)\bigg ]_2= & {} \frac{3(3B_1-4)B_1(3B_1-8)(B_1-4)^2}{2(3B_1^3+12B_1^2-152B_1+288)} \bigg (\frac{\omega _0}{\alpha }\bigg )^3\mathrm{i}\\&-\frac{2}{\alpha }\frac{(B_1-4)^5(3B_1^3+12B_1^2-152B_1+288)}{4(B_1(3B_1-8)(3B_1^3-136B_1+288))}\bigg (\beta +\frac{\gamma \omega _0}{\alpha }\mathrm{i}\bigg )\\&-\frac{2B_1(B_1-4)^4(3B_1-4)}{4(3B_1^3-136B_1+288)} \bigg (\frac{\omega _0}{\alpha }\bigg )^2 +2\frac{(B_1-4)^3}{B_1}\bigg (\frac{\omega _0}{\alpha }\bigg )^2 \bigg (\frac{\gamma }{\alpha }+3\frac{\beta }{\omega _0}\mathrm{i}\bigg ) \\ \bigg [C({\bar{q}},{\bar{q}},q)\bigg ]_3= & {} -\frac{3}{16}(B_1-4)^2(3B_1-8) \bigg (\frac{\omega _0}{\alpha }\bigg )^3\mathrm{i}-\frac{2(B_1-4)^3(2B_1^2-19B_1+36)}{(3B_1^3-136B_1+288)} \bigg (\frac{\omega _0}{\alpha }\bigg )^2\\&+\frac{2}{\alpha }\frac{(B_1-4)^5(3B_1^3+12B_1^2-152B_1+288)}{8(B_1(3B_1-8)(3B_1^3-136B_1+288))} \bigg (\beta +\frac{\gamma \omega _0}{\alpha }\mathrm{i}\bigg )\nonumber \\&-\frac{(B_1-4)^3}{B_1} \bigg (\frac{\omega _0}{\alpha }\bigg )^2\bigg (\frac{\gamma }{\alpha }+3\frac{\beta }{\omega _0}\mathrm{i}\bigg ) \end{aligned}$$
$$\begin{aligned} \bigg [B({\bar{q}},A^{-1}B({\bar{q}},q))\bigg ]_1= & {} \frac{(B_1-4)(3B_1-8)(3B_1^3-136B_1+288)}{2(3B_1^3+12B_1^2-152B_1+288)}\bigg (r_3\frac{\omega _0}{\alpha }\bigg )\mathrm{i}\\&\quad +\frac{1}{2}(B_1-4)^2\bigg (r_3-r_1\frac{\omega _0}{\alpha }\mathrm{i}\bigg )\\ \bigg [B({\bar{q}},A^{-1}B({\bar{q}},q))\bigg ]_2= & {} \frac{B_1(3B_1-4)(B_1-4)(3B_1-8)}{(3B_1^3+12B_1^2-152B_1+288)}\bigg (r_3\frac{\omega _0}{\alpha }\bigg )\mathrm{i}\\&+ \frac{(3B_1^3+12B_1^2-152B_1+288)(B_1-4)^3}{2((3B_1^3-136B_1+288)(3B_1-8))} \bigg (r_2+r_1\frac{\gamma }{\alpha }+r_1\frac{\beta }{\omega _0}\mathrm{i}\bigg )\\&- \frac{(B_1-4)^3B_1(3B_1-4)}{4(3B_1^3-136B_1+288)} \bigg (r_3-r_1\frac{\omega _0}{\alpha }\mathrm{i}\bigg )\\&\quad +\frac{(B_1-4)^2}{B_1}\bigg [r_3\frac{\gamma }{\alpha }+ \bigg (r_3\frac{\beta }{\omega _0}-r_2\frac{\omega _0}{\alpha }\mathrm{i}\bigg )\bigg ] \\ \bigg [B({\bar{q}},A^{-1}B({\bar{q}},q))\bigg ]_3= & {} -\frac{1}{8}(3B_1^2-20B_1+16)) \bigg (r_3\frac{\omega _0}{\alpha }\bigg )\mathrm{i}\\&-\frac{(B_1-4)^2(2B_1^2-19B_1+36)}{(3B_1^3-136B_1+288)}\bigg (r_3-r_1\frac{\omega _0}{\alpha }\mathrm{i}\bigg )\\&- \frac{(3B_1^3+12B_1^2-152B_1+288)(B_1-4)^3}{4((3B_1^3-136B_1+288)(3B_1-8))}\bigg (r_2+r_1\frac{\gamma }{\alpha }+r_1\frac{\beta }{\omega _0}\mathrm{i}\bigg )\\&-\frac{(B_1-4)^2}{2B_1}\left[ r_3\frac{\gamma }{\alpha }+\bigg (r_3\frac{\beta }{\omega _0}-r_2\frac{\omega _0}{\alpha }\bigg )\mathrm{i}\right] \end{aligned}$$
$$\begin{aligned} r= & {} A^{-1}B({\bar{q}},q)=\left( \begin{array}{c} r_1 \\ r_2 \\ r_3 \\ \end{array} \right) ,\\ \bigg [B({\bar{q}},q)\bigg ]_1= & {} -\frac{(B_1-4)(3B_1-8)(3B_1^3-136B_1+288)}{3B_1^3+12B_1^2-152B_1+288} \bigg (\frac{\omega _0}{\alpha }\bigg )^2\\ \bigg [B({\bar{q}},q)\bigg ]_2= & {} -\frac{2B_1(3B_1-4)(B_1-4)(3B_1-8)}{(3B_1^3+12B_1^2-152B_1+288)} \bigg (\frac{\omega _0}{\alpha }\bigg )^2\\&+ \frac{(3B_1^3+12B_1^2-152B_1+288)(B_1-4)^3}{(3B_1^3-136B_1+288)(3B_1-8)}\bigg (\frac{\gamma }{\alpha }\bigg )\\&- \frac{2(B_1-4)^2}{B_1}\bigg (\frac{\beta }{\alpha }\bigg ) \\ \bigg [B({\bar{q}},q)\bigg ]_3= & {} \frac{1}{4}(3B_1^2-20B_1+16)) \bigg (\frac{\omega _0}{\alpha }\bigg )^2\\&- \frac{(3B_1^3+12B_1^2-152B_1+288)(B_1-4)^3}{2(3B_1^3-136B_1+288)(3B_1-8)} \bigg (\frac{\gamma }{\alpha }\bigg )+\frac{(B_1-4)^2}{B_1}\bigg (\frac{\beta }{\alpha }\bigg ). \end{aligned}$$

Corollary 2

Let \(c={\tilde{c}}\), where

$$\begin{aligned} c={\tilde{c}}= & {} \frac{(3B_1^3+12B_1^2-152B_1+288)(B_1-4)^3}{B_1(3B_1-8)(3B_1^3-136B_1+288)},\\ B_1\ne & {} \frac{4}{3},~\frac{8}{3},~4,~\frac{4\sqrt{34}}{3}\sin \left( \frac{1}{3}\tan ^{-1} \left( \frac{\sqrt{3256}}{81}\right) +\frac{\pi }{6}\right) ,\\&\frac{2\sqrt{34}}{3}\left( \sqrt{3}\cos \left( \frac{1}{3}\tan ^{-1} \left( \frac{\sqrt{3256}}{81}\right) +\frac{\pi }{6}\right) -\sin \left( \frac{1}{3}\tan ^{-1}\left( \frac{\sqrt{3256}}{81}\right) + \frac{\pi }{6}\right) \right) . \end{aligned}$$

If \(l_1(0)\ne 0\), given by (3.8), then equilibrium \(E^*\) of the system (1.2) undergoes a generic Hopf bifurcation.

Remark 3.2

We note that the above corollary refers to critical normal form of Hopf bifurcation of equilibrium \(E^*\) at \(c={\tilde{c}}\), where the explicit formula of critical coefficient is obtained by (3.8). Actually the curve

$$\begin{aligned} c={\tilde{c}} = \frac{(3B_1^3+12B_1^2-152B_1+288)(B_1-4)^3}{B_1(3B_1-8)(3B_1^3-136B_1+288)}, \end{aligned}$$

when

$$\begin{aligned} B_1\ne & {} \frac{4}{3},~\frac{8}{3},~4,~\frac{4\sqrt{34}}{3}\sin \left( \frac{1}{3}\tan ^{-1} \left( \frac{\sqrt{3256}}{81}\right) +\frac{\pi }{6}\right) ,\\&\frac{2\sqrt{34}}{3}\left( \sqrt{3}\cos \left( \frac{1}{3}\tan ^{-1} \left( \frac{\sqrt{3256}}{81}\right) +\frac{\pi }{6}\right) -\sin \left( \frac{1}{3}\tan ^{-1} \left( \frac{\sqrt{3256}}{81}\right) +\frac{\pi }{6}\right) \right) \end{aligned}$$

represents a curve of Hopf bifurcations. The numerical results also confirm non-degeneracy of the computed Hopf point.

3.3 Hopf-zero bifurcation in the appearance of the rate of conflict

If \((c,B_1)=(\frac{32}{9},\frac{4}{3})\) then by Theorem 3.1, part (iii), roots of the characteristics polynomial (3.1) are \(\pm \mathrm{i}\omega _0,~0\), in which \(\omega _0=\frac{\sqrt{6}}{3}\). Therefore, at \((c,B_1)=(\frac{32}{9},\frac{4}{3})\) the equilibrium \(E^*\) of the system (1.2) may undergo a generic Hopf-zero bifurcation. But this bifurcation is degenerate (the coefficient C(0) corresponding to the normal form of Hopf-zero becomes zero). Due to this degeneracy, we modify the model.

Let the predator y is affected under the rate of conflict in the prey z with rates \(\zeta \). For this purpose, near the equilibrium \(E^*=(x^*,y^*,z^*)\), we consider the following model,

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}=x\left( \dfrac{A_{1}z}{\dfrac{1}{2}+z}-B_{1}\right) \\ {\dot{y}}=y\left( \dfrac{A_{2}z(1+cx)}{\dfrac{1}{2}+z}-B_{2}\right) +\zeta (z-z^*)^2\\ {\dot{z}}=z(1-z)-\left( \dfrac{z}{\dfrac{1}{2}+z}\right) (x+(1+cx)y) \end{array} \right. \end{aligned}$$
(3.9)

where \(\zeta \) is a parameter and

$$\begin{aligned} z^*=\dfrac{B_1}{2(A_1-B_1)}. \end{aligned}$$

Remark 3.3

Notice that when \((c,B_1)=(\frac{32}{9},\frac{4}{3})\), the equilibrium \(E^*\) is reduced to a boundary equilibrium.

For simplicity let \(\zeta =1\). We notice that the characteristics polynomial of the corresponding Jacobian matrix at equilibrium \(E^*\) for both models (1.2) and (3.9) are the same. If \((c,B_1)=(\frac{32}{9},\frac{4}{3})\) then by Theorem 3.1, part (iii), roots of the characteristics polynomial (3.1) are \(\pm \mathrm{i}\omega _0,~0\), where \(\omega _0=\frac{\sqrt{6}}{3}\). Therefore, the system (3.9) undergoes a Hopf-zero bifurcation at \((c,B_1)=(\frac{32}{9},\frac{4}{3})\). We investigate the normal form of Hopf-zero bifurcation at \((c,B_1)=(\frac{32}{9},\frac{4}{3})\). If we use the translations \((x,y,z)=(X,Y,Z)+E^*\) and \((c,B_1)=({\mathcal {C}},{\mathcal {B}}_1)+(\frac{32}{9},\frac{4}{3})\) then system (3.9) reduces to

$$\begin{aligned} \left( \begin{array}{c} {\dot{X}} \\ {\dot{Y}} \\ {\dot{Z}} \\ \end{array} \right) =H_{{\mathcal {C}}{\mathcal {B}}_1}\left( \begin{array}{c} X \\ Y \\ Z \\ \end{array} \right) , \end{aligned}$$
(3.10)

where the origin is an equilibrium at \(({\mathcal {C}},{\mathcal {B}}_1)=(0,0)\). By Kuznetsov (2004), restriction of the vector field \(H_{{\mathcal {C}}{\mathcal {B}}_1}\) to center manifold at the critical value \(({\mathcal {C}},{\mathcal {B}}_1)=(0,0)\), for \((u,w)\in {\mathbb {R}}\times {\mathbb {C}}\), has the form

$$\begin{aligned} {\dot{u}}= & {} B(0)u^2+C(0)|w|^2+{\mathcal {O}}(||(u,w,{\bar{w}})||), \end{aligned}$$
(3.11)
$$\begin{aligned} {\dot{w}}= & {} \mathrm{i} \omega _0w+D(0)uw+E(0)u^2w+{\mathcal {O}}(||(u,w,{\bar{w}})||), \end{aligned}$$
(3.12)

where

$$\begin{aligned} B(0)= & {} G_{200}(0)\\ C(0)= & {} G_{011}(0)\\ D(0)= & {} H_{110}(0)-\mathrm{i}\omega _0\frac{G_{300}(0)}{G_{200}(0)}\\ E(0)= & {} \Re \left[ H_{210}(0)+H_{110}(0)\left( \frac{\Re H_{021}(0)}{G_{011}(0)}-\frac{3G_{300}(0)}{2G_{200}(0)}+\frac{G_{111}(0)}{2G_{011}(0)}\right) -\frac{H_{021}(0)G_{200}(0)}{G_{011}(0)}\right] \end{aligned}$$

with

$$\begin{aligned} G_{200}= & {} \frac{1}{2}<p_0,B(q_0,q_0)>,~~H_{110}=<p_1,B(q_0,q_1)>,~~G_{011}=<p_0,B(q_1,{\bar{q}}_1)>, \\ h_{200}= & {} -A^{INV}[B(q_0,q_0)-<p_0,B(q_0,q_0)>q_0],\\ h_{020}= & {} (2\mathrm{i}\omega _0I-A)^{-1}B(q_1,q_1),\\ h_{110}= & {} (\mathrm{i}\omega _0I-A)^{INV}[B(q_0,q_1)-<p_1,B(q_0,q_1)>q_1],\\ h_{011}= & {} -A^{INV}[B(q_1,{\bar{q}}_1)-<p_0,B(q_1,{\bar{q}}_1)>q_0] \end{aligned}$$

and

$$\begin{aligned} G_{300}= & {} \frac{1}{6}<p_0,C(q_0,q_0,q_0)+3B(q_0,h_{200})>,\\ G_{111}= & {} <p_0,C(q_0,q_1,{\bar{q}}_1)+B(q_1,{\bar{h}}_{110})+B({\bar{q}}_1,h_{110})+B(q_0,h_{011})>,\\ H_{210}= & {} \frac{1}{2}<p_1,C(q_0,q_0,q_1)+2B(q_0,h_{110})+B(q_1,h_{200})>,\\ H_{021}= & {} \frac{1}{2}<p_1,C(q_1,q_1,{\bar{q}}_1)+2B(q_1,h_{011})+B({\bar{q}}_1,h_{020})> \end{aligned}$$

and \(Aq_0=0,~Aq_1=\mathrm{i}\omega _0q_1\), \(A^tp_0=0,~A^tp_1=-\mathrm{i}\omega _0p_1\) and \(<p_0,q_0>=<p_1,q_1>=1\), \(<p_0,q_1>=<p_1,q_0>=0\).

The non-degeneracy of the Hopf-zero bifurcation of system (3.10), are given by

  1. ZH1.

    \(B(0)C(0)E(0)\ne 0\);

  2. ZH2.

    the map \((X,Y,Z,c,B_1)\rightarrow (H_{{\mathcal {C}}{\mathcal {B}}_1},Tr(\frac{\partial H_{{\mathcal {C}}{\mathcal {B}}_1}}{\partial X\partial Y \partial Z}),det(\frac{\partial H_{{\mathcal {C}}{\mathcal {B}}_1}}{\partial X\partial Y \partial Z}))(X,Y,Z,c,B_1)\) is regular at \((X,Y,Z,c,B_1)=(0,0,0,0,0)\).

Here, we have

$$\begin{aligned} A=\left( \begin{array}{ccc} 0 &{} 0 &{} 2 \\ 0 &{} 0 &{} 0 \\ -\frac{1}{3} &{} -1 &{} 0 \\ \end{array} \right) ,~~q_0=\left( \begin{array}{c} -3 \\ -1 \\ 0 \\ \end{array} \right) ,~q_1=\left( \begin{array}{c} -\frac{\sqrt{6}}{2}\mathrm{i} \\ 0 \\ \frac{1}{2} \\ \end{array} \right) ,~p_0=\left( \begin{array}{c} 0 \\ 1 \\ 0 \\ \end{array} \right) ,~p_1=\left( \begin{array}{c} -\frac{\sqrt{6}}{6}\mathrm{i} \\ -\frac{\sqrt{6}}{2}\mathrm{i} \\ 1 \\ \end{array} \right) . \end{aligned}$$

Therefore,

$$\begin{aligned} B(q_0,q_0)=\left( \begin{array}{c} 0 \\ -\frac{128}{9} \\ \frac{64}{9} \end{array} \right) ,~~B(q_0,q_1)=\left( \begin{array}{c} -\frac{16}{3} \\ \frac{8}{3}-\frac{32\sqrt{6}}{27}\mathrm{i} \\ \frac{16\sqrt{6}}{27}\mathrm{i} \end{array} \right) , \\ B(q_1,q_1)=\left( \begin{array}{c} -\frac{4}{3}-\frac{16\sqrt{6}}{9}\mathrm{i} \\ \frac{1}{2} \\ -\frac{1}{6}+\frac{4\sqrt{6}}{9}\mathrm{i} \end{array} \right) ,~~B(q_1,{\bar{q}}_1)=\left( \begin{array}{c} -8 \\ \frac{1}{2} \\ -\frac{1}{6} \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} B(0)=G_{200}=-\frac{64}{9},~~H_{110}=\frac{32}{9}-\frac{28\sqrt{6}}{27}\mathrm{i},~~C(0)=G_{011}=\frac{1}{2}. \end{aligned}$$

Also \(h_{200},~h_{011},~h_{110},\) are the solutions of the following nonsingular 4-dimensional real bordered systems, respectively,

$$\begin{aligned} \left( \begin{array}{cc} A &{} q_0 \\ p^T_0 &{} 0 \\ \end{array} \right) \left( \begin{array}{c} h_{200} \\ s \\ \end{array} \right) =\left( \begin{array}{c} -B(q_0,q_0)+<p_0,B(q_0,q_0)>q_0 \\ 0 \\ \end{array} \right) ,\\ \left( \begin{array}{cc} A &{} q_0 \\ p^T_0 &{} 0 \\ \end{array} \right) \left( \begin{array}{c} h_{011} \\ s \\ \end{array} \right) =\left( \begin{array}{c} -B(q_1,{\bar{q}}_1)+<p_0,B(q_1,{\bar{q}}_1)>q_0 \\ 0 \\ \end{array} \right) ,\\ \left( \begin{array}{cc} \mathrm{i}\omega _0{I_3}-A &{} q_1 \\ {\bar{p}}^T_1 &{} 0 \\ \end{array} \right) \left( \begin{array}{c} h_{110} \\ s \\ \end{array} \right) =\left( \begin{array}{c} B(q_0,q_1)-<p_1,B(q_0,q_1)>q_1 \\ 0 \\ \end{array} \right) , \end{aligned}$$
Fig. 1
figure 1

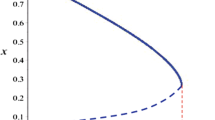
The continuation curve of the equilibrium \(E^*\) of the system (1.2)

Full size image
Fig. 2
figure 2

Phase diagram for the Hopf bifurcation of the equilibrium \(E^*\) of the system (1.2): the projection of family of limit cycles in (x, z)-plane with respect to parameter c

Full size image
Fig. 3
figure 3

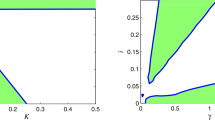
H curve in \((c,B_1)\)-plane for the system (1.2)

Full size image
Fig. 4
figure 4

The continuation curve of the equilibrium \(E^*\) of the system (3.9)

Full size image
Fig. 5
figure 5

Phase diagram for the Hopf bifurcation of the equilibrium \(E^*\) of the system (3.9): the projection of a family of limit cycles in (x, z)-plane with respect to parameter c

Full size image
Fig. 6
figure 6

H curve in \((c,B_1)\)-plane for the system (3.9)

Full size image

where s is a one-dimensional stack variable. Thus

$$\begin{aligned} h_{200}=\left( \begin{array}{c} \frac{64}{3} \\ 0 \\ -\frac{64}{3} \end{array} \right) ,~~h_{011}=\left( \begin{array}{c} -\frac{1}{2} \\ 0 \\ \frac{191}{4} \end{array} \right) ,~~h_{110}=\left( \begin{array}{c} 8+\frac{37\sqrt{6}}{9}\mathrm{i}\\ -\frac{32}{9}-\frac{4\sqrt{6}}{3}\mathrm{i}\\ \frac{1}{9}+\frac{4\sqrt{6}}{9}\mathrm{i} \end{array} \right) . \end{aligned}$$

We also have

$$\begin{aligned}&C(q_0,q_0,q_0)=C(q_0,q_0,q_1)=\left( \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right) ,\\&C(q_0,q_1,{\bar{q}}_1)=\left( \begin{array}{c} \frac{64}{9} \\ \frac{32}{9} \\ -\frac{32}{9} \end{array} \right) ,~~C(q_1,q_1,{\bar{q}}_1)=\left( \begin{array}{c} \frac{8}{3}+\frac{32\sqrt{6}}{27}\mathrm{i} \\ 0 \\ -\frac{2}{3}-\frac{8\sqrt{6}}{27}\mathrm{i} \end{array} \right) , \\&h_{020}=\left( \begin{array}{c} \frac{1}{3}+\frac{32}{9}\sqrt{6}- \left( \frac{8}{3}+\frac{8}{9}\sqrt{6}\right) \mathrm{i} \\ \mathrm{i} \\ \frac{1}{18}-\frac{8}{9}\sqrt{6}-\left( \frac{1}{3}+\frac{16}{27}\sqrt{6}\right) \mathrm{i} \end{array} \right) ,\\&B(q_0,h_{200})=\left( \begin{array}{c} \frac{2048}{9} \\ \frac{5120}{81} \\ -\frac{7744}{81} \end{array} \right) ,~~B(q_1,{\bar{h}}_{110})=\left( \begin{array}{c} \frac{248}{27}-\frac{512\sqrt{6}}{81}\mathrm{i} \\ \frac{1}{9}+\frac{1780\sqrt{6}}{243}\mathrm{i} \\ -\frac{65}{27}-\frac{452\sqrt{6}}{243}\mathrm{i} \end{array} \right) , \\&B({\bar{q}}_1,h_{110})=\left( \begin{array}{c} \frac{248}{27}+\frac{512\sqrt{6}}{81}\mathrm{i} \\ \frac{1}{9}-\frac{1780\sqrt{6}}{243}\mathrm{i} \\ -\frac{65}{27}+\frac{452\sqrt{6}}{243}\mathrm{i} \end{array} \right) ,~~B(q_0,h_{011})=\left( \begin{array}{c} -\frac{1528}{3} \\ -\frac{6844}{27} \\ \frac{6860}{27} \end{array} \right) ,\\&B(q_0,h_{110})=\left( \begin{array}{c} -\frac{32}{27}-\frac{128\sqrt{6}}{27}\mathrm{i} \\ \frac{464}{81}-\frac{640\sqrt{6}}{243}\mathrm{i} \\ -\frac{208}{81}+\frac{608\sqrt{6}}{243}\mathrm{i} \end{array} \right) ,~~B(q_1,h_{200})=\left( \begin{array}{c} \frac{2560}{27}+\frac{1024\sqrt{6}}{27}\mathrm{i} \\ -\frac{64}{3} \\ -\frac{64}{27}-\frac{256\sqrt{6}}{27}\mathrm{i} \end{array} \right) , \\&B(q_1,h_{011})=\left( \begin{array}{c} -\frac{1154}{9}-\frac{764\sqrt{6}}{9}\mathrm{i} \\ \frac{191}{4} \\ -\frac{565}{36}+\frac{191\sqrt{6}}{9}\mathrm{i} \end{array} \right) , \\&B({\bar{q}}_1,h_{020})=\left( \begin{array}{c} \left( \frac{212}{243}\sqrt{6}+\frac{512}{243}\sqrt{3}+\frac{16}{27}\sqrt{2} +\frac{4}{9}\right) +\left( -\frac{256}{81}\sqrt{3}+\frac{8}{81}\sqrt{2}-\frac{104}{27}\right) \mathrm{i}\\ \left( -\frac{56}{27}\sqrt{6}+\frac{1}{18}\right) + \left( -\frac{16}{27}\sqrt{6}+\frac{7}{3}\right) \mathrm{i} \\ -\left( \frac{56}{81}\sqrt{6}+\frac{128}{243}\sqrt{3} +\frac{4}{27}\sqrt{2}+\frac{1}{6}\right) +\left( \frac{16}{27}\sqrt{6}+\frac{64}{81}\sqrt{3}-\frac{2}{81}\sqrt{2}-\frac{1}{27}\right) \mathrm{i} \end{array} \right) . \end{aligned}$$

Therefore

$$\begin{aligned} G_{300}= & {} \frac{2560}{81},~~G_{111}=-\frac{6742}{27},\\ H_{210}= & {} -\frac{424}{81}\sqrt{6}-\frac{304}{81}+\left( \frac{512}{81}+\frac{544}{243}\sqrt{6}\right) \mathrm{i},\\ H_{021}= & {} -\left( \frac{253}{81}\sqrt{6}+\frac{88}{243}\sqrt{3}+\frac{146}{243}\sqrt{2} +\frac{1153}{81}\right) -\left( \frac{6839}{324}\sqrt{6}+\frac{92}{243}\sqrt{3}+\frac{7}{9}\sqrt{2} +\frac{511}{6}\right) \mathrm{i}. \end{aligned}$$

Finally,

$$\begin{aligned}&E(0)=-\left( \frac{17464}{243}\sqrt{6}+\frac{5632}{729}\sqrt{3}+\frac{9344}{729}\sqrt{2}+\frac{10544}{9}\right)<0,\\&s=\mathrm{sign}(B(0)C(0))=-1,~~\theta (0)=\frac{\Re H_{110}}{B(0)}=-\frac{1}{4}<0, \end{aligned}$$

and therefore we have subcritical Hopf bifurcations and no tori.

4 Numerical continuation analysis for original model

This section deals with the numerical continuation method using the matlab package matcont. This matlab package can be found in Dhooge et al. (2003). We compute several bifurcation curves emanating from the detected bifurcation points, to examine the obtained analytical results as well as to reveal more complicated dynamics of the system which can not be achieved by analytical argument.

We now do a numerical continuation of the equilibrium \(E^*\) of the system (1.2) by using matcont, by fixing \(A_1 = 4,~A_2 = 2,~B_1=1.7,~B_2 = 2\) and c free with the initial value \(c =2 .7\). The matcont reports are: (for this continuation the initial point in state space is \(x(0)=0.45,~y(0)=0.02,~z(0)=0.35\))

figure a

The corresponding curve is plotted in the Figure 1. A supercritical Hopf bifurcation is detected with the first Lyapunov coefficient \(l_1(0)= -1.049516<0\) and therefore there is a unique and stable limit cycle for each c after bifurcation point.

The projection of limit cycles in (x, z)-plane with respect to parameter c is plotted in Fig. 2. We also compute a branch point BP when \(c=2.467951\).

We select the Hopf (H) point to start a continuation of a Hopf bifurcation curve in two control parameters c and \(B_1\) and keep all other parameters fixed. The matcont reports are:

figure b

The Hopf curve is depicted in Fig. 3.

Notice that ZH and GH indicate Hopf-zero bifurcation and generalized Hopf bifurcation, respectively. We have a generalized Hopf (GH) on the Hopf curve with corresponding second Lyapunov coefficient in the matcont report.

5 Numerical continuation analysis for modified model

In this section, we do a numerical continuation of the equilibrium \(E^*\) of the system (3.9) by using matcont, by fixing \(A_1 = 4,~A_2 = 2,~B_1=1.7,~B_2 = 2\) and c free with the initial value \(c =2 .7\). The matcont reports are: (for this continuation the initial point in state space is \(x(0)=0.45,~y(0)=0.02,~z(0)=0.35\))

figure c

The corresponding curve is depicted in the Fig. 4. A subcritical Hopf bifurcation is detected with the first Lyapunov coefficient \(l_1(0)= 6.231433>0\) and therefore a unique and unstable limit cycle emerges beyond c before bifurcation point.

The projection of limit cycles in (x, z)-plane with respect to parameter c is plotted in Fig. 5.

We select the Hopf point (H) point to start a continuation of a Hopf bifurcation curve in two control parameters c and \(B_1\) and keep all other parameters the same. The matcont reports are:

figure d

The Hopf curve is shown in Fig. 6.

6 Conclusion and biological discussion

In this paper we first consider a predator-prey model consisting of a resource-consumer with two consumer species. We investigate the stability of interior equilibrium and identify codimension one generic bifurcations, i.e, fold and Hopf. However, continuation with two free parameters gives a degenarate Hopf-zero bifurcation. We then modify the model by adding the rate of conflict with the same equilibrium to obtain the non-degenerate Hopf-zero bifurcation. For all these bifurcations we compute the critical normal form coefficients and the corresponding parameter dependent normal forms of the reduced system to the center manifold and then conclude the non-degeneracy conditions of generic bifurcations. Finally, we numerically analyze the bifurcations by the toolbox matcont. On the Hopf bifurcation curve we detect codimension two bifurcations, namely a Hopf-zero bifurcation and a generalized Hopf bifurcation. Also, for the modified model on the Hopf bifurcation curve we detect codimension two bifurcations, i.e., Hopf-zero and generalized Hopf bifurcations.

Concerning to the biological implication of the system at \(E^*\), both predators (consumers) x,  y and prey (resource) z are in stationary cases with positive populations. Parameter c in the model (1.2) backs to rate that modifies consumers per-capita catch rates to include consumer mutualism. The fixed parameters \(A_1 = 4,~A_2 = 2,~B_2 = 2\), are valid in point of ecological view by the results of Assaneo et al. (2013). By Corollary 1, at \(c={\hat{c}}\) the equilibrium \(E^*\) of the system (1.2) undergoes a generic fold bifurcation and therefore in a neighborhood of \(c={\hat{c}}\) a curve of stable equilibria and a curve of unstable equilibria were born from \(E^*\), in which they exhibit stable and unstable stationary cases of populations and they collide and both disappear at \(E^*\). Therefore, at a slight parameter variation, some populations can suddenly disappear or equivalently extinction occurs. Ecologically, we can refer to Scheffer et al. (2001) for this catastrophic shift.

Also, by Corollary 2, at \(c={\tilde{c}}\) the equilibrium \(E^*\) of the system (1.2) undergoes a generic Hopf bifurcation and naturally if the first Lyapunov coefficient is negative, there is a unique and stable limit cycle for each c after bifurcation point, i.e., stable populations of predators x,  y and prey z oscillate and have periodic behaviour. In an equivalent phrase, all the three species coexist and have densities that vary periodically over time with a common period. Near the Hopf-zero bifurcation and generalized Hopf bifurcation, generally we have complex dynamics and complexity in populations.