Stability and bifurcation of a discrete predator-prey system with Allee effect and other food resource for the predators

Abstract

Concerned in this paper is a discrete predator-prey system with Allee effect and other food resources for the predators. The conditions on the existence and stability of fixed points are obtained. It is shown that the system can undergo fold bifurcation and flip bifurcation by using the center manifold theorem and bifurcation theory. Numerical simulations are provided to illustrate the feasibility of the main results and the influence of Allee effect on the stability of the system. Our study indicates that other food resources for the predator can enrich the dynamical behaviours of the system, including cascades of period-doubling bifurcation in orbits of period-2, 4, 8, and chaotic sets.

1 Introduction

The predation relationship between predator and prey is one of the dominant themes in ecology, due to its universal existence and importance. Predator-prey models have been extensively studied with the first one being proposed by Lotka and Volterra. A general Lotka-Volterra predator-prey model can be written as

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}=x(b_1-a_{11}x-a_{12}y),\\ {\dot{y}}=y(b_2+a_{21}x-a_{22}y), \end{array} \right. \end{aligned}$$

(1)

where $b_1$ and $a_{ij}$’s are positive constants, $b_2>0$ means that the predator has other food resources and $b_2<0$ otherwise. According to Ma [1], a positive fixed point must be globally stable when exists.

Allee effect [2] is a crucial phenomenon that has been studied by many scholars [3,4,5,6,7,8,9,10]. It can be regarded as a negative density dependence of the per capita growth rate of a population when its density is smaller than a critical value. It may be caused by many factors including the difficulty in finding a mate, reduced defence against predators at low densities, special trends of social dysfunction, etc. Allee effect may enhance [11, 12] or decrease [13,14,15,16,17,18,19,20,21] the stability of the system. By the biological meanings, the Allee function f(u, x) should satisfy the following requirements:

$$\begin{aligned} f(u,0)=0, \quad \lim _{x\rightarrow \infty }f(u,x)=1, \quad \frac{\partial f(u,x)}{\partial x}>0, \end{aligned}$$

where u is the Allee constant, x is the population density. Noting that $f(u,x)=\frac{x}{u+x}$ meets the above requirements.

For a bio-mathematical model, when species have non-overlapping generations or the population densities are too small, discrete models described by difference equations are more realistic than the continuous–time models. The dynamic behaviours of discrete predator-prey systems have been extensively studied over the past decades. To name a few, see [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] and references therein. All these works have demonstrated that discrete systems indeed have more complex dynamic behaviours than the continuous ones. In particular, several discrete models with Allee effect are discussed in [11, 12, 38,39,40,41]. Among these investigations, Celik and Duman [11] studied the following discrete predator-prey system with the prey population subject to an Allee effect,

$$\begin{aligned} \begin{array}{lcl} \left\{ \begin{array}{lll} N_{n+1}=N_{n}+rN_{n}\left( 1-N_{n}\right) \frac{N_{n}}{u+N_{n}}-aN_{n}P_{n},\\ P_{n+1}=P_{n}+aP_{n}\left( N_{n}-P_{n}\right) . \end{array} \right. \end{array} \end{aligned}$$

(2)

They showed that the Allee effect has a stabilizing effect for system (2) and the positive fixed point arrives stability much faster due to the Allee effect.

The models mentioned above are all based on a one-to-one relationship between the predator and the prey, i.e., the predator species takes the prey species as its unique food resource. Thus the extinction of the prey species will lead to the extinction of the predator species. However, predators are generally polyphagies and do not hunt for only one type of prey. Based on this, Zhu et al. [42] and Chen et al. [36] proposed respectively continuous and discrete models where the predator species has other food resources and the prey species is subject to fear effect. So far, little has been done for discrete predator-prey systems with both Allee effect and other food resources for predators.

Motivated by the above discussion and works, we propose a continuous predator-prey system with Allee effect and other food resources for the predator and study the dynamical behaviours of its discrete version obtained by the forward Euler scheme. The continuous model is

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dx}{dt}=rx\left( 1-\frac{x}{K}\right) \frac{x}{u_1+x}-axy,\\ \frac{dy}{dt}=pxy+ey-hy^2, \end{array}\right. } \end{aligned}$$

(3)

where x and y are the densities of the prey and the predator at time t, respectively. Here r, K, $u_1$, a, p, e, and h are all positive constants. r and e represent the intrinsic growth rates of the prey and predator, respectively; K is the carrying capacity of the prey in the absence of the predator; a denotes the maximum predation rate of the predator and $\frac{p}{a}$ stands for the conversion rate of prey’s biomass to predator’s biomass; $u_1$ is the Allee effect constant of the prey; and h describes the death rate due to intra-species competition of the predator.

For the sake of simplicity, we make the following change of variables,

$$\begin{aligned} {\bar{x}}=\frac{x}{K},\quad {\bar{y}}=\frac{h}{r}y,\quad {\bar{t}}=rt. \end{aligned}$$

Denote

$$\begin{aligned} u=\frac{u_1}{K},\quad b=\frac{a}{h},\quad c=\frac{pK}{r},\quad m=\frac{e}{r}. \end{aligned}$$

After dropping the bars, system (3) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dx}{dt} =x\left( 1-x\right) \frac{x}{u+x}-bxy, \\ \frac{dy}{dt} =cxy+my-y^2. \end{array}\right. } \end{aligned}$$

(4)

Applying the forward Euler scheme to system (4) and taking the step size $\delta \rightarrow 1$, we obtain the following discrete system,

$$\begin{aligned} {\left\{ \begin{array}{ll} x\rightarrow x+x\left( 1-x\right) \frac{x}{u+x}-bxy, \\ y\rightarrow y+cxy+my-y^2. \end{array}\right. } \end{aligned}$$

(5)

The aim of this paper is to study the dynamical behaviours of system (5), which include the existence and stability of fixed points, and the bifurcation phenomena.

The rest of this paper is arranged as follows. Sect. 2 is devoted to the existence and stability of fixed points. Then, in Sect. 3, we show that system (5) can undergo fold bifurcation and flip bifurcation under appropriate conditions on the parameters. Numerical simulations are provided in Sect. 4 to illustrate the feasibility of the main results. The paper ends with a brief conclusion.

2 The existence and stability of fixed points

2.1 The existence of fixed points

The fixed points of system (5) satisfy the following equations,

$$\begin{aligned} {\left\{ \begin{array}{ll} x=x+x\left( 1-x\right) \frac{x}{u+x}-bxy, \\ y=y+cxy+my-y^2. \end{array}\right. } \end{aligned}$$

Obviously, system (5) always admits the boundary fixed points $E_0(0,0)$, $E_1(0,m)$, and $E_2(1,0)$. For the positive fixed points, we only need to consider positive solutions of the following equations,

$$\begin{aligned} {\left\{ \begin{array}{ll} (bc+1)x^2+(bcu+bm-1)x+bmu=0, \\ y=cx+m. \end{array}\right. } \end{aligned}$$

(6)

For positive fixed points, x must satisfy $0<x<1$. Let $\Delta$ denote the discriminant of the first equation of (6) and express $\Delta$ in terms of m, i.e.,

$$\begin{aligned} \Delta (m)=b^2m^2-2(b^2cu+2bu+b)m+(bcu-1)^2. \end{aligned}$$

Then $\Delta (m)$ has two roots,

$$\begin{aligned} m^*=\frac{\left( \sqrt{u(bc+1)}-\sqrt{u+1}\right) ^2}{b},\quad m^{**}=\frac{\left( \sqrt{u(bc+1)}+\sqrt{u+1}\right) ^2}{b}. \end{aligned}$$

Note that $0\le m^*<m^{**}$.

Theorem 1

The following statements on positive fixed points of system (5) hold.

• 1. If either $m>m^*$ or $bcu\ge 1$, then there is no positive fixed point.

• 2. If $m=m^*$ and $bcu<1$, then there is a unique positive fixed point $E_{31}(x_{31},y_{31})$, where $x_{31}=\sqrt{\frac{u(u+1)}{bc+1}}-u$ and $y_{31}=cx_{31}+m$.

• 3. If $0<m<m^*$ and $bcu<1$, then there are two distinct positive fixed points $E_{32}(x_{32},y_{32})$ and $E_{33}(x_{33},y_{33})$, where $x_{32}=\frac{1-bcu-bm-\sqrt{\Delta (m)}}{2(bc+1)}$, $x_{33}=\frac{1-bcu-bm+\sqrt{\Delta (m)}}{2(bc+1)}$, $y_{32}=cx_{32}+m$, and $y_{33}=cx_{33}+m$.

Proof

Let $f(x)=(bc+1)x^2+(bcu+bm-1)x+bmu$. We only need to show when f has positive zeros in (0, 1). Note that $f'(x)=2(bc+1)x+bcu+bm-1$. It follows that $f'({\bar{x}})=0$ with ${\bar{x}}=\frac{1-bm-bcu}{2(bc+1)}$. If $bcu\ge 1$, then ${\bar{x}} {\le }-\frac{bm}{2(bc+1)}<0$. This, combined with $f(0)=bmu>0$, implies that f(x) has no positive zeros when $bcu\ge 1$. So in the following, we assume that $bcu< 1$, which implies that $m^*\ne 0$.

If $m^*<m<m^{**}$, then $\Delta (m)<0$, which means that f(x) has no real zeros.

If $m\ge m^{**}$, then ${\bar{x}} =\frac{1-bm-bcu}{2(bc+1)}\le \frac{1-bm^{**}-bcu}{2(bc+1)} =\frac{-2u(bc+1)-2\sqrt{u(bc+1)(u+1)}}{2(bc+1)}<0$. It follows from the argument at the beginning of the proof that f(x) has no positive zeros.

If $m=m^{*}$, then $\Delta (m)=0$. In addition, ${\bar{x}}=\frac{1-bm^*-bcu}{2(bc+1)}=\sqrt{\frac{u(u+1)}{bc+1}}-u >0$ since $bcu<1$. It is easy to see that ${\bar{x}}<1$. Therefore, ${\bar{x}}$ is the only positive real zero of f. It follows that system (5) has a unique positive fixed point $E_{31}(x_{31},y_{31})$ when $m=m^*$ and $bcu<1$, where $x_{31}={\bar{x}}$ and $y_{31}=cx_{31}+m$.

If $0<m<m^{*}$, we have $\Delta (m)>0$. It follows from $bcu<1$ that ${\bar{x}}>\frac{1-bm^*-bcu}{2(bc+1)}>0$. Note that $f(0)>0$, $f(1)=b(1+m)(1+u)>0$, and $f'(1)=1+2bc+bcu+bm>0$. Thus $f(x)=0$ has two distinct positive roots $x_{32}=\frac{1-bcu-bm-\sqrt{\Delta (m)}}{2(bc+1)}$ and $x_{33}=\frac{1-bcu-bm+\sqrt{\Delta (m)}}{2(bc+1)}$, both in (0, 1). This shows that system (5) has two distinct positive fixed points $E_{32}(x_{32},y_{32})$ and $E_{33}(x_{33},y_{33})$, where $y_{32}=cx_{32}+m$ and $y_{33}=cx_{33}+m$. $\square$

2.2 The stability of fixed points

In this subsection, we use linearization to discuss the stability of the fixed points obtained in the previous subsection.

The Jacobian matrix of system (5) evaluated at a fixed point E(x, y) is given by

$$\begin{aligned} J(E)=\begin{pmatrix} J_{11} &{}J_{12} \\ J_{21} &{}J_{22} \end{pmatrix}, \end{aligned}$$

(7)

where

$$\begin{aligned} J_{11}= & {} 1-\frac{x(3x-2)}{u+x}-\frac{x^2(1-x)}{(u+x)^2}-by, \\ J_{12}= & {} -bx, \\ J_{21}= & {} cy, \\ J_{22}= & {} 1+cx+m-2y. \end{aligned}$$

Write the characteristic equation of J(E) as $F(\lambda )=\lambda ^2+B\lambda +C=0$. Assume that $\lambda _1$ and $\lambda _2$ are the two roots of $F(\lambda )=0$. Then E is classified as follows.

Definition 1

The fixed point E of (5) is

• 1. locally asymptotically stable if $\max \{\vert \lambda _1\vert , \vert \lambda _2\vert \}<1$ and it is called a sink;

• 2. unstable if ${\max }\{\vert \lambda _1\vert , \vert \lambda _2\vert \}>1$;

• 3. non-hyperbolic if either $\vert \lambda _1\vert =1$ or $\vert \lambda _2\vert =1$.

The following results tell us how to determine the type of the fixed point E.

Lemma 1

([43, Lemma 2]) Assume that $F(1)>0$. Then

• 1. $|\lambda _1|<1$ and $|\lambda _2|<1$ if and only if $F(-1)>0$ and $C<1$;

• 2. $|\lambda _1|>1$ and $|\lambda _2|>1$ if and only if $F(-1)>0$ and $C>1$;

• 3. ($|\lambda _1|>1$ and $|\lambda _2|<1$) or ($|\lambda _1|<1$ and $|\lambda _2|>1$) if and only if $F(-1)<0$;

• 4. $\lambda _1=-1$ and $|\lambda _2|\ne 1$ if and only if $F(-1)=0$ and $B\ne 0,2$;

• 5. $\lambda _1$ and $\lambda _2$ are conjugate complex roots and $|\lambda _1|=|\lambda _2|=1$ if and only if $B^2-4C<0$ and $C=1$.

Note that $F(1)>0$ and $F(-1)=0$ imply that $B\ne 0$. Hence $B\ne 0$ is redundant in (iv) of Lemma 1, which will be ignored in the coming discussion.

The following result can be proved in the same manner as Lemma 1 and hence the detail is omitted here.

Lemma 2

Assume that $F(1)<0$. Then

• 1. $|\lambda _1|>1$ and $|\lambda _2|>1$ if and only if $F(-1)<0$;

• 2. ($|\lambda _1|>1$ and $|\lambda _2|<1$) or ($|\lambda _1|<1$ and $|\lambda _2|>1$) if and only if $F(-1)>0$;

• 3. $\lambda _1=-1$ and $|\lambda _2|\ne 1$ if and only if $F(-1)=0$.

For the boundary fixed points $E_0(0,0)$, $E_1(0,m)$, and $E_2(1,0)$, we have $J(E_0)= \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 1+m \end{pmatrix}$, $J(E_1)= \begin{pmatrix} 1-bm &{}\quad 0 \\ cm &{}\quad 1-m \end{pmatrix}$, and $J(E_2)= \begin{pmatrix} \frac{u}{u+1} &{}\quad -b\\ 0 &{}\quad 1+c+m \end{pmatrix}$, respectively. Then we can easily get their stability, which is summarized below.

Theorem 2

For the three boundary fixed points $E_0$, $E_1$, and $E_2$ of system (5),

• 1. $E_0(0,0)$ is always non-hyperbolic;

• 2. $E_1(0,m)$ is

  • (a) stable if $m<\min \{\frac{2}{b},2\}$;

  • (b) non-hyperbolic if $m=\frac{2}{b}$ or $m=2$;

  • (c) unstable for the other cases;

• 3. $E_2(1,0)$ is always unstable.

Now, we turn to the positive fixed points of (5). Recall that the positive fixed points $E_{3i}$ ($i=1$, 2, 3) satisfy

$$\begin{aligned} \frac{x_{3i}(1-x_{3i})}{u+x_{3i}}=by_{3i}, \quad y_{3i}=cx_{3i}+m. \end{aligned}$$

(8)

Substitute (8) into (7) to simplify the Jacobian matrix evaluated at $E_{3i}$ as

$$\begin{aligned} J(E_{3i})= \begin{pmatrix} 1+\alpha _ix_{3i} &{}\quad -bx_{3i} \\ cy_{3i} &{}\quad 1-y_{3i} \end{pmatrix}, \end{aligned}$$

where $\alpha _i=\frac{u(1-x_{3i})}{(u+x_{3i})^2}-\frac{x_{3i}}{u+x_{3i}}$. Thus the characteristic equation of $J(E_{3i})$ is

$$\begin{aligned} F(\lambda )=\lambda ^2+P\lambda +Q=0, \end{aligned}$$

where $P=-2-\alpha _i x_{3i}+y_{3i}$ and $Q=1+\alpha _i x_{3i}-y_{3i}+\left( bc-\alpha _i\right) x_{3i}y_{3i}$. In particular,

$$\begin{aligned} F(1)= & {} \left( bc-\alpha _i\right) x_{3i}y_{3i}\triangleq H(x_{3i})x_{3i}y_{3i}, \\ F(-1)= & {} 4+\left( bc-\alpha _i\right) x_{3i}y_{3i}+2\left( \alpha _i x_{3i}-y_{3i}\right) . \end{aligned}$$

Theorem 3

Under the conditions on the existence of positive fixed points of (5) in Theorem 1,

• 1. $E_{31}$ is always non-hyperbolic;

• 2. $E_{32}$ is

  • (a) non-hyperbolic if $(bc-\alpha _2)cx_{32}^2+2(\alpha _2-c)x_{32}+4>0$ and

    $$\begin{aligned} m=\frac{(bc-\alpha _2)cx_{32}^2 +2(\alpha _2-c)x_{32}+4}{2-(bc-\alpha _2)x_{32}}; \end{aligned}$$

  • (b) unstable for the other cases;

• 3. The properties of $E_{33}$ are listed in Table 1.

Table 1 Conditions on the stability of the fixed point $E_{33}$

Proof

Note that $H(x_{3i})=\frac{h(x_{3i})}{(u+x_{3i})^2}$, where

$$\begin{aligned} {h(x)} =(bc+1)x^2+(2bcu+2u)x+bcu^2-u. \end{aligned}$$

Then the sign of F(1) is determined by that of $h(x_{3i})$.

• (i) At $E_{31}$, $x_{31}=\sqrt{\frac{u(u+1)}{bc+1}}-u$. A simple calculation gives $h(x_{31})=0$ and hence $F(1)=0$. Therefore, $E_{31}$ is always non-hyperbolic.

  Recall from Theorem 1 that one of the conditions on the existence of $E_{32}$ and $E_{33}$ is $bcu<1$. Then $h(0)=bcu^2-u<0$. Since the vertex of h(x) is at the left of the y-axis, h(x) is monotonically increasing for $x>0$. Moreover, since $0<m<m^*$, it follows from

  $$\begin{aligned} f(x_{31})= & {} (bc+1)x^2_{31}+(bcu+bm-1)x_{31}+bmu \\= & {} [(bc+1)x^2_{31}+(bcu+bm^*-1)x_{31}+bm^*u]+b(m-m^*)(x_{31}+u) \\< & {} 0 \end{aligned}$$

  that $x_{32}<x_{31}<x_{33}$.

• (ii) For $E_{32}$, by the above discussion, $h(x_{32})<h(x_{31})=0$ and hence $F(1)=(bc-\alpha _2)x_{32}y_{32}<0$, which implies that $bc-\alpha _2<0$. By Lemma 2, if $F(-1)=0$ then $E_{32}$ is non-hyperbolic and otherwise it is unstable. Noting

  $$\begin{aligned} F(-1)=(bc-\alpha _2)x_{32}^2+2(\alpha _2-c)x_{32}+4-m[2-(bc-\alpha _2)x_{32}], \end{aligned}$$

  we easily see that $F(-1)=0$ if and only if $(bc-\alpha _2)x_{32}^2+2(\alpha _2-c)x_{32}+4>0$ and $m=\frac{(bc-\alpha _2)x_{32}^2+2(\alpha _2-c)x_{32}+4}{2-(bc-\alpha _2)x_{32}}$. Then 2(a) and 2(b) follow immediately.

• (iii) For $E_{33}$, we have $h(x_{33})>h(x_{31})=0$ and hence $F(1)>0$. Express $F(-1)$ and $Q-1$ as

  $$\begin{aligned} F(-1)= & {} \left[ (bc-\alpha _3)x_{33}-2\right] m +(bc-\alpha _3)cx_{33}^2+2(\alpha _3-c)x_{33}+4 \\\triangleq & {} \left[ (bc-\alpha _3)x_{33}-2\right] m+{\widetilde{m}} \end{aligned}$$

  and

  $$\begin{aligned} Q-1= & {} \left[ (bc-\alpha _3)x_{33}-1\right] m +(bc-\alpha _3)cx_{33}^2+(\alpha _3-c)x_{33} \\\triangleq & {} \left[ (bc-\alpha _3)x_{33}-1\right] m+{\overline{m}}, \end{aligned}$$

  respectively. Then the result on stability of $E_{33}$ follows easily from Lemma 1. $\square$

3 Bifurcation analysis

In this section, we investigate the possible bifurcations occurring at the fixed points of system (5) by using the center manifold theorem [44] and bifurcation theory [45, 46]. We start with the fold bifurcation.

3.1 Fold bifurcation

Recall from Theorem 1(ii) that if

$$\begin{aligned} m_1=m^*=\frac{\left( \sqrt{u(bc+1)}-\sqrt{u+1}\right) ^2}{b} \qquad \text{ and }\qquad bcu<1 \end{aligned}$$

(9)

then system (5) has only one positive fixed point $E_{31}(x_{31},y_{31})$ and the eigenvalues of the Jacobian matrix $J(E_{31})$ are $\lambda _1=1$ and $\lambda _2=1+\alpha _1x_{31}-(cx_{31}+m_1)$. Suppose that

$$\begin{aligned} m_1\ne (\alpha _1-c)x_{31},\qquad m_1\ne (\alpha _1-c)x_{31}+2. \end{aligned}$$

(10)

Then $|\lambda _2 |\ne 1$.

Let $w=x-x_{31}$, $v=y-y_{31}$, and $\eta =m-m_1$. Then system (5) can be rewritten as

$$\begin{aligned} \begin{array}{rcl} \begin{pmatrix} w \\ \eta \\ v \end{pmatrix} &{} \rightarrow &{}\begin{pmatrix} 1+\alpha _1x_{31} &{} 0 &{} -bx_{31}\\ 0 &{} 1 &{}0\\ cy_{31} &{} y_{31} &{} 1-y_{31} \end{pmatrix} \begin{pmatrix} w \\ \eta \\ v \end{pmatrix} \\ &{}&{}+ \begin{pmatrix} \beta w^2-bwv+O\big ((|w|+|v|+|\eta |)^{3}\big ) \\ 0 \\ cwv-v^2+\eta v \end{pmatrix}, \end{array} \end{aligned}$$

(11)

where $\beta =\frac{u^3+u^2}{(u+x_{31})^3}-1$. We choose

$$\begin{aligned} T_1= \begin{pmatrix} -bx_{31} &{} 0 &{} -bx_{31} \\ 0 &{} \frac{1-\lambda _2}{y_{31}} &{} 0 \\ -\alpha _1x_{31} &{} 1 &{} -y_{31} \end{pmatrix}, \end{aligned}$$

which is invertible. Then with the transformation

$$\begin{aligned} \begin{pmatrix} w \\ \eta \\ v \end{pmatrix} =T_1\begin{pmatrix} {\tilde{x}} \\ \eta _1 \\ {\tilde{y}} \end{pmatrix}, \end{aligned}$$

we transform (11) into

$$\begin{aligned} \begin{pmatrix} {\tilde{x}}\\ \eta _1 \\ {\tilde{y}} \end{pmatrix} \rightarrow \begin{pmatrix} 1 &{} 1 &{}0\\ 0 &{} 1 &{}0\\ 0 &{} 0 &{}\lambda _{2} \end{pmatrix} \begin{pmatrix} {\tilde{x}}\\ \eta _1 \\ {\tilde{y}} \end{pmatrix} + \begin{pmatrix} \phi \left( {\tilde{x}}, {\tilde{y}}, \eta _1\right) \\ 0 \\ \psi \left( {\tilde{x}}, {\tilde{y}}, \eta _1\right) \end{pmatrix}, \end{aligned}$$

(12)

where

$$\begin{aligned} \phi \left( {\tilde{x}}, {\tilde{y}}, \eta _1\right)= & {} \frac{\beta y_{31}}{bx_{31}(\lambda _2-1)}w^2 -\frac{by_{31}+bcx_{31}}{bx_{31}(\lambda _2-1)}wv +\frac{v^2}{\lambda _2-1}-\frac{\eta v}{\lambda _2-1} \\&+O\big ((|{\tilde{x}} |+|{\tilde{y}} |+|\eta _1 |)^{3}\big ), \\ \psi \left( {\tilde{x}}, {\tilde{y}}, \eta _1\right)= & {} -\frac{\beta \alpha _1x_{31}}{bx_{31}(\lambda _2-1)}w^2 +\frac{b\alpha _1x_{31}+bcx_{31}}{bx_{31}(\lambda _2-1)}wv -\frac{v^2}{\lambda _2-1}+\frac{\eta v}{\lambda _2-1}, \\ w= & {} -\,bx_{31}({\tilde{x}}+{\tilde{y}}),\qquad \eta =\frac{1-\lambda _2}{y_{31}}\eta _1, \\ v= & {} -\,\alpha _1x_{31}{\tilde{x}}+\eta _1-y_{31}{\tilde{y}}. \end{aligned}$$

By the center manifold theory, in a small neighborhood of $\eta _1=0$, there exists a center manifold $W^c(0)$ of (12) at the fixed point $({\tilde{x}},{\tilde{y}})=(0,0)$, which can be represented as

$$\begin{aligned} W^c(0)=\left\{ \left( {\tilde{x}}, {\tilde{y}}, \eta _1\right) \in {\mathbb {R}}^{3}\vert {\tilde{y}}=h\left( {\tilde{x}}, \eta _1\right) , h(0,0)=0, D h(0,0)=0\right\} , \end{aligned}$$

where ${\tilde{x}}$ and $\eta _1$ are sufficiently small. Suppose that the expression of h is

$$\begin{aligned} h\left( {\tilde{x}}, \eta _1\right) =n_1 {\tilde{x}}^{2}+n_2 {\tilde{x}} \eta _1+n_3\eta _1^2+O\big ((|{\tilde{x}} |+|\eta _1 |)^{3}\big ), \end{aligned}$$

(13)

which must satisfy

$$\begin{aligned} h\left( {\tilde{x}}+\eta _1+\phi \left( {\tilde{x}}, h\left( {\tilde{x}}, \eta _1\right) , \eta _1\right) , \eta _1\right) =\lambda _{2} h\left( {\tilde{x}}, \eta _1\right) +\psi \left( {\tilde{x}}, h\left( {\tilde{x}}, \eta _1\right) , \eta _1\right) . \end{aligned}$$

(14)

Substituting (13) into (14) and comparing the coefficients of the like terms ${\tilde{x}}^k\eta _1^l$, we get

$$\begin{aligned} n_1= & {} \frac{\alpha _1x_{31}^2(b\beta +\alpha _1-\alpha _1b-bc)}{(\lambda _2-1)^2}, \\ n_2= & {} \frac{2\alpha _1x_{31}^2(b\beta +\alpha _1-\alpha _1b-bc)}{(\lambda _2-1)^3} +\frac{x_{31}(\alpha _1b+bc-2\alpha _1)}{(\lambda _2-1)^2} -\frac{\alpha _1x_{31}}{y_{31}(\lambda _2-1)}, \\ n_3= & {} \frac{1}{(\lambda _2-1)^2}+\frac{1}{y_{31}(\lambda _2-1)} +\frac{\alpha _1x_{31}^2(b\beta +\alpha _1-\alpha _1b-bc)}{(\lambda _2-1)^3} \\&+\frac{2\alpha _1x_{31}^2(b\beta +\alpha _1-\alpha _1b-bc)}{(\lambda _2-1)^4} +\frac{x_{31}(\alpha _1b+bc-2\alpha _1)}{(\lambda _2-1)^3} -\frac{\alpha _1x_{31}}{y_{31}(\lambda _2-1)^2}. \end{aligned}$$

Therefore, the map (12) restricted to the center manifold $W^c(0)$ can be written as

$$\begin{aligned} F_{1}: {\tilde{x}} \rightarrow {\tilde{x}}+\eta _1+k_{1} {\tilde{x}}^{2}+k_{2} {\tilde{x}} \eta _1+k_{3} \eta _1^2+O\left( \left( |{\tilde{x}} |+|\eta _1 |\right) ^{3}\right) , \end{aligned}$$

where

$$\begin{aligned} k_1= & {} \frac{x_{31}(\alpha _1^2x_{31}+b\beta y_{31})}{\lambda _2-1} -\frac{b\alpha _1x_{31}(cx_{31}+y_{31})}{\lambda _2-1}, \\ k_2= & {} \frac{bcx_{31}-2\alpha _1x_{31}+by_{31}}{\lambda _2-1}-\frac{\alpha _1x_{31}}{y_{31}}, \\ k_3= & {} \frac{1}{\lambda _2-1}+\frac{1}{y_{31}}. \end{aligned}$$

Since $F_1(0,0)=0$, $\frac{\partial F_{1}}{\partial {\tilde{x}}}(0,0)=1$, $\frac{\partial F_{1}}{\partial \eta _1}(0,0)=1$, and $\frac{\partial ^2 F_{1}}{\partial {\tilde{x}}^2}(0,0)=2k_1\ne 0$, we obtain the following result.

Theorem 4

The system (5) undergoes a fold bifurcation at $E_{31}$ if conditions (9) and (10) hold. Moreover, the fixed points $E_{32}$ and $E_{33}$ bifurcate from $E_{31}$ for $m<m_1$, coalesce at $E_{31}$ for $m=m_1$, and disappear for $m>m_1$.

3.2 Flip bifurcation

Now we discuss the flip bifurcations of system (5).

System (5) can undergo flip bifurcation at the boundary fixed point $E_1(0,m)$ when parameters vary in a small neighborhood of $m=2$ or $m=\frac{2}{b}$. Since a center manifold of system (5) at $E_1$ is $x=0$ and system (5) restricted to it is the logistic model,

$$\begin{aligned} y\rightarrow g(y)=(1+m)y-y^2. \end{aligned}$$

Its nontrivial fixed point is $y_1=m$. If $g'(y_1)=1-m\ne 0$ when parameters vary in a small neighborhood of $m=2$ or $m=\frac{2}{b}$, then flip bifurcation can occur (see Fig. 2). In this case, the prey species becomes extinct and, by choosing m as the bifurcation parameter, the predator species undergoes the flip bifurcation to chaos due to the other food resources.

Since $E_{32}$ is always unstable, with the biological significance in mind, in the following we focus on the flip bifurcation at $E_{33}$. Here we again choose m as the bifurcation parameter.

Rewrite the conditions in rows 8 to 10 of Table 1 as the following three subsets,

$$\begin{aligned} F_{A1}= & {} \left\{ (b, c, u, m)\Bigg \vert \begin{array}{l} {b, c, u, m>0, (bc-\alpha _3)x_{33}<2, {\widetilde{m}}>0,} \\ {m=\frac{{\widetilde{m}}}{2-(bc-\alpha _3)x_{33}}, m\ne (\alpha _3-c)x_{33}+4} \end{array} \right\} , \\ F_{A2}= & {} \left\{ (b, c, u, m)\Bigg \vert \begin{array}{l} {b, c, u, m>0, (bc-\alpha _3)x_{33}>2, {\widetilde{m}}<0,} \\ {m=\frac{{\widetilde{m}}}{2-(bc-\alpha _3)x_{33}}, m\ne (\alpha _3-c)x_{33}+4} \end{array} \right\} , \\ F_{A3}= & {} \left\{ (b, c, u, m)\Bigg \vert \begin{array}{l} {b, c, u, m>0, (bc-\alpha _3)x_{33}=2,} \\ {\alpha _3x_{33}+2=0, m\ne (\alpha _3-c)x_{33}+4 } \end{array} \right\} . \end{aligned}$$

We show that flip bifurcation may undergo when parameters vary in one of $F_{A1}$, $F_{A2}$ and $F_{A3}$.

Take parameter values $(b, c, u, m_2)$ arbitrarily from $F_{A1}$, $F_{A2}$, or $F_{A3}$. Then the eigenvalues of $J(E_{33})$ are $\lambda _1=-1$ and $\lambda _2\ne \pm 1$. Let $w=x-x_{33}$, $v=y-y_{33}$, and $\mu =m-m_2$. Then system (5) can be rewritten as

$$\begin{aligned} \begin{array}{rcl}\begin{pmatrix} w \\ v \\ \mu \end{pmatrix} &{}\rightarrow &{} \begin{pmatrix} 1+\alpha _3x_{33} &{} -bx_{33} &{} 0\\ cy_{33} &{} 1-y_{33} &{} y_{33}\\ 0 &{} 0 &{}1 \end{pmatrix} \begin{pmatrix} w \\ v \\ \mu \end{pmatrix} \\ &{}&{}+ \begin{pmatrix} \beta _1 w^2-bwv+O\big ((|w|+|v|+|\mu |)^{3}\big ) \\ cwv-v^2+\mu v \\ 0 \end{pmatrix}, \end{array} \end{aligned}$$

(15)

where $\beta _1=\frac{u^3+u^2}{(u+x_{33})^3}-1$. We choose

$$\begin{aligned} T_2= \begin{pmatrix} -bx_{33} \quad &{} \quad -bx_{33} \quad &{} \quad -bx_{33}y_{33} \\ -\alpha _3x_{33}-2 \quad &{} \quad 2-y_{33} \quad &{} \quad -\alpha _3x_{33}y_{33} \\ 0 \quad &{} \quad 0\quad &{} \quad 2-2\lambda _2 \end{pmatrix}, \end{aligned}$$

which is invertible. With the transformation

$$\begin{aligned} \begin{pmatrix} w \\ v \\ \mu \end{pmatrix} =T_2\begin{pmatrix} X \\ Y \\ \mu _1 \end{pmatrix}, \end{aligned}$$

the map (15) becomes

$$\begin{aligned} \begin{pmatrix} X\\ Y \\ \mu _1 \end{pmatrix} \rightarrow \begin{pmatrix} -1 &{} 0 &{}0\\ 0 &{} \lambda _2 &{}0\\ 0 &{} 0 &{} 1 \end{pmatrix} \begin{pmatrix} X\\ Y \\ \mu _1 \end{pmatrix} + \begin{pmatrix} f\left( X, Y, \mu _1\right) \\ g\left( X, Y, \mu _1\right) \\ 0 \end{pmatrix}, \end{aligned}$$

(16)

where

$$\begin{aligned} f\left( X, Y, \mu _1\right)= & {} \frac{\beta _1 (y_{33}-2)}{bx_{33}(\alpha _3x_{33}-y_{33}+4)}w^2 -\frac{cx_{33}+y_{33}-2}{x_{33}(\alpha _3x_{33}-y_{33}+4)}wv \\&+\frac{v^2}{\alpha _3x_{33}-y_{33}+4} -\frac{\mu v}{\alpha _3x_{33}-y_{33}+4}+O\big ((|w |+|v |+|\mu |)^{3}\big ), \\ g\left( X, Y, \mu _1\right)= & {} -\frac{\beta _1 (\alpha _3x_{33}+2)}{bx_{33}(\alpha _3x_{33}-y_{33}+4)}w^2 -\frac{cx_{33}+\alpha _3x_{33}+2}{x_{33}(\alpha _3x_{33}-y_{33}+4)}wv \\&-\frac{v^2}{\alpha _3x_{33}-y_{33}+4} +\frac{\mu v}{\alpha _3x_{33}-y_{33}+4}, \\ w= & {} -bx_{33}(X+Y+y_{33}\mu _1), \\ v= & {} -(\alpha _3x_{33}+2)X+(2-y_{33})Y-\alpha _3x_{33}y_{33}\mu _1, \\ \mu= & {} (2-2\lambda _2)\mu _1. \end{aligned}$$

Now we determine the center manifold $W^c(0)$ of (16) at the fixed point $(X,Y)=(0,0)$ in a small neighborhood of $\mu _1=0$, which can be expressed as

$$\begin{aligned} W^{c}(0)=\left\{ \left( X, Y, \mu _1\right) \in {\mathbb {R}}^{3}\vert Y=h\left( X,\mu _1\right) , h(0,0)=0, D h(0,0)=0\right\} \end{aligned}$$

for X and $\mu _1$ sufficiently small. h must satisfy

$$\begin{aligned} h\left( -X+f\left( X, h\left( X, \mu _1\right) , \mu _1\right) , \mu _1\right) =\lambda _{2} h\left( X, \mu _1\right) +g\left( X, h\left( X, \mu _1\right) , \mu _1\right) . \end{aligned}$$

(17)

We suppose that h has the form

$$\begin{aligned} h\left( X, \mu _1\right) =s_1 X^{2}+s_2 X \mu _1+s_3 \mu _1^2+O\big ((|X|+|\mu _1 |)^{3}\big ). \end{aligned}$$

(18)

Substituting (18) into (17) and comparing the corresponding coefficients of the like terms in the left-hand and right-hand sides of the resultant, we can obtain

$$\begin{aligned} s_1= & {} \frac{(\alpha _3x_{33}+2) \left\{ \alpha _3x_{33}+2-b\left[ (\alpha _3+c-\beta _1)x_{33}+2\right] \right\} }{\lambda _2^2-1}, \\ s_2= & {} \frac{\begin{array}{l} -2by_{33}(\alpha _3x_{33}+1)[(\alpha _3+c)x_{33}+2] \\ +2(\alpha _3x_{33}+2)[(b\beta _1+\alpha _3)x_{33}y_{33} -\alpha _3x_{33}+y_{33}-2] \end{array}}{(\lambda _2+1)^2}, \\ s_3= & {} \frac{ \begin{array}{l} x_{33}y_{33}\{(\alpha _3x_{33}+2)b\beta _1y_{33} -[(\alpha _3+c)x_{33}+2]b\alpha _3y_{33} \\ +\alpha _3^2x_{33}y_{33} +2\alpha _3(y_{33}-\alpha _3x_{33}-2)\} \end{array}}{\lambda _2^2-1}. \end{aligned}$$

Therefore, the restricted map of (16) on the center manifold $W^c(0)$ is

$$\begin{aligned} F_{2}: X \rightarrow -X+c_{1} X^{2}+c_{2} X \mu _1+c_{3} \mu _1^2+c_{4} X^3+O\left( \left( |X |+|\mu _1 |\right) ^{3}\right) , \end{aligned}$$

(19)

where

$$\begin{aligned} c_1= & {} \frac{(\alpha _3x_{33}+2)[2b+2-by_{33}-(bc-\alpha _3)x_{33}] +b\beta _1x_{33}(y_{33}-2)}{\lambda _2+1}, \\ c_2= & {} \frac{\begin{array}{l} 2(y_{33}-2)b\beta _1x_{33}y_{33} -2by_{33}(\alpha _3x_{33}+1)(cx_{33}+y_{33}-2) \\ +2(\alpha _3x_{33}+2)[\alpha _3x_{33}(y_{33}-1)+y_{33}-2] \end{array}}{\lambda _2+1}, \\ c_3= & {} \frac{\begin{array}{l} x_{33}y_{33}[b\beta _1y_{33}(y_{33}-2)-(cx_{33}+y_{33}-2)b\alpha _3y_{33} \\ +\alpha _3^2x_{33}y_{33}+2\alpha _3(y_{33}-\alpha _3x_{33}-2)] \end{array}}{\lambda _2+1}, \\ c_4= & {} \frac{s_1[2(y_{33}-2)(b\beta _1x_{33}+\alpha _3x_{33}+2) -b(cx_{33}+y_{33}-2)(\alpha _3x_{33}+y_{33})]}{\lambda _2+1}. \end{aligned}$$

In order for map (19) to undergo a flip bifurcation, we require that the two discriminatory quantities $\gamma _1$ and $\gamma _2$ are not zero, where

$$\begin{aligned} \gamma _{1}= & {} \left( \frac{\partial ^{2} F_{2}}{\partial X \mu _1}+\frac{1}{2} \frac{\partial F_{2}}{\partial \mu _1} \frac{\partial ^{2} F_{2}}{\partial X^{2}}\right) \Bigg \vert _{(0,0)}=c_{2}, \\ \gamma _{2}= & {} \left( \frac{1}{6} \frac{\partial ^{3} F_{2}}{\partial X^{3}}+\left( \frac{1}{2} \frac{\partial ^{2} F_{2}}{\partial X^{2}}\right) ^{2}\right) \Bigg \vert _{(0,0)}=c_{4}+c_{1}^{2}. \end{aligned}$$

In summary, from the above discussion and theory in [45, 46], we have derived the following result.

Theorem 5

If $\gamma _1\ne 0$ and $\gamma _2\ne 0$, then system (5) undergoes a flip bifurcation at the fixed point $E_{33}$ when the parameter m varies in a small neighborhood of $m_2$. Moreover, if $\gamma _2>0$ (resp., $\gamma _2<0$), then the period-2 orbits that bifurcate from $E_{33}$ are stable (resp., unstable).

4 Numerical simulations

This section presents the bifurcation diagrams and phase portraits of system (5) to confirm the feasibility of the main results. Further, numerical simulations are provided to investigate the influence of Allee effect on the stability of system (5).

Example 1

(Fold bifurcation at the positive fixed point $E_{31}$) We choose m as the bifurcation parameter. With

$$\begin{aligned} m\in [0,1],\quad b=0.5, \quad c=0.3, \quad u=0.2, \end{aligned}$$

(20)

one obtains the bifurcation value $m_1\approx 0.759$ and system (5) only has one positive fixed point $E_{31}(0.257,0.836)$. It is easy to verify (9) and (10). Further, the eigenvalues of $J(E_{31})$ are $\lambda _1=1$ and $\lambda _2=0.203$. All the conditions of Theorem 4 hold and hence fold bifurcation occurs at $E_{31}$. Fig. 1 agrees very well with Theorem 4. Moreover, we can see that $E_{32}$ is unstable while $E_{33}$ is stable when $m<m_1$ and they disappear when $m>m_1$.

Fig. 1

Fold bifurcation diagram of system (5) in the mx-plane where parameter values are given in (20) with the initial value (0.5, 0.6). The dash curve corresponds to the unstable fixed point $E_{32}$ and the solid curve corresponds to the stable fixed point $E_{33}$. The fold bifurcation value is $m_1\approx 0.759$

Fig. 2

Bifurcation diagram of the logistic model $y\rightarrow (1+m)y-y^2$ with $m\in [1,3]$

Example 2

(Flip bifurcation at the boundary fixed point $E_{1}$) System (5) always has a boundary fixed point $E_{1}(0,m)$. Take $b=0.5$, $c=0.3$, and $u=0.2$. From sect 3.2, we know that flip bifurcation emerges from the fixed point $E_1$ at $m=2$ (see Fig. 2).

Example 3

(Flip bifurcation at the positive fixed point $E_{33}$) Now we choose

$$\begin{aligned} m\in [0,3], \quad b=0.08, \quad c=0.05, \quad u=0.2. \end{aligned}$$

(21)

According to Theorem 1(3.), system (5) has two distinct positive fixed points $E_{32}$ and $E_{33}$ when $m<m^*=5.238$. After some simple calculations, we can find that the flip bifurcation emerges from $E_{33}$ at $m\approx 1.96$. With $m\in [0,3]$, the discriminatory quantities $\gamma _1\ne 0$ and $\gamma _2>0$, and $(b,c,u,m)=(0.08,0.05,0.2,1.96)\in F_{A1}$. Fig. 3 shows the feasibility of Theorem 5. It is easy to see that $E_{33}$ is stable for $m<1.96$. When m reaches 1.96, with the increase of m, two points with a period-2 cycle are bifurcated, and then points with period-4 and period-8 are bifurcated in sequence. Some phase portraits related to Fig. 3 are displayed in Fig. 4, which include orbits of periods 2, 4, and 8. When $m=2.9$, we can see chaotic sets in Fig. 4f.

Fig. 3

The flip bifurcation diagram of system (5) with parameter values given in (21) and the initial value (0.5, 0.6)

Fig. 4

Phase portraits for various values of m corresponding to Fig. 3

Example 4

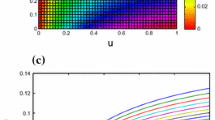
(Effect of Allee effect) We now investigate the influence of Allee effect on the stability of system (5) through numerical simulations. Take the parameter values as

$$\begin{aligned} b=0.08, \quad c=0.05, \quad m=1, \quad u\in \{0,0.5,1,3,5,10\}. \end{aligned}$$

Figure 5 shows the graphs of the prey densities and the predator densities for various u. We considered the cases where system (5) has Allee effect ($u\ne 0$) and no Allee effect ($u=0$), and set up the control groups $u=0.5$ and $u=1$ as a way to see the effect of the magnitude of the Allee constant on properties of system (5). From Fig. 5, we observe that the Allee effect has little influence on the predator species while the local stability of the prey species decreases and its density arrives equilibrium value more slowly as the Allee constant u increases. What’s more, it is clear to see that the larger u is, the lower is the prey level at the fixed point.

Fig. 5

Effect of Allee effect on the prey species and the predator species

5 Conclusion

In this paper, a discrete predator-prey system with Allee effect (on the prey species) and other food resources for predator has been proposed and studied. Conditions on the existence and the stability of fixed points are obtained. Moreover, taking the ratio of the intrinsic growth rates of predator to prey (m) as the bifurcation parameter, the model can undergo fold and flip bifurcations. For fold bifurcation, the number of the positive fixed points changes from two to one and eventually to 0 as m increases (see Fig. 1). According to theoretical analysis and Example 2, we obtain that flip bifurcation can occur at the boundary fixed point $E_1(0,m)$, which means that the prey species is driven to extinct while the predator species first remains stable when m is small and gradually becomes chaotic as m increases through flip bifurcation (see Fig. 2). Further, it is shown that flip bifurcation will occur at the positive fixed point $E_{33}$, which includes orbits of period-2, 4, 8 (see Fig. 3). This means that the positive fixed point $E_{33}$ is stable if m is small, and when m is large enough, system (5) becomes unstable and even chaotic. Such a result is contrary to the conclusion drawn by Ma [1]. In other words, when the prey species is subject to Allee effect, a positive fixed point is likely to be unstable under certain conditions, rather than globally stable, that is, the Allee effect would decrease the stability of system (5), at least for the discrete systems.

In [11], Celik showed that Allee effect has a stabilizing force to system (2) and the fixed points reach stable steady state much faster when the prey species is subject to Allee effect. In this paper, however, we find that Allee effect reduces the population density of prey species at the stable steady state and it takes a longer time to reach the stable steady state when the Allee effect constant increases in the range of low values. Namely, the trajectories of system (5) take more time to arrive at the constant solution as the Allee effect increases in the range of low values, which is different from the results of Celik. Therefore, the discrete predator-prey system where the predator has other food resources presents more complex dynamical behaviors than systems in which the predator only takes the prey species as its unique food resource. When the Allee effect constant is large enough, the prey species becomes extinct because of low reproduction rate. Moreover, the larger the Allee effect constant is, the faster the prey species becomes extinct (see Fig. 5a). It is shown that Allee effect has little impact on predator species (stable steady state levels decrease by only 0.04) (see 5b).

In summary, our results show that the Allee effect and ratio of intrinsic growth rates m combined play an important role on the dynamic behaviors of the proposed model.