A class of accurate Newton–Jarratt-like methods with applications to nonlinear models

Abstract

We propose a class of composite Newton–Jarratt iterative methods with increasing convergence order for approximating the solutions of systems of nonlinear equations. Novelty of the methods is that in each step the order of convergence is increased by an amount of two at the cost of only one additional function evaluation. Moreover, the use of only a single inverse operator in each iteration makes the algorithms computationally more efficient. Theoretical results regarding convergence and computational efficiency are verified through numerical problems, including those that arise from boundary value problems. By way of comparison, it is shown that the novel methods are more efficient than their existing counterparts, especially when applied to solve the large systems of equations.

1 Introduction

Construction of fixed point iterative methods for solving nonlinear equations or systems of nonlinear equations is an interesting and challenging task in numerical analysis and many applied scientific branches. The importance of this subject has led to the development of many numerical methods, most frequently of iterative nature (see Ortega and Rheinboldt 1970; Argyros 2007). With the advancement of computer hardware and software, the problem of solving nonlinear equations by numerical methods has gained an additional importance. In this paper, we consider the problem of approximating a solution $t^*$ of the equation $\mathrm {F}(t)=0$, where $\mathrm {F}:\Omega \subset {\mathbb {R}}^m\rightarrow {\mathbb {R}}^m$, by iterative methods of a high order of convergence. The solution $t^*$ can be obtained as a fixed point of some function $\phi :\Omega \subset {\mathbb {R}}^m\rightarrow {\mathbb {R}}^m$ by means of fixed point iteration

$$\begin{aligned} {t}_{k+1}=\phi (t_k), \quad k= 0,\,1,\,2,\ldots . \end{aligned}$$

There are a variety of iterative methods for solving nonlinear equations. A basic method is the well-known quadratically convergent Newton’s method (Argyros 2007)

$$\begin{aligned} t_{k+1}=M_1^{(2)}(t_k)=t_k-\mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k), \end{aligned}$$

(1)

where $\mathrm {F'}({t})^{-1}$ is the inverse of Fréchet derivative $\mathrm {F'}(t)$ of the function $\mathrm {F}(t).$ This method converges if the initial approximation $t_0$ is closer to solution $t^*$ and $\mathrm {F'}({t})^{-1}$ exists in the neighborhood $\Omega$ of $t^*.$ To achieve the higher order of convergence, a number of modified Newton’s or Newton-like methods have been proposed in the literature, see, for example (Cordero and Torregrosa 2006; Babajee et al. 2010; Behl et al. 2017; Homeier 2004; Darvishi and Barati 2007; Cordero and Torregrosa 2007; Cordero et al. 2010, 2012; Esmaeili and Ahmadi 2015; Noor and Waseem 2009; Alzahrani et al. 2018; Xiao and Yin 2017, 2018; Sharma et al. 2016; Lotfi et al. 2015; Choubey et al. 2018) and references therein. Throughout this paper, we use $M_i^{(p)}$ to denote an i-th iteration method of convergence order p.

The principal goal and motivation in developing iterative methods is to achieve convergence order as high as possible by utilizing number of evaluations as small as possible so that the methods may possess high efficient character. The most obvious barrier in the development of efficient methods is the evaluation of inverse of a matrix since it requires a lengthy calculation work. Therefore, it will turn out to be judicious if we use minimum number of such inversions as possible (Argyros and Regmi 2019; Regmi 2021). With these considerations, here we propose multi-step iterative methods with increasing order of convergence. First, we present a cubically convergent two-step scheme with first step as Jarratt iteration and second is Newton-like iteration. Then on the basis of this scheme a three-step scheme of fifth-order convergence is proposed. Furthermore, in quest of more fast convergence the scheme is generalized to $q+1$ Newton–Jarratt steps with increasing convergence order $2q+1$ $(q \in {\mathbb {N}})$. The novel feature is that in each step the order of convergence is increased by an amount of two at the cost of only one additional function evaluation. Evaluation of the inverse operator $\mathrm {F'}({t})^{-1}$ remains the same throughout which also points to the name ‘methods with frozen inverse operator’.

Rest of the paper is structured as follows. Some basic definitions relevant to the present work are provided in Sect. 2. Section 3 includes development of the third- and fifth-order methods with their analysis of convergence. Then the generalized version consisting of $q+1$-step scheme with convergence order $2q+1$ is presented in Sect. 4. The computational efficiency is discussed and compared with the existing methods in Sect. 5. In Sect. 6, various numerical examples are considered to confirm the theoretical results. Concluding remarks are given in Sect. 7.

2 Basic definitions

2.1 Order of convergence

Let $\{t_k\}_{k\ge 0}$ be a sequence in ${\mathbb {R}}^m$ which converges to $t^*$. Then convergence is called of order p, $p > 1,$ if there exists M, $M > 0,$ and $k_0$ such that

$$\begin{aligned} \Vert t_{k+1}-t^*\Vert \le M \Vert t_k-t^*\Vert ^p \ \ \text {for all} \ \ k\ge k_0 \end{aligned}$$

or

$$\begin{aligned} \Vert \epsilon _{k+1}\Vert \le M \Vert \epsilon _k\Vert ^p \ \ \text {for all} \ \ k\ge k_0, \end{aligned}$$

where $\epsilon _k = t_k - t^*$. The convergence is called linear if $p = 1$ and there exists M such that $0< M < 1$.

2.2 Error equation

Let $\epsilon _k = t_k - t^*$ be the error in the k-th iteration, we call the relation

$$\begin{aligned} \epsilon _{k+1} = L \epsilon _k^p + O(\epsilon _k^{p+1}), \end{aligned}$$

as the error equation. Here, p is the order of convergence, L is a p -linear function, i.e. $L\in {\mathcal {L}}({\mathbb {R}}^m \times {\mathop {\cdot \,\cdot \,\cdot \,\cdot }\limits ^{p-times}}\times {\mathbb {R}}^m, {\mathbb {R}}^m )$, ${\mathcal {L}}$ denotes the set of bounded linear functions.

2.3 Computational order of convergence

Let $t^*$ be a zero of the function $\mathrm {F}$ and suppose that $t_{n-1}$, $t_{n}$, $t_{n+1}$ and $t_{n+2}$ are the four consecutive iterations close to $t^*.$ Then, the computational order of convergence (COC) can be approximated using the formula (see Weerkoon and Fernando 2000)

$$\begin{aligned} \mathrm{COC}=\frac{\log \big (\Vert t_{k+2}-t_{k+1}\Vert /\Vert t_{k+1}-t_{k}\Vert \big )}{\log \big (\Vert t_{k+1}-t_{k}\Vert /\Vert t_{k}-t_{k-1}\Vert \big )}. \end{aligned}$$

2.4 Computational efficiency

Computational efficiency of an iterative method is measured by the efficiency index $E = p^{1/C}$ or $E=\frac{\log p}{C}$ (see Ostrowski 1960), where p is the order of convergence and C is the computational cost per iteration.

3 Formulation of basic methods

In what follows first we will introduce the basic third- and fifth-order iterative methods. These are called basic methods since they pave the way for the generalized algorithm to be presented in next section.

3.1 Third-order scheme

Our aim is to develop a method which accelerates the convergence rate of Newton method (1) using minimum number of function evaluations and inverse operators. Thus, it will turn out to be judicious if we consider the two-step iteration scheme of the type

$$\begin{aligned}&w_k = \ t_k- \frac{2}{3}\mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\nonumber \\&t_{k+1} = \ w_k-(a_1 \, \text {I} +a_2 Q_k)\mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k), \end{aligned}$$

(2)

where $Q_{k}=\mathrm {F'}(t_k)^{-1}\mathrm {F'}(w_k)$, $a_1$ and $a_2$ are arbitrary constants and $\text {I}$ is an $m\times m$ identity matrix. Idea of the first step is taken from the well-known Jarratt method (Cordero et al. 2010) whereas the second step is based on Newton-like iteration.

We introduce some known notations and results (Cordero et al. 2010), which are needed to obtain the convergence order of new method. Let $\mathrm {F}:\Omega \subseteq {\mathbb {R}}^{m}\rightarrow {\mathbb {R}}^{m}$ be sufficiently differentiable in $\Omega$. The q-th derivative of $\mathrm {F}$ at $u\in {\mathbb {R}}^m$, $q\ge 1$, is the q-linear function $\mathrm {F}^{(q)}(u): {\mathbb {R}}^{m}\times \cdots \times {\mathbb {R}}^{m}\rightarrow {\mathbb {R}}^{m}$ such that $\mathrm {F}^{(q)}(u)(v_1,\ldots ,v_q )\in {\mathbb {R}}^m$. It is easy to observe that

• (i) $\mathrm {F}^{(q)}(u)(v_1,\ldots ,v_{q})\in {\mathcal {L}}({\mathbb {R}}^m)$,

• (ii) $\mathrm {F}^{(q)}(u)(v_{\sigma (1)},\ldots ,v_{\sigma (q)} )=\mathrm {F}^{(q)}(u)(v_1,\ldots ,v_{q})$, for all permutation $\sigma$ of $\{1,2,\ldots ,q\}$.

From the above properties, we can use the following notation:

• (a) $\mathrm {F}^{(q)}(u)(v_1,\ldots ,v_{q})=\mathrm {F}^{(q)}(u)v_1,\ldots ,v_{q}$,

• (b) $\mathrm {F}^{(q)}(u)v^{q-1}\mathrm {F}^{(p)}v^p =\mathrm {F}^{(q)}(u)\mathrm {F}^{(p)}(u)v^{q+p-1}$.

On the other hand, for $t^*+h\in {\mathbb {R}}^{m}$ lying in a neighborhood of a solution $t^*$ of $\mathrm {F}(t)=0$, we can apply Taylor’s expansion and assuming that the Jacobian matrix $\mathrm {F'}(t^*)$ is nonsingular, we have

$$\begin{aligned} \mathrm {F}(t^*+h)=\mathrm {F'}(t^*)\bigg [h+\sum _{q=2}^{p-1}K_qh^q \bigg ]+O(h^p), \end{aligned}$$

where $K_q=\frac{1}{q!}\mathrm {F'}(t^*)^{-1}\mathrm {F}^{(q)}(t^*)$, $q\ge 2$. We observe that $K_qh^q\in {\mathbb {R}}^m$ since $\mathrm {F}^{(q)}(t^*)\in {\mathcal {L}}({\mathbb {R}}^{m}\times \cdots \times {\mathbb {R}}^{m}, {\mathbb {R}}^{m})$ and $\mathrm {F'}(t^*)^{-1}\in {\mathcal {L}}({\mathbb {R}}^{m})$. In addition, we can express $\mathrm {F'}$ as

$$\begin{aligned} \mathrm {F'}(t^*+h)=\mathrm {F'}(t^*)\bigg [ \text {I}+\sum _{q=2}^{p-1}qK_qh^{q-1} \bigg ]+O(h^{p-1}), \end{aligned}$$

(3)

where $\text {I}$ is the identity matrix. Therefore, $qK_qh^{q-1}\in {\mathcal {L}}({\mathbb {R}}^{m})$. From (3), we obtain

$$\begin{aligned} \mathrm {F'}(t^*+h)^{-1}=\, \big [ \text {I}+X_2h+X_3h^2+X_4h^3+\cdots \big ]\mathrm {F'}(t^*)^{-1}+O(h^{p}), \end{aligned}$$

(4)

where

$$\begin{aligned} X_2=&\, -2K_2,\nonumber \\ X_3=&\,\ 4K_2^2-3K_3,\nonumber \\ X_4=&\, -8K_2^3+6K_2K_3+6K_3K_2-4K_4,\nonumber \\ \vdots \end{aligned}$$

(5)

To analyze the convergence properties of scheme (2), we prove the following theorem:

Theorem 1

Let the function $\mathrm {F}:\Omega \subset {\mathbb {R}}^m\rightarrow {\mathbb {R}}^m$ be sufficiently differentiable in an open neighborhood $\Omega$ of its zero $t^*$. Suppose that $\mathrm {F'}(t)$ is continuous and nonsingular in $t^*$. If an initial approximation $t_0$ is sufficiently close to $t^*$, then order of convergence of method (2) is at least 3, provided $a_1=\frac{13}{12}$ and $a_2=-\frac{3}{4}$.

Proof

Let $\epsilon _k = t_k- t^*$ and $\Gamma =\mathrm {F'}(t^*)^{-1}$ exist. Developing $\mathrm {F}(t_k)$ in a neighborhood of $t^*$, we have that

$$\begin{aligned} \mathrm {F}(t_k)=\mathrm {F'}(t^*)[\epsilon _k+A_2 \epsilon _k^2+A_3 \epsilon _k^3+A_4 \epsilon _k^4+A_5 \epsilon _k^5+O(\epsilon _k^6)], \end{aligned}$$

(6)

where $A_q=\frac{1}{q!}\Gamma \mathrm {F}^{(q)}(t^*)$, $q=2, 3, \ldots$, $\mathrm {F}^{(q)}(t^*) \in {\mathcal {L}}({\mathbb {R}}^m \times {\mathop {\cdot \,\cdot \,\cdot \,\cdot }\limits ^{q-times}}\times {\mathbb {R}}^m, {\mathbb {R}}^m )$, $\Gamma \in {\mathcal {L}}({\mathbb {R}}^m, {\mathbb {R}}^m)$ and $A_q (\epsilon _k)^q= A_q(\epsilon _k,\epsilon _k,{\mathop {\cdot \,\cdot \,\cdot \,\cdot }\limits ^{q-times}},\epsilon _k)\in {\mathbb {R}}^m$ with   $\epsilon _k \in {\mathbb {R}}^m$. Also,

$$\begin{aligned} \mathrm {F'}(t_k)&= \mathrm {F'}(t^*)[ \, \text {I}+2 A_2 \epsilon _k+3A_3 \epsilon _k^2+4A_4 \epsilon _k^3+5A_5 \epsilon _k^4+O(\epsilon _k^5)], \end{aligned}$$

(7)

$$\begin{aligned} \mathrm {F'}(t_k)^{-1}&= [ \, \text {I}+B_1 \epsilon _k +B_2 \epsilon _k^2+B_3 \epsilon _k^3+B_4 \epsilon _k^4+O(\epsilon _k^5)]\Gamma , \end{aligned}$$

(8)

where $B_1 = -2A_2$, $B_2 = 4A_2^2-3A_3$, $B_3 = -(8A_2^3-6A_2A_3-6A_3A_2+4A_4)$ and $B_4 = (16A_2^4+9A_3^2-12A_2^2A_3-12A_2A_3A_2-12A_3A_2^2+8A_2A_4+8A_4A_2-5A_5).$ Applying (6) and (8) in the first step of (2), we have

$$\begin{aligned} \epsilon _{w_k} =&w_k-t^* \nonumber \\ =&\frac{1}{3} \epsilon _k+ \frac{2}{3} A_2 \epsilon _k^2 -\frac{4}{3}(A_2^2-A_3) \epsilon _k^3+\frac{2}{3}(4A_2^3-4A_2A_3-3A_3A_2+3A_4)\epsilon _k^4 +O(\epsilon _k^5). \end{aligned}$$

(9)

Taylor expansions of $\mathrm {F}(w_k)$ and $\mathrm {F'}(w_k)$ about $t^*$ yield

$$\begin{aligned} \mathrm {F}(w_k)=\mathrm {F'}(t^*)[\epsilon _{w_k}+A_2 \epsilon _{w_k}^2+A_3 \epsilon _{w_k}^3+A_4 \epsilon _{w_k}^4+A_5 \epsilon _{w_k}^5+O(\epsilon _{w_k}^6)], \end{aligned}$$

(10)

and

$$\begin{aligned} \mathrm {F'}(w_k)=\mathrm {F'}(t^*)[ \, \text {I}+2 A_2 \epsilon _{w_k}+3A_3 \epsilon _{w_k}^2+4A_4 \epsilon _{w_k}^3+5A_5 \epsilon _{w_k}^4+O(\epsilon _{w_k}^5)]. \end{aligned}$$

(11)

Combining (8) and (11),

$$\begin{aligned} Q_k= \ \mathrm {F'}(t_k)^{-1}\mathrm {F'}(w_k) =&\text {I} -\frac{4}{3} A_2 \epsilon _k+\frac{4}{3} (3A_2^2-2A_3)\epsilon _k^2 \nonumber \\&-\frac{8}{27} (36A_2^3-27A_2A_3-18A_3A_2+13A_4)\epsilon _k^3+O(\epsilon _k^4). \end{aligned}$$

(12)

Then simple calculations yield

$$\begin{aligned} a_1 \text {I} +a_2 Q_k&= (a_1+a_2) \, \text {I}-\frac{4a_2}{3} A_2 \epsilon _k+\frac{4a_2}{3} (3A_2^2-2A_3)\epsilon _k^2 \nonumber \\&\quad -\frac{8 a_2}{27}(36A_2^3-27A_2A_3-18A_3A_2+13A_4)\epsilon _k^3+O(\epsilon _k^4). \end{aligned}$$

(13)

Substituting (6), (8), (9) and (13) in second step of (2), we obtain

$$\begin{aligned} \epsilon _{k+1} =&\Big (\frac{1}{3}-a_1-a_2\Big ) \epsilon _k+ \frac{1}{3}(2+3a_1+7 a_2)A_2 \epsilon _k^2\nonumber \\&-\frac{2}{3}\big ((2+3a_1+11a_2)A_2^2-(2+3a_1+7a_2)A_3\big )\epsilon _k^3 \nonumber \\&+O(\epsilon _k^4). \end{aligned}$$

(14)

It easy to prove that for the parameters $a_1=\frac{13}{12}$ and $a_2=-\frac{3}{4}$, the error equation (14) produces the maximum order of convergence. For these values of parameters above equation reduces to

$$\begin{aligned} \epsilon _{k+1} = \ 2A_2^2 \epsilon _k^3+O(\epsilon _k^4). \end{aligned}$$

(15)

This proves the third order of convergence. $\square$

Thus, the proposed Newton–Jarratt third-order method (2) is finally presented as

$$\begin{aligned}&w_k = \ t_k- \frac{2}{3} \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\nonumber \\&x_{k+1} = \ M_1^{(3)}(t_k,w_k) = \ w_k-\frac{1}{12}(13 \ \text {I} -9 Q_k)\mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k). \end{aligned}$$

(16)

In terms of computational cost this formula uses one function, two derivatives and one matrix inversion per iteration.

3.2 Fifth-order scheme

Based on the third-order scheme (16), we consider the following three-step Newton–Jarratt composition:

$$\begin{aligned}&w_k = \ t_k- \frac{2}{3} \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\nonumber \\&y_k = \ M_1^{(3)}(t_k,w_k),\nonumber \\&t_{k+1} = \ y_k- \big (d_1 \, \text {I} +d_2 Q_k\big )\mathrm {F'}(t_k)^{-1}\mathrm {F}(y_k), \end{aligned}$$

(17)

where $d_1$ and $d_2$ are some parameters to be determined. This new scheme requires one extra function evaluation in addition to the evaluations of scheme (16). Following theorem proves convergence properties of (17).

Theorem 2

Let the function $\mathrm {F}:\Omega \subset {\mathbb {R}}^m\rightarrow {\mathbb {R}}^m$ be sufficiently differentiable in an open neighborhood $\Omega$ of its zero $t^*$. Suppose that $\mathrm {F'}(t)$ is continuous and nonsingular in $t^*$. If an initial approximation $t_0$ is sufficiently close to $t^*$, then order of convergence of method (17) is at least 5, provided that $d_1=\frac{5}{2}$ and $d_2=-\frac{3}{2}$.

Proof

From (15), error equation of second step of (16) can be written as

$$\begin{aligned} \epsilon _{y_k} = \ 2A_2^2 \epsilon _k^3+O(\epsilon _k^4). \end{aligned}$$

(18)

Let $\epsilon _{y_k}= y_k- t^*.$ Then, the Taylor expansion of $\mathrm {F}(y_k)$ about $t^*$ yields

$$\begin{aligned} \mathrm {F}(y_k)= \ \mathrm {F'}(t^*)[\epsilon _{y_k}+A_2 \epsilon _{y_k}^2+O(\epsilon _{y_k}^3)]. \end{aligned}$$

(19)

Using Eqs.  (8), (12), (18) and (19) in third step of (17), we obtain

$$\begin{aligned} \epsilon _{k+1}&= -2(d_1+d_2-1)A_2^2\epsilon _k^3+\frac{1}{9} \bigg (3(39d_1+47d_2-27)A_2^2-36(d_1+d_2-1)A_2A_3 \nonumber \\&\quad -27(d_1+d_2-1)A_3A_2-(d_1+d_2-1)A_4\bigg )\epsilon _k^4-\frac{2}{27} \bigg (9(84d_1+122d_2-45)A_2^4 \nonumber \\&\quad -18(48d_1+59d_2-33)A_3A_2^2+(123d_1+121d_2-126)A_2A_4\nonumber \\&\quad +(d_1+d_2-1) (81A_3^2+4A_5)\bigg )\epsilon _k^5 \nonumber \\&\quad +O(\epsilon _k^6). \end{aligned}$$

(20)

It can be easily shown that for parameters $d_1 =\frac{5}{2}$ and $d_2 =-\frac{3}{2}$, the error equation (20) produces the maximum order of convergence. For this set of parameters, Eq. (20) reduces to

$$\begin{aligned} \epsilon _{k+1} = \ 2(6A_2^2-A_3)A_2^2 \epsilon _k^5+O(\epsilon _k^6). \end{aligned}$$

(21)

Hence the required result follows. $\square$

Thus, the Newton–Jarratt fifth-order method is expressed as

$$\begin{aligned} w_k&= \ t_k- \frac{2}{3}\mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\nonumber \\ y_k&= \ M_1^{(3)}(t_k,w_k),\nonumber \\ t_{k+1}&= \ M_1^{(5)}(t_k,w_k, y_k) = \ y_k-\frac{1}{2}\big (5 \, \text {I} -3 \, Q_k\big )\mathrm {F'}(t_k)^{-1}\mathrm {F}(y_k). \end{aligned}$$

(22)

In terms of computational cost this formula requires two functions, two derivatives and one inverse operator per iteration.

4 Generalized method

The generalized $q+1$-step Newton–Jarratt composite scheme, with the base as three-step scheme (22), can be expressed as follows:

$$\begin{aligned} w_k^{(0)}&= \ t_k - \frac{2}{3}\mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\nonumber \\ w_k^{(1)}&= \ w_k - \frac{1}{12}(13 \ \text {I}-9 Q_k)\mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\nonumber \\ w_k^{(2)}&= \ w_k^{(1)} - \varphi (t_k,w_k)\mathrm {F'}(t_k)^{-1}\mathrm {F}(w_k^{(1)}),\nonumber \\ w_k^{(3)}&= \ w_k^{(2)}-\varphi (t_k,w_k)\mathrm {F'}(t_k)^{-1}\mathrm {F}(w_k^{(2)}),\nonumber \\ w_k^{(4)}&= \ w_k^{(3)}-\varphi (t_k,w_k)\mathrm {F'}(t_k)^{-1}\mathrm {F}(w_k^{(3)}),\nonumber \\ ......&.........................................................\nonumber \\ w_k^{(q-1)}&= \ w_k^{(q-2)}-\varphi (t_k,w_k)\mathrm {F'}(t_k)^{-1}\mathrm {F}(w_k^{(q-2)}),\nonumber \\ w_k^{(q)}&= \ t_{k+1}= \ w_k^{(q-1)}-\varphi (t_k,w_k)\mathrm {F'}(t_k)^{-1}\mathrm {F}(w_k^{(q-1)}), \ \ \end{aligned}$$

(23)

where $q\ge 2$, $w_k^{(0)}=w_k$, $Q_{k}=\mathrm {F'}(t_k)^{-1}\mathrm {F'}(w_k)$ and $\varphi (t_k,w_k)= \frac{1}{2}\big (5 \, \text {I} -3 \, Q_k\big ).$

To analyze the convergence property, we prove the following theorem:

Theorem 3

Let the function $\mathrm {F}:\Omega \subset {\mathbb {R}}^m\rightarrow {\mathbb {R}}^m$ be sufficiently differentiable in an open neighborhood $\Omega$ of its zero $t^*$. Suppose $\mathrm {F'}(t)$ is continuous and nonsingular in $t^*$. If an initial approximation $t_0$ is sufficiently close to $t^*$, the sequence $\{t_k\}$ generated by method (23) for $t_0\in \Omega$ converges to $t^*$ with order $2q+1$ for $q\in {\mathbb {N}}$.

Proof

Let $\epsilon _k= \, t_k-t^*,$ $\epsilon _{w_k^{(q-1)}}= w_k^{(q-1)}- t^*.$ Taylor’s expansion of $\mathrm {F}(w_k^{(q-1)})$ about $t^*$ yields

$$\begin{aligned} \mathrm {F}(w_k^{(q-1)})=\mathrm {F'}(t^*)\big [(w_k^{(q-1)}-t^*)+A_2(w_k^{(q-1)}-t^*)^2+\cdots \big ]. \end{aligned}$$

(24)

Using (8) and (24), we have that

$$\begin{aligned} \mathrm {F'}(t_k)^{-1}\mathrm {F}(w_k^{(q-1)})&= [\,\text {I}+B_1 \epsilon _k+B_2 \epsilon _k^2+B_3 \epsilon _k^3+B_4 \epsilon _k^4+O(\epsilon _k^5)]\Gamma \nonumber \\&\quad \times \mathrm {F'}(t^*)\bigg [(w_k^{(q-1)}-t^*)+A_2(w_k^{(q-1)}-t^*)^2+\cdots \bigg ] \nonumber \\&= (w_k^{(q-1)}-t^*) -\bigg (2A_2 \epsilon _k-(4A_2^2-3A_3)\epsilon _k^2\nonumber \\&\quad +(8A_2^3-6A_2A_3-6A_3A_2+4A_4)\epsilon _k^3+\cdots \bigg ) \nonumber \\&\quad \times (w_k^{(q-1)}-t^*)+ A_2 (w_k^{(q-1)}-t^*)^2-2A_2 \epsilon _k A_2 (w_k^{(q-1)}-t^*)^2+\cdots . \end{aligned}$$

(25)

We write Eq. (13) as

$$\begin{aligned} \varphi (t_k,w_k)= & {} \text {I}+2 A_2 \epsilon _k-2 (3A_2^2-2A_3)\epsilon _k^2\nonumber \\&+\frac{4}{9}(36A_2^3-27A_2A_3-18A_3A_2+13A_4)\epsilon _k^3+O(\epsilon _k^4). \end{aligned}$$

(26)

Using Eqs. (25) and (26), we get

$$\begin{aligned}&\varphi (t_k,w_k) \mathrm {F'}(t_k)^{-1}\mathrm {F}(w_k^{(q-1)}) \nonumber \\&\quad = (w_k^{(q-1)}-t^*)+\Big ((-6A_2^2+A_3)\epsilon _{k}^2+\frac{2}{9}\bigg (216A_2^3-108A_2A_3-99A_3A_2 \nonumber \\&\qquad +44A_4\bigg )\epsilon _{k}^3+O(\epsilon _{k}^4)\Big )(w_k^{(q-1)}-t^*)+\cdots . \end{aligned}$$

(27)

Then last step of (23) yields

$$\begin{aligned} w_k^{(q)}-t^*= & {} \Bigg [(6A_2^2-A_3)\epsilon _{k}^2-\frac{2}{9}\bigg (216A_2^3-108A_2A_3\\&\quad -99A_3A_2+44A_4\bigg ) \epsilon _{k}^3+\cdots \Bigg ](w_k^{(q-1)}-t^*)+\cdots . \end{aligned}$$

For $q=3,4,5$, we obtain the corresponding error equations as

$$\begin{aligned} w_k^{(3)}-t^* =&\Bigg [(6A_2^2-A_3)\epsilon _{k}^2-\frac{2}{9}\bigg (216A_2^3-108A_2A_3\\&\quad -99A_3A_2+44A_4\bigg )\epsilon _{k}^3+\cdots \Bigg ](w_k^{(2)}-t^*)+\cdots \\ =&2 (6A_2^2-A_3)^2 A_2^2 \epsilon _k^{7}+O(\epsilon _k^{8}),\\ w_k^{(4)}-t^* =&\Bigg [(6A_2^2-A_3)\epsilon _{k}^2-\frac{2}{9}\bigg (216A_2^3-108A_2A_3\\&\quad -99A_3A_2+44A_4\bigg )\epsilon _{k}^3+\cdots \Bigg ](w_k^{(3)}-t^*)+\cdots \\ =&2 (6A_2^2-A_3)^3 A_2^2 \epsilon _k^{9}+O(\epsilon _k^{10}) \end{aligned}$$

and

$$\begin{aligned} w_k^{(5)}-t^* =&\Bigg [(6A_2^2-A_3)\epsilon _{k}^2-\frac{2}{9}\bigg (216A_2^3-108A_2A_3\\&\quad -99A_3A_2+44A_4\bigg )\epsilon _{k}^3+\cdots \Bigg ](w_k^{(4)}-t^*)+\cdots \\ =&2 (6A_2^2-A_3)^4 A_2^2 \epsilon _k^{11}+O(\epsilon _k^{12}). \end{aligned}$$

Proceeding by induction, we have

$$\begin{aligned} \epsilon _{k+1} = w_k^{(q)}-t^* = 2 (6A_2^2-A_3)^{q-1} A_2^2 \epsilon _k^{2q+1}+O(\epsilon _k^{2q+2}). \end{aligned}$$

Hence, the result follows. $\square$

It is clear that the generalized scheme requires the information of q functions, two derivatives and only one matrix inversion per iteration. The single use of inverse operator throughout the iteration also justifies the name ‘method with frozen inverse operator’ of the above scheme

5 Computational efficiency

Ranking of numerical methods, based on their computational efficiency, is in many cases a difficult task since the quality of an algorithm depends on many parameters. Considering root-solvers, Brent (1973) said that “...the method with the higher efficiency is not always the method with the higher order". Sometimes a great accuracy of the sought results is not a main target whereas in many cases numerical stability of implemented algorithms is the preferable feature.

Computational efficiency of a root-solver can be defined in various manners, but always proportional to order of convergence p and inversely proportional to computational cost C per iteration—the number of function evaluations taking with certain weights. Traub (1964) introduced coefficient of efficiency by the ratio

$$\begin{aligned} E_T = \frac{p}{C}, \end{aligned}$$

whereas Ostrowski (1960) dealt with alternative definitions

$$\begin{aligned} E_{O_1} = p^{1/C} \ \text {and} \ E_{O_2} = \frac{\log p}{C}. \end{aligned}$$

An interesting question arises: Which of these definitions describes computational efficiency in the best way in practice when iterative methods are implemented on digital computers? This will be clarified in what follows.

To solve nonlinear equations, assuming that the tested equation has a solution $t^*$ contained in an interval (n-cube or n-ball in general) of unit diameter. Starting with an initial approximation $t_0$ to $t^*$, a stopping criterion is given by

$$\begin{aligned} ||t_k -t^* || \le \tau = 10^{-d}, \end{aligned}$$

where k is the iteration index, $\tau$ is the required accuracy, and d is the number of significant decimal digits of the approximation $t_k$. Assume that $||t_0 -t^* || \approx 10^{-1}$ and let p be the order of convergence of the applied iterative method. Then the (theoretical) number of iterative steps, necessary to reach the accuracy $\tau$, can be calculated approximately from the relation $10^{-d} = 10^{-p^k}$ as $k \approx \log d/\log p.$ Taking into account that the computational efficiency is proportional to the reciprocal value of the total computational cost kC of the completed iterative process consisting of k iterative steps, one gets the estimation of computer efficiency,

$$\begin{aligned} E = \frac{1}{kC} = \frac{1}{\log d}\frac{\log p}{C}. \end{aligned}$$

(28)

For the function $F(t)=(f_1(t), f_2(t),\ldots , f_m(t))^\mathrm{{T}}$, where $t=(t_1, t_2, \ldots , t_m)^\mathrm{{T}}$, the computational cost C is computed as

$$\begin{aligned} \text{ C }(\mu _0,\mu _1,m,l)=P_0(m)\mu _0+P_1(m)\mu _1+P(m,l), \end{aligned}$$

(29)

where $P_0(m)$ represents the number of evaluations of scalar functions used in the evaluation of F, $P_1(m)$ is the number of evaluations of scalar functions of $F'$, i.e. $\frac{\partial f_i}{\partial t_j}$, $1\leqslant i,j \leqslant m$ and P(m, l) represents the number of products or quotients needed per iteration. To express the value of $C(\mu _0,\mu _1,m,l)$ in terms of products, the ratios $\mu _0>0$ and $\mu _1>0$ between products and evaluations and a ratio $l\ge 1$ between products and quotients are required.

It is clear form the above discussion that estimating the computational efficiency of iterative methods for some fixed accuracy, it is sufficient to compare the values of $\log p/C$. This means that the second Ostrowski’s formula $E_{O_2} = \log p/C$ is preferable in the sense of the best fitting a real CPU time. Let us note that this formula was used in many manuscripts and books, see, e.g., Brent (1973) and McNamee (2007).

We shall make use of the Definition (28) for assessing the computational efficiency of presented methods. To do this we must consider all possible factors which contribute to the total cost of computation. For example, to compute F in any iterative method we need to calculate m scalar functions. The number of scalar evaluations is $m^2$ for any new derivative $F'$. To compute an inverse linear operator we solve a linear system, where we have $m(m - 1)(2m - 1)/6$ products and $m(m - 1)/2$ quotients in the LU decomposition and $m(m - 1)$ products and m quotients in the resolution of two triangular linear systems. We must add $m^2$ products for multiplication of a matrix with a vector or of a matrix by a scalar and m products for multiplication of a vector by a scalar.

To demonstrate the computational efficiency we consider the third, fifth- and seventh-order methods of the family (23) and compare the efficiency with existing third, fifth- and seventh-order methods. For example, third-order method $M_1^{(3)}$ is compared with third-order methods by Homeier (2004), Cordero and Torregrosa (2007), Noor and Waseem (2009) and Xiao and Yin (2017); fifth-order method $M_1^{(5)}$ with fifth-order methods by Cordero et al. (2010, 2012), Sharma and Gupta (2014) and Xiao and Yin (2018); and seventh-order $M_1^{(7)}$ with seventh-order method by Xiao and Yin (2015). In addition, the new methods are also compared with each other. The considered existing methods are expressed as follows.

Third-order Homeier method (Homeier 2004):

$$\begin{aligned} y_k&= \ t_k-\frac{1}{2} \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\\ t_{k+1}&= \ M_2^{(3)}(t_k,y_k) = \ t_k- \mathrm {F'}(y_k)^{-1}\mathrm {F}(t_k). \end{aligned}$$

Third-order methods by (Cordero and Torregrosa 2007):

$$\begin{aligned} y_k&= \ t_k- \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\\ t_{k+1}&= \ M_3^{(3)}(t_k,y_k) = \ t_k-6\bigg [\mathrm {F'}(t_k)+4\mathrm {F'}\bigg (\frac{t_k+y_k}{2}\bigg )+\mathrm {F'}(y_k)\bigg ]^{-1}\mathrm {F}(t_k) \end{aligned}$$

and

$$\begin{aligned} y_k&= \ t_k- \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\\ t_{k+1}&= \ M_4^{(3)}(t_k,y_k) = \ t_k-3\bigg [2\mathrm {F'}\bigg (\frac{3t_k+y_k}{4}\bigg )-\mathrm {F'}\bigg (\frac{t_k+y_k}{2}\bigg )+2\mathrm {F'}\bigg (\frac{t_k+3y_k}{4}\bigg )\bigg ]^{-1} \mathrm {F}(t_k). \end{aligned}$$

Third-order Noor–Waseem method (Noor and Waseem 2009):

$$\begin{aligned} y_k&= \ t_k- \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\\ t_{k+1}&= \ M_5^{(3)}(t_k,y_k) = \ t_k-4\bigg [3\mathrm {F'}\bigg (\frac{2t_k+y_k}{3}\bigg )+\mathrm {F'}(y_k)\bigg ]^{-1}\mathrm {F}(t_k). \end{aligned}$$

Third-order Xiao–Yin method (Xiao and Yin 2017):

$$\begin{aligned} y_k&= \ t_k- \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\\ t_{k+1}&= \ M_6^{(3)}(t_k,y_k) = \ t_k-\frac{2}{3}\big (\big (3\mathrm {F'}(y_k)-\mathrm {F'}(t_k)\big )^{-1}+\mathrm {F'}(t_k)^{-1}\big )\mathrm {F}(t_k). \end{aligned}$$

Fifth-order methods by (Cordero et al. 2010, 2012):

$$\begin{aligned} y_k&= \ t_k- \frac{2}{3} \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\\ z_k&= \ t_k-\frac{1}{2}\big (3\mathrm {F'}(y_{k})-\mathrm {F'}(t_{k})\big )^{-1}\big (3\mathrm {F'}(y_{k})+\mathrm {F'}(t_{k})\big )\mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\\ t_{k+1}&= \ M_2^{(5)}(t_k,y_k, z_k) = \ z_k-\big (\alpha \mathrm {F'}(y_{k})+\beta \mathrm {F'}(t_k)\big )^{-1}\mathrm {F}(z_k) \end{aligned}$$

and

$$\begin{aligned} y_k&= \ t_k- \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\\ z_k&= \ t_k-2\big (\mathrm {F'}(y_{k})+\mathrm {F'}(t_{k})\big )^{-1}\mathrm {F}(t_k),\\ t_{k+1}&= \ M_3^{(5)}(t_k,y_k, z_k) = \ z_k-\mathrm {F'}(y_{k})^{-1}\mathrm {F}(z_k), \end{aligned}$$

where $\alpha = \beta =0.5$.

Fifth-order Sharma–Gupta method (Sharma and Gupta 2014):

$$\begin{aligned} y_k&= \ t_k- \frac{1}{2} \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\\ z_k&= \ t_k- \mathrm {F'}(y_k)^{-1}\mathrm {F}(t_k),\\ t_{k+1}&= \ M_4^{(5)}(t_k,y_k,z_k) = z_k-\big (2\mathrm {F'}(y_k)^{-1}-\mathrm {F'}(t_k)^{-1}\big )\mathrm {F}(z_k). \end{aligned}$$

Fifth-order Xiao–Yin method (Xiao and Yin 2018):

$$\begin{aligned} y_k&= \ t_k- \frac{2}{3} \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\\ z_k&= \ t_k- \frac{1}{4} \big (3\mathrm {F'}(y_k)^{-1}+\mathrm {F'}(t_k)^{-1}\big )\mathrm {F}(t_k),\\ t_{k+1}&= \ M_5^{(5)}(t_k,y_k,z_k) = z_k-\frac{1}{2}\big (3 \, \mathrm {F'}(y_k)^{-1}-\mathrm {F'}(t_k)^{-1}\big )\mathrm {F}(z_k). \end{aligned}$$

Seventh-order Xiao–Yin method (Xiao and Yin 2015):

$$\begin{aligned} y_k&= \ t_k- \frac{1}{2} \mathrm {F'}(t_k)^{-1}\mathrm {F}(t_k),\\ z_k&= \ t_k- \mathrm {F'}(y_k)^{-1}\mathrm {F}(t_k),\\ x_k&= \ z_k- \big (2\mathrm {F'}(y_k)^{-1}-\mathrm {F'}(t_k)^{-1}\big )\mathrm {F}(z_k),\\ t_{k+1}&= \ M_2^{(7)}(t_k,y_k,z_k,x_k) = x_k-\big (2\mathrm {F'}(y_k)^{-1}-\mathrm {F'}(t_k)^{-1}\big )\mathrm {F}(x_k). \end{aligned}$$

Denoting the efficiency indices of the methods $M_i^{(p)}$ ($p=3,5,7$ and $i=1,2,3,4,5$) by ${\mathcal {E}}_i^{(p)}$ and computational costs by $C_i^{(p)}$. Then taking into account above considerations, we obtain

$$\begin{aligned} C_1^{(3)}&= \ m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 15m+7+3l(3+m)) \ \text {and} \ {\mathcal {E}}_1^{(3)}= \frac{1}{D}\frac{\log 3}{C_1^{(3)}}, \\ C_2^{(3)}&= \ m \mu _0+2 m^2 \mu _1 + \frac{m}{3} (2m^2 + 3m-2+3l(1+m)) \ \text {and} \ {\mathcal {E}}_2^{(3)}= \frac{1}{D}\frac{\log 3}{C_2^{(3)}}, \\ C_3^{(3)}&= \ m \mu _0+3 m^2 \mu _1 + \frac{m}{3} (2m^2 + 6m+1+3l(1+m)) \ \text {and} \ {\mathcal {E}}_3^{(3)}= \frac{1}{D}\frac{\log 3}{C_3^{(3)}}, \\ C_4^{(3)}&= \ m \mu _0+4 m^2 \mu _1 + \frac{m}{3} (2m^2 + 9m+13+3l(1+m)) \ \text {and} \ {\mathcal {E}}_4^{(3)}= \frac{1}{D}\frac{\log 3}{C_4^{(3)}}, \\ C_5^{(3)}&= \ m \mu _0+3 m^2 \mu _1 + \frac{m}{3} (2m^2 + 6m+4+3l(1+m)) \ \text {and} \ {\mathcal {E}}_5^{(3)}= \frac{1}{D}\frac{\log 3}{C_5^{(3)}}, \\ C_6^{(3)}&= \ m \mu _0+2 m^2 \mu _1 + \frac{m}{3} (2m^2 + 6m-2+3l(1+m)) \ \text {and} \ {\mathcal {E}}_6^{(3)}= \frac{1}{D}\frac{\log 3}{C_6^{(3)}}, \\ C_1^{(5)}&= \ 2 m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 33m+7+3l(7+m)) \ \text {and} \ {\mathcal {E}}_1^{(5)}= \frac{1}{D}\frac{\log 5}{C_1^{(5)}}, \\ C_2^{(5)}&= \ 2 m \mu _0+2 m^2 \mu _1 + \frac{m}{2} (2m^2 + 7m+1+3l(1+m)) \ \text {and} \ {\mathcal {E}}_2^{(5)}= \frac{1}{D}\frac{\log 5}{C_2^{(5)}}, \\ C_3^{(5)}&= \ 2 m \mu _0+2 m^2 \mu _1 + \frac{m}{2} (2m^2 + 3m-3+3l(1+m)) \ \text {and} \ {\mathcal {E}}_3^{(5)}= \frac{1}{D}\frac{\log 5}{C_3^{(5)}}, \\ C_4^{(5)}&= \ 2 m \mu _0+2 m^2 \mu _1 + \frac{m}{3} (2m^2 + 9m-5+3l(3+m)) \ \text {and} \ {\mathcal {E}}_4^{(5)}= \frac{1}{D}\frac{\log 5}{C_4^{(5)}}, \\ C_5^{(5)}&= \ 2 m \mu _0+2 m^2 \mu _1 + \frac{m}{3} (2m^2 + 9m+1+3l(3+m)) \ \text {and} \ {\mathcal {E}}_5^{(5)}= \frac{1}{D}\frac{\log 5}{C_5^{(5)}}, \\ C_1^{(7)}&= \ 3 m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 51m+7+3l(11+m)) \ \text {and} \ {\mathcal {E}}_1^{(7)}= \frac{1}{D}\frac{\log 5}{C_1^{(7)}}, \\ C_2^{(7)}&= \ 3 m \mu _0+2 m^2 \mu _1 + \frac{m}{3} (2m^2 + 15m-8+3l(5+m)) \ \text {and} \ {\mathcal {E}}_2^{(7)}= \frac{1}{D}\frac{\log 5}{C_2^{(7)}}, \end{aligned}$$

wherein $D = \log d$.

5.1 5.1 Comparison between efficiencies

To compare the efficiencies of iterative methods, say $M_i^{(p)}$ against $M_j^{(q)}$, we consider the ratio

$$\begin{aligned} R_{i,j}^{p,q}=\frac{{\mathcal {E}}_i^{(p)}}{{\mathcal {E}}_j^{(q)}}=\frac{C_j^{(q)}\log p}{C_i^{(p)}\log q}. \end{aligned}$$

It is clear that if $R_{i,j}^{p,q}>1$, the iterative method $M_i^{(p)}$ is more efficient than $M_j^{(q)}$. Mathematically this fact will be denoted by $M_i^{(p)}\gtrdot M_j^{(q)}$. Taking into account that the border between two computational efficiencies is given by $R_{i,j}^{p,q}=1,$ this boundary will be given by the equation $\mu _0$ written as a function of $\mu _1$, m and l; $(\mu _0,\mu _1)\in (0,+\infty )\times (0,+\infty ),$ m is a positive integer $\ge 2$ and $l\ge 1.$ In the sequel, we consider the comparison of computational efficiencies of the methods as expressed above.

$M_1^{(3)}$ versus $M_2^{(3)}$ case:

In this case, the ratio

$$\begin{aligned} R_{1,2}^{3,3}= \frac{m \mu _0+2 m^2 \mu _1 + \frac{m}{3} (2m^2 + 3m-2+3l(1+m))}{m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 15m+7+3l(3+m))}>1, \end{aligned}$$

for $m\ge 5$, which implies that ${\mathcal {E}}_1^3 > {\mathcal {E}}_2^3$ and hence $M_1^3 \gtrdot M_2^3$ for all $m\ge 5$ and $l\ge 1.$

$M_1^{(3)}$ versus $M_3^{(3)}$ case:

In this case, the ratio

$$\begin{aligned} R_{1,3}^{3,3}= \frac{m \mu _0+3 m^2 \mu _1 + \frac{m}{3} (2m^2 + 6m+1+3l(1+m))}{m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 15m+7+3l(3+m))}>1, \end{aligned}$$

for $m\ge 2$, which implies that ${\mathcal {E}}_1^3 > {\mathcal {E}}_3^3$ and hence $M_1^3 \gtrdot M_3^3$ for all $m\ge 2$ and $l\ge 1.$

$M_1^{(3)}$ versus $M_4^{(3)}$ case:

For this case, the ratio

$$\begin{aligned} R_{1,4}^{3,3}= \frac{m \mu _0+4 m^2 \mu _1 + \frac{m}{3} (2m^2 + 9m+13+3l(1+m))}{m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 15m+7+3l(3+m))}>1. \end{aligned}$$

It is easy to prove that $R_{1,4}^{3,3}> 1$ for $m\ge 1.$ Thus, we conclude that ${\mathcal {E}}_1^3 > {\mathcal {E}}_4^3$ and consequently $M_1^3 \gtrdot M_4^3$ for all $m\ge 2$ and $l\ge 1.$

$M_1^{(3)}$ versus $M_5^{(3)}$ case:

For this case, the ratio

$$\begin{aligned} R_{1,5}^{3,3}= \frac{m \mu _0+3 m^2 \mu _1 + \frac{m}{3} (2m^2 + 6m+4+3l(1+m))}{m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 15m+7+3l(3+m))}>1. \end{aligned}$$

We have that $R_{1,5}^{3,3}> 1$ for $m\ge 1,$ which shows ${\mathcal {E}}_1^3 > {\mathcal {E}}_5^3$ and consequently $M_1^3 \gtrdot M_5^3$ for all $m\ge 2$ and $l\ge 1.$

$M_1^{(3)}$ versus $M_6^{(3)}$ case:

In this case, the ratio

$$\begin{aligned} R_{1,6}^{3,3}= \frac{m \mu _0+2 m^2 \mu _1 + \frac{m}{3} (2m^2 + 6m-2+3l(1+m))}{m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 15m+7+3l(3+m))}>1, \end{aligned}$$

for $m\ge 3$, which implies that ${\mathcal {E}}_1^3 > {\mathcal {E}}_6^3$ for all $m\ge 3$ and $l\ge 1$, that is $M_1^3 \gtrdot M_6^3$.

$M_1^{(5)}$ versus $M_2^{(5)}$ case:

In this case, the ratio

$$\begin{aligned} R_{1,2}^{5,5}= \frac{2 m \mu _0+2 m^2 \mu _1 + \frac{m}{2} (2m^2 + 7m+1+3l(1+m))}{2 m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 33m+7+3l(7+m))}>1, \end{aligned}$$

for $m\ge 3$, which implies that ${\mathcal {E}}_1^5 > {\mathcal {E}}_2^5$ for all $m\ge 3$ and $l\ge 1.$ Therefore $M_1^5 \gtrdot M_2^5$.

$M_1^{(5)}$ versus $M_3^{(5)}$ case:

In this case, the ratio

$$\begin{aligned} R_{1,3}^{5,5}= \frac{2 m \mu _0+2 m^2 \mu _1 + \frac{m}{2} (2m^2 + 3m-3+3l(1+m))}{2 m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 33m+7+3l(7+m))}>1, \end{aligned}$$

for $m\ge 6$, which implies that ${\mathcal {E}}_1^5 > {\mathcal {E}}_3^5$ and $M_1^5 \gtrdot M_3^5$ for all $m\ge 6$ and $l\ge 1.$

$M_1^{(5)}$ versus $M_4^{(5)}$ case:

In this case, the ratio

$$\begin{aligned} R_{1,4}^{5,5}= \frac{2 m \mu _0+2 m^2 \mu _1 + \frac{m}{3} (2m^2 + 9m-5+3l(3+m))}{2 m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 33m+7+3l(7+m))}>1, \end{aligned}$$

for $m\ge 8$, which implies that ${\mathcal {E}}_1^5 > {\mathcal {E}}_4^5$ and $M_1^5 \gtrdot M_4^5$ for all $m\ge 8$ and $l\ge 1.$

$M_1^{(5)}$ versus $M_5^{(5)}$ case:

In this case, the ratio

$$\begin{aligned} R_{1,5}^{5,5}= \frac{2 m \mu _0+2 m^2 \mu _1 + \frac{m}{3} (2m^2 + 9m+1+3l(3+m))}{2 m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 33m+7+3l(7+m))}>1, \end{aligned}$$

for $m\ge 7$, which implies that ${\mathcal {E}}_1^5 > {\mathcal {E}}_5^5$ and $M_1^5 \gtrdot M_5^5$ for all $m\ge 7$ and $l\ge 1.$

$M_1^{(7)}$ versus $M_2^{(7)}$ case:

In this case, the ratio

$$\begin{aligned} R_{1,2}^{7,7}= \frac{3 m \mu _0+2 m^2 \mu _1 + \frac{m}{3} (2m^2 + 15m-8+3l(5+m))}{3 m \mu _0+2 m^2 \mu _1 + \frac{m}{6} (2m^2 + 51m+7+3l(11+m))}>1, \end{aligned}$$

for $m\ge 11$, which implies that ${\mathcal {E}}_1^7 > {\mathcal {E}}_2^7$ and $M_1^7 \gtrdot M_2^7$ for all $m\ge 11$ and $l\ge 1.$

$M_1^{(3)}$ versus $M_1^{(5)}$ case:

For this case, it is judicious to consider the boundary $R_{1,1}^{3,5} = 1$, which is given by

$$\begin{aligned} \mu _0 = \frac{-(14 + 18 m + m^2) r + (8 + 9 m + m^2) s + 6 m (s-r)\mu _1}{6 r-3 s}, \end{aligned}$$

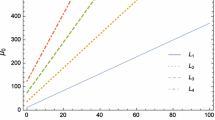
where $r=\log 3$ and $s=\log 5$. The comparison of efficiencies ${\mathcal {E}}_1^3$ and ${\mathcal {E}}_1^5$ is shown in the $(\mu _1,\mu _0)$-plane by drawing some particular boundaries corresponding to $m = 2, 5, 10 \ \text {and} \ 20$ taking $l=1$, where ${\mathcal {E}}_1^3 > {\mathcal {E}}_1^5$ (that is $M_1^3 \gtrdot M_1^5)$ on the left (above) and ${\mathcal {E}}_1^5 > {\mathcal {E}}_1^3$ (that is, $M_1^5 \gtrdot M_1^3)$ on the right (below) of each line (see Fig. 1).

Fig. 1

Boundary lines in $(\mu _1,\mu _0)$ - plane for $M_1^3$ versus $M_1^5$

$M_1^{(3)}$ versus $M_1^{(7)}$ case:

Like the previous case we consider the boundary $R_{1,1}^{3,7} = 1$, which yields

$$\begin{aligned} \mu _0 = \frac{-20 r - 27 m r - m^2 r + 8 t + 9 m t + m^2 t - 6 m r \mu _1 + 6 m t\mu _1}{3 (3 r - t)}, \end{aligned}$$

where $r=\log 3$ and $t=\log 7$. To compare the efficiencies ${\mathcal {E}}_1^3$ and ${\mathcal {E}}_1^7$ in the $(\mu _1,\mu _0)$-plane, we draw some particular boundaries corresponding to $m = 2, 5, 10 \ \text {and} \ 20$ taking $l=1$. These boundaries are shown in Fig. 2, wherein ${\mathcal {E}}_1^3 > {\mathcal {E}}_1^7$ (that is $M_1^3 \gtrdot M_1^7)$ on the left (above) and ${\mathcal {E}}_1^7 > {\mathcal {E}}_1^3$ (that is $M_1^7 \gtrdot M_1^3$) on the right (below) of each line.

Fig. 2

Boundary lines in $(\mu _1,\mu _0)$ - plane for $M_1^3$ versus $M_1^7$

$M_1^{(5)}$ versus $M_1^{(7)}$ case:

The boundary $R_{1,1}^{5,7} = 1$ is given by

$$\begin{aligned} \mu _0 = \frac{-20 s - 27 m s - m^2 s + 14 t + 18 m t + m^2 t -6 m s \mu _1 + 6 m t\mu _1}{3 (3 s - 2 t)}, \end{aligned}$$

where $s=\log 5$ and $t=\log 7$. As before we draw boundary lines in $(\mu _1,\mu _0)$-plane corresponding to cases $m = 2, 5, 10 \ \text {and} \ 20$ taking $l=1$. Boundaries are shown in Fig. 3, wherein ${\mathcal {E}}_1^5 > {\mathcal {E}}_1^7$ (that is $M_1^5 \gtrdot M_1^7$) on the left (above) and ${\mathcal {E}}_1^7 > {\mathcal {E}}_1^5$ (that is $M_1^7 \gtrdot M_1^5$) on the right (below) of each line.

Fig. 3

Boundary lines in $(\mu _1,\mu _0)$ - plane for $M_1^5$ versus $M_1^7$

We summarize the preceding results in following theorem:

Theorem 4

(a) For all $\mu _0$, $\mu _1>0$ and $l\ge 1$ we have that:

$$\begin{aligned} \mathrm{{(i)}}&{\mathcal {E}}_1^3> {\mathcal {E}}_2^3 \Longleftrightarrow M_1^3 \gtrdot M_2^3 \ \forall \ m\ge 5. \\ \mathrm{{(ii)}}&\ \{{\mathcal {E}}_1^3> {\mathcal {E}}_3^3, {\mathcal {E}}_1^3> {\mathcal {E}}_4^3, {\mathcal {E}}_1^3> {\mathcal {E}}_5^3\} \Longleftrightarrow \{M_1^3 \gtrdot M_3^3, M_1^3 \gtrdot M_4^3, M_1^3 \gtrdot M_5^3\} \ \forall \ m\ge 2. \\ \mathrm{{(iii)}}&{\mathcal {E}}_1^3> {\mathcal {E}}_6^3 \Longleftrightarrow M_1^3 \gtrdot M_6^3 \ \forall \ m\ge 3. \\ \mathrm{{(iv)}}&{\mathcal {E}}_1^5> {\mathcal {E}}_2^5 \Longleftrightarrow M_1^5 \gtrdot M_2^5 \ \forall \ m\ge 3 \ and \ {\mathcal {E}}_1^5> {\mathcal {E}}_3^5 \Longleftrightarrow M_1^5 \gtrdot M_3^5 \ \forall \ m\ge 6. \\ \mathrm{{(v)}}&{\mathcal {E}}_1^5> {\mathcal {E}}_4^5 \Longleftrightarrow M_1^5 \gtrdot M_4^5 \ \forall \ m\ge 8 \ and \ {\mathcal {E}}_1^5> {\mathcal {E}}_5^5 \Longleftrightarrow M_1^5 \gtrdot M_5^5 \ \forall \ m\ge 7. \\ \mathrm{{(vi)}}&{\mathcal {E}}_1^7 > {\mathcal {E}}_2^7 \Longleftrightarrow M_1^7 \gtrdot M_2^7 \ \forall \ m\ge 11. \end{aligned}$$

Otherwise, the comparison depends on $\mu _0$, $\mu _1$ and l.

(b) For all $m\ge 2$ we have:

$$\begin{aligned} \mathrm{{(i)}}&{\mathcal {E}}_1^3> {\mathcal {E}}_1^5 \Longleftrightarrow M_1^3 \gtrdot M_1^5 \ \forall \ \mu _0> \beta _1 \ and \ {\mathcal {E}}_1^5> {\mathcal {E}}_1^3 \Longleftrightarrow M_1^5 \gtrdot M_1^3 \ \forall \ \mu _0< \beta _1, \\ \mathrm{{(ii)}}&{\mathcal {E}}_1^3> {\mathcal {E}}_1^7 \Longleftrightarrow M_1^3 \gtrdot M_1^7 \ \forall \ \mu _0> \beta _2 \ and \ {\mathcal {E}}_1^7> {\mathcal {E}}_1^3 \Longleftrightarrow M_1^7 \gtrdot M_1^3 \ \forall \ \mu _0< \beta _2, \\ \mathrm{{(iii)}}&{\mathcal {E}}_1^5> {\mathcal {E}}_1^7 \Longleftrightarrow M_1^5 \gtrdot M_1^7 \ \forall \ \mu _0> \beta _3 \ and \ {\mathcal {E}}_1^7 > {\mathcal {E}}_1^5 \Longleftrightarrow M_1^7 \gtrdot M_1^5 \ \forall \ \mu _0 < \beta _3, \end{aligned}$$

where $\beta _1 = \frac{-(14 + 18 m + m^2) r + (8 + 9 m + m^2) s + 6 m (s-r)\mu _1}{3(2r-s)}, \beta _2 = \frac{-(20+27 m +m^2) r + (8 + 9 m+ m^2) t +6 m (t-r) \mu _1}{3 (3 r - t)}$ and $\beta _3 = \frac{-(20+27 m+ m^2) s + (14+ 18 m + m^2) t+6 m (t-s) \mu _1}{3 (3 s - 2 t)}.$

6 Numerical results

To illustrate the convergence behavior and computational efficiency of the proposed methods $M_1^{(3)}$, $M_1^{(5)}$ and $M_1^{(7)}$, we consider some numerical examples and compare the performance with $M_2^{(3)}$, $M_3^{(3)}$, $M_4^{(3)}$, $M_5^{(3)}$, $M_6^{(3)}$, $M_2^{(5)}$, $M_3^{(5)}$, $M_4^{(5)}$, $M_5^{(5)}$ and $M_2^{(7)}$. All computations are performed in the programming package Mathematica (Wolfram 2003) in a PC with Intel(R) Pentium(R) CPU B960 @ 2.20 GHz, 2.20 GHz (32-bit Operating System) Microsoft Windows 7 Professional and 4 GB RAM. For every method, we analyze the number of iterations (k) needed to converge to the solution such that $\Vert t_{k+1}- t_k\Vert + \Vert \mathrm {F}(t_k)\Vert < 10^{-100}.$ To verify the theoretical order of convergence (p), we calculate the computational order of convergence COC by using the formula given in Definition 2.3. In numerical results, we also include CPU time (e-time) utilized in the execution of program which is computed by the Mathematica command TimeUsed[ ]. To calculate ${\mathcal {E}}_i^p$ for all methods in numerical examples we take $D =10^{-5}$ and $A(\pm m)$ denotes $A\times 10^{\pm m}.$

The results of theorem 4 are also verified through numerical experiments. To do this, we need an estimation of the factors $\mu _0$ and $\mu _1$. To claim this estimation, we express the cost of the evaluation of the elementary functions in terms of products, which depends on the computer, the software and the arithmetics used (Fousse et al. 2007). In Table 1, an estimation of the cost of the elementary functions in product unit is shown, where the running time of the one product is measured in milliseconds (ms). It is evident from Table 1 that the computational cost of the quotient with respect to product is, $l \approx 2.4.$

Table 1 CPU time and estimation of computational cost of the elementary functions, where $x = \sqrt{3}-1$ and $y = \sqrt{5}$

For numerical tests we consider the following examples:

Example 1

Consider a system of 2 equations (Sharma and Arora 2016a):

$$\begin{aligned} e^{-t_1^2} + 8 \, t_1 \, \sin t_2=&\, 0,\\ t_1 + t_2-1=&\, 0. \end{aligned}$$

With the initial approximations $t_0 = \{\frac{4}{10}, -\frac{4}{10}\}^\mathrm{{T}}$, we obtain the solution $t^* =\{1.0407\ldots , -0.0407\ldots \}^\mathrm{{T}}$. The concrete values of parameters $(m, \mu _0,\mu _1)$, obtained with the help of estimates of elementary functions displayed in Table 1, are (2, 46.8527, 36.6426). These values are used to calculate computational costs and efficiency indices of the methods shown in previous section.

Example 2

Consider a system of 3 equations (Sharma and Arora 2016c):

$$\begin{aligned}&10 \, t_1+ \sin (t_1+t_2)-1= \, 0,\\&8 \, t_2 - \cos ^2(t_3-t_2)-1= \, 0 \\&12 \, t_3 + \sin (t_3)-1= \, 0. \end{aligned}$$

The initial approximation $t_0 = \{0, 1, 0\}^\mathrm{{T}}$ is chosen to find the solution

$$\begin{aligned} t^* =\{0.0690\ldots ,0.2464\ldots , 0.0769\ldots \}^\mathrm{{T}}. \end{aligned}$$

Corresponding calculated values of the parameters $(m, \mu _0,\mu _1)$ are (3, 49.2469, 22.3370).

Example 3

Let us consider the Van der Pol equation (see Burden and Faires 2001), which is defined as follows:

$$\begin{aligned} t'' - \mu (t^2-1)t'+t = 0, \ \mu > 0, \end{aligned}$$

(30)

which governs the flow of current in a vacuum tube, with the boundary conditions $t(0)=0,$ $t(2)=1.$ Further, we consider the partition of the given interval [0, 2], which is given by

$$\begin{aligned} y_0 = 0< y_1< y_2<\cdots< y_{n-1} < y_n, \ \text {where} \ \ y_{i} = y_0 + i h, \ \ h = \frac{2}{n}. \end{aligned}$$

Moreover, we assume that

$$\begin{aligned} t_0 = t(y_0) =0 ,t_1 = t(y_1),\ldots , \ t_{n-1} = t(y_{n-1}), \ t_n = t(y_n) = 1. \end{aligned}$$

If we discretize the problem (30) using the second-order divided difference for the first and second derivatives, which are given by

$$\begin{aligned} t'_k = \frac{t_{k+1} - t_{k-1}}{2h}, \ \ t''_k = \frac{t_{k-1} - 2t_k + t_{k+1}}{h^2}, \ \ (k = 1, 2, 3,\ldots ,n - 1), \end{aligned}$$

then we obtain a system of $(n-1)$ nonlinear equations

$$\begin{aligned} 2 h^2 t_k -h \mu (t_k^2-1)(t_{k+1}-t_{k-1}) +2(t_{k-1}+t_{k+1}-2t_{k})=0, \ \ (k = 1, 2, 3,\ldots ,n - 1). \end{aligned}$$

Let us consider $\mu =\frac{1}{2}$ and initial approximation $t_0 = (\frac{1}{2},\frac{1}{2},\ldots ,\frac{1}{2})^\mathrm{{T}}$. In particular, we solve this problem for $n = 6$ so we obtain a system of 5 nonlinear equations. The solution of this problem is

$$\begin{aligned} t^* = \{0.4393\ldots ,0.7775\ldots ,1.0105\ldots ,1.1319\ldots ,1.1302\ldots \}^\mathrm{{T}} \end{aligned}$$

and parametric values are $(m, \mu _0,\mu _1) = (5,6.9784,1.3157).$

Example 4

Next, consider a system of 10 equations (Xiao and Yin 2016):

$$\begin{aligned} \tan ^{-1}(t_i)+1- 2\sum _{j=1, j\ne i}^{10}t_j^2, \, \, 1\le i\le 10. \end{aligned}$$

The solution $t^* =\{0.2644\ldots , 0.2644\ldots , \,{\mathop {\cdots }\limits ^{10}},\, 0.2644\ldots \}^\mathrm{{T}}$ is obtained by assuming the initial approximations $t_0 = \{\frac{7}{10}, \frac{7}{10} \,{\mathop {\cdots }\limits ^{10}},\, \frac{7}{10}\}^\mathrm{{T}}$. Computed values of the parameters $(m, \mu _0,\mu _1)$ are (10, 90.9400, 0.4446).

Example 5

The boundary value problem (see Ortega and Rheinboldt 1970):

$$\begin{aligned} t'' + a^2(t')^2 + 1 = 0, \ \ t(0) = 0, \ \ t(1) = 0 \end{aligned}$$

is studied. Consider the following partitioning of the interval [0,1]:

$$\begin{aligned} y_0 = 0< y_1< y_2<\cdots< y_{n-1} < y_n = 1, \ \ y_{j+1} = y_j + h, \ \ h = 1/n. \end{aligned}$$

Let us define $t_0 = t(y_0) = 0, \ t_1 = t(y_1),\ldots , \ t_{n-1} = t_(y_{n-1}), \ t_n = t(y_n) = 1.$ If we discretize the problem by using the numerical formulae for first and second derivatives

$$\begin{aligned} t'_k = \frac{t_{k+1} - t_{k-1}}{2h}, \ \ t''_k = \frac{t_{k-1} - 2t_k + t_{k+1}}{h^2}, \ \ (k = 1, 2, 3,\ldots ,n - 1), \end{aligned}$$

we obtain a system of $n-1$ nonlinear equations in $n-1$ variables:

$$\begin{aligned} t_{k-1} -2t_k + t_{k+1} + \frac{a^2}{4}(t_{k+1} - t_{k-1})^2 + h^2 = 0, \ \ (k = 1, 2, 3,\ldots ,n - 1). \end{aligned}$$

In particular, we solve this problem for $n = 51$ so that $k = 50$ by selecting $t_0 = (2,2,\,{\mathop {\cdots }\limits ^{50}},\,2)^\mathrm{{T}}$ as the initial value and $a =2$. Solution of this problem is

$$\begin{aligned} t^* =&\bigg \{0.9584\ldots ,0.9719\ldots ,0.9843\ldots ,0.9958\ldots ,1.0063\ldots ,\\&1.0161\ldots ,1.0252\ldots ,1.0335\ldots , \\&1.0412\ldots ,1.0483\ldots ,1.0549\ldots ,1.0609\ldots ,1.0664\ldots ,1.0714\ldots ,\\&1.0759\ldots ,1.0799\ldots ,1.0835\ldots , \\&1.0867\ldots ,1.0895\ldots ,1.0918\ldots ,1.0938\ldots ,1.0953\ldots ,1.0965\ldots ,\\&1.0972\ldots ,1.0976\ldots ,1.0976\ldots , \\&1.0972\ldots ,1.0965\ldots ,1.0953\ldots ,1.0938\ldots ,1.0918\ldots ,1.0895\ldots ,\\&1.0867\ldots ,1.0835\ldots ,1.0799\ldots , \\&1.0759\ldots ,1.0714\ldots ,1.0664\ldots ,1.0609\ldots ,1.0549\ldots ,1.0483\ldots ,\\&1.0412\ldots ,1.0335\ldots ,1.0252\ldots , \\&1.0161\ldots ,1.0063\ldots ,0.9958\ldots ,0.9843\ldots ,0.9719\ldots ,0.9584\ldots \bigg \}^\mathrm{{T}} \end{aligned}$$

and $(m, \mu _0,\mu _1)=(50,3,0.0392)$.

Example 6

Consider the following Burger’s equation (see Sauer 2012):

$$\begin{aligned} \frac{\partial ^2 f}{\partial u^2}+f\frac{\partial f}{\partial u}-\frac{\partial f}{\partial v}+g(u,v)=0, \, \, \, (u,v)\in [0,1]^2, \end{aligned}$$

where $g (u,v) = -10e^{-2v}[e^v(2 -u + u^2) + 10u(1-3u + 2u^2)]$ and function $f = f(u,v)$ satisfies the boundary conditions

$$\begin{aligned} f(0,v) = f(1,v) = 0, f(u,0) = 10u(u - 1) \, \, \text {and} \, \, f(u,1) = 10u(u-1)/e. \end{aligned}$$

Assuming the following partitioning of the domain $[0,1]^2:$

$$\begin{aligned}&0 =u_0< u_1< u_2< \cdots< u_{n-1}< u_n = 1, \, u_{k+1} = u_k + h, \\&0 =v_0< v_1< v_2< \cdots< v_{n-1} < v_n = 1, \, v_{l+1} = v_l + h, \, h = 1/n. \end{aligned}$$

Let us define $f_{k,l} = f(u_k, v_l)$ and $g_{k,l} = g(u_k, v_l)$ for $k, l = 0, 1, 2, \ldots , n.$ Then the boundary conditions will be $f_{0,l} = f(u_0, v_l ) = 0,$ $f_{n,l} = f (u_n, v_l ) = 0$, $f_{k,0} = f(u_k, v_0) = 10 u_k(u_k - 1)$ and $f_{k,n} = f(u_k, v_n) = 10u_k(u_k - 1)/e.$ If we discretize Burger’s equation by using the numerical formulae for the partial derivatives, we obtain the following system of $(n - 1)^2$ nonlinear equations in $(n - 1)^2$ variables:

$$\begin{aligned} f_{i-1,j}(2-h f_{i,j}) + h(f_{i,j-1} - f_{i,j+1})-f_{i,j}(4 - h f_{i+1,j}) + 2 f_{i+1,j} + 2 h^2 g_{i,j} = 0, \end{aligned}$$

(31)

where $i,j = 1, 2,\ldots , n-1$. In particular, we solve the nonlinear system (31) for $n = 11$ so that $m = 100$ by selecting $f_{i,j} = -\frac{5}{2}$ (for $i,j = 1, 2,\ldots , 10$) as the initial value towards the required solution $t^*$ given by

$$\begin{aligned}&\bigg \{-0.7546\ldots ,-0.6892\ldots ,-0.6290\ldots ,-0.5750\ldots ,-0.5235\ldots ,\\&\quad -0.4817\ldots ,-0.4306\ldots ,-0.4213\ldots , \\&\quad -0.2583\ldots , -0.3068\ldots , -1.3583\ldots ,-1.2405\ldots ,-1.1322\ldots ,\\&\quad -1.0351\ldots ,-0.9422\ldots ,-0.8675\ldots , \\&\quad -0.7741\ldots ,-0.7598\ldots ,-0.4358\ldots ,-0.5505\ldots , -1.8111\ldots ,\\&\quad -1.6541\ldots ,-1.5096\ldots ,-1.3803\ldots , \\&\quad -1.2559\ldots ,-1.1573\ldots ,-1.0309\ldots ,-1.0110\ldots ,-0.6951\ldots ,\\&\quad -0.7356\ldots , -2.1130\ldots ,-1.9298\ldots , \\&\quad -1.7611\ldots , -1.6106\ldots ,-1.4649\ldots ,-1.3511\ldots ,-1.2014\ldots ,\\&\quad -1.1768\ldots ,-0.8755\ldots ,-0.8605\ldots , \\&\quad -2.2639\ldots ,-2.0678\ldots ,-1.8869\ldots ,-1.7258\ldots ,-1.5690\ldots ,\\&\quad -1.4485\ldots ,-1.2860\ldots ,-1.2582\ldots , \\&\quad -0.9783\ldots ,-0.9244\ldots , -2.2639\ldots ,-2.0678\ldots ,-1.8868\ldots ,\\&\quad -1.7261\ldots ,-1.5686\ldots ,-1.4494\ldots , \\&\quad -1.2850\ldots , -1.2558\ldots ,-1.0040\ldots ,-0.9268\ldots , -2.1129\ldots ,\\&\quad -1.9300\ldots ,-1.7609\ldots ,-1.6112\ldots , \\&\quad -1.4637\ldots ,-1.3534\ldots ,-1.1987\ldots ,-1.1700\ldots ,-0.9534\ldots ,\\&\quad -0.8672\ldots , -1.8111\ldots ,-1.6544\ldots , \\&\quad -1.5093\ldots ,-1.3812\ldots ,-1.2544\ldots ,-1.1604\ldots ,-1.0272\ldots ,\\&\quad -1.0010\ldots ,-0.8270\ldots ,-0.7454\ldots , \\&\quad -1.3583\ldots ,-1.2408\ldots ,-1.1320\ldots ,-1.0359\ldots ,-0.9407\ldots ,\\&\quad -0.8704\ldots ,-0.7706\ldots ,-0.7492\ldots , \\&\quad -0.6255\ldots ,-0.5609\ldots , -0.7546\ldots ,-0.6893\ldots ,-0.6289\ldots ,\\&\quad -0.5755\ldots ,-0.5227\ldots ,-0.4834\ldots , \\&\quad -0.4285\ldots ,-0.4152\ldots ,-0.3496\ldots ,-0.3128\ldots \bigg \}^\mathrm{{T}}. \end{aligned}$$

The approximate solution found is also plotted in Fig. 4. The concrete values of parameters for this system are $(m, \mu _0,\mu _1) = (100,10.0503,0.0492).$

Fig. 4

Approximate solution of Burger equation

Example 7

Next, the methods are applied to solve the Poisson equation (Cordero et al. 2015)

$$\begin{aligned} u_{xx}+u_{yy}=u^2, \ \ (x,y)\in [0,1]\times [0,1], \end{aligned}$$

(32)

with boundary conditions

$$\begin{aligned}&u(x,0) = 2x^2-x+1, \ \ u(x,1) = 2, \nonumber \\&u(0,y) = 2y^2-y+1, \ \ u(1,y)=2. \end{aligned}$$

(33)

The solution can be found using finite difference discretization. Let $u = u(x, y)$ be the exact solution of this Poisson equation. Let $w_{i,j} =u(x_i,y_j)$ be its approximate solution at the grid points of the mesh. Let M and N be the number of steps in x and y directions, and h and k be the respective step size ($h=\frac{1}{M}$, $k=\frac{1}{N}$). If we discretize the problem by using the central divided differences, i.e., $u_{xx}(x_i,y_j)=(w_{i+1,j} -2w_{i,j}+w_{i-1,j})/h^2$ and $u_{yy}(x_i,y_j)=(w_{i,j+1}-2w_{i,j} +w_{i,j-1})/k^2$, we get the following system of nonlinear equations:

$$\begin{aligned} w_{i+1,j} -4w_{i,j} +w_{i-1,j} +&w_{i,j+1}+w_{i,j-1}-h^2 w_{i,j}^2 =0, \nonumber \\&i=1,\ldots ,M-1, j=1,\ldots ,N-1. \end{aligned}$$

(34)

We consider $M=15$ and $N= 15$ and thereby solve the resulting nonlinear system of 196 equations in 196 unknowns. The approximate solution

$$\begin{aligned}&\bigg \{0.9306\ldots ,0.9209\ldots ,0.9193\ldots ,0.9289\ldots ,0.9513\ldots ,0.9873\ldots ,\\&\quad 1.0377\ldots , 1.1030\ldots ,1.1834\ldots , \\&\quad 1.2793\ldots , 1.3909\ldots ,1.5185\ldots ,1.6623\ldots ,1.8226\ldots ,0.9209\ldots ,0.9351\ldots ,\\&\quad 0.9513\ldots , 0.9734\ldots , \\&\quad 1.0039\ldots ,1.0446\ldots ,1.0965\ldots ,1.1606\ldots ,1.2375\ldots ,\\&\quad 1.3279\ldots ,1.4322\ldots ,1.5510\ldots ,1.6847\ldots , \\&\quad 1.8341\ldots ,0.9193\ldots ,0.9513\ldots ,0.9815\ldots ,1.0137\ldots ,\\&\quad 1.0510\ldots ,1.0954\ldots ,1.1484\ldots ,1.2113\ldots , \\&\quad 1.2851\ldots ,1.3704\ldots , 1.4682\ldots ,1.5791\ldots ,1.7041\ldots ,\\&\quad 1.8439\ldots ,0.9289\ldots ,0.9734\ldots ,1.0137\ldots , \\&\quad 1.0535\ldots ,1.0958\ldots ,1.1429\ldots ,1.1964\ldots ,1.2578\ldots ,\\&\quad 1.3283\ldots ,1.4089\ldots ,1.5006\ldots ,1.6044\ldots , \\&\quad 1.7214\ldots ,1.8528\ldots ,0.9513\ldots , 1.0039\ldots ,1.0510\ldots ,\\&\quad 1.0958\ldots ,1.1413\ldots ,1.1897\ldots , 1.2428\ldots , \\&\quad 1.3022\ldots ,1.3692\ldots , 1.4451\ldots ,1.5310\ldots ,1.6280\ldots ,\\&\quad 1.7375\ldots ,1.8609\ldots ,0.9873\ldots ,1.0446\ldots , \\&\quad 1.0954\ldots , 1.1429\ldots ,1.1897\ldots ,1.2380\ldots ,1.2897\ldots ,\\&\quad 1.3465\ldots ,1.4097\ldots ,1.4806\ldots ,1.5606\ldots , \\&\quad 1.6509\ldots ,1.7531\ldots ,1.8688\ldots ,1.0377\ldots ,1.0965\ldots ,\\&\quad 1.1484\ldots ,1.1964\ldots ,1.2428\ldots , 1.2897\ldots , \\&\quad 1.3391\ldots ,1.3924\ldots ,1.4512\ldots ,1.5168\ldots ,1.5906\ldots ,\\&\quad 1.6741\ldots ,1.7689\ldots , 1.8768\ldots ,1.1030\ldots , \\&\quad 1.1606\ldots ,1.2113\ldots ,1.2578\ldots ,1.3022\ldots ,1.3465\ldots ,\\&\quad 1.3924\ldots , 1.4415\ldots ,1.4952\ldots ,1.5550\ldots , \\&\quad 1.6222\ldots ,1.6984\ldots ,1.7854\ldots ,1.8852\ldots ,1.1834\ldots ,\\&\quad 1.2375\ldots ,1.2851\ldots ,1.3283\ldots , 1.3692\ldots , \\&\quad 1.4097\ldots ,1.4512\ldots ,1.4952\ldots ,1.5432\ldots ,1.5965\ldots ,\\&\quad 1.6565\ldots ,1.7248\ldots , 1.8034\ldots ,1.8943\ldots , \\&\quad 1.2793\ldots ,1.3279\ldots ,1.3704\ldots , 1.4089\ldots ,1.4451\ldots ,\\&\quad 1.4806\ldots ,1.5167\ldots ,1.5550\ldots ,1.5965\ldots , \\&\quad 1.6425\ldots ,1.6946\ldots , 1.7543\ldots ,1.8234\ldots ,1.9044\ldots ,\\&\quad 1.3909\ldots ,1.4322\ldots ,1.4682\ldots ,1.5006\ldots , \\&\quad 1.5310\ldots , 1.5606\ldots ,1.5906\ldots ,1.6222\ldots ,1.6565\ldots ,\\&\quad 1.6946\ldots , 1.7379\ldots ,1.7879\ldots ,1.8465\ldots , \\&\quad 1.9162\ldots ,1.5185\ldots ,1.5510\ldots ,1.5791\ldots ,1.6044\ldots ,\\&\quad 1.6280\ldots ,1.6509\ldots ,1.6741\ldots , 1.6984\ldots , \\&\quad 1.7248\ldots ,1.7543\ldots ,1.7879\ldots ,1.8270\ldots ,1.8736\ldots ,\\&\quad 1.9301\ldots ,1.6623\ldots , 1.6847\ldots ,1.7041\ldots , \\&\quad 1.7214\ldots ,1.7375\ldots ,1.7531\ldots ,1.7689\ldots ,1.7854\ldots ,\\&\quad 1.8034\ldots , 1.8234\ldots ,1.8465\ldots , 1.8736\ldots , \\&\quad 1.9064\ldots ,1.9472\ldots ,1.8226\ldots ,1.8341\ldots ,1.8439\ldots ,\\&\quad 1.8528\ldots ,1.8609\ldots ,1.8688\ldots ,1.8768\ldots , \\&\quad 1.8852\ldots ,1.8943\ldots ,1.9044\ldots ,1.9162\ldots , 1.9301\ldots ,1.9472\ldots ,1.9693\ldots \bigg \}^\mathrm{{T}} \end{aligned}$$

is evaluated with the initial vector $w_{i,j} =\{2,2, \, {\mathop {\cdot \cdots }\limits ^{196}}, \, 2\}^\mathrm{{T}}$ ($i,j = 1, 2,\ldots , 14$). The approximate solution found has also been displayed in Fig. 5. For this problem the concrete values of parameters are $(m, \mu _0,\mu _1) = (196,3,0.005102).$

Fig. 5

Approximate solution of Poisson equation

Example 8

Consider a system of 200 nonlinear equations (see Sharma and Arora 2016b)

$$\begin{aligned} \sum _{j=1, j\ne i}^{200}t_j-e^{-t_i}=0, \, \, 1\le i\le 200, \end{aligned}$$

with initial value $t_0=(\frac{3}{2},\frac{3}{2}, \,{\mathop {\cdots }\limits ^{m}},\, \frac{3}{2})^\mathrm{{T}}$ towards the required solution $t^*=(0.0050\ldots ,\, {\mathop {\cdots }\limits ^{200}}, \, 0.0050\ldots )^\mathrm{{T}}$. The concrete values of parameters are $(m, \mu _0,\mu _1) = (200,44.2674,0.2213).$

Example 9

Lastly, consider a system of 500 equations (see Sharma and Arora 2016b)

$$\begin{aligned} \left\{ \begin{array}{l} t_i^2 t_{i+1}-1=0, \ 1\le i\le 499,\\ t_{i}^2 t_1-1=0, \ i =500. \end{array}\right. \end{aligned}$$

To obtain the required solution $t^* =\{1,1, \,{\mathop {\cdot \cdots }\limits ^{500}},\, 1\}^\mathrm{{T}}$ of the system, the initial value chosen is $t_0=(\frac{18}{10},\frac{18}{10}, \,{\mathop {\cdot \cdots }\limits ^{500}},\, \frac{18}{10})^\mathrm{{T}}$. Computed values of the parameters $(m, \mu _0,\mu _1)$ are (500, 2, 0.006).

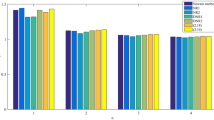
The numerical results of the performance of various methods, applied to solve the above mentioned problems, are displayed in Tables 2 and 3. Here the values like $A(\pm m)$ denote $A\times 10^{\pm m}$. The numerical results clearly indicate the stable convergence behavior of the methods. Also observe that in each method the computational order of convergence overwhelmingly supports the theoretical order of convergence. The elapsed CPU time (e-time in seconds) used in the execution of program shows the efficient nature of proposed methods as compared to other methods. In fact speaking of the efficient nature of an iterative method we mean that the method with high efficiency uses less computing time than that of the method with low efficiency. Similar numerical experimentations, carried out for a number of problems of different type, confirmed the above conclusions to a large extent.

7 Conclusions

In the foregoing study, we have considered the problem of solving systems of nonlinear equations and developed two- and three-step composite Newton–Jarratt iterative methods of convergence order three and five, respectively. Furthermore, in quest of fast algorithms a generalized $q+1$-step scheme with increasing convergence order $2q+1$ is proposed and analyzed. Novelty of the $q+1$-step algorithm is that in each step order of convergence is increased by an amount of two at the cost of only one additional function evaluation. Moreover, evaluation of inverse operator remains the same throughout the iteration which makes the algorithm more attractive and computationally efficient.

Table 2 Comparison of performance between third-order methods

Table 3 Comparison of performance between fifth- and seventh-order methods

Computational efficiency of the methods is discussed in its general form. Then a comparison of efficiencies of the new schemes with existing schemes is shown. It is observed that the presented methods are more efficient than similar existing methods in general. Numerical examples are presented and the performance is compared with existing methods. Theoretical order of convergence is verified in the examples by calculating computational order of convergence. Comparison of the elapsed CPU time shows that, in general, the method with large efficiency uses less computing time than the method with small efficiency. This shows that the efficiency results are in agreement with the CPU time utilized in the execution of program.