1 Introduction

The basic idea of non-integer order calculus which is believed to be a generalization of traditional calculus has attracted a considerable interest in modeling real physical phenomena (Akinyemi and Iyiola 2020a, b; Belgacem et al. 2019; Bokharia et al. 2020; Senol et al. 2019a; Maitama and Zhao 2019c; Akinyemi et al. 2021). However, when a real physical phenomena possess uncertain behavior, it is very difficult to accurately capture its reliable solution using the well-known fractional calculus. This motivated Agarwal et al. to first introduced the concept of fractional differential equations with uncertainty which is based on fuzzy set theory (Agarwal et al. 2010). In 1965, the theory of fuzzy set, fuzzy mathematics, and the fuzzy logic was first introduced by Azerbaijan mathematics Lotfi Aliasker Zadeh (1965). In the same year, L-relation Salii (1965) was presented, which is more general in a theoretical context and applies to decision-making (Kuzmin 1982; Khana et al. 2019a, b; Yen and Langari 1995), clustering (Bezdek 1978), and the linguistic (Zadeh 1975; Langari 1992). Puri and Ralescu introduced the notion of fuzzy random variables and the expectation of a fuzzy random variables (see Puri and Ralescu 1986). Recently, the fuzzy set theory has attracted a lot attention in the field of computer science (Khana et al. 2020a, b), engineering (Khana et al. 2020c; Fatihu et al. 2017), pure and applied mathematics (Gong and Hao 2018), and medical diagosis (Khana et al. 2020d). The fuzzy risk analysis and similarity measure of sequence of fuzzy numbers are discussed in Khana et al. (2020e), Zararsız (2015). In the fuzzy literature, the basic idea of the fuzzy derivative was first proposed by Chang and Zadeh (1972). Fuzzy fractional differential equations were derived by replacing the classical bivalent sets called crisp sets with the fuzzy quantities to described imprecision and uncertainty behavior (Zureigat et al. 2019). A recent review of the non-integer order derivatives can found in Machado et al. (2011), Tarasov (2011), de Oliveira et al. (2014), Valerio et al. (2013). In 2020, the analytical and numerical solutions of one-dimensional fuzzy fractional partial differential equations were successfully constructed using the fuzzy Laplace transform (Shah et al. 2020). Due to the great freedom of non-integer order operator, the fuzzy fractional partial differential equations have been used to model more complex phenomena with uncertainty behavior (Kahraman et al. 2020).

The concept of non-integer order differential equations with uncertainty was extended to definitions of H-differentiability by Allahviranloo et al. (2012), Salahshour et al. (2012). In finance, fuzzy sets were applied to study the European option pricing models (Appadoo and Thavaneswaran 2013). Dubois et al. (2004) discussed the fuzzy or possibility of measures of uncertainty based on probability transformations. In recent years, due to the importance of fuzzy differential equations in physical science and engineering, many analytical and numerical techniques, such as the Runge–Kutta method (Akbarzadeh and Mohseni 2011), the Adomian decomposition method (Chakraverty et al. 2012), and the homotopy analysis transform method (Salah et al. 2013), the variational iteration method (Jafari et al. 2012), have been proposed and efficiently applied to many applications in the literature. In Bede and Gal (2005), introduced the weak and strong generalized differentiability of a fuzzy-number-valued function. In 2014, Allahviranhoo et al. studied the concept of Caputo generalized Hukuhara derivative (Allahviranloo et al. 2014). Recently, Senol et al. (2019b) developed a perturbation-iteration algorithm using the Caputo derivative under generalized Hukuhara difference.

In this work, using the recently proposed Shehu transform in fuzzy context (Maitama and Zhao 2019a, b), we introduce a suitable iterative algorithm for solving fuzzy fractional models. The algorithm is a combination of the homotopy analysis method (Liao 1995) which was first devised by Liao in 1992 and the FSTM which is a generalization of the fuzzy Laplace transform (Allahviranloo and Ahmadi 2010) and the fuzzy Sumudu transform (Jafari and Razvarz 2019). Applications are provided to justify the efficiency and the simplicity of the proposed iterative algorithm.

Other sections of this article are organized as follows. In the Sect. 2, we provide some notations of the fuzzy calculus used in this paper. In the Sect. 3, we discussed the absolute error analysis and convergence of the method. In the Sect. 4, applications of the proposed method are presented. The results and discussion section is presented in the Sect. 5, and finally, in the Sect. 6, we give the conclusion of this article.

2 Preliminaries notations and fuzzy calculus

Definition 1

The function \(f: \mathfrak {I}\rightarrow E, \mathfrak {I}\in {\mathbb {R}}\) is called a fuzzy function and the \(\beta \)-level set of f is represented by the function \(f(t,\beta )=\left[ {\bar{f}}(t,\beta ),\underline{f}(t,\beta )\right] ,\,\,\forall \beta \in [0,1]\). Besides, a fuzzy function always has a domain and fuzzy range. Thus,a function \(f: E\rightarrow E\) is also a fuzzy function (see Salahshour et al. 2012).

Definition 2

(Senol et al. 2019b) Let \(v: A\rightarrow [0,1]\), be a membership function, where A is a nonempty fuzzy subset defined as \(\{(t,v(t)) :t\in A\}\), of \(A\times [0,1]\). Let set E be the family of all such fuzzy sets, where \(v\in {\mathbb {R}}\times [0,1]\).

Suppose v satisfies the following conditions.

  1. 1.

    \(\forall t_0\in {\mathbb {R}}\), the membership function v is normal and \(v(t_0)=1 (crisp value)\).

  2. 2.

    \(\forall t_0,y_0\in {\mathbb {R}}\) and \(x\in [0,1]\), the membership function v is convex and satisfies \(v[xt+(1-x)y]\ge \min \{v(t),v(y)\}\).

  3. 3.

    The set \(\{t\in {\mathbb {R}}, v(t)>0 \}\) is called closure of v and denoted \(v^0\) which is compact.

  4. 4.

    The membership function v is upper semi continuous.

If the conditions mentioned above are satisfied, then the function v is called a fuzzy number.

Based on the principle of Zadeh’s extension of addition on \({\mathbb {E}}\), we obtain:

$$\begin{aligned} (v+w)(t)=\sup _{y\in {\mathbb {R}}}\min \{v(y),w(t-y)\},\,\,t\in \mathbb R, \end{aligned}$$
(1)

and the scalar multiplication is:

$$\begin{aligned} (\beta \odot \upsilon )(t)={\left\{ \begin{array}{ll} \upsilon (t/\beta ),\,\,\beta >0,\\ {\tilde{0}},\,\,\beta =0, \end{array}\right. } \end{aligned}$$
(2)

where \({\tilde{0}}\in {\mathbb {E}}\) (Salahshour et al. 2012).

According to Puri and Ralescu (1986), the Hausdorff distance between fuzzy numbers in the set \(d: \mathbb E\times {\mathbb {E}}\rightarrow [0,+\infty ]\) is defined by:

$$\begin{aligned} d(v,w)=\sup _{r\in [0,1]}\max \{|\underline{v}(\beta )-\underline{w}(\beta )|,\,|{\bar{v}}(\beta )-{\bar{w}}(\beta )|\}, \end{aligned}$$
(3)

where \(v={(\underline{v}(\beta ),{\bar{v}}(\beta ))}, w={(\underline{w}(\beta ),{\bar{w}}(\beta ))}\subset {\mathbb {R}}\) was applied in Bede and Gal (2005). Based on this definition, it is obvious to see that d is a metric in \({\mathbb {E}}\) and satisfied the following properties:

  • \(d(v\oplus w,q\oplus w)=d(v,q),\,\forall \,v,w,q \in \mathbb E\).

  • \(d(v\oplus w,q\oplus e)\le d(v,w)+d(w,e),\,\forall v,w,q,e \in \mathbb E\).

  • \(d(\beta \odot v, \beta \odot w)=|\beta |d(v,w),\,\forall \beta \in {\mathbb {R}}, v,w\in \mathbb E.\)

  • \((d,{\mathbb {E}})\) is a complete metric space.

The following definition of differentiability was first introduced by Bede and Gal (2005)

Definition 3

Let \(\Lambda :(a,b)\rightarrow {\mathbb {E}}\) and \(t_0\in (a,b)\). Then, we say that \(\Lambda \) is strongly generalized differentiability at \(t_0\) if there exists an element \(\Lambda '(t_0)\in {\mathbb {E}}\), such that for all \(\zeta >0\) sufficiently small, then:

  1. 1.
    $$\begin{aligned} \lim _{\zeta \searrow 0}\frac{\Lambda (t_0+\zeta )\ominus \Lambda (t_0)}{\zeta }=\lim _{\zeta \searrow 0}\frac{\Lambda (t_0)\ominus \Lambda (t_0-\zeta )}{\zeta }=\Lambda '(t_0). \end{aligned}$$
    (4)

    or

  2. 2.
    $$\begin{aligned} \lim _{\zeta \searrow 0}\frac{\Lambda (t_0)\ominus \Lambda (t_0+\zeta )}{-\zeta }=\lim _{\zeta \searrow 0}\frac{\Lambda (t_0-\zeta )\ominus \Lambda (t_0)}{-\zeta }=\Lambda '(t_0). \end{aligned}$$
    (5)

    or

  3. 3.
    $$\begin{aligned} \lim _{\zeta \searrow 0}\frac{\Lambda (t_0+\zeta )\ominus \Lambda (t_0)}{\zeta }=\lim _{\zeta \searrow 0}\frac{\Lambda (t_0-\zeta )\ominus \Lambda (t_0)}{-\zeta }=\Lambda '(t_0). \end{aligned}$$
    (6)

    or

  4. 4.
    $$\begin{aligned} \lim _{\zeta \searrow 0}\frac{\Lambda (t_0)\ominus \Lambda (t_0+\zeta )}{-\zeta }=\lim _{\zeta \searrow 0}\frac{\Lambda (t_0)\ominus \Lambda (t_0-\zeta )}{\zeta }=\Lambda '(t_0). \end{aligned}$$
    (7)

The definition of second-order derivative under generalized H-differentiability is defined as Najeeb et al. (2015)

Definition 4

Let \(\Lambda :(a,b)\rightarrow {\mathbb {E}}\) and \(t_0\in (a,b)\). Then, we say that \(\Lambda \) is strongly generalized differentiability of the second-order derivative at \(t_0\) if there exists an element \(\Lambda ''(t_0)\in {\mathbb {E}}\), such that for all \(\zeta >0\) sufficiently small, then:

  1. 1.
    $$\begin{aligned} \lim _{\zeta \searrow 0}\frac{\Lambda '(t_0+\zeta )\ominus \Lambda '(t_0)}{\zeta }=\lim _{\zeta \searrow 0}\frac{\Lambda '(t_0)\ominus \Lambda '(t_0-\zeta )}{\zeta }=\Lambda ''(t_0). \end{aligned}$$
    (8)

    or

  2. 2.
    $$\begin{aligned} \lim _{\zeta \searrow 0}\frac{\Lambda '(t_0)\ominus \Lambda '(t_0+\zeta )}{-\zeta }=\lim _{\zeta \searrow 0}\frac{\Lambda '(t_0-\zeta )\ominus \Lambda '(t_0)}{-\zeta }=\Lambda ''(t_0). \end{aligned}$$
    (9)

    or

  3. 3.
    $$\begin{aligned} \lim _{\zeta \searrow 0}\frac{\Lambda '(t_0+\zeta )\ominus \Lambda '(t_0)}{\zeta }=\lim _{\zeta \searrow 0}\frac{\Lambda '(t_0-\zeta )\ominus \Lambda '(t_0)}{-\zeta }=\Lambda ''(t_0). \end{aligned}$$
    (10)

    or

  4. 4.
    $$\begin{aligned} \lim _{\zeta \searrow 0}\frac{\Lambda '(t_0)\ominus \Lambda '(t_0+\zeta )}{-\zeta }=\lim _{\zeta \searrow 0}\frac{\Lambda '(t_0)\ominus \Lambda '(t_0-\zeta )}{\zeta }=\Lambda ''(t_0). \end{aligned}$$
    (11)

Definition 5

(Salahshour et al. 2012) Let \(v,w\in {\mathbb {E}}.\) Suppose there exists \(u\in {\mathbb {E}}\), such that \(v=w+u\), and then, u is called H-difference of v and w and is denoted by \(v\ominus w\) and \(v+(-1)w \ne v\ominus w\), where the notation \(\ominus \) denotes H-difference.

Definition 6

(Allahviranloo et al. 2014) The gH-difference u of two fuzzy numbers \(v,w\in {\mathbb {R}}\) is defined as:

$$\begin{aligned} v\ominus _{gH}w=u\Longleftrightarrow {\left\{ \begin{array}{ll} (i)\,v=w+u,\\ or\,\,(ii)\,w=v+(-1)u. \end{array}\right. } \end{aligned}$$
(12)

Definition 7

The fuzzy time-fractional diffusion equation is defined as: Zureigat et al. (2019)

$$\begin{aligned} \frac{\partial ^\alpha {\tilde{v}}(\varsigma ,t)}{\partial t^\alpha } ={\tilde{a}}(\varsigma )\frac{\partial ^2 {\tilde{v}}(\varsigma ,t)}{\partial \varsigma ^2}+{\tilde{b}}(\varsigma ),\,\,0<\varsigma <l,\,\,t>0, \end{aligned}$$
(13)

with boundary and initial conditions:

$$\begin{aligned} {\tilde{v}}(\varsigma ,0)={\tilde{f}},\,\,{\tilde{v}}(0,t)={\tilde{g}},\,\,{\tilde{v}}(l,0)={\tilde{z}}, \end{aligned}$$
(14)

where \(\tilde{v}(\varsigma ,t)\) represents \(\underline{v}(\varsigma ,0)\) and \({\bar{v}}(\varsigma ,0)\) (the lower and upper functional derivatives), \(\frac{\partial ^\alpha \tilde{v}(\varsigma ,t)}{\partial t^\alpha }\) denotes the non-integer order fuzzy functional derivative of order \(\alpha \), \(\frac{\partial ^2\tilde{v}(\varsigma ,t)}{\partial \varsigma ^2}\) is the fuzzy partial Hukuhara derivative with respect to \(\varsigma \), \(\tilde{v}(\varsigma ,0)\), \(\,\,\tilde{v}(0,t)\), and \(\tilde{v}(l,0)\) represents the initial and boundary conditions.

In general, Eq. (13) can be re-written as upper and lower bound equations as Zureigat et al. (2019):

  • Upper bound equation:

    $$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial ^\alpha {\bar{v}}(\varsigma ,t)}{\partial t^\alpha } ={\bar{a}}(\varsigma )\frac{\partial ^2 {\bar{v}}(\varsigma ,t)}{\partial \varsigma ^2} +{\bar{b}}(\varsigma ) &{} \\ {\bar{v}}(\varsigma ,0,\beta )={\bar{f}}(\beta ),\,\,{\bar{v}}(0,t)={\bar{g}}(\beta ),\,\,{\bar{v}}(l,0)={\bar{z}}(\beta ).&{} \end{array} \right. \end{aligned}$$
    (15)

  • Lower bound equation:

    $$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial ^\alpha \underline{v}(\varsigma ,t)}{\partial t^\alpha }= \underline{\mathrm{a}}(\varsigma )\frac{\partial ^2 \underline{v}(\varsigma ,t)}{\partial \varsigma ^2}+\underline{b}(\varsigma ) &{} \\ \underline{v}(\varsigma ,0)=\underline{f}(\beta ),\,\,\underline{v}(0,t)=\underline{g}(\beta ),\,\,\underline{v}(l,0)=\underline{z}(\beta ).&{} \end{array} \right. \end{aligned}$$
    (16)

Let \(C^\mathfrak {I}[a,b]\) be the space of all continuous fuzzy-valued function on the interval [a, b], and let \(L^\mathfrak {I}[a,b]\) be the space of all Lebesgue integrable fuzzy-valued function on the interval \([a,b]\subset {\mathbb {R}}\), and then, we have the following definition.

Definition 8

(Allahviranloo et al. 2014) Let assume \(f_{gH}^{(n)}=f^{(n)}\in C^\mathfrak {I}[a,b]\cap L^\mathfrak {I}[a,b]\). Then, the fuzzy gH-fractional Caputo differentiability of fuzzy-valued function f is defined as:

$$\begin{aligned}&\left( _{gH}^{C}D^\vartheta f\right) (t)= J_a^{n-\vartheta }\odot \left( f^{(n)}\right) (t)\nonumber \\&\quad =\frac{1}{n-\vartheta }\odot \int _{a}^{t}\left( t-\zeta \right) ^{n-\vartheta -1}\odot \left( f^{(n)}\right) (\zeta )\mathrm{d}\zeta , \end{aligned}$$
(17)

where \(n-1<\vartheta \le n,\,\,n\in {\mathbb {N}},\,\,t>a\).

Besides, by virtue of Theorem 1 and any arbitrary fixed \(r\in [0,1]\) Eq. (16) can be written as the following relation:

$$\begin{aligned} \left( _{gH}^{C}D^\vartheta f\right) (t)=\left[ \left( _{gH}^{C}D^\vartheta {\bar{f}}\right) (t,r),{\left( _{gH}^{C}D^\vartheta \underline{f}\right) }(t,r)\right] , \end{aligned}$$
(18)

where:

$$\begin{aligned} \left( _{gH}^{C}D^\vartheta {\bar{f}}\right) (t,r)=\frac{1}{n-\vartheta }\int _{a}^{t}\left( t-\tau \right) ^{n-\vartheta -1}\left( {\bar{f}}^{(n)}\right) (\tau ,r)\mathrm{d}\tau , \,\,r\in [0,1], \end{aligned}$$
(19)

and

$$\begin{aligned} \left( _{gH}^{C}D^\vartheta \underline{f}\right) (t,r)=\frac{1}{n-\vartheta }\int _{a}^{t}(t-\tau )^{n-\vartheta -1}\left( \underline{f}^{(n)}\right) (\tau ,r)\mathrm{d}\tau ,\,\,r\in [0,1]. \end{aligned}$$
(20)

In the next definition, we define a Laplace-type integral transform called the Shehu transform (Maitama and Zhao 2019a, b) in fuzzy context.

Definition 9

Let \(\tilde{f}\) be continuous fuzzy-valued function and suppose that \(\exp \left( \frac{-p}{q}t\right) \odot \tilde{f}(t)\) is a improper fuzzy Riemann-integrable on the interval \([0,\infty )\), and then, \(\int _{0 }^{\infty }\exp \left( \frac{-p}{q}t\right) \odot \tilde{f}(t)\mathrm{d}t\) is called the fuzzy Shehu transform and is defined over the set of functions:

\(A=\left\{ \tilde{f}(t):\exists \, \, {\mathcal {N}},\, \zeta _{1} ,\, \zeta _{2} >0,\, \, \left| \tilde{f}(t)\right| <{\mathcal {N}}\exp \left( \frac{\left| t\right| }{\zeta _{i} }\right) ,\, \, \text {if}\, \, t\in (-1)^{i} \times \left[ 0,\infty \right) \right\} \),

as

$$\begin{aligned} \mathbf{S }\left[ \tilde{f}(t)\right] =F(p,q)= & {} \int _{0 }^{\infty }\exp \left( \frac{-p}{q}t\right) \odot \tilde{f}(t)\mathrm{d}t,\, \, \, \, p\,>0,\,\, q>0. \end{aligned}$$
(21)

Remark 1

In Eq. (21), \(\tilde{f}\) satisfied the cases of the decreasing diameter \((\,\underline{f}\,)\) and the increasing diameter \((\,{\bar{f}}\,)\) of a fuzzy function f. When the variable \(q=1\), the fuzzy Shehu transform converges to well-known fuzzy Laplace transform.

By virtue of Theorem 1 in Salahshour et al. (2012), we have:

$$\begin{aligned} \int _{0 }^{\infty }\exp \left( \frac{-p}{q}t\right) \odot \tilde{f}(t)\mathrm{d}t= & {} \left( \int _{0 }^{\infty }\exp \left( \frac{-p}{q}t\right) \underline{f}(t;r)\mathrm{d}t,\int _{0 }^{\infty }\exp \left( \frac{-p}{q}t\right) {\bar{f}}(t;r)\mathrm{d}t\right) . \end{aligned}$$
(22)

Moreover, using the classical Shehu transform (Maitama and Zhao 2019a, b), we get:

$$\begin{aligned}&{{\mathbb {S}}}\left[ \underline{f}(t;r)\right] =\int _{0 }^{\infty }\exp \left( \frac{-p}{q}t\right) \underline{f}(t;r)\mathrm{d}t\,\, \text {and}\nonumber \\&\,\, {\mathbb S}\left[ {\bar{f}}(t;r)\right] =\int _{0 }^{\infty }\exp \left( \frac{-p}{q}t\right) {\bar{f}}(t;r)\mathrm{d}t. \end{aligned}$$
(23)

Then, we have the following relations:

$$\begin{aligned} \mathbf{S }\left[ \tilde{f}(t)\right]= & {} \left( {\mathbb S}\left[ \underline{f}(t;r)\right] ,{\mathbb S}\left[ {\bar{f}}(t;r)\right] \right) \nonumber \\= & {} \left( {\underline{F}}(p,q),{\bar{F}}(p,q)\right) . \end{aligned}$$
(24)

2.1 Basic properties of the fuzzy Shehu transform

Theorem 1

(Derivative operator). Suppose \(\tilde{f}^{(n)}(t)\) be an integrable fuzzy-valued function, and \(\tilde{f}(t)\) is the primitive of \(\tilde{f}^{(n)}(t)\) on \([0,\infty )\), and then:

$$\begin{aligned} \mathbf{S } \left[ \tilde{f}^{(n)}(t)\right] =\left( \frac{p}{q}\right) ^n\odot \mathbf{S } \left[ \tilde{f}(t)\right] \ominus \sum _{k=0}^{n-1}\left( \frac{p}{q}\right) ^{n-(k+1)}\odot \tilde{f}^{(k)}(0). \end{aligned}$$
(25)

Some few terms of Eq. (25) are:

$$\begin{aligned}&\mathbf{S }\left[ \tilde{f}'(t)\right] =\frac{p}{q}\odot F(p,q)\ominus \tilde{f}(0). \end{aligned}$$
(26)
$$\begin{aligned}&\mathbf{S }\left[ \tilde{f}''(t)\right] =\left( \frac{p}{q}\right) ^2\odot F(p,q)\ominus \frac{p}{q}\odot \tilde{f}(0)\ominus \tilde{f}'(0). \end{aligned}$$
(27)
$$\begin{aligned}&\mathbf{S }\left[ \tilde{f}'''(t)\right] =\left( \frac{p}{q}\right) ^3\odot F(p,q)\ominus \left( \frac{p}{q}\right) ^2\odot \tilde{f}(0)\ominus \frac{p}{q}\odot \tilde{f}'(0)\ominus \tilde{f}''(0). \end{aligned}$$
(28)

Proof

Let \(r\in [0,1]\) be arbitrary, and then, we deduce:

$$\begin{aligned}&\left( \frac{p}{q}\right) ^n\odot \mathbf{S }\left[ \tilde{f}(t)\right] \ominus \sum _{k=0}^{n-1}\left( \frac{p}{q}\right) ^{n-(k+1)}\odot \tilde{f}^{(k)}(0)\nonumber \\&\quad =\left( \left( \frac{p}{q}\right) ^n{\mathbb S}\left[ {\bar{f}}(t;r)\right] -\sum _{k=0}^{n-1}\left( \frac{p}{q}\right) ^{n-(k+1)}{\bar{f}}^{(k)}(0;r),\nonumber \right. \\&\left. \left( \frac{p}{q}\right) ^n{\mathbb S}\left[ \underline{f}(t;r)\right] -\sum _{k=0}^{n-1}\left( \frac{p}{q}\right) ^{n-(k+1)}\ \underline{f}^{(k)}(0;r)\right) . \end{aligned}$$
(29)

By Theorem 1, we have:

$$\begin{aligned}&\left( \frac{p}{q}\right) ^n\odot \mathbf{S } \left[ \tilde{f}(t)\right] \ominus \sum _{k=0}^{n-1}\left( \frac{p}{q}\right) ^{n-(k+1)}\odot \tilde{f}^{(k)}(0)\nonumber \\&\quad =\left( {{\mathbb {S}}} \left[ {\bar{f}}^{(n)}(t;r)\right] ,{{\mathbb {S}}} \left[ \underline{f}^{(n)}(t;r)\right] \right) , \end{aligned}$$
(30)

where \(\left( {{\mathbb {S}}} \left[ {\bar{f}}^{(n)}(t;r)\right] ,{\mathbb S} \left[ \underline{f}^{(n)}(t;r)\right] \right) \) are, respectively, defined in Eq. (23).

Using induction hypothesis, Eq. (25) holds for \(n=k\), and then, using Eq. (26), we get:

$$\begin{aligned}&\mathbf{S } \left[ (\tilde{f}^{(k)}(t))'\right] =\frac{p}{q}\odot \mathbf{S} \left[ \tilde{f}^{(k)}(t)\right] \ominus \tilde{f}^{(k)}(0)\nonumber \\&\quad =\frac{p}{q}\odot \left[ \left( \frac{p}{q}\right) ^k\odot \mathbf{S} \left[ \tilde{f}(t)\right] \ominus \sum _{i=0}^{k-1}\left( \frac{p}{q}\right) ^{k-(i+1)}\odot \tilde{f}^{(i)}(0)\right] \ominus \tilde{f}^{(k)}(0)\nonumber \\&\quad =\left( \frac{p}{q}\right) ^{k+1}\odot \mathbf{S} \left[ \tilde{f}(t)\right] \ominus \sum _{i=0}^{k}\left( \frac{p}{q}\right) ^{k-i}\odot \tilde{f}^{(i)}(0), \end{aligned}$$
(31)

Thus, Eq. (25) is true when \(n=k+1\). This complete the proof. \(\square \)

To demonstrate the assertion of Theorem 1, we consider the following second-order fuzzy initial value problem (see Khastan et al. 2009; Najeeb et al. 2015):

$$\begin{aligned} \left\{ \begin{array}{ll} \tilde{v}''(\tau )=\zeta _0,\,\,\zeta _0=(\beta -1,1-\beta ), &{} \\ \tilde{v}(0;\beta )=(\beta -1,1-\beta ), &{} \\ \tilde{v}'(0;\beta )=(\beta -1,1-\beta ).&{} \\ \end{array} \right. \end{aligned}$$
(32)

Let us consider the four cases of strongly generalized H-differentiability given in Definition 4

Case I: Suppose \(\tilde{v}(\tau )\) and \(\tilde{v}'(\tau )\) in Eq. (32) are (1)-differentiable. Then, computing the fuzzy Shehu transform, we get:

$$\begin{aligned} \frac{p^2}{q^2}\odot \mathbf{S} \left[ \tilde{v}(\tau )\right] \ominus \frac{p}{q}\odot \tilde{v}(0)\ominus \tilde{v}'(0)=\frac{q}{p}\zeta _0. \end{aligned}$$
(33)

Then, for any fixed \(\beta \in [0,1]\), we obtain the following \(\beta \)-cuts representations of the lower and upper bound equations as:

$$\begin{aligned} \frac{p^2}{q^2} \mathbf{S} \left[ \underline{v}(\tau ;\beta )\right] -\frac{p}{q} \underline{v}(0;\beta )- \underline{v}'(0;\beta )=\frac{q}{p}\zeta _0, \end{aligned}$$
(34)

and

$$\begin{aligned} \frac{p^2}{q^2} \mathbf{S} \left[ {\bar{v}}(\tau ;\beta )\right] -\frac{p}{q} {\bar{v}}(0;\beta )- {\bar{v}}'(0;\beta )=\frac{q}{p}\zeta _0. \end{aligned}$$
(35)

After simplifying Eqs. (34) and (35), we get:

$$\begin{aligned}&\underline{v}(\tau ;\beta )=\mathbf{S} ^{-1}\left( \frac{q}{p}\right) \underline{v}(0;\beta )+ \mathbf{S} ^{-1}\left( \frac{q^2}{p^2}\right) \underline{v}'(0;\beta )+\mathbf{S} ^{-1}\left( \frac{q^3}{p^3}\right) \zeta _0, \end{aligned}$$
(36)
$$\begin{aligned}&{\bar{v}}(t;\beta )=\mathbf{S} ^{-1}\left( \frac{q}{p}\right) {\bar{v}}(0;\beta )+\mathbf{S} ^{-1}\left( \frac{q^2}{p^2}\right) {\bar{v}}'(0;\beta )+\mathbf{S} ^{-1}\left( \frac{q^3}{p^3}\right) \zeta _0. \end{aligned}$$
(37)

Finally, we obtain the expected results of Case I as:

$$\begin{aligned} \left\{ \begin{array}{ll} \underline{v}(\tau ;\beta )=(\beta -1)\left( 1+\tau +\frac{\tau ^2}{2}\right) , &{} \\ {\bar{v}}(\tau ;\beta )=(1-\beta )\left( 1+\tau +\frac{\tau ^2}{2}\right) .&{} \\ \end{array} \right. \end{aligned}$$
(38)

Case II: Suppose \(\tilde{v}(\tau )\) is (1)-differentiable and \(\tilde{v}'(\tau )\) is (2)-differentiable in Eq. (32). Then, applying the fuzzy Shehu transform, we deduce:

$$\begin{aligned} -\frac{p}{q}\odot \tilde{v}(0)-\tilde{v}'(0)\ominus \left( -\frac{p^2}{q^2}\right) \odot \mathbf{S} \left[ \tilde{v}(\tau )\right] =\frac{q}{p}\zeta _0. \end{aligned}$$
(39)

For any fixed \(\beta \in [0,1]\), we get the following \(\beta \)-cuts representations of the lower and upper bound equations as:

$$\begin{aligned}&-\frac{p}{q}\odot \underline{v}(0;\beta )-\underline{v}'(0;\beta )\ominus \left( -\frac{p^2}{q^2}\right) \odot \mathbf{S} \left[ \underline{v}(\tau ;\beta )\right] =\frac{q}{p}\zeta _0, \end{aligned}$$
(40)
$$\begin{aligned}&-\frac{p}{q}\odot {\bar{v}}(0;\beta )-{\bar{v}}'(0;\beta )\ominus \left( -\frac{p^2}{q^2}\right) \odot \mathbf{S} \left[ {\bar{v}}(\tau ;\beta )\right] =\frac{q}{p}\zeta _0. \end{aligned}$$
(41)

After simplifying and inverting the transform, we obtain the following results:

$$\begin{aligned} \left\{ \begin{array}{ll} \underline{v}(\tau ;\beta )=(\beta -1)\left( 1+\tau -\frac{\tau ^2}{2}\right) , &{} \\ \bar{v}(\tau ;\beta )=(1-\beta )\left( 1+\tau -\frac{\tau ^2}{2}\right) .&{} \\ \end{array} \right. \end{aligned}$$
(42)

Case III: Suppose \(\tilde{v}(\tau )\) is (2)-differentiable and \(\tilde{v}'(\tau )\) is (1)-differentiable in Eq. (32). Then, computing the fuzzy Shehu transform, we get:

$$\begin{aligned} -\frac{p}{q}\odot \tilde{v}(0)\ominus \tilde{v}'(0)\ominus \left( -\frac{p^2}{q^2}\right) \odot \mathbf{S} \left[ \tilde{v}(\tau )\right] =\frac{q}{p}\zeta _0. \end{aligned}$$
(43)

Then, for any fixed \(\beta \in [0,1]\), we obtain the following \(\beta \)-cuts representations of the lower and upper bound equations as:

$$\begin{aligned}&-\frac{p}{q}\odot \underline{v}(0;\beta )\ominus \underline{v}'(0;\beta )\ominus \left( -\frac{p^2}{q^2}\right) \odot \mathbf{S} \left[ \underline{v}(\tau ;\beta )\right] =\frac{q}{p}\zeta _0, \end{aligned}$$
(44)
$$\begin{aligned}&-\frac{p}{q}\odot \bar{v}(0;\beta )\ominus \bar{v}'(0;\beta )\ominus \left( -\frac{p^2}{q^2}\right) \odot \mathbf{S} \left[ \bar{v}(\tau ;\beta )\right] =\frac{q}{p}\zeta _0. \end{aligned}$$
(45)

After some algebraic simplifications, we obtain the following results:

$$\begin{aligned} \left\{ \begin{array}{ll} \underline{v}(\tau ;\beta )=(\beta -1)\left( 1-\tau -\frac{\tau ^2}{2}\right) , &{} \\ \bar{v}(\tau ;\beta )=(1-\beta )\left( 1-\tau -\frac{\tau ^2}{2}\right) .&{} \\ \end{array} \right. \end{aligned}$$
(46)

Finally, Case IV: Suppose \(\tilde{v}(\tau )\) and \(\tilde{v}'(\tau )\) are (2)-differentiable in Eq. (32). Then, taking the fuzzy Shehu transform, we have:

$$\begin{aligned} -\tilde{v}'(0)\ominus \frac{p}{q}\odot \tilde{v}(0)+\frac{p^2}{q^2}\odot \mathbf{S} \left[ \tilde{v}(\tau )\right] =\frac{q}{p}\zeta _0. \end{aligned}$$
(47)

For any fixed \(\beta \in [0,1]\), we obtain the following \(\beta \)-cuts representations of the lower and upper bound equations as:

$$\begin{aligned}&-\underline{v}'(0;\beta )\ominus \frac{p}{q}\odot \underline{v}(0;\beta )+\frac{p^2}{q^2}\odot \mathbf{S} \left[ \underline{v}(\tau ;\beta )\right] =\frac{q}{p}\zeta _0, \end{aligned}$$
(48)
$$\begin{aligned}&-\bar{v}'(0;\beta )\ominus \frac{p}{q}\odot \bar{v}(0;\beta )+\frac{p^2}{q^2}\odot \mathbf{S} \left[ \bar{v}(\tau ;\beta )\right] =\frac{q}{p}\zeta _0. \end{aligned}$$
(49)

After some algebraic manipulations, the following results are obtain:

$$\begin{aligned} \left\{ \begin{array}{ll} \underline{v}(\tau ;\beta )=(\beta -1)\left( 1-\tau +\frac{\tau ^2}{2}\right) , &{} \\ \bar{v}(\tau ;\beta )=(1-\beta )\left( 1-\tau +\frac{\tau ^2}{2}\right) .&{} \\ \end{array} \right. \end{aligned}$$
(50)

In the next theorem, we prove the convolution theorem of the fuzzy Shehu transform.

Theorem 2

(Convolution theorem). Suppose \(\tilde{f}(t)\) and \(\tilde{g}(t)\) be integrable fuzzy-valued functions, and let F(p, q)  and G(p, q) be the fuzzy Shehu transform of the functions \(\tilde{f}(t)\) and \(\tilde{g}(t)\), respectively, and then:

$$\begin{aligned} \mathbf{S} \left[ (\tilde{f}*\tilde{g})(t)\right] =F(p,q)\odot G(p,q), \end{aligned}$$
(51)

where the convolution of \(f*g\) is:

$$\begin{aligned} \int _{0 }^{t }\tilde{f}(\zeta )\odot \tilde{g}(t-\zeta )\mathrm{d}\zeta =\int _{0 }^{t }\tilde{f}(t-\zeta )\odot \tilde{g}(\zeta )\mathrm{d}\zeta . \end{aligned}$$
(52)

Proof

Based on Eqs. (22), (51) and Eq. (52), we deduce:

$$\begin{aligned}&\mathbf{S} \left[ \int _{0}^{t}\tilde{f}(\zeta )\odot \tilde{g}(t-\zeta )\mathrm{d}\zeta \right] =\int _{0 }^{\infty }\exp \left( \frac{-pt}{q}\right) \odot \left( \int _{0}^{t}\tilde{f}(\zeta )\odot \tilde{g}(t-\zeta )\right) \mathrm{d}\zeta . \end{aligned}$$

Interchanging the order and the limit of the integration, we have:

$$\begin{aligned}&\mathbf{S} \left[ \int _{0}^{t}\tilde{f}(\zeta )\odot \tilde{g}(t-\zeta )\mathrm{d}\zeta \right] =\int _{0 }^{\infty }\left( \tilde{f}(\zeta )\odot \int _{\zeta }^{\infty }\exp \left( \frac{-pt}{q}\right) \odot \tilde{g}(t-\zeta )\mathrm{d}t\right) \mathrm{d}\zeta . \end{aligned}$$

Setting \(\vartheta =t-\zeta \), we get:

$$\begin{aligned}&\int _{\zeta }^{\infty }\exp \left( \frac{-pt}{q}\right) \odot \tilde{g}(t-\zeta )\mathrm{d}t=\int _{0 }^{\infty }\exp \left( -\frac{(\vartheta +\zeta )}{q}p\right) \odot \tilde{g}(\vartheta )\mathrm{d}\vartheta \\&\quad =\exp \left( -\frac{\zeta p}{q}\right) \odot \int _{0}^{\infty }\exp \left( -\frac{\vartheta p}{q}\right) \odot \tilde{g}(\vartheta )\mathrm{d}\vartheta \\&\quad =\exp \left( -\frac{\zeta p}{q}\right) \odot G(p,q). \end{aligned}$$

Hence:

$$\begin{aligned}&\mathbf{S} \left[ \int _{0}^{t}\tilde{f}(\zeta )\odot \tilde{g}(t-\zeta )\mathrm{d}\zeta \right] =\int _{0 }^{\infty }\tilde{f}(\zeta )\odot \exp \left( \frac{-p\zeta }{q}\right) \odot G(p,q)\mathrm{d}\zeta \nonumber \\&\quad =G(p,q)\odot \int _{0 }^{\infty }\tilde{f}(\zeta )\odot \exp \left( \frac{-p\zeta }{q}\right) \mathrm{d}\zeta \nonumber \\&\quad =F(p,q)\odot G(p,q); \end{aligned}$$
(53)

thus, the proof is complete. \(\square \)

To illustrate the assertion of Theorem 1, let us consider the following fuzzy Volterra integral equation of the second kind of the form:

$$\begin{aligned} \tilde{v}(\tau )=(1+\beta ,2-\beta )\odot \exp (-2\tau )+\int _{0}^{\tau }\sin (\tau -\zeta )\odot \tilde{v}(\zeta )\mathrm{d}\zeta . \end{aligned}$$
(54)

Applying Theorem 2 on Eq. (54) yields:

$$\begin{aligned} \mathbf{S} \left[ \tilde{v}(\tau )\right] =\mathbf{S} \left[ (1+\beta ,2-\beta )\odot \exp (-2\tau )\right] +\mathbf{S} \left[ \sin (\tau )\right] \odot \mathbf{S} \left[ \tilde{v}(\tau )\right] . \end{aligned}$$
(55)

Then, for any fixed \(\beta \in [0,1]\), we obtain the following \(\beta \)-cuts representations of the lower and upper bound equations as:

$$\begin{aligned} \mathbf{S} \left[ \underline{v}(\tau ;1+\beta )\right] =\mathbf{S} \left[ (1+\beta )\odot \exp (-2\tau )\right] +\mathbf{S} \left[ \sin (\tau )\right] \odot \mathbf{S} \left[ \underline{v}(\tau ;\beta )\right] , \end{aligned}$$
(56)

and

$$\begin{aligned} \mathbf{S} \left[ \bar{v}(\tau ;2-\beta )\right] =\mathbf{S} \left[ (2-\beta )\odot \exp (-2\tau )\right] +\mathbf{S} \left[ \sin (\tau )\right] \odot \mathbf{S} \left[ \bar{v}(\tau ;\beta )\right] . \end{aligned}$$
(57)

After simplifying the above equations, we get:

$$\begin{aligned} \underline{v}(\tau ;\beta )= & {} (1+\beta )\mathbf{S} ^{-1}\left( -\frac{q}{4p}+\frac{q^2}{2p^2}+\frac{5q}{4(p+2q)}\right) \nonumber \\= & {} (1+\beta )\left( -\frac{1}{4}+\frac{1}{2}\tau +\frac{5}{4}\exp (-2\tau )\right) . \end{aligned}$$
(58)

and

$$\begin{aligned} \bar{v}(\tau ;\beta )= & {} (2-\beta )\mathbf{S} ^{-1}\left( -\frac{q}{4p}+\frac{q^2}{2p^2}+\frac{5q}{4(p+2q)}\right) \nonumber \\= & {} (2-\beta )\left( -\frac{1}{4}+\frac{1}{2}\tau +\frac{5}{4}\exp (-2\tau )\right) . \end{aligned}$$
(59)

In the following theorem, we prove the fuzzy Shehu transform of Caputo generalize Hukuhara derivative \(_{gH}^{C}D_t^{\vartheta } f(t)\), (see Allahviranloo et al. 2014 and the references therein).

Theorem 3

Let \(_{gH}^{C}D_t^{\vartheta } \tilde{f}(t)\) be an integrable fuzzy-valued function, and f(t) is the primitive of \(_{gH}^{C}D_t^{\vartheta } \tilde{f}(t)\) on \([0,\infty )\), and then, the Caputo fractional derivative operator of order \(\vartheta \) holds:

$$\begin{aligned} \mathbf{S} \left[ _{gH}^{C}D_t^{\vartheta } \tilde{f}(t)\right] =\left( \frac{p}{q}\right) ^\vartheta \odot \mathbf{S} \left[ \tilde{f}(t)\right] \ominus \sum _{k=0}^{n-1}\left( \frac{p}{q}\right) ^{\vartheta -k-1}\odot \tilde{f}^{(k)}(0), \end{aligned}$$
(60)

\(n-1<\vartheta \le 1\).

Proof

Applying Definition 9 and Theorem 2, we deduce:

$$\begin{aligned} _{gH}^{C}D_t^{\vartheta } \tilde{f}(t)= & {} \frac{1}{\Gamma (n-\vartheta )}\odot \int _{0}^{t}(t-\tau )^{n-\vartheta -1}\odot \frac{\partial ^n \tilde{f}(\tau )}{\partial \tau ^n}\mathrm{d}\tau \\&=\frac{1}{\Gamma (n-\vartheta )}\odot \tilde{f}^{(n)}(t)\odot t^{n-\vartheta -1}. \end{aligned}$$

Then, by Definition 9 and Theorem 1, we get:

$$\begin{aligned} \mathbf{S} \left[ _{gH}^{C}D_t^{\vartheta }\tilde{f}(t)\right]= & {} \frac{1}{\Gamma (n-\vartheta )}\odot \mathbf{S} \left[ t^{n-\vartheta -1}\odot \tilde{f}^{(n)}(t)\right] \\= & {} \left( \frac{p}{q}\right) ^\vartheta \odot \mathbf{S} \left[ \tilde{f}(t)\right] \ominus \sum _{k=0}^{n-1}\left( \frac{p}{q}\right) ^{\vartheta -k-1}\odot \tilde{f}^{(k)}(0). \end{aligned}$$

Finally, by the virtue of Theorem 1 in Salahshour et al. (2012) and any arbitrary fixed \(r\in [0,1]\), we have:

$$\begin{aligned}&\left( \frac{p}{q}\right) ^\vartheta \odot \mathbf{S} \left[ \tilde{f}(t)\right] \ominus \sum _{k=0}^{n-1}\left( \frac{p}{q}\right) ^{\vartheta -(k+1)}\odot \tilde{f}^{(k)}(0)\nonumber \\&\quad =\left( \left( \frac{p}{q}\right) ^\vartheta \mathbf{S} \left[ \bar{f}(t;r)\right] -\sum _{k=0}^{n-1}\left( \frac{p}{q}\right) ^{\vartheta -(k+1)}\bar{f}^{(k)}(0;r),\nonumber \right. \\&\left. \left( \frac{p}{q}\right) ^\vartheta \mathbf{S} \left[ \underline{f}(t;r)\right] -\sum _{k=0}^{n-1}\left( \frac{p}{q}\right) ^{\vartheta -(k+1)}\underline{f}^{(k)}(0;r)\right) . \end{aligned}$$

The proof ends.\(\square \)

The generalization of the fuzzy Laplace transform (Allahviranloo and Ahmadi 2010) and the fuzzy Sumudu transform (Jafari and Razvarz 2019) is verified in the following theorems.

Theorem 4

Let F(p, q) and F(p) be the fuzzy Shehu transform and the fuzzy Laplace transform of the function \(\tilde{f}(t)\in A\), and then:

$$\begin{aligned} F(p,q)=F\left( \frac{p}{q}\right) . \end{aligned}$$
(61)

Proof

The proof follows directly from Eq. (22) and Definition 3.1 in Allahviranloo and Ahmadi (2010). \(\square \)

Theorem 5

Let F(p, q) and G(q) be the fuzzy Shehu transform and the fuzzy Sumudu transform of the function \(\tilde{f}(t)\in A\), and then:

$$\begin{aligned} F(p,q)=\frac{q}{p}\odot G\left( \frac{q}{p}\right) . \end{aligned}$$
(62)

Proof

Let \(r\in [0,1]\). Setting \(\zeta =\frac{p}{q}t\) in Eq. (22), we deduce:

$$\begin{aligned}&F(p,q)=\frac{q}{p}\odot \int _{0 }^{\infty }\exp \left( -\zeta \right) \odot \tilde{f}(\frac{q}{p}\zeta )\mathrm{d}\zeta \nonumber \\&\quad =\left( \frac{q}{p}\int _{0 }^{\infty }\exp \left( -\zeta \right) \underline{f}\left( \frac{q}{p}\zeta ;r\right) \mathrm{d}\zeta ,\frac{q}{p}\int _{0 }^{\infty }\exp \left( -\zeta \right) \bar{f}\left( \frac{q}{p}\zeta ;r\right) \mathrm{d}\zeta \right) \nonumber \\&\quad =\left( \frac{q}{p}\underline{G}\left( \frac{q}{p}\right) ,\frac{q}{p}\bar{G}\left( \frac{q}{p}\right) \right) =\frac{q}{p}\odot G\left( \frac{q}{p}\right) . \end{aligned}$$
(63)

\(\square \)

The inverse fuzzy Shehu transform is defined in the next theorem.

Theorem 6

(Inverse fuzzy Shehu transform). Let the function \(f(t)\in A\) and F(p, q) be the fuzzy Shehu transform of the function f(t), and then, its inverse transform \(\mathbf{S} ^{-1}\) is given by:

$$\begin{aligned} \mathbf{S} ^{-1}\left[ F(p,q)\right] =\tilde{f}(t),\, \, forall\,\,t\ge 0. \end{aligned}$$
(64)

Equivalently, the complex inverse fuzzy Shehu transform is:

$$\begin{aligned}&\tilde{f}(t)=\lim _{\beta \rightarrow \infty }\frac{1}{2\pi i}\odot \int _{\vartheta -i\beta }^{\vartheta +i\beta }\frac{1}{q}\odot \exp \left( \frac{pt}{q}\right) \odot F(p,q)\mathrm{d}p. \end{aligned}$$
(65)

The basic idea of the proposed algorithm is illustrated in the following section.

3 Algorithm of HASTM

Consider the fuzzy fractional partial differential equation:

$$\begin{aligned}&\frac{\partial ^\vartheta \tilde{v}(\varsigma ,t)}{\partial t^\vartheta }=\tilde{a}(\varsigma )\frac{\partial ^2 \tilde{v}(\varsigma ,t)}{\partial \varsigma ^2}+\tilde{b}(\varsigma ),\,\,{\varsigma \in {\mathbb {R}},}\,\,\,0<\varsigma <{1,\,\,t>0,\,\,\,\vartheta \in (0,1],} \end{aligned}$$
(66)

where \(\frac{\partial ^\vartheta \tilde{v}(\varsigma ,t)}{\partial t^\vartheta }\) is the Caputo gH-derivative.

Operating the fuzzy Shehu transform on Eq. (66), we have:

$$\begin{aligned}&\mathbf{S} \left[ \frac{\partial ^\vartheta \tilde{v}(\varsigma ,t)}{\partial t^\vartheta }\right] - \mathbf{S} \left[ \tilde{a}(\varsigma )\frac{\partial ^2 \tilde{v}(\varsigma ,t)}{\partial \varsigma ^2}\right] =\mathbf{S} \left[ \tilde{b}(\varsigma )\right] . \end{aligned}$$
(67)

Using Theorem 3, we have:

$$\begin{aligned}&\left( \frac{p}{q}\right) ^\vartheta \mathbf{S} \left[ \tilde{v}(\varsigma ,t)\right] -\sum _{k=0}^{m-1}\left( \frac{p}{q}\right) ^{\vartheta -k-1}\tilde{v}^{(k)}(0,t)- \mathbf{S} \left[ \tilde{a}(\varsigma )\frac{\partial ^2 \tilde{v}(\varsigma ,t)}{\partial \varsigma ^2}\right] =\mathbf{S} \left[ \tilde{b}(\varsigma )\right] .\nonumber \\ \end{aligned}$$
(68)

Equivalently:

$$\begin{aligned}&\mathbf{S} \left[ \tilde{v}(\varsigma ,t)\right] =\left( \frac{q}{p}\right) ^\vartheta \sum _{k=0}^{m-1}\left( \frac{p}{q}\right) ^{\vartheta -k-1}\tilde{v}^{(k)}(0,t)-\left( \frac{q}{p}\right) ^\vartheta \left( \mathbf{S} \left[ \tilde{a}(\varsigma )\frac{\partial ^2 \tilde{v}(\varsigma ,t)}{\partial \varsigma ^2}\right] +\mathbf{S} \left[ \tilde{b}(\varsigma )\right] \right) .\nonumber \\ \end{aligned}$$
(69)

In this case, the nonlinear operator is:

$$\begin{aligned}&{\mathcal {N}}[{\tilde{\varphi }}(\varsigma ,t;\lambda )]=\mathbf{S} \left[ {\tilde{\varphi }}(\varsigma ,t;\lambda )\right] -\left( \frac{q}{p}\right) ^\vartheta \sum _{k=0}^{m-1}\left( \frac{p}{q}\right) ^{\vartheta -k-1}\tilde{v}^{(k)}(0,t)\nonumber \\&\quad -\left( \frac{q}{p}\right) ^\vartheta \left( \mathbf{S} \left[ \tilde{a}(\varsigma )\frac{\partial ^2 \tilde{v}(\varsigma ,t)}{\partial \varsigma ^2}\right] +\mathbf{S} \left[ \tilde{b}(\varsigma )\right] \right) , \end{aligned}$$
(70)

where \(\lambda \in [0,1]\), \({\tilde{\varphi }}(\varsigma ,t;\lambda )\) represent a real-valued function, and \(\lambda \in [0,1]\) denotes an auxiliary parameter. The homotopy of Eq. (66) is:

$$\begin{aligned} (1-\lambda )\mathbf{S} \left[ {\tilde{\varphi }}(\varsigma ,t;\lambda )-\tilde{v}_0(\varsigma ,t)\right] =\xi \lambda {\mathcal {H}}(\varsigma ,t){\mathcal {N}}[{\tilde{\varphi }}(\varsigma ,t)], \end{aligned}$$
(71)

where \(\mathbf{S} \), \({\mathcal {H}}(\varsigma ,t)\), denotes the fuzzy Shehu transform and the auxiliary function, respectively. \(\lambda \in [0,1]\) denotes the embedding parameter and \(\xi \ne 0\) represent the auxiliary parameter (non-zero convergent control parameter). Finally, \(\tilde{v_0}(\varsigma ,t)\) is the initial approximation of \(\tilde{v}(\varsigma ,t)\), and \({\tilde{\varphi }}(\varsigma ,t;\lambda )\) represent the unknown function to be computed later.

The most significant advantage of the algorithm is the freedom to control the series solutions, select the auxiliary parameter, and the initial guess, respectively. When \(\lambda =1\), and \(\lambda =0\) in Eq. (71), the following conditions hold:

$$\begin{aligned} {\tilde{\varphi }}(\varsigma ,t;0)=\tilde{v}_0(\varsigma ,t),\,\,\,\,\mathrm{and}\,\,\,\,{\tilde{\varphi }}(\varsigma ,t;1)=\tilde{v}(\varsigma ,t). \end{aligned}$$
(72)

Then, the solution \({\tilde{\varphi }}(\varsigma ,t;\lambda )\) changes from the guess \(\tilde{v_0}(\varsigma ,t)\) to the solution \(\tilde{v}(\varsigma ,t)\) as \(\lambda \) varies from 0 to 1. Thanks to Taylor series expanding of \({\tilde{\varphi }}(\varsigma ,t;\lambda )\) with respect to \(\lambda \) which help us to get:

$$\begin{aligned} {\tilde{\varphi }}(\varsigma ,t;\lambda )=\tilde{v}_0(\varsigma ,t)+\sum _{m=1}^{+\infty }\tilde{v}_m(\varsigma ,t)\lambda ^{m}, \end{aligned}$$
(73)

where:

$$\begin{aligned} \tilde{v}_m(\varsigma ,t)=\left[ \frac{1}{\Gamma (m+1)}\frac{\partial ^ {m}{\tilde{\varphi }}(\varsigma ,t;\lambda )}{\partial \lambda ^{m}}\right] _{\lambda =0}. \end{aligned}$$
(74)

Choosing a suitable auxiliary parameter, initial guess, auxiliary linear operator, and the auxiliary function, Eq. (73) converge at \(\lambda =1\), and:

$$\begin{aligned} {\tilde{\varphi }}(\varsigma ,t)=\tilde{v}_0(\varsigma ,t)+\sum _{m=1}^{+\infty }\tilde{v}_m(\varsigma ,t). \end{aligned}$$
(75)

Besides, we obtain the governing equation from the zero deformation Eq. (71) based on Eq. (75).

The vectors \(\vec {\tilde{v}}_m\) are defined as:

$$\begin{aligned} \vec {\tilde{v}}_m=\left\{ \tilde{v}_0(\varsigma ,t),\,\,\tilde{v}_1(\varsigma ,t),\,\,\tilde{v}_2(\varsigma ,t),\ldots ,\,\,\tilde{v}_n(\varsigma ,t)\right\} . \end{aligned}$$
(76)

Then, differentiating Eq. (71) m-times with respect to \(\lambda \) and choosing \(\lambda =0\), and dividing by \(\Gamma (m+1)\), yields the M\(^{th}\)-order deformation equation:

$$\begin{aligned} \mathbf{S} \left[ \tilde{v}_m(\varsigma ,t)-\chi _m\tilde{v}_{m-1}(\varsigma ,t)\right] =\xi {\mathcal {H}}(\varsigma ,t)R_m(\vec {\tilde{v}}_{m-1},\varsigma ,t), \end{aligned}$$
(77)

where:

$$\begin{aligned} R_m(\vec {\tilde{v}}_{m-1},\varsigma ,t)=\left[ \frac{1}{\Gamma (m)}\frac{\partial ^ {{(m-1)}}{\mathcal {N}}\left[ {\tilde{\varphi }}(\varsigma ,t;\lambda )\right] }{\partial \lambda ^{{(m-1)}}}\right] _{\lambda =0}, \end{aligned}$$
(78)

and

$$\begin{aligned} \chi _m= \left\{ \begin{array}{ll} 0 &{} \quad m \le 1 \\ 1 &{} \quad m > 1. \end{array} \right. \end{aligned}$$
(79)

Taking the inverse fuzzy Shehu transform of Eq. (77), we deduce:

$$\begin{aligned} \tilde{v}_m(\varsigma ,t)=\chi _m\tilde{v}_{m-1}(\varsigma ,t)+\mathbf{S} ^{-1}\left[ \xi {\mathcal {H}}(\varsigma ,t)R_m(\vec {\tilde{v}}_{m-1},\varsigma ,t)\right] , \end{aligned}$$
(80)

where \(R_m(\vec {\tilde{v}}_{m-1},\varsigma ,t)\) is defined as:

$$\begin{aligned} R_m(\vec {\tilde{v}}_{m-1},\varsigma ,t)=\frac{\partial ^\vartheta \tilde{v}_{m-1}(\varsigma ,t)}{\partial t^\vartheta }- \tilde{a}(\varsigma )\frac{\partial ^2 \tilde{v}_{m-1}(\varsigma ,t)}{\partial \varsigma ^2}-(1-\chi _m)\tilde{b}(\varsigma ). \end{aligned}$$
(81)

Solving Eq. (80) for \(m\ge 1\), using any mathematical software (Mathematica, Maple, or Matlab), we obtain the series solution:

$$\begin{aligned} \tilde{v}(\varsigma ,t)=\tilde{v}_0(\varsigma ,t)+\sum _{m=0}^{M}\tilde{v}_m(\varsigma ,t), \end{aligned}$$
(82)

which converge with the help of \(\xi \).

Finally, the upper and lower bound solutions of Eq. (66) are given by:

$$\begin{aligned} \bar{v}(\varsigma ,t)=\sum _{m=0}^{+\infty }\bar{v}_m(\varsigma ,t), \end{aligned}$$
(83)

and

$$\begin{aligned} \underline{v}(\varsigma ,t)=\sum _{m=0}^{+\infty }\underline{v}_m(\varsigma ,t), \end{aligned}$$
(84)

respectively.

The following theorems discuss the convergence analysis and error analysis of the original problem [Eq. (66)] based on the procedure of the method.

Theorem 7

Convergence analysis. Suppose the series of Eq. (82) converges to \(\psi (\varsigma ,t)\) as \(M\rightarrow \infty \), where \(\tilde{v}_m(\varsigma ,t)\) is computed using Eq. (77) and the conditions of Eqs. (71) and (78). Then, \(\phi (\varsigma ,t)\) must be the exact solution of the original problem (Eq. (66)).

Proof

Let the series:

$$\begin{aligned} \sum _{m=0}^{\infty }\tilde{v}_m(\varsigma ,t)=\tilde{v}_0(\varsigma ,t)+\sum _{m=1}^{+\infty }\tilde{v}_m(\varsigma ,t)={\tilde{\phi }}(\varsigma ,t). \end{aligned}$$
(85)

Then, we deduce \(\lim _{M\rightarrow \infty }\sum _{m=1}^{M}\tilde{v}_m(\varsigma ,t)=0\). From Eq. (77), we have:

$$\begin{aligned}&\lim _{M\rightarrow \infty }\left[ \xi {\mathcal {H}}(\varsigma ,t)\sum _{m=1}^{M}R_m(\vec {\tilde{v}}_{m-1},\varsigma ,t)\right] =\lim _{M\rightarrow \infty }\left[ \sum _{m=1}^{M}{} \mathbf{S} \left[ \tilde{v}_m(\varsigma ,t)-\chi _m\tilde{v}_{m-1}(\varsigma ,t)\right] \right] \\&\quad =\mathbf{S} \left[ \lim _{M\rightarrow \infty }\sum _{m=1}^{M}\tilde{v}_m(\varsigma ,t)-\lim _{M\rightarrow \infty }\sum _{m=1}^{M}\chi _m\tilde{v}_{m-1}(\varsigma ,t)\right] \\&\quad =\mathbf{S} \left[ \lim _{M\rightarrow \infty }\sum _{m=1}^{M}\tilde{v}_m(\varsigma ,t)\right] =0, \end{aligned}$$

Using the linearity property of Eq. (71) and the fact that \({\mathcal {H}}(\varsigma ,t)\ne 0\),  \(\xi \ne 0\), we get:

$$\begin{aligned} \lim _{M\rightarrow \infty }\sum _{m=1}^{M}R_m(\vec {\tilde{v}}_{m-1},\varsigma ,t)=0. \end{aligned}$$
(86)

Similarly, according to Eq. (81), we get:

$$\begin{aligned}&\lim _{M\rightarrow \infty }\sum _{m=1}^{M}R_m(\vec {\tilde{v}}_{m-1},\varsigma ,t)=\lim _{M\rightarrow \infty }\sum _{m=1}^{M}\left[ \frac{\partial ^\vartheta \tilde{v}_{m-1}(\varsigma ,t)}{\partial t^\vartheta }- \tilde{a}(\varsigma )\frac{\partial ^2 \tilde{v}_{m-1}(\varsigma ,t)}{\partial \varsigma ^2}-(1-\chi _m)\tilde{b}(\varsigma )\right] \nonumber \\&\quad =\frac{\partial ^\vartheta }{\partial t^\vartheta }\lim _{M\rightarrow \infty }\sum _{m=1}^{M}\tilde{v}_{m-1}(\varsigma ,t)-\tilde{a}(\varsigma )\frac{\partial ^2}{\partial \varsigma ^2}\lim _{M\rightarrow \infty }\sum _{m=1}^{M} \tilde{v}_{m-1}(\varsigma ,t)- \lim _{M\rightarrow \infty }\sum _{m=1}^{M}(1-\chi _m)\tilde{b}(\varsigma )\nonumber \\&\quad =\frac{\partial ^\vartheta \tilde{v}_{m-1}(\varsigma ,t)}{\partial t^\vartheta }- \tilde{a}(\varsigma )\frac{\partial ^2 \tilde{v}_{m-1}(\varsigma ,t)}{\partial \varsigma ^2}-(1-\chi _m)\tilde{b}(\varsigma )=0. \end{aligned}$$
(87)

Finally, Eq. (87) above proved that \(\phi (\varsigma ,t)\) satisfies the result of the original problem [Eq. (66)]. \(\square \)

Theorem 8

Let \({\mathcal {X}}\) be a Banach space and let \(\tilde{v}_n(\tau ,t)\) and \(\tilde{v}_m(\varsigma ,t)\) be in \({\mathcal {X}}\). Suppose \(\Lambda \in (0,1)\), then the series solution \(\{\tilde{v}_m(\varsigma ,t)\}^\infty _{m=0}\) which is defined from \(\sum _{m=0}^{\infty }\tilde{v}m(\varsigma ,t)\) converges to the solution of Eq. (77) whenever \(\tilde{v}_m(\varsigma ,t)\le \Lambda \tilde{v}_{m-1}(\varsigma ,t)\,\,\forall \,\,m> {\mathbb {N}}\), that is for any given \(\varepsilon >0\), there exists a positive number \({\mathbb {N}}\), such that \(\left\| \tilde{v}_{m+n}(\varsigma ,t)\right\| \le \varepsilon \,\,\,\forall m,n>{\mathbb {N}}\).

Proof

Let us first define a sequence of partial sum \(\{{\mathcal {S}}_m(\varsigma ,t)\}^\infty _{m=0}\) as:

$$\begin{aligned} {\mathcal {S}}_0(\varsigma ,t)= & {} \tilde{v}_0(\varsigma ,t)\\ {\mathcal {S}}_1(\varsigma ,t)= & {} \tilde{v}_0(\varsigma ,t)+\tilde{v}_1(\varsigma ,t)\\ {\mathcal {S}}_2(\varsigma ,t)= & {} \tilde{v}_0(\varsigma ,t)+\tilde{v}_1(\varsigma ,t)+\tilde{v}_2(\varsigma ,t)\\ {\mathcal {S}}_3(\varsigma ,t)= & {} \tilde{v}_0(\varsigma ,t)+\tilde{v}_1(\varsigma ,t)+\tilde{v}_2(\varsigma ,t)+\tilde{v}_3(\varsigma ,t)\\ \vdots \\ {\mathcal {S}}_m(\varsigma ,t)= & {} \tilde{v}_0(\varsigma ,t)+\tilde{v}_1(\varsigma ,t)+\tilde{v}_2(\varsigma ,t)+\tilde{v}_3(\varsigma ,t)+\cdots +\tilde{v}_m(\varsigma ,t). \end{aligned}$$

We only need to show that \({\mathcal {S}}_m(\varsigma ,t)\) is a Cauchy sequence in \({\mathcal {X}}\). To prove the claim, since \(\Lambda \in (0,1)\), the following inequality holds:

$$\begin{aligned}&\left\| {\mathcal {S}}_{m+1}(\varsigma ,t)-{\mathcal {S}}_m(\varsigma ,t)\right\| =\left\| \tilde{v}_{m+1}(\varsigma ,t)\right\| \le \Lambda \left\| \tilde{v}_{m}(\varsigma ,t)\right\| \le \Lambda ^2\left\| \tilde{v}_{m-1}(\varsigma ,t)\right\| \nonumber \\\nonumber \\&\quad \le \Lambda ^3\left\| \tilde{v}_{m-2}(\varsigma ,t)\right\| \le \Lambda ^4\left\| \tilde{v}_{m-3}(\varsigma ,t)\right\| \le \cdots \le \Lambda ^{m+1}\left\| \tilde{v}_{0}(\varsigma ,t)\right\| . \end{aligned}$$
(88)

Then, for any \(m,n\in {\mathbb {N}},\,\,\,\,n>m\), we obtain:

$$\begin{aligned}&\left\| {\mathcal {S}}_{m}(\varsigma ,t)-{\mathcal {S}}_n(\varsigma ,t)\right\| =\left\| \tilde{v}_{m+n}(\varsigma ,t)\right\| =\left\| \left( {\mathcal {S}}_{m}(\varsigma ,t)-{\mathcal {S}}_{m-1}(\varsigma ,t)\right) \right. \nonumber \\&\quad \left. +\left( {\mathcal {S}}_{m-1}(\varsigma ,t)-{\mathcal {S}}_{m-2}(\varsigma ,t)\right) +\left( {\mathcal {S}}_{m-2}(\varsigma ,t)-{\mathcal {S}}_{m-3}(\varsigma ,t)\right) \right. \nonumber \\&\quad \left. +\cdots +\left( {\mathcal {S}}_{n+1}(\varsigma ,t)-{\mathcal {S}}_{n}(\varsigma ,t)\right) \right\| \le \left\| {\mathcal {S}}_{m}(\varsigma ,t)-{\mathcal {S}}_{m-1}(\varsigma ,t)\right\| \nonumber \\&\quad +\left\| {\mathcal {S}}_{m-1}(\varsigma ,t)-{\mathcal {S}}_{m-2}(\varsigma ,t)\right\| +\left\| {\mathcal {S}}_{m-2}(\varsigma ,t)-{\mathcal {S}}_{m-3}(\varsigma ,t)\right\| \nonumber \\&\quad +\cdots + \left\| {\mathcal {S}}_{n+1}(\varsigma ,t)-{\mathcal {S}}_{n}(\varsigma ,t)\right\| \le \Lambda ^m\left\| \tilde{v}_{0}(\varsigma ,t)\right\| +\Lambda ^{m-1}\left\| \tilde{v}_{0}(\varsigma ,t)\right\| \nonumber \\&\quad +\Lambda ^{m-2}\left\| \tilde{v}_{0}(\varsigma ,t)\right\| + \Lambda ^{m-3}\left\| \tilde{v}_{0}(\varsigma ,t)\right\| +\cdots +\Lambda ^{m+1}\left\| \tilde{v}_{0}(\varsigma ,t)\right\| \nonumber \\&=\quad \left\| \tilde{v}_{0}(\varsigma ,t)\right\| \frac{1-\Lambda ^{m-n}}{1-\Lambda }\Lambda ^{n+1}. \end{aligned}$$
(89)

Choosing \(\varepsilon =\frac{1-\Lambda }{\left( 1-\Lambda ^{m-n}\right) \Lambda ^{n+1}\left\| \tilde{v}_0(\varsigma ,t)\right\| }\), since \(\Lambda \in (0,1)\), \(1>1-\Lambda ^{m-n}\) and \(\tilde{v}_{0}(\varsigma ,t)\) is bounded, we obtain:

$$\begin{aligned} \left\| \tilde{v}_{m+n}(\varsigma ,t)\right\| \le \varepsilon \,\,\, \forall n,m> {\mathbb {N}}. \end{aligned}$$
(90)

or

$$\begin{aligned} \lim _{m,n\rightarrow \infty } \left\| \tilde{v}_{m+n}(\varsigma ,t)\right\| =0. \end{aligned}$$
(91)

Thus, the sequence \(\{{\mathcal {S}}_m(\varsigma ,t)\}^\infty _{m=0}\) is a Cauchy sequence in \({\mathcal {X}}\). This completes the proof. \(\square \)

Theorem 9

Error estimate. Let \(\sum _{i=0}^{j}\tilde{v}_i(\varsigma ,t)\) be finite and \(\tilde{v}(\varsigma ,t)\) be its approximate solution. Suppose \(\Lambda >0\), such that \(\left\| \tilde{v}_{i+1}(\varsigma ,t)\right\| \le \Lambda \left\| \tilde{v}_{i}(\varsigma ,t)\right\| \),  \(\Lambda \in (0,1)\),  for \(\forall i\), then the maximum absolute error is:

$$\begin{aligned} \left\| \tilde{v}(\varsigma ,t)-\sum _{i=0}^{j}\tilde{v}_i(\varsigma ,t)\right\| \le \frac{\Lambda ^{j+1}}{1-\Lambda }\left\| \tilde{v}_{0}(\varsigma ,t)\right\| . \end{aligned}$$
(92)

Proof

Let the series \(\sum _{i=0}^{j}\tilde{v}_i(\varsigma ,t)<\infty \), and then:

$$\begin{aligned}&\left\| \tilde{v}(\varsigma ,t)-\sum _{i=0}^{j}\tilde{v}_i(\varsigma ,t)\right\| =\left\| \sum _{i=j+1}^{\infty }\tilde{v}_i(\varsigma ,t)\right\| \\&\quad \le \sum _{i=j+1}^{\infty }\left\| \tilde{v}_i(\varsigma ,t)\right\| \le \sum _{i=j+1}^{\infty }\Lambda ^i\left\| \tilde{v}_0(\varsigma ,t)\right\| \le \left\| \tilde{v}_0(\varsigma ,t)\right\| \Lambda ^{j+1}\left( 1+\Lambda +\Lambda ^2+\cdots \right) \\&\quad \le \frac{\Lambda ^{j+1}}{1-\Lambda }\left\| \tilde{v}_{0}(\varsigma ,t)\right\| . \end{aligned}$$

The proof is complete. \(\square \)

Test examples were provided in the next section to justify the efficiency and high accuracy of the algorithm.

4 Applications of the HASTM

In this section, we illustrate the efficiency of the proposed analytical technique to fuzzy time-fractional models.

Example 1

Consider the following one-dimensional fuzzy fractional partial differential equation:

$$\begin{aligned} \frac{\partial ^\vartheta \tilde{v}(\varsigma ,t)}{\partial t^\vartheta }=\frac{1}{2}\varsigma ^2\frac{\partial ^2 \tilde{v}(\varsigma ,t)}{\partial \varsigma ^2},\,\,\,{\varsigma \in {\mathbb {R}},}\,\,\,0<\varsigma <{1,\,\,t>0,\,\,\,\vartheta \in (0,1],} \end{aligned}$$
(93)

with initial condition and boundary conditions:

$$\begin{aligned} \tilde{v}(\varsigma ,0)=\tilde{k}(\beta )\varsigma ^2,\,\,\tilde{v}(0,t)=\tilde{v}(1,t)=0,\,\,0 \le \varsigma \le 1, \end{aligned}$$
(94)

where   \(\tilde{k}(\beta )=\left( \underline{k}(\beta ),\,\,\bar{k}(\beta )\right) =\left( \beta -1,1-\beta \right) ,\,\,\beta \in [0,1].\)

Applying the procedure of the HASTM presented in section 3, when \({\mathcal {H}}(\varsigma ,t)=1\), we get the following approximations:

$$\begin{aligned} \tilde{v}_0(\varsigma ,t;\beta )= & {} \varsigma ^2\tilde{k}(\beta )\\ \tilde{v}_1(\varsigma ,t;\beta )= & {} -\xi \varsigma ^2\tilde{k}(\beta )\frac{t^{\vartheta }}{\Gamma (\vartheta +1)}\\ \tilde{v}_2(\varsigma ,t;\beta )= & {} -\xi (\xi +1)\varsigma ^2\tilde{k}(\beta )\frac{t^{\vartheta }}{\Gamma (\vartheta +1)}+\xi ^2\varsigma ^2\tilde{k}(\beta )\frac{t^{2\vartheta }}{\Gamma (2\vartheta +1)}\\ \vdots \end{aligned}$$

and so on.

Setting \(\xi =-1\), the series solutions of Eq. (93) are:

$$\begin{aligned} \tilde{v}(\varsigma ,t;\beta )= & {} \displaystyle \tilde{v}_0(\varsigma ,t;\beta )+\tilde{v}_1(\varsigma ,t;\beta )+\tilde{v}_2(\varsigma ,t;\beta )+\cdots \nonumber \\= & {} \varsigma ^2\tilde{k}(\beta )\sum _{m=0}^{+\infty }\frac{t^{m\vartheta }}{\Gamma (m\vartheta +1)}. \end{aligned}$$
(95)

Hence, the upper and lower bounds solutions of Eq. (93) are given by:

  • Upper bound solution:

    $$\begin{aligned} \bar{v}(\varsigma ,t;\beta )=\varsigma ^2\bar{k}(\beta )\sum _{m=0}^{+\infty }\frac{t^{m\vartheta }}{\Gamma (m\vartheta +1)}. \end{aligned}$$
    (96)

  • Lower bound solution:

    $$\begin{aligned} \displaystyle \underline{v}(\varsigma ,t;\beta )=\varsigma ^2\underline{k}(\beta )\sum _{m=0}^{+\infty }\frac{t^{m\vartheta }}{\Gamma (m\vartheta +1)}. \end{aligned}$$
    (97)
Table 1 Comparison of the upper bound solutions   \(\left( \bar{v}_{10}(\varsigma ,t;\beta )\right) \)  of Eq. (93) using HASTM, ADM (Allahviranloo 2008), and HPM (Wang 2008) at \(\varsigma =0.45,\,\,t=0.7,\) and  \(\beta \in [0,1]\)
Full size table
Table 2 Comparison of the lower bound solutions   \(\left( \underline{v}_{10}(\varsigma ,t;\beta )\right) \)  of Eq. (93) using HASTM, ADM (Allahviranloo 2008), and HPM (Wang 2008) at \(\varsigma =0.45,\,\,t=0.7,\) and  \(\beta \in [0,1]\)
Full size table

Moreover, when \(\vartheta =1\) in Eqs. (96) and (97), we get the following exact solutions:

  • Upper bound solution:

    $$\begin{aligned} \bar{v}(\varsigma ,t;\beta )=\displaystyle \bar{k}(\beta )\varsigma ^2\exp \left( t\right) . \end{aligned}$$
    (98)

  • Lower bound solution:

    $$\begin{aligned} \displaystyle \underline{v}(\varsigma ,t;\beta )=\displaystyle \underline{k}(\beta )\varsigma ^2\exp \left( t\right) . \end{aligned}$$
    (99)

The numerical simulations of the exact and approximate solutions behavior are given in Tables 1 and  2 respectively.

Example 2

Consider the following one-dimensional fuzzy time-fractional partial differential equation:

$$\begin{aligned} \frac{\partial ^\vartheta \tilde{v}(\varsigma ,t)}{\partial t^\vartheta }+\frac{\partial \tilde{v}(\varsigma ,t)}{\partial \varsigma }=\zeta \frac{\partial ^2 \tilde{v}(\varsigma ,t)}{\partial \varsigma ^2},\,\,{\varsigma \in {\mathbb {R}},}\,\,\,0<\varsigma <{1,\,\,t>0,\,\,\,\vartheta \in (0,1],}\qquad \end{aligned}$$
(100)

with initial condition and boundary conditions:

$$\begin{aligned} \tilde{v}(\varsigma ,0)=\tilde{k}(\beta )\exp \left( -\varsigma \right) ,\,\,\tilde{v}(0,t)=\tilde{v}({1},t)=0,\,\,0\le \varsigma \le 1, \end{aligned}$$
(101)

where \(\zeta \) is constant and     \(\tilde{k}(\beta )=\left( \underline{k}(\beta ),\,\,\bar{k}(\beta )\right) =\left( 0.85+0.15\beta ,\,\,1.50-0.5\beta \right) ,\,\,\beta \in [0,1].\)

Employing the procedure of the HASTM discussed in Sect. 3, when \({\mathcal {H}}(\varsigma ,t)=1\), we get the following iterations:

$$\begin{aligned} \tilde{v}_0(\varsigma ,t;\beta )= & {} \tilde{k}(\beta )\exp \left( -\varsigma \right) \\ \tilde{v}_1(\varsigma ,t;\beta )= & {} -\xi \tilde{k}(\beta )(\zeta +1)\exp \left( -\varsigma \right) \frac{t^{\vartheta }}{\Gamma (\vartheta +1)}\\ \tilde{v}_2(\varsigma ,t;\beta )= & {} -\xi (\xi +1)\tilde{k}(\beta )(\zeta +1)\exp \left( -\varsigma \right) \frac{t^{\vartheta }}{\Gamma (\vartheta +1)}\\&+\,\xi ^2\tilde{k}(\beta )(\zeta +1)^2\exp \left( -\varsigma \right) \frac{t^{2\vartheta }}{\Gamma (2\vartheta +1)}\\ \vdots \end{aligned}$$

and so on.

Table 3 Comparison of the upper bound solutions   \(\left( \bar{v}_{10}(\varsigma ,t;\beta )\right) \)  of Eq. (100) using HASTM, ADM (Allahviranloo 2008), and HPM (Wang 2008) at \(\varsigma =0.45,\,\,t=0.045,\,\,\zeta =0.001\) and  \(\beta \in [0,1]\)
Full size table
Table 4 Comparison of the lower bound solutions   \(\left( \underline{v}_{10}(\varsigma ,t;\beta )\right) \)  of Eq. (100) using HASTM, ADM (Allahviranloo 2008), and HPM (Wang 2008) at \(\varsigma =0.45,\,\,t=0.045,\,\,\zeta =0.001\) and  \(\beta \in [0,1]\)
Full size table

Taking \(\xi =-1\), the series solutions of Eq. (100) are:

$$\begin{aligned} \tilde{v}(\varsigma ,t;\beta )= & {} \displaystyle \tilde{v}_0(\varsigma ,t;\beta )+\tilde{v}_1(\varsigma ,t;\beta )+\tilde{v}_2(\varsigma ,t;\beta )+\cdots \nonumber \\= & {} \displaystyle \tilde{k}(\beta )\exp \left( -\varsigma \right) E_\vartheta \left[ (\zeta +1)t^\vartheta \right] . \end{aligned}$$
(102)

Hence, the upper and lower bounds solutions of Eq. (100) are given by:

  • Upper bound solution:

    $$\begin{aligned} \bar{v}(\varsigma ,t;\beta )=\displaystyle \bar{k}(\beta )\exp \left( -\varsigma \right) E_\vartheta \left[ (\zeta +1)t^\vartheta \right] . \end{aligned}$$
    (103)

  • Lower bound solution:

    $$\begin{aligned} \displaystyle \underline{v}(\varsigma ,t;\beta )=\displaystyle \underline{k}(\beta )\exp \left( -\varsigma \right) E_\vartheta \left[ (\zeta +1)t^\vartheta \right] . \end{aligned}$$
    (104)

When \(\vartheta =1\) in Eqs. (103) and (104), we successfully obtain the following exact solutions:

  • Upper bound solution:

    $$\begin{aligned} \bar{v}(\varsigma ,t;\beta )=\displaystyle \bar{k}(\beta )\exp \left( -\varsigma \right) \exp \left( (\zeta +1)t\right) . \end{aligned}$$
    (105)

  • Lower bound solution:

    $$\begin{aligned} \displaystyle \underline{v}(\varsigma ,t;\beta )=\displaystyle \underline{k}(\beta )\exp \left( -\varsigma \right) \exp \left( (\zeta +1)t\right) . \end{aligned}$$
    (106)

The numerical simulations of the exact and approximate solutions behavior are presented in Tables 3 and  4 respectively.

5 Results and discussion

In this section, we discuss the efficiency and accuracy of the results obtained using the proposed technique and compare it with the results of the existing methods.

Fig. 1
figure 1

Numerical simulations

Full size image

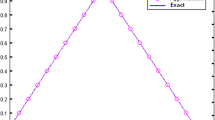
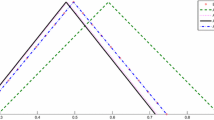
Figure 1: The numerical simulations of the upper and lower bounds solutions of Eq. (93) are given at varying values of \(\vartheta \). In Fig. 1a, the exact solutions of Eqs. (96) and (97) when \(\vartheta =1,\,\,\beta \in [0,1]\),   and  \(r\in [0,1]\) are provided. In Fig. 1b, the 2D surface solutions of Eq. (93) when \(\vartheta =1\) (exact solutions) are illustrated. In Fig. 1c, the \(10^{th}\)-order approximate solutions of the upper and lower bound solutions of Eq. (93) when \(\vartheta =0.5,\,\,\beta \in [0,1]\),  and \(r\in [0,1]\) are illustrated. In Fig. 1d, the \(10^\mathrm{th}\)-order approximate solutions of Eqs. (96) and (97) when \(\vartheta =0.75,\,\,\beta \in [0,1]\),  and \(r\in [0,1]\) are given. In Fig. 1e, the upper and lower bound approximate solutions of Eq. (93) when \(m=10,\,\,\vartheta =0.85,\,\,\beta \in [0,1]\),  and \(r\in [0,1]\) are presented. In Fig. 1f, the \(10^{th}\)-order approximations of \(\bar{v}(\varsigma ,t)\) and \(\underline{v}(\varsigma ,t)\) when \(\vartheta =0.95\) are depicted. From the analytical and the numerical solutions of Eq. (93) using the HASTM, it is clear that both the exact and the approximate solutions fully satisfied the fuzzy number properties. The graphical solutions show a clear triangular fuzzy number shape. Moreover, the exact and approximate solutions of the HASTM are in good agreement with ADM and HPM when the non-zero convergence control parameter \(\xi =-1.\) Besides, the numerical comparison of the exact and the approximate solutions of Eq. (93) at \(\varsigma =0.45,\,\,t=0.7,\,\,\xi =-1,-1.5\)  and different \(\vartheta 's\) are presented in Tables 1 and Table 2, respectively. In Fig. 1g, the upper bound absolute error \(E_{10}(\bar{v}(\varsigma ,t))=|\bar{v}_{ext.}(\varsigma ,t)-\bar{v}_{appr.}(\varsigma ,t)|\), is provided. In Fig. 1(h), the absolute error \(E_{10}(\underline{v}(\varsigma ,t))=|\underline{v}_{ext.}(\varsigma ,t)-\underline{v}_{appr.}(\varsigma ,t)|\) is illustrated. The series solutions of Eqs. (96) and (97) are in excellent agreement with the results found in Salah et al. (2013), Zureigat et al. (2019).

Fig. 2
figure 2

Numerical simulations

Full size image

Figure 2: The numerical simulations of Eq. (100) are given at varying values of \(\vartheta \). In Fig. 2a, the exact solutions of Eq. (100) when \(\vartheta =1,\,\,\zeta =0.001,\,\,\beta \in [0,1]\),   and  \(r\in [0,1]\) are provided. In Fig. 2b, the 2D surface solutions’ behavior of Eq. (100) when \(\vartheta =1,\,\,\zeta =0.001\) is illustrated. In Fig. 2c, the \(10^\mathrm{th}\)-order approximate solutions behavior of Eqs. (103) and (104) when \(\vartheta =0.5,\,\,\zeta =0.001,\,\,\beta \in [0,1]\),  and \(r\in [0,1]\) are illustrated. In Fig. 2d, the \(10^{th}\)-order approximate solutions of the upper and lower bound solutions of Eq. (100) when \(\vartheta =0.75,\,\,\zeta =0.001,\,\,\beta \in [0,1]\),  and \(r\in [0,1]\) are given. In Fig. 2e, the upper and lower bound approximate solutions of Eq. (100) when \(m=10,\,\,\vartheta =0.85,\,\,\zeta =0.001,\,\,\beta \in [0,1]\),  and \(r\in [0,1]\) are provided. In Fig. 2f, the \(10^\mathrm{th}\)-order approximations of \(\bar{v}(\varsigma ,t)\) and \(\underline{v}(\varsigma ,t)\) when \(\vartheta =0.95,\,\,\zeta =0.001\) are depicted. The graphical solutions of Eq. (100) satisfy the fuzzy number properties and triangular fuzzy number shape. Besides, the obtained results are in excellent agreement with HPM and ADM when the non-zero convergence control parameter \(\xi =-1.\) Moreover, the numerical comparison of the exact and the approximate solutions of Eq. (100) at \(\varsigma =0.45,\,\,t=0.045,\,\,\zeta =0.001,\,\,\xi =-1,-1.5\)  and different \(\vartheta 's\) are presented in Tables 3 and Table 4, respectively. In Fig. 2g, the upper bound absolute error \(E_{10}(\bar{v}(\varsigma ,t))=|\bar{v}_{ext.}(\varsigma ,t)-\bar{v}_\mathrm{appr.}(\varsigma ,t)|\), is provided. In Fig. 2(h), the absolute error \(E_{10}(\underline{v}(\varsigma ,t))=|\underline{v}_{ext.}(\varsigma ,t)-\underline{v}_\mathrm{appr.}(\varsigma ,t)|\) is illustrated. The results of Eqs. (103) and (104) are in complete agreement with the results found in Salah et al. (2013), Zureigat et al. (2019).

At this stage, we highlight the important feature or advantage of the proposed iterative method before we list the limitations or disadvantage of the suggested technique in the conclusion section. The proposed iterative method have the following feature advantage

  • Unlike the implicit finite difference method where discretization of space, time, and fractional derivatives are necessary, the HASTM can be used directly to linear and nonlinear fuzzy fractional differential equations without any discretization of space, time, and fractional order derivatives.

  • Unlike the perturbation techniques where perturbation parameter plays a significant role, the proposed HASTM does not require any small or large perturbation parameter which is not available in many fuzzy models of integer and non-integer order derivatives.

  • Using the numerical methods, we can only get a very good approximations. However, the series solutions of the HASTM lead to approximate or exact solution which give us chance to further analyze the error estimate of any given problem.

  • The proposed fuzzy Shehu transform can easily be coupled with the well-known Adomian decomposition method, and the homotopy perturbation method to solve more complex fuzzy differential equations of fractional and non-fractional order derivatives.

  • The convergence of the series solutions of the suggested HASTM can algebraically be control using the initial approximation, the deformation equation, the auxiliary function, and the non-zero convergence control parameter.

  • When the non-zero convergence control parameter \(\xi =-1\), the HASTM reduces to Adomian Decomposition Method and the Homotopy Perturbation Method as a special case.

6 Conclusion

We proposed an efficient iterative technique called the HASTM based on homotopy analysis technique and the fuzzy Shehu integral transform for solving integer and non-integer order fuzzy differential equations. The fuzzy Shehu transform is defined on fuzzy environment based on zadeh’s decomposition theorem via fuzzy Riemann integrals of real-valued functions on finite intervals. The proposed iterative technique is applied directly without discretization of variables, transformations, or linearization. Besides, it reduces the volume of computations and errors. The fractional derivative is computed using Caputo generalized Hukuhara derivative. We discussed the convergence analysis of the proposed technique, and proved many interesting properties of the suggested technique. Examples of integer and non-integer order fuzzy differential equations are provided to validate the efficiency of the method. The graphical solutions of the exact and the approximate solutions are also illustrated. Furthermore, it was found that the proposed HASTM converges to ADM and HPM when the non-zero convergence control parameter \(\xi =-1\) as a special case. Based on the procedure and findings using the HASTM, it proved to be highly efficient. We conclude that the basic idea can easily be extended to related problems in physical science and engineering models. However, the proposed HASTM has the following limitations.

  • The HASTM cannot be applied to some discontinuous fuzzy differential equations, since the fuzzy Shehu transform is defined based on zadeh’s decomposition theorem and fuzzy Riemann integral of real-valued functions on finite intervals.

  • The proposed HASTM does not provide a unique solution (it provides us with two solutions which sometime become an advantage to choose the best result for a given model).

  • Since the HASTM is an iterative method, it is only applicable to fuzzy differential equations with the initial and boundary conditions.

Moreover, in the future, to analyze the solutions of a more complex discontinuous fuzzy differential equations, one may define fuzzy Shehu transform based on Henstock integrals on infinite intervals (Henstock 1963; Gong and Wang 2012) which is a fuzzy integral in the sense of Lebesgue.