1 Introduction

Fractional differential equations have attracted considerable attention for the past 10 years or so. This is evident from the number of publications on such equations in various mathematical and scientific databases. Crisp quantities in the fractional differential equations which are deemed imprecise and uncertain can be replaced by fuzzy quantities to reflect imprecision and uncertainty. This leads to fuzzy fractional differential equations (FFDEs). There have been a number of recent studies on the solutions of FFDEs [1,2,3,4,5,6,7]. Agarwal et al. [8] considered the solution of fractional differential equation with uncertainty. The problem in question was an initial value problem involving a fractional ordinary differential equation. The fractional derivative was evaluated using the Riemann–Liouville formula. Later, Allahviranlo et al. [9] introduced the concept of Riemann–Liouville H-differentiability, which is a direct generalization of the fractional Riemann–Liouville derivative using Hukuhara difference to solve uncertain fractional differential equations (UFDEs) using Mittag-Leffer functions. The obtained explicit solutions of UFDEs were derived by applying the equivalent integral forms of UFDEs. Then, Takaci et al. [10] used the fuzzy Laplace transform to construct exact and approximate solutions of FFDEs in the sense of Caputo Hukuhara differentiability, i.e. the fractional derivative was evaluated using Caputo formula and fuzzy differentiability evaluated using the Hukuhara approach. The obtained results were expressed in the form of fuzzy Mittag-Leffer function. Salahshour et al. [11] then used the fuzzy Laplace transform definition to solve FFDEs under Riemann–Liouville H-differentiability and investigated the efficiency and utility of the Laplace transform method. Later, Ghazanfari and Ebrahimi [12] applied the differential transformation method (DTM) to solve fuzzy fractional diffusion equations. The DTM is an iterative procedure for obtaining analytic series solution of differential equations. It was found that the DTM was a highly effective and simple scheme for obtaining approximate analytical solutions of fuzzy fractional diffusion equations. Chakraverty and Tampaswini [13] later proposed a new computational technique to handle the fuzzy fractional diffusion equations. These approaches convert the fuzzy diffusion equation into interval-based finite difference equations (FDEs) and then transform the obtained equation into crisp form by using the double parametric form of fuzzy numbers. Finally, this crisp form is solved by the Adomian decomposition method (ADM) to obtain the uncertain bounds of the solution.

Salah et al. [14] developed the homotopy analysis transform method (HATM) to solve fuzzy fractional heat and wave equations. The HATM is a combination of the homotopy analysis method and the Laplace decomposition method. HATM yields approximate analytical solution in the form of a series. It was found that the HATM is efficient, simple and involves less computational work as compared to other analytical methods. To the best of our knowledge, there seems to have been no attempt to solve fuzzy fractional diffusion equations by using finite difference schemes. Most of the papers on the solution of fuzzy fractional diffusion equations involve approximate analytical methods. Our paper will investigate the use of a finite difference scheme for solving fuzzy time fractional diffusion equations. The availability of a reliable and efficient finite difference scheme will facilitate the numerical solution of fuzzy time fractional diffusion equations.

2 Fuzzy time fractional diffusion equation

In this section, we present the general form of time fractional diffusion equation in a fuzzy environment by using the basic concepts of fuzzy properties [15,16,17,18]. Consider the one-dimensional fuzzy time fractional diffusion equation with the initial and boundary conditions

$$\begin{aligned} \frac{{\partial }^{\alpha }\tilde{u}(x,t,\alpha )}{{\partial }^{\alpha }t}=\, & {} \tilde{a}\left( x\right) \frac{{\partial }^2\tilde{u}\left( x,t\right) }{\partial x^2}+\tilde{b}\left( x\right), \quad 0<x<l,\ t>0\nonumber \\ \tilde{u}\left( x,0\right)= \,& {} \tilde{f}\left( x\right), \tilde{u}\left( 0,t\right) =\tilde{g}, \tilde{u}\left( l,0\right) =\tilde{z} \end{aligned},$$
(1)

where \(\tilde{u}\left( x,t\right) \)is a fuzzy function [16] of crisp variables\(\ t\) and x, \(\frac{{\partial }^{\alpha }\tilde{u}(x,t,\alpha )}{{\partial }^{\alpha }t}\) is the fuzzy time fractional derivative of order \(\alpha\), \(\frac{{\partial }^2\tilde{u}(x,t)}{\partial x^2}\) is a fuzzy partial Hukuhara derivative [9] with respect to x. \(\tilde{a}\left( x\right) \)and\(\ \widetilde{\ b}(x)\) are fuzzy functions for the crisp variable x. \(\tilde{u}\left( 0,x\right) \) is the fuzzy initial condition, and \(\tilde{u}\left( 0,t\right)\)as well as \(\tilde{u}\left( l,0\right) \)is fuzzy boundary conditions with\(\ \widetilde{g\ }\), \(\tilde{z}\) being fuzzy convex numbers. Finally in Eq. 1, the fuzzy functions\(\ \tilde{a}(x)\), \(\tilde{b}(x)\) and \(\tilde{f}\left( x\right)\) are defined as follows [19]:

$$\begin{aligned} \left\{ \begin{array}{l} \tilde{a}\left( x\right) ={\widetilde{\theta }}_1s_1(x) \\ \tilde{b}\left( x\right) ={\widetilde{\theta }}_2s_2(x) \\ \tilde{f}\left( x\right) ={\widetilde{\theta }}_3s_3(x) \end{array} \right. \end{aligned},$$
(2)

where \(s_1(x)\), \(s_2(x)\) and \(s_3(x)\) are the crisp functions of the crisp variable x with \({\widetilde{\theta }}_1\), \({\widetilde{\theta }}_2\) and \({\widetilde{\theta }}_3\) being the fuzzy convex numbers. The fuzzification of Eq. 1 for all \(r\in \left[ 0,1\right] \) is as follows [19]

$$\begin{aligned} {\left[ \tilde{u}(x,t)\right] }_r= \,& {} \underline{u}\left( x,t;r\right),\overline{u}(x,t;r) \end{aligned}$$
(3)
$$\begin{aligned} {\left[ \frac{{\partial }^{\alpha }\tilde{u}(x,t,\alpha )}{{\partial }^{\alpha }t}\right] }_r=\, & {} \frac{{\partial }^{\alpha }\underline{u}\left( x,t,\alpha ;r\right) }{{\partial }^{\alpha }t},\frac{{\partial }^{\alpha }\overline{u}(x,t,\alpha ;r)}{{\partial }^{\alpha }t} \end{aligned}$$
(4)
$$\begin{aligned} {\left[ \frac{{\partial }^2\tilde{u}(x,t)}{\partial x^2}\right] }_r=\, & {} \frac{{\partial }^2\underline{u}\left( x,t;r\right) }{\partial x^2},\frac{{\partial }^2\overline{u}(x,t;r)}{\partial x^2} \end{aligned}$$
(5)
$$\begin{aligned} {\left[ a(x)\right] }_r= \,& {} \underline{k}\left( x;r\right),\overline{k}(x;r) \end{aligned}$$
(6)
$$\begin{aligned} {\left[ \tilde{b}(x)\right] }_r= \,& {} \underline{b}\left( x;r\right),\overline{b}(x;r) \end{aligned}$$
(7)
$$\begin{aligned} {\left[ \tilde{u}(x,0)\right] }_r=\, & {} \underline{u}\left( x,0;r\right),\overline{u}(x,0;r) \end{aligned}$$
(8)
$$\begin{aligned} {\left[ \tilde{u}(0,t)\right] }_r=\, & {} \underline{u}\left( 0,t;r\right),\overline{u}(0,t;r) \end{aligned}$$
(9)
$$\begin{aligned} {\left[ \tilde{u}(l,t)\right] }_r= \,& {} \underline{u}\left( l,t;r\right),\overline{u}(l,t;r) \end{aligned}$$
(10)
$$\begin{aligned} {\left[ \tilde{f}(x)\right] }_r= \,& {} \underline{f}\left( x;r\right),\overline{f}(x;r) \end{aligned}$$
(11)
$$\begin{aligned}&\left\{ \begin{array}{l} {\left[ \tilde{g}\right] }_r\,=\,\underline{g}\left( r\right),\overline{g}(r) \\ {\left[ \tilde{z}\right] }_r\,=\,\underline{z}\left( r\right),\overline{z}(r) \end{array} \right. \end{aligned},$$
(12)

where

$$\begin{aligned} \left\{ \begin{array}{l} {\left[ \tilde{a}(x)\right] }_r=\left[ {\underline{\theta }\left( r\right) }_1,{\overline{\theta }}_1(r)\right] s_1(x) \\ {\left[ \tilde{b}(x)\right] }_r=\left[ {\underline{\theta }\left( r\right) }_2,{\overline{\theta }}_2(r)\right] s_2(x) \\ {\left[ \tilde{f}(x)\right] }_r=\left[ {\underline{\theta }\left( r\right) }_3,{\overline{\theta }}_3(r)\right] s_3(x) \end{array} \right. \end{aligned}$$
(13)

The membership function is defined by using the fuzzy extension principle [19]

$$\begin{aligned} \left\{ \begin{array}{l} \underline{u}\left( x,t;r\right) =\min \left\{ \tilde{u}\left( \widetilde{\mu }(r),t)\right) | \widetilde{\mu }(r)\in \tilde{u}(x,t;r)\right\} \\ \overline{u}\left( x,t;r\right) =\max \left\{ \tilde{u}\left( \widetilde{\mu }(r),t\right) |\widetilde{\mu }(r)\in \tilde{u}(x,t;r)\right\} \end{array} \right. \end{aligned}$$
(14)

According to [19], by fuzzfication of Eq. 1 and defuzzfication of Eqs. (2–14), we can rewrite the Eq. 1 in the following new formula. The Lower bound of Eq. 1

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{\partial }^{\alpha }\underline{u}(x,t,\alpha )}{{\partial }^{\alpha }t}=\left[ {\underline{\theta }\left( r\right) }_1\right] s_1(x)\frac{{\partial }^2\underline{u}\left( x,t;r\right) }{\partial x^2}+\left[ {\underline{\theta }\left( r\right) }_2\right] s_2(x) \\ \underline{u}\left( x,0;r\right) ={\underline{\theta }\left( r\right) }_3s_3\left( x\right) \\ \underline{u}\left( 0,t;r\right) =\underline{g}\left( r\right),\underline{u}\left( l,t;r\right) =\underline{z}\left( r\right) \end{array} \right. \end{aligned}$$
(15)

The upper bound of Eq. 1

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{\partial }^{\alpha }\overline{u}(x,t,\alpha )}{{\partial }^{\alpha }t}=\left[ {\overline{\theta }}_1(r)\right] s_1(x)\frac{{\partial }^2\overline{u}\left( x,t;r\right) }{\partial x^2}+\left[ {\overline{\theta }}_2(r)\right] s_2(x)\ \ \ \ \ \ \ \\ \overline{u}\left( x,0;r\right) ={{\overline{\theta }}_3\left( r\right) }_3s_3\left( x\right) \\ \overline{u}\left( 0,t;r\right) =\overline{g}\left( r\right),\overline{u}\left( l,t;r\right) =\overline{z}(r) \end{array} \right. \end{aligned}$$
(16)

We next consider a discretization of Eqs. 15 and 16.

3 The fuzzy implicit finite difference method

In this section, we present a fuzzy implicit scheme using Caputo formula for time fractional derivative and central difference approximation for second-order space derivative to solve the fuzzy time fractional diffusion equations.

Following the definition of Caputo formula, we discretize the time fractional derivative in Eq. 1 such that [20]:

$$\begin{aligned} \frac{{\partial }^{\alpha }\tilde{u}(x,t,\alpha )}{{\partial }^{\alpha }t}={\Delta t}^{-\alpha }\sum ^n_{j=0}{v_j\ (u^{n-j}_i-u^0_i)}+o(\Delta t) \end{aligned},$$
(17)

where \(v_0=1,\ {\ v}_j=\left( 1-\frac{\alpha +1}{j}\right) v_{j-1}, \quad j=1,2,\ldots\)

Also by using the central difference approximation definition, we can discretize the second partial derivatives \(\frac{{\partial }^2\underline{u}\left( x,t\right) }{\partial x^2},\frac{{\partial }^2\overline{u}\left( x,t\right) }{\partial x^2}\) as follows:

$$\begin{aligned} \frac{{\partial }^2{\underline{u}}_{i,n}(x,t;r)}{\partial x^2}= & {} \frac{{\underline{u}}_{i+1,n}\left( x,t;r\right) -2{\underline{u}}_{i,n}\left( x,t;r\right) +{\underline{u}}_{i-1,n}(x,t;r)}{h^2} \end{aligned}$$
(18)
$$\begin{aligned} \frac{{\partial }^2{\overline{u}}_{i,n}(x,t;r)}{\partial x^2}= & {} \frac{{\overline{u}}_{i+1,n}\left( x,t;r\right) -2{\overline{u}}_{i,n}\left( x,t;r\right) +{\overline{u}}_{i-1,n}(x,t;r)}{h^2} \end{aligned}$$
(19)

i indicates a spatial grid point and n a temporal one.

Equations (17, 18, 19) are substituted in Eqs. (14, 15) to obtain:

$$\begin{aligned}&{\Delta t}^{-\alpha }\sum ^n_{j=0}{v_j\ \left( {\underline{u}}^{n-j}_i-{\underline{u}}^0_i\right) }\nonumber \\&\quad =\ \underline{a}\left( x,r\right) \frac{{\underline{u}}_{i+1,n}\left( x,t;r\right) -2{\underline{u}}_{i,n}\left( x,t;r\right) +{\underline{u}}_{i-1,n}\left( x,t;r\right) }{h^2}+\underline{b}(x,r) \end{aligned}$$
(20)
$$\begin{aligned}&{\Delta t}^{-\alpha }\sum ^n_{j=0}{v_j\ \left( {\overline{u}}^{n-j}_i-{\overline{u}}^0_i\right) }\nonumber \\&\quad =\overline{a}\left( x,r\right) \frac{{\overline{u}}_{i+1,n}\left( x,t;r\right) -2{\overline{u}}_{i,n}\left( x,t;r\right) +{\overline{u}}_{i-1,n}\left( x,t;r\right) }{h^2}+\overline{b}(x,r) \end{aligned}$$
(21)

Now we let \(p\left( r\right) =\frac{\underline{a}\left( x,r\right) {\Delta t}^{\alpha }}{h^2}\), and from Eqs. (21, 22), we obtain for all\(\ r\in [0,1]\)

$$\begin{aligned}&-\,p{\underline{u}}_{i+1,n}\left( x,t;r\right) +\left( 1+2p\right) {\underline{u}}_{i,n}\left( x,t;r\right) -p{\underline{u}}_{i-1,n}\left( x,t;r\right) \nonumber \\&\quad = \,-\,\sum ^{n-1}_{j=1}{v_j{\underline{u}}_{i,n-j} +\left( \sum ^{n-1}_{j=0}{v_j}\right) {\underline{u}}_{i,0}+}{\Delta t}^{\alpha }\underline{b}\left( x,r\right) \end{aligned}$$
(22)
$$\begin{aligned}&-\,p{\overline{u}}_{i+1,n}\left( x,t;r\right) +\left( 1+2p\right) {\overline{u}}_{i,n}\left( x,t;r\right) -p{\overline{u}}_{i-1,n}\left( x,t;r\right) \nonumber \\&\quad =\,-\,\sum ^{n-1}_{j=1}{v_j{\overline{u}}_{i,n-j} +\left( \sum ^{n-1}_{j=0}{v_j}\right) {\overline{u}}_{i,0}+}{\Delta t}^{\alpha }\underline{b}\left( x,r\right) \end{aligned}$$
(23)

For each spatial grid point, Eqs. (22, 23) are evaluated to yield linear equations. At the end of each time level, a system of linear equations is obtained. This system is then solved to obtain the values \(\tilde{u}(x,t,\alpha )\) for that particular time level.

4 Stability analysis

Ma [21] developed implicit finite difference schemes for the crisp time fractional diffusion equation with source terms. Wang and Qin [22] developed a fuzzy finite difference scheme for heat conduction problem which did not involve fractional derivative. In addition, the stability properties of the scheme were also investigated. We shall follow the approaches to analyse stability in [21, 22] in our investigation of the stability of the implicit finite difference schemes proposed in the present for the fuzzy time fractional diffusion equations.

It is first assumed that the discretization of initial condition introduces the fuzzy error \(\ {\widetilde{\varepsilon }}^0_i\).

Let \(\ {\tilde{g}}^0_i=\ \acute{\ {\tilde{g}}^0_i}-\ {\widetilde{\varepsilon }}^0_i\), \({\tilde{u}}^n_i\) and \(\acute{{\tilde{u}}^n_i}\) be the fuzzy numerical solutions of scheme in Eqs. (22, 23) with respect to the initial data’s \({\tilde{g}}^0_i\) and \(\acute{\ {\tilde{g}}^0_i}\), respectively.

Let \(\ {{[\tilde{u}}^n_{i+1}(x,t;\alpha )]}_r={[\ \underline{u}}^n_{i+1}\left( r\right),{\ \overline{u}}^n_{i+1}\left( r\right) ],\) where\(\ r\in \left[ 0,1\right]\).

The error bound is defined as:

$$\begin{aligned} {\left[ {\widetilde{\varepsilon }}^n_i\right] }_r={\left[ \acute{{\tilde{u}}^n_i} - \ {\tilde{u}}^n_i\right] }_r \end{aligned},$$
(24)

where

$$\begin{aligned} {\left[ {\widetilde{\varepsilon }}^n_i\right] }_r=\left\{ {\underline{\varepsilon }}^n_i\left( r\right) ,{\overline{\varepsilon }}^n_i(r)\right\} =\left\{ \begin{array}{l} {{\ \underline{u}}^n_i}' \left( r\right) -{\underline{u}}^n_i\left( r\right) \\ {{\ \overline{u}}^n_i}' \left( r\right) -{\ \overline{u}}^n_i\left( r\right) \end{array} \right. \end{aligned}$$
(25)

which satisfies the finite difference Eq. 1.

For \(n=1\)

$$\begin{aligned} \left\{ \begin{array}{l} -\,p{\underline{\varepsilon }}^1_i\left( r\right) +\left( 1+2p\right) {\underline{\varepsilon }}^1_i\left( r\right) -s\ {\underline{\varepsilon }}^n_{i-1}\left( r\right) ={\underline{\varepsilon }}^0_i\left( r\right) \ \\ -p{\overline{\varepsilon }}^1_i\left( r\right) +\left( 1+2p\right) {\overline{\varepsilon }}^1_i\left( r\right) -s\ {\overline{\varepsilon }}^n_{i-1}\left( r\right) ={\overline{\varepsilon }}^0_i\left( r\right) \end{array} \right. \end{aligned}$$
(26)

For \(n\ge 2\)

$$\begin{aligned} \left\{ \begin{array}{l} -s\ {\underline{\varepsilon }}^n_{i+1}+\left( 1+2p\right) {\underline{\varepsilon }}^n_i-r\ {\underline{\varepsilon }}^n_{i-1}=\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\underline{\varepsilon }}^{n-j}_i}+(\sum ^{n-1}_{j=0}{v_{j\ })\ {\underline{\varepsilon }}^0_i}\ \\ -s\ {\overline{\varepsilon }}^n_{i+1}+\left( 1+2p\right) {\overline{\varepsilon }}^n_i-r\ {\overline{\varepsilon }}^n_{i-1}=\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\overline{\varepsilon }}^{n-j}_i}+(\sum ^{n-1}_{j=0}{v_{j\ })\ {\overline{\varepsilon }}^0_i} \end{array} \right. \ \end{aligned}$$
(27)

Suppose that

$$\begin{aligned} \left\{ \begin{array}{l} {\underline{\varepsilon }}^n_i=\ {\underline{\lambda }}^n(r){\ e}^{\sqrt{-\underline{\theta }\ (r)i}}\ \\ {\overline{\varepsilon }}^n_i={\overline{\lambda }}^n(r)\ e^{\sqrt{-\overline{\theta }(r)i}} \end{array} \right. \end{aligned}$$
(28)

Substituting Eq. 28 into Eqs. (26, 27) to obtain:

For \(n=1\)

$$\begin{aligned} \ \ \left\{ \begin{array}{l} -p\ \underline{\lambda }(r)e^{\sqrt{-\underline{\theta }\ (r)\left( i+1\right) }}+\left( 1+2p\right) \underline{\lambda }(r)e^{\sqrt{-\underline{\theta }\ (r)i}}-p\ \underline{\lambda }(r)\ e^{\sqrt{-\underline{\theta }\ (r)\left( i-1\right) }}=\ e^{\sqrt{-\underline{\theta }\ (r)i}}\ \\ -p\ \overline{\lambda }(r)e^{\sqrt{-\overline{\theta }(r)\left( i+1\right) }}+\left( 1+2p\right) \overline{\lambda }(r)e^{\sqrt{-\overline{\theta }(r)i}}-\ p\ \overline{\lambda }(r)\ e^{\sqrt{-\overline{\theta }(r)\left( i-1\right) }}=\ e^{\sqrt{-\overline{\theta }(r)i}} \end{array} \right. \end{aligned}$$
(29)

For \(n\ge 2\)

$$\begin{aligned} \left\{ \begin{array}{l} -p\ {\underline{\lambda }}^n(r)e^{\sqrt{-\underline{\theta }\ (r)\left( i+1\right) }}\ +\left( 1+2p\right) {\underline{\lambda }}^n(r)e^{\sqrt{-\underline{\theta }\ (r)i}}\ -p\ \ (r)e^{\sqrt{-\underline{\theta }\ (r)(i-1)}}= \\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\underline{\lambda }}^{n-j}\ e^{\sqrt{-\underline{\theta }\ (r)i}}}+\left( \sum ^{n-1}_{j=0}{v_{j\ }}\right) \ e^{\sqrt{-\underline{\theta }\ (r)i}}\ \\ -p\ {\overline{\lambda }}^n(r)\ e^{\sqrt{-\overline{\theta }(r)\left( i+1\right) }}\ +\left( 1+2p\right) {\overline{\lambda }}^n(r)e^{\sqrt{-\overline{\theta }(r)i}}\ -p\ {\overline{\lambda }}^n(r)e^{\sqrt{-\overline{\theta }(r)(i-1)}}=\\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\overline{\lambda }}^{n-j}\left( r\right) \ e^{\sqrt{-\overline{\theta }(r)i}}}+\left( \sum ^{n-1}_{j=0}{v_{j\ }}\right) \ e^{\sqrt{-\overline{\theta }(r)i}} \end{array} \right. \end{aligned}$$
(30)

Begin with \(\ n=1\), in Eq. 29 to obtain

$$\begin{aligned} \ \left\{ \begin{array}{l} -p\ \underline{\lambda }(r)e^{\sqrt{-\underline{\theta }\ (r)\left( i+1\right) }}+\left( 1+2p\right) \underline{\lambda }(r)e^{\sqrt{-\underline{\theta }\ (r)i}}-p\ \underline{\lambda }(r)\ e^{\sqrt{-\underline{\theta }\ (r)\left( i-1\right) }}=\ e^{\sqrt{-\underline{\theta }\ (r)i}}\ \\ -p\ \overline{\lambda }(r)e^{\sqrt{-\overline{\theta }(r)\left( i+1\right) }}+\left( 1+2p\right) \overline{\lambda }(r)e^{\sqrt{-\overline{\theta }(r)i}}-p\ \overline{\lambda }(r)\ e^{\sqrt{-\overline{\theta }(r)\left( i-1\right) }}=\ e^{\sqrt{-\overline{\theta }(r)i}} \end{array} \right. \end{aligned}$$
(31)

Divide Eq. 31 on \({\ e}^{\sqrt{-\theta i}}\) to obtain:

$$\begin{aligned}&\left\{ \begin{array}{l} -p\ \underline{\lambda }(r)e^{\sqrt{-\underline{\theta }\ (r)i}}+\left( 1+2p\right) \underline{\lambda }(r)-p\ \underline{\lambda }(r)\ e^{-\sqrt{-\underline{\theta }\ (r)i}}=\ 1\ \\ -p\ \overline{\lambda }(r)e^{\sqrt{-\overline{\theta }(r)i}}+\left( 1+2p\right) \overline{\lambda }(r)-p\ \overline{\lambda }(r)\ e^{-\sqrt{-\overline{\theta }(r)i}}=\ 1\ \end{array} \right. \nonumber \\&\quad \left\{ \begin{array}{l} \underline{\lambda }(r)[\left( 1+2p\right) -p\ \left( e^{\sqrt{-\underline{\theta }\ (r)i}}+\ e^{-\sqrt{-\underline{\theta }\ (r)i}}\right) ]=\ 1\ \\ \overline{\lambda }(r)[\left( 1+2p\right) -p\ \left( e^{\sqrt{-\overline{\theta }(r)i}}+\ e^{-\sqrt{-\overline{\theta }(r)i}}\right) ]=\ 1\ \end{array} \right. \nonumber \\&\quad \left\{ \begin{array}{l} \underline{\lambda }(r)[\ \left( 1+2p\right) -\ 2\ p\ cos\underline{\theta }\ (r)]=\ 1\ \\ \overline{\lambda }(r)[\ \left( 1+2p\right) -\ 2\ p\ cos\overline{\theta }(r)]=\ 1\ \ \end{array} \right. \nonumber \\&\quad \left\{ \begin{array}{l} \underline{\lambda }(r)[\ 1+\ 2\ p\ (1-cos\underline{\theta }\ (r))]=1\ \\ \overline{\lambda }(r)[\ 1+\ 2\ p\ (1-cos\overline{\theta }(r))]=1\ \ \end{array} \right. \end{aligned}$$
(32)

According to the Zadeh extension principle [21], we obtain:

$$\begin{aligned} \left\{ \begin{array}{l} \underline{\lambda }(r)={\text {Min}}\left[ \frac{1}{1+\ 2\ p\ (1-cos\underline{\theta }\ (r))},\frac{1}{1+\ 2\ p\ (1-cos\overline{\theta }(r))}\right] \le 1 \\ \overline{\lambda }(r)={\text {Max}}\left[ \frac{1}{1+\ 2\ p\ (1-cos\underline{\theta }\ (r))},\ \frac{1}{1+\ 2\ p\ (1-cos\overline{\theta }(r))} \right] \le 1 \end{array} \right. \end{aligned}$$

Now let \(\left\{ \begin{array}{l} \left| {\underline{\lambda }}^m\right| \le 1, \quad m=1,\ 2,\ 3,\ \dots , n-1\ \\ \left| {\overline{\lambda }}^m\right| \le 1, \quad m=1,\ 2, 3,\ \ldots , n-1\ \ \end{array} \right. .\)

In [17], there is a lemma which states:

The coefficients \(v_j={(-1)}^j\left( \begin{array}{l} \alpha \\ j \end{array} \right)\)\((j=0,\ 1,\ 2,\ \dots )\) satisfy:

  1. 1.

    \({{v}}_0=1, \,\,{{v}}_{{j}} < 0 \quad j=1,\ 2, 3,\ldots\)

  2. 2.

    \(\sum ^{k-1}_{j=0}{{ {v}}_{ {j}}} >0 \quad k=2,\ 3,\ \dots\)

  3. 3.

    From this lemma and Eq. 30, we obtain

  4. 4.
    $$\begin{aligned} \left\{ \begin{array}{l} -p\ {\underline{\lambda }}^n\left( r\right) e^{\sqrt{-\underline{\theta }\ \left( r\right) \left( i+1\right) }}\ +\left( 1+2p\right) {\underline{\lambda }}^n\left( r\right) e^{\sqrt{-\underline{\theta }\ \left( r\right) i}}\ --p\ {\underline{\lambda }}^n\left( r\right) e^{\sqrt{-\underline{\theta }\ \left( r\right) \left( i-1\right) }}=\ \ \ \\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\underline{\lambda }}^{n-j}(r)e^{\sqrt{-\underline{\theta }\ (r)i}}}+\left( \sum ^{n-1}_{j=0} v_{j\ }\right) \ e^{\sqrt{-\underline{\theta }\ (r)i}}\ \\ --p\ {\overline{\lambda }}^n\left( r\right) e^{\sqrt{-\overline{\theta }\left( r\right) \left( i+1\right) }}\ +\left( 1+2p\right) {\overline{\lambda }}^n\left( r\right) e^{\sqrt{-\overline{\theta }\left( r\right) i}}\ --p\ {\overline{\lambda }}^n\left( r\right) e^{\sqrt{-\overline{\theta }\left( r\right) \left( i-1\right) }}= \\ \ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\overline{\lambda }}^{n-j}(r)\ e^{\sqrt{-\overline{\theta }(r)i}}}+\left( \sum ^{n-1}_{j=0} v_{j\ }\right) \ e^{\sqrt{-\overline{\theta }(r)i}} \ \ \end{array} \right. \end{aligned}$$
    (33)

Divide Eq. 33 on \(\left\{ \begin{array}{l} {\ e}^{\sqrt{-\underline{\theta }i}} \\ {\ e}^{\sqrt{-\overline{\theta }i}}\ \ \end{array} \right.\) to obtain:

$$\begin{aligned}&\left\{ \begin{array}{l} -p\ {\underline{\lambda }}^n(r)e^{\sqrt{-\underline{\theta }\ (r)i}}\ +\left( 1+2p\right) {\underline{\lambda }}^n(r)\ -p\ {\underline{\lambda }}^n(r)e^{-\sqrt{-\theta i}}=\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\underline{\lambda }}^{n-j}(r)} +\sum ^{n-1}_{j=0}{v_{j\ }\ }\ \\ -p\ {\overline{\lambda }}^n(r)e^{\sqrt{-\overline{\theta }(r)i}}\ +\left( 1+2p\right) {\overline{\lambda }}^n(r)\ -p\ {\overline{\lambda }}^n(r)e^{-\sqrt{-\overline{\theta }(r)i}}=\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\overline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\ \ \end{array} \right. \end{aligned}$$
(34)
$$\begin{aligned}&\quad \left\{ \begin{array}{l} {\underline{\lambda }}^n(r)[\ \left( 1+2p\right) -{p\ (e}^{\sqrt{-\underline{\theta }\ (r)i}}+{\ e}^{-\sqrt{-\underline{\theta }\ (r)i}})]=\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\underline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\ \\ {\overline{\lambda }}^n(r)[\ \left( 1+2p\right) -{p\ (e}^{\sqrt{-\overline{\theta }(r)i}}+{\ e}^{-\sqrt{-\overline{\theta }(r)i}})]=\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\overline{\lambda }}^n(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\ \ \end{array} \right. \nonumber \\&\quad \left\{ \begin{array}{l} {\underline{\lambda }}^n(r)[\ \left( 1+2p\right) -p\ (2\ cos\underline{\theta }\ (r))]\ =\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\underline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\ \\ {\overline{\lambda }}^n(r)[\ \left( 1+2p\right) -p\ (2\ cos\overline{\theta }(r))]=\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\overline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\ \ \end{array} \right. \nonumber \\&\left\{ \begin{array}{l} {\underline{\lambda }}^n(r)[\ 1+2p(1-\ cos\underline{\theta }\ (r))]=\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\underline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\ \\ {\overline{\lambda }}^n(r)[\ 1+2p(1-\ cos\overline{\theta }(r))]=\ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\overline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\ \ \end{array} \right. \end{aligned}$$
(35)

So, \(\left\{ \begin{array}{l} {\underline{\lambda }}^n\left( r\right) =\ \frac{1}{1+2p(1-\ cos \underline{\theta }\ (r))}*\left[ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\underline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\right] \\ {\underline{\lambda }}^n\left( r\right) =\frac{1}{1+2p(1-\ cos\overline{\theta }\ (r))}*\left[ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\overline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\right] \ \ \end{array} \right.\)

Therefore, \(\left\{ \begin{array}{l} \left| {\underline{\lambda }}^n\left( r\right) \right| =\ \frac{1}{1+2p(1-\ cos\underline{\theta }\ (r))}* \left[ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\underline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\right] \\ \left| {\underline{\lambda }}^n\left( r\right) \right| =\frac{1}{1+2p(1-\ cos\overline{\theta }\ (r))}*\left[ -\sum ^{n-1}_{j=1}{v_{j\ }\ {\overline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\right] \ \ \end{array} \right.\)

$$\begin{aligned}&\left\{ \begin{array}{l} {\underline{\lambda }}^n\left( r\right) =\frac{1}{1+2p(1-\ cos\overline{\theta }\ (r))}*\left[ \sum ^{n-1}_{j=1}{{(-v}_{j\ })\ {\underline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\right] \\ {\overline{\lambda }}^n\left( r\right) =\frac{1}{1+2p(1-\ cos\overline{\theta }\ (r))}*\left[ \sum ^{n-1}_{j=1}{{(-v}_{j\ })\ {\overline{\lambda }}^{n-j}(r)}+\sum ^{n-1}_{j=0}{v_{j\ }\ }\right] \ \ \end{array} \right. \\&\quad \left\{ \begin{array}{l} {\underline{\lambda }}^n\left( r\right) \le \frac{1}{1+2p(1-\ cos\overline{\theta }\ (r))}*\left[ \sum ^{n-1}_{j=1}{{(-v}_{j\ })\ \left| {\underline{\lambda }}^{n-j}(r)\right| }+\sum ^{n-1}_{j=0}{v_{j\ }\ }\right] \\ {\ \overline{\lambda }}^n\left( r\right) \le \frac{1}{1+2p(1-\ cos\overline{\theta }\ (r))}*\left[ \sum ^{n-1}_{j=1}{{(-v}_{j\ })\ \left| {\overline{\lambda }}^{n-j}(r)\right| }+\sum ^{n-1}_{j=0}{v_{j\ }\ }\right] \ \ \end{array} \right. \\&\quad \left\{ \begin{array}{l} {\underline{\lambda }}^n(r)\le \left[ \sum ^{n-1}_{j=1}{{(-v}_{j\ })\ }+\sum ^{n-1}_{j=0}{v_{j\ }\ }\right] *\frac{1}{1+2p(1-\ cos\underline{\theta }\ (r))} \\ {\overline{\lambda }}^n(r)\le \left[ \sum ^{n-1}_{j=1}{{(-v}_{j\ })\ }+\sum ^{n-1}_{j=0}{v_{j\ }\ }\right] *\frac{1}{1+2p(1-\ cos\overline{\theta }\ (r))}\ \ \end{array} \right. \\&\quad \left\{ \begin{array}{l} {\underline{\lambda }}^n(r)=\frac{1}{1+2p(1-\ cos\underline{\theta }\ (r))}\ [\ \left( -v_1\right) +\left( -v_2\right) +\dots +\left( -v_{n-1}\right) +v_0+v_1+v_2+\dots +v_{n-1}] \\ {\overline{\lambda }}^n(r)=\frac{1}{1+2p(1-\ cos\overline{\theta }\ (r))}\ [\ \left( -v_1\right) +\left( -v_2\right) +\dots +\left( -v_{n-1}\right) +v_0+v_1+v_2+\dots +v_{n-1}]\ \ \end{array} \right. \\&\left\{ \begin{array}{l} {\underline{\lambda }}^n\left( r\right) =\frac{1}{1+2p(1-\ cos\underline{\theta }\ (r))}*v_0 \\ {\overline{\lambda }}^n\left( r\right) =\frac{1}{1+2p(1-\ cos\overline{\theta }\ (r))}*v_0\ \end{array} \right. \\&\left\{ \begin{array}{l} {\underline{\lambda }}^n\left( r\right) ={\text {Min}}\left[ \frac{1}{1+2p(1-\ cos\underline{\theta }\ (r))}\right] \le 1 \\ {\overline{\lambda }}^n\left( r\right) ={\text {Max}}\left[ \frac{1}{1+2p(1-\ cos\overline{\theta }\ (r))}\right] \le 1\ \end{array} \right. \end{aligned}$$

Thus, \(\ \ \ \ \left\{ \begin{array}{l} \left| {\underline{\lambda }}^n\left( r\right) \right| \le 1 \\ \left| {\overline{\lambda }}^n\left( r\right) \right| \le 1\ \end{array} \right.\)

Therefore, according to Von Neumann’s criterion for stability, the fuzzy implicit finite difference scheme defined by Eq. 1 is unconditionally stable for all r-level set and for all \(0<\alpha <1\).

5 Numerical example

In this section, we implement the implicit finite difference approximations to solve fuzzy time fractional diffusion equations for different orders of\(\ \alpha\) to investigate the implicit finite difference method. The Wolfram Mathematica10 software was used to conduct the numerical experiment for the proposed method.

Example 1

Consider fuzzy time fractional diffusion equations [10]

$$\begin{aligned} \frac{{\partial }^{\alpha }\tilde{u}\left( x,t\right) }{\partial t^{\alpha }}=\ \frac{{\partial }^2\tilde{u}\left( x,t\right) }{\partial x^2},\quad 0<x<l,\ t>0 \end{aligned}$$
(36)

subject to the boundary conditions \(\tilde{u}\left( 0,t\right) =\tilde{u}\left( 1,t\right) =0\) and initial condition

$$\begin{aligned} \tilde{u}\left( x,0\right) =\tilde{k}{ {\sin} \left( \pi x\right),\ \ 0<\ x<1\ }\end{aligned},$$
(37)

where\(\widetilde{\ \alpha }\left( r\right) =\left[ 0.1r-0.1, 0.1-0.1r\right] \)for all \(r\in \left[ 0,1\right]\). The exact solution of Eq. 36 was given in [10]:

$$\begin{aligned} \tilde{u}\left( x,t,\alpha ;r\right) =\sum ^{\infty }_{n=0}{\frac{({-1)}^n{\pi }^{2n}t^{n\alpha }}{\Gamma (n\alpha +1)}\tilde{k}\left( r\right) {{\sin} \left( \pi x\right) \ }} \end{aligned}$$
(38)

The absolute error of the solution of Eq. 36 can be defined as:

$$\begin{aligned} {\left[ \tilde{E}\right] }_r=\left| \tilde{u}\left( t,x;r\right) -\tilde{u}\left( t,x;r\right) \right| =\left\{ \begin{array}{l} {\left[ \underline{E}\right] }_r=\left| \underline{u}\left( t,x;r\right) -\underline{u}\left( t,x;r\right) \right| \\ {\left[ \overline{E}\right] }_r=\left| \overline{U}\left( t,x;r\right) -\overline{u}\left( t,x;r\right) \right| \end{array} \right. \end{aligned}$$
(39)

According to Eqs. (20, 21) in Sect. 3 the implicit finite difference method formula for solving Eq. 36 is as follows:

$$\begin{aligned}&{\Delta t}^{-\alpha }\sum ^n_{j=0}{v_j\ \left( {\underline{u}}^{n-j}_i-{\underline{u}}^0_i\right) }\ =\ \frac{{\underline{u}}_{i+1,n}\left( x,t;r\right) -2{\underline{u}}_{i,n}\left( x,t;r\right) +{\underline{u}}_{i-1,n}\left( x,t;r\right) }{h^2} \end{aligned}$$
(40)
$$\begin{aligned}&{\Delta t}^{-\alpha }\sum ^n_{j=0}{v_j\ \left( {\overline{u}}^{n-j}_i-{\overline{u}}^0_i\right) }\ =\frac{{\overline{u}}_{i+1,n}\left( x,t;r\right) -2{\overline{u}}_{i,n}\left( x,t;r\right) +{\overline{u}}_{i-1,n}\left( x,t;r\right) }{h^2} \end{aligned}$$
(41)

As explained in Sect. 3 we obtain

$$\begin{aligned}&-p{\underline{u}}_{i+1,n}\left( x,t;r\right) +\left( 1+2p\right) {\underline{u}}_{i,n}\left( x,t;r\right) -p{\underline{u}}_{i-1,n}\left( x,t;r\right) =\ \ \ \ -\sum ^{n-1}_{j=1}{v_j{\underline{u}}_{i,n-j}+\left( \sum ^{n-1}_{j=0}{v_j}\right) {\underline{u}}_{i,0}} \end{aligned}$$
(42)
$$\begin{aligned}&-p{\overline{u}}_{i+1,n}\left( x,t;r\right) +\left( 1+2p\right) {\overline{u}}_{i,n}\left( x,t;r\right) -p{\overline{u}}_{i-1,n}\left( x,t;r\right) =\ \ \ \ -\sum ^{n-1}_{j=1}{v_j{\overline{u}}_{i,n-j}+\left( \sum ^{n-1}_{j=0}{v_j}\right) {\overline{u}}_{i,0}} \end{aligned}$$
(43)

At \(\Delta x=h=0.1\ {\mathrm {and\ \ }}{\Delta t}^{\alpha }={\left( 0.01\right) }^{0.5}=0.1\ {\mathrm {to\ get\ \ }}p\left( r\right) =\frac{{\Delta t}^{\alpha }}{h^2}=\frac{0.1}{{0.1}^2}\) we have the following results:

Table 1 Lower solution of Eq. 36 by implicit FDM at \(t=0.05\), \(\alpha =0.5\) and for all \(r \in [0,1]\)
Full size table
Table 2 Upper solution of Eq. 36 by implicit FDM at \(t=0.05\), \(\alpha =0.5\) and for all \(r\in [0,1]\)
Full size table

Tables 1 and 2 and Figs. 1, 2, 3, 4 and 5 show that both the implicit finite difference and exact solution at \(t=0.05\), \(\alpha =0.5\) and for all \(r\in [0,1]\) attain the triangular fuzzy number shape and thus satisfy the fuzzy number properties as explained in [21].

Fig. 1
figure 1

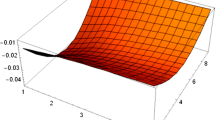
The exact solution for the lower bound of Eq. 36 at \(\Delta t=0.01\), \(h=0.1\) and \(r =0\)

Full size image
Fig. 2
figure 2

The exact solution for the upper bound of Eq. 36 at \(\Delta t=0.01\), \(h=0.1\) and \(r=0\)

Full size image
Fig. 3
figure 3

Exact and implicit FDM of the solution of Eq. 36 at \({\alpha }= 0.5,\)\(x=0.9\), \(t=0.05\) for all \(r \in [0,1]\)

Full size image
Fig. 4
figure 4

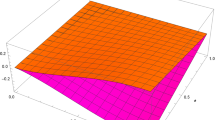
the lower implicit FDM of the solution of Eq. 36 at \(\alpha\) = 0.5 for all \(r \in [0,1]\)

Full size image
Fig. 5
figure 5

the upper implicit FDM of the solution of Eq. 36 at \(\alpha\) = 0.5 for all \(r \in [0,1]\)

Full size image

Now we compare between the numerical and exact solutions of Eq. 36, for different orders of \(\alpha\).

Figures 6, 7 and 8 shows that both the implicit finite difference and exact solutions satisfy the fuzzy number properties by attaining the triangular fuzzy number shape. Also, the exact solution agrees with the implicit finite difference solutions for different values of \(\alpha\). The comparison of numerical and exact solutions when \(\alpha =\ 0.4,\ 0.5,\ 0.6\) shows that the scheme is accurate and the results confirm our theoretical analysis.

Fig. 6
figure 6

Exact and implicit FDM of the solution of Eq. 36 at different values of \(\alpha\) for all \(r \in [0,1]\)

Full size image
Fig. 7
figure 7

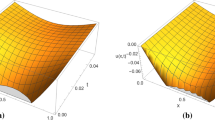
the lower implicit FDM of the solution of Eq. 36 at \(\alpha\) = 0.2 for all \(r \in [0,1]\)

Full size image
Fig. 8
figure 8

the upper implicit FDM of the solution of Eq. 36 at \(\alpha\) = 0.2 for all \(r \in [0,1]\)

Full size image

Example 2

Consider fuzzy time fractional diffusion equations [14]

$$\begin{aligned} \frac{{\partial }^{\alpha }\tilde{u}\left( x,t\right) }{\partial t^{\alpha }}=\frac{1}{2}.x^{2} \ \frac{{\partial }^2\tilde{u}\left( x,t\right) }{\partial x^2},\ \ \ \ \ \ \ \ \ \ \ 0<x<l,\ t>0 \end{aligned}$$
(44)

subject to the boundary conditions \(\tilde{u}\left( 0,t\right) =\tilde{u}\left( 1,t\right) =0\) and initial condition

$$\begin{aligned} \tilde{u}\left( x,0\right) =\tilde{k}{x^{2},\ \ 0<\ x<1,\ }\end{aligned}$$
(45)

where\(\widetilde{\ \alpha }\left( r\right) =\left[ 0.1r-0.01,\ 0.01-0.01r\right] \)for all \(r\in \left[ 0,1\right]\). The exact solution of Eq. 44 was given in [10] :

$$\begin{aligned} \tilde{u}\left( x,t,\alpha ;r\right) =\sum ^{\infty }_{n=0}{\frac{t^{n\alpha }}{\Gamma (n\alpha +1)}\tilde{k}\left( r\right) {x^{2} }} \end{aligned}$$
(46)

The absolute error of the solution of Eq. 44 can be defined as:

$$\begin{aligned} {\left[ \tilde{E}\right] }_r=\left| \tilde{u}\left( t,x;r\right) -\tilde{u}\left( t,x;r\right) \right| =\left\{ \begin{array}{l} {\left[ \underline{E}\right] }_r=\left| \underline{u}\left( t,x;r\right) -\underline{u}\left( t,x;r\right) \right| \\ {\left[ \overline{E}\right] }_r=\left| \overline{U}\left( t,x;r\right) -\overline{u}\left( t,x;r\right) \right| \end{array} \right. \end{aligned}$$
(47)

According to Eqs. (20, 21) in Sect. 3 the implicit finite difference method formula for solving Eq. 44 is as follows:

$$\begin{aligned}&{\Delta t}^{-\alpha }\sum ^n_{j=0}{v_j\ \left( {\underline{u}}^{n-j}_i-{\underline{u}}^0_i\right) }\ =\frac{1}{2} x^{2} \frac{{\underline{u}}_{i+1,n}\left( x,t;r\right) -2{\underline{u}}_{i,n}\left( x,t;r\right) +{\underline{u}}_{i-1,n}\left( x,t;r\right) }{h^2} \end{aligned}$$
(48)
$$\begin{aligned}&{\Delta t}^{-\alpha }\sum ^n_{j=0}{v_j\ \left( {\overline{u}}^{n-j}_i-{\overline{u}}^0_i\right) }\ = \frac{1}{2} x^{2} \frac{{\overline{u}}_{i+1,n}\left( x,t;r\right) -2{\overline{u}}_{i,n}\left( x,t;r\right) +{\overline{u}}_{i-1,n}\left( x,t;r\right) }{h^2} \end{aligned}$$
(49)

As explained in Sect. 3 we obtain

$$\begin{aligned}&-p{\underline{u}}_{i+1,n}\left( x,t;r\right) +\left( 1+2p\right) {\underline{u}}_{i,n}\left( x,t;r\right) -p{\underline{u}}_{i-1,n}\left( x,t;r\right) =\ \ \ \ -\sum ^{n-1}_{j=1}{v_j{\underline{u}}_{i,n-j}+\left( \sum ^{n-1}_{j=0}{v_j}\right) {\underline{u}}_{i,0}} \end{aligned}$$
(50)
$$\begin{aligned}&-p{\overline{u}}_{i+1,n}\left( x,t;r\right) +\left( 1+2p\right) {\overline{u}}_{i,n}\left( x,t;r\right) -p{\overline{u}}_{i-1,n}\left( x,t;r\right) =\ \ \ \ -\sum ^{n-1}_{j=1}{v_j{\overline{u}}_{i,n-j}+\left( \sum ^{n-1}_{j=0}{v_j}\right) {\overline{u}}_{i,0}} \end{aligned}$$
(51)

At \(\Delta x=h=0.1\ {\mathrm {and\ \ }}{\Delta t}^{\alpha }={\left( 0.001\right) }^{0.5}=0.01\ {\mathrm {to\ get\ \ }}p\left( r\right) =\frac{1}{2}x^{2}\frac{{\Delta t}^{\alpha }}{h^2}\) we have the following results:

Table 3 Lower solution of Eq. 44 by implicit FDM at \(t=0.05,\)\(\alpha =0.7\) and for all \(r \in [0,1]\)
Full size table
Table 4 Upper solution of Eq. 44 by implicit FDM at \(t=0.05\), \(\alpha =0.7\) and for all \(r\in [0,1]\)
Full size table

Tables 3 and 4 and Fig. 9 show that both the implicit finite difference and exact solution at \(t=0.05\), \(\alpha =0.7\) and for all \(r\in [0,1]\) attain the triangular fuzzy number shape and thus satisfy the fuzzy number properties as explained in [21].

Fig. 9
figure 9

Exact and implicit FDM of the solution of Eq. 44 at \(\alpha= 0.7,\)\(x=0.9\), \(t=0.05\) and for all \(r \in [0,1]\)

Full size image

Now we compare between the numerical and exact solutions of Eq. 44, for different orders of \(\alpha\).

Figure 10 shows that both the implicit finite difference and exact solutions satisfy the fuzzy number properties by attaining the triangular fuzzy number shape. Also, the exact solution agrees with the implicit finite difference solutions for different values of \(\alpha\). The comparison of numerical and exact solutions when \(\alpha =\ 0.7,\ 0.8,\ 0.9\) shows that the scheme is accurate and the results confirm our theoretical analysis.

Fig. 10
figure 10

Exact and implicit FDM of the solution of Eq. 44 at different values of \(\alpha\) for all \(r \in [0,1]\)

Full size image

6 Conclusions

In this paper, an implicit finite difference scheme has been implemented to obtain the numerical solution for a fuzzy time fractional diffusion equations. The Caputo formula was used for the time fractional derivative. The obtained results by the implicit finite difference scheme satisfy the fuzzy number properties by taking the triangular fuzzy number shape. We have also shown that the implicit finite difference scheme is unconditionally stable. A comparative study of the numerical and exact solution at different values of \(\alpha\) indicates that the scheme is feasible and accurate. The proposed implicit scheme can be used to obtain accurate numerical solutions of fuzzy time fractional diffusion equations. The presented scheme may be extended to nonlinear fuzzy fractional diffusion equations, and this will be investigated in detail at a later stage.