A Novel Numerical Approach for Fredholm Integro-Differential Equations

Abstract

We examine the numerical solution of a second-order linear Fredholm integro-differential equation (FIDE) by a finite difference method. The discretization of the problem is obtained by a finite difference method on a uniform mesh. We construct the method using the integral identity method with basis functions and dealing with the integral terms by interpolating quadrature rules with remainder terms. We further employ the factorization method to establish the algorithm. We demonstrate the error estimates and the convergence of the method. The numerical results are enclosed to verify the order of accuracy.

1 INTRODUCTION

Integro-differential equations (IDEs) are one of the essential tools having applications in many science fields, such as physics, engineering, biology, chemistry [9, 11]. IDEs are classified with respect to the range of their integral terms. Namely, Fredholm integro-differential equations (FIDEs) have a finite range in the integral term while Volterra integro-differential equations (VIDEs) have an integral term with a bound in terms of a variable.

In this paper, our main focus is to construct a new accurate numerical scheme to obtain the numerical solution of the following boundary value problem with a type of second order Fredholm integro-differential equation

$$Lu: = u{\kern 1pt} ''(t) + a(t)u{\kern 1pt} '(t) + \lambda \int\limits_0^T {K(t,s)u(s)ds} = f(t),\quad t \in I = (0,T),$$

(1.1)

$$u(0) = A,\quad u(T) = B,$$

(1.2)

where $a(t) \geqslant \alpha > 0$, $f(t)$, $K(t,s)$ are sufficiently smooth functions in $t \in \bar {I}$ and in $(t,s) \in \bar {I} \times \bar {I}$.

Various analytical and numerical methods have been developed to obtain exact and approximate solutions of FIDEs. In addition the classical analytical methods such as the direct computation method and the series solution method for FIDEs, one can find many other novel well-developed numerical methods for FIDEs in the literature. For instance, the variational iteration method [11], the Adomian decomposition method [12] and B-spline collocation method [13], Galerkin method [5], Taylor polynomial method [1], the generalized minimal residual method [3], the method of moments based on B-spline wavelet method [8] are some of the recently studied methods for the approximate solutions of FIDEs. It is also known that fitted difference schemes are efficient to maintain accurate numerical results for IDEs. In [7], the author constructed a uniform convergent difference scheme on a graded mesh to achieve the numerical solution of a non-linear VIDE with a boundary layer. A non-linear first order singularly perturbed VIDE with a delay is handled by a finite difference scheme in [12]. In [4], it is also shown that finite difference schemes are reliable tools to treat non-linear VIDEs. Recently, a finite difference scheme is constructed to solve a boundary value problem of a second order singularly perturbed FIDE in [6].

To the best of our knowledge, a difference scheme we presented in this paper has not been performed on FIDEs in the literature yet. In this paper, we essentially establish a convergent finite difference method for the given problem in (1.1)–(1.2) on a uniform mesh. The remaining sections of this work is presented in the following organization. In Section 2, a priori estimations of the continuous problem (1.1)–(1.2) are provided. In Section 3, a finite difference scheme is derived using the integral identity method with basis functions and dealing with the integral terms by interpolating quadrature formulas including residues. In Section 4, after we calculate the error estimates we conclude that the proposed scheme is convergent. The scheme is implemented and tested on a couple of numerical examples in Section 5.

Throughout this paper, for any continuous function $g(t)$ defined on $[0,T]$ we will consider the norms ${{\left\| g \right\|}_{\infty }} = \mathop {\max }\limits_{t \in [0,T]} \left| {g(t)} \right|$, ${{\left\| g \right\|}_{1}} = \int_0^T {\left| {g(t)} \right|dt}$ and we take $\bar {K} = \mathop {\max }\limits_{t \in \bar {I}} \int_0^T \left| {K(t,s)} \right|ds$.

2 A PRIORI ESTIMATES

In this section, we present the estimates on the exact solution to the problem (1.1)–(1.2) which describe the asymptotic behavior of the solution and will be considered in the background calculations of the derivation of the numerical scheme.

Lemma 2.1. Let $a,f \in C(\bar {I})$, $K \in {{C}^{1}}(\bar {I} \times \bar {I})$ and $a(t) \geqslant \alpha > 0$. Then, the solution $u$ to the problem (1.1)–(1.2) holds the estimates

$$\left\| u \right\| \leqslant {{C}_{0}},$$

(2.1)

and where ${{C}_{0}} = \frac{{\left| A \right| + \left| B \right| + {{\alpha }^{{ - 1}}}{{{\left\| f \right\|}}_{1}}}}{{1 - {{\alpha }^{{ - 1}}}\bar {K}T}}$ and

$$\left| {u{\kern 1pt} '(t)} \right| \leqslant {{C}_{1}},\quad t \in \bar {I},$$

(2.2)

where ${{C}_{1}} = C{{e}^{{ - \alpha t}}} + {{\alpha }^{{ - 1}}}\left[ {{{{\left\| f \right\|}}_{\infty }} + \left| \lambda \right|{{C}_{0}}\bar {K}} \right](1 - {{e}^{{\alpha t}}})$.

Proof. We begin the proof by establishing the estimate (2.1). We first rewrite (1.1)–(1.2) as the following

$$u{\kern 1pt} ''(t) + a(t)u{\kern 1pt} '(t) + F(t) = 0,$$

(2.3)

$$u(0) = A,\quad u(T) = B,$$

(2.4)

where $F(t) = - f(t) + \lambda \int_0^T K(t,s)u(s)ds$. Solving (2.3)–(2.4) we obtain

$$u{\kern 1pt} '(t) = u{\kern 1pt} '(0){{e}^{{ - \int_0^t {a(\nu )d\nu } }}} - \int\limits_0^t {F(\xi ){{e}^{{ - \int_\xi ^t {a(\nu )d\nu } }}}d\xi } .$$

(2.5)

Integrating (2.5) over $(0,t)$ provides

$$\begin{gathered} u(t) = A + \int\limits_0^t {u{\kern 1pt} '(0){{e}^{{\int_0^\tau {a(\nu )d\nu } }}}d\tau } - \int\limits_0^t {d\tau } \int\limits_0^\tau {F(\xi ){{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\xi } \\ = A + \int\limits_0^t {u{\kern 1pt} '(0){{e}^{{\int_0^\tau {a(\nu )d\nu } }}}d\tau } - \int\limits_0^t {d\xi F(\xi )} \int\limits_\xi ^t {{{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\tau } {\kern 1pt} . \\ \end{gathered} $$

(2.6)

Since $u(T) = B$ and from (2.6),

$$u{\kern 1pt} '{\kern 1pt} (0) = \frac{{B - A + \int\limits_0^T {d\xi F(\xi )} \int\limits_\xi ^T {{{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\tau } }}{{\int\limits_0^T {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }}.$$

(2.7)

Inserting (2.7) into (2.6) we obtain

$$u(t) = A + \left( {B - A + \int\limits_0^T {d\xi F(\xi )} \int\limits_\xi ^T {{{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\tau } } \right)\frac{{\int\limits_0^t {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }}{{\int\limits_0^T {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }} - \int\limits_0^t {d\xi F(\xi )} \int\limits_\xi ^t {{{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\tau } .$$

(2.8)

Here, using the Green’s function

$$\begin{gathered} G(t,\xi ) = \int\limits_\xi ^T {{{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\tau } \frac{{\int\limits_0^t {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }}{{\int\limits_0^T {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }} - {{T}_{0}}(t - \xi )\int\limits_\xi ^t {{{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\tau } \\ ({{T}_{0}}(\lambda ) = 1,\quad \lambda \geqslant 0;\quad {{T}_{0}}(\lambda ) = 0,\quad \lambda < 0), \\ \end{gathered} $$

(2.9)

we rewrite (2.8) as the following

$$u(t) = A\left( {1 - \frac{{\int\limits_0^t {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }}{{\int\limits_0^T {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }}} \right) + B\frac{{\int\limits_0^t {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }}{{\int\limits_0^T {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }} + \int\limits_0^T {G(t,\xi )F(\xi )d\xi } .$$

(2.10)

As an alternative to this formulation of Green’s function, a Green’s function formula for the operator

$$\mathcal{L}u: = - u{\kern 1pt} ''(t) - a(t)u(t),\quad 0 < t < T,$$

$$u(0) = 0,\quad u(T) = 0,$$

is given by

$$G(t,\xi ) = \frac{1}{{\omega (\xi )}}\left( \begin{gathered} {{\varphi }_{1}}(\xi ){{\varphi }_{2}}(t),\quad 0 \leqslant \xi \leqslant t \leqslant T, \hfill \\ {{\varphi }_{1}}(t){{\varphi }_{2}}(\xi ),\quad 0 \leqslant t \leqslant \xi \leqslant T, \hfill \\ \end{gathered} \right.$$

(2.11)

where $\omega (\xi ) = \frac{{\phi (\xi )}}{{Q(T)}}$, $Q(t) = \int_0^t \,\phi (s)ds$ and $\phi (s) = {{e}^{{ - \int_0^s {a(\nu )d\nu } }}}$ and ${{\varphi }_{1}}(t)$ and ${{\varphi }_{2}}(t)$ are respectively the solutions to

$$\mathcal{L}{{\varphi }_{1}} = 0,\quad {{\varphi }_{1}}(0) = 0,\quad {{\varphi }_{1}}(T) = 1,$$

$$\mathcal{L}{{\varphi }_{2}} = 0,\quad {{\varphi }_{2}}(0) = 1,\quad {{\varphi }_{2}}(T) = 0.$$

Formula (2.11) implies that $G(t,\xi ) \geqslant 0$ and in accordance with (2.9) we have

$$\begin{gathered} \mathop {\max }\limits_{t;\xi \in \bar {I}} G(t,\xi ) = \mathop {\max }\limits_{t;\xi \in \bar {I}} \left( {\int\limits_\xi ^T {{{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\tau } \frac{{\int\limits_0^t {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }}{{\int\limits_0^T {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }} - {{T}_{0}}(t - \xi )\int\limits_\xi ^t {{{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\tau } } \right) \\ \leqslant \mathop {\max }\limits_{t;\xi \in \bar {I}} \left( {\int\limits_\xi ^T {{{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\tau } \frac{{\int\limits_0^t {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }}{{\int\limits_0^T {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }}} \right) \leqslant {{\alpha }^{{ - 1}}}(1 - {{e}^{{ - \alpha (T - \xi )}}}). \\ \end{gathered} $$

(2.12)

From (2.12), we conclude that $G(t,\xi ) \leqslant {{\alpha }^{{ - 1}}}$ and utilizing this in (2.10) we find

$$\left| {u(t)} \right| \leqslant \left| A \right| + \left| B \right| + \mathop {\max }\limits_{t;\xi \in \bar {I}} \left| {G(t,\xi )} \right|\int\limits_0^T {\left| {F(\xi )} \right|d\xi } \leqslant \left| A \right| + \left| B \right| + {{\alpha }^{{ - 1}}}\int\limits_0^T {\left| {F(\xi )} \right|d\xi } .$$

(2.13)

Here, we obtain the following bound for $F(t)$

$$\left| {F(t)} \right| \leqslant \left| {f(t)} \right| + \left| \lambda \right|\int\limits_0^T {\left| {K(t,s)} \right|\left| {u(s)} \right|ds} \leqslant \left| {f(t)} \right| + \left| \lambda \right|\bar {K}{{\left\| u \right\|}_{\infty }},$$

and inserting this bound into (2.13) we have

$$\begin{gathered} \left| {u(t)} \right| \leqslant \left| A \right| + \left| B \right| + \mathop {\max }\limits_{t;\xi \in \bar {I}} \left| {G(t,\xi )} \right|\int\limits_0^T {\left| {F(\xi )} \right|d\xi } \leqslant \left| A \right| + \left| B \right| + {{\alpha }^{{ - 1}}}\int\limits_0^T {\left| {F(\xi )} \right|d\xi } \\ \leqslant \left| A \right| + \left| B \right| + {{\alpha }^{{ - 1}}}{{\left\| f \right\|}_{1}} + {{\alpha }^{{ - 1}}}\bar {K}{{\left\| u \right\|}_{\infty }}T, \\ \end{gathered} $$

(2.14)

which provides the desired result in (2.1). To prove (2.2), it suffices to establish a bound for $u{\kern 1pt} '{\kern 1pt} (0)$ given in (2.7) and insert that bound in the formula of $u{\kern 1pt} '{\kern 1pt} (t)$ provided in (2.5). Since

$$\int\limits_0^T {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } \geqslant \int\limits_0^T {{{e}^{{ - {{{\left\| a \right\|}}_{\infty }}\tau }}}d\tau } $$

(2.15)

$$ = \frac{1}{{{{{\left\| a \right\|}}_{\infty }}}}(1 - {{e}^{{ - {{{\left\| a \right\|}}_{\infty }}T}}}) \equiv {{C}_{2}},$$

(2.16)

and

$$\begin{gathered} \int\limits_0^T {d\xi \left| {F(\xi )} \right|} \int\limits_\xi ^T {{{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\tau } \leqslant \int\limits_0^T {d\xi \left| {F(\xi )} \right|} \int\limits_\xi ^T {{{e}^{{ - \alpha (\tau - \xi )}}}d\tau } \leqslant \int\limits_0^T {({{\alpha }^{{ - 1}}}(1 - {{e}^{{ - \alpha (T - \xi )}}}))\left| {F(\xi )} \right|d\xi } \\ \leqslant {{\alpha }^{{ - 1}}}\int\limits_0^T {\left| {F(\xi )} \right|d\xi } \leqslant {{\alpha }^{{ - 1}}}{{\left\| f \right\|}_{1}} + {{\alpha }^{{ - 1}}}\bar {K}{{\left\| u \right\|}_{\infty }}T \equiv {{C}_{3}}, \\ \end{gathered} $$

(2.17)

and from (2.7) it follows that

$$\left| {u{\kern 1pt} '{\kern 1pt} (0)} \right| \leqslant \frac{{\left| A \right| + \left| B \right| + \int\limits_0^T {d\xi \left| {F(\xi )} \right|} \int\limits_\xi ^T {{{e}^{{ - \int_\xi ^\tau {a(\nu )d\nu } }}}d\tau } }}{{\int\limits_0^T {{{e}^{{ - \int_0^\tau {a(\nu )d\nu } }}}d\tau } }} \leqslant C_{2}^{{ - 1}}(\left| A \right| + \left| B \right| + {{C}_{3}}) \equiv {{C}_{4}}.$$

(2.18)

Hence, we have

$$\begin{gathered} \left| {u{\kern 1pt} '{\kern 1pt} (t)} \right| \leqslant {{C}_{4}}{{e}^{{ - \int_0^t {a(\nu )d\nu } }}} + \int\limits_0^t {\left| {F(\xi )} \right|{{e}^{{ - \int_\xi ^t {a(\nu )d\nu } }}}d\xi } \leqslant {{C}_{4}}{{e}^{{ - \alpha t}}} + \int\limits_0^t {\left[ {\left| {f(\xi )} \right| + \left| \lambda \right|{{C}_{0}}\int\limits_0^T {\left| {K(\xi ,s)} \right|ds} } \right]{{e}^{{ - \alpha (t - \xi )}}}d\xi } \\ \leqslant {{C}_{4}}{{e}^{{ - \alpha t}}} + {{\alpha }^{{ - 1}}}\left[ {{{{\left\| f \right\|}}_{\infty }} + \left| \lambda \right|{{C}_{0}}\bar {K}} \right](1 - {{e}^{{\alpha t}}}), \\ \end{gathered} $$

(2.19)

which yields the result in (2.2).

3 DERIVATION OF THE DIFFERENCE SCHEME

In this section, we develop a finite difference scheme for the problem (1.1)–(1.2). Before we proceed to the derivation process of the finite difference scheme we provide the necessary notation we use throughout the paper. Let ${{\omega }_{N}}$ be a uniform mesh on $(0,T)$ defined as

$${{\omega }_{N}} = \left\{ {0 < {{t}_{1}} < \cdots < {{t}_{{N - 1}}} < T,\;h = {{t}_{i}} - {{t}_{{i - 1}}} = \frac{T}{N}} \right\},$$

and ${{\bar {\omega }}_{N}} = {{\omega }_{N}} \cup \{ {{t}_{0}} = 0,\;{{t}_{N}} = T\}$. For any mesh function $v(x)$ defined on ${{\bar {\omega }}_{N}}$, let

$${{{v}}_{i}} = {v}({{t}_{i}}),\quad {{{v}}_{{t,i}}} = \frac{{{{{v}}_{{i + 1}}} - {{{v}}_{i}}}}{h},\quad {{{v}}_{{\bar {t},i}}} = \frac{{{{{v}}_{i}} - {{{v}}_{{i - 1}}}}}{h},\quad {{{v}}_{{\mathop t\limits^ \circ ,i}}} = \frac{{{{{v}}_{{t,i}}} + {{{v}}_{{\bar {t},i}}}}}{2},\quad {{{v}}_{{\bar {t}t,i}}} = \frac{{{{{v}}_{{t,i}}} - {{{v}}_{{\bar {t},i}}}}}{h},$$

and

$${{\left\| {v} \right\|}_{\infty }} = {{\left\| {v} \right\|}_{{\infty ,{{{\bar {\omega }}}_{N}}}}}: = \mathop {\max }\limits_{0 \leqslant i \leqslant N} \left| {{{{v}}_{i}}} \right|,\quad {{\left\| {v} \right\|}_{{1,{{\omega }_{N}}}}}: = h\sum\limits_{i = 1}^{N - 1} \left| {{{{v}}_{i}}} \right|.$$

In order to discretize the problem (1.1)–(1.2), we use the following integral identity

$${{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {Lu(t){{\varphi }_{i}}(t)dt} = {{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {f(t){{\varphi }_{i}}(t)dt} ,$$

(3.1)

with the basis functions

$${{\varphi }_{i}}(t) = \left( \begin{gathered} \varphi _{i}^{{(1)}}(t) = \frac{{{{e}^{{{{a}_{i}}(t - {{t}_{{i - 1}}})}}} - 1}}{{{{e}^{{{{a}_{i}}h}}} - 1}},\quad {{t}_{{i - 1}}} < t < {{t}_{i}}, \hfill \\ \varphi _{i}^{{(2)}}(t) = \frac{{1 - {{e}^{{ - {{a}_{i}}({{t}_{{i + 1}}} - t)}}}}}{{1 - {{e}^{{ - {{a}_{i}}h}}}}},\quad {{t}_{i}} < t < {{t}_{{i + 1}}}, \hfill \\ 0,\quad t \notin ({{t}_{{i - 1}}},{{t}_{{i + 1}}}). \hfill \\ \end{gathered} \right.$$

(3.2)

We note that the functions $\varphi _{i}^{{(1)}}$ and $\varphi _{i}^{{(2)}}$ are respectively the solutions to the problems

$$\begin{gathered} \varphi {\kern 1pt} ''(t) - {{a}_{i}}\varphi {\kern 1pt} '(t) = 0,\quad {{t}_{{i - 1}}} < t < {{t}_{i}},\quad \varphi ({{t}_{{i - 1}}}) = 0,\quad \varphi ({{t}_{i}}) = 1, \hfill \\ \varphi {\kern 1pt} ''(t) - {{a}_{i}}\varphi {\kern 1pt} '(t) = 0,\quad {{t}_{{i - 1}}} < t < {{t}_{i}},\quad \varphi ({{t}_{i}}) = 1,\quad \varphi ({{t}_{{i + 1}}}) = 0 \hfill \\ \end{gathered} $$

and it is obvious that

$${{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {{{\varphi }_{i}}(t)dt} = 1.$$

(3.3)

To achieve the finite difference scheme from the integral identity given in (3.1), we proceed by dealing with the first two terms on the left hand side of the equality. Rearranging these two terms and applying the appropriate interpolating quadrature rules provided in [2] we obtain

$$\begin{gathered} {{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {[u{\kern 1pt} ''{\kern 1pt} (t) + a(t)u{\kern 1pt} '{\kern 1pt} (t)]{{\varphi }_{i}}(t)dt} = {{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {[u{\kern 1pt} ''{\kern 1pt} (t) + {{a}_{i}}u{\kern 1pt} '{\kern 1pt} (t)]{{\varphi }_{i}}(t)dt} + R_{i}^{{(1)}} \\ = - {{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {u{\kern 1pt} '{\kern 1pt} (t)\varphi _{i}^{'}(t)} + {{a}_{i}}{{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {{{\varphi }_{i}}(t)u{\kern 1pt} '{\kern 1pt} (t)dt} + R_{i}^{{(1)}} \\ = {{u}_{{\bar {t}t,i}}} + {{a}_{i}}(\chi _{i}^{{(1)}}{{u}_{{\bar {t},i}}} + \chi _{i}^{{(2)}}{{u}_{{t,i}}}) + R_{i}^{{(1)}}, \\ \end{gathered} $$

(3.4)

where

$$R_{i}^{{(1)}} = {{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {[a(t) - {{a}_{i}}]{{\varphi }_{i}}(t)u{\kern 1pt} '{\kern 1pt} (t)dt,} $$

(3.5)

where

$$\chi _{i}^{{(1)}} = {{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{i}}} {\varphi _{i}^{{(1)}}(t)dt} = \frac{1}{{h{{a}_{i}}}} - \frac{1}{{{{e}^{{{{a}_{i}}h}}} - 1}},$$

and

$$\chi _{i}^{{(2)}} = {{h}^{{ - 1}}}\int\limits_{{{t}_{i}}}^{{{t}_{{i + 1}}}} {\varphi _{i}^{{(2)}}(t)dt} = \frac{1}{{1 - {{e}^{{ - {{a}_{i}}h}}}}} - \frac{1}{{h{{a}_{i}}}}.$$

Since

$${{u}_{{\bar {t},i}}} = {{u}_{{\mathop t\limits^ \circ ,i}}} - \frac{h}{2}{{u}_{{\bar {t}t,i}}},\quad {{u}_{{t,i}}} = {{u}_{{\mathop t\limits^ \circ ,i}}} + \frac{h}{2}{{u}_{{\bar {t}t,i}}},$$

we have the relation

$${{u}_{{\bar {t}t,i}}} + {{a}_{i}}(\chi _{i}^{{(1)}}{{u}_{{\bar {t},i}}} + \chi _{i}^{{(2)}}{{u}_{{t,i}}}) = {{\theta }_{i}}{{u}_{{\bar {t}t,i}}} + {{a}_{i}}{{u}_{{\mathop t\limits^ \circ ,i}}},$$

(3.6)

where

$${{\theta }_{i}} = 1 + {{a}_{i}}h(\chi _{i}^{{(2)}} - \chi _{i}^{{(1)}}) = {{\gamma }_{i}}\coth {{\gamma }_{i}},\quad {{\gamma }_{i}} = \frac{{{{a}_{i}}h}}{2}.$$

(3.7)

Hence, inserting (3.6) in (3.8) provides

$${{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {[u{\kern 1pt} ''{\kern 1pt} (t) + a(t)u{\kern 1pt} '{\kern 1pt} (t)]{{\varphi }_{i}}(t)dt} = {{\theta }_{i}}{{u}_{{\bar {t}t,i}}} + {{a}_{i}}{{u}_{{\mathop t\limits^ \circ ,i}}} + R_{i}^{{(1)}}.$$

(3.8)

Furthermore, for the integral term in (3.1) we first utilize the appropriate interpolating quadrature rules provided in [2] and then apply the right side triangle rule which yield

$${{h}^{{ - 1}}}\lambda \int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {{{\varphi }_{i}}(t)dt} \int\limits_0^T {K(t,s)u(s)ds} = \lambda \int\limits_0^T {K({{t}_{i}},s)u(s)ds} + R_{i}^{{(2)}} = \lambda h\sum\limits_{j = 1}^N \,{{K}_{{ij}}}{{u}_{j}} + R_{i}^{{(2)}} + R_{i}^{{(3)}},$$

(3.9)

where

$$R_{i}^{{(2)}} = {{h}^{{ - 1}}}\lambda \int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {{{\varphi }_{i}}(t)dt} \int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {\left[ {{{T}_{0}}(t - \xi ) - \frac{1}{2}{{h}^{{ - 1}}}(t - {{t}_{{i - 1}}})} \right]\left( {\int\limits_0^T {\frac{\partial }{{\partial \xi }}K(\xi ,s)u(s)ds} } \right)d\xi } ,$$

(3.10)

and

$$R_{i}^{{(3)}} = - \lambda \sum\limits_{j = 1}^N {\kern 1pt} {\kern 1pt} \int\limits_{{{t}_{{j - 1}}}}^{{{t}_{j}}} {(\xi - {{t}_{{j - 1}}})\frac{\partial }{{\partial \xi }}(K({{t}_{i}},\xi )u(\xi ))d\xi } .$$

(3.11)

Separately, by rearranging the right hand side of (3.1), we attain

$${{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {f(t){{\varphi }_{i}}(t)dt} = {{f}_{i}} + R_{i}^{{(4)}},$$

(3.12)

where

$$R_{i}^{{(4)}} = {{h}^{{ - 1}}}\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {[f(t) - f({{t}_{i}})]{{\varphi }_{i}}(t)dt} .$$

(3.13)

Inserting the equations (3.8), (3.9) and (3.12) in (3.1) provides the difference relation

$$\ell {{u}_{i}}: = {{\theta }_{i}}{{u}_{{\bar {t}t,i}}} + {{a}_{i}}{{u}_{{\mathop t\limits^ \circ ,i}}} + \lambda h\sum\limits_{j = 1}^N \,{{K}_{{ij}}}{{u}_{j}} = {{f}_{i}} + {{R}_{i}},\quad i = 1,2, \ldots ,N,$$

(3.14)

where

$${{R}_{i}} = R_{i}^{{(4)}} - R_{i}^{{(1)}} - R_{i}^{{(2)}} - R_{i}^{{(3)}}.$$

(3.15)

Once we disregard the error term ${{R}_{i}}$ in (3.14), this leads to the difference scheme for (1.1)–(1.2)

$$\ell {{y}_{i}}: = {{\theta }_{i}}{{y}_{{\bar {t}t,i}}} + {{a}_{i}}{{y}_{{\mathop t\limits^ \circ ,i}}} + \lambda h\sum\limits_{j = 1}^N \,{{K}_{{ij}}}{{y}_{j}} = {{f}_{i}},\quad i = 1,2, \ldots ,N - 1,$$

(3.16)

$${{y}_{0}} = A,\quad {{y}_{N}} = B,$$

(3.17)

where ${{\theta }_{i}}$ is defined in (3.7).

4 CONVERGENCE ANALYSIS OF THE METHOD

We provide the necessary error estimates and convergence results of the proposed scheme given in (3.16)–(3.17). The error function of the scheme, ${{z}_{i}} = {{y}_{i}} - {{u}_{i}}$, $0 \leqslant i \leqslant N$, is the solution of

$$\ell {{z}_{i}}: = {{\theta }_{i}}{{z}_{{\bar {t}t,i}}} + {{a}_{i}}{{z}_{{\mathop t\limits^ \circ ,i}}} + \lambda h\sum\limits_{j = 1}^N \,{{K}_{{ij}}}{{z}_{j}} = {{R}_{i}},\quad i = 1,2, \ldots ,N - 1,$$

(4.1)

$${{z}_{0}} = A,\quad {{z}_{N}} = B.$$

(4.2)

Lemma 4.1. Suppose that $a,f \in {{C}^{1}}(\bar {I})$, $K \in {{C}^{1}}(\bar {I} \times \bar {I})$ and $a(t) \geqslant \alpha > 0$. Then, the error ${{R}_{i}}$ holds the following estimate

$${{\left\| R \right\|}_{{1,{{\omega }_{N}}}}} \leqslant Ch.$$

(4.3)

Proof. To establish the estimate (4.3), we handle each $R_{i}^{{(k)}}$, for $k = 1,2,3,4$ respectively. Applying the Mean Value Theorem to function $a(t)$ in (3.5) we obtain

$$\left| {R_{i}^{{(1)}}} \right| = C\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {\left| {{{\varphi }_{i}}(t)} \right|\left| {u{\kern 1pt} '{\kern 1pt} (t)} \right|dt} .$$

(4.4)

It is easy to see that $0 < {{\varphi }_{i}}(t) \leqslant 1$ by its definition given in (3.2) and taking this and (2.2) into account in (4.4) it follows that

$${{\left\| {{{R}^{{(1)}}}} \right\|}_{{1,{{\omega }_{N}}}}} \leqslant Ch\sum\limits_{i = 1}^{N - 1} {\kern 1pt} {\kern 1pt} \int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {\left| {u{\kern 1pt} '{\kern 1pt} (t)} \right|dt} \leqslant Ch\int\limits_0^T {\left| {u{\kern 1pt} '{\kern 1pt} (t)} \right|dt} \leqslant Ch.$$

(4.5)

We have an upper bound for $R_{i}^{{(2)}}$ given in (3.10) as the following

$$\left| {R_{i}^{{(2)}}} \right| \leqslant {{h}^{{ - 1}}}\left| \lambda \right|\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {{{\varphi }_{i}}(t)dt} \int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {\left( {\int\limits_0^T {\left| {\frac{\partial }{{\partial \xi }}K(\xi ,s)} \right|\left| {u(s)} \right|ds} } \right)d\xi } .$$

Then, from (3.3) we have

$$\left| {R_{i}^{{(2)}}} \right| \leqslant \left| \lambda \right|\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {\left( {\int\limits_0^T {\left| {\frac{\partial }{{\partial \xi }}K(\xi ,s)} \right|\left| {u(s)} \right|ds} } \right)d\xi } ,$$

and since $\left| u \right| \leqslant {{C}_{0}}$ and $\left| {\frac{\partial }{{\partial \xi }}K(\xi ,s)} \right| \leqslant C$ it follows that

$${{\left\| {{{R}^{{(2)}}}} \right\|}_{{1,{{\omega }_{N}}}}} \leqslant h\left| \lambda \right|\sum\limits_{i = 1}^{N - 1} {\kern 1pt} {\kern 1pt} \int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {\left( {\int\limits_0^T {\left| {\frac{\partial }{{\partial \xi }}K(\xi ,s)} \right|\left| {u(s)} \right|ds} } \right)d\xi } \leqslant {{C}_{3}}h\sum\limits_{i = 1}^{N - 1} \,({{t}_{{i + 1}}} - {{t}_{{i - 1}}}) = 2{{C}_{3}}{{h}^{2}}(N - 1) \leqslant Ch.$$

(4.6)

For the third remainder term $R_{i}^{{(3)}}$ defined in (3.11), we first get the following bound

$$\begin{gathered} \left| {R_{i}^{{(3)}}} \right| \leqslant \left| \lambda \right|\sum\limits_{j = 1}^N {\kern 1pt} {\kern 1pt} \int\limits_{{{t}_{{j - 1}}}}^{{{t}_{j}}} {(\xi - {{t}_{{j - 1}}})\left| {\frac{\partial }{{\partial \xi }}(K({{t}_{i}},\xi )u(\xi ))} \right|d\xi } \leqslant \left| \lambda \right|h\int\limits_0^T {\left| {\frac{\partial }{{\partial \xi }}(K({{t}_{i}},\xi )u(\xi ))} \right|d\xi } \\ \leqslant \left| \lambda \right|h\int\limits_0^T {\left[ {{\kern 1pt} \left| {\frac{\partial }{{\partial \xi }}K({{t}_{i}},\xi )} \right|\left| {u(\xi )} \right| + \left| {K({{t}_{i}},\xi )} \right|\left| {u{\kern 1pt} '{\kern 1pt} (\xi )} \right|} \right]d} \xi {\kern 1pt} . \\ \end{gathered} $$

Here, utilizing the bounds $\left| u \right| \leqslant {{C}_{0}}$, $\left| {\frac{d}{{d\xi }}K(\xi ,s)} \right| \leqslant C$ and (2.2) we get

$${{\left\| {{{R}^{{(3)}}}} \right\|}_{{1,{{\omega }_{N}}}}} \leqslant Ch.$$

(4.7)

For the last remainder term $R_{i}^{{(4)}}$ defined in (3.13), we apply the Mean Value Theorem to function $f(t)$ and get

$$\left| {{{R}^{{(4)}}}} \right| \leqslant C\int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {\left| {{{\varphi }_{i}}(t)} \right|dt} $$

which follows

$$\begin{array}{*{20}{l}} {{{{\left\| {{{R}^{{(4)}}}} \right\|}}_{{1,{{\omega }_{N}}}}}}&{ \leqslant Ch} \end{array}.$$

(4.8)

As a result, considering (4.5)–(4.8) in (3.15) we get the desired result given in (4.3).

Lemma 4.2. Suppose that the error function ${{z}_{i}}$ solves the problem in (4.1)–(4.2). Then, the error function ${{z}_{i}}$ holds the following estimate

$${{\left\| z \right\|}_{{\infty ,{{\omega }_{N}}}}} \leqslant {{\left\| R \right\|}_{{1,{{\omega }_{N}}}}}.$$

(4.9)

Proof. In [10], it is provided that the discrete Green’s function $G({{t}_{i}},{{\eta }_{k}})$ for the difference operator

$${{\ell }^{h}}{{z}_{i}}: = {{\theta }_{i}}{{z}_{{\bar {t}t,i}}} + {{a}_{i}}{{z}_{{\mathop t\limits^ \circ ,i}}},\quad i = 1,2, \ldots ,N - 1,\quad {{z}_{0}} = 0,\quad {{z}_{N}} = 0$$

is the solution to the problem

$${{\ell }^{h}}G({{t}_{i}},{{\eta }_{k}}) = \frac{{{{\delta }_{{ik}}}}}{h},\quad i,k = 1,2, \ldots ,N - 1,\quad {{y}_{0}} = 0,\quad {{y}_{N}} = 0$$

for fixed $k = 1,2, \ldots ,N - 1$ where ${{\delta }_{{ik}}}$ is the Kronecker delta. Rewriting the problem (4.1)–(4.2) and by the Green’s function, the solution to the problem (4.1)–(4.2) is obtained as

$${{z}_{i}} = \sum\limits_{k = 1}^{N - 1} \,hG({{t}_{i}},{{\eta }_{k}})\left( {\lambda h\sum\limits_{j = 1}^N \,{{K}_{{kj}}}{{z}_{j}} - {{R}_{k}}} \right),\quad {{t}_{i}} \in {{\omega }_{N}}.$$

(4.10)

It is also known that the Green’s function $G({{t}_{i}},{{\eta }_{k}})$ is bounded, namely, $0 \leqslant G({{t}_{i}},{{\eta }_{k}}) \leqslant c{{\alpha }^{{ - 1}}}$. Taking this into account with (4.10) we have

$$\begin{gathered} {{\left\| z \right\|}_{{{{\omega }_{N}},\infty }}} \leqslant c{{\alpha }^{{ - 1}}}\left( {\left| \lambda \right|{{{\left\| z \right\|}}_{{{{\omega }_{N}},\infty }}}\sum\limits_{k = 1}^{N - 1} \,{{h}^{2}}{\kern 1pt} \sum\limits_{j = 1}^N \left| {{{K}_{{kj}}}} \right| + {{{\left\| R \right\|}}_{1}}} \right) \leqslant c{{\alpha }^{{ - 1}}}\left( {\tilde {K}\left| \lambda \right|{{{\left\| z \right\|}}_{{{{\omega }_{N}},\infty }}}\sum\limits_{k = 1}^{N - 1} \,h + {{{\left\| R \right\|}}_{1}}} \right) \\ \leqslant c{{\alpha }^{{ - 1}}}\left( {\tilde {K}\left| \lambda \right|T{{{\left\| z \right\|}}_{{{{\omega }_{N}},\infty }}} + {{{\left\| R \right\|}}_{1}}} \right), \\ \end{gathered} $$

where $\tilde {K} = \mathop {\max }\limits_{0 \leqslant i \leqslant N} h\sum\nolimits_{j = 1}^N {\left| {{{K}_{{ij}}}} \right|}$ and this leads to the desired result given in (4.9).

Theorem 4.3. Suppose that $a,f \in {{C}^{1}}(\bar {I})$, $K \in {{C}^{1}}(\bar {I} \times \bar {I})$, $u$ is the solution of (1.1)–(1.2) and $y$ is the solution of (3.16)–(3.17). Then, y satisfies the following estimate

$${{\left\| {y - u} \right\|}_{{\infty ,{{{\bar {\omega }}}_{N}}}}} \leqslant Ch.$$

Proof. This statement follows from Lemma 4.1 and Lemma 4.2.

5 ALGORITHM AND NUMERICAL RESULTS

The numerical results on a couple of problems are demonstrated to support the analysis we made in the previous sections. Since the scheme given in (3.16)–(3.17) is a boundary value problem with a difference equation consisting of three points, we employ the factorization method as introduced in (3.16) and iteration simultaneously. For this purpose, we rearrange the difference scheme in (3.16) in the following form

$${{A}_{i}}{{y}_{{i - 1}}} - {{C}_{i}}{{y}_{i}} + {{B}_{i}}{{y}_{{i + 1}}} = - {{F}_{i}},\quad i = 1, \ldots ,N - 1,$$

(5.1)

$${{y}_{0}} = A,\quad {{y}_{N}} = B,$$

(5.2)

where

$${{A}_{i}} = \lambda hK({{x}_{i}},{{x}_{{i - 1}}}) + \frac{{{{\theta }_{i}}}}{{{{h}^{2}}}} - \frac{{{{a}_{i}}}}{{2h}},$$

$${{B}_{i}} = \lambda hK({{x}_{i}},{{x}_{{i + 1}}}) + \frac{{{{\theta }_{i}}}}{{{{h}^{2}}}} + \frac{{{{a}_{i}}}}{{2h}},$$

$${{C}_{i}} = \frac{{2{{\theta }_{i}}}}{{{{h}^{2}}}} - \lambda hK({{x}_{i}},{{x}_{i}}),$$

and

$${{F}_{i}} = \lambda h\sum\limits_{j = 0}^{i - 2} \,K({{x}_{i}},{{x}_{j}})y_{j}^{{(n - 1)}} + \lambda h\sum\limits_{j = i + 2}^n \,K({{x}_{i}},{{x}_{j}})y_{j}^{{(n - 1)}} - {{f}_{i}}.$$

Then, the solution to (5.1)–(5.2) is determined by the algorithm

$${{y}_{i}} = {{\alpha }_{{i + 1}}}{{y}_{{i + 1}}} + {{\beta }_{{i + 1}}},\quad i = N - 1, \ldots ,0,$$

where

$${{\alpha }_{{i + 1}}} = \frac{{{{B}_{i}}}}{{{{C}_{i}} - {{\alpha }_{i}}{{A}_{i}}}},\quad {{\alpha }_{1}} = 0,\quad i = 1, \ldots ,N - 1,$$

$${{\beta }_{{i + 1}}} = \frac{{{{A}_{i}}{{\beta }_{i}} + {{F}_{i}}}}{{{{C}_{i}} - {{\alpha }_{i}}{{A}_{i}}}},\quad {{\beta }_{1}} = A,\quad i = 1, \ldots ,N - 1.$$

Example 1. We study the following boundary value problem

$$u{\kern 1pt} ''{\kern 1pt} (t) + 2u{\kern 1pt} '{\kern 1pt} (t) + \frac{1}{4}\int\limits_0^{\pi /2} {{{e}^{{s - t}}}u(s)ds} = \frac{1}{4}({{e}^{{ - t}}} - {{e}^{{ - (1 + t)}}}),\quad 0 < t < 1,\quad u(0) = 1,\quad u(1) = {{e}^{{ - 2}}},$$

with an exact solution

$$u(x) = {{e}^{{ - 2x}}}.$$

We calculate the error by the formula

$$e_{\varepsilon }^{N} = {{\left\| {{{y}^{N}} - u} \right\|}_{\infty }},$$

where ${{y}^{N}}$ is the numerical solution for various $N$ values. The order of convergence is calculated by

$${{r}^{N}} = \frac{{\ln ({{e}^{N}}{\text{/}}{{e}^{{2N}}})}}{{\ln 2}}.$$

(5.3)

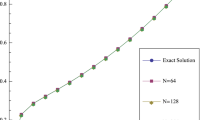
For various values of N, the maximum errors and the convergence rates of the approximate solution are enclosed in Table 1.

Table 1.   Error terms ${{e}^{N}}$, ${{e}^{{2N}}}$ and convergence order $r$ for Example 1

Example 2. The second test problem is

$$u{\kern 1pt}'' + 2u{\kern 1pt} ' + \frac{1}{4}\int\limits_0^1 {\sin (ts)u(s)ds} = {{\sinh }^{2}}(t) + {{t}^{2}} + 4,\quad 0 < t < 1,\quad u(0) = 0,\quad u(1) = 1,$$

and the exact solution to this problem is unknown. Hence, the approximate solution ${{y}^{N}}$ is computed and then, the double mesh principle is involved in the computation to estimate the errors and to calculate the convergence. The double mesh principle is taking the error as the difference between the approximate solution on mesh size $N$ and the approximate solution calculated on double mesh 2N, namely

$$e_{{}}^{N} = {{\left\| {{{y}^{N}} - {{y}^{{2N}}}} \right\|}_{\infty }},$$

where ${{y}^{N}}$ is the numerical solution on mesh $N$ and ${{y}^{{2N}}}$ is the numerical solution on mesh 2N. Further, the formula of convergence rate given in (5.3) is used for the order of convergence.

The error estimations and the convergence study of the approximate solution for various values of $N$ are provided in Table 2.

Table 2.   Error terms ${{e}^{N}}$, ${{e}^{{2N}}}$ and convergence order $r$ for Example 2

6 CONCLUSIONS

In this study, we mainly derived a finite difference scheme to examine a boundary value problem for a linear second-order Fredholm integro-differential equation. After we studied the asymptotic behavior of the exact solution of the problem, we constructed the difference scheme and established the error estimates and the rate of convergence of the scheme. Further, we provided the numerical results in Tables 1, 2 and Fig. 1 which also match the analytical results on the error estimates and convergence order. Hence, it is analytically and practically shown that the difference scheme is a first order convergent numerical method.

Fig. 1.

The graphs of the exact solution and the computed solution for $N = 256$.