1 Introduction

The theory of fuzzy set was introduced by Zadeh (1965). A fuzzy set basically consists of subjects with a series of grades. The fuzzy set is described by a function(commonly termed as membership function) from any non-empty set to the closed interval [0, 1]. The set-theocratic ideas of relation, union, inclusion, complement, intersection, convexity, etc. are extended to fuzzy sets. Moreover, several characteristics of all those notions are established in the context of the fuzzy sets. After the introduction of fuzzy set, the fuzzy logic (FL) has been used in several substantial applications to address the uncertainty (Singh et al. 2013). The extension of FS to intutionistic fuzzy set was given by Atansassov (1986).

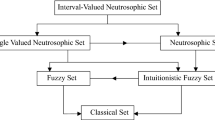
To exhibit the inexact, uncertain, incoherent and indefinite information that is faced by the world, the notion of neutrosophic set was proposed for philosophical perspectives by Smarandache (1999). The neutrosophic sets are the prevailing frameworks that generalize the ideas of a fuzzy set (Zadeh 1965), classic set, interval-valued fuzzy set (Turksen 1986), intuitionistic fuzzy set (Atansassov 1986), paraconsistent set, interval-valued intuitionistic fuzzy set, tautological set and the paradoxist set. Single-valued neutrosophic set is the case of neutrosophic set which is utilized in the engineering and scientific application. Indeterminacy is associated with the uncertainty that everyone faces in every domain of life. Double-refined neutrosophic sets and triple-refined neutrosophic sets are believed to handle incomplete and inconsistent information more efficiently than single-valued neutrosophic set (Kandasamy and Smarandache 2016; Zadeh 2018). Further generalizations such as single- and double-valued neutrosophic set and neutrosophic logic are studied by Smarandache (2013). These generalizations have made research more sensitive and realistic by introducing the uncertain aspect of the life as an idea.

In previous optimization methods, all parameters are assumed to be exactly known and fixed. However, these types of assumptions are not adequate to tackle various problems of real life, where most parameters are inexact and inexplicit. Zimmermann (1978) was the first to model such situations and acquainted the concept of fuzzy linear programming problem. One can consider Zimmermann’s work as an extension of Zadeh and Bellman’s (1970) work which proposes the basic concept of fuzzy goals, fuzzy constraints and fuzzy decisions. Many researchers have studied and applied the optimization in fuzzy and generalized fuzzy environment. For this matter, Tanaka and Asai (1984) presented the fuzzy solutions of fuzzy linear programming problem. Moreover, in addition to that, Chanas (1983), Verdegay (1984), Carlsson and Korhonen (1986), Campos (1989), Luhandjula (1989), Sakawa and Yano (1989), Jain and Deb (2013), Guu and Wu (2018), Zhou et al. (2018), Ghodousian (2019), etc., worked on linear and non-linear, single and multi-objective fuzzy optimization. A short survey of studies of different researchers on optimization under impression can be found in the work of Sahinidis (1983). Chakrabortty et al. (2013) and Wan et al. (2017) applied intuitionistic fuzzy optimization to find the optimal solution of manufacturing inventory models and group decision making with interval-valued fuzzy preference relations. Bharati (2018a, b), in his recent work, proposed a new computational algorithm for multi-objective linear programming problem in interval-valued intuitionistic fuzzy and hesitant fuzzy environments. Das and Roy (2015) and Sarkar and Roy (2018) presented an algorithm for non-linear programming problem in neutrosophic environment and also applied the proposed method on riser design and welded beam problems.

Uncertain programming has been widely applied in engineering, management, and design problems. These prevailing methods dealing with uncertain data do not successfully imply indeterminate solutions. Latitude is actually provided by introducing indeterminacy in decision making which acquire an indeterminate optimal solution for the objective function as well as for decision variables. Hence, it is important to see how to deal with indeterminate real life situation and yield indeterminate solutions. Whenever optimization was carried out in neutrosophic and generalized neutrosophic environment, we get better and refined results. These models are based on the conversion of objective functions into neutrosophic fuzzy constraints. The refined neutrosophic set handles impression and inconsistency more efficiently. Our motivation is to establish a refined neutrosophic model, which could be more efficiently applied in the decision-making process to get effective results. This model is proficient when it is required to express an ill-known quantity with some uncertain numerical value or in situations where decision makers have to abstain from expressing their assessments. In this study, we define the four-valued refined neutrosophic set and set-theoretic operators and also furnish them with various properties of four-valued refined neutrosophic set. We also aim to give a computational algorithm for solving multi-objective non-linear programming problem by four-valued refined neutrosophic optimization approach. In addition, we have made a comparative study between the new and some of the existing techniques.

2 Preliminaries

2.1 Fuzzy set

A fuzzy set (Zadeh 1965) is a set that can contain elements partially, that is, the property that an element belongs to the set under consideration can be true with a partial degree of truth. Given a universe set X, a fuzzy set \({\tilde{A}}^{F}\) is an ordered set (universe-element, truth degree of membership of that element denoted mathematically as

$$\begin{aligned} {\tilde{A}}^{F} = \{(x, T _{{\tilde{A}}^{F}}(x) ): x \; \in \; X \}, \end{aligned}$$

where \(T_{{\tilde{A}}^{F}}(x)\; \in \; [0,1]\).

2.2 Intuitionistic fuzzy set (IFS)

Given a universe X, an intuitionistic fuzzy set (Atansassov 1986) is a set of triplet \((x, T _{{\tilde{A}}^{I}}(x), F_{{\tilde{A}}^{I}}(x))\), where \(T _{{\tilde{A}}^{I}}(x), F_{{\tilde{A}}^{I}}(x)\) represents the truth and falsity grades, respectively, and \(0 \le T _{{\tilde{A}}^{I}}(x)+F_{{\tilde{A}}^{I}}(x) \le 1\) , \(T _{{\tilde{A}}^{I}}(x), F_{{\tilde{A}}^{I}}(x) \; \in [0,1]\). Clearly, one can obtain a fuzzy set when \(T _{{\tilde{A}}^{I}}(x)+F_{{\tilde{A}}^{I}}(x)=1.\)

2.3 Neutrosophic set

Neutrosophic set (Smarandache 1995) is a generalized concept in which each component \(x\in X\) to a set \(\tilde{A^N}\) has a membership degree \(T_{\tilde{A^N}}(x)\), nonmembership degree \(F_{\tilde{A^N}}(x)\) as well as a degree of indeterminacy \(I_{\tilde{A^N}}(x)\), where \(T_{\tilde{A^N}}(x), I_{\tilde{A^N}}(x)\) and \(F_{\tilde{A^N}}(x)\) are real standard or nonstandard subsets of \(]0^-,1^+[\).

2.4 Single-valued neutrosophic set (SVNS)

In single-valued neutrosophic set (Smarandache 1998), each \(x \in X\) to a set \({\tilde{A}}^{\text {SN}}\) is characterized by \(T_{{\tilde{A}}^{\text {SN}}}(x),I_{{\tilde{A}}^{\text {SN}}}(x),F_{{\tilde{A}}^{\text {SN}}}(x)\), where \(T_{{\tilde{A}}^{\text {SN}}}(x)\), \(I_{{\tilde{A}}^{\text {SN}}}(x)\), \(F_{{\tilde{A}}^{\text {SN}}}(x)\) belongs to [0, 1] and \(0 \le T_{{\tilde{A}}^{\text {SN}}}(x)+I_{{\tilde{A}}^{\text {SN}}}(x)+F_{{\tilde{A}}^{\text {SN}}}(x) \le 3.\)

Thus, a single-valued neutrosophic set \({\tilde{A}}^{\text {SN}}\) is expressed as

$$\begin{aligned} {\tilde{A}}^{\text {SN}}=\{(x, T_{{\tilde{A}}^{\text {SN}}}(x),I_{{\tilde{A}}^{\text {SN}}}(x), F_{{\tilde{A}}^{\text {SN}}}(x)) : x\in X\}. \end{aligned}$$

2.5 Fuzzy optimization

Fuzzy optimization is a process to solve the fuzziness model “optimally” using existing optimization tools and techniques, purely depending on the formulation of fuzzy information in terms of membership functions. There are seven stages introduced by Tang et al. (2004) to carry out fuzzy optimization. These steps can be used for any kind of problem whether it is linear or non-linear, single or multi-objective and decision variables are discrete or continuous:

  • Understanding the problem, identifying constraints and objectives of the framework and connections among them.

  • Formulation of fuzzy coefficient, fuzzy objective and fuzzy constraints based on the fuzzy information in the problem.

  • Using fuzzy coefficient, fuzzy objective, fuzzy constraints and mathematical techniques development of a fuzzy optimization model.

  • Formulation of fuzzy membership function based on the problem and decision makers’ choice to transform fuzzy model into fuzzy optimization.

  • Transformation of the fuzzy optimization model into an equivalent or an approximate crisp optimization model.

  • Solution of the crisp optimization model by using appropriate optimization techniques.

  • Upgradation of fuzzy optimization system iteratively if the attained optimal solution is not satisfactory.

3 Four-valued refined neutrosophic set (FVRNS)

Refinement of any of T, I, and F involves the extenics (Zadeh 2018). Four-valued refined neutrosophic set can be defined in a number of ways by splitting indeterminacy in different manners. Here in the present work, we only focus on the below mentioned criteria. A four-valued refined neutrosophic set is such a type of neutrosophic set in which indeterminacy is split into two parts as \(U=\)uncertain and \(C=\) contradiction, where \(C=T\wedge F\). The values of T, I, C and F belong to [0, 1] and \(0 \le T+U+C+F \le 4.\) Thus, FVRNS is represented as

$$\begin{aligned} {\tilde{A}}^{\text {RN}}=\{(x,T_{{\tilde{A}}^{\text {RN}}}(x),U_{{\tilde{A}}^{\text {RN}}}(x),C_{{\tilde{A}}^{\text {RN}}}(x),F_{{\tilde{A}}^{\text {RN}}}(x)) : x \in X\}. \end{aligned}$$

When X is continuous, then

$$\begin{aligned} {\tilde{A}}^{\text {RN}}=\int _X \{x,T_{{\tilde{A}}^{\text {RN}}}(x),U_{{\tilde{A}}^{\text {RN}}}(x),C_{{\tilde{A}}^{\text {RN}}}(x),F_{{\tilde{A}}^{\text {RN}}}(x)\diagup \mathrm{d}x : x\in X\}, \end{aligned}$$

and when X is discrete, its representation will be

$$\begin{aligned} {\tilde{A}}^{\text {RN}}=\sum _{i=1}^{n} \{T_{{\tilde{A}}^{\text {RN}}}(x_i),U_{{\tilde{A}}^{\text {RN}}}(x_i),C_{{\tilde{A}}^{\text {RN}}}(x_i),F_{{\tilde{A}}^{\text {RN}}}(x_i)\diagup x_i : x_i\in X\}. \end{aligned}$$

The complement of the four-valued refined neutrosophic set is denoted by \(C_r\) and is defined as

$$\begin{aligned} T_{C_r}(x)&=F_{{\tilde{A}}^{\text {RN}}}(x), \\ U_{C_r}(x)&=1-U_{{\tilde{A}}^{\text {RN}}}(x),\\ C_{C_r}(x)&=1-C_{{\tilde{A}}^{\text {RN}}}(x),\\ F_{C_r}(x)&=T_{{\tilde{A}}^{\text {RN}}}(x), \end{aligned}$$

for all \(x\in X\).

The definition of FVRNS and the complement guarantees the following results.

Theorem 1

For two FVRNS \({\tilde{A}}^{\text {RN}}\) and \({B}^{\text {RN}}\), \({\tilde{A}}^{\text {RN}}\subseteq {B}^{\text {RN}}\) if and only if

$$\begin{aligned} T_{{\tilde{A}}^{\text {RN}}}(x)\le & {} T_{{\tilde{B}}^{\text {RN}}}(x),\\ U_{{\tilde{A}}^{\text {RN}}}(x)\le & {} U_{{\tilde{B}}^{\text {RN}}}(x),\\ C_{{\tilde{A}}^{\text {RN}}}(x)\le & {} C_{{\tilde{B}}^{\text {RN}}}(x),\\ F_{{\tilde{A}}^{\text {RN}}}(x)\ge & {} F_{{\tilde{B}}^{\text {RN}}}(x). \end{aligned}$$

Theorem 2

\({{\tilde{A}}}^{\text {RN}}\subseteq {\tilde{B}}^{\text {RN}}\) if and only if \(C_r({{\tilde{B}}^{\text {RN}}})\subseteq C_r({{\tilde{A}}^{\text {RN}}})\).

The union of two four-valued refined neutrosophic sets \({\tilde{A}}^{\text {RN}}\) and \({\tilde{B}}^{\text {RN}}\) is a four-valued refined neutrosophic set \({\tilde{C}}^{\text {RN}}\), indicated as \({\tilde{C}}^{\text {RN}}={\tilde{A}}^{\text {RN}}\cup {\tilde{B}}^{\text {RN}}\), whose truth membership T, uncertainty U, contradictory C and falsity memberships F are identified with those of \({\tilde{A}}^{\text {RN}}\) and \({\tilde{B}}^{RN}\) as follow:

$$\begin{aligned} T_{{\tilde{C}}^{\text {RN}}}(x)= & {} \max (T_{{\tilde{A}}^{\text {RN}}}(x),T_{{\tilde{B}}^{\text {RN}}}(x));\\ U_{{\tilde{C}}^{\text {RN}}}(x)= & {} \max (U_{{\tilde{A}}^{\text {RN}}}(x),U_{{\tilde{B}}^{\text {RN}}}(x));\\ C_{{\tilde{C}}^{\text {RN}}}(x)= & {} \max (C_{{\tilde{A}}^{\text {RN}}}(x),C_{{\tilde{B}}^{\text {RN}}}(x));\\ F_{{\tilde{C}}^{\text {RN}}}(x)= & {} \min (F_{{\tilde{A}}^{\text {RN}}}(x),F_{{\tilde{B}}^{\text {RN}}}(x)). \end{aligned}$$

Theorem 3

\({\tilde{A}}^{\text {RN}}\cup {\tilde{B}}^{\text {RN}} \) is the smallest four-valued refined neutrosophic set containing both \({\tilde{A}}^{\text {RN}}\) and \({\tilde{B}}^{\text {RN}}\).

Proof

It is unvarnished from the concept of the union operator. \(\square \)

The intersection of two four-valued refined neutrosophic set \({\tilde{A}}^{\text {RN}}\) and \({\tilde{B}}^{\text {RN}}\) is a four-valued refined neutrosophic set \({\tilde{C}}^{\text {RN}}\), indicated as \({\tilde{C}}^{\text {RN}}={\tilde{A}}^{\text {RN}}\cap {\tilde{B}}^{\text {RN}}\), whose truth membership, uncertainty U, contradictory C, and falsity memberships are identified with those of \({\tilde{A}}^{\text {RN}}\) and \({\tilde{B}}^{\text {RN}}\) as follows.

$$\begin{aligned} T_{{\tilde{C}}^{\text {RN}}}(x)&=\min (T_{{\tilde{A}}^{\text {RN}}}(x),T_{{\tilde{B}}^{\text {RN}}}(x));\\ U_{{\tilde{C}}^{\text {RN}}}(x)&=\min (U_{{\tilde{A}}^{\text {RN}}}(x),U_{{\tilde{B}}^{\text {RN}}}(x));\\ C_{{\tilde{C}}^{\text {RN}}}(x)&=\min (C_{{\tilde{A}}^{\text {RN}}}(x),C_{{\tilde{B}}^{\text {RN}}}(x));\\ F_{{\tilde{C}}^{\text {RN}}}(x)&=\max (F_{{\tilde{A}}^{\text {RN}}}(x),F_{{\tilde{B}}^{\text {RN}}}(x)). \end{aligned}$$

Theorem 4

\({\tilde{A}}^{\text {RN}}\cap {\tilde{B}}^{\text {RN}} \) is the largest four-valued refined neutrosophic set containing both \({\tilde{A}}^{\text {RN}}\) and \({\tilde{B}}^{\text {RN}}\).

Proof

It is unvarnished from the concept of intersection operator.\(\square \)

The difference of two four-valued refined sets \({\tilde{A}}^{\text {RN}}\) and \({\tilde{B}}^{\text {RN}}\) is FVRNS \({\tilde{C}}^{\text {RN}}\), indicated as \({\tilde{C}}^{\text {RN}}={\tilde{A}}^{\text {RN}}{\setminus }{\tilde{B}}^{\text {RN}}\), whose truth membership, uncertainty U, contradictory C, and falsity memberships are identified with those of \({\tilde{A}}^{\text {RN}}\) and \({\tilde{B}}^{\text {RN}}\) as follows.

$$\begin{aligned} T_{{\tilde{C}}^{\text {RN}}}(x)&=\min (T_{{\tilde{A}}^{\text {RN}}}(x),F_{{\tilde{B}}^{\text {RN}}}(x));\\ U_{{\tilde{C}}^{\text {RN}}}(x)&=\min (U_{{\tilde{A}}^{\text {RN}}}(x),1-U_{{\tilde{B}}^{\text {RN}}}(x));\\ C_{{\tilde{C}}^{\text {RN}}}(x)&=\min (C_{{\tilde{A}}^{\text {RN}}}(x),1-C_{{\tilde{B}}^{\text {RN}}}(x));\\ F_{{\tilde{C}}^{\text {RN}}}(x)&=\max (F_{{\tilde{A}}^{\text {RN}}}(x),T_{{\tilde{B}}^{\text {RN}}}(x)). \end{aligned}$$

It can easily be checked that four-valued refined neutrosophic set satisfies most properties such as associativity, distributivity, idempotency, absorption, involution and De Morgan’s laws, but it does not satisfy the principle of excluded middle like fuzzy set, IFS and SNVS.

All of the above defined operations can be verified by example as given below.

Example 1

Semantic web service quality evaluation Zadeh (2018) is done by some domain experts. Assume \(A=[a_1, a_2, a_3 ]\) in which \(a_1\) is capability, \(a_2\) is trustworthiness and \(a_3\) is price, where \(a_1, a_2, a_3\) are in [0, 1]. From the experts’ questionnaire, the option could be a grade of “ excellent service”, a grade of “intermediate service”, a grade of “ contradictory service” and a grade of “bad service”. X and Y are four-valued refined neutrosophic sets of A defined by

$$\begin{aligned} X= & {} \frac{\langle 0.2,0.6,0.3,0.5 \rangle }{a_1}+\frac{\langle 0.5,0.3,0.7,0.4 \rangle }{a_2}+\frac{\langle 0.7,0.3,0.4,0.2 \rangle }{a_3}\\ Y= & {} \frac{\langle 0.4,0.7,0.3,0.5 \rangle }{a_1}+\frac{\langle 0.2,0.8,0.3,0.5 \rangle }{a_2}+\frac{\langle 0.3,0.6,0.8,0.5 \rangle }{a_3}. \end{aligned}$$

4 Four-valued refined neutrosophic optimization technique

Consider a non-linear multi-objective optimization problem,

$$\begin{aligned} \mathrm{Minimize} \; \{f_i(x)\}\qquad \qquad i=1,2,\ldots ,p, \end{aligned}$$

such that

$$\begin{aligned} g_j(x)\le b_j \qquad \qquad j=1,2,\ldots , q, \end{aligned}$$

where x are decision variables, \(f_i(x)\) represents objective functions, \(g_j(x)\) represents the constraint functions, and p and q represent the number of objective functions and constraints, respectively. Now the decision set \({\tilde{D}},\) a conjunction of four-valued neurotrophic objectives and constraints, is defined as

$$\begin{aligned} {\tilde{D}}=(\cap _{p=1}^{k} {\tilde{O}}_k)\cap ( \cap _{p=1}^{k}{\tilde{L}}_j) = \{x,T_{{\tilde{D}}},U_{{\tilde{D}}},C_{{\tilde{D}}},F_{{\tilde{D}}})\}, \end{aligned}$$

where

$$\begin{aligned} T_{{\tilde{D}}}(x)= & {} \min ( T_{{\tilde{O}}_1}(x), T_{{\tilde{O}}_2}(x),\ldots ,T_{{\tilde{O}}_p}(x);T_{{\tilde{L}}_1}(x),T_{{\tilde{L}}_2}(x),\ldots , T_{{\tilde{L}}_q}(x))\\ U_{{\tilde{D}}}(x)= & {} \min ( U_{{\tilde{O}}_1}(x), U_{{\tilde{O}}_2}(x), \ldots ,U_{{\tilde{O}}_p}(x);U_{{\tilde{L}}_1}(x),U_{{\tilde{L}}_2}(x), \ldots ,U_{{\tilde{L}}_q}(x))\\ C_{{\tilde{D}}}(x)= & {} \min ( C_{{\tilde{O}}_1}(x), C_{{\tilde{O}}_2}(x), \ldots ,C_{{\tilde{O}}_p}(x);C_{{\tilde{L}}_1}(x),C_{{\tilde{L}}_2}(x),\ldots , C_{{\tilde{L}}_q}(x))\\ F_{{\tilde{D}}}(x)= & {} \max ( F_{{\tilde{O}}_1}(x), F_{{\tilde{O}}_2}(x), \ldots ,F_{{\tilde{O}}_p}(x);F_{{\tilde{L}}_1}(x),F_{{\tilde{L}}_2}(x), \ldots ,F_{{\tilde{L}}_q}(x)) \end{aligned}$$

for all \(x\in X\).

Where \(T_{{\tilde{D}}},\) \(U_{{\tilde{D}}}\), \(C_{{\tilde{D}}}\), and \(F_{{\tilde{D}}}\) represent truth, uncertainty, contradictory and falsity grade of membership of four-valued refined neutrosophic decision set, respectively. Now using the four-valued refined neutrosophic optimization, the above problem is remodeled into a non-linear optimization as

$$\begin{aligned} \mathrm{Max} \, \alpha ,\quad \mathrm{Max} \, \gamma ,\quad \mathrm{Min} \, \beta ,\quad \mathrm{Max} \, \delta , \end{aligned}$$

Such that

$$\begin{aligned}&T_{\tilde{O_k}}(x)\ge \alpha ,\quad T_{\tilde{L_j}}(x)\ge \alpha ,\\&U_{\tilde{O_k}}(x)\ge \gamma ,\quad U_{\tilde{L_j}}(x)\ge \gamma ,\\&F_{\tilde{O_k}}(x)\le \beta ,\quad F_{\tilde{L_j}}(x)\le \beta ,\\&C_{\tilde{O_k}}(x)\ge \delta , \quad C_{\tilde{L_j}}(x)\ge \delta ,\\&\alpha \ge \beta , \quad \alpha \ge \gamma \quad \alpha \ge \delta ,\\&\alpha +\beta +\gamma +\delta \le 4, \\&\alpha ,\; \beta ,\; \gamma , \; \delta \in [0,1],\\&g_j(x)\le b_j, \quad x\ge 0, \quad j=1,2,\dots ,q. \end{aligned}$$

Computational Algorithm

Step 1: Solve the first objective function as a single objective function taken from set of K objectives. The values of decision variables and objective functions will be computed subject to the given constraints.

Step 2: Now compute the values of the unresolved objective, i.e., \((k-1)\) using the decision variables from step 1.

Step 3: Continue to the remaining \((k-1)\) objective function by going through step 1 and step 2.

$$\begin{aligned} \begin{bmatrix} f^*_1({x^1})&f_2({x^1})&\cdots&f_p({x^1}) \\ f_1({x^2})&f^*_2({x^2})&\cdots&f_1({x^2}) \\ \vdots&\vdots&\ddots&\vdots \\ f_1({x^r})&f_2({x^r})&\cdots&f^*_p({x^r}) \end{bmatrix}. \end{aligned}$$

Step 4: Find the lower bound \({{\hat{L}}_p}^{T}\) and the upper bound \({{\hat{U}}_p}^{T}\) corresponding to each objective \(f_k(x)\). The lower and upper bounds for truth membership of objectives are

$$\begin{aligned} {{\hat{U}}_p}^{T}=\max \{f_p(x^r)\}\qquad \text { and } \qquad {{\hat{L}}_p}^{T}=\min \{f_p(x^r)\}, \end{aligned}$$

where \(r=1,2,\ldots ,p\).

The upper \({{\hat{U}}_p}^{F}\) and lower \({{\hat{L}}_p}^{F}\) bounds for falsity membership of objectives are

$$\begin{aligned} {{{\hat{U}}}_p}^{F}={{\hat{U}}_p}^{T} \qquad \text { and } \qquad {{\hat{L}}_p}^{F}={{\hat{L}}_p}^{T}+t({{\hat{U}}_p}^{T}-{{\hat{L}}_p}^{T}) \end{aligned}$$

Upper \({{\hat{U}}_p}^{U}\) and lower \({{\hat{L}}_p}^{U}\) bounds for uncertainty membership of objectives are

$$\begin{aligned} {{\hat{L}}_p}^{U}={{\hat{L}}_p}^{T} \qquad \text { and } \qquad {{\hat{U}}_p}^{U}={{\hat{L}}_p}^{T}+s({{\hat{U}}_p}^{T}-{{\hat{L}}_p}^{T}), \end{aligned}$$

and the upper and lower bounds for contradictory membership of objectives are

$$\begin{aligned} {{\hat{L}}_p}^{C}={{\hat{L}}_p}^{T}\wedge {{\hat{L}}_p}^{F} \qquad \text { and } \qquad {{\hat{U}}_p}^{C}={{\hat{L}}_p}^{T}\wedge {{\hat{L}}_p}^{F}+l({{\hat{U}}_p}^{T}\wedge {{\hat{U}}_p}^{F}-{{\hat{L}}_p}^{T}\wedge {{\hat{L}}_p}^{F}), \end{aligned}$$

where t, s, \(l \in (0,1)\).

Step 5: In this step, we will define truth, uncertainty, falsity, and contradictory membership functions as follows:

$$\begin{aligned} {T}_p(f_p(x))= & {} \left\{ \begin{array}{ll} 1 &{} \quad f_p(x)\le {{\hat{L}}_p}^{T} \\ \frac{{{\hat{U}}_p}^{T}-f_p(x)}{{{\hat{U}}_p}^{T}-{{\hat{L}}_p}^{T}} &{} \quad {{\hat{L}}_p}^{T}\le f_p(x)\le {{\hat{U}}_p}^{T} \\ 0 &{} \quad f_p(x)\ \ge {{\hat{U}}_p}^{T} \\ \end{array} \right. ,\\ {U}_p(f_p(x))= & {} \left\{ \begin{array}{ll} 1 &{}\quad f_p(x)\le {{\hat{L}}_p}^{U} \\ \frac{{{\hat{U}}_p}^{U}-f_p(x)}{{{\hat{U}}_p}^{U}-{{\hat{L}}_p}^{U}} &{} \quad {{\hat{L}}_p}^{U}\le f_p(x)\le {{\hat{U}}_p}^{U} \\ 0 &{}\quad f_p(x)\ \ge {{\hat{U}}_p}^{U} \\ \end{array} \right. ,\\ {F}_p(f_p(x))= & {} \left\{ \begin{array}{ll} 0 &{}\quad f_p(x)\le {{\hat{L}}_p}^{F} \\ \frac{f_p(x)-{{\hat{L}}_p}^{F}}{{{\hat{U}}_p}^{F}-{{\hat{L}}_p}^{F}} &{}\quad {{\hat{L}}_p}^{F}\le f_p(x)\le {{\hat{U}}_p}^{F} \\ 1 &{}\quad f_p(x)\ \ge {{\hat{U}}_p}^{F} \\ \end{array} \right. , \\ {C}_p(f_p(x))= & {} \left\{ \begin{array}{ll} 1 &{}\quad f_p(x)\le {{\hat{L}}_p}^{C} \\ \frac{{{\hat{U}}_p}^{C}-f_p(x)}{{{\hat{U}}_p}^{C}-{{\hat{L}}_p}^{C}} &{} \quad {{\hat{L}}_p}^{C}\le f_p(x)\le {{\hat{U}}_p}^{C} \\ 0 &{}\quad f_p(x)\ \ge {{\hat{U}}_p}^{C} \\ \end{array} \right. . \end{aligned}$$

Step 6: Now four-valued refined neutrosophic optimization method for multi-objective non-linear programming problem gives a corresponding non-linear problem as

Max \(\alpha -\beta +\gamma +\delta ,\) such that

$$\begin{aligned} {T}_p(f_p(x))\ge & {} \alpha ,\\ {U}_p(f_p(x))\ge & {} \gamma ,\\ {F}_p(f_p(x))\le & {} \beta ,\\ {C}_p(f_p(x))\ge & {} \delta , \end{aligned}$$

with

$$\begin{aligned} \alpha +\beta +\gamma +\delta \le 4, \end{aligned}$$

and

$$\begin{aligned} \alpha \ge \beta ,\quad \alpha \ge \gamma , \quad \alpha \ge \delta , \end{aligned}$$

where

$$\begin{aligned}&\alpha ,\; \beta ,\; \gamma , \; \delta \in [0,1].\\&g_j(x)\le b_j, \qquad x\ge 0, \quad j=1,2,\dots ,q. \end{aligned}$$

This corresponds to non-linear programming as:

$$\begin{aligned} \mathrm{Max} \qquad \alpha -\beta +\gamma +\delta , \end{aligned}$$

such that

$$\begin{aligned} f_p(x)+ ({{\hat{U}}_p}^{T}-{{\hat{L}}_p}^{T}).\alpha\le & {} {{\hat{U}}_p}^{T},\\ f_p(x)+ ({{\hat{U}}_p}^{U}-{{\hat{L}}_p}^{U}).\gamma\le & {} {{\hat{U}}_p}^{U},\\ f_p(x)- ({{\hat{U}}_p}^{F}-{{\hat{L}}_p}^{F})\ .\beta\le & {} {{\hat{L}}_p}^{F},\\ f_p(x)+ ({{\hat{U}}_p}^{C}-{{\hat{L}}_p}^{C}).\delta\le & {} {{\hat{U}}_p}^{C}, \end{aligned}$$

for \(p=1,2,\ldots ,k.\) We have

$$\begin{aligned} \alpha +\beta +\gamma +\delta \le 4 \end{aligned}$$

and

$$\begin{aligned} \alpha \ge \beta ,\quad \alpha \ge \gamma ,\quad \alpha \ge \delta , \end{aligned}$$

where

$$\begin{aligned}&\alpha ,\; \beta ,\; \gamma , \; \delta \in [0,1]\\&g_j(x)\le b_j, \qquad x\ge 0,j=1,2,\dots ,q. \end{aligned}$$

Numerical example

Consider the following optimization problem:

$$\begin{aligned} \hbox {Min }f_1(x_1,x_2)= & {} {x_1}^{-1}{x_2}^{-2},\\ \hbox {Min }f_2(x_1,x_2)= & {} 2{x_1}^{-2}{x_2}^{-3}, \end{aligned}$$

such that

$$\begin{aligned} x_1+x_2\le 1. \end{aligned}$$

Step 1: Solve the first objective function as a single objective non-linear programming problem subject to given constraints, then we get the value of \(x_1=0.33\), \(x_2=0.67\), \((f_1)_1=6.75\).

Step 2: By using these decision variables, we compute the other remaining objective functions whose values are \((f_2)_1=60.78\)

Step 3: Now, repeat step 1 and step 2 for other remaining objective functions. The ideal solution is given as

$$\begin{aligned} P=\begin{bmatrix} 6.75&60.78 \\ 6.94&57.87 \end{bmatrix}. \end{aligned}$$

Step 4: Find the lower bound and the upper bound corresponding to each objective \(f_p(x)\).

$$\begin{aligned} {{\hat{U}}_1}^{T}&={{\hat{U}}_1}^{F}=6.94,\\ {{\hat{U}}_1}^{C}&=6.75+t(0.19)=6.845,\\ {{\hat{L}}_1}^{T}&=6.75 {{\hat{L}}_1}^{F}=6.75+(0.19)r=6.807,\\ {{\hat{U}}_1}^{U}&=6.75+(.19)s=6.826,\\ {{\hat{L}}_1}^{U}&={{\hat{L}}_1}^{C}=6.75,\\ {{\hat{U}}_2}^{T}&={U_2}^{F}=60.78,\\ {{\hat{U}}_2}^{C}&=57.87+t(2.91)=59.325,\\ {{\hat{L}}_2}^{T}&=57.87,\\ {{\hat{L}}_2}^{F}&=57.87+(2.91)r=58.743,\\ {{\hat{U}}_2}^{U}&=57.87+(2.91)s=59.034,\\ {{\hat{L}}_2}^{U}&={{\hat{L}}_2}^{C}=57.87, \end{aligned}$$

where \(r,s,t=(0,1)\), taking \(r=0.3\), \(s=0.4\), and \(t=0.5.\)

Step 5: Now, we define the membership functions for T, F, U and C as:

$$\begin{aligned} {T}_1({x_1}^{-1}{x_2}^{-2})= & {} \left\{ \begin{array}{ll} 1 &{}\quad {x_1}^{-1}{x_2}^{-2}\le 6.75 \\ \frac{6.94-{x_1}^{-1}{x_2}^{-2}}{6.94-6.75} &{}\quad 6.75\le {x_1}^{-1}{x_2}^{-2}\le 6.94 \\ 0 &{}\quad {x_1}^{-1}{x_2}^{-2}\ \ge 6.94 \\ \end{array} \right. , \\ {T}_2(2{x_1}^{-2}{x_2}^{-3})= & {} \left\{ \begin{array}{ll} 1 &{}\quad 2{x_1}^{-2}{x_2}^{-3}\le 57.87 \\ \frac{60.78-2{x_1}^{-2}{x_2}^{-3}}{60.78-57.87} &{} \quad 57.87\le 2{x_1}^{-2}{x_2}^{-3}\le 60.78 \\ 0 &{}\quad {x_1}^{-1}{x_2}^{-2}\ \ge 60.78 \\ \end{array} \right. , \\ {U}_1({x_1}^{-1}{x_2}^{-2})= & {} \left\{ \begin{array}{ll} 1 &{}\quad {x_1}^{-1}{x_2}^{-2}\le 6.75 \\ \frac{6.826-{x_1}^{-1}{x_2}^{-2}}{6.826-6.75} &{}\quad 6.75\le {x_1}^{-1}{x_2}^{-2}\le 6.826 \\ 0 &{}\quad {x_1}^{-1}{x_2}^{-2}\ \ge 6.826 \\ \end{array} \right. , \\ {U}_2(2{x_1}^{-2}{x_2}^{-3})= & {} \left\{ \begin{array}{ll} 1 &{}\quad 2{x_1}^{-2}{x_2}^{-3}\le 57.87 \\ \frac{59.034-2{x_1}^{-2}{x_2}^{-3}}{59.034-57.87} &{}\quad 57.87\le 2{x_1}^{-2}{x_2}^{-3}\le 59.034 \\ 0 &{}\quad 2{x_1}^{-2}{x_2}^{-3}\ \ge 59.034 \\ \end{array} \right. , \\ {F}_1({x_1}^{-1}{x_2}^{-2})= & {} \left\{ \begin{array}{ll} 0 &{}\quad {x_1}^{-1}{x_2}^{-2}\le 6.807 \\ \frac{{x_1}^{-1}{x_2}^{-2}-6.807}{6.94-6.807} &{}\quad 6.807\le {x_1}^{-1}{x_2}^{-2}\le 6.94 \\ 1 &{}\quad {x_1}^{-1}{x_2}^{-2}\ \ge 6.94 \\ \end{array} \right. , \\ {F}_2(2{x_1}^{-2}{x_2}^{-3})= & {} \left\{ \begin{array}{ll} 0 &{}\quad 2{x_1}^{-2}{x_2}^{-3}\le 58.743 \\ \frac{2{x_1}^{-2}{x_2}^{-3}-58.743}{60.78-58.743} &{}\quad 58.743\le 2{x_1}^{-2}{x_2}^{-3}\le 60.78 \\ 1 &{}\quad 2{x_1}^{-2}{x_2}^{-3}\ \ge 60.78 \\ \end{array} \right. , \\ {C}_1({x_1}^{-1}{x_2}^{-2})= & {} \left\{ \begin{array}{ll} 1 &{}\quad {x_1}^{-1}{x_2}^{-2}\le 6.75 \\ \frac{6.75-{x_1}^{-1}{x_2}^{-2}}{6.845-6.75} &{}\quad 6.75\le {x_1}^{-1}{x_2}^{-2}\le 6.845 \\ 0 &{}\quad {x_1}^{-1}{x_2}^{-2}\ \ge 6.845 \\ \end{array} \right. , \\ {C}_2(2{x_1}^{-2}{x_2}^{-3})= & {} \left\{ \begin{array}{ll} 1 &{}\quad 2{x_1}^{-2}{x_2}^{-3}\le 57.87 \\ \frac{59.325-2{x_1}^{-2}{x_2}^{-3}}{59.325-57.87} &{}\quad 57.87\le 2{x_1}^{-2}{x_2}^{-3}\le 59.325 \\ 0 &{}\quad 2{x_1}^{-2}{x_2}^{-3}\ \ge 59.325 \\ \end{array} \right. . \end{aligned}$$

Step 6: Non-linear programming problem in FVRN is

$$\begin{aligned} \mathrm{Maximize} \qquad \alpha -\beta +\gamma +\delta \end{aligned}$$

such that

$$\begin{aligned} {x_1}^{-1}{x_2}^{-2}+(0.19)\alpha&\le 6.94,\\ 2{x_1}^{-2}{x_2}^{-3}+(2.91)\alpha&\le 60.78,\\ {x_1}^{-1}{x_2}^{-2}+(0.076)\gamma&\le 6.826,\\ 2{x_1}^{-2}{x_2}^{-3}+(1.164)\gamma&\le 59.034,\\ {x_1}^{-1}{x_2}^{-2}+(0.095)\delta&\le 6.845,\\ 2{x_1}^{-2}{x_2}^{-3}+(1.455)\delta&\le 59.325,\\ {x_1}^{-1}{x_2}^{-2}-(0.133)\beta&\le 6.807,\\ 2{x_1}^{-2}{x_2}^{-3}-(2.037)\beta&\le 58.743,\\ x_1+x_2&\le 1,\\ 0\le \alpha&\le 1,\\ 0\le \beta&\le 1,\\ 0\le \gamma&\le 1,\\ 0\le \delta&\le 1.\\ \end{aligned}$$

Comparison of the proposed optimal solution with those of intuitionistic fuzzy optimization and neutrosophic optimization techniques is given as below.

5 Application of four-valued refined neutrosophic set

In this section, we present application of FVRNS in riser design and car-side impact problem.

5.1 Riser design

A riser is a part of gating system in the mold and it is used for ensuring the complete filling of the mold cavity. It compensates shrinkage happening during the solidification. Generally, the porosity of the shrinkage occurs either in the cope or in a part of the casting under the surface. Casting is a procedure where the melted material is permitted to freeze and yields its final form. It depends upon the surface area and the rate of heat transfer. Solidification of the molten metal is built upon how quickly heat is transferred to mold wall. Solidification associates the solubility of metals back into the solid metal. There are three stages of solidification in a mold.

  1. 1.

    Liquid contraction.

  2. 2.

    Transformation from liquid to solid contraction.

  3. 3.

    Solid contractions.

Risers are used to compensate the contractions in the first stage and second stage. In the third stage, allowance is used to take care of contractions. Riser supplies redundant metal to compensate for the shrinkage of volume.

There are different types of risers. In this research, the cylindrical riser is considered because it has a large area with a broad inlet and molten metal fills the shrinkage cavity as quickly as possible. The metal solidifies in the mold earlier than the riser, so by using Chvorinov’s rule the volume and solidification time of the riser can be calculated,

$$\begin{aligned} S_t=k\bigg (\frac{v}{A_s}\bigg )^2, \end{aligned}$$

where “k” is solidification factor (seconds/meter square), V is the volume of the riser, \(A_s\) is the surface area of the riser, \(s_t=\) solidification time, volume of riser\(=\frac{\pi }{4}\cdot d^2 \cdot h\), surface area of riser \(=2.\frac{\pi }{4}\cdot d^2+(\pi \cdot d\cdot h).\)

The solidification time depends on the shape of the casting. In cylindrical casting:

$$\begin{aligned} s_t= \frac{\pi \cdot \, d^2\,\cdot h}{4}. \end{aligned}$$

Our objective is to design a smaller riser in such a way that solidification of the riser takes place after the solidification of the casting, that is,

$$\begin{aligned} t_r \ge t_c, \end{aligned}$$

which means the time taken by the riser to solidify will be greater than the time taken by the casting to solidify.

$$\begin{aligned} k_r\bigg (\frac{v_r}{A_s^{r}}\bigg )^2 \ge k_c\bigg (\frac{v_c}{A_s^{c}}\bigg )^2. \end{aligned}$$

It is assumed that the riser and casting are made up of the same metal. Then,

$$\begin{aligned} k_r= & {} k_c,\\ \frac{v_r}{A_s^{r}}= & {} \frac{v_c}{A_s^{c}}. \end{aligned}$$

If the casting has a specified volume and surface area, then

$$\begin{aligned}&\displaystyle \frac{v_c}{A_s^{c}}=m_c= \mathrm{constant} .\\&\displaystyle \frac{v_r}{A_s^{r}}\ge m_c.\\&\displaystyle \frac{dh}{4h+2d} \ge m_c. \end{aligned}$$

Take \(v_c=2.8.6=96\) cube inches, and \(A_s^{c}=2.(2.8+2.6+6.8)=152\) square inches, then

$$\begin{aligned} \frac{48}{19}d^{-1}+\frac{24}{19}h^{-1} \le 1. \end{aligned}$$

The multi-objective non-linear problem is

$$\begin{aligned} \hbox {Minimize }v_r(d,h)=\frac{\pi d^2h}{4}\,;\hbox { Minimize } s_t(d,h)=\frac{dh}{4h+2d}, \end{aligned}$$

such that

$$\begin{aligned} \frac{48}{19}d^{-1}+\frac{24}{19}h^{-1} \le 1. \end{aligned}$$

Here, the pay-off matrix is

$$\begin{aligned} P=\begin{bmatrix} 42.75642&0.631579 \\ 12.510209&0.6315786 \end{bmatrix}. \end{aligned}$$

5.2 Car-side impact

Jain and Deb (2013) discussed the car-side impact problem by defining evolutionary many-objective optimization algorithm using reference point-based non-dominated sorting approach. Car-side impact test aims to minimizing the weight of the car, the pubic force experienced by a passenger and the average velocity of the V-Pillar responsible for withstanding the impact load. These three objectives are conflicting; several constraints including body weight, structure and movement, pubic force and velocity, and design variables of car turn it into a complex engineering design optimization problem. The mathematical formulation is given as:

$$\begin{aligned} s_1(y)&=1.98+4.9y_1+6.67y_2+6.98y_3+4.01y_4+1.78x_5+0.00001y_6+2.73y_7,\\ s_2(y)&=F,\\ s_3(y)&=0.5(V_\mathrm{MBP}+V_\mathrm{FD}), \end{aligned}$$

such that

$$\begin{aligned} c_1(y)&=1.16-0.3717y_2y_4-0.0092928y_3\le 1,\\ c_2(y)&=0.261-0.0159y_1y_2-0.06486y_1-0.019y_2y_7+0.0144y_3y_5\\&\quad +0.0154464y_6\le 0.32,\\ c_3(y)&=0.214+0.00817y_5-0.045195y_1-0.0135168y_1+0.03099y_2y_6-0.018y_2y_7,\\&\quad +0.007176y_3+0.023232y_3-0.00364y_5y_6-0.018{y_2}^{2}\le 0.32,\\ c_4(y)&=0.74-0.61y_2-0.031296y_3-0.013872y_7+0.227{y_2}^2\le 0.32,\\ c_5(y)&=28.98+3.818y_3-4.2y_1y_2+1.27296y_6-2.68065y_7\le 32,\\ c_6(y)&=33.86+2.95y_3-5.057y_1y_2-3.795y_2-3.4431y_7+1.45728\le 32,\\ c_7(y)&=46.36-9.9x_2-4.4505y_1\le 32,\\ c_8(y)&=F=4.72-0.5y_4-0.19y_2y_3\le 4,\\ c_9(y)&=V_{MBP}=10.58-0.674y_1y_2-0.67275y_2\le 9.9,\\ c_{10}(y)&=V_{FD}=16.45-0.489y_3y_7-0.843y_5y_6\le 15.7\\&0.5\le y_1 \le 1.5, \qquad 0.45\le y_2 \le 1.35,\\&0.5 \le y_3\le 1.5, \qquad 0.5 \le y_4\le 1.5,\\&0.875 \le y_5\le 2.625, \qquad 0.4 \le y_6\le 1.2,\\&0.4\le y_7 \le 1.2, \end{aligned}$$

where \(s_1, s_2, s_3\) are objective functions; \(y_i\)s are decision variables and \(c_i\)s are constraints. Here, the pay-off matrix is

$$\begin{aligned} =\begin{bmatrix} 23.5857&4.0000&-3.1642 \\ 39.9449&3.5853&-2.9400 \\ 33.4058&3.8440&-3.6965 \end{bmatrix}. \end{aligned}$$

6 Conclusion

In this paper, first, we have defined a four-valued refined neutrosophic set, set-theoretic operators over this extenics of a neutrosophic set were studied. Secondly to find the optimal solution of multi-objective non-linear optimization model, we give a computational algorithm in a four-valued refined neutrosophic environment by defining truth (T), uncertain (U), contradiction (C) and falsity (F) grades of memberships which are independent of each other. Comparison of the results obtained from the proposed optimization method for the riser design and car-side impact problems proves the superiority of four-valued optimization method over intuitionistic fuzzy optimization as well as single-valued neutrosophic optimization. Results of Tables 1, 2, 3 and 4 also prove the authenticity of the four-valued refined neutrosophic optimization technique. Thus, the proposed method is reliable, efficient and a more generalized optimization technique for solving the non-linear multi-objective optimization problem in the less certain environment.

Table 1 Comparison of optimal solutions
Full size table
Table 2 Percentage gap for different fuzzy optimization techniques
Full size table
Table 3 Comparison of optimal solutions
Full size table
Table 4 Comparison of optimal solutions
Full size table
Fig. 1
figure 1

Comparison of the proposed methodology with percentage gap

Full size image
Fig. 2
figure 2

Comparison of proposed methodology with percentage gap

Full size image

Performance evaluation of the proposed methodology

The riser design problem was already solved with two different fuzzy optimization techniques: intuitionistic fuzzy optimization and neutrosophic fuzzy optimization. To analyze the performance of the proposed methodology, we need to find the percentage gap of all the objective functions by using the equation that is given below:

$$\begin{aligned} \text {Percentage gap}=\frac{\text { Acheived Value }- \text { Best Value }}{\text { Acheived Value }}\times 100. \end{aligned}$$

By Figs. 1 and 2, we can analyze that the percentage gap of the proposed algorithm is less than that of the existing algorithm.

The car-side impact problem was solved as crisp optimization problem by using multi-objective genetic algorithm and multi-objective goal attainment. The results in Table 4 show that the proposed methodology is more efficient to attain the desired goals with conflicting objectives.

The work presented here opens the gates for future research not only in optimization, but also to establish improved methods in sampling survey analysis, cost function estimation analysis, and engineering.