A New Approach to Solve Multi Objective Linear Programming Problem Under Neutrosophic Environment

Abstract

In the present era, the idea of nonlinearity plays a crucial and fundamental role in an intuitionistic fuzzy world. The goal of this paper is to develop some novel and valuable concepts for the ability to effectively convey challenging and ambiguous information in real life issues. In order to achieve this goal, this work investigated the interval valued pentagonal intuitionistic fuzzy multi-objective linear programming problem under neutrosophic uncertainty. This study provides solutions to such uncertainty and assists in the relative decision-making processes. The major objective of this paper is to develop some novel and useful concepts of nonlinear interval valued pentagonal intuitionistic fuzzy numbers and their classification in different situations. Additionally, the new de-intuitification (Ranking) method is formulated in decision-making by reducing complexions and addresses the graphical illustration. The proposed technique based on neutrosophic fuzzy approaches provides the potential value to decision makers of optimization problems under three distinct membership degrees, such as truth, indeterminacy, and falsity membership degrees. Therefore, this paper implemented methodologies with the help of numerical examples and addressed the effectiveness of several membership functions as linear, parabolic, and hyperbolic types of membership functions. A comparative study of existing approaches has been done to show the efficiency of the proposed approach. Finally, based on suggested study, conclusions and future research directions are discussed.

Introduction

In the real world, tackling optimization problems requires the use of several prominent and important optimization techniques. There are various optimization techniques that can be used to handle various real-world mathematical model according to circumstances and difficulties. As a result, the mathematical models include one or more specified objective functions and a set of clearly defined constraints that the problems must be optimized under (maximized or minimized). In recent years, researchers from a variety of disciplines, including science and technology, financial mathematics, medical experimentation, inventory control, transportation problem (TP), assignment problems, manufacturing system, supplier selection, supply chain management, etc., have integrated the assumption of vagueness in their pertinent and significant fields. When dealing with many objectives, it is difficult to find a single solution that effectively optimizes all of objectives. However, in practice, there is frequently ambiguity or uncertainty in real life daily problem. A tremendous amount of research has been presented in the past era on the context of multi objective optimization problem (MOOP). In MOOP, the challenging work as a decision maker is to find suitable compromised solution set from a list of potential Pareto-optimal solutions.

Literature Review

In 1965, the idea of fuzzy sets (FS) was created by Professor Zadeh [50] and is an essential tool for displaying ambiguity, has been used in the engineering and management sectors [17, 20]. It is the most significant and beneficial area of study for decision-making. Later, Zimmermann [4] proposed a fuzzy programming approach (FPA) for several objective optimization problems. A few years later, in 1972, Chang and Zadeh [14] proposed the idea of fuzzy numbers. Since then, numerous studies in this field of study have received recognition [12, 13, 25], along with the numerous advancements and upgrades of fuzzy logic postulates. Furthermore, it is noted that the FS does not address the circumstances of doubt and hesitation, both of which are real-world issues. FS is characterized only by a degree of acceptance between 0 and 1, but not the degree of rejection. As a result, Professor Atanassov [2] proposed the intuitionistic fuzzy set (IFS) in 1986, which is a generalization and extension of the FS. In IFS, the degree of acceptance and the degree of rejection are both incorporated, and their sum is less than one. Angelov [1] presented the intuitionistic fuzzy programming technique (IFPT), which is based on the IFS, to resolve the MOPP. In this approach, the membership and non-membership functions of each objective function determine its marginal assessment. Several researchers [22, 32, 33, 35, 36, 40, 41] have used an intuitionistic fuzzy set to address issues with collective decision-making. Singh et al. [45] introduced the modelling and optimization methodology for MOPP in an intuitionistic fuzzy environment with both pessimistic and optimistic perspectives. After this, Cuong [18] characterized a new idea by putting an additional grade which is a grade of neutral membership, and named it to picture FS (PFS). It triply contains positive membership, neutral membership, and negative membership. Jan et al. [28,29,30] extended this into complex picture fuzzy soft information in different fields like adversarial networks, human–computer interaction and analysis of networks and digital systems respectively. In 1995, Smrandache [46] developed a brand-new idea known as the neutrosophic set (NS for short). The characteristics of NS are the degree of truth membership, indeterminacy membership, and falsity membership. Chakraborty et al. [9] discussed different forms of triangular neutrosophic numbers and its de-neutrosophication procedure techniques. A computational approach to solve a transportation problem with pentagonal neutrosophic numbers was proposed in [10]. Chakraborty et al. [11] suggested a de-neutrosophication technique for pentagonal neutrosophic number and applied its application to find a minimal spanning tree. Recently, a multi-objective non-linear riser design problem based on neutrosophic optimization technique was proposed by Das et al. [19]. Whereas Sarkar et al. [42] demonstrated a comparative study based on neutrosophic optimization in the field of structural design.

Interval Valued Intuitionistic Fuzzy Number (IVIFN)

In 1989, Interval-valued intuitionistic fuzzy sets (IVIFSs) were introduced by Atanassov et al. [3] for the first time in front of the researcher community. This new concept includes interval-valued fuzzy sets and intuitionistic fuzzy sets. They define their concept is characterized by a membership function and a non-membership function that uses interval values rather than real number. IVIFS is more powerful in dealing with vagueness and uncertainty than IFS. The activities of IVIFSs and a few other intriguing IVIFSs characteristics have been considered in the research filed like MADM [48], MCDM [16, 24], transportation [5] etc. Following this, Zhang et al. [51] demonstrated the idea of IVIFN and thoroughly analyzed its relevance as an annex of IFS. Later, researchers extended their creativity to handle the different complicated characteristics of many real-world problems with the different shapes of IFNs like triangles [31], trapezoids [38], and pentagons [43] etc. Dong et al. [23] discussed three kinds of interval-valued intuitionistic linguistic arithmetic average operators and their application in their work. Maoying et al. [37] also used interval-valued intuitionistic trapezoidal fuzzy numbers as the foundation to tackle multiple attribute decision-making problems. Also, Bromi et al. [6] combine IVIFN and the hesitant fuzzy concept in their work because hesitant fuzzy set can be considered as a useful tool allowing several possible degrees of membership of an element to a set.

Motivation for that Research

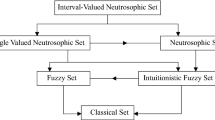
According to our review of the literature, researchers mostly concentrated on linear IVIFNs, neglecting to consider non-linearity in the context of IVIFNs. But there are numerous situations where we need non-linear membership functions, particularly when the data contains any geometric concavity or convexity. In order to effectively capture and manage the underlying uncertainties, we need to take into consideration nonlinear IVIFNs (NLIVPIFN). A generalized NLIVPIFN has been proposed in this research study to provide for greater decision-maker flexibility. We presented a NLIVPIFN with symmetric and as well as asymmetric representations, and it was effectively applied to a MOLPP where objective solutions were subjected to rework. From this perspective, we attempt to define interval valued pentagonal intuitionistic fuzzy numbers (IVPIFNs) which may be a superior option for decision-makers. The Flow Fig. 1 illustrates the specifics of taking an uncertain parameter into consideration.

Fig. 1

Flowchart for the membership function of an uncertain parameter

Contribution of Our Work

Many scholars are working continuously to find the best solution to multi objective linear programming problems (MOLPPs). A large amount of the literature is composed of fuzzy-based optimization approaches that use the generalized concept of a FS to solve MOLPPs. Many researchers optimize the MOLPPs using an intuitionistic fuzzy-based optimization technique. Although there are some articles that define and apply IVPIFSs and numbers to diverse fields. The study focused on IVPIFNs, assuming different $\alpha$ and $\beta$ cut values from them. After that, accuracy is used to convert the IVIFMOLPP into equivalent crisp MOLPP and can be solve by using proposed neutrosophic optimization approach. However, following are the few major aspects that guarantee a significant contribution to the field of multi objective optimization techniques.

• IVPIFN formation in the pentagonal shape is made simpler.

• There are several types of IVPIFN that have been developed, including linear pentagonal intuitionistic fuzzy number with symmetric (LPIFNAS), linear pentagonal intuitionistic fuzzy number with asymmetric (LPIFNAS), nonlinear pentagonal intuitionistic fuzzy number with symmetric (NLPIFNS), and nonlinear pentagonal intuitionistic fuzzy number with asymmetric (NLPIFNAS).

• The IVPIFNs in their parametric form.

• Arithmetic operations on IVPIFNs.

• Defuzzification of linear or non-linear symmetric and asymmetry IVPIFNs were done.

• The current approaches to resolving MOLPPs [44, 45] considered both the membership and non-membership degrees of every objective function. When making decisions, they ignore the degree of ambiguity. We were able to successfully deal with the concept of neutrality, leading to the simultaneous suggestion of degrees of membership and non-membership as well as indeterminacy.

• We have developed MOLPP under neutrosophic environment (NEv). Using NS optimization approach, a computational algorithm has been developed to solve MOLPPs

• The suggested neutrosophic set under different membership functions like linear, parabolic, and hyperbolic type were discussed and solved MOLPPs under NEv.

Structure of the Article

The rest of the paper has been summarized as follows: In Section “Mathematical Preliminaries”, some basic preliminary concepts are provided for IFS, neutrosophic numbers, PIFNs, IVPIFNs. Section “Arithmetic Operations of IVPIFN” represent some operations of IVPIFNs. Section “De-intuitification of Non-linear Interval Valued Pentagonal Intuitionistic Fuzzy Number with Symmetry (NLIVPIFNS)” is the most significant section, here the formulation of the IVIFMOLPP is discussed. Section “Proposed Neutrosophic Fuzzy Approach” presents the suggested neutrosophic optimization strategy and solution methodology to solve MOLPP. An illustrative example is examined in Section “Numerical Illustrations”, which reflects the applicability and validity of the proposed approach efficiently. Finally, Section “Conclusions” and Section “Future Research Scope”, presents concluding remarks and future research directions.

Mathematical Preliminaries

Definition 2.1

Chakraborty et al. [10] Intuitionistic fuzzy set (IFS): Let X be the fixed set. An IFS $\tilde{A}^{i}$ in $X$ is an object with the form $\tilde{A}^{i} = \left\{ {\left( {x,\mu_{{\tilde{A}^{i} }} (x),\nu_{{\tilde{A}^{i} }} (x)} \right):x \in X} \right\}$ where $\mu_{{\tilde{A}^{i} }} (x):X \to [0,1]$ and $\nu_{{\tilde{A}^{i} }} (x):X \to [0,1][0,1]$ specify the degree of membership and degree of non-membership respectively, of the element x ∈ X to the set $\tilde{A}^{i}$, which is a subset of $X$, for every element of x ∈ X, $0 \le \mu_{{\tilde{A}^{i} }} (x) + \nu_{{\tilde{A}^{i} }} (x) \le 1$.

Definition 2.2

Smarandache [47] (Neutrosophic Set (NS)) Assume there is a universe discourse $X$ in which $x \in X$. A NS $\tilde{A}^{n}$ in $X$ is characterized by three membership functions: truth $\mu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$, indeterminacy $\nu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$ and a falsity $\lambda_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$ and is denoted by the following form:

$$ \tilde{A}^{n} = \{ \left( {x,\mu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right),\nu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right),\lambda_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)} \right):x \in X\} $$

where the subsets $\mu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$,$\nu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$ and $\lambda_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$ are truth, indeterminacy and falsity membership function lies in ${\rm E} = ]^{ - } 0,1^{ + } [$,also given as, $\mu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right):X \to {\rm E},\nu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right):X \to {\rm E},\;and \, \lambda_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right):X \to {\rm E}$.There is no restriction on the sum of $\mu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$,$\nu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$ and $\lambda_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$,so we have, ${0}^{ - } \le \sup \mu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right) + \sup \nu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right) + \sup \lambda_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right) \le 3^{ + }$

Definition 2.3

Smarandache [47] (Single valued neutrosophic set) Let $X$ be a universe set. A single valued neutrosophic set (SVNS) $\tilde{A}^{n}$ over $X$ is given by $\tilde{A}^{n} = \{ \left( {x,\mu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right),\nu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right),\lambda_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)} \right):x \in X\}$.

where $\mu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$,$\nu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$ and $\lambda_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right)$ and ${0} \le \mu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right) + \nu_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right) + \lambda_{{{\tilde{\text{A}}}^{{\text{n}}} }} \left( x \right) \le {3}$ for every $x \in X$.

Definition 2.4

Guijun and Xiaoping [25] Interval-Valued Intuitionistic Fuzzy set (IVIFS): Let $E[0,1]$ be the set of all closed subintervals of the interval $[0,1]$ and $X$ be a given set. An IVIFS $\tilde{A}^{I}$ in $X$ is defined by $\tilde{A}^{I} = \left\{ {\left( {x,\mu_{{\tilde{A}^{I} }} (x),\nu_{{\tilde{A}^{I} }} (x)} \right):x \in X} \right\}$ where $\mu_{{\tilde{A}^{I} }} (x_{i} ) = \left[ {\mu_{{\tilde{A}^{L} }} (x_{i} ),\mu_{{\tilde{A}^{U} }} (x_{i} )} \right]:X \to E[0,1]$ and $\nu_{{\tilde{A}^{I} }} (x_{i} ) = \left[ {\nu_{{\tilde{A}^{L} }} (x_{i} ),\nu_{{\tilde{A}^{U} }} (x_{i} )} \right]:X \to E[0,1]$ with the condition $0 \le \sup \mu_{{\tilde{A}^{I} }} (x_{i} ) + \sup \nu_{{\tilde{A}^{I} }} (x_{i} ) \le 1$ for any $x \in X$.

Definition 2.5

Shapique [43] Pentagonal intuitionistic fuzzy number (PIFN): A LPIFNAS $\tilde{A}_{LAS}^{I} = \left\{ {\left( {a_{1} ,a_{2} ,a_{3} ,a_{4} ,a_{5} ;\omega ,r_{1} ,r_{2} } \right),\left( {b_{1} ,b_{2} ,b_{3} ,b_{4} ,b_{5} ;\sigma ,s_{1} ,s_{2} } \right)} \right\}$ is defined as an intuitionistic fuzzy set in R with the membership and non-membership function (Shown in Fig. 2) as follows:

Fig. 2

Diagram of LPIFNAS

$$ \begin{gathered} \mu _{{\tilde{A}_{{LAS}}^{I} }} (x) = \left\{ {\begin{array}{*{20}c} {r_{1} \frac{{x - a_{1} }}{{a_{2} - a_{1} }}} &\quad {\it if}\,\, {a_{1} \le x \le a_{2} } \\ {\omega - \left( {\omega - r_{1} } \right)\frac{{x - a_{2} }}{{c - a_{2} }}} &\quad {\it if}\,\, {a_{2} \le x \le c} \\ \omega &\quad {\it if}\,\, {x = c} \\ {\omega - \left( {\omega - r_{2} } \right)\frac{{a_{4} - x}}{{a_{4} - c}}} &\quad {\it if}\,\, {c \le x \le a_{4} } \\ {r_{2} \frac{{a_{5} - x}}{{a_{5} - a_{4} }}} &\quad {\it if}\,\, {a_{4} \le x \le a_{5} } \\ 0 &\quad {\it if}\,\, {x > a_{5} } \\ \end{array} } \right. \hfill \\ \nu _{{\tilde{A}_{{LAS}}^{I} }} (x) = \left\{ {\begin{array}{*{20}c} {\sigma - \left( {\sigma - s_{1} } \right)\frac{{x - b_{1} }}{{b_{2} - b_{1} }}} &\quad {\it if}\,\, {b_{1} \le x \le b_{2} } \\ {s_{1} \frac{{c - x}}{{c - b_{2} }}} &\quad {\it if}\,\, {b_{2} \le x \le c} \\ \sigma &\quad {\it if}\,\, {x = c} \\ {s_{2} \frac{{b_{4} - x}}{{b_{4} - c}}} &\quad {\it if}\,\, {c \le x \le b_{4} } \\ {\sigma - \left( {\sigma - s_{2} } \right)\frac{{b_{5} - x}}{{b_{5} - b_{4} }}} &\quad {\it if}\,\, {b_{4} \le x \le b_{5} } \\ 1 &\quad {\it if}\,\, {x > b_{5} } \\ \end{array} } \right. \hfill \\ \end{gathered} $$

Definition 2.6

Chakraborty et al. [11] $\left( {\alpha ,\beta } \right)$-cut or parametric form of LPIFNAS: $\left( {\alpha ,\beta } \right)$-cut or parametric form of LPIFNAS is represented as follows

$$ \begin{aligned} \left( {\tilde{A}_{LAS}^{I} } \right)_{\alpha ,\beta }&= \left\{ {x \in X:\mu_{{\tilde{A}_{LAS}^{I} }} (x) \ge \alpha ,\nu_{{\tilde{A}_{LAS}^{I} }} (x) \le \beta } \right\} \\& = \left[ \left\{ {\left( {A_{1L} (\alpha ),A_{2L} (\alpha )}\right),\left( {A_{2R} (\alpha ),A_{1R} (\alpha )} \right)}\right\};\right.\\& \left. \left\{ \left( {A_{1L} (\beta ),A_{2L} (\beta )}\right),\left( {A_{2R} (\beta ),A_{1R} (\beta )} \right) \right\}\right]\end{aligned} $$

where

$$ \begin{aligned} & A_{1L} (\alpha ) = a_{1} + \frac{\alpha }{{r_{1} }}\left( {a_{2} - a_{1} } \right)\; \text{for}\;\alpha \in \left[ {0,r_{1} } \right];\\ & A_{1L} (\beta ) = b_{1} + \frac{\sigma - \beta }{{\sigma - s_{1} }}\left( {b_{2} - b_{1} } \right)\;\text{for}\;\beta \in \left[ {s_{1} ,1} \right] \\ & A_{2L} (\alpha ) = a_{2} + \frac{\omega - \alpha }{{\omega - r_{1} }}\left( {c - a_{2} } \right)\;\text{for}\;\alpha \in \left[ {r_{1} ,\omega } \right];\\ & A_{2L} (\beta ) = b_{2} + \frac{\beta }{{s_{1} }}\left( {c - b_{2} } \right)\;\text{for}\;\beta \in \left[ {\sigma ,s_{1} } \right] \\ & A_{2R} (\alpha ) = a_{4} - \frac{\omega - \alpha }{{\omega - r_{2} }}\left( {a_{4} - c} \right)\;\text{for}\;\alpha \in \left[ {r_{2} ,\omega } \right];\\ & A_{2R} (\beta ) = b_{4} - \frac{\beta }{{s_{2} }}\left( {b_{4} - c} \right)\;\;\text{for}\;\beta \in \left[ {\sigma ,s_{2} } \right] \\ & A_{1R} (\alpha ) = a_{5} - \frac{\alpha }{{r_{2} }}\left( {a_{5} - a_{4} } \right)\;\text{for}\;\alpha \in \left[ {0,r_{2} } \right];\\ & A_{1R} (\beta ) = b_{5} - \frac{\sigma - \beta }{{\sigma - s_{2} }}\left( {b_{5} - b_{4} } \right)\;\text{for}\;\beta \in \left[ {s_{2} ,1} \right] \end{aligned} $$

Note that $A_{1L} (\alpha ),A_{2L} (\alpha ),A_{2R} (\beta ),A_{1R} (\beta )$ are increasing functions and $A_{2R} (\alpha ),A_{1R} (\alpha ),A_{1L} (\beta ),A_{2L} (\beta )$ are decreasing functions.

Note 01

If $r_{1} = r_{2}$ and $s_{1} = s_{2}$ then the LPIFNAS becomes linear pentagonal intuitionistic fuzzy number with partial symmetry (LPIFNPS) (Shown in Fig. 3).

Fig. 3

Diagram of LPIFNPS

Note 02

If $r_{1} = r_{2} = s_{1} = s_{2} = r$ then the LPIFNAS becomes linear pentagonal intuitionistic fuzzy number with symmetry (LPIFNS) (Shown in Fig. 4).

Fig. 4

Diagram of LPIFNS

Definition 2.7

Deng et al. [21] Nonlinear Pentagonal Intuitionistic fuzzy number with asymmetry: A NLPIFNAS can be written as, $\tilde{A}_{NLAS}^{I} = \left\{ {\left( {a_{1} ,a_{2} ,c,a_{4} ,a_{5} ;\omega ,r_{1} ,r_{2} } \right)_{{\left( {g_{1} ,g_{2} ,h_{1} ,h_{2} } \right)}} ,\left( {b_{1} ,b_{2} ,c,b_{4} ,b_{5} ;\sigma ,s_{1} ,s_{2} } \right)_{{\left( {g_{1} ,g_{2} ,h_{1} ,h_{2} } \right)}} } \right\}$ where membership and non-membership function (Shown in Fig. 5) can be explained as,

Fig. 5

Diagram of NLPIFNAS

$$ \begin{gathered} \mu _{{\tilde{A}_{{NLAS}}^{I} }} (x) = \left\{ {\begin{array}{*{20}c} {r_{1} \left( {\frac{{x - a_{1} }}{{a_{2} - a_{1} }}} \right)^{{g_{1} }} } &\quad {\it if}\,\, {a_{1} \le x \le a_{2} } \\ {\omega - \left( {\omega - r_{1} } \right)\left( {\frac{{x - a_{2} }}{{c - a_{2} }}} \right)^{{g_{2} }} } &\quad {\it if}\,\, {a_{2} \le x \le c} \\ \omega &\; {\it if}\,\, {x = c} \\ {\omega - \left( {\omega - r_{2} } \right)\left( {\frac{{a_{4} - x}}{{a_{4} - c}}} \right)^{{h_{1} }} } &\quad {\it if}\,\, {c \le x \le a_{4} } \\ {r_{2} \left( {\frac{{a_{5} - x}}{{a_{5} - a_{4} }}} \right)^{{h_{2} }} } &\quad {\it if}\,\, {a_{4} \le x \le a_{5} } \\ 0 &\; {\it if}\,\, {x > a_{5} } \\ \end{array} } \right. \hfill \\ \nu _{{\tilde{A}_{{NLAS}}^{I} }} (x) = \left\{ {\begin{array}{*{20}c} {\sigma - \left( {\sigma - s_{1} } \right)\left( {\frac{{x - b_{1} }}{{b_{2} - b_{1} }}} \right)^{{g_{1} }} } &\quad {\it if}\,\, {b_{1} \le x \le b_{2} } \\ {s_{1} \left( {\frac{{c - x}}{{c - b_{2} }}} \right)^{{g_{2} }} } &\quad {\it if}\,\, {b_{2} \le x \le c} \\ \sigma &\; {\it if}\,\, {x = c} \\ {s_{2} \left( {\frac{{b_{4} - x}}{{b_{4} - c}}} \right)^{{h_{1} }} } &\quad {\it if}\,\, {c \le x \le b_{4} } \\ {\sigma - \left( {\sigma - s_{2} } \right)\left( {\frac{{b_{5} - x}}{{b_{5} - b_{4} }}} \right)^{{h_{2} }} } &\quad {\it if}\,\, {b_{4} \le x \le b_{5} } \\ 1 &\; {\it if}\,\, {x > b_{5} } \\ \end{array} } \right. \hfill \\ \end{gathered} $$

Definition 2.8

Chakraborty et al. [11] $\left( {\alpha ,\beta } \right)$-cut or parametric form of NLPIFNAS: $\left( {\alpha ,\beta } \right)$-cut or parametric form of NLPIFNAS is represented as follows

$$\begin{aligned}\left( {\tilde{A}_{NLAS}^{I} } \right)_{\alpha ,\beta } & = \left\{x \in X:\mu_{{\tilde{A}_{LAS}^{I} }} (x) \ge \alpha ,\nu_{{\tilde{A}_{LAS}^{I} }} (x) \le \beta \right\} \\& = \left[\left\{ \left( {A_{1L} (\alpha ),A_{2L} (\alpha )} \right),\left({A_{2R} (\alpha ),A_{1R} (\alpha )} \right) \right\};\right.\\&\left. \left\{ \left( {A_{1L} (\beta ),A_{2L} (\beta )}\right),\left( {A_{2R} (\beta ),A_{1R} (\beta )} \right) \right\}\right]\end{aligned} $$

where

$$ \begin{aligned} & A_{1L} (\alpha ) = a_{1} + \left( {\frac{\alpha }{{r_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{1} }}} \right. \kern-0pt} {g_{1} }}}} \left( {a_{2} - a_{1} } \right)\;\text{for}\;\alpha \in \left[ {0,r_{1} } \right]\\ & A_{1L} (\beta ) = b_{1} + \left( {\frac{\sigma - \beta }{{\sigma - s_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{1} }}} \right. \kern-0pt} {g_{1} }}}} \left( {b_{2} - b_{1} } \right)\;\text{for}\;\beta \in \left[ {s_{1} ,1} \right] \\ & A_{2L} (\alpha ) = a_{2} + \left( {\frac{\omega - \alpha }{{\omega - r_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{2} }}} \right. \kern-0pt} {g_{2} }}}} \left( {c - a_{2} } \right)\;\text{for}\;\alpha \in \left[ {r_{1} ,\omega } \right]\\ & A_{2L} (\beta ) = b_{2} + \left( {\frac{\beta }{{s_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{2} }}} \right. \kern-0pt} {g_{2} }}}} \left( {c - b_{2} } \right)\;\text{for}\;\beta \in \left[ {\sigma ,s_{1} } \right] \\ & A_{2R} (\alpha ) = a_{4} - \left( {\frac{\omega - \alpha }{{\omega - r_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{1} }}} \right. \kern-0pt} {h_{1} }}}} \left( {a_{4} - c} \right)\;\text{for}\;\alpha \in \left[ {r_{2} ,\omega } \right]\\ & A_{2R} (\beta ) = b_{4} - \left( {\frac{\beta }{{s_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{1} }}} \right. \kern-0pt} {h_{1} }}}} \left( {b_{4} - c} \right)\;\;\text{for}\;\beta \in \left[ {\sigma ,s_{2} } \right] \\ & A_{1R} (\alpha ) = a_{5} - \left( {\frac{\alpha }{{r_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{2} }}} \right. \kern-0pt} {h_{2} }}}} \left( {a_{5} - a_{4} } \right)\;\text{for}\;\alpha \in \left[ {0,r_{2} } \right]\\ & A_{1R} (\beta ) = b_{5} - \left( {\frac{\sigma - \beta }{{\sigma - s_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{2} }}} \right. \kern-0pt} {h_{2} }}}} \left( {b_{5} - b_{4} } \right)\;\text{for}\;\beta \in \left[ {s_{2} ,1} \right] \end{aligned} $$

Note that $A_{1L} (\alpha ),A_{2L} (\alpha ),A_{2R} (\beta ),A_{1R} (\beta )$ are increasing functions and $A_{2R} (\alpha ),A_{1R} (\alpha ),A_{1L} (\beta ),A_{2L} (\beta )$ are decreasing functions.

Note 03

If $g_{1} = g_{2} = h_{1} = h_{2} = 1$, as a result of the NLPIFNAS becomes LPIFNAS (see in Fig. 2).

Note 04

If $r_{1} = r_{2}$ and $s_{1} = s_{2}$ then the NLPIFNAS is converted into nonlinear pentagonal intuitionistic fuzzy number with partial symmetry (NLPIFNPS) (See in Fig. 6).

Fig. 6

Diagram of NLPIFNPS

Note 05

If $g_{1} = g_{2} = h_{1} = h_{2} = 1$, $r_{1} = r_{2}$ and $s_{1} = s_{2}$ then the NLPIFNAS is converted into LPIFNPS (see in Fig. 3).

Note 06

If $g_{1} = g_{2} = h_{1} = h_{2} = 1$, $r_{1} = r_{2} = s_{1} = s_{2} = r$ then the NLPIFNAS is converted into LPIFNS (see in Fig. 4).

The geometrical representation of different form of PIFN is shown as follows:

Definition 2.9

Non Linear Interval-Valued Pentagonal Intuitionistic Fuzzy Number with Asymmetry (NLIVPIFNAS) (see in Fig. 7): A nonlinear interval valued intuitionistic fuzzy number is written as

Fig. 7

Diagram of NLIVPIFNAS

$$ \tilde{A}_{NLIVAS} = \left\{ \begin{gathered} \left( {\left( {a_{1} ,a_{2} ,c,a_{4} ,a_{5} } \right),\left( {a^{\prime}_{1} ,a^{\prime}_{2} ,c,a^{\prime}_{4} ,a^{\prime}_{5} } \right);\omega ,\omega^{\prime},r_{1} ,r_{2} ,r^{\prime}_{1} ,r^{\prime}_{2} } \right)_{{\left( {g_{1} ,g_{2} ,h_{1} ,h_{2} } \right)}} , \hfill \\ \left( {\left( {b_{1} ,b_{2} ,c,b_{4} ,b_{5} } \right),\left( {b^{\prime}_{1} ,b^{\prime}_{2} ,c,b^{\prime}_{4} ,b^{\prime}_{5} } \right);\sigma ,\sigma^{\prime},s_{1} ,s_{2} ,s^{\prime}_{1} ,s^{\prime}_{2} } \right)_{{\left( {g_{1} ,g_{2} ,h_{1} ,h_{2} } \right)}} \hfill \\ \end{gathered} \right\} $$

where $0 < \omega \le \omega^{\prime} \le 1,0 < \sigma \le \sigma^{\prime} \le 1,0 < \omega + \sigma^{\prime} \le 1,0 < \omega^{\prime} + \sigma \le 1$.

The upper and lower membership function is defined by

$$ \begin{gathered} \mu _{{\tilde{A}_{{NLIVAS}}^{U} }} (x) = \left\{ {\begin{array}{*{20}c} {r_{1} \left( {\frac{{x - a_{1} }}{{a_{2} - a_{1} }}} \right)^{{g_{1} }} } &\quad {\it if}\,\, {a_{1} \le x \le a_{2} } \\ {\omega - \left( {\omega - r_{1} } \right)\left( {\frac{{x - a_{2} }}{{c - a_{2} }}} \right)^{{g_{2} }} } &\quad {\it if}\,\, {a_{2} \le x \le c} \\ \omega &\quad {\it if}\,\, {x = c} \\ {\omega - \left( {\omega - r_{2} } \right)\left( {\frac{{a_{4} - x}}{{a_{4} - c}}} \right)^{{h_{1} }} } &\quad {\it if}\,\, {c \le x \le a_{4} } \\ {r_{2} \left( {\frac{{a_{5} - x}}{{a_{5} - a_{4} }}} \right)^{{h_{2} }} } &\quad {\it if}\,\, {a_{4} \le x \le a_{5} } \\ 0 &\quad {\it if}\,\, {x > a_{5} } \\ \end{array} } \right. \hfill \\ \mu _{{\tilde{A}_{{NLIVAS}}^{L} }} (x) = \left\{ {\begin{array}{*{20}c} {r^{\prime}_{1} \left( {\frac{{x - a^{\prime}_{1} }}{{a^{\prime}_{2} - a^{\prime}_{1} }}} \right)^{{g_{1} }} } &\quad {\it if}\,\, {a^{\prime}_{1} \le x \le a^{\prime}_{2} } \\ {\omega ^{\prime} - \left( {\omega ^{\prime} - r^{\prime}_{1} } \right)\left( {\frac{{x - a^{\prime}_{2} }}{{c - a^{\prime}_{2} }}} \right)^{{g_{2} }} } &\quad {\it if}\,\, {a^{\prime}_{2} \le x \le c} \\ {\omega ^{\prime}} &\quad {\it if}\,\, {x = c} \\ {\omega ^{\prime} - \left( {\omega ^{\prime} - r^{\prime}_{2} } \right)\left( {\frac{{a^{\prime}_{4} - x}}{{a^{\prime}_{4} - c}}} \right)^{{h_{1} }} } &\quad {\it if}\,\, {c \le x \le a^{\prime}_{4} } \\ {r_{2} \left( {\frac{{a^{\prime}_{5} - x}}{{a^{\prime}_{5} - a^{\prime}_{4} }}} \right)^{{h_{2} }} } &\quad {\it if}\,\, {a^{\prime}_{4} \le x \le a^{\prime}_{5} } \\ 0 &\quad {\it if}\,\, {x > a^{\prime}_{5} } \\ \end{array} } \right. \hfill \\ \end{gathered} $$

Upper and lower for non-membership function are defined as

$$ \begin{gathered} \nu _{{\tilde{A}_{{NLIVAS}}^{U} }} (x) = \left\{ {\begin{array}{*{20}c} {\sigma - \left( {\sigma - s_{1} } \right)\left( {\frac{{x - b_{1} }}{{b_{2} - b_{1} }}} \right)^{{g_{1} }} } &\quad {\it if}\,\, {b_{1} \le x \le b_{2} } \\ {s_{1} \left( {\frac{{c - x}}{{c - b_{2} }}} \right)^{{g_{2} }} } &\quad {\it if}\,\, {b_{2} \le x \le c} \\ \sigma &\quad {\it if}\,\, {x = c} \\ {s_{2} \left( {\frac{{b_{4} - x}}{{b_{4} - c}}} \right)^{{h_{1} }} } &\quad {\it if}\,\, {c \le x \le b_{4} } \\ {\sigma - \left( {\sigma - s_{2} } \right)\left( {\frac{{b_{5} - x}}{{b_{5} - b_{4} }}} \right)^{{h_{2} }} } &\quad {\it if}\,\, {b_{4} \le x \le b_{5} } \\ 1 &\quad {\it if}\,\, {x > b_{5} } \\ \end{array} } \right. \hfill \\ \nu _{{\tilde{A}_{{NLIVAS}}^{L} }} (x) = \left\{ {\begin{array}{*{20}c} {\sigma ^{\prime} - \left( {\sigma ^{\prime} - s^{\prime}_{1} } \right)\left( {\frac{{x - b^{\prime}_{1} }}{{b^{\prime}_{2} - b^{\prime}_{1} }}} \right)^{{g_{1} }} } &\quad {\it if}\,\, {b^{\prime}_{1} \le x \le b^{\prime}_{2} } \\ {s^{\prime}_{1} \left( {\frac{{c - x}}{{c - b^{\prime}_{2} }}} \right)^{{g_{2} }} } &\quad {\it if}\,\, {b^{\prime}_{2} \le x \le c} \\ {\sigma ^{\prime}} &\quad {\it if}\,\, {x = c} \\ {s^{\prime}_{2} \left( {\frac{{b^{\prime}_{4} - x}}{{b^{\prime}_{4} - c}}} \right)^{{h_{1} }} } &\quad {\it if}\,\, {c \le x \le b^{\prime}_{4} } \\ {\sigma ^{\prime} - \left( {\sigma ^{\prime} - s^{\prime}_{2} } \right)\left( {\frac{{b^{\prime}_{5} - x}}{{b^{\prime}_{5} - b^{\prime}_{4} }}} \right)^{{h_{2} }} } &\quad {\it if}\,\, {b^{\prime}_{4} \le x \le b^{\prime}_{5} } \\ 1 &\quad {\it if}\,\, {x > b^{\prime}_{5} } \\ \end{array} } \right. \hfill \\ \end{gathered} $$

Definition 2.10

$\left( {\alpha ,\beta } \right)$-cut or parametric form of NLIVPIFNAS: $\left( {\alpha ,\beta } \right)$-cut or parametric form of NLIVPIFNAS is represented as follows

$$ \left( {\tilde{A}_{NLIVAS}^{I} } \right)_{\alpha ,\beta } = \left[ \begin{gathered} \left\{ {A_{1L}^{U} (\alpha_{2} ),A_{2L}^{U} (\alpha_{2} ),A_{2R}^{U} (\alpha_{2} ),A_{1R}^{U} (\alpha_{2} );A_{1L}^{L} (\alpha_{1} ),A_{2L}^{L} (\alpha_{1} ),A_{2R}^{L} (\alpha_{1} ),A_{1R}^{L} (\alpha_{1} )} \right\}; \hfill \\ \left\{ {\left\{ {A_{1L}^{U} (\beta_{2} ),A_{2L}^{U} (\beta_{2} ),A_{2R}^{U} (\beta_{2} ),A_{1R}^{U} (\beta_{2} );A_{1L}^{L} (\beta_{1} ),A_{2L}^{L} (\beta_{1} ),A_{2R}^{L} (\beta_{1} ),A_{1R}^{L} (\beta_{1} )} \right\}} \right\} \hfill \\ \end{gathered} \right] $$

where

$$\begin{aligned} & A_{{1L}}^{U} (\alpha _{2} ) = a_{1} + \left( {\frac{{\alpha _{2} }}{{r_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{1} }}} \right. \kern-\nulldelimiterspace} {g_{1} }}}} \left( {a_{2} - a_{1} } \right)\;for\;\alpha _{2} \in \left[ {0,r_{1} } \right];\,\\ & A_{{1L}}^{L} (\alpha _{1} ) = a^{\prime}_{1} + \left( {\frac{{\alpha _{1} }}{{r^{\prime}_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{1} }}} \right. \kern-\nulldelimiterspace} {g_{1} }}}} \left( {a^{\prime}_{2} - a^{\prime}_{1} } \right)\;for\;\alpha _{1} \in \left[ {0,r^{\prime}_{1} } \right]\\ & A_{{2L}}^{U} (\alpha _{2} ) = a_{2} + \left( {\frac{{\omega - \alpha _{2} }}{{\omega - r_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{2} }}} \right. \kern-\nulldelimiterspace} {g_{2} }}}} \left( {c - a_{2} } \right)\;for\;\alpha _{2} \in \left[ {r_{1} ,\omega } \right];\\ & A_{{2L}}^{L} (\alpha _{1} ) = a^{\prime}_{2} + \left( {\frac{{\omega ^{\prime} - \alpha _{1} }}{{\omega ^{\prime} - r^{\prime}_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{2} }}} \right. \kern-\nulldelimiterspace} {g_{2} }}}} \left( {c - a^{\prime}_{2} } \right)\;for\;\alpha _{1} \in \left[ {r^{\prime}_{1} ,\omega ^{\prime}} \right] \\ & A_{{2R}}^{U} (\alpha _{2} ) = a_{4} - \left( {\frac{{\omega - \alpha _{2} }}{{\omega - r_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{1} }}} \right. \kern-\nulldelimiterspace} {h_{1} }}}} \left( {a_{4} - c} \right)\;for\;\alpha _{2} \in \left[ {r_{2} ,\omega } \right];\\ & A_{{2R}}^{L} (\alpha _{1} ) = a^{\prime}_{4} - \left( {\frac{{\omega ^{\prime} - \alpha _{1} }}{{\omega ^{\prime} - r^{\prime}_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{1} }}} \right. \kern-\nulldelimiterspace} {h_{1} }}}} \left( {a^{\prime}_{4} - c} \right)\;for\;\alpha _{1} \in \left[ {r^{\prime}_{2} ,\omega ^{\prime}} \right] \\ & A_{{1R}}^{U} (\alpha _{2} ) = a_{5} - \left( {\frac{{\alpha _{2} }}{{r_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{2} }}} \right. \kern-\nulldelimiterspace} {h_{2} }}}} \left( {a_{5} - a_{4} } \right)\;for\;\alpha _{2} \in \left[ {0,r_{2} } \right];\\ &A_{{1R}}^{L} (\alpha _{1} ) = a^{\prime}_{5} - \left( {\frac{{\alpha _{1} }}{{r^{\prime}_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{2} }}} \right. \kern-\nulldelimiterspace} {h_{2} }}}} \left( {a^{\prime}_{5} - a^{\prime}_{4} } \right)\;for\;\alpha _{1} \in \left[ {0,r^{\prime}_{2} } \right] \\ & A_{{1L}}^{U} (\beta _{2} ) = b_{1} + \left( {\frac{{\sigma - \beta _{2} }}{{\sigma - s_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{1} }}} \right. \kern-\nulldelimiterspace} {g_{1} }}}} \left( {b_{2} - b_{1} } \right)\;for\;\beta _{2} \in \left[ {s_{1} ,1} \right];\\ & A_{{1L}}^{L} (\beta _{1} ) = b^{\prime}_{1} + \left( {\frac{{\sigma ^{\prime} - \beta _{2} }}{{\sigma ^{\prime} - s^{\prime}_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{1} }}} \right. \kern-\nulldelimiterspace} {g_{1} }}}} \left( {b^{\prime}_{2} - b^{\prime}_{1} } \right)\;for\;\beta _{1} \in \left[ {s^{\prime}_{1} ,1} \right] \\ & A_{{2L}}^{U} (\beta _{2} ) = b_{2} + \left( {\frac{{\beta _{2} }}{{s_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{2} }}} \right. \kern-\nulldelimiterspace} {g_{2} }}}} \left( {c - b_{2} } \right)\;for\;\beta _{2} \in \left[ {\sigma ,s_{1} } \right];\\ & A_{{2L}}^{L} (\beta _{1} ) = b^{\prime}_{2} + \left( {\frac{{\beta _{2} }}{{s^{\prime}_{1} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {g_{2} }}} \right. \kern-\nulldelimiterspace} {g_{2} }}}} \left( {c - b^{\prime}_{2} } \right)\;for\;\beta _{1} \in \left[ {\sigma ^{\prime},s^{\prime}_{1} } \right] \\ & A_{{2R}}^{U} (\beta _{2} ) = b_{4} - \left( {\frac{{\beta _{2} }}{{s_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{1} }}} \right. \kern-\nulldelimiterspace} {h_{1} }}}} \left( {b_{4} - c} \right)\;\;for\;\beta _{2} \in \left[ {\sigma ,s_{2} } \right];\\ & A_{{2R}}^{L} (\beta _{1} ) = b^{\prime}_{4} - \left( {\frac{{\beta _{2} }}{{s^{\prime}_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{1} }}} \right. \kern-\nulldelimiterspace} {h_{1} }}}} \left( {b^{\prime}_{4} - c} \right)\;\;for\;\beta _{1} \in \left[ {\sigma ^{\prime},s^{\prime}_{2} } \right] \\ & A_{{1R}}^{U} (\beta _{2} ) = b_{5} - \left( {\frac{{\sigma - \beta _{2} }}{{\sigma - s_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{2} }}} \right. \kern-\nulldelimiterspace} {h_{2} }}}} \left( {b_{5} - b_{4} } \right)\;for\;\beta _{2} \in \left[ {s_{2} ,1} \right];\\ & A_{{1R}}^{L} (\beta _{1} ) = b^{\prime}_{5} - \left( {\frac{{\sigma ^{\prime} - \beta _{2} }}{{\sigma ^{\prime} - s^{\prime}_{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {h_{2} }}} \right. \kern-\nulldelimiterspace} {h_{2} }}}} \left( {b^{\prime}_{5} - b^{\prime}_{4} } \right)\;for\;\beta _{1} \in \left[ {s^{\prime}_{2} ,1} \right] \end{aligned} $$

where $A_{1L}^{U} (\alpha_{2} ),A_{2L}^{U} (\alpha_{2} ),A_{1L}^{L} (\alpha_{1} ),A_{2L}^{L} (\alpha_{1} ),A_{2R}^{U} (\beta_{2} ),A_{1R}^{U} (\beta_{2} ),A_{2R}^{L} (\beta_{1} ),A_{1R}^{L} (\beta_{1} )$ are increasing function based on $\alpha_{i} ,\beta_{i} (i = 1,2)$ and $A_{2R}^{U} (\alpha_{2} ),A_{1R}^{U} (\alpha_{2} ),A_{2R}^{L} (\alpha_{1} ),A_{1R}^{L} (\alpha_{1} ),A_{1L}^{U} (\beta_{2} ),A_{2L}^{U} (\beta_{2} ),A_{1L}^{L} (\beta_{1} ),A_{2L}^{L} (\beta_{1} )$ are decreasing function based on $\alpha_{i} ,\beta_{i} (i = 1,2)$.

Note 07

If $g_{1} = g_{2} = h_{1} = h_{2} = 1$,$a_{i} = a^{\prime}_{i} ,b_{i} = b^{\prime}_{i} \;,\omega = \omega^{\prime},\;\sigma = \sigma^{\prime},r_{1} = r_{1}^{\prime } ,r_{2} = r_{2}^{\prime } ,s_{1} = s^{\prime},s_{2} = s^{\prime}for\;i = 1,2,3,4\;$, then the NLIVPIFNAS is converted into LPIFNAS (See in Fig. 2).

Note 08

If $g_{1} = g_{2} = h_{1} = h_{2} = 1$,$a_{i} = a^{\prime}_{i} ,b_{i} = b^{\prime}_{i} \;,\omega = \omega^{\prime},\;\sigma = \sigma^{\prime},r_{1} = r_{1}^{\prime } = r_{2} = r_{2}^{\prime } ,s_{1} = s^{\prime} = s_{2} = s^{\prime}for\;i = 1,2,3,4\;$, then the NLIVPIFNAS is converted into LPIFNS (see in Fig. 4).

Note 09

If $g_{1} = g_{2} = h_{1} = h_{2} = 1$, as a result of NLIVPIFNAS becomes linear interval valued pentagonal intuitionistic fuzzy number with asymmetry (LIVPIFNAS). (See in Fig. 9).

Note 10

If $r_{1} = r_{2} ,r^{\prime}_{1} = r^{\prime}_{2}$$,s_{1} = s_{2} ,s^{\prime}_{1} = s^{\prime}_{2}$ then the NLIVPIFNAS is converted into nonlinear interval valued pentagonal intuitionistic fuzzy number with partial symmetry (NLIVPIFNPS). (See in Fig. 8).

Fig. 8

Diagram of Non-linear Interval Valued pentagonal intuitionistic fuzzy number having partial symmetry

Note 11

If $g_{1} = g_{2} = h_{1} = h_{2} = 1$ then the NLIVPIFNPS is converted into linear interval valued pentagonal intuitionistic fuzzy number with partial symmetry (LIVPIFNPS) (See in Fig. 9).

Fig. 9

Diagram of LIVPIFNAS

Note 12

If $g_{1} = g_{2} = h_{1} = h_{2} = 1$, $r_{1} = r_{2}$ and $s_{1} = s_{2}$ then the NLIVPIFNAS is converted into LIVPIFNPS (See in Fig. 10).

Fig. 10

Diagram of Linear Interval Valued pentagonal intuitionistic fuzzy number having partial symmetry

Note 13

If $g_{1} = g_{2} = h_{1} = h_{2} = 1$, $r_{1} = r_{2} = s_{1} = s_{2}$, $r^{\prime}_{1} = r^{\prime}_{2} = s^{\prime}_{1} = s^{\prime}_{2}$ then the NLIVPIFNAS is converted into LPIFNS (See in Fig. 4).

The following diagram illustrates the geometric representation of several IVPIFN forms:

Arithmetic Operations of IVPIFN

There are several researchers contributing to the field where they discover the arithmetic operation on various types of IFN. IFNs [27] are included in the existing interval arithmetic methods on fuzzy numbers [39]. It is comparable to combining two separate generalized IVIFNs.

Consider two IVPIFN

$$ \tilde{A}_{\text{NLIVS}} = \left[ \begin{gathered} \left\{ {\left( {a_{11} ,a_{12} ,c,a_{14} ,a_{15} ;\omega_{11} ,r_{11} } \right),\left( {a_{21} ,a_{22} ,c,a_{24} ,a_{25} ;\omega_{12} ,r_{12} } \right)} \right\}, \hfill \\ \left\{ {\left( {b_{11} ,b_{12} ,c,b_{14} ,b_{15} ;\sigma_{11} ,s_{11} } \right),\left( {b_{21} ,b_{22} ,c,b_{24} ,b_{25} ;\sigma_{12} ,s_{12} } \right)} \right\} \hfill \\ \end{gathered} \right] $$

and

$$ \tilde{B}_{\text{NLIVS}} = \left[ \begin{gathered} \left\{ {\left( {p_{11} ,p_{12} ,d,p_{14} ,p_{15} ;\omega_{21} ,r_{21} } \right),\left( {p_{21} ,p_{22} ,d,p_{24} ,p_{25} ;\omega_{22} ,r_{22} } \right)} \right\}, \hfill \\ \left\{ {\left( {q_{11} ,q_{12} ,d,q_{14} ,q_{15} ;\sigma_{21} ,s_{21} } \right),\left( {q_{21} ,q_{22} ,d,q_{24} ,q_{25} ;\sigma_{22} ,s_{22} } \right)} \right\} \hfill \\ \end{gathered} \right] $$

• (i) Addition

  $$ \tilde{A}_{\text{NLIVS}} \oplus \tilde{B}_{\text{NLIVS}} = \left[ \begin{gathered} \left\{ {\left( {w_{11} ,w_{12} ,e,w_{14} ,w_{15} ;\omega_{01} ,r_{01} } \right),\left( {w_{21} ,w_{22} ,e,w_{24} ,w_{25} ;\omega_{02} ,r_{02} } \right)} \right\}, \hfill \\ \left\{ {\left( {u_{11} ,u_{12} ,e,u_{14} ,u_{15} ;\sigma_{01} ,s_{01} } \right),\left( {u_{21} ,u_{22} ,e,u_{24} ,u_{25} ;\sigma_{02} ,s_{02} } \right)} \right\} \hfill \\ \end{gathered} \right] $$

where

$$ \begin{gathered} w_{11} = a_{11} + p_{11} ,w_{12} = a_{12} + p_{12} ,e = c + d,w_{14} = a_{14} + p_{14} ,w_{15} = a_{15} + p_{15} , \hfill \\ w_{21} = a_{21} + p_{21} ,w_{22} = a_{22} + p_{22} ,w_{24} = a_{24} + p_{24} ,w_{25} = a_{25} + p_{25} , \hfill \\ u_{11} = b_{11} + q_{11} ,u_{12} = b_{12} + q_{12} ,u_{14} = b_{14} + q_{14} ,u_{15} = b_{15} + q_{15} , \hfill \\ u_{21} = b_{21} + q_{21} ,u_{22} = b_{22} + q_{22} ,u_{24} = b_{24} + q_{24} ,u_{25} = b_{25} + q_{25} , \hfill \\ \omega_{01} = \min \left( {\omega_{11} ,\omega_{21} } \right),\omega_{02} = \min \left( {\omega_{12} ,\omega_{22} } \right),r_{01} = \min \left( {r_{11} ,r_{21} } \right),r_{02} = \min \left( {r_{12} ,r_{22} } \right), \hfill \\ \sigma_{01} = \max \left( {\sigma_{11} ,\sigma_{21} } \right),\sigma_{02} = \max \left( {\sigma_{12} ,\sigma_{22} } \right),s_{01} = \max \left( {s_{11} ,s_{21} } \right),s_{02} = \max \left( {s_{12} ,s_{22} } \right) \hfill \\ \end{gathered} $$

• (ii) Subtraction

  $$ \tilde{A}_{\text{NLIVS}} - \tilde{B}_{\text{NLIVS}} = \left[ \begin{gathered} \left\{ {\left( {y_{11} ,y_{12} ,j,y_{14} ,y_{15} ;\omega_{01} ,r_{01} } \right),\left( {y_{21} ,y_{22} ,j,y_{24} ,y_{25} ;\omega_{02} ,r_{02} } \right)} \right\}, \hfill \\ \left\{ {\left( {z_{11} ,z_{12} ,j,z_{14} ,z_{15} ;\sigma_{01} ,s_{01} } \right),\left( {z_{21} ,z_{22} ,j,z_{24} ,z_{25} ;\sigma_{02} ,s_{02} } \right)} \right\} \hfill \\ \end{gathered} \right] $$

where

$$ \begin{aligned} & y_{11} = \max (a_{11} - p_{15} ,L_{l} ),y_{12} = \max (a_{12} - p_{14} ,L_{l} ),j = \max (c - d,L_{l} ),\\ & y_{14} = \max (a_{14} - p_{12} ,L_{l} ),y_{15} = \max (a_{15} - p_{11} ,L_{l} ), \\ & y_{21} = \max (a_{21} - p_{25} ,L_{l} ),y_{22} = \max (a_{22} - p_{24} ,L_{l} ),y_{24} = \max (a_{24} - p_{22} ,L_{l} ),\\ &y_{25} = \max (a_{25} - p_{21} ,L_{l} ), \\ & z_{11} = \max (b_{11} - q_{15} ,L_{l} ),z_{12} = \max (b_{12} - q_{14} ,L_{l} ),z_{14} = \max (b_{14} - q_{12} ,L_{l} ),\\ &z_{15} = \max (b_{15} - q_{11} ,L_{l} ), \\ & z_{21} = \max (b_{21} - q_{25} ,L_{l} ),z_{22} = \max (b_{22} - q_{24} ,L_{l} ),z_{24} = \max (b_{24} - q_{22} ,L_{l} ),\\ & z_{25} = \max (b_{25} - q_{21} ,L_{l} ), \\ &\omega_{01} = \min \left( {\omega_{11} ,\omega_{21} } \right),\omega_{02} = \min \left( {\omega_{12} ,\omega_{22} } \right),r_{01} = \min \left( {r_{11} ,r_{21} } \right),r_{02} = \min \left( {r_{12} ,r_{22} } \right), \\ & \sigma_{01} = \max \left( {\sigma_{11} ,\sigma_{21} } \right),\sigma_{02} = \max \left( {\sigma_{12} ,\sigma_{22} } \right),s_{01} = \max \left( {s_{11} ,s_{21} } \right),s_{02} = \max \left( {s_{12} ,s_{22} } \right) \hfill \\ \end{aligned} $$

Here $L_{l}$ is the lower scale of PIFNs.

• (iii) Multiplication

  Multiplication by some crisp number

  $$ \begin{aligned} \tilde{Z}_{\text{NLIVS}} &= k\tilde{A}_{\text{NLIVS}}\\ &= k\left[ \begin{gathered} \left\{ {\left( {a_{11} ,a_{12} ,c,a_{14} ,a_{15} ;\omega_{11} ,r_{11} } \right),\left( {a_{21} ,a_{22} ,c,a_{24} ,a_{25} ;\omega_{12} ,r_{12} } \right)} \right\}, \hfill \\ \left\{ {\left( {b_{11} ,b_{12} ,c,b_{14} ,b_{15} ;\sigma_{11} ,s_{11} } \right),\left( {b_{21} ,b_{22} ,c,b_{24} ,b_{25} ;\sigma_{12} ,s_{12} } \right)} \right\} \hfill \\ \end{gathered} \right] \hfill \\ & = \left[ \begin{gathered} \left\{ {\left( {ka_{11} ,ka_{12} ,kc,ka_{14} ,ka_{15} ;\omega_{11} ,r_{11} } \right),\left( {ka_{21} ,ka_{22} ,kc,ka_{24} ,ka_{25} ;\omega_{12} ,r_{12} } \right)} \right\}, \hfill \\ \left\{ {\left( {kb_{11} ,kb_{12} ,kc,kb_{14} ,kb_{15} ;\sigma_{11} ,s_{11} } \right),\left( {kb_{21} ,kb_{22} ,kc,kb_{24} ,kb_{25} ;\sigma_{12} ,s_{12} } \right)} \right\} \hfill \\ \end{gathered} \right]\;for\;k > 0 \hfill \\ &= \left[ \begin{gathered} \left\{ {\left( {ka_{15} ,ka_{14} ,kc,ka_{12} ,ka_{11} ;\omega_{11} ,r_{11} } \right),\left( {ka_{25} ,ka_{24} ,kc,ka_{22} ,ka_{21} ;\omega_{12} ,r_{12} } \right)} \right\}, \hfill \\ \left\{ {\left( {kb_{15} ,kb_{14} ,kc,kb_{12} ,kb_{11} ;\sigma_{11} ,s_{11} } \right),\left( {kb_{25} ,kb_{24} ,kc,kb_{22} ,kb_{21} ;\sigma_{12} ,s_{12} } \right)} \right\} \hfill \\ \end{gathered} \right]\;for\;k < 0 \hfill \\ \end{aligned} $$

De-intuitification of Non-linear Interval Valued Pentagonal Intuitionistic Fuzzy Number with Symmetry (NLIVPIFNS)

Defuzzification is the process of converting fuzzy numbers into crisp ones. In other words, defuzzification is a method for assigning a crisp value to a fuzzy number. There are various common and conventional defuzzification methods, such as the Centre of Area method [47], the Largest of Maxima method [15], the Smallest of Maxima method [34], the Bisector of Area method [26], the Mean of Maxima method [21], the Centre of Approximated Interval method, and so on. The defuzzification procedure is crucial for two key reasons:

• Anyone can understand the relationship between fuzzy number and the crisp number.

• Determining the crispified value of fuzzy solutions.

De-intuitification of NLIVPIFNS Based on Mean of $\left( {\alpha ,\beta } \right)$- Cut Method

The left and right $\left( {\alpha ,\beta } \right)$-cut of a nonlinear interval valued pentagonal intuitionistic fuzzy number (NLIVPIFN) are,

For Upper membership and non-membership functions:

$$ \begin{aligned} & L_{1}^{ - 1} \left( \alpha \right) = a_{1} + \left( {\frac{\alpha }{{r_{1} }}} \right)^{{\phi_{1} }} \left( {a_{2} - a_{1} } \right)\;for\;\alpha \in \left[ {0,r_{1} } \right]\\ & L_{1}^{ - 1} (\beta ) = b_{1} + \left( {\frac{\sigma - \beta }{{\sigma - s_{1} }}} \right)^{{\phi_{1} }} \left( {b_{2} - b_{1} } \right)\;for\;\beta \in \left[ {s_{1} ,1} \right] \\ & L_{1}^{ - 1} \left( \alpha \right) = a_{2} + \left( {\frac{\omega - \alpha }{{\omega - r_{1} }}} \right)^{{\phi_{2} }} \left( {c - a_{2} } \right)\;for\;\alpha \in \left[ {r_{1} ,\omega } \right]\\ &L_{1}^{ - 1} (\beta ) = b_{2} + \left( {\frac{\beta }{{s_{1} }}} \right)^{{\phi_{2} }} \left( {c - b_{2} } \right)\;for\;\beta \in \left[ {\sigma ,s_{1} } \right] \\ & R_{1}^{ - 1} \left( \alpha \right) = a_{4} - \left( {\frac{\omega - \alpha }{{\omega - r_{1} }}} \right)^{{\psi_{1} }} \left( {a_{4} - c} \right)\;for\;\alpha \in \left[ {r_{1} ,\omega } \right]\\ & R_{1}^{ - 1} (\beta ) = b_{4} - \left( {\frac{\beta }{{s_{1} }}} \right)^{{\psi_{1} }} \left( {b_{4} - c} \right)\;\;for\;\beta \in \left[ {\sigma ,s_{1} } \right] \\ & R_{1}^{ - 1} \left( \alpha \right) = a_{5} - \left( {\frac{\alpha }{{r_{1} }}} \right)^{{\psi_{2} }} \left( {a_{5} - a_{4} } \right)\;for\;\alpha \in \left[ {0,r_{1} } \right]\\ & R_{1}^{ - 1} (\beta ) = b_{5} - \left( {\frac{\sigma - \beta }{{\sigma - s_{1} }}} \right)^{{\psi_{2} }} \left( {b_{5} - b_{4} } \right)\;for\;\beta \in \left[ {s_{1} ,1} \right] \end{aligned} $$

For Lower membership and non-membership functions:

$$ \begin{aligned} & L_{2}^{ - 1} \left( \alpha \right) = a^{\prime}_{1} + \left( {\frac{\alpha }{{r_{2} }}} \right)^{{\phi_{1} }} \left( {a^{\prime}_{2} - a^{\prime}_{1} } \right)\;for\;\alpha \in \left[ {0,r_{2} } \right]\\ & L_{2}^{ - 1} (\beta ) = b^{\prime}_{1} + \left( {\frac{{\sigma^{\prime} - \beta }}{{\sigma^{\prime} - s_{2} }}} \right)^{{\phi_{1} }} \left( {b^{\prime}_{2} - b^{\prime}_{1} } \right)\;for\;\beta \in \left[ {s_{2} ,1} \right] \\ & L_{2}^{ - 1} \left( \alpha \right) = a^{\prime}_{2} + \left( {\frac{{\omega^{\prime} - \alpha }}{{\omega^{\prime} - r_{2} }}} \right)^{{\phi_{2} }} \left( {c - a^{\prime}_{2} } \right)\;for\;\;for\;\alpha \in \left[ {r_{2} ,\omega^{\prime}} \right]\\ & L_{2}^{ - 1} (\beta ) = b^{\prime}_{2} + \left( {\frac{\beta }{{s_{2} }}} \right)^{{\phi_{2} }} \left( {c - b^{\prime}_{2} } \right)\;for\;\beta \in \left[ {\sigma^{\prime},s_{2} } \right] \\ & R_{2}^{ - 1} \left( \alpha \right) = a^{\prime}_{4} - \left( {\frac{{\omega^{\prime} - \alpha }}{{\omega^{\prime} - r_{2} }}} \right)^{{\psi_{1} }} \left( {a^{\prime}_{4} - c} \right)\;for\;\alpha \in \left[ {r_{2} ,\omega^{\prime}} \right]\\ & R_{2}^{ - 1} (\beta ) = b^{\prime}_{4} - \left( {\frac{\beta }{{s_{2} }}} \right)^{{\psi_{1} }} \left( {b^{\prime}_{4} - c} \right)\;\;for\;\beta \in \left[ {\sigma^{\prime},s_{2} } \right] \\ & R_{2}^{ - 1} \left( \alpha \right) = a^{\prime}_{5} - \left( {\frac{\alpha }{{r_{2} }}} \right)^{{\psi_{2} }} \left( {a^{\prime}_{5} - a^{\prime}_{4} } \right)\;for\;\alpha \in \left[ {0,r_{2} } \right]\\ & R_{2}^{ - 1} (\beta ) = b^{\prime}_{5} - \left( {\frac{{\sigma^{\prime} - \beta }}{{\sigma^{\prime} - s_{2} }}} \right)^{{\psi_{2} }} \left( {b^{\prime}_{5} - b^{\prime}_{4} } \right)\;for\;\beta \in \left[ {s_{2} ,1} \right] \end{aligned} $$

We proposed the mean of interval method for de-intuitification as follows:

$$ \begin{gathered} Sc\left( {\tilde{A}_{{NLIVPS}} } \right) = \frac{{\left( {\int\limits_{{\alpha = 0}}^{\omega } {\left( {\frac{{L_{1}^{{ - 1}} (\alpha ) + R_{1}^{{ - 1}} (\alpha )}}{2}} \right)d\alpha } + \int\limits_{{\alpha = 0}}^{{\omega ^{\prime}}} {\left( {\frac{{L_{2}^{{ - 1}} (\alpha ) + R_{2}^{{ - 1}} (\alpha )}}{2}} \right)d\alpha } } \right)/2 + \left( {\int\limits_{{\beta = \sigma }}^{1} {\left( {\frac{{L_{1}^{{ - 1}} (\beta ) + R_{1}^{{ - 1}} (\beta )}}{2}} \right)d\beta + \int\limits_{{\beta = \sigma ^{\prime}}}^{1} {\left( {\frac{{L_{2}^{{ - 1}} (\beta ) + R_{2}^{{ - 1}} (\beta )}}{2}} \right)d\beta } } } \right)2}}{2} \hfill \\ \quad \quad \quad \quad \quad \quad = \left( \begin{gathered} \int\limits_{{\alpha = 0}}^{{r_{1} }} {\left( {\frac{{L_{1}^{{ - 1}} (\alpha ) + R_{1}^{{ - 1}} (\alpha )}}{2}} \right)d\alpha } + \int\limits_{{\alpha = r_{1} }}^{\omega } {\left( {\frac{{L_{1}^{{ - 1}} (\alpha ) + R_{1}^{{ - 1}} (\alpha )}}{2}} \right)d\alpha } + \int\limits_{{\alpha = 0}}^{{r_{2} }} {\left( {\frac{{L_{2}^{{ - 1}} (\alpha ) + R_{2}^{{ - 1}} (\alpha )}}{2}} \right)d\alpha + \int\limits_{{\alpha = r_{2} }}^{{\omega ^{\prime}}} {\left( {\frac{{L_{2}^{{ - 1}} (\alpha ) + R_{2}^{{ - 1}} (\alpha )}}{2}} \right)d\alpha } } \hfill \\ + \;\int\limits_{{\beta = \sigma }}^{{s_{1} }} {\left( {\frac{{L_{1}^{{ - 1}} (\beta ) + R_{1}^{{ - 1}} (\beta )}}{2}} \right)d\beta + \int\limits_{{\beta = s_{1} }}^{1} {\left( {\frac{{L_{1}^{{ - 1}} (\beta ) + R_{1}^{{ - 1}} (\beta )}}{2}} \right)d\beta + \;\int\limits_{{\beta = \sigma ^{\prime}}}^{{s_{2} }} {\left( {\frac{{L_{2}^{{ - 1}} (\beta ) + R_{2}^{{ - 1}} (\beta )}}{2}} \right)d\beta + \int\limits_{{\beta = s_{2} }}^{1} {\left( {\frac{{L_{2}^{{ - 1}} (\beta ) + R_{2}^{{ - 1}} (\beta )}}{2}} \right)d\beta } } } } \hfill \\ \end{gathered} \right)/4 \hfill \\ \quad \quad \quad \quad \quad \quad = \left( \begin{gathered} \int\limits_{{\alpha = 0}}^{{r_{1} }} {\left( {\frac{{a_{1} + \left( {\frac{\alpha }{{r_{1} }}} \right)^{{\phi _{1} }} \left( {a_{2} - a_{1} } \right) + a_{5} - \left( {\frac{\alpha }{{r_{1} }}} \right)^{{\psi _{2} }} \left( {a_{5} - a_{4} } \right)}}{2}} \right)d\alpha } + \int\limits_{{\alpha = r_{1} }}^{\omega } {\left( {\frac{{a_{2} + \left( {\frac{{\omega - \alpha }}{{\omega - r_{1} }}} \right)^{{\phi _{2} }} \left( {c - a_{2} } \right) + a_{4} - \left( {\frac{{\omega - \alpha }}{{\omega - r_{1} }}} \right)^{{\psi _{1} }} \left( {a_{4} - c} \right)}}{2}} \right)d\alpha } \hfill \\ + \int\limits_{{\alpha = 0}}^{{r_{2} }} {\left( {\frac{{a^{\prime}_{1} + \left( {\frac{{\alpha _{1} }}{{r_{2} }}} \right)^{{\phi _{1} }} \left( {a^{\prime}_{2} - a^{\prime}_{1} } \right)\; + a^{\prime}_{5} - \left( {\frac{{\alpha _{1} }}{{r_{2} }}} \right)^{{\psi _{2} }} \left( {a^{\prime}_{5} - a^{\prime}_{4} } \right)}}{2}} \right)d\alpha + \int\limits_{{\alpha = r_{2} }}^{{\omega ^{\prime}}} {\left( {\frac{{a^{\prime}_{2} + \left( {\frac{{\omega ^{\prime} - \alpha _{1} }}{{\omega ^{\prime} - r_{2} }}} \right)^{{\phi _{2} }} \left( {c - a^{\prime}_{2} } \right)\; + a^{\prime}_{4} - \left( {\frac{{\omega ^{\prime} - \alpha _{1} }}{{\omega ^{\prime} - r_{2} }}} \right)^{{\psi _{1} }} \left( {a^{\prime}_{4} - c} \right)\;}}{2}} \right)d\alpha } } \hfill \\ + \;\int\limits_{{\beta = s_{1} }}^{1} {\left( {\frac{{b_{1} + \left( {\frac{{\sigma - \beta }}{{\sigma - s_{1} }}} \right)^{{\phi _{1} }} \left( {b_{2} - b_{1} } \right) + b_{5} - \left( {\frac{{\sigma - \beta }}{{\sigma - s_{1} }}} \right)^{{\psi _{2} }} \left( {b_{5} - b_{4} } \right)}}{2}} \right)d\beta \; + \int\limits_{{\beta = \sigma }}^{{s_{1} }} {\left( {\frac{{b_{2} + \left( {\frac{\beta }{{s_{1} }}} \right)^{{\phi _{2} }} \left( {c - b_{2} } \right)\; + b_{4} - \left( {\frac{\beta }{{s_{1} }}} \right)^{{\psi _{1} }} \left( {b_{4} - c} \right)}}{2}} \right)d\beta } } \hfill \\ + \int\limits_{{\beta = s_{2} }}^{1} {\left( {\frac{{b^{\prime}_{1} + \left( {\frac{{\sigma ^{\prime} - \beta }}{{\sigma ^{\prime} - s_{2} }}} \right)^{{\phi _{1} }} \left( {b^{\prime}_{2} - b^{\prime}_{1} } \right) + b^{\prime}_{5} - \left( {\frac{{\sigma ^{\prime} - \beta }}{{\sigma ^{\prime} - s_{2} }}} \right)^{{\psi _{2} }} \left( {b^{\prime}_{5} - b^{\prime}_{4} } \right)}}{2}} \right)d\beta } + \int\limits_{{\beta = \sigma ^{\prime}}}^{{s_{2} }} {\left( {\frac{{b^{\prime}_{2} + \left( {\frac{\beta }{{s_{2} }}} \right)^{{\phi _{2} }} \left( {c - b^{\prime}_{2} } \right) + b^{\prime}_{4} - \left( {\frac{\beta }{{s_{2} }}} \right)^{{\psi _{1} }} \left( {b^{\prime}_{4} - c} \right)}}{2}} \right)d\beta } \hfill \\ \end{gathered} \right)/4 \hfill \\ \quad \quad \quad \quad \quad \quad = \left\{ \begin{gathered} \frac{{a_{1} r_{1} + \frac{{r_{1} }}{{\phi _{1} + 1}}\left( {a_{2} - a_{1} } \right) + a_{5} r_{1} - \frac{{r_{1} }}{{\psi _{2} + 1}}\left( {a_{5} - a_{4} } \right)}}{2} + \frac{{a_{2} (\omega - r_{1} ) + \frac{{(\omega - r_{1} )\left( {c - a_{2} } \right)}}{{\phi _{2} + 1}} + a_{4} (\omega - r_{1} ) - \frac{{(\omega - r_{1} )\left( {a_{4} - c} \right)}}{{\psi _{1} + 1}}}}{2} \hfill \\ + \frac{{a^{\prime}_{1} r_{2} + \frac{{r_{2} }}{{\phi _{1} + 1}}\left( {a^{\prime}_{2} - a^{\prime}_{1} } \right) + a^{\prime}_{5} r_{2} - \frac{{r_{2} }}{{\psi _{2} + 1}}\left( {a^{\prime}_{5} - a^{\prime}_{4} } \right)}}{2} + \frac{{a^{\prime}_{2} (\omega ^{\prime} - r_{2} ) + \frac{{(\omega ^{\prime} - r_{2} )\left( {c - a^{\prime}_{2} } \right)}}{{\phi _{2} + 1}} + a^{\prime}_{4} (\omega ^{\prime} - r_{2} ) - \frac{{(\omega ^{\prime} - r_{2} )\left( {a^{\prime}_{4} - c} \right)}}{{\psi _{1} + 1}}}}{2} \hfill \\ + \frac{{b_{1} (1 - s_{1} ) + \frac{{\left( {b_{2} - b_{1} } \right)}}{{\left( {\sigma - s_{1} } \right)^{{\phi _{1} }} \left( {\phi _{1} + 1} \right)}}\left\{ {1 - \left( {\frac{{\sigma - 1}}{{\sigma - s_{1} }}} \right)^{{\phi _{1} + 1}} } \right\} + b_{5} (1 - s_{1} ) - \frac{{\left( {b_{5} - b_{4} } \right)}}{{\left( {\sigma - s_{1} } \right)^{{\psi _{2} }} \left( {\psi _{2} + 1} \right)}}\left\{ {1 - \left( {\frac{{\sigma - 1}}{{\sigma - s_{1} }}} \right)^{{\psi _{2} + 1}} } \right\}}}{2} \hfill \\ + \frac{{b^{\prime}_{1} (1 - s_{2} ) + \frac{{\left( {b^{\prime}_{2} - b^{\prime}_{1} } \right)}}{{\left( {\sigma ^{\prime} - s_{2} } \right)^{{\phi _{1} }} \left( {\phi _{1} + 1} \right)}}\left\{ {1 - \left( {\frac{{\sigma ^{\prime} - 1}}{{\sigma ^{\prime} - s_{2} }}} \right)^{{\phi _{1} + 1}} } \right\} + b^{\prime}_{5} (1 - s_{2} ) - \frac{{\left( {b^{\prime}_{5} - b^{\prime}_{4} } \right)}}{{\left( {\sigma ^{\prime} - s_{2} } \right)^{{\psi _{2} }} \left( {\psi _{2} + 1} \right)}}\left\{ {1 - \left( {\frac{{\sigma ^{\prime} - 1}}{{\sigma ^{\prime} - s_{2} }}} \right)^{{\psi _{2} + 1}} } \right\}}}{2} \hfill \\ + \frac{{b_{2} (s_{1} - \sigma ) + \frac{{s_{1} \left( {c - b_{2} } \right)}}{{\phi _{2} + 1}}\left\{ {1 - \left( {\frac{\sigma }{{s_{1} }}} \right)^{{\phi _{2} + 1}} } \right\} + b_{4} (s_{1} - \sigma ) - \frac{{s_{1} \left( {b_{4} - c} \right)}}{{\psi _{1} + 1}}\left\{ {1 - \left( {\frac{\sigma }{{s_{1} }}} \right)^{{\psi _{1} + 1}} } \right\}}}{2} \hfill \\ + \frac{{b^{\prime}_{2} (s_{2} - \sigma ^{\prime}) + \frac{{s_{2} \left( {c - b^{\prime}_{2} } \right)}}{{\phi _{2} + 1}}\left\{ {1 - \left( {\frac{{\sigma ^{\prime}}}{{s_{2} }}} \right)^{{\phi _{2} + 1}} } \right\} + b^{\prime}_{4} (s_{2} - \sigma ^{\prime}) - \frac{{s_{2} \left( {b^{\prime}_{4} - c} \right)}}{{\psi _{1} + 1}}\left\{ {1 - \left( {\frac{{\sigma ^{\prime}}}{{s_{2} }}} \right)^{{\psi _{1} + 1}} } \right\}}}{2} \hfill \\ \end{gathered} \right\}/4 \hfill \\ \end{gathered} $$

(1)

If $\phi_{1} = \phi_{2} = \psi_{1} = \psi_{2} = 1$ then NLIVPIFN is reduced to LIVPIFNS.

Definition 4.1

Let $\tilde{A}_{{\text{NLIVPS}}} = \left[ \begin{array}{llll} \left\{( \left({a_{{11}} ,a_{{12}} ,c,a_{{14}} ,a_{{15}} ;\omega _{{11}} ,r_{{11}}} \right),\right.\\ \left.\left( {a_{{21}} ,a_{{22}} ,c,a_{{24}},a_{{25}} ;\omega _{{12}} ,r_{{12}} } \right) )_{{\left({g_{1} ,g_{2} ,h_{1} ,h_{2} } \right)}} \right\}, \hfill \\\left\{( \left( b_{{11}} ,b_{{12}} ,c,b_{{14}} ,b_{{15}} ;\sigma _{{11}} ,s_{{11}} \right),\right.\\ \left.\left( {b_{{21}},b_{{22}} ,c,b_{{24}} ,b_{{25}} ;\sigma _{{12}} ,s_{{12}} }\right))_{{\left({g_{1} ,g_{2} ,h_{1} ,h_{2} } \right)}} \right\} \hfill \\\end{array} \right]$ and $\tilde{B}_{{\text{NLIVPS}}} = \left[ \begin{array}{llll}\left\{(\left({p_{{11}} ,p_{{12}} ,d,p_{{14}} ,p_{{15}} ;\omega _{{21}} ,r_{{21}} } \right),\right.\\ \left.\left( {p_{{21}},p_{{22}} ,d,p_{{24}} ,p_{{25}} ;\omega _{{22}} ,r_{{22}} }\right))_{{\left({g_{1} ,g_{2} ,h_{1} ,h_{2} } \right)}} \right\}, \hfill \\\left\{ ( \left( {q_{{11}} ,q_{{12}} ,d,q_{{14}} ,q_{{15}} ;\sigma _{{21}} ,s_{{21}} } \right),\right.\\ \left. \left( {q_{{21}},q_{{22}} ,d,q_{{24}} ,q_{{25}} ;\sigma _{{22}} ,s_{{22}} }\right))_{{\left( {g_{1} ,g_{2} ,h_{1} ,h_{2} } \right)}} \right\} \hfill \\ \end{array} \right]$ be two NLIVPIFNs. Then we have define the ordering between $\tilde{A}_{\text{NLIVS}}$ and $\tilde{B}_{\text{NLIVS}}$ as:

$$ \begin{gathered} ({\text{i}})\;\;\;Sc\left( {k\tilde{A}_{\text{NLIVPS}} + \tilde{B}_{\text{NLIVPS}} } \right) = kSc\left( {\tilde{A}_{\text{NLIVPS}} } \right) + Sc\left( {\tilde{B}_{\text{NLIVPS}} } \right) \hfill \\ ({\text{ii}})\;\;Sc\left( {\tilde{A}_{\text{NLIVPS}} } \right) \le Sc\left( {\tilde{B}_{\text{NLIVPS}} } \right) \Rightarrow \tilde{A}_{\text{NLIVPS}} \le \tilde{B}_{\text{NLIVPS}} \hfill \\ ({\text{iii}})\;Sc\left( {\tilde{A}_{\text{NLIVPS}} } \right) \ge Sc\left( {\tilde{B}_{\text{NLIVPS}} } \right) \Leftrightarrow \tilde{A}_{\text{NLIVPS}} \ge \tilde{B}_{\text{NLIVPS}} \hfill \\ ({\text{iv}})\;\;Sc\left( {\tilde{A}_{\text{NLIVPS}} } \right) = Sc\left( {\tilde{B}_{\text{NLIVPS}} } \right) \Leftrightarrow (ii)\;and\;(iii) \hfill \\ \end{gathered} $$

Example 1

Let $\tilde{A}_{{\text{NLIVPS}}} = \left[ \begin{array}{llll} \left\{ ( \left( {4.2,4.5,5,6,6.7;0.85,0.15} \right),\right.\\ \left.\left( {4.3,4.8,5,5.5,6.5;0.65,0.05} \right) )_{{\left( {g_{1} ,g_{2} ,h_{1} ,h_{2} } \right)}} \right\}, \hfill \\ \left\{ ( \left( {4.4,4.7,5,5.8,6.2;0.25,0.65} \right),\right.\\ \left.\left( {4.6,4.9,5,5.7,6.1;0.05,0.45} \right))_{{\left( {g_{1} ,g_{2} ,h_{1} ,h_{2} } \right)}} \right\} \hfill \\ \end{array} \right]$ and $\tilde{B}_{{\text{NLIVPS}}} = \left[ \begin{array}{llll}\left\{(\left({3,3.5,4,4.5,5.7;0.75,0.65} \right),\right.\\\left.\left( {3.3,3.6,4,4.4,5.5;0.75,0.55} \right))_{{\left( {g_{1},g_{2} ,h_{1} ,h_{2} } \right)}} \right\}, \hfill \\\left\{(\left( {3.2,3.7,4,4.8,5.2;0.05,0.35} \right),\right.\\ \left.\left( {3.6,3.9,4,4.7,5.1;0.20,0.45} \right) )_{{\left({g_{1},g_{2} ,h_{1} ,h_{2} } \right)}} \right\} \hfill \\\end{array} \right]$ be two NLIVIFNs then $Sc\left( {\tilde{A}_{\text{NLIVPS}} } \right) = 4.864$ and $Sc\left( {\tilde{B}_{\text{NLIVPS}} } \right) = 3.922$.

Therefore, $Sc\left( {\tilde{A}_{\text{NLIVPS}} } \right) \ge Sc\left( {\tilde{B}_{\text{NLIVPS}} } \right) \Rightarrow \tilde{A}_{\text{NLIVPS}} \ge \tilde{B}_{\text{NLIVPS}}$. Similarly it can be satisfied all other properties of Definition 4.1.

Interval Valued Pentagonal Intuitionistic Fuzzy Multi Objective Linear Programming Problem (IVPIFMOLPP)

The majority of the time, real-world challenges show the simultaneous optimization of many objectives. The best compromise solution is the most promising solution set that effectively addresses each objective. A MOLPP with $k$ objectives may be taken:

$$ \begin{aligned} & \text{Minimum}\;\;\Theta \left( x \right) = \left[ {\Theta_{1} \left( x \right),\Theta_{2} \left( x \right), \ldots \Theta_{k} \left( x \right)} \right]^{T} \\ & {\text{Subject}}\;{\text{to}} \\ & \quad \quad \quad \quad \sum\limits_{q = 1}^{Q} {a_{pq} x_{q} \left( x \right)} \ge b_{p} ,\;p = 1,2,...,P_{1} \\ & \quad \quad \quad \quad \sum\limits_{q = 1}^{Q} {a_{pq} x_{q} \left( x \right)} \le b_{p} ,\;p = P_{1} + 1,P_{1} + 2,...,P_{2} \\ & \quad \quad \quad \quad \sum\limits_{q = 1}^{Q} {a_{pq} x_{q} \left( x \right)} = b_{p} \,,\;p = P_{2} + 1,P_{2} + 2,...,Q \\ & \quad \quad \quad \quad x_{q} \ge 0,q = 1,2,..,Q \end{aligned} $$

(2)

where $\Theta_{k} \left( x \right) = \sum\limits_{k = 1}^{K} {c_{kq} x_{q} } \;\forall k = 1,2,...,K$ the k-th objective is linear function $b_{p} ,\;\forall \;p = 1,2,...,P$ and $x_{q} ,\;\forall \;q = 1,2,...,Q$ are the right hand sides and the decision variables, respectively.

Definition 4.1

Suppose $\Lambda$ be the collection of feasible solution for (2) of MOSOP. Then a point $x^{*}$ is considered to be a Pareto optimal or efficient solution of (2) iff there exists no $x \in \Lambda$ such that $\Theta_{k} (x^{*} ) \ge \Theta_{k} (x)$ for all $k$ and $\Theta_{k} (x^{*} ) > \Theta_{k} (x)$ for at least one $k$.

Definition 4.2

A point $x^{*} \in \Lambda$ is called a weak Pareto optimal solution of (2) iff there exists no $x \in \Lambda$ such that $\Theta_{k} (x^{*} ) \ge \Theta_{k} (x)$ for all $k$.

In MOLPP (2), if all the parameters are IVIFN then it is termed as intuitionistic fuzzy MOLPP. It is supposed that all of the parameters in problem (3) are IVPIFN. As a result, the mathematical formulation of IVIFMOLPP is as follows:

$$ \begin{gathered} {\text{Minimum}}\;\;\tilde{\Theta }^{\text{IVPEN}} \left( x \right) = \left[ {\tilde{\Theta }_{1}^{\text{IVPEN}} \left( x \right),\tilde{\Theta }_{2}^{\text{IVPEN}} \left( x \right), \ldots \tilde{\Theta }_{k}^{\text{IVPEN}} \left( x \right)} \right]^{T} \hfill \\ {\text{Subject}}\;{\text{to}} \hfill \\ \quad \quad \quad \quad \sum\limits_{q = 1}^{Q} {\tilde{a}_{pq}^{\text{IVPEN}} x_{q} \left( x \right)} \ge \tilde{b}_{q}^{\text{IVPEN}} ,\;p = 1,2,...,P_{1} \hfill \\ \quad \quad \quad \quad \sum\limits_{q = 1}^{Q} {\tilde{a}_{pq}^{\text{IVPEN}} x_{q} \left( x \right)} \le \tilde{b}_{p}^{\text{IVPEN}} ,\;p = P_{1} + 1,P_{1} + 2,...,P_{2} \hfill \\ \quad \quad \quad \quad \sum\limits_{q = 1}^{Q} {\tilde{a}_{pq}^{\text{IVPEN}} x_{q} \left( x \right)} = \tilde{b}_{p}^{\text{IVPEN}} ,\;p = P_{2} + 1,P_{2} + 2,...,Q \hfill \\ \quad \quad \quad \quad x_{q} \ge 0,q = 1,2,..,Q \hfill \\ \end{gathered} $$

(3)

where $\tilde{\Theta }_{k}^{\text{IVPEN}} = \sum\nolimits_{k = 1}^{K} {\tilde{c}_{kq}^{\text{IVPEN}} x_{q} } \;\forall k = 1,2,...,K$ the k-th objective nonlinear function with interval is valued pentagonal intuitionistic fuzzy parameters.

Using mean of interval method for de-intuitification Problem (3) is transformed to the following crisp MOLPP:

$$ \begin{aligned} & \text{Minimum}\;\;\Theta ^{\prime}\left( x \right) = \left[ {\Theta ^{\prime}_{1} \left( x \right),\Theta ^{\prime}_{2} \left( x \right), \ldots \Theta ^{\prime}_{k} \left( x \right)} \right]^{T} \\ & {\text{Subject}}\;{\text{to}} \\ & \quad \quad \quad \quad \sum\limits_{{q = 1}}^{Q} {a^{\prime}_{{pq}} x_{q} \left( x \right)} \ge b^{\prime}_{p} ,\;p = 1,2, \ldots ,P_{1} \\ & \quad \quad \quad \quad \sum\limits_{{q = 1}}^{Q} {a^{\prime}_{{pq}} x_{q} \left( x \right)} \le b^{\prime}_{p} ,\;p = P_{1} + 1,P_{1} + 2, \ldots ,P_{2} \\ & \quad \quad \quad \quad \sum\limits_{{q = 1}}^{Q} {a^{\prime}_{{pq}} x_{q} \left( x \right)} = b^{\prime}_{p} ,\;p = P_{2} + 1,P_{2} + 2, \ldots ,Q \\ & \quad \quad \quad \quad x_{q} \ge 0,q = 1,2, \ldots ,Q \end{aligned} $$

(4)

where $\Theta^{\prime}_{k} \left( x \right) = \sum\limits_{k = 1}^{K} {c^{\prime}_{kq} x_{q} } \;\forall k = 1,2,...,K$ the k-th objective is nonlinear function $b^{\prime}_{p} ,\;\forall \;p = 1,2,...,P$ and $x_{q} ,\;\forall \;q = 1,2,...,Q$ are the crisp version of all the objective functions and parameters.

Theorem 4.1

[49] An efficient solution for deterministic MOLPP is an efficient solution for (4).

As a result, using the mean of the interval approach for de-intuitification, the best solution for an intuitionistic fuzzy LPP may be readily turned into a deterministic LPP. Now we will move on to the MOLPP (4) solution techniques in a NEv.

Proposed Neutrosophic Fuzzy Approach

There are several approaches to solving a MOLPP. Based on the fuzzy set, several fuzzy optimization approaches have been developed. In the fuzzy programming technique, each objective function's marginal evaluation is solely represented by the membership functions, and it can be reached by maximization. By including approaches for intuitionistic fuzzy optimization, the fuzzy optimization method is expanded significantly because the membership and non-membership functions, which may be obtained by maximizing the membership and minimizing the non-membership functions, respectively, represent the marginal assessment of each objective function, it is significantly more sophisticated than the fuzzy technique. The complexity of real-life events creates the indeterminacy scenario while making the most appropriate decisions. Thus, Smarandache [47] investigated a neutrosophic set to cover the indeterminacy degree of the element into the feasible solution set. The NS incorporates three types of membership functions into the feasible solution set: truth, indeterminacy, and a falsity degree. The NS research domain would gain exposure in the future and aid in dealing with uncertainty in decision-making. Under the neutrosophic decision set, the truth, indeterminacy, and falsity membership functions quantify the marginal evaluation of each objective function.

Zimmermann [4] established that the MOPP can be solved using fuzzy programming techniques.

The following steps are used to solve the MOLPP.

Step 1: Calculate the MOLPP (4) as a single objective linear programming problem (SOLPP) by focusing on one goal at a time and overlooking the other objective functions which are called ideal solutions.

Step 2: The result obtained in step 1, the pay-off matrix can be constructed by determining the corresponding tabulated values for every objective function as follows:

In this case $x_{1} ,x_{2} , \ldots ,x_{k}$ are the optimal solutions of the objective functions $\Theta^{\prime}_{1} \left( x \right)$, $\Theta^{\prime}_{2} \left( x \right)$,…,$\Theta^{\prime}_{k} \left( x \right)$ correspondingly.

Step 3: The highest possible value in each column $U_{k}$ represents upper tolerance, upper bound, or greatest acceptable degree of success for the $k{\text{th}}$ objective function $\Theta^{\prime}_{k} \left( x \right)$, where $U_{k} = \max \left\{ {\Theta^{\prime}_{k} \left( {x_{{^{1} }} } \right),\Theta^{\prime}_{k} \left( {x_{{^{2} }} } \right), \ldots ,\Theta^{\prime}_{k} \left( {x_{{^{k} }} } \right)} \right\}$ and the minimum value of every column $L_{k}$ gives lower tolerance or lower bound limit for the $k^{th}$ objective function $\Theta^{\prime}_{k} \left( x \right)$, where $L_{k} = \min \left\{ {\Theta^{\prime}_{k} \left( {x_{{^{1} }} } \right),\Theta^{\prime}_{k} \left( {x_{{^{2} }} } \right), \ldots ,\Theta^{\prime}_{k} \left( {x_{{^{K} }} } \right)} \right\}$ for $k \in {\rm E}\;where\;{\rm E} = \left\{ {1,2, \ldots ,K} \right\}$.

$$ U_{k}^{\mu } = U_{k} ,L_{k}^{\mu } = L_{k} \;{\text{for}}\;{\text{truth}}\;{\text{membership}} $$

$$ L_{k}^{\nu } = U_{k}^{\mu } - s_{k} ,U_{k}^{\nu } = U_{k}^{\mu } \;{\text{for}}\;{\text{indeterminacy}}\;{\text{membership}} $$

$$ U_{k}^{\lambda } = U_{k}^{\mu } ,L_{k}^{\lambda } = L_{k}^{\mu } + t_{k} \;{\text{for}}\;{\text{falsity}}\;{\text{membership}} $$

where $0 \le s_{k} \le \left( {U_{k} - L_{k} } \right)$ and $0 \le t_{k} \le \left( {U_{k} - L_{k} } \right)$ are specific real numbers in $\left( {0,1} \right)$.

Step 4: Under a NF environment, we can now define the various membership functions as linear, parabolic, and hyperbolic. Each of them appears to be more accurate for the membership functions truth, indeterminacy, and falsity.

Linear Type Membership Function Technique (LTMFT)

The truth membership function of linear type $\mu_{k}^{LT} (\Theta^{\prime}(x))$, indeterminacy membership of linear type $\nu_{k}^{LT} (\Theta^{\prime}_{k} (x))$ and a falsity membership of linear type $\lambda_{k}^{LT} (\Theta^{\prime}_{k} (x))$ functions under NF environment can be explained in the following way

$$ \mu_{k}^{LT} \left( {\Theta^{\prime}_{k} \left( x \right)} \right) = \left\{ \begin{gathered} {1}\quad \quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{{\text{k}}} \left( x \right) \le L_{k}^{\mu } \hfill \\ \frac{{U_{k}^{\mu } - \Theta^{\prime}_{{\text{k}}} \left( x \right)}}{{U_{k}^{\mu } - L_{k}^{\mu } }} \, \;\;{\text{if }}L_{k}^{\mu } \le \Theta^{\prime}_{{\text{k}}} \left( x \right) \le U_{k}^{\mu } \hfill \\ {0}\quad \quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{{\text{k}}} \left( x \right) \ge U_{k}^{\mu } \hfill \\ \end{gathered} \right. $$

$$ \nu_{k}^{LT} \left( {\Theta^{\prime}_{k} \left( x \right)} \right) = \left\{ \begin{gathered} {1}\quad \quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{k} \left( x \right) \le L_{k}^{\nu } \hfill \\ \frac{{U_{k}^{\nu } - \Theta^{\prime}_{k} \left( x \right)}}{{U_{k}^{\nu } - L_{k}^{\nu } }} \, \;\;{\text{if }}L_{k}^{\nu } \le \Theta^{\prime}_{k} \left( x \right) \le U_{k}^{\nu } \hfill \\ {0}\quad \quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{k} \left( x \right) \ge U_{k}^{\nu } \hfill \\ \end{gathered} \right. $$

$$ \lambda_{k}^{LT} \left( {\Theta^{\prime}_{k} (x)} \right) = \left\{ \begin{gathered} {0}\quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{k} (x) \le L_{k}^{\lambda } \hfill \\ \frac{{\Theta^{\prime}_{k} (x) - L_{k}^{\lambda } }}{{U_{k}^{\lambda } - L_{k}^{\lambda } }}{\text{ if }}L_{k}^{\lambda } \le \Theta^{\prime}_{k} (x) \le U_{k}^{\lambda } \hfill \\ {1}\quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{k} (x) \ge U_{k}^{\lambda } \hfill \\ \end{gathered} \right. $$

The mathematical formula for objective functions is as follows

$$ \begin{gathered} {\text{Max }}\mathop {{\text{min}}}\limits_{{{\text{k = 1,2,}}..{\text{,K}}}} \mu_{k}^{LT} (\Theta^{\prime}_{k} (x)) \hfill \\ {\text{Max }}\mathop {{\text{min}}}\limits_{{{\text{k = 1,2,}}..{\text{,K}}}} \nu_{k}^{LT} (\Theta^{\prime}_{k} (x)) \hfill \\ {\text{Min }}\mathop {{\text{max}}}\limits_{{{\text{k = 1,2,}}..{\text{,K}}}} \lambda_{k}^{LT} (\Theta^{\prime}_{k} (x)) \hfill \\ \end{gathered} $$

(5)

$\left( {p = 1\;to\;P \in N} \right)$, subject to all constraints of (4).

Also assume that $\mu_{k}^{LT} (\Theta^{\prime}_{k} (x)) \ge \alpha ,\nu_{k}^{LT} (\Theta^{\prime}_{k} (x)) \ge \beta ,\lambda_{k}^{LT} (\Theta^{\prime}_{k} (x)) \le \gamma$ for all $k$.

Applying auxiliary parameters $\alpha ,\beta$ and $\gamma$, the following problem (5) may be changed to (6)

$$ \begin{gathered} {\text{Max}}\;\;\alpha + \beta - \gamma \hfill \\ s.t,\;\;\Theta^{\prime}_{k} (x) + \left( {U_{k}^{\mu } - L_{k}^{\mu } } \right)\alpha \le U_{k}^{\mu } , \hfill \\ \;\;\;\;\;\Theta^{\prime}_{k} (x) + \left( {U_{k}^{\nu } - L_{k}^{\nu } } \right)\beta \le U_{k}^{\nu } , \hfill \\ \;\;\;\;\;\Theta^{\prime}_{k} (x) - \left( {U_{k}^{\lambda } - L_{k}^{\lambda } } \right)\gamma \le L_{k}^{\lambda } , \hfill \\ \;\;\;\;\alpha \ge \beta ,\alpha \ge \gamma ,\alpha + \beta + \gamma \le 3,\alpha ,\beta ,\gamma \in \left( {0,1} \right) \hfill \\ \end{gathered} $$

(6)

all constraints of (4).

Parabolic Type Membership Function Technique (PTMFT)

The truth membership function of parabolic type $\mu_{k}^{PT} (\Theta^{\prime}(x))$, indeterminacy membership of parabolic type $\nu_{k}^{PT} (\Theta^{\prime}_{k} (x))$ and a falsity membership of parabolic type $\lambda_{k}^{PT} (\Theta^{\prime}_{k} (x))$ functions under NF environment can be explained in the following way

$$ \mu_{k}^{PT} \left( {\Theta^{\prime}_{k} \left( x \right)} \right) = \left\{ \begin{gathered} {1}\quad \quad \quad \quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{k} (x) \le L_{k}^{\mu } \hfill \\ \left( {\frac{{U_{k}^{\mu } - \Theta^{\prime}_{k} (x)}}{{U_{k}^{\mu } - L_{k}^{\mu } }}} \right)^{{2}} \, \;\;{\text{if }}L_{k}^{\mu } \le \Theta^{\prime}_{k} (x) \le U_{k}^{\mu } \hfill \\ {0}\quad \quad \quad \quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{k} (x) \ge U_{k}^{\mu } \hfill \\ \end{gathered} \right. $$

$$ \nu_{k}^{PT} \left( {\Theta^{\prime}_{k} \left( x \right)} \right) = \left\{ \begin{gathered} {1}\quad \quad \quad \quad \quad \quad \quad \;{\text{if }}\Theta^{\prime}_{k} \left( x \right) \le L_{k}^{\nu } \hfill \\ \left( {\frac{{U_{k}^{\nu } - \Theta^{\prime}_{k} \left( x \right)}}{{U_{k}^{\nu } - L_{k}^{\nu } }}} \right)^{{2}} {\text{ if }}L_{k}^{\nu } \le \Theta^{\prime}_{k} \left( x \right) \le U_{k}^{\nu } \hfill \\ {0}\quad \quad \quad \quad \quad \quad \quad \;{\text{if }}\Theta^{\prime}_{k} \left( x \right) \ge U_{k}^{\nu } \hfill \\ \end{gathered} \right. $$

$$ \lambda_{k}^{PT} \left( {\Theta^{\prime}_{k} (x)} \right) = \left\{ \begin{gathered} {0}\quad \quad \quad \quad \quad \quad \;\;{\text{if }}\Theta^{\prime}_{k} (x) \le L_{k}^{\lambda } \hfill \\ \left( {\frac{{\Theta^{\prime}_{k} (x) - L_{k}^{\lambda } }}{{U_{k}^{\lambda } - L_{k}^{\lambda } }}} \right)^{{2}} {\text{ if }}L_{k}^{\lambda } \le \Theta^{\prime}_{k} (x) \le U_{k}^{\lambda } \hfill \\ {1}\quad \quad \quad \quad \quad \quad \;\;{\text{if }}\Theta^{\prime}_{k} (x) \ge U_{k}^{\lambda } \hfill \\ \end{gathered} \right. $$

The mathematical formula for objective functions is as follows

$$ \begin{gathered} {\text{Max }}\mathop {{\text{min}}}\limits_{{{\text{k = 1,2,}}..{\text{,K}}}} \mu_{k}^{PT} (\Theta^{\prime}_{k} (x)) \hfill \\ {\text{Max }}\mathop {{\text{min}}}\limits_{{{\text{k = 1,2,}}..{\text{,K}}}} \nu_{k}^{PT} (\Theta^{\prime}_{k} (x)) \hfill \\ {\text{Min }}\mathop {{\text{max}}}\limits_{{{\text{k = 1,2,}}..{\text{,K}}}} \lambda_{k}^{PT} (\Theta^{\prime}_{k} (x)) \hfill \\ \end{gathered} $$

(7)

$\left( {p = 1\;to\;P \in N} \right)$, subject to all constraints of (4).

Also assume that $\mu_{k}^{PT} (\Theta^{\prime}_{k} (x)) \ge \alpha ,\nu_{k}^{PT} (\Theta^{\prime}_{k} (x)) \ge \beta ,\lambda_{k}^{PT} (\Theta^{\prime}_{k} (x)) \le \gamma$ for all $k$.

Applying auxiliary parameters $\alpha ,\beta$ and $\gamma$, the following problem (7) may be changed to (8)

$$ \begin{gathered} {\text{Max}}\;\;\alpha + \beta - \gamma \hfill \\ s.t,\;\;\left( {U_{k}^{\mu } - \Theta ^{\prime}_{k} (x)} \right)^{2} \ge \alpha \left( {U_{k}^{\mu } - L_{k}^{\mu } } \right)^{2} , \hfill \\ \;\;\;\;\;\left( {U_{k}^{\nu } - \Theta ^{\prime}_{k} \left( x \right)} \right)^{2} \ge \beta \left( {U_{k}^{\nu } - L_{k}^{\nu } } \right)^{2} , \hfill \\ \;\;\;\;\;\left( {\Theta ^{\prime}_{k} (x) - L_{k}^{\lambda } } \right)^{2} \le \gamma \left( {U_{k}^{\lambda } - L_{k}^{\lambda } } \right)^{2} , \hfill \\ \;\;\;\;\alpha \ge \beta ,\alpha \ge \gamma ,\alpha + \beta + \gamma \le 3,\alpha ,\beta ,\gamma \in \left( {0,1} \right) \hfill \\ \end{gathered} $$

(8)

all constraints of (4).

Hyperbolic type membership function technique (HTMFT)

The truth membership function of hyperbolic type $\mu_{k}^{HT} (\Theta^{\prime}(x))$, indeterminacy membership of hyperbolic type $\nu_{k}^{HT} (\Theta^{\prime}_{k} (x))$ and a falsity membership of hyperbolic type $\lambda_{k}^{HT} (\Theta^{\prime}_{k} (x))$ functions under NF environment can be explained in the following way

$$ \mu_{k}^{HT} \left( {\Theta^{\prime}_{k} \left( x \right)} \right) = \left\{ \begin{gathered} {1}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{{\text{k}}} \left( x \right) \le L_{k}^{\mu } \hfill \\ \frac{1}{2} + \frac{1}{2}\tanh \left\{ {\left( {\frac{{U_{k}^{\mu } + L_{k}^{\mu } }}{2} - \Theta^{\prime}_{{\text{k}}} \left( x \right)} \right)\tau_{k} } \right\}{\text{ if }}L_{k}^{\mu } \le \Theta^{\prime}_{{\text{k}}} \left( x \right) \le U_{k}^{\mu } \hfill \\ {0}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{{\text{k}}} \left( x \right) \ge U_{k}^{\mu } \hfill \\ \end{gathered} \right. $$

$$ \nu_{k}^{HT} \left( {\Theta^{\prime}_{k} \left( x \right)} \right) = \left\{ \begin{gathered} {1}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{{\text{k}}} \left( x \right) \le L_{k}^{\nu } \hfill \\ \frac{1}{2} + \frac{1}{2}\tanh \left\{ {\left( {\frac{{U_{k}^{\nu } + L_{k}^{\nu } }}{2} - \Theta^{\prime}_{{\text{k}}} \left( x \right)} \right)\tau_{k} } \right\}{\text{ if }}L_{k}^{\nu } \le \Theta^{\prime}_{{\text{k}}} \left( x \right) \le U_{k}^{\nu } \hfill \\ {0}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{if }}\Theta^{\prime}_{{\text{k}}} \left( x \right) \ge U_{k}^{\nu } \hfill \\ \end{gathered} \right. $$

$$ \lambda_{k}^{HT} \left( {\Theta^{\prime}_{k} (x)} \right) = \left\{ \begin{gathered} {0}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;{\text{if }}\Theta^{\prime}_{k} (x) \le L_{k}^{\lambda } \hfill \\ \frac{1}{2} + \frac{1}{2}\tanh \left\{ {\left( {\Theta^{\prime}_{k} (x) - \frac{{U_{k}^{\lambda } + L_{k}^{\lambda } }}{2}} \right)\tau_{k} } \right\}{\text{ if }}L_{k}^{\lambda } \le \Theta^{\prime}_{k} (x) \le U_{k}^{\lambda } \hfill \\ {1}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;{\text{if }}\Theta^{\prime}_{k} (x) \ge U_{k}^{\lambda } \hfill \\ \end{gathered} \right. $$

The mathematical formula for objective functions is as follows

$$ \begin{gathered} {\text{Max }}\mathop {{\text{min}}}\limits_{{{\text{k = 1,2,}}..{\text{,K}}}} \mu_{k}^{HT} (\Theta^{\prime}_{k} (x)) \hfill \\ {\text{Max }}\mathop {{\text{min}}}\limits_{{{\text{k = 1,2,}}..{\text{,K}}}} \nu_{k}^{HT} (\Theta^{\prime}_{k} (x)) \hfill \\ {\text{Min }}\mathop {{\text{max}}}\limits_{{{\text{k = 1,2,}}..{\text{,K}}}} \lambda_{k}^{HT} (\Theta^{\prime}_{k} (x)) \hfill \\ \end{gathered} $$

(9)

$\left( {p = 1\;to\;P \in N} \right)$, subject to all constraints of (4).

Also assume that $\mu_{k}^{HT} (\Theta^{\prime}_{k} (x)) \ge \alpha ,\nu_{k}^{HT} (\Theta^{\prime}_{k} (x)) \ge \beta ,\lambda_{k}^{HT} (\Theta^{\prime}_{k} (x)) \le \gamma$ for all $k$.

Where the parameter $t > 0$. Applying auxiliary parameters $\alpha ,\beta$ and $\gamma$, the following problem (9) can be transformed to (10)

$$ \begin{gathered} {\text{Max}}\;\;\alpha + \beta - \gamma \hfill \\ s.t,\;\;\Theta^{\prime}_{k} (x)\tau_{k} + \tanh^{ - 1} \left( {2\alpha - 1} \right) \le \frac{{\tau_{k} }}{2}\left( {U_{k}^{\mu } + L_{k}^{\mu } } \right), \hfill \\ \;\;\;\;\;\Theta^{\prime}_{k} (x)\tau_{k} + \tanh^{ - 1} \left( {2\beta - 1} \right) \le \frac{{\tau_{k} }}{2}\left( {U_{k}^{\nu } + L_{k}^{\nu } } \right), \hfill \\ \;\;\;\;\;\Theta^{\prime}_{k} (x)\tau_{k} - \tanh^{ - 1} \left( {2\gamma - 1} \right) \le \frac{{\tau_{k} }}{2}\left( {U_{k}^{\lambda } + L_{k}^{\lambda } } \right), \hfill \\ \;\;\;\tau_{k} = \frac{6}{{U_{k} - L_{k} }}\;,\alpha \ge \beta ,\alpha \ge \gamma ,\alpha + \beta + \gamma \le 3,\alpha ,\beta ,\gamma \in \left( {0,1} \right) \hfill \\ \end{gathered} $$

(10)

all constraints of (3).

Computational Algorithm for MOLPP using NFPA

Step 1. Formulate the IVIFMOLPP in the manner given in the issue (3).

Step 2. Using the mean of interval method for defuzzification, produce the crisp version of IVIFMOLPP as shown in (4).

Step 3.Solve each objective function separately and use the above payoff matrix to get the upper and lower limits.

Step 4. Determine the upper and lower limit for the truth, indeterminacy, and falsity membership functions in a NEv using $U_{k}$ and $L_{k}$.

Step 5. Elicit the various sorts of membership functions in a NEv by using Eqs. (5–6), (7–8) and (9–10) according to decision-makers’ preference respectively.

Step 6. Create the neutrosophic optimization models such as LTMFT, PTMFT and HTMFT under the given set of well-defined constraints.

Step 7. Apply the proper techniques or various optimization software packages to the neutrosophic MOLPPs (5), (7) and (9) to find the best compromise outcomes.

Numerical Illustrations

This numerical example assumes that the IVPIFN represents all the parameters. Thus the mathematical formulation of the problem is as follows:

$$ \begin{gathered} \text{Minimize}\,\widetilde{{Z_{1} }}^{\text{IVPFN}} \left( {x_{1} ,x_{2} } \right) = \widetilde{{5_{a} }}^{\text{IVPFN}} x_{1} + \widetilde{3}^{\text{IVPFN}} x_{2} \hfill \\ Minimize\, \widetilde{{Z_{2} }}^{\text{IVPFN}} \left( {x_{1} ,x_{2} } \right) = \widetilde{{2_{a} }}^{\text{IVPFN}} x_{1} + \widetilde{7}^{\text{IVPFN}} x_{2} \hfill \\ \text{subject}\,\,to\,\widetilde{{2_{b} }}^{\text{IVPFN}} x_{1} + \widetilde{{4_{a} }}^{\text{IVPFN}} x_{2} \ge \widetilde{25}^{\text{IVPFN}} \hfill \\ \widetilde{{1_{a} }}^{\text{IVPFN}} x_{1} + \widetilde{{1_{b} }}^{\text{IVPFN}} x_{2} \ge \widetilde{10}^{\text{IVPFN}} \hfill \\ \widetilde{{4_{b} }}^{\text{IVPFN}} x_{1} + \widetilde{{5_{b} }}^{\text{IVPFN}} x_{2} \le \widetilde{50}^{\text{IVPFN}} \hfill \\ x_{1} ,x_{2} \ge 0 \hfill \\ \end{gathered} $$

(11)

Using the mean of interval method for de-intuitification (where, $\phi_{1} = \phi_{2} = \psi_{1} = \psi_{2} = 2$), the crisp version of the Problem (11) can be depicted as follows:

$$ \begin{gathered} {\text{Minimize}}\,\,\,Z_{1}^{\prime } \left( {x_{1} ,x_{2} } \right) = {4}{\text{.809625}}x_{1} + {3}{\text{.328582}}x_{2} \hfill \\ {\text{Minimize}}\,\,Z_{2}^{\prime } \left( {x_{1} ,x_{2} } \right) = {2}{\text{.375412}}x_{1} + {6}{\text{.403215}}x_{2} \hfill \\ {\text{subject}}\;to\,\,\,{1}{\text{.865901}}x_{1} + {3}{\text{.624509}}x_{2} \ge {23}{\text{.87733}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;{0}{\text{.8950513}}x_{1} + {1}{\text{.082045}}x_{2} \ge {9}{\text{.031410}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;\;{3}{\text{.826359}}x_{1} + {5}{\text{.117060}}x_{2} \le {51}{\text{.34778}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x_{1} ,x_{2} \ge 0 \hfill \\ \end{gathered} $$

(12)

The optimal solution for addressing the neutrosophic optimization models (5), (7), and (9), are compiled in Table 1. It is obvious that for all membership functions, the objective values outperform the [44] technique. Additionally, the suggested neutrosophic performance metrics of different membership functions may be shown as Hyperbolic > Parabolic > Linear.

Table 1 Optimal solution

The presented approach is based on the neotrosophic fuzzy approach (NFA), which includes different membership functions, which provide more flexibility in a decision-making process than intuitionistic fuzzy approach (IFA). To show the efficiency of proposed NFA based on de-intuitification method on MOLPP has been compared to other existing approach IFA based on de-intuitification method. The proposed method applied in three different membership functions: linear type, parabolic type and hyperbolic type under NFA. The obtained result has been summarized in Table 2. From Table 2, it is clear that the objective values of proposed approached under different type membership functions are minimum as compared to the IFA. Thus, the proposed method is superior as compared to IFA.

Table 2 Comparative result analysis based on de-intuitification method

Conclusions

In this paper, we introduced the idea of NLIVPIFNs along with their graphical classifications. Here, many IVPIFN configurations and their geometrical symmetry and asymmetry-based scenarios are discussed. Additionally, a new de-intuitification technique utilizing the alpha/beta cut approach is created in the nonlinear IVPIFN arena. In this study, an effective modeling and optimization framework for the IVPIFMOLPP is described under neutrosophic fuzzy uncertainty. The IVPIFMOLPP is transformed to crisp version of MOLPP by using the mean of interval method for de-intuitification. The suggested optimization method was developed in a NEv with a degree of independent indeterminacy in decision-making. Introduction of a variety of membership functions gives the DM the freedom to select the membership function that best fits the challenge. Due to the degree of uncertainty, the usage of linear, parabolic, and hyperbolic membership functions makes decision-making procedures more flexible and realistic while achieving the ideal compromise solution. The solution obtained results by our suggested neutrosophic optimization technique outperforms as compared to others numerical example as we discussed. Table 1 shows that solutions are superior in the case of a hyperbolic membership function for the given numerical problem. Thus, the model’s efficiency in terms of DM satisfaction or achievement may be categorized as Hyperbolic > Parabolic > Linear. The other flexibility in this situation is the option to select a solution based on the importance of the goals. In other aspects, the DM can use the membership function, which offers a more appropriate solution for the higher-priority objective function. The proposed method addresses these deficiencies and provides a worldwide solution.

Future Research Scope

Multi objective optimization is one of the most and widely utilized decision making methods. MOOP became very helpful and popular due to its intriguing philosophy and great applicability in resolving actual decision-making issues involving several objective structures. Our proposed approach might be used in the following fields of research:

• Our proposed method may be used in nonlinear optimization problems with hesitantly and uncertainty.

• It may use in real life decision making of multi objective nonlinear programming, transportations, and assignment problems.

• It can be expanded to handle issues involving multi objective fractional programming.

• For better decision making, it might be applied in game theory as well as goal programming problem with uncertainty and hesitation.

• It may be implemented in multi objective stochastic linear programming problem.

• Our suggested computational technique can be further enhanced for the agricultural, industrial and health management sectors as well, and it may be successfully applied in the variety of field like design of aircraft control system, chemical engineering with multiple objectives, supply chain management, and industrial neural network design.

• It may be applied in the new domain of fermatean neutrosophic environment like Interval- valued fermatean neutrosophic environment [8], Complex fermatean neutrosophic environment [7] etc.