1 Introduction

In today’s highly competitive market, the pressure on a construction agency is to find better ways to attain the optimal solution. In conventional optimization problems, it is assumed that the decision maker is sure about the precise values of data involved in the model. But in real-world applications, all the parameters of the optimization problems may not be known precisely due to uncontrollable factors. Such type of imprecise data is well represented by fuzzy number introduced by Zadeh [1].

In reality, a decision maker may assume that an object belongs to a set to a certain degree, but it is probable that he is not sure about it. In other words, there may be uncertainty about the membership degree. The main premise is that the parameters’ demand across the problem is uncertain. So, they are known to fall within a prescribed uncertainty set with some attributed degree. In fuzzy set (FS) theory, there is no means to incorporate this hesitation in the membership degree. To incorporate the uncertainty in the membership degree, intuitionistic fuzzy set (IFS) proposed by Atanassov [2] is an extension of FS theory. In IFS theory along with degree of membership, a degree of non-membership is usually considered to express ill-known quantity. This degree of membership and non-membership functions are so defined as they are independent to each other, and sum of them is less or equal to one. Hence, IFS is playing an important role in decision making under uncertainty and has gained popularity in recent years. However, an application of the IFSs to optimization problems is introduced by Angelov [3]. His technique is based on maximizing the degree of membership and minimizing the degree of non-membership, and the crisp model is formulated using the IF aggregation operator.

Now the fact is that in IFS indeterminate information is partially lost, as hesitant information is taken in consideration by default. So indeterminate information should be considered in decision-making process. Smarandache [4] defined neutrosophic set that could handle indeterminate and inconsistent information. In neutrosophic sets, indeterminacy is quantified explicitly as indeterminacy membership along with truth membership and falsity membership functions which are independent. Wang et al. [5] define single-valued neutrosophic set which represents imprecise, incomplete, indeterminate, inconsistent information. Thus, taking the universe as a real line, we can develop the concept of single-valued neutrosophic set as special case of neutrosophic sets. This set is able to express ill-known quantity with uncertain numerical value in decision-making problem. It helps more adequately to represent situations where decision makers abstain from expressing their assessments.

In this way, neutrosophic set provides a richer tool to grasp impression and ambiguity than the conventional FS as well as IFSs. Although exactly known, partially unknown and uncertain information handled by fully utilizing the properties of transition rate matrices, together with the convexification of uncertain domains [6,7,8], NSO is more realistic in application of optimum design. These characteristics of neutrosophic set led to the extension of optimization methods in neutrosophic environment (NSE).

Besides, it has been seen that the current research on fuzzy mathematical programming is limited to the range of linear programming introduced by Ziemmermann [9]. It has been shown that the solutions of fuzzy linear programming problems (FLPPs) are always efficient. The most common approach for solving fuzzy linear programming problem is to change it into corresponding crisp linear programming problem.

But practically there exist so many nonlinear structural designs such as welded beam design problem in various fields of engineering. So development of nonlinear programming is also essential. Recently, a robust and reliable static output feedback (SOF) control for nonlinear systems [24] and for continuous-time nonlinear stochastic systems [25] with actuator fault in a descriptor system framework has been studied. However, welding can be defined as a process of joining metallic parts by heating to a suitable temperature with or without the application of pressure. This cost of welding should be economical, and welded beam should be durable one.

Since decades, deterministic optimization has been widely used in practice for optimizing welded connection design. These include mathematical traditional optimization algorithms such as David–Fletcher–Powell with a penalty function (DAVID) [10], Griffith and Stewart’s successive linear approximation (APPROX) [10], simplex method with penalty function (SIMPLEX) [10], Recherdson’s random method (RANDOM) [10], harmony search method [11], GA-based method [12, 13], improved harmony search algorithm [14], simple constrained particle swarm optimizer (SiC-PSO) [15], Mezura [16], constrained optimization via PSO algorithm (COPSO) [17], GA based on a coevolution model (GA1) [13], GA through the use of dominance-based tournament selection (GA2) [18], evolutionary programming with a cultural algorithm (EP) [19], coevolutionary particle swarm optimization (CPSO) [20], hybrid particle swarm optimization (HPSO) with a feasibility-based rule [21], hybrid Nelder–Mead simplex search method and particle swarm optimization (NM-PSO) [22], particle swarm optimization (PSO) [23], simulate anneling (SA) [23], Goldlike (GL) [23], cuckoo search (Cuckoo) [23], firefly algorithm (FF), flower pollination (FP) [23], ant lion optimizer (ALO) [23], gravitational search algorithm (GSA) [23], multi-verse optimizer (MVO) [23]. All these deterministic optimizations aim to search the optimum solution under given constraints without consideration of uncertainties.

So these traditional techniques cannot be applicable in optimizing welded beam design when impreciseness is involved in information. Thus, the research on optimization for nonlinear programming under fuzzy, IF and neutrosophic environment is not only necessary in the fuzzy optimization theory but also has great and wide value in application to welded beam design problem of conflicting and imprecise nature. This is the motivation of our present investigation.

In this regard, it can be cited that Das et al. [26] developed neutrosophic nonlinear programming with numerical example and application of real-life problem recently. A single-objective plane truss structure [27] and a multi-objective plane truss structure [28] have been optimized in IF environment. A multi-objective structural model has been optimized by IF mathematical programming with IF number for truss structure [29], welded beam structure [36] and neutrosophic number for truss design [35] as coefficient of objective by Sarkar et al. With the help of linear membership [30] and nonlinear membership [31, 32], single-objective truss design and multi-objective truss design [33] have been optimized in neutrosophic environment. A multi-objective goal programming technique [34], T-norm and T-conorm-based IF optimization technique [37] have been developed to optimize cost of welding in neutrosophic and IF environment, respectively.

The aim of this paper is to show the efficiency of single-objective NSO technique in finding optimum cost of welding of welded beam in imprecise environment and to make a comparison of results obtained from different deterministic methods.

The paper is organized as follows. In Sect. 2, we have presented mathematical preliminaries on neutrosophic set.

In Sect. 3, we have developed mathematical algorithm to solve a single-objective nonlinear programming problem. In Sect. 4, we have studied in detail formulation of welded beam by solving it using NSO technique. In Sect. 5, we have solved welded beam design model numerically. Lastly in Sect. 6, we arrive at a conclusion.

2 Mathematical Preliminaries

In the following, we briefly describe some basic concepts and basic operational laws related to neutrosophic set [1, 2, 5, 26].

2.1 Fuzzy Set (FS) [1]

Let X be a fixed set. A fuzzy set \(\tilde{A}\) of X is an object having the form

$$\tilde{A} = \left\{ {\left. {\left( {x,T_{{\tilde{A}}} \left( x \right)} \right)} \right|x \in X} \right\}$$
(1)

where the function \(T_{{\tilde{A}}} :X \to \left[ {0,1} \right]\) stands for the truth membership of the element to the set \(\tilde{A}\).

2.2 Intuitionistic Fuzzy Set (IFS) [2]

Let a set X be fixed. An intuitionistic fuzzy set or IFS \(\tilde{A}^{i}\) in X is an object of the form

$$\tilde{A}^{i} = \left\{ {\left( {X,T_{{\tilde{A}^{i} }} \left( x \right),F_{{\tilde{A}^{i} }} \left( x \right)} \right)\left| {x \in X} \right.} \right\}$$
(2)

where \(T_{{\tilde{A}^{i} }} :X \to \left[ {0,1} \right]\) and \(F_{{\tilde{A}^{i} }} :X \to \left[ {0,1} \right]\) define the truth membership and falsity membership, respectively, for every element of \(x \in X\) such that \(0 \le T_{{\tilde{A}^{i} }} \left( x \right) + F_{{\tilde{A}^{i} }} \left( x \right) \le 1\).

2.3 Single-Valued Neutrosophic Set (SVNS) [5]

Let a set X be the universe of discourse. A single-valued neutrosophic set \(\tilde{A}^{n}\) over X is an object having the form

$$\tilde{A}^{n} = \left\{ {\left( {x,T_{{\tilde{A}^{n} }} \left( x \right),I_{{\tilde{A}^{n} }} \left( x \right),F_{{\tilde{A}^{n} }} \left( x \right)} \right)\left| {x \in X} \right.} \right\}$$
(3)

where \(T_{{\tilde{A}^{n} }} :X \to \left[ {0,1} \right],\;\,I_{{\tilde{A}^{n} }} :X \to \left[ {0,1} \right]\) and \(F_{{\tilde{A}^{n} }} :X \to \left[ {0,1} \right]\) are truth indeterminacy and falsity membership functions, respectively, so as to \(0 \le T_{{\tilde{A}^{n} }} \left( x \right) + I_{{\tilde{A}^{n} }} \left( x \right) + F_{{\tilde{A}^{n} }} \left( x \right) \le 3\) for all \(x \in X\).

2.4 Union of Neutrosophic Sets (NSs) [26]

The union of two single-valued neutrosophic sets \(\tilde{A}^{n}\) and \(\tilde{B}^{n}\) is a single-valued neutrosophic set \(\tilde{U}^{n}\) denoted by

$$\tilde{U}^{n} = \tilde{A}^{n} \cup \tilde{B}^{n} = \left\{ {\left( {x,T_{{\tilde{U}^{n} }} \left( x \right),I_{{\tilde{U}^{n} }} \left( x \right),F_{{\tilde{U}^{n} }} \left( x \right)} \right)\left| {x \in X} \right.} \right\}$$
(4)

and is defined by the following conditions

(i) \(T_{{\tilde{U}^{n} }} \left( x \right) = \hbox{max} \left( {T_{{\tilde{A}^{n} }} \left( x \right),T_{{\tilde{B}^{n} }} \left( x \right)} \right),\)

(ii) \(I_{{\tilde{U}^{n} }} \left( x \right) = \hbox{max} \left( {I_{{\tilde{A}^{n} }} \left( x \right),I_{{\tilde{B}^{n} }} \left( x \right)} \right),\)

(iii) \(F_{{\tilde{U}^{n} }} \left( x \right) = \hbox{min} \left( {F_{{\tilde{A}^{n} }} \left( x \right),F_{{\tilde{B}^{n} }} \left( x \right)} \right)\) for all \(x \in X\) for Type-I

Or in another way by defining following conditions

(i) \(T_{{\tilde{U}^{n} }} \left( x \right) = \hbox{max} \left( {T_{{\tilde{A}^{n} }} \left( x \right),T_{{\tilde{B}^{n} }} \left( x \right)} \right),\)

(ii) \(I_{{\tilde{U}^{n} }} \left( x \right) = \hbox{min} \left( {I_{{\tilde{A}^{n} }} \left( x \right),I_{{\tilde{B}^{n} }} \left( x \right)} \right)\)

(iii) \(F_{{\tilde{U}^{n} }} \left( x \right) = \hbox{min} \left( {F_{{\tilde{A}^{n} }} \left( x \right),F_{{\tilde{B}^{n} }} \left( x \right)} \right)\) for all \(x \in X\) for Type-II, where \(T_{{\tilde{U}^{n} }} \left( x \right),\;I_{{\tilde{U}^{n} }} \left( x \right),\;I_{{\tilde{U}^{n} }} \left( x \right),\;F_{{\tilde{U}^{n} }} \left( x \right)\) represent truth membership, indeterminacy membership and falsity membership functions of union of neutrosophic sets.

Example

Let \(\tilde{A}^{n} = <0.3,0.4,0.5{>}{/}x_{1} + <0.5,0.2,0.3{>}{/}x_{2} + <0.7,0.2,0.2{>}{/}x_{3}\) and \(\tilde{B}^{n} = <0.6,0.1,0.2{>}{/}x_{1} + <0.3,0.2,0.6{>}{/}x_{2} + <0.4,0.1,0.5{>}{/}x_{3}\) be two neutrosophic sets. Then, the union of \(\tilde{A}^{n}\) and \(\tilde{B}^{n}\) is a single-valued neutrosophic set that can be calculated for Type-I as

$$\tilde{A}^{n} \cup \tilde{B}^{n} = < 0.6,0.4,0.2{>}{/}x_{1} + < 0.5,0.2,0.3{>}{/}x_{2} + < 0.7,0.2,0.2{>}{/}x_{3}$$
(5)

and for Type-II as

$$\tilde{A}^{n} \cup \tilde{B}^{n} = < 0.6,0.1,0.2{>}{/}x_{1} + < 0.5,0.2,0.3{>}{/}x_{2} + < 0.7,0.1,0.2{>}{/}x_{3}$$
(6)

2.5 Intersection of Neutrosophic Sets [26]

The intersection of two single-valued neutrosophic sets \(\tilde{A}^{n}\) and \(\tilde{B}^{n}\) is a single-valued neutrosophic set \(\tilde{E}^{n}\) that is denoted by

$$\tilde{E}^{n} = \tilde{A}^{n} \cap \tilde{B}^{n} = \left\{ {\left( {x,T_{{\tilde{E}^{n} }} \left( x \right),I_{{\tilde{E}^{n} }} \left( x \right),F_{{\tilde{E}^{n} }} \left( x \right)} \right)\left| {x \in X} \right.} \right\}$$
(7)

and is defined by the following conditions

(i) \(T_{{\tilde{E}^{n} }} \left( x \right) = \hbox{min} \left( {T_{{\tilde{A}^{n} }} \left( x \right),T_{{\tilde{B}^{n} }} \left( x \right)} \right),\)

(ii) \(I_{{\tilde{E}^{n} }} \left( x \right) = \hbox{min} \left( {I_{{\tilde{A}^{n} }} \left( x \right),I_{{\tilde{B}^{n} }} \left( x \right)} \right),\)

(iii) \(F_{{\tilde{E}^{n} }} \left( x \right) = \hbox{max} \left( {F_{{\tilde{A}^{n} }} \left( x \right),F_{{\tilde{B}^{n} }} \left( x \right)} \right)\) for all \(x \in X\) for Type-I

Or in another way by defining following conditions

(i) \(T_{{\tilde{E}^{n} }} \left( x \right) = \hbox{min} \left( {T_{{\tilde{A}^{n} }} \left( x \right),T_{{\tilde{B}^{n} }} \left( x \right)} \right),\)

(ii) \(I_{{\tilde{E}^{n} }} \left( x \right) = \hbox{max} \left( {I_{{\tilde{A}^{n} }} \left( x \right),I_{{\tilde{B}^{n} }} \left( x \right)} \right)\)

(iii) \(F_{{\tilde{E}^{n} }} \left( x \right) = \hbox{max} \left( {F_{{\tilde{A}^{n} }} \left( x \right),F_{{\tilde{B}^{n} }} \left( x \right)} \right)\) for all \(x \in X\) for Type-II, where \(T_{{\tilde{E}^{n} }} \left( x \right),\) \(I_{{\tilde{E}^{n} }} \left( x \right),\) \(F_{{\tilde{E}^{n} }} \left( x \right)\) represent truth membership, indeterminacy membership and falsity membership functions of union of neutrosophic sets.

Example

Let \(\tilde{A}^{n} = < 0.3,0.4,0.5 {>}{/}x_{1} + < 0.5,0.2,0.3 {>}{/}x_{2} + < 0.7,0.2,0.2 {>}{/}x_{3}\) and \(\tilde{B}^{n} = < 0.6,0.1,0.2 {>}{/}x_{1} + < 0.3,0.2,0.6 {>}{/}x_{2} + < 0.4,0.1,0.5 {>}{/}x_{3}\) be two neutrosophic sets. Then, the intersection of \(\tilde{A}^{n} and \,\tilde{B}^{n}\) is a single-valued neutrosophic set that can be measured for Type-I as

$$\tilde{A}^{n} \cap \tilde{B}^{n} = < 0.3,0.1,0.5{>}{/}x_{1} + < 0.3,0.2,0.6{>}{/}x_{2} + < 0.4,0.1,0.5{>}{/}x_{3}$$
(8)

and for Type-II as

$$\tilde{A}^{n} \cap \tilde{B}^{n} = < 0.3,0.4,0.5{>}{/}x_{1} + < 0.3,0.2,0.6 {>}{/}x_{2} + < 0.4,0.2,0.5 {>}{/}x_{3}$$
(9)

3 Mathematical Analysis

Decision making is nothing but a process of solving the problem that achieves goals under constraints. The outcome of the problem is a decision which should in an action. Decision making plays an important role in different subjects such as field of economic and business, management sciences, engineering and manufacturing, social and political science, biology and medicine, military, computer science. It faces difficulty in progress due to factors like incomplete and imprecise information which is often present in real-life situations. In the decision-making process, the decision maker’s main target is to find the value from the selected set with the highest degree of membership in the decision set and these values support the goals under constraints only. But while vegueness exists in available information there may arise situations where some values from selected set cannot support, rather such values strongly against the goals under constraints which are non-admissible. In this case, we find such values from the selected set with least degree of non-membership in the decision sets. IFSs can only handle incomplete information not the indeterminate information and inconsistent information which exists commonly belief in system. In neutrosophic set, indeterminacy is quantified explicitly and truth membership, indeterminacy membership and falsity membership are independent to each other. So it is natural to adopt for that purpose the value from the selected set with highest degree of truth membership, highest degree or least degree of indeterminacy membership and least degree of falsity membership on the decision set. These factors indicate that a decision-making process takes place in neutrosophic environment.

3.1 Neutrosophic Optimization (NSO) Technique to Solve Single-Objective Nonlinear Programming Problem (SONLPP)

A nonlinear programming problem (NLPP) may be considered in the following form

$${\text{Minimize}}\;g(x)$$
(10)

subject to,

$$g_{j} \left( x \right) \le b_{j} ;j = 1,2, \ldots ,m$$
(11)
$$x \ge 0$$
(12)

Usually constraint goals are considered as fixed quantity. But in real-life problems, the constraint goals cannot be always exact. So we can consider the constraint goals for minimization type non-linear programming problem at least \(b_{j}\), and it may be possible to extend to \(b_{j} + b_{j}^{0}\) for \(j = 1,2, \ldots ,m\). This fact seems to take the constraint goals as a neutrosophic set, and it will be more realistic descriptions than others. Then, NSO problem with neutrosophic goals can be described as follows:

$${\text{Minimize}}\,\,\,\,g\left( x \right)$$
(13)

subject to,

$$g_{j} \left( x \right)\tilde{ \le }^{n} b_{j} ,\;j = 1,2, \ldots ,m$$
(14)
$$x \ge 0\;{\text{where}}\;\tilde{ \le }^{n} \;{\text{represents inequality in neutrosophic sense}}.$$
(15)

In the case of degree of falsity membership and indeterminacy membership, it is to define simultaneously with degree of truth membership of the objective and constraint and while all these three degrees are independent of each other, NSO can be used as a more general tool to describe this uncertainty. Considering maximization of the degree of truth membership together with minimization or maximization of the degree of indeterminacy as per decision maker’s choice and minimizing degree of falsity membership of neutrosophic fuzzy objective and constraints, we can formulate a NSO technique to solve a neutrosophic nonlinear programming (NSNLP) (Eqs. 13–15) problem.

To solve the NSNLP (Eqs. 13–15), following Warner’s [38] and Angelov [3] we are presenting a solution procedure by successive steps as follows:

Step-1 Following Warner’s approach, solve the SONLPP without tolerance in constraints, with tolerance of truth membership in constraints (i.e., \(g_{j} \left( x \right) \le b_{j} + b_{j}^{0}\)) by appropriate nonlinear programming technique. Here they are,

Subproblem 1

$${\text{Minimize}}\,\,\,\,g\left( x \right)$$
(16)

subject to,

$$\,g_{j} \left( x \right) \le b_{j} ;\;j = 1,2, \ldots ,m$$
(17)
$$x \ge 0$$
(18)

Subproblem 2

$${\text{Minimize}}\,\,\,\,g\left( x \right)$$
(19)

subject to,

$$g_{j} \left( x \right) \le b_{j} + b_{j}^{0} ,\;j = 1,2, \ldots ,m$$
(20)
$$x \ge 0$$
(21)

we may get optimal solutions \(x^{*} = x^{1} ,g\left( {x^{*} } \right) = g\left( {x^{1} } \right)\) and \(x^{*} = x^{2} ,g\left( {x^{*} } \right) = g\left( {x^{2} } \right)\) for subproblems 1 and 2, respectively.

Step-2 From the result of step 1, we now find the lower bound and upper bound of objective functions. Let \(U_{g\left( x \right)}^{T} ,U_{g\left( x \right)}^{I} ,U_{g\left( x \right)}^{F}\) be the upper bounds of truth, indeterminacy, falsity membership function for the objective, respectively, and \(L_{g\left( x \right)}^{T} ,L_{g\left( x \right)}^{I} ,L_{g\left( x \right)}^{F}\) be the lower bound of truth, indeterminacy, falsity membership functions of objective, respectively, using following rules

$$U_{g\left( x \right)}^{T} = \hbox{max} \left\{ {g\left( {x^{1} } \right),g\left( {x^{2} } \right)} \right\}$$
(22)
$$L_{g\left( x \right)}^{T} = \hbox{min} \left\{ {g\left( {x^{1} } \right),g\left( {x^{2} } \right)} \right\}$$
(23)

But in single-valued NSO technique, the degree of truth, indeterminacy and falsity membership are considered so that the sum of these degree of membership values is less than three. To define the falsity and indeterminacy membership function of NLP (Eqs. 10–12), let us consider \(U_{g\left( x \right)}^{F} ,\;L_{g\left( x \right)}^{F}\) and \(U_{g\left( x \right)}^{I} ,\;L_{g\left( x \right)}^{I}\) be the upper and lower bounds of objective function \(g\left( x \right)\) such that

$$U_{g\left( x \right)}^{F} = U_{g\left( x \right)}^{T}$$
(24)
$$L_{g\left( x \right)}^{F} = L_{g\left( x \right)}^{T} + t\left( {U_{g\left( x \right)}^{T} - L_{g\left( x \right)}^{T} } \right)\,\,\,{\text{where}}\,\,0 < t < 1$$
(25)
$$L_{g\left( x \right)}^{I} = L_{g\left( x \right)}^{T}$$
(26)
$$U_{g\left( x \right)}^{I} = L_{g\left( x \right)}^{T} + s\left( {U_{g\left( x \right)}^{T} - L_{g\left( x \right)}^{T} } \right)\,\,\,{\text{where}}\,\,0 < s < 1$$
(27)

The initial neutrosophic model (Model-I) with aspiration levels of objectives can be formulated as

$${\text{Find}}\;x$$
(28)

So as to satisfy

$$g\left( x \right) \le^{n} L_{g\left( x \right)}^{T} \;{\text{with tolerance}}\;\left( {U_{g\left( x \right)}^{T} - L_{g\left( x \right)}^{T} } \right)\;{\text{for degree of truth membership}}$$
(29)
$$g\left( x \right) \le^{n} L_{g\left( x \right)}^{I} \;{\text{with tolerance}}\;\left( {U_{g\left( x \right)}^{I} - L_{g\left( x \right)}^{I} } \right)\;{\text{for degree of indeterminacy membership}}$$
(30)
$$g\left( x \right) \ge^{n} U_{g\left( x \right)}^{F} \,{\text{with tolerance}}\;\left( {U_{g\left( x \right)}^{F} - L_{g\left( x \right)}^{F} } \right)\;{\text{for degree of falsity membership}}$$
(31)
$$g_{j} \left( x \right) \le^{n} b_{j} \;{\text{with tolerance}}\;b_{j}^{0} \;{\text{for degree of truth membership}}$$
(32)
$$g_{j} \left( x \right) \le^{n} b_{j} \;{\text{with tolerance}}\;\left( {\xi_{{g_{j} \left( x \right)}} } \right)\;{\text{for degree of indeterminacy membership}}$$
(33)
$$g_{j} \left( x \right) \ge^{n} b_{j} + b_{j}^{0} \;{\text{with tolerance}}\;\left( {\left( {b_{j} + b_{j}^{0} } \right) - \left( {b_{j} + \varepsilon_{{g_{j} \left( x \right)}} } \right)} \right)\;{\text{for degree of falsity membership}}$$
(34)

for \(j = 1,2, \ldots m,\;\varepsilon_{{g_{j} \left( x \right)}} = t\left( {U_{{g_{j} \left( x \right)}}^{T} - L_{{g_{j} \left( x \right)}}^{T} } \right);t \in \left( {0,1} \right)\) and \(\xi_{{g_{j} \left( x \right)}} = s\left( {U_{{g_{j} \left( x \right)}}^{T} - L_{{g_{j} \left( x \right)}}^{T} } \right);s \in \left( {0,1} \right)\) and for Mode-II, it can be formulated as

$${\text{Find}}\;x$$
(35)

So as to satisfy

$$g\left( x \right) \le^{n} L_{g\left( x \right)}^{T} \;{\text{with tolerance}}\;\left( {U_{g\left( x \right)}^{T} - L_{g\left( x \right)}^{T} } \right)\;{\text{for degree of truth membership}}$$
(36)
$$g\left( x \right) \ge^{n} U_{g\left( x \right)}^{I} \;{\text{with tolerance}}\;\left( {U_{g\left( x \right)}^{I} - L_{g\left( x \right)}^{I} } \right)\;{\text{for degree of indeterminacy membership}}$$
(37)
$$g\left( x \right) \ge^{n} U_{g\left( x \right)}^{F} \;{\text{with tolerance}}\;\left( {U_{g\left( x \right)}^{F} - L_{g\left( x \right)}^{F} } \right)\;{\text{for degree of falsity membership}}$$
(38)
$$g_{j} \left( x \right) \le^{n} b_{j} \;{\text{with tolerance}}\;b_{j}^{0} \;{\text{for degree of truth membership}}$$
(39)
$$g_{j} \left( x \right) \ge^{n} \left( {b_{j} + \xi_{{g_{j} \left( x \right)}} } \right)\;{\text{with tolerance}}\;\left( {\xi_{{g_{j} \left( x \right)}} } \right)\;{\text{for degree of indeterminacy membership}}$$
(40)
$$g_{j} \left( x \right) \ge^{n} b_{j} + b_{j}^{0} \;{\text{with tolerance}}\;\left( {\left( {b_{j} + b_{j}^{0} } \right) - \left( {b_{j} + \varepsilon_{{g_{j} \left( x \right)}} } \right)} \right)\;{\text{for degree of falsity membership}}$$
(41)

for \(j = 1,2, \ldots m,\;\varepsilon_{{g_{j} \left( x \right)}} = t\left( {U_{{g_{j} \left( x \right)}}^{T} - L_{{g_{j} \left( x \right)}}^{T} } \right);t \in \left( {0,1} \right)\) and \(\xi_{{g_{j} \left( x \right)}} = s\left( {U_{{g_{j} \left( x \right)}}^{T} - L_{{g_{j} \left( x \right)}}^{T} } \right);s \in \left( {0,1} \right)\)

Here ‘\(\ge^{n}\)’ denotes inequality in neutrosophic sense.

Step-3 Here for simplicity linear membership \(T_{g\left( x \right)}\) for truth, \(I_{g\left( x \right)}\) for indeterminacy and \(F_{g\left( x \right)}\) for falsity membership functions of objective function are defined as follows:

$$T_{g\left( x \right)} \left( {g\left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;{\text{if}}\,\,g\left( x \right) \le L_{g\left( x \right)}^{T} } \\ {\left( {\frac{{U_{g\left( x \right)}^{T} - g\left( x \right)}}{{U_{g\left( x \right)}^{T} - L_{g\left( x \right)}^{T} }}} \right)\,\,\,\,\,\,\;{\text{if}}\,\,\,L_{g\left( x \right)}^{T} \le g\left( x \right) \le U_{g\left( x \right)}^{T} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\,{\text{if}}\,\,\,g\left( x \right) \ge U_{g\left( x \right)}^{T} } \\ \end{array} } \right.$$
(42)
$$I_{g\left( x \right)} \left( {g\left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g\left( x \right) \le L_{g\left( x \right)}^{I} } \\ {\left( {\frac{{U_{g\left( x \right)}^{I} - g\left( x \right)}}{{U_{g\left( x \right)}^{I} - L_{g\left( x \right)}^{I} }}} \right)\,\,\,\,{\text{if}}\,\,\,L_{g\left( x \right)}^{I} \le g\left( x \right) \le U_{g\left( x \right)}^{I} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g\left( x \right) \ge U_{g\left( x \right)}^{I} } \\ \end{array} } \right.$$
(43)
$$F_{g\left( x \right)} \left( {g\left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {0\,\,\,\,\,\,\,\,\,\;{\text{if}}\,\,g\left( x \right) \le L_{g\left( x \right)}^{F} } \\ {\frac{{g\left( x \right) - L_{g\left( x \right)}^{F} }}{{U_{g\left( x \right)}^{F} - L_{g\left( x \right)}^{F} }}\,\,\;\;{\text{if}}\,\,\,L_{g\left( x \right)}^{F} \le g\left( x \right) \le U_{g\left( x \right)}^{F} } \\ {1\,\,\,\,\,\,\,\,\,\,\,\;{\text{if}}\,\,g\left( x \right) \ge U_{g\left( x \right)}^{F} } \\ \end{array} } \right.$$
(44)

Step-4 Using linear membership function \(T_{{g_{j} \left( x \right)}}\) for truth, \(I_{{g_{j} \left( x \right)}}\) for indeterminacy and \(F_{{g_{j} \left( x \right)}}\) for falsity membership functions, we can calculate the membership functions of constraints as follows:

$$T_{{g_{j} \left( x \right)}} \left( {g_{j} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g_{j} \left( x \right) \le b_{j} } \\ {\left( {\frac{{b_{j} + b_{j}^{0} - g_{j} \left( x \right)}}{{b_{j}^{0} }}} \right)\,\,\,\,\,\;\;\;\;\;\,{\text{if}}\,\,\,b_{j} \le g_{j} \left( x \right) \le b_{j} + b_{j}^{0} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{j} \left( x \right) \ge b_{j}^{0} } \\ \end{array} } \right.$$
(45)
$$I_{{g_{j} \left( x \right)}} \left( {g_{j} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g_{j} \left( x \right) \le b_{j} } \\ {\frac{{\left( {b_{j} + \xi_{{g_{j} \left( x \right)}} } \right) - g_{j} \left( x \right)}}{{\xi_{{g_{j} \left( x \right)}} }}\,\,\,\,\,\,{\text{if}}\,\,\,b_{j} \le g_{j} \left( x \right) \le b_{j} + \xi_{{g_{j} \left( x \right)}} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{j} \left( x \right) \ge b_{j} + \xi_{{g_{j} \left( x \right)}} } \\ \end{array} } \right.$$
(46)
$$F_{{g_{j} \left( x \right)}} \left( {g_{j} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g_{j} \left( x \right) \le b_{j} + \varepsilon_{{g_{j} \left( x \right)}} } \\ {\frac{{g_{j} \left( x \right) - b_{j} - \varepsilon_{{g_{j} \left( x \right)}} }}{{b_{j}^{0} - \varepsilon_{{g_{j} \left( x \right)}} }}\,\,\,\,{\text{if}}\,\,\,b_{j} + \varepsilon_{{g_{j} \left( x \right)}} \le g_{j} \left( x \right) \le b_{j} + b_{j}^{0} } \\ {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{j} \left( x \right) \ge b_{j} + b_{j}^{0} } \\ \end{array} } \right.$$
(47)

for \(j = 1,2, \ldots m\,\,\,\,0 < \varepsilon_{{g_{j} \left( x \right)}} ,\xi_{{g_{j} \left( x \right)}} < b_{j}^{0}\). and

Step-5 Now using NSO [30] for single-objective optimization with linear truth, indeterminacy and falsity membership functions, the NSNLP (Eqs. 13–15) can be formulated as

Model-I

$${\text{Maximize}}\,\,\left( {T_{g\left( x \right)} \left( {g\left( x \right)} \right),T_{{g_{j} \left( x \right)}} \left( {g_{j} \left( x \right)} \right)} \right)$$
(48)
$${\text{Maximize}}\,\,\left( {I_{g\left( x \right)} \left( {g\left( x \right)} \right),I_{{g_{j} \left( x \right)}} \left( {g_{j} \left( x \right)} \right)} \right)$$
(49)
$${\text{Minimize}}\,\,\left( {F_{g\left( x \right)} \left( {g\left( x \right)} \right),F_{{g_{j} \left( x \right)}} \left( {g_{j} \left( x \right)} \right)} \right)$$
(50)

Such that

$$T_{g\left( x \right)} \left( x \right) + I_{g\left( x \right)} \left( x \right) + F_{g\left( x \right)} \left( x \right) \le 3;$$
(51)
$$T_{{g_{j} }} \left( x \right) + I_{{g_{j} }} \left( x \right) + F_{{g_{j} }} \left( x \right) \le 3;$$
(52)
$$T_{g\left( x \right)} \left( x \right) \ge I_{{_{g\left( x \right)} }} \left( x \right);$$
$$T_{g\left( x \right)} \left( x \right) \ge F_{{_{g\left( x \right)} }} \left( x \right);$$
(53)
$$T_{{g_{j} }} \left( x \right) \ge I_{{g_{j} }} \left( x \right);$$
(54)
$$T_{{g_{j} }} \left( x \right) \ge F_{{g_{j} }} \left( x \right);$$
(55)
$$T_{g\left( x \right)} \left( x \right),I_{g\left( x \right)} \left( x \right),F_{g\left( x \right)} \left( x \right) \in \left[ {0,1} \right]$$
$$T_{{g_{j} }} \left( x \right),I_{{g_{j} }} \left( x \right),F_{{g_{j} }} \left( x \right) \in [0,1]$$
$$x > 0\;j = 1,2, \ldots ,m$$
(56)

Model-II

$${\text{Maximize}}\,\,\left( {T_{g\left( x \right)} \left( {g\left( x \right)} \right),T_{{g_{j} \left( x \right)}} \left( {g_{j} \left( x \right)} \right)} \right)$$
(57)
$${\text{Minimize}}\,\,\left( {I_{g\left( x \right)} \left( {g\left( x \right)} \right),I_{{g_{j} \left( x \right)}} \left( {g_{j} \left( x \right)} \right)} \right)$$
(58)
$${\text{Minimize}}\,\,\left( {F_{g\left( x \right)} \left( {g\left( x \right)} \right),F_{{g_{j} \left( x \right)}} \left( {g_{j} \left( x \right)} \right)} \right)$$
(59)

subject to the same constraints as Model-I.

All these crisp nonlinear programming problems (Model-I) and (Model-II) can be solved by appropriate mathematical algorithm.

4 Welded Beam Design (WBD) and its Optimization in Neutrosophic Environment

Welding, a process of joining metallic parts with the application of heat or pressure or the both, with or without added material, is an economical and efficient method for obtaining permanent joints in the metallic parts. These welded joints are generally used as a substitute for riveted joint or can be used as an alternative method for casting or forging. The welding processes can broadly be classified into following two groups: the welding process that uses heat alone to join two metallic parts and the welding process that uses a combination of heat and pressure for joining (Bhandari. V. B). However, above all the design of welded beam should preferably be economical and durable one.

4.1 WBD Formulation

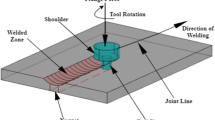
The optimum welded beam design ([37], Fig. 1) can be formulated considering some design criteria such as cost of welding, i.e., cost function, shear stress, bending stress and deflection, derived as follows:

Fig. 1
figure 1

Shear stresses in the weld group

Full size image

4.1.1 Cost Function Formulation

The performance index appropriate to this design is the cost of weld assembly. The major cost components of such an assembly are (i) setup labor cost, (ii) welding labor cost, (iii) material cost, i.e.,

$$C\left( X \right) \equiv C_{0} + C_{1} + C_{2}$$
(60)

where \(C\left( X \right) =\) cost function; \(C_{0} =\) setup cost; \(C_{1} =\) welding labor cost; \(C_{2} =\) material cost. Now

Setup cost \(C_{0}\) The company has chosen to make this component a weldment, because of the existence of a welding assembly line. Furthermore, assume that fixtures for setup and holding of the bar during welding are readily available. The cost \(C_{0}\) can therefore be ignored in this particular total cost model.

Welding labor cost \(C_{1}\) Assume that the welding will be done by machine at a total cost of $10/h (including operating and maintenance expense). Furthermore, suppose that the machine can lay down a cubic inch of weld in 6 min. The labor cost is then

$$C_{1} = \left( {10\frac{\$ }{\text{h}}} \right)\left( {\frac{1}{60}\frac{\$ }{\hbox{min} }} \right)\left( {6\frac{\hbox{min} }{{{\text{in}}^{3} }}} \right)V_{w} = 1\left( {\frac{\$ }{{{\text{in}}^{3} }}} \right)V_{w}$$
(61)

where V w  = weld volume, in3

$${\text{Material cost}}\;C_{2} :C_{2} = C_{3} V_{w} + C_{4} V_{B}$$
(62)

where C 3 = cost per volume per weld material, \(\$ /{\text{in}}^{3} = (0.37)(0.283);\) C 4 = cost per volume of bar stock, \(\$ /{\text{in}}^{3} = (0.37)(0.283)\); V B  = volume of bar, in3.

From geometry \(V_{w} = h^{2} l\); volume of the weld material, in3; \(V_{\text{weld}} = x_{1}^{2} x_{2}\) and \(V_{B} = tb\left( {L + l} \right)\); volume of bar, in3; \(V_{\text{bar}} = x_{3} x_{4} \left( {L + x_{2} } \right)\).

Therefore, cost function become

$$C\left( X \right) = h^{2} l + C_{3} h^{2} l + C_{4} tb\left( {L + l} \right) = 1.10471x_{1}^{2} x_{2} + 0.04811x_{3} x_{4} \left( {14.0 + x_{2} } \right)$$
(63)

4.1.2 Constraints Derivation from Engineering Relationship

Figure 1.

4.1.3 Maximum Shear Stress in Weld Group

To complete the model, it is necessary to define important stress states

Direct or primary shear stress, i.e.,

$$\tau_{1} = \frac{\text{Load}}{{{\text{Throat}}\,\,{\text{area}}}} = \frac{P}{A} = \frac{P}{\sqrt 2 hl} = \frac{P}{{\sqrt 2 x_{1} x_{2} }}$$
(64)

Since the shear stress produced due to turning moment \(M = P \cdot e\) at any section is proportional to its radial distance from center of gravity of the joint ‘G’, stress due to \(M\) is proportional to \(R\) and is in a direction at right angles to \(R\). In other words,

$$\frac{{\tau_{2} }}{R} = \frac{\tau }{r} = {\text{constant}}$$
(65)
$${\text{Therefore}}\;R = \sqrt {\left( {\frac{l}{2}} \right)^{2} + \left( {\frac{h + t}{2}} \right)^{2} } = \sqrt {\frac{{x_{2}^{2} }}{4} + \frac{{\left( {x_{1} + x_{3} } \right)^{2} }}{4}}$$
(66)

where \(\tau_{2}\) is the shear stress at the maximum distance R and \(\tau\) is the shear stress at any distance r. Consider a small section of the weld having area dA at a distance r from ‘G.’ Therefore, shear force on this small section is \(= \tau \times dA\) and turning moment of the shear force about center of gravity is

$$dM = \tau \times dA \times r = \frac{{\tau_{2} }}{R} \times dA \times r^{2}$$
(67)

Therefore, total turning moment over the whole weld area is

$$M = \frac{{\tau_{2} }}{R}\int {dA} \times r^{2} = \frac{{\tau_{2} }}{R}J.$$
(68)

where J = polar moment of inertia of the weld group about center of gravity.

Therefore, shear stress due to the turning moment is

$${\text{Secondary shear stress}},\;\tau_{2} = \frac{MR}{J}$$
(69)

In order to find the resultant stress, the primary and secondary shear stresses are combined vectorially. Therefore, the maximum resultant shear stress that will be produced at the weld group is

$$\tau = \sqrt {\tau_{1}^{2} + \tau_{2}^{2} + 2\tau_{1} \tau_{2} \cos \theta } ,$$
(70)

where θ = angle between \(\tau_{1}\) and \(\tau_{2}\).

$${\text{As}}\;\cos \theta = \frac{{{l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0pt} 2}}}{R} = \frac{{x_{2} }}{2R};$$
(71)
$$\tau = \sqrt {\tau_{1}^{2} + \tau_{2}^{2} + 2\tau_{1} \tau_{2} \frac{{x_{2} }}{2R}} .$$
(72)

Now the polar moment of inertia of the throat area \(\left( A \right)\) about the center of gravity is obtained by parallel axis theorem,

$$J = 2\left[ {I_{xx} + A + x^{2} } \right] = 2\left[ {\frac{{A \times l^{2} }}{12} + A \times x^{2} } \right] = 2A\left( {\frac{{l^{2} }}{12} + x^{2} } \right) = 2\left\{ {\sqrt 2 x_{1} x_{2} \left[ {\frac{{x_{2}^{2} }}{12} + \frac{{\left( {x_{1} + x_{3} } \right)^{2} }}{2}} \right]} \right\}$$
(73)

where A = throat area =  \(\sqrt 2 x_{1} x_{2}\), l = length of the weld,

$$x = {\text{Perpendicular distance between two parallel axes}} = \frac{t}{2} + \frac{h}{2} = \frac{{x_{1} + x_{3} }}{2}$$
(74)

4.1.4 Maximum Bending Stress in Beam

Now maximum bending moment = PL, maximum bending stress =  \(\frac{T}{Z}\), where T = PL; Z = section modulus =  \(\frac{I}{y};\) \(I =\)  moment of inertia \(= \frac{{bt^{3} }}{12};\) \(y =\)  distance of extreme fiber from center of gravity of cross section =  \(\frac{t}{2};\) therefore, \(Z = \frac{{bt^{2} }}{6}\).

$${\text{So bar bending stress}}\;\sigma \left( x \right) = \frac{T}{Z} = \frac{6PL}{{bt^{2} }} = \frac{6PL}{{x_{4} x_{3}^{2} }}.$$
(75)

4.1.5 Maximum Deflection in Beam

$${\text{Maximum deflection at cantilever tip}}\;\delta \left( x \right) = \frac{{PL^{3} }}{3EI} = \frac{{PL^{3} }}{{3E\frac{{bt^{3} }}{12}}} = \frac{{4PL^{3} }}{{Ebt^{3} }} = \frac{{4PL^{3} }}{{Ex_{4} x_{3}^{2} }}$$
(76)

4.1.6 Buckling Load of Beam

$${\text{Buckling load can be approximated by}}\;P_{C} \left( x \right) = \frac{{4.013\sqrt {\text{EIC}} }}{{l^{2} }}\left( {1 - \frac{a}{l}\sqrt {\frac{El}{C}} } \right)$$
(77)
$$= \frac{{4.013\sqrt {E\frac{{t^{2} b^{6} }}{36}} }}{{L^{2} }}\left( {1 - \frac{t}{2L}\sqrt {\frac{E}{4G}} } \right) = \frac{{4.013\sqrt {EGx_{3}^{6} x_{4}^{6} /36} }}{{L^{2} }}\left( {1 - \frac{{x_{3} }}{2L}\sqrt {\frac{E}{4G}} } \right)$$
(78)

where I = moment of inertia  \(= \frac{{bt^{3} }}{12};\) torsional rigidity \(C = GJ = \frac{1}{3}tb^{3} G;\) \(l = L;a = \frac{t}{2}.\)

4.2 Crisp Formulation of WBD

In design formulation, a welded beam ([10], Fig. 2) has to be designed at minimum cost whose constraints are shear stress in weld \(\left( \tau \right)\), bending stress in the beam \(\left( \sigma \right)\), buckling load on the bar (P) and deflection of the beam \(\left( \delta \right)\). The design variables are \(\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ {x_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} h \\ l \\ t \\ b \\ \end{array} } \right]\) where h is the weld size, l is the length of the weld, t is the depth of the welded beam, and b is the width of the welded beam.

Fig. 2
figure 2

Design of the welded beam

Full size image

The single-objective crisp welded beam optimization problem can be formulated as follows:

$${\text{Minimize}}\,\,C\left( X \right) \equiv 1.10471x_{1}^{2} x_{2} + 0.04811\left( {14 + x_{2} } \right)x_{3} x_{4}$$
(79)

such that

$$g_{1} \left( x \right) \equiv \tau \left( x \right) - \tau_{\hbox{max} } \le 0$$
(80)
$$g_{2} \left( x \right) \equiv \sigma \left( x \right) - \sigma_{\hbox{max} } \le 0$$
(81)
$$g_{3} \left( x \right) \equiv x_{1} - x_{4} \le 0$$
(82)
$$g_{4} \left( x \right) \equiv 0.10471x_{1}^{2} x_{2} + 0.04811x_{3} x_{4} \left( {14 + x_{2} } \right) - 5 \le 0$$
(83)
$$g_{5} \left( x \right) \equiv 0.125 - x_{1} \le 0$$
(84)
$$g_{6} \left( x \right) \equiv \delta \left( x \right) - \delta_{\hbox{max} } \le 0$$
(85)
$$g_{7} \left( x \right) \equiv P - P_{C} \left( x \right) \le 0$$
(86)
$$x_{1} ,x_{2} ,x_{3} ,x_{4} \in \left[ {0,1} \right]$$
(87)

where \(\tau \left( x \right) = \sqrt {\tau_{1}^{2} + 2\tau_{1} \tau_{2} \frac{{x_{2} }}{2R} + \tau_{2}^{2} }\); \(\tau_{1}\,=\,\frac{P}{{\sqrt 2 x_{1} x_{2} }}\); \(\tau_{2}\,=\,\frac{MR}{J}\);  \(M\,=\,P\left( {L + \frac{{x_{2} }}{2}} \right)\); \(R\,=\,\sqrt {\frac{{x_{2}^{2} }}{4} + \left( {\frac{{x_{1} + x_{3} }}{2}} \right)^{2} }\); \(J\,=\, \left\{ {\frac{{x_{1} x_{2} }}{\sqrt 2 }\left[ {\frac{{x_{2}^{2} }}{12} + \left( {\frac{{x_{1} + x_{3} }}{2}} \right)^{2} } \right]} \right\};\)  \(\sigma \left( x \right)\, =\, \frac{6PL}{{x_{4} x_{3}^{2} }};\)  \(\delta \left( x \right)\, = \,\frac{{4PL^{3} }}{{Ex_{4} x_{3}^{2} }};\)  \(P_{C} \left( x \right)\,= \,\frac{{4.013\sqrt {EGx_{3}^{6} x_{4}^{6} /36} }}{{L^{2} }}\left( {1 - \frac{{x_{3} }}{2L}\sqrt {\frac{E}{4G}} } \right)\) as derived as Eqs. (70), (64), (69), (68), (66), (73), (75), (76), (78), respectively. Again \(P\,=\,\) Force on beam; \(L\,=\,\)  Beam length beyond weld; \(x_{1}\,=\,\) Height of the welded beam; \(x_{2}\,=\,\) Length of the welded beam; \(x_{3}\,=\,\) Depth of the welded beam; \(x_{4}\,=\,\) Width of the welded beam; \(\tau \left( x \right)\,=\,\) Design shear stress; \(\sigma \left( x \right)\,=\,\) Design normal stress for beam material; M = Moment of P about the center of gravity of the weld, J = Polar moment of inertia of weld group; G = Shearing modulus of Beam Material; E = Young modulus; \(\tau_{\hbox{max} }\,=\,\) Design Stress of the weld; \(\sigma_{\hbox{max} }\,=\,\) Design normal stress for the beam material; \(\delta_{\hbox{max} }\,=\,\) Maximum deflection; \(\tau_{1}\,=\,\) Primary stress on weld throat; \(\tau_{2}\,=\,\) Secondary torsional stress on weld.

4.3 WBD Formulation in Neutrosophic Environment

Sometimes slight change in stress or deflection enhances the weight of structures and indirectly cost of processing. In such situation when decision maker (DM) is in doubt to decide the stress constraint goal, the DM can induce the idea of acceptance boundary, hesitancy response or negative response margin of constraints goal. This fact seems to take the constraint goal as a NS instead of FS and IFS. It may be more realistic description than FS and IFS. When the sheer stress, normal stress and deflection constraint goals are NS in nature, the above crisp welded beam design (Eqs. 79–87) can be formulated as

$${\text{Minimize}}\,\,C\left( X \right) \equiv 1.10471x_{1}^{2} x_{2} + 0.04811\left( {14 + x_{2} } \right)x_{3} x_{4}$$
(88)

Such that

$$g_{1} \left( x \right) \equiv \tau \left( x \right)\tilde{ \le }^{n} \tau_{\hbox{max} }$$
(89)
$$g_{2} \left( x \right) \equiv \sigma \left( x \right)\tilde{ \le }^{n} \sigma_{\hbox{max} }$$
(90)
$$g_{3} \left( x \right) \equiv x_{1} - x_{4} \le 0$$
(91)
$$g_{4} \left( x \right) \equiv 0.10471x_{1}^{2} x_{2} + 0.04811x_{3} x_{4} \left( {14 + x_{2} } \right) - 5 \le 0$$
(92)
$$g_{5} \left( x \right) \equiv 0.125 - x_{1} \le 0$$
(93)
$$g_{6} \left( x \right) \equiv \delta \left( x \right)\tilde{ \le }^{n} \delta_{\hbox{max} }$$
(94)
$$g_{7} \left( x \right) \equiv P - P_{C} \left( x \right) \le 0$$
(95)
$$x_{1} ,x_{2} ,x_{3} ,x_{4} \in \left[ {0,1} \right]$$
(96)

where all the parameters have their usual meaning as stated in Sect. 4.2. Here constraint goals are characterized by neutrosophic sets

$$\tilde{\tau }_{\hbox{max} }^{n} = \left( {\tau_{\hbox{max} } \left( {x_{1} ,x_{2} } \right),T_{{\tilde{\tau }_{\hbox{max} }^{n} }} \left( {\tau_{\hbox{max} } \left( {x_{1} ,x_{2} } \right)} \right),I_{{\tilde{\tau }_{\hbox{max} }^{n} }} \left( {\tau_{\hbox{max} } \left( {x_{1} ,x_{2} } \right)} \right),F_{{\tilde{\tau }_{\hbox{max} }^{n} }} \left( {\tau_{\hbox{max} } \left( {x_{1} ,x_{2} } \right)} \right)} \right)$$
(97)

with \(T_{{\tilde{\tau }_{\hbox{max} }^{n} }} \left( {\tau_{\hbox{max} } \left( {x_{1} ,x_{2} } \right)} \right),\) \(I_{{\tilde{\tau }_{\hbox{max} }^{n} }} \left( {\tau_{\hbox{max} } \left( {x_{1} ,x_{2} } \right)} \right),\)   \(F_{{\tilde{\tau }_{\hbox{max} }^{n} }} \left( {\tau_{\hbox{max} } \left( {x_{1} ,x_{2} } \right)} \right)\) as the degree of truth, indeterminacy and falsity membership functions of neutrosophic set \(\tilde{\tau }_{\hbox{max} }^{n}\);

$$\tilde{\sigma }_{\hbox{max} }^{n} = \left( {\sigma_{\hbox{max} } \left( {x_{3} ,x_{4} } \right),T_{{\tilde{\sigma }_{\hbox{max} }^{n} }} \left( {\sigma_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right),I_{{\tilde{\sigma }_{\hbox{max} }^{n} }} \left( {\sigma_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right),F_{{\tilde{\sigma }_{\hbox{max} }^{n} }} \left( {\sigma_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right)} \right)$$
(98)

with \(T_{{\tilde{\sigma }_{\hbox{max} }^{n} }} \left( {\sigma_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right),\) \(I_{{\tilde{\sigma }_{\hbox{max} }^{n} }} \left( {\sigma_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right),\) \(F_{{\tilde{\sigma }_{\hbox{max} }^{n} }} \left( {\sigma_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right)\) as the degree of truth, indeterminacy and falsity membership functions of neutrosophic set \(\tilde{\sigma }_{\hbox{max} }^{n}\); and

$$\tilde{\delta }_{\hbox{max} }^{n} = \left( {\delta_{\hbox{max} } \left( {x_{3} ,x_{4} } \right),T_{{\tilde{\delta }_{\hbox{max} }^{n} }} \left( {\delta_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right),I_{{\tilde{\delta }_{\hbox{max} }^{n} }} \left( {\delta_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right),F_{{\tilde{\delta }_{\hbox{max} }^{n} }} \left( {\delta_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right)} \right)$$
(99)

with \(T_{{\tilde{\delta }_{\hbox{max} }^{n} }} \left( {\delta_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right),\) \(I_{{\tilde{\delta }_{\hbox{max} }^{n} }} \left( {\delta_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right),\) \(F_{{\tilde{\delta }_{\hbox{max} }^{n} }} \left( {\delta_{\hbox{max} } \left( {x_{3} ,x_{4} } \right)} \right)\) as the degree of truth, indeterminacy and falsity membership functions of neutrosophic set \(\tilde{\delta }_{\hbox{max} }^{n}\)

4.4 Optimization of WBD in Neutrosophic Environment

To solve the WBD (Eqs. 88–96), step 1 of Sect. 3.1 is used and we will get optimum solutions of two subproblem as \(X^{1}\) and \(X^{2}\). After that according to step 2, we find upper and lower bounds of membership function of objective function as \(U_{C\left( X \right)}^{T} ,U_{C\left( X \right)}^{I} ,U_{C\left( X \right)}^{F}\) and \(L_{C\left( X \right)}^{T} ,L_{C\left( X \right)}^{I} ,L_{C\left( X \right)}^{F}\) where \(U_{C\left( X \right)}^{T} = \hbox{max} \left\{ {C\left( {X^{1} } \right),C\left( {X^{2} } \right)} \right\},\;L_{C\left( X \right)}^{T} = \hbox{min} \left\{ {C\left( {X^{1} } \right),C\left( {X^{2} } \right)} \right\},\)

therefore,

$$U_{C\left( X \right)}^{F} = U_{C\left( X \right)}^{T} ,L_{C\left( X \right)}^{F} = L_{C\left( X \right)}^{T} + \varepsilon_{C\left( X \right)} \;{\text{where}}\;0 < \varepsilon_{C\left( X \right)} < \left( {U_{C\left( X \right)}^{T} - L_{C\left( X \right)}^{T} } \right)$$
(100)
$$L_{C\left( X \right)}^{I} = L_{C\left( X \right)}^{T} ,U_{C\left( X \right)}^{I} = L_{C\left( X \right)}^{T} + \xi_{C\left( X \right)} \;{\text{where}}\;0 < \xi_{C\left( X \right)} < \left( {U_{C\left( X \right)}^{T} - L_{C\left( X \right)}^{T} } \right)$$
(101)

Let the linear membership functions for objective be,

$$T_{C\left( X \right)} \left( {C\left( X \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,\,C\left( X \right) \le L_{C\left( X \right)}^{T} } \\ {\left( {\frac{{U_{C\left( X \right)}^{T} - C\left( X \right)}}{{U_{C\left( X \right)}^{T} - L_{C\left( X \right)}^{T} }}} \right)\,\,\,\,\,\,{\text{if}}\,\,\,L_{C\left( X \right)}^{T} \le C\left( X \right) \le U_{C\left( X \right)}^{T} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,C\left( X \right) \ge U_{C\left( X \right)}^{T} } \\ \end{array} } \right.$$
(102)
$$I_{C\left( X \right)} \left( {C\left( X \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,\,\,C\left( X \right) \le L_{WT\left( A \right)}^{T} } \\ {\left( {\frac{{\left( {L_{C\left( X \right)}^{T} + \xi_{C\left( X \right)} } \right) - C\left( X \right)}}{{\xi_{C\left( X \right)} }}} \right)\,\,\,\,{\text{if}}\,\,\,L_{C\left( X \right)}^{T} \le C\left( X \right) \le L_{C\left( X \right)}^{T} + \xi_{C\left( X \right)} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,WT\left( A \right) \ge L_{C\left( X \right)}^{T} + \xi_{C\left( X \right)} } \\ \end{array} } \right.$$
(103)
$$F_{C\left( X \right)} \left( {C\left( X \right)} \right) = \left\{ {\begin{array}{*{20}l} {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,C\left( X \right) \le L_{C\left( X \right)}^{T} + \varepsilon_{C\left( X \right)} } \\ {\left( {\frac{{C\left( X \right) - \left( {L_{C\left( X \right)}^{T} + \varepsilon_{C\left( X \right)} } \right)}}{{U_{C\left( X \right)}^{T} - L_{C\left( X \right)}^{T} - \varepsilon_{C\left( X \right)} }}} \right)\,\,\,\,\,{\text{if}}\,\,\,L_{C\left( X \right)}^{T} + \varepsilon_{C\left( X \right)} \le C\left( X \right) \le U_{C\left( X \right)}^{T} } \\ {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,C\left( X \right) \ge U_{C\left( X \right)}^{T} } \\ \end{array} } \right.$$
(104)

and constraints be,

$$T_{{\sigma_{i} \left( X \right)}} \left( {\sigma_{i} \left( X \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\sigma_{i} \left( X \right) \le \sigma_{i} } \\ {\left( {\frac{{\left( {\sigma_{i} + \sigma_{i}^{0} } \right) - \sigma_{i} \left( X \right)}}{{\sigma_{i}^{0} }}} \right)\,\,\,\,{\text{if}}\,\,\,\sigma_{i} \le \sigma_{i} \left( X \right) \le \sigma_{i} + \sigma_{i}^{0} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,\sigma_{i} \left( X \right) \ge \sigma_{i} + \sigma_{i}^{0} } \\ \end{array} } \right.$$
(105)
$$I_{{\sigma_{i} \left( X \right)}} \left( {\sigma_{i} \left( X \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\sigma_{i} \left( X \right) \le \sigma_{i} } \\ {\left( {\frac{{\left( {\sigma_{i} + \xi_{{\sigma_{i} \left( X \right)}} } \right) - \sigma_{i} \left( X \right)}}{{\xi_{{\sigma_{i} \left( X \right)}} }}} \right)\,\,\,\,\,\,{\text{if}}\,\,\,\sigma_{i} \le \sigma_{i} \left( X \right) \le \sigma_{i} + \xi_{{\sigma_{i} \left( X \right)}} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,\sigma_{i} \left( X \right) \ge \sigma_{i} + \xi_{{\sigma_{i} \left( X \right)}} } \\ \end{array} } \right.$$
(106)
$$F_{{\sigma_{i} \left( X \right)}} \left( {\sigma_{i} \left( X \right)} \right) = \left\{ {\begin{array}{*{20}l} {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\sigma_{i} \left( X \right) \le \sigma_{i} + \varepsilon_{{\sigma_{i} \left( X \right)}} } \\ {\left( {\frac{{\sigma_{i} \left( X \right) - \sigma_{i} - \varepsilon_{{\sigma_{i} \left( X \right)}} }}{{\sigma_{i}^{0} - \varepsilon_{{\sigma_{i} \left( X \right)}} }}} \right)\,\,\,\,{\text{if}}\,\,\,\sigma_{i} + \varepsilon_{{\sigma_{i} \left( X \right)}} \le \sigma_{i} \left( X \right) \le \sigma_{i} + \sigma_{i}^{0} } \\ {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,\sigma_{i} \left( X \right) \ge \sigma_{i} + \sigma_{i}^{0} } \\ \end{array} } \right.$$
(107)

for \(j = 1,2, \ldots ,m\,\,\,\,0 < \varepsilon_{{\sigma_{i} \left( X \right)}} ,\xi_{{\sigma_{i} \left( X \right)}} < \sigma_{i}^{0}\) then NSO problem (Eqs. 88–96) can be formulated as the following crisp linear programming problem by considering linear membership as follows:

Type-I

$${\text{Maximize}}\,\,\left( {\alpha - \beta + \gamma } \right)$$
(108)

Such that

$$C\left( X \right) + \alpha \left( {U_{C\left( X \right)}^{T} - L_{C\left( X \right)}^{T} } \right) \le U_{C\left( X \right)}^{T} ;$$
(109)
$$C\left( X \right) + \gamma \left( {U_{C\left( X \right)}^{T} - L_{C\left( X \right)}^{T} - \xi_{C\left( X \right)} } \right) \le L_{C\left( X \right)}^{T} + \xi_{C\left( X \right)} ;$$
(110)
$$C\left( X \right) - \beta \left( {U_{C\left( X \right)}^{T} - L_{C\left( X \right)}^{T} - \varepsilon_{C\left( X \right)} } \right) \le L_{C\left( X \right)}^{T} + \varepsilon_{C\left( X \right)} ;$$
(111)
$$\sigma_{i} \left( X \right) + \alpha \left( {U_{{\sigma_{i} \left( X \right)}}^{T} - L_{{\sigma_{i} \left( X \right)}}^{T} } \right) \le U_{{\sigma_{i} \left( X \right)}}^{T} ;$$
(112)
$$\sigma_{i} \left( X \right) + \gamma \left( {U_{{\sigma_{i} \left( X \right)}}^{T} - L_{{\sigma_{i} \left( X \right)}}^{T} - \xi_{{\sigma_{i} \left( X \right)}} } \right) \le U_{{\sigma_{i} \left( X \right)}}^{T} + \xi_{{\sigma_{i} \left( X \right)}} ;$$
(113)
$$\sigma_{i} \left( X \right) - \beta \left( {U_{{\sigma_{i} \left( X \right)}}^{T} - L_{{\sigma_{i} \left( X \right)}}^{T} - \varepsilon_{{\sigma_{i} \left( X \right)}} } \right) \le L_{{\sigma_{i} \left( X \right)}}^{T} + \varepsilon_{{\sigma_{i} \left( X \right)}} ;$$
(114)
$$\alpha + \beta + \gamma \le 3;\alpha \ge \beta ;\alpha \ge \gamma ;\alpha ,\beta ,\gamma \in \left[ {0,1} \right]$$

Model-II

$${\text{Maximize}}\,\,\left( {\alpha - \beta - \gamma } \right)$$
(115)

Subject to the same constraints as Model-I (Eqs. 108–115). All these crisp nonlinear programming problems can be solved by appropriate mathematical algorithm.

5 Numerical Illustration

Input data of welded beam design problem (Eqs. 79–87) are given in Table 1 as follows:

Table 1 Input data for neutrosophic model [Eqs. (88–96)]
Full size table

Solution: According to step 2 of Sect. 3.1, we find upper and lower bound of membership function of objective function as \(U_{C\left( X \right)}^{T} ,U_{C\left( X \right)}^{I} ,U_{C\left( X \right)}^{F}\) and \(L_{C\left( X \right)}^{T} ,L_{C\left( X \right)}^{I} ,L_{C\left( X \right)}^{F}\) where \(U_{C\left( X \right)}^{T} = 1.861642 = U_{C\left( X \right)}^{F} ,L_{C\left( X \right)}^{T} = 1.858613 = L_{C\left( X \right)}^{I} ,\) \(L_{C\left( X \right)}^{F} = 1.858613 + \varepsilon_{C\left( X \right)}\), with \(0 < \varepsilon_{C\left( X \right)} < .003029;\) and \(U_{C\left( X \right)}^{I} = L_{C\left( X \right)}^{T} + \xi_{C\left( X \right)}\) with \(0 < \xi_{C\left( X \right)} < .003029\)

Now using the bounds, we calculate the membership functions for objective as follows:

$$T_{C\left( X \right)} \left( {C\left( X \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,C\left( X \right) \le 1.858613} \\ {\left( {\frac{1.861642 - C\left( X \right)}{.003029}} \right)\,\,\,\;\;\;{\text{if}}\,\,1.858613 \le C\left( X \right) \le 1.861642} \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,C\left( X \right) \ge 1.861642} \\ \end{array} } \right.$$
(116)
$$\begin{aligned} I_{C\left( X \right)} \left( {C\left( X \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,\,C\left( X \right) \le 1.858613} \\ {\left( {\frac{{\left( {1.858613 + \xi_{C\left( X \right)} } \right) - g\left( x \right)}}{{\xi_{C\left( X \right)} }}} \right)\,\,\,\,\,\,if\,\,\,1.858613 \le C\left( X \right) \le 1.858613 + \xi_{C\left( X \right)} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,\,\,C\left( X \right) \ge 1.858613 + \xi_{C\left( X \right)} } \\ \end{array} } \right. \hfill \\ \end{aligned}$$
(117)
$$F_{C\left( X \right)} \left( {C\left( X \right)} \right) = \left\{ {\begin{array}{*{20}l} {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,C\left( X \right) \le 1.858613 + \varepsilon_{C\left( X \right)} } \\ {\left( {\frac{{C\left( X \right) - 1.858613 - \varepsilon_{C\left( X \right)} }}{{.003029 - \varepsilon_{C\left( X \right)} }}} \right)\;\;\;\,\,\,{\text{if}}\,\,\,1.858613 + \varepsilon_{C\left( X \right)} \le C\left( X \right) \le 1.861642} \\ {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,C\left( X \right) \ge 1.861642} \\ \end{array} } \right.$$
(118)

similarly the membership functions for shear stress constraint are,

$$T_{{g_{1} \left( x \right)}} \left( {g_{1} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g_{1} \left( x \right) \le 13,600} \\ {\left( {\frac{{13600 - g_{1} \left( x \right)}}{50}} \right)\,\,\,\,\;\;{\text{if}}\,\,\,13,600 \le g_{1} \left( x \right) \le 13,650} \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{1} \left( x \right) \ge 13,650} \\ \end{array} } \right.$$
(119)
$$I_{{g_{1} \left( x \right)}} \left( {g_{1} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g_{1} \left( x \right) \le 13,600} \\ {\left( {\frac{{\left( {13600 + \xi_{{g_{1} \left( x \right)}} } \right) - g_{1} \left( x \right)}}{{\xi_{{g_{1} \left( x \right)}} }}} \right)\,\,\,\,\,\,\;\;{\text{if}}\,\,\,13600 \le g_{1} \left( x \right) \le 13,600 + \xi_{{g_{1} \left( x \right)}} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{1} \left( x \right) \ge 13,600 + \xi_{{g_{1} \left( x \right)}} } \\ \end{array} } \right.$$
(120)
$$F_{{g_{1} \left( x \right)}} \left( {g_{1} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g_{1} \left( x \right) \le 13,600 + \varepsilon_{{g_{1} \left( x \right)}} } \\ {\left( {\frac{{g_{1} \left( x \right) - 13600 - \varepsilon_{{g_{1} \left( x \right)}} }}{{50 - \varepsilon_{{g_{1} \left( x \right)}} }}} \right)\,\,\,\,\,\,{\text{if}}\,\,\,13600 + \varepsilon_{{g_{1} \left( x \right)}} \le g_{1} \left( x \right) \le 13,650} \\ {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{1} \left( x \right) \ge 13,650} \\ \end{array} } \right.$$
(121)
$${\rm where}\,\,0 < \varepsilon_{{g_{1} \left( x \right)}} ,\xi_{{g_{1} \left( x \right)}} < .003209$$

and the membership functions for normal stress constraint are,

$$T_{{g_{2} \left( x \right)}} \left( {g_{2} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\;g_{2} \left( x \right) \le 30,000} \\ {\left( {\frac{{30000 - g_{2} \left( x \right)}}{50}} \right)\,\,\,\,\;\;\;{\text{if}}\,\,\,30,000 \le g_{2} \left( x \right) \le 30,050} \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{2} \left( x \right) \ge 30,050} \\ \end{array} } \right.$$
(122)
$$I_{{g_{2} \left( x \right)}} \left( {g_{2} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g_{2} \left( x \right) \le 30,000} \\ {\left( {\frac{{\left( {30000 + \xi_{{g_{2} \left( x \right)}} } \right) - g_{2} \left( x \right)}}{{\xi_{{g_{2} \left( x \right)}} }}} \right)\,\,\;\;\;\,{\text{if}}\,\,\,30,000 \le g_{2} \left( x \right) \le 30,000 + \xi_{{g_{2} \left( x \right)}} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{2} \left( x \right) \ge 30,000 + \xi_{{g_{2} \left( x \right)}} } \\ \end{array} } \right.$$
(123)
$$F_{{g_{2} \left( x \right)}} \left( {g_{2} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g_{2} \left( x \right) \le 30000 + \varepsilon_{{g_{2} \left( x \right)}} } \\ {\left( {\frac{{g_{2} \left( x \right) - 30000 - \varepsilon_{{g_{2} \left( x \right)}} }}{{50 - \varepsilon_{{g_{2} \left( x \right)}} }}} \right)\,\,\,\,\,\,\;{\text{if}}\,\,\,30000 + \varepsilon_{{g_{2} \left( x \right)}} \le g_{2} \left( x \right) \le 30050} \\ {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{2} \left( x \right) \ge 30050} \\ \end{array} } \right.$$
(124)
$${\rm where}\,\,0 < \varepsilon_{{g_{2} \left( x \right)}} ,\xi_{{g_{2} \left( x \right)}} < 50$$

and the membership functions for deflection constraint are,

$$T_{{g_{6} \left( x \right)}} \left( {g_{6} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g_{6} \left( x \right) \le 0.25} \\ {\left( {\frac{{0.25 - g_{6} \left( x \right)}}{0.05}} \right)\,\,\,\,\;{\text{if}}\,\,\,0.25 \le g_{6} \left( x \right) \le 0.3} \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{6} \left( x \right) \ge 0.3} \\ \end{array} } \right.$$
(125)
$$I_{{g_{6} \left( x \right)}} \left( {g_{6} \left( x \right)} \right) = \left\{ {\begin{array}{*{20}l} {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g_{6} \left( x \right) \le 0.25} \\ {\left( {\frac{{\left( {0.25 + \xi_{{g_{6} \left( x \right)}} } \right) - g_{6} \left( x \right)}}{{\xi_{{g_{6} \left( x \right)}} }}} \right)\,\,\,\;\;\;{\text{if}}\,\,\,0.25 \le g_{6} \left( x \right) \le 0.25 + \xi_{{g_{6} \left( x \right)}} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{6} \left( x \right) \ge 0.25 + \xi_{{g_{6} \left( x \right)}} } \\ \end{array} } \right.$$
(126)
$$\begin{aligned} F_{{g_{6} \left( x \right)}} \left( {g_{6} \left( x \right)} \right) = \hfill \\ \left\{ {\begin{array}{*{20}l} {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,g_{6} \left( x \right) \le 0.25 + \varepsilon_{{g_{6} \left( x \right)}} } \\ {\left( {\frac{{g_{6} \left( x \right) - 0.25 - \varepsilon_{{g_{6} \left( x \right)}} }}{{0.05 - \varepsilon_{{g_{6} \left( x \right)}} }}} \right)\,\,\,\,\,\,\;{\text{if}}\,\,\,0.25 + \varepsilon_{{g_{6} \left( x \right)}} \le g_{6} \left( x \right) \le 0.3} \\ {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,g_{6} \left( x \right) \ge 0.3} \\ \end{array} } \right. \hfill \\ \end{aligned}$$
(127)
$${\rm where}\,\,0 < \varepsilon_{{g_{6} \left( x \right)}} ,\xi_{{g_{6} \left( x \right)}} < .05$$

Now, using above-mentioned truth, indeterminacy and falsity linear membership function NLP (Eqs. 79–87) can be solved for Model-I and Model-II, by fuzzy, intuitionistic fuzzy and NSO technique with different values of \(\varepsilon_{C\left( X \right)} ,\varepsilon_{{g_{1} \left( x \right)}} ,\varepsilon_{{g_{2} \left( x \right)}} ,\varepsilon_{{g_{6} \left( x \right)}}\) and \(\xi_{C\left( X \right)} ,\xi_{{g_{1} \left( x \right)}} ,\xi_{{g_{2} \left( x \right)}} ,\xi_{{g_{6} \left( x \right)}}\). The optimum height, length, depth, width and cost of welding of welded beam design (Eqs. 79–87) are given in Table 2, and the solution are compared with other deterministic optimization methods.

Table 2 Comparison of optimal solution of welded beam design (Eqs. 79–87) based on fuzzy and IF and NSO technique (Model-I and Model-II) with different methods
Full size table

A detailed comparison has been made among several deterministic optimization methods for optimizing welding cost with imprecise optimization methods such as fuzzy, IF and NSO methods in Table 2. It has been observed that fuzzy nonlinear optimization provides better result in comparison with IF and NSO methods. Although it has been seen that in this method cost of welding is minimum than in other the methods studied in this paper, as far as non-deterministic optimization methods concern, fuzzy, IF and NSO are providing a valuable result in imprecise environment in this paper and the literature. It has been seen that improved harmony search algorithm [14], COPSO [17], EP [19], HPSO [21] are providing minimum most cost of welding where all the parameters have been considered as exact in nature. However, it may also be noted that the efficiency of the proposed method depends on the model chosen to a greater extent because it is not always expected that NSO will provide better results over fuzzy and IF optimization. So overall NSO is an efficient method in finding best optimal solution in imprecise environment. It has been studied that same results have been obtained while indeterminate membership tried to be maximize (Model-I) or minimize (Model-II) in NSO for this particular problem.

6 Conclusion

In this paper, a single-objective NSO algorithm has been developed by defining truth, indeterminacy and falsity membership functions which are independent to each other. Using this method, firstly optimum height length depth, width and cost of welding have been calculated and finally the results are compared with different deterministic methods. So given example of welded beam design illustrates the optimization procedure, effectiveness and advantages of the proposed NSO method. The comparison of NSO technique with other optimization techniques has enhanced the acceptability of proposed method. The result obtained in proposed neutrosophic optimization method is not absurd related to other deterministic methods and the results have been obtained in imprecise environment, so realistic.