1 Introduction

The problem of achieving synchronization in a multi-agent system (MAS), where the goal is to design a distributed protocol, such that some variables of interest, either states or output trajectories, become the same asymptotically, has been substantially studied in last decade (see Bai et al. (2011), Ding et al. (2018), You et al. (2020) and references therein). Various applications can be cast in this framework, including distributed computation, swarming and flocking , the coordination or platooning of autonomous vehicles, and many others (for example, Tanner et al., 2007, Bernardo et al., 2015, Viana et al., 2017, Jaoura et al., 2022).

For a MAS of identical agent models (i.e., homogeneous network), an amount of efforts has been put in, first for simple agent dynamics and topology, then progressing to general higher-order agent dynamics and time-varying topology, for example (Li et al., 2010; Liu et al., 2018; Zhang et al., 2019; You et al., 2020). While for a MAS of non-identical models (i.e., heterogeneous network), more and more attention has been given. One reason is that it can accommodate parameter uncertainty or small disturbances in the agent dynamics. The other is that the heterogeneous MAS represents more general systems. The work has been focused on output synchronization, that is, all the agents should agree on a set of pre-selected outputs, and leader-following consensus, that is, all agents converge asymptotically to a priori given leader’s trajectory. It is commonly assumed that agents are introspective, that is, agents possess some knowledge about their own states (see Kim et al. (2011), Yang et al. (2014), Xu et al. (2017), Wang et al. (2020) for example). In both Xu et al. (2017) and Wang et al. (2020), another layer of communication is needed in the controller design. The synchronization problem for a network of non-introspective agents is more challenging, yet effort has already been made in this direction (Peymani et al., 2014; Zhang et al., 2016). A specific class of heterogenous networks is studied in Panteley and Loria (2017) with static output feedback, showing that the synchronization involves the stability of two orthogonal dynamical systems.

In the practical applications, agent systems are easily affected by disturbances, which might result from sensor bias or noise, processing errors or system uncertainties. Li et al. (2014) considers agents with both external disturbances and system uncertainties and a static protocol is designed to ensure the network disagreement is uniformly ultimately bounded (UUB). The literature uses the \({\mathcal {H}}_\infty \) norm of the transfer function from the external disturbance to the disagreement as a measurement for the synchronization among agents (see Wang and Ding (2016), Zhang et al. (2019), Zhang et al. (2018) for example). Wang and Ding (2016) analyzes homogeneous network with constant input delay while using full state feedback in the controller. In Zhang et al. (2019), event-triggered controller using output feedback for a general heterogeneous network is investigated and linear matrix inequality (LMI) theory is utilized for choosing controller parameters. The \({\mathcal {H}}_\infty \) almost synchronization is brought forth in Peymani et al. (2014) for a network of introspective, right-invertible linear time-invariant (LTI) agents. The impact of disturbances on the synchronization error dynamics is attenuated to an arbitrarily small value in the sense of the \({\mathcal {H}}_\infty \) norm. After that, the problem of \({\mathcal {H}}_\infty \) almost synchronization for networks of identical non-introspective agents is also studied in Peymani et al. (2013), where the only available information for each agent is the network measurement which is a linear combination of relative outputs.

Synchronization under time-varying communication topologies, where the links among agents might vanish, come up, become stronger or weaker, has been studied in the literature. In Shi and Johansson (2013); Meng et al. (2013), the conditions for synchronization are derived under switching signal with an arbitrarily given dwell time. In Li et al. (2021), the switching of topology follows a Markov process and aperiodic intermittent control strategy is investigated. Intermittent communication topology is also a kind of time-varying topology, but it tackles the synchronization problem with discontinuous information from the network (see Cheng et al. (2016), Yu et al. (2018) for example).

So far, the results on the synchronization problem for heterogeneous networks of the general, linear, non-introspective agents under switching topologies in the presence of external disturbance can be seen in Zhang et al. (2015). Since no agents’ states are available for the protocol design, all agents’ outputs are almost regulated to an external trajectory generated by an autonomous system. In this paper, partial states are allowed to be utilized in the protocol. Hence, agents’ outputs can be directly synchronized with an arbitrary degree of accuracy (i.e., the disagreement dynamic is asymptotically smaller than any desired bound). In particular, the notion of almost output synchronization for heterogeneous networks of the general, linear, introspective agents under time-varying topologies is formulated. It is assumed that the external disturbances have power less than a prior given bound and the time-varying topology switches among a finite number of directed graphs that contain a directed spanning tree with an a priori given dwell time. Then, a family of parameterized distributed protocols is designed for each agent such that almost synchronization is achieved among agents and the network disagreement can be squeezed by tuning the parameter in the protocol.

The remainder of this paper is organized as follows. In the rest of this section, we introduce some notations and recall some results of algebraic graph theory. In Sect. 2, heterogeneous multi-agent networks are discussed, together with the switching topologies and some assumptions on the network. The problem of almost output synchronization is formulated and solved in Sect. 3. In Sect. 4, we solve the almost regulated output synchronization problem. In Sect. 5, the results are illustrated via simulation examples.

1.1 Notations and Definitions

A matrix \(A \in {\mathbb {C}}^{m \times n}\) has its conjugate transpose denoted by \({\bar{A}}^{'}\). When \(m=n\), the eigenvalues are represented by \(\lambda _i(A)\) \((i=1,\ldots ,n)\). And if all its eigenvalues are in the open left-half complex plane, the matrix A is Hurwitz stable. For \(A_i\in {\mathbb {C}}^{m \times n}\) \((i=1,\ldots ,n)\), \({{\,\mathrm{blkdiag}\,}}\{A_i\}\) denotes a block-diagonal matrix with \(A_i\) as the diagonal elements. The Kronecker product between two matrices is marked by \(\otimes \). \(I_n\) is the identity matrix, \(0_n\) means the zero square matrix, and \(\mathbf{1}_n\) denotes a column vector with all entries equal to one. The subscript n of the dimension is dropped if it is clear in the context. \([x_1; \cdots ; x_n]\) denotes the column vector by stacking the elements of \(x_1, \ldots , x_n\). Finally, \({\mathcal {H}}_{\infty }\) norm of a transfer function T is indicated by \(\Vert T \Vert _{\infty }\).

A triple \(({\mathcal {V}}, {\mathcal {E}}, {\mathcal {A}})\) is used to define a graph \({\mathcal {G}}\), where \({\mathcal {V}}=\{1,\ldots , N\}\) is a node set, \({\mathcal {E}}\) is a set of node pairs (i, j), and \({\mathcal {A}}=[a_{ij}]\) is the weighted adjacency matrix with \(a_{ij}\in {\mathbb {R}}\ge 0\) standing for the weigh between node i and j. \({\mathcal {G}}\) is undirected if \((i, j)\in {\mathcal {E}}\Rightarrow (j, i)\in {\mathcal {E}}\); otherwise, directed. A directed path from node \(i_1\) to \(i_k\) is a sequence of vertices \(\{i_1,\ldots , i_k\}\) such that \((i_q, i_{q+1})\in {\mathcal {E}}\) for \(q=1,\ldots , k-1\). A directed graph \({\mathcal {G}}\) contains a directed spanning tree if there is a node r such that a directed path exists between node r and every other node. A weighted graph \({\mathcal {G}}\) is linked with a Laplacian matrix \(L=\{\ell _{ij}\}\) with \(\ell _{ij}=\sum _{j=1}^{N} a_{ij}\) for \( i=j\); otherwise \(-a_{ij}\). Since the graph \({\mathcal {G}}\) has non-negative weights, L has all its eigenvalues in the closed right-half plane and at least one eigenvalue at zero associated with right eigenvector \({\textbf {1}}_N\) (Godsi & Royle, 2001). If \({\mathcal {G}}\) has a directed spanning tree, L has a simple eigenvalue at zero and all the other eigenvalues have strictly positive real parts (Ren & Beard, 2005).

The following definitions will be used in this paper (see Saberi et al., 2022).

Definition 1

For given \(\alpha ,\beta >0\), \({\mathbb {G}}_{\alpha ,\beta }^{N}\) is the set of fixed directed graphs composed of N nodes such that for every \({\mathcal {G}}\in {\mathbb {G}}_{\alpha ,\beta }^{N}\), the graph has a directed spanning tree and the associated eigenvalues of its Laplacian, denoted by \(\lambda _1,\ldots ,\lambda _N\), that satisfy \( Re(\lambda _i)>\beta \) and \(\mid \lambda _i\mid <\alpha \) whenever \(\lambda _i\ne 0\).

Definition 2

An LTI dynamics (A, B, C, D) is right-invertible if given a reference output \(y_r(t)\), there exist an initial condition x(0) and an input u(t) such that \(y(t)=y_r(t)\) for all \(t\ge 0\). For example, every single-input single-output system is right-invertible, unless its transfer function is identically zero.

Definition 3

An LTI dynamics (A, B, C, D) is minimum-phase when the invariant zeros of the quadruple are all in the open left-half complex plane.

2 Multi-agent Systems

A MAS with N non-identical under external disturbances is considered, with the agent i described by an LTI dynamics:

$$\begin{aligned} \Sigma _i: \left\{ \begin{array}{ll} \dot{{\bar{x}}}_i = A_i{\bar{x}}_i+B_i{\bar{u}}_i+G_i{\bar{w}}_i,\\ y_i = C_i{\bar{x}}_i,\\ z_{m,i} = C_{m,i}{\bar{x}}_i, \end{array}\right. \end{aligned}$$
(1)

for \(i=1,\ldots ,N\), where \({\bar{x}}_i \in {\mathbb {R}}^{n_i}\), \({\bar{u}}_i \in {\mathbb {R}}^{m_i}\), and \(y_i \in {\mathbb {R}}^p\) are states, inputs and outputs of the agent i, respectively. \(z_{m,i}\in {\mathbb {R}}^{p_{m,i}}\) is the part of states that can be accessed by agent i. While, \({\bar{w}}_i \in {\mathbb {R}}^{{\bar{w}}_i}\) is the external disturbance, the power of which is finite, i.e., \( \lim _{T\rightarrow \infty }\dfrac{1}{2T}\int _{-T}^{T}{\bar{w}}_i^{'}{\bar{w}}_i \mathrm{d}t<\infty \). Matrices \(A_i\), \(B_i\), \(C_i\), \(G_i\), \(C_{m,i}\) have proper dimensions and satisfy the following assumption:

Assumption 1

For each agent \(i \in {\mathcal {V}}\):

  1. 1.

    \((A_i, B_i, C_i)\) is right-invertible and minimum-phase;

  2. 2.

    \((A_i, B_i)\) is stabilizable and \((A_i, C_i)\) is detectable;

  3. 3.

    \((A_i, C_{m,i})\) is detectable.

The time-varying topology \({\mathcal {G}}(t)\) is defined by a triple \(({\mathcal {V}},{\mathcal {E}}(t), {\mathcal {A}}(t))\), where both \({\mathcal {E}}(t)\) and \({\mathcal {A}}(t)\) are functions of time t and each node in \({\mathcal {V}}\) stands for an agent. Moreover, the time-varying weighed adjacency matrix \({\mathcal {A}}(t)= [a_{ij}(t)]\) with \(a_{ij}(t)\) being a piecewise constant and right-continuous in time t. The time-varying topology \({\mathcal {G}}(t)\) supplies each agent with a quantity \(\zeta _i(t)\), which is a linear, time-varying combination of its own output relative to that of its neighboring agents, i.e.,

$$\begin{aligned} \zeta _i(t) = \sum _{j=1}^{N}a_{ij}(t)(y_i(t)-y_j(t))=\sum _{j=1}^{N}\ell _{ij}(t)y_j(t), \end{aligned}$$
(2)

for agent \(i\in {\mathcal {V}}\), where \(a_{ij}(t)\ge 0\) and \(a_{ii}(t)=0\) with \(i,j \in {\mathcal {V}}\). And \(L(t)=[\ell _{ij}(t)]\) is corresponding time-varying Laplacian matrix, which is also piecewise constant and right-continuous functions of t.

The assumptions for the switching topology are given as follows:

Assumption 2

Let \(\{t_k\}\) be the time sequence of the discontinuities of the piecewise constant weighted adjacency matrix \({\mathcal {A}}(t)\) such that \(0=:t_0<t_1<\cdots<t_k<\cdots \). Assume that the switching time sequence has minimum dwell time \(\tau ^{*}>0\) such that \(t_{k+1}-t_{k}\ge \tau ^{*}\) for \(k=0, 1, 2,\ldots \).

Assumption 3

Let \({\mathbb {G}}=\{{\mathcal {G}}_1,{\mathcal {G}}_2,\ldots ,{\mathcal {G}}_M\}\) be a set of finite directed graphs and \({\mathbb {G}}\subset {\mathbb {G}} _{\alpha ,\beta }^{N}\). Assume that \({\mathcal {G}}(t)\) remains constant during interval \([t_{k-1},t_{k})\), and switches among the finite graph set \({\mathbb {G}}\) at \(t=t_{k}\), \(k=1,2,\ldots \).

The switching topology can be easily presented with a piecewise constant, right-continuous function \(\sigma (t):[0,\infty )\rightarrow {\mathcal {M}}:=\{1,2,\ldots ,M\}\), where \(\sigma (t)\in {\mathcal {M}}\) for \(t\in [t_{k-1},t_k)\) and \(\sigma (t)\) changes at \(t=t_k\), \(k=1,2,\ldots \). Suppose, for each \({\mathcal {G}}_i\in {\mathbb {G}} \,(i=1,\ldots ,M)\), we denote the associated weighted matrix by \({\mathcal {A}}_i\) and Laplacian matrix by \(L_i\). Then, by using the function \(\sigma (t)\), we have \({\mathcal {G}}(t)={\mathcal {G}}_{\sigma (t)}\). And similarly, we have \({\mathcal {A}}(t)={\mathcal {A}}_{\sigma (t)}\), and \(L(t)=L_{\sigma (t)}\), which implies that \(a_{ij}(t)=a_{ij,\sigma (t)}\) and \(\ell _{ij}(t)=\ell _{ij,\sigma (t)}\).

3 Almost Output Synchronization Under Switching Topologies

In this section, we consider almost output synchronization under switching topologies for a MAS described in Sect. 2.

Define variables for the entire MAS \( {\bar{w}} := {{\,\mathrm{col}\,}}\{{\bar{w}}_i\},\, {\bar{u}} := {{\,\mathrm{col}\,}}\{{\bar{u}}_i\},\, \zeta := {{\,\mathrm{col}\,}}\{\zeta _i\} \). Synchronization among agents is measured by the mutual disagreement. That is, the disagreement between agent i and agent N is denoted by \({\mathbf {e}}_i := y_N-y_i\) for \(i\in {\mathcal {V}}\), and \({\mathbf {e}} := {{\,\mathrm{col}\,}}\{{\mathbf {e}}_i \}\) is the disagreement vector for the whole MAS.

Before giving the problem formulation, a set of disturbances presented in the system is defined as:

Definition 4

A set of piecewise continuous noises with power less than \(\kappa \) is defined as \(\Gamma _{\kappa }=\{{\bar{w}}: \Vert {\bar{w}}\Vert _{rms}=\lim _{T\rightarrow \infty }\dfrac{1}{2T} \int _{-T}^{T}{\bar{w}}_i^{'}{\bar{w}}_i \mathrm{d}t<\kappa \}\).

We now formulate the problem of almost output synchronization under switching topologies as follows:

Problem 1

Consider a MAS with non-identical and introspective agents described by (1) and (2), in the presence of external disturbances and under a switching topology \({\mathcal {G}}(t)\). Suppose Assumptions 2 to 1 are satisfied, and the switching topology has a minimum dwell time \(\tau ^{*}\) and the disturbance has a limit power \(\kappa \). Then, the problem of almost output synchronization under the switching topology \({\mathcal {G}}(t)\) is to find, if possible, for any \(\kappa >0\), any \(\gamma >0\), an LTI distributed dynamic protocol, such that the disagreement among agents satisfies \(\limsup _{t\rightarrow \infty }\Vert {\mathbf {e}}(t)\Vert <\gamma \).

The main result in this section is given in the following theorem.

Theorem 1

Consider a MAS with non-identical and introspective agents described by (1) and (2). Under Assumptions 2 to 1, with any a priori given minimum dwell time \(\tau ^{*}\), for any given \(\kappa >0\), the problem of almost output synchronization under a switching topology \({\mathcal {G}}(t)\) is solvable, i.e., there exists a family of LTI dynamic protocols, parameterized in terms of low-and-high gain parameters \(\delta ,\, \varepsilon \in (0,1]\), of the form

$$\begin{aligned} \left\{ \begin{array}{cl} \dot{\chi }_i&{}={\mathcal {A}}_i(\delta ,\varepsilon )\chi _i+{\mathcal {B}}_i(\delta ,\varepsilon ){{\,\mathrm{col}\,}}\{\zeta _i,z_{m,i}\},\\ {\bar{u}}_i&{}= {\mathcal {C}}_i(\delta ,\varepsilon )\chi _i+{\mathcal {D}}_i(\delta ,\varepsilon ){{\,\mathrm{col}\,}}\{\zeta _i,z_{m,i}\}, \end{array}\right. \end{aligned}$$
(3)

for \( i\in {\mathcal {V}}\), where \(\chi _i \in {\mathbb {R}}^{q_i}\), such that, for any given \(\gamma >0\), there exists a \(\delta ^{*} \in (0,1]\) such that, for each \(\delta \in (0,\delta ^{*} ]\), there exists an \(\varepsilon ^{*} (\delta ,\tau ^{*})\in (0, 1]\) such that for any \(\varepsilon \in (0,\varepsilon ^{*}(\delta ,\tau ^{*})]\), the protocol (3) achieves almost output synchronization under the switching topology, i.e., \(\limsup _{t\rightarrow \infty }\Vert {\mathbf {e}}(t)\Vert <\gamma \).

Remark 1

For the distributed protocol (3), we only need to know the lower bound on the real parts of the non-zero eigenvalues of all the Laplacian matrices \(L_i\), \(i \in {\mathcal {M}}\), (i.e., \(\beta \)), the upper bound of the magnitude of the eigenvalues of all the Laplacian matrices \(L_i\), \(i \in {\mathcal {M}}\), (i.e., \(\alpha \)), the number of agents N, and the minimum dwell time \(\tau ^{*}\).

We will prove Theorem 1 in the following subsequent sections in a constructive way.

3.1 Homogenization via a Pre-compensator

In this section, we show that non-identical agents represented by (1) can be shaped into asymptotically identical agents via a dynamic pre-compensator, using the local measurements \(z_{m,i}\), which is called homogenization.

Lemma 1

Consider a MAS of N non-identical agents described by (1). Let Assumption 1 hold. We denote by \(n_{qi}\) the maximal order of infinite zeros of \((C_i,A_i,B_i)\), \(i \in \{1,\ldots ,N\}\). Suppose a triple (C, A, B) is given such that

  1. 1.

    \({{\,\mathrm{rank}\,}}(C)=p\),

  2. 2.

    (C, A, B) is invertible, of uniform rank \(n_q \ge n_{qi}\), and has no invariant zero.

Then for each agent \(i \in \{1,\ldots , N\}\), there exist a dynamic pre-compensator for each agent \(i\in {\mathcal {V}}\):

$$\begin{aligned} \left\{ \begin{array}{cl} {\dot{x}}_{p,i}&{}=A_{p,i}x_{p,i}+B_{p1,i}u_i+B_{p2,i}z_{m,i},\\ {\bar{u}}_i&{}=C_{p,i}x_{p,i}+D_{p1,i}u_i+D_{p2,i}z_{m,i}, \end{array}\right. \end{aligned}$$
(4)

where \(u_i\in {\mathbb {R}}^{p}\) is a new input, \(x_{p,i}\in {\mathbb {R}}^{p_i}\) is the state for pre-compensator i. The cascade of the pre-compensator (4) and the agent (1) is then presented as:

$$\begin{aligned} \left\{ \begin{array}{cl} {\dot{x}}_i&{}=Ax_i+B(Mu_i+Rx_i)+E_{i,d}{\bar{w}}_i+\rho _i,\\ y_i&{}=Cx_i, \end{array}\right. \end{aligned}$$
(5)

where \(u_i,\,y_i \in {\mathbb {R}}^{p},\,x_i\in {\mathbb {R}}^{pn_q}\); A, B, and C are given as:

$$\begin{aligned} A= \begin{pmatrix} 0 &{} I_{p(n_q-1)}\\ 0 &{} 0 \end{pmatrix}, \quad B= \begin{pmatrix} 0\\ I_p \end{pmatrix},\quad C=(I_p\,\,0). \end{aligned}$$
(6)

Moreover, \(M \in {\mathbb {R}}^{p\times p}\) is an arbitrary and non-singular matrix and \(R \in {\mathbb {R}}^{p\times pn_q}\) is a matrix of appropriate dimension and can be chosen arbitrarily. \(E_{i,d}\) can be chosen appropriately and \(\rho _i\) is generated by an exponentially stable system of the following form:

$$\begin{aligned} \dot{{\tilde{x}}}_{i}= & {} H_{i}{\tilde{x}}_{i}+E_{o,i}{\bar{w}}_i,\nonumber \\ \rho _i= & {} W_{i}{\tilde{x}}_{i}, \end{aligned}$$
(7)

where \(H_{i}\), \(E_{o,i}\), \(W_{i}\) can be found appropriately and \(H_i\) is Hurwitz stable.

Proof

The proof is in “Appendix.” \(\square \)

We then define

$$\begin{aligned} E_iw_i:= \begin{pmatrix} E_{i,d}&W_i \end{pmatrix} \begin{pmatrix} {\bar{w}}_i\\ {\tilde{x}}_i \end{pmatrix}. \end{aligned}$$

Then, the augmented agent can be rewritten as follows:

$$\begin{aligned} \left\{ \begin{array}{cl} {\dot{x}}_i &{}=Ax_i+B(Mu_i+Rx_i)+E_iw_i,\\ y_i &{}= Cx_i. \end{array}\right. \end{aligned}$$
(8)

Note that if \(n_q=1\), then \(A=0\), \(B=C=I_p\). For \(i\in {\mathcal {V}}\), the measurement \(\zeta _i\) is available, the local measurement \(z_{m,i}\) will no longer be used. They only play a role in homogenizing the non-identical agents.

3.2 Protocol Design

In this section, we design a protocol for each augmented agent (8) using a low-gain parameter \(\delta \in (0,1]\) and a high-gain parameter \(\varepsilon \in (0,1]\).

First, select K to ensure that \(A-KC\) is Hurwitz. Next, choose \(F_{\delta }=-B^{'}P_\delta \), where \(P_\delta =P_\delta ^{'}>0\) is the unique solution of the following algebraic Riccati equation:

$$\begin{aligned} P_\delta A+A^{'}P_\delta -\tau P_\delta BB^{'}P_\delta +\delta I=0, \end{aligned}$$
(9)

where \(\tau >0\) is the lower bound on the real parts of the non-zero eigenvalues of all Laplacian matrices \(L_i\), \(i \in {\mathcal {M}}\) (i.e., \(\tau \le \beta \)). Next, define \(S_\varepsilon ={{\,\mathrm{blkdiag}\,}}\{I_p,\varepsilon I_p,\ldots ,\varepsilon ^{n_q-1}I_p\}\), \(K_\varepsilon =\varepsilon ^{-1}S_\varepsilon ^{-1}K\) and \(F_{\delta \varepsilon }=\varepsilon ^{-pn_q}F_{\delta }S_\varepsilon \).

Then, we define the dynamic controller for each agent \(i \in {\mathcal {V}}\):

$$\begin{aligned} \dot{\hat{x}}_{i}= & {} A{\hat{x}}_i+BR{\hat{x}}_i+K_\varepsilon (\zeta _i-C{\hat{x}}_i),\nonumber \\ u_i= & {} M^{-1}F_{\delta \varepsilon }{\hat{x}}_i. \end{aligned}$$
(10)

The state \({\hat{x}}_i\) is an observer estimate of a linear combination of other agents’ relative states with the same weights as in the measurement \(\zeta _i\). The following Lemma provides a constructive proof of Theorem 1.

Lemma 2

For any given \(\gamma >0\), there exists a \(\delta ^{*} \in (0,1]\) such that, for each \(\delta \in (0,\delta ^{*} ]\), there exists an \(\varepsilon ^{*} (\delta ,\tau ^{*})\in (0, 1]\) such that for any \(\varepsilon \in (0,\varepsilon ^{*}(\delta ,\tau ^{*})]\), the dynamic protocol (10) solves the problem of almost output synchronization for a MAS of the form (8) under the switching topology \({\mathcal {G}}(t)\).

Proof

For each \(i \in \{1,\ldots ,N-1\}\), let \({\bar{x}}_{i}:=x_{N}-x_{i}\) and \(\hat{{\bar{x}}}_{i}:={\hat{x}}_{N}-{\hat{x}}_{i}\). Moreover, define \({\hat{w}}_i=E_Nw_N-E_iw_i\). Then, using (8), we can write down the error dynamics as follows:

$$\begin{aligned} \dot{{\bar{x}}}_i= & {} A{\bar{x}}_i+B(F_{\delta \varepsilon }\hat{{\bar{x}}}_i+R{\bar{x}}_i)+{\hat{w}}_i,\nonumber \\ {\mathbf {e}}_{i}= & {} C{\bar{x}}_i. \end{aligned}$$
(11)

Define \({\bar{g}}_{ij,\sigma (t)}=\ell _{ij,\sigma (t)}-\ell _{Nj,\sigma (t)}\), \(i,j \in \{1,\ldots ,N-1\}\). From (10), we obtain the following dynamics:

$$\begin{aligned} \dot{\hat{{\bar{x}}}}_{i}=A\hat{{\bar{x}}}_{i}+BR\hat{{\bar{x}}}_{i}+ \sum _{j=1}^{N-1}{\bar{g}}_{ij,\sigma (t)}K_{\varepsilon }C{\bar{x}}_{j}-K_{\varepsilon }C\hat{{\bar{x}}}_{i}. \end{aligned}$$
(12)

Next, define \(\xi _{i}=S_\varepsilon {\bar{x}}_{i}\), and \({\hat{\xi }}_{i}=S_\varepsilon \hat{{\bar{x}}}_{i}\). Then, the dynamics (11) and (12) become

$$\begin{aligned} \varepsilon \dot{\xi }_{i}= & {} A\xi _{i}+BF_{\delta }{\hat{\xi }}_{i}+ V_{\varepsilon i}\xi _{i}+\varepsilon {\bar{E}}_{\varepsilon i}{\hat{w}}_i,\nonumber \\ \varepsilon \dot{{\hat{\xi }}}_{i}= & {} A{\hat{\xi }}_{i}+V_{\varepsilon i}{\hat{\xi }}_{i}+ \sum _{j=1}^{N-1}{\bar{g}}_{ij,\sigma (t)}KC\xi _{j}-KC{\hat{\xi }}_{i}, \end{aligned}$$
(13)

where \(V_{\varepsilon i}=\varepsilon ^{n_q}BR S_{\varepsilon }^{-1}\), \({\bar{E}}_{\varepsilon i}=S_{\varepsilon }\).

Now define \({\bar{G}}_{\sigma (t)}=[{\bar{g}}_{ij,\sigma (t)}]\), \(i,j \in \{1,\ldots ,N-1\}\). Moreover, let \( \xi ={{\,\mathrm{col}\,}}\{\xi _i\}\), \({\hat{\xi }}={{\,\mathrm{col}\,}}\{{\hat{\xi }}_i\}\), \({\hat{w}}={{\,\mathrm{col}\,}}\{{\hat{w}}_i\} \). Then, we obtain the overall system dynamics as follows:

$$\begin{aligned} \varepsilon \dot{\xi }= & {} (I_{N-1}\otimes A)\xi +(I_{N-1}\otimes BF_{\delta }) {\hat{\xi }}+V_{\varepsilon }\xi +\varepsilon {\bar{E}}_{\varepsilon }{\hat{w}},\nonumber \\ \varepsilon \dot{{\hat{\xi }}}= & {} (I_{N-1}\otimes (A-KC)){\hat{\xi }}+V_{\varepsilon }{\hat{\xi }}+ ({\bar{G}}_{\sigma (t)}\otimes KC)\xi , \end{aligned}$$
(14)

where \( V_{\varepsilon }={{\,\mathrm{blkdiag}\,}}\{V_{\varepsilon i}\}\) and \({\bar{E}}_{\varepsilon }={{\,\mathrm{blkdiag}\,}}\{{\bar{E}}_{\varepsilon i}\}\).

Define \(U_{\sigma (t)}^{-1}{\bar{G}}_{\sigma (t)}U_{\sigma (t)}=J_{\sigma (t)}\), where \(J_{\sigma (t)}\) is the Jordan canonical form of \({\bar{G}}_{\sigma (t)}\), and let

$$\begin{aligned} v=(J_{\sigma (t)}U_{\sigma (t)}^{-1}\otimes I_{pn_q})\xi ,\qquad {\tilde{v}}=v-(U_{\sigma (t)}^{-1}\otimes I_{pn_q}){\hat{\xi }}. \end{aligned}$$

Then, the new overall system dynamics can be written,

$$\begin{aligned} \varepsilon {\dot{v}}= & {} (I_{N-1}\otimes A)v+(J_{\sigma (t)}\otimes BF_{\delta }) (v-{\tilde{v}})+W_{\varepsilon }v+\varepsilon {\bar{E}}{\hat{w}},\nonumber \\ \varepsilon \dot{{\tilde{v}}}= & {} (I_{N-1}\otimes (A-KC)){\tilde{v}}+(J_{\sigma (t)}\otimes BF_{\delta })(v-{\tilde{v}})+ W_{\varepsilon }v\nonumber \\&+\varepsilon {\bar{E}}{\hat{w}}-{\hat{W}}_{\varepsilon }(v-{\tilde{v}}), \end{aligned}$$
(15)

where \( {\bar{E}}=(J_{\sigma (t)}U_{\sigma (t)}^{-1}\otimes I_{pn_q}){\bar{E}}_{\varepsilon }, \), \(W_{\varepsilon }=(J_{\sigma (t)}U_{\sigma (t)}^{-1}\otimes I_{pn_q})V_{\varepsilon }(U_{\sigma (t)}J_{\sigma (t)}^{-1}\otimes I_{pn_q})\), and \({\hat{W}}_{\varepsilon }=(U_{\sigma (t)}^{-1}\otimes I_{pn_q})V_{\varepsilon }(U_{\sigma (t)}\otimes I_{pn_q})\). Finally, define Z as

$$\begin{aligned} Z= \begin{pmatrix} e_1&{}0\\ 0&{}e_1\\ \vdots &{}\vdots \\ e_{N-1}&{}0\\ 0&{}e_{N-1} \end{pmatrix}\otimes I_{pn_q}, \end{aligned}$$

such that a vector variable \(\eta \) can be defined in such a way,

$$\begin{aligned} \eta :=Z \begin{pmatrix} v \\ {\tilde{v}} \end{pmatrix}= \begin{pmatrix} v_{1}&{\tilde{v}}_{1}&\ldots&v_{N-1}&{\tilde{v}}_{N-1} \end{pmatrix}', \end{aligned}$$

where \(e_{i} \in {\mathbb {R}}^{N-1}\) is the i’th standard basis vector whose elements are all equal to zero except for the i’th element which is equal to 1. Then, the dynamics of \(\eta \) can be written from (15):

$$\begin{aligned} \varepsilon \dot{\eta }={\tilde{A}}_{\delta ,\sigma (t)}\eta +{\tilde{W}}_{\varepsilon }\eta +\varepsilon {\tilde{E}}{\hat{w}}, \end{aligned}$$
(16)

where

$$\begin{aligned} {\tilde{A}}_{\delta ,\sigma (t)}= & {} I_{N-1}\otimes \begin{pmatrix} A &{} 0\\ 0 &{} A-KC \end{pmatrix}+ J_{\sigma (t)}\otimes \begin{pmatrix} BF_{\delta } &{} -BF_{\delta }\\ BF_{\delta } &{} -BF_{\delta } \end{pmatrix}, \\ {\tilde{W}}_{\varepsilon }= & {} Z \begin{pmatrix} W_{\varepsilon } &{} 0\\ W_{\varepsilon }-{\hat{W}}_{\varepsilon } &{} {\hat{W}}_{\varepsilon } \end{pmatrix}Z^{-1}, \,\text {and}\,\,\, {\tilde{E}}=Z \begin{pmatrix} {\bar{E}}\\ {\bar{E}} \end{pmatrix} \end{aligned}$$

For \(t\in [t_{k-1},t_k)\), we denote the value of \(\sigma (t)\) as \(\varrho \), where \(\varrho \in {\mathcal {M}}\). It follows from the proof of (Grip et al., 2014, Theorem 1), that for each \(\varrho \in {\mathcal {M}}\), there exists a small \(\delta ^{*}\), for any \(\delta \in (0,\delta ^{*}]\), \({\tilde{A}}_{\delta ,\varrho }\) in (16) is Hurwitz stable. We pick a \(\delta \in (0,\delta ^{*}]\) and let it be fixed. Then there exists \({\tilde{P}}_{\delta ,\varrho }={\tilde{P}}_{\delta ,\varrho }^{'}>0\) satisfying

$$\begin{aligned} {\tilde{A}}_{\delta ,\varrho }^{'}{\tilde{P}}_{\delta ,\varrho }+ {\tilde{P}}_{\delta ,\varrho }{\tilde{A}}_{\delta ,\varrho }= -3I_{2(N-1)pn_q}. \end{aligned}$$
(17)

Define Lyapunov function \(V_{\varrho }=\varepsilon \eta ^{'}{\tilde{P}}_{\delta ,\varrho }\eta \) for this interval. Evaluating its derivative along the trajectory of (16) yields that

$$\begin{aligned} {\dot{V}}_{\varrho }&= -3\Vert \eta \Vert ^{2}+2{{\,\mathrm{Re}\,}}(\eta ^{*}{\tilde{P}}_{\delta ,\varrho }{\tilde{W}}_{\varepsilon }\eta ) +2\varepsilon {{\,\mathrm{Re}\,}}(\eta ^{*}{\tilde{P}}_{\delta ,\varrho }{\tilde{E}}{\hat{w}})\\&\le -3\Vert \eta \Vert ^{2}+2\Vert {\tilde{P}}_{\delta ,\varrho }\Vert \Vert {\tilde{W}}_{\varepsilon }\Vert \Vert \eta \Vert ^{2}+ 2\rho \varepsilon \Vert {\hat{w}}\Vert \Vert \eta \Vert \\&=-(2-2\Vert {\tilde{P}}_{\delta ,\varrho }\Vert \Vert {\tilde{W}}_{\varepsilon }\Vert )\Vert \eta \Vert ^{2}\\&\quad - (\Vert \eta \Vert -\rho \varepsilon \Vert {\hat{w}}\Vert )^{2}+\varepsilon ^{2}\rho ^{2}\Vert {\hat{w}}\Vert ^{2}\\&\le -(2-2\Vert {\tilde{P}}_{\delta ,\varrho }\Vert \Vert {\tilde{W}}_{\varepsilon }\Vert )\Vert \eta \Vert ^{2}+ \varepsilon ^{2}\rho ^{2}\Vert {\hat{w}}\Vert ^{2}, \end{aligned}$$

where \(\rho \ge \lambda _{\max }({\tilde{P}}_{\delta ,\varrho })\Vert {\tilde{E}}\Vert \ge \Vert {\tilde{P}}_{\delta ,\varrho }{\tilde{E}}\Vert \). Moreover, since \({\tilde{W}}_{\varepsilon }\) shrinks to zero as \(\varepsilon \) goes to zero, there exists an \(\varepsilon _1^{*}\) such that, for any \(\varepsilon \in (0,\varepsilon _1^{*}]\), \(2-2\Vert {\tilde{P}}_{\delta ,\varrho }\Vert \Vert {\tilde{W}}_{\varepsilon }\Vert >1\) holds for any \(\varrho \in {\mathcal {M}}\). Then,

$$\begin{aligned} {\dot{V}}_{\varrho }\le & {} -(2-2\Vert {\tilde{P}}_{\delta ,\varrho }\Vert \Vert {\tilde{W}}_{\varepsilon }\Vert ) \Vert \eta \Vert ^{2}+\varepsilon ^{2}\rho ^{2}\Vert {\hat{w}}\Vert ^{2}\nonumber \\\le & {} -\Vert \eta \Vert ^{2}+\varepsilon ^{2}\rho ^{2}\Vert {\hat{w}}\Vert ^{2}. \end{aligned}$$
(18)

So,

$$\begin{aligned} {\dot{V}}_{\varrho }+\Vert \eta \Vert ^{2}-\varepsilon ^{2}\rho ^{2}\Vert {\hat{w}}\Vert ^{2}\le 0. \end{aligned}$$
(19)

From Kalman–Yakubovich–Popov Lemma (Zhou & Doyle, 1998), we conclude that (19) implies that \(\Vert T_{{\hat{w}}\eta }\Vert _{\infty }\le \varepsilon \rho \). Next, we will show that this implies that the transfer function from the original disturbance to the network disagreement satisfies that \(\Vert T_{{\bar{w}}{\mathbf {e}}}\Vert _{\infty }\le \varepsilon \rho _{1}\), for certain \(\rho _{1}\).

Recall that \({\hat{w}}_i=E_Nw_N-E_iw_i\) which implies that \({\hat{w}}=T_ww\), where

$$\begin{aligned} T_w= \begin{pmatrix} -E_1 &{} 0 &{}\ldots &{} 0 &{} E_N\\ 0 &{} -E_2 &{}\ldots &{} 0 &{} E_N\\ \vdots &{} \vdots &{}\vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{}\ldots &{}-E_{N-1} &{} E_N \end{pmatrix}. \end{aligned}$$

Following the proof above, we find that

$$\begin{aligned} {\mathbf {e}}&= (I_{N-1}\otimes C)(I_{N-1}\otimes S_{\varepsilon }^{-1})(U_{\varrho }J_{\varrho }^{-1}\otimes I_{pn_q})\\&\begin{pmatrix} I_{(N-1)pn_q}&0 \end{pmatrix} Z^{-1}\eta \\&=(U_{\varrho }J_{\varrho }^{-1}\otimes C)\begin{pmatrix} I_{(N-1)pn_q}&0 \end{pmatrix} Z^{-1}\eta . \end{aligned}$$

Let \(\Theta =(U_{\varrho }J_{\varrho }^{-1}\otimes C)\begin{pmatrix} I_{(N-1)pn_q}&0 \end{pmatrix} Z^{-1}\). Since the norm of \(\Theta \) is bounded, we have that

$$\begin{aligned} \Vert {\mathbf {e}}\Vert =\Vert \Theta \eta \Vert \le \Vert \Theta \Vert \Vert T_{{\hat{w}}\eta }\Vert _{\infty }\Vert T_w\Vert \Vert w\Vert \le \varepsilon \rho \Vert \Theta \Vert \Vert T_w\Vert \Vert w\Vert . \end{aligned}$$

According to Sect. 3.1 of homogenization, we have that \(w_i = \begin{pmatrix} {\bar{w}}_i \\ {\tilde{x}}_i \end{pmatrix}\), and that \({\tilde{x}}_i\) is defined via

$$\begin{aligned} \dot{{\tilde{x}}}_i = H_i {\tilde{x}}_i + E_{o,i} {\bar{w}}_i, \end{aligned}$$

where \(H_i\) is Hurwitz and thus there exists \(\Theta ^{'}\) such that \(\Vert w \Vert \le \Vert {\bar{w}} \Vert \le \Theta ^{'} \Vert w \Vert \). This implies that there exists \(\rho _{1}\) such that

$$\begin{aligned} \Vert T_{{\bar{w}}{\mathbf {e}}}\Vert _{\infty }\le \varepsilon \rho _{1}, \end{aligned}$$
(20)

which can be made arbitrarily small by an appropriate choice of the high gain \(\varepsilon \).

Let us first consider (16) without the disturbance w, and denote the state as \({\tilde{\eta }}\) and Lyapunov function as \({\tilde{V}}_{\varrho }=\varepsilon {\tilde{\eta }}^{'}{\tilde{P}}_{\delta ,\varrho }{\tilde{\eta }}\) for interval \(t\in [t_{k-1},t_k)\). We then have

$$\begin{aligned} \dot{{\tilde{V}}}_{\varrho }&\le -(2-2\Vert {\tilde{P}}_{\delta ,\varrho }\Vert \Vert {\tilde{W}}_{\varepsilon }\Vert )\Vert {\tilde{\eta }}\Vert ^{2} \\&\le -\dfrac{(2-2\Vert {\tilde{P}}_{\delta ,\varrho }\Vert \Vert {\tilde{W}}_{\varepsilon }\Vert )}{\varepsilon \Vert {\tilde{P}}_{\delta ,\varrho }\Vert }{\tilde{V}}_{\varrho }\\&\le -\dfrac{1}{\varepsilon \lambda _{\max }({\tilde{P}}_{\delta ,\varrho })}{\tilde{V}}_{\varrho }. \end{aligned}$$

Define \(\lambda _{c}=\min _{\varrho \in {\mathcal {M}}}\dfrac{1}{\lambda _{\max }({\tilde{P}}_{\delta ,\varrho })}\), then \(\dot{{\tilde{V}}}_{\varrho } \le -\frac{\lambda _{c}}{\varepsilon }{\tilde{V}}_{\varrho }\).

According to Liberzon and Morse (1999), we define multiple Lyapunov function for (16) as \({\tilde{V}}=\varepsilon {\tilde{\eta }}^{'}{\tilde{P}}_{\delta ,\sigma (t)}{\tilde{\eta }}\). Then, for \(t\in [t_{k-1},t_k)\), we have

$$\begin{aligned} {\tilde{V}}(t)&\le e^{-\lambda _{\sigma (t)}(t-t_{k-1})}{\tilde{V}}(t_{k-1})\\&\le e^{-\frac{1}{\varepsilon }\lambda _{c}(t-t_{k-1})}{\tilde{V}}(t_{k-1}). \end{aligned}$$

Let \(b=\sup _{i,j\in {\mathcal {M}}}\dfrac{\lambda _{\max }({\tilde{P}}_{\delta ,i})}{\lambda _{\min }({\tilde{P}}_{\delta ,j})}\). Let \(s_t\) be the switching times during \([t_0, t)\). Then \(s_t\le \dfrac{t-t_0}{\tau ^{*}}\). And we have

$$\begin{aligned} {\tilde{V}}(t)&\le b^{s_t}e^{-\frac{\lambda _{c}}{\varepsilon }(t-t_0)}{\tilde{V}}(t_0)\\&\le b^{\frac{t-t_0}{\tau ^{*}}}e^{-\frac{\lambda _{c}}{\varepsilon }(t-t_0)}{\tilde{V}}(t_0)\\&\le e^{-(\frac{\lambda _{c}}{\varepsilon }-\frac{\ln b}{\tau ^{*}})(t-t_0)}{\tilde{V}}(t_0). \end{aligned}$$

There exist \(\varepsilon _2^{*} = \frac{\lambda _c\tau ^*}{\ln b+\tau ^*}\) such that for any \(\varepsilon \in (0, \varepsilon _2^{*}]\), \(V(t)\le e^{-(t-t_0)}V(t_0)\). Since \(\varepsilon \max _{\varrho \in {\mathcal {M}}}\lambda _{\max }({\tilde{P}}_{\delta ,\varrho })\Vert {\tilde{\eta }}(t)\Vert ^{2} \ge {\tilde{V}}(t) \ge \varepsilon \min _{\varrho \in \mathcal {M}}\lambda _{\min }({\tilde{P}}_{\delta ,\varrho })\Vert {\tilde{\eta }}(t)\Vert ^{2}\), we have

$$\begin{aligned} \Vert {\tilde{\eta }}(t)\Vert \le \sqrt{\dfrac{\max _{\varrho \in \mathcal {M}}\lambda _{\max }({\tilde{P}}_{\delta ,\varrho }) }{\min _{\varrho \in \mathcal {M}}\lambda _{\min }({\tilde{P}}_{\delta ,\varrho })}} e^{-\frac{1}{2}(t-t_0)}\Vert {\tilde{\eta }}(t_0)\Vert . \end{aligned}$$
(21)

Hence, we can choose \(\varepsilon ^{*}=\min \{\varepsilon _1^{*}, \varepsilon _2^{*}\}\), such that for each fixed \(\varepsilon \in (0, \varepsilon ^{*}]\), \(\lim _{t\rightarrow \infty }\Vert {\tilde{\eta }}(t)\Vert =0\).

We now consider the affect of the external disturbance on the network disagreement. Define state transition matrix from \(t_{k-1}\) to \(t_k\) as \(\phi (t_k, t_{k-1})\), it is easy to find that \(\Vert \phi (t_k, t_{k-1})\Vert <1\) for any k. Let \(T_{\phi }=\max _k\Vert \phi (t_k, t_{k-1})\Vert \).

When adding the affect of disturbance, during an interval, \(t \in [t_{k-1},t_k)\), \(\eta (t_k)=\phi (t_k, t_{k-1})\eta (t_{k-1})+ \int _{t_{k-1}}^{t_k} T_{{\hat{w}}\eta }(t){\hat{w}}(t_{k}-t)\mathrm{d}t \).

Then we have

$$\begin{aligned} \Vert \eta (t_k)\Vert&\le \Vert \phi (t_k, t_{k-1})\eta (t_{k-1})\Vert +\Vert \int _{t_{k-1}}^{t_k} T_{{\hat{w}}\eta }(t){\hat{w}}(t_{k}-t)\mathrm{d}t \Vert \\&\le T_{\phi }\Vert \eta (t_{k-1})\Vert +\varepsilon \rho \kappa \Vert T_w\Vert \\&\le T_{\phi }^{k}\Vert \eta (t_{0})\Vert + \dfrac{1-T_{\phi }^{k-1}}{1-T_{\phi }}\varepsilon \rho \kappa \Vert T_w\Vert . \end{aligned}$$

Thus, \(\limsup _{k\rightarrow \infty } \Vert \eta (t_k)\Vert =\dfrac{1}{1- T_{\phi }}\varepsilon \rho \kappa \). Therefore,

$$\begin{aligned} \Vert \eta (t)\Vert \le \Vert \phi (t,t_{k-1})\eta (t_{k-1})\Vert +\varepsilon \rho \kappa \Vert T_w\Vert , \end{aligned}$$
(22)

for \(0\le t-t_{k-1} < \tau ^{*}\). Hence, \(\limsup _{t\rightarrow \infty } \Vert \eta (t)\Vert \le \dfrac{2-T_{\phi }}{1- T_{\phi }}\varepsilon \rho \kappa \Vert T_w\Vert \).

Next, we will show that, there exists a \(\rho _2\) such that \(\limsup _{t\rightarrow \infty }\Vert {\mathbf {e}}(t)\Vert \le \varepsilon \rho _2 \kappa \). From the above, we already know that \({\mathbf {e}}=\Theta \eta \) and the norm of \(\Theta \) is bounded. Thus, we have

$$\begin{aligned} \limsup _{t\rightarrow \infty }\Vert {\mathbf {e}}(t)\Vert = \Theta \limsup _{t\rightarrow \infty }\Vert \eta (t)\Vert \le \varepsilon \rho _2\kappa , \end{aligned}$$
(23)

where \(\rho _2=\Theta \rho \). Let \(\varepsilon =\gamma /(\rho _2\kappa )\), then \(\limsup _{t\rightarrow \infty }\Vert {\mathbf {e}}(t)\Vert \le \gamma \). \(\square \)

4 Almost Regulated Output Synchronization Under Switching Topologies

In this section, we consider the case where the goal is that the agents follow a particular trajectory in the presence of external disturbances under a time-varying topology. In general, the reference trajectory is generated by an autonomous system of the form:

$$\begin{aligned} {\bar{\Sigma }}_0: \left\{ \begin{array}{cl} \dot{{\bar{x}}}_0&{}={\bar{A}}_0{\bar{x}}_0,\\ y_0&{}={\bar{C}}_0{\bar{x}}_0, \end{array}\right. \end{aligned}$$
(24)

where \({\bar{x}}_0\in {\mathbb {R}}^{n_0}\), \(y_0\in {\mathbb {R}}^{p}\). We assume that \(({\bar{A}}_0,{\bar{C}}_0)\) is observable, and all eigenvalues of \({\bar{A}}_0\) are in the closed-right half complex plane, and \({\bar{C}}_0\) has full row rank.

Let \(e_{i0}:=y_i-y_0\) be the regulation error for agent \(i\in {\mathcal {V}}\) and \({\mathbf {e}}_0={{\,\mathrm{col}\,}}\{e_{i0}\}\). In order to achieve regulated output synchronization for all agents, the following assumption is clearly necessary:

Assumption 4

Every agent of the direct graph \({\mathcal {G}}_i\), \(i\in {\mathcal {M}}\), is a member of a directed spanning tree with root contained in a subset \(\pi \subset {\mathcal {V}}\).

To regulate all agents in the network to a reference trajectory, it is necessary that agents in the root set \(\pi \) will receive the regulation error \(e_{i0}\). It implies that the quantity available to each agent is altered to

$$\begin{aligned} {\tilde{\zeta }}_i=\sum _{j=1}^{N}a_{ij}(t)(y_i-y_j)+\varphi _i(y_i-y_0), \end{aligned}$$
(25)

where \(\varphi _i=1\) for \(i\in \pi \) and \(\varphi _i=0\) for \(i\notin \pi \). Note that the reference system can be viewed as a new root agent, denoted as 0. This expanded graph will be referred to as the augmented graph and will be denoted by \(\tilde{{\mathcal {G}}}(t)\). The associated Laplacian matrix \({\tilde{L}}(t)=[{\tilde{\ell }}_{ij}(t)]\) is then

$$\begin{aligned} {\tilde{L}}(t)= \begin{pmatrix} 0 &{} 0\\ -{{\,\mathrm{col}\,}}\{\varphi _i\}&{}L(t)+{{\,\mathrm{diag}\,}}\{\varphi _i\} \end{pmatrix}. \end{aligned}$$

Thus, in terms of the Laplacian matrix \({\tilde{L}}(t)\), (25) can be rewritten as \( {\tilde{\zeta }}_i=\sum _{j=0}^{N}{\tilde{l}}_{ij}(t)y_j \).

Note that \(\tilde{\mathcal {G}}(t)\) switches among the finite graph set \(\tilde{\mathbb {G}}=\{\tilde{\mathcal {G}}_1,\tilde{\mathcal {G}}_2,\ldots ,\tilde{\mathcal {G}}_M\}\), with associated Laplacian matrix \({\tilde{L}}_i\) for each \(\tilde{\mathcal {G}}_i\). Also note that, from Assumption 4, each graph \(\tilde{\mathcal {G}}_i\) contains a directed spanning tree with agent 0 as the root (Grip et al., 2012).

We will define almost regulated output synchronization problem under the switching topology as follows.

Problem 2

Consider a MAS with non-identical and introspective agents described by (1) and (2) and an autonomous system described by (24). Suppose Assumptions 2 to 4 are satisfied, and the switching topology has minimum dwell time \(\tau ^*\) and the disturbance has a limit power \(\kappa \). Then, the problem of almost regulated output synchronization under switching topology \(\tilde{\mathcal {G}}(t)\) with respect to a reference trajectory \(y_0\) is to find, if possible, for any \(\kappa >0\) and any \(\gamma >0\), an LTI dynamic protocol such that, the disagreement among agents satisfies that \(\limsup _{t\rightarrow \infty }\Vert {\mathbf {e}}_0(t)\Vert <\gamma \).

Here is the main result in this section:

Theorem 2

Consider a MAS with non-identical and introspective agents described by (1) and (2) and an autonomous system described by (24). Under Assumption 2 to 4 with any a priori given minimum dwell time \(\tau ^{*}\), for any given \(\kappa >0\), the problem of almost regulated output synchronization under a switching topology \(\tilde{\mathcal {G}}(t)\) is solvable, i.e., there exits a family of LTI dynamic protocols, parameterized in terms of low-and-high gain parameters \(\delta ,\,\varepsilon \in (0,1]\), of the form:

$$\begin{aligned} \left\{ \begin{array}{cl} \dot{{\tilde{\chi }}}_i &{}= \mathcal {A}_i(\delta ,\varepsilon ){\tilde{\chi }}_i+ {\mathcal {B}}_i(\delta ,\varepsilon ){{\,\mathrm{col}\,}}\{{\tilde{\zeta }}_i,z_{m,i}\},\\ {\bar{u}}_i &{}= {\mathcal {C}}_i(\delta ,\varepsilon ){\tilde{\chi }}_i+ {\mathcal {D}}_i(\delta ,\varepsilon ){{\,\mathrm{col}\,}}\{{\tilde{\zeta }}_i,z_{m,i}\}, \end{array}\right. \end{aligned}$$
(26)

for\(i\in {\mathcal {V}}\), where \({\tilde{\chi }}_i \in {\mathbb {R}}^{{\tilde{q}}_i}\), such that given any \(\gamma >0\), there exists a \(\delta ^{*} \in (0,1]\) such that, for each \(\delta \in (0,\delta ^{*} ]\), there exists an \(\varepsilon ^{*} (\delta ,\tau ^{*})\in (0, 1]\) such that for any \(\varepsilon \in (0,\varepsilon ^{*}(\delta ,\tau ^{*})]\), the protocol (26) achieves almost regulated output synchronization under switching topology, i.e., we have \(\limsup _{t\rightarrow \infty }\Vert {\mathbf {e}}_0(t)\Vert <\gamma \).

Proof

The proof is constructive and similar to the proof of Theorem 1, except that the autonomous system needs to be rank-uniformed first. In what follows, we will give such a design procedure.

Let the largest observability index of the pair \(({\bar{A}}_0,{\bar{C}}_0)\) be denoted by \(n_{q_0}^*\). There exist a series of state manipulations for (24) and a matrix \(B_0\) such that the resulting system characterized by \((A_0, B_0, C_0)\) is invertible, of the uniform rank \(n_q\ge \max \{n_{q_i}, n_{q_0}^{*}\}\), and have no invariant zeros (Yang et al., 2014, Appendix C). According to Peymani et al. (2014, Lemma 4), we can then transform the autonomous system into the following form:

$$\begin{aligned} \Sigma _0: \left\{ \begin{array}{cl} {\dot{x}}_0&{}=Ax_0+B(M_0u_0+R_0x_0),\\ y_0&{}=Cx_0, \end{array}\right. \end{aligned}$$
(27)

where \(x_0\in {\mathbb {R}}^{pn_q}\), \(u_0\in {\mathbb {R}}^{p}\), A, B, and C are given by (6), and \(M_0\in {\mathbb {R}}^{p\times p}\) is an arbitrary non-singular matrix. Since it is an autonomous system, we choose \(u_0=0\). Finally, \(R_0\in {\mathbb {R}}^{p\times pn_q}\) such that (27) can generate the same outputs as (24). By adding a term \(E_0w_0\) with \(E_0=0\) in (27), we obtain the same form for the autonomous system as the agents in the system (8), with \(i\in \{{0},{\mathcal {V}}\}\).

The protocol designed here is similar to the one (10) used in the synchronization case, except that \(\alpha \) and \(\beta \) used in (9) are set to the proper bounds associated with \({\tilde{L}}_i\), \(i\in {\mathcal {M}}\). The dynamic protocol used for each agent in the augmented system is given by:

$$\begin{aligned} \dot{{\hat{x}}}_{i}= & {} A{\hat{x}}+BR_0{\hat{x}}_i+K_\varepsilon ({\tilde{\zeta }}_i-C{\hat{x}}_i),\nonumber \\ u_i= & {} M_0^{-1}F_{\delta \varepsilon }{\hat{x}}_i, \end{aligned}$$
(28)

where \(K_{\varepsilon }=\varepsilon ^{-1}S_{\varepsilon }^{-1}K\) and \(F_{\delta \varepsilon }=\varepsilon ^{-pn_q}F_{\delta }S_{\varepsilon }\), with K and \(F_{\delta }\) are chosen in the same way in Sect. 3. Notice that setting \({\hat{x}}_0(0)=0\) leads to \({\hat{x}}_0(t)=0\) and \(u_0(t)=0\) for all \(t\ge 0\).

The remaining of the proof is then the same as the proof of Theorem 1. \(\square \)

5 Examples

In this section, we illustrate our results on a MAS of \(N=10\) agents, in which there are four different dynamics:

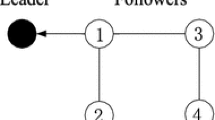
$$\begin{aligned}\text {I}: A= & {} \begin{pmatrix} -1 &{} 2 &{} 0\\ 0 &{} 0 &{} 1\\ 2 &{} 1 &{}1 \end{pmatrix}, B= \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}, C^{'}= \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, C_{m}^{'}= \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}, G= \begin{pmatrix} 1\\ 0\\ 1 \end{pmatrix}, \\\text {II}: A= & {} \begin{pmatrix} -2 &{} 1 &{} 0\\ 0 &{} 0 &{} 1\\ 1 &{} 1 &{}2 \end{pmatrix}, B= \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}, C^{'}= \begin{pmatrix} 0 \\ 1\\ 0 \end{pmatrix}, C_{m}^{'}= \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}, G= \begin{pmatrix} 2\\ 1\\ 2 \end{pmatrix}, \\\text {III}: A= & {} \begin{pmatrix} -3 &{} 2 &{} 0\\ 0 &{} 0 &{} 1\\ 2&{} 2 &{}1 \end{pmatrix}, B= \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}, C^{'}= \begin{pmatrix} 0 \\ 1\\ 0 \end{pmatrix}, C_{m}^{'}= \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}, G= \begin{pmatrix} 2\\ 3\\ 4 \end{pmatrix}, \\\text {IV}: A= & {} \begin{pmatrix} -2 &{} 3 &{} 0\\ 0 &{} 0 &{} 1\\ 3 &{} 1 &{}2 \end{pmatrix}, B= \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}, C^{'}= \begin{pmatrix} 0 \\ 1\\ 0 \end{pmatrix}, C_{m}^{'}= \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}, G= \begin{pmatrix} 4\\ 1\\ 3 \end{pmatrix}. \end{aligned}$$

Agents 1, 2, and 3 have type I dynamics, Agents 4, 5, and 6 have type II dynamics, Agents 7 and 8 have type III dynamics, and Agents 9 and 10 have type IV dynamics. The topology switches among three directed graphs presented in Fig. 1 in a circular manner. The minimum dwell time \(\tau ^{*}\) is equal to 3 second. The external disturbances are chosen as \({\bar{w}}_1(t)=\sin (9t)\), \({\bar{w}}_2(t)=1.5\), \({\bar{w}}_3(t)=\cos (6t)\), \({\bar{w}}_4(t)=1\), \({\bar{w}}_5(t)=\cos (3t)\), \({\bar{w}}_6(t)=\sin (6t)\), \({\bar{w}}_7(t)=\sin (5t)\), \({\bar{w}}_8(t)=\cos (t)\), \({\bar{w}}_9(t)=\sin (10t)\), \({\bar{w}}_{10}(t)=\cos (2t)\). The degree of the infinite zeros for each agent is equal to 2.

Fig. 1
figure 1

The topologies of multi-agent systems

Full size image

After homogenization, the agents have dynamics of the form (8) with

$$\begin{aligned} A= & {} \begin{pmatrix} 0 &{} 1\\ 0 &{} 0 \end{pmatrix},\qquad B= \begin{pmatrix} 0\\ 1 \end{pmatrix},\qquad C= \begin{pmatrix} 1&0 \end{pmatrix}, \\ E_1w_{i1}= & {} \begin{pmatrix} 0 &{}0&{}0&{}0\\ 1&{}2&{}3&{}4 \end{pmatrix} \begin{pmatrix} {\bar{w}}_{i1}\\ {\tilde{x}}_1 \end{pmatrix} ,\quad E_2w_{i2}= \begin{pmatrix} 1 &{}0&{}0&{}0\\ 2&{}1&{}3&{}5 \end{pmatrix} \begin{pmatrix} {\bar{w}}_{i2}\\ {\tilde{x}}_2 \end{pmatrix}, \\ E_3w_{i3}= & {} \begin{pmatrix} 3 &{}0&{}0&{}0\\ 4&{}2&{}4&{}4 \end{pmatrix} \begin{pmatrix} {\bar{w}}_{i3}\\ {\tilde{x}}_3 \end{pmatrix},\quad E_4w_{i4}= \begin{pmatrix} 1 &{}0&{}0&{}0\\ 3&{}3&{}4&{}6 \end{pmatrix} \begin{pmatrix} {\bar{w}}_{i4}\\ {\tilde{x}}_4 \end{pmatrix}, \end{aligned}$$

where \(i1\in \{1, 2, 3\}\), \(i2\in \{4, 5, 6\}\), \(i3\in \{7, 8\}\), \(i4\in \{9, 10\}\).

Almost output synchronization: Choose \(K=\begin{pmatrix} 3&2\end{pmatrix}\) to place eigenvalues at \(\{-1,\,-2\}\), and select \(\delta =10^{-5}\). Figure 2 shows the results for \(\varepsilon =0.0002\) and \(\varepsilon =0.0007\). It is clearly that when \(\varepsilon \) is smaller, the effect of disturbance on the network disagreement is squeezed much more.

Fig. 2
figure 2

Almost output synchronization

Full size image

Almost regulated output synchronization: In this case, the reference system of the form (24) has \( A_0=\begin{pmatrix} 0&{}0.5\\ -0.5&{}0 \end{pmatrix},\, C_0=\begin{pmatrix} 1&0 \end{pmatrix} \) and the initial condition \(x_0=\begin{pmatrix} 0\\ 1 \end{pmatrix}\), which is connected to the root Agent 2. After homogenization, we get \(R_0=[-0.5^2\,\,0]\), \(M_0=1\), A, B, and C are the same as above for (27). We use the same K matrix, and choose \(\delta =10^{-5}\). Figure 3 also shows that when \(\varepsilon \) is smaller, the effect of disturbance on the regulation error is attenuated much more.

Fig. 3
figure 3

Almost regulated output synchronization

Full size image

6 Conclusion

In this paper, we have formulated the notion of almost synchronization for heterogeneous networks of introspective agents under directed switching topologies. That means the problem of almost synchronization for heterogeneous networks of both introspective and non-introspective agents under a directed switching topologies has been done. The future research will be focused on agents in the presence of actuator saturation and input delay while under switching topologies.

The author has no conflicts of interest to disclose.