1 Introduction

Recently, the synchronization/consensus theory and applications for multi-agent systems have been attracting great interest from many areas [1]. This is due to its many important applications, such as network synchronization [2, 3], formation control [4, 5], attitude alignment [6, 7], cooperative attack of multiple missiles [8], flocking [9, 10]. The synchronization of multi-agent systems means that all the agents’ states converge to a same state. To guarantee that the final synchronization state is the reference state, the method of adding a virtual leader is usually employed. In this case, the system is called leader-following multi-agent systems.

As for the leader-following multi-agent systems, the leader can be divided into two cases: One is stationary leader, and the other one is dynamic leader. In the case when the leader is stationary, in [11], the consensus problem under switching topologies was studied for double-integrator systems. To guarantee all the follower can track a dynamic leader, the consensus control algorithms were designed for single and double-integrator multi-agent systems in [12–17], respectively. For the second-order nonlinear leader-following multi-agent systems, the corresponding consensus control algorithms were discussed in [18–20].

Nevertheless, the aforementioned results on consensus results are based on continuous-time state feedback. In practice, since more and more sensors and controllers are being implemented through digital computers, how to design a consensus algorithm only using sampled-data information becomes imperative. To this end, in [21], the consensus problem via sampled-data control for the multi-agent systems with double-integrator dynamics was discussed. When the communication topology is time-varying, the corresponding sampled-data control-based consensus algorithm was proposed in [22]. When only the position information is available at the sampling instants, the consensus algorithm was given in [23]. Under the consideration of communication delay between agents, the corresponding delayed consensus algorithm via sampled-data control was proposed in [24]. In [25], some necessary and sufficient conditions were derived to guarantee states consensus via pinning control. When the sampling is aperiodic, the consensus problem was also proposed in [26].

Note that the previous listed consensus control algorithms via sampled-data information are mainly applicable to first-order or second-order multi-agent systems. This paper considers a more general case, i.e., a class of high-order nonlinear multi-agent systems. Nevertheless, because of the presence of the unknown nonlinearities, we cannot directly obtain the exact discrete-time model for the nonlinear multi-agent systems under sampled-data control. To this end, a continuous-time consensus controller is first designed to achieve states consensus. Then the controller is discretized and implemented digitally where the key issue is to compute the maximum allowable sampling period (MASP) that guarantees the closed-loop system’s stability. Under the proposed sampled-data controller and some assumptions, it is shown that the consensus for the considered second-order nonlinear multi-agent systems can be achieved by choosing appropriate gains and sampling period. The main contribution of this paper lies in two aspects: (i) A distributed sampled-data controller is constructed step by step to solve the synchronization problem for a class of high-order nonlinear multi-agent systems whose nonlinearities are allowable to be unknown and (ii) the explicit formula for the maximum allowable sampling period (MASP) is given.

2 Preliminaries and problem formulation

2.1 Problem formulation

This paper investigates the problem of synchronization via sampled-data control for a class of high-order nonlinear multi-agent systems described by:

$$\begin{aligned}&\dot{x}_{i,1}=x_{i,2},~~\nonumber \\&\vdots \nonumber \\&\dot{x}_{i,n-1}=x_{i,n},~~\nonumber \\&\dot{x}_{i,n}= f(t,x_{i,1},\ldots ,x_{i,n})+ u_i, \quad i\in \varGamma =\{1,2,\ldots ,n\}, \end{aligned}$$
(1)

where \((x_{i,1},\ldots ,x_{i,n})\in R^n\) is the i-th agent’s state, \(u_i\) is the control input to be designed, \(f(\cdot )\) is a unknown nonlinear continuous function. Considering in practice, many agents only send and receive information at sampling instant points, and the controller is usually digitally implemented, e.g., the most popular zero-order hold device

$$\begin{aligned} \begin{aligned} u(t)&=u(t_k), \quad \forall t\in [t_k,t_{k+1}),\nonumber \\ t_{k+1}&=t_k+ T, \quad \ k\in N=\{0,1,2,\ldots \}, \end{aligned} \end{aligned}$$

where the time instants \(t_k,t_{k+1}\) are the sampling points, and T is the sampling period. Motivated by this reason, the objective of this paper is to design a distributed sampled-data controller \(u(t_k)\) which is only based on the itself and neighbors’ sampled-data information such that the states of all agents reach synchronization. And the final synchronization state is a referenced state, which is represented by a virtual leader described by

$$\begin{aligned}&\dot{x}_1^d=x_2^d,~~\nonumber \\&\vdots \nonumber \\&\dot{x}_{n-1}^d=x_n^d,~~\nonumber \\&\dot{x}_n^d=f(t,x_1^d,\ldots ,x_n^d) \end{aligned}$$
(2)

From a mathematical viewpoint, the synchronization means that for all \(i\in \varGamma ,\)

$$\begin{aligned} \lim _{t\rightarrow \infty }\left\| (x_{i,1}(t),\ldots ,x_{i,n}(t))-(x_1^d(t),\ldots ,x_n^d(t))\right\| \!=\!0, \end{aligned}$$

where \(\Vert \cdot \Vert \) denotes the Euclidean norm, i.e., \(\Vert x\Vert =\sqrt{x^Tx}\) for a vector x.

2.2 Graph theory

For the considered multi-agent systems, i.e., leader–follower multi-agent systems (1)–(2), assume that each agent is a node and the information exchange of n follower agents is denoted by an undirected graph \(G=\{V,E,A\}\). \(V=\{v_i,i=1,\ldots ,n\}\) is the set of vertices, \(E\subseteq V\times V\) is the set of edges, and \(A=[a_{ij}]\in R^{n\times n}\) is the weighted adjacency matrix of the graph G. The node indexes belong to a finite index set \(\varGamma =\{1,\ldots ,n\}\). If there is an edge between agent i and j, i.e., \((v_i,v_j)\in E\), then \(a_{ij}=a_{ji}>0\). If there is not any edge between agent i and j, then \(a_{ij}=a_{ji}=0\). Moreover, we assume that \(a_{ii}=0\) for all \(i\in \varGamma \). The set of neighbors of node \(v_i\) is denoted by \(N_i=\{j:(v_i,v_j)\in E\}\). The out-degree of node \(v_i\) is defined as \(\mathrm{deg}_{\mathrm{out}}(v_i)=d_i=\sum _{j=1}^{n}a_{ij}=\sum _{j\in N_i}a_{ij}\). Then the degree matrix of digraph G is \(D=\mathrm{diag}\{ d_1,\ldots ,d_n\}\), and the Laplacian matrix of digraph G is \(L=D-A\). A path in the graph G from \(v_i\) to \(v_j\) is a sequence of distinct vertices starting with \(v_i\) and ending with \(v_j\) such that consecutive vertices are adjacent. The graph G is connected if there is a path between any two vertices.

Assume that the leader (labeled by 0) is represented by the vertex \(v_0\). If the i-th follower is connected to the leader, i.e., this follower can directly obtain the information of the leader, then \(b_i>0\), otherwise, \(b_i=0\). Define the matrix \(B=\mathrm{diag}\{b_1,\ldots ,b_n\}\).

2.3 Some assumptions

Firstly, as that in [18, 19], it is assumed that the unknown nonlinear function \(f(\cdot )\) satisfies the Lipschitz condition.

Assumption 1

There is a known positive constant \(\rho \) such that

(3)

Secondly, as that in [14, 17], an assumption on communication topology is presented.

Assumption 2

For the leader–follower multi-agent systems (1) and (2), the graph G for the followers is connected and there is at least one follower connected to the leader, i.e., \(B\ne 0\).

2.4 Useful lemma

Lemma 1

([12]). For the leader–follower multi-agent systems (1) and (2), if Assumption 2 holds, then \(L+B>0\), i.e., the matrix \(L+B\) is positive definite.

3 Main results

In this section, it is shown that the synchronization problem of high-order nonlinear multi-agent systems (1)–(2) only using sampled-data information is solvable under Assumptions 1–2. To achieve this control objective, at the first step, a consensus controller based on continuous-time state feedback is proposed. Then, by discretizing the continuous-time controller, it is shown that there is a maximum allowable sampling period (MASP) \(T^*>0\) (\(\sup _{k\in N} \) \(\{t_{k+1}-t_k\}\le T^*\)) such that the sampled-data control system is globally asymptotically stable.

Theorem 1

For the high-order nonlinear multi-agent systems (1)–(2), if Assumptions 1–2 are satisfied and \(u_i\) is designed as

$$\begin{aligned}&u_{i}(t)=\nonumber \\&\quad -\,k_1\Big [\sum _{j\in N_i}a_{ij} (x_{i,1}(t_k)-x_{j,1}(t_k))+b_i(x_{i,1}(t_k)\nonumber \\&\qquad -\,x_1^d(t_k))\Big ]\nonumber \\&\quad -\,k_2\Big [\sum _{j\in N_i}a_{ij}(x_{i,2}(t_k)-x_{j,2}(t_k))+b_i(x_{i,2}(t_k)\nonumber \\&\qquad -\,x_2^d(t_k))\Big ]\nonumber \\&\quad -\cdots \nonumber \\&\quad -\,k_n\Big [\sum _{j\in N_i}a_{ij} (x_{i,n}(t_k)-x_{j,n}(t_k))+b_i(x_{i,n}(t_k)\nonumber \\&\qquad -\,x_n^d(t_k))\Big ], \quad \forall t\in [t_k,t_{k+1}),~~i\in \varGamma , \end{aligned}$$
(4)

then the states synchronization can be achieved provided that the control gains and the sampling period T satisfy

(5)

where \(\lambda _{\mathrm{max}}(L+B)\), \(\lambda _{\mathrm{min}}(L+B)\) are the maximum and minimum eigenvalues of matrix \(L+B\),

$$\begin{aligned} c_1=&n,\nonumber \\ c_2=&\beta _1(c_1)+n-1,\beta _1(c_1)=\frac{(1+c_1^4)}{2}+c_1, \nonumber \\ c_i=&\left[ \beta _{i-1}(c_1,\ldots ,c_{i-1})+n-i+1\right] ,\nonumber \\&\quad i=3,\ldots ,n-1, \end{aligned}$$
(6)

with

(7)

Proof

Denote the tracking error between the followers and the leader as:

$$\begin{aligned} \bar{x}_{i,1}=x_{i,1}-x_1^d,\ldots ,\bar{x}_{i,n}=x_{i,n}-x_n^d,~~i\in \varGamma . \end{aligned}$$
(8)

It follows from (1) and (2) that the tracking error dynamic equation is:

(9)

Next, by integrating the graph theory and Lyapunov design method together, a sampled-data controller is first designed.

A: Design of a sampled-data controller

An inductive argument is employed.

Step 1 For the Lyapunov function

$$\begin{aligned} V_1=\frac{1}{2}\sum _{i=1}^n\overline{x}_{i,1}^2, \end{aligned}$$
(10)

the derivative of \(V_1\) along system (9) is

$$\begin{aligned} \dot{V}_1&= \sum _{i=1}^n\overline{x}_{i,1}\overline{x}_{i,2}^*+\sum _{i=1}^n\overline{x}_{i,1} \left( \overline{x}_{i,2}-{\overline{x}_{i,2}^*}\right) , \end{aligned}$$
(11)

where \({\overline{x}_{i,2}^*}\) is a virtual control law. Design a virtual controller \(\overline{x}_{i,2}^*\) as

$$\begin{aligned} {\overline{x}_{i,2}^*}=-c_1 \xi _{i,1} \quad \mathrm{with}~c_1=n,~\xi _{i,1}=\overline{x}_{i,1}, \end{aligned}$$
(12)

which results in

$$\begin{aligned} \dot{V}_1 = -n\sum _{i=1}^n\xi _{i,1}^2+\sum _{i=1}^n\xi _{i,1} \left( \overline{x}_{i,2}-{\overline{x}_{i,2}^*}\right) . \end{aligned}$$
(13)

Inductive Step Assume that at step \(j-1\), under the virtual controller

$$\begin{aligned} {\overline{x}_{i,j}^*}=-c_{j-1}\xi _{i,j-1}, \end{aligned}$$
(14)

we have the following inequality

$$\begin{aligned} \dot{V}_{j-1}\le & {} -[n-(j-2)]\sum _{i=1}^n\left( \xi _{i,1}^{2}+\ldots +\xi _{i,j-1}^{2}\right) \nonumber \\&\quad +\sum _{i=1}^n\xi _{i,j-1}\left( \overline{x}_{i,j}-\overline{x}_{i,j}^*\right) , \end{aligned}$$
(15)

where

$$\begin{aligned} \xi _{i,1}&=\overline{x}_{i,1}, \nonumber \\ \xi _{i,l}&=\overline{x}_{i,l}-{\overline{x}_{i,l}^*}, \nonumber \\ \overline{x}_{i,l}^*&=-c_{l-1}\xi _{i,l-1},\quad l=2,\ldots ,\quad j-1, \end{aligned}$$
(16)

and

$$\begin{aligned} {V}_{j-1}=\frac{1}{2}\sum _{i=1}^n \left( \xi _{i,1}^2+\cdots +\xi _{i,j-1}^2\right) . \end{aligned}$$
(17)

Next, it is shown that (15) also holds at step j. To this end, define

$$\begin{aligned} V_j&=V_{j-1}+\frac{1}{2}\sum _{i=1}^n\left( \overline{x}_{i,j}-{\overline{x}_{i,j}^*}\right) ^2\nonumber \\&=V_{j-1}+\frac{1}{2}\sum _{i=1}^n\xi _{i,j}^2, \end{aligned}$$
(18)

where \(\xi _{i,j}=\overline{x}_{i,j}-\overline{x}_{i,j}^*\).

The derivative of \(V_j\) along system (9) is

$$\begin{aligned} \dot{V}_j\le & {} -[n-(j-2)]\sum _{i=1}^n\left( \xi _{i,1}^{2}+\cdots +\xi _{i,j-1}^{2}\right) \nonumber \\&\quad +\sum _{i=1}^n\left( \xi _{i,j-1}\xi _{i,j}+\xi _{i,j}\overline{x}_{i,j+1}-\xi _{i,j}\dot{\overline{x}}_{i,j}^*\right) \nonumber \\ \quad\le & {} -[n-(j-2)]\sum _{i=1}^n\left( \xi _{i,1}^{2}+\cdots +\xi _{i,j-1}^{2}\right) \nonumber \\&\quad +\frac{1}{2}\sum _{i=1}^n\left( \xi _{i,j-1}^2+\xi _{i,j}^2\right) +\sum _{i=1}^n\xi _{i,j}\overline{x}_{i,j+1}\nonumber \\&\quad +\sum _{i=1}^n|\xi _{i,j}\dot{\overline{x}}_{i,j}^*|. \end{aligned}$$
(19)

According to the definition of \(\overline{x}_{i,j}^*\), it can be obtained that

$$\begin{aligned} \dot{\overline{x}}_{i,j}^*&=-c_{j-1}\overline{x}_{i,j}-c_{j-1}c_{j-2}\overline{x}_{i,j-1}-\ldots \\&\quad -(c_{j-1}c_{j-2}\ldots c_1)\overline{x}_{i,2}\\&=-c_{j-1}(\xi _{i,j}-c_{j-1}\xi _{i,j-1})\\&\quad -c_{j-1}c_{j-2}(\xi _{i,j-1}-c_{j-2}\xi _{i,j-2})-\ldots \nonumber \\&\quad -(c_{j-1}c_{j-2}\ldots c_1)(\xi _{i,2}-c_{1}\xi _{i,1})\\&=-c_{j-1}\xi _{i,j}+c_{j-1}(c_{j-1}-c_{j-2})\xi _{i,j-1}\\&\quad +c_{j-1}c_{j-2}(c_{j-2}-c_{j-3})\xi _{i,j-2}+\cdots \\&\quad +(c_{j-1}c_{j-2}\cdots c_2)(c_2-c_1)\xi _{i,2}\\&\quad +(c_{j-1}c_{j-2}\cdots c_1)c_1\xi _{i,1}. \end{aligned}$$

Based on this relation, completing the square for each individual cross-term leads to

$$\begin{aligned} |\xi _{i,j}\dot{\overline{x}}_{i,j}^* |&\le c_{j-1} \xi _{i,j}^2+ \frac{1}{2}\xi _{i,j-1}^2+\frac{c_{j-1}^2(c_{j-1}-c_{j-2})^2 }{2}\xi _{i,j}^2\nonumber \\&\quad +\xi _{i,j-2}^2+\frac{c_{j-1}^2c_{j-2}^2(c_{j-2}-c_{j-3})^2 }{4}\xi _{i,j}^2\nonumber \\&\quad +\cdots +\xi _{i,2}^2+\frac{(c_{j-1}^2c_{j-2}^2\cdots c_2^2)(c_2-c_1)^2}{4}\xi _{i,j}^2\nonumber \\&\quad +\xi _{i,1}^2+\frac{(c_{j-1}^2c_{j-2}^2\ldots c_1^2)c_{1}^2}{4}\xi _{i,j}^2 \nonumber \\&=\xi _{i,1}^2+\cdots +\xi _{i,j-2}^2 +\frac{1}{2}\xi _{i,j-1}^2+c_{j-1}\xi _{i,j}^2\nonumber \\&\quad +\left( \frac{c_{j-1}^2(c_{j-1}-c_{j-2})^2}{2}\right. \nonumber \\&\quad \left. ~~~~+\,\sum _{l=1}^{j-2}\frac{(c_{j-1}^2\ldots c_l^2)(c_{l}-c_{l-1})^2 }{4}\right) \xi _{i,j}^2 \nonumber \\&=\xi _{i,1}^2+\cdots +\xi _{i,j-2}^2+\frac{1}{2}\xi _{i,j-1}^2+{\beta _{j-1}(\cdot )}\xi _{i,j}^2, \end{aligned}$$
(20)

where \(\beta _{j-1}\) is a function defined in (7). Based on (20), it follows from (19) that

$$\begin{aligned} \dot{V}_j\le & {} -[n-(j-1)]\sum _{i=1}^n\left( \xi _{i,1}^{2}+\cdots +\xi _{i,j-1}^{2}\right) \nonumber \\&+\sum _{i=1}^n\Big [\beta _{j-1}(\cdot )\xi _{i,j}^2+\xi _{i,j}\overline{x}_{i,j+1}\Big ]. \end{aligned}$$
(21)

Since \(c_j=[\beta _{j-1}(\cdot )+n-j+1]\) as chosen in (6), the virtual controller

$$\begin{aligned} \overline{x}_{i,j+1}^*=-c_j\xi _{i,j}, \end{aligned}$$
(22)

yields

$$\begin{aligned} \dot{V}_j\le & {} -[n-(j-1)]\sum _{i=1}^n \left( \xi _{i,1}^{2}+\cdots +\xi _{i,j}^{2}\right) \nonumber \\&+\sum _{i=1}^n\xi _{i,j}\left( \overline{x}_{i,j+1}-\overline{x}_{i,j+1}^*\right) . \end{aligned}$$
(23)

This completes the inductive proof. \(\square \)

Following the inductive procedure between (14)–(23), the following inequality is obtained for the step n

$$\begin{aligned} \dot{V}_n\le & {} -\sum _{i=1}^n\left( \xi _{i,1}^{2}+\cdots +\xi _{i,n-1}^{2}\right) \nonumber \\&+ \sum _{i=1}^n\Big [\beta _{n-1}(\cdot )\xi _{i,n}^2+\xi _{i,n}\bar{f}_i+\xi _{i,n}u_i\Big ], \end{aligned}$$
(24)

where

$$\begin{aligned}&\xi _{i,1}=\overline{x}_{i,1}, ~~\xi _{i,j}=\overline{x}_{i,j}-{\overline{x}_{i,j}^*}, \nonumber \\&\overline{x}_{i,j}^* =-c_{j-1}\xi _{j-1}, ~~j=2,\ldots ,n,\nonumber \\&{V}_{n}=\frac{1}{2}\sum _{i=1}^n\left( \xi _{i,1}^{2}+\cdots +\xi _{i,n}^{2}\right) , \end{aligned}$$
(25)

and

$$\begin{aligned} \bar{f}_i=f\left( t,x_{i,1},\ldots ,x_{i,n}\right) -f\left( t,x_1^d,\ldots ,x_n^d\right) . \end{aligned}$$
(26)

Under Assumption 1, it can be obtained that

$$\begin{aligned} \sum _{i=1}^n\xi _{i,n}\bar{f}_i\le & {} \sum _{i=1}^n |\xi _{i,n}|\cdot \rho \left( |\bar{x}_{i,1}|+|\bar{x}_{i,2}|+\cdots +|\bar{x}_{i,n}|\right) \nonumber \\ \quad\le & {} \sum _{i=1}^n |\xi _{i,n}|\cdot \rho \left( |\xi _{i,1}|+|\xi _{i,2}-c_1\xi _{i,1}|+\cdots \right. \nonumber \\&\left. \quad +\,|\xi _{i,n}-c_{n-1}\xi _{i,n-1}|\right) \nonumber \\ \quad\le & {} \sum _{i=1}^n |\xi _{i,n}|\cdot \rho \Big [(1+c_1)|\xi _{i,1}|+(1+c_2)|\xi _{i,2}|\nonumber \\&\quad +\cdots +(1+c_{n-1})|\xi _{i,n-1}|+|\xi _{i,n}|\Big ]\nonumber \\ \quad\le & {} \frac{1}{2}\sum _{i=1}^n\left( \xi _{i,1}^{2}+\cdots +\xi _{i,n-1}^{2}\right) \nonumber \\&\quad +\left( \frac{\rho ^2\left[ (1+c_1)^2+\cdots +(1+c_{n-1})^2\right] }{2}+\rho \right) \nonumber \\&\quad \times \sum _{i=1}^n\xi _{i,n}^{2}. \end{aligned}$$
(27)

As a result, this together with (24) leads to

$$\begin{aligned} \dot{V}_n\le & {} -\frac{1}{2}\sum _{i=1}^n\left( \xi _{i,1}^{2}+\cdots +\xi _{i,n-1}^{2}\right) \nonumber \\&+\,[\beta _{n-1}(\cdot )+{\gamma }_{1}]\sum _{i=1}^n\xi _{i,n}^2+\sum _{i=1}^n\xi _{i,n}u_i\nonumber \\ \quad= & {} -\frac{1}{2}\sum _{i=1}^n\left( \xi _{i,1}^{2}+\cdots +\xi _{i,n-1}^{2}\right) \nonumber \\&+\left[ \beta _{n-1}(\cdot )+{\gamma }_{1}\right] \xi _n^T\xi _n+\xi _n^Tu. \end{aligned}$$
(28)

In the literature, for nonlinear systems, there are usually two approaches to design a sampled-data controller. One approach is to design a discrete-time controller based on the discrete-time model of the nonlinear plant [27]. The other approach, which is called the emulation method, is to design a continuous-time controller at the first step and then discretize it [28]. Considering there are unknown nonlinear terms in the system (1), it is almost impossible to get an accurate discrete-time model of the nonlinear plant. So we employ the second approach to design a sampled-data controller.

With the relation (28) in mind, a continuous-time state feedback controller is designed as follows:

$$\begin{aligned} u_i^{*}=&-c_n\left[ \sum _{j\in N_i}a_{ij} \left( \xi _{i,n}-\xi _{j,n}\right) +b_i\xi _{i,n}\right] ,~~i\in \varGamma . \end{aligned}$$
(29)

Define

$$\begin{aligned} \xi _{n}=\left[ \xi _{1,n},\ldots ,\xi _{n,n}\right] ^T. \end{aligned}$$

By the definition of \(L+B\), \(u^*\) can be rewritten as

$$\begin{aligned} u^*=&\left[ u_{1}^*,\ldots ,u_{n}^*\right] ^T=-c_n(L+B)\xi _n. \end{aligned}$$
(30)

With (30) in mind, it follows from (28) that

$$\begin{aligned} \dot{V}_n\le & {} -\frac{1}{2}\sum _{i=1}^n\left( \xi _{i,1}^{2}+\cdots +\xi _{i,n-1}^{2}\right) \nonumber \\&+\left[ \beta _{n-1}(\cdot )+{\gamma }_{1}\right] \xi _n^T\xi _n\nonumber \\&-c_n\xi _n^T(L+B)\xi _n+\xi _n^T\left( u-u^*\right) . \end{aligned}$$
(31)

By discretizing the continuous-time controller (30), the sampled-data controller can be obtained as follows:

$$\begin{aligned} u(t)=u(t_k)= & {} -c_n(L+B)\xi _n(t_k), ~\forall t\in [t_k,t_{k+1}),\nonumber \\&i\in \varGamma , \end{aligned}$$
(32)

which is equivalent to (4). Substituting the sampled-data control law (32) into (31) leads to

$$\begin{aligned} \dot{V}_n\le & {} -\frac{1}{2}\sum _{i=1}^n\left( \xi _{i,1}^{2}+\cdots +\xi _{i,n-1}^{2}\right) \nonumber \\&+\,\left[ \beta _{n-1}(\cdot )+{\gamma }_{1}\right] \xi _n^T\xi _n-c_n\xi _n^T(L+B)\xi _n\nonumber \\&-\,c_n\xi _n^T(L+B)\left( \xi _n(t_k)-\xi _n(t)\right) . \end{aligned}$$
(33)

Chose the gain \(c_n\) such that \(c_n\ge \frac{\beta _{n-1}(\cdot )+{\gamma }_{1}+\frac{1}{2}}{\lambda _{\mathrm{min}}(L+B)}\), then

$$\begin{aligned} \dot{V}_n\le & {} -\frac{1}{2}\sum _{i=1}^n\left( \xi _{i,1}^{2}+\cdots +\xi _{i,n}^{2}\right) \nonumber \\&-\,\,c_n\xi _n^T(L+B)\left( \xi _n(t_k)-\xi _n(t)\right) , \quad \forall t\!\in \![t_k,t_{k+1}),\nonumber \\ \end{aligned}$$
(34)

which means that the global states’ synchronization can be achieved if the sampling period \(T=0\). The key issue for emulation method is to find the maximum allowable sampling period. Next, we will show that there exists a maximum allowable sampling period (MASP) \(T^*>0\) (\(\sup _{k\in N} \) \(\{t_{k+1}-t_k\}\le T^*\)) such that the states’ synchronization is globally reached.

Step 2: Selection of a sampling period

To handle the term of \(\xi _n(t)-\xi _n(t_k)\) in (34), without loss of generality, we estimate the i-th element of \(\xi _n(t)-\xi _n(t_k)\) as follows:

$$\begin{aligned} \left| \xi _{i,n}(t)-\xi _{i,n}(t_k)\right| \le \int _{t_k}^t\left| \dot{\xi }_{i,n}(\tau )\right| \mathrm{d}\tau , \quad t\in [t_k,t_{k+1}).\nonumber \\ \end{aligned}$$
(35)

Since

$$\begin{aligned} \xi _{i,n}(\tau )=\overline{x}_{i,n}+c_{n-1}\overline{x}_{i,n-1}+\cdots +(c_{n-1}\cdots c_1)\overline{x}_{i,1}, \end{aligned}$$
(36)

then it follows from (9) that

$$\begin{aligned} |\dot{\xi }_{i,n}(\tau )|= & {} |c_{n-1}\overline{x}_{i,n}+\cdots +(c_{n-1}\cdots c_1)\overline{x}_{i,2}+u_i+\bar{f}_i|\nonumber \\&\quad \le (\rho \!+\!c_{n-1})|\overline{x}_{i,n}|\!+\!(\rho \!+\!c_{n-1}c_{n-2})|\overline{x}_{i,n-1}|\!+\!\cdots \nonumber \\&\qquad +[\rho +(c_{n-1}\cdots c_1)]|\overline{x}_{i,2}|+\rho |\overline{x}_{i,1}|+|u_i|\nonumber \\ \quad= & {} (\rho +c_{n-1})|\xi _{i,n}-c_{n-1}\xi _{i,n-1}|\nonumber \\&\qquad +(\rho +c_{n-1}c_{n-2})|\xi _{i,n-1}-c_{n-2}\xi _{i,n-2}|+\cdots \nonumber \\&\qquad +[\rho +(c_{n-1}\cdots c_1)]|\xi _{i,2}-c_{1}\xi _{i,1}|+\rho |\overline{x}_{i,1}|\nonumber \\&\qquad +|u_i|\nonumber \\&\quad \le (\rho +c_{n-1})|\xi _{i,n}|\nonumber \\&\qquad +[(\rho +c_{n-1}+c_{n-2})c_{n-1}+\rho ]|\xi _{i,n-1}|\nonumber \\&\qquad +[(\rho +c_{n-1}c_{n-2}+c_{n-1}c_{n-3})c_{n-2}+\rho ]|\xi _{i,n-2}|\nonumber \\&\qquad +\cdots \nonumber \\&\qquad +[(\rho +(c_{n-1}\cdots c_2))c_2+\rho +c_n\cdots c_1]|\xi _{i,2}|\nonumber \\&\qquad +[(\rho +(c_{n-1}\cdots c_1))c_1+\rho ]|\xi _{i,1}|\nonumber \\&\qquad +|u_i| \nonumber \\&\quad \le {\gamma }_{2}(|\xi _{i,1}|+\cdots +|\xi _{i,n}|)+|u_i| \end{aligned}$$
(37)

where \({\gamma }_{2}=[\rho +(c_{n-1}\cdots c_1)](c_1+\cdots +c_{n-1})+\rho +(c_{n-1}\ldots c_1)\). By the control law (32), we get

$$\begin{aligned} |u_i|\le \Vert u\Vert =c_n\Vert L+B\Vert \cdot \Vert \xi (t_k)\Vert \end{aligned}$$
(38)

which results in

$$\begin{aligned} |\dot{\xi }_i(\tau )|\le & {} {\gamma }_{2}\sqrt{2n} \sqrt{V(\tau )}+ \sqrt{2}c_n\Vert L+B\Vert \sqrt{V(t_k)}\nonumber \\&\quad \le {\gamma }_{3}\sqrt{V_{\mathrm{max}}(t)} \end{aligned}$$
(39)

where \(V_{\mathrm{max}}(t)=\max _{\forall \tau \in [t_k,t]} V(\tau ),{\gamma }_{3}={\gamma }_{2}\sqrt{2n} + \sqrt{2}c_n\Vert L+B\Vert \). With this in mind, it follows from (35) that

$$\begin{aligned} |\xi _i(t)-\xi _i(t_k)|\le (t-t_k){\gamma }_{3}\sqrt{V_{\mathrm{max}}(t)}. \end{aligned}$$
(40)

Substituting (40) into (34) leads to that for any \(t\in [t_k,t_{k+1})\), the following inequality holds:

$$\begin{aligned} \dot{V}(t)\le & {} -V(t)+(t-t_k) \sqrt{2n}c_n\nonumber \\&\times \, \Vert L+B\Vert {\gamma }_{3} \sqrt{V(t)}\sqrt{V_{\mathrm{max}}(t)}. \end{aligned}$$
(41)

The sampling time T is chosen to satisfy the following condition:

$$\begin{aligned} \sqrt{2n}c_n\Vert L+B\Vert {\gamma }_{3} T=\sqrt{2n}c_n\lambda _{\mathrm{max}}(L+B) {\gamma }_{3} T<1. \end{aligned}$$
(42)

In the sequel, based on the relation (41) and the sampling period condition (42), it is shown that

$$\begin{aligned} \max _{\forall \tau \in [t_k,t_{k+1}]} V(\tau )=V(t_k). \end{aligned}$$

Otherwise, assume that there exists a time instant \(t'\in [t_k,t_{k+1}]\) such that \(V(t')>V(t_k)\). Firstly, it follows from (41) that for \(V(t_k) \not =0\), \(\dot{V}(t_k)<0\). That is to say that V(t) will decrease in a short time starting from \(t_k\). As a result, there is a time instant \(t{''} \in [t_k,t']\) such that

$$\begin{aligned} (i) ~&V(t{''})= V(t_k),~~ (ii)~ \dot{V}(t{''})>0,\nonumber \\&\text{ and }~~ (iii) V(t)\le V(t_k), ~\forall t\in [t_k, t{''}]. \end{aligned}$$
(43)

With this relations in mind, it follows from (41) that

$$\begin{aligned} \dot{V}(t{''})\le & {} -V(t{''}) \nonumber \\&+(t{''}\!-\!t_k)\sqrt{2n}c_n\Vert L\!+\!B\Vert {\gamma }_{3} \sqrt{V(t{''})}\sqrt{V_{\mathrm{max}}(t)}\nonumber \\ \quad\le & {} -V(t{''})\nonumber \\&+(t{''}-t_k)\sqrt{2n}c_n\Vert L+B\Vert {\gamma }_{3} \sqrt{V(t{''})}\sqrt{V(t{''})}\nonumber \\\le & {} -[1-T\sqrt{2n}c_n\Vert L+B\Vert {\gamma }_{3}]V(t{''})<0 \end{aligned}$$
(44)

which contradicts to the assumption \(\dot{V}(t{''})>0\). Thus,

$$\begin{aligned} \max _{\forall \tau \in [t_k,t_{k+1}]} V(\tau )=V(t_k). \end{aligned}$$
(45)

Based on this fact, by (41), we further get

$$\begin{aligned} \dot{V}(t)\le & {} -V(t)+(t-t_k) \sqrt{2n}c_n\nonumber \\&\times \,\Vert L+B\Vert {\gamma }_{3} \sqrt{V(t)}\sqrt{V(t_k)}. \end{aligned}$$
(46)

For the sake of brevity, denote \(\mu (t)=\sqrt{\frac{{V}(t)}{V(t_k)}}\), which results in

$$\begin{aligned} \dot{\mu }(t) \le -\mu (t)+T\sqrt{2n}c_n\Vert L+B\Vert {\gamma }_{3} . \end{aligned}$$
(47)

By the fact \(\mu (t_k)=1\), it follows (47) that

$$\begin{aligned} \mu (t_{k+1})\le & {} e^{-T}+\left( 1-e^{-T}\right) T\sqrt{2n}c_n\nonumber \\&\times \, \Vert L+B\Vert {\gamma }_{3}:=\Delta . \end{aligned}$$
(48)

That is to say that

$$\begin{aligned} V(t_{k+1})\le \Delta ^2{V}(t_k). \end{aligned}$$
(49)

On the other hand, using the condition (42) leads to that the constant \(\Delta <1\). Therefore, \(V(t_k)\) will converge zero as k tends to infinity. Hence, it can be concluded that the closed-loop system (9) with (4) is globally asymptotically stable, i.e., \(x_i\rightarrow x_d\), \(v_i\rightarrow v_d\) as \(t\rightarrow \infty \). That is to say the consensus for systems (1)-(2) is achieved. The proof is completed. \(\square \)

Fig. 1
figure 1

The information exchange among agents

Full size image
Fig. 2
figure 2

Response curves of agents positions

Full size image
Fig. 3
figure 3

Response curves of agents velocities

Full size image
Fig. 4
figure 4

Response curves of agents control signals

Full size image

Remark 1

Note that for each follower agent, the proposed sampled-data controller (4) only use neighbors’ and itself’s sampling-data information. And only part of followers can have access to the leader’s state. That is to say that the proposed control in this paper is a distributed control law. The distributed control has many advantages such as greater efficiency, higher robustness, and fewer communication requirements, etc.

Remark 2

Our design procedure of distributed sampled-data controller for the nonlinear multi-agent systems (1)–(2) can be divided into three steps:

Step 1:

Design a distributed sampled-data controller in the form of (4).

Step 2:

Select the gains \(k_i\)’s according to the gains condition (5).

Step 3:

Compute the maximum allowable sampling period T according to (5).

4 Numerical examples and simulations

As that in [19], consider multiple coupled forced pendulums with four follower agents and one leader agent. Each agent’s dynamic is governed by:

$$\begin{aligned}&{\dot{x}}_i=v_i,\nonumber \\&{\dot{v}}_i=-\sin (x_i)-0.25v_i+1.5\cos (2.5t)+ u_i,\nonumber \\&\quad i\in \varGamma =\{1,2,\ldots ,n\}, \end{aligned}$$
(50)

from which it can be found that the nonlinear term \(f(t,x_i,v_i)=-\sin (x_i)-0.25v_i+1.5\cos (2.5t)\) satisfies Assumption 1 with a Lipschitz constant \(\rho =1\).

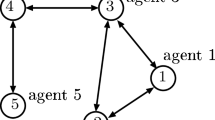
The information exchange among agents is shown in Fig. 1 with \(a_{12}=a_{21}=a_{13}=a_{31}=a_{34}=a_{43}=b_1=1\). The initial conditions of the four followers are selected as follows: \(x(0)=[0,1,3,1.5]^T,\) \(v(0)=[-1,0,1,2]^T.\) And the initial condition for leader is \(x_d(0)=-1,v_d(0)=2.\)

According to Theorem 1, we can design a consensus control algorithm (4) only using sampled-data information to achieve global states consensus with appropriate gain and sampling period. The control gain is chosen as \(k_1=k_2=10\), and the sampling period is chosen as \(T=0.05\, \mathrm{s}\). The response curves are shown in Figs. 2, 3 and 4. Clearly, all the agents’ states can reach consensus.

5 Conclusion

In this paper, we have discussed the states consensus problem for a class of high-order nonlinear multi-agent systems with unknown nonlinearities. By utilizing graph theory and feedback domination method, a distributed sampled-data controller has been proposed. An explicit formula for the MASP is computed to guarantee global stability of closed-loop systems under the proposed sampled-data controller with appropriate gains.