Stochastic Almost Output Synchronization for Time-Varying Networks of Nonidentical and Non-introspective Agents Under External Stochastic Disturbances and Disturbances with Known Frequencies

Abstract

We consider stochastic almost output synchronization for time-varying directed networks of nonidentical and non-introspective (i.e., agents have no access to their own states or outputs) agents under external stochastic disturbances. The network experiences switches at unknown moments in time without chattering. A purely decentralized (i.e., the additional communication channel among agents is dispensed) time-invariant protocol based on a low- and high-gain method is designed for each agent to achieve stochastic almost output synchronization, while reducing the impact of stochastic disturbances. Moreover, we extend the problem to the case where stochastic disturbances can have nonzero mean or other disturbances are present with known frequencies. Another purely decentralized protocol is designed to completely reject the impact of disturbances with known frequencies on the synchronization error.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

6.1 Introduction

Almost disturbance decoupling has a long history. It was the main topic of the Ph.D. thesis of Harry Trentelman. Anton Stoorvogel was, as a Ph.D. student of Harry, also looking at almost disturbance decoupling in connection to $H_2$ and $H_\infty$ control. Ali Saberi was in this period working on the same class of problems. This paper looks at a version of almost disturbance decoupling in the context of multiagent systems.

In the last decade, the topic of synchronization in a multiagent system has received considerable attention. Its potential applications can be seen in cooperative control on autonomous vehicles, distributed sensor network, swarming and flocking, and others. The objective of synchronization is to secure an asymptotic agreement on a common state or output trajectory through decentralized control protocols (see [1, 12, 18, 28]). Research has mainly focused on the state synchronization based on full-state/partial-state coupling in a homogeneous network (i.e., agents have identical dynamics), where the agent dynamics progress from single- and double-integrator dynamics to more general dynamics (e.g., [7, 14, 15, 21, 24–26, 29]). The counterpart of state synchronization is output synchronization, which is mostly done on heterogeneous networks (i.e., agents are nonidentical). When the agents have access to part of their own states it is frequently referred to as introspective and, otherwise, non-introspective. Quite a few of the recent works on output synchronization have assumed agents are introspective (e.g., [3, 6, 27, 30]) while few have considered non-introspective agents. For non-introspective agents, the paper [5] addressed the output synchronization for heterogeneous networks.

In [7] for homogeneous networks a controller structure was introduced which included not only sharing the relative outputs over the network but also sharing the relative states of the protocol over the network. This was also used in our earlier work such as [5, 16, 17]. This type of additional communication is not always natural. Some papers such as [21] (homogeneous network) and [6] (heterogeneous network but introspective) already avoided this additional communication of controller states.

Almost synchronization is a notion that was brought up by Peymani and his coworkers in [17] (introspective) and [16] (homogeneous, non-introspective), where it deals with agents that are affected by external disturbances. The goal of their work is to reduce the impact of disturbances on the synchronization error to an arbitrary degree of accuracy (expressed in the $\mathscr {H}_{\infty }$ norm). But they assume availability of an additional communication channel to exchange information about internal controller or observer states between neighboring agents. The earlier work on almost synchronization for introspective, heterogeneous networks was extended in [31] to design a dynamic protocol to avoid exchange of controller states.

The majority of the works assumes that the topology associated with the network is fixed. Extensions to time-varying topologies are done in the framework of switching topologies. Synchronization with time-varying topologies is studied utilizing concepts of dwell time and average dwell time (e.g., [11, 22, 23]). It is assumed that time-varying topologies switch among a finite set of topologies. In [32], switching laws are designed to achieve synchronization.

This paper also aims to solve the almost regulated output synchronization problem for heterogeneous networks of non-introspective agents under switching graphs. However, instead of deterministic disturbances with finite power, we consider stochastic disturbances with bounded variance. We name this problem as stochastic almost regulated output synchronization. Moreover, we extend this problem by allowing nonzero mean stochastic disturbances and other disturbances with known frequencies.

6.1.1 Notations and Definitions

Given a matrix A, $A'$ denotes its conjugate transpose and $\Vert A\Vert$ is the induced 2-norm. For square matrices, $\lambda _i(A)$ denotes its i’th eigenvalue, and it is said to be Hurwitz stable if all eigenvalues are in the open left half complex plane. We denote by ${\text {blkdiag}}\{A_i\}$, a block diagonal matrix with $A_1,\ldots ,A_N$ as the diagonal elements, and by ${\text {col}}\{x_i\}$ or $[x_{1};\ldots ;x_{N}]$, a column vector with $x_1,\ldots ,x_N$ stacked together, where the range of index i can be identified from the context. $A\otimes B$ depicts the Kronecker product between A and B. $I_n$ denotes the n-dimensional identity matrix and $0_n$ denotes the $n\times n$ zero matrix; sometimes we drop the subscript if the dimension is clear from the context. Finally, the $\mathscr {H}_{\infty }$ norm of a transfer function T is indicated by $\Vert T \Vert _{\infty }$.

A weighted directed graph $\mathscr {G}$ is defined by a triple $(\mathscr {V}, \mathscr {E}, \mathscr {A})$ where $\mathscr {V}=\{1,\ldots , N\}$ is a node set, $\mathscr {E}$ is a set of pairs of nodes indicating connections among nodes, and $\mathscr {A}=[a_{ij}]\in \mathbb {R}^{N\times N}$ is the weighting matrix, and $a_{ij}>0$ iff $(i,j)\in \mathscr {E}$. Each pair in $\mathscr {E}$ is called an edge. A path from node $i_1$ to $i_k$ is a sequence of nodes $\{i_1,\ldots , i_k\}$ such that $(i_j, i_{j+1})\in \mathscr {E}$ for $j=1,\ldots , k-1$. A directed tree with root r is a subset of nodes of the graph $\mathscr {G}$ such that a path exists between r and every other node in this subset. A directed spanning tree is a directed tree containing all the nodes of the graph. For a weighted graph $\mathscr {G}$, a matrix $L=[\ell _{ij}]$ with

$$ \ell _{ij}= \left\{ \; \begin{array}{cl} \sum _{k=1}^{N} a_{ik}, &{} i=j,\\ -a_{ij}, &{} i\ne j, \end{array} \right. $$

is called the Laplacian matrix associated with the graph $\mathscr {G}$. Since our graph $\mathscr {G}$ has nonnegative weights, we know that L has all its eigenvalues in the closed right half plane and at least one eigenvalue at zero associated with right eigenvector $\mathbf 1$.

Definition 6.1

Let $\mathscr {L}_N\subset \mathbb {R}^{N\times N}$ be the family of all possible Laplacian matrices associated to a graph with N nodes. We denote by $\mathscr {G}_L$ the graph associated with a Laplacian matrix $L\in \mathscr {L}_N$. A time-varying graph $\mathscr {G}(t)$ with N nodes is such that

$$ \mathscr {G}(t)=\mathscr {G}_{\sigma (t)} $$

where $\sigma : \mathbb {R}\rightarrow \mathscr {L}_N$ is a piecewise constant, right-continuous function with minimal dwell time $\tau$ (see [8]), i.e., $\sigma (t)$ remains fixed for $t \in [t_k, t_{k+1})$, $k \in \mathbb {Z}$ and switches at $t=t_k$, $k=1,2,\ldots$ where $t_{k+1}-t_{k} \ge \tau$ for $k=0,1,\ldots$. For ease of presentation we assume $t_0=0$.

Definition 6.2

A matrix pair (A, C) is said to contain the matrix pair (S, R) if there exists a matrix $\varPi$ such that $\varPi S=A\varPi$ and $C\varPi =R$.

Remark 6.3

Definition 6.2 implies that for any initial condition $\omega (0)$ of the system

$$ \dot{\omega }=S\omega ,\qquad y_{r}=R\omega , $$

there exists an initial condition x(0) of the system

$$ \dot{x}=Ax,\qquad y=Cx, $$

such that $y(t)=y_{r}(t)$, for all $t\ge 0$ (see [10]).

6.2 Stochastic Disturbances

In this section, we consider the problem of almost output synchronization for time-varying networks (i.e., multiagent systems) with nonidentical and non-introspective agents under stochastic disturbances. The time-varying network is constrained in the sense that we exclude chattering by imposing an, arbitrary small, minimal dwell time. Our agents need not be the same and are non-introspective (i.e., they have no access to any of their own states). We will achieve stochastic almost output synchronization in such a way that outputs of agents are asymptotically regulated to a reference trajectory generated by an autonomous system.

6.2.1 Multiagent System Description

Suppose a multiagent system/network consists of N nonidentical, non-introspective agents $\tilde{\varSigma }_i$ with $i\in \{1,\ldots ,N\}$ described by the stochastic differential equation:

$$\begin{aligned} \tilde{\varSigma }_i: \left\{ \; \begin{array}{ccl} \text {d}\tilde{x}_i &{}=&{} \tilde{A}_i\tilde{x}_i\text {d}t +\tilde{B}_i \tilde{u}_i\text {d}t+\tilde{G}_i \text {d}w_i,\qquad \tilde{x}_{i}(0)=\tilde{x}_{i0}, \\ y_i &{}=&{} \tilde{C}_i\tilde{x}_i, \end{array} \right. \end{aligned}$$

(6.1)

where $\tilde{x}_i \in \mathbb {R}^{\tilde{n}_i}$, $\tilde{u}_i \in \mathbb {R}^{m_i}$, and $y_i \in \mathbb {R}^{p}$ are the state, input, and output of agent i, and $w={\text {col}}\{w_i\}$ is a Wiener process (a Brownian motion) with mean 0 and rate $Q_{0}$, that is, ${\text {Cov}}[w(t)]=t Q_{0}$ and the initial condition $\tilde{x}_{i0}$ of (6.1) is a Gaussian random vector which is independent of $w_i$. Here $Q_0$ is block diagonal such that $w_i$ and $w_j$ are independent for any $i\ne j$. Its solution $\tilde{x}_i$ is rigorously defined through Wiener integrals and is a Gauss–Markov process. See, for instance, [13]. We denote by $\tilde{\rho }_i$ the maximal order of the infinite zeros of (6.1) with input $\tilde{u}_i$ and output $y_i$.

Remark 6.4

If we have an agent described by:

$$\begin{aligned} \breve{\varSigma }_i: \left\{ \; \begin{array}{ccl} \dot{\breve{x}}_i &{}=&{} \breve{A}_i\breve{x}_i +\breve{B}_i \tilde{u}_i+\breve{G}_i \breve{w}_i,\\ y_i &{}=&{} \breve{C}_i\breve{x}_i, \end{array} \right. \end{aligned}$$

(6.2)

with $\breve{w}_i$ stochastic colored noise, then we assume that $\breve{w}_i$ can be (approximately) modeled by a linear model:

$$\begin{aligned} \breve{\varSigma }_{wi}: \left\{ \; \begin{array}{ccl} \text {d}\breve{p}_i &{}=&{} \breve{A}_{wi}\breve{p}_i\text {d}t +\breve{G}_{wi} \text {d}w_i,\\ \breve{w}_i &{}=&{} \breve{C}_{wi}\breve{p}_i. \end{array} \right. \end{aligned}$$

(6.3)

Combining (6.2) and (6.3) we get a model of the form (6.1).

The time-varying network provides each agent with a linear combination of its own output relative to those of other neighboring agents, that is, agent $i\in \mathscr {V}$, has access to the quantity

$$\begin{aligned} \zeta _i(t) = \sum _{j=1}^{N}a_{ij}(t)(y_i(t)-y_j(t)), \end{aligned}$$

(6.4)

which is equivalent to

$$\begin{aligned} \zeta _i(t) = \sum _{j=1}^{N}\ell _{ij}(t)y_j(t). \end{aligned}$$

(6.5)

We make the following assumption on the agent dynamics.

Assumption 6.5

For each agent $i\in \mathscr {V}$, we have:

• $(\tilde{A}_i,\tilde{B}_i,\tilde{C}_i)$ is right-invertible and minimum-phase;

• $(\tilde{A}_i,\tilde{B}_i)$ is stabilizable, and $(\tilde{A}_i,\tilde{C}_i)$ is detectable;

Remark 6.6

Right invertibility of a triple $(\tilde{A}_i, \tilde{B}_i, \tilde{C}_i)$ means that, given a reference output $y_{r}(t)$, there exist an initial condition $\tilde{x}_{i}(0)$ and an input $\tilde{u}_{i}(t)$ such that $y_{i}(t)=y_{r}(t)$, for all $t\ge 0$.

6.2.2 Problem Formulation

As described at the beginning of this section, the outputs of agents will be asymptotically regulated to a given reference trajectory in the presence of external stochastic disturbances. The reference trajectory is generated by an autonomous system

$$\begin{aligned} \varSigma _{0}:\left\{ \; \begin{array}{ccl} \dot{x}_r &{}=&{} S_{r}x_r,\qquad x_r(0)=x_{r0}, \\ y_r &{}=&{} R_{r}x_r, \end{array} \right. \end{aligned}$$

(6.6)

where $x_r \in \mathbb {R}^{n_r}$, $y_r\in \mathbb {R}^{p}$. Moreover, we assume that $(S_{r},R_{r})$ is observable and all eigenvalues of $S_{r}$ are in the closed right half complex plane.

Define $e_{i}:=y_i-y_r$ as the regulated output synchronization error for agent $i\in \mathscr {V}$ and $\mathbf {e}={\text {col}}\{e_{i}\}$ for the complete network. In order to achieve our goal, it is clear that a nonempty subset $\pi$ of agents must have knowledge of their output relative to the reference trajectory $y_r$ generated by the reference system. Specially, each agent has access to the quantity

$$\begin{aligned} \psi _i=\iota _i(y_i-y_r),\qquad \iota _i= {\left\{ \begin{array}{ll} 1, &{}\qquad i\in \pi ,\\ 0, &{}\qquad i\notin \pi , \end{array}\right. } \end{aligned}$$

(6.7)

where $\pi$ is a subset of $\mathscr {V}$.

Assumption 6.7

Every node of the network graph $\mathscr {G}$ is a member of a directed tree with the root contained in $\pi$.

In the following, we will refer to the node set $\pi$ as root set in view of Assumption 6.7 (A special case is when $\pi$ consists of a single element corresponding to the root of a directed spanning tree of $\mathscr {G}$).

Based on the Laplacian matrix L(t) of our time-varying network graph $\mathscr {G}(t)$, we define the expanded Laplacian matrix as

$$ \bar{L}(t)=L(t)+{\text {blkdiag}}\{\iota _i\} = [\bar{\ell }_{ij}(t)]. $$

Note that $\bar{L}(t)$ is clearly not a Laplacian matrix associated to some graph since it does not have a zero row sum. From [5, Lemma 7], all eigenvalues of $\bar{L}(t)$ are in the open right half complex plane for all $t\in \mathbb {R}$.

It should be noted that, in practice, perfect information of the communication topology is usually not available for controller design and only some rough characterization of the network can be obtained. Next, we will define a set of time-varying graphs based on some rough information of the graph. Before doing so, we first define a set of fixed graphs, based on which the set of time-varying graphs will be defined.

Definition 6.8

For given root set $\pi$, $\alpha ,\beta , \varphi >0$ and positive integer N, $\mathbb {G}_{\alpha ,\beta ,\pi }^{\varphi ,N}$ is the set of directed graphs $\mathscr {G}$ composed of N agents satisfying the following properties:

• The eigenvalues of the associated expanded Laplacian $\bar{L}$, denoted by $\lambda _1,\ldots ,\lambda _N$, satisfy ${\text {Re}}\{\lambda _i\}>\beta$ and $|\lambda _i|<\alpha$.

• The condition number¹ of the expanded Laplacian $\bar{L}$ is less than $\varphi$.

Remark 6.9

In order to achieve regulated output synchronization for all agents, the first condition is obviously necessary.

Note that for undirected graphs the condition number of the Laplacian matrix is always bounded. Moreover, if we have a finite set of possible directed graphs each of which has a spanning tree then there always exists a set of the graph $\mathbb {G}_{\alpha ,\beta ,\pi }^{\varphi ,N}$ for suitable $\alpha ,\beta , \varphi >0$ and N containing these graphs. The only limitation is that we cannot find one protocol for a sequence of graphs converging to a graph without a spanning tree or whose Laplacian matrix either diverges or approaches some ill-conditioned matrix.

Definition 6.10

Given a root set $\pi$, $\alpha ,\beta ,\varphi , \tau >0$ and positive integer N, we define the set of time-varying network graphs $\tilde{\mathbb {G}}_{\alpha ,\beta ,\pi }^{\varphi ,\tau ,N}$ as the set of all time-varying graphs $\mathscr {G}$ with minimal dwell time $\tau$ for which

$$ \mathscr {G}(t)=\mathscr {G}_{\sigma (t)} \in \mathbb {G}_{\alpha ,\beta ,\pi }^{\varphi ,N} $$

for all $t\in \mathbb {R}$.

Remark 6.11

Note that a minimal dwell time is assumed to avoid chattering problems. However, it can be arbitrarily small.

We will define the stochastic almost regulated output synchronization problem under switching graphs as follows.

Problem 6.12

Consider a multiagent system (6.1) and (6.4) under Assumption 6.5, and reference system (6.6) and (6.7) under Assumption 6.7. For any given root set $\pi$, $\alpha ,\beta ,$ $\varphi ,\tau >0$ and positive integer N defining a set of time-varying network graphs $\tilde{\mathbb {G}}_{\alpha ,\beta ,\pi }^{\varphi ,\tau ,N}$, the stochastic almost regulated output synchronization problem is to find, if possible, for any $\gamma >0$, a linear time-invariant dynamic protocol such that, for any $\mathscr {G}\in \tilde{\mathbb {G}}_{\alpha ,\beta ,\pi }^{\varphi ,\tau ,N}$, for all initial conditions of agents and reference system, the stochastic almost regulated output synchronization error satisfies

$$\begin{aligned}&\lim _{t\rightarrow \infty } {\mathbb {E}}\mathbf {e}(t) =0,\nonumber \\&\limsup _{t\rightarrow \infty } {\text {Var}}[\mathbf {e}(t)] = \limsup _{t\rightarrow \infty }\, {\mathbb {E}}\mathbf {e}'(t)\mathbf {e}(t)<\gamma \,{\text {trace}}\, Q_0. \end{aligned}$$

(6.8)

Remark 6.13

Clearly, we can also define (6.8) in terms of the RMS, (see, e.g., [2]) as:

$$ \limsup _{T\rightarrow \infty }\, \frac{1}{T} {\mathbb {E}}\int _0^T \mathbf {e}(t)'\mathbf {e}(t) \, \text {d}t < \gamma \,{\text {trace}}\,Q_0. $$

Remark 6.14

Note that because of the time-varying graph the complete system is time variant and hence the variance of the error signal might not converge as time tends to infinity. Hence we use in the above a $\limsup$ instead of a regular limit.

6.2.3 Distributed Protocol Design

The main result in this section is given in the following theorem.

Theorem 6.15

Consider a multiagent system (6.1) and (6.4), and reference system (6.6) and (6.7). Let a root set $\pi$, $\alpha ,\beta ,\varphi ,\tau >0$ and positive integer N be given, and hence a set of time-varying network graphs $\tilde{\mathbb {G}}_{\alpha ,\beta ,\pi }^{\varphi ,\tau ,N}$ be defined.

Under Assumptions 6.5 and 6.7, the stochastic almost regulated output synchronization problem is solvable, i.e., for any given $\gamma >0$, there exists a family of distributed dynamic protocols, parametrized in terms of low- and high-gain parameters $\delta ,\,\varepsilon$, of the form

$$\begin{aligned} \left\{ \; \begin{array}{cl} \dot{\chi }_i &{}= \mathscr {A}_i(\delta ,\varepsilon )\chi _i+ \mathscr {B}_i(\delta ,\varepsilon )\begin{pmatrix}\zeta _i \\ \psi _i\end{pmatrix}\\ \tilde{u}_i &{}= \mathscr {C}_i(\delta ,\varepsilon )\chi _i+ \mathscr {D}_i(\delta ,\varepsilon )\begin{pmatrix}\zeta _i \\ \psi _i\end{pmatrix} \end{array} \right. ,\qquad i\in \mathscr {V} \end{aligned}$$

(6.9)

where $\chi _i \in \mathbb {R}^{q_i}$, such that for any time-varying graph $\mathscr {G}\in \tilde{\mathbb {G}}_{\alpha ,\beta ,\pi }^{\varphi ,\tau ,N}$, for all initial conditions of agents, the stochastic almost regulated output synchronization error satisfies (6.8).

Specifically, there exits a $\delta ^{*}\in (0,1]$ such that for each $\delta \in (0,\delta ^{*}]$, there exists an $\varepsilon ^{*} \in (0,1]$ such that for any $\varepsilon \in (0,\varepsilon ^{*}]$, the protocol (6.9) achieves stochastic almost regulated output synchronization.

Remark 6.16

In the above, we would like to stress that the initial condition of the reference system is deterministic while the initial conditions of the agents are stochastic. Our protocol yields (6.8) independent of the initial condition of the reference system and independent of the stochastic properties for the agents, i.e., we do not need to impose bounds on the second-order moments.

In the next section, we will present a more general problem after which we will present a joint proof of these two cases in Sect. 6.4.

6.3 Stochastic Disturbances and Disturbances with Known Frequencies

In this section, the agent model (6.1) is modified as follows:

$$\begin{aligned} \tilde{\varSigma }_i: \left\{ \; \begin{array}{ccl} \text {d}\tilde{x}_i &{}=&{} \tilde{A}_i\tilde{x}_i\text {d}t +\tilde{B}_i \tilde{u}_i\text {d}t + \tilde{G}_{i}\text {d}w_{i} + \tilde{H}_i^1d_i\text {d}t,\\ y_i &{}=&{} \tilde{C}_i\tilde{x}_i+\tilde{H}_i^2d_i, \end{array} \right. \end{aligned}$$

(6.10)

where $\tilde{x}_i$, $\tilde{u}_i$, $y_i$, and $w_{i}$ are the same as those in (6.1), while $d_i\in \mathbb {R}^{m_{d_i}}$ is an external disturbance with known frequencies, which can be generated by the following exosystem:

$$\begin{aligned} \begin{array}{cl} x_{id}&{}=S_{id}x_{id},\quad x_{id}(0)=x_{id0}\\ d_i&{}=R_{id}x_{id}, \end{array} \end{aligned}$$

(6.11)

where $x_{id}\in \mathbb {R}^{n_{d_i}}$ and the initial condition $x_{id0}$ can be arbitrarily chosen.

In Remark 6.4 we considered colored noise. However, the model we used in that remark to generate colored noise, clearly cannot incorporate bias terms. This is one of the main motivations of the model (6.10) since the above disturbance term $d_i$ can generate bias terms provided $S_{id}$ has zero eigenvalues. However, it clearly can also handle other cases where we have disturbances with known frequency content.

Note that we have two exosystems (6.6) and (6.11) which generate the reference signal $y_r$ and the disturbance $d_i$, respectively. We can unify the two in one exosystem:

$$\begin{aligned} \begin{array}{cl} x_{ie} &{}=S_{i}x_{ie},\qquad x_{ie}(0)=x_{ie0}\\ d_i &{}=R_{ie}x_{ie},\\ y_r &{}=R_{re}x_{ie}, \end{array} \end{aligned}$$

(6.12)

where

$$\begin{aligned} S_i = \begin{pmatrix} S_{id} &{} 0 \\ 0 &{} S_r \end{pmatrix},\quad R_{ie} = \begin{pmatrix} R_{id}&0 \end{pmatrix},\quad R_{re} = \begin{pmatrix} 0&R_r \end{pmatrix}. \end{aligned}$$

(6.13)

Note that

$$ x_{ie0} = \begin{pmatrix} x_{id0} \\ x_{r0} \end{pmatrix} $$

and therefore the second part of the initial condition has to be the same for each agent while the first part might be different for each agent. Note that in case we have no disturbances with known frequencies (as in the previous section) then we can still use the model (6.12) but with

$$\begin{aligned} S_i = S_r,\qquad R_{ie} = 0,\qquad R_{re} = R_r \end{aligned}$$

(6.14)

while $x_{ie0} = x_{r0}$.

The time-varying topology $\mathscr {G}(t)$ has exactly the same structure as in Sect. 6.2, and it also belongs to a set of time-varying graph $\tilde{\mathbb {G}}_{\alpha ,\beta ,\pi }^{\varphi ,\tau , N}$ as defined in Definition 6.10. The network defined by the time-varying topology also provides each agent with the measurement $\zeta _{i}(t)$ given in (6.4).

6.3.1 Distributed Protocol Design

Here is the main result in this section:

Theorem 6.17

Consider a multiagent system described by (6.10), (6.4), (6.7), and reference system (6.12). Let a root set $\pi$, $\alpha ,\beta ,\varphi , \tau >0$ and positive integer N be given, and hence a set of time-varying network graphs $\tilde{\mathbb {G}}_{\alpha ,\beta ,\pi }^{\varphi ,\tau , N}$ be defined.

Under Assumptions 6.5 and 6.7, the stochastic almost regulated output synchronization problem is solvable, i.e., there exists a family of distributed dynamic protocols, parametrized in terms of low- and high-gain parameters $\delta ,\,\varepsilon$, of the form

$$\begin{aligned} \left\{ \; \begin{array}{cl} \dot{\chi }_i &{}= \mathscr {A}_i(\delta ,\varepsilon )\chi _i+ \mathscr {B}_i(\delta ,\varepsilon )\begin{pmatrix}\zeta _i \\ \psi _i\end{pmatrix}\\ \tilde{u}_i &{}= \mathscr {C}_i(\delta ,\varepsilon )\chi _i+ \mathscr {D}_i(\delta ,\varepsilon )\begin{pmatrix}\zeta _i \\ \psi _i\end{pmatrix} \end{array} \right. ,\qquad i\in \mathscr {V} \end{aligned}$$

(6.15)

where $\chi _i \in \mathbb {R}^{q_i}$, such that for any time-varying graph $\mathscr {G}\in \tilde{\mathbb {G}}_{\alpha ,\beta ,\pi }^{\varphi ,\tau ,N}$, for all initial conditions of agents, the stochastic almost regulated output synchronization error satisfies (6.8).

Specifically, there exits a $\delta ^{*}\in (0,1]$ such that for each $\delta \in (0,\delta ^{*}]$, there exists an $\varepsilon ^{*} \in (0,1]$ such that for any $\varepsilon \in (0,\varepsilon ^{*}]$, the protocol (6.15) solves the stochastic almost regulated output synchronization problem.

The proof will be presented in a constructive way in the following section.

6.4 Proof of Theorems 6.15 and 6.17

Note that Theorem 6.15 is basically a corollary of Theorem 6.17 if we replace (6.13) by (6.14) and still use exosystem (6.12). In this section, we will present a constructive proof in three steps. As noted, we can concentrate on the proof of Theorem 6.17.

In Step 1, precompensators are designed for each agent to make the interconnection of an agent and its precompensator square, uniform rank (i.e., all the infinite zeros are of the same order) and such that it can generate the reference signal for all possible initial condition of the joint exosystem (6.12). In Step 2, a distributed linear dynamic protocol is designed for each interconnection system obtained from Step 1. Finally, in Step 3, we combine the precompensator from Step 1 and the protocol for the interconnection system in Step 2, and get a protocol of the form (6.15) for each agent in the network (6.10) (if disturbances with known frequencies are present) or a protocol of the form (6.9) for each agent in the network (6.1) (if disturbances with known frequencies are not present).

Step 1: In this step, we augment agent (6.10) with a precompensator in such a way that the interconnection is square, minimum-phase uniform rank such that it can generate the reference signal for all possible initial condition of the joint exosystem (6.12).

To be more specific, we need to find precompensators

$$\begin{aligned} \left\{ \; \begin{array}{ccl} \dot{z}_i &{}=&{} A_{ip} z_i + B_{ip} u_i, \\ \tilde{u}_i &{}=&{} C_{ip} z_i+ D_{ip} u_i, \end{array} \right. \end{aligned}$$

(6.16)

for each agent $i=1,\ldots , N$, such that agent (6.10) plus precompensator (6.16) can be represented as:

$$\begin{aligned} \left\{ \; \begin{array}{cl} \text {d}x_i &{}=A_ix_i\text {d}t + B_iu_i\text {d}t + G_i\text {d}w_i + H_i^1d_i\text {d}t,\\ y_i&{}=C_ix_i+H_i^2d_i, \end{array} \right. \end{aligned}$$

(6.17)

where $x_{i}\in \mathbb {R}^{n_{i}}$, $u_{i}\in \mathbb {R}^{p},\,y_{i}\in \mathbb {R}^{p}$ are states, inputs, and outputs of the interconnection of agent (6.10) and precompensator (6.16). Moreover,

• There exists $\varPi _i$ such that

  $$\begin{aligned} A_i\varPi _i + H_i^1 R_{ie}&= \varPi _i S_i \nonumber \\ C_i\varPi _i + H_i^2 R_{ie}&= R_{re} \end{aligned}$$

  (6.18)

• $(A_i, B_i,C_i)$ is square and has uniform rank $\rho \ge 1$.

The first condition implies that for any initial condition of (6.12) there exists an initial condition for (6.17) such that for $u_i=0$, we have that ${\mathbb {E}}y_i= y_r$. We could, equivalently, impose $w_i=0$ in which case, we should have $y_i=y_r$. In the special case where we do not have disturbances with known frequencies (Theorem 6.15) we have $R_{ie}=0$ and $S_i=S_r$. In that case, the first condition reduces to the condition that $(C_i,A_i)$ contains $(S_{r},R_{r})$.

For our construction of precompensator (6.16), we first note that the following regulator equation

$$\begin{aligned} \tilde{A}_i\tilde{\varPi }_i+\tilde{B}_i\tilde{\varGamma }_i + \tilde{H}_i^1 R_{ie} = \tilde{\varPi }_i S_i, \qquad \tilde{C}_i\tilde{\varPi }_i + \tilde{H}_i^2 R_{ie} = R_{re}. \end{aligned}$$

(6.19)

has a unique solution $\tilde{\varPi }_i$ and $\tilde{\varGamma }_i$ since $(\tilde{A}_i,\tilde{B}_i,\tilde{C}_i)$ is right-invertible and minimum-phase while $S_i$ has no stable eigenvalues (see [19]). Let $\varGamma _{oi},S_{oi})$ be the observable subsystem of $(\tilde{\varGamma }_i,S_i)$. Then we consider the following precompensator:

$$\begin{aligned} \dot{p}_{i,1}=S_{oi} p_{i,1}+B_{i,1}u^1_i,\qquad \tilde{u}_i =\varGamma _{oi} p_{i,1} +D_{i,1} u^1_i \end{aligned}$$

(6.20)

where $B_{i,1}$ and $D_{i,1}$ are chosen according to the technique presented in [9] to guarantee that the interconnection of (6.10) and (6.20) is minimum-phase and right-invertible. It is not hard to verify that the interconnection of (6.10) and (6.20) is a system of the form (6.17) for which there exists $\varPi _i$ satisfying (6.18). However, we still need to guarantee that this interconnection is square and uniform rank.

Let $\rho _i$ be the maximal order of the infinite zeros for the interconnection of (6.20) and (6.10). For $i=1,\ldots , N$ and set $\rho =\max \{\rho _{i}\}$. According to [20, Theorem 1], a precompensator of the form

$$\begin{aligned} \begin{array}{cl} \dot{p}_{i_2} &{}= A_{ip2} p_{i_2} + B_{ip2} u_i^{2},\\ u_i^1 &{}= C_{ip2} p_{i_2} + D_{ip2} u_i^{2}, \end{array} \end{aligned}$$

(6.21)

exists such that the interconnection of (6.20), (6.21), and (6.10) is square, minimum-phase, and has uniform rank $\rho$. This interconnection of (6.20) and (6.21) is of the form (6.16) while the interconnection of (6.20), (6.21), and (6.10) is of the form (6.17) which has the required properties.

Without loss of generality, we assume that $(A_i, B_i, C_i)$ is already in the SCB form, i.e., the system has a specific form where $x_{i}=[x_{ia};x_{id}]$, with $x_{ia}\in \mathbb {R}^{n_{i}-p\rho }$ representing the finite zero structure and $x_{id}\in \mathbb {R}^{p\rho }$ the infinite zero structure. We obtain that (6.17) can be written as:

$$\begin{aligned} \left\{ \; \begin{array}{cl} \text {d}x_{ia} &{}=A_{ia}x_{ia}\text {d}t+L_{iad}y_i\text {d}t +G_{ia}\text {d}w_{i} +H_{ia}^1d_i\text {d}t,\\ \text {d}x_{id} &{}=A_dx_{id}\text {d}t+B_d(u_i +E_{ida}x_{ia} +E_{idd}x_{id})\text {d}t +G_{id}\text {d}w_i+H_{id}^1d_i\text {d}t,\\ y_i&{}=C_dx_{id}+H_i^2d_i\text {d}t, \end{array} \right. \end{aligned}$$

(6.22)

for $i=1,\ldots ,N$, where $A_{d}$, $B_{d}$, and $C_{d}$ have the special form

$$\begin{aligned} A_d= \begin{pmatrix} 0 &{} I_{p(\rho -1)} \\ 0 &{} 0 \end{pmatrix}, \qquad B_d= \begin{pmatrix} 0 \\ I_p \end{pmatrix},\qquad C_d= \begin{pmatrix} I_p&0 \end{pmatrix}. \end{aligned}$$

(6.23)

Furthermore, the eigenvalues of $A_{ia}$ are the invariant zeros of $(A_i, B_i, C_i)$, which are all in the open left half complex plane.

Step 2: Each agent after applying the precompensator (6.16) is of the form (6.22). For this system, we will design a purely decentralized controller based on a low- and high-gain method. Let $\delta \in (0,1]$ be the low-gain parameter and $\varepsilon \in (0,1]$ be the high-gain parameter as in [4]. First, select K such that $A_d-KC_d$ is Hurwitz stable. Next, choose $F_{\delta }=-B_d'P_d$ where $P_d'=P_{d}>0$ is uniquely determined by the following algebraic Riccati equation:

$$\begin{aligned} P_d A_d+A_d'P_d-\beta P_d B_dB_d'P_d+\delta I=0, \end{aligned}$$

(6.24)

where $\beta >0$ is the lower bound on the real parts of all eigenvalues of expanded Laplacian matrices $\bar{L}(t)$, for all t. Next, define

$$ S_\varepsilon ={\text {blkdiag}}\{I_p,\varepsilon I_p,\ldots ,\varepsilon ^{\rho -1} I_p \}, $$

$$ K_\varepsilon =\varepsilon ^{-1}S_\varepsilon ^{-1}K\; \text { and }\; F_{\delta \varepsilon }=\varepsilon ^{-\rho }F_{\delta }S_{\varepsilon }. $$

Then, we design the dynamic controller for each agent $i \in \mathscr {V}$:

$$\begin{aligned} \begin{array}{ccl} \dot{\hat{x}}_{id} &{}=&{} A_d\hat{x}_{id}+K_{\varepsilon }(\zeta _i+\psi _i-C_d\hat{x}_{id}),\\ u_i &{}=&{} F_{\delta \varepsilon }\hat{x}_{id}, \end{array} \end{aligned}$$

(6.25)

where $\psi _i$ is defined in (6.7).

The state $\hat{x}_{id}$ is not an estimator for $x_{id}$ but actually an estimator for

$$\begin{aligned} \sum _{j=1}^N \bar{\ell }_{ij}(t) x_{id}(t). \end{aligned}$$

(6.26)

The following lemma then provides a constructive proof of Theorem 6.17. However, by replacing (6.13) with (6.14) it also provides a constructive proof of Theorem 6.15.

Lemma 6.18

Consider the agents in SCB format (6.22) obtained after applying the precompensators (6.16). For any given $\gamma >0$, there exits a $\delta ^{*}\in (0,1]$ such that, for each $\delta \in (0,\delta ^{*}]$, there exists an $\varepsilon ^{*} \in (0,1]$ such that for any $\varepsilon \in (0,\varepsilon ^{*}]$, the protocol (6.25) solves the stochastic almost regulated output synchronization problem for any time-varying graph $\mathscr {G}\in \tilde{\mathbb {G}}^{\varphi ,\tau ,N}_{\alpha , \beta ,\pi }$, for all initial conditions.

Proof

Recall that $x_i=[x_{ia};x_{id}]$ and that (6.17) is a shorthand notation for (6.22). For each $i \in \mathscr {V}$, let $\bar{x}_{i}=x_{i}-\varPi _ix_r$, where $\varPi _i$ is defined by (6.18). Then

$$\begin{aligned} \text {d}\bar{x}_i&=A_ix_i\text {d}t-\varPi _iS_ix_r\text {d}t + B_iu_i\text {d}t + H_i^1 d_i \text {d}t + G_i\text {d}w_i \\&= A_i\bar{x}_i\text {d}t + B_iu_i\text {d}t+G_i\text {d}w_i \end{aligned}$$

and

$$ e_i=y_i-y_r = C_ix_i+H_i^2R_{ie}-R_{re}x_r=C_ix_i-C_i\varPi _ix_r=C_i\bar{x}_i. $$

Since the dynamics of the $\bar{x}_i$ system with output $e_i$ is governed by the same dynamics as the dynamics of agent i, we can present $\bar{x}_i$ in the same form as (6.22), with $\bar{x}_i=[\bar{x}_{ia};\bar{x}_{id}]$, where

$$ \begin{array}{cl} \text {d}\bar{x}_{ia}&{}=A_{ia}\bar{x}_{ia}\text {d}t+L_{iad}e_i\text {d}t + G_{ia}\text {d}w_i,\\ \text {d}\bar{x}_{id}&{}=A_d\bar{x}_{id}\text {d}t+B_d(u_i+E_{ida}\bar{x}_{ia}+E_{idd}\bar{x}_{id})\text {d}t +G_{id}\text {d}w_i ,\\ e_i&{}=C_d\bar{x}_{id}. \end{array} $$

Define $\xi _{ia}=\bar{x}_{ia}$, $\xi _{id}=S_\varepsilon \bar{x}_{id}$, and $\hat{\xi }_{id}=S_\varepsilon \hat{x}_{id}$. Then

$$ \begin{array}{ccl} \text {d}\xi _{ia}&{}=&{}A_{ia}\xi _{ia}\text {d}t+V_{iad}\xi _{id}\text {d}t+G_{ia}\text {d}w_{i},\\ \varepsilon \text {d}\xi _{id} &{}=&{}A_d\xi _{id}\text {d}t+B_dF_{\delta }\hat{\xi }_{id}\text {d}t+V_{ida}^{\varepsilon }\xi _{ia}\text {d}t +V_{idd}^{\varepsilon }\xi _{id}\text {d}t+ \varepsilon G_{id}^{\varepsilon } \text {d}w_i,\\ e_i &{}=&{} C_d\xi _{id}, \end{array} $$

where $V_{iad}=L_{iad}C_d$, $V_{ida}^{\varepsilon }=\varepsilon ^{\rho }B_dE_{ida}$, $V_{idd}^{\varepsilon }=\varepsilon ^{\rho }B_dE_{idd}S_{\varepsilon }^{-1}$ and $G_{id}^{\varepsilon }=S_{\varepsilon }G_{id}$.

Then,

$$ \zeta _i+\psi _i=\sum _{j=1}^{N}\ell _{ij}(t)(y_j-y_r)+\iota _i(y_i-y_r)= \sum _{j=1}^{N}\bar{\ell }_{ij}(t)e_j. $$

Similarly, the controller (6.25) can be rewritten as

$$ \varepsilon \text {d}\hat{\xi }_{id}=A_d\hat{\xi }_{id}\text {d}t+ K\sum _{j=1}^{N}\bar{\ell }_{ij}(t)C_d\xi _{jd}\text {d}t- KC_d\hat{\xi }_{id}\text {d}t. $$

Let

$$ \xi _a={\text {col}}\{\xi _{ia}\},\, \xi _d={\text {col}}\{\xi _{id}\},\,\hat{\xi }_d={\text {col}}\{\hat{\xi }_{id}\},\, w={\text {col}}\{w_i\}. $$

Then we have,

$$ \begin{array}{ccl} \text {d}\xi _a&{}=&{} A_a\xi _a\text {d}t+V_{ad}\xi _d\text {d}t+G_a\text {d}w,\\ \varepsilon \text {d}\xi _d&{}=&{} (I_{N}\otimes A_d)\xi _d\text {d}t+(I_{N}\otimes B_dF_{\delta }) \hat{\xi }_d\text {d}t+V_{da}^{\varepsilon }\xi _a\text {d}t+ V_{dd}^{\varepsilon }\xi _d\text {d}t+\varepsilon G_{d}^{\varepsilon }\text {d}w,\\ \varepsilon \text {d}\hat{\xi }_d&{}=&{} (I_{N}\otimes A_d)\hat{\xi }_d\text {d}t+ (\bar{L}(t)\otimes KC_d)\xi _d\text {d}t-(I_{N}\otimes KC_d)\hat{\xi }_d\text {d}t, \end{array} $$

where $A_a={\text {blkdiag}}\{A_{ia}\}$, and $V_{ad}$, $V_{da}^{\varepsilon }$, $V_{dd}^{\varepsilon }$, $G_a$, $G_d^{\varepsilon }$ are similarly defined.

Define $U_{t}^{-1}\bar{L}(t)U_{t}=J_{t}$, where $J_{t}$ is the Jordan form of $\bar{L}(t)$, and let

$$ v_a=\xi _a,\qquad v_d=(J_{t}U_{t}^{-1}\otimes I_{p\rho })\xi _d,\qquad \tilde{v}_d=v_d-(U_{t}^{-1}\otimes I_{p\rho })\hat{\xi }_d. $$

By our assumptions on the graph, we know that $J_t$ and $J_t^{-1}$ are bounded. Moreover, by the assumption on the condition number we can guarantee that $U_t$ and $U_t^{-1}$ are both bounded as well. Note that when a switching of the network graph occurs then $v_d$ and $\tilde{v}_d$ will in most case experience a discontinuity (because of a sudden change in $J_t$ and $U_t$) while $v_a$ remains continuous. There exists $m_1,m_2>0$ such that we will have:

$$ \Vert v_d(t_k^+) \Vert \le m_1 \Vert v_d(t_k^-) \Vert ,\qquad \Vert \tilde{v}_d(t_k^+) \Vert \le m_2 \Vert \tilde{v}_d(t_k^-) \Vert $$

for any switching time $t_k$ because of our bounds on $U_t$ and $J_t$. Here

$$ f(t^+)=\lim _{h\downarrow 0} f(t+h), \quad f(t^-)=\lim _{h\downarrow 0} f(t-h) $$

Between switching, the behavior of $v_a,v_d$, and $\tilde{v}_d$ is described by the following stochastic differential equations:

$$\begin{aligned} \begin{array}{cl} \text {d}v_a&{}=A_av_a\text {d}t+W_{ad,t}v_d\text {d}t+G_a\text {d}w,\\ \varepsilon \text {d}v_d &{}=(I_{N}\otimes A_d)v_d\text {d}t+(J_{t}\otimes B_dF_{\delta }) (v_d-\tilde{v}_d)\text {d}t\\ &{}\qquad +W_{da,t}^{\varepsilon }v_a\text {d}t+W_{dd,t}^{\varepsilon }v_d\text {d}t+\varepsilon \bar{G}_{d,t}^{\varepsilon } \text {d}w,\\ \varepsilon \text {d}\tilde{v}_d&{}=(I_{N}\otimes (A_d-KC_d))\tilde{v}_d\text {d}t+(J_{t}\otimes B_dF_{\delta })(v_d-\tilde{v}_d)\text {d}t\\ &{}\qquad +W_{da,t}^{\varepsilon }v_a\text {d}t+ W_{dd,t}^{\varepsilon }v_d\text {d}t+\varepsilon \bar{G}_{d,t}^{\varepsilon } \text {d}w,\\ \end{array} \end{aligned}$$

(6.27)

where $W_{ad,t}=V_{ad}(U_{t}J_{t}^{-1}\otimes I_{p\rho })$, $W_{da,t}^{\varepsilon }=(J_{t}U_{t}^{-1}\otimes I_{p\rho })V_{da}^{\varepsilon }$, $W_{dd,t}^{\varepsilon }=(J_{t}U_{t}^{-1}\otimes I_{p\rho })V_{dd}^{\varepsilon }(U_{t}J_{t}^{-1}\otimes I_{p\rho })$, and $\bar{G}_{d,t}^{\varepsilon }=(J_{t}U_{t}^{-1}\otimes I_{p\rho })G_{d}^{\varepsilon }$.

Finally, let $\eta _a=v_a$, and define $N_d$ such that

$$ \eta _d:=N_d \begin{pmatrix} v_d \\ \tilde{v}_d \end{pmatrix}= \begin{pmatrix} v_{1d} \\ \tilde{v}_{1d} \\ \vdots \\ v_{Nd} \\ \tilde{v}_{Nd} \end{pmatrix} \text { where } N_d= \begin{pmatrix} e_1&{}0\\ 0&{}e_1\\ \vdots &{}\vdots \\ e_{N} &{} 0\\ 0 &{} e_{N} \end{pmatrix}\otimes I_{p\rho }, $$

where $e_{i} \in \mathbb {R}^{N}$ is the i’th standard basis vector whose elements are all zero except for the i’th element which is equal to 1. Again the switching can only cause discontinuities in $\eta _d$ (and not in $\eta _a$). There exists $m_3>0$ such that we will have:

$$\begin{aligned} \Vert \eta _d(t_k^+) \Vert \le m_3 \Vert \eta _d(t_k^-) \Vert , \end{aligned}$$

(6.28)

for any switching time $t_k$. Between switching the stochastic differential equation (6.27) can be rewritten as:

$$\begin{aligned} \begin{array}{cl} \text {d}\eta _a&{}=A_a\eta _a\text {d}t+\tilde{W}_{ad,t}\eta _d\text {d}t+G_a\text {d}w,\\ \varepsilon \text {d}\eta _d&{}=\tilde{A}_{\delta ,t}\eta _d\text {d}t+\tilde{W}_{da,t}^{\varepsilon }\eta _a\text {d}t+ \tilde{W}_{dd,t}^{\varepsilon }\eta _d\text {d}t+\varepsilon \tilde{G}_{d,t}^{\varepsilon }\text {d}w, \end{array} \end{aligned}$$

(6.29)

where

$$\begin{aligned} \tilde{A}_{\delta ,t}=I_{N}\otimes \begin{pmatrix} A_d &{} 0\\ 0 &{} A_d-KC_d \end{pmatrix}+ J_{t}\otimes \begin{pmatrix} B_dF_{\delta } &{} -B_dF_{\delta }\\ B_dF_{\delta } &{} -B_dF_{\delta } \end{pmatrix}, \end{aligned}$$

(6.30)

and

$$\begin{aligned} \tilde{W}_{ad,t}&= \begin{pmatrix} W_{ad,t}&0 \end{pmatrix}N_d^{-1},\qquad&\tilde{G}_{d,t}^{\varepsilon }&=N_d \begin{pmatrix} \bar{G}_{d,t}^{\varepsilon }\\ \bar{G}_{d,t}^{\varepsilon } \end{pmatrix},\\ \tilde{W}_{da,t}^{\varepsilon }&= N_d \begin{pmatrix} W_{da,t}^{\varepsilon } \\ W_{da,t}^{\varepsilon } \end{pmatrix},\qquad&\tilde{W}_{dd,t}^{\varepsilon }&= N_d \begin{pmatrix} W_{dd,t}^{\varepsilon } &{} 0\\ W_{dd,t}^{\varepsilon }&{}0 \end{pmatrix}N_d^{-1}. \end{aligned}$$

Lemma 6.19

Consider the matrix $\tilde{A}_{\delta ,t}$ defined in (6.30). For any $\delta$ small enough the matrix $\tilde{A}_{\delta ,t}$ is asymptotically stable for any Jordan matrix $J_{t}$ whose eigenvalues satisfy ${\text {Re}}\{\lambda _{ti}\}>\beta$ and $|\lambda _{ti}|<\alpha$. Moreover, there exists $P_\delta >0$ and $\nu >0$ such that

$$\begin{aligned} \tilde{A}_{\delta ,t}' P_\delta + P_\delta \tilde{A}_{\delta ,t} \le -\nu P_\delta - 4I \end{aligned}$$

(6.31)

is satisfied for all possible Jordan matrices $J_{t}$ and such that there exists $P_a>0$ for which

$$\begin{aligned} P_aA_a+A_a'P_a=-\nu P_a-I. \end{aligned}$$

(6.32)

Proof

First note that if $\nu$ is small enough such that $A_a+\tfrac{\nu }{2}I$ is asymptotically stable then there exists $P_a>0$ satisfying (6.32).

For the existence of $P_\delta$ and the stability of $\tilde{A}_{\delta ,t}$ we rely on techniques developed earlier in [4, 21]. If we define

$$ \bar{A}_{\delta ,ti} = \begin{pmatrix} A_d + \lambda _{ti} B_d F_\delta &{} -\lambda _{ti} B_d F_\delta \\ \lambda _{ti} B_d F_\delta &{} A_d-KC_d - \lambda _{ti} B_d F_\delta \end{pmatrix} $$

and

$$ \bar{B} = \begin{pmatrix} B_d F_\delta &{} -B_d F_\delta \\ B_d F_\delta &{} -B_d F_\delta \end{pmatrix} $$

then

$$ \tilde{A}_{\delta ,t} = \begin{pmatrix} \bar{A}_{\delta ,t1} &{} \mu _1 \bar{B} &{} 0 &{} \cdots &{} 0 \\ 0 &{} \bar{A}_{\delta ,t2} &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} 0 \\ \vdots &{} &{} \ddots &{} \ddots &{} \mu _{N-1} \bar{B} \\ 0 &{} \cdots &{} \cdots &{} 0 &{} \bar{A}_{\delta ,tN} \end{pmatrix}, $$

where $\lambda _{t1},\ldots ,\lambda _{tN}$ are the eigenvalues of $J_{t}$ and $\mu _i\in \{ 0,1 \}$ is determined by the Jordan structure of $J_{t}$. Define

$$ \bar{P}_\delta = \rho \begin{pmatrix} P_d &{} 0 \\ 0 &{} \sqrt{\Vert P_d \Vert } P \end{pmatrix}, $$

where $P_d$ is the solution of the Riccati equation (6.24) and P is uniquely defined by the Lyapunov equation:

$$ P(A_d - KC_d) + (A_d- KC_d)'P = -I. $$

In the above we choose $\rho$ such that $\rho \delta >1$ and $\rho \sqrt{\Vert P_d\Vert } >2$. As shown in [4] we then have:

$$ \bar{A}_{\delta ,ti} '\bar{P}_\delta +\bar{P}_\delta \bar{A}_{\delta ,ti} \le -\rho \begin{pmatrix} \delta I &{} 0 \\ 0 &{} \tfrac{1}{2}\sqrt{\Vert P_d \Vert } I \end{pmatrix}\le - I. $$

Via Schur complement, it is easy to verify that if matrices $A_{11}<-kI$, $A_{22}<0$ and $A_{12}$ are given then there exists $\mu$ sufficiently large such that the matrix

$$ \begin{pmatrix} A_{11} &{} A_{12} \\ A_{12}' &{} \mu A_{22} \end{pmatrix} < -(k-1) I. $$

Define the matrix:

$$ P_{\delta } = \begin{pmatrix} \alpha _1 \bar{P}_\delta &{} 0 &{} \cdots &{} 0 \\ 0 &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} 0 \\ 0 &{} \cdots &{} 0 &{} \alpha _N \bar{P}_\delta \end{pmatrix}. $$

Then we have that $P_{\delta } \tilde{A}_{\delta ,t} + \tilde{A}_{\delta ,t}' P_{\delta }$ is less than or equal to:

$$ \begin{pmatrix} -\alpha _1 I &{} \alpha _1 \mu _{1}\bar{P}_{\delta }\bar{B} &{} 0 &{} \ldots &{} 0 \\ \alpha _1 \mu _{1}\bar{B}'\bar{P}_{\delta } &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} \ddots &{} \ddots &{} \ddots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \alpha _{N-1}\mu _{N-1} \bar{P}_{\delta }\bar{B} \\ 0 &{} \cdots &{} 0 &{} \alpha _{N-1} \mu _{N-1}\bar{B}'\bar{P}_{\delta } &{} -\alpha _N I \end{pmatrix}. $$

Using the above Schur argument, it is not hard to show that if

$$ \begin{pmatrix} -\alpha _1 I &{} \alpha _1 \mu _{1}\bar{P}_{\delta }\bar{B} &{} 0 &{} \ldots &{} 0 \\ \alpha _1 \mu _{1}\bar{B}'\bar{P}_{\delta } &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} \ddots &{} \ddots &{} \ddots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \alpha _{N-2}\mu _{N-2} \bar{P}_{\delta }\bar{B} \\ 0 &{} \cdots &{} 0 &{} \alpha _{N-2} \mu _{N-2}\bar{B}'\bar{P}_{\delta } &{} -\alpha _{N-1} I \end{pmatrix} \le -6 I, $$

then there exists $\alpha _N$ such that:

$$ \begin{pmatrix} -\alpha _1 I &{} \alpha _1 \mu _{1}\bar{P}_{\delta }\bar{B} &{} 0 &{} \ldots &{} 0 \\ \alpha _1 \mu _{1}\bar{B}'\bar{P}_{\delta } &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} \ddots &{} \ddots &{} \ddots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \alpha _{N-1}\mu _{N-1} \bar{P}_{\delta }\bar{B} \\ 0 &{} \cdots &{} 0 &{} \alpha _{N-1} \mu _{N-1}\bar{B}'\bar{P}_{\delta } &{} -\alpha _N I \end{pmatrix} \le -5 I. $$

Using a recursive argument, we can then prove there exists $\alpha _1,\ldots , \alpha _N$ such that:

$$ P_{\delta } \tilde{A}_{\delta ,t} + \tilde{A}_{\delta ,t}' P_{\delta } \le -5I. $$

This obviously implies that for $\nu$ small enough we have (6.31). If this $\nu$ is additionally small enough such that $A_a+\tfrac{\nu }{2} I$ is asymptotically stable (recall that $A_a$ is asymptotically stable) then we obtain that there also exists $P_a$ satisfying (6.32). $\blacksquare$

Define $V_a=\varepsilon ^2 \eta _a'P_a\eta _a$ as a Lyapunov function for the dynamics of $\eta _a$ in (6.29). Similarly, we define $V_d=\varepsilon \eta _d'P_{\delta }\eta _d$ as a Lyapunov function for the $\eta _d$ dynamics in (6.29). Then the derivative of $V_a$ is bounded by:

$$\begin{aligned} \text {d}V_a&=-\nu V_a\text {d}t -\varepsilon ^2 \Vert \eta _a\Vert ^2\text {d}t+2\varepsilon ^2{\text {Re}}(\eta _a'P_a\tilde{W}_{ad,t}\eta _d) \text {d}t\nonumber \\&\quad +\varepsilon ^2 \,{\text {trace}}(P_aG_aQ_0G_a' )\text {d}t+2\varepsilon ^2{\text {Re}}(\eta _a'P_aG_a)\text {d}w \nonumber \\&\le -\nu V_a\text {d}t +\varepsilon c_3 V_d \text {d}t\nonumber \\&\quad +\varepsilon ^2 r_5 \,{\text {trace}}(Q_0) \text {d}t + 2\varepsilon ^2 {\text {Re}}(\eta _a'P_aG_a)\text {d}w , \end{aligned}$$

(6.33)

where $r_5$ and $c_3$ are such that:

$$ {\text {trace}}(P_aG_aQ_0G_a' ) \le r_5 \,{\text {trace}}\,Q_0 $$

and

$$ 2 {\text {Re}}(\eta _a'P_a\tilde{W}_{ad,t}\eta _d) \le 2 r_4 \Vert \eta _a\Vert \Vert \eta _d\Vert \le \tfrac{1}{2}\Vert \eta _a \Vert ^2 + 2 r_4^2 \Vert \eta _d \Vert ^2 \le \tfrac{1}{2}\Vert \eta _a \Vert ^2 + \varepsilon ^{-1} c_3 V_d. $$

Note that we can choose $r_4$, $r_5$, and $c_3$ independent of the network graph but only depending on our bounds on the eigenvalues and condition number of our expand Laplacian $\bar{L}(t)$. Taking the expectation, we get:

$$ \text {d} {\mathbb {E}}V_a \le -\nu {\mathbb {E}}V_a\text {d}t +\varepsilon c_3 {\mathbb {E}}V_d \text {d}t +\varepsilon ^2 r_5 \,{\text {trace}}(Q_0) \text {d}t. $$

Next, the derivative of $V_d$ is bounded by

$$\begin{aligned} \text {d}V_d&=-\nu \varepsilon ^{-1} V_d \text {d}t -4\Vert \eta _d\Vert ^{2}\text {d}t+ 2{\text {Re}}(\eta _d'P_{\delta }\tilde{W}_{da,t}^{\varepsilon }\eta _a)\text {d}t \nonumber \\&\qquad +2{\text {Re}}(\eta _d'P_{\delta }\tilde{W}_{dd,t}^{\varepsilon }\eta _d)\text {d}t + \varepsilon \,{\text {trace}}(P_{\delta }\tilde{G}_{d,t}^{\varepsilon }Q_0(\tilde{G}_{d,t}^{\varepsilon })') \text {d}t \nonumber \\&\qquad + 2\varepsilon {\text {Re}}(\eta _d'P_{\delta }\tilde{G}_{d,t}^{\varepsilon })\text {d}w\nonumber \\&\le c_2 V_a \text {d}t -(\nu \varepsilon ^{-1} +\nu - \varepsilon ^2 \frac{c_2c_3}{\nu } ) V_d\text {d}t -\Vert \eta _d\Vert ^{2}\text {d}t \nonumber \\&\qquad +\varepsilon r_3\,{\text {trace}}(Q_0) \text {d}t + 2\varepsilon {\text {Re}}(\eta _d'P_{\delta }\tilde{G}_d^{\varepsilon })\text {d}w, \end{aligned}$$

(6.34)

where

$$ 2{\text {Re}}(\eta _d'P_{\delta }\tilde{W}_{dd,t}^{\varepsilon }\eta _d) \le \Vert \eta _d \Vert ^2 $$

for small $\varepsilon$ and

$$ 2{\text {Re}}(\eta _d'P_{\delta }\tilde{W}_{da,t}^{\varepsilon }\eta _a) \le \varepsilon r_1\Vert \eta _a\Vert \Vert \eta _d\Vert \le \varepsilon ^2r_1^2 \Vert \eta _a\Vert ^2+ \Vert \eta _d\Vert ^2 \le c_2 V_a + \Vert \eta _d\Vert ^2, $$

provided $r_1$ is such that we have $\varepsilon r_1\ge \Vert P_{\delta }\tilde{W}_{da,t}^{\varepsilon }\Vert$ and $c_2$ sufficiently large. Finally

$$ {\text {trace}}(P_{\delta }\tilde{G}_{d,t}^{\varepsilon }Q_0(\tilde{G}_{d,t}^{\varepsilon })') \le r_3 \,{\text {trace}}\, Q_0 $$

for suitably chosen $r_3$. Taking the expectation, we get:

$$ \text {d} {\mathbb {E}}V_d \le c_2 {\mathbb {E}}V_a \text {d}t -(\nu \varepsilon ^{-1} +\nu - \varepsilon ^2 \frac{c_2c_3}{\nu } ) {\mathbb {E}}V_d\text {d}t \\ \quad \quad \quad -{\mathbb {E}}\Vert \eta _d\Vert ^{2}\text {d}t +\varepsilon r_3\,{\text {trace}}(Q_0) \text {d}t. $$

We get:

$$ \frac{\text {d}}{\text {d}t} \begin{pmatrix} {\mathbb {E}}V_a \\ {\mathbb {E}}V_d \end{pmatrix} \le A_e \begin{pmatrix} {\mathbb {E}}V_a \\ {\mathbb {E}}V_d \end{pmatrix} + \begin{pmatrix} \varepsilon ^2 r_5 \,{\text {trace}}(Q_0) \\ \varepsilon r_3\,{\text {trace}}(Q_0) \end{pmatrix}, $$

where

$$ A_e={ \begin{pmatrix} -\nu &{} \varepsilon c_3 \\ c_2 &{} -\varepsilon ^{-1}\nu -\nu + \varepsilon ^2\frac{c_2c_3}{\nu } \end{pmatrix}}. $$

Note that the inequality here is componentwise. We find by integration that

$$ \begin{pmatrix} {\mathbb {E}}V_a \\ {\mathbb {E}}V_d \end{pmatrix}(t_k^-) \le e^{A_e (t_k-t_{k-1})} \begin{pmatrix} {\mathbb {E}}V_a \\ {\mathbb {E}}V_d \end{pmatrix} (t_{k-1}^+) + \int _{t_{k-1}}^{t_k} e^{A_e (t_k-s)} \begin{pmatrix} \varepsilon ^2 r_5 \,{\text {trace}}(Q_0) \\ \varepsilon r_3\,{\text {trace}}(Q_0) \end{pmatrix}\text {d}s $$

componentwise. In our case:

$$ e^{A_et} = \frac{1}{1+\varepsilon ^3 \frac{c_2c_3}{\nu ^2}} \begin{pmatrix} e^{\lambda _1 t} + \varepsilon ^3 \frac{c_2c_3}{\nu ^2}e^{\lambda _2t} &{} \varepsilon ^2 \frac{c_3}{\nu } \left( e^{\lambda _1t} -e^{\lambda _2t} \right) \\ \varepsilon \frac{c_2}{\nu } \left( e^{\lambda _1t} -e^{\lambda _2t} \right) &{} e^{\lambda _2 t} + \varepsilon ^3 \frac{c_2c_3}{\nu ^2}e^{\lambda _1t} \end{pmatrix}, $$

where $\lambda _1=-\nu +\varepsilon ^2\frac{c_2c_3}{\nu }$ and $\lambda _2=-\varepsilon ^{-1}\nu -\nu$. We have a potential jump at time $t_{k-1}$ in $V_d$. However, there exists m such that

$$ V_d(t_{k-1}^+) \le m V_d(t_{k-1}^-), $$

while $V_a$ is continuous. Using our explicit expression for $e^{A_et}$ and the fact that $t_k-t_{k-1} > \tau$ we find:

$$ \begin{pmatrix} 1&1 \end{pmatrix} e^{A_e (t_k-t_{k-1})} \begin{pmatrix} {\mathbb {E}}V_a \\ {\mathbb {E}}V_d \end{pmatrix} (t_{k-1}^+) \le e^{\lambda _3 (t_k-t_{k-1})} \left[ {\mathbb {E}}V_a(t_{k-1}^-) + {\mathbb {E}}V_d(t_{k-1}^-) \right] , $$

where $\lambda _3=-\nu /2$. Moreover, it can be easily verified that:

$$ \begin{pmatrix} 1&1 \end{pmatrix} \int _{t_{k-1}}^{t_k} e^{A_e (t_k-s)} \begin{pmatrix} \varepsilon ^2 r_5 \,{\text {trace}}(Q_0) \\ \varepsilon r_3\,{\text {trace}}(Q_0) \end{pmatrix}\text {d}s \le r \varepsilon ^2 \,{\text {trace}}(Q_0), $$

where r is a sufficiently large constant. We find

$$ \left[ {\mathbb {E}}V_a(t_{k}^-) + {\mathbb {E}}V_d(t_{k}^-) \right] \le e^{\lambda _3 (t_k-t_{k-1})} \left[ {\mathbb {E}}V_a(t_{k-1}^-) + {\mathbb {E}}V_d(t_{k-1}^-) \right] + r \varepsilon ^2 \,{\text {trace}}(Q_0). $$

Combining these time intervals, we get:

$$ \left[ {\mathbb {E}}V_a(t_{k}^-) + {\mathbb {E}}V_d(t_{k}^-) \right] \le e^{\lambda _3 t_k} \left[ {\mathbb {E}}V_a(0) + {\mathbb {E}}V_d(0) \right] + \frac{r \varepsilon ^2}{1-\mu } \,{\text {trace}}(Q_0), $$

where $\mu <1$ is such that

$$ e^{\lambda _3 (t_k-t_{k-1})} \le e^{\lambda _3\tau } \le \mu $$

for all k. Assume $t_{k+1}>t>t_k$. Since we do not necessarily have that $t-t_k>\tau$ we use the bound:

$$ e^{A_e (t-t_{k})} \begin{pmatrix} {\mathbb {E}}V_a \\ {\mathbb {E}}V_d \end{pmatrix} (t_k^{+}) \le 2\,m e^{\lambda _3 (t-t_{k})} \begin{pmatrix} {\mathbb {E}}V_a \\ {\mathbb {E}}V_d \end{pmatrix} (t_{k}^-), $$

where the factor m is due to the potential discontinuous jump. Combining all together, we get:

$$ \left[ {\mathbb {E}}V_a(t) + {\mathbb {E}}V_d(t) \right] \le 2m e^{\lambda _3 t} \left[ {\mathbb {E}}V_a(0) + {\mathbb {E}}V_d(0) \right] + (2m+1) \frac{r \varepsilon ^2}{1-\mu } \,{\text {trace}}(Q_0). $$

This implies:

$$ \lim _{t\rightarrow \infty } {\mathbb {E}}[ \eta _d'(t)\eta _{d}(t) ] \le \frac{2m+1}{\sigma _{\min }(P_\delta )} \frac{r \varepsilon }{1-\mu } \,{\text {trace}}(Q_0). $$

Following the proof above, we find that

$$\begin{aligned} \mathbf {e}&= (I_{N}\otimes C_d)(I_{N}\otimes S_{\varepsilon }^{-1})(U_{t}J_{t}^{-1}\otimes I_{p\rho })\begin{pmatrix} I_{Np\rho }&\quad 0 \end{pmatrix} N_d^{-1}\eta _d\\&=(U_{t}J_{t}^{-1}\otimes C_d)\begin{pmatrix} I_{Np\rho }&\quad 0 \end{pmatrix}N_d^{-1}\eta _d\\&=\Theta _{t}\eta _d, \end{aligned}$$

for suitably chosen matrix $\Theta _{t}$. Although $\Theta _{t}$ is time-varying, it is uniformly bounded, because for graphs in $\mathbb {G}_{\alpha ,\beta ,\pi }^{\varphi ,N}$ the matrices $U_{t}$ and $J_{t}$ are bounded. The fact that we can make the asymptotic variance of $\eta _d$ arbitrarily small then immediately implies that the asymptotic variance of $\mathbf {e}$ can be made arbitrarily small. Because all agents and protocols are linear it is obvious that the expectation of $\mathbf {e}$ is equal to zero. $\blacksquare$

Step 3: Combining the precompensator (6.16) and the controller (6.25) in Step 2, we obtain the protocol in the form of (6.15) in Theorem 6.17 (or if we replaced (6.13) by (6.14) we find the protocol for Theorem 6.15) as:

$$\begin{aligned} \begin{array}{cl} \mathscr {A}_i&{}={\begin{pmatrix} A_d-K_{\varepsilon }C_d &{}\quad 0\\ B_{ip}F_{\delta \varepsilon } &{}\quad A_{ip} \end{pmatrix}},\qquad \mathscr {B}_i= {\begin{pmatrix} K_{\varepsilon } &{}\quad K_{\varepsilon }\\ 0 &{}\quad 0 \end{pmatrix}},\\ \mathscr {C}_i&{}={\begin{pmatrix} 0 &{}\quad C_{ip} \end{pmatrix}},\qquad \qquad \qquad \mathscr {D}_i={\begin{pmatrix} 0&\quad 0 \end{pmatrix}}. \end{array} \end{aligned}$$

(6.35)

6.5 Examples

In this section, we will present two examples. The first example is connected to Theorem 6.15 (without disturbances with known frequencies). The second example is connected to Theorem 6.17 (with disturbances with known frequencies).

6.5.1 Example 1

We illustrate the result in this section on a network of 10 nonidentical agents, which are of the form (6.1) with

$$ A_{i_1}= \begin{pmatrix} -1 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1\\ 0.1 &{}\quad 0 &{}\quad 0.1 \end{pmatrix}, B_{i_1}= \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}, C_{i_1}'= \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, G_{i_1}= \begin{pmatrix} 1\\ 0\\ 1.5 \end{pmatrix}, $$

$$ A_{i_2}= \begin{pmatrix} -3 &{}\quad 1 &{}\quad 0\\ 0&{}\quad 0 &{}\quad 1\\ 1 &{}\quad 0.5 &{}\quad 1 \end{pmatrix}, B_{i_2}= \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}, C_{i_2}'= \begin{pmatrix} 0 \\ 1\\ 0 \end{pmatrix}, G_{i_2}= \begin{pmatrix} 0.5\\ 1\\ 1 \end{pmatrix}, $$

$$ A_{i_3}= \begin{pmatrix} -2 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1\\ 2&{}\quad 2 &{}\quad 2 \end{pmatrix}, B_{i_3}= \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}, C_{i_3}'= \begin{pmatrix} 0 \\ 1\\ 0 \end{pmatrix}, G_{i_3}= \begin{pmatrix} 2\\ 1\\ 2 \end{pmatrix}, $$

and $i_1\in \{1,2,3\}$, $i_2\in \{4,5,6\}$, $i_3\in \{7,8,9,10\}$, which will also be used as indices for the following precompensators and interconnection systems. The degree of the infinite zeros for each of the agent is equal to 2.

Assume the reference system as $y_0=1$, which is in the form of (6.6) with $S_{r}=0, R_{r}=1, x_r(0)=1$. By using the method given in Sect. 6.4, precompensators are designed of the form (6.16) as

$$ A_{i_1p}= 0,\quad B_{i_1p}= 10,\quad C_{i_1p}= -0.1, $$

$$ A_{i_2p}= 0,\quad B_{i_2p}= -1.2,\quad C_{i_2p}= -\frac{5}{6}, $$

$$ A_{i_3p}= 0,\quad B_{i_3p}= -\frac{1}{3},\quad C_{i_3p}= -3. $$

The interconnection of the above precompensators and agents have the degree of the infinite zeros equal to 3, and can be written in SCB form:

$$ A_{i_1}= \begin{pmatrix} -1 &{}\quad 1.4142 &{}\quad 0&{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ -0.0707 &{}\quad 0.1&{}\quad 0 &{}\quad 0.1 \end{pmatrix}, B_{i_1}= \begin{pmatrix} 0\\ 0\\ 0\\ 1 \end{pmatrix}, C_{i_1}'= \begin{pmatrix} 0 \\ 1 \\ 0\\ 0 \end{pmatrix}, G_{i_1}= \begin{pmatrix} 1.4142\\ 0\\ 1.5\\ 0.25 \end{pmatrix}, $$

$$ A_{i_2}= \begin{pmatrix} -3 &{}\quad 1.562 &{}\quad 0&{}\quad 0\\ 0&{}\quad 0 &{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ -1.9206&{}\quad 1 &{}\quad 0.5 &{}\quad 1 \end{pmatrix}, B_{i_2}= \begin{pmatrix} 0\\ 0\\ 0\\ 1 \end{pmatrix}, C_{i_2}'= \begin{pmatrix} 0 \\ 1\\ 0\\ 0 \end{pmatrix}, G_{i_2}= \begin{pmatrix} 0.781\\ 1\\ 1\\ 2 \end{pmatrix}, $$

$$ A_{i_3}= \begin{pmatrix} -2 &{}\quad 1.2019 &{}\quad 0&{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ -3.3282&{}\quad 2&{}\quad 2 &{}\quad 2 \end{pmatrix}, B_{i_3}= \begin{pmatrix} 0\\ 0\\ 0\\ 1 \end{pmatrix}, C_{i_3}'= \begin{pmatrix} 0 \\ 1\\ 0\\ 0 \end{pmatrix}, G_{i_3}= \begin{pmatrix} 2.4037\\ 1\\ 2\\ 10 \end{pmatrix}. $$

We select $K=(\begin{matrix} 3&7&3 \end{matrix})^{'}$ such that eigenvalues of $(A_{d}-KC_{d})$ are given by $(-0.5265,\,-1.2367\pm j2.0416)$, and then choose $\delta =10^{-10}$, $\varepsilon =0.01$ such that

$$ F_{\delta \varepsilon }=\begin{pmatrix} -0.0018&-0.0021&-0.0012\end{pmatrix},\, K_{\varepsilon }=\begin{pmatrix} 300 \\ 70000 \\ 3000000\end{pmatrix}. $$

Together with $A_{d},\,C_{d}$ with $\rho =3$, we get the controller of the form (6.25) for each interconnection system.

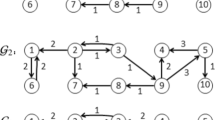
As stated in Theorem 6.15, the time-varying network topology switches in a set of network graph $\mathbb {G}_{\alpha ,\beta ,\pi }^{\varphi , N}$ with minimum dwell time $\tau$, and a priori given $\alpha ,\beta ,\pi ,\varphi , N$. In this example, we assume a graph set consists of three directed graphs $\mathscr {G}_1,\,\mathscr {G}_2,\,\mathscr {G}_3$, with $N=10, \alpha =10, \beta =0.3$, $\pi$ only contains node of agent 2, and $\varphi$ can be any bounded real number for this set is finite (with only 3 graphs). These graphs are shown in Fig. 6.1. The reference system is connected to agent 2, which is in the root set.

Fig. 6.1

The network topologies

Figure 6.2 shows the outputs of 10 agents with reference system $y_0=1$ with $\varepsilon =0.01, \delta =10^{-10}$. When tuning parameter $\varepsilon$ to 0.001, regulated output synchronization errors are squeezed to small and outputs of agents are much closer to the reference trajectory, shown in Fig. 6.3.

Fig. 6.2

Low- and high-gain parameters $\varepsilon =0.01,\delta =10^{-10}$

Fig. 6.3

Low- and high-gain parameters $\varepsilon =0.001,\delta =10^{-10}$

6.5.2 Example 2

In this section, we will modify Sect. 6.5.1 by adding disturbances with known frequencies. The $\tilde{H}_{i}^{1}$, $\tilde{H}_{i}^{2}$, $S_{id}$, and $R_{id}$ for agent i are given by:

$$ \tilde{H}_{i_{1}}^{1}=\begin{pmatrix} 0 &{}\quad 1\\ 0 &{}\quad 0\\ 0 &{}\quad 1.5\end{pmatrix},\, \tilde{H}_{i_{1}}^{2}=\begin{pmatrix} 1&0\end{pmatrix},\, S_{i_{1}d}=\begin{pmatrix} 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 9\\ 0 &{}\quad -9 &{}\quad 0\end{pmatrix},\, R_{i_{1}d}=\begin{pmatrix} 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0&{}\quad 1\end{pmatrix}, $$

$$ \tilde{H}_{i_{2}}^{1}=\begin{pmatrix} 0 &{}\quad 0.5\\ 0 &{}\quad 1\\ 0 &{}\quad 1\end{pmatrix},\, \tilde{H}_{i_{2}}^{2}=\begin{pmatrix} 1&0\end{pmatrix},\, S_{i_{2}d}=\begin{pmatrix} 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 3\\ 0 &{}\quad -3 &{}\quad 0\end{pmatrix},\, R_{i_{2}d}=\begin{pmatrix} 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1&{}\quad 0\end{pmatrix}, $$

$$ \tilde{H}_{i_{3}}^{1}=\begin{pmatrix} 0 &{}\quad 2\\ 0 &{}\quad 1\\ 0 &{}\quad 2\end{pmatrix},\, \tilde{H}_{i_{3}}^{2}=\begin{pmatrix} 1&0\end{pmatrix},\, S_{i_{3}d}=\begin{pmatrix} 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 5\\ 0 &{}\quad -5 &{}\quad 0\end{pmatrix},\, R_{i_{3}d}=\begin{pmatrix} 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0&{}\quad 1\end{pmatrix}, $$

where from $S_{id}$ we find that the disturbances with known frequencies are constant and sinusoid waves. Please note that $i_1\in \{1,2,3\}$, $i_2\in \{4,5,6\}$, $i_3\in \{7,8,9,10\}$. Assume we also have the constant reference trajectory $y_{0}=1$. By applying the method given in Sect. 6.4, we get precompensators

$$ A_{i_1p}= \begin{pmatrix} 0 &{}\quad -0.8441 &{}\quad 0 \\ 0.8441 &{}\quad 0 &{}\quad -8.9603 \\ 0&{}\quad 8.9603 &{}\quad 0 \end{pmatrix}, B_{i_1p}= \begin{pmatrix} 0.7779 \\ 0.5959 \\ 0.6631 \end{pmatrix}, C_{i_1p}'= \begin{pmatrix} 0\\ 0 \\ 1.5079 \end{pmatrix}, $$

$$ A_{i_2p}= \begin{pmatrix} 0 &{}\quad -1.1235 &{}\quad 0 \\ 1.1235 &{}\quad 0 &{}\quad -2.7817 \\ 0&{}\quad 2.7817 &{}\quad 0 \end{pmatrix}, B_{i_2p}= \begin{pmatrix} 0.2106\\ 0.2285\\ 0.3177 \end{pmatrix}, C_{i_2p}'= \begin{pmatrix} 0\\ 0\\ 3.1469 \end{pmatrix}, $$

$$ A_{i_3p}= \begin{pmatrix} 0 &{}\quad -3.5038 &{}\quad 0 \\ 3.5038 &{}\quad 0 &{}\quad -3.5670\\ 0&{}\quad 3.5670 &{}\quad 0 \end{pmatrix}, B_{i_3p}= \begin{pmatrix} 0.0353\\ 0.1059\\ 0.1652 \end{pmatrix}, C_{i_3p}'= \begin{pmatrix} 0\\ 0\\ 6.0544 \end{pmatrix}. $$

We also use the same parameters as those in Sect. 6.5.1, i.e., $K=(\begin{matrix} 3&\quad 7&\quad 3 \end{matrix})^{'}$, $\delta =10^{-10}$, $\varepsilon =0.01$. Then, we have

$$F_{\delta \varepsilon }=\begin{pmatrix} -18.2574&\quad -20.7160&\quad -11.7519\end{pmatrix},\, K_{\varepsilon }=\begin{pmatrix} 300 \\ 70000 \\ 3000000 \end{pmatrix}. $$

For $A_{d},\,C_{d}$ with $\rho =3$ given, we can get the controller of the form (6.25) for each interconnection system.

Fig. 6.4

Low- and high-gain parameters $\varepsilon =0.01,\delta =10^{-10}$

Fig. 6.5

Low- and high-gain parameters $\varepsilon =0.001,\delta =10^{-10}$

The network topology also switches among the set of graph shown in Fig. 6.1 in the same way. Figure 6.4 shows the outputs of 10 agents with reference system $y_0=1$ with $\varepsilon =0.01, \delta =10^{-10}$. When tuning parameter $\varepsilon$ to 0.001, regulated output synchronization errors are squeezed to small and outputs of agents are much closer to the reference trajectory, shown in Fig. 6.5. We can find that even agents are affected by any constant and any sinusoid wave with known frequencies, stochastic almost regulated output synchronization is still obtained.