On the Stochastic Modeling of the NSVR–IAF–PNLMS Algorithm for Correlated Gaussian Input Data

Abstract

This paper presents a stochastic model for the normalized smoothed variation rate individual-activation-factor proportionate normalized least-mean-square (NSVR–IAF–PNLMS) algorithm. Specifically, taking into account correlated Gaussian input data, model expressions are derived for predicting the mean weight vector, gain distribution matrix, NSVR metric, learning curve, weight-error correlation matrix, and steady-state excess mean-square error. Such expressions are obtained by considering the time-varying characteristics of the gain distribution matrix. Simulation results are shown confirming the accuracy of the proposed model for different operating conditions.

1 Introduction

Although the least-mean-square (LMS) and the normalized LMS (NLMS) algorithms have been commonly used in many real-world applications (Sayed 2009; Farhang-Boroujeny 2013; Haykin 2014), these algorithms exhibit slow convergence and poor tracking capability when the plant impulse response is sparse (as compared with other algorithms designed to exploit the sparse nature of the plant) (Martin et al. 2002; Paleologu et al. 2010; Wagner and Doroslovački 2013). For instance, Duttweiler (2000) introduced the proportionate NLMS (PNLMS) algorithm, in which each adaptive coefficient is updated proportionally to its magnitude in order to improve the algorithm convergence speed. Nevertheless, it has been observed that the PNLMS algorithm exhibits slow convergence for plants with low and medium sparseness (Benesty and Gay 2002), and improved convergence characteristics are not preserved over the whole adaptation process (Deng and Doroslovački 2006). So, to overcome the aforementioned problems, several PNLMS-type algorithms have been discussed in the open literature, such as the improved PNLMS (IPNLMS) (Benesty and Gay 2002), the µ-law PNLMS (MPNLMS) (Deng and Doroslovački 2006), the sparseness-controlled PNLMS (SC-PNLMS) (Loganathan et al. 2008), and the individual-activation-factor PNLMS (IAF–PNLMS) (de Souza et al. 2010a).

In particular, the IAF–PNLMS algorithm (de Souza et al. 2010a) presents faster convergence in comparison with other algorithms from the literature for plants with high sparseness. Such an improvement in the convergence speed is due to the use of proportional gain for both active and inactive adaptive coefficients. However, given that gains assigned to active coefficients are maintained high even after achieving the vicinity of their optimal values, inactive coefficients receive very small gain during the whole adaptation process. As a consequence, the fast initial convergence is significantly compromised after the convergence of the active coefficients (de Souza et al. 2012). So, since assigning larger gains to coefficients that reached the vicinity of their optimal values have almost no effect on the convergence of the adaptive filter, Perez et al. (2017) have devised the normalized smoothed variation rate IAF–PNLMS (NSVR–IAF–PNLMS) algorithm. In this algorithm, gain allocated to coefficients that have achieved the vicinity of their optimal values is transferred to other coefficients that have not yet converged, thus enhancing the algorithm convergence and reducing the steady-state misalignment.

A convenient way to provide a theoretical basis for the study of a given adaptive algorithm is through its stochastic model. In the stochastic modeling of adaptive algorithms, the aim is to derive expressions describing (with certain accuracy) the algorithm behavior under different operating conditions (Duttweiler 2000; Rupp 1993; Doroslovački and Deng 2006; Wagner and Doroslovački 2008a, b; Loganathan et al. 2010; de Souza et al. 2010b; Kuhn et al. 2014a; Haddad and Petraglia 2014). So, from the model expressions, cause-and-effect relationships between algorithm parameters and performance metrics can be established, resulting in useful design guidelines (Abadi and Husøy 2009; Kuhn et al. 2014b; Kuhn et al. 2015; Matsuo and Seara 2016). Moreover, model expressions can help in identifying anomalous and/or undesired behavior, allowing to modify the algorithm to circumvent such an issue (Kolodziej et al. 2009). In this context, focusing on the stochastic modeling of the NSVR–IAF–PNLMS algorithm, the present research work has the following goals:

• (i) To obtain a stochastic model for predicting the algorithm behavior considering correlated Gaussian input data and time-varying characteristics of the gain distribution matrix;

• (ii) To provide model expressions describing the mean weight vector, gain distribution matrix, NSVR metric, learning curve, and weight-error correlation matrix;

• (iii) To derive model expressions characterizing the excess mean-square error (EMSE) in steady state and misadjustment; and

• (iv) To assess the accuracy of the model for different operating conditions.

Note that the proposed stochastic model presented here extends the results given in Perez et al. (2017).

This paper is organized as follows. Section 2 describes briefly the system identification setup considered and revisits the NSVR–IAF–PNLMS algorithm. In Sect. 3, based on some assumptions and approximations, the proposed stochastic model is derived and discussed. Section 4 presents simulation results, aiming to assess the accuracy of the proposed model under different operating scenarios. Finally, Sect. 5 presents concluding remarks.

Throughout this paper, the mathematical notation adopted follows the standard practice of using lower-case boldface letters for vectors, upper-case boldface letters for matrices, and both italic Roman and Greek letters for scalar quantities. In addition, superscript T stands for the transpose, ${\text{diag}}( \cdot {\kern 1pt} )$ denotes the diagonal operator, and $E( \cdot )$ characterizes the expected value.

2 Problem Statement

In this section, a brief description of the environment considered in the development of the proposed model is firstly presented. Next, the general expressions describing the NSVR–IAF–PNLMS algorithm are introduced.

2.1 System Identification Setup

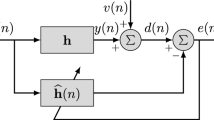
In a system identification setup (as depicted in Fig. 1), the adaptive filter is used to produce an estimate of an unknown system (plant) impulse response (Sayed 2009; Farhang-Boroujeny 2013; Haykin 2014). In this kind of setup, both the plant (system to be identified) ${\mathbf{w}}^{\text{o}}$ and the adaptive filter ${\mathbf{w}}(k)$ are driven by the same input signal $x(k).$ In turn, the plant output signal is corrupted by an additive measurement noise $v(k),$ which results in the desired signal $d(k).$ Thereby, the error signal can be expressed as

$$ \begin{aligned} e(k) & = d(k) - {\mathbf{w}}^{\text{T}} (k)\,{\mathbf{x}}(k) \\ & = [{\mathbf{w}}^{\text{o}} - {\mathbf{w}}(k)]^{\text{T}} \,{\mathbf{x}}(k) + v(k) \\ \end{aligned} $$

(1)

where ${\mathbf{w}}(k) = [w_{1} (k)\;w_{2} (k)\; \cdots \;w_{N} (k)]^{\text{T}}$ characterizes the adaptive coefficient vector, ${\mathbf{w}}^{\text{o}}$ is the plant coefficient vector, and ${\mathbf{x}}(k) = [x(k)\;\;x(k - 1)\; \cdots \;x(k - N + 1)]^{\text{T}}$ denotes the input vector with the $N$ most recent input samples. Note that the order of the adaptive filter and the plant is assumed the same for the sake of simplicity.

Fig. 1

Block diagram of a typical system identification setup

2.2 Revisiting the NSVR–IAF–PNLMS Algorithm

For PNLMS-type algorithms, the coefficient update rule is expressed as (Duttweiler 2000; Benesty and Gay 2002)

$$ {\mathbf{w}}(k + 1) = {\mathbf{w}}(k) + \frac{{\beta \,{\mathbf{G}}(k)\,{\mathbf{x}}(k)\,e(k)}}{{{\mathbf{x}}^{\text{T}} (k)\,{\mathbf{G}}(k)\,{\mathbf{x}}(k) + \xi }} $$

(2)

where $\beta$ denotes the step-size control parameter, $\xi > 0$ is a regularization parameter that prevents division by zero, while

$$ {\mathbf{G}}(k) = {\text{diag[}}g_{1} (k) \, g_{2} (k) \, \cdots \, g_{N} (k)] $$

(3)

represents a diagonal gain distribution matrix. Note that the individual gain governing the step-size adjustment of the ith adaptive filter coefficient is obtained as

$$ g_{i} (k) = \frac{{\gamma_{i} (k)}}{{\sum\limits_{j = 1}^{N} {\gamma_{j} (k)} }},\quad i = 1,2,3, \ldots $$

(4)

with $\gamma_{i} (k)$ characterizing a proportionality function, which is defined in different ways depending on the particulars of the algorithm considered (e.g., see Duttweiler 2000; Benesty and Gay 2002; Deng and Doroslovački 2006; Loganathan et al. 2008; de Souza et al. 2010a).

For the NSVR–IAF–PNLMS algorithm, the proportionality function associated with the ith adaptive filter coefficient is given by (Perez et al. 2017)

$$ \gamma_{i} (k) = \left\{ {\begin{array}{ll}{{\displaystyle{\frac{1}{N}}},} &{V_{i} (k) \le \varepsilon } \\ {\lambda_{i} (k),} & {\text{otherwise}} \end{array} } \right. $$

(5)

where $\varepsilon$ is a convergence threshold parameter,

$$ V_{i} (k) = \left\{ {\begin{array}{ll} {{\displaystyle{\frac{{|Q_{i} (k) - P_{i} (k)|}}{{\text{min} [Q_{i} (k),P_{i} (k)] + \zeta }}}},} & {k = m\Delta ,\;\; m = 1,2,3, \ldots }\\ {V_{i} (k - 1),} &{\text{otherwise}} \end{array} } \right. $$

(6)

with $\zeta > 0$ denoting a regularization parameter,

$$ Q_{i} (k) = \;\sum\limits_{j = 0}^{(\Delta - 2)/2} {|w_{i} (k - j)|} $$

(7)

and

$$ P_{i} (k) = \;\sum\limits_{j = \Delta /2}^{\Delta - 1} {|w_{i} (k - j)|} $$

(8)

in which $\Delta$ defines the number of samples of $w_{i} (k)$ considered to assess the individual-coefficient convergence, while

$$ \lambda_{i} (k) = \hbox{max} [f_{i} (k),\;|w_{i} (k)|] $$

(9)

and

$$ f_{i} (k) = \left\{ {\begin{array}{ll} {{\displaystyle{\frac{1}{2}}}|w_{i} (k)| + {\displaystyle{\frac{1}{2}}}\lambda_{i} (k - 1),} &{k = mN,\;\; m = 1,2,3, \ldots } \\ {f_{i} (k - 1),} & {\text{otherwise}}\end{array} } \right. $$

(10)

arise from the IAF–PNLMS algorithm given in de Souza et al. (2010a).

Notice that (6) characterizes the NSVR metric of the ith adaptive coefficient, which is used to capture the individual-coefficient convergence behavior during the adaptation process [see (7) and (8)]. In turn, ε represents the percentage value of coefficient magnitude variation for which one assumes that the coefficient has reached the vicinity of its optimal value [see (5)]. Then, the value chosen for ε must ensure that gain assigned to adaptive coefficients that have reached the vicinity of their optimal values is transferred to other coefficients that have not yet converged, thus improving the algorithm convergence. Therefore, the choice of ∆ and ε affects the change of the gain distribution policy and, hence, the algorithm performance [typical values for ∆ and ε are discussed in Perez et al. (2017)].

3 Proposed Stochastic Model

To derive the stochastic model of the NSVR–IAF–PNLMS algorithm [given by (1)–(10)], the following simplifying assumptions and approximations are stated:

• (A1) The input signal $x(k)$ is obtained from a zero-mean correlated Gaussian process with variance $\sigma_{x}^{2}$ and autocorrelation matrix ${\mathbf{R}} = E[{\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k)]$ (Sayed 2009; Farhang-Boroujeny 2013; Haykin 2014).

• (A2) Regularization parameters $0 < \xi \ll 1$ and $0 < \zeta \ll 1$ are neglected during the model development for the sake of simplicity (Kuhn et al. 2014c).

• (A3) The measurement noise $v(k)$ is obtained from a zero-mean independent and identically distributed (i.i.d.) Gaussian process with variance $\sigma_{v}^{2} ,$ which is uncorrelated with any other signal (Sayed 2009; Farhang-Boroujeny 2013; Haykin 2014).

• (A4) For slow adaptation (small step size), the adaptive weight vector ${\mathbf{w}}(k)$ and the input vector ${\mathbf{x}}(k)$ are assumed statistically independent (Sayed 2009; Farhang-Boroujeny 2013; Haykin 2014).

• (A5) Due to the piecewise-constant nature of the gain distribution matrix [see (3)–(10)], variables ${\mathbf{G}}(k),$${\mathbf{w}}(k),$ and ${\mathbf{x}}(k)$ are assumed uncorrelated (de Souza et al. 2010b; Kuhn et al. 2014a).

Note that these assumptions and approximations have been commonly used in the stochastic modeling of adaptive algorithms and are required to make the development mathematically tractable.

3.1 Mean Weight Vector

To derive an expression that describes the mean weight vector of the algorithm, let us substitute (1) into (2) and take the expected value of both sides of the resulting expression, which yields

$$ \begin{aligned} E[{\mathbf{w}}(k + 1)] & = E[{\mathbf{w}}(k)] + \beta E\left[ {\frac{{{\mathbf{G}}(k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi }}} \right]{\mathbf{w}}^{\text{o}} \\ & \quad - \beta E\left[ {\frac{{{\mathbf{G}}(k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{w}}(k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi }}} \right] \\ & \quad+ \beta E\left[ {\frac{{{\mathbf{G}}(k){\mathbf{x}}(k)v(k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi }}} \right]. \\ \end{aligned} $$

(11)

Then, taking into account Assumptions (A2)–(A5), (11) can be simplified to

$$ E[{\mathbf{w}}(k + 1)] \cong [{\mathbf{I}} - \beta {\mathbf{R}}_{1} (k) ]E[{\mathbf{w}}(k)] + \beta {\mathbf{R}}_{1} (k){\mathbf{w}}^{\text{o}} $$

(12)

where ${\mathbf{I}}$ denotes the identity matrix and

$$ {\mathbf{R}}_{1} (k) \cong E\left[ {\frac{{{\bar{\mathbf{G}}}(k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k)}}{{{\mathbf{x}}^{\text{T}} (k){\bar{\mathbf{G}}}(k){\mathbf{x}}(k)}}} \right] $$

(13)

in which ${\bar{\mathbf{G}}}(k)$ characterizes the mean gain distribution matrix. Therefore, using the solution presented in Kuhn et al. (2014a) for computing ${\mathbf{R}}_{1} (k)$ [see Assumption (A1)], the behavior of the mean weight vector can be predicted through (12) if the mean gain distribution matrix is known.

3.2 Mean Gain Distribution Matrix

An expression that describes the mean gain distribution matrix can be obtained by taking the expected value of both sides of (3)–(10) and assuming that $E[|w_{i} (k)|] \cong \,|E[w_{i} (k)]|$ (Kuhn et al. 2014a). Thereby,

$$ {\bar{\mathbf{G}}}(k) = {\text{diag}}[\bar{g}_{1} (k)\;\bar{g}_{2} (k)\; \cdots \;\bar{g}_{N} (k)] $$

(14)

in which

$$ \bar{g}_{i} (k) \cong \frac{{E[\gamma_{i} (k)]}}{{\sum\limits_{j = 1}^{N} {E[\gamma_{j} (k)]} }} $$

(15)

with

$$ E[\gamma_{i} (k)] \cong \left\{ {\begin{array}{ll} {{\displaystyle{\frac{1}{N}}},}& {E[V_{i} (k)] \le \varepsilon } \\ {E[\lambda_{i} (k)],} &{\text{otherwise}} \end{array} } \right. $$

(16)

where

$$ E[\lambda_{i} (k)] \cong \hbox{max} \{ E[f_{i} (k)],\;|E[w_{i} (k)]|\} $$

(17)

and

$$ \begin{aligned} & E[f_{i} (k)] \\ & \cong \left\{ {\begin{array}{ll} {{\displaystyle{\frac{1}{2}}}|E[w_{i} (k)]| + {\displaystyle{\frac{1}{2}}}E[\lambda_{i} \,(k - 1)],} &{k = mN,\;\; m = 1,2,3, \ldots } \\ {E[f_{i} (k - 1)],}&{{\text{otherwise}} .} \end{array} } \right. \end{aligned} $$

(18)

So, considering (12), the evolution of the mean gain distribution matrix can be predicted through (14)–(18) if the mean behavior of the NSVR metric is known.

3.3 Mean Behavior of the NSVR Metric

Aiming to determine an expression that describes the evolution of the NSVR metric $V_{i} (k)$ for active coefficients, let us start by taking the expected value of both sides of (6) along with Assumption (A2), i.e.,

$$ \begin{aligned} & E[V_{i} (k)] \\ &\quad\cong \left\{ {\begin{array}{ll} {E\left[ {{\displaystyle{\frac{{|Q_{i} (k) - P_{i} (k)|}}{{\text{min} [Q_{i} (k),P_{i} (k)]}}}}} \right],} &{k = m\Delta ,\;\; m = 1,2, \ldots }\\ {E[V_{i} (k - 1)],}&{{\text{otherwise}} .} \end{array} } \right. \end{aligned} $$

(19)

Next, considering that the numerator varies slowly with respect to the denominator in such a way that the averaging principle (AP) (Samson and Reddy 1983) can be invoked, one gets

$$ E\left[ {\frac{{|Q_{i} (k) - P_{i} (k)|}}{{\text{min} [Q_{i} (k),P_{i} (k)]}}} \right] \cong \frac{{E[|Q_{i} (k) - P_{i} (k)|]}}{{E\{ \text{min} [Q_{i} (k),P_{i} (k)]\} }}. $$

(20)

Also, assuming that coefficients hold the same algebraic sign during the whole adaptation process, (20) becomes

$$ E\left[ {\frac{{|Q_{i} (k) - P_{i} (k)|}}{{\text{min} [Q_{i} (k),P_{i} (k)]}}} \right] \cong \frac{{|E[Q_{i} (k)] - E[P_{i} (k)]|}}{{\text{min} \{ E[Q_{i} (k)],E[P_{i} (k)]\} }}. $$

(21)

Finally, substituting (21) into (19), the mean behavior of the NSVR for the ith (active) adaptive coefficient can be approximated to

$$ \begin{aligned} & E[V_{i} (k)] \\ & \cong \left\{ {\begin{array}{ll} {{\displaystyle{\frac{{|E[Q_{i} (k)] - E[P_{i} (k)]|}}{{\text{min} \{ E[Q_{i} (k)],E[P_{i} (k)]\} }}}},} &{k = m\Delta ,\;\; m = 1,2,3, \ldots }\\ {E[V_{i} (k - 1)],} &{\text{otherwise}}\end{array} } \right. \end{aligned} $$

(22)

with

$$ E[Q_{i} (k)] \cong \sum\limits_{j = 0}^{(\Delta - 2)/2} {|E[w_{i} (k - j)} ]| $$

(23)

and

$$ E[P_{i} (k)] \cong \sum\limits_{j = \Delta /2}^{\Delta - 1} {|E[w_{i} (k - j)} ]| $$

(24)

obtained by taking the expected value of both sides of (7) and (8), respectively. Thereby, using (12), the mean behavior of the NSVR metric can be predicted from (22) to (24).

3.4 Learning Curve

An expression that describes the algorithm learning curve [mean-square error (MSE)] can be derived by rewriting (1) in terms of the weight-error vector

$$ {\mathbf{z}}(k) = {\mathbf{w}}(k) - {\mathbf{w}}^{\text{o}} $$

(25)

as

$$ e(k) = - {\mathbf{z}}^{\text{T}} (k)\,{\mathbf{x}}(k) + v(k) $$

(26)

determining $e^{2} (k),$ taking the expected value of both sides of the resulting expression, and considering Assumptions (A3) and (A4) (Sayed 2009; Farhang-Boroujeny 2013; Haykin 2014). Thus,

$$ \begin{aligned} J(k) &= E[e^{2} (k)] \\ &= J_{\text{min} } + J_{\text{ex}} (k) \\ \end{aligned} $$

(27)

where

$$ J_{\text{min} } = \sigma_{v}^{2} $$

(28)

denotes the minimum MSE, while

$$ J_{\text{ex}} (k) = {\text{tr}}[{\mathbf{RK}}(k)] $$

(29)

characterizes the excess MSE (EMSE). Note in (29) that the weight-error correlation matrix is defined as

$$ {\mathbf{K}}(k) = E[{\mathbf{z}}(k){\mathbf{z}}^{\text{T}} (k)]. $$

(30)

Therefore, the learning curve (MSE) can be predicted through (27)–(29) if the weight-error correlation matrix is known.

3.5 Weight-Error Correlation Matrix

Since the expression that describes the behavior of the algorithm learning curve requires knowledge of the weight-error covariance matrix, a recursive expression characterizing the evolution of ${\mathbf{K}}(k)$ is derived now. To this end, using (2) and (26), the weight update equation is first rewritten in terms of the weight-error vector ${\mathbf{z}}(k)$ [defined in (25)] as

$$ \begin{aligned} & {\mathbf{z}}(k + 1) = \\ & \quad {\mathbf{z}}(k) - \beta \frac{{{\mathbf{G}}(k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{z}}(k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi }} + \beta \frac{{{\mathbf{G}}(k){\mathbf{x}}(k)v(k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi }}. \\ \end{aligned} $$

(31)

Then, determining ${\mathbf{z}}(k + 1){\mathbf{z}}^{\text{T}} (k + 1),$ taking the expected value of both sides of the resulting expression, and considering (30), one obtains

$$ \begin{aligned} & {\mathbf{K}}(k + 1)\\ &\quad = {\mathbf{K}}(k) - \beta E\left[ {\frac{{{\mathbf{z}}(k){\mathbf{z}}^{\text{T}} (k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi }}} \right] \\ & \quad - \,\beta E\left[ {\frac{{{\mathbf{G}}(k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{z}}(k){\mathbf{z}}^{\text{T}} (k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi }}} \right] \\ & \quad - \,\beta^{2} E\left\{ {\frac{{v(k){\mathbf{G}}(k){\mathbf{x}}(k){\mathbf{z}}^{\text{T}} (k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k)}}{{[{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi ]^{2} }}} \right\} \\ & \quad + \,\beta^{2} E\left[ {\frac{{v(k){\mathbf{G}}(k){\mathbf{x}}(k){\mathbf{z}}^{\text{T}} (k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi }}} \right] \\ & \quad - \,\beta^{2} E\left\{ {\frac{{v(k){\mathbf{G}}(k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{z}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k)}}{{[{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi ]^{2} }}} \right\} \\ & \quad + \,\beta^{2} E\left\{ {\frac{{v^{2} (k){\mathbf{G}}(k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k)}}{{[{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi ]^{2} }}} \right\} \\ & \quad + \,\beta^{2} E\left\{ {\frac{{{\mathbf{G}}(k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{z}}(k){\mathbf{z}}^{\text{T}} (k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k)}}{{[{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi ]^{2} }}} \right\} \\ & \quad + \,\beta^{2} E\left[ {\frac{{v(k){\mathbf{z}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi }}} \right]. \\ \end{aligned} $$

(32)

Finally, due to the statistical characteristics of the measurement noise [see Assumption (A3)], all terms involving $v(k)$ in (32) are equal to zero, except that with $v^{2} (k).$ Additionally, using Assumptions (A2)–(A5), (32) reduces to

$$ \begin{aligned} {\mathbf{K}}(k + 1) &\cong {\mathbf{K}}(k) - \beta {\mathbf{K}}(k){\mathbf{R}}_{1}^{\text{T}} (k) - \beta {\mathbf{R}}_{1} (k){\mathbf{K}}(k) \\ & \quad + \beta^{2} J_{\text{min} } {\mathbf{R}}_{2} (k) + \beta^{2} {\mathbf{R}}_{3} (k) \\ \end{aligned} $$

(33)

with

$$ {\mathbf{R}}_{2} (k) \cong E\left[ {\frac{{{\bar{\mathbf{G}}}(k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\bar{\mathbf{G}}}(k)}}{{[{\mathbf{x}}^{\text{T}} (k){\bar{\mathbf{G}}}(k){\mathbf{x}}(k)]^{2} }}} \right] $$

(34)

and

$$ {\mathbf{R}}_{3} (k) \cong E\left[ {\frac{{{\bar{\mathbf{G}}}(k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\mathbf{K}}(k){\mathbf{x}}(k){\mathbf{x}}^{\text{T}} (k){\bar{\mathbf{G}}}(k)}}{{[{\mathbf{x}}^{\text{T}} (k){\bar{\mathbf{G}}}(k){\mathbf{x}}(k)]^{2} }}} \right]. $$

(35)

So, using the solutions presented in Kuhn et al. (2014a) for computing ${\mathbf{R}}_{1} (k),$${\mathbf{R}}_{2} (k),$ and ${\mathbf{R}}_{3} (k)$ [see Assumption (A1)], along with (14)–(24), the evolution of the weight-error correlation matrix can now be predicted through (33); consequently, the algorithm learning curve can also be predicted from (27).

3.6 Steady-State Analysis

Based on energy-conservation arguments (Sayed 2009), an expression characterizing the steady-state EMSE $J_{\text{ex}} (\infty )$ can be derived by rewriting (2) in terms of the weight-error vector ${\mathbf{z}}(k)$ [defined in (25)], which results in

$$ {\mathbf{z}}(k + 1) = {\mathbf{z}}(k) + \beta \frac{{{\mathbf{G}}(k){\mathbf{x}}(k)e(k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi }}. $$

(36)

Then, calculating ${\mathbf{z}}^{\text{T}} (k + 1){\mathbf{G}}^{ - 1} (k){\mathbf{z}}(k + 1)$ from (36), i.e.,

$$ \begin{aligned} & {\mathbf{z}}^{\text{T}} (k + 1){\mathbf{G}}^{ - 1} (k){\mathbf{z}}(k + 1) = {\mathbf{z}}^{\text{T}} (k){\mathbf{G}}^{ - 1} (k){\mathbf{z}}(k) \\ & \quad + 2\beta \frac{{{\mathbf{z}}^{\text{T}} (k){\mathbf{x}}(k)e(k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi }} + \beta^{2} \frac{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k)e^{2} (k)}}{{[{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k) + \xi ]^{2} }} \\ \end{aligned} $$

(37)

taking the expected value of both sides, letting $k \to \infty ,$ assuming convergence, considering (26), as well as Assumptions (A2) and (A3), the following variance relation is obtained:

$$ 2\mathop {\lim }\limits_{k \to \infty } E\left\{ {\frac{{[{\mathbf{z}}^{\text{T}} (k){\mathbf{x}}(k)]^{2} }}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k)}}} \right\} = \beta \mathop {\lim }\limits_{k \to \infty } E\left[ {\frac{{e^{2} (k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k)}}} \right]. $$

(38)

Now, recalling the definition of the EMSE [given in (29)], taking into account Assumptions (A4) and (A5), as well as assuming that $M$ is large in such a way that the AP (Samson and Reddy 1983) can be used, the left-hand side term of (38) is approximated by

$$ \mathop {\lim }\limits_{k \to \infty } E\left\{ {\frac{{[{\mathbf{z}}^{\text{T}} (k){\mathbf{x}}(k)]^{2} }}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k)}}} \right\} \cong \frac{{J_{\text{ex}} (\infty )}}{{{\text{tr}}[{\mathbf{R}}{\bar{\mathbf{G}}}(\infty )]}} $$

(39)

with

$$ {\bar{\mathbf{G}}}(\infty ) = \,\mathop {\lim }\limits_{k \to \infty } E[{\mathbf{G}}(k)] $$

(40)

denoting the mean gain distribution matrix in steady state. Similarly, using (26), (28), (29), and (40), along with Assumptions (A3)–(A5), the right-hand side term of (38) is simplified to

$$ \mathop {\lim }\limits_{k \to \infty } E\left[ {\frac{{e^{2} (k)}}{{{\mathbf{x}}^{\text{T}} (k){\mathbf{G}}(k){\mathbf{x}}(k)}}} \right] \cong \frac{{J_{\text{ex}} (\infty )}}{{{\text{tr}}[{\mathbf{R}}{\bar{\mathbf{G}}}(\infty )]}} + J_{ \text{min} } E_{1} (\infty ) $$

(41)

where

$$ \,E_{1} (\infty ) = E\left[ {\frac{1}{{{\mathbf{x}}^{\text{T}} (k){\bar{\mathbf{G}}}(\infty ){\mathbf{x}}(k)}}} \right]. $$

(42)

So, substituting (39) and (41) into (38), and solving the resulting expression for $J_{\text{ex}} (\infty ),$ the steady-state EMSE is obtained according to

$$ J_{\text{ex}} (\infty ) \cong \frac{\beta }{(2 - \beta )}J_{\text{min} } \,{\text{tr[}}{\mathbf{R}}{\bar{\mathbf{G}}}(\infty ) ]\,E_{1} (\infty ). $$

(43)

Finally, to determine the steady-state behavior of the mean gain distribution matrix ${\bar{\mathbf{G}}}(\infty )$ [required in (42) and (43)], let $k \to \infty$ of both sides of (15) in such a way that

$$ \bar{g}_{i} (\infty ) \cong \frac{{E[\gamma_{i} (\infty )]}}{{\sum\limits_{j = 1}^{N} {E[\gamma_{j} (\infty )]} }} $$

(44)

with

$$ E[\gamma_{i} (\infty )] = \mathop {\lim }\limits_{k \to \infty } E[\gamma_{i} (k)]. $$

(45)

Note from (45) that knowledge of the mean value of the proportionality function in steady state is required. Then, recalling from (22) to (24) that

$$ \mathop {\lim }\limits_{k \to \infty } E[V_{i} (k)] \to 0 $$

(46)

since the adaptive coefficients do not change significantly as the algorithm tends to the steady state, it can be verified [from (16)] that

$$ \mathop {\lim }\limits_{k \to \infty } E[\gamma_{i} (k)] \to \frac{1}{N\,}. $$

(47)

Consequently, the mean gain distribution matrix in steady state reduces to

$$ {\bar{\mathbf{G}}}(\infty ) \cong \frac{1}{N}{\mathbf{I}}. $$

(48)

Therefore, using the solution presented in Kuhn et al. (2014b) for computing $E_{1} (\infty )$ [see Assumption (A1)], along with the expression characterizing the mean gain distribution matrix in steady state ${\bar{\mathbf{G}}}(\infty )$ [given by (48)], the steady-state EMSE can be predicted through (43); likewise, the misadjustment can be straightforwardly determined.

4 Simulation Results

To verify the accuracy of the proposed model, three examples are presented considering distinct operating scenarios in a system identification setup. In these examples, the results obtained from Monte Carlo (MC) simulations (average of 200 independent runs) are compared with those predicted through the proposed stochastic model. The zero-mean and unit variance Gaussian input signal $x(k)$ [see Assumption (A1)] is obtained from (Haykin 2014)

$$ x(k) = - a_{1} x(k - 1) - a_{2} x(k - 2) + \eta (k) $$

(49)

where $a_{1}$ and $a_{2}$ denote the AR(2) coefficients, and $\eta (k)$ is a white Gaussian noise with variance

$$ \sigma_{\eta }^{2} = \left( {\frac{{1 - a_{2} }}{{1 + a_{2} }}} \right)[(1 + a_{2} )^{2} - a_{1}^{2} ]. $$

(50)

The signal-to-noise ratio (SNR) is defined here as

$$ {\text{SNR}} = 10\log_{10} \left( {\frac{{\sigma_{x}^{2} }}{{\sigma_{v}^{2} }}} \right). $$

(51)

Two plants ${\mathbf{w}}_{\text{A}}^{\text{o}}$ and ${\mathbf{w}}_{\text{B}}^{\text{o}}$ (with $N = 128$ weights) obtained from echo-path models for testing of speech echo cancellers defined in the (ITU-T Recommendation G.168 2009, Models 1 and 4) are used. (Note that ${\mathbf{w}}_{\text{A}}^{\text{o}}$ has been formed by zero padding the echo-path model.) Sparseness degrees (Hoyer 2004) of such plants are $S({\mathbf{w}}_{\text{A}}^{\text{o}} ) = 0.78$ and $S({\mathbf{w}}_{\text{B}}^{\text{o}} ) = 0.42,$ respectively. Unless otherwise stated, parameter values of the algorithm are $\beta = 0.01,$$\xi = 10^{ - 6} ,$$f_{i} (0) = \lambda_{i} (0) = 10^{ - 4} ,$$\Delta = N,$$\varepsilon = 10^{ - 2} ,$ and $\zeta = 10^{ - 4} ,$ while ${\mathbf{w}}(0) = {\mathbf{0}}$ and $V_{i} (0) = 0.$ Still, to ensure the stability in the computation of ${\mathbf{R}}_{1} (k),$${\mathbf{R}}_{2} (k),$${\mathbf{R}}_{3} (k),$ and $E_{1} (\infty ),$ the threshold value used for discarding less significant eigenvalues is $5 \times 10^{ - 4}$ (Kuhn et al. 2014a).

4.1 Example 1

Here, the accuracy of the model expressions characterizing the mean weight vector (12), NSVR metric (22), and the algorithm learning curve (27) is assessed for different input data correlation levels. To this end, we consider plant ${\mathbf{w}}_{\text{A}}^{\text{o}}$$[S({\mathbf{w}}_{\text{A}}^{\text{o}} ) = 0.78]$ and 30 dB SNR. The eigenvalue spread values¹ of the input autocorrelation matrix are $\chi = 71.71$ [obtained from (49) for $a_{1} = - 0.75$ and $a_{2} = 0.68]$ and $\chi = 338.23$ [obtained from (49) by changing $a_{2}$ to 0.85]. Figure 2 shows the results obtained by MC simulations and predicted through the proposed model. Specifically, Fig. 2a, b depicts the mean behavior of four adaptive weights (for the sake of clarity). Figure 2c, d illustrates the evolution of the NSVR metric for one active coefficient. Figure 2e, f presents the algorithm learning curve (MSE). Notice from these figures that the proposed model satisfactorily predicts the algorithm behavior for both transient and steady-state phases, irrespective of the input data correlation level considered. This result also confirms the accuracy of the methodology used for computing the normalized autocorrelation-like matrices ${\mathbf{R}}_{1} (k),$${\mathbf{R}}_{2} (k),$ and ${\mathbf{R}}_{3} (k).$

Fig. 2

Example 1: Algorithm behavior obtained by MC simulations (gray-ragged lines) and through the proposed model (dark-solid lines) considering $\chi = 71.71$ (left) and $\chi = 338.23$ (right). a, b Mean weight behavior of four adaptive coefficients. c, d Evolution of the NSVR metric associated with coefficient $w_{7} (k).$e, f Learning curve

4.2 Example 2

This example verifies the accuracy of the proposed model (via learning curve) for plants with different sparseness degrees and two distinct SNR values. For this operating scenario, plants ${\mathbf{w}}_{\text{A}}^{\text{o}}$$[S({\mathbf{w}}_{\text{A}}^{\text{o}} ) = 0.78]$ and ${\mathbf{w}}_{\text{B}}^{\text{o}}$$[S({\mathbf{w}}_{\text{B}}^{\text{o}} ) = 0.42]$ are used, considering 20 and 30 dB SNR. The input signal is obtained from (49) with $a_{1} = - 0.75$ and $a_{2} = 0.75,$ which yields an eigenvalue spread of $\chi = 120.25$ for the input autocorrelation matrix. Figure 3 depicts the results obtained through MC simulations and from model predictions. Specifically, Fig. 3a shows the results obtained for plant ${\mathbf{w}}_{\text{A}}^{\text{o}}$$[S({\mathbf{w}}_{\text{A}}^{\text{o}} ) = 0.78],$ while Fig. 3b for plant ${\mathbf{w}}_{\text{B}}^{\text{o}}$$[S({\mathbf{w}}_{\text{B}}^{\text{o}} ) = 0.42].$ From these figures, very good match between MC simulations and model predictions can also be verified for both transient and steady-state phases, irrespective of the plant sparseness degrees and SNR values considered.

Fig. 3

Example 2: Learning curves (MSE) obtained by MC simulations (gray-ragged lines) and through the proposed model (dark-solid lines). a Plant ${\mathbf{w}}_{\text{A}}^{\text{o}}$$[S({\mathbf{w}}_{\text{A}}^{\text{o}} ) = 0.78].$b Plant ${\mathbf{w}}_{\text{B}}^{\text{o}}$$[S({\mathbf{w}}_{\text{B}}^{\text{o}} ) = 0.42]$

4.3 Example 3

In this last example, considering plants with different sparseness degrees and a wide range of SNR values, the accuracy of the model expressions characterizing the steady-state EMSE (43) is assessed for step-size values ranging from 0.01 to 1.96. To this end, we consider plants ${\mathbf{w}}_{\text{A}}^{\text{o}}$$[S({\mathbf{w}}_{\text{A}}^{\text{o}} ) = 0.78]$ and ${\mathbf{w}}_{\text{B}}^{\text{o}}$$[S({\mathbf{w}}_{\text{B}}^{\text{o}} ) = 0.42],$ as well as four different SNR values (i.e., 10, 20, 30, and 40 dB SNR). The remaining parameter values are the same as in Example 2. [Note also that the last 100 EMSE values in steady state have been averaged to provide a better visualization of the experimental results obtained from MC simulations (Sayed 2009, pp. 250).] Figure 4 shows the steady-state EMSE curves obtained by MC simulations along with those predicted from the model expressions. Specifically, Fig. 4a illustrates the results obtained for plant ${\mathbf{w}}_{\text{A}}^{\text{o}}$$[S({\mathbf{w}}_{\text{A}}^{\text{o}} ) = 0.78],$ while Fig. 4b for plant ${\mathbf{w}}_{\text{B}}^{\text{o}}$$[S({\mathbf{w}}_{\text{B}}^{\text{o}} ) = 0.42].$ Observe from such figures that the proposed model predicts very well the steady-state algorithm behavior for a wide range of step-size values, irrespective of the plant sparseness degrees and SNR values considered.

Fig. 4

Example 3: Steady-state EMSE obtained by MC simulations (gray-cross marker) and through the proposed model (dark-solid lines). a Plant ${\mathbf{w}}_{\text{A}}^{\text{o}}$$[S({\mathbf{w}}_{\text{A}}^{\text{o}} ) = 0.78].$b Plant ${\mathbf{w}}_{\text{B}}^{\text{o}}$$[S({\mathbf{w}}_{\text{B}}^{\text{o}} ) = 0.42]$

5 Concluding Remarks

In this paper, considering correlated Gaussian input data, a stochastic model was obtained for the NSVR–IAF–PNLMS algorithm. Specifically, we derived expressions describing the mean weight vector, gain distribution matrix, NSVR metric, learning curve, weight-error correlation matrix, and steady-state EMSE. To this end, a reduced number of assumptions were used, leading to expressions that predict satisfactorily both the algorithm transient and steady-state phases. Simulation results confirmed the accuracy of the model for different operating conditions, i.e., covering different plants, SNR and step-size values, and several eigenvalue spreads. Note that the methodology discussed here can be extended to other PNLMS-type algorithms from the literature.