1 Introduction

Nowadays, adaptive filtering techniques have been used in a large variety of real-world applications such as adaptive control, noise and echo cancelation, channel equalization, and adaptive beamforming [4, 6, 7, 13,14,15, 34]. These applications often require the use of an adaptive filter to obtain (in real-time) an approximate input–output relationship representation of an unknown system (to be identified). Such adaptive filter uses an algorithm responsible for adjusting the weights of a filtering structure in order to optimize a given performance measure [13,14,15, 34]. Among the existing adaptive algorithms, the least-mean-square (LMS) [40, 41] and normalized LMS (NLMS) [3, 20, 30] are well-established and have been extensively used in practical applications, due mainly to their low computational complexity and numerical robustness. Nevertheless, the adjustment of the step-size parameter in these algorithms raises a crucial tradeoff between convergence speed and steady-state performance.

Aiming to address this tradeoff, an approach from the practical point-of-view is given by variable step-size algorithms [2, 9, 11, 17, 24, 25, 28, 35, 37, 39, 42, 43]. These algorithms make use of strategies for adjusting the step-size value during adaptation, by starting with a large step size (within the stability conditions) that allows for faster initial convergence, and then gradually reducing it (slowing down the convergence speed) for achieving smaller error in steady state. Among such algorithms, the nonparametric variable step-size NLMS (NP-VSS-NLMS) [9] exhibits interesting convergence and steady-state characteristics when compared to others from the literature [10], which makes it suitable for different practical applications. However, to the best of our knowledge, the performance and robustness of this algorithm have been assessed only through Monte Carlo (MC) simulations and through model expressions derived under very strong simplifying assumptions.

In this context, a stochastic model serves as a convenient tool for supporting a more rigorous and comprehensive theoretical analysis of an adaptive algorithm. Based on such a model, the behavior of an algorithm can be predicted (through model expressions) under different operating conditions, facilitating the identification of anomalous behavior, cause-and-effect relationships between parameters and performance metrics, as well as design guidelines for parameter tuning (for further details, see [1, 21,22,23, 26, 27, 32, 33]). So, focusing on the NP-VSS-NLMS [9] algorithm, the goals of this research work are:

  1. (i)

    to derive a stochastic model for the algorithm, considering a system identification problem and Gaussian input data;

  2. (ii)

    to obtain expressions for predicting the mean weight behavior, the evolution of the variable step-size parameter, learning curves, as well as some correlation-like matrices;

  3. (iii)

    to investigate the algorithm behavior in steady state based on the model expressions derived;

  4. (iv)

    to assess the model’s accuracy and algorithm characteristics for different operating conditions; and

  5. (v)

    to provide performance comparisons against other recent and relevant variable step-size algorithms from the literature.

The remainder of this paper is organized as follows. Section 2 introduces the problem formulation, revisiting the NP-VSS-NLMS algorithm and the operating scenario considered. Section 3 presents the proposed model, including assumptions, mathematical development, and design guidelines. Section 4 shows simulation results assessing the model’s accuracy and the algorithm’s performance. Section  5 presents concluding remarks and suggestions for future research works.

Throughout this paper, the adopted mathematical notation follows the standard practice of using lower-case boldface letters for vectors, upper-case boldface letters for matrices, and both italic Roman and Greek letters for scalar quantities. Superscript \((\,\cdot \,)^{\textrm{T}}\) stands for the transpose operator, \(\textrm{Tr}(\,\cdot \,)\) characterizes the trace operator, while \(\textrm{E}(\,\cdot \,)\) denotes the expected value, and \(\textrm{P}(\,\cdot \,)\) represents the probability of a random event.

2 Problem Formulation

Considering a system identification problem (see the block diagram shown in Fig. 1) [13,14,15, 34], let us assume that the output signal y(n) of the system to be identified, which is corrupted by the measurement noise v(n), can be expressed as

$$\begin{aligned} \begin{aligned} d(n)&= y(n) + v(n)\\&= {\textbf{h}}^\textrm{T}{\textbf{x}}(n) + v(n) \end{aligned} \end{aligned}$$
(1)

where \({\textbf{h}}\) denotes an L-dimensional (unknown) system impulse response, and

$$\begin{aligned} {\textbf{x}}(n) = [x(n)\,\, x(n-1) \,\, \cdots \,\,x(n-L+1)]^\textrm{T} \end{aligned}$$
(2)

is a vector containing the L most recent time samples of the input signal x(n). Then, consider that the NP-VSS-NLMS [9] algorithm is used to update the adaptive filter weight vector \(\widehat{{\textbf{h}}}(n)\) (of length L), through

$$\begin{aligned} \widehat{{\textbf{h}}}(n) = \widehat{{\textbf{h}}}(n-1) + \mu (n) \frac{{\textbf{x}}(n) e(n)}{\delta + {\textbf{x}}^\textrm{T}(n){\textbf{x}}(n)} \end{aligned}$$
(3)

with the error signal given by

$$\begin{aligned} e(n) = d(n) - \widehat{{\textbf{h}}}^\textrm{T}(n-1){\textbf{x}}(n) \end{aligned}$$
(4)

and the step-size adjustment rule by

$$\begin{aligned} \mu (n) = {\left\{ \begin{array}{ll} 1 - \dfrac{\widehat{\sigma }_v}{\zeta + \widehat{\sigma }_e(n)}, &{}\widehat{\sigma }_e(n) \ge \widehat{\sigma }_v \\ 0, &{}\textrm{otherwise} \end{array}\right. } \end{aligned}$$
(5)

where \(\widehat{\sigma }_v^2\) denotes an estimate of the measurement noise variance, while

$$\begin{aligned} \widehat{\sigma }_e^2(n) = \kappa \widehat{\sigma }_e^2(n-1) + (1-\kappa )e^2(n) \end{aligned}$$
(6)

is an estimate of the error signal variance with parameter \(0\ll \kappa <1\) representing a forgetting factor. Note, in (3) and (6), that \(\delta \) and \(\zeta \) are the regularization parameters. Therefore, based on the setup described here, the proposed stochastic model can now be developed.

Fig. 1
figure 1

Block diagram of a system identification problem

Full size image

3 Proposed Model

Here, the proposed model describing the behavior of the NP-VSS-NLMS [9] algorithm is derived, which includes expressions for predicting the mean weight behavior, the evolution of the variable step-size parameter, learning curves, some correlation-like matrices related to the input data and weight-error vector, as well as analytical expressions characterizing the variable step size and MSE in steady state. Based on such expressions, some interesting characteristics of the algorithm behavior are further discussed, aiming to provide useful design guidelines. To this end, one considers the following commonly used assumptions and approximations to make the mathematical development tractable [13,14,15, 22, 23, 26, 27, 33, 34]:

  1. (A1)

    The input data are obtained through a real-valued Gaussian process with zero mean, variance \(\sigma _x^2\), and autocorrelation matrix \({\textbf{R}} = \textrm{E}[{\textbf{x}}(n){\textbf{x}}^\textrm{T}(n)]\).

  2. (A2)

    The measurement noise v(n) is obtained through a white Gaussian process of zero mean and variance \(\sigma _v^2\).

  3. (A3)

    The adaptive weight vector \(\widehat{{\textbf{h}}}(n)\) is considered independent of any other variable in the system.

  4. (A4)

    The variable step-size parameter \(\mu (n)\) is considered independent of any other variable in the system.

  5. (A5)

    The parameters \(\delta \) and \(\zeta \) are considered small, so their effect can be neglected.

These assumptions and approximations yield satisfactory results as shown later in Sect. 4.

3.1 Mean Weight Behavior

Substituting (1) and (4) into (3), applying the expected value, and using Assumptions (A2)–(A5) to simplify the resulting expression, we get

$$\begin{aligned} \textrm{E}[\widehat{{\textbf{h}}}(n)] = \{{\textbf{I}} - \textrm{E}[\mu (n)]{\textbf{R}}_1\}\textrm{E}[\widehat{{\textbf{h}}}(n-1)] + \textrm{E}[\mu (n)]{\textbf{R}}_1{\textbf{h}} \end{aligned}$$
(7)

where \(\mathrm {{\textbf {I}}}\) is an \(L \times L\) identity matrix, \(\textrm{E}[\mu (n)]\) characterizes the mean behavior of the variable step size, and [32]

$$\begin{aligned} {\textbf{R}}_1 = \textrm{E}\left[ \frac{{\textbf{x}}(n){\textbf{x}}^\textrm{T}(n)}{{\textbf{x}}^\textrm{T}(n){\textbf{x}}(n)}\right] . \end{aligned}$$
(8)

So, using the results presented in [23, Appendix A] for computing the normalized correlation-like matrix \({\textbf{R}}_1\) vis-à-vis (uncorrelated and correlated) Gaussian input data, the mean weight behavior of the adaptive filter can be predicted through (7) if \(\textrm{E}[\mu (n)]\) is known.

3.2 Learning Curves

Rewriting (4) in terms of the weight-error vector:

$$\begin{aligned} {\textbf{v}}(n) = {\textbf{h}} - \widehat{{\textbf{h}}}(n) \end{aligned}$$
(9)

as

$$\begin{aligned} e(n) = {\textbf{v}}^\textrm{T}(n-1){\textbf{x}}(n) + v(n) \end{aligned}$$
(10)

calculating \(e^2(n)\), applying the expected value, and using Assumption (A3), the following expression is obtained for predicting the evolution of the mean-square error (MSE) [13,14,15, 34]:

$$\begin{aligned} J(n) =J_{\textrm{min}} + J_{\textrm{ex}}(n) \end{aligned}$$
(11)

with the minimum MSE given by

$$\begin{aligned} J_{\textrm{min}} = \sigma _v^2 \end{aligned}$$
(12)

and the excess MSE (EMSE) by

$$\begin{aligned} \begin{aligned} J_{\textrm{ex}}(n)&= \textrm{Tr}[{\textbf{R}}{\textbf{K}}(n-1)]\\&= \varvec{\lambda }^\textrm{T}{\textbf{k}}^\prime (n-1) \end{aligned} \end{aligned}$$
(13)

where vector \(\varvec{\lambda }\) contains the eigenvalues arising from the eigendecomposition \({\textbf{R}}={\textbf{Q}}\varvec{\Lambda }{\textbf{Q}}^\textrm{T}\) [13,14,15, 34],

$$\begin{aligned} {\textbf{K}}(n) = \textrm{E}[{\textbf{v}}(n){\textbf{v}}^\textrm{T}(n)] \end{aligned}$$
(14)

denotes the autocorrelation matrix of the weight-error vector, while \({\textbf{k}}^\prime (n)\) represents a vector containing the diagonal elements of \({\textbf{K}}^\prime (n) = {\textbf{Q}}^\textrm{T} {\textbf{K}}(n) {\textbf{Q}}\). Note that the mean-square deviation (MSD) [13,14,15, 34] can be straightforwardly determined [from (9)] as

$$\begin{aligned} m(n) = \textrm{Tr}[{\textbf{K}}(n)]. \end{aligned}$$
(15)

Therefore, based on (11)–(13) and (15), the (MSE, EMSE, and MSD) learning curves can be predicted if \({\textbf{k}}^\prime (n)\) is known.

3.3 Weight-Error Autocorrelation Matrix

Subtracting \({\textbf{h}}\) from both sides of (3), considering (9) and (10), determining \({\textbf{v}}(n){\textbf{v}}^\textrm{T}(n)\), taking the expected value, using (14), and applying Assumptions (A2)–(A5) to simplify both sides of the resulting expression, one gets

$$\begin{aligned} \begin{aligned} {\textbf{K}}(n)&= {\textbf{K}}(n-1) - \textrm{E}[\mu (n)][{\textbf{K}}(n-1){\textbf{R}}_1+{\textbf{R}}_1{\textbf{K}}(n-1)]\\&~~~+ \textrm{E}[\mu ^2(n)]{\textbf{R}}_2(n) + \textrm{E}[\mu ^2(n)]{\textbf{R}}_3\sigma _v^2 \end{aligned} \end{aligned}$$
(16)

with the normalized correlation-like matrices \({\textbf{R}}_2(n)\) and \({\textbf{R}}_3(n)\) [32] given as

$$\begin{aligned} {\textbf{R}}_2(n) = \textrm{E}\left\{ \frac{{\textbf{x}}(n){\textbf{x}}^\textrm{T}(n){\textbf{K}}(n-1){\textbf{x}}(n){\textbf{x}}^\textrm{T}(n)}{[{\textbf{x}}^\textrm{T}(n){\textbf{x}}(n)]^2}\right\} \end{aligned}$$
(17)

and

$$\begin{aligned} {\textbf{R}}_3 = \textrm{E}\left\{ \frac{{\textbf{x}}(n){\textbf{x}}^\textrm{T}(n)}{[{\textbf{x}}^\textrm{T}(n){\textbf{x}}(n)]^2}\right\} . \end{aligned}$$
(18)

Then, pre- and post-multiplying (16) by \({\textbf{Q}}^\textrm{T}\) and \({\textbf{Q}}\), respectively, taking the diagonal elements, and considering the results presented in [22] for computing \({\textbf{R}}_1\), \({\textbf{R}}_2\), and \({\textbf{R}}_3\), we obtain

$$\begin{aligned} {\textbf{k}}^\prime (n) = \{ {\textbf{I}} - 2\textrm{E}[\mu (n)]{\textbf{H}} + \textrm{E}[\mu ^2(n)](2{\textbf{T}} + {\textbf{P}})\}{\textbf{k}}^\prime (n-1) + \textrm{E}[\mu ^2(n)]{\textbf{s}}\sigma _v^2 \end{aligned}$$
(19)

where the diagonal matrices \({\textbf{H}}\) and \({\textbf{T}}\), the full matrix \({\textbf{P}}\), as well as the vector \({\textbf{s}}\) are determined as in [23, Appendix A] for (uncorrelated and correlated) Gaussian input data. Therefore, the evolution of \({\textbf{k}}^\prime (n)\) can be computed if \(\textrm{E}[\mu (n)]\) and \(\textrm{E}[\mu ^2(n)]\) are known, thus making it possible to predict (in a recursive way) the mean-square behavior of the algorithm.

3.4 Variable Step-Size Behavior

Using Assumption (A5) and introducing the quantity:

$$\begin{aligned} \delta _e(n) = \widehat{\sigma }_e^2(n) - \textrm{E}[\widehat{\sigma }_e^2(n)] \end{aligned}$$
(20)

to rewrite the nonzero part of (5) as

$$\begin{aligned} {\widetilde{\mu }}(n) \cong 1 - \frac{\widehat{\sigma }_v}{\sqrt{\textrm{E}[\widehat{\sigma }_e^2(n)]+\delta _e(n)}} \end{aligned}$$
(21)

one can write the expected value of the variable step size and its squared version as [31, 36]

$$\begin{aligned} \begin{aligned} \textrm{E}[\mu ^i(n) | \mu (n) > 0]&= \int _{-\infty }^{\infty } \mu ^i(n) f[\delta _e(n)] d\delta _e(n) \\&= \int _{\widehat{\sigma }_v^2 - \textrm{E}[\widehat{\sigma }_e^2(n)]}^{\infty } \widetilde{\mu }^i(n)f[\delta _e(n)] d\delta _e(n) \end{aligned} \end{aligned}$$
(22)

for \(i = 1,2\) where the probability density function (PDF) of \(\delta _e(n)\) is assumed to follow a Gaussian distribution, i.e.,

$$\begin{aligned} f[\delta _e(n)] \cong \frac{1}{\sqrt{2\pi \textrm{E}[\delta _e^2(n)]}}\textrm{exp}\left\{ \frac{-\delta _e^2(n)}{2\textrm{E}[\delta _e^2(n)]}\right\} \end{aligned}$$
(23)

due to the central limit theorem [31, 36]. Next, we resort to second-order Taylor polynomials [38] to approximate \(\widetilde{\mu }^i(n)\) for \(i=1,2\) [given by (21)] as

$$\begin{aligned} \widetilde{\mu }(n) \cong 1 - \frac{\widehat{\sigma }_v}{\sqrt{\textrm{E}[\widehat{\sigma }_e^2(n)]}}\left\{ 1 - \frac{1}{2}\frac{\delta _e(n)}{\textrm{E}[\widehat{\sigma }_e^2(n)]} + \frac{3}{8}\frac{\delta _e^2(n)}{\textrm{E}[\widehat{\sigma }_e^2(n)]^2}\right\} \end{aligned}$$
(24)

and

$$\begin{aligned} \begin{aligned} \widetilde{\mu }^2(n)&\cong 1 - \frac{2\widehat{\sigma }_v}{\sqrt{\textrm{E}[\widehat{\sigma }_e^2(n)]}}\left\{ 1 - \frac{1}{2}\frac{\delta _e(n)}{\textrm{E}[\widehat{\sigma }_e^2(n)]} + \frac{3}{8}\frac{\delta _e^2(n)}{\textrm{E}[\widehat{\sigma }_e^2(n)]^2}\right\} \\&~~~+ \frac{\widehat{\sigma }_v^2}{\textrm{E}[\widehat{\sigma }_e^2(n)]}\left\{ 1 - \frac{\delta _e(n)}{\textrm{E}[\widehat{\sigma }_e^2(n)]} + \frac{\delta _e^2(n)}{\textrm{E}[\widehat{\sigma }_e^2(n)]^2}\right\} . \end{aligned} \end{aligned}$$
(25)

Then, substituting (23) and (24) into (22) and solving the resulting expression, we have

$$\begin{aligned} \begin{aligned}&\textrm{E}[\mu (n)| \mu (n)> 0] = \textrm{P}[\mu (n)> 0] - \frac{\widehat{\sigma }_v}{\sqrt{\textrm{E}[\widehat{\sigma }_e^2(n)]}}\times \\&\bigg \{\textrm{P}[\mu (n)> 0] - \frac{1}{2}\frac{\textrm{E}[\delta _e(n) | \mu (n)> 0]}{\textrm{E}[\widehat{\sigma }_e^2(n)]} + \frac{3}{8}\frac{\textrm{E}[\delta _e^2(n) | \mu (n) > 0]}{\textrm{E}[\widehat{\sigma }_e^2(n)]^2}\bigg \} \end{aligned} \end{aligned}$$
(26)

while, from (25),

$$\begin{aligned} \begin{aligned}&\textrm{E}[\mu ^2(n)| \mu (n)> 0] = \textrm{P}[\mu (n)> 0] - \frac{2\widehat{\sigma }_v}{\sqrt{\textrm{E}[\widehat{\sigma }_e^2(n)]}}\times \\&\bigg \{\textrm{P}[\mu (n)> 0] - \frac{1}{2}\frac{\textrm{E}[\delta _e(n) | \mu (n)> 0]}{\textrm{E}[\widehat{\sigma }_e^2(n)]} + \frac{3}{8}\frac{\textrm{E}[\delta _e^2(n) | \mu (n)> 0]}{\textrm{E}[\widehat{\sigma }_e^2(n)]^2}\bigg \} \\&+ \frac{\widehat{\sigma }_v^2}{\textrm{E}[\widehat{\sigma }_e^2(n)]}\bigg \{\textrm{P}[\mu (n)> 0] - \frac{\textrm{E}[\delta _e(n) | \mu (n)> 0]}{\textrm{E}[\widehat{\sigma }_e^2(n)]} + \frac{\textrm{E}[\delta _e^2(n) | \mu (n) > 0]}{\textrm{E}[\widehat{\sigma }_e^2(n)]^2}\bigg \} \end{aligned} \end{aligned}$$
(27)

with

$$\begin{aligned}{} & {} \textrm{P}[\mu (n) > 0] = \frac{1}{2} \textrm{erfc}\left\{ \frac{\widehat{\sigma }_v^2 - \textrm{E}[\widehat{\sigma }_e^2(n)]}{\sqrt{2\textrm{E}[\delta _e^2(n)]}}\right\} \end{aligned}$$
(28)
$$\begin{aligned}{} & {} \textrm{E}[\delta _e(n) | \mu (n) > 0] = \sqrt{\frac{\textrm{E}[\delta _e^2(n)]}{2\pi }}\textrm{exp}\left( -\frac{\{\widehat{\sigma }_v^2 - \textrm{E}[\widehat{\sigma }_e^2(n)]\}^2}{2\textrm{E}[\delta _e^2(n)]}\right) \end{aligned}$$
(29)

and

$$\begin{aligned} \textrm{E}[\delta _e^2(n) | \mu (n)> 0]= \{\widehat{\sigma }_v^2 - \textrm{E}[\widehat{\sigma }_e^2(n)]\} \textrm{E}[\delta _e(n) | \mu (n)> 0] + \textrm{E}[\delta _e^2(n)] \textrm{P}[\mu (n) > 0].\nonumber \\ \end{aligned}$$
(30)

Finally, notice that (26)–(30) require knowledge of \(\textrm{E}[\widehat{\sigma }_e^2(n)]\) and \(\textrm{E}[\delta _e^2(n)]\). So, taking the expected value, one gets from (6) that

$$\begin{aligned} \textrm{E}[\widehat{\sigma }_e^2(n)] = \kappa \textrm{E}[\widehat{\sigma }_e^2(n-1)] + (1-\kappa )J(n). \end{aligned}$$
(31)

In turn, substituting (6) and (31) into (20), squaring both sides of the resulting expression, taking the expected value, and approximating \(\textrm{E}[\delta _e(n-1)e^2(n)] \cong \textrm{E}[\delta _e(n-1)]\textrm{E}[e^2(n)] = 0\), it is possible to show that

$$\begin{aligned} \textrm{E}[\delta _e^2(n)] = \kappa ^2\textrm{E}[\delta _e^2(n-1)] + (1-\kappa )^2\{\textrm{E}[e^4(n)] - J^2(n)\} \end{aligned}$$
(32)

where [from (10)]

$$\begin{aligned} \begin{aligned} \textrm{E}[e^4(n)]&\cong 2\varvec{\lambda }^\textrm{T}{{\textbf{K}}^\prime }^2(n-1)\varvec{\lambda } + [\varvec{\lambda }^\textrm{T}{\textbf{k}}^\prime (n-1)]^2 \\&~~~+ 6\sigma _v^2\varvec{\lambda }{\textbf{k}}^\prime (n-1) + 3\sigma _v^4 \end{aligned} \end{aligned}$$
(33)

due to the factorization theorem of a fourth-order moment of Gaussian variables [31, 36]. Still, by substituting (33) into (32) and approximating \(\varvec{\lambda }^\textrm{T}{{\textbf{K}}^\prime }^2(n-1)\varvec{\lambda } \cong J_{\textrm{ex}}^2(n)\), (32) can be further simplified to

$$\begin{aligned} \textrm{E}[\delta _e^2(n)] \cong \kappa ^2\textrm{E}[\delta _e^2(n-1)]+ 2(1-\kappa )^2 J^2(n). \end{aligned}$$
(34)

So, given that \(\textrm{E}[\mu (n)]\) and \(\textrm{E}[\mu ^2(n)]\) can be computed recursively through (26)–(31) and (34), the behavior of the algorithm is completely characterized now during the transient phase.

3.5 Variable Step Size in Steady State

Assuming convergence, letting \(n\rightarrow \infty \), considering from (31) and (34) that

$$\begin{aligned} \textrm{E}[\widehat{\sigma }_e^2(\infty )] = J(\infty ) \end{aligned}$$
(35)

and

$$\begin{aligned} \textrm{E}[\delta _e^2(\infty )] = 2\rho J^2(\infty ) \end{aligned}$$
(36)

hold, and substituting into (28), (29), and (30), we have [from (26)] that

$$\begin{aligned} \begin{aligned} \textrm{E}[\mu (\infty )| \mu (\infty ) > 0]&= \frac{1}{2} \textrm{erfc}\left( \frac{\tau }{2\sqrt{\rho }}\right) \left( 1 - \frac{\widehat{\sigma }_v}{\sqrt{J(\infty )}} - \frac{3\rho \widehat{\sigma }_v}{4\sqrt{J(\infty )}} \right) \\&~~~- \frac{\widehat{\sigma }_v}{2\sqrt{J(\infty )}} \sqrt{\frac{\rho }{2\pi }}\textrm{exp}\left( -\frac{\tau ^2}{4\rho }\right) \left( \frac{3}{4}\tau - 1\right) \end{aligned} \end{aligned}$$
(37)

while, from (27),

$$\begin{aligned} \begin{aligned} \textrm{E}[\mu ^2(\infty ) | \mu (\infty ) > 0]&= \frac{1}{2} \textrm{erfc}\left( \frac{\tau }{2\sqrt{\rho }}\right) \left[ 1 - \frac{2\widehat{\sigma }_v}{\sqrt{J(\infty )}} \left( 1 + \frac{3\rho }{4}\right) + \frac{\widehat{\sigma }_v^2}{J(\infty )} (1 + 2\rho ) \right] \\&~~~+ \sqrt{\frac{\rho }{2\pi }}\textrm{exp}\left( -\frac{\tau ^2}{4\rho }\right) \left[ \frac{\widehat{\sigma }_v^2}{J(\infty )} \left( \tau - 1\right) -\frac{\widehat{\sigma }_v}{\sqrt{J(\infty )}} \left( \frac{3}{4}\tau - 1\right) \right] \end{aligned}\nonumber \\ \end{aligned}$$
(38)

in which

$$\begin{aligned} \rho = \frac{1-\kappa }{1+\kappa } \end{aligned}$$
(39)

and

$$\begin{aligned} \tau = \frac{\widehat{\sigma }_v^2 - J(\infty )}{J(\infty )}. \end{aligned}$$
(40)

So, the variable step size \(\textrm{E}[\mu (\infty )]\) and its squared version \(\textrm{E}[\mu ^2(\infty )]\) in steady state can be predicted from (37)–(40) if \(J(\infty )\) is known.

3.6 MSE in Steady State

Using (9) and (10) to express (3) in terms of \({\textbf{v}}(n)\), determining \({\textbf{v}}^\textrm{T}(n){\textbf{v}}(n)\), applying the expected value, making \(n\rightarrow \infty \) on both sides, considering Assumptions (A2)–(A5) to simplify the resulting expression, and approximating [12]

$$\begin{aligned} {\textbf{R}}_1 \cong \textrm{E}\left[ \frac{1}{{\textbf{x}}^\textrm{T}(n){\textbf{x}}(n)}\right] {\textbf{R}} \end{aligned}$$
(41)

one obtains

$$\begin{aligned} -2\textrm{E}[\mu (\infty )| \mu (\infty )>0][J(\infty ) - \sigma _v^2] + \textrm{E}[\mu ^2(\infty )| \mu (\infty ) > 0]J(\infty ) = 0 \end{aligned}$$
(42)

with \(\textrm{E}[\mu (\infty )| \mu (\infty )>0]\) and \(\textrm{E}[\mu ^2(\infty )| \mu (\infty )>0]\) depending intrinsically on \(J(\infty )\). Now, substituting (37) and (38) into (42), we get

$$\begin{aligned} J^{3/2}(\infty ) - \sigma _v^2[2 + \alpha \gamma (\epsilon )]J^{1/2}(\infty ) + 2\sqrt{\alpha }\beta (\epsilon )\sigma _v^3 = 0 \end{aligned}$$
(43)

in which \(\epsilon \) denotes an auxiliary variable included to make it possible to obtain an approximate solution through a perturbation method [16],

$$\begin{aligned} \alpha = \frac{\widehat{\sigma }_v^2}{\sigma _v^2} \end{aligned}$$
(44)

defines the ratio between the estimate of the measurement noise variance and its true value, while

$$\begin{aligned} \beta (\epsilon )= & {} 1 + \frac{3}{4}\rho + \epsilon \sqrt{\frac{\rho }{\pi }}\left( \frac{3}{4}\tau - 1\right) g\left( \frac{\tau }{2\sqrt{\rho }}\right) \end{aligned}$$
(45)
$$\begin{aligned} \gamma (\epsilon )= & {} 1 + 2\rho + 2\epsilon \sqrt{\frac{\rho }{\pi }}\left( \tau - 1\right) g\left( \frac{\tau }{2\sqrt{\rho }}\right) \end{aligned}$$
(46)

and

$$\begin{aligned} g(z) = \frac{\exp (-z^2)}{\textrm{erfc}(z)}. \end{aligned}$$
(47)

Note that (43) leads to the original problem for \(\epsilon =1\) and to a cubic equation for \(\epsilon =0\), whose appropriate solution is given by [19]

$$\begin{aligned} \begin{aligned} \sqrt{J_\infty (0)}&= \sigma _v\left( \frac{1}{2} + i\frac{\sqrt{3}}{2}\right) \root 3 \of {\sqrt{\alpha }\beta (0) - \sqrt{\alpha \beta ^2(0) - \frac{[2+\alpha \gamma (0)]^3}{27}}} \\&~~~+ \sigma _v\left( \frac{1}{2} - i\frac{\sqrt{3}}{2}\right) \root 3 \of {\sqrt{\alpha }\beta (0) + \sqrt{\alpha \beta ^2(0) - \frac{[2+\alpha \gamma (0)]^3}{27}} } \end{aligned} \end{aligned}$$
(48)

with \(J_\infty (\epsilon )\) being a differentiable function. So, taking the implicit derivative with respect to \(\epsilon \) in (43), making \(\epsilon = 0\), and solving the resulting expression, we have

$$\begin{aligned} \begin{aligned} \left. \frac{d J_\infty (\epsilon )}{d\epsilon }\right| _{\epsilon = 0}&= \frac{2\sigma _v^2J_\infty ^{3/2}(0)}{J_\infty ^{3/2}(0) - \sqrt{\alpha }\sigma _v^3} \sqrt{\frac{\rho }{\pi }}g\left( \frac{\tau _0}{2\sqrt{\rho }}\right) \\&~~~\times \left\{ \tau _0\left[ \alpha - \frac{3}{4}\frac{\sqrt{\alpha }\sigma _v}{J_\infty ^{1/2}(0)}\right] - \left[ \alpha - \frac{\sqrt{\alpha }\sigma _v}{J_\infty ^{1/2}(0)}\right] \right\} \end{aligned} \end{aligned}$$
(49)

with

$$\begin{aligned} \tau _0 = \frac{\widehat{\sigma }_v^2 - J_\infty (0)}{J_\infty (0)}. \end{aligned}$$
(50)

Based on (48) and (49), the steady-state MSE can be approximated as

$$\begin{aligned} \begin{aligned} J(\infty )&\cong J_\infty (0) + \left. \frac{d J_\infty (\epsilon )}{d\epsilon }\right| _{\epsilon = 0} \end{aligned} \end{aligned}$$
(51)

which holds well for

$$\begin{aligned} \alpha \le \frac{4 - 3\sqrt{\rho \pi }}{4(1 - \sqrt{\rho \pi })}. \end{aligned}$$
(52)

Therefore, based on (37)–(40) and (44)–(51), the algorithm behavior in steady state is completely characterized now.

4 Simulation Results

In this section, the model’s accuracy and the algorithm’s performance are assessed through MC simulations (average of 200 independent runs), highlighting some interesting characteristics. To this end, four examples are presented and discussed, considering systems with different lengths, distinct input data correlation levels, several values of signal-to-noise ratio (SNR), as well as different values for parameters \(\widehat{\sigma }_v^2\) and \(\kappa \) [required in (5) and (6)]. In particular, the system impulse responses \({\textbf{h}}_{1}\) (with \(L=64\) weights) and \({\textbf{h}}_{2}\) (with \(L=128\) weights) are obtained from echo path models for testing of speech echo cancelers given in the ITU-T G.168 Recommendation [18, Models 1 and 4] (as depicted in Fig. 2). In turn, the input signal x(n) is generated through [15]

$$\begin{aligned} x(n) = -a_1x(n-1) -a_2x(n-2) + w(n) \end{aligned}$$
(53)

with \(a_1\) and \(a_2\) being the autoregressive coefficients, and w(n) a white Gaussian noise whose variance

$$\begin{aligned} \sigma _w^2 = \sigma _x^2\left( \dfrac{1-a_2}{1+a_2}\right) [(1+a_2)^2-a_1^2] \end{aligned}$$
(54)

is adjusted such that \(\sigma _x^2=1\). The SNR is defined (in dB) as [5, 8]

$$\begin{aligned} \text {SNR} = 10\log _{10}\left( \frac{\sigma _y^2}{\sigma _v^2} \right) \end{aligned}$$
(55)

with \(\sigma _y^2={\textbf{h}}^\text {T}{\textbf{R}}{\textbf{h}}\) characterizing the variance of y(n) (see Fig. 1). Lastly, the algorithm variables are initialized as \(\widehat{{\textbf{h}}}(0)=[1\,\, 0\, \ldots \, 0]^\text {T}\) and \(\widehat{\sigma }_e^2(0)=0\), while regularization parameters are set as \(\zeta =\widehat{\sigma }_v/1000\) and \(\delta =10^{-3}\).

Fig. 2
figure 2

System impulse responses obtained from echo path models for testing of speech echo cancelers given in the ITU-T G.168 Recommendation [18]. a System impulse response \({\textbf{h}}_{1}\) with \(L=64\) weights (based on [18, Model 1]). b System impulse response \({\textbf{h}}_{2}\) with \(L=128\) weights (based on [18, Model 4])

Full size image

4.1 Example 1

Here, the proposed model’s accuracy is assessed for both uncorrelated and correlated input data as well as different SNR values. In particular, we consider two eigenvalue spread values for the input data autocorrelation matrix, i.e., \(\chi =1\) [obtained from (53) for \(a_1=a_2=0\)] and \(\chi =454.09\) [obtained from (53) for \(a_1=-0.5\) and \(a_2=0.9\)]. Three SNR values are used, i.e., 20, 30, and 40 dB. The system impulse response \({\textbf{h}}_1\) with \(L=64\) weights (see Fig. 2a) is used, while the remaining algorithm parameters are \(\kappa =0.95\) and \(\widehat{\sigma }_v^2 = \sigma _v^2\) (i.e., a perfect estimate of the measurement noise variance).

Figure 3 shows the results obtained for this operating scenario. In particular, Figs. 3a and b present the mean behavior of four adaptive weights, Fig. 3c and d depict the evolution of the variable step size, while Fig. 3e and f illustrate the MSE learning curves. These figures show a very good match between MC simulations and model predictions, during the transient phase as well as in the steady state, irrespective of the input data correlation level and SNR considered. Moreover, one observes, from such figures, that \(\mu (n)\) plays an important role on the evolution of the adaptive weights and MSE learning curves. Specifically, \(\mu (n)\rightarrow 1\) at the beginning of the adaptation process, speeding up the algorithm convergence; in turn, \(\mu (n)\rightarrow 0\) as the algorithm converges, aiming to reduce the EMSE in steady state. Nevertheless, as opposed to [9, Sec. II-C], we verify that \(\mu (n)\) tends to a small positive value as \(n\rightarrow \infty \), preventing any further reduction in the EMSE in steady state. Such effect is captured by the presence of \(\delta _e(n)\) in the model expressions; so, finding ways to suppress the effect of \(\delta _e(n)\) can result in improved versions of the algorithm. Therefore, one concludes that the proposed model may be successfully used to gain insights into the algorithm behavior without resorting exclusively to extensive simulations and to support the development of improved algorithms.

Fig. 3
figure 3

Example 1. Results obtained from MC simulations (gray-ragged lines) and predicted from the proposed model (dark-dashed lines), considering uncorrelated \(\chi =1\) (left) and correlated \(\chi =454.09\) (right) Gaussian input data. a, b Evolution of (four) weights of the adaptive filter. c, d Evolution of the variable step size. e, f Evolution of the MSE learning curve

Full size image

4.2 Example 2

Now, the accuracy of the proposed model is verified (via EMSE learning curve) considering different lengths L for the system impulse response and distinct values for the smoothing parameter \(\kappa \). For such, both system impulse responses \({\textbf{h}}_1\) with \(L=64\) and \({\textbf{h}}_2\) with \(L=128\) (depicted in Fig. 2) and two values for the smoothing parameter \(\kappa = \{0.9,\; 0.999\}\) are used. Also, we consider correlated input data [obtained from (53) with \(a_1=-0.6\) and \(a_2=0.8\)], yielding an eigenvalue spread of \(\chi =144.78\) (for \(L=64\)) and \(\chi =156.40\) (for \(L=128\)) for the input autocorrelation matrix. Still, it is assumed perfect estimate of the measurement noise variance (i.e., \(\widehat{\sigma }_v^2 = \sigma _v^2\)) and SNR values of 20, 30, and 40 dB.

Figure 4 depicts the results obtained for this operating scenario. Specifically, EMSE learning curves obtained for different SNR values are presented in Fig. 4a assuming \(L=64\) and \(\kappa = 0.9\), Fig. 4b with \(L=128\) and \(\kappa = 0.9\), Fig. 4c for \(L=64\) and \(\kappa = 0.999\), while Fig. 4d considering \(L=128\) and \(\kappa = 0.999\). Notice, comparing either Fig. 4a and c or Fig. 4b and d, that smaller values of steady-state EMSE are achieved when \(\kappa \) is increased. Nevertheless, values of \(\kappa \) close to 1 slow down the update of \(\widehat{\sigma }_e^2(n)\) [see (6)], maintaining \(\mu (n)\) [see (5)] high for too long; as a consequence, one verifies a plateau in the EMSE learning curves after the initial transient phase. Despite these characteristics of the algorithm behavior, one observes that the model predictions exhibit a very good match with MC simulations, during the transient phase and in steady state, irrespective of the length L of the system impulse response, the value selected for the smoothing parameter \(\kappa \), the correlation level of the input data, and/or the SNR considered. So, one concludes that the proposed model may be considered to investigate the impact of the algorithm parameters on its performance without relying only on trial-and-error procedures.

Fig. 4
figure 4

Example 2. Results obtained from MC simulations (gray-ragged lines) and predicted from the proposed model (dark-dashed lines), considering a system impulse response with \(L=64\) (left) and \(L=128\) (right) weights. a, b Smoothing parameter \(\kappa = 0.9\). c, d Smoothing parameter \(\kappa = 0.999\)

Full size image

4.3 Example 3

This example aims to verify the accuracy of expressions describing the steady-state algorithm behavior (i.e., variable step size and EMSE in steady state), as a function of the smoothing parameter \(\kappa \) and the ratio \(\alpha \) between the estimate of the measurement noise variance and its true value [see (44)]. To this end, we assume either (i) different values for parameter \(\kappa \) ranging from 0.9 to 0.9999 while \(\alpha =1\) is kept fixed; or (ii) the ratio \(\alpha \) ranging from 0.7 to 1.3 while \(\kappa =0.99\) is fixed. Note that, following the approach described in [34, pp. 250], we have averaged the last 100 values in steady state for each variable of interest to visualize better the experimental results. The remaining parameter values are the same as in Example 2 with \(L=128\), except for the SNR which is assumed here equal to 30 dB for simplicity.

Figure 5 exhibits the results obtained for this operating scenario. Particularly, Fig. 5a and c present curves characterizing the step size and EMSE in steady state as a function of \(\kappa \) with \(\alpha =1\) (fixed), while Fig. 5b and d depict curves assuming \(\kappa =0.99\) (fixed) and varying \(\alpha \). Notice, from Fig. 5a and c, that model predictions match satisfactorily the experimental results over a wide range of values of \(\kappa \), when the measurement noise variance is perfectly estimated (i.e., when \(\widehat{\sigma }_v^2=\sigma _v^2\) which implies \(\alpha =1\)). In turn, although Fig. 5b confirms that the steady-state step-size value can be satisfactorily predicted, observe from Fig. 5d that the model expression describing the steady-state EMSE fails as \(\alpha \) increases above the condition given in (52) (i.e., when \(\widehat{\sigma }_v^2\) overestimates \(\sigma _v^2\)). Despite these aspects, one verifies from Fig. 5c that the EMSE achieved in steady state decreases as \(\kappa \rightarrow 1\). In addition, Fig. 5d highlights how an imperfect estimate of the measurement noise variance affects the steady-state EMSE achieved; in other words, the steady-state EMSE increases, whereas \(\widehat{\sigma }_v^2\) moves away from \(\sigma _v^2\), thus affecting the algorithm performance. Hence, one concludes that parameters \(\kappa \) and \(\widehat{\sigma }_v^2\) must be determined carefully.

Fig. 5
figure 5

Example 3. Results obtained from MC simulations (gray-cross markers) and predicted from the proposed model (dark-dashed lines), considering different values of \(\kappa \) with \(\alpha =1\) (left) and different values of \(\alpha \) with \(\kappa =0.99\) (right). a, b Steady-state value of the variable step size. c, d Steady-state EMSE. [Condition (52) is depicted (as a shaded area) in b and d.]

Full size image
Fig. 6
figure 6

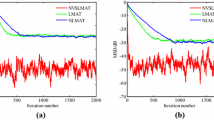
Example 4. Results obtained from MC simulations comparing the performance of the NP-VSS-NLMS algorithm (dark-ragged lines) with important algorithms from the literature (gray-ragged lines) for the same steady-state EMSE. a Algorithm given in [42]. b Algorithm given in [28]. c Algorithm given in [17]. d Algorithm given in [11]. e Algorithm given in [37]. f Algorithm given in [39]

Full size image

4.4 Example 4

In this last example, performance comparisons are conducted between the NP-VSS-NLMS algorithm and the algorithms given in [11, 17, 28, 37, 39, 42]. For such, we employ the system impulse response \({\textbf{h}}_2\) with \(L=128\) (see Fig. 2b), correlated input data [obtained from (53) with \(a_1=-0.6\) and \(a_2=0.8\)] with eigenvalue spread of \(\chi =156.40\) for the input autocorrelation matrix, and SNR values of 20 and 40 dB. Parameters of the algorithms are adjusted manually for achieving the same steady-state EMSE, in order to obtain fair comparisons [29]. In particular, the parameter values are: \(\kappa = 0.99\) for the NP-VSS-NLMS; \(\alpha = 0.99\), \(\gamma = 0.01\), \(a = 0.99\), \(b = 0.9993\), \(A_0 = 0\), and \(B_0 = 0.01\) for [42]; \(\gamma = 0.994\), \(\eta _0 = 0\), and \(\rho _0 = 0.1\) for [28]; \(\alpha = 0.99\), \(\beta = 15\), and \(\zeta _{\textrm{th}} = 0.35\), \(\mu _0 = 1\), and \(\mu _{\textrm{max}} = 1\) for [17]; \(m_0 = 2\widehat{\sigma }_v^2\) and \(\sigma _{w,0} = 0\) for [11]; \(\mu _{\textrm{ref}} = 1\), \(\gamma = 8\), \(\alpha ^+ = 4\), and \(\alpha _0 = 0\) for [37]; while \(\lambda =0.8\) for 20 dB and 0.99992 for 40 dB SNR, \(\epsilon = 10^{-12}\), and \(\sigma ^2_{e,0} = 0\) for [39]. Perfect estimate of the measurement noise variance (i.e., \(\widehat{\sigma }_v^2 = \sigma _v^2\)) is assumed. Tracking performance is assessed by multiplying \({\textbf{h}}_2\) by \(-1\) after the algorithms have reached convergence.

Figure 6 presents performance comparisons involving the NP-VSS-NLMS algorithm and other recent and relevant algorithms from the literature. Specifically, EMSE learning curves obtained from the NP-VSS-NLMS and from the algorithms given in [11, 17, 28, 37, 39, 42] are depicted in Fig. 6a–f, respectively. Notice that the NP-VSS-NLMS algorithm outperforms the algorithms given in [17, 28, 39, 42] in terms of convergence speed when algorithms are properly adjusted to reach the same steady-state EMSE. Although the NP-VSS-NLMS exhibits similar transient characteristics in comparison to the algorithm given in [11], it is observed that the EMSE achieved by this latter continues to reduce as \(n\rightarrow \infty \). Lastly, one verifies that both the NP-VSS-NLMS and the algorithm given in [37] demonstrate comparable performance; nevertheless, the latter requires the fine tuning of more parameters. Therefore, even when compared to other variable step-size algorithms from the literature, we conclude that the NP-VSS-NLMS is suitable in practice, requiring the tuning of fewer parameters for proper operation.

5 Conclusions

In this paper, a stochastic model for the NP-VSS-NLMS algorithm was presented. Specifically, model expressions were derived for predicting the algorithm behavior in the transient phase and the steady state, considering a system identification problem and (uncorrelated and correlated) Gaussian input data. These expressions revealed interesting algorithm characteristics and provided some design guidelines. For instance, it was observed that small steady-state EMSE values are achieved by making the smoothing parameter close to 1. Also, it was found that an imperfect estimate of the measurement noise variance significantly affects the steady-state EMSE achieved by the algorithm. Simulation results for various operating scenarios attested both the model’s accuracy and the algorithm’s superior performance relative to other recent and relevant algorithms from the literature. Note that, based on the obtained results, further research works could address the derivation of models for other algorithms which incorporate rules for estimating the measurement noise variance as well as the development of improved variable step-size algorithms.