Two-Stage Algorithm for Estimation of Nonlinear Functions of State Vector in Linear Gaussian Continuous Dynamical Systems

Abstract

This paper focuses on the optimal minimum mean square error estimation of a nonlinear function of state (NFS) in linear Gaussian continuous-time stochastic systems. The NFS represents a multivariate function of state variables which carries useful information of a target system for control. The main idea of the proposed optimal estimation algorithm includes two stages: the optimal Kalman estimate of a state vector computed at the first stage is nonlinearly transformed at the second stage based on the NFS and the minimum mean square error (MMSE) criterion. Some challenging theoretical aspects of analytic calculation of the optimal MMSE estimate are solved by usage of the multivariate Gaussian integrals for the special NFS such as the Euclidean norm, maximum and absolute value. The polynomial functions are studied in detail. In this case the polynomial MMSE estimator has a simple closed form and it is easy to implement in practice. We derive effective matrix formulas for the true mean square error of the optimal and suboptimal quadratic estimators. The obtained results we demonstrate on theoretical and practical examples with different types of NFS. Comparison analysis of the optimal and suboptimal nonlinear estimators is presented. The subsequent application of the proposed estimators demonstrates their effectiveness.

INTRODUCTION

Estimation and filtering are powerful techniques for building models of complex control systems. The Kalman filtering and its variations are well-known state estimation techniques in wide use in a variety of applications such as navigation, target tracking, communications engineering, biomedical and chemical processing and other areas [1–6]. However, in many applications it is of interest to estimate not only a state vector ${{x}_{t}} \in {{\mathbb{R}}^{n}}$ but also a nonlinear function of the state vector (NFS), ${{z}_{t}} = f\left( {{{x}_{t}}} \right),$ which expresses practical and worthwhile information for control systems. The first motivating example of the NFS is the location of a target and radar. An angle (φ) and distance (d) from radar to target are shown in Fig. 1:

$$\begin{array}{*{20}{c}} {\varphi = f(x) = {\text{arctan}}\left( {\frac{{{{x}_{3}}}}{{\sqrt {x_{1}^{2} + x_{2}^{2}} }}} \right),} \\ {d = f(x) = \sqrt {x_{1}^{2} + x_{2}^{2} + x_{3}^{2}} ~.} \end{array}$$

Fig. 1.

Location of radar and target: $A({{x}_{1}},{{x}_{2}},{{x}_{3}})$, d = OA, ${\text{tan}}\varphi = \frac{{AK}}{{OK}}$.

The second example can be an arbitrary quadratic form, $f({{x}_{t}}) = x_{t}^{T}{\Omega }{{x}_{t}}$, representing an energy-like function of an object [7], or the Euclidean distance (2-norm), $f({{x}_{t}}) = {\text{||}}{{x}_{t}} - x_{t}^{n}{\text{||}}$, between the current ${{x}_{t}}$ and nominal $x_{t}^{n}$ states, respectively. So estimation and prediction of quantities represented by an NFS can be helpful in different applications, such as system control and target tracking.

The problem of estimation of nonlinear functions with unknown parameters and signals based on the minimax theory has been studied by many authors [8–11] and the references therein. Estimation of parameters of nonlinear functional model with known error covariance matrix is presented in [12]. Minimax quadratic estimate for integrated squared derivative of a periodic function is derived in [13]. In [14, 15], the optimal matrix of a quadratic function is searching based on cumulant criterions. Estimation of penalty considered as a quadratic cost functional for quantum harmonic oscillator is given in [16]. Estimators for integrals of nonlinear functions of a probability density are developed in [17, 18]. We also mention estimation of nonlinear functions of spectral density, periodogram of a stationary linear signals [19–21]. Some extension of these results obtained by [22]. In [23] an unknown distance between a target and radar is approximated by Taylor polynomial to subsequent estimation of its coefficients. For algorithms and theory for estimation information measures representing an nonlinear function of signals the reader is referred to [24, 25]. However, most authors have not focused on estimation of an NFS for vector signals defined by dynamical models, such as stochastic differential systems.

The aim of this paper is to develop an optimal two-stage minimum mean square error (MMSE) estimator for an arbitrary NFS in a linear Gaussian stochastic differential systems, and considerably study a special polynomial estimators for which one can obtain an important mean square estimation results. The main contributions of the paper are listed in the following:

1. This paper studies the estimation problem of an NFS within the continuous Kalman filtering framework. Using the mean square estimation approach, an optimal two-stage nonlinear estimator is proposed.

2. The optimal MMSE estimator for a polynomial functions (quadratic, cubic and quartic) is derived. We establish that the polynomial estimator represents a compact closed-form formula depends only on the Kalman estimate and error covariance.

3. Important class of quadratic estimators is comprehensively investigated, including derivation of a matrix equation for its true mean square error (MSE).

4. Performance of the proposed estimators for real NFS illustrates their theoretical and practical usefulness.

This paper is organized as follows. Section 1 presents a statement of the MMSE estimation problem for an NFS within the Kalman filtering framework. In Section 2, the general optimal MMSE estimator is proposed. Here we study the comparative analysis of the optimal and suboptimal estimators via several theoretical examples with a practical NFS. In Section 3, the importance of obtaining an optimal estimator in a closed form is studied. An optimal polynomial estimator represents a closed form expression in terms of the Kalman estimate and its error covariance. For an optimal and suboptimal quadratic estimators we derive matrix formulas for the true MSEs. The efficiency of the quadratic estimators is studied for a scalar random signal and on real model of the wind tunnel system.

1. PROBLEM STATEMENT

The Kalman framework involves estimation of the state of a continuous-time linear Gaussian dynamic system with additive white noise,

$$\begin{gathered} {{{\dot {x}}}_{t}} = {{F}_{t}}{{x}_{t}} + {{G}_{t}}{{v}_{t}},\quad t \geqslant 0, \hfill \\ {{y}_{t}} = {{H}_{t}}{{x}_{t}} + {{w}_{t}}. \hfill \\ \end{gathered} $$

((1.1))

Here, ${{x}_{t}} \in {{\mathbb{R}}^{n}}$ is a state vector, ${{y}_{t}} \in {{\mathbb{R}}^{m}}$ is an observation vector, ${{v}_{t}} \in {{\mathbb{R}}^{r}}$ and ${{w}_{t}} \in {{\mathbb{R}}^{m}}$ are zero-mean Gaussian white noises with intensities Q_t and R_t, respectively, i.e., ${\mathbf{E}}({{v}_{t}}v_{s}^{{\text{T}}}) = {{Q}_{t}}{{\delta }_{{t - s}}}$, ${\mathbf{E}}({{w}_{t}}w_{s}^{{\text{T}}}) = {{R}_{t}}{{\delta }_{{t - s}}}$, ${{\delta }_{t}}$ is the Dirac delta-function, ${{F}_{t}} \in {{\mathbb{R}}^{{n \times n}}}$, ${{G}_{t}} \in {{\mathbb{R}}^{{n \times r}}}$, ${{Q}_{t}} \in {{\mathbb{R}}^{{r \times r}}}$, ${{R}_{t}} \in {{\mathbb{R}}^{{m \times m}}}$ and ${{H}_{t}} \in {{\mathbb{R}}^{{m \times n}}}$, ${\mathbf{E}}(X)$ is the expectation of a random vector X.

We assume that the initial state ${{x}_{0}}\sim \mathbb{N}\left( {{{{\bar {x}}}_{0}},{{P}_{0}}} \right),$ and system and observation noises ${{v}_{t}}$, ${{w}_{t}}$ are mutually uncorrelated.

A problem associated with such system (1.1) is that of estimation of the nonlinear function of state vector

$${{z}_{t}} = f({{x}_{t}}):{{\mathbb{R}}^{n}} \to \mathbb{R}$$

((1.2))

from the overall noisy observations $y_{0}^{t} = \left\{ {{{y}_{s}}:0 \leqslant s \leqslant t} \right\}.$

There are a multitude of statistics-based methods to estimate an unknown function $z = f(x)$ from real sensor observations $y_{0}^{t}.$ We focus on choosing the best estimate$\hat {z}$ minimizing MSE: $\mathop {\min }\limits_{\hat {z}} {\mathbf{E}}[{{\left\| {z - \hat {z}} \right\|}^{2}}].$ In general the optimal MMSE solution (further “estimate” or “estimator”) is given by the conditional mean, $\hat {z} = {\mathbf{E}}(z {\text{|}}{\kern 1pt} y_{0}^{t})$ [26, 27]. The most challenging problem is how to calculate the conditional mean. In this paper, we solve this problem for the NFS (1.2) within the Kalman filtering framework.

We propose optimal and suboptimal MMSE estimation algorithms for the NFS and their implementation in next section.

2. OPTIMAL TWO-STAGE MMSE ESTIMATOR FOR GENERAL NFS

Here the optimal two-stage estimator for the general NFS is derived. Also we propose a simple suboptimal estimator. The both estimators include two stages: the optimal Kalman estimate of the state vector ${{\hat {x}}_{t}}$, computed at the first stage is used at the second stage for estimation of the NFS (1.2).

2.1. Optimal Two-Stage Algorithm

First stage (calculation of Kalman estimate). The estimate ${{\hat {x}}_{t}} = {\mathbf{E}}({{x}_{t}}|y_{0}^{t})$ of the state x_t based on the observations $y_{0}^{t}$, and its error covariance ${{P}_{t}} = {\mathbf{E}}({{e}_{t}}e_{t}^{{\text{T}}}),~\;{{e}_{t}} = {{x}_{t}} - {{\hat {x}}_{t}},$ are given by the continuous Kalman-Bucy filter (KBF) equations [4–6]:

$$\begin{array}{*{20}{c}} {{{{\dot {\hat {x}}}}_{t}} = {{F}_{t}}{{{\hat {x}}}_{t}} + {{K}_{t}}({{y}_{t}} - {{H}_{t}}{{{\hat {x}}}_{t}}),\quad {{{\hat {x}}}_{{t = 0}}} = {{{\bar {x}}}_{0}},} \\ {{{K}_{t}} = {{P}_{t}}H_{t}^{{\text{T}}}R_{t}^{{ - 1}},\quad {{{\tilde {G}}}_{t}} = {{G}_{t}}{{Q}_{t}}G_{t}^{{\text{T}}},~} \\ {{{{\dot {P}}}_{t}} = {{F}_{t}}{{P}_{t}} + F_{t}^{{\text{T}}}{{P}_{t}} - {{P}_{t}}H_{t}^{{\text{T}}}R_{t}^{{ - 1}}{{H}_{t}}{{P}_{t}} + {{{\tilde {G}}}_{t}},\quad {{P}_{{t = 0}}} = {{P}_{0}}.} \end{array}$$

((2.1))

Second stage (optimal estimator for NFS). The optimal estimate of the NFS ${{z}_{t}} = f({{x}_{t}})$ based on the observations $y_{0}^{t}$ also represents a conditional mean, that is

$${{\hat {z}}_{t}} = {\mathbf{E}}({{z}_{t}} {\text{|}}{\kern 1pt} y_{0}^{t}) = \int\limits_{{{\mathbb{R}}^{n}}} {f(x){{p}_{t}}(x {\text{|}}{\kern 1pt} y_{0}^{t})dx} ,$$

((2.2))

where ${{p}_{t}}(x {\text{|}}{\kern 1pt} y_{0}^{t}) = \mathbb{N}\left( {{{{\hat {x}}}_{t}},{{P}_{t}}} \right)$ is a multivariate conditional Gaussian probability density function determining by the conditional mean ${{\hat {x}}_{t}} = {\mathbf{E}}({{x}_{t}}|y_{0}^{t})$ and covariance ${{P}_{t}} = {\text{cov}}({{x}_{t}},{{x}_{t}} {\text{|}}{\kern 1pt} y_{0}^{t}) = {\mathbf{E}}({{e}_{t}}e_{t}^{{\text{T}}})$.

Thus, the estimate in (2.2) represents the optimal MMSE estimator for the general NFS which depends on the Kalman estimate ${{\hat {x}}_{t}}$ and its error covariance P_t.

In practice, the nonlinear function (1.2) may depend not only on the state vector, but also on its estimate. Then the NSF takes the form

$${{z}_{t}} = f({{x}_{t}},{{\hat {x}}_{t}}):{{\mathbb{R}}^{n}} \times \;{\kern 1pt} {{\mathbb{R}}^{n}} \to \mathbb{R}.$$

((2.3))

Taking into account that the state estimate ${{\hat {x}}_{t}}$ represents the known function of observations, ${{\hat {x}}_{t}}$ = ${{\hat {x}}_{t}}(y_{0}^{t})$, the MMSE estimate of an unknown function, ${{z}_{t}} = f({{x}_{t}},{{\hat {x}}_{t}})$ is given by the formula similar to (2.2). Namely

$${{\hat {z}}_{t}} = {\mathbf{E}}[f({{x}_{t}},{{\hat {x}}_{t}}(y_{0}^{t})){\text{|}}y_{0}^{t}] = \int\limits_{{{\mathbb{R}}^{n}}} {f(x,{{{\hat {x}}}_{t}}){{p}_{t}}(x {\text{|}}{\kern 1pt} y_{0}^{t})dx} = \int\limits_{{{\mathbb{R}}^{n}}} {f(x,{{{\hat {x}}}_{t}})\mathbb{N}({{{\hat {x}}}_{t}},{{P}_{t}})dx} .$$

((2.4))

Further, we consider several theoretical examples of application of the general nonlinear estimators (2.2).

2.2. Examples of Two-Stage Estimator

Let ${{x}_{t}} = {{\left[ {\begin{array}{*{20}{c}} {{{x}_{{1,t}}}}&{{{x}_{{2,t}}}} \end{array}} \right]}^{{\text{T}}}}$ be a bivariate Gaussian vector; and ${{\hat {x}}_{t}} \in {{\mathbb{R}}^{2}}$ and ${{P}_{t}} \in {{\mathbb{R}}^{{2 \times 2}}}$ are the Kalman estimate and error covariance, respectively.

Example 1 (expected value of the Euclidean norm). The overall estimation error is defined as

$$\left\| {{{e}_{t}}} \right\| = \sqrt {e_{{1,t}}^{2} + e_{{2,t}}^{2}} ,\quad {{e}_{t}} = {{x}_{t}} - {{\hat {x}}_{t}},\quad {{e}_{t}} = {{\left[ {\begin{array}{*{20}{c}} {{{e}_{{1,t}}}}&{{{e}_{{2,t}}}} \end{array}} \right]}^{{\text{T}}}}.$$

((2.5))

Taking into account that the Euclidean norm of the error depends on the difference between state vector and its estimate, ${\text{||}}{{e}_{t}}{\text{||}} = \sqrt {e_{t}^{{\text{T}}}{{e}_{t}}} = \sqrt {{{{({{x}_{t}} - {{{\hat {x}}}_{t}})}}^{{\text{T}}}}({{x}_{t}} - {{{\hat {x}}}_{t}})} ,$ one transform the formula (2.2). We have

$${{\hat {z}}_{t}} = {\mathbf{E}}[\left\| {{{e}_{t}}} \right\| {\text{|}}{\kern 1pt} y_{0}^{t}] = \int {(\sqrt {{{e}^{{\text{T}}}}e} )} {{p}_{t}}(e {\text{|}}{\kern 1pt} y_{0}^{t})de = \int {(\sqrt {{{e}^{{\text{T}}}}e} )} \,\mathbb{N}\left( {0,{{P}_{t}}} \right)de,$$

where ${{p}_{t}}(e {\text{|}}{\kern 1pt} y_{0}^{t}) = \mathbb{N}\left( {0,{{P}_{t}}} \right)$ is the conditional probability density function of the error ${{e}_{t}} = {{x}_{t}} - {{\hat {x}}_{t}}.$

Next using [28] we have the analytical expression for the MMSE estimate of the Euclidean norm z_t = ${\text{||}}{{e}_{t}}{\text{||}}{\text{,}}$

$$\begin{gathered} {{{\hat {z}}}_{t}} = {\mathbf{E}}(\left\| {{{e}_{t}}} \right\| {\text{|}}{\kern 1pt} y_{0}^{t}) = \frac{{2{{\lambda }_{{1,t}}}{{\lambda }_{{2,t}}}\sqrt \pi }}{{{{{\left( {{{\lambda }_{{1,t}}} + {{\lambda }_{{2,t}}}} \right)}}^{{3/2}}}}}{}_{2}^{{}}{{F}_{1}}\left( {\frac{3}{4},\frac{5}{4};1;q_{t}^{2}} \right), \\ q_{t}^{2} = \frac{{{{\lambda }_{{1,t}}} - {{\lambda }_{{2,t}}}}}{{{{\lambda }_{{1,t}}} + {{\lambda }_{{2,t}}}}}, \\ \end{gathered} $$

((2.6))

where ${}_{2}^{{}}{{F}_{1}}\left( {a,b;c;x} \right)~$ is the hypergeometric function, and λ_1,t and λ_2,t are the eigenvalues of P_t.

Example 2 (feedback control depends on maximum of state coordinate). In mechanical systems a piecewise feedback control law is given by

$${{u}_{t}} = \left\{ \begin{gathered} 1,\quad \max ({{x}_{{1,t}}},{{x}_{{2,t}}}) > D, \hfill \\ - 1,\quad \max ({{x}_{{1,t}}},{{x}_{{2,t}}}) \leqslant D, \hfill \\ \end{gathered} \right.$$

where D is a distance threshold. Then the MMSE estimate of the maximum ${{z}_{t}} = {\text{max}}\left( {{{x}_{{1,t}}},{{x}_{{2,t}}}} \right)$ is obtained from [29],

$$\begin{gathered} {{{\hat {z}}}_{t}} = {\mathbf{E}}[\max ({{x}_{{1,t}}},{{x}_{{2,t}}}){\text{|}}y_{0}^{t}] = {{{\hat {x}}}_{{1,t}}}\Phi \left( {\frac{{{{{\hat {x}}}_{{1,t}}} - {{{\hat {x}}}_{{2,t}}}}}{{{{\theta }_{t}}}}} \right) \\ \, + {{{\hat {x}}}_{{2,t}}}\Phi \left( {\frac{{{{{\hat {x}}}_{{2,t}}} - {{{\hat {x}}}_{{1,t}}}}}{{{{\theta }_{t}}}}} \right) + {{\theta }_{t}}\phi \left( {\frac{{{{{\hat {x}}}_{{1,t}}} - {{{\hat {x}}}_{{2,t}}}}}{{{{\theta }_{t}}}}} \right), \\ \end{gathered} $$

$${{\theta }_{t}} = \sqrt {{{P}_{{11,t}}} + {{P}_{{22,t}}} - 2{{P}_{{12,t}}}} ,\quad {{P}_{t}} = [{{P}_{{ij,t}}}],$$

where ϕ(⋅) and Φ(⋅) are the standard conditional Gaussian density and cumulative distribution function, respectively.

Example 3 (estimation of sine function). Let θ be a random unknown angle which is measured in the presence of an additive white noise. Then

$$\begin{gathered} {{{\dot {x}}}_{t}} = 0,\quad t \geqslant 0,\quad {{x}_{0}} = \theta \sim \mathbb{N}({{m}_{\theta }},\sigma _{\theta }^{2}), \hfill \\ {{y}_{t}} = {{x}_{t}} + {{w}_{t}},\quad 0 \leqslant t \leqslant T, \hfill \\ \end{gathered} $$

((2.7))

where ${{x}_{t}} = \theta ,$ and w_t is a zero-mean Gaussian white noise with intensity r.

The KBF equations (2.1) become

$$\begin{gathered} {{{\dot {\hat {x}}}}_{t}} = ~{{P}_{t}}\left( {{{y}_{t}} - {{{\hat {x}}}_{t}}} \right){\text{/}}r,~~~{{{\hat {x}}}_{0}} = {{m}_{\theta }},~ \\ {{{\dot {P}}}_{t}} = - P_{t}^{2}{\text{/}}r,\quad {{P}_{0}} = \sigma _{\theta }^{2}. \\ \end{gathered} $$

((2.8))

Integrating the Riccati equation for ${{P}_{t}} = {\mathbf{E}}[{{(\theta - {{\hat {x}}_{t}})}^{2}}]$, we obtain ${{P}_{t}} = \sigma _{\theta }^{2}{\text{/}}(1 + t\sigma _{\theta }^{2}{\text{/}}r)$. Further, we consider a sine function of an unknown angle θ. Then an NFS becomes $z = f(\theta ) = \sin \theta$.

1. Optimal estimate. Using (2.2) the optimal estimate of the sine is

$${{\hat {z}}_{t}} = {\mathbf{E}}[{\text{sin}}\theta {\text{|}}{\kern 1pt} y_{0}^{t}] = \int\limits_\mathbb{R} {{\text{sin}}\theta \mathbb{N}({{{\hat {\theta }}}_{t}},{{P}_{t}})d\theta = {{e}^{{ - {{P}_{t}}/2}}}{\text{sin}}{{{\hat {\theta }}}_{t}}} ,$$

((2.9))

where ${{\hat {\theta }}_{t}} = {{\hat {x}}_{t}}$ and P_t are determined by (2.8).

2. Suboptimal estimate. In parallel with the optimal mean square estimate (2.9) we consider a simple suboptimal estimate, ${{\tilde {z}}_{t}} = f({{\hat {\theta }}_{t}}) = {\text{sin}}{{\hat {\theta }}_{t}}$.

To compare estimation accuracy of two estimates, we derive the analytical formulas for their MSE: $P_{{z,t}}^{{{\text{opt}}}} = {\mathbf{E}}[{{({\text{sin}}\theta - {{\hat {z}}_{t}})}^{2}}]$ and $P_{{z,t}}^{{{\text{sub}}}} = {\mathbf{E}}[{{\left( {\sin \theta - {{{\tilde {z}}}_{t}}} \right)}^{2}}],$ and demonstrate a comparative analysis. We obtain

$$P_{{z,t}}^{{{\text{opt}}}} = k_{t}^{{\left( 1 \right)}} - 2{{e}^{{ - {{P}_{t}}/2}}}k_{t}^{{\left( 2 \right)}} + {{e}^{{ - {{P}_{t}}}}}k_{t}^{{\left( 3 \right)}},\quad P_{{z,t}}^{{{\text{sub}}}} = k_{t}^{{\left( 1 \right)}} - 2k_{t}^{{\left( 2 \right)}} + k_{t}^{{\left( 3 \right)}},$$

where

$$\begin{gathered} k_{t}^{{\left( 1 \right)}} = {\mathbf{E}}[{\text{si}}{{{\text{n}}}^{2}}\theta ] = (1 - {{e}^{{ - 2\sigma _{\theta }^{2}}}}){\text{cos}}\left( {2{{m}_{{\theta }}}} \right){\text{/}}2, \\ k_{t}^{{\left( 2 \right)}} = {\mathbf{E}}[{\text{sin}}\theta {\text{sin}}{{{\hat {\theta }}}_{t}}] = [{{e}^{{ - {{P}_{t}}/2}}} - {{e}^{{ - (4\sigma _{\theta }^{2} - 3{{P}_{t}})/2}}}{\text{cos}}\left( {2{{m}_{\theta }}} \right)]{\text{/}}2,~ \\ k_{t}^{{\left( 3 \right)}} = {\mathbf{E}}[{\text{si}}{{{\text{n}}}^{2}}{{{\hat {\theta }}}_{t}}] = [1 - {{e}^{{ - 2(\sigma _{\theta }^{2} - {{P}_{t}})}}}{\text{cos}}\left( {2{{m}_{\theta }}} \right)]{\text{/}}2. \\ \end{gathered} $$

Figure 2 illustrates the exact MSEs $P_{{z,t}}^{{{\text{opt}}}}$ and $P_{{z,t}}^{{{\text{sub}}}}$ for the parameters ${{m}_{\theta }} = 0$; $\sigma _{\theta }^{2} = 2$; $r = 1$ and Fig. 3 shows the relative error, ${{\Delta }_{t}} = {\text{|}}(P_{{z,t}}^{{{\text{opt}}}} - P_{{z,t}}^{{{\text{sub}}}}){\text{/}}P_{{z,t}}^{{{\text{opt}}}}{\text{|}} \cdot 100\% .$ Not surprisingly, Figs. 2 and 3 illustrate that the optimal estimate is better than suboptimal one, i.e., $P_{{z,t}}^{{{\text{opt}}}} < P_{{z,t}}^{{{\text{sub}}}}.$ We also observe that the difference between two estimates becomes negligible as the time increases.

Fig. 2.

Optimal MSE (dotted curve) and suboptimal MSE (solid curve) for z = sinθ.

Fig. 3.

Relative error Δ_t, % between optimal and suboptimal MSEs for z = sinθ.

Example 4 (estimation of distance between random location θ and given point a). In this case an NFS becomes $z = \left| {\theta - a} \right|$. Under the model (2.7) for a random location ${{x}_{t}} = \theta$ we use the best estimate (2.2) for the distance $\left| {\theta - a} \right|$. Then

$${{\hat {z}}_{t}} = {\mathbf{E}}[\left| {\theta - a} \right| {\text{|}}{\kern 1pt} y_{0}^{t}] = \mathop \smallint \limits_{ - \infty }^\infty \left| {\theta - a} \right|\mathbb{N}({{\hat {\theta }}_{t}},{{P}_{t}})d\theta = \sqrt {\frac{{2{{P}_{t}}}}{\pi }} {\text{exp}}\left[ { - \frac{{{{{(a - {{{\hat {\theta }}}_{t}})}}^{2}}}}{{2{{P}_{t}}}}} \right] + (a - {{\hat {\theta }}_{t}})\left[ {2\Phi \left( {\frac{{a - {{{\hat {\theta }}}_{t}}}}{{\sqrt {{{P}_{t}}} }}} \right) - 1} \right],~$$

where ${{\hat {\theta }}_{t}} = {{\hat {x}}_{t}}$ and P_t are determined by (2.8).

In the particular case with a = 0 the MMSE estimate of an unknown modulus, $z = f\left( \theta \right) = \left| \theta \right|$, takes the form

$${{\hat {z}}_{t}} = \sqrt {\frac{{2{{P}_{t}}}}{\pi }} {\text{exp}}\left( { - \frac{{\hat {\theta }_{t}^{2}}}{{2{{P}_{t}}}}} \right) + {{\hat {\theta }}_{t}}\left[ {1 - 2\Phi \left( { - \frac{{{{{\hat {\theta }}}_{t}}}}{{\sqrt {{{P}_{t}}} }}} \right)} \right].$$

In addition we can consider a simple suboptimal estimate ${{\tilde {z}}_{t}} = f({{\hat {\theta }}_{t}}) = {\text{|}}{{\hat {\theta }}_{t}}{\text{|}}.$

To study the behavior of the MSEs, $P_{t}^{{{\text{opt}}}} = {\mathbf{E}}[{{\left( {\left| \theta \right| - {{{\hat {z}}}_{t}}} \right)}^{2}}]$ and $P_{t}^{{{\text{sub}}}} = {\mathbf{E}}[{{\left( {\left| \theta \right| - {{{\tilde {z}}}_{t}}} \right)}^{2}}]$ set ${{m}_{\theta }} = 1$; $~\sigma _{\theta }^{2} = 1$; $r = 0.2$. To compute the MSEs the Monte-Carlo simulation with 1000 runs was used. As shown in Fig. 4, the optimal estimate ${{\hat {z}}_{t}}$ has a great improvement over the suboptimal one ${{\tilde {z}}_{t}}$.

Fig. 4.

MSEs for estimates of absolute value z = |θ|: $P_{t}^{{{\text{opt}}}}$ (solid curve), $P_{t}^{{{\text{sub}}}}$ (dotted curve).

2.3. Alternative Idea of Suboptimal Estimation of NFS

In contrast to the proposed optimal MMSE solution (2.1) and (2.2) there is an alternative idea to estimate an NFS. In this case the NFS, ${{z}_{t}} = f({{x}_{t}})$, is considered as additional state variable z_t which is determined by the nonlinear stochastic equation ${{\dot {z}}_{t}} = a\left( {{{x}_{t}},{{z}_{t}}} \right) + b\left( {{{x}_{t}},{{z}_{t}}} \right){{v}_{t}},$ in which the drift coefficient $a\left( {{{x}_{t}},{{z}_{t}}} \right)$ and diffusion matrix $b\left( {{{x}_{t}},{{z}_{t}}} \right)$ are determined by the Ito formula applied to the complex function f(x_t), in which the argument is given by the equation ${{\dot {x}}_{t}} = {{F}_{t}}{{x}_{t}} + {{G}_{t}}{{v}_{t}}$ [30]. Including the variable z_t into the state of a system ${{x}_{t}} \in {{\mathbb{R}}^{n}},$ we obtain system with the augmented state ${{X}_{t}} = [\begin{array}{*{20}{c}} {x_{t}^{{\text{T}}}}&{{{z}_{t}}} \end{array}] \in {{\mathbb{R}}^{{n + 1}}}$. Thus the problem of estimation of the NFS is reduced to the nonlinear filtering problem by replacing the original state x_t by the augmented one X_t. And approximate nonlinear filtering techniques can be used for simultaneously estimation of x_t and z_t. Many different approximate filters have been proposed [5, 6, 30–35], among which we distinguish the extended Kalman filter [5], the conditionally optimal Pugachev filter with given and optimal structures [30–32] and the unscented Kalman filter [33]. But computational complexity of the approximate nonlinear filters is considerably greater than complexity of the linear Kalman-Bucy filter. The proposed two-stage procedure (2.1) and (2.2) is more promising than estimation of the augmented state X_t.

2.4. Simple Suboptimal Estimator for NFS

In parallel to the optimal estimator ${{\hat {z}}_{t}} = {\mathbf{E}}({{z}_{t}} {\text{|}}{\kern 1pt} y_{0}^{t})$ we propose a simple suboptimal estimate of the NFS, such as ${{\tilde {z}}_{t}} = f({{\hat {x}}_{t}})$ which depends only on the Kalman estimate of state ${{\hat {x}}_{t}}$ and does not require its error covariance P_t in contrast to the optimal one ${{\hat {z}}_{t}}$. The numerical results show that the suboptimal estimate ${{\tilde {z}}_{t}}$ may be either close to the optimal one (Example 3) or seriously worse (see Example 4 and further Example 6).

2.5. Real-Time Implementation of MMSE Estimator

The error covariance P_t can be pre-computed, because it does not depend on the sensor observations $y_{0}^{t} = \left\{ {{{y}_{s}}:0 \leqslant s \leqslant t} \right\},$ but only on the noise statistics ${{Q}_{t}}$, R_t, the system matrices ${{F}_{t}},\;{{G}_{t}},\;{{H}_{t}}$ and the initial condition P₀, which are the part of system and observation model (1.1). Thus, once the observation schedule has been settled, the real-time implementation of the MMSE estimator, ${{\hat {z}}_{t}} = {{\hat {z}}_{t}}\left( {{{{\hat {x}}}_{t}},{{P}_{t}}} \right)$, requires only the computation of the Kalman estimate ${{\hat {x}}_{t}}$.

2.6. Closed-Form MSE Estimator

For the general NFS, ${{z}_{t}} = f\left( {{{x}_{t}}} \right)$, calculation of the optimal MMSE estimate is reduced to calculation of the multivariate integral (2.2). Analytic calculation of the integral (closed-form MSE estimator) is possible only in special cases as in Examples 1–4.

Further, we consider a polynomial function of state (polynomial form) for which it is possible to obtain a simple closed-form MSE estimators that depend only on the Kalman statistics $\left( {{{{\hat {x}}}_{t}},{{P}_{t}}} \right)$.

3. OPTIMAL CLOSED-FORM MMSE ESTIMATOR FOR POLYNOMIAL FUNCTIONS

Let consider a special NFS (1.2) that represents an arbitrary multivariate polynomial function (form) such as,

$$\begin{array}{*{20}{c}} {{\text{a}})\,\,{\text{Linear}}\,{\text{form:}}}&{f(x) = Ax;} \\ {{\text{b}})\,\,{\text{Quadratic}}\,{\text{form:}}}&{f(x) = {{x}^{{\text{T}}}}Ax,\quad A = {{A}^{{\text{T}}}};} \\ {{\text{c}})\,\,{\text{Cubic}}\,{\text{form:}}}&{f(x) = Ax{{x}^{{\text{T}}}}Bx;} \\ {{\text{d}})\,\,{\text{Quartic}}\,{\text{form:}}}&{f(x) = {{x}^{{\text{T}}}}Ax{{x}^{{\text{T}}}}Bx,} \\ {}&{A = {{A}^{{\text{T}}}},\quad B = {{B}^{{\text{T}}}},} \end{array}$$

((3.1))

where $x \in {{\mathbb{R}}^{n}}$, and $A,B \in {{\mathbb{R}}^{{n \times n}}}$. For simplicity, we ignore the subscript t in this Section.

3.1. Optimal Polynomial Estimators

In case of the polynomial forms (3.1), the optimal estimate $\hat {z} = {\mathbf{E}}[f\left( x \right) {\text{|}}{\kern 1pt} y_{0}^{t}]$ has a closed-form solution since the conditional expectation depends on high-order moments of a conditional Gaussian distribution $\mathbb{N}({{\hat {x}}_{t}},{{P}_{t}})$, which can be explicitly calculated in terms of first- and second-order moments, namely, the Kalman estimate and its error covariance $(\hat {x},P)$. The following theorem gives the best polynomial estimators.

Theorem 1.The optimal MMSE estimators $\hat {z} = {\mathbf{E}}[f\left( x \right) {\text{|}}{\kern 1pt} y_{0}^{t}]$  for the polynomial forms (3.1) are given by the following analytical formulas:

$$\begin{array}{*{20}{c}} {{\text{a}})\,\,linear\,estimator{\text{:}}}&{\hat {z} = A\hat {x};} \\ {{\text{b}})\,\,quadratic\,estimator{\text{:}}}&{\hat {z} = {\text{tr}}(AP) + {{{\hat {x}}}^{{\text{T}}}}A\hat {x};} \\ {{\text{c}})\,\,cubic\,estimator{\text{:}}}&{\hat {z} = 2APB\hat {x} + A\hat {x}{{{\hat {x}}}^{{\text{T}}}}B\hat {x} + A\hat {x}{\text{tr}}({\text{BP}});} \\ {{\text{d}})\,\,quartic\,estimator{\text{:}}}&{\hat {z} = 2{\text{tr(}}APBP) + 4{{{\hat {x}}}^{{\text{T}}}}APB\hat {x}} \\ {}&{\, + [{\text{tr}}(AP) + {{{\hat {x}}}^{{\text{T}}}}A\hat {x}][{\text{tr}}(BP) + {{{\hat {x}}}^{{\text{T}}}}B\hat {x}].} \end{array}$$

((3.2))

The derivation of the estimators (3.2) is given in Appendix.

Example 5 (optimal and suboptimal estimation of the Euclidean norm). To determine an optimal relative location in wireless sensor networks we need to evaluate the cost function representing the Euclidean norm of an overall error,

$$z = \left\| {{\kern 1pt} e{\kern 1pt} } \right\| = \sqrt {{{e}^{{\text{T}}}}e} ,$$

where e is n-dimensional random error, $e\sim \mathbb{N}(0,P)$

If n = 2 the optimal MMSE estimate $\hat {z}$ determined by formulas (2.5) and (2.6),

$$\hat {z} = {\mathbf{E}}({{e}_{t}} {\text{|}}{\kern 1pt} y_{0}^{t}) = \frac{{2{{\lambda }_{1}}{{\lambda }_{2}}\sqrt \pi }}{{{{{\left( {{{\lambda }_{1}} + {{\lambda }_{2}}} \right)}}^{{3/2}}}}}{}_{2}^{{}}{{F}_{1}}\left( {\frac{3}{4},\frac{5}{4};1;{{q}^{2}}} \right),\quad q = \frac{{{{\lambda }_{1}} - {{\lambda }_{2}}}}{{{{\lambda }_{1}} + {{\lambda }_{2}}}}.$$

((3.3))

If n > 2 then it is difficult to derive an analytical formula for the optimal estimate $\hat {z}$ such as (3.3). In this case we propose a simple suboptimal estimate $\tilde {z}$ for the Euclidean norm. First, using the quadratic estimator (3.2) we calculate the MMSE estimate of the square norm ${{\left\| {{\kern 1pt} e{\kern 1pt} } \right\|}^{2}} = {{e}^{{\text{T}}}}e,$ and then extract the square root. We have

$$\tilde {z} = \sqrt {{\text{||}}{{{\hat {e}}}^{2}}{\text{||}}} = \sqrt {{\mathbf{E}}({{e}^{{\text{T}}}}e {\text{|}}{\kern 1pt} y_{0}^{t})} = \sqrt {{\text{tr}}\left( P \right)} ,$$

((3.4))

where tr(P) denotes the trace of a matrix P.

To study behavior of the optimal and suboptimal estimates (3.3) and (3.4) at n = 2 we set

$$\begin{array}{*{20}{c}} {P = \left[ {\begin{array}{*{20}{c}} {1.5}&{ - 0.5} \\ { - 0.5}&{1.5} \end{array}} \right],\quad {{\lambda }_{1}} = 1,~~{{\lambda }_{2}} = 2,} \\ {q = - \frac{1}{3},\quad {}_{2}^{{}}{{F}_{1}}\left( {\frac{3}{4},\frac{5}{4};1;{{q}^{2}}} \right) = 1.1169.} \end{array}$$

Then $\hat {z} = 1.524$, $\tilde {z} = 1.732$. The relative error $\left| {\frac{{\tilde {z} - \hat {z}}}{{\tilde {z}}}} \right| \cdot 100\% = 13.6\%$ shows that the suboptimal estimate $\tilde {z}$ is more worse than the optimal one $\hat {z}$.

3.2. Exact Matrix Formulas for Quadratic Estimators

Consider an arbitrary quadratic form (QF)

$${{z}_{t}} = f({{x}_{t}}) = x_{i}^{{\text{T}}}A{{x}_{t}}.$$

((3.5))

Using Theorem 1, the optimal quadratic estimator (3.2) can be explicitly calculated in terms of the state estimate ${{\hat {x}}_{t}}$ and error covariance P_t,

$${{\hat {z}}_{t}} = {\text{tr}}\left( {A{{P}_{t}}} \right) + \hat {x}_{t}^{{\text{T}}}A{{\hat {x}}_{t}}.$$

((3.6))

In parallel to the optimal estimate we propose a suboptimal estimate $\tilde {z}$ of the QF which depends only on the Kalman estimate ${{\hat {x}}_{t}}$ and does not require its error covariance P_t in contrast to the optimal one (3.6). The suboptimal estimate is obtained by direct calculation of the QF at the point ${{x}_{t}} = {{\hat {x}}_{t}}$ such as,

$${{\tilde {z}}_{t}} = f({{\hat {x}}_{t}}) = \hat {x}_{t}^{{\text{T}}}A{{\hat {x}}_{t}}.$$

((3.7))

Let compare estimation accuracy of the optimal (3.6) and suboptimal (3.7) estimates. The following result completely defines the MSEs,

$$\begin{array}{*{20}{c}} {P_{{z,t}}^{{{\text{opt}}}} = {\mathbf{E}}[{{{\left( {{{z}_{t}} - {{{\hat {z}}}_{t}}} \right)}}^{2}}],} \\ {~P_{{z,t}}^{{{\text{sub}}}} = {\mathbf{E}}[{{{\left( {{{z}_{t}} - {{{\tilde {z}}}_{t}}} \right)}}^{2}}].} \end{array}~$$

Theorem 2.The mean square errors $P_{{z,t}}^{{{\text{opt}}}}$ and $P_{{z,t}}^{{{\text{sub}}}}$ are given by

$$P_{{z,t}}^{{{\text{opt}}}} = 4{\text{tr}}\left( {A{{P}_{t}}A{{C}_{t}}} \right) - 2{\text{tr}}\left( {A{{P}_{t}}A{{P}_{t}}} \right) + 4\mu _{t}^{{\text{T}}}A{{P}_{t}}A{{\mu }_{t}},$$

((3.8))

and

$$P_{{z,t}}^{{{\text{sub}}}} = 4{\text{tr}}\left( {A{{P}_{t}}A{{C}_{t}}} \right) - 2{\text{tr}}\left( {A{{P}_{t}}A{{P}_{t}}} \right) + {\text{t}}{{{\text{r}}}^{2}}\left( {A{{P}_{t}}} \right) + 4\mu _{t}^{{\text{T}}}A{{P}_{t}}A{{\mu }_{t}}$$

((3.9))

respectively. Here the unconditional mean ${{\mu }_{t}} = {\mathbf{E}}\left( {{{x}_{t}}} \right)$ and covariance ${{C}_{t}} = {\text{cov}}\left( {{{x}_{t}},{{x}_{t}}} \right)$ of the state vector x_tare determined by the equations of the method of moments [6],

$$\begin{gathered} {{{\dot {\mu }}}_{t}} = {{F}_{t}}{{\mu }_{t}},\quad t \geqslant 0,\quad {{\mu }_{0}} = {{{\bar {x}}}_{0}}, \\ {{{\dot {C}}}_{t}} = {{F}_{t}}{{C}_{t}} + {{C}_{t}}F_{t}^{{\text{T}}} + {{G}_{t}}{{Q}_{t}}G_{t}^{{\text{T}}},\quad {{C}_{0}} = {{P}_{0}}. \\ \end{gathered} $$

((3.10))

The derivation of the MSEs (3.8) and (3.9) is given in Appendix.

Note that the difference between $P_{{z,t}}^{{{\text{opt}}}}$ and $P_{{z,t}}^{{{\text{sub}}}}$ is equal $P_{{z,t}}^{{{\text{sub}}}} - P_{{z,t}}^{{{\text{opt}}}} = {\text{t}}{{{\text{r}}}^{2}}(A{{P}_{t}}).$

Thus, equations (3.8)–(3.10) completely define the true MSEs of the optimal and suboptimal quadratic estimators, respectively.

3.3. Theoretical and Practical Examples of Application of Quadratic Estimators

Example 6 (theoretical example—estimation of power of scalar signal). Let x_t be a scalar random signal measured in additive white noise. Then the system model is

$$\begin{gathered} {{{\dot {x}}}_{t}} = a{{x}_{t}} + {{v}_{t}},\quad t \geqslant 0,\quad a < 0,~~~~~ \\ {{y}_{t}} = {{x}_{t}} + {{w}_{t}}, \\ \end{gathered} $$

where ${{{v}}_{t}}$ and w_t are the uncorrelated white Gaussian noises with intensities q and r, respectively, and x₀ ~ $\mathbb{N}({{m}_{0}},\sigma _{0}^{2}).$

The KBF equations (2.1) give the following

$$\begin{gathered} {{{\hat {x}}}_{t}} = ~\;a{{{\hat {x}}}_{t}} + {{P}_{t}}\left( {{{y}_{t}} - {{{\hat {x}}}_{t}}} \right){\text{/}}r,\quad {{{\hat {x}}}_{0}} = {{m}_{0}}, \\ {{{\dot {P}}}_{t}} = 2a{{P}_{t}} - P_{t}^{2}{\text{/}}r + q,\quad {{P}_{0}} = \sigma _{0}^{2}. \\ \end{gathered} $$

Let consider power of the signal x_t, which is proportional to its square. Then ${{z}_{t}} = f({{x}_{t}}) = x_{t}^{2}$

Using (3.6) and (3.7) we obtain the optimal and suboptimal estimates of power of the signal, respectively,

$${{\hat {z}}_{t}} = \hat {x}_{t}^{2} + {{P}_{t}},\quad {{\tilde {z}}_{t}} = f({{\hat {x}}_{t}}) = \hat {x}_{t}^{2}.$$

Compare accuracy of the estimates. Using Theorem 2, we obtain the true MSEs,

$$\begin{gathered} P_{{z,t}}^{{{\text{opt}}}} = 4{{P}_{t}}{{C}_{t}} - 2P_{t}^{2} + 4\mu _{t}^{2}{{P}_{t}}, \\ P_{{z,t}}^{{{\text{sub}}}} = 4{{P}_{t}}{{C}_{t}} - P_{t}^{2} + 4\mu _{t}^{2}{{P}_{t}}, \\ \end{gathered} $$

where the mean μ_t and covariance C_t of the signal x_t are determined by (3.10) as follows:

$$\begin{array}{*{20}{c}} {{{{\dot {\mu }}}_{t}} = a{{\mu }_{t}},~\quad {{\mu }_{0}} = {{m}_{0}},} \\ {{{{\dot {C}}}_{t}} = 2a{{C}_{t}} + q,~\quad {{C}_{0}} = \sigma _{0}^{2}.} \end{array}$$

Figure 5 shows the relative error ${{\Delta }_{t}} = {\text{|}}(P_{{z,t}}^{{{\text{opt}}}} - P_{{z,t}}^{{{\text{sub}}}}){\text{/}}P_{{z,t}}^{{{\text{opt}}}}{\text{|}} \cdot 100\%$ for the values $a = - 1$, $q = 0.5$, ${{m}_{\theta }} = 0$, $\sigma _{\theta }^{2} = 4$, r = 0.1 From Fig. 5 we observe that the relative error Δ_t varies from 3 to 6% within the time zone $t \in [0.1;~~1.1]$, and then it increases. In steady-state regime t > 4 the relative error reaches the value ${{\Delta }_{\infty }} = 20.4{{\% }}$ and at the same time zone the absolute values of the MSEs are equal $P_{\infty }^{{{\text{opt}}}} = 0.1029$ and $P_{\infty }^{{{\text{sub}}}}$ = 0.1239. Thus the numerical results show that the suboptimal estimate ${{\tilde {z}}_{t}} = \hat {x}_{t}^{2}$ may be seriously worse than the optimal one ${{\hat {z}}_{t}} = \hat {x}_{t}^{2} + {{P}_{t}}.$

Fig. 5.

Relative error ${{\Delta }_{t}}$, % between optimal and suboptimal MSEs for quadratic estimators.

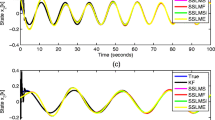
Example 7 (practical example—wind tunnel system). Here an experimental analysis of the quadratic estimators is considered on example of a total kinetic energy of the high-speed closed-air unit wind tunnel system [36]. The state vector ${{x}_{t}} \in {{\mathbb{R}}^{3}}$ consists of the state variables ${{x}_{{1t}}},\;~{{x}_{{2t}}}$ and ${{x}_{{3t}}},$ representing derivatives from a chosen equilibrium point of the following quantities: x₁—Mach number, x₂—actuator position guyde vane angle in a driving fan, and x₃—actuator rate. Then the system model is given by

$${{\dot {x}}_{t}} = \left[ {\begin{array}{*{20}{c}} {0.4032}&0&0 \\ 0&{0.1245}&{0.0701} \\ 0&{ - 2.5247}&{ - 0.5488} \end{array}} \right]{{x}_{t}} + {{v}_{t}},$$

where the initial conditions are ${{\bar {x}}_{0}} = {{\left[ {3~\;28\;10} \right]}^{{\text{T}}}}$ and ${{P}_{0}} = {\text{diag}}\left[ {1\;~1\;~0} \right]$.

Two sensory measurement model is given

$${{y}_{t}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&0&1 \end{array}} \right]{{x}_{t}} + {{w}_{t}}.$$

The intensities of the white noises ${{v}_{t}} \in {{\mathbb{R}}^{3}}$ and ${{w}_{t}} \in {{\mathbb{R}}^{2}}$ are subjected to $Q = {\text{diag}}\left[ {0.01\;0.01~\;0.01} \right]$ and $R = {\text{diag[}}0.05\,\,0.05{\text{]}}$, respectively.

The total kinetic energy of an actuator can be expressed as sum of the translational kinetic energy of the center of mass, ${{E}^{{tr}}} = mv_{t}^{2}{\text{/}}2$ and the rotational kinetic energy about the center of mass, ${{E}^{r}} = {\mathbf{I}}\omega _{t}^{2}{\text{/}}2$ where I is rotational inertia, ${{\omega }_{t}} = {{\dot {x}}_{{2t}}}$ is angular velocity, m is mass and ${{v}_{t}} = {{x}_{{3t}}}$ is linear velocity. Then the energy can be expressed in the following QF,

$$\begin{array}{*{20}{c}} {{{z}_{t}} = {{E}^{r}} + {{E}^{{tr}}} = \frac{1}{2}{\mathbf{I}}\dot {x}_{{2,t}}^{2} + \frac{1}{2}mx_{{3,t}}^{2} = X_{t}^{{\text{T}}}A{{X}_{t}},} \\ {{{X}_{t}} = {{{\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{x}_{{1,t}}}}&{{{x}_{{2,t}}}} \end{array}}&{\begin{array}{*{20}{c}} {{{x}_{{3,t}}}}&{{{{\dot {x}}}_{{2,t}}}} \end{array}} \end{array}} \right]}}^{{\text{T}}}},~} \\ {A = {\text{diag}}\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&0 \end{array}}&{\begin{array}{*{20}{c}} {m{\text{/}}2}&{{\mathbf{I}}{\text{/}}2} \end{array}} \end{array}} \right],} \end{array}$$

where ${{X}_{t}} \in {{\mathbb{R}}^{4}}$ is the extended state vector, and I= 0.136 kgm², m = 7.39 kg.

Using Theorem 1 the optimal and suboptimal quadratic estimators take the form

$${{\hat {z}}_{t}} = {\text{tr}}\left( {A{{P}_{t}}} \right) + \hat {X}_{t}^{{\text{T}}}A{{\hat {X}}_{t}},~~~{{\tilde {z}}_{t}} = \hat {X}_{t}^{{\text{T}}}A{{\hat {X}}_{t}},$$

where the estimate of the state ${{\hat {X}}_{t}} \in {{\mathbb{R}}^{4}}$ and error covariance ${{P}_{t}} \in {{\mathbb{R}}^{{4 \times 4}}}$ are determined by (2.1).

Our point of interest is behavior of the MSEs, $P_{{z,t}}^{{{\text{opt}}}}$ = E[(z_t – ${{\hat {z}}_{t}}$)²] and $P_{{z,t}}^{{{\text{sub}}}}$ = E[(z_t – ${{\tilde {z}}_{t}}$)²] which can be calculated by using Theorem 2. We observe in Figure 6 that the optimal estimator has the best performance in contrast to the suboptimal one, i.e., $P_{{z,t}}^{{{\text{opt}}}}$ < $P_{{z,t}}^{{{\text{sub}}}}$. The relative error Δ_t varies from 6.2 to 10% within the initial zone, t ∈ [0.02; 0.07] of operation of the system, and then it decreases. In time zone, t > 0.07 the values of the MSEs and relative error are equal $P_{{z,t}}^{{{\text{opt}}}}$ = 0.89, $P_{{z,t}}^{{{\text{sub}}}}$ = 0.94, and Δ_t = 5.6%, respectively.

Fig. 6.

Comparison of MSEs for total kinetic energy z_t with using optimal and suboptimal quadratic estimators: $P_{t}^{{{\text{opt}}}}$ (solid curve), $P_{t}^{{{\text{sub}}}}$ (dotted curve).

As a result, we confirm that the proposed optimal quadratic estimator is more suitable for data processing in practice.

CONCLUSIONS

In some application problems, nonlinear function of state variables contains useful information of the target systems for control. In order to estimate an arbitrary NFS, an optimal two-stage MMSE estimation algorithm is proposed. At the first stage, a preliminary state estimate from the standard KBF method is calculated. And next the computed estimate is used at the second stage for the MMSE estimation of an NFS.

Particular attention is given for a polynomial functions of a state. In this case, it is possible to derive a closed-form polynomial estimator, which depends only on a parameters of the KBF. Interpretation of a quadratic functional as power or energy is considered in Examples 6 and 7.

In a view of importance of an NFS for practice, the proposed estimation algorithms are illustrated on theoretical and numerical examples for a real NFS. The examples show that the optimal MMSE estimator yields reasonably good estimation accuracy.

Using the MMSE method, an optimal two-stage nonlinear estimator is proposed. We establish that the polynomial estimators (quadratic, cubic and quartic) can be represented a compact closed-forms which depend only on the KBF characteristics (Theorem 1). An important class of quadratic functional is comprehensively investigated, including derivation of a matrix equations for a true MSE (Theorem 2). Performance of the proposed estimators for real NFS illustrates their theoretical and practical usefulness.

APPENDIX

Proof of Theorem 1. The derivation of the polynomial estimators (3.2) is based on the Lemma 1.

Lemma 1. Let $x \in {{\mathbb{R}}^{n}}$ be a Gaussian random vector, $x \sim \mathbb{N}(\mu ,S)$ and $A,B \in {{\mathbb{R}}^{{n \times n}}}$ be an arbitrary matrices. Then it holds that

$$\begin{gathered} {\mathbf{E}}(Ax) = A\mu ; \\ {\mathbf{E}}({{x}^{{\text{T}}}}Ax) = {\text{tr}}(AS) + {{\mu }^{{\text{T}}}}A\mu ,\quad A = {{A}^{{\text{T}}}}; \\ {\mathbf{E}}(Ax{{x}^{{\text{T}}}}Bx) = 2ASB\mu + A\mu {{\mu }^{{\text{T}}}}B\mu + A\mu {\text{tr}}(BS); \\ E({{x}^{T}}Ax{{x}^{T}}Bx) = 2tr(ASBS) + 4{{\mu }^{T}}ASB\mu \\ \, + [{\text{tr}}(AS) + {{\mu }^{T}}A\mu {\text{][tr}}(BS) + {{\mu }^{T}}B\mu ],\quad A = {{A}^{{\text{T}}}},\quad B = {{B}^{{\text{T}}}}. \\ \end{gathered} $$

((A.1))

The derivation of the formulas (A.1) is based on their scalar versions given in [37, 38], and standard transformations on random vectors.

This completes the proof of Lemma 1.

Next, replacing in (A.1) an unconditional expectations and covariance by their conditional versions, for example, $\mu \to {\mathbf{E}}(x {\text{|}}{\kern 1pt} y_{0}^{t}) = \hat {x}$, S → ${\text{cov(}}\hat {x},\hat {x} {\text{|}}{\kern 1pt} y_{0}^{t}{\text{)}}$ = P we obtain (3.2).

This completes the proof of Theorem 1.

Proof of Theorem 2. The derivation of the MSEs is based on the Lemma 2.

Lemma 2.Let $X \in {{\mathbb{R}}^{{3n}}}$ be a composite multivariate Gaussian vector, ${{X}^{{\text{T}}}} = [{{U}^{{\text{T}}}}\;{{V}^{T}}\;{{W}^{T}}]$:

$$\begin{gathered} X\sim \mathbb{N}(\mu ,S),\quad U,V,W \in {{\mathbb{R}}^{n}}, \\ \mu = \left[ \begin{gathered} {{\mu }_{u}} \\ {{\mu }_{{v}}} \\ {{\mu }_{w}} \\ \end{gathered} \right],\quad S = \left[ {\begin{array}{*{20}{c}} {{{S}_{{uu}}}}&{{{S}_{{u{v}}}}}&{{{S}_{{uw}}}} \\ {{{S}_{{{v}u}}}}&{{{S}_{{{vv}}}}}&{{{S}_{{{v}w}}}} \\ {{{S}_{{wu}}}}&{{{S}_{{w{v}}}}}&{{{S}_{{ww}}}} \end{array}} \right]. \\ \end{gathered} $$

((A.2))

Then the third- and fourth-order vector moments of the composite random vector are given by

$$\begin{gathered} {\mathbf{E}}({{U}^{{\text{T}}}}VW) = \mu _{u}^{{\text{T}}}{{\mu }_{{v}}}{{\mu }_{w}} + {\text{tr}}({{S}_{{u{v}}}})\mu _{w}^{{\text{T}}} + \mu _{{v}}^{{\text{T}}}{{S}_{{uw}}} + \mu _{u}^{{\text{T}}}{{S}_{{{v}w}}}; \\ {\mathbf{E}}({{U}^{{\text{T}}}}U{{V}^{{\text{T}}}}V) = \mu _{u}^{{\text{T}}}{{\mu }_{u}}\mu _{{v}}^{{\text{T}}}{{\mu }_{{v}}} + 2{\text{tr}}({{S}_{{u{v}}}}{{S}_{{{v}u}}}) + {\text{tr}}({{S}_{{uu}}}){\text{tr}}({{S}_{{{vv}}}}) \\ \, + {\text{tr}}({{S}_{{uu}}})\mu _{{v}}^{{\text{T}}}{{\mu }_{{v}}} + {\text{tr}}({{S}_{{{vv}}}})\mu _{u}^{{\text{T}}}{{\mu }_{u}} + 4\mu _{u}^{{\text{T}}}{{S}_{{u{v}}}}{{\mu }_{{v}}}; \\ {\mathbf{E}}({{U}^{{\text{T}}}}V{{V}^{{\text{T}}}}U) = \mu _{u}^{{\text{T}}}{{\mu }_{{v}}}\mu _{{v}}^{{\text{T}}}{{\mu }_{u}} + {\text{tr}}({{S}_{{uu}}}{{S}_{{{vv}}}}) + {\text{tr}}({{S}_{{u{v}}}}){\text{tr}}({{S}_{{{v}u}}}) \\ \, + {\text{tr}}(S_{{u{v}}}^{2}) + \mu _{{v}}^{{\text{T}}}{{S}_{{uu}}}{{\mu }_{{v}}} + \mu _{u}^{{\text{T}}}{{S}_{{{vv}}}}{{\mu }_{u}} + \mu _{u}^{{\text{T}}}{{S}_{{u{v}}}}{{\mu }_{u}} + \mu _{u}^{{\text{T}}}{{S}_{{{v}u}}}{{\mu }_{{v}}} + 2{\text{tr}}({{S}_{{u{v}}}})\mu _{u}^{{\text{T}}}{{\mu }_{{v}}}; \\ {\mathbf{E}}({{U}^{{\text{T}}}}V{{W}^{{\text{T}}}}U) = \mu _{u}^{{\text{T}}}{{\mu }_{{v}}}\mu _{w}^{{\text{T}}}{{\mu }_{u}} + {\text{tr}}({{S}_{{u{v}}}}){\text{tr}}({{S}_{{uw}}}) + {\text{tr}}({{S}_{{uu}}}{{S}_{{w{v}}}}) \\ \, + {\text{tr}}({{S}_{{uw}}}{{S}_{{u{v}}}}) + {\text{tr}}({{S}_{{u{v}}}})\mu _{u}^{{\text{T}}}{{\mu }_{w}} + {\text{tr}}({{S}_{{uw}}})\mu _{u}^{{\text{T}}}{{\mu }_{{v}}} \\ \, + \mu _{{v}}^{{\text{T}}}{{S}_{{uu}}}{{\mu }_{w}} + \mu _{{v}}^{{\text{T}}}{{S}_{{uw}}}{{\mu }_{u}} + \mu _{u}^{{\text{T}}}{{S}_{{{v}u}}}{{\mu }_{w}} + \mu _{u}^{{\text{T}}}{{S}_{{{v}w}}}{{\mu }_{u}}. \\ \end{gathered} $$

((A.3))

The derivation of the vector formulas (A.3) is based on their scalar versions, and standard matrix manipulations,

$$\begin{gathered} {\mathbf{E}}\left( {{{x}_{i}}{{x}_{j}}{{x}_{k}}} \right) = {{\mu }_{i}}{{\mu }_{j}}{{\mu }_{k}} + {{\mu }_{i}}{{S}_{{jk}}} + {{\mu }_{j}}{{S}_{{ik}}} + {{\mu }_{k}}{{S}_{{ij}}};~~~ \\ {\mathbf{E}}\left( {{{x}_{i}}{{x}_{j}}{{x}_{k}}{{x}_{\ell }}} \right) = {{\mu }_{i}}{{\mu }_{j}}{{\mu }_{k}}{{\mu }_{\ell }} + {{S}_{{ij}}}{{S}_{{k\ell }}} + {{S}_{{ik}}}{{S}_{{\ell j}}} + {{S}_{{i\ell }}}{{S}_{{jk}}} + {{\mu }_{i}}{{\mu }_{j}}{{S}_{{k\ell }}} + {{\mu }_{i}}{{\mu }_{k}}{{S}_{{j\ell }}} + {{\mu }_{i}}{{\mu }_{\ell }}{{S}_{{jk}}} \\ \, + \;~{{\mu }_{j}}{{\mu }_{k}}{{S}_{{i\ell }}} + {{\mu }_{j}}{{\mu }_{\ell }}{{S}_{{ik}}} + {{\mu }_{k}}{{\mu }_{\ell }}{{S}_{{ij}}},~ \\ \end{gathered} $$

((A.4))

where ${{\mu }_{h}} = {\mathbf{E}}({{x}_{h}})$, ${{S}_{{pq}}} = {\text{cov(}}{{x}_{p}},{{x}_{q}}{\text{)}}$.

This completes the proof of Lemma 2.

Further, we derive the formula (3.8). Using (3.5) and (3.6), the error can be written as

$$\begin{gathered} {{e}_{z}} = z - \hat {z} = {{x}^{{\text{T}}}}Ax - {\text{tr}}\left( {AP} \right) - {{{\hat {x}}}^{{\text{T}}}}A\hat {x} = {{\left( {e + \hat {x}} \right)}^{{\text{T}}}}A\left( {e + \hat {x}} \right) - {{{\hat {x}}}^{{\text{T}}}}A\hat {x} - {\text{tr}}\left( {AP} \right)~ \\ \; = {{e}^{{\text{T}}}}Ae + 2{{e}^{{\text{T}}}}A\hat {x} - {\text{tr}}\left( {AP} \right),\quad e = x - \hat {x},\quad {{{\hat {x}}}^{{\text{T}}}}Ae = {{e}^{{\text{T}}}}A\hat {x}. \\ \end{gathered} $$

((A.5))

Next, using the unbiased and orthogonality properties of the Kalman estimate ${\mathbf{E}}\left( e \right) = {\mathbf{E}}(e{{\hat {x}}^{{\text{T}}}}) = 0,$ we obtain

$$\begin{gathered} P_{z}^{{{\text{opt}}}} = {\mathbf{E}}({{e}^{{\text{T}}}}Ae{{e}^{{\text{T}}}}Ae) + 2{\mathbf{E}}({{e}^{{\text{T}}}}A\hat {x}{{e}^{{\text{T}}}}Ae) \\ \, - {\text{tr}}(AP){\mathbf{E}}({{e}^{{\text{T}}}}Ae) + 2{\mathbf{E}}({{e}^{{\text{T}}}}Ae{{e}^{{\text{T}}}}A\hat {x}) \\ \, + 4{\mathbf{E}}({{e}^{{\text{T}}}}A\hat {x}{{e}^{{\text{T}}}}A\hat {x}) - 2{\text{tr}}(AP){\mathbf{E}}({{e}^{{\text{T}}}}A\hat {x}) \\ \, - {\text{tr}}(AP){\mathbf{E}}({{e}^{{\text{T}}}}Ae) - 2{\text{tr}}(AP){\mathbf{E}}({{e}^{{\text{T}}}}A\hat {x}) + {\text{t}}{{{\text{r}}}^{2}}(AP). \\ \end{gathered} $$

((A.6))

Using Lemma 2 we can calculate high-order moments in (A.6). We have

$$\begin{gathered} {\mathbf{E}}({{e}^{{\text{T}}}}Ae) = {\text{tr}}\left( {AP} \right),~~~{\mathbf{E}}({{e}^{{\text{T}}}}A\hat {x}) = 0,\quad {\mathbf{E}}({{e}^{{\text{T}}}}Ae{{e}^{{\text{T}}}}Ae) = {\text{t}}{{{\text{r}}}^{2}}\left( {AP} \right) + 2{\text{tr}}\left( {APAP} \right), \\ {\mathbf{E}}({{e}^{{\text{T}}}}A\hat {x}{{e}^{{\text{T}}}}Ae) = {\mathbf{E}}({{e}^{{\text{T}}}}Ae{{e}^{{\text{T}}}}A\hat {x}) = 0,\quad {\mathbf{E}}({{e}^{{\text{T}}}}A\hat {x}{{e}^{{\text{T}}}}A\hat {x}) = {\mathbf{E}}({{e}^{{\text{T}}}}A\hat {x}{{{\hat {x}}}^{{\text{T}}}}Ae) = {\text{tr}}\left( {PA{{C}_{{\hat {x}\hat {x}}}}A} \right) + {{\mu }^{{\text{T}}}}AP\mu , \\ \end{gathered} $$

((A.7))

where

$$\begin{gathered} \mu = {\mathbf{E}}\left( x \right) = {\mathbf{E}}\left( {\hat {x}} \right),\quad {\text{cov}}\left( {Ae,Ae} \right) = AP{{A}^{{\text{T}}}}, \\ {{C}_{{\hat {x}\hat {x}}}} = C - P,~~~P = {\text{cov}}\left( {e,e} \right),\quad C = {\text{cov}}\left( {x,x} \right). \\ \end{gathered} $$

((A.8))

Substituting (A.7) in (A.6), and after some manipulations, we get the optimal MSE (3.8).

In the case of the suboptimal estimate $\tilde {z},$ the derivation of the MSE (3.9) is similar.

This completes the proof of Theorem 2.