A Dynamic-State Feedback Approach Employing a New State-Space Description for the Fast Wavelet Transform with Multiple Decomposition Levels

Abstract

This research paper proposes a wavelet-based dynamic-state feedback control strategy in the discrete time domain. In this proposal, the state feedback employs a state-space description for the fast wavelet transform, which is also developed in this article. The feedback gains are obtained through a linear quadratic regulator formulation, with cost weights adjusted according to suitable performance metrics. This proposal brings forward efficient results, as well as more robust systems to external perturbations and sensor noises.

1 Introduction

Linear quadratic regulator (LQR) is an automated way of finding an appropriate state feedback controller, which has been used in various applications (Zhang and Fu 1996; Fernando and Kumarawadu 2015; Pradhan and Ghosh 2015; Liu et al. 2013; Zhang et al. 2014). The LQR provides a key role in many control design methods. Besides being a powerful design method, it is in many aspects the principle of several current systematic control design procedures. Both the linear quadratic Gaussian or $H_2$ , and $H_\infty$ controller design procedures have usage and philosophy similar to the LQR methodology (Lublin and Athans 1996; Maccari et al. 2014).

Improving stability margins via dynamic-state feedback for systems is well studied in Zhang and Fu (1996), Schmitendorf and Stalford (1997), Holmberg et al. (2001), Ulsoy (2013), Ulsoy (2015) and Verdea et al. (2013). By analyzing robustness properties of the LQR, in Schmitendorf and Stalford (1997), Holmberg et al. (2001), it has shown that the guaranteed gain/phase margins of LQR need to be carefully interpreted. This analysis leads to the discussion of using dynamic-state feedback. Furthermore, the stability margin for a linear system with constant uncertainty can be increased beyond that attainable by a static-state feedback with the use of a dynamic-state feedback controller (Zhang and Fu 1996).

In this paper, a dynamic-state feedback control approach employing a new state-space description for the multi-level fast wavelet transform (FWT) is proposed. The main characteristic that makes the proposed approach efficient and easy to implement is the use of the standard discrete linear quadratic regulator. This proposal is justified by the fact of getting more robust systems resistant to perturbations and measuring noise.

The state-space description mentioned is developed from a previous paper that presents the state-space description for single-level decomposition of the FWT algorithm (Uzinski et al. 2015). In the state-space description for the entire filter bank with M decomposition levels, the outputs are the approximation in the last level and the details in all levels as in the FWT algorithm. The main characteristics presented by the single-level formulation are carried to the description for multi-level decomposition, as the explicit presence of parameters that can be freely adjusted holding the guarantees of perfect reconstruction and orthogonality. The state-space realization proposed to represent the filter bank with M levels is controllable and observable.

The paper is organized into three main parts: Sect. 2 deals with the development of the state-space for multi-level wavelet filter bank and its background, Sect. 3 presents the proposed dynamic-state feedback approach, and Sect.  4 contains results and analysis.

2 State-Space for Multi-Level FWT

2.1 On the Space of Orthonormal Wavelets

By adapting the work of Vaidyanathan (1993) on the factorization of paraunitary matrices and parameterizing the space of orthonormal wavelets by a set of angular parameters, Sherlock and Monro (1998) devised a simple and elegant framework to parameterize the space of orthonormal wavelets by a set of angular parameters (Paiva et al. 2009; Paiva and Galvão 2012). Sherlock and Monro’s formulation is presented in the following.

Let $H^{(N)}(z)$ and $G^{(N)}(z)$ be the transfer functions of the low-pass and high-pass filters, respectively, for an orthonormal filter bank with length-2N, such that

$$\begin{aligned} H^{(N)}(z)=\sum _{i=0}^{2N-1}h_i^{(N)}z^{-i} \end{aligned}$$

(1)

and

$$\begin{aligned} G^{(N)}(z)=\sum _{i=0}^{2N-1}g_i^{(N)}z^{-i}, \end{aligned}$$

(2)

where

$$\begin{aligned} g_i^{(N)}=(-1)^{i+1}h^{(N)}_{2N-1-i}, \qquad i=0,1,\cdots ,2N-1, \end{aligned}$$

(3)

and

$$\begin{aligned} \begin{array}{ll} h_0^1=\cos (\alpha _1)\\ h_1^1=\sin (\alpha _1)\\ h_0^{N+1}=\cos (\alpha _{N+1})h_0^N\\ h_{2i}^{N+1}=\cos (\alpha _{N+1})h_{2i}^N-\sin (\alpha _{N+1})h_{2i-1}^N,\\ h_{2N}^{N+1}=-\sin (\alpha _{N+1})h_{2N-1}^N\\ h_1^{N+1}=\sin (\alpha _{N+1})h_0^N\\ h_{2i+1}^{N+1}=\sin (\alpha _{N+1})h_{2i}^N+\cos (\alpha _{N+1})h_{2i-1}^N,\\ h_{2N+1}^{N+1}=\cos (\alpha _{N+1})h_{2N-1}^N \end{array} \end{aligned}$$

(4)

with $i=0,1,\cdots ,N-1$. In (4), $\alpha =\left[ \begin{array}{cccc} \alpha _1&\alpha _2&\cdots&\alpha _N \end{array} \right]$ is the angular parameter set, following the notation defined in the original work of Sherlock and Monro (1998.)

Let u[k] be an input signal processed in a level of the discrete wavelet transform (DWT). It has two outputs, $y_1$ and $y_2$ corresponding to the input signal filtered by the low-pass filter and by the high-pass filter, respectively. This filtering process for one decomposition level can be seen through the implementation of these filters in lattice structure, Fig. 1.

Fig. 1

A DWT decomposition level represented by a lattice structure. Adapted from Akansu and Haddad (2001)

In Fig. 1, symbols $C_i$ and $S_i$ denote $\sin ({\varTheta }_i)$ and $\cos ({\varTheta }_i)$, respectively, where

${\varTheta }= \left[ \begin{array}{cccc} {\varTheta }_1&{\varTheta }_2&\cdots&{\varTheta }_N \end{array} \right]$ and ${\varTheta }_1 =\alpha _N$, ${\varTheta }_2=\alpha _{N-1}$, $\cdots$, ${\varTheta }_N=\alpha _1$.

2.2 A State-Space Description for One Single Decomposition Level of a Wavelet Filter Bank

According to Uzinski et al. (2015), the model for a single-level in the state-space takes the form

$$\begin{aligned}&\mathbf{x }[k+1] = \mathbf{Ax }[k]+\mathbf{Bu }[k] \end{aligned}$$

(5)

$$\begin{aligned}&\mathbf{y }[k] = \mathbf{Cx }[k]+\mathbf{Du }[k]. \end{aligned}$$

(6)

where $\mathbf{x }=[\begin{array}{cccc}x_1&x_2&\cdots&x_{2N-1}\end{array}]^T$ and k denotes the kth sampling instant. This state-space description was obtained through the procedure shown in Fig. 2.

Fig. 2

Parameterization of the filter bank in the state-space. Adapted from Uzinski et al. (2015)

In (5) and (6), $\mathbf{A }$, $\mathbf{B }$, $\mathbf{C }$ and $\mathbf{D }$ are given by (7), (8), (9) and (10), respectively.

$$\begin{aligned} \mathbf{A }= & {} \left[ \begin{array}{ccccccccccc} 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 1\\ C_1 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 \\ -S_2S_1 &{} C_2 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 \\ -S_3C_2S_1 &{} -S_3S_2 &{} C_3 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ S_{N-1}S_1\prod _{i=2}^{N-2}C_i &{} S_{N-1}S_2\prod _{i=3}^{N-2}C_i &{} S_{N-1}S_3\prod _{i=4}^{N-2}C_i &{} \cdots &{} C_{N-1} &{} 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 \end{array} \right] , \end{aligned}$$

(7)

$$\begin{aligned} \mathbf{B }= & {} \left[ \begin{array}{c} 1 \\ 0 \\ \vdots \\ 0 \\ -S_1\\ -S_2C_1\\ \vdots \\ -S_{N-1}\prod _{i=1}^{N-2}C_i \end{array} \right] . \end{aligned}$$

(8)

$$\begin{aligned} \mathbf{C }= & {} \left[ \begin{array}{ccccccccc} S_1\prod _{i=2}^NC_i &{} S_2\prod _{i=3}^NC_i &{} \cdots &{} S_{N-2}\prod _{i=N-1}^NC_i &{} S_{N-1}C_N &{} S_N &{} 0 &{} \cdots &{} 0\\ -S_NS_1\prod _{i=2}^{N-1}C_i &{} -S_NS_2\prod _{i=3}^{N-1}C_i &{} \cdots &{} -S_NS_{N-2}\prod _{i=N-1}^{N-1}C_i &{} -S_NS_{N-1} &{} C_N&{} 0 &{} \cdots &{} 0 \end{array}\right] \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$

(9)

$$\begin{aligned} \mathbf{D }= & {} \left[ \begin{array}{c} \prod _{i=1}^NC_i \\ -S_N\prod _{i=1}^{N-1}C_i \end{array}\right] , \end{aligned}$$

(10)

Fig. 3

Three-level binary tree-structured quadrature mirror filter (QMF) bank. Adapted from Vaidyanathan (1993)

The sizes of matrices A, B, C and D are $(2N-1)\times (2N-1)$, $(2N-1)\times 1$, $2 \times (2N-1)$ and $2\times 1$, respectively. An important feature of this realization ($\mathbf{A }$, $\mathbf{B }$, $\mathbf{C }$, $\mathbf{D }$) is that it is minimal, namely reachable and observable. Further discussions, proof and illustrative examples can be found in Uzinski et al. (2015).

2.3 Wavelet Filter Bank and the Algorithme à Trous

After recalling the theory about the parameterization for the ith decomposition level, it is necessary to show how the fast wavelet transform (FWT) works. This method uses digital filter banks in a tree structure, as shown as an example with three decomposition levels, in Fig. 3. In this figure, H(z) and G(z) indicate the low-pass and high-pass filters and $\downarrow 2$ denotes the downsampling operators (Vaidyanathan 1993).

An equivalent implementation for the FWT, Fig. 3, avoiding the downsampling operations in each decomposition level is the Algorithme à Trous (algorithm with “holes”) (Vetterli and Kovačevi 1995), Fig. 4.

Fig. 4

Equivalent filter bank to the one in Fig. 3 using the Algorithme à Trous. Adapted from Vetterli and Kovačevi (1995)

As stated by Paiva (2005), Vetterli and Kovačevi (1995), the relationship between the coefficients $\mathbf y _i[k]$ (FWT) and $\underline{\mathbf{y }}_i[k]$ (Algorithme à Trous) is

$$\begin{aligned} \mathbf y _i[k]=(\downarrow 2^i)\underline{\mathbf{y }}_i[k]. \end{aligned}$$

(11)

The Algorithme à Trous is used in the new state-space description for the multi-level FWT proposed in this paper.

2.4 The State-Space Parameterization for Multiple Decomposition Levels

In this subsection, the parameterization for one single decomposition level of a wavelet filter bank presented in Uzinski et al. (2015) is extended for M decomposition levels of a perfect-reconstruction wavelet filter bank, which is known as fast wavelet transform. The Algorithme à Trous, which was described in Sect. 2.3, was adopted to overcome the difficulties associated with the downsampling operations.

The state vector associated with the lattice in the ith decomposition level has $2N-1$ states and it is denoted by

$$\begin{aligned} \mathbf{x }_i[k]=\left[ \begin{array}{c} x_{i,1}[k] \\ x_{i,2}[k] \\ x_{i,3}[k] \\ \vdots \\ x_{i,2N-1}[k] \end{array} \right] , \end{aligned}$$

(12)

the output in the ith decomposition level with $\underline{y}_{i,1}[k]$ and $\underline{y}_{i,2}[k]$ associated with the low-pass and high-pass channels, respectively, by

$$\begin{aligned} {{{\underline{\varvec{y}}}}}_i[k]=\left[ \begin{array}{c} \underline{y}_{i,1}[k] \\ \underline{y}_{i,2}[k] \end{array} \right] , \end{aligned}$$

(13)

and the matrices C and D are conveniently rewritten as

$$\begin{aligned} \mathbf C =\left[ \begin{array}{c} \mathbf C _1 \\ \mathbf C _2 \end{array}\right] \end{aligned}$$

and

$$\begin{aligned} \mathbf D =\left[ \begin{array}{c} D_1 \\ D_2 \end{array}\right] . \end{aligned}$$

The state-space description for a single decomposition level i of a wavelet filter bank as previously presented and its denotations are shown in Fig. 5.

Fig. 5

Representation of the state-space description for a single decomposition level i of a wavelet filter bank

In Fig. 5, the input $\underline{y}_{i-1,1}[k]$ at level i is the low-pass output at the level $i-1$. The elements $\mathbf x _i[k]$, $\underline{y}_{i,1}[k]$ and $\underline{y}_{i,2}[k]$ are the state variable and two outputs in the ith decomposition level (algorithm with “holes”), respectively.

By considering the state-space description for the ith decomposition level and recalling the Algorithme à Trous, the lattice model in the first decomposition level has the form

$$\begin{aligned}&\mathbf{x }_1[k+1] = \mathbf{Ax }_1[k]+\mathbf{B }u[k],\end{aligned}$$

(14)

$$\begin{aligned}&{{{\underline{\varvec{y}}}}}_1[k] = \left[ \begin{array}{c} \mathbf{C }_1 \\ \mathbf{C }_2 \end{array} \right] \mathbf{x }_1[k]+\left[ \begin{array}{c} D_1 \\ D_2 \end{array} \right] u[k], \end{aligned}$$

(15)

while for $i>1$ it is

$$\begin{aligned}&\mathbf{x }_i[k+2^{i-1}]= \mathbf{Ax }_i[k]+\mathbf{B }\underline{y}_{i-1,1}[k],\end{aligned}$$

(16)

$$\begin{aligned}&{{{\underline{\varvec{y}}}}}_i[k] = \left[ \begin{array}{c} \mathbf{C }_1 \\ \mathbf{C }_2 \end{array} \right] \mathbf{x }_i[k]+\left[ \begin{array}{c} D_1 \\ D_2 \end{array} \right] \underline{y}_{i-1,1}[k]. \end{aligned}$$

(17)

The Algorithme à Trous (Fig. 4) employs filters of the form $H(z^2)$, $H(z^4)$, $H(z^8)$ and so on. It should be noted that $H(z^2)$ is twice as longer as H(z). This difference in the filter length is taken into account in (16). In fact, to understand this point, consider $i = 2$ in (16). In this case

$$\begin{aligned} \mathbf x _{2}[k+2] = \mathbf Ax _{2} [k] + \mathbf B \underline{y}_{1,1} [k]. \end{aligned}$$

(18)

Considering an additional state vector $\mathbf w [k] = \mathbf x _{2}[k+1]$, (18) could be rewritten as

$$\begin{aligned}&{} \mathbf w [k+1] = \mathbf Ax _{2} [k] + \mathbf B \underline{y}_{1,1} [k] \end{aligned}$$

(19)

$$\begin{aligned}&{} \mathbf x _{2}[k+1] = \mathbf w [k], \end{aligned}$$

(20)

that is:

(21)

where I is an identity matrix and 0 is a null matrix. Therefore, using $\mathbf x _{2}[k+2]$ in (16) is equivalent to using more states to describe a longer filter. For $i=2$, $\mathbf x _2[k+2]$ it is necessary to use twice as many states. For $i=3$, $\mathbf x _3[k+4]$ it means that four times as many states are necessary and so on.

Taking the entire analysis filter bank, the following state vector can be defined as the filter bank with M decomposition levels, Fig. 6,

$$\begin{aligned} \mathbf{x }[k]=\left[ \begin{array}{c} \mathbf{x }_1[k] \\ \mathbf{x }_2[k] \\ \mathbf{x }_3[k] \\ \vdots \\ \mathbf{x }_M[k] \end{array} \right] . \end{aligned}$$

(22)

When the “holes” are considered, the equation for the filter bank can be written as

$$\begin{aligned} \left[ \begin{array}{c} \mathbf{x }_1[k+1] \\ \mathbf{x }_2[k+2] \\ \vdots \\ \mathbf{x }_M[k+2^{M-1}] \end{array} \right]= & {} \left[ \begin{array}{c} \mathbf{Ax }_1[k]+\mathbf{B }u[k] \\ \mathbf{Ax }_2[k]+\mathbf{B }\underline{y}_{1,1}[k] \\ \vdots \\ \mathbf{Ax }_M[k]+\mathbf{B }\underline{y}_{M-1,1}[k] \end{array} \right] , \end{aligned}$$

then

$$\begin{aligned}&\left[ \begin{array}{c} \mathbf{x }_1[k+1] \\ \mathbf{x }_2[k+2] \\ \vdots \\ \mathbf{x }_M[k+2^{M-1}] \end{array} \right] \nonumber \\&\quad =\left[ \begin{array}{cccc} \mathbf{A } &{} 0 &{} \cdots &{} 0 \\ \mathbf{BC }_1 &{} \mathbf{A } &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \mathbf{B }D_1^{M-2}\mathbf{C }_1 &{} \cdots &{} \mathbf{BC }_1 &{} \mathbf{A } \end{array} \right] \left[ \begin{array}{c} \mathbf{x }_1[k] \\ \mathbf{x }_2[k] \\ \vdots \\ \mathbf{x }_M[k] \end{array} \right] \nonumber \\&\quad +\left[ \begin{array}{c} \mathbf{B } \\ \mathbf{B }D_1 \\ \vdots \\ \mathbf{B }D_1^{M-1} \end{array} \right] u[k]. \end{aligned}$$

(23)

Fig. 6

Wavelet filter bank with M decomposition levels seen as state-space description

Let ${{{\underline{\varvec{y}}}}}[k]$ be the output vector, comprising the approximation in the last level and details in all levels, defined as

$$\begin{aligned} {{{\underline{\varvec{y}}}}}[k]=\left[ \begin{array}{c} \underline{y}_{M,1}[k] \\ \underline{y}_{M,2}[k] \\ \underline{y}_{M-1,2}[k] \\ \vdots \\ \underline{y}_{1,2}[k] \end{array} \right] , \end{aligned}$$

(24)

the output equation can be finally written for the filter bank as follows:

$$\begin{aligned} {{{\underline{\varvec{y}}}}}[k]= & {} \left[ \begin{array}{c} \mathbf{C }_1\mathbf{x }_M[k]+D_1\underline{y}_{M-1,1}[k] \\ \mathbf{C }_2\mathbf{x }_M[k]+D_2\underline{y}_{M-1,1}[k] \\ \mathbf{C }_2\mathbf{x }_{M-1}[k]+D_2\underline{y}_{M-2,1}[k] \\ \vdots \\ \mathbf{C }_2\mathbf{x }_1[k]+D_2u[k] \end{array} \right] , \end{aligned}$$

thus

$$\begin{aligned} \left[ \begin{array}{c} \underline{y}_{M,1}[k] \\ \underline{y}_{M,2}[k] \\ \underline{y}_{M-1,2}[k] \\ \vdots \\ \underline{y}_{1,2}[k] \end{array} \right]= & {} \left[ \begin{array}{ccccc} D_1^{M-1}\mathbf{C }_1 &{} \cdots &{} D_1^{2}\mathbf{C }_1 &{} D_1\mathbf{C }_1 &{} \mathbf{C }_1 \\ D_2D_1^{M-2}\mathbf{C }_1 &{} \cdots &{} D_2D_1\mathbf{C }_1 &{} D_2\mathbf{C }_1 &{} \mathbf{C }_2 \\ D_2D_1^{M-3}\mathbf{C }_1 &{} \cdots &{} D_2\mathbf{C }_1 &{} \mathbf{C }_2 &{} 0 \\ \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots \\ \mathbf{C }_2 &{} \cdots &{} 0 &{} 0 &{} 0 \end{array} \right] \left[ \begin{array}{c} \mathbf{x }_1[k] \\ \mathbf{x }_2[k] \\ \mathbf{x }_3[k] \\ \vdots \\ \mathbf{x }_M[k] \end{array} \right] \nonumber \\&+\left[ \begin{array}{c} D_1^M \\ D_2D_1^{M-1} \\ D_2D_1^{M-2} \\ \vdots \\ D_2 \end{array} \right] u[k]. \end{aligned}$$

(25)

After all, the version to Fig. 5 for the M decomposition levels proposal, as previously obtained, is presented in Fig. 6.

However, (23) is not the state equation for multi-level FWT, some changes are required, and changes in (23) will imply other changes in (25).

Suitably defining

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} x_{M+1}[k]=x_2[k+1],\\ \end{array}\right. \\ \\ \left\{ \begin{array}{l} x_{M+2}[k]=x_3[k+1],\\ x_{M+3}[k]=x_{M+2}[k+1],\\ x_{M+4}[k]=x_{M+3}[k+1],\\ \end{array}\right. \\ \\ \left\{ \begin{array}{l} x_{M+5}[k]=x_4[k+1],\\ x_{M+6}[k]=x_{M+5}[k+1],\\ \qquad \vdots \\ x_{M+11}[k]=x_{M+10}[k+1],\\ \end{array}\right. \\ \\ \qquad \mathbf \vdots \\ \\ \left\{ \begin{array}{l} x_{M+\varepsilon +1}[k]=x_M[k+1],\\ x_{M+\varepsilon +2}[k]=x_{M+\varepsilon +1}[k+1],\\ \qquad \vdots \\ x_{M+\varepsilon +2^{M-1}-1}[k]=x_{M+\varepsilon +2^{M-1}-2}[k+1], \end{array}\right. \end{array} \end{aligned}$$

(26)

where $\varepsilon =\sum \limits _{i=2}^{M-1}\left[ 2^{i-1}-1\right]$, hence

$$\begin{aligned} \left\{ \begin{array}{llll} x_{M+1}[k+1]=x_2[k+2],\\ x_{M+4}[k+1]=x_{3}[k+4],\\ x_{M+11}[k+1]=x_{4}[k+8],\\ \qquad \vdots \\ x_{M+\varepsilon +2^{M-1}-1}[k+1]=x_{M}[k+2^{M-1}]. \end{array}\right. \end{aligned}$$

(27)

In this way, vector $\mathbf x [k]$ becomes

$$\begin{aligned} \mathbf x [k]=\left[ \begin{array}{c} \mathbf{x }_1[k] \\ \mathbf{x }_2[k] \\ \vdots \\ \mathbf{x }_M[k]\\ \mathbf{x }_{M+1}[k]\\ \mathbf{x }_{M+2}[k]\\ \vdots \\ \mathbf{x }_{\eta }[k] \end{array} \right] , \end{aligned}$$

(28)

with $\eta = M+\sum \limits _{i=2}^{M-1}\left[ 2^{i-1}-1\right] +2^{M-1}-1$, namely, $\eta =M+\varepsilon +2^{M-1}-1$.

Matrices of the state-space realization for M decomposition levels are denoted as $\mathbf A _M$, $\mathbf B _M$, $\mathbf C _M$ and $\mathbf D _M$.

From (23), (25), (26) and (27), matrix $\mathbf A _M$ takes the form

$$\begin{aligned} \mathbf A _M=\left[ \begin{array}{ccccccccc} \mathbf A &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} \cdots &{} 0 &{} \mathbf I &{} 0 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ \mathbf BC _1 &{} \mathbf A &{} \cdots &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} \mathbf I &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} \cdots &{} \mathbf I \\ \mathbf B D_1^{M-2}{} \mathbf C _1 &{} \mathbf B D_1^{M-3}{} \mathbf C _1 &{} \cdots &{} \mathbf A &{} 0 &{} 0 &{} \cdots &{} 0 \end{array} \right] , \end{aligned}$$

(29)

where $\mathbf I$ is the $(2N-1)\times (2N-1)$ identity matrix. In the same way, each element denoted by 0 is a $(2N-1)\times (2N-1)$ null matrix. While $\mathbf B _M$ is defined as

$$\begin{aligned} \mathbf B _M=\left[ \begin{array}{c} \mathbf{B } \\ 0\\ \vdots \\ \mathbf{B }D_1 \\ 0\\ \vdots \\ 0\\ \mathbf{B }D_1^{M-1} \end{array} \right] , \end{aligned}$$

(30)

with 0 being a $(2N-1)\times 1$ null vector. Matrix $\mathbf C _M$ is given by

$$\begin{aligned} \mathbf C _M=\left[ \begin{array}{cccccccc} D_1^{M-1}\mathbf{C }_1 &{} \cdots &{} D_1^{2}\mathbf{C }_1 &{} D_1\mathbf{C }_1 &{} \mathbf{C }_1 &{}0 &{}\cdots &{} 0\\ D_2D_1^{M-2}\mathbf{C }_1 &{} \cdots &{} D_2D_1\mathbf{C }_1 &{} D_2\mathbf{C }_1 &{} \mathbf{C }_2 &{}0 &{}\cdots &{} 0\\ D_2D_1^{M-3}\mathbf{C }_1 &{} \cdots &{} D_2\mathbf{C }_1 &{} \mathbf{C }_2 &{} 0 &{}0 &{}\cdots &{} 0\\ \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ \mathbf{C }_2 &{} \cdots &{} 0 &{} 0 &{} 0 &{}0 &{}\cdots &{} 0 \end{array} \right] , \end{aligned}$$

(31)

with 0 being an $1\times (2N-1)$ null vector. Vector $\mathbf D _M$ is equal to

$$\begin{aligned} \mathbf D _M=\left[ \begin{array}{c} D_1^M \\ D_2D_1^{M-1} \\ D_2D_1^{M-2} \\ \vdots \\ D_2 \end{array} \right] . \end{aligned}$$

(32)

Finally, matrices (29), (30), (31) and (32) are the description in the state-space for analysis wavelet FIR filter banks with multiple decomposition levels. This proposal is based on Algorithme à Trous; therefore, it is necessary to remember that the relationship among the coefficients $\mathbf y _i[k]$ (FWT) and $\underline{\mathbf{y }}_i[k]$ (Algorithme à Trous ) is given by (11); in other words, the convenient decimation must be done after state-space description.

Dimensions of the matrices in the state-space description are:

• $\dim (\mathbf A _M)=\eta (2N-1)\times \eta (2N-1)$;

• $\dim (\mathbf B _M)=\eta (2N-1)\times 1$;

• $\dim (\mathbf C _M)=(M+1)\times \eta (2N-1)$;

• $\dim (\mathbf D _M)=(M+1)\times 1$,

and if $\mathcal {R}_{{\mathbf{A }}_{M}},\mathbf{B }_{M}$ and $\mathcal {S}_{{\mathbf{C }}_{M}},\mathbf{A }_{M}$ are respectively controllability and observability matrices, then

• $\dim (\mathcal {R}_{{\mathbf{A }}_{M}},\mathbf{B }_{M}) =\eta (2N-1)\times \eta (2N-1)$;

• $\dim (\mathcal {S}_{{\mathbf{C }}_{M}},\mathbf{A }_{M}) =(M+1)\eta (2N-1)\times \eta (2N-1)$.

An important result about the state-space description is the minimality condition, which is the combination of controllability and observability conditions. For $M=1$, the proposed state-space description is minimal, and this can be checked in Uzinski et al. (2015). For an arbitrary M, the minimality condition is exploited in Theorem 2. The proof of this theorem is made by using mathematical induction. For this reason, Lemma 1 states that the proposed state-space description is minimal for $M=2$ (for $M=1$ there is no delay operators included in the parameterization).

Lemma 1

A realization ($\mathbf A _M$, $\mathbf B _M$, $\mathbf C _M$, $\mathbf D _M$) for $M=2$ given by (29), (30), (31) and (32), respectively, with all angles different from 0, $\pi /2$, $\pi$ and $3\pi /2$ ¹, is minimal.

Proof

For $M=2$ matrices $\mathbf A _M$, $\mathbf B _M$ and $\mathbf C _M$ become

$$\begin{aligned} \mathbf A _M= & {} \left[ \begin{array}{ccc} \mathbf A &{} 0 &{} 0 \\ 0 &{} 0 &{} \mathbf I \\ \mathbf BC _1 &{} \mathbf A &{} 0 \end{array} \right] , \end{aligned}$$

(33)

$$\begin{aligned} \mathbf B _M= & {} \left[ \begin{array}{c} \mathbf B \\ 0 \\ \mathbf B D_1 \end{array}\right] \end{aligned}$$

(34)

and

$$\begin{aligned} \mathbf C _M=\left[ \begin{array}{ccc} D_1\mathbf C _1 &{} \mathbf C _1 &{} 0 \\ \mathbf C _2\mathbf C _1 &{} \mathbf C _2 &{} 0 \\ \mathbf C _2 &{} 0 &{} 0 \end{array} \right] . \end{aligned}$$

(35)

By the mathematical induction principle, it is necessary to verify that the lemma is true for $N=1$ and if it holds for a certain N this implies that it will be true for $N+1$. It is made as follows.

• For $N=1$: $\mathbf A =0$, $\mathbf B =1$, $\mathbf C =[\begin{array}{cc} S_1&C_1 \end{array} ]^T$ and $\mathbf D =[\begin{array}{cc} C_1&S_1 \end{array} ]^T$. By replacing these values in (33), (34) and (35):

  $$\begin{aligned}&\mathbf A _M=\left[ \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 \\ S_1 &{} 0 &{} 0 \end{array} \right] , \qquad \mathbf B _M=\left[ \begin{array}{c} 1 \\ 0 \\ C_1 \end{array} \right] \\&\quad \text {and} \qquad \mathbf C _M=\left[ \begin{array}{ccc} C_1S_1 &{} S_1 &{} 0 \\ C_1C_1 &{} C_1 &{} 0 \\ C_1 &{} 0 &{} 0 \end{array}\right] , \end{aligned}$$

  and after that computing the controllability and observability matrices, both of them have three linearly independent rows and columns.

• Let N be an arbitrary positive integer number. For $N+1$ matrices (33), (34) and (35) hold the same form that for N, only the dimensions of these matrices will be changed. Consequently, the same fact is valid for matrices $\mathcal {R}_{{\mathbf{A }}_{M}},\mathbf{B }_{M}$ and $\mathcal {S}_{{\mathbf{C }}_{M}},\mathbf{A }_{M}$. Therefore, if matrices $\mathcal {R}_{{\mathbf{A }}_{M}},\mathbf{B }_{M}$ and $\mathcal {S}_{{\mathbf{C }}_{M}},\mathbf{A }_{M}$ have $\eta (2N-1)$ linearly independent rows and columns for N, they have $\eta (2(N+1)-1)$ linearly independent rows and columns for $N+1$ (in $\eta$, $M=2$).

By the mathematical induction principle, it is demonstrated that matrices $\mathcal {R}_{{\mathbf{A }}_{M}},\mathbf{B }_{M}$ and $\mathcal {S}_{{\mathbf{C }}_{M}},\mathbf{A }_{M}$ have $\eta (2N-1)$ linearly independent rows and columns. Thus, any realization ($\mathbf A _M$, $\mathbf B _M$, $\mathbf C _M$, $\mathbf D _M$) (with all angles different from 0, $\pi /2$, $\pi$ and $3\pi /2$) for $M=2$ is minimal.

Theorem 2

A realization ($\mathbf A _M$, $\mathbf B _M$, $\mathbf C _M$, $\mathbf D _M$) given by (29), (30), (31) and (32), respectively, with all angles different from 0, $\pi /2$, $\pi$ and $3\pi /2$, is minimal because it is reachable and observable.

Proof

By the mathematical induction principle and the following conclusions, the proof of the theorem is achieved as follows.

• For $M=1$, it is demonstrated by Uzinski et al. (2015) that $\mathcal {R}_{{\mathbf{A }}_{M}},\mathbf{B }_{M}$ and $\mathcal {S}_{{\mathbf{C }}_{M}},\mathbf{A }_{M}$ have $\eta (2N-1)$ linearly independent rows and columns (in $\eta$, $M=1$).

• For $M=2$, it is demonstrated by Lemma 1 that $\mathcal {R}_{{\mathbf{A }}_{M}},\mathbf{B }_{M}$ and $\mathcal {S}_{{\mathbf{C }}_{M}},\mathbf{A }_{M}$ have $\eta (2N-1)$ linearly independent rows and columns (in $\eta$, $M=2$).

• For any $M\ge 2$, the forms of $\mathbf A _M$, $\mathbf B _M$ and $\mathbf C _M$ are the same as stated by (29), (30), (31) and (32), only the dimensions change according to M. The same fact is valid for the matrices $\mathcal {R}_{{\mathbf{A }}_{M}},\mathbf{B }_{M}$ and $\mathcal {S}_{{\mathbf{C }}_{M}},\mathbf{A }_{M}$. Therefore, if $\mathcal {R}_{{\mathbf{A }}_{M}},\mathbf{B }_{M}$ and $\mathcal {S}_{{\mathbf{C }}_{M}},\mathbf{A }_{M}$ have $\eta (2N-1)$ linearly independent rows and columns, it implies that $\mathcal {R}_{{\mathbf{A }}_{M+1}},\mathbf{B }_{M+1}$ and $\mathcal {S}_{{\mathbf{C }}_{M+1}},\mathbf{A }_{M+1}$ have $\eta (2N-1)$ (in $\eta$, the value of M is $M+1$) linearly independent rows and columns.

By the mathematical induction principle, it is demonstrated that matrices $\mathcal {R}_{{\mathbf{A }}_{M}},\mathbf{B }_{M}$ and $\mathcal {S}_{{\mathbf{C }}_{M}},\mathbf{A }_{M}$ have $\eta (2N-1)$ linearly independent rows and columns. Thus, any realization ($\mathbf A _M$, $\mathbf B _M$, $\mathbf C _M$, $\mathbf D _M$) (with all angles different from 0, $\pi /2$, $\pi$ and $3\pi /2$) is minimal.

Remark 1

When the designer considers that the dynamical system has a large number of states and for some reason it can be unsatisfactory, an order reduction method can be applied to the states $\mathbf x _M$ of the description (29), (30), (31) and (32).

3 Proposed Dynamic-State Feedback Approach

3.1 Preliminaries: Discrete Linear Quadratic Regulator (DLQR)

Consider a plant described by a discrete-time model of the form

$$\begin{aligned} \mathbf x _p[k+1]= & {} \mathbf A _p\mathbf x _p[k]+\mathbf B _p\mathbf u _p[k], \end{aligned}$$

(36)

where $\mathbf x _p[k] \in \mathbb {R}^n$, $\mathbf u _p[k] \in \mathbb {R}^p$ are the state and control vectors, and $\mathbf A _p$, $\mathbf B _p$ are matrices of compatible dimensions. It is assumed that the plant is controllable and the state $\mathbf x _p[k]$ is available for feedback.

Given the following quadratic cost function:

$$\begin{aligned} J= \sum _{k=0}^{\infty }{} \mathbf x _p^T[k]\mathbf Q _p\mathbf x _p[k]+\mathbf u _p^T[k]\mathbf R _p\mathbf u _p[k], \end{aligned}$$

(37)

with positive-definite state and control weight matrices $\mathbf Q _p, \mathbf R _p$, the optimal control law is of the form

$$\begin{aligned} \mathbf u _p[k] = -\mathbf K _p\mathbf x _p[k], \end{aligned}$$

(38)

with feedback gain $\mathbf K _p$ calculated as

$$\begin{aligned} \mathbf K _p = (\mathbf B _p^T \mathbf P \mathbf B _p + \mathbf R _p)^{-1} \mathbf B _p^T \mathbf P \mathbf A _p , \end{aligned}$$

(39)

where $\mathbf P$ is the positive-definite solution of the following Riccati equation (Lewis 1986).

$$\begin{aligned} \mathbf P =\mathbf A _p^T \mathbf P \mathbf A _p - \mathbf A ^T_p \mathbf P \mathbf B _p (\mathbf R _p + \mathbf B _p^T \mathbf P \mathbf B _p)^{-1} \mathbf B _p^T \mathbf P \mathbf A _p +\mathbf Q _p.\nonumber \\ \end{aligned}$$

(40)

Fig. 7 shows the block diagram for the resulting control loop. As will be discussed in Sect. 4 (Case study), the weight matrices $\mathbf Q _p, \mathbf R _p$ can be adjusted in order to optimize a robustness or performance metric of interest.

Fig. 7

Discrete linear quadratic regulator

3.2 Discrete Linear Quadratic Regulator Employing a Wavelet Filter Bank (DLQR-WFB)

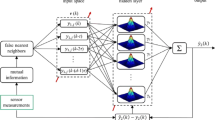
In the DLQR-WFB approach proposed herein, a filter bank is included in the feedback path, as illustrated in Fig. 8. More specifically, each state of the plant is decomposed by the fast wavelet transform, in order to obtain an augmented state vector $\mathbf x _{pw} = [\mathbf x _p^T ~~\mathbf x _w^T]^T$, with $\mathbf x _w$ comprising the state variables of the filter bank. Since the fast wavelet transform is applied to each of the n components of the plant state $\mathbf x _p$, the filter bank state $\mathbf x _w$ is formed as

$$\begin{aligned} \mathbf x _w=\left[ \begin{array}{c} \mathbf x _{FB_1} \\ \mathbf x _{FB_2} \\ \vdots \\ \mathbf x _{FB_n} \end{array} \right] , \end{aligned}$$

(41)

where $\mathbf x _{FB_i}$ is a vector with the filter bank states involved in the decomposition of the ith plant state.

The dynamics of the plant coupled with the filter bank can then be described by a state equation of the form

$$\begin{aligned} \mathbf x _{pw}[k+1] = \mathbf A _{pw} \mathbf x _{pw}[k] + \mathbf B _{pw} \mathbf u _p[k], \end{aligned}$$

(42)

where

$$\begin{aligned} {x}_{pw}[k]= & {} \left[ \begin{array}{c} \mathbf x _p[k] \\ \mathbf x _w[k] \end{array} \right] , \; \; \mathbf A _{pw}= \left[ \begin{array}{cc} \mathbf A _p &{} 0 \\ \mathbf B _w &{} \mathbf A _w \end{array} \right] , \;\; \nonumber \\ \mathbf B _{pw}= & {} \left[ \begin{array}{c} \mathbf B _p\\ 0 \end{array} \right] , \end{aligned}$$

(43)

with $\mathbf A _w$ and $\mathbf B _w$ obtained from the filter bank equations as

$$\begin{aligned} \mathbf A _w=\left[ \begin{array}{cccc} \mathbf A _M &{} 0 &{} \cdots &{} 0 \\ 0 &{} \mathbf A _M &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} \mathbf A _M \end{array} \right] , \; \; \mathbf B _w= \left[ \begin{array}{cccc} \mathbf B _M &{} 0 &{} \cdots &{} 0 \\ 0 &{} \mathbf B _M &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} \mathbf B _M \end{array} \right] . \end{aligned}$$

(44)

Fig. 8

Discrete linear quadratic regulator employing a wavelet filter bank

A discrete linear quadratic regulator with weight matrices $\mathbf Q _{pw}, \mathbf R _{pw}$ can be designed for the augmented system (42) in order to obtain a feedback gain $\mathbf K _{pw}$, as illustrated in Fig. 8.

4 Case Study

Consider a two-mass-spring system described by a continuous-time state equation of the form $\dot{x}_p = A_\mathrm{pc} x_p + B_\mathrm{pc} u_p$, with

$$\begin{aligned} \mathbf A _\mathrm{pc}= & {} \left[ \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ -\frac{K_s}{m_\mathrm{ac}} &{} \frac{K_s}{m_\mathrm{ac}} &{} -\frac{b_\mathrm{ac}+\frac{K_g^2K_mK_t}{R_mr_\mathrm{mp}^2}}{m_\mathrm{ac}} &{} 0 \\ \frac{K_s}{m_\mathrm{pc}} &{} -\frac{K_s}{m_\mathrm{pc}} &{} 0 &{} -\frac{b_\mathrm{pc}}{m_\mathrm{pc}} \end{array} \right] , \; \;\nonumber \\ \mathbf B _\mathrm{pc}= & {} \left[ \begin{array}{cccc} 0&0&\frac{K_gK_t}{R_mr_\mathrm{mp}}&0 \end{array} \right] ^T, \end{aligned}$$

(45)

with parameter values given in Table 1 (Colombo Junior et al. 2016). This model was discretized into the form (36) by using the zero-order hold method with a sampling period $T = 15$ ms, as in Colombo Junior et al. (2016).

Table 1 Model parameters

In the present example, the proposed DLQR-WFB approach for dynamic-state feedback will be illustrated by using a db3 wavelet filter bank with $M = 2$ levels. This filter bank can be described by a state-space model with $\mathbf A _M$, $\mathbf B _M$, $\mathbf C _M$, $\mathbf D _M$ matrices as in (29), (30), (31), (32) where $\mathbf A$, $\mathbf B$, $\mathbf C$, $\mathbf D$ are given by (7), (8), (9), (10). The numerical values for the coefficients in $\mathbf A$, $\mathbf B$, $\mathbf C$, $\mathbf D$ can be found in Uzinski et al. (2015). By using a balanced realization and removing the states corresponding to small Hankel singular values (Laub et al. 1987), the model order for the filter bank was reduced from 15 to 10. It is worth noting that four separate filter banks will be employed in the control loop (one for each of the four plant states). Therefore, the overall order of the augmented system will be $4 + 10 + 10 +10 +10 = 44$.

In what follows, the DLQR (Fig. 7) and DLQR-WFB (Fig. 8) methods will be compared in two numerical investigations using different evaluation metrics.

The numerical results were obtained by using the Matlab$^{\circledR }$ software, with the Optimization and Control System Toolboxes$^{TM}$.

4.1 Sensitivity

Let S(z) be a sensitivity function defined for the DLQR case as

$$\begin{aligned} S(z) = \frac{1}{1+\mathbf K _{p}(z\mathbf I -\mathbf A _{p})^{-1}{} \mathbf B _{p}}, \end{aligned}$$

(46)

with a similar definition in the DLQR-WFB case (replacing $\mathbf K _{p}$, $\mathbf A _{p}$, $\mathbf B _{p}$ with $\mathbf K _{pw}$, $\mathbf A _{pw}$, $\mathbf B _{pw}$, respectively) (Franklin et al. 1998).

This sensitivity function can be used as a robustness measure, since the value $|S(e^{j\omega })|$ is the reciprocal of the distance between the Nyquist curve and the critical point $-1$, considering the loop broken at the plant input (Franklin et al. 1998). In this sense, a possible design goal may consist of obtaining small values of $|S(e^{j\omega })|$ at a given set of frequencies $\omega$. This can be achieved by using a numerical optimization method to adjust the control and state weights in the DLQR or DLQR-WFB formulations.

In this example, diagonal weight matrices were adopted for simplicity. The control weight was set to one and a diagonal form was adopted for the state weight matrix, with diagonal elements optimized by using the sequential quadratic programming (SQP) method (Nocedal and Wright 2006). For this purpose, the fmincon function of the MATLAB Optimization Toolbox$^{TM}$ was employed, with default settings for the numerical search procedure. The weights corresponding to the four plant states were initialized by using 81 different combinations of the values $10^{-4}$, $10^0$ and $10^4$. In the DLQR-WFB case, the weights corresponding to the filter bank states were initialized with null values. The index to be minimized was defined as $\vert S(e^{j\omega _1})\vert + \rho \vert S(e^{j\omega _2})\vert$, where $\omega _1 = 0.15$, $\omega _2 = 0.60$ and $\rho$ is a positive scalar that can be adjusted to place larger emphasis on the minimization of $\vert S(e^{j\omega _1})\vert$ or $\vert S(e^{j\omega _2})\vert$.

Fig. 9 presents the DLQR and DLQR-WFB results obtained by varying the value of $\rho$. As can be seen, smaller values of $\vert S(e^{j\omega _1})\vert$ and $\vert S(e^{j\omega _2})\vert$ can be achieved by using the proposed DLQR-WFB formulation. Line segments connecting the non-dominated solutions (in the usual multi-objective sense) are included in the graphs, for better visualization.

Fig. 9

Sensitivity values at $\omega _1 = 0.15$ and $\omega _2 = 0.60$ obtained by optimizing the state weights in the DLQR and DLQR-WFB formulations

4.2 Effect of External Disturbances and Measurement Noise

Consider the plant model (45) with a scalar output $y_p$ defined as

$$\begin{aligned} y_p[k] = \mathbf C _p \mathbf x _p[k], \end{aligned}$$

(47)

where $\mathbf C _p$ is a row vector of compatible dimension. In the present example, the output will be defined as the first state variable, i.e., $\mathbf C _p = [1 \; \; 0 \; \; 0 \; \; 0]$.

Assume that a disturbance d is applied at the plant input. In the DLQR case, the effect of the disturbance on the plant output $y_p$ can be evaluated by replacing (38) with

$$\begin{aligned} u_p[k] = - \mathbf K _p \mathbf x _p[k] + d[k]. \end{aligned}$$

(48)

From (36), (47) and (48), a transfer function $H_{dy}(z)$ can be obtained as

$$\begin{aligned} H_{dy}(z) = \frac{Y_p(z)}{D(z)}= \mathbf C _p(z\mathbf I - \mathbf A _p + \mathbf B _p \mathbf K _p)^{-1}{} \mathbf B _p. \end{aligned}$$

(49)

The effect of the disturbance on the plant output can then be evaluated in terms of the $H_2$ norm of $H_{dy_p}(z)$, which is defined as, (Bunse-Gerstner et al. 2010),

$$\begin{aligned} \Vert H_{dy}\Vert _2=\sqrt{\frac{1}{2\pi }\int _{0}^{2\pi } |H_{dy}(e^{j\omega })|^2 d\omega }. \end{aligned}$$

(50)

A similar transfer function can be obtained in the DLQR-WFB case, by replacing $\mathbf K _{p}$, $\mathbf A _{p}$, $\mathbf B _{p}$ and $\mathbf C _p$ with $\mathbf K _{pw}$, $\mathbf A _{pw}$, $\mathbf B _{pw}$ and $[\mathbf C _p \; \; 0]$, respectively.

Now, instead of considering an input disturbance, assume that the state values employed in the feedback control law are corrupted with a measurement noise term n such that

$$\begin{aligned} u_p[k] = - \mathbf K _p(\mathbf x _p[k] + \mathbf E _p n[k]) \end{aligned}$$

(51)

in the DLQR case, where $\mathbf E _p$ is a column vector of compatible dimension. In the present example, the noise will be included in the measurement of the first state variable, i.e., $\mathbf E _p = [1 \; \; 0 \; \;0 \; \;0 ]^T$. From (36), (47) and (51), a transfer function $H_{ny}(z)$ can be obtained as

$$\begin{aligned} H_{ny}(z) = \frac{Y_p(z)}{N(z)}= - \mathbf C _p(z\mathbf I - \mathbf A _p + \mathbf B _p \mathbf K _p)^{-1}{} \mathbf B _p \mathbf K _p \mathbf E _p. \end{aligned}$$

(52)

The $H_2$ norm of $H_{ny}(z)$ can then be used to evaluate the effect of the measurement noise on the plant output. A similar transfer function can be obtained in the DLQR-WFB case, by replacing $\mathbf K _{p}$, $\mathbf A _{p}$, $\mathbf B _{p}$, $\mathbf C _p$ and $\mathbf E _p$ with $\mathbf K _{pw}$, $\mathbf A _{pw}$, $\mathbf B _{pw}$, $[\mathbf C _p \; \; 0]$ and $[\mathbf E ^T_p \; \; 0]^T$, respectively.

As in the sensitivity study presented in Sect. 4.1, the state weights in the DLQR and DLQR-WFB formulations were optimized by using the SQP method. In this case, the index to be minimized was defined as $\Vert H_{dy}\Vert _2 + \rho \Vert H_{ny}\Vert _2$. Fig. 10 presents the DLQR and DLQR-WFB results obtained by varying the value of $\rho$. Again, the proposed DLQR-WFB approach leads to better results, in that smaller values of $\Vert H_{dy}\Vert _2$ and $\Vert H_{ny}\Vert _2$ can be achieved as compared to the DLQR formulation.

Fig. 10

Comparative evaluation of the DLQR and DLQR-WFB formulations in terms of external disturbance and measurement noise effects

5 Conclusions

This paper presented a new state-space description for wavelet filter banks (WFBs) with multiple decomposition levels, thus extending previous work on single-level decomposition schemes. The proposed description can be used to design dynamic-state feedback control laws involving the decomposition of the plant states by the filter bank. A simple synthesis procedure consists of designing a discrete linear quadratic regulator (DLQR) for the augmented system incorporating the plant model and the filter bank.

A numerical example was presented to illustrate the potential advantages of the proposed DLQR-WFB approach. For this purpose, a standard DLQR design was employed for comparison. As a result, the proposed approach was shown to provide better results in terms of sensitivity values, as well as rejection of external disturbances and measurement noise.

Future research could be concerned with the development of guidelines for choosing the type of wavelet and the number of decomposition levels in view of the design requirements for the closed-loop system. The use of WFBs with control design methods other than DLQR could also be investigated.