Variable input observer for nonstationary high-rate dynamic systems

Abstract

Engineering systems experiencing events of amplitudes higher than 100 g_n for a duration under 100 ms, here termed high-rate dynamics, can undergo rapid damaging effects. If the structural health of such systems could be accurately estimated in a timely manner, preventative measures could be employed to minimize adverse effects. For complex high-rate problems, adaptive observers have shown promise due to their capability to deal with nonstationary, noisy, and uncertain systems. However, adaptive observers have slow convergence rates, which impede their applicability to the high-rate problems. To improve on the convergence rate, we propose a variable input space concept for optimizing the use of data history of high-rate dynamics, with the objective to produce an optimal representation of the system of interest. Using the embedding theory, the algorithm sequentially selects and adapts a vector of inputs that preserves the essential dynamics of the high-rate system. In this paper, the variable input space is integrated in a wavelet neural network, which constitutes a variable input observer. The observer is simulated using experimental data from a high-rate system. Different input space adaptation methods are studied, and the performance is also compared against an optimized fixed input strategy. It is found that a smooth transition of the input space eliminates error spikes and yields faster convergence. The variable input observer is further studied in a hybrid model-/data-driven formulation, and results demonstrate significant improvement in performance gained from the added physical knowledge.

1 Introduction

High-rate dynamics, here defined as events of amplitudes higher than 100 g_n for a duration under 100 ms, can be highly detrimental to modern engineering systems. Examples of such systems include civil structures exposed to blast, passenger vehicles experiencing collisions, and aerial or spacecraft vehicles impacting foreign objects [1]. High-rate dynamics can cause rapid plastic deformation propagating through the structure and to electronics and sensors, which in turn can cause catastrophic failures and endanger human lives [2]. Precise and on-time state estimation is a necessary first step to prevent further damage and complete failure [3]. However, state estimation of high-rate dynamics is a challenging problem. A well-designed estimator must converge very fast (high-rate) and be capable of coping with the following unique complexities that characterize the high-rate problem:

• Large uncertainties in the external loads;

• High levels of nonstationarities and heavy disturbances; and

• Generation of unmodeled dynamics from changes in system configuration.

In particular, an estimator must be capable of operating through noise, uncertainty, time-varying parameters/states, and disturbances. Noise is a common issue that can arise from flexing of electronics. There is uncertainty in how a system may respond to very large excitations. In the case of a spontaneous blast or impact, little is known about the inputs. Plastic deformation or damage leads to time-varying parameters or states. Lastly, large excitations can resonate the system or components resulting in disturbances. Sophistication in the algorithm is required to overcome the negative effects of the combined complexities leading to slower convergence rates [4,5,6,7,8].

Classic observers are constructed to estimate one or more states from sensor inputs. Typically, inputs are preselected and rarely optimized, contributing to a sub-optimal observer design. Hong et al. [1] discussed promising properties of adaptive observers (AOs), in general, to perform well in the presence of various system complexities (e.g., noise, uncertainty, time-varying parameters, and disturbance mentioned above). However, it was also discussed that these observers are characterized by slower convergence rates due to their adaptive architecture. Various methods have been developed to increase the convergence rate of AOs, see [9,10,11] for instance. While such research has yielded important contributions in ameliorating the convergence of AOs, all of the methods focused on altering the estimation and adaptation algorithm, while the input space selection and construction are vastly overlooked [12].

Typical observers employ representations that are tuned to fixed types of inputs to attain an appropriate level of performance [13, 14]. The choice of inputs influences computation time, adaptation speed, effects of the curse of dimensionality, understanding of the representation, and model complexity [15, 16]. Although in practice only limited states in a system can be observed, the essential dynamics may be preserved through a proper selection of the input space vector based on limited measurements [17, 18]. Bowden et al. [13] argued that proper input space selection can lead to superior estimators by bypassing modeling inaccuracies due to nonlinearities. The benefits of essential dynamics present in an input space have been studied in fields of structural health monitoring [19,20,21] and control [22,23,24,25,26].

It follows that a strategy is to employ a dynamic input space to provide stability of the adaptive algorithm. The change in the input types and numbers can help target inputs that would contain the essential dynamics of the system. A critical advantage of such methodology is that the essential dynamics can be extracted from nonstationary systems [12] using limited sensors [27]. The authors have studied varying input space strategies for structural control applications [12, 18, 28], and recently for high-rate state estimation [29].

The decision to take an adaptive algorithm approach was determined from an overview study of observers and their general applications [1]. Due to the difficulties in creating a representation of high-rate systems, adaptive data-driven observers were found to have a unique advantage of adapting to large levels of uncertainties and complexities through pattern recognition capabilities [30]. The downfall of adaptive methods, however, is their slow convergence rates. In order to accelerate the convergence times, the input space of observers was studied [29]. It was determined that the input space of observers was critical to the quality of estimates observers can produce for high-rate systems.

The method of varying the input space produces a variable input observer (VIO) when used as an estimator. Here, the estimator is comprised of the variable input space coupled with a self-organizing single-layer wavelet neural network. The single-layer wavelet architecture is selected for its known universal approximation capabilities [31], ideal for mapping complex nonlinear dynamics [32], and real-time computations due to fewer number of calculations [33]. The input space of the estimator is varied sequentially in real-time, to adapt to complexities of high-rate dynamics, including nonlinearities and nonstationarities. Such variation allows the state estimation function to adapt to changing dynamics resulting in a minimum number of inputs that preserve the system’s essential dynamics leading to faster convergence rates.

Systems that initially behave in a linear manner can respond nonlinearly when damaged [19]. Such nonstationarities are inherent attributes of high-rate systems. Liu et al. [21] verified that damage assessment using an embedding strategy provided superior results compared with the same strategy without embedding. Previous embedding techniques were only applicable to stationary systems where offline processing was used to determine the embedding parameters [34, 35]. Through the VIO, we extend the embedding strategy to nonstationary systems through the online computation of the embedding over stationary segments of data.

In prior work presented in conference proceedings, a preliminary version of the VIO showed promise when compared with a typical fixed input space observer [36]. However, the rapid input space adaptation produced undesirable error spikes in the estimations, and the authors demonstrated that a slower transition of the input space reduced these error spikes [37].

In this paper, we introduce a smooth transition technique between input spaces by applying a c^∞ type function to the time delay values with the objective to eliminate error spikes, and also further previous studies by examining the effects of added physical knowledge into the system by creating a hybrid data-/model-driven VIO. Lastly, we explore the possibility of using this hybrid observer for system identification applications through pre-training.

The rest of the paper is organized as follows. Section 2 will present the methodology used in constructing the VIO, model, and hybrid VIO. Section 3 will describe the experimental setup used for acquiring data used in the numerical simulations and discuss simulation results. Section 4 will conclude the paper with a summary of major findings.

2 Background

2.1 Variable input observer

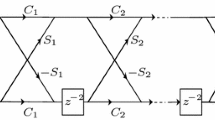
The variable input space strategy is combined with a wavelet neural network (WNN) to perform state estimation, therefore constituting the VIO. Its architecture is illustrated in Fig. 1. A single layer of Mexican hat wavelet network is used to produce the estimate $\hat{y}_{2} (k)$

$$ \hat{y}_{2} (k) = \mathop \sum \limits_{j = 1}^{h} \gamma_{j} \varphi_{j} (\varvec{\nu}(k)) $$

(1)

where ν is the input vector also termed delay vector, τ the time delay, d the embedding dimension, h is the number of nodes or activation functions, γ the nodal weights, and φ is the Mexican hat wavelet activation function

$$ \varphi (\varvec{\nu}(k)) = \left( {1 - \frac{{\|\varvec{\nu}(k) -\varvec{\mu}_{j2}\| }}{{\varvec{\sigma}_{j}^{2} }}} \right)e^{{ - \frac{{\|\varvec{\nu}(k) -\varvec{\mu}_{j}\|_{2} }}{{\varvec{\sigma}_{j}^{2} }}}} $$

(2)

where $\varvec{\mu}_{j}$ and $\varvec{\sigma}_{j}$ are the center and bandwidth of the jth node, respectively, and $|| \cdot ||_{2}$ is the 2-norm. The VIO is specifically designed to self-organize based on Kohonen’s self-organizing map (SOM) theory [38], and to perform self-adaptation. The SOM functionality consists of adding nodes when a new sample falls outside the region covered by the WNN. When a new node j is added, it is given a weight $\gamma_{j}$ initially equal to zero, a center $\varvec{\mu}_{j}$ at the location of the new observation, and a bandwidth $\varvec{\sigma}_{j}$ set at the user-defined value σ(0). Self-adaptation consists of sequentially adapting the WNN parameters γ and σ following a stable back-propagation rule [39]:

$$ \begin{aligned} \dot{\gamma }_{j} \left( k \right) & = - \varGamma_{{\gamma_{j} }} \frac{\partial E\left( k \right)}{{\partial \gamma_{j} }} \\ \dot{\varvec{\sigma }}_{j} \left( k \right) & = - \varGamma_{{\varvec{\sigma}_{\varvec{j}} }} \frac{\partial E\left( k \right)}{{\partial\varvec{\sigma}_{j} }} \\ \end{aligned} $$

(3)

where $\varGamma_{{\gamma_{j} }}$ and $\varGamma_{{\varvec{\sigma}_{\varvec{j}} }}$ are positive learning rates for $\gamma_{j}$ and $\varvec{\sigma}_{j}$ and E is the error function

$$ E\left( k \right) = \frac{1}{2}\left( {\tilde{y}_{2} \left( k \right)} \right)^{2} = \frac{1}{2}\left( {\mathop \sum \limits_{j = 1}^{h} \gamma_{j} \varphi_{j} \left( {\varvec{\nu}\left( k \right)} \right) - y_{2} \left( k \right)} \right)^{2} $$

(4)

and $\tilde{y}_{2} (k) = \tilde{y}_{2} (k) - y_{2} (k)$ is the estimation error.

Fig. 1

Variable input observer’s architecture

Substituting Eqs. (4) into (3) gives

$$ \begin{aligned} \dot{\gamma }_{j} (k) & = - \varGamma_{{\gamma_{j} }} \frac{{\partial \left( {\frac{1}{2}\left( {\mathop \sum \nolimits_{j = 1}^{h} \gamma_{j} \varphi_{j} \left( {\varvec{\nu}(k)} \right) - y_{2} (k)} \right)^{2} } \right)}}{{\partial \gamma_{j} }} \\ & = - \varGamma_{{\gamma_{j} }} \left( {\mathop \sum \limits_{j = 1}^{h} \varphi_{j} \left( {\varvec{\nu}(k)} \right)} \right)\left( {\mathop \sum \limits_{j = 1}^{h} \gamma_{j} \varphi_{j} \left( {\varvec{\nu}(k)} \right) - y_{2} (k)} \right) \\ & = - \varGamma_{{\gamma_{j} }} \left( {\mathop \sum \limits_{j = 1}^{h} \varphi_{j} \left( {\varvec{\nu}(k)} \right)} \right)\tilde{y}_{2} (k) \\ \end{aligned} $$

(5)

and

$$ \begin{aligned} \dot{\varvec{\sigma }}_{j} (k) & = - \varGamma_{{\varvec{\sigma}_{j} }} \frac{{\partial \left( {\frac{1}{2}\left( {\mathop \sum \nolimits_{j = 1}^{h} \gamma_{j} \varphi_{j} \left( {\varvec{\nu}(k)} \right) - y_{2} (k)} \right)^{2} } \right)}}{{\partial\varvec{\sigma}_{j} }} \\ & = - \varGamma_{{\varvec{\sigma}_{j} }} \frac{{\partial \left( {\frac{1}{2}\left( {\mathop \sum \nolimits_{j = 1}^{h} \gamma_{j} \left( {1 - \frac{{\|\varvec{\nu}(k) -\varvec{\mu}_{j}\|_{2} }}{{\varvec{\sigma}_{j}^{2} }}} \right)e^{{ - \frac{{\|\varvec{\nu}(k) -\varvec{\mu}_{j}\|_{2} }}{{\varvec{\sigma}_{j}^{2} }}}} - y_{2} (k)} \right)^{2} } \right)}}{{\partial\varvec{\sigma}_{j} }} \\ & = - \varGamma_{{\varvec{\sigma}_{j} }} \left( {\mathop \sum \limits_{j = 1}^{h} \gamma_{j} \left( {\frac{1}{{\sigma_{j}^{5} }}e^{{\frac{{ -\|\varvec{\nu}(k) -\varvec{\mu}_{j}\|_{2} }}{{\varvec{\sigma}_{j}^{2} }}}} \left( {4\varvec{\sigma}_{j}^{2}\|\varvec{\nu}(k) -\varvec{\mu}_{j}\|_{2} - 2\|\varvec{\nu}(k) -\varvec{\mu}_{j}\|_{2}^{2} } \right)} \right)} \right)\tilde{y}_{2} (k) \\ \end{aligned} $$

(6)

Using $\dot{x}\left( k \right) = \left( {x\left( {k + 1} \right) - x\left( k \right)} \right)/\Delta k$ with $\Delta k = 1$ yields a discrete formulation for the adaptation rules

$$ \begin{aligned} \gamma_{j} (k + 1) & = \gamma_{j} (k) - \varGamma_{{\gamma_{j} }} \left( {\mathop \sum \limits_{j = 1}^{h} \varphi_{j} \left( {\varvec{\nu}(k)} \right)} \right)\tilde{y}_{2} (k) \\ \sigma_{j} (k + 1) & = \sigma_{j} (k) - \varGamma_{{\varvec{\sigma}_{j} }} \left( {\mathop \sum \limits_{j = 1}^{h} \gamma_{j} \left( {\frac{1}{{\sigma_{j}^{5} }}e^{{\frac{{ -\|\varvec{\nu}\left( k \right) -\varvec{\mu}_{j}\|_{2} }}{{\varvec{\sigma}_{j}^{2} }}}} \left( {4\varvec{\sigma}_{j}^{2}\|\varvec{\nu}(k) -\varvec{\mu}_{j}\|_{2} - 2\|\varvec{\nu}(k) -\varvec{\mu}_{j}\|_{2}^{2} } \right)} \right)} \right)\tilde{y}_{2} (k) \\ \end{aligned} $$

(7)

The delay vector ν is variable, and its selection and adaptation is described in what follows.

2.1.1 Embedding of high-rate data

The embedding theorem [40, 41] is the fundamental principle underlying the variable input space formulation. The theorem, developed by Takens [40], states the phase space of an unknown autonomous system can be geometrically reconstructed using an observation y delayed by τ in an embedding dimension d forming a delay vector, ν

$$ \begin{aligned} \varvec{\nu}(k) &= \left[ y_{1} (k),\;y_{1} (k - \tau ),\;y_{1} (k - 2\tau ),\, \ldots , \right. \\ & \quad \left. y_{1} (k - (d - 1)\tau ) \right] \end{aligned}$$

(8)

where $\varvec{\nu}\in {\mathbb{R}}^{dx1}$ and k is the discrete time step. From this formulation, there exists a one-to-one map between the phase space produced by ν and the phase space of the unknown system, provided ν is constructed appropriately with the optimal parameters τ* and d*, yielding v*. Because such a map exists, the essential dynamics of the unknown system are preserved in v*. It is hypothesized that, because v* preserves the essential dynamics of the system, it can be used as a minimal input space to an estimator, producing more computationally efficient system representations. Originally developed for autonomous systems, the theorem has been extended to stationary systems with forcings [42], and applied to nonstationary high-rate systems through the calculation of the input spaces over stationary segments of data [12]. Here, the system of interest is nonstationary due to rapid changes in system configuration or from possible damage. Our solution is to vary v* in real time using τ*(t) and d*(t). It follows that a challenge is in the selection of τ* and d*. It was demonstrated in the literature that a combination of the mutual information (MI) test for τ* and the false nearest neighbors (FNN) test for d* yielded the most accurate results [43].

The MI test [44] is based on Shannon’s information theory. The algorithm selects τ* such that maximum level of information can be extracted between y₁(k) and $y_{1} \left( {k - \tau^{*} } \right)$. Mathematically,

$$ {\text{MI}}\left( {y_{1} \left( k \right),y_{1} \left( {k - \tau } \right)} \right) = \mathop \sum \limits_{{y_{1} \left( k \right),y_{1} \left( {k - \tau } \right)}} p\left( {y_{1} \left( k \right),y_{1} \left( {k - \tau } \right)} \right){ \log }\frac{{p\left( {y_{1} \left( k \right),y_{1} \left( {k - \tau } \right)} \right)}}{{p\left( {y_{1} \left( k \right)} \right)p\left( {y_{1} \left( {k - \tau } \right)} \right)}} $$

(9)

where y₁(k) and $y_{1} \left( {k - \tau } \right)$ are discrete observations of the time series, p(·) denotes a probability, and p(·,·) denotes a joint probability. The value τ* is taken as the first local minimum of the mutual information function.

The false nearest neighbor (FNN) test [45] is used to calculate the optimal embedding dimension d*. The FNN test calculates the Euclidean distances between the rth neighboring points of a vector for increasing dimensions. If the distance between neighboring points is greater than some threshold, the point is considered a false neighbor. Mathematically,

$$ \frac{{R_{d + 1}^{2} \left( {k,r} \right) - R_{d}^{2} \left( {k,r} \right)}}{{R_{d}^{2} \left( {k,r} \right)}} > R_{\text{tol}} $$

(10)

where R_tot is a user-defined threshold and $R_{d}^{2} \left( {k,r} \right)$ and $R_{d + 1}^{2} \left( {k,r} \right)$ are the Euclidean distances between measurement y₁(k) and its rth nearest neighbor $y_{1}^{\left( r \right)} \left( k \right)$ for dimensions d and d + 1. To increase accuracy, a second condition was added

$$ \frac{{R_{d + 1} (k)}}{{R_{A} }} > A_{\text{tol}} $$

(11)

with

$$ R_{A}^{2} = \frac{1}{n}\mathop \sum \limits_{k = 1}^{n} \left( {y_{1} \left( k \right) - \bar{y}_{1} } \right)^{2} $$

(12)

where $\bar{y}_{1}$ is the mean of observations y₁ and A_tot is a user-defined value. If both conditions are satisfied, the points are considered false neighbors. The value d* is taken at the point when the percentage of FNN drops below an acceptable value.

2.1.2 Smooth transition of the input space

The values for τ and d in constructing ν are updated based on computed τ* and d*. In a previous study by the authors, it was demonstrated that rapid variation of the input space led to error spikes in the estimation [37]. To overcome this challenge, a slow transition of the input space was implemented. The slow transition allowed τ to vary by ± 10 and d to vary by ± 1 with the restrictions that τ remains positive and d does not drop below an embedding dimension of 2. For the smooth input space transition, we apply a sigmoid function S(x) when adapting τ and allow d to vary by d ± 1. New τ and d values are calculated every 10 iterations for a data history of 200 points. The 200 point data history is a sliding window of data used to calculate the input space for stationary segments of data. In real time, τ would have units of seconds. In this study, we use discrete time, which makes τ the corresponding number of past data points. A transition region of 10 points is selected to smooth the transition from the previous τ, τ_old to the new τ, τ_new, with

$$ S\left( x \right) = \frac{1}{{1 + e^{ - x} }} $$

(13)

where $x = - 4{:}1{:}5$, and τ updated as follows:

$$ \tau \left( k{:}k + 10 \right) = S\left( x \right)\left( {\tau_{\text{new}} - \tau_{\text{old}} } \right) + \tau_{\text{old}} $$

(14)

where values for τ are rounded to the closest integer, and τ(k:k + 10) are the next ten τ values providing the smooth transition. Figure 2 illustrates the smooth transitioning of τ. Since d has to be an integer, it varies by ± 1 with no further manipulation.

Fig. 2

Smooth transition of τ

2.2 Hybrid VIO

The VIO described above is a pure data-driven technique. While the system of interest is complex, it is possible that a certain level of physical knowledge be available. This gives rise to an opportunity to integrate such knowledge in the VIO, therefore creating a hybrid data-/model-driven observer. Here, this is done by using the data-driven VIO in parallel with a model-based observer constructed using the partial physical knowledge. It results that, in this configuration illustrated in Fig. 3, the VIO is used to estimate only the unmodeled dynamics, the difference between the model and the system output measured by the sensor. The difference is further used to train the VIO. The estimates from the VIO and model are summed to produce the hybrid VIO’s estimate.

Fig. 3

Block diagram of the hybrid data-/model-driven observer

To study the effect of adding physical knowledge, the experimental data from the high-rate system of interest are modeled using a state-space representation

$$ \begin{aligned} {\dot{\mathbf{x}}}(t) &= {\mathbf{A}}{\mathbf{x}}(t) + {\mathbf{B}}{\mathbf{u}}(t) + {\mathbf{K}}{\mathbf{w}}(t) \hfill \\ {\mathbf{y}}(t) &= {\mathbf{Cx}}(t) + {\mathbf{Du}}(t) + {\mathbf{w}}(t) \hfill \\ \end{aligned} $$

(15)

where A, B, C, D, and K are the state-space matrices and u(t), y(t), w(t), and x(t) are the input, output, disturbance, and state vectors. A six degrees-of-freedom (DOF) representation will be used to synthetically create partial physical knowledge from the system. The representation is constructed using the function ssest from the MATLAB system identification toolbox by feeding the time series of the input and output measurements and specifying the DOFs.

3 Numerical simulations

Simulations were conducted on high-rate experimental data gathered from a mechanical shock test on an electronics unit. The various input space transition techniques of the VIO (fast, slow, and smooth transitions) are compared along with a traditional pre-optimized fixed input strategy as a baseline. Simulations are also conducted on the hybrid data-/model-based observer.

3.1 Experimental data

The experimental setup is shown in Fig. 4. An electronics unit (Fig. 4c) houses four circuit boards each equipped with a high-g Meggitt 72 accelerometers. These high-g accelerometers are capable of accurately measuring upward accelerations up to 120,000 g_n or 120 kg_n [46], where 1 g_n = 9.81 m/s² = 32.2 ft/s². The electronics in the unit are potted in high-density polystyrene for shock survivability. The unit is securely held in a fixture (Fig. 4b) with a threaded lock ring. The fixture is bolted to an accelerated drop tower (Fig. 4a), which creates an impact condition. In this study, only the top (accel 2) and bottom (accel 1) accelerometer data sets are used.

Fig. 4

Experimental setup: a MTS-66 drop tower; b unit mounting fixture; and c electronics unit

Data were acquired using a Precision Filters signal conditioner coupled with a National Instruments data acquisition system. Precision Filter 28,000 chassis with 28144A Quad-Channel Wideband Transducer Conditioner is operated in constant voltage excitation mode with an anti-aliasing filter of 204.6 kHz. A National Instruments chassis with a PXI-6133 acquisition card sampling at 1 MSa/s is used for the acquisition of data.

This high-rate experiment contains many complexities. Noise is added to the data from the cable whip from the operation of the drop tower. The uncertainties are in the unknown high-rate material response of the unit and boundary conditions. It is unsure whether or not the potting material stays bonded to the inner wall of the electronics unit. The precise input to the system from the drop tower impact is unknown. Only the response to the impact is measured. There are time-varying properties in the system response observed through back-to-back test results. Lastly, disturbances are created from sensor and system resonance from vibrations of threaded interfaces.

The experimental data are plotted in Figs. 5 and 6. The data are collected from five back-to-back tests of the same test condition. The entire high-rate dynamic event happens within 1 ms and produces deceleration responses ranging between − 60 kg_n to above 50 kg_n. The overall response of the system is distinct from the similarities between the tests. However, from the zoomed in plots of both accel 1 (inputs) and accel 2 (outputs), there is evidence of time-varying properties. Figures 5c and 6d show the amplitudes increasing and the response delay varies as the test numbers increase.

Fig. 5

Time history of accel 1: a over 1 ms; b zoom on 0.11–0.21 ms; c zoom on 0.3 0.4 ms; and d zoom on 0.41–0.47 ms

Fig. 6

Time history of accel 2: a over 1 ms; b zoom on 0.14–0.22 ms; c zoom on 0.32–0.37 ms; and d zoom on 0.44–0.53 ms

3.2 Simulation results

3.2.1 Comparison of the VIO input space transition strategies

First, the performance of the different input space transitioning techniques is studied. Their performance is investigated relative to a traditional fixed input strategy. The fixed input space observer used the same WNN architecture as that of the VIO, but v is pre-optimized over the range τ = [1, 500] and d = [2, 5] to obtained the smallest root-mean-square error (RMSE). The optimal fixed input observer used τ = 46 and d = 3. Data from accel 1 (Fig. 4) are used as the input and accel 2 as the output to construct a representation.

The same parameters were used to simulate all observers for a direct comparison to determine which input space adaptation performs best. The parameter values are tabulated in Table 1. Values $\varGamma_{\gamma }$ and $\varGamma_{\sigma }$ are, respectively, the learning rates for γ and σ, σ(0) is the initial σ assigned to newly added nodes, R_tot and A_tot are threshold values suggested by Kennel [45] to determine if a neighbor is a false nearest neighbor, the FNN percentage is the upper percentage threshold in which to determine the proper embedding dimension, and the sliding window size is the history data size used to calculate the input space.

Table 1 Parameter values for all observer variations

Figure 7 is a plot of typical estimation time histories. The experimental data of accel 2 are represented by the gray solid line, the fixed input observer by the solid orange line, the fast transitioning VIO by the red solid line, the slow transitioning VIO by the green dashed line, and the smooth transitioning VIO by the blue dashed line. The overall estimations for the observers are plotted in Fig. 7a, with zoomed portions in Fig. 7b–d. Visual inspections of results show error spikes detected in the fixed observer, and in the fast and slow transitioning observers. The nonstationary nature of the high-rate experiment requires the input space to adapt to the dynamics. The proposed technique of using the sigmoid function to provide a smooth transition between input spaces shows superior to the previous versions based on the elimination of the error spikes. Another observable feature is that the data-driven methods did poorly in capturing the rise time of the initial pulse, but later was able to converge and produce good results.

Fig. 7

Estimation time histories: a over 0.9 ms; b zoom on 0–0.13 ms; c zoom on 0.4–0.52 ms; d zoom on 0.52–0.58 ms

Three more simulations were conducted to evaluate the robustness in the smooth transitioning VIO’s choice of parameters. The second simulation used the same parameters as listed in Table 1, but with changing σ(0) to 105% (5% increase) of the value listed in Table 1. Likewise, the third and forth simulations changed $\varGamma_{\gamma }$ and $\varGamma_{\sigma }$ to 105% of the value listed in Table 1, respectively. The performance of the observers is assessed through performance metrics listed in Table 2. A smaller number of nodes (J1) represent a more compact representation of the essential dynamics of the high-rate system, and thus a faster computation time. Note that the computation time itself is not part of this study. The RMSE of the entire trace (J2) gives an indication of overall fitting error. The RMSE of the first 0.13 ms (J3) is selected to compare the initial pulses of the estimations. The convergence time (J4) is determined from the start of the event (time = 0 ms) to when the absolute error falls and remains under 10% of the initial pulse value (3.7 kg_n). The error (J5–J6) is defined as the difference between the experimental data and the estimations produced by the different observers.

Table 2 Performance metrics

Figure 8 compares the performance metrics (J1–J6) of the observers for the different simulations on radar plots. All the performance metrics are defined such that a smaller number exhibits a better performance. Results show that the smooth transitioning input space VIO outperforms all other observers over all performance metrics for every simulations, except for metric J4 under 105% of $\varGamma_{\gamma }$. A cross-comparison between simulations shows that the wavelet neural network-based representation is relative robust to the studied changes in parameters.

Fig. 8

Radar plots of performance metrics J1–J6: a simulation using parameters in Table 1; b 105% of σ(0); c 105% of $\varGamma_{\gamma }$; d 105% of $\varGamma_{\sigma }$

Figure 9 plots the evolution of τ and d for the smooth transitioning input space technique. The input space is constantly fluctuating throughout the simulation due to the nonstationary dynamics of the high-rate system. Remark that prior studies have shown the stabilization of these parameters over stationary excitations (see [18], for instance). Early in the simulation at approximately 0.1 ms, there is a spike in τ attributable to a noisy low-amplitude excitation, after which τ drops and fluctuates at values under 50 points, later converging around 10 when the excitation becomes more stationary between 0.75 and 0.9 ms. The value for d increases from 2 when the excitation becomes more chaotic, oscillating between 2 and 3 for the majority of the excitation. It oscillates between 2 and 4 at the end of the simulation due to the higher level of chaos in the signal.

Fig. 9

Evolution of τ and d

The performance of the smooth transitioning VIO is further validated on a high impact velocity test using the same electronics unit (see Fig. 4). The unit was shot out of a smooth bore Howitzer impacting a concrete specimen. The estimation is compared with the same fixed input observer with τ = 46 and d = 3. The same observer parameters listed in Table 1 were used. Figure 10 plots the time histories.

Fig. 10

Estimation time histories: a over 80 ms; b zoom on 0–10 ms; c zoom on 25–35 ms; d zoom on 55–65 ms

The smooth transitioning VIO outperformed the fixed input observer in the initial convergence (Fig. 10b), eliminated the error spikes (Fig. 10c), and yielded a smaller overall RMSE of 1.38 kg_n compared with the fixed observer’s RMSE of 1.93 kg_n (a 29% improvement). The smooth transitioning VIO was capable of achieving better results while using a more compact representation of 33 nodes compared with 38 nodes for the fixed observer.

3.2.2 Model estimate of high-rate dynamics

The result for modeling high-rate dynamics with a six degrees-of-freedom representation is shown in Fig. 11. Figure 11 shows that the modeling approach produces an acceptable fit with a better estimate than the pure data-driven observer early on, but that the high-rate complexities are not captured by the model.

Fig. 11

Modeled estimate of the high-rate experimental data

3.2.3 Hybrid VIO study

Now, we study the exploitation of physical knowledge to create a hybrid VIO. Figure 12 shows the comparison between the hybrid VIO estimate versus the smooth transitioning VIO (pure data-driven). It can be observed in Fig. 12b that better initial convergence is achieved through the addition of the physical knowledge. The hybrid VIO outperformed the smooth transitioning VIO using a fewer number of nodes and smaller overall RMSE, RMSE of the initial pulse, maximum absolute error, and average absolute error, and a similar convergence time as illustrated in the radar plot on Fig. 13.

Fig. 12

Hybrid observer versus smooth transitioning VIO: a over 0.9 ms; b zoom on 0–0.13 ms

Fig. 13

Radar plot of performance metrics J1–J6 comparing the hybrid VIO with the smooth transitioning VIO

The combination of the model and VIO is capable of producing a representation between accel 1 (the input) and accel 2 (the output) for test 3. Test 3 was chosen as the training data set to be consistent with previous VIO studies. Using the different tests shown in Figs. 5 and 6, we verify the robustness of the representation. The inputs of tests 1, 2, 4, and 5 were used to estimate the outputs of the corresponding tests through a pre-trained hybrid VIO, using the data from test 3. The absolute errors are plotted in Fig. 14. The majority of the errors fall below 20% of the initial pulse value with some peak errors occurring just under 15 kg_n. These maximum absolute errors are much smaller than those displayed in Fig. 8’s J5 metric.

Fig. 14

Absolute errors of estimates of tests 1, 2, 4, 5 using the learned representation from the hybrid observer

4 Conclusion

State estimation of high-rate dynamic systems is challenging due to multiple system complexities such as noise, uncertainties, time-varying parameters/states, and disturbances. Examples of these systems include civil structures exposed to blast and aerial vehicles exposed to in-flight anomalies such as contact with foreign objects. Adaptive observers showed to be an important tool for estimating complex systems. However due to the high-rate nature, adaptive observers would require faster convergence rates to be applicable.

As a potential solution, we presented a variable input observer (VIO) which optimized the use of past data. By doing so, we optimize the inputs to an estimator with the objective to enable faster convergence through an optimized representation. The variable input concept was based on the embedding theorem, whereas the input space is designed through a delay vector that preserves the essential dynamics of the system of interest. By allowing the delay vector to vary as sensor measurements become available, the embedding theorem is applied to complex nonstationary high-rate problems.

Three different input space transitioning strategies were studied. Those included fast, slow, and smooth transitioning input spaces. The fast transition applied no restriction on the input space adaptation allowing the time delay τ and embedding dimension d to vary as the calculations were made. The slow transitioning input space limited τ to vary by ± 10 and d by ± 1. The smooth transitioning input space applied a sigmoid function to τ to allow a smooth transition between input spaces.

Demonstrated in the simulations of high-rate experimental data, the smooth transitioning VIO outperformed all other methods, including a typical pre-optimized fixed input space observer in terms of number of nodes, RMSE of the entire trace, RMSE of the first 0.13 ms, convergence time, maximum absolute error, and average absolute error. The error spikes are eliminated through the smooth transition and through a more accurate representation of the nonstationary high-rate system.

The training speed of the a neural network depends on many parameters such as the number of nodes used to build the representation, CPU speed, quality of the coding, etc. Through the smooth transitioning VIO, the number of nodes was minimized and provided more efficient training as observed through the faster convergence times. The real-time application of the VIO is currently under investigation.

A six degrees-of-freedom model of the high-rate data, representing a level of physical knowledge about the system, was added to the VIO to create a hybrid VIO. Results showed that the hybrid observer was capable of producing superior representations of the system compared with either a pure data- or model-driven observer. To validate the representation, inputs from consecutive tests were used to estimate the corresponding outputs. The study showed the majority of absolute errors were below the 20% of the initial pulse value. Furthermore, the peak absolute errors were much smaller than those seen using other observers.

Based on this study, the VIO has shown great promise for the use in nonstationary high-rate applications. The VIO, through the adaptive input space, is capable of sequentially learning chaotic representations improving the performance of an adaptive observer including its convergence time.