1 Introduction

In many industries, the competition between firms has become chain-to-chain or channel-to-channel competition, in which an upstream or downstream firm in one supply chain not only competes with its counterpart in the other chain but also interacts with the entire other chain. Chain-to-chain competition is seen in a variety of industries such as fast food, fashion clothing, automobiles, electronics, and telecom industries. For these industries, how a supply chain is structured—vertically integrated or decentralized—critically impacts the supply chain’s performance in the competition. This paper aims to analyze how the choice of supply chain structure affects firms’ strategic behaviors and what supply chain structure may emerge as an equilibrium choice.

We consider the inventory competition between two competing supply chains. Each chain has one manufacturer and two exclusive retailers. The two manufacturers produce differentiated products, which can be either substitutable or complementary. Each retailer faces random demand and, before the demand is realized, the retail inventory decision must be made by the retailer (if its supply chain is decentralized) or by the entire integrated chain. A retailer’s inventory affects the probability distributions of the demands at all retailers. For substitutable products, a retailer’s inventory stimulates its own demand while having demand-stealing effect on all other retailers; for complementary products, a retailer’s inventory stimulates (instead of stealing) the competing chain’s demand. The two chains engage in inventory competition by making newsvendor type of decisions. Our setting may be applied to capacity investment competition, where a high service capacity has demand-stealing effect on other service providers.

When a chain is integrated, the inventory decision is made by the entire chain; when a chain is decentralized, each retailer makes its own inventory decision, but all firms in the chain can coordinate their decisions via supply contracts. We examine three possible supply chain structures: two integrated chains, two decentralized chains, and the mixed structure with one integrated chain and one decentralized chain. These structures are also compared with the first-best structure where one decision-maker decides inventory for both chains. The key questions are: How do firms compete under a given supply chain structure? Which structure outperforms other structures in terms of supply chain profitability, and under what conditions? What is the equilibrium supply chain structure choice? What is the impact of demand uncertainty on the supply chain structure choice?

The chain-to-chain or channel-to-channel competition has been studied in the analytical marketing literature. McGuire and Staelin [1] analyze various retail distribution structures in the context of two competing manufacturers, each selling products through an independent retailer. They explain that a strategic reason for manufacturers to use intermediaries is to shield themselves from possibly ruinous price competition. Coughlan [2] extends this research to a more general demand function and applied it to the electronic industry. Moorthy [3] links the value of decentralization to the concept of strategic interaction. Zhao et al. [4] endogenize the product differentiation and examine the supply chain structure under both price and service competition. There are also models for the industry settings where retailers carry an assortment of products from multiple manufacturers. Choi [5] considers two manufacturers selling their products through a common retailer. Lee and Staelin [6] and Trivedi [7] generalize the above work to a competitive environment with two manufacturers and two common retailers. We also analyze the competition among manufacturers and (exclusive) retailers, but we focus on a setting where demands are uncertain and retail inventories must be decided prior to the realization of the demands.

Supply chain contracts and industry structure choices under demand uncertainty have been considered in the literature. Kranton and Minehart [8] compare vertical integration versus networks. (Vertically integrated firms make their own inputs, while firms in networks procure inputs from several suppliers who, in turn, sell to several network firms.) They model demand uncertainty as incorporated in firms’ random valuation of the supply, and there is no inventory decision in their framework. They show that firms are likely to form networks when they experience large idiosyncratic demand shocks. Ai et al. [9] examine a setting where manufacturers in two competing supply chains may choose either a wholesale price contract in which the retailer’s demand forecasting information is not shared, or a revenue-sharing contract in which the retailer’s demand forecasting information is shared. They find that supply chain contract choice depends on the degree of product substitution and demand uncertainty.

Competition among newsvendors has been studied in the literature. Parlar [10] models a duopoly of two newsvendors selling substitutable products. When either newsvendor experiences stockout, a fraction of the excess demand switches to the other. Lippman and McCardle [11] start with aggregate industry demand and specify a variety of rules to split the realized aggregate demand among firms. Mahajan and van Ryzin [12] derive the demand from dynamic consumer choice. There are also simple allocation rules that lead to more explicit solution. Cachon [13] considers proportional demand allocation rule and reaches qualitatively consistent insights.

In a competitive environment, inventory has demand-stealing effect and demand-stimulating effect. Cachon [13] finds that “Competition makes the retailers order more inventory because of the demand-stealing effect: each retailer ignores the fact that ordering more means the other retailers’ demands stochastically decrease. \(\cdots \)Furthermore, if retailers sell complements, rather than substitutes, then the demand-stealing effect is reversed: each retailer tends to understock because it ignores the additional demand it creates for other retailers.” Dana and Petruzzi [14] point out that consumers are more likely to purchase from stores that have fewer stockouts. They provide a consumer choice model in which consumers maximize expected utility by taking into account the inventory available at the firm. In this paper, we model the demand distribution as a linear function of the inventory levels. This linear approximation allows us to model both demand-stealing and stimulating effects as well as both substitutable and complementary products. Furthermore, the research efforts in the literature suggest the difficulty in obtaining explicit formulas for equilibrium analysis. This paper aims to explicitly derive and compare equilibria under various supply chain structures, and our demand model makes such analysis tractable.

In this paper, we do not consider price competition nor transshipment between retailers. For models with both price and inventory competition, see [15], and for models with transshipment after the realization of demand, see [16].

2 The Model

We analyze two competing supply chains, indexed by \(i=1,2\), with chain i supplying product i. The two products can be either substitutable or complementary. Chain i has one manufacturer, referred to as manufacturer i, and two exclusive retailers, indexed by (i, j), \(j=1,2\). As a convention, we use \(-i\) to refer to the other chain/manufacturer/product, and use \((i,-j)\) to refer to the other retailer of chain i.

We consider a single-period setting where both supply chains produce and stock their products before the selling season starts. Let \(c_i\) denote manufacturer i’s per-unit production cost, and let \(v_i\) denote the per-unit salvage value (if \(0<v_i<c_i\)) or disposal cost (if \(v_i<0\)) at the end of the selling season. The retail prices for the two products, \(p_1\) and \(p_2\), are assumed to be exogenous.

2.1 Demand Model

The two chains compete by deciding inventory levels before the selling season. Let \(q_{ij}\) denote the inventory level at retailer (i, j) and let \({\varvec{q}}= (q_{11},q_{12},q_{21},q_{22})\). Let random variable \(\xi _{ij}\) represent retailer (i, j)’s natural demand, which is the demand occurring at the retailer (i, j) when no retailer carries any inventory (\({\varvec{q}}=0\)). The random variables \(\xi _{ij}\)’s may be dependent. For analytical simplicity, we assume the demands facing retailers in the same chain, \(\xi _{i1}\) and \(\xi _{i2}\), have the same probability distribution, with cumulative distribution function denoted as \(F_i(x)\), \(i=1,2\).

The probability distribution of the demand at any retailer is affected by the inventory available at all retailers. To facilitate the analysis, we assume these effects have a linear form. Specifically, the random demand facing retailer (i, j) is modeled as

$$\begin{aligned} D_{ij}({\varvec{q}}) \&= \ \xi _{ij} \, +\, \alpha _i q_{ij} \, -\, \beta _i q_{i,-j} \, -\, \frac{1}{2}\, \gamma _{-i} (q_{-i,1}+q_{-i,2}),\quad i,j=1,2, \end{aligned}$$
(2.1)

where

$$\begin{aligned}&1 > \alpha _i \geqslant \beta _i \geqslant 0, \quad \ \beta _i \geqslant \gamma _i, \quad \ 1>\alpha _i-\beta _i-\gamma _i \geqslant 0, \nonumber \\&\quad \text {for } i=1,2, \quad \text {and} \quad \gamma _1\gamma _2 \geqslant 0. \end{aligned}$$
(2.2)

In model (2.1), inventory levels shift the natural demand in the following ways:

  • The term \(\alpha _i q_{ij}\) suggests that inventory availability stimulates retailer’s own demand.

  • The term \(-\beta _i q_{i,-j}\) reflects a within-chain demand-stealing effect: the availability of product i at a retailer reduces the demand at the other retailer of the same chain.

  • The last term \(-\frac{1}{2}\gamma _{-i} (q_{-i,1}+q_{-i,2})\) captures the between-chain demand-stealing effect when \(\gamma _1>0\) and \(\gamma _2>0\) (i.e., substitutable products) or demand-stimulating effect when \(\gamma _1<0\) and \(\gamma _2<0\) (i.e., complementary products).

The assumption of \(\alpha _i \geqslant \beta _i\) in (2.2) indicates that raising inventory level \({q}_{ij}\) does not reduce chain’s own demand. We refer to \(\alpha _i - \beta _i\) as inventory’s net stimulating effect on own chain’s demand.

Because \(\gamma _1\) and \(\gamma _2\) have the same signs (assumption of \(\gamma _1\gamma _2 \geqslant 0\)), we use \(\gamma >0\) and \(\gamma <0\) to indicate substitutable and complementary products, respectively, throughout the paper. For substitutable products, \(\beta _i \geqslant \gamma _i>0\) in (2.2) implies that the demand-stealing effect is stronger within chains than between chains, because the retailers of the same chain carry the same product.

The total effect of inventory \(q_{ij}\) on all demands is \(\alpha _i-\beta _i-\gamma _i\), assumed to be in [0, 1) in (2.2). That is, one unit of inventory does not reduce the total demand, nor does it stimulate more than one unit of demand.

We assume \(q_{ij}\in [0, q_{ij}^{\max }]\) and denote the strategy set as \(Q=\big \{{\varvec{q}}: q_{ij}\in [0, q_{ij}^{\max }] \big \}\). Throughout the paper, we assume \(D_{ij}({\varvec{q}}) \geqslant 0\), for \({\varvec{q}}\in Q\) and all equilibria are attained within the interior of Q.

The assumption of linear effects of inventory on demand allows us to explicitly analyze the competition between the two chains and derive useful insights.

2.2 Service Level and Inventory

Let \(S_{ij}\) denote the service level of retailer (i, j). That is,

$$\begin{aligned} S_{ij}&= \mathsf{P}\big [D_{ij}({\varvec{q}})\leqslant q_{ij} \big ]\nonumber \\&= F_{i}\Big ((1-\alpha _i)q_{ij} + \beta _i q_{i,-j}+ \frac{1}{2}\gamma _{-i} (q_{-i,1}+q_{-i,2})\Big ), \quad i,j=1,2. \end{aligned}$$
(2.3)

Assume \(F_i(x)\) is continuous and strictly increasing in x for \(F_i(x)\in (0,1)\). Thus, \(F_i^{-1}(y) = \inf \big \{ x : F(x) \geqslant y\}\) is continuous and strictly increasing in y for \(y\in (0,1)\). Then, (2.3) leads to a system of linear equations for \({\varvec{q}}\):

$$\begin{aligned} (1-\alpha _i)q_{ij} + \beta _i q_{i,-j}+ \frac{1}{2}\gamma _{-i} (q_{-i,1}+q_{-i,2}) = F^{-1}_{i}(S_{ij}), \quad i,j=1,2. \end{aligned}$$
(2.4)

For given retail service levels \(S_{ij}\in (0,1)\), \(i,j=1,2\), the system of equations in (2.4) uniquely determines the inventory level \({\varvec{q}}\). In particular, if the two retailers in chain i achieve service level \(S_i\), i.e., \(S_{i1}=S_{i2}=S_i\), for \(i = 1, 2\), then system in (2.4) determines the corresponding inventory levels:

$$\begin{aligned} q_{i1} = q_{i2} = \frac{1}{\eta }\Big [ (1-\alpha _{-i}+\beta _{-i})F^{-1}_i(S_i) - \gamma _{-i} F^{-1}_{-i}(S_{-i}) \Big ],\quad i=1,2, \end{aligned}$$
(2.5)

where \(\eta = (1-\alpha _1+\beta _1)(1-\alpha _2+\beta _2)-\gamma _1\gamma _2\). Note that the relations in (2.2) imply that \(\eta >0\).

3 Supply Chain Structures and Strategic Interactions

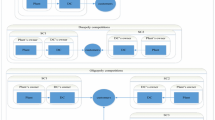
This section analyzes the firms’ strategic behaviors under various supply chain structures. Four structures are analyzed and illustrated in Fig. 1.

  1. (a)

    Integrated industry: The entire industry is integrated and decision-making is centralized.

  2. (b)

    II: Each manufacturer is integrated with its own retailers.

  3. (c)

    DD: Both chains are decentralized.

  4. (d)

    DI: One chain is integrated and the other is decentralized.

Fig. 1
figure 1

Industry structures (a) integrated industry; (b) two integrated chains (II); (c) two decentralized chains (DD); (d) a decentralized chain and an integrated chain (DI)

Full size image

3.1 Integrated Industry

We first consider a benchmark case where an integrated industry centrally decides the stocking levels at all retailers to maximize the total expected profit. Throughout the paper, we use \(\sum \nolimits _{i,j}\) as an abbreviation for \(\sum \nolimits _{i=1}^2 \sum \nolimits _{j=1}^2 \), use \(\sum \nolimits _{i}\) for \(\sum \nolimits _{i=1}^2\), and use \(\sum \nolimits _{j}\) for \(\sum \nolimits _{j=1}^2\). The industry aims to maximize the expected total profit:

$$\begin{aligned} \max _{\varvec{q}}\ \sum _{i,j} \Big \{(p_i-c_i)q_{ij} - (p_i-v_i) \mathrm{E}\big [ (q_{ij} - D_{ij}({\varvec{q}}))^+\big ] \Big \}. \end{aligned}$$
(3.1)

Note that \( (q_{ij} - D_{ij}({\varvec{q}}))^+\) is jointly convex in \({\varvec{q}}\) because \(D_{ij}({\varvec{q}})\) is linear in \({\varvec{q}}\). Hence, the objective in (3.1) is jointly concave in \({\varvec{q}}\).

Theorem 3.1

The industry optimal service levels and inventory levels are given by \(S_{ij} = S_i^*\) and \(q_{ij} = q_i^*\), for \(i,j=1,2\), where

$$\begin{aligned} S_i^*&\overset{{\mathrm{def}}}{=} \frac{p_i-c_i-\frac{\gamma _i(p_{-i}-c_{-i})}{1-\alpha _{-i}+\beta _{-i}}}{(p_i-v_i)\left( 1-\alpha _i+\beta _i-\frac{\gamma _1\gamma _2}{1-\alpha _{-i}+\beta _{-i}}\right) }, \end{aligned}$$
(3.2)
$$\begin{aligned} q_i^*&\overset{{\mathrm{def}}}{=} \frac{1}{\eta } \left[ (1-\alpha _{-i}+\beta _{-i})F^{-1}_i(S_i^*) - \gamma _{-i} F^{-1}_{-i}(S_{-i}^*) \right] . \end{aligned}$$
(3.3)

The resulting optimal profit of the industry is

$$\begin{aligned} \pi ^*&= \sum _i \bigg [ 2(p_i-c_i)q_i^* - 2(p_i-v_i)\int _0^{F_i^{-1}(S_i^*)}F_i(u)\mathrm{d}u \bigg ]. \end{aligned}$$
(3.4)

Furthermore, \(S_i^*\) and \(q_i^*\) increase in \(\alpha _i-\beta _i\) and decrease (increase) in \(\alpha _{-i}-\beta _{-i}\) if \(\gamma >0~(\gamma <0)\). The total profit \(\pi ^*\) increases in \(\alpha _i-\beta _i\) and decreases in \(\gamma _i\).

Note that if \(\alpha _i=\beta _i=\gamma _i=0\), then \(S_i^*=(p_i-c_i)/(p_i-v_i)\), the standard newsvendor’s service level.

The monotonicity properties of \(S^*_i\) and \(q^*_i\) in Theorem 3.1 reveal that if inventory’s net stimulating effect on own chain’s demand, \(\alpha _i-\beta _i\), increases for product i, the industry should raise product i’s inventory and service level, and reduce (raise) the substitutable (complementary) product’s inventory and service level.

The monotonicity properties of \(\pi ^*\) also justify our intuition that strong net demand-stimulating effect (high \(\alpha _i-\beta _i\)) and weak product substitution or strong product complementarity (low \(\gamma \)) are favorable conditions for industry profitability.

3.2 Two Integrated Chains (II)

In this structure, each manufacturer vertically integrates with its exclusive retailers. The two integrated chains engage in inventory competition. Given chain \((-i)\)’s inventory levels \(q_{-i,1}\) and \(q_{-i,2}\), chain i’s best response problem is

$$\begin{aligned} \max _{q_{i1},q_{i2}}\ \sum _j \left\{ (p_i-c_i)q_{ij} - (p_i-v_i) \mathrm{E}\left[ (q_{ij} - D_{ij}({\varvec{q}}))^+\right] \right\} . \end{aligned}$$
(3.5)

The first-order condition for (3.5) leads to chain i’s optimal service level, which in turn determines the best response in terms of inventory levels. The equilibrium inventory levels can then be found, which is also stated in Theorem 3.2.

Theorem 3.2

(II equilibrium) When each chain is vertically integrated, the equilibrium service levels and inventory levels are given by \(S_{ij} = S^{\mathrm{II}}_i \) and \(q_{ij} = q_i^{\mathrm{II}}\), for \(i,j=1,2\), where

$$\begin{aligned} S_i^{\mathrm{II}}&\overset{{\mathrm{def}}}{=} \frac{p_i-c_i}{(p_i-v_i)(1-\alpha _i+\beta _i)}, \end{aligned}$$
(3.6)
$$\begin{aligned} q_i^{\mathrm{II}}&\overset{{\mathrm{def}}}{=} \frac{1}{\eta } \Big [ (1-\alpha _{-i}+\beta _{-i})F^{-1}_i\big (S^{\mathrm{II}}_i\big ) - \gamma _{-i} F^{-1}_{-i}\big (S^{\mathrm{II}}_{-i}\big ) \Big ]. \end{aligned}$$
(3.7)

Chain i’s profit in the eqilibrium is

$$\begin{aligned} \pi _i^{\mathrm{II}}= 2(p_i-c_i)q_i^{\mathrm{II}}- 2(p_i-v_i)\int _0^{F_i^{-1}(S^{\mathrm{II}}_i)}F_i(u)\mathrm{d}u. \end{aligned}$$
(3.8)

Furthermore, \(S_i^{\mathrm{II}}\), \(q_i^{\mathrm{II}}\), and \(\pi _i^{\mathrm{II}}\) increase in \(\alpha _i-\beta _i\); \(q_i^{\mathrm{II}}\) and \(\pi _i^{\mathrm{II}}\) decrease (increase) in \(\alpha _{-i}-\beta _{-i}\) if \(\gamma >0~(\gamma <0)\).

Note that if the two products are independent (\(\gamma _1=\gamma _2=0\)), the service level \(S_i^{\mathrm{II}}\) in (3.6) is identical to \(S_i^*\) in (3.2). It can be shown that for substitutable products, \(S_i^{\mathrm{II}}> S_i^*\), whereas for complementary products, \(S_i^{\mathrm{II}}< S_i^*\). (See Corollary 4.1 in Sect. 4.1.) Intuitively, both chains focus on inventory’s net stimulating effect on own chain’s demand and ignore the negative (positive) impact of its inventory on the substitutable (complementary) product, whereas the service level \(S_i^*\) in (3.2) internalizes the inventory effect between chains.

From Theorem 3.2, an increases in the net stimulating effect \(\alpha _i-\beta _i\) results in a higher profit for chain i, while it reduces (improves) the profit of the substitutable (complementary) product.

3.3 Two Decentralized Chains (DD)

Suppose that both chains are decentralized and, within each chain, the manufacturer and its retailers are coordinated via supply contracts. As discussed in Sect. 1, the focus of this paper is chain-to-chain competition, not competition between manufacturers. Thus, we assume the manufacturer and retailers are coordinated to maximize their chain’s own profit. For many channel-coordinating contracts, the contract parameters can be adjusted to achieve various allocations of the supply chain profit between the manufacturer and the retailers.

The chain-to-chain competition in DD structure involves two stages. In the first stage, both chains decide their target service levels (via coordinating contracts). In the second stage, the four retailers compete in inventories under the given contracts.

In the first stage, various forms of contracts can serve the purpose of setting target service level. For example, under a buyback contract with wholesale price \(w_i\) and buyback rate \(b_i\), retailer (i, j)’s problem becomes

$$\begin{aligned} \max _{q_{ij} \geqslant 0} (p_i-w_i)q_{ij}- (p_i-b_i) \mathrm{E}\big [ (q_{ij} - D_{ij}({\varvec{q}}))^+\big ]. \end{aligned}$$
(3.9)

It can be verified that the above retailer’s problem leads to the following service level:Footnote 1

$$\begin{aligned} S^c_i = \frac{p_i-w_i}{(p_i-b_i)(1-\alpha _i)}. \end{aligned}$$

From this point onward, we do not assume any specific contract form. We let \(S_i^c\) denote the target service level chosen by chain i in the first stage. Then, using (2.5), the second-stage equilibrium inventory levels are

$$\begin{aligned} q_{i1} = q_{i2}&= \frac{(1-\alpha _{-i}+\beta _{-i})F^{-1}_i\big (S^c_i\big ) - \gamma _{-i} F^{-1}_{-i}\big (S^c_{-i}\big )}{\eta }. \end{aligned}$$
(3.10)

In the first-stage game, each chain anticipates the retailers’ equilibrium decisions in (3.10) and chooses service levels simultaneously. Chain i’s problem can be written as (using (3.10)):

$$\begin{aligned}&\max _{S^c_i} \ 2 (p_i-c_i) \frac{(1-\alpha _{-i}+\beta _{-i})F^{-1}_i\big (S^c_i\big ) - \gamma _{-i} F^{-1}_{-i}\big (S^c_{-i}\big )}{\eta } \nonumber \\&\quad - 2(p_i-v_i) \int _0^{F_i^{-1}\big (S^c_i\big )}F_i(u)\mathrm{d}u. \end{aligned}$$
(3.11)

The objective in (3.11) is generally not concave, but the proof of Theorem 3.3 shows that this objective is quasi-concave in \(S^c_i\). Hence, the optimal service level is determined by the first-order condition:

$$\begin{aligned} \frac{2(p_i-c_i)(1-\alpha _{-i}+\beta _{-i})}{\eta } \frac{\partial F^{-1}_i\big (S^c_i\big )}{\partial S^c_i} - 2(p_i-v_i) S^c_i \frac{\partial F^{-1}_i\big (S^c_i\big )}{\partial S^c_i}&= 0, \end{aligned}$$
(3.12)

which leads to the optimal service level given in the following theorem.

Theorem 3.3

(DD equilibrium) When both chains are decentralized, the equilibrium service levels and inventory levels are given by \(S_{ij} = S^{\mathrm{DD}}_i \) and \(q_{ij} = q_i^{\mathrm{DD}}\), for \(i,j=1,2\), where

$$\begin{aligned} S_i^{\mathrm{DD}}&\overset{{\mathrm{def}}}{=} \frac{p_i-c_i}{(p_i-v_i)(1-\alpha _i+\beta _i-\frac{\gamma _1\gamma _2}{1-\alpha _{-i}+\beta _{-i}})}, \end{aligned}$$
(3.13)
$$\begin{aligned} q_i^{\mathrm{DD}}&\overset{{\mathrm{def}}}{=} \frac{1}{\eta } \Big [(1-\alpha _{-i}+\beta _{-i})F^{-1}_i\big (S_i^{\mathrm{DD}}\big ) - \gamma _{-i} F^{-1}_{-i}\big (S_{-i}^{\mathrm{DD}}\big )\Big ]. \end{aligned}$$
(3.14)

Chain i’s profit in the equilibrium is

$$\begin{aligned} \pi _i^{\mathrm{DD}}= 2(p_i-c_i)q_i^{\mathrm{DD}}- 2(p_i-v_i) \int _0^{F_i^{-1}(S^{\mathrm{DD}}_i)}F_i(u)\mathrm{d}u. \end{aligned}$$
(3.15)

Furthermore, \(S_i^{\mathrm{DD}}\) increases in \(\alpha _i-\beta _i\) and \(\alpha _{-i} - \beta _{-i}\). If \(\gamma <0\), then \(q_i^{\mathrm{DD}}\) and \(\pi _i^{\mathrm{DD}}\) increase in \(\alpha _i - \beta _i\) and \(\alpha _{-i} - \beta _{-i}\).

In Theorems 3.1 and 3.2, \(q_i^*\) and \(q_i^{\mathrm{II}}\) increase in \(\alpha _i - \beta _i\), but in the DD structure when \(\gamma >0\), \(q_i^{\mathrm{DD}}\) does not necessarily increase in \(\alpha _i-\beta _i\). This is because the competing chain’s service level \(S_{-i}^{\mathrm{DD}}\) increases in \(\alpha _i-\beta _i\), which may cause \(q_i^{\mathrm{DD}}\) in (3.14) to decrease, and \(\pi _i^{\mathrm{DD}}\) may decline as well. When \(\gamma <0\), as \(\alpha _i-\beta _i\) increases, inventory levels and profits of both chains increase.

It is important to note that the coordinated decentralized chains do not behave as the integrated chains in the II structure. Integrated chains compete directly using inventory levels: In the II equilibrium, chain i’s inventory levels are optimized given by the other chain’s inventory decisions. However, decentralized chains do not decide inventory directly, but decide service levels in the first stage. Both chains recognize that their own service levels will influence the competing chain’s inventory levels in the second stage, reflected by (2.5) and elaborated below:

  • If the two products are substitutes, then a high chain’s own service level reduces the competing chain’s inventory. This effect provides incentives for both decentralized chains to raise their service levels above those in the II equilibrium.

  • If the two products are complements, then a high own chain’s service level increases the competing chain’s inventory, which in turn stimulate own chain’s demand. This effect also provides incentives for both chains to raise their service levels above those in the II equilibrium.

Summarizing the above discussion, the service level \(S_i^{\mathrm{DD}}\) in (3.13) is higher than \(S_i^{\mathrm{II}}\) in (3.6), regardless of the whether the products are substitutes or complements. The only situation that \(S_i^{\mathrm{DD}}=S_i^{\mathrm{II}}\) is when the two products are independent (\(\gamma =0\)).

3.4 A Decentralized Chain Competing with an Integrated Chain (DI)

Suppose that chain 1 is decentralized and chain 2 is integrated. In the decentralized chain, the manufacturer and the retailers are coordinated via contracts. Unlike the DD structure where neither chain can decide inventory levels in the first-stage game, in the DI structure, the integrated chain decides inventory levels, while the decentralized chain decides its service level. In the second stage, the decentralized retailers decide inventory levels.

We first discuss the intuitions on the equilibrium behavior, and then formally prove these intuitions. Focus on the decentralized chain (chain 1) first. If the competing chain (chain 2) is also decentralized, the analysis on DD structure shows that chain 1 chooses service level to influence the chain 2’s inventory decisions in the second stage. If the chain 2 is integrated, however, it commits inventory levels in the first stage, and thus, the best response of chain 1 is to induce its retailers to choose the best inventory levels in response to chain 2’s inventory, which coincides with the best response problem of an integrated chain in the II structure. Therefore, chain 1’s behavior may be similar to an integrated chain in the II structure even though it is decentralized.

We now turn to the integrated chain 2 in the DI structure. Chain 2 understands that it makes inventory decisions earlier than chain 1’s retailers decide inventory. Chain 2 also recognizes that its service level influences chain 1’s inventory decision, reflected by (2.5). Hence, chain 2’s problem is similar to that in the DD structure. Therefore, chain 2’s behavior may be similar to a decentralized chain in the DD structure even though it is integrated.

We now formalize the above intuitions. In the first-stage game, chain 1 chooses coordinating contract and chain 2 decides inventory. Consider chain 1’s best response problem to chain 2’s inventory \(q_{21}\) and \(q_{22}\). Chain 1 aims to maximize its profit by choosing a contract and its parameters. This contract should induce chain 1’s retailers to choose the best inventory levels in response to chain 2’s inventory levels. From the II structure in Theorem 3.2, we know that the service level that maximizes chain 1’s profit is given by \(S_1^{\mathrm{II}}\) in (3.6). Hence, chain 1 will set a contract such that

$$\begin{aligned} S_{1j} =S_1^{\mathrm{II}}. \end{aligned}$$
(3.16)

This confirms our intuition that the behavior of the decentralized chain in the DI structure is similar to an integrated chain in the II structure.

Using (2.3), we can write the condition (3.16) as

$$\begin{aligned} S_{1j} = F_{1}\Big ((1-\alpha _1))q_{1j} + \beta _1 q_{1,-j}+\frac{1}{2}\gamma _2(q_{21}+q_{22})\Big ) = S_1^{\mathrm{II}},\quad j=1,2. \end{aligned}$$

From the above equation, we can find chain 1’s inventory level as a best response to chain 2’s inventory \(q_{21}+q_{22}\):

$$\begin{aligned} q_{11}+q_{12}&= \frac{-\gamma _2(q_{21}+q_{22})+2F_{1}^{-1}\big (S_1^{\mathrm{II}}\big )}{1-\alpha _1+\beta _1}. \end{aligned}$$
(3.17)

Clearly, for substitutable (complementary) products, inventories are also strategic substitutes (complements).

Next, we consider the integrated chain 2 making inventory decisions in anticipation of chain 1’s response in (3.17). Using (3.17), chain 2’s problem can be written as

$$\begin{aligned} \max _{q_{21},q_{22}} \ \sum _j \left\{ (p_2-c_2)q_{2j} -(p_2-v_2) \mathrm{E}\big [ \big (q_{2j} - D_{2j}( q_{12}, q_{22}) \big )^+\big ] \right\} , \end{aligned}$$
(3.18)

where

$$\begin{aligned}&D_{2j}(q_{21}, q_{22}) \nonumber \\ \overset{{\mathrm{def}}}{=}&\ \xi _{2j} + \alpha _2 q_{2j} - \beta _2 q_{2,-j} +\frac{\gamma _1\gamma _2(q_{21}+q_{22})}{2(1-\alpha _1+\beta _1)} -\frac{\gamma _1F_{1}^{-1}\big (S_1^{\mathrm{II}}\big )}{1-\alpha _1+\beta _1}. \end{aligned}$$
(3.19)

Because \(D_{2j}(q_{21}, q_{22}) \) is linear in \(q_{21}\) and \(q_{22}\), the objective function in (3.18) is concave in \(q_{21}\) and \(q_{22}\).

Using (3.19), the objective in (3.18) can be written as

$$\begin{aligned}&\sum _j \left[ (p_2-c_2)q_{2j} -(p_2-v_2) \int _0^{q_{2j}} F_{2}\left( u-\alpha _2q_{2j}+ \beta _2 q_{2,-j}\right. \right. \\&\quad \left. \left. -\,\frac{\gamma _1\gamma _2(q_{21}+q_{22})}{2(1-\alpha _1+\beta _1)} +\frac{\gamma _1F_{1}^{-1}(S_1^{\mathrm{II}})}{1-\alpha _1+\beta _1}\right) \mathrm{d}u \right] . \end{aligned}$$

The first-order condition is

$$\begin{aligned} \frac{p_2-c_2}{p_2-v_2}&= \Big (1-\alpha _2-\frac{\gamma _1\gamma _2}{2(1-\alpha _1+\beta _1)}\Big ) S_{2j}\\&\quad +\Big (\beta _2-\frac{\gamma _1\gamma _2}{2(1-\alpha _1+\beta _1)}\Big ) S_{2,-j}, \quad j=1,2. \end{aligned}$$

The above optimality condition is equivalent to

$$\begin{aligned} S_{2j}&= S_2^{\mathrm{DD}}, \quad j=1,2, \end{aligned}$$

where \(S_2^{\mathrm{DD}}\) is defined in (3.13). This proves our intuition that the behavior of the integrated chain in the DI structure is similar to a decentralized chain in the DD structure.

The above results are summarized in the following theorem.

Theorem 3.4

(DI structure) When chain 1 is decentralized and chain 2 is integrated, the equilibrium service level and inventory level are given by \(S_{ij} = S^{\mathrm{DI}}_i \) and \(q_{ij} = q_i^{\mathrm{DI}}\), for \(i,j=1,2\), where

$$\begin{aligned} S_1^{\mathrm{DI}}&= S_1^{\mathrm{II}}= \frac{p_1-c_1}{(p_1-v_1)(1-\alpha _1+\beta _1)}, \end{aligned}$$
(3.20)
$$\begin{aligned} S_2^{\mathrm{DI}}&= S_2^{\mathrm{DD}}= \frac{p_2-c_2}{(p_2-v_2)\left( 1-\alpha _2+\beta _2-\frac{\gamma _1\gamma _2}{1-\alpha _1+\beta _1}\right) } , \end{aligned}$$
(3.21)
$$\begin{aligned} q_i^{\mathrm{DI}}&\overset{{\mathrm{def}}}{=} \frac{1}{\eta } \Big [(1-\alpha _{-i}+\beta _{-i})F^{-1}_i\big (S_i^{\mathrm{DI}}\big ) - \gamma _{-i} F^{-1}_{-i}\big (S_{-i}^{\mathrm{DI}}\big )\Big ]. \end{aligned}$$
(3.22)

Chain i’s profit in the equilibrium is

$$\begin{aligned} \pi _i^{\mathrm{DI}}&= 2(p_i-c_i)q_i^{\mathrm{DI}}- 2(p_i-v_i) \int _0^{F_i^{-1}(S^{\mathrm{DI}}_i)}F_i(u)\mathrm{d}u. \end{aligned}$$
(3.23)

Furthermore, \(S_2^{\mathrm{DI}}\), \(q_2^{\mathrm{DI}}\), and \(\pi _2^{\mathrm{II}}\) increase in \(\alpha _2-\beta _2\); \(q_1^{\mathrm{DI}}\) and \(\pi _1^{\mathrm{DI}}\) decrease (increase) in \(\alpha _2-\beta _2\) if \(\gamma >0~(\gamma <0)\); \(S_1^{\mathrm{DI}}\) and \(S_2^{\mathrm{DI}}\) increase in \(\alpha _1-\beta _1\); \(q_1^{\mathrm{DI}}\) and \(\pi _1^{\mathrm{DI}}\) increase in \(\alpha _1 - \beta _1\) if \(\gamma <0\).

The effects of integrated chain’s \(\alpha _2-\beta _2\) on the DI equilibrium are qualitatively the same as the II equilibrium in Theorem 3.2, because \(\alpha _2-\beta _2\) affects the service levels in the same way as in the II equilibrium. On the other hand, an increase in \(\alpha _1-\beta _1\) raises both \(S_1^{\mathrm{DI}}\) and \(S_2^{\mathrm{DI}}\), and thus, the effects of \(\alpha _1-\beta _1\) on the DI equilibrium are qualitatively the same as the DD equilibrium in Theorem 3.3.

4 Equilibrium Supply Chain Structures

The previous section analyzes the firms’ strategic interactions under any given supply chain structure. In this section, we consider supply chain structure choice game, in which both chains simultaneously choose to be either integrated or decentralized. We identify the equilibrium supply chain structure and further analyze the impact of demand uncertainty on the equilibrium choice.

4.1 Comparison of Industry Structures

With the equilibria solved in Sects. 3.2–3.4, we compare the equilibrium service levels, inventory levels, and profits in this section.

Corollary 4.1

If \(\gamma >0\), then \(S_i^* < S_i^{\mathrm{II}}< S_i^{\mathrm{DD}}\);   if \(\gamma <0\), then \(S_i^{\mathrm{II}}< S_i^{\mathrm{DD}}< S_i^*\).

The inequality \(S_i^{\mathrm{II}}< S_i^{\mathrm{DD}}\) means that the decentralized chains raise service levels to either reduce the demand-stealing effect of competing chain’s inventory or increase the demand-stimulating effect of competing chain’s inventory. These are discussed in detail after Theorem 3.3.

For substitutable products, chain-to-chain competition results in a higher service levels than if the entire industry is integrated. For complementary products, each supply chain enjoys the demand-stimulating effect from the other chain’s inventory and thus offers lower service level than if the industry is integrated.

Next, we compare the total industry profit. Let \(\mathrm{X}\) denote a supply chain structure, \(\mathrm{X}\in \{*, {\mathrm{II}}, {\mathrm{DD}}, {\mathrm{DI}}\}\), where “\(*\)” denotes the integrated industry structure. Let \(\pi ^\mathrm{X}\) denote the expected profit of the industry under structure \(\mathrm{X}\), which can be written as

$$\begin{aligned} \pi ^\mathrm{X}&=\pi _1^\mathrm{X}+\pi _2^\mathrm{X}\\&= \sum _i \bigg [ 2(p_i-c_i)q_i^\mathrm{X}- 2(p_i-v_i) \int _0^{F_i^{-1}\big (S^\mathrm{X}_i\big )}F_i(u)\mathrm{d}u \bigg ] \nonumber \\&= \sum _i \bigg [ \frac{2(p_i-c_i)}{\eta } \Big [(1-\alpha _{-i}+\beta _{-i})F^{-1}_i\big (S_i^\mathrm{X}\big ) - \gamma _{-i} F^{-1}_{-i}\big (S_{-i}^\mathrm{X}\big )\Big ]\\&\quad - 2(p_i-v_i) \int _0^{F_i^{-1}\big (S^\mathrm{X}_i\big )}F_i(u)\mathrm{d}u \bigg ] \\&= \sum _i \bigg \{\frac{2}{\eta }\Big [(p_i-c_i)(1-\alpha _{-i}+\beta _{-i})-\gamma _i(p_{-i}-c_{-i})\Big ]F_i^{-1}(S^\mathrm{X}_i)\\&\quad - 2(p_i-v_i) \int _0^{F_i^{-1}\big (S^\mathrm{X}_i\big )}F_i(u)\mathrm{d}u \bigg \}. \end{aligned}$$

Note that \(S_i^* \) in (3.2) can be written as

$$\begin{aligned} S_i^* = \frac{ (p_i-c_i)(1-\alpha _{-i}+\beta _{-i}) - \gamma _i(p_{-i}-c_{-i})}{(p_i-v_i) {\eta } }. \end{aligned}$$

Hence, we obtain an expression for the total industry profit:

$$\begin{aligned} \pi ^\mathrm{X}= \sum _i\ 2(p_i-v_i)\, g_i\big (S^\mathrm{X}_i\big ), \end{aligned}$$
(4.1)

where

$$\begin{aligned} g_i(S) \ \overset{{\mathrm{def}}}{=} \ S_i^* F_i^{-1}(S)-\int ^{F_i^{-1}(S)}_0 F_i(u)\mathrm{d}u. \end{aligned}$$
(4.2)

The slope of \(g_i(S)\) is

$$\begin{aligned} \frac{\mathrm{d}g_i(S)}{\mathrm{d}S}= (S_i^*-S)\frac{\mathrm{d} F_i^{-1}(S)}{\mathrm{d}S}. \end{aligned}$$
(4.3)

Using Corollary 4.1 and (4.3), it can be seen that when \(\gamma >0\), \(g_i(S)\) strictly decreases in S for \(S\in [S_i^*, S_i^{\mathrm{DD}}]\), and thus, \( g_i(S_i^{\mathrm{II}}) > g_i(S_i^{\mathrm{DD}})\). Therefore, (4.1) implies that \(\pi ^{\mathrm{DD}}< \pi ^{\mathrm{DI}}< \pi ^{\mathrm{II}}\). On the other hand, when \(\gamma <0\), \(g_i(S)\) strictly increases in S for \(S\in [S_i^{\mathrm{II}}, S_i^*]\), and thus, \(g_i(S_i^{\mathrm{II}}) < g_i(S_i^{\mathrm{DD}})\). Therefore, (4.1) implies that \(\pi ^{\mathrm{II}}< \pi ^{\mathrm{DI}}< \pi ^{\mathrm{DD}}\).

The above results are summarized in the following corollary.

Corollary 4.2

If \(\gamma >0\), then \(\pi ^{\mathrm{DD}}< \pi ^{\mathrm{DI}}< \pi ^{\mathrm{II}}< \pi ^*\). If \(\gamma <0\), then \(\pi ^{\mathrm{II}}< \pi ^{\mathrm{DI}}< \pi ^{\mathrm{DD}}< \pi ^*\).

The order of profits in Corollary 4.2 is consistent with the order of service levels in Corollary 4.1 in the following sense: The more the industry service level deviates from the industry optimal service level, the lower the total industry profit is.

The above two corollaries compare the industry-wide service levels and profits. Next, we compare supply chains’ inventory levels and profits.

Corollary 4.3

If two products are complements \((\gamma <0)\),

$$\begin{aligned} q_i^{\mathrm{II}}&\ <\ q_i^{\mathrm{DI}}\ <\ q_i^{\mathrm{DD}}<\ q_i^* , \\ \pi _i^{\mathrm{II}}&\ <\ \pi _i^{\mathrm{DI}}\ <\ \pi _i^{\mathrm{DD}}<\ \pi _i^*. \end{aligned}$$

If two products are substitutes \((\gamma >0)\),

$$\begin{aligned} q_1^{\mathrm{DI}}&< \min \big \{ q_1^{\mathrm{II}},\, q_1^{\mathrm{DD}}\big \}, \quad q_2^{\mathrm{DI}}> \max \big \{ q_2^{\mathrm{II}},\, q_2^{\mathrm{DD}}\big \},\\ \pi _1^{\mathrm{DI}}&< \min \big \{ \pi _1^{\mathrm{II}},\,\pi _1^{\mathrm{DD}}\big \}, \quad \pi _2^{\mathrm{DI}}> \max \big \{\pi _2^{\mathrm{II}},\, \pi _2^{\mathrm{DD}}\big \}. \end{aligned}$$

When \(\gamma >0\), the comparison between \(q_i^{\mathrm{II}}\), \(q_i^{\mathrm{DD}}\), and \(q_i^*\) depends on the demand distribution. To see this dependence, note that \(\displaystyle q_i^\mathrm{X}= \frac{1}{\eta } \Big [ (1-\alpha _{-i}+\beta _{-i})F^{-1}_i(S_i^\mathrm{X}) - \gamma _{-i} F^{-1}_{-i}(S_{-i}^\mathrm{X}) \Big ], \) for \(\mathrm{X}\in \{*, {\mathrm{II}},{\mathrm{DD}}\}\). Because \(\gamma >0\) and \(S_i^* < S_i^{\mathrm{II}}< S_i^{\mathrm{DD}}\), the order of \(q_i^{\mathrm{II}}\), \(q_i^{\mathrm{DD}}\), and \(q_i^*\) depends on the shape of \(F_i^{-1}(S)\) and \(F_{-i}^{-1}(S)\) for \(S\in [S_i^*, S_i^{\mathrm{DD}}]\). Similar indeterminacy occurs for ordering the profit under \(\mathrm{X}\in \{*, {\mathrm{II}},{\mathrm{DD}}\}\).

Corollary 4.3 reveals that, for complementary products, the individual chain’s inventory and profit under various structures have the same order as the industry-wide inventory and profit. However, for substitutable products, although the industry’s profits are ordered as \(\pi ^{\mathrm{DD}}< \pi ^{\mathrm{DI}}< \pi ^{\mathrm{II}}\) (see Corollary 4.2), individual supply chains’ profits do not have the same order. The integrated chain in the DI structure has the highest inventory and profit, whereas the decentralized chain in the DI structure has the lowest inventory and profit.

4.2 Equilibrium Supply Chain Structures

We now consider a supply chain structure game, in which both supply chains simultaneously choose to be integrated or decentralized, in anticipation of the profits given in the previous sections.

Consider substitutable products (\(\gamma >0\)) first. Corollary 4.3 shows that \(\pi _1^{\mathrm{II}}> \pi _1^{\mathrm{DI}}\), i.e., if chain 2 is integrated, then chain 1 prefers integration as well. By symmetry, if chain 1 is integrated, then chain 2 also prefers integration. These together imply that II structure is a Nash equilibrium supply chain structure.

When \(\gamma >0\), Corollary 4.3 also shows that \(\pi _2^{\mathrm{DD}}< \pi _2^{\mathrm{DI}}\), i.e., if chain 1 is decentralized, then chain 2 prefers integration, which asserts that integration is a dominant strategy for each supply chain when the two products are substitutable.

Next, consider the case of complementary products (\(\gamma <0\)). Corollary 4.3 shows that \(\pi _i^{\mathrm{DI}}< \pi _i^{\mathrm{DD}}\), i.e., if one chain is decentralized, then the other chain prefers to be decentralized. Furthermore, \(\pi _i^{\mathrm{II}}< \pi _i^{\mathrm{DI}}\) implies that if one chain is integrated, then the other chain still prefers decentralization. This reveals that decentralization is a dominant strategy for each supply chain when the two products are complementary.

The above discussions are summarized in the following theorem.

Theorem 4.4

If two products are substitutable, \({\mathrm{II}}\) is the unique equilibrium supply chain structure. If two products are complementary, \({\mathrm{DD}}\) is the unique equilibrium supply chain structure.

Corollary 4.2 implies that for substitutable (complementary) products, the II (DD) structure brings the industry the highest profit among all duopoly structures, and Theorem 4.4 further confirms that the II (DD) structure is the industry’s only equilibrium structure.

The reasons for II and DD to be the equilibria under different product characteristics are explained below.

Note that when a chain is decentralized, its inventory decision is delayed compared to an integrated chain, because the chain members need to negotiate on the contract terms in the first stage. This is why in the DI structure, the decentralized retailers choose their inventories after the integrated chain decides inventory levels. In fact, the DI equilibrium coincides with the equilibrium of a Stakelberg game, in which one chain chooses inventory first, and the other chain follows.

For substitutable products (\(\gamma >0\)), inventories are strategic substitutes (see equation (3.17)) and the first-mover advantage emerges. Therefore, both chains want to be the leader by committing inventory levels as early as possible, and resulting in II being the equilibrium industry structure. Neither chain has an incentive to decentralize because a delayed inventory decision will bring disadvantage to the chain when products are substituable.

For complementary products (\(\gamma <0\)), inventories are strategic complements and the first-mover advantage disappears. Both supply chains want to be the followers, resulting in DD being the equilibrium. Neither chain has an incentive to integrate because with two complementary products, early inventory decision only brings disadvantage to the integrated chain.

4.3 Impact of Demand Uncertainty

Finally, we explore the impact of demand uncertainty on supply chain’s profits. A common definition of variability order can be found in [17]. Let X and Y be random variables. X is said to be more variable than Y, denoted by \(X \geqslant _vY\), if \(\mathrm{E}[h(X)] \geqslant \mathrm{E}[h(X)]\), for all increasing convex h. If X and Y are non-negative random variables with distributions F and G, respectively, then \(X \geqslant _vY\) if and only if \(\displaystyle \int _a^\infty (G(x)-F(x))\mathrm{d}x \geqslant 0\), for all \(a \geqslant 0\).

In this paper, we use a different stochastic ordering, which we call dispersion. For simplicity, we focus on the case where distributions and inverse distributions are all continuous functions.

Definition 4.5

Let X and Y be random variables with cumulative distributions F and G, respectively, and suppose that F, G, \(F^{-1}\) and \(G^{-1}\) are continuous. X is said to be more dispersed than Y, denoted by \(X \geqslant _dY\) or \(F \geqslant _dG\), if

$$\begin{aligned} F^{-1}(b)-F^{-1}(a)&\geqslant G^{-1}(b) - G^{-1}(a), \quad \text{ for } \text{ all } 0<a < b<1. \end{aligned}$$
(4.4)

If the inverse distributions are differentiable, then Definition 4.5 is equivalent to

$$\begin{aligned} \frac{\mathrm{d} F^{-1}(y)}{\mathrm{d}y}&\geqslant \frac{\mathrm{d} G^{-1}(y)}{\mathrm{d}y}, \quad \text{ for } \text{ all } y\in (0,1). \end{aligned}$$
(4.5)

That is, X is more dispersed than Y if \(F^{-1}\) is steeper than \(G^{-1}\) (or F is flatter than G) everywhere. It can be shown that \( \geqslant _d\) is a complete order for most of commonly used class of distributions, and that \( \geqslant _d\) coupled with \(\mathrm{E}[X] \geqslant \mathrm{E}[Y]\) implies \( \geqslant _v\), as stated below.

Lemma 4.6

If \(X \geqslant _d Y\), then

  1. (a)

    If \(F(\widehat{x}) = G(\widehat{x})=\widehat{y}\in (0,1)\) for some \(\widehat{x}\), then \(F(x) \geqslant G(x)\) for all \(x \leqslant \widehat{x}\) and \(F(x) \leqslant G(x)\) for all \(x \geqslant \widehat{x}\); \(F^{-1}(y) \leqslant G^{-1}(y)\), for all \(0<y \leqslant \widehat{y}\), and \(F^{-1}(y) \geqslant G^{-1}(y)\), for all \(\widehat{y} \leqslant y <1\).

  2. (b)

    If X and Y are non-negative, and \(\mathrm{E}[X] \geqslant \mathrm{E}[Y]\), then \(X \geqslant _v Y\).

  3. (c)

    For \(y\in (0,1)\), \(\displaystyle \int _0^{F^{-1}(y)} \!\! F(u)\mathrm{d}u \geqslant \! \int _0^{G^{-1}(y)} \!\!G(u)\mathrm{d}u\), and \(\displaystyle \int ^\infty _{F^{-1}(y)}\! (1-F(u))\mathrm{d}u \geqslant \! \int ^\infty _{G^{-1}(y)} \! (1-G(u))\mathrm{d}u\).

To emphasize the dependence on demand uncertainty, we rewrite (4.1) and (4.2) as

$$\begin{aligned} \pi ^\mathrm{X}(F_1,F_2)&= \sum _i 2(p_i-v_i)g_i\big (S^\mathrm{X}_i; F_i\big ),\\ g_i(y;F)&= S_i^* F^{-1}(y)-\int ^{F^{-1}(y)}_0 F(u)\mathrm{d}u. \end{aligned}$$

Now consider two demand systems of the form specified in (2.1). All parameters are the same and the mean demands are also the same, except that one system is more dispersed than the other.

Specifically, the two demand systems are labeled by superscript F and G; we assume \(\xi ^F_{ij}\sim F_i\), \(\xi ^G_{ij}\sim G_i\), and that \(\mathrm{E}[\xi _{ij}^F] = \mathrm{E}[\xi _{ij}^G]\), for \(i,j=1,2\).

The following theorem addresses the impact of demand dispersion on the expected supply chain profit.

Theorem 4.7

If \(F_i \geqslant _d G_i\), \(i=1,2\), then for any structure \(\mathrm{X}\), \( \pi ^\mathrm{X}(F_1,F_2) \leqslant \pi ^\mathrm{X}(G_1,G_2). \) Furthermore, if \(F_i \geqslant _d G_i\) and \(F_{-i} = G_{-i}\), then for any structure \(\mathrm{X}\), \( \pi _i^\mathrm{X}(F_1,F_2) \leqslant \pi _i^\mathrm{X}(G_1,G_2). \)

We essentially prove that \(g_i(y, F)\) decreases when F becomes more dispersed, by exploring the properties of dispersion order stated in Lemma 4.6. The theorem shows that the expected industry profit is lower under larger demand dispersion (with mean demand kept constant). The theorem also shows that a high own-demand dispersion reduces own chain’s profit. However, the impact of the other chain’s demand dispersion on own profit is ambiguous. It depends on how the dispersion is shaped.

Finally, we explore the impact of demand uncertainty on the relative profit when comparing two different structures.

Theorem 4.8

If \(F_i \geqslant _d G_i\) for \(i=1,2\), then for any two structures \(\mathrm{X}_1\) and \(\mathrm{X}_2\),

$$\begin{aligned} \left| \pi ^{\mathrm{X}_1}(F_1,F_2) - \pi ^{\mathrm{X}_2}(F_1,F_2)\right|&\geqslant \left| \pi ^{\mathrm{X}_1}(G_1,G_2) - \pi ^{\mathrm{X}_2}(G_1,G_2)\right| . \end{aligned}$$
(4.6)

For individual supply chain, when \(\gamma >0\), \(F_2 \geqslant _dG_2\), and \(F_1 = G_1\),

$$\begin{aligned} \pi _1^{\mathrm{II}}(F_1,F_2) - \pi _1^{\mathrm{DI}}(F_1,F_2) \ \geqslant \ \pi _1^{\mathrm{II}}(G_1,G_2) - \pi _1^{\mathrm{DI}}(G_1,G_2); \end{aligned}$$
(4.7)

and when \(\gamma <0\), \(F_1 \geqslant _dG_1\), and \(F_2 = G_2\),

$$\begin{aligned} \pi _2^{\mathrm{DD}}(F_1,F_2) - \pi _2^{\mathrm{DI}}(F_1,F_2) \ \geqslant \ \pi _2^{\mathrm{DD}}(G_1,G_2) - \pi _2^{\mathrm{DI}}(G_1,G_2). \end{aligned}$$
(4.8)

The first part of the theorem shows that the profit differences of different industry structures are increasing as the demand becomes more uncertain.

Inequality (4.7) shows that for substitutable products, if the other chain is integrated, the advantage of integration over decentralization to own chain increases as the demand of the other chain becomes more dispersed. Inequality (4.8) shows that for complementary products, if the other chain is decentralized, the advantage of decentralization over integration to own chain increases as the demand of the other chain becomes more uncertain.

In summary, a high demand uncertainty reinforces the equilibrium supply chain structure stated in Theorem 4.4.

5 Conclusions

In this paper, we link the analytical marketing literature on channel structures to the operations management literature on inventory decisions under demand uncertainty. We examine the relations between supply chain structures, supply chain performance, product substitutability/complementarity, and demand uncertainty.

We consider three duopoly structures: two integrated chains (II), two decentralized chains (DD), and a mixed structure with one decentralized chain and one integrated chain (DI). We derive firms’ equilibrium strategies in explicit forms, which allow us to compare different supply chain structures and further analyze the equilibrium structure choice. We assume fixed prices and focus on inventory competition, in which inventory levels impact retailers’ demands through both stealing and stimulating effects.

We find that the DD structure always induces higher service levels than the II structure, regardless whether the products are substitutes or complements. This is because in the DD structure, committing to a higher service level in the first stage can reduce (increase) the competing chain’s inventory of substitutable (complementary) products in the second stage, which incentivizes both decentralized chains to raise their service levels higher than in the II structure. In the DI structure, decentralization delays a chain’s inventory decision, allowing the integrated chain to decide inventory first. As a result, the decentralized chain’s best service level is the same as a follower in the inventory competition.

In terms of supply chain profits, we find that for substitutable products, the integrated chain (leading in inventory decision) in DI structure earns more profit than it would earn in the II and DD structures, while the decentralized chain in the DI structure earns less than in the other two structures. Therefore, integration is a dominant strategy for each supply chain when the two products are substitutable. The equilibrium structure choice is II, which is also the most profitable duopoly structure (the industry profits are ordered as II \(>\) DI \(>\) DD). On the other hand, when the products are complements, the industry profits are ordered as DD \(>\) DI \(>\) II, and the individual supply chain profit has the same order. Hence, decentralization is a dominant strategy for each supply chain. The equilibrium structure choice is DD, which is also the most profitable duopoly structure.

Finally, we find that when demands become more uncertain, the cost of deviating from the equilibrium supply chain structure is larger. Thus, demand uncertainty reinforces the equilibrium supply chain structure.