Introduction

There is no vulnerability that numerous scenarios in nature can be outlined beneath the modeling of nonlinear partial differential equations (\({\mathbb {N}}{\mathbb {P}}{\mathbb {D}}{\mathbb {E}}\)s) with their explanatory or numerical arrangements. To understand such scenarios to \({\mathbb {N}}{\mathbb {P}}{\mathbb {D}}{\mathbb {E}}\)s by their explanatory arrangements (analytic solutions), mathematicians, engineers, and researchers have a common connection in examining the traveling wave solutions to \({\mathbb {N}}{\mathbb {P}}{\mathbb {D}}{\mathbb {E}}\)s by expository strategies due to their critical part and pertinence in liquid mechanics, scientific material science, plasma material science, nonlinear optics, and other related building sciences [1,2,3,4,5,6,7,8]. Many recent studies have employed fractional-order calculus as a tool in studying the fractional-order differential equations and their obtained solutions [9, 10, 40,41,42,43, 45].

Coupled nonlinear Schrödinger–KdV equations (Schrödinger–Korteweg–de vries) are considered as one of the vital models related to such of inquire about areas. Colorado [11] investigated the presence of bound and ground states for a framework of coupled nonlinear Schrödinger–KdV equations. A few studies have been conducted on developing modern traveling wave solutions for a system of coupled Schrödinger–KdV equations by utilizing different expository and numerical strategies, such as the strategy of generalized amplified \(\tanh\) function, Laplace decomposition, Petrov–Galerkin, homotopy perturbation, Adomian’s decomposition, homotopy analysis, Nehari manifold, and solitary wave and Bifurcation [12,13,14,15,16, 6, 18, 46]. Ma provided a brief overview of soliton solutions obtained through the Hirota direct method, discussed bilinear formulation of soliton solutions in both (1+1)-dimensions and (2+1)-dimensions together with applications to various integrable equations and analyzed the Hirota conditions for N-soliton solutions [19]. In [20], they discussed about how to construct and classify nonlocal PT-symmetric integrable equations via nonlocal group reductions of matrix spectral problems which are used to formulate a kind of Riemann–Hilbert problems and thus inverse scattering transforms (for more instance, consider [21, 22, 44]).

Kaya et al. and Alomari et al. considered the following Schrödinger–KdV equations

$$\begin{aligned} i\mathfrak {g}_{\textrm{s}} + \mathfrak {g}_{\textrm{yy}} - \mathfrak {g}\mathfrak {h}&=0,\\ \mathfrak {h}_{\textrm{s}} + 6\mathfrak {g}\mathfrak {h}_{\textrm{y}} + \mathfrak {h}_{\textrm{yyy}} - \left( | \mathfrak {g}|^2 \right) _{\textrm{y}}&= 0, \end{aligned}$$

under an initial condition \(\mathfrak {g}(\textrm{y},0)= \uprho _1(\textrm{y})\) and \(\mathfrak {h}(\textrm{y},0)= \uprho _2(\textrm{y})\) [12, 17]. In 2015, Colorado introduced the dimensionless form of a system of coupled nonlinear Schrödinger–KdV equations

$$\begin{aligned} i\mathfrak {g}_{\textrm{s}} + \mathfrak {g}_{\textrm{yy}} - \eta \mathfrak {g}\mathfrak {h} + \left( |\mathfrak {g}|^2 \right) \mathfrak {g}&=0, \end{aligned}$$
(1a)
$$\begin{aligned} i \mathfrak {h}_{\textrm{s}} + \mathfrak {h}_{\textrm{yyy}} + \mathfrak {h} \mathfrak {h}_{\textrm{y}} - \frac{1}{2} \eta \left( | \mathfrak {g}|^2 \right) _{\textrm{y}}&= 0, \end{aligned}$$
(1b)

where \(\eta\) is a real coupling constant, \(\mathfrak {g}(\textrm{y}, \textrm{s})\) and \(\mathfrak {h}(\textrm{y}, \textrm{s})\) are complex functions that stand for the short wave profile and real function that represents long wave profile, respectively [11]. Equation (1a) and (b) is well-known models that have been shown up within the marvels of intelligent between brief and long dispersive waves emerging from liquid mechanics, particularly the intuitive of capillary-gravity water waves. Álvarez-Caudevilla et al. in [13] analyzed the existence of solutions of the following higher-order system, coupling nonlinear Schrödinger–KdV equations

$$\begin{aligned} i\mathfrak {g}_{\textrm{s}} - \mathfrak {g}_{\textrm{yyyy}} + |\mathfrak {g}|^2 \mathfrak {g} + \eta \mathfrak {g} \mathfrak {g} \mathfrak {h}&=0,\\ \mathfrak {h}_{\textrm{s}} - \mathfrak {h}_{\textrm{yyyyy}} + \frac{1}{2} \left( |\mathfrak {h}|\mathfrak {h}\right) _{\textrm{y}} + \frac{1}{2}\eta \left( |\mathfrak {g}|^2\right) _{\textrm{y}}&= 0, \end{aligned}$$

with \(\mathfrak {g}=\mathfrak {g}(\textrm{y}, \textrm{s}) \in \mathbb (C)\), \(\mathfrak {h}= \mathfrak {h}(\textrm{y}, \textrm{s}) \in {\mathbb {R}}\) and \(\eta \in {\mathbb {R}}\) the coupling parameter. Also, Baskonus et al. extracted some optical soliton solutions from the following decoupled nonlinear Schrödinger–KdV equation with Kerr law nonlinearity arising in dual-core optical fibers by using the extended sinh-Gordon equation expansion method,

$$\begin{aligned} i\left( \mathfrak {g}_{\textrm{y}} + \eta _1 \mathfrak {h}_{\textrm{s}} \right) + \eta _2\mathfrak {g}_{\textrm{ss}} + \eta _3 |\mathfrak {g}|^2 \mathfrak {g} + \eta _4 \mathfrak {h}&=0,\\ i\left( \mathfrak {h}_{\textrm{y}} + \eta _1 \mathfrak {g}_{\textrm{s}} \right) + \eta _2\mathfrak {h}_{\textrm{ss}} + \eta _3 |\mathfrak {h}|^2 \mathfrak {h} + \eta _4 \mathfrak {g}&= 0, \end{aligned}$$

where \(\mathfrak {g}, \, \mathfrak {h}\) are field envelopes, \(\textrm{y}\) is the propagation co-ordinate, \(\frac{1}{\eta _1}\) is the group velocity mismatch, \(\eta _2\) is the group velocity dispersion, \(\eta _4\) is the linear coupling coefficient, and \(\eta _3\) is defined as \(\eta _3 = \frac{2\pi m_2}{kB_{eff}}\), where \(m_2\) is the nonlinear refractive index, k is the wavelength, and \(B_{eff}\) is effective mode area of each wavelength [23]. Soliton is characterized as a localized waveform that engenders along the framework with steady speed and undeformed shape [24]. It can be found in all fields of nonlinear dynamics for a variety of shapes, such as singular, combined singular soliton, dark, bright, combined dark–bright, and many other related forms. Such soliton shapes are explored with various nonlinear integer and fractional-order evolution equations via newly generalized or modified integration schemes such as the extended Jacobi’s elliptic function approach [25], the sinh-Gordon equation expansion method [26, 27], the generalized \(\exp (\varrho (\tau ))\)-expansion method [28], the modified Kudryashov method [29], and the semi-inverse variational principle [30].

The extended sinh-Gordon equation expansion method has never been considered in the framework of Equ. 1a) and (b). In any case, there are a few investigations that have been considered on understanding other frameworks of \({\mathbb {N}}{\mathbb {P}}{\mathbb {D}}{\mathbb {E}}\)s by extended sinh-Gordon equation expansion method [23, 31,32,33,34]. Extended sinh-Gordon equation expansion method could be considered as a vigorous and capable method that can be effectively connected to both numbers and fragmentary arranged \({\mathbb {P}}{\mathbb {D}}{\mathbb {E}}\)s to build different shapes of soliton arrangements such as particular, singular, combined singular soliton, dark, bright, combined dark–bright, and other related solutions, and to overcome some challenges emerging from utilizing the single wave ansatz method [35, 36]. In addition, Bulut et al. [37] applied the extended sinh-Gordon equation expansion method for their formulated space-time fractional nonlinear Schrödinger equation in the sense of conformable derivatives, and they successfully obtained several solitons solutions such as dark, bright, combined dark–bright, singular, combined-singular, and singular periodic wave solutions. For more information about conformable derivative which is a type of local fractional derivative and some approximate-analytical methods for solving second-order wave equation, we refer to [38].

The most objective of this investigation is to explore some novel shapes of unequivocal complex hyperbolic and complex trigonometric work arrangements by utilizing the extended sinh-Gordon equation expansion method in different shapes such as dull, shinning, combined dark–bright, particular, combined particular optical, occasional wave, dipole soliton and other related arrangements in a framework of coupled nonlinear Schrödinger–KdV Equ. 1).

This work is organized as: In Sect. 2, we step-by-step examine \({\mathbb {N}}{\mathbb {P}}{\mathbb {D}}{\mathbb {E}}\)s. The arrangement strategy of the overseeing framework of coupled nonlinear Schrödinger–KdV equations is explored in Sect. 3 through the extended sinh-Gordon equation expansion method. In Section 3, we build different shapes of soliton arrangements such as singular, combined singular optical, dark, bright, combined dark–bright, periodic wave, dipole soliton and other arrangements. The found soliton arrangements and their graphical representations are discussed in Sect. 4. In Sect. 5, we conclude our investigation.

Outlines of the extended sinh-Gordon equation expansion method

In this portion, a point-by-point portrayal of the extended sinh-Gordon equation expansion method is displayed. The exp-function method has been introduced to nonlinear equations, particularly KdV equation, and it has been discussed in detail in [39] where generalized solitary and periodic solutions can be resulted from the usage of this method. To utilize our strategy, we require the following steps from [32, 33].

Step 1: Consider the common shape of a coupled \({\mathbb {N}}{\mathbb {P}}{\mathbb {D}}{\mathbb {E}}\)s:

$$\begin{aligned} \mathfrak {G}_{1} \left( \mathfrak {g},\mathfrak {h},\mathfrak {g}_{\textrm{y}}, \mathfrak {h}_{\textrm{y}}, \mathfrak {g}_{\textrm{s}}, \mathfrak {h}_{\textrm{s}}, \mathfrak {g}_{{\textrm{yy}}}, \mathfrak {h}_{{\textrm{yy}}}, \mathfrak {g}_{{\textrm{ys}}}, \mathfrak {h}_{{\textrm{ys}}}, \mathfrak {g}_{{\textrm{ss}}}, \mathfrak {h}_{{\textrm{ss}}}, \dots \right)&=0, \end{aligned}$$
(2)
$$\begin{aligned} \mathfrak {G}_{2} \left( \mathfrak {g}, \mathfrak {h}, \mathfrak {g}_{\textrm{y}}, \mathfrak {h}_{\textrm{y}}, \mathfrak {g}_{\textrm{s}}, \mathfrak {h}_{\textrm{s}}, \mathfrak {g}_{{\textrm{yy}}}, \mathfrak {h}_{{\textrm{yy}}}, \mathfrak {g}_{{\textrm{ys}}}, \mathfrak {h}_{{\textrm{ys}}}, \mathfrak {g}_{{\textrm{ss}}}, \mathfrak {h}_{{\textrm{ss}}}, \dots \right)&= 0, \end{aligned}$$
(3)

where \(\mathfrak {g} =\mathfrak {g}({\textrm{y}},{\textrm{s}})\), \(\mathfrak {h} =\mathfrak {h}({\textrm{y}}, {\textrm{s}})\) are characterized in Equation (1), and each of \(\mathfrak {G}_{1}\) and \(\mathfrak {G}_{2}\) may be a polynomial work, with respect to a few capacities or indicated factors, which contains the nonlinear terms and most elevated arranged subordinates of \(\mathfrak {g}\) and \(\mathfrak {h}\). We begin by presenting the complex wave changes:

$$\begin{aligned} \mathfrak {u}(\textrm{y},\textrm{s})&= \upphi (\tau ) \exp (\textrm{i} \varrho \left( \textrm{y},\textrm{s} \right) ), \end{aligned}$$
(4)
$$\begin{aligned} \mathfrak {U}(\textrm{y},\textrm{s})&= \Phi (\tau ), \end{aligned}$$
(5)

where \(\tau = \textrm{y} - \nu \textrm{s}\) and \(\varrho \left( \textrm{y}, \textrm{s}\right) = k\textrm{y} + \omega \textrm{s}+ \vartheta _{0}\). Then, by substituting Equs. (4) and (5) into Equs. (2) and (3), we have:

$$\begin{aligned} \mathfrak {H}_{1}\left( \upphi , \Phi , \frac{\textrm{d}}{\textrm{d}\tau }\upphi , \frac{\textrm{d}}{\textrm{d}\tau }\Phi , \frac{\textrm{d}^2}{\textrm{d}\tau ^2}\upphi , \frac{\textrm{d}^2}{\textrm{d}\tau ^2}\Phi , \dots \right)&= 0, \end{aligned}$$
(6)
$$\begin{aligned} \mathfrak {H}_{2}\left( \upphi , \Phi , \frac{\textrm{d}}{\textrm{d}\tau }\upphi , \frac{\textrm{d}}{\textrm{d}\tau }\Phi , \frac{\textrm{d}^2}{\textrm{d}\tau ^2}\upphi , \frac{\textrm{d}^2}{\textrm{d}\tau ^2}\Phi , \dots \right)&= 0, \end{aligned}$$
(7)

here each of \(\mathfrak {H}_{\imath }\, (\imath =1,2)\) is a polynomial of \(\upphi (\tau )\) and \(\Phi (\tau )\). The delineations of k, \(\nu\), \(\omega\) and \(\vartheta\) are shown in Sect. 3.

Step 2: Presently, we consider the formal arrangements of Equs. (6) and (7) as takes after:

$$\begin{aligned} \upphi \left( \wp \right)&= \sum _{\imath = 1}^{ \textrm{N}_1} \cosh ^{\imath - 1} \wp \left[ \bar{b}_\imath \sinh \wp +\bar{a}_\imath \cosh \wp \right] + \bar{a}_0, \end{aligned}$$
(8)
$$\begin{aligned} \Phi \left( \wp \right)&= \sum _{ \imath =1}^{ \textrm{N}_2} \cosh ^{\imath -1} \wp \left[ \bar{B}_\imath \sinh \wp +\bar{A}_\imath \cosh \wp \right] + \bar{A}_0, \end{aligned}$$
(9)

here \(\wp (\tau )\) satisfies the following equation [32]:

$$\begin{aligned} \wp ^\prime = \sqrt{\mu + \lambda \sinh ^2\wp }. \end{aligned}$$
(10)

This is a transformed form of sinh-Gordon equation. The parameters \(\mu\) and \(\lambda\) have different values in the following two cases:

Case I. ( Equ.10) is reduced to

$$\begin{aligned} \wp ^\prime = \sinh \left( \wp \right) , \end{aligned}$$
(11)

whenever \(\mu =0\) and \(\lambda =1\). This can be a streamlined shape of the sinh-Gordon equation. Thus, Equ. (11) concedes the following solutions [32]

$$\begin{aligned} \sinh \left( \wp \right) = \pm \textrm{i} {{\,\textrm{sech}\,}}\tau ,\qquad \cosh \wp = -\tanh \tau , \end{aligned}$$
(12)

here \((\textrm{i}=\sqrt{-1})\), and

$$\begin{aligned} \sinh \wp = \pm {{\,\textrm{csch}\,}}\tau , \qquad \cosh \wp = -\coth \tau . \end{aligned}$$
(13)

Therefore, from \(\upphi (\tau )\) and \(\Phi (\tau )\) in Equs. (8) and (9), we obtain:

$$\begin{aligned} \upphi (\tau )&= \sum _{\imath =1}^{\textrm{N}_1} \left( - \tanh \tau \right) ^{\imath - 1} \left[ \pm \textrm{i} \, \overline{b}_\imath {{\,\textrm{sech}\,}}\tau - \overline{a}_\imath \tanh \tau \right] +\overline{a}_0, \end{aligned}$$
(14)
$$\begin{aligned} \Phi (\tau )&= \sum _{\imath =1}^{\textrm{N}_2} \left( - \tanh \tau \right) ^{\imath -1} \left[ \pm \textrm{i} \, \overline{B}_\imath {{\,\textrm{sech}\,}}\tau - \overline{A}_\imath \tanh \tau \right] +\overline{A}_0, \end{aligned}$$
(15)

and

$$\begin{aligned} \upphi (\tau )&= \sum _{\imath =1}^{\textrm{N}_1 } \left( - \coth \tau \right) ^{\imath -1}\left[ \pm \overline{b}_\imath {{\,\textrm{csch}\,}}\tau - \overline{a}_\imath \coth \tau \right] + \overline{a}_0, \end{aligned}$$
(16a)
$$\begin{aligned} \Phi (\tau )&= \sum _{\imath =1}^{\textrm{N}_2} \left( - \coth \tau \right) ^{\imath - 1} \left[ \pm \overline{B}_\imath {{\,\textrm{csch}\,}}\tau -\overline{A}_\imath \coth \tau \right] + \overline{A}_0. \end{aligned}$$
(16b)

Case II. Equ. (10) becomes

$$\begin{aligned} \wp ^\prime = \cosh \wp , \end{aligned}$$
(17)

whenever \(\mu =1\) and \(\lambda =1\). Typically too a streamlined shape of the sinh-Gordon equation. Essentially, Equation (17) concedes the following solutions [32]:

$$\begin{aligned} \sinh \wp = \tan \tau , \qquad \cosh \wp = \pm \sec \tau , \end{aligned}$$
(18)

and

$$\begin{aligned} \sinh \wp = - \cot \tau ,\qquad \cosh \wp = \pm \csc \tau . \end{aligned}$$
(19)

So, from Equs.8) and (9), we obtain

$$\begin{aligned} \upphi (\tau )&= \sum _{\imath =1}^{\textrm{N}_1} \left( \pm \sec \tau \right) ^{\imath -1} \left[ \overline{b}_\imath \tan \tau \pm \overline{a}_\imath \sec \tau \right] +\overline{a}_0, \end{aligned}$$
(20)
$$\begin{aligned} \Phi (\tau )&= \sum _{\imath =1}^{\textrm{N}_2} \left( \pm \sec \tau \right) ^{\imath -1} \left[ \overline{B}_\imath \tan \tau \pm \overline{A}_\imath \sec \tau \right] + \overline{A}_0, \end{aligned}$$
(21)

and

$$\begin{aligned} \upphi \left( \tau \right)&= \sum _{\imath =1}^{\textrm{N}_1} \left( \pm \csc \tau \right) ^{\imath -1} \left[ - \overline{b}_\imath \cot \tau \pm \overline{a}_\imath \csc \tau \right] + \overline{a}_0, \end{aligned}$$
(22)
$$\begin{aligned} \Phi \left( \tau \right)&= \sum _{\imath =1}^{\textrm{N}_2} \left( \pm \csc \tau \right) ^{\imath -1} \left[ - \overline{B}_\imath \cot \tau \pm \overline{A}_j \csc \tau \right] + \overline{A}_0. \end{aligned}$$
(23)

Step 3: By substituting the values of \({N}_1\) and \({N}_2\) into Equs. (8) and (9), which are determined by using the homogeneous balance principle, along with Equation (11), we have a nonlinear framework of conditions in terms of \(\sinh ^\imath (\wp )\) and \(\cosh ^\imath (\wp )\). Setting up the coefficients of \(\sinh ^\imath (\wp )\) and \(\cosh ^\imath (\wp )\) to zero, we have frameworks of conditions and the values of \(\overline{A}_\imath\), \(\overline{B}_\imath\), \(\overline{a}_\imath\), \(\overline{b}_\imath\) and \(\omega\), \(\nu\) are found. Now, by substituting the results into Equs. (14) and (15), we can retrieve the solitary wave solutions of Equs. (2) and (3) (as in Case I). As a result, one may continue the same way for Case II and can get the particular and occasional wave arrangements of Equs. (2) and (3).

Investigation of single and other wave arrangements

We consider Equs. (1a) and (b) as traveling wave transformations such that k is the soliton frequency, while \(\omega\) is the wave number of the soliton and \(\vartheta _0\) is a phase constant [11]. On the other hand, \(\nu\) is the speed of the soliton [11]. By part the real and imaginary parts of Equ. 1a) and (b), individually, we have

$$\begin{aligned} \upphi ^{\prime \prime } - \left( k^{2} + \omega \right) \upphi - \sigma \upphi \Phi + \upphi ^3&= 0, \end{aligned}$$
(24)
$$\begin{aligned} \Phi ^{\prime \prime } - 2 k \Phi - \frac{1}{2} \sigma \upphi ^2 + \frac{1}{2} \Phi ^2&=0, \end{aligned}$$
(25)

and \(\nu \upphi ^{\prime } - 2 k \upphi ^{\prime } = 0\). Indeed, \(\nu =2k\). It gives the speed of the soliton in terms of the soliton recurrence.

Here, a recently compelling adaptation of the extended sinh-Gordon equation expansion method is utilized to investigate modern single wave and other arrangements of Equs. (24) and (25).

For case I: \(\wp ^{\prime } = \sinh \wp\)

If we take \(\textrm{N}_1=1\) and \(\textrm{N}_2=2\) in Equs. (8)–(9), (14)–(15) and (16a)–(b), at that point, we get the formal arrangements of Equs. (24) and (25) as taken after:

$$\begin{aligned} \upphi (\wp )&= \overline{b}_1 \sinh \wp + \overline{a}_1 \cosh \wp + \overline{a}_0, \end{aligned}$$
(26)
$$\begin{aligned} \Phi (\wp )&= \overline{B}_1 \sinh \wp + \overline{B}_2 \sinh \wp \cosh \wp \nonumber \\&\quad + \overline{A}_1 \cosh \wp + \overline{A}_2 \cosh ^2 \wp + \overline{A}_0, \end{aligned}$$
(27)

and

$$\begin{aligned} \upphi (\tau )&= \textrm{i} \, \overline{b}_1 {{\,\textrm{sech}\,}}\tau -\overline{b}_1 \tanh \tau + \overline{b}_0, \end{aligned}$$
(28)
$$\begin{aligned} \Phi (\tau )&= \textrm{i} \, \overline{B}_1 {{\,\textrm{sech}\,}}\tau - \textrm{i} \, \overline{B}_2 \tanh \tau {{\,\textrm{sech}\,}}\nonumber \\&\quad - \overline{A}_1 \tanh \tau + \overline{A}_2 \tanh ^2\overline{A} +\overline{A}_0, \end{aligned}$$
(29)
$$\begin{aligned} \upphi (\tau )&= \overline{b}_1 {{\,\textrm{csch}\,}}\tau - \overline{a}_1 \coth \tau + \tau _0, \end{aligned}$$
(30)
$$\begin{aligned} \Phi (\tau )&= \overline{B}_1 {{\,\textrm{csch}\,}}\overline{B} - \overline{B}_2 \coth \tau {{\,\textrm{csch}\,}}\tau \nonumber \\&\quad - \overline{A}_1 \coth \tau + \overline{A}_2 \coth ^2 \tau + \overline{A}_0, \end{aligned}$$
(31)

where either \(\overline{A}_1\) or \(\overline{A}_2\) or \(\overline{B}_1\) or \(\overline{B}_2\) or \(\overline{a}_1\) or \(\overline{b}_1\) may be zero, but not all of them ended up zero at the same time. By substituting Equs. (26) and (27) into Equs. (24) and (25), we obtain a system of nonlinear algebraic equation (\({\mathbb {N}}{\mathbb {A}}{\mathbb {E}}\)). Then, by solving the system, we have the following results:

Set 1:

$$\begin{aligned} -\omega&= \frac{1}{2} \sigma ^3 + k^2 + 2 k \sigma + \frac{1}{12} \sigma ^2 + 8 \sigma + 2,\\ \overline{A}_{0}&= \frac{1}{2} \sigma ^2 + 2 k + \frac{1}{12} \sigma + 8, \end{aligned}$$

where

$$\begin{aligned} \overline{A}_1=\overline{B}_1=\overline{B}_2=\overline{a}_{0}=\overline{b}_1=0, \end{aligned}$$

and \(\overline{A}_2 = -12\), \(\overline{a}_1 = \pm \textrm{i} \, \sqrt{12 \sigma + 2}\). By substituting Set 1 into Equations (28)–(29) and (30)–(31), the following solitary wave solutions for Equ. (1a)–(b) which can be determined as:

$$\begin{aligned}&\mathfrak {u}_{1,2} (\textrm{y},\textrm{s}) \nonumber \\&\quad = \pm \textrm{i} \, \left( \sqrt{12\sigma + 2} \tanh (\textrm{y} - 2 k \textrm{s} ) \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( k \textrm{y}\right. \right. \nonumber \\&\qquad \quad \left. \left. - \left( \frac{1}{2} \sigma ^3 + k^2 + 2 k \sigma + \frac{1}{12} \sigma ^2 + 8 \sigma + 2 \right) \textrm{s}+ \vartheta _{0} \right) \right) , \end{aligned}$$
(32)
$$\begin{aligned}&\mathfrak {U}_{1,2} ( \textrm{y}, \textrm{s} ) = \frac{1}{2} \sigma ^2 + 2 k + \frac{1}{12} \sigma + 8 - 12 \tanh ^2 (\textrm{y} - 2 k \textrm{s} ), \end{aligned}$$
(33)

and

$$\begin{aligned}&\mathfrak {u}_{3,4} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad =\pm \textrm{i} \, \left( \sqrt{12 \sigma + 2} \coth (\textrm{y} - 2 k \textrm{s} ) \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( k \textrm{y} \right. \right. \nonumber \\&\qquad \quad \left. \left. - \left( \frac{1}{2} \sigma ^3 + k^2 + 2k \sigma + \frac{1}{12} \sigma ^2 + 8\sigma + 2\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(34)
$$\begin{aligned}&\mathfrak {U}_{3,4} (\textrm{y}, \textrm{s}) = \frac{1}{2} \sigma ^2+ 2 k + \frac{1}{12} \sigma + 8 - 12 \coth ^2 (\textrm{y} -2 k \textrm{s}). \end{aligned}$$
(35)

Set 2:

$$\begin{aligned} -\omega =\frac{1}{2} \sigma ^3 + k^2 + 2 k \sigma + \frac{1}{12} \sigma ^2 - 4 \sigma - 1, \end{aligned}$$

where

$$\begin{aligned}{} & {} \overline{A}_0 = \frac{1}{2} \sigma ^2 + 2 k + \frac{1}{12} \sigma + 8,\\{} & {} \overline{A}_{1}=\overline{B}_1=\overline{B}_2=\overline{a}_0=\overline{a}_1=0, \end{aligned}$$

and \(\overline{A}_{2}=-12\), \(\overline{b}_{1}=\pm \textrm{i} \, \sqrt{12\sigma + 2}\). Again by substituting Set 2 into Equs. (28)–(29) and (30)–(31), we obtain here wave solutions

$$\begin{aligned}&\mathfrak {u}_{5,6} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad = \mp \textrm{i} \, \left( \sqrt{12 \sigma + 2} {{\,\textrm{sech}\,}}(\textrm{y}- 2 k \textrm{s} ) \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( k \textrm{y} \right. \right. \nonumber \\&\qquad \left. \left. - \left( \frac{1}{2} \sigma ^3 + k^2 + 2 k \sigma + \frac{1}{12} \sigma ^2 - 4\sigma - 1 \right) \textrm{s} + \theta _{0} \right) \right) , \end{aligned}$$
(36)
$$\begin{aligned}&\mathfrak {U}_{5,6} (\textrm{y}, \textrm{s} ) = \frac{1}{2} \sigma ^2 + 2 k +\frac{1}{12} \sigma + 8-12 \tanh ^2 ( \textrm{y} - 2 k \textrm{s}), \end{aligned}$$
(37)

and

$$\begin{aligned}&\mathfrak {u}_{7,8} (\textrm{y},\textrm{s}) \nonumber \\&\quad =\mp \textrm{i} \, \left( \sqrt{12 \sigma + 2 } {{\,\textrm{csch}\,}}(\textrm{y} - 2 k\textrm{s}) \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( k \textrm{y} \right. \right. \nonumber \\&\qquad \left. \left. - \left( \frac{1}{2} \sigma ^3 + k^2 + 2 k\sigma + \frac{1}{12} \sigma ^2 - 4\sigma - 1\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(38)
$$\begin{aligned}&\mathfrak {U}_{7,8} (\textrm{y}, \textrm{s}) = \frac{1}{2} \sigma ^2 + 2 k +\frac{1}{12} \sigma + 8 - 12 \coth ^2 (\textrm{y} - 2 k \textrm{s}). \end{aligned}$$
(39)

Set 3-a:

$$\begin{aligned} -\omega = \frac{1}{2} \sigma ^3 + k^2 + 2 k \sigma + \frac{1}{12} \sigma ^2 + 2 \sigma + \frac{1}{2}, \end{aligned}$$

where

$$\begin{aligned} \overline{A}_0 = \frac{1}{2} \sigma ^2 + 2 k + \frac{1}{12} \sigma + 5, \end{aligned}$$

\(\overline{A}_1 =\overline{B}_{1} = \overline{a}_0=0\), \(\overline{A}_{2}=-6\), \(\overline{B}_2=6\) and

$$\begin{aligned} \overline{a}_{1}= \mp \textrm{i} \, \sqrt{ 3 \sigma + 0.5 }, \qquad \overline{b}_1 = \pm \textrm{i} \, \sqrt{3 \sigma + 0.5 }. \end{aligned}$$

After substituting the arrangement in Set 3-a into Equs. 28)–(29) and (30)–(31), we construct the following wave solutions:

$$\begin{aligned}&\mathfrak {u}_{9,10} (\textrm{y},\textrm{s} ) \nonumber \\&\quad = \pm \textrm{i} \, \left( \sqrt{3 \sigma + \frac{1}{2}} \tanh (\textrm{y}- 2 k\textrm{s} ) - \sqrt{3\sigma + \frac{1}{2} } {{\,\textrm{sech}\,}}(\textrm{y}- 2 k\textrm{s})\right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( k \textrm{y} \right. \right. \nonumber \\&\qquad \quad \left. \left. - \left( \frac{1}{2} \sigma ^3 + k^2 + 2 k \sigma + \frac{1}{12} \sigma ^2 + 2 \sigma + \frac{1}{2} \right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(40)
$$\begin{aligned}&\mathfrak {U}_{9,10} (\textrm{y},\textrm{s} ) \nonumber \\&\quad = \frac{1}{2} \sigma ^2 + 2 k +\frac{1}{12} \sigma + 5 \nonumber \\&\qquad - 6 \tanh ^2 (\textrm{y}- 2 k\textrm{s}) + 6 \textrm{i} \, \tanh (\textrm{y}-2 k \textrm{s}) {{\,\textrm{sech}\,}}(\textrm{y} - 2k\textrm{s}), \end{aligned}$$
(41)

and

$$\begin{aligned}&\mathfrak {u}_{11,12} (\textrm{y},\textrm{s} ) \nonumber \\&\quad ={\pm \textrm{i} \, \left( \sqrt{3\sigma + \frac{1}{2}} \coth (\textrm{y}- 2k\textrm{s} ) - \sqrt{ 3\sigma + \frac{1}{2}} {{\,\textrm{csch}\,}}(\textrm{y}- 2 k\textrm{s} )\right) }\nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( k \textrm{y} \right. \right. \nonumber \\&\qquad \left. \left. - \left( \frac{1}{2} \sigma ^{3} + k^{2}+ 2k\sigma +\frac{1}{12}\sigma ^{2}+2\sigma +\frac{1}{2} \right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(42)
$$\begin{aligned}&\mathfrak {U}_{11,12} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad = \frac{1}{2} \sigma ^{2}+2k+\frac{1}{12}\sigma + 5 \nonumber \\&\qquad -6 \coth ^2 (\textrm{y}- 2 k\textrm{s}) - 6 \coth (\textrm{y}- 2 k\textrm{s}) {{\,\textrm{csch}\,}}(\textrm{y}-2k\textrm{s}). \end{aligned}$$
(43)

Set 3-b:

$$\begin{aligned} -\omega = \frac{1}{2}\sigma ^{3}+k^{2}+2k\sigma +\frac{1}{12} \sigma ^{2}+2\sigma +\frac{1}{2}, \end{aligned}$$

where

$$\begin{aligned} \overline{A}_{0} = \frac{1}{2} \sigma ^{2}+2k+\frac{1}{12}\sigma +5, \end{aligned}$$

\(\overline{A}_{1}=0\), \(\overline{A}_{2}=-6\), \(\overline{B}_{1}=0\), \(\overline{B}_{2}=-6\), \(\overline{a}_{0}=0\) and

$$\begin{aligned} \overline{a}_{1}=\mp \textrm{i} \, \sqrt{3\sigma +\frac{1}{2}}, \qquad \overline{b}_{1} =\pm \textrm{i} \, \sqrt{3\sigma +\frac{1}{2}}. \end{aligned}$$

By substituting Set 3-b into Equs. 28)–(29) and (30)–(31), we extract the following wave solutions:

$$\begin{aligned}&\mathfrak {u}_{13,14} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad =\pm \left( \textrm{i} \, \sqrt{3\sigma +\frac{1}{2} } \tanh (\textrm{y}-2k\textrm{s}) -\sqrt{3\sigma +\frac{1}{2}} {{\,\textrm{sech}\,}}( \textrm{y}-2k\textrm{s})\right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( k\textrm{y} \right. \right. \nonumber \\&\qquad \left. \left. - \left( \frac{1}{2} \sigma ^{3}+k^{2}+2 k \sigma +\frac{1}{12} \sigma ^{2}+2\sigma + \frac{1}{2}\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(44)
$$\begin{aligned}&\mathfrak {U}_{13,14} \left( \textrm{y},\textrm{s}\right) \nonumber \\&\quad = \frac{1}{2} \sigma ^{2}+2k+\frac{1}{12}\sigma +5 \nonumber \\&\qquad -6 \tanh ^{2}(\textrm{y}-2k\textrm{s}) -6 \tanh (\textrm{y}-2k\textrm{s}) {{\,\textrm{sech}\,}}(\textrm{y}-2k\textrm{s}), \end{aligned}$$
(45)

and

$$\begin{aligned}&\mathfrak {u}_{15,16}\left( x,t\right) \nonumber \\&\quad =\pm \textrm{i} \, \left( \sqrt{3\sigma +\frac{1}{2}} \coth (\textrm{y}-2k\textrm{s}) - \sqrt{3\sigma +\frac{1}{2}} {{\,\textrm{csch}\,}}(\textrm{y}-2kt\textrm{s})\right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( k\textrm{y} \right. \right. \nonumber \\&\qquad \left. \left. - \left( \frac{1}{2} \sigma ^3+k^{2}+2k\sigma +\frac{1}{12}\sigma ^{2}+2\sigma +\frac{1}{2}\right) \textrm{s}+\vartheta _{0} \right) \right) , \end{aligned}$$
(46)
$$\begin{aligned}&\mathfrak {U}_{15,16}\left( \textrm{y},\textrm{s}\right) \nonumber \\&\quad =\frac{1}{2} \sigma ^{2}+2k+\frac{1}{12}\sigma +5 \nonumber \\&\qquad -6 \coth ^2 (\textrm{y}-2k\textrm{s})+6 \coth (\textrm{y}-2k\textrm{s}) {{\,\textrm{csch}\,}}(\textrm{y}-2k\textrm{s}), \end{aligned}$$
(47)

For case-II: \(\wp ^{\prime } = \cosh (\wp )\)

If we take \({N}_1=1\) and \({N}_2=2\) in Equs. 8)–(9), (20)–(21) and (22)–(23), we obtain the following formal solutions of Equs. 24) and (25):

$$\begin{aligned} \upphi (\wp )&= \overline{b}_1 \sinh \wp + \overline{a}_1 \cosh \wp +\overline{a}_0, \end{aligned}$$
(48)
$$\begin{aligned} \Phi (\wp )&= \overline{B}_1 \sinh \wp + \overline{B}_2 \sinh \wp \cosh \wp \nonumber \\&\quad + \overline{A}_1 \cosh \wp + \overline{A}_2 \cosh ^2 \wp + \overline{A}_0, \end{aligned}$$
(49)

and

$$\begin{aligned} \upphi (\tau )&=\overline{b}_1 \sec \tau + \overline{a}_1 \tan \tau + \overline{a}_0, \end{aligned}$$
(50)
$$\begin{aligned} \Phi (\tau )&= \overline{B}_1 \sec \tau + \overline{B}_2 \tan \tau \sec \tau \nonumber \\&\quad + \overline{A}_1 \tan \tau + \overline{A}_2 \tan ^2 \tau + \overline{A}_0, \end{aligned}$$
(51)
$$\begin{aligned} \upphi (\tau )&= -\overline{b}_1 \cot \wp + \overline{a}_1 \csc \tau + \overline{a}_0, \end{aligned}$$
(52)
$$\begin{aligned} \Phi (\tau )&= -\tau _1 \cot \tau -\overline{B}_2 \cot \tau \csc \tau \nonumber \\&\quad + \overline{A}_1 \csc \tau + \overline{A}_2 \csc ^2 \tau + \overline{A}_0, \end{aligned}$$
(53)

where either \(\overline{A}_1\) or \(\overline{A}_2\) or \(\overline{B}_1\) or \(\overline{B}_2\) or \(\overline{a}_1\) or \(\overline{b}_1\) may be zero, but not all of them ended up zero at the same time. By substituting Equs. 46)–(47) into Equs. 24)–(25), we get a framework of \({\mathbb {N}}{\mathbb {A}}{\mathbb {E}}\) and by tackling the frameworks we have the taking after three sets.

Set 1:

$$\begin{aligned} -k&=\frac{1}{4} \sigma ^{2}+\frac{1}{24}\sigma +2,\\ - \omega&= \frac{1}{16} \sigma ^{4}+\frac{1}{48} \sigma ^{3}+\frac{577}{576}\sigma ^{2}+\frac{1}{6}\sigma +5, \end{aligned}$$

where

$$\begin{aligned} \overline{A}_0 =\overline{A}_{1} =\overline{B}_{1}=\overline{B}_{2}=\overline{a}_{0}=\overline{b}_1=0, \end{aligned}$$

and \(\overline{A}_{2}=-12, \, \overline{a}_{1}=\pm \textrm{i} \, \sqrt{12\sigma +2}\). Again by substituting Set 1 into Equs. 48)–(49) and (50)–(51), we can determine the following trigonometric work arrangements for Equs. 1a)–(b):

$$\begin{aligned}&\mathfrak {u}_{15,16} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad =\pm \textrm{i} \, \left( \sqrt{ 12\sigma +2} \sec \left( \textrm{y} + 2\left( \frac{1}{4} \sigma ^{2}+\frac{1}{24}\sigma +2\right) \textrm{s} \right) \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( - \left( \frac{1}{4} \sigma ^{2}+\frac{1}{24}\sigma +2\right) \textrm{y} \right. \right. \nonumber \\&\qquad \left. \left. - \left( \frac{1}{16}\sigma ^{4}+ \frac{1}{48}\sigma ^{3}+\frac{577}{576}\sigma ^{2}+\frac{1}{6}\sigma +5 \right) \textrm{s}+\vartheta _{0} \right) \right) , \end{aligned}$$
(54)
$$\begin{aligned}&\mathfrak {U}_{15,16} (\textrm{y},\textrm{s}) =-12 \sec ^2 \left( \textrm{y} +2\left( \frac{1}{4}\sigma ^{2}+\frac{1}{24}\sigma +2\right) \textrm{s}\right) , \end{aligned}$$
(55)

and

$$\begin{aligned}&\mathfrak {u}_{17,18} (\textrm{y},\textrm{s} ) \nonumber \\&\quad =\pm \textrm{i} \, \left( \sqrt{12\sigma +2} \csc \left( \textrm{y} + 2\left( \frac{1}{4} \sigma ^{2} + \frac{1}{24} \sigma +2 \right) \textrm{s} \right) \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( - \left( \frac{1}{4}\sigma ^{2}+\frac{1}{24}\sigma +2\right) \textrm{y} \right. \right. \nonumber \\&\qquad \left. \left. - \left( \frac{1}{16} \sigma ^{4}+\frac{1}{48}\sigma ^{3}+\frac{577}{576} \sigma ^{2}+\frac{1}{6}\sigma +5\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(56)
$$\begin{aligned}&\mathfrak {U}_{17,18} \left( \textrm{y}, \textrm{s} \right) =-12 \csc ^{2} \left( \textrm{y} + 2 \left( \frac{1}{4} \sigma ^{2} +\frac{1}{24}\sigma +2\right) \textrm{s} \right) . \end{aligned}$$
(57)

Set 2:

$$\begin{aligned} k&=\frac{1}{4}\sigma ^{2}+\frac{1}{24}\sigma +2,\\ -\omega&= \frac{1}{16}\sigma ^{4} + \frac{49}{48} \sigma ^{3} + \frac{673}{576} \sigma ^{2}+\frac{49}{6} \sigma + 5, \end{aligned}$$

where

$$\begin{aligned}{} & {} \overline{A}_0 = \sigma ^{2} + \frac{1}{6}\sigma +8, \\{} & {} \overline{A}_{1}=\overline{B}_{1}=\overline{B}_{2} =\overline{a}_{0}= \overline{b}_{1}=0, \end{aligned}$$

and \(\overline{A}_{2} =-12\), \(\overline{a}_{1}=\pm \textrm{i} \, \sqrt{12\sigma +2}\). By substituting Set 2 into Equs. 48)–(49) and (50)–(51), again, we determine the following trigonometric work arrangements:

$$\begin{aligned}&\mathfrak {u}_{19,20} (\textrm{y},\textrm{s}) \nonumber \\&\quad =\pm \textrm{i} \, \left( \sqrt{ 12\sigma +2 } \sec \left( \textrm{y} + 2\left( \frac{1}{4} \sigma ^{2}+\frac{1}{24}\sigma +2\right) t \right) \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( - \left( \frac{1}{4}\sigma ^{2} + \frac{1}{24}\sigma +2\right) \textrm{y} \right. \right. \nonumber \\&\qquad \left. \left. - \left( \frac{1}{16}\sigma ^{4}+\frac{49}{48}\sigma ^{3} + \frac{673}{576}\sigma ^{2} + \frac{49}{6}\sigma +5\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(58)
$$\begin{aligned}&\mathfrak {U}_{19,20} (\textrm{y},\textrm{s} ) \nonumber \\&\quad = \sigma ^{2} +\frac{1}{6}\sigma +8-12 \sec ^{2} \left( \textrm{y}+ 2 \left( \frac{1}{4}\sigma ^{2} +\frac{1}{24}\sigma +2\right) \textrm{s}\right) , \end{aligned}$$
(59)

and

$$\begin{aligned}&\mathfrak {u}_{21,22} (\textrm{y},\textrm{s} ) \nonumber \\&\quad =\pm \textrm{i} \, \left( \sqrt{ 12 \sigma +2 } \csc \left( \textrm{y}+ 2 \left( \frac{1}{4}\sigma ^{2} + \frac{1}{24} \sigma +2\right) t\right) \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( -\left( \frac{1}{4}\sigma ^{2}+\frac{1}{24}\sigma +2\right) \textrm{y} \right. \right. \nonumber \\&\qquad \left. \left. - \left( \frac{1}{16}\sigma ^{4}+\frac{49}{48}\sigma ^{3}+\frac{673}{576} \sigma ^{2}+\frac{49}{6}\sigma +5\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(60)
$$\begin{aligned}&\mathfrak {U}_{21,22} (\textrm{y},\textrm{s} )\nonumber \\&\quad = \sigma ^{2}+\frac{1}{6}\sigma +8 - 12 \csc ^{2} \left( \textrm{y}+ 2\left( \frac{1}{4}\sigma ^{2} +\frac{1}{24}\sigma +2\right) \textrm{s}\right) . \end{aligned}$$
(61)

Set 3-a:

$$\begin{aligned} k&=\pm \sqrt{\Delta },\\ \omega&= - \frac{1}{16} \sigma ^{4}-\frac{1}{48} \sigma ^{3} + \frac{287}{576}\, \sigma ^{2}\\&\quad - \sigma \left( \frac{1}{2}\sigma ^{2} + \frac{1}{12}\sigma +1 + \frac{1}{12} \sqrt{\Delta } \right) + \frac{37}{12} \sigma +\frac{1}{4}, \end{aligned}$$

where

$$\begin{aligned} \overline{A}_{0} = \frac{1}{2}\sigma ^{2} + \frac{1}{12}\sigma +1 +\frac{1}{12}\sqrt{ \Delta }, \end{aligned}$$

\(\overline{A}_{1}=\overline{B}_{1}=\overline{a}_{0} =0\), \(\overline{A}_{2}=-6\), \(\overline{B}_{2}=6\),

$$\begin{aligned} \overline{a}_{1}= - \textrm{i} \, \sqrt{3\sigma +\frac{1}{2}}, \qquad \overline{b}_{1} =\textrm{i} \, \sqrt{3\sigma +\frac{1}{2}}, \end{aligned}$$

and

$$\begin{aligned} \Delta = 36\sigma ^{4}+12\sigma ^{3}-287\sigma ^{2}-48\sigma +144. \end{aligned}$$
(62)

After substituting Set 3-a into Equs. 48)–(49) and (50)–(51), we produce the following trigonometric work arrangements:

$$\begin{aligned}&\mathfrak {u}_{23,24} (\textrm{y},\textrm{s} ) \nonumber \\&\quad = -\textrm{i} \, \sqrt{3\sigma +\frac{1}{2}} \tan \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s} \right) +\textrm{i} \, \sqrt{ 3\sigma +\frac{1}{2} } \sec \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{y} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Delta } \textrm{y}+ \left( -\frac{1}{16}\sigma ^{4}- \frac{1}{48} \sigma ^{3} +\frac{287}{576}\sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - \sigma \left( \frac{1}{2} \sigma ^{2}+\frac{1}{12} \sigma +1 + \frac{1}{12} \sqrt{\Delta } \right) + \frac{37}{12}\sigma + \frac{1}{4}\right) \textrm{s}+ \vartheta _{0} \right) \right) , \end{aligned}$$
(63)
$$\begin{aligned}&\mathfrak {U}_{23,24} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad = \frac{1}{2}\sigma ^{2} + \frac{1}{12}\sigma +1 + \frac{1}{12}\sqrt{\Delta } \nonumber \\&\qquad - 6 \tan ^{2} \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s} \right) +6 \tan \left( \textrm{y} \pm 2 \sqrt{\Delta }\textrm{y} \right) \sec \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s}\right) , \end{aligned}$$
(64)

and

$$\begin{aligned}&\mathfrak {u}_{25,26} (\textrm{y},\textrm{s} ) \nonumber \\&\quad = -\textrm{i} \, \sqrt{3\sigma +\frac{1}{2} } \csc \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{s} \right) - \textrm{i} \, \sqrt{3 \sigma +\frac{1}{2} } \cot \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Delta } \textrm{y} + \left( -\frac{1}{16}\sigma ^{4} - \frac{1}{48}\sigma ^{3} + \frac{287}{576}\sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - \sigma \left( \frac{1}{2} \sigma ^{2} + \frac{1}{12}\sigma +1 + \frac{1}{12} \sqrt{\Delta } \right) +\frac{37}{12}\sigma +\frac{1}{4}\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(65)
$$\begin{aligned}&\mathfrak {u}_{27,28} ( \textrm{y},\textrm{s} ) \nonumber \\&\quad = \frac{1}{2} \sigma ^{2}+\frac{1}{12}\sigma +1+\frac{1}{12} \sqrt{\Delta } \nonumber \\&\qquad -6 \csc ^{2}\left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{y} \right) - 6 \cot \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s} \right) \csc \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s} \right) . \end{aligned}$$
(66)

Set 3-b:

$$\begin{aligned} k&=\pm \sqrt{\Delta },\\ \omega&= - \frac{1}{16} \sigma ^{4}-\frac{1}{48} \sigma ^{3} + \frac{287}{576}\, \sigma ^{2} \\&\quad - \sigma \left( \frac{1}{2}\, \sigma ^{2} + \frac{1}{12}\sigma +1+\frac{1}{12} \sqrt{\Delta } \right) + \frac{37}{12} \sigma +\frac{1}{4}, \end{aligned}$$

where

$$\begin{aligned} \overline{A}_{0} = \frac{1}{2} \sigma ^{2}+\frac{1}{12}\sigma +1+\frac{1}{12}\sqrt{\Delta }, \end{aligned}$$

\(\overline{A}_{1}=0\), \(\overline{A}_{2}=-6\), \(\overline{B}_{1}=0\), \(\overline{B}_{2}=6\), \(\overline{A}_{0}=0\), and

$$\begin{aligned} \overline{a}_{1}=\textrm{i} \, \sqrt{3 \sigma +\frac{1}{2}}, \qquad \overline{b}_{1} = -\textrm{i} \, \sqrt{3\sigma +\frac{1}{2}}. \end{aligned}$$

After substituting Set 3-b into Equs. 48)–(49) and (50)–(51), we extract the following trigonometric work arrangements:

$$\begin{aligned}&\mathfrak {u}_{29,30} (\textrm{y} ,\textrm{s}) \nonumber \\&\quad = \textrm{i} \, \sqrt{3 \sigma + \frac{1}{2}} \tan \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{s} \right) - {\textrm{i} \sqrt{3\sigma +\frac{1}{2}} } \sec \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{y} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Delta } \textrm{y}+ \left( -\frac{1}{16}\sigma ^{4} - \frac{1}{48}\sigma ^{3} + \frac{287}{576}\sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - \sigma \left( \frac{1}{2}\sigma ^{2} + \frac{1}{12}\sigma +1 + \frac{1}{12}\sqrt{\Delta } \right) + \frac{37}{12} \sigma + \frac{1}{4}\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(67)
$$\begin{aligned}&\mathfrak {U}_{29,30} (\textrm{y},\textrm{s} ) \nonumber \\&\quad = \frac{1}{2} \sigma ^{2}+\frac{1}{12}\sigma +1 + \frac{1}{12} \sqrt{\Delta } \nonumber \\&\qquad - 6 \tan ^{2} \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{S} \right) + 6 \tan \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{y} \right) \sec \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{s} \right) , \end{aligned}$$
(68)

and

$$\begin{aligned}&\mathfrak {u}_{31,32} (\textrm{y},\textrm{s}) \nonumber \\&\quad = \textrm{i} \, \sqrt{3 \sigma + \frac{1}{2} } \csc \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{y} \right) + \textrm{i} \, \sqrt{3 \sigma +\frac{1}{2}} \cot \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{s} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Delta } \textrm{y} + \left( -\frac{1}{16} \sigma ^{4} - \frac{1}{48}\sigma ^{3} + \frac{287}{576}\sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - \sigma \left( \frac{1}{2} \sigma ^{2} + \frac{1}{12}\sigma +1 + \frac{1}{12}\sqrt{\Delta } \right) +\frac{37}{12}\sigma + \frac{1}{4}\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(69)
$$\begin{aligned}&\mathfrak {U}_{31,32} (\textrm{y},\textrm{s} ) \nonumber \\&\quad =\frac{1}{2} \sigma ^{2}+\frac{1}{12} \sigma +1+\frac{1}{12} \sqrt{\Delta } \nonumber \\&\qquad - 6 \csc ^{2} \left( \textrm{y}\pm 2 \sqrt{\Delta } \textrm{s} \right) - 6 \cot \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{s} \right) \csc \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s} \right) . \end{aligned}$$
(70)

Set 3-c:

$$\begin{aligned} k&=\pm \sqrt{\Delta },\\ \omega&= - \frac{1}{16} \sigma ^{4}-\frac{1}{48} \sigma ^{3} \, + \frac{287}{576}\, \sigma ^{2} \\&\quad - \sigma \left( \frac{1}{2}\, \sigma ^{2} \, + \frac{1}{12}\, \sigma +1+\frac{1}{12} \sqrt{\Delta } \right) + \frac{37}{12} \sigma +\frac{1}{4}, \end{aligned}$$

where

$$\begin{aligned} \overline{A}_{0} = \frac{1}{2}\sigma ^{2}+\frac{1}{12}\sigma +1+\frac{1}{12}\sqrt{\Delta }, \end{aligned}$$

\(\overline{A}_{1}=0\), \(\overline{A}_{2}=-6\), \(\overline{B}_{1}=0\), \(\overline{B}_{2}=-6\), \(\overline{A}_{0}=0\) and

$$\begin{aligned} \overline{a}_{1}=-\textrm{i} \, \sqrt{3 \sigma +\frac{1}{2} }, \qquad \overline{b}_{1} = \textrm{i} \, \sqrt{3\sigma +\frac{1}{2}}. \end{aligned}$$

By substituting the Set 3-c into Equs. 48)–(49) and (50)–(51), we obtain the following trigonometric work arrangements:

$$\begin{aligned}&\mathfrak {u}_{33,34} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad = - \textrm{i} \, \sqrt{ 3 \sigma + \frac{1}{2} } \tan \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{s} \right) + \textrm{i} \, \sqrt{ 3 \sigma +\frac{1}{2}} \sec \left( \textrm{y} \pm 2\sqrt{\Delta }\textrm{s} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Delta } \textrm{y} + \left( - \frac{1}{16} \sigma ^{4} - \frac{1}{48} \sigma ^{3} + \frac{287}{576} \sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - \sigma \left( \frac{1}{2} \sigma ^{2}+\frac{1}{12}\sigma + 1 +\frac{1}{12} \sqrt{\Delta } \right) + \frac{37}{12}\sigma +\frac{1}{4}\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(71)
$$\begin{aligned}&\mathfrak {U}_{33,34} (\textrm{y},\textrm{s} )\nonumber \\&\quad = \frac{1}{2}\sigma ^{2} +\frac{1}{12}\sigma +1 + \frac{1}{12} \sqrt{\Delta } \nonumber \\&\qquad -6 \tan ^{2} \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s} \right) - 6 \tan \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s} \right) \sec \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s} \right) , \end{aligned}$$
(72)

and

$$\begin{aligned}&\mathfrak {u}_{35,36} (\textrm{y},\textrm{s} ) \nonumber \\&\quad = -\textrm{i} \, \sqrt{3\sigma +\frac{1}{2}} \csc \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s} \right) - \textrm{i} \, \sqrt{ 3\sigma +\frac{1}{2} } \cot \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{s} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Delta } \textrm{y} + \left( - \frac{1}{16}\sigma ^{4} - \frac{1}{48}\sigma ^{3} +\frac{287}{576}\sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - \sigma \left( \frac{1}{2}\sigma ^{2} + \frac{1}{12}\sigma +1 + \frac{1}{12}\sqrt{\Delta } \right) + \frac{37}{12} \sigma +\frac{1}{4}\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(73)
$$\begin{aligned}&\mathfrak {U}_{35,36} (\textrm{y},\textrm{s} ) \nonumber \\&\quad = \frac{1}{2}\sigma ^{2}+\frac{1}{12}\sigma +1 + \frac{1}{12}\sqrt{\Delta } \nonumber \\&\qquad -6 \csc ^{2} \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{s} \right) -6 \cot \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{s} \right) \csc \left( \textrm{y}\pm 2\sqrt{\Delta }\textrm{s}\right) . \end{aligned}$$
(74)

Set 3-d:

$$\begin{aligned} k&=\pm \sqrt{\Delta },\\ \omega&= - \frac{1}{16} \sigma ^{4}-\frac{1}{48} \sigma ^{3} +\frac{287}{576} \, \sigma ^{2} \\&\quad - \sigma \, \left( \frac{1}{2}\sigma ^{2} + \frac{1}{12}\sigma +1 +\frac{1}{12} \sqrt{\Delta } \right) + \frac{37}{12} \sigma +\frac{1}{4}, \end{aligned}$$

where

$$\begin{aligned} \overline{A}_{0} = \frac{1}{2}\sigma ^{2} +\frac{1}{12}\sigma +1+\frac{1}{12}\sqrt{\Delta }, \end{aligned}$$

\(\overline{A}_{1}=\overline{B}_{1}=\overline{a}_{0}=0\), \(\overline{A}_{2}=-6\), \(\overline{B}_{2}=-6\) and

$$\begin{aligned} \overline{a}_{1}=\textrm{i} \, \sqrt{3 \sigma + \frac{1}{2} }, \qquad \overline{b}_{1} = -\textrm{i} \, \sqrt{3\sigma +\frac{1}{2} }. \end{aligned}$$

By substituting the Set 3-d into Equations (48)–(49) and (50)–(51), we extract the following trigonometric work arrangements:

$$\begin{aligned}&\mathfrak {u}_{37,38} (\textrm{y}, \textrm{s}) \nonumber \\&\quad = \textrm{i} \, \sqrt{3 \sigma + \frac{1}{2}} \tan \left( \textrm{y} \pm 2 \sqrt{\Delta } \textrm{s} \right) - \textrm{i} \, \sqrt{3 \sigma + \frac{1}{2}} \sec \left( \textrm{y} \pm 2 \sqrt{\Delta } \textrm{s} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Delta }\textrm{y} + \left( - \frac{1}{16}\sigma ^{4} - \frac{1}{48} \sigma ^{3} + \frac{287}{576} \sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - \sigma \left( \frac{1}{2} \sigma ^{2} + \frac{1}{12} \sigma + 1 + \frac{1}{12} \sqrt{\Delta }\right) +\frac{37}{12} \sigma + \frac{1}{4}\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(75)
$$\begin{aligned}&\mathfrak {U}_{37,38} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad =\frac{1}{2}\sigma ^{2}+\frac{1}{12}\sigma +1 + \frac{1}{12}\sqrt{\Delta } \nonumber \\&\qquad -6 \tan ^{2} \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s}\right) - 6 \tan \left( \textrm{y}\pm 2\sqrt{\Delta } \textrm{s}\right) \sec \left( \, \textrm{y}\, \pm 2 \sqrt{\Delta } \textrm{s}\right) , \end{aligned}$$
(76)

and

$$\begin{aligned}&\mathfrak {u}_{39,40} (\textrm{y},\textrm{s}) \nonumber \\&\quad =\textrm{i} \, \sqrt{ 3\sigma +\frac{1}{2} } \csc \left( \textrm{y} \pm 2\sqrt{\Delta } \textrm{s} \right) + \textrm{i} \, \sqrt{3 \sigma +\frac{1}{2} } \cot \left( \textrm{y} \pm 2\sqrt{\Delta }\textrm{s} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Delta } \textrm{y} + \left( - \frac{1}{16}\sigma ^{4} - \frac{1}{48} \sigma ^{3} + \frac{287}{576} \sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. -\sigma \left( \frac{1}{2} \sigma ^{2} + \frac{1}{12} \sigma + 1 + \frac{1}{12} \sqrt{\Delta } \right) + \frac{37}{12} \sigma + \frac{1}{4} \right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(77)
$$\begin{aligned}&\mathfrak {U}_{39,40} (\textrm{y},\textrm{s} ) \nonumber \\&\quad = \frac{1}{2} \sigma ^{2} + \frac{1}{12} \sigma + 1 + \frac{1}{12} \sqrt{\Delta } \nonumber \\&\qquad - 6 \csc ^{2} \left( \textrm{y} \pm 2\sqrt{\Delta }\textrm{s}\right) - 6 \cot \left( \textrm{y}\pm 2\sqrt{\Delta }\textrm{s}\right) \csc \left( \textrm{y} \pm 2\sqrt{\Delta }\textrm{s} \right) , \end{aligned}$$
(78)

Set 4-a:

$$\begin{aligned} k&=\pm \sqrt{\Lambda },\\ \omega&= -\frac{1}{16} \sigma ^{4} - \frac{1}{48} \sigma ^{3} + \frac{1151}{576} \sigma ^{2} \\&\quad - \sigma \left( \frac{1}{2} \sigma ^{2} +\frac{1}{12} \sigma + 4 + \frac{1}{12} \sqrt{\Lambda }\right) + \frac{37}{3} \sigma -2, \end{aligned}$$

where

$$\begin{aligned}{} & {} \overline{A}_{0} =\frac{1}{2} \sigma ^{2} + \frac{1}{12}\sigma + 4 + \frac{1}{12} \sqrt{\Lambda },\\{} & {} \overline{A}_{1} = \overline{B}_{1} = \overline{B}_{2} = \overline{a}_{0} = \overline{a}_{1}=0, \end{aligned}$$

\(\overline{A}_{2}=-12\), \(\overline{b}_{1} = \textrm{i} \, \sqrt{12 \sigma + 2}\) and

$$\begin{aligned} \Lambda = 36\sigma ^{4}+12\sigma ^{3}-1151\sigma ^{2} - 192\sigma + 2304. \end{aligned}$$
(79)

By substituting the Set 4-a into Equs. (48)–(49) and (50)–(51), we explore the following trigonometric work arrangements:

$$\begin{aligned}&\mathfrak {u}_{41,42} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad = \textrm{i} \, \sqrt{ 12\sigma +2} \sec \left( \textrm{y} \mp 2 \sqrt{\Lambda } \textrm{s} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Lambda } \textrm{y}+ \left( - \frac{1}{16} \sigma ^{4} - \frac{1}{48} \sigma ^{3} + \frac{1151}{576} \sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - \sigma \left( \frac{1}{2}\sigma ^{2} + \frac{1}{12}\sigma + 4 + \frac{1}{12} \sqrt{\Lambda } \right) + \frac{37}{3} \sigma -2\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(80)
$$\begin{aligned}&\mathfrak {U}_{41,42} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad = \frac{1}{2} \sigma ^{2} + \frac{1}{12}\sigma + 4 + \frac{1}{12}\sqrt{\Lambda }\nonumber \\&\qquad -12\tan ^{2} \left( \textrm{y}\mp 2\sqrt{\Lambda } \textrm{s} \right) , \end{aligned}$$
(81)

and

$$\begin{aligned}&\mathfrak {u}_{43,44} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad = \textrm{i} \, \sqrt{ 12\sigma +2} \cot \left( \textrm{y} \mp 2 \sqrt{\Lambda } \textrm{s} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Lambda } \textrm{y} + \left( - \frac{1}{16} \sigma ^{4} - \frac{1}{48} \sigma ^{3} + \frac{1151}{576} \sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - \sigma \left( \frac{1}{2} \sigma ^{2} + \frac{1}{12} \sigma + 4 + \frac{1}{12}\sqrt{\Lambda }\right) +\frac{37}{3} \sigma -2 \right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(82)
$$\begin{aligned}&\mathfrak {U}_{43,44} (\textrm{y}, \textrm{s} ) \nonumber \\&\quad = \frac{1}{2} \sigma ^{2} + \frac{1}{12} \sigma + 4 + \frac{1}{12} \sqrt{\Lambda } \nonumber \\&\qquad -12 \csc ^{2} \left( \textrm{y} \mp 2\sqrt{\Lambda }\textrm{s} \right) . \end{aligned}$$
(83)

Set 4-b:

$$\begin{aligned} k&=\pm \sqrt{\Lambda },\\ \omega&=-\frac{1}{16} \sigma ^{4}-\frac{1}{48} \sigma ^{3} + \frac{1151}{576} \sigma ^{2} \\&\quad - \sigma \left( \frac{1}{2} \sigma ^{2} + \frac{1}{12} \sigma + 4+ \frac{1}{12} \sqrt{\Lambda } \right) + \frac{37}{3}\sigma -2, \end{aligned}$$

where

$$\begin{aligned} \overline{A}_{0} = \frac{1}{2}\sigma ^{2} + \frac{1}{12}\sigma + 4 + \frac{1}{12} \sqrt{\Lambda }, \end{aligned}$$

\(\overline{A}_{1}=0\), \(\overline{A}_{2}=-12\), \(\overline{B}_{1}=0\), \(\overline{B}_{2}=0\), \(\overline{a}_{0}=0\), \(\overline{a}_{1}=0\) and \(\overline{b}_{1} = - \textrm{i} \, \sqrt{12 \sigma + 2}\). By substituting the Set 4-b into Equs. (48)–(49) and (50)–(51), we obtain the following trigonometric work arrangements:

$$\begin{aligned}&\mathfrak {u}_{41,42} (\textrm{y},\textrm{s} ) \nonumber \\&\quad =-\textrm{i} \, \sqrt{ 12\sigma +2 } \sec \left( \textrm{y} \mp 2\sqrt{\Lambda } \textrm{S} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Lambda } \textrm{y}+ \left( -\frac{1}{16} \sigma ^{4} - \frac{1}{48} \sigma ^{3} + \frac{1151}{576} \sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - \sigma \left( \frac{1}{2} \sigma ^{2} + \frac{1}{12} \sigma + 4+ \frac{1}{12} \sqrt{\Lambda }\right) + \frac{37}{3} \sigma -2 \right) \textrm{S} + \vartheta _{0} \right) \right) , \end{aligned}$$
(84)
$$\begin{aligned}&\mathfrak {U}_{41,42} (\textrm{y},\textrm{s} ) \nonumber \\&\quad = \frac{1}{2} \sigma ^{2} +\frac{1}{12}\sigma +4 + \frac{1}{12} \sqrt{\Lambda } \nonumber \\&\qquad -12\tan ^{2} \left( \textrm{y} \mp 2\sqrt{\Lambda } \textrm{s} \right) , \end{aligned}$$
(85)

and

$$\begin{aligned}&\mathfrak {u}_{43,44} (\textrm{y},\textrm{s}) \nonumber \\&\quad = -\textrm{i} \, \sqrt{ 12 \sigma +2} \cot \left( \textrm{y} \mp 2 \sqrt{\Lambda } \textrm{s} \right) \nonumber \\&\qquad \times \exp \left( \textrm{i} \, \left( \pm \sqrt{\Lambda } \textrm{y} + \left( - \frac{1}{16} \sigma ^{4} - \frac{1}{48} \sigma ^{3} + \frac{1151}{576} \sigma ^{2} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - \sigma \left( \frac{1}{2}\sigma ^{2} + \frac{1}{12} \sigma +4+\frac{1}{12} \sqrt{\Lambda } \right) + \frac{37}{3} \sigma -2\right) \textrm{s} + \vartheta _{0} \right) \right) , \end{aligned}$$
(86)
$$\begin{aligned}&\mathfrak {U}_{43,44} (\textrm{y},\textrm{s} )\nonumber \\&\quad =\frac{1}{2}\sigma ^{2}+\frac{1}{12} \sigma +4 +\frac{1}{12}\sqrt{\Lambda } \nonumber \\&\qquad -12 \csc ^{2} \left( \textrm{y}\mp 2\sqrt{\Lambda }\textrm{s}\right) , \end{aligned}$$
(87)

Discussion and graphical illustration of the attained solutions

This section discusses our attained results and their three-dimensional (3D) and two-dimensional (2D) graphical representations that can be helpful in understanding the proper physical meaning of the coupled Schrödinger–KdV equations. The extended sinh-Gordon equation expansion method is successfully employed by constructing various types of wave solutions to coupled Schrödinger–KdV equations. The specified governing equations of (1a)–(1b) have been previously investigated by diverse methods [12, 13, 11, 14, 16, 6].

According to all previous studies, singular, dark, bright, and periodic waves solutions have not been constructed yet. In our work, we have developed some particular, singular, combined singular, dark, bright, combined dark–bright, periodic, singular periodic wave solutions, and other solutions to the coupled Schrödinger–KdV equations through the extended sinh-Gordon equation expansion method. For the first time ever, this research paper can be assured that all singular, combined-singular, combined dark–bright, periodic, and singular periodic wave solutions have been discussed and investigated. It too ought to be specified that the legitimacy of the extricated solutions is examined by substituting each of the precise solutions back into its comparing equation.

Fig. 1
figure 1

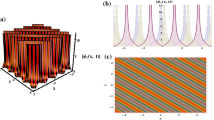
3D plot \(\mathfrak {u}( \textrm{x}, \textrm{t})\) with forms for Equation (32): a real portion, b imaginary portion with \(k=0.5\), \(\sigma =1\), \(\vartheta _{0}=0\), and c, d: 2D line plot of a and b individually at \(t=0\)

Full size image
Fig. 2
figure 2

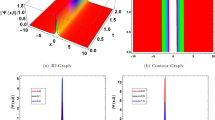
3D plot \(\mathfrak {U}(\textrm{x}, \textrm{t})\) with forms for (33): a real part with \(k=0.5\), \(\sigma =1\), and b: 2D line plot of a at \(t=0\)

Full size image

All of our generated solutions have some physical significance. To ensure such types of realization, we have displayed some 3D graphs with contour and 2D line graphs among the detected singular solitons, combined-singular solitons, dark solitons, bright solitons, combined dark–bright solitons, periodic, and singular- periodic wave solutions for different values of their arbitrary parameters, which are indicated in Figs. 1, 2, 3, 4, 5, 6, 7, 8.

Fig. 3
figure 3

3D plot \(\mathfrak {u}( \textrm{x}, \textrm{t})\) with forms for Equation (40): a real part, b imaginary part with \(k=1\), \(\sigma =2\), \(\vartheta _{0}=0\), and c, d: 2D line plot of a and b individually at \(t=0\)

Full size image
Fig. 4
figure 4

3D plot \(\mathfrak {U}( \textrm{x}, \textrm{t})\) with forms for Equation (41): a real part, b imaginary part with \(k=1\), \(\sigma =2\), and c, d: (2D) line plot of a and b individually at \(t=0\)

Full size image
Fig. 5
figure 5

3D plot \(\mathfrak {u}( \textrm{x}, \textrm{t})\) with contours for Equation (42): a real part, b imaginary part with \(k=1\), \(\sigma =2\), \(\vartheta _{0}=0\), and c, d: 2D line plot of a and b individually at \(t=0\)

Full size image
Fig. 6
figure 6

3D plot \(\mathfrak {u}( \textrm{x}, \textrm{t})\) with forms for (43): a real part with \(k=1\), \(\sigma =2\), and b: 2D line plot of a at \(t=0\)

Full size image
Fig. 7
figure 7

3D plot \(\mathfrak {u}( \textrm{x}, \textrm{t})\) with forms for (54): a real part, b imaginary part with \(\sigma =1\), \(\vartheta _{0}=0\), and c, d: 2D line plot of a and b individually at \(t=0\)

Full size image
Fig. 8
figure 8

3D plot \(\mathfrak {U}( \textrm{x}, \textrm{t})\) with forms for (55): a real part with \(\sigma =1\), and b: 2D line plot of a at \(t=0\)

Full size image

For Equs. (1a) and (b), dark solitons, bright solitons, combined dark–bright solitons, singular solitons, combined singular solitons, and singular periodic wave solutions are reported in Equs. (32)–(33), (46)–(47) and Equs. (54)–(55), (86)–(87). In order to have a good understanding of the physical properties, the 3D graphs with contour and 2D line graphs are included among the obtained solutions under the choice of suitable values of arbitrary parameters. The perspective view of the obtained solutions prescribed by Equs. (32)–(33), (40)–(41), (42)–(43) and (54)–(55) can be seen in the 3D and 2D graphs at \(t=0\), which appear in Figs. 1, 2, 3, 4, 5, 6, 78, respectively.

Therefore, it is clear from the graphical outputs that the procedure of the extended sinh-Gordon equation expansion method will contribute for other related equations for obtaining more new soliton and other solutions.

Conclusions

Extended sinh-Gordon equation expansion method has been applied in this study to generate novel soliton and other solutions of the coupled Schrödinger–KdV equations. As a result, unused unequivocal complex hyperbolic and complex trigonometric work arrangements have been found, which are communicated by singular, combined singular, dark, bright, combined dark–bright, periodic wave soliton, and other shapes. All obtained arrangements fulfill their comparing condition. The 3D charts with form and 2D charts have been appeared for a few of the found solutions. All our results are fundamental in clarifying the physical meaning of some nonlinear models emerging from nonlinear sciences. The constructed solitons have never been discussed in any of the previous studies [12, 13, 11, 14, 16, 6] in Schrödinger–KdV systems. In this manner, it is very apparent that this work gives a great contribution to this field of research due to its significance in numerous areas of material science.