1 Introduction

This study focuses on the following nonlinear variety of Boussinesq-like equations (Wazwaz 2012; Eslami and Mirzazadeh 2014; Lee and Rathinasamy 2014; Darvishi et al. 2017a, b):

$$\begin{aligned}&u_{tt} - u_{xx} - {(6u^2u_x+u_{xxx})}_x =0,\\&u_{tt} - u_{xx} - {(6u^2u_x+u_{xtt})}_x =0,\\&u_{tt} - u_{xt} - {(6u^2u_x+u_{xxt})}_x =0, \end{aligned}$$

and

$$\begin{aligned} u_{tt} - {(6u^2u_x+u_{xxx})}_x =0, \end{aligned}$$

which play a prominent role in the propagation of long waves in shallow water and arises also in other physical applications such as nonlinear lattice waves, the propagation of waves in elastic rods, in vibrations in a nonlinear string, the dynamics of the thin inviscid layers with free surface, the shape-memory alloys and in the coupled electrical circuits (Wazwaz 2012; Eslami and Mirzazadeh 2014; Lee and Rathinasamy 2014; Darvishi et al. 2017a, b).

During last several years, exact solutions of the Boussinesq and its related equations in shallow water are significantly important for coastal scientists and engineers to apply the nonlinear water wave, port-offshore and harbors modelling in the field of coastal and ocean engineering. These equations are also appeared in many scientific applications such as nonlinear fiber optics, plasma physics, fluid dynamics, and ocean engineering (Wazwaz 2012; Eslami and Mirzazadeh 2014; Lee and Rathinasamy 2014; Darvishi et al. 2017a, b; Wazwaz 2007; Bulut et al. 2016). Due to rapid expansion of some powerful symbolic computations based mathematical packages such as Maple and Mathematica, extraction process of exact solutions is very much easier than the past. In this context, researchers have gained a platform to produce new exact solutions of well-known partial differential equations (PDEs) that arise in applied sciences by numerous robust influential methods such as the first integral method (Eslami and Mirzazadeh 2014), modified tanh–coth method (Lee and Rathinasamy 2014), extended Jacobi elliptic function expansion method (Lee and Rathinasamy 2014), the semi-inverse variational principle (Darvishi et al. 2017b), the sine–cosine method (Darvishi et al. 2017a), the Darboux transform method (Gu et al. 1999), Backlund transformation and inverse scattering method (Vakhnenko et al. 2003), the homogenous balance method (Wang 1995), exp-function method (Liu 2009), multiple exp-function method (Ma et al. 2010), sine–Gordon expansion method (Kumar et al. 2017a), Qimproved \(\tanh (\phi {}(\xi {})/2)\)-expansion method (Lakestani and Manafian 2017), the exponential rational function method (Bekir and Kaplan 2016), the modified simple equation method (Roshid 2017), the extended simple equation method (Lu et al. 2017), the modified Kudryashov method (Kumar et al. 2017b), the hyperbolic function method (Xie et al. 2001), the \((\frac{G'}{G})\)-expansion method (Wang et al. 2008), the improved \((\frac{G'}{G})\)-expansion method (Hawlader and Kumar 2017), the solitary ansatz method (Guner et al. 2017), the auxiliary equation method (Kumar et al. 2008) and the \((\frac{G'}{G},\frac{1}{G})\)-expansion method (Miah et al. 2017).

Several researchers work out some new solutions from the family of variety of Boussinesq-like equations using different analytical methods. We review some literatures about Boussinesq-like equations and analytical methods. In this respect, Wazwaz (2012) first introduced a variety of Boussinesq-like equations and investigated to determine one soliton solutions and one singular soliton solutions for each Boussinesq-like model. After that, Eslami and Mirzazadeh (2014) applied the first integral method and obtained exact 1-soliton solutions for each Boussinesq-like equation. Later on, Lee and Rathinasamy (2014) obtained exact traveling wave solutions of a variety of Boussinesq-like equations by using two distinct methods, namely, modified tanh–coth method and the extended Jacobi elliptic function method with the aid of symbolic computation Maple package. In fact, by employing the modified tanh–coth method and the extended Jacobi elliptic function method, they obtained single soliton solutions and doubly periodic wave solutions, respectively. They also recommended that soliton solutions and triangular solutions can be established as the limits of the Jacobi doubly periodic wave solutions. Recently, Darvishi et al. (2017b) adopted the semi-inverse variational principle (SVP) to search soliton solutions of the Boussinesq-like equations with spatio-temporal dispersion. The derived soliton solutions depicted the dynamics of thin inviscid layers with free surface, solitons solutions, and other nonlinear phenomena. Very recently, Darvishi et al. (2017a) derived some new traveling wave solutions for the four distinct non-integrable Boussinesq-like equations with the effect of spatial dispersion for two variants of the Boussinesq equation, and with the effect of spatial–temporal dispersion for other two variants by using the sine–cosine method. As a matter of fact, authors of Refs. Wazwaz (2012), Eslami and Mirzazadeh (2014), Lee and Rathinasamy (2014) and Darvishi et al. (2017a, b) explored the exact solutions for a variety of Boussinesq-like equations with integer order.

In this paper, we will introduce and solve a variety of the fractional order of Boussinesq-like equations especially the conformable fractional derivative and fractional complex transform sense via the modified Kudryashov method.

Recently, many researchers have introduced and solved the nonlinear conformable time-fractional Boussinesq equation using various analytical techniques in the sense of conformable fractional derivative and fractional complex transform such as Jacobi elliptic function expansion method (Tasbozan et al. 2016), the \(\exp (-\phi {}(\xi {}))\)-expansion method (Hosseini et al. 2017a), the modified simple equation method and the exponential rational function method (Kaplan 2017). More works (Eslami and Rezazadeh 2016; Hosseini et al. 2017b; Iyiola et al. 2017; Cenesiz and Kurt 2016; Kurt et al. 2015, 2017; Cenesiz et al. 2017), have been found about conformable fractional derivative and complex transforms for converting nonlinear PDEs to ordinary differential equations (ODEs) and then solving fractional differential equations with the aid of different methods. For instance, Eslami and Rezazadeh (2016) implemented the first integral method for Wu–Zhang system with conformable time-fractional derivative. Hosseini et al. (2017b) executed the modified Kudryashov method for seeking new exact solutions of the conformable time-fractional Klein Gordon equations with quadratic and cubic nonlinearities and Iyiola et al. (2017) solved the system of conformable time-fractional Robertson equations with one-dimensional diffusion coefficients with the help of the q-homotopy analysis method (q-HAM). Finally, Darvishi et al. (2018) solved conformable time–space fractional Schrödinger model by sine–cosine method.

Now, we consider the following form of the space–time-fractional Boussinesq-like equations (Rahmat et al. 2017):

$$\begin{aligned}&D^{2\alpha }_t{\text {u}}-D^{2\beta }_x{\text {u}}-D^\beta _x(6u^2D^\beta _x{\text {u}}+D^{3\beta }_x{\text {u}}) =0, \end{aligned}$$
(1)
$$\begin{aligned}&D^{2\alpha }_t{\text {u}}-D^{2\beta }_x{\text {u}}-D^\beta _x(6u^2D^\beta _x{\text {u}}+D^\beta _xD^{2\alpha }_t{\text {u}}) =0,\end{aligned}$$
(2)
$$\begin{aligned}&D^{2\alpha }_t{\text {u}}-D^\beta _xD^\alpha _t{\text {u}}-D^\beta _x(6u^2D^\beta _x{\text {u}}+D^{2\beta }_xD^\alpha _t{\text {u}}) =0, \end{aligned}$$
(3)

and

$$\begin{aligned} D^{2\alpha }_t{\text {u}}-D^\beta _x(6u^2D^\beta _x{\text {u}}+D^{3\beta }_x{\text {u}}) =0, \end{aligned}$$
(4)

where \(D_t^\alpha\), \(D_x^\beta\) denote the conformable fractional derivative of order \(\alpha\), \(\beta\) with respect to t and x, respectively, and \(0<\alpha {}\le {}1\), \(0<\beta {}\le {}1\). Also, u(x, t) is a differentiable function in respect with two independent variables x and t.

Very recently, Rahmat et al. (2017) solved these fractional equations by using Exp-function method with the help of fractional complex transformation and modified Riemann–Liouville fractional order operator.

When we substitute \(\alpha =1\) and \(\beta =1\) in Eqs. (1)–(4), the variety of space–time-fractional Boussinesq-like equations convert to the nonlinear integer order variety of Boussinesq-like equations. In this purpose, researchers in Wazwaz (2012), Eslami and Mirzazadeh (2014), Lee and Rathinasamy (2014) and Darvishi et al. (2017a, b) have received the distinct new abundant analytical solutions and distinct physical phenomena which have already discussed in the literature review section.

The main aim of this study is to introduce the variety of space–time-fractional Boussinesq-like equations with conformable fractional derivative for converting the fractional differential equations into the ordinary differential equations with integer order with the help of fractional complex transform (Cenesiz and Kurt 2016). Besides, we explore the new exact solutions for the variety of space–time-fractional Boussinesq-like equations with the aid of modified Kudryashov method. The obtained solutions of the variety of space–time-fractional Boussinesq-like equations are expressed by exponential function forms. The exponential function is based on an arbitrary variable a in which \(a\ne 0\) and \(a\ne 1\).

The remainder of the paper is organized as follows. A brief discussion about the conformable fractional derivative and the modified Kudryashov method is presented in Sect. 2. Section 3 and its sub-sections deal with the applications of the modified Kudryashov method to look for new closed form exact solutions for the variety of space–time-fractional Boussinesq-like equations. Finally, we draw a conclusion about executed method and the generated results in Sect. 4.

2 Conformable fractional derivative and the modified Kudryashov method

2.1 A brief description of conformable fractional derivative

The definition of conformable fractional derivative with the limit operator is as follows (Khalil et al. 2014):

Definition 1

Let \(f:(0,\infty {})\rightarrow \mathbb {R}\), the conformable fractional derivative of f from order \(\alpha {}\) is defined as

$$\begin{aligned} D_t^{\alpha }(f)(t)=\lim _{\epsilon {}\rightarrow 0}{\frac{f(t+\epsilon {}t^{1-\alpha {}})-f(t)}{\epsilon {}}},\quad {\text {for}}\ {\text {all}}\ t>0,\quad 0<\alpha {}\le {}1. \end{aligned}$$

Further, f is called an \(\alpha\)-conformable differentiable function at a point \(t>0\).

For this differentiation, the chain rule, exponential functions, Gronwalls inequality, integration by parts, Taylor power series expansions and Laplace transform are introduced by Abdeljawad (2015). Also, the conformable fractional derivative satisfies some feasible features which are mentioned in the following theorems (for more details see Khalil et al. 2014; Abdeljawad 2015):

Theorem 1

Let \(\alpha \in (0,1]\), and \(f=f(t),\ g=g(t)\) be \(\alpha\)-conformable differentiable functions at a point \(t>0\), then:

$$\begin{aligned}&({\text {i}})\quad D^\alpha _t(c_1f+c_2g)=c_1D^\alpha _tf+c_2D^\alpha _tg,\quad {{\text {for}}\ {\text {all}}}\ c_1,c_2\in \mathbb {R}. \\&({\text {ii}})\quad D_t^{\alpha {}}(t^{\mu {}})=\mu {}t^{\mu {}-\alpha {}}, \quad {{\text {for}}\ {\text {all}}}\ \mu {}\in {}\mathbb {R}. \\&({\text {iii}})\quad D^\alpha _t(fg)=gD^\alpha _t(f)+fD^\alpha _t(g). \\&({\text {iv}})\quad D^\alpha _t\left( \frac{f}{g}\right) =\frac{gD^\alpha _t(f)-fD^\alpha _t(g)}{g^2}. \end{aligned}$$

Furthermore, if f is differentiable, then \(D^\alpha _t(f(t))=t^{1-\alpha }\frac{df}{dt}\).

Theorem 2

Let \(f:(0,\infty )\rightarrow \mathbb {R}\) be a function such that f is differentiable and \(\alpha\)-conformable differentiable. Also, let g be a differentiable function defined in the range of f. Then

$$\begin{aligned} D^\alpha _t(fog)(t)=t^{1-\alpha }{g(t)}^{\alpha -1}g'(t)D^\alpha _t{(f(t))}_{t=g(t)}, \end{aligned}$$

where prime denotes the classical derivatives with respect to t.

The above definition of conformable fractional derivative and some of its properties are also used by several researchers (Tasbozan et al. 2016; Eslami and Rezazadeh 2016; Kaplan 2017; Hosseini et al. 2017a, b; Iyiola et al. 2017; Kurt et al. 2015, 2017; Cenesiz et al. 2017; Rahmat et al. 2017).

It is worth noting that recently a various significance study appeared in the cited references on conformable fractional derivative (Kurt et al. 2017; Zhao and Luo 2017; Zhou et al. 2018; Yang et al. 2018). Zhao and Luo (2017) explained the geometric and physical interpretation of the conformable fractional derivatives. The definition of the generalized conformable fractional derivative (GCFD) to general conformable derivative by means of linear extended Gateaux derivative, and employed this definition to describe that the physical interpretation of the conformable derivative is a modification of classical derivative in direction and magnitude (Zhao and Luo 2017). After that, Zhou et al. (2018) described the anomalous diffusion based on the conformable derivative (Zhao and Luo 2017) and analytical solutions of the conformable derivative model are obtained in terms of Error function and Gauss kernel. Finally, authors conclude that the conformable derivative model results good agreements with experimental data than the conventional diffusion equation. Very recently, Yang et al. (2018) developed the Swartzendruber model for description of non-Darcian flow in porous media by considering conformable derivative. Authors also explained that the proposed conformable Swartzendruber models are solved employing the Laplace transform method and validated on the basis of water flow in compacted fine-grained soils. The obtained results of fitting analysis present a good agreement with experimental data. The physical significance of conformable derivative is also described in Refs. Eslami et al. (2017a, b).

2.2 A brief description of the modified Kudryashov method

In this sub-section, we will describe all procedures of the modified Kudryashov method (Tasbozan et al. 2016) for solving fractional differential equations. The essential steps of this method are described as follows:

Consider a general form of a nonlinear fractional differential equation (FDE), say in two independent variables x and t as

$$\begin{aligned} F(u,D^\alpha _tu,D^\beta _xu,D^{2\alpha }_tu,D^{2\beta }_xu,D^\alpha _tD^\beta _xu, \ldots )=0, \quad t>0, \quad 0<\alpha ,\quad 0<\beta \le 1. \end{aligned}$$
(5)

In Eq. (5) \(D^\alpha _tu\) and \(D^\beta _xu\) are conformable fractional derivatives of u, \(u=u(x,t)\) is an unknown function, F is a polynomial in u(x, t) and its various partial derivatives, in which the nonlinear terms and highest order derivatives are involved. The main steps of the modified Kudryashov method are as follows:

Step-1 Conversion of the nonlinear FDE into an ordinary differential equation (ODE) has been overcome by using simple fractional calculus. In this respect, first we introduce the wave transformation

$$\begin{aligned} u(x,t)=U(\xi {}),\quad \xi = k\frac{x^{\beta }}{\beta }-l\frac{t^{\alpha }}{\alpha }, \end{aligned}$$
(6)

where k and l are arbitrary constants to be determined later. After that, implementing the transformation of Eq. (6) into Eq. (5), converts the latter to the following nonlinear ODE:

$$\begin{aligned} Q(U, U', U'',\ldots .)=0, \end{aligned}$$
(7)

where Q is a polynomial of U and its derivatives and the superscripts indicate the ordinary derivatives with respect to \(\ \xi\). If possible, we should integrate Eq. (7) term by term one or more times.

Step-2 It is supposed that the solution of Eq. (7) can be demonstrated as follows

$$\begin{aligned} U(\xi )=a_0+a_1Q(\xi )+\cdots +a_NQ^N(\xi ), \end{aligned}$$
(8)

wherein the arbitrary constants \(a_i, (i=1,2,\ldots ,N)\) are evaluated later but \(a_N\not =0\) and \(Q(\xi {})=\frac{1}{1+da^{\xi {}}}\) is a function satisfying the following auxiliary equation:

$$\begin{aligned} Q'(\xi )=(Q^2(\xi )-Q(\xi ))\ln a, \end{aligned}$$
(9)

where N is a natural number which is determined by the homogeneous balance principle and \(a\ne 0,1\).

Step-3 Inserting new solution from Eq. (8) into Eq. (7) along with Eq. (9) and comparing the terms results in a set of nonlinear equations which by solving it using Maple, we will acquire new exact solutions for the fractional partial differential equation (5).

3 Application of the modified Kudryashov method

In this section, the modified Kudryashov method will be performed to handle the space–time-fractional variety of Boussinesq-like equations for acquiring new soliton solutions.

3.1 Exact solutions of the first fractional Boussinesq-like equation

By setting the complex transformation (6) into Eq. (1), we obtain

$$\begin{aligned} (l^2-k^2)\,U-2k^2\,(U)^3-k^4\,U''=0. \end{aligned}$$
(10)

Now, balancing between \({\text {U}}''\) and \(U^3\), gives \(N=1.\) Then we consider solution of Eq. (10) as

$$\begin{aligned} U(\xi )=a_0+a_1Q(\xi ). \end{aligned}$$
(11)

Substituting Eq. (11) along with its first and second derivatives into Eq. (10) and equating the coefficients of similar powers of \({\text {Q}}(\xi )\) in the obtained equation, results in

$$\begin{aligned}&-2{(\ln a)}^2k^4a_1-2k^2a^3_1=0, \\&3{(\ln a)}^2k^4a_1-6k^2a_0a^2_1=0, \\&{-(\ln a)}^2k^4a_1-k^2a_1-6k^2a^2_0a_1+l^2a_1=0, \\&-k^2a_0-2k^2a^3_0+l^2a_0=0. \end{aligned}$$

By solving the above nonlinear system using symbolic computation package, the following cases are determined:

Set-1:

$$\begin{aligned} a_0=-\frac{1}{2}ik \ln a,\quad a_1=ik\, \ln a, \,{\text {and }}\, l=\pm k\sqrt{1-\frac{1}{2} {(\ln a)}^2k^2}. \end{aligned}$$

Substituting the values of Set-1 into Eq. (11) along with the general solution of Eq. (6), the following exact soliton solutions of the first fractional Boussinesq-like equation is obtained:

$$\begin{aligned} u_{1,2}(x,t)=-\frac{1}{2}ik \ln a+\frac{ik \ln a}{1+da^{k\left( \frac{x^{\beta }}{\beta }\mp \sqrt{1-\frac{1}{2}{(\ln a)}^2k^2}\ \frac{t^{\alpha }}{\alpha }\right) }}. \end{aligned}$$
(12)

Set-2:

$$\begin{aligned} a_0=\frac{1}{2}ik \ln a,\ a_1=-ik \ln a, \,{\text {and }}\, l=\pm k\sqrt{1-\frac{1}{2}{(\ln a)}^2k^2}. \end{aligned}$$

By substituting the values of Set-2 into Eq. (11) along with the general solution (6), we receive the following exact soliton solutions of the first fractional Boussinesq-like equation:

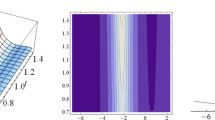
$$\begin{aligned} u_{3,4}(x,t)=\frac{1}{2}ik \ln a-\frac{ik \ln a}{1+da^{k\left( \frac{x^{\beta }}{\beta }\mp \sqrt{1-\frac{1}{2}{(\ln a)}^2k^2}\ \frac{t^{\alpha }}{\alpha }\right) }}. \end{aligned}$$
(13)

The 3D and 2D modulus snapshots of solutions (12) and (13) are shown in Figs. 1 and 2, respectively, with free choices of arbitrary parameters in different fractional values of \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\) and \(\alpha =\beta =1\). The figures demonstrate the anti-bell or dark soliton profile. The behavior of the solitons depends on the free choices of arbitrary parameters.

Fig. 1
figure 1

a–c 3D snapshots for the solution of the first fractional Boussinesq-like equation extracted by the modified Kudryashov method for the free choices of arbitrary parameters \(a=3\), \(d=1.5\), and \(k=0.5\) with \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\); \(\alpha =\beta =1\), respectively. d 2D snapshots of a–c at \(t=0\)

Full size image
Fig. 2
figure 2

a–c 3D snapshots for the solution of the first fractional Boussinesq-like equation constructed by the modified Kudryashov method for the free choices of arbitrary parameters \(a=3\), \(d=1.5\), and \(k=1\) with \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\); \(\alpha =\beta =1\), respectively. d 2D snapshots of a–c at \(t=1\)

Full size image

3.2 Exact solutions of the second fractional Boussinesq-like equation

By considering the traveling wave transformation (6) into Eq. (2), we obtain

$$\begin{aligned} (l^2-k^2)\,U-2k^2\,(U)^3-k^2l^2\,U''=0. \end{aligned}$$
(14)

Using homogeneous balance principle, we obtain \(N=1\). Then we assume that solution of Eq. (14) is

$$\begin{aligned} U(\xi )=a_0+a_1Q(\xi ). \end{aligned}$$
(15)

Substituting Eq. (15) along with its first and second derivatives into Eq. (14) and equating the coefficients of same powers of \({\text {Q}}(\xi )\) in the resulting equation, gives

$$\begin{aligned}&-2{(\ln a)}^2k^2{l^2a}_1-2{k^2a}^3_1=0, \\&3{(\ln a)}^2k^2{l^2a}_1-6{k^2a}_0a^2_1=0, \\&{-(\ln a)}^2k^2{l^2a}_1-k^2a_1-6{k^2a}^2_0a_1+l^2a_1=0, \\&-k^2a_0-2k^2a^3_0+l^2a_0=0. \end{aligned}$$

By solving the above nonlinear system using symbolic computation package, the following cases are determined:

Set-1:

$$\begin{aligned} a_0={\frac{k\ln a}{\sqrt{-(2\,{k}^{2}\left( \ln a \right) ^{2}+4)}}},\quad a_1={\frac{k\ln a\sqrt{-(2\,{k}^{2}\left( \ln a\right) ^{2}+4)}}{{k}^{2}\left( \ln a\right) ^{2}+2}}, {\text {and }}\, l=\pm {\frac{2k}{\sqrt{2\,{k}^{2}\left( \ln a\right) ^{2}+4}}}. \end{aligned}$$

Substituting the values of Set-1 into Eq. (15) along with the general solution of Eq. (6), we determine the following exact soliton solutions of the second fractional Boussinesq-like equation:

$$\begin{aligned} u_{1,2}(x,t)= \frac{k\ln a}{\sqrt{-(2\,{k}^{2}\left( \ln a\right) ^{2}+4)}}+\frac{k\ln a\sqrt{-(2\,{k}^{2}\left( \ln a\right) ^{2}+4)}}{{k}^{2}\left( \ln a\right) ^{2}+2}\left( \frac{1}{1+da^{k\left( \frac{x^{\beta }}{\beta }\mp \frac{2}{\sqrt{2\,{k}^{2}\left( \ln a\right) ^{2}+4}}\frac{t^{\alpha }}{\alpha }\right) }}\right) . \end{aligned}$$
(16)

Set-2:

$$\begin{aligned} a_0=-{\frac{k\ln a}{\sqrt{-(2\,{k}^{2}\left( \ln a\right) ^{2}+4)}}},\quad a_1=-{\frac{k\ln a\sqrt{-(2\,{k}^{2}\left( \ln a\right) ^{2}+4)}}{{k}^{2}\left( \ln a\right) ^{2}+2}}, {\text {and }}\, l=\pm {\frac{2k}{\sqrt{2\,{k}^{2}\left( \ln a\right) ^{2}+4}}}. \end{aligned}$$

Substituting the values of Set-2 into Eq. (15) along with the general solution (6), the following exact soliton solutions of the second fractional Boussinesq-like equation are explored:

$$\begin{aligned} u_{3,4}(x,t)= -\frac{k\ln a}{\sqrt{-(2\,{k}^{2}\left( \ln a\right) ^{2}+4)}}- \frac{k\ln a\sqrt{-(2\,{k}^{2}\left( \ln a\right) ^{2}+4)}}{{k}^{2}\left( \ln a\right) ^{2}+2} \left( \frac{1}{1+da^{k\left( \frac{x^{\beta }}{\beta } \mp \frac{2}{\sqrt{2\,{k}^{2}\left( \ln a\right) ^{2}+4}}\frac{t^{\alpha }}{\alpha }\right) }}\right) . \end{aligned}$$
(17)

The 3D and 2D modulus snapshots of solutions (16) and (17) are exhibited in Figs. 3 and 4, respectively, with free choices of arbitrary parameters in different fractional values of \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\) and \(\alpha =\beta =1\). The figures also demonstrate the anti-bell or dark soliton profile.

Fig. 3
figure 3

a–c 3D snapshots for the solution of second fractional Boussinesq-like equation obtained by the modified Kudryashov method for the free choice of arbitrary parameters \(a=3\), \(d=1.5\), and \(k=0.5\) with \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\); \(\alpha =\beta =1\), respectively. d 2D snapshots of a–c at \(t=0\)

Full size image
Fig. 4
figure 4

a–c 3D snapshots for the solution of second fractional Boussinesq-like equation found by the modified Kudryashov method for the free choices of arbitrary parameters \(a=3\), \(d=1.5\), and \(k=1\) with \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\); \(\alpha =\beta =1\), respectively. d 2D snapshots of a–c at \(t=1\)

Full size image

3.3 Exact solutions of the third fractional Boussinesq-like equation

Putting the transformation (6) into Eq. (3), yields

$$\begin{aligned} (l^2+lk)\,U-2k^2\,(U)^3+k^3l\,U''=0. \end{aligned}$$
(18)

Homogeneous balance principle gives \(N=1\). As usual the solution of Eq. (18) is taken as

$$\begin{aligned} U(\xi )=a_0+a_1Q(\xi ). \end{aligned}$$
(19)

Substituting Eq. (19) along with its first and second derivatives into Eq. (18) and equating the coefficients of same powers of \({\text {Q}}(\xi )\) in the resulting equation, yields

$$\begin{aligned}&2{(\ln a)}^2k^3{la}_1-2k^2a^3_1=0,\\&-3{(\ln a)}^2k^2{la}_1-6k^2a_0a^2_1=0,\\&{(\ln a)}^2k^3{la}_1+kla_1-6k^2a^2_0a_1+l^2a_1=0,\\&l^2a_0-2{k^2a}^3_0+kla_0=0. \end{aligned}$$

After solving the above nonlinear system by using Maple, the following cases are determined:

Set-1:

$$\begin{aligned} a_0=\frac{1}{4}k\ln a\sqrt{{2k^2(\ln a)}^2-4},\quad a_1=-\frac{k\ln a (({\ln a)}^2k^2-2)}{\sqrt{{2(\ln a)}^2k^2-4}}, {\text {and }}\, l=k\left( \frac{1}{2}{(\ln a)}^2k^2-1\right) . \end{aligned}$$

Substituting the values of Set-1 into Eq. (19) along with the general solution of Eq. (6), we extract the following exact soliton solutions of the third fractional Boussinesq-like equation:

$$\begin{aligned}&u_1(x,t)=\frac{1}{4}k\ln a\sqrt{2{(\ln a)}^2k^2-4}-\frac{k\ln a (({\ln a)}^2k^2-2)}{\sqrt{{2(\ln a)}^2k^2-4}} \frac{1}{1+da^{k\left( \frac{x^{\beta }}{\beta }\mp \left( \frac{1}{2}{(\ln a)}^2k^2-1\right) \frac{t^{\alpha }}{\alpha }\right) }}. \end{aligned}$$
(20)

Set-2:

$$\begin{aligned} a_0=-\frac{1}{4}k\ln a\sqrt{{2k^2(\ln a)}^2-4},\ a_1=\frac{k\ln a (({\ln a)}^2k^2-2)}{\sqrt{{2(\ln a)}^2k^2-4}}, {\text {and }}\, l=k\left( \frac{1}{2}{(\ln a)}^2k^2-1\right) . \end{aligned}$$

Substituting the values of Set-2 into Eq. (19) along with the general solution (6), we generate the following exact soliton solutions of the third fractional Boussinesq-like equation:

$$\begin{aligned} u_2(x,t)=-\frac{1}{4}k\ln a\sqrt{2{(\ln a)}^2k^2-4}+\frac{k\ln a (({\ln a)}^2k^2-2)}{\sqrt{{2(\ln a)}^2k^2-4}} \frac{1}{1+da^{k\left( \frac{x^{\beta }}{\beta }\mp \left( \frac{1}{2}{(\ln a)}^2k^2-1\right) \frac{t^{\alpha }}{\alpha }\right) }}. \end{aligned}$$
(21)

The 3D and 2D modulus snapshots of solutions (20) and (21) are shown in Figs. 5 and 6, respectively, with free choices of arbitrary parameters in different fractional values of \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\) and \(\alpha =\beta =1\). The figures also demonstrate the anti-bell or dark soliton profile.

Fig. 5
figure 5

a–c 3D snapshots for the solution of third fractional Boussinesq-like equation generated by the modified Kudryashov method for the free choices of arbitrary parameters \(a=3\), \(d=1.5\), and \(k=1\) with \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\); \(\alpha =\beta =1\), respectively. d 2D snapshots of a–c at \(t=1\)

Full size image
Fig. 6
figure 6

a–c 3D snapshots for the solution of third fractional Boussinesq-like equation acquired by the modified Kudryashov method for the free choices of arbitrary parameters \(a=4\), \(d=1.5\), and \(k=1\) with \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\); \(\alpha =\beta =1\), respectively. d 2D snapshots of a–c at \(t=0\)

Full size image

3.4 Exact solutions of the fourth fractional Boussinesq-like equation

Similar to the previous parts, we use the same transformation (6) into Eq. (4), which yields

$$\begin{aligned} l^2\,U-2k^2\,U^3-k^4\,U{''}=0. \end{aligned}$$
(22)

We obtain \(N=1\) using homogeneous balance principle. Then solution of Eq. (22) is assumed as

$$\begin{aligned} U(\xi )=a_0+a_1Q(\xi ). \end{aligned}$$
(23)

Substituting Eq. (23) along with its first and second derivatives into Eq. (22) and equating the coefficients of same powers of \({\text {Q}}(\xi )\) in the resulting equation, results in

$$\begin{aligned}&-2{(\ln a)}^2k^4a_1-2k^2a^3_1=0,\\&3{(\ln a)}^2k^4a_1-6{k^2a}_0a^2_1=0,\\&{-(\ln a)}^2k^4a_1+l^2a_1-6k^2a^2_0a_1=0,\\&l^2a_0-2k^2a^3_0=0. \end{aligned}$$

Solution sets of the above nonlinear system which have obtained by Maple are:

Set-1:

$$\begin{aligned} a_0=-\frac{1}{2}ik \ln a,\ a_1=ik \ln a, {\text {and}}\, l=\pm \frac{1}{\sqrt{2}}ik^2 \ln a. \end{aligned}$$

Substituting the values of Set-1 into Eq. (23) along with the general solution (6) gives the following exact soliton solutions of the fourth fractional Boussinesq-like equation:

$$\begin{aligned} u_{1,2}(x,t)=-\frac{1}{2}ik \ln a+\frac{ik \ln a}{1+da^{k\left( \frac{x^{\beta }}{\beta }\mp \frac{1}{\sqrt{2}}ik \ln a\ \frac{t^{\alpha }}{\alpha }\right) }}. \end{aligned}$$
(24)

Set-2:

$$\begin{aligned} a_0=\frac{1}{2}ik \ln a,\ a_1=-ik \ln a, {\text {and}}\, l=\pm \frac{1}{\sqrt{2}}ik^2 \ln a. \end{aligned}$$

Substituting the values of Set-2 into Eq. (23) along with the general solution (6), we obtain the following exact soliton solutions of the fourth fractional Boussinesq-like equation:

$$\begin{aligned} u_{3,4}(x,t)=\frac{1}{2}ik \ln a-\frac{ik \ln a}{1+da^{k\left( \frac{x^{\beta }}{\beta }\mp \frac{1}{\sqrt{2}}ik \ln a\ \frac{t^{\alpha }}{\alpha }\right) }}. \end{aligned}$$
(25)

The 3D and 2D modulus snapshots of  solutions (24) and (25) are presented in Figs. 7 and 8, respectively, with free choices of arbitrary parameters in different fractional values of \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\) and \(\alpha =\beta =1\). The figures also demonstrate the periodic behaviors.

Fig. 7
figure 7

a–c 3D snapshots for the solution of fourth fractional Boussinesq-like equation produced by the modified Kudryashov method for the free choices of arbitrary parameters \(a=4\), \(d=1.5\), and \(k=1\) with \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\); \(\alpha =\beta =1\), respectively. d 2D snapshots of a–c at \(t=0\)

Full size image
Fig. 8
figure 8

a–c 3D snapshots for the solution of fourth fractional Boussinesq-like equation extracted by the modified Kudryashov method for the free choice of arbitrary parameters \(a=4\), \(d=1.5\), and \(k=1\) with \(\alpha =\beta =0.5\); \(\alpha =\beta =0.75\); \(\alpha =\beta =1\), respectively. d 2D snapshots of a–c at \(t=0\)

Full size image

4 Conclusions

The basic goal of this work was to execute the modified Kudryashov method for exactly solving the variety of space–time-fractional Boussinesq-like equations. As a result, we received many new exact soliton solutions for the space–time-fractional variety of Boussinesq-like equations which are expressed by exponential function forms. The exponential function is based on an arbitrary variable a in which \(a\ne 0\) and \(a\ne 1\). To the best of our knowledge, the received results have not been reported in other studies on the fractional case of Boussinesq-like equations. Therefore, the obtained results show that the implemented method along with the symbolic computation package suggest a promising, robust, and well-built mathematical tool to handle for any nonlinear partial differential equations with integer and fractional order arising in mathematical physics and other applied fields.