1 Introduction

The dispersion (or diffusion) process of a soluble matter in the flow of fluids plays a pertinent role in chemical industry and biological systems, especially in the gel chromatography, tubular flow reactors, indicator dilution technique and in the study of blood circulation. It is well understood that in blood, the substances such as nutrients, oxygen, metabolic waste products, drugs, etc., are transported by means of diffusive mechanisms. Motivated by the study of Griffith [1], Taylor [2, 3] have mathematically developed the modest approach to investigate the dispersion process of a solute in a Newtonian fluid (a solvent) flowing slowly through a circular tube. It is revealed that the coefficient of effective dispersion of solute becomes a function of the radius of the tube, mean velocity and molecular diffusion coefficient, when it is diffused relative to a reference plane moving with the average velocity of the fluid flow. Aris [4] has extended the results obtained by Taylor [2, 3] and predicted that the growth rate of the solute spreading is directly proportionate to the sum of the molecular dispersion coefficient and Taylor dispersion coefficient. Further, Aris [4] took an effort to remove the limitations imposed by Taylor [2, 3]. In view of understanding the basic concepts of physiological organisms, Wageningen [5] proposed a novel generalised approach. In the aforementioned studies, the rheology of solvents is assumed to obey the law of Newtonian. It is of interest to note that the simple rheological behaviour of Newtonian fluid is inadequate to represent the real characteristics of biological fluids and several types of fluids used in industry, which are suspensions of particulate substances in continuous fluids. In view of this, a study on the dispersion of a solute in solvent (fluid) flowing in a tube has to be made by taking into account the rheology of solvent as a non-Newtonian fluid.

Fan and Hwang [6] have examined the nature of dispersion in a power law fluid, whereas Fan and Wang [7] explored this problem for Bingham plastic and Ellis modells by adopting Taylor’s approach [2]. Ghoshal [8] has considered a Reiner-Philippoff modell fluid, and Shah and Cox [9] have analysed the dispersion in Eyring modell fluid. The values of effective dispersion coefficient for a Newtonian fluid are higher than those for an Eyring modell fluid [9]. Using Aris’ method, Prenosil et al. [10] have solved the problem of dispersion of a soluble matter in the flow of a power law fluid. Assuming the rheology of non-Newtonian fluids (solvents) as power-law, Bingham plastic and Casson modells, the performance of shear-augmented dispersion of solutes in solvents is carried out by adopting the dispersion theory developed by Taylor and Aris. Sharp [11] has observed that the value of yield stress of the solvent fluid has a predominate effect on the relative axial diffusivity. Using the methodology developed by Sharp [11], Sankar et al. [12] have studied the shear augmented dispersion of a solute in blood flow by assuming the rheology of blood as a Herschel-Bulkley fluid modell. The effective axial diffusivity of a solute is shown to be higher for the flow of blood in a tube as compared to that of the flow between two parallel plates. All the research works mentioned above are regarded with flows where the solute does not chemically react with the liquid through which it is dispersed. It is practically significant to mention that one has to deal with a broad assortment of chemical engineering problems in which dispersion of a solute takes place in the presence of irreversible chemical reactions, namely, absorption of a frugally soluble gas in an agitated tank with irreversible first-order chemical reaction, ester hydrolysis, etc. [10].

Katz [13], Walker [14], Soloman et al. [15], Gill et al. [16, 17], Gupta et al. [18] and Scherer et al. [19] examined the dispersion of a soluble matter in the flow of a Newtonian fluid by taking into account both homogeneous and heterogeneous chemical reactions. Shukla et al. [20] have investigated the effects of homogeneous chemical reaction on the Taylor dispersion in flowing non-Newtonian fluids by considering Bingham plastic, power law and Casson fluids. The effective dispersion coefficient is found to be enhanced as the value of the rate of chemical reaction decreases. Singh et al. [21] have developed a mathematical modell to analyse the combined effects of the width of the flow region and the chemical reaction on dispersion coefficient in three types of non-Newtonian fluids (power law, Bingham plastic and Casson) flowing through a channel. The influences of chemical reaction and the rheology of blood as a Herschel-Bulkley modell on the axial diffusivity have been analysed by Jaafar et al. [22], and it is seen that the effective axial diffusivity tends to increase with the increase of Peclet number. Kumar et al. [23] have examined the influence of both types of chemical reactions (homogeneous and heterogeneous) on the solute dispersion in composite porous medium by taking into account immiscible fluids with different viscosities. Further, they perceived that dispersion coefficient is decreased as the value of chemical reaction rate parameter increases, and they indicated that the concept of solute dispersion with the chemical reaction has wide physiological applications in the circulatory system.

It is well understood that several circulatory medications are therapeutic when the concentration is stumpy, but toxic at higher concentration, hence, it is of interest to identify the dispersion rate of medicines in the cardiovascular system. The injection of medicines (solute) into the flow of blood causes the remarkable disorders in the normal blood flow through an artery or veins. Blood exposes anomalous viscid behaviour when it flows in the arteries of numerous diameters. Chien [24] has experimentally revealed that under some diseased conditions, e.g. patients suffering from hypertension, myocardial infarction, cerebrovascular diseases and renal ailment, blood shows remarkable non-Newtonian properties. Hence, a more or less realistic rheological modell for blood is to be considered while investigating the problem of dispersion of passive species (solute) with the chemical reaction in flowing blood in order to have crystal clear understanding of the physiological process of the hemodialysis and molecular transport of oxygen from blood plasma to the living tissues of brain, heart and lungs.

As mentioned above, numerous investigators have extended the mathematical technique developed by Taylor [2] to various types of non-Newtonian fluids including Herscel-Bulkley fluids. As compared to rheological behaviour of Hershel-Bulkley fluid, the constitutive equation of thixotropic fluids has one more parameter known as a thixotropic parameter α1 (a scalar structural parameter of materials) in addition to yield stress, shear thinning and shear thickening property [25]. For other values of α1 (\(0 < \alpha_{1} < 1)\), the degree of complexity or severity of the combined rheological behaviour of yield stress, consistency factor and power index is altered which could represent various complex behaviour of fluid (blood) to adequately investigate the theory of dispersion of a solute.

Based on the aforementioned views, an attempt has been made to investigate the solute diffusion in blood flow through a tube with homogeneous biochemical reaction, considering blood as thixotropic modell which has, to the best of authors knowledge, not carried out in the earlier literature. The role of thixotropic fluid modell with the first-order biochemical reaction on the equivalent dispersion coefficient of the solute is brought out in the present work.

2 Formulation of the Problem

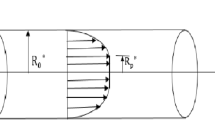
Consider the dispersion of soluble pieces (solute) in the steady, axisymmetric, laminar and fully developed flow of blood (a non-Newtonian fluid) with a uniform pressure gradient through a circular tube of radius \(R_{0}^{*}\), as shown in Fig. 1. We take the circular cylindrical polar coordinate system (\(r^{*} ,\theta^{*} ,z^{*}\)), where \(r^{*}\) denotes the radial coordinate, \(\theta^{*}\) represents the circumferential coordinate, and \(z^{*}\) indicates the axial coordinate. Bugliarello and Sevilla [26] have reported that the radial velocity is insignificantly small and can be ignored for a low Reynolds number flow through a microvessel (narrow artery). This type of flow condition is valid when we deal with the problem of investigating the dispersion of a drug into blood stream in small-diameter blood vessels (arterioles) and capillaries. It is assumed that the diluted solute having a small concentration diffuses and concurrently undertakes a first order irreversible chemical reaction in a non-Newtonian fluid under isothermal condition.

Fig. 1
figure 1

Geometry of an artery

Full size image

2.1 Governing Equation and Boundary Conditions

Neglecting the axial diffusion as compared to the radial diffusion term which is termed as Taylor’s approximation [2, 3], the equation for the concentration of the dispersing solute is given by [18, 20]

$$\frac{{\partial c^{*} }}{{\partial t^{*} }} + u^{*} \frac{{\partial c^{*} }}{{\partial z^{*} }} = \frac{{D_{m}^{*} }}{{r^{*} }}\frac{\partial }{{\partial r^{*} }}\left( {r^{*} \frac{{\partial c^{*} }}{{\partial r^{*} }}} \right) - \alpha^{*} c^{*}$$
(1)

where \(c^{*}\) is the concentration of a solute, \(t^{*}\) is the time, \(u^{*}\) is the axial velocity in the unidirectional flow, \(D_{m}^{* }\) is the constant molecular diffusion coefficient, and \(\alpha^{*}\) is the first order homogeneous chemical reaction rate constant.

Following Taylor [2] and introducing \(z_{1}^{*} \left( { = z^{*} - \overline{u}^{*} t^{*} } \right)\), Eq. (1) relative to a plane moving with the mean speed of the flow (\(\overline{u }^{*} )\) can be written as

$$\frac{{\partial c^{*} }}{{\partial t^{*} }} + \left( {u^{*} - \overline{u }^{*} } \right)\frac{{\partial c^{*} }}{{\partial z_{1}^{*} }} = \frac{{D_{m}^{* } }}{{r^{*} }}\frac{\partial }{{\partial r^{*} }}\left( {r^{*} \frac{{\partial c^{*} }}{{\partial r^{*} }}} \right) - \alpha^{*} c^{*}$$
(2)

Supposing that the limiting condition of Taylor is valid [2], that is, the partial equilibrium state in any cross section of the circular tube is well recognised, Eq. (2) may be reduced to

$$\left( {u^{*} - \overline{u }^{*} } \right)\frac{{\partial c^{*} }}{{\partial z_{1}^{*} }} = \frac{{D_{m}^{* } }}{{r^{*} }}\frac{\partial }{{\partial r^{*} }}\left( {r^{*} \frac{{\partial c^{*} }}{{\partial r^{*} }}} \right) - \alpha^{*} c^{*}$$
(3)

where \(\frac{{\partial c^{*} }}{{\partial z_{1}^{*} }}\) is independent of the radial distance \(r^{*}\) and \(\frac{{\partial c^{*} }}{{\partial t^{*} }} = 0.\)

Non-dimensional variables are defined as

$$r = \frac{{r^{*} }}{{R_{0}^{*} }} , u = \frac{{u^{*} }}{{u_{0}^{*} }} , z_{1} = \frac{{z_{1}^{*} }}{{R_{0}^{*} }} ,\overline{u } = \frac{{\overline{u }^{*} }}{{u_{0}^{*} }} ,\; pe = \frac{{R_{0}^{*} u_{0}^{*} }}{{D_{m}^{*} }},\; \tau = \frac{{\tau^{*} R_{0}^{*} }}{{\mu^{*} u_{0}^{*} }},\; \tau_{0} = \frac{{\tau_{0}^{*} R_{0}^{*} }}{{\mu^{*} u_{0}^{*} }},\; \tau_{0} = \frac{{\tau_{0}^{*} R_{0}^{*} }}{{\mu^{*} u_{0}^{*} }},\; p = \frac{{p^{*} R_{0}^{*} }}{{\mu^{*} u_{0}^{*} }},\;k = \frac{{k^{*} }}{{\mu^{*} }}\left( {\frac{{u_{0}^{*} }}{{R_{0}^{*} }}} \right){ }^{n - 1} ,$$
(4)

where \(u_{0}^{*}\) is the average velocity of Newtonian fluid, \(\mu^{*}\) denotes the viscosity of Newtonian fluid, and \(Pe\) is the Peclet number, \(p^{*}\) is the pressure, \(\tau^{*}\) is the shear stress, \(k^{*}\) is the consistency index, n denotes the power law index or fluid behaviour index, and \(\tau_{0}^{*}\) is the yield stress (\(*\) denotes the corresponding dimensional quantity).

Using Eq. (4), the governing Eq. (3) transforms to

$$\frac{{\partial^{2} c^{*} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial c^{*} }}{\partial r} - Pe\alpha^{2} c^{*} = Pe \overline{u } \frac{{\partial c^{*} }}{{\partial z_{1} }}f\left( r \right)$$
(5)

where \(\alpha^{2} = \frac{{\alpha^{*} R_{0}^{*} }}{{u_{0}^{*} }}\) and \(f\left( r \right) = \frac{u}{{\overline{u } }} - 1.\)

The corresponding boundary conditions for the present study are

$$\frac{{\partial c^{*} }}{\partial r} = 0 \;{\text{at}}\;r = 0,$$
(6)
$$\frac{{\partial c^{*} }}{\partial r} = 0 \;{\text{at}}\;r = 1.$$
(7)

2.2 Constitutive Equation for Thixotropic Fluid and Momentum Equation

The dimensionless form of rheological behaviour of thixotropic fluid may be expressed as [25]

$$\left( { - \frac{\partial u}{{\partial r}}} \right)^{n} = \frac{{\tau - \alpha_{1} \tau_{0} }}{{\left( {1 - \alpha_{1} } \right)k}} , {\text{ if}}\;\tau \ge \tau_{0} ,$$
(8)
$$\left( {\frac{\partial u}{{\partial r}}} \right) = 0 ,\;{\text{ if}}\; \tau \le \tau_{0 } ,$$
(9)

where n is the fluid behaviour index (power law index), \(\tau\) indicates the shear stress, \(\alpha_{1}\) is the scalar structural parameter of materials or thixotropic parameter, \(\tau_{0}\) is the yield stress, and k denotes the consistency index of the fluid.

Equation (9) corresponds to disappearing of velocity gradient in the region where the shear stress \(\tau\) is less than the yield stress \(\tau_{0}\), which implies that a region of plug flow exists whenever \(\tau \le \tau_{0 }\).

The dimensionless version of equation of momentum for the flow of fluid is written as

$$- \frac{\partial p}{{\partial z}} - \frac{1}{r}\frac{\partial }{\partial r}\left( {r\tau } \right) = 0,$$
(10)

where \(p\) is the pressure.

The boundary conditions are

$$\left( {\text{i}} \right)\; \tau \;{\text{is }}\;{\text{finite}}\;{\text{at}}\; r = 0 \;{\text{and}}\;\left( {{\text{ii}}} \right) \; u = 0 \;{\text{ at}}\; r = 1.$$
(11)

3 Solution Method

3.1 Velocity Distribution for the Flow of Thixotropic Fluid

Integrating Eq. (10) with respect to \(r\) and applying the boundary condition (i) of Eq. (11), we get

$$\tau = \frac{{r P_{0} }}{2},$$
(12)

where \(P_{0} = - \frac{{{\text{d}}p}}{{{\text{d}}z}}\).

With the help of Eqs. (8), (9), (11) and (12), the analytic expression for velocity profile in the flow region may be obtained as

$$u = \frac{2n}{{P_{0} \left( {n + 1} \right)\left( {\left( {1 - \alpha_{1} } \right)k} \right)^{\frac{1}{n}} }}\left[ {\left( {\frac{{P_{0} }}{2} - \alpha_{1} \tau_{0} } \right)^{{\frac{n + 1}{n}}} - \left( {\frac{{rP_{0} }}{2} - \alpha_{1} \tau_{0} } \right)^{{\frac{n + 1}{n}}} } \right] ; \;{\text{if}}\;R_{p} \le r \le 1,$$
(13)

By substituting \(r = R_{p}\) into Eq. (13), the velocity profile in the plug core region can be obtained as

$$u_{p} = \frac{2n}{{P_{0} \left( {n + 1} \right)\left( {\left( {1 - \alpha_{1} } \right)k} \right)^{\frac{1}{n}} }}\left[ {\left( {\frac{{P_{0} }}{2} - \alpha_{1} \tau_{0} } \right)^{{\frac{n + 1}{n}}} - \left( {\frac{{P_{0} R_{p} }}{2} - \alpha_{1} \tau_{0} } \right)^{{\frac{n + 1}{n}}} } \right];\;{\text{if}}\;0 \le r \le R_{p } ,$$
(14)

where \(R_{p}\) is the plug core radius, and it is expressed as \(R_{p} = \frac{{2\tau_{0} }}{{P_{0} }}\).

The mean velocity of the fluid in dimensionless form is given by

$$\overline{u} = 2\mathop \smallint \limits_{0}^{1} ru{\text{d}}r$$
(15)
$$\begin{gathered} \overline{u } = \frac{{2n\left( {\frac{{P_{0} }}{2} - \alpha_{1} \tau_{0} } \right)^{{\frac{n + 1}{n}}} }}{{P_{0} \left( {n + 1} \right)\left( {\left( {1 - \alpha_{1} } \right)k} \right)^{\frac{1}{n}} }} - \frac{{8n^{2} \left( {\frac{{P_{0} }}{2} - \alpha_{1} \tau_{0} } \right)^{{\frac{2n + 1}{n}}} }}{{P_{0}^{2} \left( {n + 1} \right)\left( {2n + 1} \right)\left( {\left( {1 - \alpha_{1} } \right)k} \right)^{\frac{1}{n}} }} + \frac{{16n^{3} \left( {\frac{{P_{0} }}{2} - \alpha_{1} \tau_{0} } \right)^{{\frac{3n + 1}{n}}} }}{{P_{0}^{3} \left( {n + 1} \right)\left( {2n + 1} \right)\left( {3n + 1} \right)\left( {\left( {1 - \alpha_{1} } \right)k} \right)^{\frac{1}{n}} }} \hfill \\ - \frac{{2nR_{p}^{2} \left( {\frac{{P_{0} R_{p} }}{2} - \alpha_{1} \tau_{0} } \right)^{{\frac{n + 1}{n}}} }}{{P_{0} \left( {n + 1} \right)\left( {\left( {1 - \alpha_{1} } \right)k} \right)^{\frac{1}{n}} }} + \frac{{8n^{2} R_{p} \left( {\frac{{P_{0} R_{p} { }}}{2} - \alpha_{1} \tau_{0} } \right)^{{\frac{2n + 1}{n}}} }}{{P_{0}^{2} \left( {n + 1} \right)\left( {2n + 1} \right)\left( {\left( {1 - \alpha_{1} } \right)k} \right)^{\frac{1}{n}} }} - \frac{{16n^{3} \left( {\frac{{P_{0} R_{p} { }}}{2} - \alpha_{1} \tau_{0} } \right)^{{\frac{3n + 1}{n}}} }}{{P_{0}^{3} \left( {n + 1} \right)\left( {2n + 1} \right)\left( {3n + 1} \right)\left( {\left( {1 - \alpha_{1} } \right)k} \right)^{\frac{1}{n}} }} \hfill \\ \end{gathered}$$
(16)

3.2 Dispersion in Thixotropic Fluid

Equation (5) is a generalised Bessel equation, and its solution along with the boundary conditions (6) and (7), gives the concentration profile as follows:

$$c^{*} \left( r \right) = Pe\frac{{\partial c^{*} }}{{\partial z_{1} }}\overline{u } c_{1} \left( r \right)$$
(17)

where

$$c_{1} \left( r \right) = A_{1} I_{0} \left( {\lambda r} \right) + \mathop \smallint \limits_{0}^{r} \left[ {I_{0} \left( {\lambda r} \right)K_{0} \left( {\lambda x} \right) - I_{0} \left( {\lambda x} \right)K_{0} \left( {\lambda r} \right)} \right]xf\left( x \right){\text{d}}x,$$
(18)
$$A_{1} = - \frac{1}{{I_{1} \left( \lambda \right)}}\mathop \smallint \limits_{0}^{1} \left[ {I_{1} \left( \lambda \right)K_{0} \left( {\lambda x} \right) + I_{0} \left( {\lambda x} \right)K_{1} \left( \lambda \right)} \right] xf\left( x \right){\text{d}}x,$$
(19)

\(\lambda = \alpha \left( {\sqrt {Pe} } \right)\), \(I_{0 } , K_{0} , \;{\text{and}}\; I_{1}\), \(K_{1}\) are the first and second kind modified Bessel functions of zeroth and first order, respectively.

The average solute flux \(\overline{Q }\), across the tube moving with the mean speed of the flow can be written as,

$$\overline{Q } = Pe\frac{{\partial c^{*} }}{{\partial z_{1} }}\overline{u }^{2} \mathop \smallint \limits_{0}^{1} 2c_{1} \left( r \right)f\left( r \right)r{\text{d}}r$$
(20)

Comparing Eq. (20) with Fick’s law of diffusion \(J^{*} = - D\left( {\frac{{\partial C^{*} }}{{\partial z^{*} }}} \right)\), the  effective dispersion coefficient, \(D\) is given by

$$D = - 2Pe\overline{u }^{2} M$$
(21)

where

$$M = \mathop \smallint \limits_{0}^{1} c_{1} \left( r \right)f\left( r \right)r{\text{d}}r$$
(22)

and M is termed as the equivalent dispersion coefficient.

4 Results and Discussion

In the present study, an effort is undertaken to analyse the dispersion process of a nanoparticle (solute) in the laminar flow of thixotropic fluid modell through a tube with the effect of homogeneous chemical reaction. The nature of dispersion process is being carried out by adopting Taylor’s approach. The effect of chemical reaction rate constant on equivalent dispersion coefficient in Thixotropic fluid is investigated. Integrals involved in the solution of dispersion coefficient \(D\) and concentration \(c_{1} \left( r \right)\) are evaluated numerically by Simpson’s \(\frac{1}{3}\) rule.

Figures 2, 3, 4, 5 show the effects of various parameters on the equivalent dispersion coefficient (M) in the presence of homogeneous chemical reaction in the flow of thixotropic fluid as solvent. The homogeneous chemical reaction rate constant (α) dependent nature of the equivalent dispersion coefficient (M) with a variation in the fluid behaviour index (n) for the dispersion process is observed in Fig. 2. It is noticed that as α or n increases, the effective dispersion coefficient decreases. The percentage decrease in M is found to be higher for a small value of α and a strongly shear thinning fluid whereas it becomes less for a larger value of α and Newtonian fluid. The combined influence of yield stress \(\left( {\tau_{0 } } \right)\) and the scalar structural parameter of materials or thixotropic parameter (\(\alpha_{1}\)) on M is revealed in Fig. 3. Figures 2 and 3 show that the equivalent dispersion coefficient (M) is higher in power law fluid as compared to thixotropic fluid.

Fig. 2
figure 2

The variation of equivalent dispersion coefficient (M) with power law index (n) for different values of first order chemical reaction rate constant (\(\alpha\)) for power law fluid (k = 0.8; \(\tau_{0 } = 0; \alpha_{1} = 0 )\)

Full size image
Fig. 3
figure 3

The variation of equivalent dispersion coefficient (M) with power law index (n) for different values of first order chemical reaction rate constant (\(\alpha\)) for thixotropic fluid (k = 0.8; \(\tau_{0 } = 0.1; \alpha_{1} = 0.3 )\)

Full size image
Fig. 4
figure 4

The variation of equivalent dispersion coefficient (M) with yield stress for different values of first order chemical reaction rate constant (\(\alpha\)) for thixotropic fluid (n = 0.8; \(k = 0.8; \alpha_{1} = 0.3 )\)

Full size image
Fig. 5
figure 5

The variation of equivalent dispersion coefficient (M) with \(\alpha_{1}\) (the scalar structural parameter of materials) for different values of first order chemical reaction rate constant (\(\alpha\)) for thixotropic fluid (n = 0.8; \(k = 0.8; \tau_{0 } = 0.2)\)

Full size image

The variation of equivalent dispersion coefficient (M) with respect to power law index (n) for different values of yield stress (\(\tau_{0}\)) and the scalar structural parameter of materials or thixotropic parameter (\(\alpha_{1}\)) is, respectively, illustrated in Figs. 4 and 5. The value of M decreases as the values of \(\tau_{0}\) and \(\alpha_{1}\) increase. The information concerning the decrease of the equivalent dispersion coefficient (M) with the increase in the scalar structural parameter of materials or thixotropic parameter (\(\alpha_{1}\)) is, for the first time, reported in the literature.

5 Conclusions

The effect of the homogeneous chemical reaction with thixotropic fluid through a circular tube has been studied under Taylor's approach. This study is noteworthy to understand the spreading of nutrients and drugs in cardiovascular system and to measure the cardiac output by means of Indicator Dilution Technique. We observed that the equivalent dispersion coefficient decreases as the reaction rate constant increases. The remarkable result is that the increase in the scalar structural parameter of materials or thixotropic parameter (\(\alpha_{1}\)) tends to decrease the equivalent dispersion coefficient (M) which is the new observation reported to the literature of biological system. During the drug delivery process, the nanoparticles (solute) should reach the sites of diseases by means of convective and diffusive transport within the microvessels in order to kill the diseased cells. It is, therefore, hoped that the present analytical study provides the useful information which, in turn, leads to understand in evaluating healing effectiveness and considers to be a significant subject in the modelling of nanoparticle drug delivery.