Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The longitudinal dispersion of a tracer in a tube has many applications in the fields of chemical engineering, environmental dynamics, and biomedical engineering. Taylor [6] was first to initiate the study on contaminant dispersion in a circular tube flow and showed that when a soluble substance is introduced into a fluid moving slowly and steadily through a circular tube it spreads out due to the combined action of molecular diffusion and the variation of velocity over the cross section. Aris [1] extended this by the method of moments including the effect of axial molecular diffusion. These theories are applicable only for large time after the introduction of solute and did not provide any idea about variation of the dispersion coefficient immediately after the injection of solute. Gill and Sankarasubramanian [3] developed a method to study the dispersion of a solute in a tube and this model is widely called as a generalized dispersion model, which holds for all times after the solute injection. Later this model is extended in the case of wall absorption by Sankarasubramanian and Gill [4]. They showed that the three effective transport coefficients namely absorption, convection, and dispersion coefficient are affected by interphase mass transfer. Dash et al. [2] gave a model to understand the dispersion process in a Casson fluid by considering the flowing fluid as steady and showed that the dispersion coefficient in the case of Cason fluid depends not only on time but also on yield stress. They also discussed the applications of their study in understanding the dispersion process in blood flows.

The existed models in the literature explain the effects of non-Newtonian rheology on dispersion of solute but not the other properties of blood flow. Blood flow in arteries and veins exhibits not only the non-Newtonian nature but also many other fluid dynamic complexities such as pulsatility, curvature, branching, and elasticity of the walls. The dispersion of any solute in blood flow is affected by these phenomena as well as the wall reaction mechanisms and the multiphase character of the blood. Hence, in this chapter, an attempt is made to study the dispersion process in a tube with wall absorption by considering the flow as unsteady and flowing fluid as Casson fluid. The purpose of this study is to explore the combined effects of yield stress, Womersley parameter, fluctuating pressure component, and absorption parameter on dispersion coefficient in a Casson fluid flowing through a tube.

2 Mathematical Formulation

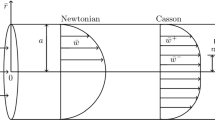
We considered axisymmetric, fully developed, pulsatile flow in a pipe of radius “a” by modeling the flow as a Casson fluid flow. We assumed that the rate of disappearance of solute at the tube wall is due to an irreversible first-order reaction catalyzed by the wall and is proportional to the solute concentration of the wall. The unsteady convective diffusion equation that describes the local concentration C of a solute as a function of axial distance z, radial distance r, and time t in the nondimensional form can be written as follows:

$$\begin{aligned} \frac{\partial C}{\partial t}+w(r,t) \frac{\partial C}{\partial z}= \left(\frac{1}{r}\frac{\partial}{\partial r} (r\frac{\partial}{\partial r})+\frac{1}{Pe^{2}} \frac{\partial^{2}}{\partial z^{2}}\right)C\end{aligned}$$
(1)

with the nondimensional variables as follows:

$$\begin{aligned} {\displaystyle{\displaystyle C=\frac{\overline{C}}{C_{0}},}\,w={\displaystyle \frac{\overline{w}}{w_{0}},}{\displaystyle \,r=\frac{\overline{r}}{a},}{\displaystyle \,z=\frac{D_{m}\overline{z}}{a^{2}w_{0}},}\,t={\displaystyle \frac{D_{m}\overline{t}}{a^{2}}},{\displaystyle Pe=\frac{aw_{0}}{D_{m}}}}\end{aligned}$$
(2)

where w is the nondimensional axial velocity of the fluid, D m is the coefficient of molecular diffusion (molecular diffusivity) which is assumed to be constant, C 0 is the reference concentration, w 0 is the characteristic velocity and Pe is the Peclet number. The variables with bar indicate the corresponding variables in dimensional form. For the slug input of solute length z s under consideration, the initial and boundary conditions in dimensionless form for the given model will be of the form:

$$\begin{aligned} C(0,z,r) =\left\{\begin{array}{ll} 1 & \mbox{if}|z|\le\frac{z_{s}}{2}\\ 0 & |z|>\frac{z_{s}}{2},\end{array}\right.\end{aligned}$$
(3)
$$\begin{aligned} {\displaystyle \frac{\partial C}{\partial r}\left(t,z,0\right)=0},\end{aligned}$$
(4)
$$\begin{aligned} {\displaystyle \frac{\partial C}{\partial r}\left(t,z,1\right)=-\beta C},\end{aligned}$$
(5)
$$\begin{aligned} {\displaystyle C\left(t,\infty,r\right)=0},\end{aligned}$$
(6)

where β is the wall absorption parameter.

The constitutive equation for a Casson fluid relating the stress \((\tau)\) and shear rate \(\left(\frac{\partial w}{\partial r}\right)\) in nondimensional form is given by

$$\begin{aligned} {\displaystyle \tau}^{\frac{1}{2}}=\tau_{y}^{\frac{1}{2}}+(-{\displaystyle \frac{\partial w}{\partial r})^{\frac{1}{2}}}\text {if} \tau\geq\tau_{y},\end{aligned}$$
(7)
$$\begin{aligned} \frac{\partial w}{\partial r}=0\,\text{if}\,\tau\leq\tau_{y},\end{aligned}$$
(8)

where \({\displaystyle \tau_{y}={\displaystyle \frac{\overline{\tau}_{y}}{\mu(w_{0}/a)}}}\)and \({\displaystyle \tau={\displaystyle \frac{\overline{\tau}}{\mu(w_{0}/a)}}}\)are the nondimensional yield stress and shear stress, respectively. The above relations correspond to vanishing of velocity gradient in the region where the shear stress is less than the yield stress which implies a plug flow for \(\tau\leq\tau_{y}\). The nondimensional velocity distribution for axisymmetric, fully developed, unsteady flow of a Casson fluid in tube is given by [5] as follows:

$$\begin{aligned} w = w_{-}= w_{p} = & {\displaystyle \frac{1}{2}p(t)}\left\{1-\frac{8}{3}r_{p}^{\frac{1}{2}}+2r_{p}-\frac{1}{3}r_{p}^{2}\right\} \nonumber\\ & -\alpha^{2}\frac{p^{\prime}(t)}{32}\left\{3-\frac{1144}{147}r_{p}^{\frac{1}{2}}+\frac{320}{63}r_{p}+ \frac{4}{3}r_{p}^{2}-\frac{16}{9}r_{p}^{\frac{5}{2}}+\frac{65}{441}r_{p}^{4}\right\}\nonumber\\ & \text{\,\,\,if } 0\leq r\leq r_{p},\end{aligned}$$
(9)
$$\begin{aligned} w = w_{+}= & \frac{1}{2}p(t)\left\{\left(1-r^{2}\right)-\frac{8}{3}r_{p}^{\frac{1}{2}} \left(1-r^{\frac{3}{2}}\right)+2r_{p}\left(1-r\right)\right\}\nonumber\\ &-\frac{\alpha^{2}}{2}p^{'}(t)\left\{\frac{3}{16}-\frac{r^{2}}{16} \left(4-r^{2}\right)\right. - \frac{r_{p}^{\frac{1}{2}}}{16} \left[\frac{1144}{147}-\frac{16}{3}\left(r^{2} +r^{\frac{3}{2}}\right)+\frac{424}{147}r^{\frac{7}{2}}\right]\nonumber\\ & + \frac{r_{p}}{16}\left.\left[\frac{320}{63}+\frac{128}{63}r^{3}-\frac{64}{9}r^{\frac{3}{2}} \right]\right\}\,\,\,\, \qquad\qquad if\,\, r_{p}\leq r\leq1,\end{aligned}$$
(10)

where \({\displaystyle r_{p}=\frac{\tau_{y}}{p(t)}}\) is the dimensionless plug radius and \({\displaystyle p(t)=1+e\cos\alpha^{2}Sct}\). Also the subscripts “-” and “+” corresponds the values for plug flow and shear flow, respectively and α represents the Womersley parameter, \({\displaystyle Sc=\frac{\nu}{D_{m}}}\) represents the Schmidt number, e is the amplitude of the pressure fluctuating component.

The solution of the convective diffusion Eq. (1) along with the given set of initial and boundary conditions (3–6) by following the analysis of [3] can be assumed as follows:

$$\begin{aligned} \sum_{i=0}^{\infty}f_{i}(t,r)\frac{\partial^{i}C_{m}}{\partial z^{i}},\end{aligned}$$
(11)

where the dimensionless mean concentration C m is defined as follows:

$$\begin{aligned} C_{m}=2\int_{0}^{1}Cr\, dr.\end{aligned}$$
(12)

Multiplying Eq. (1) by 2r and integrating with respect to r from 0 to 1, we get

$$\begin{aligned} \frac{\partial C_{m}}{\partial t}=\sum_{i=0}^{\infty}K_{i}(t)\frac{\partial^{i}C_{m}}{\partial z^{i}}\end{aligned}$$
(13)

with transport coefficients K i ’s as function of time t and

$$\begin{aligned} K_{i}(t)=\frac{\partial_{i2}}{Pe^{2}}-2\int_{0}^{1}f_{i-1}(t,r)w(t,r)r\, dr+2\frac{\partial f_{i}}{\partial r}(t,1),\, i=0,1,2,3\ldots,\end{aligned}$$
(14)

where \(\delta_{ij}\) denotes Kronecker delta and \(K_{0}(t), K_{1}(t)\), and \(K_{2}(t)\) are called as the absorption coefficient, convection coefficient, and dispersion coefficient, respectively. Also the following set of differential equations for f n is obtained as follows:

$$\begin{aligned} \frac{\partial f_{n}}{\partial t}=\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial f_{n}}{\partial r}\right)-w(t,r)f_{n-1}+\frac{1}{Pe^{2}}f_{n-2}-\sum_{i=0}^{n}K_{i}f_{n-i}\hspace{1cm}n=0,1,2,\ldots.\end{aligned}$$
(15)

The initial and boundary conditions are obtained from Eqs. (3–6) as follows:

$$\begin{aligned} f_{n}(0,r) & = \left\{\begin{array}{ll} 1 & \mbox{for}n=0\\ 0 & \mbox{for}n=1,2,3\ldots,\end{array}\right.\end{aligned}$$
(16)
$$\begin{aligned} \frac{\partial f_{n}}{\partial r}(t,0) & = 0,\end{aligned}$$
(17)
$$\begin{aligned} \frac{\partial f_{n}}{\partial r}(t,1) & = -\beta f_{n}(t,1).\end{aligned}$$
(18)

In order to solve the transport coefficient one has to solve \(f_{n}s\) simultaneously. These coupled equations are not conformable to an analytic solution, so a finite difference scheme is used to study the dispersion phenomena and is explained in Sect. 3. By neglecting terms involved \(K_{3},K_{4}\), etc., in Eq. (13) and solving we can get the expression for C m .

3 Numerical Scheme

Equation (15) for \(n=0,1,2\) for f n ’s are discretized in radial direction r and time t. The Crank–Nicolson method is applied for each time step. The finite difference scheme for derivatives and other terms are written at the mesh \((i,j),\) where \(0\leq j\leq m\) and \(0\leq i\leq n\). The resultant finite difference equations become linear simultaneous equations with a tridiagonal matrix in the form \(A_{i}f_{n}(i+1,j+1)+B_{i}f_{n}(i,j+1)+C_{i}f_{n}(i-1,j+1)=D_i\), where \(A_{i},B_{i},C_{i}\), and D i are the matrix elements. This tridiagonal matrices can be solved by using the Gauss Seidel method with the help of initial and boundary conditions.

4 Results and Discussion

The effect of yield stress, Womersley parameter, fluctuating pressure component, and absorption parameter on dispersion coefficient is analyzed. From Fig. 1a–d, it can be seen that due to the oscillatory flow the dispersion coefficient changes cyclically and initially increase with time. From Fig. 1b, c one can observe that fluctuations and the magnitude of K 2 increase with e and also as β increases the dispersion coefficient K 2 decreases. We also observed that as the yield stress increases the amplitude of the fluctuations of K 2 decreases.

5 Conclusions

The expression for dispersion coefficient is obtained for dispersion of a solute in Casson fluid flow with wall absorption by using the generalized dispersion model. The dispersion coefficient has been found to depend on yield stress, absorption parameter, frequency parameter, and the fluctuating component.

Fig. 1
figure 1

Variation of dispersion coefficient K 2with t when \(Pe=Sc=1000\) for different a \(\tau_{y}\) for \(e=0.1,\,\beta=1, \textrm{and} \,\alpha=0.1\) b e for \(\tau_{y}=0.02,\,\beta=1,\, \textrm{and} \alpha=0.1\) c β for \(\tau_{y}=0.05,\, e=0.2, \textrm{and}\,\alpha=0.1\) d α for \(\tau_{y}=0.05,\, e=0.2,\textrm{and}\,\beta=1\)

Full size image