Introduction

The dispersion of a solute in fluids has various applications in bio science particularly in the study of blood flow. Griffith [1] was the first to experimentally observe the motion of a coloured index along a capillary (circular tube). After his initial experimental work,the mathematical treatment of dispersion problem was initiated by Taylor [2, 3]. He has noticed that the solute diffused depends upon parameters such as tube radius, mean velocity and coefficient of molecular diffusion. Aris [4] has extended the results of Taylor and shown that the rate of growth of the solute distribution is proportional to the sum of the coefficient of molecular diffusion and Taylor’s coefficient of diffusion. His analysis pulled out the restriction given by Taylor. In view of understanding the basic concepts of physiological organisms, Wageningen [5] offered a novel generalized approach. The Taylor’s approach is used to study the dispersion process in non-Newtonian flows due to the fact that non-Newtonian fluids has vital applications in bio-fluids.

Fan and Hwang [6] have analysed the process of dispersion in a non-Newtonian fluid (power law fluid). Fan and Wang [7] have investigated the solute dispersion in the flow of Bingham plastic and Ellis fluids. By implementing Taylor’s methodology, Ghoshal [8] has obtained the analytic expression for effective dispersion coefficient by taking into account a Reiner-Philippoff model fluid and the development of dispersion in Eyring model fluid is studied by Shah and Cox [9]. Using Aris’ method, Prenosil et al. [10] have solved the problem of dispersion of a soluble matter in the power law fluid flow model. Assuming the rheology of non-Newtonian fluids (solvents) as power-law, Bingham plastic and Casson models, the performance of shear-augmented dispersion of solutes in solvents is carried out by adopting the dispersion theory developed by Taylor and Aris. Sharp [11] has noticed that the value of relative axial diffusivity is markedly influenced by the presence of yield stress in the solvent fluid. By means of the methodology developed by Sharp [11], the shear augmented dispersion of a solute in the flow of blood by supposing the rheological behaviour of blood as a Herschel–Bulkley fluid model has been investigated (Sankar et al. [12]). The effective axial diffusivity of a solute is found to be lower for the flow of blood between two parallel plates as compared to that of the flow in a tube. In the aforementioned works, flows are considered where the solute dispersed does not chemically react with the solvent.

Several investigations [13,14,15,16,17,18,19] have been done on dispersion in steady and non-steady flow of Newtonian fluids by for homogeneous and heterogeneous chemical reactions. Applying Taylor’s theory, the influence of homogeneous chemical reaction on the process of dispersion in non-Newtonian fluids such as power law, Bingham and Casson models has been analysed by Shukla et al. [20]. Singh et al. [21] have established a mathematical model to see the impact of the combined effects of the thickness of the flow region and the chemical reaction on dispersion coefficient in three types of non-Newtonian fluids (power law, Bingham plastic and Casson) flowing through a channel. Jaafar et al. [22] have studied the shear-augmented nature of dispersion in solvent (Herschel–Bulkley fluid) in a channel and in circular pipe. It is seen that the effective value of axial diffusivity and relative value of axial diffusivity are lower in flow through channel than the pipe. Chien [23] has experimentally revealed that blood shows noteworthy non-Newtonian properties in patients suffering from diseases like from hypertension, cerebrovascular diseases and renal ailment.

From the literature, it is understood that many investigators have extended the mathematical scheme developed by Taylor [2] and Aris [4] to different types of non-Newtonian fluids including Casson fluid. The three parameter constitutive equation of K-L fluid has been determined by Luo and Kuang [24] based on the data obtained from the experimental studies on human blood (Cokelet et al. [25], Cokelet [26], Bate [27] and Easthope and Brooks [28]). Ponakala and Sebastian [29] have investigated the unsteady dispersion of a solute in a tube by assuming the fluid as a Casson fluid. The axial dispersion of solute in a pulsatile fluid flow of Herschel–Bulkley fluid through a straight circular tube is investigated in [30] considering reaction at the tube wall. The K-L fluid model has been recommended in [24] which is an improvement of the Casson model. When the value of yield stress is treated as zero, the Casson model reduces to Newtonian fluid, but the K-L fluid model still narrates the shear thinning property. Hence, it is significant to note that K-L model fluid is of general type, and is a non-Newtonian fluid characterized by three parameters, the yield stress, and the parameters of K-L fluid. The rheological equation of K-L fluid has an additional parameter compared to Casson model; it is therefore anticipated that more relevant detailed information about the rheology of blood can be obtained from the K-L model. Under these circumstances, Casson and Herschel–Bulkley fluids characterizing blood may no longer be appropriate.

Zhang and Kuang [32] have found that the K-L model is in good agreement with hemorheological characteristics of human. The Lattice Boltzmann simulation has been applied to the K-L model by Asharafizaadeh and Bakhshaei [33]. Sriyab [34] has investigated the flow of blood in narrow arteries with bell-shaped mild stenosis treating blood as non-Newtonian fluid by using the K-L model. Bali and Gupta [35] have investigated a constitutive equation for blood carrying nanoparticles in a stenosed microvessel assuming blood as K-L fluid.

Keeping this in view, a modest effort has been made to explore the process of solute dispersion in the flow of blood along a tube with homogeneous biochemical reaction, considering blood as K-L model which has, to the best of authors knowledge, not carried out in the earlier studies. The significance of K-L fluid model with the first-order biochemical reaction on the equivalent dispersion coefficient is brought out in the present work.

The solute dispersion phenomenon has a lot of applications in the chemical industries and the medical field. The solute dispersion process in blood flow ultimately leads to measuring the transport of medicine, oxygen, and nutrients into the tissues. We want to emphasize that the current research could help with the design and development of artificial bio-processors and gain some insight into the drug transportation mechanism of the circulatory system.

Formulation of the Problem

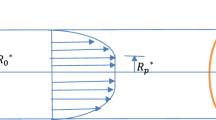
The dispersion of soluble pieces (solute) in the blood flow has been considered in the present model. Blood flow has been treated as one-dimensional steady, axi-symmetric, laminar and fully developed with a uniform pressure gradient through a circular tube of radius \(R_0^*\) (Fig. 1). The rheology of blood is taken as non-Newtonian fluid. We take the circular cylindrical polar coordinate system \((r^*, \theta ^*, z^*)\) , where \(r^*\) represents the radial coordinate, \(\theta ^*\) symbolizes the circumferential coordinate and \(z^*\) designates the axial coordinate. Bugliarello and Sevilla [31] have reported that the radial velocity is insignificantly small and can be ignored for a low Reynolds number flow through a microvessel (narrow artery). This type of flow condition is valid when we deal with the problem of investigating the dispersion of a drug into blood stream in small-diameter blood vessels (arterioles) and capillaries. It is assumed that the diluted solute having a small concentration diffuses and concurrently undertakes a first order irreversible chemical reaction in a non-Newtonian fluid under isothermal condition.

Fig. 1
figure 1

Geometry of an artery

Full size image

Governing Equation and Boundary Conditions

Based on the arguments made by Taylor [2, 3], the axial diffusion term in comparison with the radial diffusion term can be neglected. In view of this, the governing equation involving the concentration of the dispersing solute is given by [18, 20].

$$\begin{aligned} \frac{\partial C^*}{\partial t^*}+u^*\frac{\partial C^*}{\partial z^*} = \frac{D_m^*}{r^*}\frac{\partial }{\partial r^*}\left( r^*\frac{\partial C^*}{\partial r^*}\right) -\alpha ^*C^* \end{aligned}$$
(1)

where \(C^*\) denotes the concentration of a solute, \(t^*\) is the time, \(u^*\) indicates the axial velocity in the unidirectional flow, \(D_m^*\) symbolizes the constant coefficient of molecular diffusion and \(\alpha ^*\) denotes the constant rate of first order homogeneous chemical reaction.

By taking \(z_1^* (=z^*-\bar{u}^*t^*)\), Eq. (1) relative to a plane moving with the mean speed of the flow \((\bar{u}^*)\) can be written as

$$\begin{aligned} \frac{\partial C^*}{\partial t^*}+(u^*-\bar{u}^*)\frac{\partial C^*}{\partial z_1^*} = \frac{D_m^*}{r^*}\frac{\partial }{\partial r^*}\left( r^*\frac{\partial C^*}{\partial r^*}\right) -\alpha ^*C^* \end{aligned}$$
(2)

Assuming the validity of Taylor’s [2] limiting condition, Eq. (2) becomes

$$\begin{aligned} (u^*-\bar{u}^*)\frac{\partial C^*}{\partial z_1^*} = \frac{D_m^*}{r^*}\frac{\partial }{\partial r^*}\left( r^*\frac{\partial C^*}{\partial r^*}\right) -\alpha ^*C^* \end{aligned}$$
(3)

where \(\frac{\partial C^*}{\partial z_1^*}\) is independent of the radial distance \(r^*\).

Non-dimensional variables are defined as

$$\begin{aligned}&r = \frac{r^*}{R_0^*},\; u = \frac{u^*}{u_0^*},\; z_1 = \frac{z_1^*}{R_0^*},\; \bar{u} = \frac{\bar{u}^*}{u_0^*}, \; Pe = \frac{R_0^*u_0^*}{D_m^*}, \nonumber \\&\mu _l = \frac{\mu _l^*}{\mu ^*},\; t = \frac{D_m^*t^*}{(R_0^*)^2},\;\tau = \frac{\tau ^* R_0^*}{\mu ^*u_0^*},\; \tau _0 = \frac{\tau _0^* R_0^*}{\mu ^*u_0^*},\nonumber \\&p = \frac{p^*R_0^*}{\mu ^*u_0^*},\; \mu _k = \frac{\mu _k^*}{\mu ^*\left( \frac{u_0^*}{R_0^*}\right) ^{\frac{1}{2}}}. \end{aligned}$$
(4)

where \(u_0^*\) indicates the average velocity of Newtonian fluid, \(\mu ^*\) denotes the viscosity of Newtonian fluid and Pe is the Peclet number, \(p^*\) represents the pressure, \(\tau ^*\) is the shear stress, \(\tau _0^*\) signifies the yield stress, \(\mu _l^*\) and \(\mu _k^*\) are the K-L fluid parameters.(* denotes the corresponding dimensional quantity). With the help of Eq. (4), the governing equation (3) becomes

$$\begin{aligned} \frac{\partial ^2 C^*}{\partial r^2}+\frac{1}{r}\frac{\partial C^*}{\partial r}-Pe\alpha ^2C^* = Pe\bar{u}\frac{\partial C^*}{\partial z_1} f(r) \end{aligned}$$
(5)

where \(\alpha ^2 = \frac{\alpha ^* R_0^*}{u_0^*}\) and \(f(r) = \frac{u}{\bar{u}}-1\).

The boundary conditions are

$$\begin{aligned}&\frac{\partial C^*}{\partial r} = 0 \text { at } r = 0, \end{aligned}$$
(6)
$$\begin{aligned}&\frac{\partial C^*}{\partial r} = 0 \text { at } r = 1. \end{aligned}$$
(7)

The Rheological Equation of KL Fluid

The dimensional form of constitutive equation for a K-L fluid is written as [24]

$$\begin{aligned}&\tau ^* = \tau _0^*+\mu _k^*\left( -\frac{\partial u^*}{\partial r^*}\right) ^{\frac{1}{2}}+\mu _l^*\left( -\frac{\partial u^*}{\partial r^*}\right) ,\quad \text {if } \tau \ge \tau _0, \end{aligned}$$
(8)
$$\begin{aligned}&\frac{\partial u^*}{\partial r^*} = 0,\quad \text {if} \tau \le \tau _0. \end{aligned}$$
(9)

where \(\tau ^*\) is the shear stress, \(\tau _0^*\) is the yield stress, \(\mu _k^*\) and \(\mu _l^*\) are the K-L fluid parameters and \(\frac{\partial u^*}{\partial r^*}\) is the shear rate. Equations (8) and (9) may be, in dimensionless form, expressed as

$$\begin{aligned}&-\frac{\partial u}{\partial r} = \frac{\mu _k^2}{4\mu _l^2}+\frac{\mu _k^2-4\mu _l(\tau _0-\tau )}{4\mu _l^2}\nonumber \\&-\frac{\mu _k(\mu _k^2-4\mu _l(\tau _0-\tau ))^{\frac{1}{2}}}{2\mu _l^2},\quad \text {if} \tau \ge \tau _0, \end{aligned}$$
(10)
$$\begin{aligned}&\frac{\partial u}{\partial r} = 0, \quad \text {if} \tau \le \tau _0, \end{aligned}$$
(11)

Equation (11) relates to disappearing of velocity gradient in the domain where the shear stress \(\tau \) is less than the yield stress \(\tau _0\), which infers that a region of plug flow exists whenever \(\tau \le \tau _0\). For the present flow conditions stated above, the momentum equation for the fluid flow may be written as

$$\begin{aligned} -\frac{\partial p}{\partial z}-\frac{1}{r} \frac{\partial (r\tau )}{\partial r} = 0 \end{aligned}$$
(12)

where p is the pressure.

The dimensionless boundary conditions are

$$\begin{aligned} (i)\; \tau {\text { is finite at }}r = 0 {\text { and }} (ii)\; u = 0 {\text { at }} r = 1. \end{aligned}$$
(13)

Solution

Velocity Distribution for the Flow of K-L Fluid

Integrating Eq. (12) with respect to r and applying the boundary condition (i) of Eq. (13), we get

$$\begin{aligned} \tau = \frac{rp_0}{2} \end{aligned}$$
(14)

where \(p_0 = -\frac{dp}{dz}\). Using Eqs. (10), (11), (13) and (14), the velocity profile in the flow zone is expressed as

$$\begin{aligned} \begin{aligned} u&= \frac{\mu _k^2(1-r)}{2\mu _l^2}-\frac{\tau _0(1-r)}{\mu _l}+\frac{p(1-r^2)}{4\mu _l}\\&\quad -\frac{\mu _k\left\{ \left( \mu _k^2-4\tau _0\mu _l+2p\mu _l\right) ^{\frac{3}{2}}-\left( \mu _k^2-4\tau _0\mu _l+2pr \mu _l\right) ^{\frac{3}{2}}\right\} }{6p\mu _l^3}, \\&\quad R_p\le r \le 1 \end{aligned} \end{aligned}$$
(15)

Substituting \(r = R_p\) into equation (15) ,the velocity profile in the plug core region can be obtained as

$$\begin{aligned} \begin{aligned} u_p&= \frac{\mu _k^2(1-R_p)}{2\mu _l^2}-\frac{\tau _0(1-R_p)}{\mu _l}+\frac{p(1-R_p^2)}{4\mu _l}\\&\quad -\frac{\mu _k\left\{ \left( \mu _k^2-4\tau _0\mu _l+2p\mu _l\right) ^{\frac{3}{2}}-\left( \mu _k^2-4\tau _0\mu _l+2pR_p \mu _l\right) ^{\frac{3}{2}}\right\} }{6p\mu _l^3}, \\&\quad 0\le r \le R_P, \end{aligned} \end{aligned}$$
(16)

where \(R_p\) denotes the radius of plug core region and it is given by \(R_p = \frac{2\tau _0}{p}\). The average velocity of the fluid can be obtained from

$$\begin{aligned} \bar{u}= & {} 2\int _0^1 rudr \end{aligned}$$
(17)
$$\begin{aligned} \bar{u}= & {} \frac{p(1-R_p^4)}{8\mu _l}-\frac{\tau _0(1-R_p^3)}{3\mu _l}+\frac{\mu _k^2(1-R_p^2)}{6\mu _l^2}\nonumber \\&\quad +\frac{\mu _k\left\{ R_p^2\left( \mu _k^2-4\tau _0\mu _l+2pR_p\mu _l\right) ^{\frac{3}{2}}-\left( \mu _k^2-4\tau _0\mu _l+2p\mu _l\right) ^{\frac{3}{2}}\right\} }{6p\mu _l^3}\nonumber \\&\quad +\frac{\mu _k\left\{ \left( \mu _k^2-4\tau _0\mu _l+2p\mu _l\right) ^{\frac{5}{2}}-R_p\left( \mu _k^2-4\tau _0\mu _l+2pR_p\mu _l\right) ^{\frac{5}{2}}\right\} }{15p^2\mu _l^4}\nonumber \\&\quad +\frac{\mu _k\left\{ \left( \mu _k^2-4\tau _0\mu _l+2pR_p\mu _l\right) ^{\frac{7}{2}}-\left( \mu _k^2-4\tau _0\mu _l+2p\mu _l\right) ^{\frac{7}{2}}\right\} }{15p^3\mu _l^5} \end{aligned}$$
(18)

Dispersion in K-L Fluid

By incorporating the boundary conditions (6) and (7), the analytic expression for the concentration profile may be obtained as

$$\begin{aligned} C^*(r) = Pe \bar{u}c_1(r)\left( \frac{\partial C^*}{\partial z_1}\right) \end{aligned}$$
(19)

where

$$\begin{aligned} c_1(r)= & {} A_1I_0(\lambda r)\nonumber \\&\quad +\int _0^r y\left( I_0(\lambda r)K_0(\lambda y)-I_0(\lambda y)K_0(\lambda r)\right) f(y)dy \end{aligned}$$
(20)
$$\begin{aligned} A_1= & {} -\frac{1}{I_1(\lambda )}\int _0^1 y\left( I_1(\lambda )K_0(\lambda y)\right. \nonumber \\&\quad \left. +I_0(\lambda y)K_1(\lambda )\right) f(y)dy \end{aligned}$$
(21)

where \(\lambda = \alpha \left( \sqrt{Pe}\right) \), \(I_0, K_0\) and \(I_1, K_1\) are the first and second kind modified Bessel functions of zeroth and first order respectively. Here y denotes the variation of parameter technique variable.

The average solute flux \(\bar{Q}\) , over the tube on the move with the average speed of the flow can be written as

$$\begin{aligned} \bar{Q} = Pe \bar{u}^2\left( \frac{\partial C^*}{\partial z_1}\right) \int _0^1 2rc_1(r)f(r)dr \end{aligned}$$
(22)

Relating Eq. (22) with the Fick’s law of diffusion, i.e. \(J^* = -D\left( \frac{\partial C^*}{\partial z}\right) \) , we achieve that the soluble matter is dispersed relative to a plane in motion with the average speed of the flow via an effective dispersion coefficient, D given by

$$\begin{aligned} D = -2Pe \bar{u}^2M \end{aligned}$$
(23)

where

$$\begin{aligned} M = \int _0^1 c_1(r)f(r) r dr \end{aligned}$$
(24)

and M indicates the equivalent dispersion coefficient.

Results and Discussion

The present study throws some light on analysing the process of solute dispersion in the steady flow of K-L fluid in a circular tube under the impact of homogeneous chemical reaction. The nature of dispersion process is studied by considering Taylor’s approach. Integral involved in the solution of dispersion coefficient D has been evaluated numerically by Simpson’s 1/3 rule. The variation of equivalent dispersion coefficient (M) with respect to first order chemical reaction rate constant (\(\alpha \)), yield stress (\(\tau _0\)) and the parameters of K-L fluid (\(\mu _l\) and \(\mu _k\)) has been computed and shown graphically (Figs. 2, 3, 4).

Table 1 Range of controlling parameter in the present study
Full size table

A comparative study on the equivalent dispersion coefficient (M) for different rheological behaviour of solvents is made and depicted in Fig. 2. Figure 2 reveals that for a given rheology of solvent (fluid), the value of M decreases with an increase in \(\alpha \). The reason is that as \(\alpha \) increases, the rate of chemical reaction takes a predominant role, while the value of \(\alpha \) reduces, molecular diffusion of the fluid becomes dominant. As \(\alpha \) increases, the percentage decrease in the value of M becomes higher in Newtonian fluid (\(\tau _0 = 0.0, \mu _k = 0.0, \mu _l = 1.0\)) as compared to that of Bingham plastic fluid (\(\tau _0 = 0.02, \mu _k = 0.0, \mu _l = 1.0\)), K-L fluid (\(\mu _k = 0.1, \mu _l = 1.0\)), Casson fluid (\(\tau _0 = 0.02, \mu _k = 0.2828, \mu _l = 1.0\)) and K-L fluid (\(\tau _0 = 0.02, \mu _k = 0.4, \mu _l = 1.0\)) respectively. It is noteworthy that for a given \(\alpha \), Newtonian fluid (\(\tau _0 = 0.0, \mu _k = 0.0, \mu _l = 1.0\)) has a higher value of equivalent dispersion coefficient (M) when compared with respective other types of solvents taken in the present analysis. This is attributed to the fact that Newtonian fluid (\(\tau _0 = 0.0, \mu _k = 0.0, \mu _l = 1.0\)) may have the physical property of higher order molecular diffusion which, in turn, shows considerably a larger dispersion of the soluble matter.

Figure 3 is prepared to show how the equivalent dispersion coefficient (M) is influenced with respect to the yield stress (\(\tau _0\)) for various values of K-L parameters \(\mu _k\) and \(\mu _l\). It is found for given values of \(\mu _k\) and \(\mu _l\) that the value of M decreases as the parameter \(\tau _0\) increases. This is because the increase in \(\tau _0\) (or an increase in the non-Newtonian parameter) tends to decrease the distribution of fluid velocity. The magnitude of M is reduced with the increase in \(\mu _k\) (K-L fluid parameter) while it is enhanced with the other K-L fluid parameter (\(\mu _l\)) when the value of \(\tau _0\) is held fixed. As the magnitude of yield stress \(\tau _0\) increases, the rate of decrease of M is higher for a lower value of \(\mu _l\) while it becomes lower for a higher value of \(\mu _l\). By increasing or decreasing the value of \(\mu _k\), the percentage decrease of M with respect to the yield value is observed to be unaltered. The combined impacts of rheological behaviour of K-L fluid model and the first order homogeneous chemical reaction rate constant (\(\alpha \)) on the dispersion coefficient (M) is revealed in Fig. 4. It is observed that K-L fluid parameter (\(\mu _l\)) tends to increase the dispersion coefficient (M) when other rheological parameters of K-L fluid and \(\alpha \) are considered to be fixed. This is due to the fact that an increase in \(\mu _l\) enhances the value of the function f(r) defined in Eq. (5). Chemical reaction rate constant (\(\alpha \)) has a tendency to diminish the value of equivalent dispersion coefficient (M). The magnitude of M is boosted as the K-L fluid parameter (\(\mu _k\))decreases and the percentage decrease of M with \(\alpha \) is higher for lower value of \(\mu _k\). For a lower value of \(\alpha \), the decreasing trend of M with the increase in \(\mu _k\) or the increasing trend of M with the increase in \(\mu _l\) is predominant and these trends become somewhat less significant for a higher value of \(\alpha \). Figures 2 and 4 shows that increasing the first-order chemical reaction parameter slows down the dispersion process in the tube because a high number of molecules undergo the chemical reaction process.

Fig. 2
figure 2

The variation of equivalent dispersion coefficient (M) with first order chemical reaction rate constant (\(\alpha \)) for different fluids

Full size image
Fig. 3
figure 3

The variation of equivalent dispersion coefficient (M) with Yield Stress (\(\tau _0\)) for different values of \(\mu _k, \mu _l\) and \(\alpha = 0.1\)

Full size image
Fig. 4
figure 4

The variation of equivalent dispersion coefficient (M) with first order chemical reaction rate constant (\(\alpha \)) for different values of \(\mu _k, \mu _l\) and \(\tau _0 = 0.02\)

Full size image

Conclusion

Dispersion of solute in K-L fluid flow in a circular tube has been investigated by Taylor’s dispersion model. Assuming blood as K-L fluid, the present study brings out some important result of dispersion process and hemorheological characteristics of human blood. We observed a decrease in equivalent dispersion coefficient as the chemical reaction rate constant is increased. For the first time, it is observed that the one of the K-L fluid parameters (\(\mu _l\)) helps to increase the equivalent dispersion coefficient (M) which, in turn, implies that a huge amount of mass of the substance diffuses into a stream of blood flow. The K-L fluid model has provided the detailed information about the rheology of blood. Further, the study of dispersion enables to understand the distribution of nutrients in blood stream and several artificial devices. Thus, it is hoped that the present analytical study provides useful information to the hemodialysis and dispersion processes of drugs in the arterial blood flow of the circulatory system.