1 Introduction

In the COVID-19 pandemic, the whole world was apparently unprepared or did not pay attention well at the earlier stage after spreading in Wuhan, China. The disease caused by SARS-CoV-2 had a devastating impact across the world. On August 22, 2022, almost all countries and territories had victims, with a total of 605,199,562 reported cases with 6,486,276 deaths, and this is a global health emergency [1, 2].

The outbreak of severe acute respiratory syndrome (SARS) appeared in November 2002 in China. A newly emerged coronavirus was responsible for this outbreak which is known as SARS-CoV [3]. Middle East respiratory syndrome coronavirus (MERS-CoV) took place in Saudi Arabia in 2012 where dromedary camels were thought to be the intermediate source for the transmission of the virus [4]. As a continuation, the virus SARS-CoV-2 was related to the coronavirus responsible for the SARS outbreak of 2003, and the transmission of the virus was also zoonotic [5]. In March 13, 2020, the World Health Organization considered Europe as a hotspot of the 2019–2020 coronavirus pandemic, and by April 24 (2020), the maximum part of the globe was affected by the outbreak [1, 2]. The daily reported cases were being doubled over periods of 2 to 4 days by countries across Europe, North America, and Asia [6], and specially the phenomenon drew a lot of attention for these zones.

Since the world is dealing with a highly contagious disease without proper medication, right now the only effective way for us to protect ourselves is prevention. Social and physical distancing, partial lockdown, and testing are some measures prescribed by WHO to control the outbreak. Data analysis and mathematical modeling are one of the core components to study these undertaken policies for the best outcome. In mathematical modeling of the COVID-19 outbreak, some recent studies provided estimation of the basic reproduction number (\(R_0\)), disease dynamics, models fit to COVID data, identification of important model parameters, and control strategies to combat the infection [7,8,9,10,11, 13, 14, 22]. In [7], the authors studied COVID-19 dynamics in Wuhan, China, for the first wave. In [8], Chowdhury et al. showed the effect of quarantine and social distancing policy on COVID-19 transmission in developing or under poverty-level countries. An SAIQHR model has been considered to study COVID-19 dynamics in India [9]. A study for COVID-19 pandemic with intervention strategies is shown in [10]. A COVID-19 model was developed to describe the outbreak of COVID-19 in India with seven compartments which analyzed both theoretically and numerically by evaluating the equilibrium points and their stability analysis [11]. The dynamics of the SEIR model and estimation of the reproduction number of COVID-19 in Italy were studied in [12]. An ODE compartmental model with saturated treatment due to the limited medical facilities such as lack of hospital beds and oxygen cylinder, in Italy, was studied to drag down the spread of COVID-19, where the prescribed model determines the scenario of COVID-19 handled by maintaining a lockdown [13]. A study for COVID-19 transmission and its control in Hong Kong is discussed in [14].

In this paper, we have studied the scenario of Spain from 24 February 2020 to 28 April 2020, considering a six-compartmental model with saturated treatment due to limited medical facilities in Spain. The study presents an analysis of various control mechanisms using a mathematical model and abridged data fitting based on the ongoing viral epidemic. The key objective of this study is as follows: we will work with real-life available discrete data of Spain to understand the dynamics of COVID-19 outbreak and possible preventive measures to control the infection. The main novelties in this study are

  1. 1.

    Analytical and theoretical results are established and presented in terms of reproductive ratio, \(R_0\). We have obtained the stable DFE for \(R_0<1\) and stable endemic solution for \(R_0>1\).

  2. 2.

    We have established the results for backward bifurcation at \(R_0 = 1\) with some other conditions.

  3. 3.

    We have fitted the proposed model with real reported data of COVID-19 in Spain from 24 February, 2020, to 28 April, 2020.

  4. 4.

    Sensitivity analysis has been performed to find out most effective model parameters which have more impact on spreading and controlling the infection.

  5. 5.

    The basic reproduction numbers for the actual epidemic, \(R_0\), and time evolution outbreak, R(t), are calculated and their respective results are established.

  6. 6.

    Using optimal control theory, it concludes that social distancing is highly effective for controlling the disease.

  7. 7.

    Besides data analysis, the proposed model shows that the human population can control and protect the spread of infectious diseases by creating social isolation, hospitalization, and physical distancing.

The paper is organized as follows: The mathematical model is formulated in Section 2. Positivity and boundedness of solutions are discussed in Section 3. Stability analysis and bifurcation analysis are prescribed in Section 4. Parameter estimation, model validation, effective parameter, and the estimation of \(R_0\) are discussed in Section 5. We have studied the optimal control theory for COVID-19 in Section 6. Finally, Section 7 outlines the summary and discussion of the results.

In the following section, we will discuss our mathematical model and formulation of the model elaborately.

2 Model Formulation

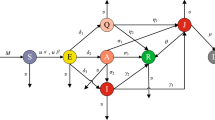
Scientifically, it is proven and well established that mathematical and computational models can help in understanding biological scenarios and can predict epidemiological aspects. In the proposed model, let the total population be divided into six compartments: these are the susceptible population (S), exposed population (E), asymptomatic population (A), quarantined population (Q), infectious population (I), and recovered population (R). We assume that the birth rate of susceptible human is constant. The disease COVID-19 spreads mainly from A & I compartments and the rate of incidence is of the form \((\alpha A+\beta I)S\). Asymptomatic infected humans become infectious at a rate \(\delta _1\) as they have no symptoms therefore they can transmit the disease with other people easily. Also, quarantined persons become infectious at a rate \(\mu _1\) as they can infect the health staff and other persons who stay in the same quarantine center. Since a large number of persons is infected by this disease in a very short span of time but the number of hospitals is limited, therefore due to limited medical facility, we consider the saturated treatment which is of the form \(\frac{aI}{1+bI}\). The flow diagram of the proposed model is given in Fig. 1 and the corresponding mathematical equations are given in (2.1).

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dS}{dt}=&{} \Lambda -(\alpha A+\beta I)S - \epsilon S \\ \frac{dE}{dt}=&{} (\alpha A+\beta I)S-(\gamma _1+\gamma _2+\gamma _3+\gamma _4+\epsilon ) E \\ \frac{dA}{dt}=&{} \gamma _1E-(\delta _1+\delta _2+\epsilon )A \\ \frac{dQ}{dt}=&{} \gamma _2E-(\mu _1+\mu _2+\epsilon )Q \\ \frac{dI}{dt}=&{} \delta _1 A+\gamma _3E+\mu _1Q-( \epsilon +d +\sigma _1 )I-\frac{aI}{1+bI} \\ \frac{dR}{dt}=&{} \gamma _4 E+\delta _2 A+\mu _2 Q +\sigma _1I -\epsilon R+\frac{aI}{1+bI} \end{array}\right. } \end{aligned}$$
(2.1)

with the initial conditions \(S(0)>0\), \(E(0)\ge 0\), \(A(0)\ge 0\), \(Q(0)\ge 0\), \(I(0)> 0\), and \(R(0)\ge 0\), where the interpretation of parameters is presented in Table 1.

Table 1 Model parameters and their descriptions
Full size table
Fig. 1
figure 1

Flow diagram of the proposed model

Full size image

In the next section, we shall establish the positivity and boundedness of solutions of (2.1). Positivity of the solution in biological model is most important because it establishes the non-negativity of the solution curve, i.e., non-negativity of the considered compartments.

3 Positivity and Boundedness of Solutions

We consider the first equation of (2.1) and multiply it by integrating factor \(\exp (\alpha A(t)+\beta I(t) + \epsilon )\), then integrating and using the initial condition, we get

$$\begin{aligned} S(t)=\exp (-(\alpha A(t)+\beta I(t) + \epsilon ))\left\{ S(0)+\Lambda \int _{t_0}^t \exp (\alpha A(u)+\beta I(u) + \epsilon )du\right\} . \end{aligned}$$

It is obvious from the above expression that \(S(t)\ge 0\). Using similar arguments, it can be easily shown that other variables are also non-negative.

To prove the boundedness of the solutions, we add the equations in (2.1) and using the notation for total population, \(N(t)=S(t)+E(t)+A(t)+Q(t)+I(t)+R(t)\), we have

$$\begin{aligned} \begin{aligned} \frac{dN}{dt}&=\Lambda -\epsilon N-dI\\&\le \Lambda -\epsilon N. \end{aligned} \end{aligned}$$

Integrating and using the initial conditions and taking \(\limsup\) as \(t\rightarrow \infty ,\) we get

$$\limsup \limits _{t\rightarrow \infty } N(t)\le \frac{\Lambda }{\epsilon }.$$

Thus, we can summarize the above results in the following theorem:

Theorem 1

All the solutions are feasible and the set

\(\Omega =\left\{ (S,E,A,Q,I,R)\in \mathbb {R}^6_{+}:S+E+A+Q+I+R\le \frac{\Lambda }{\epsilon } \right\}\) is a positively invariant set for the system (2.1).

In the next section, we shall study the stability and bifurcation analyses of the proposed model.

4 Stability and Bifurcation Analyses

In this section, we first find the disease-free equilibrium point (DFE) and then using the next-generation matrix approach, the basic reproduction number will be found. The stability of the equilibrium points will be discussed in terms of the basic reproductive number. The backward bifurcation will be discussed also.

4.1 Basic Reproduction Number, DFE, and EEP

The basic reproduction number is denoted by \(R_0\) and is defined as the expected number of secondary infections that a single infected individual generates [15, 16]. In the epidemic system, it has great importance as it is the indicator of persistence or eradication of disease. Using the next-generation matrix [16, 17], the basic reproduction number of (2.1) has been found here. Since the DFE is \(E_0\left( \frac{\Lambda }{\epsilon },0,0,0,0,0\right)\), hence the basic reproduction number can be found through the following analytical approach.

Let \(\mathscr {F}=\left( \begin{array}{c} S(A\alpha +I\beta ) \\ 0 \\ 0\\ 0 \end{array} \right)\) represent the vector of rate of new infections and \(\mathscr {V}=\left( \begin{array}{c} D_0 E \\ A D_1-\gamma _1E \\ D_2Q-E\gamma _2 \\ -\gamma _{3} E-\delta _1 A-\mu _1 Q+D_3 J+\frac{aI}{1+bI} \end{array} \right)\) denote the vector of remaining transitional terms.

Let us define \(F= \frac{\partial \mathscr {F} }{\partial x_j }(E_0)\) and \(V= \frac{\partial \mathscr {V} }{\partial x_j }(E_0)\), where \(x_j\) represents the infected compartment. Then, the next-generation matrix is \(FV^{-1}\) and the spectral radius of \(FV^{-1}\) is the basic reproduction number \(R_0\), which is given below

$$\begin{aligned} R_0=\frac{\Lambda \alpha \gamma _1}{\epsilon D_0D_1}+\frac{\Lambda \beta (D_1D_2\gamma _3+D_1\gamma _2\mu _1+D_2\delta _1\gamma _1)}{\epsilon D_0D_1D_2(D_3+a)}, \end{aligned}$$

where \(D_0=\epsilon +\gamma _1+\gamma _2+\gamma _3+\gamma _4\), \(D_1=\delta _1+\delta _2+\epsilon\), \(D_2=\mu _1+\mu _2+\epsilon\), \(D_3=d+\epsilon +\sigma _1\).

Let \(E^*(S^*,E^*,A^*,Q^*,I^*,R^*)\) be the endemic equilibrium point (EEP) of the considered system. Then, it satisfies the steady-state condition for the system (2.1). Solving the steady-state equations, we obtain \(I^*=\frac{A^*(A^*D_0D_1\alpha +D_0D_1\epsilon -\alpha \gamma _1\Lambda )}{\beta (\gamma _1\Lambda -A^* D_0D_1)}\), \(A^*=\frac{\gamma _1E^*}{D_1}\), \(S^*=\frac{\Lambda }{A^*\alpha +I^*\beta +\epsilon }\), \(Q^*=\frac{\gamma _2E^*}{D_2}\), \(\epsilon R^*=\gamma _{4} E^*+\delta _2 A^*+\mu _2 Q^*+\frac{aI^*}{1+bI^*}+\sigma _1I^*\) and \(E^*\) satisfies the equation

$$\begin{aligned} C_0x^3+C_1x^2+C_2x+C_3=0, \end{aligned}$$
(4.1)

where

$$\begin{aligned} C_0&= \gamma _1 (\beta (D_2 \gamma _4 + \gamma _2 \mu _2) D_1+D_2 \gamma _1(-\alpha \sigma _1+ \beta \delta _2)) D_0^2 \alpha b, \\ C_1&=\beta D_0^2 (b \epsilon - \beta ) (D_2 \gamma _4+ \gamma _2 \mu _2) D_1^2+(-D_2 \delta _2 \beta ^2 D_0\\&+ (D_2(\delta _2 b \epsilon + \alpha (\sigma _1+a)) D_0- 2 b \alpha \Lambda \\&(D_2 \gamma _4+ \gamma _2 \mu _2)) \beta - 2 D_2 \sigma _1 b \alpha D_0 \epsilon ) \gamma _1 D_1 D_0 \\&- 2 D_0 D_2 \gamma _1^2 b \alpha \Lambda (-\alpha \sigma _1+ \beta \delta _2), \\ C_2&=-(-2 \Lambda (D_2 \gamma _4 + \gamma _2 \mu _2) \beta ^2 + \epsilon (-D_2 (\sigma _1+a) D_0 \\&+b \Lambda (D_2 \gamma _4 + \gamma _2 \mu _2)) \beta + D_2 \sigma _1 b D_0 \epsilon ^2) D_0 D_1^2\\&-(-2 D_2 \delta _2 \beta ^2 D_0 +(D_2 (\delta _2 b \epsilon +2 \alpha (\sigma _1+a)) D_0\\&- b \alpha \Lambda (D_2 \gamma _4+ \gamma _2 \mu _2)) \beta -2 D_2 \sigma _1 b \alpha D_0 \epsilon ) \Lambda \gamma _1 D_1\\&+D_2 \gamma _1^2 b \alpha \Lambda ^2 (-\alpha \sigma _1+ \beta \delta _2), \\ C_3&= D_0D_1^2D_2\beta \epsilon \Lambda (D_3+a)(1-R_0). \end{aligned}$$

It is clear from the expressions of coefficients the equation (4.1) that it may have either two positive roots or no positive root if \(R_0<1\). For \(R_0>1\), the number of positive roots is one or three if the positivity condition of \(I^*\) is satisfied. Thus, when \(R_0<1\), the model (2.1) has at most two endemic equilibrium points and for \(R_0>1\) the number of endemic equilibrium points is three or one.

4.2 Stability of Disease-Free Equilibrium State (\(E_0\))

To eradicate the disease from the system, the stability of the DFE is essential.

Theorem 2

The DFE will be locally asymptotically stable if \(R_0<1\) and unstable if \(R_0>1\).

Proof

The Jacobian matrix corresponding to the system (2.1) at DFE point \(E_0(\frac{\Lambda }{\epsilon }, 0, 0, 0, 0, 0)\) is

$$\begin{aligned} J(E_0)=\left( \begin{array}{cccccc} -\epsilon &{}0 &{}-\frac{\Lambda \alpha }{\epsilon }&{} 0 &{}-\frac{\Lambda \beta }{\epsilon } &{}0 \\ 0 &{}-D_0 &{}\frac{\Lambda \alpha }{\epsilon }&{}0&{}\frac{\Lambda \beta }{\epsilon }&{} 0 \\ 0 &{} \gamma _1 &{} -D_1&{}0&{}0&{}0 \\ 0&{}\gamma _2&{}0&{}-D_2&{}0&{}0\\ 0&{}\gamma _3&{}\delta _1&{}\mu _1&{}-D_3-a&{}0\\ 0&{}\gamma _4&{}\delta _2&{}\mu _2&{}a+\sigma _1&{}-\epsilon \\ \end{array}\right) . \end{aligned}$$

The eigenvalues of the Jacobian matrix \(J(E_0)\) are \(-\epsilon ,-\epsilon ,\lambda _{1},\lambda _{2},\lambda _{3},\lambda _{4}\), where \(\lambda _{i} (i=1-4)\) are the roots of the following equation:

$$\begin{aligned} P(\lambda )&\equiv \frac{\Lambda \alpha \gamma _{1}}{\epsilon (D_{0}+\lambda )(D_{1}+\lambda )}+\frac{\Lambda \beta \gamma _{3}}{\epsilon (D_{0}+\lambda )(D_{3}+a+\lambda )}\\&+\frac{\Lambda \beta \gamma _{2} \mu _{1}}{\epsilon (D_{0}+\lambda )(D_{2}+\lambda )(D_{3}+a+\lambda )} \\&+\frac{\Lambda \beta \gamma _{1} \delta _{1}}{\epsilon (D_{0}+\lambda )(D_{1}+\lambda )(D_{3}+a+\lambda )}-1=0 . \end{aligned}$$

Thus, \(P(0)=R_{0}-1\). Now, we shall discuss the following two cases.

Case I: Suppose \(R_{0}>1\). Then \(P(0)>0\). Again, \(\lim \limits _{\lambda \rightarrow \infty } P(\lambda )=-1\). Here \(P(\lambda )\) is a continuous function of \(\lambda\) and so by applying Bolzano theorem on continuous function, we have \(P(\lambda _{k})=0\) for some \(\lambda _{k}>0\). Thus, at least one eigenvalue of the Jacobian matrix \(J(E_0)\) must be positive and so the DFE, \(E_{0}\), is unstable.

Case II: Suppose \(R_{0}<1\) which yields \(P(0)<0\).

If possible, let us assume that \(P(\lambda )=0\) has at least one root of the form \(x+iy\), where \(x\ge 0\) and \(x,y\in \mathbb {R}\). Then \(P(x+iy)=0\).

Again,

$$\begin{aligned}&\vert P(x+iy)+1 \vert \\&\le \frac{\Lambda \alpha \gamma _{1}}{\epsilon \vert D_{0}+\lambda \vert \vert D_{1}+\lambda \vert }+\frac{\Lambda \beta \gamma _{3}}{\epsilon \vert D_{0}+\lambda \vert \vert D_{3}+a+\lambda \vert }\\&+\frac{\Lambda \beta \gamma _{2} \mu _{1}}{\epsilon \vert D_{0}+\lambda \vert \vert D_{2}+\lambda \vert \vert D_{3}+a+\lambda \vert }\\ {}&+\frac{\Lambda \beta \gamma _{1} \delta _{1}}{\epsilon \vert D_{0}+\lambda \vert \vert D_{1}+\lambda \vert \vert D_{3}+a+\lambda \vert } \le \frac{\Lambda \alpha \gamma _{1}}{\epsilon (D_{0}+x)(D_{1}+x)}\\&+\frac{\Lambda \beta \gamma _{3}}{\epsilon (D_{0}+x)(D_{3}+a+x)}+\frac{\Lambda \beta \gamma _{2} \mu _{1}}{\epsilon (D_{0}+x)(D_{2}+x)(D_{3}+a+x)}\\ {}&+\frac{\Lambda \beta \gamma _{1} \delta _{1}}{\epsilon (D_{0}+x)(D_{1}+x)(D_{3}+a+x)} \\&\le \frac{\Lambda \alpha \gamma _{1}}{\epsilon D_{0} D_{1}}+\frac{\Lambda \beta \gamma _{3}}{\epsilon D_{0} (D_{3}+a)}+\frac{\Lambda \beta \gamma _{2} \mu _{1}}{\epsilon D_{0} D_{2}(D_{3}+a)}\\&+\frac{\Lambda \beta \gamma _{1} \delta _{1}}{\epsilon D_{0} D_{1}(D_{3}+a)} = R_{0} < 1, \end{aligned}$$

which implies \(1<1\), clearly a contradiction. Hence, all the roots of the equation \(P(\lambda )=0\) have the form \(x+iy\), where \(x < 0\) and \(x,y\in \mathbb {R}\). Thus, in this case, the DFE is locally asymptotically stable.

Hence, the theorem is proved.

4.3 Backward Bifurcation

In this section, we shall investigate the existence of backward bifurcation of the considered COVID-19 model. Biologically, this type of bifurcation is most important because usually the disease eradication happens when \(R_0<1\) but in this situation there exists another stable endemic equilibrium point for \(R_0<1\) and so eradication of the disease depends not only on the value of basic reproduction number but also on the initial number of infection level. When \(R_0=1\), i.e.,

$$\begin{aligned} \alpha =\frac{D_0D_1D_2D_3\epsilon +D_0D_1D_2 a \epsilon -D_1D_2\beta \gamma _3\Lambda -D_1\beta \gamma _2\Lambda \mu _1-D_2\beta \delta _1\gamma _1\Lambda }{D_2(D_3+a)\Lambda \gamma _1} \equiv \alpha ^{[BB]}, \end{aligned}$$

then one of the eigenvalues of the Jacobian matrix corresponding to the system (2.1) at DFE is 0. Using the theorem by Castillo-Chavez and Song [15, 17, 18], we shall establish the existence of backward bifurcation of the system (2.1).

Theorem 3

Suppose \(c_{3}>0\) and \(c_{1} c_{2} > c_{3}\). Then the system (2.1) undergoes the backward bifurcation at \(R_0=1\) with respect to the parameter \(\alpha\) if \(\phi >0\), where \(c_{1}, c_{2}, c_{3}\) and \(\phi\) are defined in the text.

Proof

First we set \(x_1=S,x_2=E,x_3=A,x_4=Q,x_5=I\) and \(x_6=R\), then the system (2.1) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dx_1}{dt}=&{} \Lambda -(\alpha x_3+\beta x_5)x_1 - \epsilon x_1 \equiv f_1 \\ \frac{dx_2}{dt}=&{} (\alpha x_3+\beta x_5)x_1-(\gamma _1+\gamma _2+\gamma _3+\gamma _4+\epsilon ) x_2 \equiv f_2 \\ \frac{dx_3}{dt}=&{} \gamma _1x_2-(\delta _1+\delta _2+\epsilon )x_3 \equiv f_3 \\ \frac{dx_4}{dt}=&{} \gamma _2x_2-(\mu _1+\mu _2+\epsilon )x_4 \equiv f_4 \\ \frac{dx_5}{dt}=&{} \delta _1 x_3+\gamma _3x_2+\mu _1x_4-( \epsilon +d +\sigma _1 )x_5-\frac{ax_5}{1+bx_5} \equiv f_5 \\ \frac{dx_6}{dt}=&{} \gamma _4 x_2+\delta _2 x_3+\mu _2 x_4 +\sigma _1x_5 -\epsilon x_6+\frac{ax_5}{1+bx_5} \equiv f_6 \end{array}\right. } \end{aligned}$$
(4.2)

At the DFE \(E_0\), the Jacobian matrix \(J(E_0)|_{\alpha =\alpha ^{[BB]}}\) has the eigenvalues \(-\epsilon , -\epsilon\), and the other three are the roots of the following cubic:

$$\begin{aligned} \lambda ^4+ c_1 \lambda ^{3}+c_{2} \lambda ^{2}+c_{3} \lambda +c_{4}=0, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} c_{1}&=D_{0}+D_{1}+D_{2}+D_{3}+a ,\\ c_{2}&= \frac{(((a+ D_0 +D_2+ D_3) D_1 +(a+ D_0+ D_3) D_2 + D_0 (a + D_3)) \epsilon - \Lambda (\alpha \gamma _1+ \beta \gamma _3)}{\epsilon },\\ c_{3}&=\frac{((a+ D_0 +D_3) D_1 +D_0 (a+ D_3)) D_2 +D_0 D_1 (a+D_3)) \epsilon - \Lambda ((\alpha \gamma _1 +\beta \gamma _3) D_2+ \gamma _3 \beta D_1}{\epsilon } \\ {}&\frac{+(a \alpha + \alpha D_3+ \beta \delta _1) \gamma _1+ \mu _1 \gamma _2 \beta )}{\epsilon }, \\ c_4&= \frac{((\gamma _3 \beta D_1 +(\delta _1 \beta + \alpha (a+D_3)) \gamma _1) \Lambda - D_0 \epsilon D_1 (a+D_3)) D_2+ \Lambda \beta D_1 \gamma _2 \mu _1}{\epsilon }. \end{aligned} \end{aligned}$$

It is obvious that \(c_{1}>0\) and \(R_{0}=1\) imply \(c_{2}>0\). Hence, by the given conditions, we can conclude that the three eigenvalues have negative real parts. Thus, we can apply the theorem by Castillo-Chavez and Song to determine the direction of the bifurcation. Let W and V be the right and left eigenvectors of \(J(E_0)|_{\alpha =\alpha ^{[BB]}}\) corresponding to the zero eigenvalue then \(W=(w_1,w_2,w_3,w_4,w_5,w_6)^T\) where

$$\begin{aligned} \begin{aligned}&w_1=-\frac{D_0}{\epsilon },w_2=1,w_3=\frac{\gamma _1}{D_1},w_4=\frac{\gamma _2}{D_2},\\&w_5=\frac{\gamma _3w_2+\delta _1w_3+\mu _1w_4}{D_3+a},\\&w_6=\frac{\gamma _4w_2+\delta _2w_3+\mu _2w_4+(a+\sigma _1)w_5}{\epsilon } \ \text {and} \\& V=(v_1,v_2,v_3,v_4,v_5,v_6) \ \text {where}\\&v_1=0,v_2=\frac{(D_3+a)D_2 \epsilon }{\Lambda \beta },v_3=\frac{D_2 (D_3+a+\delta _1)}{D_1},\\&v_4=\mu _1,v_5=D_2,v_6=0. \end{aligned} \end{aligned}$$

Now, the coefficient

$$\begin{aligned}&\phi =\sum _{k,i,j=1}^{6}v_k w_iw_j\frac{\partial ^2f_k}{\partial x_i \partial x_j} \\ {}&= \frac{2D_{2}ab}{(D_{3}+a)^{2}} \left( \gamma _{3}+\frac{\delta _{1} \gamma _{1}}{D_{1}}+\frac{\mu _{1} \gamma _{2}}{D_{2}}\right) ^{2}\\&-\frac{2(D_{3}+a)D_{0} D_{2}}{\Lambda \beta } \left\{ \frac{\alpha ^{[BB]} \gamma _{1}}{D_{1}}+\frac{\beta }{D_{3}+a} (\gamma _{3}+\frac{\delta _{1} \gamma _{1}}{D_{1}}+\frac{\mu _{1} \gamma _{2}}{D_{2}}) \right\} \end{aligned}$$

and the coefficient

$$\begin{aligned} \psi = \sum _{k,i=1}^{6}v_k w_i\frac{\partial ^2f_k}{\partial x_i \partial \alpha } = \frac{(D_{3}+a)D_{2} \gamma _{1}}{D_{1} \beta }. \end{aligned}$$

Since the coefficient \(\psi\) is obviously a positive number, hence the system (2.1) exhibits the backward bifurcation if \(\phi >0\). Hence, the theorem is proved.

Fig. 2
figure 2

Backward bifurcation diagram for the parametric values \(\beta =0.52, \gamma _1 = 7.81, \gamma _2 = 7.32, \gamma _3 = 7.18, \gamma _4 =0.5, \epsilon =0.25, \Lambda = 1.2, \delta _2 =0.6, \delta _3 =0.9, a = 5.1, b = 65.1, d = 0.15, \sigma _1 =0.5, \sigma _2 =0.5, \mu _1 = 1.32, \mu _2 =0.15\) with different values of \(\alpha\) (considering \(R_0\) as a function of \(\alpha\)). The red and blue lines, respectively, denote the lines of unstable and stable equilibrium points

Full size image

It is clear from Fig. 2 that if we vary the transmission rate of infection (\(\alpha\)) from the asymptomatic class, then the system generates two endemic equilibrium points for \(R_0^{*}<R_0<1\), where \(R_0^{*}\) is some positive quantity, among them one with the lower infection level is unstable along with the stable DFE and the other with the higher infection level is stable. This type of phenomenon occurs due to the presence of saturated treatment. In [13, 14, 18], we see that the infected being delayed for treatment is one of the origins that lead to the backward bifurcation. But the consideration of linear treatment function does not ensure the phenomenon of backward bifurcation [11, 19, 20].

4.4 Stability of Endemic Equilibrium State

The Jacobian matrix at the endemic equilibrium point \(E^*\) is given by

$$\begin{aligned} J(E^*)=\left( \begin{array}{cccccc} - \alpha A^*-\beta I^*-\epsilon &{}0 &{}-\alpha S^*&{} 0 &{}-\beta S^* &{}0 \\ \alpha A^*+\beta I^* &{}-D_0 &{}\alpha S^*&{}0&{}\beta S^*&{} 0 \\ 0&{}\gamma _1&{} -D_1&{}0&{}0&{}0 \\ 0&{}\gamma _2&{}0&{}-D_2&{}0&{}0 \\ 0&{}\gamma _3&{}\delta _1&{}\mu _1&{}-D_3-\frac{a}{1+bI^*}+\frac{abI^*}{(1+bI^*)^2} &{}0 \\ 0&{}\gamma _4&{}\delta _2&{}\mu _2&{}\frac{a}{1+bI^*}-\frac{abI^*}{(1+bI^*)^2}+\sigma _1&{}-\epsilon \\ \end{array}\right) . \end{aligned}$$

One characteristic root of the above matrix is \(-\epsilon\) and the other five satisfy the following equation:

$$\begin{aligned} x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5=0. \end{aligned}$$
(4.3)

Here

$$\begin{aligned} a_1&=(D_5+D_1+D_2+D_3+P+\epsilon +D_0),\\ a_2&=(P+D_5+ D_0+ \epsilon + D_2+ D_3) D_1+(P+ D_5 +D_0\\&+ \epsilon + D_3) D_2+(P+ D_5+ \epsilon + D_3) D_0\\&+(D_3+P)( D_5+ \epsilon ) -S^*(\alpha \gamma _1+ \beta \gamma _3),\\ a_3&=((P+D_5+D_0+ \epsilon + D_3) D_1+(P+D_5+ \epsilon +D_3) D_0\\&+(D_3+P)(\epsilon + D_5) \\ {}&-S^* (\alpha \gamma _1+ \beta \gamma _3)) D_2+((P+D_5+\epsilon +D_3)D_0\\&+(D_3+P)(\epsilon + D_5)\epsilon - \gamma _3 \beta S^* )D_1\\&+(D_5+ \epsilon )(P+D_3) D_0-((\alpha \gamma _1 + \beta \gamma _3) \epsilon + \gamma _1 \alpha ( D_3 +P)\\&+ \beta (\delta _1 \gamma _1+ \gamma _2 \mu _1)) S^*,\\ a_4&=(((P+D_0+D_3) \epsilon + (P+D_5+D_3)D_0- \gamma _3 \beta S^*\\&+ D_5 (P+D_3))D_1+((D_3+P)D_0\\&-S^*(\alpha \gamma _1+ \beta \gamma _3)) \epsilon + D_5(P+D_3)D_0- \gamma _1 S^* (P \alpha + \alpha D_3 \\&+ \beta \delta _1))D_2+(((D_3+P)D_0-\gamma _3 \beta S^*) \epsilon \\&+ D_5(P+D_3)D_0- \mu _1 \gamma _2 S^* \beta ) D_1- S^* \epsilon (P \gamma _1 \alpha + \alpha \gamma _1 D_3 \\&+ \beta (\delta _1 \gamma _1+ \gamma _2 \mu _1)),\\ a_5&= (((-\gamma _3 \beta S^* + D_0( P+D_3)) D_1- \gamma _1 S^*(P \alpha + \alpha D_3\\&+ \beta \delta _1)) \epsilon + D_5 D_0 D_1 (P+D_3)) D_2\\&-S^* \beta \epsilon D_1 \gamma _2 \mu _1,\\\end{aligned}$$

where \(D_5=\alpha A^*+\beta I^*,\; P=\frac{a}{1+bI^*}-\frac{abI^*}{(1+bI^*)^2}\).

Since one root of the characteristic equation is negative and so the EEP will be locally asymptotically stable if other roots are negative or have negative real parts. The other roots will be negative or have negative real parts if the Routh-Hurwitz [15] is satisfied, i.e., \(a_1,\;a_2,\;a_3,\;a_4,\;a_5>0\), \(a_1a_2a_3>a_3{^2}+a_1{^2}a_4\) and \((a_1a_4-a_5)(a_1a_2a_3-a_3{^2}-a_1{^2}a_4 )>a_5(a_1a_2-a_3)^2+a_1a_5{^2}\).

5 Parameter Estimation, Model Validation, Effective Parameter, Estimation of \(R_0\)

5.1 Fitting Model to Data

To estimate the important model parameters, we consider the cumulative number of infective cases from the real data sources and the model predicted cumulative number of infective cases. Let \(y_i\) be the cumulative number of real infective case and \(Z(t_i,\theta ),\;\theta \in \Theta (\theta _1,\theta _2,...,\theta _l)\) be the cumulative number of corresponding model predicted infective case, where \(Z(t,\theta )\) satisfies the differential equation

$$\begin{aligned} \frac{dZ}{dt}=\delta _1 A+\gamma _3E+\mu _1Q. \end{aligned}$$

Since \(Z(t_i,\theta )\) is the function of the model parameter \(\theta \in \Theta\), hence our aim in the present section is to find \(\theta \in \Theta\) such that

$$\begin{aligned} SSE(\theta )=\sum _{i=1}^{n} \left\{ (y_i-Z(t_i,\theta ))^2 \right\} \end{aligned}$$

is minimized with subject to \(\theta \in \Theta\), n is the number of observations [21]. There are several optimization techniques to minimize the error for suitable \(\theta \in \Theta\); here, we have used the Matlab package fmincon to estimate important model parameters and rest of the parameters are collected from online sources.

To study the spreading of COVID-19 in Spain, we have considered the cumulative infected cases from 24 February 2020 to 28 April 2020, and using the formula mentioned previously, we have estimated model parameters. To calibrate the numerical simulations, the initial population sizes have been taken as \(S(0)= 46,751,619\), \(E(0)= 10\), \(A(0)= 2\), \(Q(0)=1\), \(I(0)=3\), and \(R(0)=0\). The estimated model parameters have been given in Table 2.

Fig. 3
figure 3

Real data and model fitted infection cases of Spain: a cumulative infection data and model prediction, b bar diagram of daily infection data and model prediction, c residuals of the fit

Full size image

The best fitted cumulative curve with the real cumulative data, bar presentation of the daily infected cases, and the model predicted values and corresponding residuals have been given in Fig. 3. It is clear from Fig. 3c that the residuals of the fit are randomly distributed, which imply that the fitness of the data with the model is overall good [15]. The total error for estimating model parameters is \(1.79521035715286 \times 10^{6}\).

The model has been validated with real infected COVID-19 data of Algeria (in Africa) and India (in Asia) also. Since the model is fitted well for different countries from different continents; therefore, the consideration of the model is appropriate for COVID-19 transmission. The data fitting for COVID-19 in Algeria and India are given in Appendices 1 and 2, respectively. Also, we mention the sensitivity index of all the parameters in the respective table. Therefore, we can easily find out the most influential parameters which are responsible for COVID-19 pandemic. By dominating these parameters, COVID-19 can be controlled.

5.2 Sensitivity Analysis

The sensitivity analysis reveals parametric influence of the disease spreading in epidemic modeling. Usually the used methods for sensitivity analysis are the perturbation of fixed point analysis and the uncertainty in parameter estimation. Using the sensitivity index, one can estimate the rate of change of variables when the parameter changes [22,23,24]. On the other hand, the most important tool to study the dynamics of epidemic model is \(R_0\) and it is the function of the model parameters. Here, our goal is to determine the significant model parameters which are controlling \(R_0\). To study the effect of sensitivity here, we use sensitivity index [22] for \(R_0\) with respect to the model parameter \(\phi\) which is denoted by \(\Gamma _{R_0}^{\phi }\) and is defined by

$$\begin{aligned} \Gamma _{R_0}^{\phi }=\frac{\partial R_0}{\partial \phi }\frac{\phi }{R_0} . \end{aligned}$$

If \(\Gamma _{R_0}^{\phi }=\xi\) then \(y\%\) increase (decrease) of \(\phi\) will increase (decrease) \(\xi y\%\) of \(R_0\) when \(\xi\) is positive and for negative \(\xi\) increase of parameter will decrease \(R_0\).

It is clear from the Table 2 that the six parameters have a positive correlation with \(R_0\) and the rest of the parameters have a negative correlation with \(R_0\). With the increase of positive correlated model parameters, the prevalence of infection will increase and the negatively related parameters will decrease the number of infection.

Table 2 Model estimated parameters with 95 % confidence interval and their sensitivity indexes
Full size table

5.3 Effect of Significant Model Parameters

Now, we shall investigate the effect of significant model parameters in the spreading of COVID-19 in Spain. Keeping other parameters fixed as in the second column of Table 2, we varied the parameters \(\alpha ,\; \beta ,\; \mu _1,\; \gamma _1\), and \(\gamma _4\) one at a time.

  1. (a)

    Effect of \(\alpha\) (transmission rate of infection from A class)

    In Fig. 4, we present the time series of the infected population for different values of the model parameter \(\alpha\) in the estimated interval as given in Table 2. It is clear from the sensitivity index that with the increase of \(\alpha\) the basic reproduction number increases, i.e., prevalence of the disease will increase. In the figure, the red curve denotes the time series of the infected population for the model predicted parametric values, the upper and lower curves denote the same for upper limit and lower limit of \(\alpha\) in the interval, and the space between the curves denotes the prevalence of infection for different values of transmission rate between the asymptomatic and susceptible class in the estimated interval. It is clear from the figure that for higher values of \(\alpha\) the daily new infection will reach the highest value shortly then it will start to decrease.

    Fig. 4
    figure 4

    Time series of infectious persons for the model parameter \(\alpha\) in confidence interval

    Full size image
  2. (b)

    Effect of \(\beta\) (transmission rate of infection from I class)

    Figure 5 denotes the daily number of new infection for different values of \(\beta\). The description of the figure is similar as the previous figure’s. The nature of the solution for both cases shows the same result that with the increasing rate of infection, the number of infection first rapidly increases; after reaching the peak point, it starts to decrease.

    Fig. 5
    figure 5

    Time series of infectious persons for the model parameter \(\beta\) in confidence interval

    Full size image
  3. (c)

    Effect of \(\mu _1\) (rate at which Q becomes infectious)

    Figure 6 shows the time series for the I class for different values of \(\mu _1\). The description of the figure is similar as the previous figures’. Like the other two figures, it is clear from the figure that with the increase of this parameter the abundance of the infected population will increase. Thus, the infection from the quarantined class plays an important role in spreading the disease. To minimize the value of \(\mu _1\), we have to quarantine the exposed class properly, then the spreading of disease can be controlled easily.

    Fig. 6
    figure 6

    Time series of infectious persons for the model parameter \(\mu _1\) in confidence interval

    Full size image
  4. (d)

    Effect of \(\gamma _1\) (transmission rate of E to A class)

    \(\gamma _1\) is the rate at which the exposed class transfers to the asymptomatic class. If \(\gamma _1\) is higher, then a large number of exposed people will enter the asymptomatic compartment, and consequently the disease will spread among the susceptible people shortly. For lower values of \(\gamma _1\), disease spreading will be lower. In Fig. 7, we have presented the time series of the infected persons for different values of \(\gamma _1\). The description of the graph is similar as the last three. It is clear from the figure that to control the disease spreading, we have to control the parameter \(\gamma _1\).

    Fig. 7
    figure 7

    Time series of infectious persons for the model parameter \(\gamma _1\) in confidence interval

    Full size image
  5. (e)

    Effect of \(\gamma _4\) (recovery rate of E class)

    In Fig. 8, we have presented the time series of the infected population for different values of recovery rates (\(\gamma _4\)) of the exposed class of infection as given in the confidence interval. Like the previous figures, here, the red line is the model predicted daily new infection for COVID-19 but the lower line is for highest value of \(\gamma _4\) and the upper line is for the lowest value. Hence, with the increase of this parameter, the number of infected population decreases, i.e., to control the disease the recovery rate plays important role. The recovery rate will increase as the immunity of the infected person increases. So, to get recovery from the disease individuals have to gain a high immunity through a good lifestyle.

    Fig. 8
    figure 8

    Time series of infectious persons for the model parameter \(\gamma _4\) in confidence interval

    Full size image

5.4 Contribution in \(R_0\) by Infectious and Asymptomatic Persons

It is clear from the expression of \(R_0\) that the two parts of \(R_0\),

$$\begin{aligned} R_{01}=\frac{\Lambda \alpha \gamma _1}{\epsilon D_0D_1},\; \text {and}\;\;R_{02}=\frac{\Lambda \beta (D_1D_2\gamma _3+D_1\gamma _2\mu _1+D_2\delta _1\gamma _1)}{\epsilon D_0D_1D_2(D_3+a)} \end{aligned}$$

respectively, arise due to the effect of asymptomatic and infectious classes. Using the estimated parametric values, we obtain \(R_0=\)6.692558249 and the values of two parts are \(R_{01}\)=5.29611714 and \(R_{02}\)=1.396441109. It is clear from the values that the asymptomatic class gives the 79% contribution and the infectious class gives only 21% contribution in the basic reproduction number. Thus, the asymptomatic class gives the most contribution in spreading the COVID-19 infection, so the asymptomatic class takes the most important role compared to the infectious individuals. Thus, to control the disease, we have to minimize the asymptomatic persons through a huge number of testing and then we have to transfer them to the infectious compartment.

5.5 Estimation of \(R_0\) for Actual Epidemic

Here, we estimate \(R_0\) from the initial growth phase of the disease. At the primary stage of the epidemic, we assumed that the number of cumulative cases, Z(t), varies as \(Z \propto exp(\zeta t)\), where \(\zeta\) is the force of infection. In this case, the number of asymptomatic, exposed, quarantined, and infectious individuals varies similarly,

$$\begin{aligned} {\left\{ \begin{array}{ll} A(t)\sim A_0 exp(\zeta t)\\ E(t)\sim E_0 exp(\zeta t)\\ Q(t)\sim Q_0 exp(\zeta t)\\ I(t)\sim I_0 exp(\zeta t) \end{array}\right. } \end{aligned}$$
(5.1)

where \(A_0,\; E_0,\;Q_0,\; \text {and}\;\; I_0\) are constants. Also from the first equation of (2.1), the constant susceptible population is \(S_0=\frac{\Lambda }{\epsilon }\). We assume that delay in treatment is 0, i.e., \(b=0\). Moreover, the number of recovered population is 0 at the initial stage, i.e.,

$$\begin{aligned} R(t) = R_0 \end{aligned}$$
(5.2)

Substituting Eqs. (5.1) and (5.2) in the respective expression for the derivative as presented in the system (2.1), we obtain first from \(E-\) equation

$$\begin{aligned} \zeta E_0=(\alpha A_0+\beta I_o)S_0-(\gamma _1+\gamma _2+\gamma _3+\gamma _4+\epsilon )E_0 \end{aligned}$$
(5.3)

which yields

$$\begin{aligned} \left( \frac{\zeta }{\gamma _1+\gamma _2+\gamma _3+\gamma _4+\epsilon }+1\right) E_0=\frac{\Lambda (\alpha A_0+\beta I_0)}{\epsilon (\gamma _1+\gamma _2+\gamma _3+\gamma _4+\epsilon )}. \end{aligned}$$

Similarly, we obtain from \(A,\;Q\) and \(I-\) equations, respectively

$$\begin{aligned} \left( \frac{\zeta }{\delta _1+\delta _2+\epsilon }+1\right) A_0=\frac{\gamma _1}{\delta _1+\delta _2+\epsilon }E_0, \end{aligned}$$
$$\begin{aligned} \left( \frac{\zeta }{\mu _1+\mu _2+\epsilon }+1\right) Q_0=\frac{\gamma _2}{\mu _1+\mu _2+\epsilon }E_0, \end{aligned}$$
$$\begin{aligned} \left( \frac{\zeta }{\epsilon +\delta +\sigma _1+a}+1\right) I_0=\frac{\delta _1 A_0+\gamma _3 E_0+\mu _1 Q_0}{\epsilon +\delta +\sigma _1+a}. \end{aligned}$$

For simplicity, using the notations \(D_0,\;D_1,\;D_2,\;\text {and}\;D_3\) as defined in Section 4.1, we have

$$\begin{aligned} \left( \frac{\zeta }{D_0}+1\right) E_0=\frac{\Lambda (\alpha A_0+\beta I_0)}{\epsilon D_0}, \end{aligned}$$
$$\begin{aligned} \left( \frac{\zeta }{D_1}+1\right) A_0=\frac{\gamma _1}{D_1}E_0, \end{aligned}$$
$$\begin{aligned} \left( \frac{\zeta }{D_2}+1\right) Q_0=\frac{\gamma _2}{D_2}E_0, \end{aligned}$$
$$\begin{aligned} \left( \frac{\zeta }{D_3+a}+1\right) I_0=\frac{\delta _1 A_0+\gamma _3 E_0+\mu _1 Q_0}{D_3+a}. \end{aligned}$$

Using the above four relations, the association of \(R_0\) and the force of infection can be done in the form

$$\begin{aligned} R_0=\frac{S_0\alpha \gamma _1}{D_0D_1}+\frac{P_2\left( D_1P_1-S_0\alpha \gamma _1\right) (D_1D_2\gamma _3+D_1\gamma _2\mu _1+D_2\gamma _1\delta _1)}{D_0D_1 \left( D_1D_2P_1P_3\gamma _3+D_1P_1\mu _1\gamma _2+D_2P_2\delta _1\gamma _1 \right) }, \end{aligned}$$
(5.4)

where \(P_0=\frac{\zeta }{D_0}+1, P_1=\frac{\zeta }{D_1}+1, P_2=\frac{\zeta }{D_2}+1\) and \(P_3=\frac{\zeta }{D_3+a}+1\).

Now it is time to estimate the force of infection, \(\zeta\). Since the number of new cases per day, I(t), is the derivative of Z(t) in relation to time t, then at the beginning of the epidemics, \(I(t)\sim I_0 \zeta exp(\zeta t)\).

Fig. 9
figure 9

a The time series of new cases of COVID-19 in Spain from 24 February 2020 to 28 April 2020; b the daily number of cases against the cumulative number of cases for the same time period in a

Full size image

Plotting the number of new cases per day against the cumulative number of cases Z(t), the phase of exponential growth of the cumulative number of cases is evidenced by a linear growth of the curve, the slope of which is the force of infection and which can be computed by a least-square linear fit of this linear phase [26, 27]. For the data of Spain from 24 February, 2020, to 28 April, 2020, for the COVID-19 outbreak, shown in Fig. 9a, we obtain the calculated range of \(\zeta = 0.1497553492834 \pm 0.0091\) day\(^{-1}\) based on the slope shown in Fig. 9b. The straight line (red color) indicates the growing linear parts of the plots corresponding to the initial exponential growth of the epidemics.

Substituting the parametric values as presented in Table 2 in the expression (5.4), we obtain an estimation of \(R_0= 5.4925\) and the range is \(R_0 \in (5.1514, 5.8448)\).

5.6 Effective Reproduction Number

In epidemiology, the basic reproduction number (\(R_0\)) denotes the average number of secondary infection produced by one infected individual during the course of mean infection time. But usually when disease starts to spread initially, the secondary number of infected is higher and it reaches a peak point then it decreases, i.e., the reproduction number is not always fixed. Our aim in this subsection is to define the time varying reproduction, i.e., the reproduction number per day for COVID-19, and determine it using the available method.

Fig. 10
figure 10

Effective reproduction number of Spain from 24 February 2020 to 28 April 2020

Full size image

This type of estimation of the reproduction number is defined as the effective reproduction number at time t and denoted by R(t) [26,27,28]. Here, R(t) yields the information about the invasion of infection among the susceptible populations with time. To adopt the control policy of COVID-19 in Spain for day to day, it is most important to know the time varying reproduction number. The authors in [26, 27] defined the renewal equation in the form

$$\begin{aligned} F(t)=\frac{b(t)}{\int _{\tau =0}^{\infty }b(t-\tau )g(\tau )d\tau }, \end{aligned}$$

where b(t) is the number of new cases at \(t^{th}\) day and \(g(\tau )\) is the generation interval distribution for the disease. Using the procedure described in [26, 27] to the model (2.1), the generation distribution can be obtained. Let the rate of leaving of the exposed, asymptomatic, and infectious people be, respectively, \(p_1=\epsilon +\gamma _1+\gamma _2+\gamma _3+\gamma _4,\; p_2=\delta _1+\delta _2+\epsilon\) and \(p_3=d+\epsilon +\sigma _1\). The generation interval distribution can be obtained as the combination of \(p_1e^{-p_1t},\; p_2e^{-p_2t}\) and \(p_3 e^{-p_3t}\) in the form

$$\begin{aligned} g(t)=\sum _{i=1}^{3}\frac{p_1p_2p_3e^{-p_1t}}{\prod _{j=1,j\ne i}^{3}(p_j-p_i)} \end{aligned}$$

and mean of the distribution is \(T=\frac{1}{p_1}+\frac{1}{p_2}+\frac{1}{p_3}\) and \(\tau >0\). The above relation is valid when the force of infection \(\zeta >\min \left\{ -p_1,-p_2,-p_3 \right\}\). From the expression of F(t), the effective reproduction per day for the COVID-19 model can be estimated as \(R(t)=F(t)\). The value of R(t) for the present model from 24 February 2020 to 28 April 2020 of Spain COVID-19 spreading is given in Fig. 10. The value of R(t) is strictly greater than 1 up to 3 April 2020 and then it moves up and down of 1. Thus, growth of disease starts to decrease from the 3rd of April.

6 Optimal Control

In this section, we have formulated an optimal control problem by introducing time-dependent controls due to maintaining social distancing, causing the reduction of transmission rate of infections. The countries applying the lockdown policy have since faced huge financial losses; therefore, some countries are adapting a partial lockdown. Hence, control of COVID-19 infection spreading depends on how the social distancing is maintained. For the implementation of social distancing, we can replace the incidence rate \(\alpha AS+\beta IS\) in the system (2.1) by \(\alpha (1-u_{1}) AS+\beta (1-u_{2}) IS\), where two controls \(u_{1}\) and \(u_{2}\), respectively, measure the reduction of transmission from asymptomatic and infectious individuals due to social distancing. Thus, we formulate an optimal control problem as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dS}{dt}=&{} \Lambda -\lbrace \alpha (1-u_{1}) A+\beta (1-u_{2}) I \rbrace S - \epsilon S \\ \frac{dE}{dt}=&{} \lbrace \alpha (1-u_{1}) A+\beta (1-u_{2}) I \rbrace S-(\gamma _1+\gamma _2+\gamma _3+\gamma _4+\epsilon ) E \\ \frac{dA}{dt}=&{} \gamma _1E-(\delta _1+\delta _2+\epsilon )A \\ \frac{dQ}{dt}=&{} \gamma _2E-(\mu _1+\mu _2+\epsilon )Q \\ \frac{dI}{dt}=&{} \delta _1 A+\gamma _3E+\mu _1Q-( \epsilon +d +\sigma _1 )I-\frac{aI}{1+bI} \\ \frac{dR}{dt}=&{} \gamma _4 E+\delta _2 A+\mu _2 Q +\sigma _1I -\epsilon R+\frac{aI}{1+bI} \end{array}\right. } \end{aligned}$$
(6.1)

Here, we construct the cost functional as follows:

$$\begin{aligned} \min J(u_{1},u_{2})=\int _{0}^{T}(B_{1}E+B_{2}A+B_{3}Q+B_{4}I+B_{5}u_{1}^{2}+B_{6}u_{2}^{2})dt, \end{aligned}$$

where the constants \(B_{1}, B_{2}, B_{3}, B_{4}\) are, respectively, the losses due to the presence of exposed, asymptomatic, quarantined, and infectious individuals. The constants \(B_{5}\) and \(B_{6}\) are the losses associated with respective controls. The main objective of this study is to minimize the COVID-19 infections as well as the financial losses due to implementation of lockdown for the time T. In order to obtain optimal control strategies, we have to find optimal functions \(u_{1}^{*}(t)\) and \(u_{2}^{*}(t)\) such that \(J(u_{1}^{*},u_{2}^{*})=\min \lbrace J(u_{1},u_{2}),(u_{1},u_{2})\in U\rbrace ,\) where the control set \(U=\lbrace (u_{1},u_{2})/u_{i}(t)\) is Lebesgue measurable on [0, 1] and \(0\le u_{1}(t),u_{2}(t)\le 1\) for all \(t\in [0,T]\rbrace\). Now, the existence of such optimal control functions for the system (6.1) has been shown by the following theorem.

Theorem 4

There exists optimal control functions \(u_{1}^{*}(t)\) and \(u_{2}^{*}(t)\) that minimize J over U.

Proof

It is obvious that the integrand of the cost functional \(J(u_{1},u_{2})\) is a convex function of \(u_{1}\) and \(u_{2}\). Again, Theorem 1 implies that all the solutions of the system (2.1) are bounded and in a similar manner it can be easily proved that all the solutions of the system (6.1) are also bounded, which claims that the system (6.1) satisfies the Lipshitz property with respect to the state variables. Therefore, there exists an optimal pair \((u_{1}^{*}(t),u_{2}^{*}(t))\). Hence, the theorem is proved.

Now, we shall determine the optimal control functions using Pontryagin’s minimum principle [29,30,31,32]. To apply Pontryagin’s minimum principle, we construct the Hamiltonian H:

$$\begin{aligned}&H(S,E,A,Q,I,R,u_{1},u_{2},\lambda _{1},\lambda _{2},\lambda _{3},\lambda _{4},\lambda _{5},\lambda _{6})=B_{1}E\\&+B_{2}A+B_{3}Q+B_{4}I+B_{5}u_{1}^{2}+B_{6}u_{2}^{2}+\lambda _{1}(t)\frac{dS}{dt}\\&+\lambda _{2}(t)\frac{dE}{dt}+\lambda _{3}(t)\frac{dA}{dt}+\lambda _{4}(t)\frac{dQ}{dt}+\lambda _{5}(t)\frac{dI}{dt}+\lambda _{6}(t)\frac{dR}{dt}. \end{aligned}$$

Here, the adjoint variables \(\lambda _{i}\), \(i=1-6\) satisfy the equations \(\frac{d\lambda _{1}(t)}{dt}=-\frac{\partial H}{\partial S}, \frac{d\lambda _{2}(t)}{dt}=-\frac{\partial H}{\partial E}, \frac{d\lambda _{3}(t)}{dt}=-\frac{\partial H}{\partial A}\), \(\frac{d\lambda _{4}(t)}{dt}=-\frac{\partial H}{\partial Q}, \frac{d\lambda _{5}(t)}{dt}=-\frac{\partial H}{\partial I}, \frac{d\lambda _{6}(t)}{dt}=-\frac{\partial H}{\partial R}\) with the transversality conditions \(\lambda _{i}(T)=0,i=1-6\), i.e., \(\lambda _{i}\), \(i=1-6\) satisfy the adjoint equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d\lambda _{1}}{dt} =& \lbrace \alpha (1-u_{1}) A+\beta (1-u_{2}) I \rbrace (\lambda _{1}-\lambda _{2})+\epsilon \lambda _{1} \\ \frac{d\lambda _{2}}{dt} =& -B_{1}+(\gamma _{1}+\gamma _{2}+\gamma _{3}+\gamma _{4}+\epsilon ) \lambda _{2}-\gamma _{1} \lambda _{3}-\gamma _{2} \lambda _{4}\\&-\gamma _{3} \lambda _{5}-\gamma _{4} \lambda _{6} \\ \frac{d\lambda _{3}}{dt} =&-B_{2}+\alpha (1-u_{1})S(\lambda _{1}-\lambda _{2})+(\delta _{1}+\delta _{2}+\epsilon ) \lambda _{3}\\&-\delta _{1} \lambda _{5}-\delta _{2} \lambda _{6} \\ \frac{d\lambda _{4}}{dt} =& -B_{3}+(\mu _{1}+\mu _{2}+\epsilon ) \lambda _{4}-\mu _{1} \lambda _{5}-\mu _{2} \lambda _{6} \\ \frac{d\lambda _{5}}{dt} =& -B_{4}+\beta (1-u_{2})S(\lambda _{1}-\lambda _{2})+\frac{a}{(1+b I)^{2}}(\lambda _{5}-\lambda _{6})\\&+(\sigma _{1}+d+\epsilon ) \lambda _{5}-\sigma _{1} \lambda _{6} \\ \frac{d\lambda _{6}}{dt} =& \epsilon \lambda _{6} \end{array}\right. } \end{aligned}$$
(6.2)

with the transversality conditions

$$\begin{aligned} \lambda _{i}(T)=0, i=1,2,...,6. \end{aligned}$$
(6.3)

For optimality conditions, we differentiate the Hamiltonian H partially with respect to \(u_{1}, u_{2}\) and we have \(u_{1}=\frac{(\lambda _{2}-\lambda _{1})\alpha SA}{2B_{5}}\) and \(u_{2}=\frac{(\lambda _{2}-\lambda _{1})\beta SI}{2B_{6}}\). This leads to the following expressions of the optimal control functions \(u_{1}^{*}(t)\) and \(u_{2}^{*}(t)\):

\(u_{1}^{*}(t) = \max \big \{0,\min \big \{\frac{(\lambda _{2}^{*}-\lambda _{1}^{*})\alpha S^{*} A^{*}}{2B_{5}},1\big \} \big \}\) and \(u_{2}^{*}(t) = \max \big \{0,\min \big \{\frac{(\lambda _{2}^{*}-\lambda _{1}^{*})\beta S^{*} I^{*}}{2B_{6}},1\big \} \big \}\), where \(S^{*},E^{*},A^{*},Q^{*},I^{*},R^{*}\) are, respectively, the optimum values of S, E, A, Q, I, R and \((\lambda _{1}^{*},\lambda _{2}^{*},\lambda _{3}^{*},\lambda _{4}^{*},\lambda _{5}^{*},\lambda _{6}^{*})\) is the solution of the system (6.2) with the transversality conditions (6.3). Again, that critical point is indeed a minimum because \(\frac{\partial ^{2} H}{\partial u_{1}^{2}}= 2B_{5}>0\) and \(\begin{vmatrix} \frac{\partial ^{2} H}{\partial u_{1}^{2}}&\frac{\partial ^{2} H}{\partial u_{1} \partial u_{2}} \\ \frac{\partial ^{2} H}{\partial u_{2} \partial u_{1}}&\frac{\partial ^{2} H}{\partial u_{2}^{2}} \end{vmatrix}=4B_{5}B_{6}>0\). Thus, we can summarize the above in the following theorem:

Theorem 5

The optimal pair \((u_{1}^{*}(t), u_{2}^{*}(t))\) minimizes the cost functional J over the region U, where \(u_{1}^{*}(t) = \max \big \{0,\min \big \{\frac{(\lambda _{2}^{*}-\lambda _{1}^{*})\alpha S^{*} A^{*}}{2B_{5}},1\big \} \big \}\) and \(u_{2}^{*}(t) = \max \big \{0,\min \big \{\frac{(\lambda _{2}^{*}-\lambda _{1}^{*})\beta S^{*} I^{*}}{2B_{6}},1\big \} \big \}\).

Fig. 11
figure 11

Time series of the populations for both with control and without control: a exposed individuals, b asymptomatic individuals, c quarantined individuals, d infectious individuals

Full size image

Now, we have performed the numerical simulations of the optimal control problem (6.1) using the forward-backward sweep method [31] written in MATLAB programming. For this simulation, we fix the parameters given in Table 2 with the initial conditions \(S(0)= 46751619\), \(E(0)= 10\), \(A(0)= 2\), \(Q(0)=1\), \(I(0)=3\), and \(R(0)=0\). For this simulation, we also assume that \(B_{1}=0.05\), \(B_{2}=0.12\), \(B_{3}=0.1\), \(B_{4}=0.2\), \(B_{5}=15\), and \(B_{6}=15\).

Fig. 12
figure 12

The optimal control function: a \(u_{1}\), b \(u_{2}\)

Full size image

We simulate the model in two different ways, one is without using any control variables and the other is with both the control variables, and we run the programme for 65 days in both cases. We adopt this in order to see the comparison of state trajectories for with and without control in the same frame (see Fig. 11a–d). For this simulation, the optimal control functions have been illustrated in Fig. 12a, b.

7 Conclusion

This paper describes an epidemic compartmental model of COVID-19 with saturated treatment that reflects the boundedness of medical resources in Spain. Here, we have investigated the transmission dynamics of COVID-19 and provided some control strategies to combat the pandemic disease. The basic reproduction number \(R_0\) of the model has been obtained and we have identified two contributory parts of \(R_0\). We have proved that if \(R_0<1\), then the disease-free equilibrium point (DFE) is locally asymptotically stable and if \(R_0>1\) then the DFE is unstable. The system has the backward bifurcation at \(R_0=1\), i.e., there is a stable endemic equilibrium point along with stable DFE for \(R_0 \in (R_0^{*},1)\) for some \(R_0^{*}<1,\) which implies that making the basic reproduction number less than 1 is not enough to eradicate the COVID infection due to saturated treatment. The model is also validated to the COVID-19 data from 24 February, 2020, to 28 April, 2020, in Spain and we have estimated the important model parameters. The effect of significant model parameters in spreading of COVID-19 in Spain has been investigated. It is clear from the estimated values of the parameters that the asymptomatic class gives 79% contribution, whereas the infectious class gives only 21% contribution in the basic reproduction number which implies that the asymptomatic individuals take the most important role compared to the infectious individuals for the disease spreading. Here, we have estimated the basic reproduction number from the initial growth phase of COVID-19 infection in Spain and the effective reproduction number has also been estimated in Spain 24 February 2020, to 28 April 2020, which indicates that the epidemic disappears after 3 April 2020. The model is also used as an optimal control problem by introducing the controls due to the social distancing. By using optimal control theory, we have the optimal policy that minimizes the infection as well as the financial loss due to implementing a partial lockdown. Thus, the social distancing due to adapting a partial lockdown by some countries is highly effective for controlling the pandemic disease COVID-19. The model is fitted for Algeria and India also. We think our study will give some insights which will be helpful for health planners.

In this study, there is one notable limitation such that the model is appropriate for the beginning of the disease development and we have ignored the spatial distribution of population densities. Due to this limitation, the accuracy of the existing results and prediction in this paper could vary for a short period of time. For this type of pandemic, the standard modeling is the partial delay differential equations (PDDEs) which conclude both time-space distributions and incubation period. Also we have ignored the effect of vaccination though vaccination is now available for COVID-19. The final conclusion about modelling is that all mathematical models have some limitations and are not perfect for all countries.