1 Introduction

In the field of epidemiology, over the past century, infectious diseases have been a primary focus of investigation through the utilization of mathematical models. Researchers have employed these models to examine various illnesses, including HIV (Anderson 1988), TB (Wangari and Stone 2018), influenza (Baba and Hincal 2018), malaria (Abimbade et al. 2022), and most recently, COVID-19 (Buonomo 2020; Ghosh and Martcheva 2021). The SARS-CoV-2 virus, which has impacted nearly every species in the last 3 years, was declared a global pandemic by the World Health Organization on March 11, 2020 (Cucinotta and Vanelli 2020). This viral disease has been associated with symptoms such as shortness of breath and loss of taste or smell (Zhu et al. 2020; Wu et al. 2020; Chang et al. 2020). The dynamic nature of SARS-CoV-2, with its ongoing mutations, has made it challenging to comprehend its precise transmission patterns and predict the course of the disease. Several factors, such as asymptomatic transmission, variable incubation periods, diverse viral strains, and reinfection of recovered individuals, have added complexity to the pandemic’s trajectory (Li et al. 2020).

Efforts to control COVID-19, such as quarantine and isolation policies, as well as appropriate patient care, necessitate effective screening and diagnostic technologies (World Health Organization, 2020). Due to the recent outbreak, comprehensive knowledge of the disease’s transmission dynamics and spread remains elusive as new information continues to emerge. COVID-19 research is a rapidly evolving field, with new information continuously emerging. Different regions have implemented various techniques and strategies for COVID-19 control, including testing and contact tracing, vaccination, social distancing, mask-wearing, hand hygiene, isolation, and quarantine. As of February 2023, in India alone, more than 44.68 million people had contracted the virus, resulting in 530,775 deaths, based on available data (My Gov India, 2023).

Evaluating the actual effectiveness of vaccinations for any disease is challenging, and it is particularly complex for COVID-19, given the rapid distribution of vaccines in diverse socioeconomic and geographic contexts (Mills and Reis 2022). Throughout the past three years, numerous mathematical models have been proposed by researchers to understand the dynamics of COVID-19 among symptomatic and asymptomatic individuals, both those who are aware of their infection and those who are not (Ghosh and Martcheva 2021; Rai et al. 2022; Li and Zhang 2022). In the context of the virus’s evolving behavior and mutations, the bilinear incidence rate, denoted as \(\beta S I\), is considered due to the high potential for the transmission of SARS-CoV-2 to other hosts. This incidence rate function has been discussed by Hethcote (2000) and Brauer and Castillo-Chávez (2001) in their general epidemic models.

Within the realm of disease control measures, medical treatment has emerged as a prominent intervention for mitigating the disease burden. Nevertheless, when dealing with diseases of significant consequence, such as COVID-19, the widespread accessibility of treatment becomes a formidable challenge. The scarcity of hospital beds and essential laboratory equipment has resulted in treatment capacity reaching a saturation point. In the domain of epidemiological modeling, this situation is addressed by incorporating an appropriate saturation function. The availability of treatment on a large scale becomes feasible when ample resources are accessible. Various treatment modalities have been explored in the existing literature, showcasing their respective advantages. Wang and Ruan (2004), in their research, investigated a constant removal rate of infections and revealed that, under certain parameter constraints, it is conceivable to eliminate a disease over time. They also determined that the persistence of the disease is contingent upon the initial number of infected individuals, and if the initial population falls within a specific range, the disease will eventually subside. Zhonghua and Yaohong (2010) employed a saturated treatment function to illustrate the constraints imposed by limited medical resources in their epidemic models. Subsequently, various researchers have adopted diverse functions to represent saturated treatment over time, such as the Holling type-II function (Gao and Zhao 2011), Holling type-III function (Dubey et al. 2016), and the Monod-Haldane function (Kumar and Nilam 2019), among others.

Mathematical models find application in diverse fields for the representation and analysis of real-world phenomena such as economy, finance, medicine, biology, epidemiology, and many others. In epidemiology, SEIR models are valuable for predicting the patterns of disease occurrence over time for diseases with latency periods. As a result, these models hold significance for epidemiologists in the analysis of disease outbreaks, offering insights into the disease’s progression within a population (Zhou and Cui 2011; Algehyne and Ud Din 2021). Zhou and Cui (2011) investigated an SEIR model featuring a bilinear incidence rate and a saturated treatment rate. Their study revealed the potential for backward bifurcation, resulting in bistable equilibrium points. Numerous SEIR mathematical models with nonlinear incidence rates have been developed to examine the dynamics of COVID-19 transmission (Rohith and Devika 2020; Algehyne and Ud Din 2021; Kwuimy et al. 2020). Rohith and Devika (2020) introduced an incidence rate that includes a psychological component, leading to the identification of forward bifurcation. Algehyne and Ud Din (2021) proposed an SQIR model with a saturated incidence rate and natural recovery, concluding that quarantine measures are the most effective means of pandemic control. Kwuimy et al. (2020) presented an SEIRD model with a hybridized incidence rate, monitoring government action, and public response strength and demonstrated global asymptotic stability of equilibria without bifurcation behavior. The number of persons who have been re-infected by the new coronavirus is increasing, showing that immunity falls fast for certain people after having been caught the virus before. According to research, severely sick patients who initially contract COVID-19 are more likely to acquire inadequate antibodies and to contract dangerous secondary infections (Goldman et al. 2020; Wu et al. 2020a). He et al. (2020) employed a model to illustrate the progression of the epidemic in Hubei Province, demonstrating its effectiveness in predicting the future scenarios of the COVID-19 outbreak. Wang et al. (2022) considered an SEIR model that accounts for reinfections from the infected and exposed classes. Literature indicates that backward bifurcation has posed a challenge in mitigating epidemic diseases (Lu et al. 2019). Oluyori et al. (2021) investigated the dynamics of the COVID-19 pandemic using an SEIRS model with saturated incidence and treatment rates, uncovering both backward and Hopf bifurcations in their model dynamics. Omame and Abbas (2023) explored the impact of COVID-19 and dengue vaccinations while incorporating saturated incidence. Ahmed et al. (2021) developed a novel reaction-diffusion model for the study of COVID-19 and performed stability analysis in the space state of the spatiotemporal model. Additionally, various mathematical models have been developed to address interventions in different countries across the globe (Flaxman et al. 2020; Chung and Chew 2021). Khan et al. (2021) studied the COVID-19 outbreaks by employing fractional calculus through nonsingular derivative. Kumar et al. (2020a) studied the COVID-19 pandemic through both singular and nonsingular derivative. There have been various significant models using fractional calculus to study multiple diseases and disorders (Kumar et al. 2020a, 2021; Mohammadi et al. 2021) as well as ecological models (Kumar et al. 2020b). Raza et al. (2022) proposed and studied a dynamical model of COVID-19 with a nonlinear incidence rate with crowding effect. Lately, numerous researchers have been engaged in discussions regarding stochastic models of epidemic diseases and its applications across various domains in the realms of physical, biological, and other scientific fields (Hamam et al. 2022; Raza et al. 2022, 2021, 2019).

The increasing number of COVID-19 reinfections highlights the rapid decline in immunity among certain individuals who have previously contracted the virus. Research suggests that severely ill patients who initially contract COVID-19 are more susceptible to developing insufficient antibodies and contracting dangerous secondary infections. In a situation where the pandemic is characterized by high and uncontrolled infection rates, the available resources within a region become overwhelmed due to a shortage of hospital beds and essential facilities. In light of this, we have designed our proposed model by incorporating a bilinear incidence rate and a treatment rate that reaches saturation. This model can provide insights into the extent and duration of protective immunity, as well as the potential for reinfection, as discussed by (Vespignani et al. 2020). To the best of our knowledge, there has been no prior research that has integrated saturated treatment with mass action incidence and addressed the issue of COVID-19 reinfection. Given the growing concerns surrounding reinfections of COVID-19, we believe it is essential to emphasize the significance of such a scenario and thoroughly investigate its implications.

In the study conducted by Annas et al. (2020), an SEIR model with a bilinear incidence rate and perfect recovery is employed and stability analysis is performed. Mwalili et al. (2020) constructed a mathematical model with a nonlinear incidence rate along with environmental factors in symptomatic and asymptomatic compartments. Even though these external factors have an effect on the disease, the realistic nature of COVID-19 has been such that there has been a shortage of medical facilities in the duration of the pandemic because of its high transmission rate. Additionally the symptomatic and asymptomatic infected people all come under the umbrella of infectives in the sense of data in a region (Han et al. 2020). So the focus of this work has been to overcome these shortcomings can be overcome and captured by the saturated treatment function. The reinfections of COVID-19 are extremely high as shown in the aforementioned literature. We believe the proposed model is useful in capturing the dynamics of COVID-19 and hence for inventions of mitigation strategies.

We present and inspect an SEIR governing model which provides for the high rate of infections through the mass action incidence and saturated treatment in the form of Holling type-II response. The governing model is examined to comprehend the specific effect of saturation in treatment. The current paper is laid out as follows. Section 2 deals with the proposed mathematical model and its preliminary analysis. The non-negativity and boundedness of solutions are demonstrated along with the computation of the basic reproduction number (BRN) \(\mathcal {R}_0\). Section 3 focuses on the local stability of the disease-free equilibrium (DFE) and the unique endemic equilibrium (EE) by the Routh-Hurwitz (R-H) criteria. Also, the global stabilities of the DFE (by the result established by Chavez et al. 2002) as well as the unique EE with the construction of Lyapunov function are established. Sensitivity analysis of the parameters occurring in the BRN is included in Sect. 5. In Sect. 4, forward bifurcation phenomena have been observed where an EE is stable when \(\mathcal {R}_0 > 1\). Moreover, due to the presence of saturated treatment function \(T(I)=\frac{aI}{1+bI}\), the model system experiences the backward bifurcation phenomena on account of the occurrence of two endemic equilibria (one stable, one unstable) when \(\mathcal {R}_0 < 1\). Saddle-node bifurcation is also analyzed for the model system. Lastly, Sect. 6 focuses on numerical simulations of the impact of some control parameters on the rise in the infective population compartment. In this study, MATLAB’s built-in ode45 tool for solving differential equations was used for all numerical simulations.

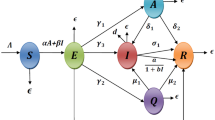
2 Description of the Model

We have divided the total population N(t) into four distinct compartments, each reflecting the individual’s disease status at any given time t, denoted as:

  • Susceptible S(t): Individuals who have not been infected and are at risk of contracting the disease.

  • Exposed E(t): Individuals who have been infected but are not yet capable of transmitting the infection. They are in the incubation phase, and after completing this period, they become infectious.

  • Infective I(t): Individuals who are currently infected and can actively transmit the disease to others.

  • Recovered R(t): Individuals that have recovered from the disease for the time being but can be exposed to reinfection.

An SEIR epidemic model is developed for COVID-19 in this paper, taking into account the saturated removed rate and assuming removed individuals do not have perpetual immunity. The entire framework for modeling the dynamics of the disease is illustrated in the schematic diagram presented in Fig. 1. This model allows us to track the flow of individuals through these compartments as the disease progresses.

Fig. 1
figure 1

The model system represented in a basic flowchart

Full size image

Assumptions:

  1. 1.

    Reinfection of the recovered population due to interaction with the infected class leads to infections rather than exposure. Due to the lack of immune response in treated individuals, it is assumed that the resulting interaction will give rise to new infections (Vespignani et al. 2020).

  2. 2.

    Treatment is a noteworthy aspect to manage and control an infectious disease. We have employed T(I) as the treatment function (Gao and Zhao 2011; Zhang and Liu 2008) for our model, which is defined to be

    $$\begin{aligned} T(I) = \dfrac{aI}{1+bI}, \end{aligned}$$

    where b is the saturation constant in the function, i.e., b determines the amount of infectives being held over in receiving treatment.

On the basis of the aforementioned determinants, the following governing nonlinear system of ordinary differential equations exhibiting mass action incidence is formed to mathematically explain the above hypotheses.

$$\begin{aligned} \begin{aligned} \dfrac{\text{d}S}{\text{d}t}&= \wedge - \beta S I - \text{d} S\\ \dfrac{\text{d}E}{\text{d}t}&= \beta S I - (\nu + d+ \mu ) E\\ \dfrac{\text{d}I}{\text{d}t}&= \nu E - (d+\delta +\gamma ) I - \frac{aI}{1+bI} + \eta R I\\ \dfrac{\text{d}R}{\text{d}t}&= \mu E + \gamma I + \frac{aI}{1+bI} - \text{d} R - \eta R I \end{aligned} \end{aligned}$$
(1)

with the initial values \(S(0)=S_0 > 0\), \(E(0)=E_0 \ge 0\), \(I(0)=I_0 \ge 0\), \(R(0)=R_0 \ge 0\). All of the parameters considered in the model are non-negative. These initial conditions are considered since at \(t=0\), the number of infections is non-negative, effectively rendering exposed and recovered individuals to be at non-negative, while the susceptible population may be prone to the disease. Table 1 contains illustrations of the parameters used in the model.

Table 1 Nomenclature of the parameters
Full size table

2.1 Non-negativity and Boundedness

The following are exhibited by the system of equations of model (1)

$$\begin{aligned} \begin{aligned} \dfrac{\text{d}S}{\text{d}t}\Bigg \vert _{S=0}&= \wedge > 0, \quad \dfrac{\text{d}E}{\text{d}t}\Bigg \vert _{E=0} = \beta S I \ge 0,\\ \dfrac{\text{d}I}{\text{d}t}\Bigg \vert _{I=0}&= \nu E \ge 0, \quad \dfrac{\text{d}R}{\text{d}t}\Bigg \vert _{R=0} = \mu E + \gamma I + \frac{aI}{1+bI} \ge 0. \end{aligned} \end{aligned}$$

All of the rates present in the model are non-negative on the planes bounding the cone of \(\mathbb {R}^4_+\). As a result, if we start from a non-negative beginning point in the inside of the non-negative cone, then the solutions will exist in the same domain of \(\mathbb {R}^4_+\) for all time t. This is the non-negativity property of all population compartments present in the system.

Theorem 1

The positively invariant set \(U=\left\{ (S,E,I,R) \in \mathbb {R}_+^4:0\le S,E,I,R \le \frac{\wedge }{d} \right\}\) is the biologically feasible region of governing model (1).

Proof

Let us consider the subdivision of the entire population \(N=S+E+I+R\) in the form of four disjoint compartments. Therefore, it follows from model system (1)

$$\frac{{{\text{d}}N}}{{{\text{d}}t}} < \wedge - {\text{d}}N.$$
(2)

This implies

$$\begin{aligned} N(t) < \dfrac{\wedge }{d} - \left( \dfrac{\wedge }{d} - N(0)\right) e^{-\text{d}t}, \end{aligned}$$

which further gives

$$\begin{aligned} 0 \le N(t) \le \dfrac{\wedge }{d}. \end{aligned}$$

This indicates that all the solutions of (1) whose initial conditions lie in \(U=\left\{ (S,E,I,R) \in \mathbb {R}_+^4:0\le S,E,I,R \le \frac{\wedge }{d} \right\}\) will persist in the same domain for all time t. \(\square\)

2.2 Existence of Equilibria and Basic Reproduction Number

The proposed model has one disease-free equilibrium state \(\varepsilon _0 = \left( \frac{\wedge }{d},0,0,0\right)\), which exists for all time t.

The basic reproduction number \(\mathcal {R}_0\) quantifies how many individuals an infected person will typically spread the illness to in a community with no resistance to it (Castillo-Chavez et al. 2002). The illness will gradually disappear if \(\mathcal {R}_0\) is smaller than one. The disease can become endemic, or persistent in the population for a very long time, if \(\mathcal {R}_0\) is higher than one (Allen et al. 2008). Making use of the next generation matrix method pioneered by Van den Driessche and Watmough (2002, 2008), we calculate the matrix containing new infections \(\mathcal {F}\) and the transitional matrix \(\mathcal {V}\) at the disease-free equilibrium. Thus,

$$\begin{aligned} \begin{aligned} \mathcal {F}&= \left( \begin{array}{cccc} 0 &{}\quad \beta \frac{\wedge }{d} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \text { and }\\ \mathcal {V}&= \left( \begin{array}{cccc} d+\mu +\nu &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ -\nu &{}\quad a+d+\gamma +\delta &{}\quad 0 &{}\quad 0 \\ -\mu &{}\quad -a-\gamma &{}\quad d+\eta &{}\quad 0 \\ 0 &{}\quad \beta \frac{\wedge }{d} &{}\quad -\eta &{}\quad d \\ \end{array} \right) . \end{aligned} \end{aligned}$$

The basic reproduction number of model system (1) is obtained as the absolute largest eigenvalue of the matrix \(\mathcal {F} \mathcal {V}^{-1}\), which is found to be

$$\begin{aligned} \mathcal {R}_0 = \frac{\beta \wedge \nu }{d (d+\mu +\nu ) (d+\delta +\gamma +a )}. \end{aligned}$$
(3)

2.3 Existence of Multiple Endemic Fixed Points

We now observe the endemic fixed point denoted by \(\varepsilon _*=(S_*,E_*,I_*,R_*)\) of governing model (1). After equating the governing equations to zero, we obtain, \(S_*=\dfrac{\wedge }{\beta I_* + d}\), \(E_* = \dfrac{\beta \wedge I_*}{(\nu +d+\mu ) (\beta I_* +d)}\), \(R_*=\dfrac{1}{d+\eta I_*} \left( \gamma I_* + \dfrac{\wedge \beta \mu I_*}{(\nu +d+\mu )(\beta I_* +d)} + \dfrac{a I_*}{1+bI_*}\right)\), where \(I_*\) is real positive root of the equation below

$$\begin{aligned} \phi (I_*) = P_0 + P_1 I_* +P_2 I_*^2 + P_3 I_*^3 = 0. \end{aligned}$$
(4)

Here,

$$\begin{aligned} P_0&= d^2 (d+\delta +\gamma +a)(\mathcal {R}_0 - 1),\\ P_1&= \eta \Bigg \{\frac{\beta \wedge \nu }{d + \nu + \mu } - d (d+\delta +\gamma +a) \Bigg \}\\&\quad + d \Bigg \{\frac{\beta \wedge \nu b}{d + \nu + \mu } - (\beta + bd) (d+\delta +\gamma ) - a \beta \Bigg \}\\&\quad + \eta \left( \gamma d + a d + \frac{\beta \wedge \mu }{d + \nu + \mu }\right) ,\\ P_2&= \eta \Bigg \{\gamma (\beta + bd) + a \beta + \frac{b \beta \wedge \mu }{d + \nu + \mu }\Bigg \} - \text{d} b \beta (d+\delta +\gamma )\\&\quad + \eta \Bigg \{ \frac{\beta \wedge \nu }{d + \nu + \mu } - d(d+\delta +\gamma ) -ad \Bigg \},\\ P_3&= - b \beta \eta (d+\delta ). \end{aligned}$$

The coefficient of the highest power \(P_3\) is always negative and the constant coefficient \(P_0 < (>) 0\) subject to \(\mathcal {R}_0 < (>) 1\). Depending on parameter values, the signs of \(P_1\) and \(P_2\) may be positive or negative. Therefore, \(\phi (I_*)\) may have several real roots which are positive. Also, from Eq. (4), it is to be noted that \(\phi (0) > 0\) and \(\phi (\infty ) < 0\); hence, by the property of continuity, there exists a positive real root such that \(\phi (I_*) = 0\) when \(\mathcal {R}_0 > 1\). Thus, atleast one endemic fixed point exists when \(\mathcal {R}_0 > 1\).

By Descartes’ rule of signs, Table 2 demonstrates the number of positive real roots of Eq. (4). It can be observed that in one case, there is an occurrence of two roots when \(\mathcal {R}_0 < 1\), thus directing toward the potential occurrence of backward bifurcation in the system.

Table 2 Possible number of real positive roots of \(\phi (I_*) = 0\)
Full size table

Theorem 2

Model system (1) possesses:

  1. 1.

    A unique endemic equilibrium \(\varepsilon _*\) if \(P_1 >0\), \(P_2 <0\), or \(P_1 >0\), \(P_2 >0\), or \(P_1 <0\), \(P_2 <0\), when \(\mathcal {R}_0 > 1\).

  2. 2.

    A maximum of two endemic equilibria \(\varepsilon _1\) and \(\varepsilon _2\) if \(P_1 >0\), \(P_2 <0\), or \(P_1 <0\), \(P_2 >0\), or \(P_1 >0\), \(P_2 > 0\), when \(\mathcal {R}_0 < 1\).

  3. 3.

    There exist atmost three endemic equilibria \(\varepsilon _1\), \(\varepsilon _2\) and \(\varepsilon _*\) when \(P_1 <0\), \(P_2 >0\) for \(\mathcal {R}_0 > 1\).

3 Stability Analysis of the Equilibria

An essential method for understanding population behavior over time is the examination of local and global stability of equilibrium points in a population model. In this section, the local and global stabilities of the fixed points are demonstrated along with the validation with numerical results in Fig. 2.

3.1 Local Asymptotic Stability of Equilibria

Theorem 3

The disease-free equilibrium point \(\varepsilon _0\) of model system (1) is locally asymptotically stable(l.a.s.) if \(\mathcal {R}_0 < 1\), and unstable otherwise.

Proof

If the real parts of all the eigenvalues of the Jacobian matrix of system (1) at the steady state are negative, then that steady state of the system will be l.a.s. Thus, the Jacobian matrix at the DFE is given by

$$\begin{aligned} J\vert _{\varepsilon _0} = \left( \begin{array}{cccc} -d &{}\quad 0 &{}\quad -\frac{\beta \wedge }{d} &{}\quad 0 \\ 0 &{}\quad -d-\mu -\nu &{}\quad \frac{\beta \Lambda }{d} &{}\quad 0 \\ 0 &{}\quad \nu &{}\quad -a-\gamma -d-\delta &{}\quad 0 \\ 0 &{}\quad \mu &{}\quad a+\gamma &{}\quad -d \\ \end{array} \right) . \end{aligned}$$
(5)

Two eigenvalues of the Jacobian matrix at the disease-free equilibrium are \(-d\) and \(-d\), which are evidently negative. The remaining two eigenvalues are rendered by the equation

$$\begin{aligned} \begin{aligned} \lambda ^2 + M_1 \lambda + M_0 = 0, \end{aligned} \end{aligned}$$
(6)

where \(M_1 = 2d+\mu +\nu +a+\delta +\gamma\), \(M_0 = (d+\mu +\nu ) (d+ a \delta + \gamma ) (1- \mathcal {R}_0)\).

For \(\mathcal {R}_0 < 1\), \(M_1,M_0 > 0\), hence Eq. (6) has two roots with negative real parts. Thus, by Routh–Hurwitz criteria (Dutta and Gupta 2018), the DFE \(\varepsilon _0\) is l.a.s. if \(\mathcal {R}_0 < 1\). \(\square\)

Theorem 4

The governing model (1) possesses an endemic steady state \(\varepsilon _*\) for \(\mathcal {R}_0>1\) when \(P_1 >0\), \(P_2 <0\), or \(P_1 >0\), \(P_2 >0\), or \(P_1 <0\), \(P_2 <0\) when \(\mathcal {R}_0 > 1\) and it is l.a.s. when \(h_0>0\), \(h_1>0\), \(h_2>0\), \(h_3>0\) and \(h_1 h_2 h_3 > h_1^2+h_0 h_3^2\) (\(h_1,h_2,h_3,h_4\) are defined in the proof below).

Proof

The Jacobian matrix of governing model (1) at the endemic fixed point \(\varepsilon _*\) is found to be

\(J\vert _{\varepsilon _*}=\)

$$\begin{aligned} \begin{aligned} \begin{pmatrix} -\beta I_* - d &{}\quad 0 &{}\quad -\beta S_* &{}\quad 0 \\ \beta I_* &{}\quad -(d+\nu +\mu ) &{}\quad \beta S_* &{}\quad 0 \\ 0 &{}\quad \nu &{}\quad -(d+\delta +\gamma )-\frac{a}{{(1+bI_*)}^2}+ \eta R_* &{}\quad \eta I_* \\ 0 &{}\quad \mu &{}\quad \gamma + \frac{a}{{(1+bI_*)}^2} - \eta R_* &{}\quad -\eta I_* \end{pmatrix}. \end{aligned} \end{aligned}$$

The characteristic equation of \(J\vert _{\varepsilon _*}\) is given below

$$\begin{aligned} u_0 + u_1 x + u_2 x^2 + u_3 x^3 + x^4 = 0. \end{aligned}$$
(7)

Here, \(u_0 = -(\beta I_* + d)[\beta ^2 \eta S_* I_*^2(d+\nu +\mu )(\nu +\mu )+\beta \eta (\nu +\mu )S_* I_* -\eta I_* (\gamma +\frac{a}{{(1+bI_*)}^2}-\eta R_*)]\), \(u_1 = [-(\beta I_* + d)(d+\mu +\nu +\eta I_*)+(d+\nu +\mu )\eta I_*](d+\delta +\gamma +\frac{a}{{(1+bI_*)}^2}-\eta R_*)-(\beta I_* + d)[\eta I_* (d+\nu +\mu )-\nu \beta S_*]-\nu \beta ^2 S_* I_*\),

\(u_2 = (d+\delta +\gamma +\frac{a}{{(1+bI_*)}^2}-\eta R_*)[-\eta I_* (\beta I_* + d)+d+\nu +\mu + \eta I_*]-(d+\nu +\mu )(\beta I_* + d) + \nu \beta S_*\), \(u_3 = d+\nu +\mu +\delta +\gamma +\frac{a}{{(1+bI_*)}^2}-\eta R_*+(\eta -\beta )I_*\).

Utilizing Routh–Hurwitz criterion given in (Martcheva 2015) for dimension \(n=4\), it can be established that every root of Eq. (7) has negative real parts on the condition that \(u_0>0\), \(u_1>0\), \(u_2>0\), \(u_3>0\) and \(u_1 u_2 u_3 > u_1^2+u_0 u_3^2\). Thus, the unique EE \(\varepsilon _*\) is l.a.s. if \(u_0>0\), \(u_1>0\), \(u_2>0\), \(u_3>0\) and \(u_1 u_2 u_3 > u_1^2+u_0 u_3^2\) in addition to its existence. \(\square\)

3.2 Global Stability of Equilibria

Theorem 5

The disease-free equilibrium point is globally asymptotically stable (g.a.s.) for \(\mathcal {R}_0 < 1\), provided \(b=\eta =0\).

Proof

By the theorem pioneered by Chavez et al. (2002), we take into consideration \(\texttt{X}={(S,R)}^T\) with \(\texttt{Y}={(E,I)}^T\) such that

$$\begin{aligned} \begin{aligned} \texttt{F}(\texttt{X},\texttt{Y})&= [\wedge - \beta S I -\text{d} S,\, \beta S I -(d+\nu +\mu )E]^T,\\ \texttt{G}(\texttt{X},\texttt{Y})&= [\nu E - (d+\delta +\gamma )I - \frac{aI}{1+bI}+\eta R I,\,\\&\mu E + \frac{aI}{1+bI} + \gamma I - \text{d} R-\eta R I]^T. \end{aligned} \end{aligned}$$
(8)

Here, the noninfected state is designated by \(\varepsilon _0=(x^*,0,0)\), where \(x^*=(\frac{\wedge }{d},0)\). It can be easily seen that \(x^*\) is g.a.s. for the subsystem \(\frac{\text{d}\texttt{X}}{\text{d}t} = \texttt{F}(\texttt{X},0)\) as \(\texttt{X} \rightarrow x^*\) when \(t \rightarrow \infty\). In addition,

$$\begin{aligned} \dfrac{\text{d}\texttt{X}}{\text{d}t} = F(\texttt{X},0)=\begin{pmatrix} \wedge - \text{d}S\\ 0 \end{pmatrix}. \end{aligned}$$

Also,

$$\begin{aligned} \begin{aligned} \texttt{A}=D_\texttt{Y} \texttt{G}(x^*,0)=\begin{pmatrix} -(d+\nu +\mu ) &{} \beta S \\ \nu &{} -(d+\delta +\gamma +a) \end{pmatrix}. \end{aligned} \end{aligned}$$

Since all nondiagonal elements are positive, \(\texttt{A}\) is a Metzler matrix.

And thus, \(\hat{\texttt{G}} (\texttt{X},\texttt{Y})\) is given by

$$\begin{aligned} \begin{aligned} \hat{\texttt{G}} (\texttt{X},\texttt{Y})&= \texttt{A} \texttt{Y}-\texttt{G} (\texttt{X},\texttt{Y}),\\ \implies \hat{\texttt{G}} (\texttt{X},\texttt{Y})&= \begin{pmatrix} 0 \\ -aI + \frac{aI}{(1+bI)} - \eta RI \end{pmatrix}. \end{aligned} \end{aligned}$$

We note that \(\hat{\texttt{G}} (\texttt{X},\texttt{Y}) \ge 0\) when \(b = \eta = 0\). Therefore, from the theorem, it follows that the disease-free state is g.a.s. provided \(\mathcal {R}_0 < 1\) when \(b=\eta =0\) (Li 2018). \(\square\)

Lemma 1

Governing model (1) is uniformly persistent, i.e., a real positive constant M exists such that

$$\begin{aligned} \lim _{t \rightarrow \infty } inf \{S(t),E(t),I(t),R(t)\} \ge M. \end{aligned}$$
(9)

Proof

It can be seen via Theorem (3) that the DFE \(\varepsilon _0\) is unstable when \(\mathcal {R}_0 >1\). Deploying the result on uniform persistence by Freedman et al. (1994), the uniform persistence of our governing system (1) is established by the fact that \(\varepsilon _0\) is unstable when \(\mathcal {R}_0 > 1\). \(\square\)

Theorem 6

The unique endemic equilibrium point \(\varepsilon _*\), provided it exists, is g.a.s. when \(\mathcal {R}_0 > 1\).

Proof

Let us take into consideration a Lyapunov function (Chavez et al. 2002; Li and Muldowney 1995)

$$\begin{aligned} \begin{aligned} \varpi&= \frac{1}{2} {(S-S_*+E-E_*+I-I_*+R-R_*)}^2 \\&+ \frac{k_1}{2} {(S-S_*+E-E_*)}^2 + \frac{k_2}{2} {(I-I_*+R-R_*)}^2. \end{aligned} \end{aligned}$$
(10)

where \(k_1\) and \(k_2\) are positive real numbers that shall be determined in due time. On differentiating \(\varTheta\) with respect to t, we obtain

$$\begin{aligned} \begin{aligned} \dfrac{\text{d} \varpi }{\text{d}t}&= (S-S_*+E-E_*+I-I_*+R-R_*)\\&\left( \dfrac{\text{d}S}{\text{d}t} +\dfrac{\text{d}E}{\text{d}t} + \dfrac{\text{d}I}{\text{d}t} + \dfrac{\text{d}R}{\text{d}t} \right) \\&+ k_1 (S-S_*+E-E_*) \left( \dfrac{\text{d}S}{\text{d}t} +\dfrac{\text{d}E}{\text{d}t} \right) \\&+ k_2 (I-I_*+R-R_*) \left( \dfrac{\text{d}I}{\text{d}t} +\dfrac{\text{d}R}{\text{d}t} \right) . \end{aligned} \end{aligned}$$
(11)

We shall determine the following relations from the system of equations (1) by using the resulting relations

$$\begin{aligned} \begin{aligned} \wedge&= \text{d}S + \text{d}E +(d+\delta ) I + \text{d}R,\\ \wedge&= \text{d}S+(\nu +d+\mu ),\\ \nu E&= (d+\delta )I - \mu E + \text{d}R. \end{aligned} \end{aligned}$$
(12)

Hence Eq. (11) becomes

$$\begin{aligned} \begin{aligned} \dfrac{\text{d} \varpi }{\text{d} t}&= (S-S_*+E-E_*+I-I_*+R-R_*) \\&\{-d(S-S_*) - d(E-E_*) - (d+\delta ) (I-I_*)\\&- d(R-R_*)\} +k_1(S-S_*+E-E_*)\{-d(S-S_*)\\&- (\nu +d+\mu )(E-E_*)\} + k_2 (I-I_*+R-R_*)\\&\{(\nu +\mu )(E-E_*) - (d+\delta ) (I-I_*) -d(R-R_*)\}. \end{aligned} \end{aligned}$$
(13)

Simplifying Eq. (13) and choosing the constants \(k_1 = 1\) and \(k_2 = \frac{d}{d+\delta }\), we get that \(\frac{\text{d} \varpi }{\text{d}t} < 0\). By LaSalle’s invariance theorem (Martcheva 2015; La Salle 1976), our analysis leads us to the conclusion that for \(\mathcal {R}_0 >1\), the unique EE is g.a.s. \(\square\)

Fig. 2
figure 2

Global stabilities of equilibrium points

Full size image

In Fig. 2, the global stability of both the DFE and the unique EE is depicted. As seen in Fig. 2a, if the parametric restrictions given in Theorem (5) along with \(\mathcal {R}_0 < 1\) are satisfied, the DFE is g.a.s. for any perturbation in the initial states of the compartments. Similarly, from Theorem (6), the EE is g.a.s., as depicted in Fig. 2b provided it exists and is unique for any disturbance in the initial conditions whenever \(\mathcal {R}_0> 1\).

Epidemiological significance: In proposed model (1), the DFE exhibits global stability when the BRN \(\mathcal {R}_0<1\) with the additional conditions \(b=0\) and \(\eta =0\), i.e., there is no saturation in treatment along with no reinfections. In the initial state of COVID-19 where there is practically no herd immunity, it is realistically feasible that all persons should get treated and the possibility of reinfections is negligible. In essence, the population will remain free from experiencing disease outbreaks, and the disease will not establish an endemic presence as shown in Fig. 2a. Moreover, the global stability of the unique EE implies that if the disease is already present within the population \((I > 0)\), it will persist over an extended period. The disease will become a sustained and recurring component of the population, resulting in the continual occurrence of outbreaks. The graphs in Fig. 2a, b signify that the global stabilities do not depend on the initial value of the population sizes if the given conditions in Theorems (5) and (6) are met.

4 Bifurcation Analysis

Bifurcation in a dynamical system happens when gradual changes in the system’s parameter values result in abrupt qualitative or topological changes in the behavior of the system. In epidemiology, there are two different sorts of branches: local and global (Ahmed et al. 2023). In one-dimensional systems, common bifurcation types such as saddle-node, tangent, transcritical and pitchfork bifurcations are displayed.

For the governing system (1), we shall consider the effective COVID-19 transmission rate \(\beta\) as the bifurcation parameter. Assuming \(\mathbb {B}_1 = d+\mu +\nu\) and \(\mathbb {B}_2 = d+\delta +\gamma +a\), the model system is rewritten as

$$\begin{aligned} \begin{aligned} \texttt{F}_1&= \wedge - \beta x_1 x_3 - \text{d} x_1\\ \texttt{F}_2&= \beta x_1 x_3 - \mathbb {B}_1 x_2\\ \texttt{F}_3&= \nu x_2 - \mathbb {B}_2 x_3 - \frac{a x_3}{1+b x_3} + \eta x_4 x_3\\ \texttt{F}_4&= \mu x_2 + \gamma x_3 + \frac{a x_3}{1+b x_3} - \text{d} x_4 - \eta x_4 x_3. \end{aligned} \end{aligned}$$
(14)

The Jacobian matrix at the DFE \(\left( \frac{\wedge }{d},0,0,0\right)\) is found to have three negative eigenvalues \(-d\), \(-d\), \(-(3d+\delta +\gamma +\mu +\nu )\) and one simple zero eigenvalue at \(\mathcal {R}_0 = 1\) at \((\varepsilon _0,\beta ^*)\). The left and right eigenvectors at the zero eigenvalue are denoted by \(\texttt{V}={[0 \quad \nu \quad \mathbb {B}_1 \quad 0]}^T\) and \(\texttt{W}={[-d \nu \mathbb {B}_1 \mathbb {B}_2 \quad \mu d\mathbb {B}_2 \quad \mu \nu d \quad \mu (\mu \mathbb {B}_2+\nu (\gamma +a))]}^T\).

By applying the center manifold theorem in the theory of bifurcation by Castillo–Chavez and Song in Carr (2012), we compute the parameters \(\text{A}\) and \(\text{B}\) as

$$\begin{aligned} \begin{aligned} \text{A}&=2 v_2 w_1 w_3 \frac{\partial ^2 \texttt{F}_2}{\partial x_1 \partial x_3} + v_3 \left( w_3^2 \frac{\partial ^2 \texttt{F}_3}{\partial x_3^2} + 2 w_3 w_4 \frac{\partial ^2 \texttt{F}_3}{\partial x_3 \partial x_4}\right) \\&=2 d \mu \nu \mathbb {B}_1 [a b d \mu \nu + \eta \mathbb {B}_1 \{\mu \mathbb {B}_2 + \nu (\gamma +a)\}] \\&- \frac{2 d^2 \nu ^2 \mathbb {B}_1^2 \mathbb {B}_2^2}{\wedge \mu },\\ \text{B}&= v_2 w_3 \frac{\partial ^2 \texttt{F}_2}{\partial x_3 \partial \beta ^*} = \nu \mu \wedge > 0. \end{aligned} \end{aligned}$$

For the occurrence of backward bifurcation (Li et al. 2015), the condition that \(\text{A} > 0\) and \(\text{B} > 0\) is essential. After evaluating the above expression for \(\text{A}\) and substituting the values of \(\mathbb {B}_1\) and \(\mathbb {B}_2\), we obtain the condition

$$\begin{aligned} \eta > \dfrac{d (d+\nu +\mu ) {(d+\delta +\gamma +a)}^2 - a b d \nu \wedge \mu ^3}{\wedge \mu ^2 (d+\delta +\gamma +a) \{\mu (d+\delta +\gamma +a) + \nu (\gamma +a)\}}. \end{aligned}$$

The above result is worded in the following theorem in a concise manner:

Theorem 7

Governing model system (1) experiences backward bifurcation when

\(\eta > \dfrac{d (d+\nu +\mu ) {(d+\delta +\gamma +a)}^2 - a b d \nu \wedge \mu ^3}{\wedge \mu ^2 (d+\delta +\gamma +a) \{\mu (d+\delta +\gamma +a) + \nu (\gamma +a)\}}\), and a forward bifurcation when

\(\eta < \dfrac{d (d+\nu +\mu ) {(d+\delta +\gamma +a)}^2 - a b d \nu \wedge \mu ^3}{\wedge \mu ^2 (d+\delta +\gamma +a) \{\mu (d+\delta +\gamma +a) + \nu (\gamma +a)\}}\).

4.1 Forward Bifurcation Phenomenon

There are two possible stable equilibria in the instance of a forward bifurcation: one in which the disease rapidly spreads and affects a significant portion of the population, and another in which the disease is controlled, leading to only a minor fraction of the population being affected. When a critical parameter value, such as the rate of effective transmission \(\beta\) or the initial count of infected individuals, is surpassed, the transition between these two equilibria occurs (Das et al. 2021). The presence of transcritical bifurcation in a system implies that if the basic reproduction number \(\mathcal {R}_0\) goes from being greater than 1 to being less than 1, then the disease can be eradicated completely. When \(\mathcal {R}_0 > 1\), the disease-free equilibrium experiences a stability transition. It is stable when \(\mathcal {R}_0 < 1\) and becomes unstable when \(\mathcal {R}_0 > 1\). Figure 3 illustrates an equivalent numerical representation of such dynamics. We choose the parameters \(\wedge =2\), \(\eta =0.01\), \(d=0.3\), \(\delta =0.1\), \(\nu =0.7\), \(\mu =0.01\), \(a=0.0001\), \(b=0.0005\), \(\gamma =0.003\). As \(\mathcal {R}_0\) moves toward unity from left to right, a stable EE is observed, whereas the DFE becomes unstable.

Fig. 3
figure 3

Forward bifurcation is observed as \(\mathcal {R}_0\) moves toward unity from left to right

Full size image

If the disease system is in a stable equilibrium with high levels of infection, even a small rise in the number of infected people or transmission rate can cause a large-scale epidemic. If, on the other hand, the system is in a stable equilibrium with low levels of infection, the disease is likely to remain localized, and only a small portion of the population will be affected.

Epidemiological significance: Forward bifurcation in the model system as in Fig. 3 suggests the presence of a critical threshold of \(\beta\) that determines the potential for a COVID-19 outbreak. Prior to the occurrence of the bifurcation, the DFE remains robust and prevents the disease from gaining a foothold in the population. Following the bifurcation, under specific parameter conditions, the DFE loses stability, allowing the disease to endure within the population. This transition holds significance as it offers valuable insights into the minimal prerequisites for the initiation of an outbreak.

4.2 Backward Bifurcation Phenomenon

Backward bifurcation is a phenomenon that gives insight into the complexities of mitigating the disease. It happens when a disease can continue to spread through a community even after transmission rates drop below a specific threshold. In some cases, when the transmission rate is reduced below the critical threshold needed for the disease to persist, the disease can still persist due to backward bifurcation. The reason behind this occurrence is the simultaneous existence of a stable endemic equilibrium and a stable disease-free equilibrium., even when \(\mathcal {R}_0\) is less than one (Moghadas 2004; Wang and Ruan 2004). We choose the parameters \(\wedge =0.01\), \(\eta =0.7\), \(d=0.001\), \(\delta =0.003\), \(\nu =0.5\), \(\mu =0.01\), \(a=0.001\), \(b=0.0005\), \(\gamma =0.003\) and \(\beta \in (0.0005,0.2)\) to numerically prove the result in Theorem (7). Upon analyzing the specified set of parameters, we notice that model system (1) satisfy condition (4) leading to the existence of two endemic equilibria \(\varepsilon _1^*=(9.99714, 5.58956 \times 10^{-6},0.000408155,,0.00121806)\) and \(\varepsilon _2^*=( 5.73275,0.00835079,9.06338,0.00539013)\) when \(\mathcal {R}_0 < 1\) as shown in Fig. 4. The EE \(\varepsilon _1^*\) is unstable, while \(\varepsilon _2^*\) is stable. This demonstrates that merely reducing the basic reproduction number to less than one is insufficient to halt the advancement of COVID-19 disease. Owing to these phenomena, additional control measures must be prioritized in addition to the main metrics, such as the transfer rate and death rate from disease. External strategies like masking, hand sanitizing and maintaining appropriate distance from other potentially infected individuals are necessary.

Fig. 4
figure 4

Backward bifurcation is observed as \(\mathcal {R}_0\) movies toward unity from right to left

Full size image

The subsistence of a high-risk population that is more prone to infection and is more responsible to propagate the outbreak may be a cause in the physical interpretation of backward bifurcation. Even if the general transmission rate is decreased, the disease may still continue if the high-risk population is not properly targeted by control methods.

Epidemiological significance: Epidemiologically this signifies that the branches of two EE are very sensitive to the initial population. For a slight change in the number of infectives, the strain might move to the unstable branch. A backward bifurcation carries implications of intricate and uncertain disease dynamics within the field of epidemiology. In Fig. 4, it becomes evident that there exists a stable DFE coexisting with a stable EE and an unstable EE concurrently. This intricacy in equilibrium coexistence can result in fluctuations in disease prevalence, rendering the prediction of disease outcomes a challenging endeavor. Consequently, this implies that the continuation or intensification of disease control measures may be necessary to avert outbreaks, even when the disease’s prevalence is relatively low. Furthermore, the presence of a backward bifurcation serves as a valuable tool for validating the accuracy of epidemiological models. The observation of real-world data aligning with a model’s projections of a backward bifurcation enhances confidence in the model’s validity and its ability to encompass the intricacies of disease dynamics.

4.3 Saddle-Node Bifurcation

We derive the condition for transversality for saddle-node bifurcation by deploying the Sotomayor’s theorem (Perko 2013), by considering \(\beta\) as the bifurcation parameter for governing model system (1). We have encountered that the occurrence and destruction of equilibria is dependent on the parameter \(\beta\). Let the critical value of \(\beta\) for the occurrence of saddle-node bifurcation be denoted by \(\beta _{SN}\). Therefore, governing model system (1) has two equilibria (\(\varepsilon _1\) and \(\varepsilon _2\)) when \(\beta >\beta _{SN}\), no equilibria when \(\beta =\beta _{SN}\) and there is a collision (\(\varepsilon _1\)=\(\varepsilon _2\)) when \(\beta <\beta _{SN}\). Let the point where both equilibrium points collide be denoted by \(\varepsilon ^* = (S^*_{SN},E^*_{SN},I^*_{SN},R^*_{SN})\). Define \(g={(g_1,g_2,g_3,g_4)}^T\), where \(g_1,g_2,g_3,g_4\) are taken to be

$$\begin{aligned} \begin{aligned} g_1&= \wedge - \beta S I - \text{d} S\\ g_2&= \beta S I - (\nu +d+\mu ) E\\ g_3&= \nu E - (d+\delta +\gamma ) I - \frac{a I}{1+b I} + \eta R I\\ g_4&= \mu E + \gamma I + \frac{a I}{1+b I} - \text{d} R - \eta R I. \end{aligned} \end{aligned}$$
(15)

Assuming that the Jacobian matrix \(J=Dg(\varepsilon ^*,\beta _{SN})\) possesses a simple eigenvalue \(\lambda =0\) with an eigenvector \(y={(y_1,y_2,y_3,y_4)}^T\), and also the transpose of the Jacobian matrix possesses an eigenvector \(z={(z_1,z_2,z_3,z_4)}^T\) for the zero eigenvalue. Further, taking the derivative of g with respect to \(\beta\), we have

$$\begin{aligned} g_\beta ={(g_{1\beta },g_{2\beta },g_{3\beta },g_{4\beta })}^T = {(-SI,SI,0,0)}^T. \end{aligned}$$

At the bifurcating equilibrium point,

$$\begin{aligned} g_\beta (\varepsilon ^*,\beta _{SN})= {(-S_{SN}^* I_{SN}^*,S_{SN}^* I_{SN}^*,0,0)}^T. \end{aligned}$$

Again,

$$\begin{aligned} z^T g_\beta (\varepsilon ^*,\beta _{SN})= -z_1 S_{SN}^* I_{SN}^* + z_2 S_{SN}^* I_{SN}^*. \end{aligned}$$

We also find

$$\begin{aligned} \begin{aligned} z^T [D^2 g (\varepsilon ^*,\beta _{SN})(y,y)] = 2\beta _{SN} y_1 y_2 (z_2-z_1) \\ + \dfrac{2 a b y_3^2 (w_3 - w_4)}{{(1+b I^*)}^3} + 2 \eta y_3 y_4 (w_3 - w_4) \ne 0. \end{aligned} \end{aligned}$$

If the following conditions given by

  1. 1.

    \(z^T g_\beta (\varepsilon ^*,\beta _{SN}) \ne 0\),

  2. 2.

    \(z^T [D^2 g (\varepsilon ^*,\beta _{SN})(y,y)] \ne 0\),

are satisfied, governing model system (1) undergoes saddle-node bifurcation.

Fig. 5
figure 5

Detection of saddle-node bifurcation points in the model

Full size image

Numerical validation: It is known that if \(det(J)<0\), the system undergoes saddle-node bifurcation. Let us consider the values of parameters as given in Table 3.

Table 3 Parameters for numerical validation
Full size table

Along with these parameters, if we consider \(\beta \in (7.2 \times 10^{-5},4.69 \times 10^{-4})\), we find that determinant of the Jacobian \(det(J) < 0\). There exist two equilibrium points \(\varepsilon _1=(385.2041,0.0733,0.9398,1.2095)\) and \(\varepsilon _2=(388.5982,0.0057,0.0145,0.2477)\) at whom value of det(J) is \(-4.3908 \times 10^{-6}\) and \(-8.9441 \times 10^{-7}\), respectively. Computing numerically, we find the eigenvalues at \(\varepsilon _1\) are \(-\)0.471653, \(-\)0.21167, \(-\)0.00891927 and 0.00493099 and those at \(\varepsilon _2\) are \(-\)0.57149, \(-\)0.112102, \(-\)0.00894602 and 0.00156058. By using MATCONT, the figure depicting these equilibrium points to be saddle nodes is depicted in Fig. 5.

5 Sensitivity Analysis

The normalized forward sensitivity index of \(\mathcal {R}_0\) in relation to a model parameter \(\Theta\) is defined to be

$$\begin{aligned} \mathbb {E}_\Theta ^{\mathcal {R}_0} = \dfrac{\Theta }{\mathcal {R}_0} \dfrac{\partial \mathcal {R}_0}{\partial \Theta } \end{aligned}$$

This definition by Chitnis et al. (2008) evaluates the normalized change in \(\mathcal {R}_0\) when one parameter changes, while the other parameters remain constant. A positive sensitivity index of a parameter indicates that \(\mathcal {R}_0\) is increasing in relation to that parameter, whereas a negative indexing suggests that \(\mathcal {R}_0\) is decreasing in relation to that parameter. The expressions for sensitivity index of every parameter present in the BRN of governing model (1) are computed as

$$\begin{aligned} \begin{aligned} \mathbb {E}_\wedge ^{\mathcal {R}_0}&=1,\quad \mathbb {E}_\beta ^{\mathcal {R}_0} =1, \quad \mathbb {E}_\nu ^{\mathcal {R}_0} =\frac{d + \mu }{d + \mu + \nu },\\ \mathbb {E}_\mu ^{\mathcal {R}_0}&=-\frac{\mu }{d + \mu + \nu }, \mathbb {E}_\delta ^{\mathcal {R}_0} =-\frac{\delta }{a + d + \delta + \gamma },\\ \mathbb {E}_\gamma ^{\mathcal {R}_0}&= -\frac{\gamma }{a + d + \delta + \gamma }, \quad \mathbb {E}_a^{\mathcal {R}_0} =-\frac{a}{a + d + \delta + \gamma }. \end{aligned} \end{aligned}$$

The initial parameter values to establish the sensitivity indices are taken from Table 4. From Fig. 6, it is seen that parameters \(\beta\), \(\wedge\) and \(\nu\) have positive indices, whereas \(\delta\), \(\gamma\), \(\mu\) and a have a negative index. From Table 4 and Fig. 6, we conclude that \(\beta\), \(\wedge\) and \(\gamma\) possess the most positive and negative correlation with \(\mathcal {R}_0\). Thus, we have established the contour plots of these parameters to better understand their influence with respect to \(\mathcal {R}_0\) in Fig. 7.

Fig. 6
figure 6

Sensitivity indices of parameters present in \(\mathcal {R}_0\)

Full size image

Sensitivity analysis results assist policymakers and public health officials in determining which parameters have the greatest impact on \(\mathcal {R}_0\) and how changes in these parameters can affect the disease transmission dynamics. This information can then be used to develop effective disease control strategies and make informed decisions about disease prevention and control resource allocation.

Fig. 7
figure 7

Contour plots of \(\mathcal {R}_0\) as a function of \(\beta\) and \(\gamma\), \(\mu\), \(\nu\) and \(\delta\) in (a), (b), (c) and (d), respectively

Full size image

The contour plots of any two parameters are easy to decipher due to the variation in the colormap of the quantity \(\mathcal {R}_0\). As shown in Fig. 7, we have plotted the effect of \(\beta\) versus four parameters viz., \(\gamma\), \(\mu\), \(\nu\) and \(\delta\) with respect to the parameters initially taken from Table 4. Figure 7a depicts the relation between \(\beta\) and \(\gamma\), it can be seen that if \(\beta\) can be lowered below 0.05 and simultaneously \(\gamma\) can lie in the interval (0, 1), the BRN can be decreased to 1 as shown by the blueish region in the colormap on the side. Likewise, as soon as \(\beta\) crosses approximately 0.1 for the same values from the interval (0, 1) for \(\gamma\), the color moves to the red region of the colormap, indicating that the value of the BRN has surpassed 1 and the region containing the population has crossed over to the endemic state. Identically for Fig. 7c, the disease remains in the disease-free zone when \(\beta\) and \(\nu\) lie approximately in (0, 0.1).

6 Numerical Simulations

In the context of modeling, control parameters are variables that are used to modify or govern the behavior of a model. These parameters can significantly influence the dynamics of the model and can have various effects depending on their values. The effects of control parameters on model dynamics can be diverse, and they are often domain-specific. Changes in behavioral dynamics of a disease with respect to parameter variations are deemed essential to thoroughly understand the progression of the disease.

Table 4 Parameter table
Full size table

These trends are proof that highly transmissible diseases like COVID-19 have multiple dynamical attributes in an endemic condition due to which they are prone to unpredictability at the onset of the spread of the illness. The data values of each parameter taken from the literature for COVID-19 are mentioned in Table 4.

This section focuses on investigating the dynamic behavior of the population under the influence of different parameters employed in model (1). Specially, the impact of the reinfection rate, the saturation constant, recovery rate of infected individuals are monitored with the help of Figs. 8, 9, 10, 11 and 12 by simulating the diagrams in MATLAB.

6.1 Effect of \(\nu\)

In Fig. 8, the effect of the proportion of individuals being infected with COVID-19 is presented while keeping the other parametric values constant. It can be observed that as \(\nu\) ranges from 0.02, 0.2, 0.4, 0.6, the infected population is obviously going higher.

Fig. 8
figure 8

Effect of \(\nu\) on compartments E, I, R

Full size image

It is interesting to see the leap as it takes the value from 0.02 to 0.2, there is a significant difference in the population size, also the peak comes in later when the proportion is lower. It is also seen that \(\nu\) has no significant impact on the compartment of recovered class.

6.2 Effect of Saturation Constant b

In Fig. 9, the impact of the saturation constant is studied with respect to the infected compartment. As the saturation constant is decreased through values 2, 0.5, 0.01, 0.001, it can be assessed that the number of infectious population is decreased. The saturated treatment function in an epidemiological mathematical model has interesting dynamics. It is integrated in our model because of the restricted accessibility of medical strategies and supplies (Hofer et al. 2021).

Fig. 9
figure 9

Effect of b on compartments E, I, R

Full size image

Since the treatment function is a Holling type-II function \(T(I)=\frac{aI}{1+bI}\), therefore when \(I \rightarrow \infty\), \(T (I) \rightarrow \frac{a}{b}\). As b is lowered significantly, \(\frac{a}{b}\) increases accordingly i.e., as the amount of treated humans from infections are increased, the rate of infection and infected can be lowered. From the figure, it is clear that if the saturation point is around 0.001, the peak is just over half the highest number of infections as it would have been had the saturation been at the value \(b=2\).

6.3 Effect of Reinfection Rate \(\eta\)

Figure 10 illustrates one of the main parameters introduced in the proposed model. The consequences of reinfection in a pandemic situation are catastrophic. Literature suggests that reinfection with COVID-19 has caused a massive dent on the health sector. On people with ages over sixty battling with comorbidities and severe illnesses, reinfection can be detrimental to their health (Goldman et al. 2020). If \(\eta\) is increased from 0.003 to 0.008, a substantial gap in the rise of sick population can be registered. It is noteworthy that in a difference of 0.005, there is a jump of around 45 infected people.

Fig. 10
figure 10

Effect of \(\eta\) on compartments E, I, R

Full size image

So, we perceive it to be one of the important control parameters in the governing model. It is worth mentioning here that the system shows backward bifurcation so it is not enough to lower the BRN to less than 1. Since \(\eta\) does not occur in the reproduction number, it is to be prioritized that reinfections are kept as less as possible. There must be treatments such as vaccination and additional doses of medicines to keep occurrence of reinfection amidst the recovered population. Additionally, it is crucial to remember that when new versions of the virus evolve and become more widespread, the situation may alter (Colson et al. 2021).

6.4 Effect of Natural Recovery Rate \(\gamma\) and Effective Transmission Rate \(\beta\)

Fig. 11
figure 11

Effect of \(\gamma\) on compartments E, I, R

Full size image

Figures 11 and 12 provide an insight into the effect of \(\gamma\), the natural recovery rate, and \(\beta\), the effective transfer rate of susceptible to infected compartment. It is noticeable that as the value of \(\gamma\) increases from 0.172, 0.40, 0.50, 0.60, the infections are slowly decreasing and then settles at a similar level after a period of time. It can be observed that \(\gamma\) does not have any noteworthy effect on the population class E, but has an enormous effect on the recovered class. On the other hand, as \(\beta\) is ranged from 0.005, 0.0258 and 0.258, the infections get far higher and settle at an endemic situation after some time. However, if \(\beta\) could be lowered to less than 0.001, it can be witnessed that the disease would eventually become extremely low and not many infected persons will remain in the population. Moreover, it is interesting to see that there is some oscillatory behavior on the infected and recovered compartment when \(\beta =0.001\). This is found subject to the other parameters made constant from previous references. It is worth pointing out that reducing \(\beta\) to 0.001 is not simple. There has to be stringent interactive measures and preventive measures like masking, use of hand sanitizers and social distancing.

Fig. 12
figure 12

Effect of \(\beta\) on compartments E, I, R

Full size image

7 Conclusion

In this article, a deterministic SEIR model is put forward which has dynamical relevance to the COVID-19 pandemic and consists of some important epidemiological factors such as a high transmission rate and factors like reinfection and natural and disease-induced death rates. The model reflects multiple transmissions from susceptible S(t) and recovered R(t) classes to the infected class I(t). The effect of restricted treatment capacity on epidemic transmission is characterized by a treatment rate given by Holling type-II functional response \(T(I)=\frac{aI}{1+bI}\). Thus, the model deliberates the impact of saturated treatment in the stage of community transmission of COVID-19 where the pandemic has reached a critical stage and the record of new infections is significantly higher than the available medical staff and resources. An observational study conducted by AIIMS, New Delhi, found that during the omicron transmission phase of COVID-19, the incidence density of reinfection was 456 per 10,000 person; however, the infection was milder than in prior instances (Malhotra et al. 2022; COVID-19 Forecasting Team 2022; Goldman et al. 2020), which is incorporated in our model (1). Initial investigations suggest that the governing model has a disease-free steady state and a maximum of upto three endemic steady states depending on sets of parameter variations. The DFE \(\varepsilon _0\) is found to be l.a.s. when \(\mathcal {R}_0 < 1\) as well as g.a.s. when the additional condition \(b=\eta =0\) holds. The presence of multiple endemic equilibria causes the model to demonstrate stability switches at equilibrium points. Local and global asymptotic stability of the unique EE is discussed in Theorems (4) and (6). The system experiences backward bifurcation at \(\mathcal {R}_0 = 1\) for the threshold value \(\beta =0.00081759\). The condition for this phenomenon is analyzed in Theorem (7) and proved numerically in Figs. 3 and 4. This suggests that lowering the reproduction number below unity is insufficient to eliminate COVID-19 from the population. The proposed model is significant because the disease is studied for the impact of the phenomenon of reinfection of COVID-19 due to its various mutations and strains in the presence of limited healthcare facilities characterized by saturated treatment. Healthcare systems frequently encounter financial limitations that impact the available funding for medical resources. Constrained budgets can lead to issues such as understaffing, outdated equipment and inadequate infrastructure. During the COVID-19 pandemic, the global supply chain disruptions have also affected the accessibility of medical resources, including medications, equipment and supplies. This study focuses on the parameters that are responsible for mitigation of COVID-19 because of its unusually high reinfections. This possibility adds more pressure on the realistic scenario of control of the disease spread. This study finds that the impacts of exposed individuals becoming actively infectious and natural recovery of infectious individuals are crucial to slow the spread of the disease along with the half-saturation constant. Determination of crucial rates which massively influence the infected and recovered population has been studied in detail. Due to the possibility of reinfection, measures to provide immunity to individuals such as vaccination, are of utmost necessity. Also, stringent preventive measures are still needed to be practiced due to the waning immunity of vaccines that are currently deployed among the masses.