1 Introduction

The study of vector-borne disease based on mathematical modeling is an important research area in mathematical epidemiology. The vector-borne disease spreads through interaction of susceptible hosts with infected vectors or infected hosts with susceptible vectors. Mosquito-borne dengue disease mainly spreads by the female mosquitoes Aedes aegypti and Aedes albopictus species mosquitoes [1]. The dengue-infected female mosquitoes bite susceptible peoples; then, susceptible peoples become infected by the disease. Symptoms of dengue fever usually appear within three to fifteen days after biting by the infectious mosquitoes [2].

Dengue virus (DENV) is mainly a RNA virus [3]. There are five different strains of dengue virus, namely DENV-1, DENV-2, DENV-3, DENV-4 and DENV-5 [4]. In particular when a person is infected with any strain of dengue, his body develops immunity with respect to that particular strain [5]; therefore, that person may be affected by another types of strains. Thus, infection by any particular strain does not imply person is protected from other types of strains. Dengue epidemic occurred in Asia, Africa, and North America first time simultaneously [6], and it was first reported in 1779–1780, later it was spread more than 127 countries. Different strains of dengue virus were first identified in different times. The DENV-1 was identified in 1977, DENV-2 in 1981, DENV-4 in 1981 and DENV-3 in 1994 [7] but in October 2013, the latest strain DENV-5 has been announced [4]. According to the report of World Health Organization (WHO), approximately 3.97 billion people are living at risk in tropical and subtropical region for this disease [8]. It becomes hyper in many countries like Thailand, Bangladesh, Malaysia, India, Singapore, Sri Lanka, etc. [8]. The peoples are terrified about dengue fever due to its high morbidity and mortality rate. The number of dengue patient has been increasing day by day. According to the report of World Health Organization (WHO), the number of dengue cases was less than one thousand in 1950, but it is highly increasing in last few years, more than 3 million in 2015 [9] and 4.2 million in 2019 [5]. The record number of dengue cases was reported in 2019 throughout the world. The co-infections of dengue occur with rate ranging from 5 to 30% as high as 40–50% for the co-circulation of different strains of dengue in the same area [10, 11]. Due to the presence of three strains, Thailand becomes in danger, total reported dengue case was 128964 from 77 provinces in 2019 [12]. First time in Philippines and Thailand, complex form of dengue, dengue shock syndrome or DHF found during epidemic of dengue in 1950 [12]. First licensed dengue vaccine Dengvaxia (CYD-TDV) [13] become commercially available in highly dengue burden countries, but it has side effects like pain and headache. In 2016, it was approved in 11 countries [14, 15], later in European Union (in 2018) and United States (in 2019) also.

Many researchers from different fields like biology, mathematics etc., are trying to investigate about the dynamics of disease spreading and its control through mathematical modeling. It is one of the most powerful tools to analyze disease transmission dynamics and its control. In 1975, Bailey [16] first proposed a basic SIR dengue model. Esteva and Vargas [17] modified the Bailey’s model considering constant population of human and constant birth rate of vectors. In their work, they established that if the basic reproduction number is less than unity, then the disease free equilibrium point is stable. The environment plays an important role in spreading of dengue disease. The spreading of this disease depends on density of mosquitoes. On the other hand, the growth of mosquitoes is highly dependent on availability of dirty water, which is gathered mainly through rainfall. To understand the effect of rainfall on the dengue transmission, Chanprasopchai [18] proposed an SEIR model in 2017. Derouich and Boutayeb [19] have developed an SIR model to characterize dengue transmission between vectors and humans. The dengue model of Derouich and Boutayeb was extended by Erikson [20] in 2010 adding exposed human class.

In recent decades, some researchers have proposed the multi-strain dengue model to investigate the effect of different strains in the same model [21, 22]. Sriprom [21] introduced a multi-strain dengue model in the presence of two strains and described the dynamics of sequential transmission of dengue virus. Mishra and Gakkar [22] formulated a two-strain dengue model and discussed the effect of vector control, awareness on dengue dynamics. Researchers included some control strategies like the vector control, awareness and treatment control, etc., in their model to identify the most important features to reduce the infection [23, 24]. The vector control policies are: use of adulticide to increase the mortality rate of adult mosquitoes, use of larvicide to kill the eggs of mosquitoes, etc. [23]. The awareness and treatment policies include: protection against mosquitoes bites, vaccination, treatment of the infected human, etc. To study the effect of vaccination, Supriatna [24] proposed a dengue model of single- and two-strain model and discussed the model with vaccination. Zheng and Nie [11] developed a mathematical model of two-strain dengue infection, describing the co-circulation of multiple strains and identified the most important control strategies using optimal control principle. Recently many researchers studied on dengue disease dynamics [25,26,27,28,29].

Optimal control becomes an important key in mathematical modelling to investigate the disease dynamics and control the influence of the infection. Optimal control is used in mathematical modelling to find out optimal value of the most effective strategy when more than one controls are used. Using optimal control, one can identify the most suitable control function which reduces the infected populations as well as minimize the implementation cost [30]. Optimal control policies on dengue disease transmission have been studied by many researchers in recent years [31,32,33,34].

This paper is the extension of the work [35]. In [35], authors considered saturated type incidence rate of the form \(\dfrac{\beta S I}{1 + \alpha I}\) as this type of incidence rate ultimately tends to \(\dfrac{\beta }{\alpha }\) as \(I \rightarrow \infty .\) For crowding effect of infected population, the rate of disease transmission ultimately decreases. For this reason, authors took this type of incidence rate. Also, they considered three types of control parameters, namely protection control against mosquito bites (\(u_1\)), treatment control for dengue-infected individuals (\(u_2\)) and insecticide spray against the mosquito (\(u_3\)). But in this paper, we have considered saturated incidence rate in the form \(\dfrac{\beta S V_I}{1 + \alpha S}\) and saturated treatment in the form \(\dfrac{a u_2 I}{1 +bu_2 I}\). This type of incidence rate ultimately tends to \(\dfrac{\beta }{\alpha }\) as \(S \rightarrow \infty .\) For inhibitory effect and psychological effect of susceptible population, the rate of disease transmission will reduce. For this reason, we have used this type of incidence rate. Here, we have also used three types of controls, namely vaccination for susceptible humans, treatment for infected humans and mosquitoes killing effort by humans. In [35], system does not exhibit backward bifurcation; moreover, authors did not show any types of bifurcation. But in this paper, we show two types of bifurcation, namely transcritical and backward bifurcation. In backward bifurcation, for \(R_0 < 1\) bistability exists (one stable disease-free equilibrium and one stable endemic). Therefore, here eradication of disease depends on model parameter as well as initial population density. In [35], authors used parameter values from some literature to study sensitivity analysis and optimal control. But, here we have estimated model parameters by fitting the model with real reported data of dengue in Singapore to study sensitivity analysis and optimal control problem. Further, to find out best control among applied controls, we have performed efficiency analysis.

Aim of the manuscript is to formulate a single-strain dengue virus transmission model in the presence of vaccination and treatment. Susceptible humans are affected by bites of infected mosquitoes in saturated form and susceptible mosquitoes are affected by infected humans in bilinear form. To include the effect of limitation of medical facility, we consider the treatment function in saturated form. Three types of controls have been considered, namely vaccination for susceptible humans, treatment for infected humans and mosquitoes killing effort by humans. After discussing qualitative analysis of the proposed model, we have estimated most of the model parameters by fitting the model with real infection data. Sensitivity analysis has been performed to find out the most effective parameters to control the infection and also effect on different model parameters on disease spreading has been discussed here. Estimation of basic reproduction number and effective reproduction number have been studied here. Finally, we have identified the optimal policy of control strategies to minimize the number of infected humans as well as reduce the implementation cost for using different controls.

The novelties of the paper are mentioned here:

  1. 1.

    Here we consider saturated type incidence and treatment.

  2. 2.

    The system (1) exhibits backward bifurcation at \(R_0 = 1\). For backward bifurcation, two endemic equilibria exist when \(R_0^{*}< R_0 < 1\) (where \(R_0^{*}\) is the critical value of \(R_0\)).

  3. 3.

    To validate the model, we have fitted the model with real reported data of dengue in Singapore from 18th week, 2014 to 1st week, 2015.

  4. 4.

    To find out most sensitive parameters and to perform optimal control problem, we go through estimated model parameters by fitting model with real data.

  5. 5.

    Further we find estimation of actual reproduction number and effective reproduction number which are generally uncommon in other literature.

  6. 6.

    To find out optimal value of applied controls to reduce infected human populations and to minimize implemented cost, we have performed optimal control analysis.

  7. 7.

    Finally we have studied efficiency analysis to know which control is best among applied controls.

Organization of this paper is as follows: Formulation of the model is discussed in Sect. 2. Positivity and boundedness of the solutions of the model, expression of basic reproduction number, existence of different types equilibrium points and their stability criteria are presented in Sects. 3, 4, and  5, respectively. Different types of bifurcation are investigated in Sect. 6. Validation of the proposed model and estimation of model parameters are studied in Sect. 7. Sensitivity analysis and effect of model parameters are discussed in Sects. 8 and  9, respectively. In Sects. 10.1 and 10.2, estimation of actual reproduction number and effective reproduction number have been discussed. Optimal control with numerical examples and efficiency analysis are studied in Sects. 11 and  12, respectively. We have summarized the results in Sect. 13.

2 Model formulation

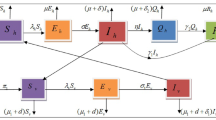
In this paper, we have formulated a single-strain dengue transmission model to study the dengue outbreak in Singapore from 18th week, 2014 to 1st week, 2015. Let total human populations be divided into three disjoint classes, namely susceptible class (S), infected class (I) and recovered class (R), and vector populations be divided into two disjoint class, namely susceptible vectors \((V_{s})\) and infected vectors \((V_{I})\). We have considered disease transmission rate by infected mosquitoes in saturated form \(\dfrac{\beta S V_I}{1 + \alpha S}\), where \(\alpha \) represents inhibitory factor of susceptible population. The above saturated incidence rate is considered here because due to the lack of knowledge about the disease, rate of disease transmission increases with number of infected vectors but for social awareness, inhibitory factor of susceptible human populations and also crowding effect of infected human populations, rate of disease transmission will decrease. To introduce the effect of limited medical resources, we have considered treatment function in saturated form \(\dfrac{a u_2}{1 + b u_2 I}\), where b represents delay in getting treatment. For lower abundance of infected human populations, treatment rate behaves like linear character but for higher abundance of infected human populations it ultimately tends to \(\dfrac{a}{b}\) where a, b both are positive constants. We assume that some of infected human populations are recovered naturally and some other are recovered using treatment. To formulate the model, we assume that the susceptible population has constant growth rate \(\omega \) and \(\omega _1\) for humans and vectors, respectively. The susceptible vectors become infected after biting infected human following mass action law. Here normal death rate of both humans and vectors is taken into consideration. Incorporating the above assumptions dynamics of flow diagram of dengue infection is presented in Fig. 1, and the corresponding model is given in the following,

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\mathrm{d}S}{\mathrm{d}t} &{}=\omega -\dfrac{\beta SV_{I}}{1+\alpha S}-(\mu + u_{1})S \\ \dfrac{\mathrm{d}I}{\mathrm{d}t} &{}=\dfrac{\beta SV_{I}}{1+\alpha S}-(\mu +d+\gamma )I-\dfrac{au_{2}I}{1+bu_{2}I} \\ \dfrac{\mathrm{d}R}{\mathrm{d}t} &{}=\dfrac{au_{2}I}{1+bu_{2}I}+\gamma I + u_{1} S-\mu R \\ \dfrac{\mathrm{d}V_{S}}{\mathrm{d}t} &{}=\omega _{1}-\mu _{1} V_{S}-cu_{3} V_{S}-\sigma V_{S} I \\ \dfrac{\mathrm{d}V_{I}}{\mathrm{d}t} &{}=\sigma V_{S}I-cu_{3}V_{I}-\mu _{1}V_{I} \end{array}\right. } \end{aligned}$$
(1)

with the initial conditions \(S(0)> 0, I(0) \ge 0, R(0) \ge 0, V_{S}(0) > 0\) and \(V_{I}(0) \ge 0\). In the next section, we shall investigate the positivity and boundedness of the proposed model to establish the well definiteness of the model. All model parameters in model system (1) are written in Table 1.

Fig. 1
figure 1

Flow diagram of dengue infection model for humans and vectors both

Full size image
Table 1 Description of model parameters
Full size table

3 Basic properties of the proposed model

First we have to check the uniform boundedness criteria of solutions of the proposed model to analyze the model. To check the uniform boundedness first we shall check the positivity of solutions, i.e., we have to establish that all solutions of the proposed model are positive starting from any nonnegative initial conditions. For establishing nonnegativity and boundedness, we shall prove the following two theorems.

Theorem 1

All solutions of the proposed model are nonnegative for any time t satisfying nonnegative initial conditions.

Proof

To prove this, we first show that \(S(t) > 0\) for all time t. From the first equation of (1), we get

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}&\ge -\frac{\beta S V_{I}}{1+\alpha S}-(\mu + u_{1})S \\ i.e. \frac{1}{S} \frac{\mathrm{d}S}{\mathrm{d}t}&\ge -(\beta V_{I}+\mu + u_{1}) . \end{aligned}$$

Integrating and using the initial conditions, we get \(S(t) \ge S(0)e^{-(\beta V_{I}+\mu + u_{1})t} > 0\). Again from the second equation of (1), we get

$$\begin{aligned} \frac{\mathrm{d}I}{\mathrm{d}t}&\ge -(\mu +d+\gamma )I-\frac{au_{2}I}{1+bu_{2}I} \\ i.e. \frac{1}{I}&\frac{\mathrm{d}I}{\mathrm{d}t}\ge -(\mu +d+\gamma +au_{2}) . \end{aligned}$$

Again integrating, we get \(I(t) \ge I(0)e^{-(\mu +d+\gamma +au_{2})t} \ge 0\). Similarly from other three equations of (1), we have \(R(t) \ge R(0)e^{-\mu t}\ge 0\) , \(V_{S}(t) \ge V_{S}(0)e^{-(\mu _{2}+cu_{3} +\sigma I)t} > 0\) and \(V_{I}(t) \ge V_{I}(0)e^{-(cu_{3}+\mu _{2})t} \ge 0\) for all t. \(\square \)

Theorem 2

All solutions of model system (1) are uniformly bounded.

Proof

Let \(H=S+I+R\) and \(V=V_{S}+V_{I}\), taking derivative of H with respect to t we get,

$$\begin{aligned} \frac{\mathrm{d}H}{\mathrm{d}t}&=\frac{\mathrm{d}S}{\mathrm{d}t}+\frac{\mathrm{d}I}{\mathrm{d}t}+\frac{\mathrm{d}R}{\mathrm{d}t} =\omega -\mu H-dI \\&\Rightarrow \frac{\mathrm{d}H}{\mathrm{d}t} +\mu H \le \omega \end{aligned}$$

Integrating both sides of above expression and then applying theory of differential inequality [18] , we have

$$\begin{aligned} 0 < H(S,I,R) \le \frac{\omega }{\mu } (1- e^{-\mu t})+H(S(0),I(0),R(0)) \end{aligned}$$

as t goes to infinity, the above inequality changes to

$$\begin{aligned} 0 < H(S,I,R) \le \frac{\omega }{\mu } +H(S(0), I(0), R(0)). \end{aligned}$$
(2)

Again derivative of V with respect to t gives

$$\begin{aligned}&\frac{\mathrm{d}V}{\mathrm{d}t} = \frac{\mathrm{d}V_{S}}{\mathrm{d}t}+\frac{\mathrm{d}V_{I}}{\mathrm{d}t} \\&\frac{\mathrm{d}V}{\mathrm{d}t}+(\mu _{2}+cu_{3})V =\omega _{1}. \end{aligned}$$

Using the similar arguments as used for H(S, I, R) , we obtain,

$$\begin{aligned} 0 < V(V_{S},V_{I}) \le \frac{\omega _{1}}{\mu _{2}+cu_{3}}+V(V_{S}(0), V_{I}(0)) \end{aligned}$$
(3)

Using the results of (2-3), we get

$$\begin{aligned} 0 < S+I+R+V_{S}+V_{I} \le M \end{aligned}$$

where \(M=\dfrac{\omega }{\mu }+\dfrac{\omega _{1}}{\mu _{2}+cu_{3}}+H(S(0),I(0),R(0))+V(V_{S}(0),V_{I}(0))\).

Hence, all solutions of the system are uniformly bounded. \(\square \)

4 Basic reproduction number \((R_0)\) and existence of different types of equilibrium points

In this section, first we shall determine the basic reproduction number of the proposed model in terms of model parameters, and then, the expression for the existence of different equilibrium points will be discussed.

The basic reproduction number (\(R_{0}\)) plays a significant role to determine whether an epidemic will ensure or not [36]. Since the system (1) has the disease-free equilibrium point (DEF) \(E_{0}(S_{0}, 0,R_{0}^{'}, V_{S_{0}}, 0)\) where \(S_{0}= \dfrac{\omega }{\mu + u_{1}}\), \(R_{0}^{'}=\dfrac{\omega u_{1}}{\mu (\mu + u_{1})}\) and \(V_{S_{0}}=\dfrac{\omega _{1}}{\mu _{1} + c u_{3}}\), hence \(R_0\) of the model exists. Here to find the expression of \(R_{0}\) by the next-generation matrix approach as proposed by Driessche and Watmough [37], we use the notation \( F_1 = (F_{11} \ F_{12})^T\) and \( F_2 = (F_{21} \ F_{22})^T\) where \( F_{11} = \dfrac{\beta S V_{I}}{1+\alpha S}\), \(F_{12} = \sigma V_{S}I \) and \(F_{21} = (\mu + d + \gamma )I + \dfrac{a u_{2}I}{1+bu_{2}I}\) , \(F_{22} = cu_{3}V_{I}+\mu _{1} V_{I}\).

Let \( {\mathbf {F}}=\frac{\partial (F_{11},F_{12})}{\partial (I,V_1)}|_{E_0}= \begin{pmatrix} 0&{}\dfrac{\beta \omega }{\mu + u_{1}+\alpha \omega }\\ \dfrac{\sigma \omega _{1}}{\mu _{1}+cu_{3}}&{}0 \end{pmatrix} \textit{and} \ {\mathbf {V}}=\frac{\partial (F_{21},F_{22})}{\partial (I,V_1)}|_{E_0}= \begin{pmatrix} \mu +d+\gamma +au_{2}&{}0\\ 0&{}\mu _{1}+cu_{3} \end{pmatrix}.\) Therefore, next-generation matrix \((F V^{- 1})\) is given by

$$\begin{aligned} \mathbf {FV^{-1}}= \begin{pmatrix} 0&{}\dfrac{\beta \omega }{(\mu + u_{1}+\alpha \omega )(\mu _{1}+cu_{3})}\\ \dfrac{\sigma \omega _{1}}{(\mu _{1}+cu_{3})(\mu +d+\gamma +au_{2})}&{}0 \end{pmatrix}. \end{aligned}$$

The spectral radius of the matrix \(FV^{-1}\) is the basic reproduction number, which is given by

$$\begin{aligned} R_{0}= \dfrac{1}{\mu _{1}+cu_{3}}\sqrt{\dfrac{\sigma \beta \omega \omega _{1}}{(\mu + u_{1}+\alpha \omega )(\mu +d+\gamma +au_{2})}} . \end{aligned}$$

Other than the DEF, the system contains the endemic equilibrium point is \( E_{*}(S_{*}, I_{*},R_{*}, V_{S_{*}}, V_{I_{*}}) \) where \(I_{*}\) satisfies the biquadratic equation

$$\begin{aligned} C_{4}I^{4}+C_{3}I^{3}+C_{2}I^{2}+C_{1}I+C_{0}=0 \end{aligned}$$
(4)

with \(S^* = \dfrac{\omega }{\mu + u_1} - \dfrac{(\mu + d + \gamma )I^*}{\mu + u_1} - \dfrac{a u_2 I^*}{(1 + b u_2 I^*)(\mu + u_1)}>0\) if \(\omega (1 + b u_2 I^*) > au_2 I^* + (\mu + d + \gamma )(1 +bu_2 I^*)\), \(V_{I^*} = \dfrac{\sigma \omega _1 I^*}{(c u_3 + \mu _1)(c u_3 + \mu _1 + \sigma I^*)}, V_{S^*} = \dfrac{\omega _1}{\mu _1 + c u_3 + \sigma I^*},\) \(R^* = \dfrac{a u_1 I^*}{\mu (1 + b u_2 I^*)} + \dfrac{\gamma I^*}{\mu } + \dfrac{u_1 S^*}{\mu }\) and the co-efficients \(C_i, i= 1,2,3,4\) are given in “Appendix I”.

It is clear from the expression of \(C_i\)’s that \(C_4\) is always positive, and depending on sign of \(C_1\), \(C_2\), \(C_3\) the number of feasible endemic equilibrium points will be calculated. The existence of endemic equilibrium point is discussed in the following theorem.

Theorem 3

An unique endemic equilibrium point \(E_{*}(S_{*}, I_{*}, R_{*}, V_{S_{*}}, V_{I_{*}})\) exists for \(R_{0} > 1\) if \(C_{1}\), \(C_{2}\) and \(C_{3}\) maintain the same sign.

Proof

To obtain the endemic equilibrium point, we have an expression of I in the form as in Eq. (4) where always \(C_{4} > 0\) and \(C_{0}\) can be expressed as \(C_{0}=(\mu _{1}+cu_{3})^{2}(\mu +d+\gamma +au_{2})(\mu + u_{1} + \alpha \omega )(1-R_{0}^{2})< 0\) if \(R_0 >1\). Therefore, by Descartes Rule of signs, Eq. (4) has at least one positive root if \(C_{1}\), \(C_{2}\) and \(C_{3}\) are of same sign for \(R_{0} > 1\). Thus, the endemic equilibrium point exists if \(C_{1}\), \(C_{2}\) and \(C_{3}\) maintain the same sign for \(R_{0} > 1\). \(\square \)

5 Stability analysis of equilibrium points

We shall now discuss the stability of the system about different equilibrium points. The eradication or persistence of the disease depends on stability of the disease-free equilibrium point and the endemic equilibrium points, respectively.

Theorem 4

The system is locally asymptotically stable around its disease-free equilibrium point if \(R_{0} < 1\).

Proof

The characteristic equation of the system at disease-free equilibrium points is given by:

$$\begin{aligned} (\lambda +\mu + u_{1})(\lambda +\mu )(\lambda +\mu _{1}+c\mu _{3})(\lambda ^{2}+\varTheta _{1}\lambda +\varTheta _{2})=0 \end{aligned}$$

where \(\varTheta _{1}=\mu +d+\gamma +\mu _{1}+au_{2}+cu_{3} > 0\) and \(\varTheta _{2}=(\mu _{1}+c u_{3})(\mu +d+\gamma +au_{2}) (1 - R_0^2)\).

It is clear from the above equation that among the five roots, three roots are negative which are \(-(\mu + u_{1})\), \(-\mu \), \(-(\mu _{1}+cu_{3})\) and other two roots satisfy the equation \(\lambda ^{2}+\varTheta _{1}\lambda +\varTheta _{2}= 0\). Since if \(R_0 < 1\) then \(\varTheta _{2} > 0\), so by Routh–Hurwitz criteria the last equation will have roots with negative real part if \(R_{0} < 1\) [38]. Thus, if \(R_{0} < 1\), then the system is locally asymptotically stable about disease-free equilibrium point. \(\square \)

Since at \( R_0=1 \) one root of the characteristic equation vanishes and other four becomes negative and the usual eigen analysis method fails. Suppose \( R_0=1 \) occurs at \(u_2=u_2^{[TC]}\) where

$$\begin{aligned} u_2^{[TC]} = \dfrac{1}{a}\left\{ \dfrac{\sigma \beta \omega \omega _{1}}{(\mu + u_{1} +\alpha \omega )(\mu _{1} +cu_{3})^{2}}-(\mu +d +\gamma )\right\} . \end{aligned}$$

Theorem 5

The system is locally asymptotically stable around its endemic equilibrium point if \(F_{2} > 0\), \(F_{3} > 0\) and \(F_{1}F_{2} > F_{3}\), where the symbolic parameters are determined in subsequent steps.

Proof

The characteristic equation of system (1) corresponding to the endemic equilibrium point is given by

$$\begin{aligned} (\lambda +\mu )(\lambda +\mu _{1}+c u_{3})(\lambda ^{3}+F_{1}\lambda ^{2}+F_{2}\lambda +F_{3})=0 \end{aligned}$$

where \(F_1,\) \(F_2,\) and \(F_3\) are given in “Appendix II”.

Clearly it has two negative real roots \(-\mu \), \(-(\mu _{1}+cu_{3})\), and remaining three roots satisfy the equation

$$\begin{aligned} \lambda ^{3}+F_{1}\lambda ^{2}+F_{2}\lambda +F_{3}=0 \end{aligned}$$
(5)

It is clear from the expressions of the coefficients that \( F_{1} \) is positive. Thus, by Routh–Hurwitz criteria all roots of the above characteristic equation will have negative real part if \(F_{2}> 0, F_{3} > 0\) and \(F_{1}F_{2} > F_{3}\) [38]. Thus, system is locally asymptotically stable around its endemic equilibrium points. \(\square \)

In biological point of view, the stability of disease-free equilibrium point implies disease eradicates from the system and stability of endemic equilibrium point implies the persistence of the disease in the system.

6 Bifurcation analysis

In this section, we investigate different types of bifurcations of the proposed model system (1). First we examine the Transcritical bifurcation at the DFE \(E_0\) in Theorem 6, and Theorem 7 is dedicated for backward bifurcation. The transcritical bifurcation will be discussed with respect to \(u_2\), and the backward bifurcation will be established considering \( \alpha \) as the bifurcation parameter.

Theorem 6

The model system (1) experiences transcritical bifurcation when the model parameter \(u_2\) passes through the critical value \( u_2=u_2^{[TC]} \) if \(\dfrac{u_2^2(\mu _1 + c u_3)^4 }{\sigma ^2 \omega _1^2} \ne \dfrac{(\mu _1 + c u_3)}{\omega _1(\mu + \mu _1 + \alpha \omega )} + \dfrac{\beta (\mu + u_1)}{(\mu + \mu _1 + \alpha \omega )^3}\).

Proof

To establish the above theorem, we have to verify transversality condition of Sotomayor’s theorem [39] for transcritical bifurcation at disease-free equilibrium point \(E_{0}\). We investigate the bifurcation with respect to the model parameter \(u_{2}\). Let \(f(S, I, R, V_S, V_I)=(f_1, f_2, f_3, f_4, f_5)^T\) where

$$\begin{aligned} {\left\{ \begin{array}{ll} f_1(S, I, R, V_S, V_I) = \omega -\frac{\beta SV_{I}}{1+\alpha S}-(\mu + u_{1})S \\ f_2(S, I, R, V_S, V_I) = \frac{\beta SV_{I}}{1+\alpha S}-(\mu +d+\gamma )I-\frac{au_{2}I}{1+bu_{2}I} \\ f_3(S, I, R, V_S, V_I) = \frac{au_{2}I}{1+bu_{2}I}+\gamma I + u_{1} S-\mu R \\ f_4(S, I, R, V_S, V_I) = \omega _{1}-\mu _{1} V_{S}-cu_{3} V_{S}-\sigma V_{S} I \\ f_5(S, I, R, V_S, V_I) = \sigma V_{S}I-cu_{3}V_{I}-\mu _{1}V_{I} \end{array}\right. } \end{aligned}$$
(6)

One of the characteristic roots of \(J(E_0)\) is zero for \(u_2 = u_2^{[TC]}\). Let \(V = (v_1 \ v_2 \ v_3 \ v_4 \ v_5)^T\) and \(W = (w_1 \ w_2 \ w_3 \ w_4 \ w_5)^T\) be eigenvectors corresponding to the zero eigenvalue of the matrices \(J(E_0)_{u_2^{[TC]}}\) and \(J^T(E_0)_{u_2^{[TC]}}\), respectively, where \(v_1 = - \dfrac{\beta S_0}{(1+\alpha S_0)(\mu + u_1)},\) \(v_2 = \dfrac{c u_3 + \mu _1}{\sigma V_{S_0}},\) \(v_3 = \dfrac{\gamma (c u_3 + \mu _1)}{\mu \sigma V_{S_0}} - \dfrac{\beta S_0 u_1}{\mu (1+\alpha S_0)(\mu + u_1)},\) \(v_4 = -1,\) \(v_5 = 1\) and \(w_1 = 0,\) \(w_2 = \dfrac{\sigma }{(\mu + d + \gamma )},\) \(w_3 = 0,\) \(w_4 = 0,\) \(w_5 = 1\).

Since for this system

$$\begin{aligned}&\left[ W^{T}f_{u_{2}}(E_{0}(S_{0}, 0,R_{0}, V_{S_{0}}, 0))\right] _{u_2^{[TC]}} =0\\&\quad \left[ W^{T}(Df_{u_{2}}(E_{0}(S_{0}, 0,R_{0}, V_{S_{0}}, 0))V)\right] _{u_2^{[TC]}} \\&\quad = -\frac{a(\mu + u_{1} +\alpha \omega )(\mu _{1} +cu_{3})^{3}}{\alpha \beta \omega \omega _{1}} \ne 0\\&\quad \left[ W^{T}(D^{2}f_{u_{2}}(E_{0}(S_{0}, 0,R_{0}, V_{S_{0}}, 0))(V,V))\right] _{u_2^{[TC]}} \\&\quad =\frac{(\mu + u_{1} +\alpha \omega )(\mu _{1} +cu_{3})}{\beta \omega } \\&\quad \left\{ \frac{2abu_{2}^{2}(\mu _{1} +cu_{3})^{4}}{\sigma ^{2} \omega _{1}^{2}} -\frac{2\beta ^{2} \omega (\mu + u_{1})}{(\mu +u_{1} +\alpha \omega )^{3}}\right\} \\&\quad -\frac{2(\mu _{1} +cu_{3})^{2}}{\omega _{1}} \ne 0 \end{aligned}$$

if the condition stated in the theorem is satisfied.

Therefore, all conditions of Sotomayor’s theorem for transcritical bifurcation are satisfied, and hence, Sotomayor’s theorem ensures the proposed system experiences transcritical bifurcation at the disease-free equilibrium point \(E_0\). \(\square \)

Fig. 2
figure 2

Transcritical bifurcation diagram with respect to \(u_2\) with \(\omega =1.95\), \(\beta =0.8\), \(\alpha =2.01\), \(\mu =0.1\), \(\mu _1=0.01\), \(d=0.19\), \(\gamma =0.15\), \(b=0.001\), \(a=1.9\), \(\omega _1=5.2\), \(u_3=0.2\), \(c=0.9\), \(\sigma =0.2\), \( \mu _2=0.2\); the blue and red lines correspond the stable equilibrium and the unstable equilibrium, respectively. (Color figure online)

Full size image

To interpret the transcritical bifurcation numerically, we have drawn the stable–unstable branches of the solution curve with respect to \(u_2\) (see Fig. 2). It is clear from Fig. 2 that for \( u_2 > u_2^{[TC]}=1.2 \) the disease-free equilibrium point is stable and for \(u_2 < u_2^{[TC]}\) the disease-free equilibrium point becomes unstable through creation of stable endemic equilibrium. Therefore, the system exchanges the stability when \( u_2 \) crosses the critical value \( u_2 = u_2^{[TC]} \). Biologically the above result has high importance, because there is a critical value of the treatment control parameter above which the disease will eradicate from the system.

Next we study backward bifurcation of the proposed model (1) at \( R_0 = 1 \) with respect to bifurcation parameter \(\alpha \). Suppose \( R_0 = 1 \) occurs at \(\alpha =\alpha ^* \) where \(\alpha ^* = \dfrac{1}{\omega }\left\{ \dfrac{\sigma \beta \omega \omega _1}{(c u_3 + \mu _1)^2 (\mu + d + \gamma + a u_2)} - (\mu + u_1) \right\} >0 \) when other parameters are fixed.

Theorem 7

The model system (1) undergoes through backward bifurcation at \( R_0 = 1 \) ( equivalently for the critical value of the bifurcation parameter \(\alpha = \alpha ^*\)) if \(\dfrac{a b u2^2 (c u_3^2 + \mu _1)^2}{\sigma ^2 S_0 (\mu + d + \gamma )} > \dfrac{\beta ^2 \sigma S_0^2 V_{S_0}}{(1+\alpha S_0)^3 (\mu + \mu _1) (\mu + d + \gamma )} + \dfrac{c u_3 + \mu _1}{V_{S_0}}. \)

Proof

Here Castillo–Chavez and Song’s theorem [40] is used to find the condition for backward bifurcation of model system (1). Again consider the function \(f(S, I, R, V_S, V_I)\) which is already defined explicitly in the previous theorem. For critical value of the bifurcation parameter \(\alpha = \alpha ^*\) ( which is equivalent to \(R_0 = 1\)) \( J(E_0) \) has one zero eigenvalue. Let \( W = (w_1 \ w_2 \ w_3 \ w_4 \ w_5)^T \) be the right eigen vector of the Jacobian matrix \( J(E_0) \) corresponding to zero eigenvalue where \( w_1 = - \dfrac{\beta S_0}{(1+\alpha S_0)(\mu + u_1)},\) \(w_2 = \dfrac{c u_3 + \mu _1}{\sigma V_{S_0}},\) \(w_3 = \dfrac{\gamma (c u_3 + \mu _1)}{\mu \sigma V_{S_0}} - \dfrac{\beta S_0 u_1}{\mu (1+\alpha S_0)(\mu + u_1)},\) \(w_4 = -1,\) \(w_5 = 1\). Also, let \(V = (v_1 \ v_2 \ v_3 \ v_4 \ v_5)\) be the left eigenvector of the Jacobian matrix \(J(E_0)\) corresponding to zero eigen value where \(v_1 = 0,\) \(v_2 = \dfrac{\sigma }{(\mu + d + \gamma )},\) \(v_3 = 0,\) \(v_4 = 0,\) \(v_5 = 1\). To use Castillo–Chavez and Song’s theorem [40], we need to find bifurcation coefficients \(\psi \) and \(\phi \) which are given by \(\psi = \varSigma _{k,i,j = 1}^5 v_k w_i w_j \dfrac{\partial ^2 f_k}{\partial x_i \ \partial x_j}=\dfrac{2 a b u2^2 (c u_3^2 + \mu _1)^2}{\sigma ^2 S_0 (\mu + d + \gamma )} - \dfrac{2 \beta ^2 \sigma S_0^2 V_{S_0}}{(1+\alpha S_0)^3 (\mu + \mu _1) (\mu + d + \gamma )} + \dfrac{2 c u_3 + \mu _1}{V_{S_0}} \) and \(\phi = \varSigma _{k,i = 1}^5 v_k w_i \dfrac{\partial ^2 f_k}{\partial x_i \ \partial \alpha }=\dfrac{\beta \sigma S_0 V_{S_0}}{(\mu + d + \gamma ) (1 + \alpha S_0)^2} > 0.\)

Now model system (1) undergoes through backward bifurcation at \(R_0 = 1 \) with respect to bifurcation parameter \(\alpha = \alpha ^*\) if \(\psi > 0\), i.e., \(\dfrac{a b u_2^2 (c u_3^2 + \mu _1)^2}{\sigma ^2 S_0 (\mu + d + \gamma )} > \dfrac{\beta ^2 \sigma S_0^2 V_{S_0}}{(1+\alpha S_0)^3 (\mu + \mu _1) (\mu + d + \gamma )} + \dfrac{c u_3 + \mu _1}{V_{S_0}}.\)

Hence the theorem is proved. \(\square \)

Fig. 3
figure 3

Backward bifurcation diagram with respect to \(R_0 (\alpha ) \) with \(\omega = 2.9\), \(\beta = 0.9\), \(\mu = 0.13\), \(\mu _1 = 0.03\), \(d = 0.0109\), \(\gamma = 0.15\), \(a = 60\), \(\omega _1 = 5.2\), \(u_3 = 0.2\), \(c = 0.9\), \(\sigma = 0.23\), \(\mu _2 = 0.2\), \(\alpha = 1.6\), \(u_2 = 0.75\), \(b = 30\)

Full size image

In Fig. 3, we have presented the one-parameter bifurcation diagram with respect to \( R_0\). In figure, the blue line corresponds to the stable branch of the solution curve and the red line corresponds to the unstable branch. It is clear from Fig. 3 that for \( R_0 < 1 \) disease-free equilibrium point is stable and for \(R_0 > 1\) disease-free equilibrium point is unstable. For \( R_0{^*}< R_0 < 1\), two endemic equilibrium points exist, endemic equilibrium point with lower density infected is unstable and endemic equilibrium point with higher density infected is stable where \(R_0{^*}\) is a critical value of \(R_0\). Biologically this bifurcation is important because for \( R_0{^*}< R_0<1 \) disease may persists in the system depending on initial population density. On the other hand, there is a critical value of the inhibitory factor above which disease will eradicate from the system and below which eradication of disease depends on initial population size.

7 Model validation and parameter estimation

In this section, we shall validate the proposed model with real reported data. To fit the model, we consider the real data of dengue outbreak in Singapore from 18th week of 2014 to 1st week of 2015 [41]. To fit the proposed model with real reported data, we have used MATLAB minimization software package fmincon [38] and estimated best-fitted model parameters. To obtain best-fitted model parameters, we have minimized the sum of squares error (SSE), which is defined as \( SSE = \sum _{j = 1}^{n}\left( Y_j - I(t_j) \right) ^2\) where \(Y_j\) is the cumulative number of real reported data of jth week and \(I(t_j)\) is model predicted cumulative infected density of the same week. By finding residuals of the data fit, we can verify about the fitness of the model. If the residuals \(\left\{ Y_j - I(t_j) | j= 1,2,...,n \right\} \) are randomly distributed, then we can say that model is well fitted.

To perform the data fit process, we consider initial number of susceptible, infected and recovered human population are 5525628, 251, 0, respectively, whereas initial number of susceptible and infected mosquitoes is 200000 and 1500, respectively. Best-fitted curve of cumulative infected data, residuals and bar diagram of new infection per week are shown in Fig. 4. From the figures, it is clear that our model fitting with real reported data is reasonably good. Among fifteen model parameters, we have estimated twelve parameters and remaining model parameters are taken from [42]. We have summarized estimated values of all model parameters in Table 2.

Fig. 4
figure 4

a Cumulative infection density: red dots represent infected reported data, blue line represents model predicted infected data. b Residuals of the data, c Bar diagram of per week infected data and model prediction. (Color figure online)

Full size image
Table 2 Estimated values of the model parameters
Full size table

8 Sensitivity analysis

Since the proposed model contains many parameters among them some of the model parameters are highly sensitive on \(R_0.\) Sensitivity analysis is performed to find out the model parameters, which have most significant affect on \(R_0.\) To perform sensitivity analysis, we apply normalized forward sensitivity index method [43, 44]. The normalized forward sensitivity index method of \( R_0 \) with respect to model parameter \( \phi \) is defined by \( \varLambda _{\phi }^{R_0} = \dfrac{\partial R_0}{\partial \phi } \dfrac{\phi }{R_0} \). Using this method, one can identify the model parameters, which have positive or negative impact on basic reproduction number. The basic reproduction number shows same behavior with the model parameters for positive sensitivity index parameter and opposite behavior for negative sensitivity index parameter. In Table 3, we have enlisted the sensitivity indexes of the model parameters. It is clear from Table 3, \(\omega \), \(\omega _1\), \(\beta \), \(\sigma \) have positive-sensitive indexes and c, \(u_3\), \(u_1\), \(\gamma \) have negative indexes.

9 Effect of different model parameters on disease spreading

In this section, we have studied the effect of highly sensitive model parameters on the disease dynamics. For this purpose, we have found abundance of infected humans changes with increasing or decreasing values of model parameters considering base value of the parameters as given in Table 2. Here we have studied the effect of four state parameters, namely \(\beta ,\) \(\sigma ,\) \(\gamma ,\) c and two control parameters \(u_2\), \(u_3.\) In the following subsections first we discuss the effect of \(\beta \) and \(\sigma \) on disease dynamics.

9.1 Effect of \(\beta \) and \(\sigma \) on disease spreading

In Fig. 5, we have presented the density of infected humans for different values of \(\beta \) and \(\sigma \). We have observed from Fig. 5a that number of infected humans increases when disease transmission rate from infected mosquitoes to susceptible humans increases and vice versa. Similarly from Fig. 5b we have seen that the number of infected humans also increases when disease transmission rate from infected humans to susceptible mosquitoes increases. Thus, the number of infected humans increases with the increase of \(\beta \) and \(\sigma \) both and vice versa. We can conclude that to control the density of infected humans, i.e., spreading of disease, we have to take policy such that \(\beta \) and \(\sigma \) both decrease. The value of \(\beta \) and \(\sigma \) will decrease if we can minimize the interaction among the humans and mosquitoes. The said interaction can be minimized if we isolate the humans from mosquitoes. The isolation can be done using mosquito nets, wearing long-covered clothes, etc.

Table 3 Sensitivity indexes of model parameters
Full size table
Fig. 5
figure 5

Time series of infected humans for different values of model parameters \(\beta \) and \(\sigma \)

Full size image

9.2 Effect of auto immune rate \((\gamma )\) and mosquito killing efficiency (c)

In Fig. 6, we have presented the time series of infected humans for different values of \(\gamma \) and c. We have seen from Fig. 6a that the number of infected humans decreases with increase of \(\gamma \). Also from Fig. 6b we have seen that the number of infected humans decreases with the increase of c. Therefore, number of infected humans decreases with the increase of both \(\gamma \), c and vice versa. This result is biologically important because the increase of \(\gamma \) and c will decrease the density of infected humans but increase of \(\gamma \) can be done taking healthy foods, proper physical exercise and increase of c can be performed by destroying mosquito larvae, killing adult mosquitoes, cleaning dirty water, increasing mortality of mosquito’s eggs, etc.

Fig. 6
figure 6

Time series of infected humans for different values of model parameters \(\gamma \) and c

Full size image

9.3 Effect of treatment control parameter \((u_2)\) and mosquitoes killing effort control parameter \((u_3)\)

In Fig. 7, we have shown density of infected humans for different values of \(u_2\) and \(u_3\). It is clear from Fig. 7a that the number of infected humans decreases with increase of \(u_2\) and vice versa. Similarly, from Fig. 7b it is clear that the number of infected humans decreases or increases with the increase or decrease of \(u_3\), respectively. Therefore, with increase in both the control parameters \(u_2\) and \(u_3\), the number of infected humans decreases and vice versa. Biologically disease transmission can be reduced taking proper treatment as well as using adulticide for killing adult mosquito, larvicide for increasing mortality of eggs, destroying mosquitoes larvae, etc.

Fig. 7
figure 7

Time series of infected humans for different values of model parameters \(u_2\) and \(u_3\)

Full size image

10 Estimation of actual and effective reproduction number

In this section, we shall estimate \( R_0 \) from actual data and estimate the values of effective reproduction number from actual data of Dengue outbreak in Singapore 2014.

10.1 Estimation of actual \( R_0 \) for dengue outbreak

There are several analytical as well as statistical methods for estimating \(R_0\) from the actual data for infectious disease. To estimate \( R_0 \) from the initial growth phase of the disease [45], we assume that at early stage of the disease, the number of cumulative cases (Q(t)) varies as exponentially with force of infection \((\varLambda )\) which can be expressed mathematically as \(Q(t) \propto \mathrm{exp}(\varLambda t).\) Similarly number of infected humans, infected mosquitoes vary as \(\mathrm{exp}(\varLambda t)\). So we have

$$\begin{aligned} {\left\{ \begin{array}{ll} I(t) \approx I_0 \mathrm{exp}(\varLambda t) \\ V_{I}(t) \approx V_{I_0} \mathrm{exp}(\varLambda t) \end{array}\right. } \end{aligned}$$
(7)

where \(I_0\) and \(V_{I_0}\) are constants. Here we assume that both susceptible populations remain constant and they are given by \(S_0 = \dfrac{\omega }{\mu + u_1}\) and \(V_{S_0} = \dfrac{\omega _1}{\mu _1 + c u_3}\). Substituting (7) in second and fifth equation of equation (1) and putting \(b = 0\), we get

$$\begin{aligned} \left( \varLambda + \zeta _1 \right) I_0 = \dfrac{\beta S_0}{1 + \alpha S_0} V_{I_0} \end{aligned}$$
(8)

and

$$\begin{aligned} \left( \varLambda + \zeta _2 \right) V_{I_0} = \sigma V_{S_0} I_{0} \end{aligned}$$
(9)

where \(\zeta _1 = \mu + d + \gamma + a u_2\) and \(\zeta _2 = \mu _1 + c u_3.\) From Eqs. (8) and (9), we get

$$\begin{aligned} \beta \sigma = \dfrac{(\varLambda + \zeta _1)(\varLambda + \zeta _2)(1 + \alpha S_0)}{S_0 V_{S_0}}. \end{aligned}$$

Putting the value of \(\beta \sigma \) from the above relation in expression of \( R_0 \), we obtain

$$\begin{aligned} R_0 = \dfrac{1}{\zeta _2}\sqrt{\dfrac{\omega \omega _1 (\varLambda + \zeta _1)(\varLambda + \zeta _2)(1 + \alpha S_0)}{S_0 V_{S_0} \zeta _1 (\mu + u_1 + \alpha \omega )}}. \end{aligned}$$
(10)

Now first we estimate the force of infection (\(\varLambda \)) and then we estimate basic reproduction number \(R_0\). The relation between new number of cases per day (q(t)) with cumulative cases per day (Q(t)) as follows \(q(t) \approx \varLambda Q(t)\).

To obtain the estimation of the force of the infection \((\varLambda )\), we maintain the following steps one by one. First we plot new number of cases along \( y- \) axis and cumulative number of cases along x-axis. Then, from scatter diagram we obtain threshold cumulative values up to which it shows exponential growth. Next using least-square method, we fit a linear regression curve based on the collected exponential growth data [46]. The slope of the regression line is force of infection \((\varLambda )\).

Fig. 8
figure 8

a Time series of new cases of dengue outbreak from 18th week, 2014 to 1st week, 2015, b daily number of cases against cumulative number of cases from 18th week, 2014 to 1st week, 2015

Full size image
Fig. 9
figure 9

Effective reproduction number

Full size image

We obtain from Fig. 8b \(\varLambda = 0.1506101534251 \pm 0.0189325690942 \) \(\mathrm{day}^{-1}\). Putting the values of \( \varLambda \) in (10) and using other parameters from Table 2, we obtain the estimated value of basic reproduction number as \(R_0 = 2.218450740\) with lower and upper limit as 2.082235564 and 2.352455166, respectively.

10.2 Effective reproduction number R(t)

In mathematical epidemiology, basic reproduction number plays a crucial role to control or eradicate the infection from the community. \(R_0\) is defined as the average number of secondary infection produced by a single infective in its entire life span as an infected host, i.e., it is a constant quantity. But in reality initially disease spreads rapidly in higher rate among population and after reaching its maximum limit position, starts to decrease that means basic reproduction number \(R_0\) is not always constant. In this section, we study time-varying reproduction number that means reproduction number per week. This type of time-varying reproduction number is known as effective reproduction number and is denoted by R(t) [47,48,49]. Based on the values of effective reproduction number R(t), researchers can predict about influence of the disease among the population and can give idea about the useful control or preventive measures to decrease the invade of the infection. For estimating effective reproduction number R(t) from per week wise infection curve of dengue outbreak data, we use the formula as follows

$$\begin{aligned} R(t) = \dfrac{b(t)}{\int _0^\infty b(t-\lambda )g(\lambda ) \mathrm{d} \lambda } \end{aligned}$$
(11)

where b(t) denotes new number of cases at t th week and \(g(\lambda )\) represents generation interval distribution of the disease. Let the rate of leaving infected humans, infected mosquitoes be represented by \(c_1 = \mu + d + \gamma + a u_2,\) \(c_2 = c u_3 + \mu _1\), respectively, and generation interval distribution is the combination of \(c_1 e^{- c_1 t}\), \(c_2 e^{- c_2 t}\) then explicit formula is given by

$$\begin{aligned} g(t)= \varSigma _{i = 1}^2\dfrac{c_1 c_2 e^{c_i t}}{\varPi _{j=1, j\ne i}^2(c_j - c_i)}. \end{aligned}$$
(12)

The above expression is valid when it satisfies the condition \(\varLambda > \mathrm{min}\left\{ - c_1, - c_2\right\} \), and mean of the above distribution is given by \(T = \dfrac{1}{c_1} + \dfrac{1}{c_2}\). Using daily new cases of dengue data and formula (11), we can estimate effective reproduction number R(t) using Eq. (12).

We have calculated effective reproduction number estimating model parameters, and the corresponding figure of effective reproduction number is presented in Fig. 9. It is clear from Fig. 9 that values of effective reproduction number oscillate and it lies near about unity except few weeks. It is also clear from the figures that value of effective reproduction number is dropped from 4.291 to 0.6942.

11 Application of optimal control technique to the proposed model

In this section, we shall apply Pontryagin’s maximum principle varying the control parameter to obtain the optimal path of the control strategies. The main objective to formulate an optimal control problem is to minimize the infected human populations as well as infected mosquitoes and also to minimize cost applied for controls [30]. There are three types of control strategies, those are: control \(u_1\) represents vaccination applied for susceptible humans, control \(u_2\) represents treatment for infected human populations and control \(u_3\) represents mosquitoes killing effort by humans. In the previous sections, we have studied the proposed model considering \(u_1, u_2, u_3\) as constants but here we are considering each of these parameters as time dependent.

11.1 Formulation of optimal control problem

To formulate optimal control problem, we consider control strategies as a function of time t. Since if applied controls are constant then implementation cost may be very high. So we have to change the control policies as time changes such that the implementation cost becomes minimum with minimum number of infected humans. Now we reformulate model system (1) in the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{Min}\ M(x,u) = \int _{0}^{T} L(t, x(t), u(t)) \mathrm{d}t \\ \mathrm{subject} \ \ \mathrm{to} \\ x^{'}(t) = f(x(t)) + g(x(t))u(t), \forall t\in [0, T] \\ u(t) \in U(t), \forall t\in [0, T]\\ x(0) = x_{0} \end{array}\right. } \end{aligned}$$
(13)

where

$$\begin{aligned}&x(0)=\left( S(0),I(0),R(0),V_S(0), V_I(0) \right) \ge 0,\\&\quad x(t) = \left( \begin{array}{c} S(t) \\ I(t) \\ R(t) \\ V_S(t) \\ V_I(t) \end{array} \right) ,u(t)= \left( \begin{array}{c} u_1(t) \\ u_2(t) \\ u_3(t) \end{array} \right) , \\&\quad g(x) = \left( \begin{array}{cccc} - S &{} 0 &{} 0 &{} 0 \\ 0 &{} - \dfrac{a u_2}{1 + b u_{2} I} &{} 0 &{} 0 \\ S &{} \dfrac{a u_2}{1 + b u_{2} I} &{} 0 &{} 0 \\ 0 &{} 0 &{} - c V_S &{} 0 \\ 0 &{} 0 &{} 0 &{} - cV_I \end{array} \right) , \\&\quad f(x)= \left( \begin{array}{c} \omega - \dfrac{\beta S V_I}{1 + \alpha S} - \mu S \\ \dfrac{\beta S V_I}{1 + \alpha S} - (\mu + d + \gamma )I \\ \gamma I - \mu R \\ \omega _1 - \mu _1 V_S - \sigma V_S I \\ \sigma V_S I - \mu _1 V_I \end{array} \right) \end{aligned}$$

and integral of cost functional is given by L(x, u) = \(A_1 S + A_2 I + A_3 V_S + A_4 V_I + \dfrac{1}{2} B_1 u_1^2 + \dfrac{1}{2} B_2 u_2^2 + \dfrac{1}{2} B_3 u_3^2\), which is also known as the Lagrangian of the optimal control problem (13). In the expression of L(t, x(t), u(t)) , the constants \( A_1(> 0),\) \(A_2(> 0) \) represent per capita loss for presence of susceptible humans and infected humans, respectively, whereas \( A_3(> 0),\) \(A_4(> 0) \) represent per capita loss for presence of susceptible mosquitoes and infected mosquitoes, respectively. \(B_1, B_2, B_3\) represent weighted cost for applying controls \(u_1(t),\) \(u_2(t),\) \(u_3(t)\), respectively. The control variables are Lebesgue-measurable function and are given as below,

$$\begin{aligned} U = \left\{ (u_1, u_2, u_3): 0\le u_i \le 1, i= 1,2,3 \, and \, t\in [0, T]\right\} . \end{aligned}$$
(14)

11.2 Existence and Uniqueness of optimal control problem

Theorem 8

The optimal control problem (13) subject to condition Eq. (1) admits optimal control variables \(u_1^*(t),\) \(u_2^*(t)\) and \(u_3^*(t)\) such that \(M(u_1^{*}(t), u_2^{*}(t), u_3^{*}(t)) = min \left\{ M(u_1(t),\right. \left. u_2(t), u_3(t)): (u_1, u_2, u_3)\in U \right\} \) where U is defined in (14).

Proof

The control variables and state variables both are non-empty and nonnegative. The control constraint set U is convex set.

Adding all equation of model (1), we get

Therefore, \(N(t) \le \dfrac{k}{\mu ^{'}} + \left( N_0 - \dfrac{k}{\mu ^{'}} \right) e^{- \mu ^{'}t}\), i.e., \(N(t) \longrightarrow \dfrac{k}{\mu ^{'}} \ as \ t \longrightarrow \infty \), which implies all state variables \(S, I, R, V_S, V_I\) are bounded.

At the same time, integrand of the objective functional \(M(u_1(t), u_2(t), u_3(t))\) is convex set with respect to \(u_1, u_2 \,\) and \( \, u_3 \).

Again system (1) can be written in the following form:

$$\begin{aligned}&\phi _{t}(t) = E \phi + G(\phi )\, where\, \phi (t) = \left( \begin{array}{c} S(t) \\ I(t) \\ R(t) \\ V_S(t) \\ V_I(t) \end{array} \right) , \phi _{t}(t) = \left( \begin{array}{c} S^{'}(t) \\ I^{'}(t) \\ R^{'}(t) \\ V_S^{'}(t) \\ V_I^{'}(t) \end{array} \right) , \qquad G(\phi ) = \left( \begin{array}{c} - \dfrac{\beta S V_I}{1 + \alpha S} \\ \dfrac{\beta S V_I}{1 + \alpha S} \\ 0 \\ - \sigma V_S I \\ \sigma V_S I \end{array} \right) ,\\&E = \left( \begin{array}{ccccc} - (\mu + u_1)S &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -(\mu + d + \gamma ) - \dfrac{a u_2}{1 + b u_{2}I} &{} 0 &{} 0 &{} 0 \\ u_1 &{} \dfrac{a u_2}{1 + b u_{2}I}+ \gamma &{} - \mu &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{}-(\mu _1 + c u_3) &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -(\mu _1 + c u_3) \end{array} \right) . \end{aligned}$$

Therefore,

$$\begin{aligned} || G(\phi _1) - G(\phi _2)||&= \left|\dfrac{\beta S_2 V_{I_2}}{1 + \alpha S_2}- \dfrac{\beta S_1 V_{I_{1}}}{1 + \alpha S_1} \right|\\&\quad + \left|\dfrac{\beta S_2 V_{I_2}}{1 + \alpha S_2}-\dfrac{\beta S_1 V_{I_{1}}}{1 + \alpha S_1} \right|\\&\quad + | \sigma V_{S_2} I_2- \sigma V_{S_1}I_1 | + | \sigma V_{S_2} I_2-\sigma V_{S_1}I_1 | \\&\le | -\beta S_1 V_{I_1} + \beta S_2 V_{I_2} | + | \beta S_1 V_{I_1} - \beta S_2 V_{I_2} | \\&\quad + | - \sigma V_{S_1}I_1 + \sigma V_{S_2} I_2 | \\&\quad + | \sigma V_{S_1}I_1 - \sigma V_{S_2} I_2 | \\&\le 2 \beta | S_1 V_{I_1} - S_2 V_{I_2} | + 2 \sigma | V_{S_1} I_1 - V_{S_2}I_2 |\\&\le 2 \beta |V_{I_1}||S_1-S_2|+ 2 \beta |S_2||V_{I_1}-V_{I_2}|\\&\quad +2 \sigma |V_{S_1}||I_1-I_2|+2 \sigma |V_{S_1}-V_{S_2}||I_2| \end{aligned}$$

i.e. \(|| G(\phi _1) - G(\phi _2) || < B || \phi _1 - \phi _2 || \ where \ B= max \left\{ \frac{2 k\beta }{\mu '}, \frac{2 k\sigma }{\mu '} \right\} \).

If we denote \(F(\phi )=E \phi + G(\phi )\), then \(||F(\phi _1) - F(\phi _2) || \le || E|| || \phi _1 - \phi _2 || + B || \phi _1 - \phi _2 || \le C || \phi _1 - \phi _2 || \ where\ \left( || E || + B \right) \le C < \infty \). So all state variables satisfy Lipschitz condition. Therefore, there exist optimal control variables \(u_1^*(t),\) \(u_2^*(t)\) and \(u_3^*(t)\) such that

$$\begin{aligned}&M(u_1^{*}(t), u_2^{*}(t), u_3^{*}(t)) \\&\quad = min \left\{ M(u_1(t), u_2(t), u_3(t)): (u_1, u_2, u_3)\in U \right\} . \end{aligned}$$

Hence the theorem is proved. \(\square \)

11.3 Characterization of optimal control problem

Theorem 9

For optimal control variables \(u_1^*(t),\) \(u_2^*(t)\), \(u_3^*(t)\) and state variables of Eq. (1) which minimizes \(M(u_1(t), u_2(t), u_3(t))\) over U, adjoint variables \(\lambda _1,\) \(\lambda _2,\) \(\lambda _3,\lambda _4\) and \(\lambda _5\) satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\mathrm{d} \lambda _1}{\mathrm{d}t} = - A_1 + \dfrac{\beta V_I}{(1 + \alpha S)^2}(\lambda _1 - \lambda _2) - u_1 (\lambda _1 - \lambda _3) - \lambda _1 \mu \\ \dfrac{\mathrm{d} \lambda _2}{\mathrm{d}t} = - A_2 + \dfrac{a u_2}{(1 + b u_2 I)^2}(\lambda _2 - \lambda _3) + \gamma (\lambda _2 - \lambda _3) \\ + (\mu _1 + d)\lambda _2 + \sigma V_S (\lambda _4 - \lambda _5) \\ \dfrac{\mathrm{d} \lambda _3}{\mathrm{d}t} = \mu \lambda _3 \\ \dfrac{\mathrm{d} \lambda _4}{\mathrm{d}t} = - A_3 + \mu _1 \lambda _4 + c u_3 \lambda _4 + \sigma I (\lambda _4 - \lambda _5) \\ \dfrac{\mathrm{d} \lambda _5}{\mathrm{d}t} = - A_4 + \dfrac{\beta S}{1 + \alpha S}(\lambda _1 - \lambda _2) + \lambda _5 c u_3 + \mu _1 \lambda _5 \end{array}\right. } \end{aligned}$$

with \(\lambda _i(T) = 0, i = 1,2,3,4,5\) and corresponding control variables \(u^*(t) = (u_1{^*}(t), u_2{^*}(t), u_3{^*}(t))\) is as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1^*(t) = \min \left( \max \left( 0, \dfrac{(\lambda _1 - \lambda _3)S}{B_1} \right) , 1 \right) \\ u_2^*(t) = \min \left( \max \left( 0, {\overline{u}}_{2} \right) , 1 \right) \\ u_3^*(t) = \min \left( \max \left( 0, \dfrac{c(\lambda _4 V_S + \lambda _5 V_I)}{B_3} \right) , 1 \right) \end{array}\right. } \end{aligned}$$

where \({\overline{u}}_{2}\) is nonnegative root of \(B_2 u_2 ( 1 + b u_2 I)^2 = a I(\lambda _2 - \lambda _3).\)

Proof

Pontryagin’s maximum principle is used to characterize the optimal control problem of the proposed model [50,51,52,53]. The Hamiltonian of the optimal control problem is given by:

$$\begin{aligned}&H(S, I, R, V_S, V_I, u_1, u_2, u_3, \lambda _1, \lambda _2, \lambda _3, \lambda _4, \lambda _5) \\&\quad = A_1 S + A_2 I + A_3 V_S + A_4 V_I + \dfrac{1}{2} B_1 u_1^2 \\&\qquad + \dfrac{1}{2} B_2 u_2^2 + \dfrac{1}{2} B_3 u_3^2 + \lambda _1 \left\{ \omega -\frac{\beta SV_{I}}{1+\alpha S}-(\mu + u_{1}) \right\} \\&\qquad + \lambda _2 \left\{ \frac{\beta SV_{I}}{1+\alpha S}-(\mu +d+\gamma )I-\frac{au_{2}I}{1+bu_{2}I} \right\} \\&\qquad + \lambda _3 \left\{ \frac{au_{2}I}{1+bu_{2}I}+\gamma I + u_{1} S-\mu R \right\} \\&\qquad +\lambda _4 \left\{ \omega _{1}-\mu _{1} V_{S}-cu_{3} V_{S}-\sigma V_{S} I \right\} \\&\qquad + \lambda _5 \left\{ \sigma V_{S}I-cu_{3}V_{I}-\mu _{1}V_{I} \right\} . \end{aligned}$$

The adjoint equations can be found using Pontryagin’s maximum principle which satisfies the following relations:

\(\dfrac{\mathrm{d} \lambda _1(t)}{\mathrm{d}t} = - \dfrac{\partial H}{\partial S},\) \(\dfrac{\mathrm{d} \lambda _2(t)}{\mathrm{d}t} = - \dfrac{\partial H}{\partial I},\) \(\dfrac{\mathrm{d} \lambda _3(t)}{\mathrm{d}t} = - \dfrac{\partial H}{\partial R},\) \(\dfrac{\mathrm{d} \lambda _4(t)}{\mathrm{d}t} = - \dfrac{\partial H}{\partial V_S},\) \(\dfrac{\mathrm{d} \lambda _5(t)}{\mathrm{d}t} = - \dfrac{\partial H}{\partial V_I}\) with \(\lambda _i(T) = 0, i = 1, 2, 3, 4, 5.\)

Using above relations, we get

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\mathrm{d} \lambda _1}{\mathrm{d}t} = - A_1 + \dfrac{\beta V_I}{(1 + \alpha S)^2}(\lambda _1 - \lambda _2) - u_1 (\lambda _1 - \lambda _3) - \lambda _1 \mu \\ \dfrac{\mathrm{d} \lambda _2}{\mathrm{d}t} = - A_2 + \dfrac{a u_2}{(1 + b u_2 I)^2}(\lambda _2 - \lambda _3) + \gamma (\lambda _2 - \lambda _3) \\ +(\mu _1 + d)\lambda _2 + \sigma V_S (\lambda _4 - \lambda _5) \\ \dfrac{\mathrm{d} \lambda _3}{\mathrm{d}t} = \mu \lambda _3 \\ \dfrac{\mathrm{d} \lambda _4}{\mathrm{d}t} = - A_3 + \mu _1 \lambda _4 + c u_3 \lambda _4 + \sigma I (\lambda _4 - \lambda _5) \\ \dfrac{\mathrm{d} \lambda _5}{\mathrm{d}t} = - A_4 + \dfrac{\beta S}{1 + \alpha S}(\lambda _1 - \lambda _2) + \lambda _5 c u_3 + \mu _1 \lambda _5 \end{array}\right. } \end{aligned}$$
(15)

with

$$\begin{aligned} \lambda _1(T) = 0, \lambda _2(T) = 0, \lambda _3(T) = 0, \lambda _4(T) = 0, \lambda _5(T) = 0. \end{aligned}$$
(16)

Using optimality conditions \(\dfrac{\partial H}{\partial u_1} = 0,\) \(\dfrac{\partial H}{\partial u_2} = 0 \) and \(\dfrac{\partial H}{\partial u_3} = 0\) we get \(u_1 = u_1^*\), \(u_2 = u_2^*\) and \(u_3 = u_3^*\) where \(u^*\) is defined in the statement of the theorem.

Now we have \(\dfrac{\partial ^2 H}{\partial u_1^2} = B_1 >0,\) \( \begin{vmatrix} \dfrac{\partial ^2 H}{\partial u_1^2}&\dfrac{\partial ^2 H}{\partial u_1 \partial u_2} \\ \dfrac{\partial ^2 H}{\partial u_2 \partial u_1}&\dfrac{\partial ^2 H}{\partial u_2^2} \end{vmatrix} = B_1 B_2 > 0 \) and \( \begin{vmatrix} \dfrac{\partial ^2 H}{\partial u_1^2}&\dfrac{\partial ^2 H}{\partial u_1 \partial u_2}&\dfrac{\partial ^2 H}{\partial u_1 \partial u_3} \\ \dfrac{\partial ^2 H}{\partial u_2 \partial u_1}&\dfrac{\partial ^2 H}{\partial u_2^2}&\dfrac{\partial ^2 H}{\partial u_2 \partial u_3} \\ \dfrac{\partial ^2 H}{\partial u_3 \partial u_1}&\dfrac{\partial ^2 H}{\partial u_3 \partial u_2}&\dfrac{\partial ^2 H}{\partial u_3^2} \end{vmatrix} = B_1 B_2 B_3 > 0. \) Thus the minimality condition for H is satisfied at \(u^* = (u_1{^*}, u_2{^*},u_3{^*})\). \(\square \)

To solve optimal control problem numerically, we use forward–backward sweep method. In this method, forward application of fourth-order Runge–Kutta method of system (1) is combined with backward application of fourth-order Runge–Kutta method of system (15) with transversality condition (16). To draw the problem numerically, we consider time interval [0, 36], i.e., after 36 weeks all the controls are terminated automatically. To solve the control effect, we consider values of model parameters as in Table 2 and the cost coefficients \(A_1 = 0.00015\), \(A_2 = 0.2\), \(A_3 = 0.000015\), \(A_4 = 0.000131\), \(B_1 = 0.01\), \(B_2 = 0.3\), \(B_3 = 0.1\) satisfying \(S(0) = 5525628\), \(I(0) = 251,\) \(R(0)= 0,\) \(V_S = 200000\), \(V_I = 1500.\) In Fig. 10 , the blue line and the red line represent time series of infected components with control and without control, respectively. From Fig. 10a, b, it is clear that number of infected decreases when controls are used. In Fig. 10c–e, time series of all controls are represented.

Fig. 10
figure 10

Time series of the population with control (blue line), without control (red line) and control variables; a Infected humans, b Infected mosquitoes, c \(Control \ u_{1}\), d \(Control \ u_{2}\), e \(Control \ u_{3}\). (Color figure online)

Full size image

12 Efficiency analysis

In this section, our target is to find out best effective control strategy using efficiency analysis. In the proposed model, three types of control strategies are used. Among three controls always \(u_2\) control is used since treatment is more essential to get recovery from the dengue disease. Therefore, two cases may arise (i) Strategy 1: \(u_1 \ne 0,\) \(u_2 \ne 0,\) \(u_3 = 0\) (ii) Strategy 2: \(u_1 = 0,\) \(u_2 \ne 0,\) \(u_3 \ne 0\). Among these two cases which strategy is better to control dengue outbreak, to know this we need to apply efficiency analysis. The efficiency index (E. I.) is defined by E. I. = \(\left( 1 - \dfrac{A^c}{A^o}\right) \times 100\), where \(A^c\) and \(A^o\) are number of cumulative infected humans with and without control, respectively. We find the value of \(A^o\) and \(A^c\) using Simpson’s \(\dfrac{1}{3}\)rd rule where \(A^o = \int _0^{36} I(t) \mathrm{d}t = 101.8026\). The values of \(A^c\) and efficiency index (E.I.) are given in Table 4 for different strategies. The strategy with highest number efficiency index (E.I.) is the best strategy [50, 52, 54]. In our problem, the best efficient policy is the second strategy. In epidemiological point of view, mosquitoes killing effort by humans with taking treatment for infected humans is the best efficient policy among the two strategies.

13 Conclusion

In this study, we have proposed a single-strain dengue model with saturated type incidence rate. To get recovery from mosquitoes bites, two types of recovery functions have been introduced for human populations, namely vaccination for susceptible populations and saturated treatment for infected populations. Three types of control functions are considered, namely vaccination for susceptible populations, treatment for infected populations and mosquitoes killing effort to recover from dengue infection. We have proved that disease-free equilibrium point is stable for \(R_0 < 1\) and unstable for \(R_0 > 1\). Similarly we have shown that endemic equilibrium point is stable under some conditions. Using Sotomayor’s theorem, we have proved that model system undergoes through transcritical bifurcation about disease-free equilibrium point when model parameter \(u_2\) passes through its critical value \(u_2^{[TC]}\). This result is biologically significant because below the critical value of the treatment parameter (i.e., \(u_2 <u_2^{[TC]}\)) disease will persist in the system. Also we have shown using Castillo–Chavez and Song’s theorem that model system has backward bifurcation at \(R_0 = 1\). We have observed that for \(R_0^{*}< R_0 < 1\) two endemic equilibrium points exist, one with smaller infected is unstable and other one with higher infected is stable where \(R_0^{*}\) is critical value of \(R_0\). Biologically we can conclude that eradication of disease depends not only on model parameter but also on initial population density.

We have fitted model with real reported data of dengue outbreak in Singapore from 18th week, 2014 to 1st week, 2015 to check the validity of the proposed model and estimated model parameters. To identify the highly effective model parameter, sensitivity analysis has been performed; these parameters need to control to reduce the disease spreading.

Table 4 Strategies with their efficiency indices
Full size table

To find the suitable path for control parameters, we have used optimal control policy which will minimize the implementation cost with minimum number of infected populations. Numerically we have shown the positive impact of the different controls for eradicating dengue transmission. Using efficiency analysis, we have found that the best effective control policy is use of treatment for infected humans and mosquitoes killing effort simultaneously. Thus from this work we can conclude that spreading of dengue can be controlled using proper preventive actions.