1 Introduction

The COVID-19 pandemic was first reported in Wuhan, in December 2019, with more than 70,000 cases of infection and 1,800 deaths within the first 50 days of the epidemic [1, 2]. As of July 30, 2021, there has been 196,553,009 confirmed cases of the pandemic with 4,200,412 confirmed deaths worldwide [3]. Some of the symptoms of the COVID-19 infection includes: difficulty in breathing, dry cough, fever and general tiredness [4]. According to clinical evidence as revealed by medical experts, the incubation period of the disease is between 2 and 14 days. During the incubation period, infected persons may be asymptomatic, yet capable of transmitting the virus to others [4]. Since the first wave of the pandemic, there have been other waves (in some countries) due to genetic mutation of the disease, thereby developing different variants. The World Health Organization (WHO) in collaboration with experts has been monitoring the evolution of the disease. The various variants have been classified as variants of concern (VOC) and variants of interest (VOI). Some of the designated VOC includes alpha, beta, gamma and delta, and that of VOI includes eta, iota, kappa and lambda [3].

As the pandemic is far from ending anytime soon, various vaccines have been developed across the globe. With 3, 839, 816, 037 vaccine doses administered globally [3], the third wave of the disease is witnessing little mortality rate. Nigeria with a population of around 206 million [5], with 178, 508 total number of COVID-19 infections [6], received approximately 8,000,000 doses of vaccine as of August 10, 2021. Just like several other countries are witnessing the third wave of the pandemic, Nigeria is also witnessing the third wave, and the Nigerian government, the Nigerian center for disease control (NCDC), in collaboration with WHO must increase its vaccination rate, for effective control of the spread of the disease.

To address COVID-19 pandemic, several mathematical approaches including Refs. [7,8,9,10,11,12,13] have been established. Reference [14] established a primer for COVID-19 mathematical model formulation, theoretical analysis and numerical simulations. Their model was then used to gain insights into transmission dynamics of the disease in the USA. Reference [15] extended a model by incorporating three parameters: use of face mask, regular washing of hands with hand sanitizer and maintenance of minimum social distancing, into their models. They corroborated their theoretical analysis with numerical simulations and proposed a control strategy on how COVID-19 disease can be eradicated. Reference [1] explored and applied a linear regression method on the mathematical model of COVID-19 in order to predict the early stage of the disease. Reference [16] established a biology-based mathematical framework to better understand clinical heterogeneity with the best treatment. Their model shows that it can be used to understand transmission dynamics of infected individuals. Reference [17] studied how COVID-19 has varied over time, by incorporating a stochastic model with data from Wuhan and international reported cases with origin from Wuhan. Reference [18] established systems of differential equations for COVID-19 analysis through a coupled system. They forecasted the peak of the pandemic in some cities using varying parameters. Reference [19] suggested a mathematical approach of the possibility of infection from dead to living humans and the potential effects of lockdown.

Consequently, in this study, we proposed mathematical model to study the transmission dynamics of COVID-19 without demographic features, i.e., birth and natural death. Demographic parameters can be excluded when investigating the dynamics of an epidemic that is occurring within a few weeks or months (see [20, 21]). We then reformulated the model by incorporating some optimal control parameters, and we conducted the theoretical analysis of the model with and without optimal control strategy. In the model without optimal control, we analyzed the disease stability and sensitivity analysis in order to identify parameters that can impact the reproduction number significantly. As for the model with control strategy, we check the necessary conditions for the model. We corroborated our theoretical findings for both models with numerical simulations.

The rest of the paper is structured as follows: Sects. 2–4 describe the formulation, theoretical insights and numerical simulations of the model without optimal control. The model with optimal control strategy and its theoretical analysis is established in Sect. 5, and Sect. 6 presents conclusion for this work.

2 Formulation of model

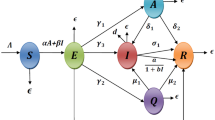
In this work, formulating a deterministic model to gain insight into the transmission dynamics of COVID-19 without demographic features such as birth and natural death, as in Refs. [20, 21], is our concern. The total human population at time \(t\), denoted by \(N\left( t \right)\), is divided into eight mutually exclusive compartments of: susceptible humans \(S\left( t \right)\), exposed humans \(E\left( t \right)\), quarantined humans \(Q\left( t \right)\), undetected asymptomatic infectious humans \(A\left( t \right)\), undetected symptomatic infectious humans \(I\left( t \right)\), undetected symptomatic infectious humans under self-medication \(M\left( t \right)\), detected and hospitalized infectious humans (via testing) \(I_{H} \left( t \right)\) and recovered humans \(R\left( t \right)\), so that we have:

$$\begin{aligned} N\left( t \right)& = S\left( t \right) + E\left( t \right) + Q\left( t \right) + A\left( t \right) + I\left( t \right)\\&\quad + M\left( t \right) + I_{H} \left( t \right) + R\left( t \right),\end{aligned} $$

It is important to state that in the model, infected humans that are detected and hospitalized are treated and carefully handled in accordance with the standard procedure and COVID-19 guidelines.

Those who are vaccinated in the susceptible class do so at the rate v, the rate of compliance to wearing of face mask, washing of hands and keeping of social distance are \(\rho_{1}\), \(\rho_{2}\) and \(\tau_{1}\), respectively, and the force of infection for acquiring the infection is given by \(\lambda = \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A + I + c_{2} M} \right)}}{N}\), while those who progressed from exposed class to quarantine class and Asymptomatic class do so at the rate \(\alpha\) and \(\sigma\), respectively. Furthermore, \(\kappa\) and \(\left( {1 - \kappa } \right)\) are the fractions of those who are undetected but asymptomatically infected and those undetected but symptomatically infected, respectively. Quarantined humans who do not develop symptoms and are not infected that progress to susceptible class again do so at the rate \(\mu\), while recovery rate of undetected asymptomatic (symptomatic) infectious humans due to strong immune system takes place at the rate \(\varepsilon_{A} \left( {\varepsilon_{I} } \right)\), respectively, while recovery rate of humans under self-medication.in their class takes place at rate \(\varepsilon_{M}\). Detection rate (via testing) for the undetected asymptomatic infectious class and sensitization rate on the danger of self-medication take place at the rate \(\omega\) and \(\phi\), respectively. Progression rate from \(M\) class to \(I_{H}\) class due to severity of COVID-19 in humans under self-medication takes place at rate \(\theta\). Disease-induced death rate of undetected symptomatic infectious humans hospitalized detected infectious humans and self-medicated humans takes place at the rate \(\delta_{I} ,\delta_{H} ,\delta_{M}\), respectively.

Consequently, the COVID-19 model is given by the following deterministic system of nonlinear differential equations:

$$ \begin{aligned} \frac{dS}{{dt}} &= - \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A + I + c_{2} M} \right)S}}{N}\\& \quad- vS + \mu Q, \hfill \\ \frac{dE}{{dt}} &= \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A + I + c_{2} M} \right)S}}{N}\\&\quad - \left( {\alpha + \sigma } \right)E, \hfill \\ \frac{dQ}{{dt}} &= \alpha E - \left( {\eta + \mu } \right)Q, \hfill \\ \frac{dA}{{dt}} &= k\sigma E - \left( {\omega + \varepsilon_{A} } \right)A, \hfill \\ \frac{dI}{{dt}} &= \left( {1 - k} \right)\sigma E - \left( {q + \delta_{I} + \varepsilon_{I} } \right)I, \hfill \\ \frac{dM}{{dt}} &= \left( {1 - \tau_{2} \phi } \right)qI - \left( {\theta + \delta_{M} + \varepsilon_{M} } \right)M, \hfill \\ \frac{{dI_{H} }}{dt} &= \eta Q + \omega A + \tau_{2} \phi qI + \theta M - \left( {\gamma + \delta_{H} } \right)I_{H} , \hfill \\ \frac{dR}{{dt}} &= \varepsilon_{A} A + \varepsilon_{I} I + \varepsilon_{M} M + \gamma I_{H} + vS, \hfill \\ \end{aligned} $$
(1)

The associated state variables and parameters are described in Table 1, and a flow diagram of the model is depicted in Fig. 1.

Table 1 Description of State Variables and parameters
Full size table
Fig. 1
figure 1

A flow chart of COVID-19 model with \(\lambda = \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A + I + c_{2} M} \right)}}{N}\)

Full size image

Some of the main assumptions made in the formulation of the third wave of COVID-19 model (1) are as itemized below:

  1. (i)

    Natural recovery can occur perhaps due to strong immune systems of humans [21].

  2. (ii)

    Self-medication increases the number of infections [20].

  3. (iii)

    The population mixed homogeneously.

3 Theoretical analysis of the model

In this section, we compute the reproduction number and prove theoretically the disease stability in its free state, and carry out sensitivity analysis of the parameters.

3.1 Basic property

It is necessary to prove that all state variable of the COVID-19 model (1) are nonnegative for all time \(\left( t \right)\), for the model to be epidemiologically and mathematically well posed in a feasible region \(D\) given by:

$$\begin{aligned} D &= \left\{ {\left( {S,E,Q,A,I,M,I_{R} ,R} \right) \in \Re_{ + }^{8} :}\right. \\ & \quad \left.{(S + E + Q + I + M + I_{R} + R) \le N}\vphantom{\Re_{ + }^{8}} \right\} \end{aligned}$$

What this means is that we need to show that the solution of the system of nonlinear differential equations in the COVID-19 model with positive initial data will remain nonnegative for all time \(\left( t \right)\) when \(t \ge 0\). This can be done as:

$$\begin{aligned} N(t) &= \left\{ {\left( {S(0),E(0),Q(0),A(0),I(0),M(0),}\right.}\right. \\&\quad\left.{\left.{\times I_{R} (0),R(0)} \right) \ge 0} \right\} \in \Re_{ + }^{8} .\end{aligned} $$

Theorem 1.

Let the initial data for the model (1) be: \(S(t) > 0,E(t) > 0,Q(t) > 0,A(t) > 0,\) \(I(t) > 0,M(t) > 0,I_{R} (t) > 0\,\,and\,\,R(t) > 0\); then, the solutions:

$$ \left( {S(t),E(t),Q(t),A(t),I(t),M(t),I_{R} (t),R(t)} \right) $$

of the model (1) with initial positive data, will remain positive for all time \(t > 0\).

Proof.

Note that initially,

$$\begin{aligned} S(t) &+ E(t) + Q(t) + A(t) + I(t) + M(t) \\&+ I_{R} (t) + R(t) = N(t)\end{aligned} $$
(2)

Thus, at any time t, \(S(t) \le N(t),\,E(t) \le N(t),Q(t) \le N(t),A(t) \le N(t),I(t) \le N(t),\) \(M(t) \le N(t),I_{R} (t) \le N(t),R(t) \le N(t)\) so that from first equation in model (1), by putting \(\lambda = \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A + I + c_{2} M} \right)}}{N}\) in it, we obtain:

$$ \begin{aligned} \frac{dS}{{dt}} & = - \lambda S - vS + \mu Q \\ & \ge - \lambda S - vS \\ & \ge - \beta S - vS \\ & \ge - \left( {\beta + v} \right)S \\ \end{aligned} $$

From here, it is clear that \(S(t) \ge S(0)e^{{ - \left( {\beta + v} \right)t}} > 0\), for \(t \ge 0\) and S > 0. By using similar approach, it can be shown that \(E(t) > 0,Q(t) > 0,A(t) > 0,\)\(I(t) > 0,M(t) > 0,I_{R} (t) > 0\,\,and\,\,R(t) > 0\), respectively. Hence, the solution of the model (1) remains nonnegative for all nonnegative initial conditions.

Lemma 1.

The solutions of the proposed system (1) are feasible for all \(t>0\), if they enter the invariant region \(D\), given by:

$$ \begin{aligned}D &= \left\{ {\left( {S,E,Q,A,I,M,I_{H} ,R} \right) \in R_{ + }^{8} :S > 0,E > 0,}\right. \\ & \quad \times \left.{Q > 0,A > 0,I > 0,I_{H} > 0,R > 0,N \le \frac{\pi }{\mu }} \right\}\end{aligned} $$
(3)

Proof: By adding all the equations in the model (1), we have:

$$ \begin{aligned} \frac{dN}{{dt}} & = - \mu N - \delta_{I} - \delta_{M} - \delta_{H} \\ = - \mu N - \left( {\delta_{I} + \delta_{M} + \delta_{H} } \right), \\ \end{aligned} $$

From which it follows that (since the state variables and parameters of the model are nonnegative)

$$ \frac{dN}{{dt}} \le - \mu N $$

Thus, \(\frac{dN}{{dt}} < 0\), whenever \(N(t) > \pi /\mu\); furthermore, \(\frac{dN}{{dt}} > 0\) whenever \(N(t) \le \pi /\mu\). Hence, since it follows from the right-hand side of the inequality that \(\frac{dN}{{dt}}\) is bounded by \(- \mu N\), a standard comparison theorem [22] can be used to show that:

$$ N\left( t \right) \le N(0)e^{ - \mu t} + \frac{\pi }{\mu }\left( {1 - e^{ - \mu t} } \right) $$
(4)

If \(N\left( 0 \right) \le \frac{\pi }{\mu }\), then \(N\left( t \right) \le \frac{\pi }{\mu }\). Thus, the region D is a positively invariant set under the flow described by the model (1). Hence, it is sufficient to consider the dynamics of the model (1) in the region D. Thus, in this region, the model can be considered as been epidemiologically and mathematically well posed [23].

3.1.1 Local asymptotic stability of the disease-free equilibrium of the model

The COVID-19 model (1) has a continuum of disease-free equilibria (DFE), given by:

$$\begin{aligned} \varepsilon_{0} &= \left( {S^{*} ,E^{*} ,Q^{*} ,A^{*} ,I^{*} ,M^{*} ,I_{H}^{*} ,R^{*} } \right) \\&= \left( {N\left( 0 \right) - R^{*} ,0,0,0,0,0,0,R^{*} } \right) \end{aligned}$$
(5)

where \(N\left( 0 \right)\) is the initial total size of the population, \(0 < S^{*} \le N\left( 0 \right)\),\(0 \le R^{*} < N\left( 0 \right)\) and \(0 < S^{*} + R^{*} \le N\left( 0 \right)\).

3.1.1.1 The basic reproduction number

The basic reproductive number \(R_{0}\) [23] is a tool that determine the potential spread of the disease in a population. In a nutshell,\(R_{0}\) is a threshold parameter that help describes the stability of the DFE of the model corresponding to the peak and final size of a pandemic. According to Ref. [24], it is “the expected number of secondary cases of infection which would occur due to a primary case in a completely susceptible population.” It is an important parameter that governs the spread of a disease. The reproductive number \(\left( {R_{0} } \right)\) can be computed using the next generation operator method described in [25]. The matrices \(F\) and \(V\), for the new infection and the remaining transition terms, respectively, for the model are:

$$ F = \left[ {\begin{array}{*{20}c} 0 & 0 & {\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)c_{1} } & {\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)} & {\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)c_{2} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] $$

And

$$ V = \left[ {\begin{array}{*{20}c} {\left( {\alpha + \sigma } \right)} & 0 & 0 & 0 & 0 & 0 \\ { - \alpha } & {\left( {\eta + \mu } \right)} & 0 & 0 & 0 & 0 \\ { - k\sigma } & 0 & {\left( {\omega + \varepsilon_{A} } \right)} & 0 & 0 & 0 \\ { - \left( {1 - k} \right)\sigma } & 0 & 0 & {\left( {q + \delta_{I} + \varepsilon_{I} } \right)} & 0 & 0 \\ 0 & 0 & 0 & { - \left( {1 - \tau_{2} \phi } \right)q} & {\left( {\theta + \delta_{M} + \varepsilon_{M} } \right)} & 0 \\ 0 & { - \eta } & { - \omega } & { - \tau_{2} \phi q} & { - \theta } & {\left( {\gamma + \delta_{H} } \right)} \\ \end{array} } \right] $$

Hence, it follows from [26] that, \(R_{0} = \rho \left( {FV^{ - 1} } \right)\), where \(\rho\) is the spectral radius or largest absolute value or modulus (in the complex case) of the eigenvalues of \(\left( {FV^{ - 1} } \right)\). Therefore,

$$\begin{aligned} R_{0} &= \beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\\ &\quad \times\left[ {\frac{{c_{1} k\sigma }}{{\left( {\alpha + \sigma } \right)\left( {\omega + \varepsilon_{A} } \right)}} + \frac{{\left( {1 - k} \right)\sigma }}{{\left( {\alpha + \sigma } \right)\left( {q + \delta_{I} + \varepsilon_{I} } \right)}} }\right. \\ & \quad \left.{+ \frac{{c_{2} \left( {1 - k} \right)\sigma \left( {1 - \tau_{2} \phi } \right)q}}{{\left( {\alpha + \sigma } \right)\left( {q + \delta_{I} + \varepsilon_{I} } \right)\left( {\theta + \delta_{M} + \varepsilon_{M} } \right)}}} \right]\end{aligned} $$
(6)

Theorem 2. The DFE of model (1) is locally asymptotically stable (LAS) if \(R_{0} < 1\) and unstable if \(R_{0} > 1\).

Epidemiologically, Theorem 2 implies that a small inflow of COVID-19 infected individuals in the population will not cause a COVID-19 outbreak if \({R}_{0}<1\). It is pertinent to note that this result is determined by the initial sizes of the infected individuals in the population. To ensure that COVID-19 elimination is independent of the initial sizes of the infected individuals in the population, it is necessary to show that the DFE is globally asymptotically stable (GAS).

3.1.2 Global asymptotic stability of the DFE of the model (1)

To examine the global stability of the COVID-19 model (1) at DFE, we consider the following theorem.

Theorem 3.

The DFE of the COVID-19 model (1) is GAS if \(R_{0} \le 1\), otherwise it will be unstable.

Proof: We consider Lyapunov function as follow

$$\begin{aligned} G &= \left( {\frac{{c_{1} k\sigma }}{{B_{1} B_{3} }} + \frac{{B_{4} }}{{B_{1} B_{5} }} + \frac{{c_{2} B_{4} B_{6} }}{{B_{1} B_{5} B_{7} }}} \right)E + \frac{{c_{1} }}{{B_{3} }}A \\&\quad+ \left( {\frac{{c_{2} B_{6} + B_{7} }}{{B_{5} B_{7} }}} \right)I + \frac{{c_{2} }}{{B_{7} }}M \end{aligned}$$
(7)

where \(B_{1} = \alpha + \sigma\),\(B_{2} = \mu + \eta\),\(B_{3} = \omega + \varepsilon_{A}\),\(B_{4} = \left( {1 - k} \right)\sigma\),\(B_{5} = q + \delta_{I} + \varepsilon_{I}\), \(B_{6} = \left( {1 - \tau_{2} \phi } \right)q\), \(B_{7} = \theta + \delta_{M} + \varepsilon_{M}\) and \(B_{8} = \gamma + \delta_{H}\).

With Lyapunov derivatives.

$$ \begin{aligned} \dot{G} & = \left( {\frac{{c_{1} k\sigma }}{{B_{1} B_{3} }} + \frac{{B_{4} }}{{B_{1} B_{5} }} + \frac{{c_{2} B_{4} B_{6} }}{{B_{1} B_{5} B_{7} }}} \right)\dot{E} + \frac{{c_{1} }}{{B_{3} }}\dot{A} \\& \quad+ \left( {\frac{{c_{2} B_{6} + B_{7} }}{{B_{5} B_{7} }}} \right)\dot{I} + \frac{{c_{2} }}{{B_{7} }}\dot{M} \\ \dot{G} &= \left( {\frac{{c_{1} k\sigma }}{{B_{1} B_{3} }} + \frac{{B_{4} }}{{B_{1} B_{5} }} + \frac{{c_{2} B_{4} B_{6} }}{{B_{1} B_{5} B_{7} }}} \right)\\ & \quad \times\left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A + I + c_{2} M} \right)S}}{N} - B_{1} E} \right) \\ &\quad + \frac{{c_{1} }}{{B_{3} }}\left( {k\sigma E - B_{3} A} \right) + \left( {\frac{{c_{2} B_{6} + B_{7} }}{{B_{5} B_{7} }}} \right)\\& \quad \times\left( {B_{4} E - B_{5} I} \right) + \frac{{c_{2} }}{{B_{7} }}\left( {B_{6} I - B_{7} M} \right) \\ \dot{G} &= \left( {\frac{{c_{1} k\sigma }}{{B_{1} B_{3} }} + \frac{{B_{4} }}{{B_{1} B_{5} }} + \frac{{c_{2} B_{4} B_{6} }}{{B_{1} B_{5} B_{7} }}} \right)\\&\quad \times\left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A + I + c_{2} M} \right)S}}{N}} \right)\\&\quad - c_{1} A - I - c_{2} M \\ \end{aligned} $$

Note that \(S\left( t \right) \le N\left( t \right)\) in the Region \(D\) for all \(t > 0\), so

$$ \begin{aligned} \dot{G} &\le \left( {c_{1} A + I + c_{2} M} \right)\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\\&\quad \times\left( {\frac{{c_{1} k\sigma }}{{B_{1} B_{3} }} + \frac{{B_{4} }}{{B_{1} B_{5} }} + \frac{{c_{2} B_{4} B_{6} }}{{B_{1} B_{5} B_{7} }}} \right) - \left( {c_{1} A + I + c_{2} M} \right) \hfill \\ \dot{G}& \le \left( {c_{1} A + I + c_{2} M} \right)\left( {\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)}\right.\\&\quad \left.{\left( {\frac{{c_{1} k\sigma }}{{B_{1} B_{3} }} + \frac{{B_{4} }}{{B_{1} B_{5} }} + \frac{{c_{2} B_{4} B_{6} }}{{B_{1} B_{5} B_{7} }}} \right) - 1} \right) \hfill \\ \dot{G} &\le \left( {c_{1} A + I + c_{2} M} \right)\left( {R_{0} - 1} \right) \hfill \\ \end{aligned} $$
(8)

Since all the model parameters are nonnegative, it follows that \(\dot{G} \le 0\) for \(R_{0} \le 1\) with \(\dot{G} = 0\) if and only if \(Q = 0,E = 0,A = 0,I = 0,M = 0\;\;{\text{and}}\;\;I_{H} = 0\). Hence, \(G\) is a Lyapunov function for the model (1). Therefore, by the LaSalle’s invariance principle [22], the DFE of the COVID-19 model (1) is globally asymptotically stable whenever \(R_{0} \le 1\).

3.1.3 Sensitivity analysis

To determine parameters with more significant contribution to the COVID-19 transmission, we carried out sensitivity analysis on the parameters of the model, by following approach in Refs. [27, 28]. This technique establish a formula to determine the sensitivity index of all the basic parameters as follows.

Definition 4.

The normalized forward sensitivity index of a variable, \(g\), that depends differentially on a parameter, \(p\), is defined as

$$ \Im_{p}^{g} = \frac{\partial g}{{\partial p}} \times \frac{p}{g} $$
(9)

so that the analytical expression for the sensitivity of the reproduction number \(\left({R}_{0}\right)\) with respect to parameter \(\mathrm{^{\prime}}p\mathrm{^{\prime}}\) is given by:

$$ \Im_{p}^{{R_{0} }} = \frac{{\partial R_{0} }}{\partial p} \times \frac{p}{{R_{0} }} $$
(10)

Therefore, we compute the sensitivity index of \({R}_{0}\) to the following basic parameters associated with the reproduction number using (10).

Here

$$\begin{aligned}R_{0} &= \beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\\&\quad\times\left[ {\frac{{c_{1} k\sigma }}{{\left( {\alpha + \sigma } \right)\left( {\omega + \varepsilon_{A} } \right)}} + \frac{{\left( {1 - k} \right)\sigma }}{{\left( {\alpha + \sigma } \right)\left( {q + \delta_{I} + \varepsilon_{I} } \right)}} }\right. \\&\quad \left.{+ \frac{{c_{2} \left( {1 - k} \right)\sigma \left( {1 - \tau_{2} \phi } \right)q}}{{\left( {\alpha + \sigma } \right)\left( {q + \delta_{I} + \varepsilon_{I} } \right)\left( {\theta + \delta_{M} + \varepsilon_{M} } \right)}}} \right] \end{aligned}$$

With

$$ \begin{aligned} \Im_{\beta }^{{R_{0} }} &= \frac{{\partial R_{0} }}{\partial \beta } \times \frac{\beta }{{R_{0} }} = 1, \hfill \\ \Im_{{\rho_{1} }}^{{R_{0} }} &= \frac{{\partial R_{0} }}{{\partial \rho_{1} }} \times \frac{{\rho_{1} }}{{R_{0} }} = - \frac{{\rho_{1} }}{{1 - \rho_{1} }} = - 0.{1111}, \hfill \\ \Im_{{\rho_{2} }}^{{R_{0} }} &= \frac{{\partial R_{0} }}{{\partial \rho_{2} }} \times \frac{{\rho_{2} }}{{R_{0} }} = - \frac{{\rho_{2} }}{{1 - \rho_{2} }} = - 0.{25}, \hfill \\ \Im_{{\tau_{1} }}^{{R_{0} }} &= \frac{{\partial R_{0} }}{{\partial \tau_{1} }} \times \frac{{\tau_{1} }}{{R_{0} }} = - \frac{{\tau_{1} }}{{1 - \tau_{1} }} = - 0.{25}, \hfill \\ \Im_{k}^{{R_{0} }} &= \frac{{k\sigma c_{1} \left( {q + \delta_{I} + \varepsilon_{I} } \right)\left( {\theta + \delta_{M} + \varepsilon_{M} } \right) - k\sigma \left( {\omega + \varepsilon_{A} } \right)\left( {\left( {\theta + \delta_{M} + \varepsilon_{M} } \right) + \left( {1 - \tau_{2} \phi } \right)qc_{2} } \right)}}{{k\sigma c_{1} \left( {q + \delta_{I} + \varepsilon_{I} } \right)\left( {\theta + \delta_{M} + \varepsilon_{M} } \right) + \left( {1 - k} \right)\sigma \left( {\omega + \varepsilon_{A} } \right)\left( {\left( {\theta + \delta_{M} + \varepsilon_{M} } \right) + \left( {1 - \tau_{2} \phi } \right)qc_{2} } \right)}} = - 0.{1976}, \hfill \\ \Im_{{c_{1} }}^{{R_{0} }}& = \frac{{k\sigma c_{1} \left( {q + \delta_{I} + \varepsilon_{I} } \right)\left( {\theta + \delta_{M} + \varepsilon_{M} } \right)}}{{k\sigma c_{1} \left( {q + \delta_{I} + \varepsilon_{I} } \right)\left( {\theta + \delta_{M} + \varepsilon_{M} } \right) + \left( {1 - k} \right)\sigma \left( {\omega + \varepsilon_{A} } \right)\left( {\left( {\theta + \delta_{M} + \varepsilon_{M} } \right) + \left( {1 - \tau_{2} \phi } \right)qc_{2} } \right)}} = 0.{4}0{1}0, \hfill \\ \Im_{{c_{2} }}^{{R_{0} }} &= \frac{{\left( {1 - k} \right)\sigma \left( {1 - \tau_{2} \phi } \right)q\left( {\omega + \varepsilon_{A} } \right)c_{2} }}{{k\sigma c_{1} \left( {q + \delta_{I} + \varepsilon_{I} } \right)\left( {\theta + \delta_{M} + \varepsilon_{M} } \right) + \left( {1 - k} \right)\sigma \left( {\omega + \varepsilon_{A} } \right)\left( {\left( {\theta + \delta_{M} + \varepsilon_{M} } \right) + \left( {1 - \tau_{2} \phi } \right)qc_{2} } \right)}} = 0.0{195}, \hfill \\ \end{aligned} $$

Similarly, we do this for the remaining basic parameters that makeup the basic reproduction number.

Interpretation of sensitivity indices: The sensitivity indices of the reproduction number with respect to basic parameters are found in Table 2 and in Fig. 2.

Table 2 Values of parameters in the model (1)
Full size table
Fig. 2
figure 2

Sensitivity index of \({R}_{0}\) against some parameters

Full size image

From the sensitivity indices, parameters with positive indices shows high impact on the burden of the disease in the community if their values are increasing. Similarly, parameters in which their sensitivity indices are negative have an effect of minimizing the burden of the disease in the community as their values increase while the others are constant. Consequently, as their values increase, the reproduction number decreases, this leads to the minimization of the endemicity of the disease in the community.

From the results of sensitivity analysis above, observe that parameters with high negative indices are \(\varpi\), \(\varphi\), \(\tau_{2}\) and \(\varepsilon_{M}\) which are: detection rate via testing for undetected asymptomatic infectious individuals, sensitization rate on danger of self-medication, fraction of undetected symptomatic infectious humans that adhered to COVID-19 safety protocols and avoided self-medication and recovery rate of those under self-medication, respectively. These are the top parameters that drives significantly the dynamics of the spread of the disease. Consequently, to control the spread of the disease, these are the top parameters to be effectively and adequately targeted by policy makers such that everything that should be done to keep their sensitivity index negative will have to be done for effective control of the disease, this means that detection rate via testing must be made higher, more people must be enlightened on the danger of self-medication and encouraged to be observing the COVID-19 safety protocols: wearing of facemasks always while in the public, washing of hands regularly with soaps and hand sanitizers, keeping of minimum social distances and early detection of those that are infected with the virus such that the recovery rate of those under self-medication must be made higher.

4 Simulations, results and discussion

In this section, the third wave of COVID-19 model (1) is simulated numerically using the parameter estimates in Table 2 in order to illustrate some of the theoretical results of the study. We estimated the parameters in the model by fitting the model with the daily number of reported cases and the number of active cases in Nigeria as obtained from NCDC [6]. The total population of Nigeria is estimated to be 206 million [5]. Therefore, the initial conditions of the state variables used for the model fitting as of July 9, 2021 is given as follows: S(0) = 206,000,000, \(E\left( 0 \right) = 200000\),\(Q\left( 0 \right) = 7000\),\(A\left( 0 \right) = 30000\),\(I\left( 0 \right) = 150000\),\(M\left( 0 \right) = 50000\),\(I_{H} \left( 0 \right) = 1719\),\(R\left( 0 \right) = 164415\).

We fit our model (1) to the cumulative number of active COVID-19 cases. Fitting is used to estimate the effective contact rate \(\left( \beta \right)\), progression rate \(\left( \eta \right)\) from \(Q\left( t \right)\) class to \(I_{H} \left( t \right)\) class, detection rate for undetected asymptomatic infectious individuals \(\left( \omega \right)\) and progression rate \(\left( \theta \right)\) from \(M\left( t \right)\) class to \(I_{H} \left( t \right)\) class. The model fitting was performed using the fmincon Algorithm in MATLAB. The model fitting was implemented for an epidemic period starting from July 9, 2021, to September 17, 2021, a period when the third wave of the pandemic pervades the air. Vaccination was introduced and actively carried out by NPHCDA [29] in Nigeria, i.e., from March 23, 2021 till date. We present the number of active COVID-19 cases and its projections in Figs. 3 and 4, respectively. Figure 4 forecasts the probable cases of COVID-19 in Nigeria for a short term only, as the federal government’s (FG) COVID-19 policies changes from time to time. The FG’s dynamic policies would lead to corresponding changes in associated parameters of the COVID-19 model. From the real data (see Fig. 3) that after September 17, 2021, we projected around 800 cases after 60 days.

Fig. 3
figure 3

Number of active cases in Nigeria

Full size image
Fig. 4
figure 4

Projections for the number of active cases in Nigeria

Full size image

Figure 5 depicts the effect of varying values of \(\phi\) on the number of active COVID-19 cases and human under self-medications, respectively. In both Fig. 5a, b, as \(\phi\) increases, the number of active cases and human under self-medications decreases faster. Figure 5a shows that as policy makers increase the sensitization rate on the danger of self-medication, the number of active cases decreases over time. Intuitively, as more and more individuals are sensitized on the danger of self-medication, the number of COVID-19 active cases will reduce. Self-medication can be dangerous as people with expert knowledge of the virus tends to use drugs that can worsen the infection or even lead to COVID-19 death. Similarly, in Fig. 5b, as \(\phi\) increases, the number of humans under self-medications decreases faster. This corroborates Fig. 5a, as policy makers increase the sensitization rate on the danger of self-medication, the number of people on self-medication reduces. This is because when people are aware of the dangers of self-medication, they are likely to consult a medical expert for advice. Sensitizing the population on the danger of self-medication will not only curb the incidence of self-medication, it will also reduce the number of active cases of COVID-19 infection. If the infected people get proper and expert advice on medication, it will certainly lead to recovery from the virus, thereby, reducing the number of active cases of infection.

Fig. 5
figure 5

Effect of \(\phi\) on the number of active cases and humans under self-medication

Full size image

Figure 6 depicts the effect of varying values of \(\omega\) on the number of active COVID-19 cases. As \(\omega\) increases, the number of active cases decreases slower within the first 50 days. In reality, some cases of COVID-19 patients are asymptomatic in nature. As the detection (testing) rate for the undetected asymptomatic infectious class increases, more cases are detected, thereby, leading to increase in the number of active cases. This is necessary since the goal of every nation is to eradicate the virus, people need to get tested, especially the undetected asymptomatic group. When the undetected asymptomatic class becomes detected, they ultimately get treated, leading to potential recovery from the disease.

Fig. 6
figure 6

Effect of \(\omega\) on the number of active cases

Full size image

5 Optimal control strategy to reducing the disease burden

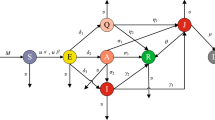
The term "optimal control strategy" refers to a measure that has been used to procure optimal approaches to be adopted against the transmission dynamics of contagious illnesses using various scientific methods. It has undoubtedly aided in the discovery of optimal strategies to help effectively control the spread of dangerous communicable diseases. Finding an approach that reduces the number of affected people as well as the associated costs is critical. As a result, we introduce and focus on the two-time varying controls: \(\left( {v\left( t \right)\;\;{\text{and}}\;\,\phi \left( t \right)} \right)\), which represent the vaccination rate and rate of sensitization on the danger of self-medication, respectively. Using this control, the COVID-19 model (1) with optimal control now becomes:

$$ \begin{aligned} \frac{dS}{{dt}} &= - \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A + I + c_{2} M} \right)S}}{N}\\&\quad - v\left( t \right)S + \mu Q, \hfill \\ \frac{dE}{{dt}} &= \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A + I + c_{2} M} \right)S}}{N}\\&\quad- \left( {\alpha + \sigma } \right)E, \hfill \\ \frac{dQ}{{dt}}&= \alpha E - \left( {\eta + \mu } \right)Q, \hfill \\ \frac{dA}{{dt}} &= k\sigma E - \left( {\omega + \varepsilon_{A} } \right)A, \hfill \\ \frac{dI}{{dt}} &= \left( {1 - k} \right)\sigma E - \left( {q + \delta_{I} + \varepsilon_{I} } \right)I, \hfill \\ \frac{dM}{{dt}} &= \left( {1 - \tau_{2} \phi \left( t \right)} \right)qI - \left( {\theta + \delta_{M} + \varepsilon_{M} } \right)M, \hfill \\ \frac{{dI_{H} }}{dt} &= \eta Q + \omega A + \tau_{2} \phi \left( t \right)qI + \theta M - \left( {\gamma + \delta_{H} } \right)I_{H} , \hfill \\ \frac{dR}{{dt}}& = \varepsilon_{A} A + \varepsilon_{I} I + \varepsilon_{M} M + \gamma I_{H} + v\left( t \right)S, \hfill \\ \end{aligned} $$
(11)

Therefore, we examine the optimal control problem in order to minimize the objective functional. Following [30], we establish the objective functional as follows:

$$\begin{aligned} J\left[ {\nu ,\phi } \right] &= \int_{0}^{{t_{f} }} \left[ {w_{1} A + w_{2} I + w_{3} M + \frac{1}{2}}\right. \\ & \quad \times\left.{\left[ {w_{4} \nu^{2} \left( t \right) + w_{5} \phi^{2} \left( t \right)} \right]} \right]dt \end{aligned}$$
(12)

Here, the parameters \(w_{i} ,\left( {i = 1,2,3,4,5} \right)\) are the weight factors to help balance each term in the integrand in (10), so that none of the terms dominate. The terms in the integrand in (12) are explained as follows:

  1. (i)

    The term \(w_{1} A + w_{2} I + w_{3} M\) denotes expense of monitoring infected people at all stages.

  2. (ii)

    The term \(w_{4} v^{2} \left( t \right)\) denotes the expense of the vaccination program at the time \(t\).

  3. (iii)

    The term \(w_{5} \phi^{2} \left( t \right)\) denotes the expense associated with the public health education awareness campaign to educate the public on the danger of self-medication.

The aim is to minimize the overall number of individuals in identified infectious classes while also keeping the cost associated with the controls \(\left( {v\left( t \right)\;\;{\text{and}}\;\;\phi \left( t \right)} \right)\) to a minimum. The goal is to find an optimal control \(\left( {v\left( t \right),\phi^{*} \left( t \right)} \right)\), such that:

$$ J\left[ {v^{*} ,\phi^{*} } \right] = \mathop {\min }\limits_{v,\phi \in \Omega } J\left[ {v,\phi } \right] $$
(13)

where \(\Omega = \left\{ {\left( {v\left( t \right)^{*} ,\phi \left( t \right)^{*} } \right) \in L^{1} \left( {0,t_{f} } \right) \times L^{1} \left( {0,t_{f} } \right)\left| {a_{1} } \right.} \right.\) \(\left.{\left.{ \le v \le b_{1} ,a_{2} \le \phi \le b_{2} } \right.} \right\}\).

5.1 Theoretical analysis of optimal control

To determine the required conditions that an optimal control must satisfy, we use Pontryagin's maximum principle (Pontryagin [31]). By applying this technique, Eqs. (11) and (12) becomes a problem of minimizing point-wise Hamiltonian (H) with respect to the control pair \(v\left( t \right)\;\;{\text{and}}\;\;\phi \left( t \right)\). The Hamiltonian is given by:

$$ \begin{aligned} {\rm H} & = w_{1} A + w_{2} I + w_{3} M + \frac{1}{2}\left[ {w_{4} v^{2} \left( t \right) + w_{5} \phi^{2} \left( t \right)} \right] \\& \quad + \lambda_{1} \left[ { - \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A + I + c_{2} M} \right)S}}{N} - v\left( t \right)S + \mu Q} \right] \\& \quad + \lambda_{2} \left[ {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A + I + c_{2} M} \right)S}}{N} - \left( {\alpha + \sigma } \right)E} \right]\\&\quad + \lambda_{3} \left[ {\alpha E - \left( {\eta + \mu } \right)Q} \right] \\& \quad + \lambda_{4} \left[ {k\sigma E - \left( {\omega + \varepsilon_{A} } \right)A} \right] + \lambda_{5} \left[ {\left( {1 - k} \right)\sigma E - \left( {q + \delta_{I} + \varepsilon_{I} } \right)I} \right] \\&\quad+ \lambda_{6} \left[ {\left( {1 - \tau_{2} \phi \left( t \right)} \right)qI - \left( {\theta + \delta_{M} + \varepsilon_{M} } \right)M} \right] \\ &\quad + \lambda_{7} \left[ {\eta Q + \omega A + \tau_{2} \phi \left( t \right)qI + \theta M - \left( {\gamma + \delta_{H} } \right)I_{H} } \right]\\&\quad+ \lambda_{8} \left[ {\varepsilon_{A} A + \varepsilon_{I} I + \varepsilon_{M} M + \gamma I_{H} + v\left( t \right)S} \right] \\ \end{aligned} $$
(14)

where \(\lambda_{i} ,\left( {i = 1,2,3,...,8} \right)\) are the adjoint functions associated with the state variables of the model (11), by applying the Pontryagin’s maximum principle [32] and the existence result for the optimal control pair \(v\left( t \right)\;\;{\text{and}}\;\;\phi \left( t \right)\), the following theorem is obtained.

Theorem 5. There exist an optimal control pair \(v^{*} \left( t \right)\;and\;\phi^{*} \left( t \right)\) and corresponding solution \(\left( {S^{*} ,E^{*} ,Q^{*} ,A^{*} ,I^{*} ,M^{*} ,I_{H}^{*} ,\;andR^{*} } \right)\) that minimize \(J\left( {v\left( t \right),\phi \left( t \right)} \right)\) over \(\Omega\). Furthermore, there exist adjoint functions,\(\lambda_{i} ,\left( {i = 1,2,3,...,8} \right)\) such that:

$$ \begin{aligned} \frac{{d\lambda_{1} }}{dt} &= \lambda_{1} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)}}{{N^{*} }} - \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }} + v\left( t \right)} \right) \hfill \\ &- \lambda_{2} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)}}{{N^{*} }} - \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right) - \lambda_{8} v\left( t \right), \hfill \\& \frac{{d\lambda_{2} }}{dt} = - \lambda_{1} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right) \hfill \\&+ \lambda_{2} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }} + \left( {\alpha + \sigma } \right)} \right) - \lambda_{3} \alpha - \lambda_{4} k\sigma - \lambda_{5} \left( {1 - k} \right)\sigma , \hfill \\& \frac{{d\lambda_{3} }}{dt} = - \lambda_{1} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }} + \mu } \right) \hfill \\& + \lambda_{2} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right) + \lambda_{3} \left( {\mu + \eta } \right) - \lambda_{7} \eta , \hfill \\ &\frac{{d\lambda_{4} }}{dt} = - w_{1} + \lambda_{1} \left( {\frac{{c_{1} \beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)S^{*} }}{{N^{*} }} - \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right) \hfill \\ & - \lambda_{2} \left( {\frac{{c_{1} \beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)S^{*} }}{{N^{*} }} - \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right)\hfill \\ & + \lambda_{4} \left( {\omega + \varepsilon_{A} } \right) - \lambda_{7} \omega - \lambda_{8} \varepsilon_{A} , \hfill \\ &\frac{{d\lambda_{5} }}{dt} = - w_{2} + \lambda_{1} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)S^{*} }}{{N^{*} }} - \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right) \hfill \\& - \lambda_{2} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)S^{*} }}{{N^{*} }} - \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right) \hfill \\ &+ \lambda_{5} \left( {q + \delta_{I} + \varepsilon_{I} } \right) - \lambda_{6} \left( {1 - \tau_{2} \phi \left( t \right)} \right)q - \lambda_{7} \tau_{2} \phi \left( t \right)q - \lambda_{8} \varepsilon_{I} , \hfill \\& \frac{{d\lambda_{6} }}{dt} = - w_{3} + \lambda_{1} \left( {\frac{{c_{2} \beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)S^{*} }}{{N^{*} }} - \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right) \hfill \\ &- \lambda_{2} \left( {\frac{{c_{2} \beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)S^{*} }}{{N^{*} }} - \frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right) \hfill \\ & + \lambda_{6} \left( {\theta + \delta_{M} + \varepsilon_{M} } \right) - \lambda_{7} \theta - \lambda_{8} \varepsilon_{M} , \hfill \\ &\frac{{d\lambda_{7} }}{dt} = - \lambda_{1} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right) \hfill \\ &+ \lambda_{2} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right) + \lambda_{7} \left( {\gamma + \delta_{H} } \right) - \gamma \lambda_{8} , \hfill \\& \frac{{d\lambda_{8} }}{dt} = - \lambda_{1} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right) \hfill \\& + \lambda_{2} \left( {\frac{{\beta \left( {1 - \rho_{1} } \right)\left( {1 - \rho_{2} } \right)\left( {1 - \tau_{1} } \right)\left( {c_{1} A^{*} + I^{*} + c_{2} M^{*} } \right)S^{*} }}{{N^{*2} }}} \right), \hfill \\ \end{aligned} $$
(15)

With transversality conditions:

$$ \lambda_{i} \left( {t_{f} } \right) = 0,i = 1,2,3,...,8 $$
(16)

And

$$ N^{*} = S^{*} + E^{*} + Q^{*} + A^{*} + I^{*} + M^{*} + I_{H}^{*} + R^{*} $$

The following characterization holds:

$$ \begin{aligned} v^{*} \left( t \right) = \min \left( {\max \left( {a_{1} ,\frac{1}{{w_{4} }}\left( {\lambda_{1} - \lambda_{8} } \right)S^{*} } \right),b_{1} } \right), \hfill \\ \phi^{*} \left( t \right) = \min \left( {\max \left( {a_{2} ,\frac{1}{{w_{5} }}\left( {\lambda_{6} - \lambda_{7} } \right)\tau_{2} qI^{*} } \right),b_{2} } \right) \hfill \\ \end{aligned} $$
(17)

Proposition 6.

Corollary 4.1 of [33] gives the existence of an optimal control pair \(\left( {v\left( t \right),\phi \left( t \right)} \right)\), due to the convexity of the integrand of \(J\) with respect to \(\left( {v,\phi } \right)\), a priori boundedness of the state solutions, and the local Lipschitz property of the state system with respect to the state variable.

Proof of Theorem 5. We apply the Pontryagin’s maximum principle to have:

$$ \begin{aligned} \frac{{d\lambda_{1} }}{dt} = - \frac{\partial H}{{\partial S}},\;\quad \lambda_{1} \left( {t_{f} } \right) = 0, \hfill \\ \frac{{d\lambda_{2} }}{dt} = - \frac{\partial H}{{\partial E}},\;\quad \lambda_{2} \left( {t_{f} } \right) = 0, \hfill \\ \frac{{d\lambda_{3} }}{dt} = - \frac{\partial H}{{\partial Q}},\;\quad \lambda_{3} \left( {t_{f} } \right) = 0, \hfill \\ \frac{{d\lambda_{4} }}{dt} = - \frac{\partial H}{{\partial A}},\;\quad \lambda_{4} \left( {t_{f} } \right) = 0, \hfill \\ \frac{{d\lambda_{5} }}{dt} = - \frac{\partial H}{{\partial I}},\;\quad \lambda_{5} \left( {t_{f} } \right) = 0, \hfill \\ \frac{{d\lambda_{6} }}{dt} = - \frac{\partial H}{{\partial M}},\;\quad \lambda_{6} \left( {t_{f} } \right) = 0, \hfill \\ \frac{{d\lambda_{7} }}{dt} = - \frac{\partial H}{{\partial I_{H} }},\;\quad \lambda_{7} \left( {t_{f} } \right) = 0, \hfill \\ \frac{{d\lambda_{8} }}{dt} = - \frac{\partial H}{{\partial R}},\;\quad \lambda_{8} \left( {t_{f} } \right) = 0, \hfill \\ \end{aligned} $$
(18)

Evaluated at the control pair \(\left( {v\left( t \right),\phi \left( t \right)} \right)\), and corresponding states which results in the stated adjoint (15) and (16).

Considering the optimality condition:

$$ \frac{\partial H}{{\partial v}} = 0,\quad \frac{\partial H}{{\partial \phi }} = 0 $$
(19)

And solving for \(v^{*} ,\phi^{*}\), subjected to the state variables, the characterizations in (15) can be obtained, taking into account the bounds on the control. By doing this, we have that:

$$ \begin{aligned} \frac{\partial H}{{\partial v}} = w_{{4_{{}} }} v - \lambda_{1} S + \lambda_{8} S = 0 \hfill \\ \Rightarrow v^{*} \left( t \right) = \frac{1}{{w_{4} }}\left( {\lambda_{1} - \lambda_{8} } \right)S^{*} \hfill \\ \end{aligned} $$
(20)

On the set \(\left\{ {t\left| {a_{1} < v^{*} \left( t \right) < b_{1} } \right.} \right\}\). To obtain the optimal control,\(\phi^{*} \left( t \right)\), we have that

$$ \begin{aligned} \frac{\partial H}{{\partial \phi }} = w_{{5_{{}} }} \phi - \lambda_{6} \tau_{2} qI + \lambda_{7} \tau_{2} qI = 0 \hfill \\ \Rightarrow \phi^{*} \left( t \right) = \frac{1}{{w_{5} }}\left( {\lambda_{6} - \lambda_{7} } \right)\tau_{2} qI^{*} \hfill \\ \end{aligned} $$
(21)

On the set \(\left\{ {t\left| {a_{2} < \phi^{*} \left( t \right) < b_{2} } \right.} \right\}\).

It is observed that the optimality condition (taking derivatives of the Hamiltonian with respect to the controls) only hold in the interior of the control set.

5.2 Numerical results for the model with optimal control

The forward–backward sweep approach, as described in [26], is used to numerically simulate the optimal control solution. The procedures start with a guess on the control variables, then the state system is solved simultaneously forward in time, and the guessed control variables and the resulting state system solutions are fed into the adjoint system, which is solved backward in time using the transversality conditions. The controls are then updated using a convex combination of the prior controls and the characterization value.

Figure 7 shows how the optimal control parameters, \(v\)* and \(\phi\)* decreases over time. Figure 7a shows that the vaccination rate is at its peak within the first 30 days, and reduces after the t = 30 days until at t = 100 days. Similarly, Fig. 7b shows that, sensitization of the danger of self-medication is at its peak in the first 60 days and reduces after 60 days until t = 100 days.

Fig. 7
figure 7

Variation of the control strategy of control parameters a \(v\)* and b \(\phi\)*

Full size image

Figure 8 depicts the solutions of all state variables without and with optimal control parameter. With the presence of control parameters, the susceptible, detected and hospitalized infectious humans, exposed, quarantined, undetected asymptomatic infectious humans, undetected symptomatic infectious humans and humans under self-medication populations decrease faster than without control parameters. Similarly, with the presence of optimal control strategy made, it was observed that the recovered population increases faster than without optimal control strategy.

Fig. 8
figure 8figure 8

Variation of population in presence and absence of control strategy

Full size image

6 Conclusion

Mathematical models has continued to be used to study the transmission dynamics of COVID-19 disease. In this work, we study the transmission dynamics of the spread of the third wave of coronavirus without and with optimal control strategy in order to reduce the disease burden. To understand the effectiveness of the model, first, we studied the disease without optimal control parameters and observe the results. We then study the disease with two optimal control parameters: the vaccination rate and rate of sensitization on the danger of self-medication. These two control parameters are important as it helps the population to understand the importance of vaccination against the disease and the danger of self-medication for infected people. Each of the models (i.e., without and with optimal control) was theoretically analyzed, the model was then fitted to data obtained from Nigerian authority pertaining to the scourge of the disease, this was followed by obtaining numerical results.

The findings from this work are:

  1. (1)

    The model without optimal control strategy was found to be locally asymptotically stable when the reproduction number is less than unity, meaning that the disease can be effectively controlled with the necessary and sufficient condition \(R_{0} < 1\).

  2. (2)

    When the model was reformulated with two control parameters incorporated into it and implemented, the number of infected populations decreases faster and there is increase in the recovered population, thereby ensuring that the COVID-19 disease can be managed effectively, such that the reproduction number will be kept within tolerable threshold..

  3. (3)

    Through sensitivity analysis conducted on the basic parameters in the model, we identify significant parameters that drive the transmission dynamic of the disease and can impact the reproduction number significantly, thereby reducing the disease transmission burden. This will be useful for policy makers in formulation of policies to combat and control the spread of the disease.

  4. (4)

    The incorporation of optimal control parameters into the model leads to significant impact on the curtailment of the spread of the disease. However, the success of these strategies rely on proper and effective implementation of these optimal control strategies. Here, we focus on two important control strategies: the vaccination rate and rate of sensitization of masses on the danger of self-medication.

However, in future work, other optimal control strategies can be incorporated and implemented as well into modeling COVID-19.