1 Introduction

In the absence of collisions, ions can still transmit vibrations to each other owing to their charge. Since the motion of massive ions is involved, these vibrations are of low frequency and are called ion acoustic (IA) waves [1]. A solitary wave is a localized wave which emerges from the balance between the nonlinear and dispersive effects. A solitary wave is called soliton if it further possesses two properties, that is, it moves with constant speed and maintains its shape. Secondly when a soliton interacts with another one, it emerges from the collision unchanged except for a phase shift (nonlinear superposition) [2]. The discovery of soliton in connection with numerical integration of Korteweg-de Vries (KdV) equation was made by Zabusky and Kruskal [3] . In a mathematical sense, solitons are basically special solutions of some integrable nonlinear partial differential equations which possess all the above mentioned properties, i.e., they are localized and stable, and survive collision, while solitary waves are solutions of near integrable partial differential equations, which are also localized, but do not possess particle-like property such as elastic collision property. Usually the terms solitary wave and soliton are used interchangeably in physics. Ion acoustic solitary waves (IASWs) are a important class of nonlinear phenomena in different plasma systems. The properties of such waves in different plasma systems are the targeted areas of many researchers. The nonlinear properties of ion acoustic waves (IAWs) in quantum plasma are studied by Misra and Bhowmik [4]. Pakzad et al. [5] studied the characteristics of IASWs in three-component plasma containing nonthermal electrons, cold electrons, and positrons. The IA solitons and supersolitons in magnetized plasma with two groups of electrons, i.e., nonthermal hot and Boltzmann cold electrons, are studied in Ref. [6]. In Ref. [7], the properties of such waves which obliquely propagate in magnetized plasma are discussed in detail.

Due to its existence in real charged particle systems, such as in space and laboratory plasmas, the field of dusty plasma is attracting increasing attention from many researchers. This interest is also due to the involvement of novel physics in its description which is mainly due to the theoretical prediction and later experimental confirmation of two new plasma modes, namely the dust-acoustic wave (DAW) and the dust-ion acoustic wave (DIAW). The detailed description of the aforementioned new acoustic modes seen in Refs. [8,9,10,11,12,13,14,15,16,17,18,19,20,21] has a unique value in astrophysical phenomena. The physical mechanism involved in DIAWs is similar to the IAWs, wherein the restoring force is provided by the inertialess electron while inertia comes from the ion mass. However, on the time scale of DIAW, the stationary dust does not contribute to the wave dynamics.

Kaniadakis introduced a new distribution function, the so-called κ-deformed distribution in Ref. [22], and demonstrated that it can cover the nonextensive distribution and conventional Maxwell-Boltzman distribution. After that, Beck and Cohen proposed that the distribution presented by Kaniadakis which is κ-deformed distribution can be represented as the result of more generalized statistics which is named superstatistics [23]. Ourabah et al. have also described that the superthermal and nonthermal empirical distributions can be recovered from superstatistics (demonstrated by Beck and Cohen) [24]. So, in this sense, the κ-deformed distribution may be considered the more general form of those distribution functions. The Kaniadakis statistics or the κ-deformed distribution has been applied to cosmic rays [25], quark-gluon plasma formation [26], kinetics of photons and interacting atoms [27], nonlinear kinetics [28], blackbody radiation [29], and in quantum entanglement [30]. Gougam and Tribeche used the κ-deformed distribution function to study the electron-acoustic solitary waves (EASWs) and have shown that the characteristics of EASWs are altered by the parameter κ of the distribution [31]. Lourek and Tribeche described the properties of IASWs in unmagnetized electron ion plasma with Kaniadakis distributed electrons by using Sagdeev approach. They showed that the κ-deformed parameter very slightly changes the structural properties of IASWs [32]. The qualitative analysis of the positron acoustic waves in four-component plasma in which electron and hot positron obey κ-deformed distribution has been carried by Saha and Tamang [33]. The use of κ-deformed Kaniadakis distribution in the context of arbitrary amplitude IASWs in a magnetized plasma (composed of cold fluid ions and non-Maxwellian electrons), where the electrons obey the κ-deformed Kaniadakis distribution, was made very recently in Ref. [34]. In our present work, we make the qualitative analysis of the DIASWs in unmagnetized dusty plasmas with κ-deformed Kaniadakis distributed electrons. For this purpose, we find the KdV equation for such a system, then the mKdV equation for the case where KdV equation fails. We also investigate the effects of different physical parameters on the solitary wave solutions of the KdV and mKdV equations.

This paper is organized as follows: In Section 2, the basic equations for the system are presented. In Section 3, the KdV equation is derived. The solitary wave solution of KdV equation is presented in Section 4. The derivation and solitary wave solution of mKdV equation are given in Section 5. The effects of parameters on solitary wave solutions are discussed in Section 6, and Section 7 is reserved for conclusion.

2 Basic Equations

We consider an unmagnetized dusty plasma consisting of fluid ions, stationary negatively charged dust grains, and nonthermal electrons. To study DIAWs, the following set of normalized fluid equations is employed:

$$ \frac{\partial n}{\partial t}+\frac{\partial }{\partial x}\left( nu\right) =0 $$
(1)
$$ \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=-\frac{\partial \phi }{\partial x} $$
(2)
$$ \frac{\partial^{2}\phi }{\partial x^{2}}=\left( 1-\mu \right) n_{e}-n+\mu $$
(3)

Here, n and ne are the ion and electron number densities which are, respectively, normalized by their equilibrium counterparts, i.e., n0 and ne0. The ion fluid velocity u is normalized by IA speed \(C_{s}=\sqrt {\frac {T_{e}}{m }}\) and \(\phi =\frac {e\phi }{T_{e}}\) is the normalized electrostatic wave potential. The space (x) and time (t) variables have been normalized by Debye length \(\lambda _{D}=\sqrt {\frac { T_{e}}{4\pi n_{0}e^{2}}}\) and \(\omega _{pi}^{-1}=\sqrt {\frac {m}{ 4\pi n_{0}e^{2}}}\), respectively, with Te representing the electron temperature and m the ion mass. Moreover, \(\mu = \frac {n_{d0}}{n_{0}}\) is the dust concentration ratio, with nd0 representing the equilibrium number density of dust grains.

The electrons follow κ-deformed Kaniadakis distribution [25], which is given as:

$$ f_{e}^{(\kappa )}(v)=A_{\kappa }\exp_{\kappa }\left( -\frac{ m_{e}v^{2}/2-e\phi }{T_{e}}\right) , $$
(4)

with

$$ \exp_{\kappa }\left( x\right) =\left( \sqrt{1+\kappa^{2}x^{2}}+\kappa x\right)^{\frac{1}{\kappa }}, $$
(5)

where Aκ is the normalized constant given by

$$ A_{\kappa }=n_{e0}\left( \frac{m_{e}\left\vert \kappa \right\vert }{\pi T_{e} }\right)^{\frac{3}{2}}\frac{\Gamma \left( \frac{1}{2\left\vert \kappa \right\vert }+\frac{3}{4}\right) }{\Gamma \left( \frac{1}{2\left\vert \kappa \right\vert }-\frac{3}{4}\right) }\left( 1+\frac{3}{2}\left\vert \kappa \right\vert \right) . $$
(6)

During the calculation of Aκ, the following standard integration was used:

$$ \begin{array}{@{}rcl@{}} &&{\int}_{0}^{\infty }x^{r-1}\exp_{\kappa }\left( -x\right) dx \\ &=&\left. \frac{\left[ 1+\left( r-2\right) \left\vert \kappa \right\vert \right] \left\vert 2\kappa \right\vert^{-r}}{\left[ 1-\left( r-1\right) \left\vert \kappa \right\vert \right]^{2}-\kappa^{2}}\frac{\Gamma \left( \frac{1}{2\left\vert \kappa \right\vert }-\frac{r}{2}\right) }{\Gamma \left( \frac{1}{2\left\vert \kappa \right\vert }+\frac{r}{2}\right) }{\Gamma} \left( r\right) ,\right. \end{array} $$
(7)

Here, κ is a real parameter which tells about the strength of deformation and Γ stands for the standard gamma function. The value of real parameter κ must follow the inequality: − 1 < κ < 1. Also, the value of κ measures the deviation from the Maxwellian distribution, that is, in the limit when \(\kappa \rightarrow 0\), the Kaniadakis distribution function is reduced to the Maxwell-Boltzmann distribution as:

$$ \lim_{\kappa \rightarrow 0}f_{e}^{(\kappa )}(v)=n_{e0}\left( \frac{m_{e}}{ 2\pi T_{e}}\right)^{\frac{3}{2}}\exp \left( -\frac{m_{e}v^{2}/2-e\phi }{ T_{e}}\right) , $$
(8)

note that \(\lim _{\kappa \rightarrow 0}\exp _{\kappa }\left (x\right ) \equiv \exp \left (x\right ) \).

Before going ahead, it is important to restrict the valid range of κ. The mean square speed \(\left \langle v^{2}\right \rangle \) must be calculated as:

$$ \begin{array}{@{}rcl@{}} \left\langle v^{2}\right\rangle &=&\frac{\int \int \int v^{2}f_{e}^{(\kappa )}(v)d^{3}v}{\int \int \int f_{e}^{(\kappa )}(v)d^{3}v}\\&=&\frac{2T_{e}/m_{e}}{ \left\vert 2\kappa \right\vert^{5/2}\left( 1+\frac{5}{2}\left\vert \kappa \right\vert \right) }\frac{\Gamma \left( \frac{1}{2\left\vert \kappa \right\vert }-\frac{5}{4}\right) }{\Gamma \left( \frac{1}{2\left\vert \kappa \right\vert }+\frac{5}{4}\right) }. \end{array} $$
(9)

As \(\left \langle v^{2}\right \rangle \) must be finite, and as the value of \(\left \langle v^{2}\right \rangle \) diverges at \(\left \vert \kappa \right \vert \rightarrow 0.4\), the acceptable value of κ must satisfy the inequality \( \left \vert \kappa \right \vert <0.4\), in order to keep the physical sense of \(\left \langle v^{2}\right \rangle \). It should be mentioned here that this limitation has been taken into account during the calculation of both Aκ and the average kinetic energy of the particles, \(m\left \langle v^{2}\right \rangle /2\), the interacting particles are ignored, i.e., ϕ = 0.

Integrating (4) over velocity space, the number density for the electrons is obtained as:

$$ n_{e}=\left( \sqrt{1+\kappa^{2}\phi^{2}}+\kappa \phi \right)^{\frac{1}{ \kappa }} $$
(10)

For ϕ ≪ 1, Taylor expansion of (10) up to third order gives:

$$ n_{e}=1+\phi +\frac{1}{2}\phi^{2}+\frac{\left( 1-\kappa^{2}\right) }{6} \phi^{3}+\cdot \cdot \cdot $$
(11)

Substitution of (11) into (3) gives:

$$ \frac{\partial^{2}\phi }{\partial x^{2}}\simeq 1-n+c_{1}\phi +c_{2}\phi^{2}+c_{3}\phi^{3}+\cdot \cdot \cdot $$
(12)

where the coefficients are \(c_{1}=\left (1-\mu \right )\), \(c_{2}=\frac {1-\mu }{2}\), and \(c_{3}=\frac {\left (1-\mu \right ) \left (1-\kappa ^{2}\right ) }{6}\).

3 Derivation of KdV Equation

To derive the KdV equation, we make use of the reductive perturbation technique. We introduce the following stretching of coordinates:

$$ \varsigma =\epsilon^{1/2}\left( x-Vt\right) \text{\ \ \ \ and \ \ \ \ }\tau =\epsilon^{3/2}t\text{\ } $$
(13)

where 𝜖 is a very small parameter and V is the phase velocity of the wave which is to be determined later.

Now, we expand the field quantities in the following form:

$$ \left[ \begin{array}{c} n \\ u \\ \phi \end{array} \right] =\left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right] +\epsilon \left[ \begin{array}{c} n_{1} \\ u_{1} \\ \phi_{1} \end{array} \right] +\epsilon^{2}\left[ \begin{array}{c} n_{2} \\ u_{2} \\ \phi_{2} \end{array} \right] +\epsilon^{3}\left[ \begin{array}{c} n_{3} \\ u_{3} \\ \phi_{3} \end{array} \right] ...... $$
(14)

Using (13) and (14) in (1), (2), and (12), we get the following set of equations in the lowest order of 𝜖 as follows:

$$ n_{1}=\frac{u_{1}}{V}=\frac{\phi_{1}}{V^{2}} $$
(15)
$$ u_{1}=\frac{\phi_{1}}{V} $$
(16)
$$ n_{1}=c_{1}\phi_{1} $$
(17)

Comparison of (15) and (17) gives the following expression for phase velocity:

$$ V=\sqrt{\frac{1}{c_{1}}} $$
(18)

We get the following set of equations in the next highest order of 𝜖:

$$ -V\frac{\partial n_{2}}{\partial \varsigma }+\frac{\partial u_{2}}{\partial \varsigma }+\frac{\partial }{\partial \varsigma }\left( n_{1}u_{1}\right) + \frac{\partial n_{1}}{\partial \tau }=0 $$
(19)
$$ -V\frac{\partial u_{2}}{\partial \varsigma }+\frac{\partial \phi_{2}}{ \partial \varsigma }+\frac{\partial u_{1}}{\partial \tau }+u_{1}\frac{ \partial u_{1}}{\partial \varsigma }=0 $$
(20)
$$ \frac{\partial^{2}\phi_{1}}{\partial \varsigma^{2}}+n_{2}=c_{1}\phi_{2}+c_{2}{\phi_{1}^{2}} $$
(21)

Multiplying (19) by V and adding with (20), we get:

$$ \begin{array}{@{}rcl@{}} &&V\frac{\partial n_{1}}{\partial \tau }-V^{2}\frac{\partial n_{2}}{\partial \varsigma }+V\frac{\partial }{\partial \varsigma }\left( n_{1}u_{1}\right) \\ &&\left. +\frac{\partial u_{1}}{\partial \tau }+u_{1}\frac{\partial u_{1}}{ \partial \varsigma }+\frac{\partial \phi_{2}}{\partial \varsigma }=0\right. , \end{array} $$
(22)

Substituting (15)–(17), and (21) in (22), we obtain the KdV equation as:

$$ \frac{\partial {\Psi} }{\partial \tau }+\alpha {\Psi} \frac{\partial {\Psi} }{ \partial \varsigma }+\beta \frac{\partial^{3}{\Psi} }{\partial \varsigma^{3}} =0 $$
(23)

with the nonlinear coefficient

$$ \alpha =\frac{3}{2V}-\frac{V}{2} $$
(24)

and dispersion coefficient

$$ \beta =\frac{V^{3}}{2} $$
(25)

It is clearly seen that both α and β depend upon the dust concentration μ. In (23), ϕ1 is replaced by Ψ.

4 Solitary Wave Solution

In order to find the nonlinear solution of (23), let us define a travelling wave transformation of the form ζ = ς − v0τ where v0 is the velocity of the nonlinear structure in comoving frame. Using this transformation, (23) takes the form:

$$ -v_{0}\frac{d{\Psi} }{d\zeta }+\alpha {\Psi} \frac{d{\Psi} }{d\zeta }+\beta \frac{ d^{3}{\Psi} }{d\zeta^{3}}=0 $$
(26)

Integrating twice (26), and using boundary conditions \({\Psi } \rightarrow 0,\ \frac {d{\Psi } }{d\zeta } \rightarrow 0\), \(\frac {d^{2}{\Psi } }{d\zeta ^{2}}\rightarrow 0\) at \( \left \vert \zeta \right \vert \rightarrow \infty \), we finally obtain the solitary wave solution:

$$ {\Psi} \left( \zeta \right) =\psi_{0}\sec h^{2}\left( \frac{\zeta }{w}\right) $$
(27)

where \(\psi _{0}=\frac {3v_{0}}{\alpha }\) and \(w=\sqrt {\frac {4\beta }{v_{0}}}\) are the peak amplitude and width of DIASW respectively.

5 Derivation of mKdV Equation

It has been pointed out that the KdV equation fails at α = 0. For example, in the present plasma model, we notice that at a critical value of μ, i.e., μc = 2/3, α vanishes [see (24)]. To investigate IAWs in such a situation, we take into account the higher order nonlinearity and derive the mKdV equation. In this context, we again use the reductive perturbation technique, and introduce the modified stretching of coordinates as:

$$ \varsigma =\epsilon \left( x-Vt\right) \text{\ \ \ \ and \ \ \ \ }\tau =\epsilon^{3}t $$
(28)

Substituting (14) and (28) into (1), (2), and (12), we get the same equations in the lowest order of 𝜖 as in the KdV derivation (i.e., (15), (16), and (17)). In the next highest order of 𝜖, the second-order momentum equation results in the following:

$$ u_{2}=\frac{\phi_{2}}{V}+\frac{1}{2V^{3}}{\phi_{1}^{2}} $$
(29)

Substituting (14) and (28) into (1), (2), and (12), the third-order terms in 𝜖 are obtained as:

$$ -V\frac{\partial n_{3}}{\partial \varsigma }+\frac{\partial u_{3}}{\partial \varsigma }+\frac{\partial n_{1}}{\partial \tau }+\frac{\partial }{\partial \varsigma }\left( n_{2}u_{1}\right) +\frac{\partial }{\partial \varsigma } \left( n_{1}u_{2}\right) =0 $$
(30)
$$ -V\frac{\partial u_{3}}{\partial \varsigma }+\frac{\partial u_{1}}{\partial \tau }+\frac{\partial }{\partial \varsigma }\left( n_{2}u_{1}\right) +\frac{ \partial \phi_{3}}{\partial \varsigma }=0 $$
(31)
$$ \frac{\partial^{2}\phi_{1}}{\partial \varsigma^{2}}+n_{3}=c_{1}\phi_{3}+2c_{2}\phi_{1}\phi_{2}+c_{3}{\phi_{1}^{3}} $$
(32)

Solving (30)–(32), along with the first- and second-order contributions, we finally obtain the mKdV equation as:

$$ \frac{\partial {\Psi} }{\partial \tau }+{\Lambda} {\Psi}^{2}\frac{\partial {\Psi} }{ \partial \varsigma }+\beta \frac{\partial^{3}{\Psi} }{\partial \varsigma^{3}} =0 $$
(33)

where

$$ {\Lambda} =\frac{3V}{4}+\frac{3}{2V^{3}}-\frac{\left( 1-\kappa^{2}\right) V}{4 } $$
(34)

Again, in (33), Ψ is used instead of ϕ1.

The solitary wave solution of mKdV equation is:

$$ {\Psi} \left( \zeta \right) =\pm \sqrt{\frac{6v_{0}}{\Lambda }}\sec h\left( \sqrt{\frac{v_{0}}{\beta }}\zeta \right) $$
(35)

6 Results and Discussion

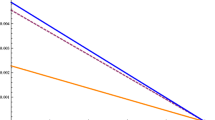
α and β given in (24) and (25), respectively, are strongly affected by as the dust concentration μ. In Fig. 1, we give a graph of how α and β vary as the dust concentration μ is increased from 0 to 0.8. It is seen that the nonlinear coefficient α takes positive as well as negative values while the dispersion coefficient β is always positive. It is pointed out that α is 0 at μ = μc = 2/3, while α is positive in the range 0 ≤ μ < μc, which defines the existence region for compressive DIASWs having positive potential. Also, α is found negative in the range μc < μ < 1 which corresponds to the existence region for rarefactive DIASWs having negative potential. Thus, in the considered model, both compressive and rarefactive solitary structures exist.

Fig. 1
figure 1

Variation of α, β versus μ

Full size image

The behavior of DIASWs for varying values of μ is shown in Figs. 2 and 3. From Fig. 2, it is clear that the width and amplitude of the positive potential DIASWs are enhanced as the value of μ is increased. However, Fig. 3 displays the opposite behavior of negative potential DIASWs in contrast to the positive potential DIASWs with increasing values of μ. Here, the increasing values of μ result in lower (in amplitude) and smaller (in width) rarefactive DIASWs. The effect of μ on DIASWs is consistent with the results of Ref. [35]. Physically, the nonlinear coefficient α decreases (increases) for positive potential (negative potential) DIASWs with increasing values of μ (see Fig. 1). As the amplitude (ψ0 = 3v0/α) has inverse relation with α, the amplitude of positive (negative) potential DIASW is enhanced (reduced) with higher values of μ.

Fig. 2
figure 2

Variation of \({\Psi } \left (\protect \zeta \right ) \) given by (27) versus ζ for different values of dust concentration μ, with v0 = 0.1

Full size image
Fig. 3
figure 3

Variation of \({\Psi } \left (\protect \zeta \right ) \) given by (27) versus ζ for different values of dust concentration μ, with v0 = 0.1

Full size image

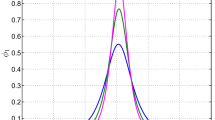
In Fig. 4, the variation of DIASW solution Ψ of mKdV equation (defined by (35)) against ζ is presented for different values of κ, i.e., κ = 0 (black curve), κ = 0.20 (dashed red curve), and κ = 0.39 (dot-dashed blue curve). The coexistence of compressive and rarefactive DIASWs is observed for the critical composition. It is seen that the width and amplitude of rarefactive and compressive DIASWs decrease with increasing values of κ. Thus, the compressive and rarefactive DIASWs abate as κ is increased, i.e., the compressive and rarefactive DIASWs shrink as the electrons evolve far away from its Maxwell–Boltzmann equilibrium. It is important to note that the value of κ has no effect on the DIASWs associated with the KdV equation (23), whereas the values of κ have a significant effect on DIASWs linked with the mKdV equation (33).

Fig. 4
figure 4

Variation of \({\Psi } \left (\protect \zeta \right ) \) given by (35) versus ζ for different values of the κ-deformed parameter κ at critical composition, with v0 = 0.1

Full size image

7 Conclusion

To conclude, we have studied the propagation characteristics of DIASWs in an unmagnetized dusty plasma consisting of fluid ions, negatively charged stationary dust grains, and Kaniadakis distributed electrons. We have derived the KdV and mKdV equations by using the famous reductive perturbation technique. The solitary wave solution of the KdV and mKdV equations is determined. Due to the variation of dust concentration μ, the KdV equation admits a combination of compressive and rarefactive wave structures in the given dusty plasma system. It was found that the nonlinear coefficient α becomes 0 at μ = μc = 2/3 and the KdV equation is not valid at α = 0. We, therefore, take into account the higher order nonlinearity in the vicinity of this critical regime, and derive the mKdV equation. It is evident from KdV equation that DIASWs have dependence only on the parameter μ, while DIASWs linked with mKdV equation depend both on μ and κ as well. Our present investigations are helpful in the context of cosmic ray spectrum [25] as well as in astrophysical plasma environments [36, 37].