1 Introduction

The anisotropic behavior of plasmas in a collisionless medium arises primarily due to a strong magnetic field, i.e., the characteristics of the plasma generally differs in parallel and perpendicular directions to the magnetic field (Baumjohann and Treumann 1997). Such anisotropies in plasmas are well described by the Chew-Goldberger-Low (CGL) theory (Chew et al. 1956) which was initially due to Chew, Goldberger and Low in 1956. The applicability of this theory is restricted to the condition that no coupling occurs between the perpendicular and parallel degrees of freedom (Parks 1991). To study the anisotropies in plasmas, two separate energy equations are needed to calculate the ion pressure i.e., the parallel ion pressure \(p_{\parallel }\) and perpendicular ion pressure \(p_{\perp }\) relative to the field. The isotropic plasma situation exists because of the strong coupling between the parallel ion pressure and perpendicular ion pressure owing to the wave-particle interactions (Choi et al. 2007; Denton et al. 1994). The anisotropy situation in space plasmas might be due to the plasma convection which gives rise to magnetic compression and/or expansion in the direction of the magnetic field lines. The magnetic compression and expansion may, respectively, result in an increase in the perpendicular temperature \(T _{\bot }\) (relative to magnetic field) of the particles and a decrease in the parallel temperature \(T_{\Vert }\) (Denton et al. 1994), i.e., \(T_{\Vert }\neq T_{\bot }\). In recent past, there are numerous investigations concerning the nonlinear electrostatic waves highlighting the effect of anisotropic ion pressure (see e.g., Choi et al. 2007; Adnan et al. 2014a,b; Manesh et al. 2017).

In recent past a great deal of attention has been paid to the study of nonlinear periodic (cnoidal) waves (Khater et al. 2005; Tiwari et al. 2007; Prudskikh 2012, 2014; Kaladze and Mahmood 2014; Kaladze et al. 2012; Singh et al. 2018; Ur-Rehman and Mahmood 2016; Ur-Rehman et al. 2017, 2018) due to their wide ranging applications in diverse areas of physics. One of these applications includes the nonlinear ion transport caused by a periodic ion acoustic wave (Ichikawa 1979). The cnoidal waves are basically worked out in terms of Jacobi-elliptical function such as cn, sn, and dn. Kauschke and Schlüter (1991) noticed that the nonlinear periodic signals detected at the edge of plasma in their experiment can be described in a befitting manner through the cnoidal waves. Konno et al. (1979) were the first who explored the ion acoustic cnoidal wave solution of the Korteweg-de Vries (KdV) equation in electron-ion (e-i) plasma. Later Yadav et al. (1994) used the reductive perturbation approach to investigate ion-acoustic nonlinear periodic waves in a magnetized plasma involving warm adiabatic ions and two temperature electron species. The dynamics therein are modeled by a KdV equation. Despite the extensive recent research work on cnoidal waves, the study of cnoidal waves in the presence of anisotropic ion pressure has not yet been explored, to the best of our knowledge. We have therefore undertaken an investigation of ion acoustic cnoidal waves and studied their dynamics in terms of intrinsic relevant plasma parameters.

In this article, we aim to explore the propagation characteristics of ion acoustic cnoidal waves in anisotropic magnetized plasmas characterized by Maxwellian electrons. The paper at hand is organized as follows: The model equations are laid out in Sect. 2. In Sect. 3, we derive the KdV equation by using the reductive perturbation technique. The cnoidal wave solution of the KdV equation is given in Sect. 4. Section 5 is devoted to the numerical analysis, while the main conclusions have been summarized in Sect. 6.

2 The model and governing equations

We are modeling ion acoustic nonlinear periodic (cnoidal) waves propagating in a magnetized plasma composed of warm ions and Maxwellian distributed electrons. The ions are assumed as inertial exhibiting pressure anisotropy relative to the external magnetic field. We assume that the plasma is immersed in a strong external magnetic field \(B=B_{0}\hat{z}\), where \(\hat{z} \) is the unit vector in the \(z\)-direction. The set of equations governing the dynamics of ion fluid are:

$$\begin{aligned}& \frac{\partial n}{\partial t}+\vec{\nabla }\cdot n\vec{v}=0 \end{aligned}$$
(1)
$$\begin{aligned}& \frac{\partial \vec{v}}{\partial t}+(\vec{v}\cdot \vec{\nabla }) \vec{v}=-\frac{Ze}{m} \vec{\nabla }\phi +\frac{Ze}{mc} ( \vec{v} \times B_{0}\hat{z} ) -\frac{1}{mn}\vec{\nabla }\cdot \widetilde{P} \end{aligned}$$
(2)

Here \(n\), \(v\), \(Z\), \(\phi \) and \(\widetilde{P}\) stand for ion density, ion velocity, ionic charge state, the electrostatic potential, and ion pressure tensor, respectively with \(e\) is electric charge and \(m\) is the ion mass. In the presence of strong magnetic field, the plasma becomes anisotropic and the pressure tensor splits into parallel and perpendicular components relative to the external magnetic field. Thus, \(\widetilde{P}\) take the form (Chew et al. 1956; Denton et al. 1994):

$$ \widetilde{P}=p_{\perp }\hat{I}+ ( p_{\parallel }-p_{\perp } ) \hat{b}\hat{b} $$
(3)

where \(\hat{b}\) is the unit vector in the direction of the external magnetic field and \(\hat{I}\) is the unit tensor. According to the CGL theory, the perpendicular and parallel ion pressures can be written as (Bittencourt 2004)

$$ p_{\perp }=p_{\perp 0} \biggl( \frac{n}{n_{0}} \biggr) \quad \text{and}\quad p _{\parallel }=p_{\parallel 0} \biggl( \frac{n}{n_{0}} \biggr) ^{3} $$
(4)

While for isotropic situation \(p_{\perp }=p_{\parallel }\) and thus \(\vec{\nabla }\cdot \widetilde{P}=\nabla p\). At equilibrium, the parallel and perpendicular ion pressures (viz., \(p_{\parallel 0}\) and \(p_{\perp 0}\)) are defined respectively as

$$ p_{\parallel 0}=n_{0}T_{\parallel }\quad \text{and}\quad p_{\perp 0}=n _{0}T_{\perp } $$
(5)

Electrons are assumed to follow the Maxwellian distribution and the electron density is thus given by

$$ n_{e}=n_{e0}\exp \biggl( \frac{e\phi }{T_{e}} \biggr) $$
(6)

The system is closed via Poisson’s equation

$$ \nabla ^{2}\phi =4\pi e(n_{e}-n) $$
(7)

2.1 Scaled evolution equations

For analytical convenience, the set of Eqs. (1), (2), (6) and (7) can be cast into a dimensionless form by making use of the appropriate normalizing quantities:

$$\begin{aligned}& \frac{\partial n}{\partial t}+\frac{\partial }{\partial x} ( nv _{x} ) + \frac{\partial }{\partial y} ( nv_{y} ) +\frac{ \partial }{\partial z} ( nv_{z} ) =0 \end{aligned}$$
(8)
$$\begin{aligned}& \frac{\partial v_{x}}{\partial t}+ \biggl( v_{x}\frac{\partial }{ \partial x}+v_{y} \frac{\partial }{\partial y}+v_{z}\frac{\partial }{ \partial z} \biggr) v_{x} \\& \quad =-\frac{\partial \phi }{\partial x}+\Omega v _{y}- \frac{p_{2}}{n}\frac{\partial n}{\partial x} \end{aligned}$$
(9)
$$\begin{aligned}& \frac{\partial v_{y}}{\partial t}+ \biggl( v_{x}\frac{\partial }{ \partial x}+v_{y} \frac{\partial }{\partial y}+v_{z}\frac{\partial }{ \partial z} \biggr) v_{y} \\& \quad =-\frac{\partial \phi }{\partial y}-\Omega v _{x}- \frac{p_{2}}{n}\frac{\partial n}{\partial y} \end{aligned}$$
(10)
$$\begin{aligned}& \frac{\partial v_{z}}{\partial t}+ \biggl( v_{x}\frac{\partial }{ \partial x}+v_{y} \frac{\partial }{\partial y}+v_{z}\frac{\partial }{ \partial z} \biggr) v_{z} \\& \quad =-\frac{\partial \phi }{\partial z}-p_{1}n\frac{ \partial n}{\partial z} \end{aligned}$$
(11)

The Poisson’s equation in normalized form is

$$ \frac{\partial ^{2}\phi }{\partial x^{2}}+\frac{\partial ^{2}\phi }{ \partial y^{2}}+\frac{\partial ^{2}\phi }{\partial z^{2}}=e^{\phi }-n $$
(12)

Here the ion number density \(n\), the ion fluid velocity \(v\) and the electrostatic wave potential \(\phi \) are normalized by the equilibrium number density \(n_{0}\), the ion-acoustic speed \(C_{s}= \sqrt{T_{e}/m}\) and \(e\phi /T_{e}\), respectively. The space variable (\(x\)) and time variable (\(t\)) have been normalized by the ion Debye length \(\lambda _{D}=\sqrt{T_{e}/4\pi n_{0}e^{2}}\) and inverse ion plasma frequency \(\omega _{pi}^{-1}=\sqrt{m_{e}/4\pi n_{0}e^{2}}\), respectively. In the above equations, we have defined the dimensionless parameters \(\Omega =\frac{\Omega _{i}}{\omega _{pi}}\), \(p_{1}=\frac{3p _{\parallel 0}}{n_{0}T_{e}}\) and \(p_{2}= \frac{p_{\perp 0}}{n_{0}T_{e}}\), where \(\Omega \) is the normalized ion gyro-frequency with \(\Omega _{i}=\frac{eB_{0}}{mc}\), while \(p_{1}\) and \(p_{2}\) are respectively the normalized ion parallel and perpendicular pressures (scaled via the thermal pressure). We have also used \(\nabla =\hat{x}\partial /\partial x+\hat{y}\partial /\partial y+ \hat{z}\partial /\partial z\), while \(v_{x},v_{y}\) and \(v_{z}\) are the ion fluid velocity along \(x\), \(y\) and \(z\) axis, respectively.

3 Derivation of KdV equation

We shall investigate the ion acoustic nonlinear periodic waves, namely, ion acoustic cnoidal waves in anisotropic magnetized e-i plasma with Maxwellian electron distribution. We use the reductive perturbation method (Yadav and Sayal 2009) involving a stretching of the spatial and temporal coordinates in terms of an infinitesimal parameter \(\epsilon \) as

$$ \xi =\epsilon ^{1/2} ( l_{x}x+l_{y}y+l_{z}z-St )\quad \text{and}\quad \tau =\epsilon ^{3/2}t $$
(13)

where \(S\) is the ion excitation speed interpreted as phase velocity of the nonlinear wave (to be determined later), and \(l_{x},l_{y}\) and \(l_{z}\) are the direction cosines along \(x\), \(y\) and \(z\) axis respectively, such that \(l_{x}^{2}+l_{y}^{2}+l_{z}^{2}=1\). Accordingly, the dependent variables are expanded about their equilibrium values in a power series in \(\epsilon \) as;

$$\begin{aligned}& \begin{aligned} &n =1+\epsilon n_{1}+\epsilon ^{2}n_{2}+ \epsilon ^{3}n_{3}+\cdots \\ &\phi =\epsilon \phi _{1}+\epsilon ^{2}\phi _{2}+\epsilon ^{3}\phi _{3}+ \cdots \\ &v_{x} =\epsilon ^{3/2}v_{x1}+\epsilon ^{2}v_{x2}+\epsilon ^{5/2}v_{x3}+ \cdots \\ &v_{y} =\epsilon ^{3/2}v_{y1}+\epsilon ^{2}v_{y2}+\epsilon ^{5/2}v_{y3}+ \cdots \\ &v_{z} =\epsilon v_{z1}+\epsilon ^{2}v_{z2}+ \epsilon ^{3}v_{z3}+\cdots \end{aligned} \end{aligned}$$
(14)

Substituting Eqs. (13) and (14) into Eqs. (8) to (12) and collecting terms of lowest orders in \(\epsilon \), we obtain

$$\begin{aligned}& n_{1}=\frac{l_{z}}{S}v_{z1}=\frac{l_{z}^{2}}{S^{2}-l_{z}^{2}p_{1}} \phi _{1} \end{aligned}$$
(15)
$$\begin{aligned}& v_{z1}=\frac{l_{z}}{S}\phi _{1}+ \frac{p_{1}l_{z}}{S}n_{1}+C_{1}(\tau ) \end{aligned}$$
(16)
$$\begin{aligned}& v_{y1}=\frac{l_{x}}{\Omega }\frac{\partial \phi _{1}}{\partial \xi }+\frac{p _{2}l_{x}}{\Omega } \frac{\partial \phi _{1}}{\partial \xi } \end{aligned}$$
(17)
$$\begin{aligned}& v_{x1}=-\frac{l_{y}}{\Omega }\frac{\partial \phi _{1}}{\partial \xi }- \frac{p _{2}l_{y}}{\Omega }\frac{\partial \phi _{1}}{\partial \xi } \end{aligned}$$
(18)

and

$$ n_{1}=\phi _{1} $$
(19)

where \(C_{1}(\tau )\) is the constant of integration and is the function of \(\tau \) only. Combination of Eqs. (15) and (19) result in the following expression for phase velocity:

$$ S=l_{z}\sqrt{1+p_{1}} $$
(20)

From Eq. (20) it is clear that phase velocity \(S\) depends on \(l_{z}\) (\(l_{z}=\cos \theta \), where \(\theta \) is the angle between the directions of the wave propagation vector \(k\) and the external magnetic field \(B_{0}\)) and parallel ion pressure \(p_{1}\). We also note that the phase velocity is independent of \(B_{0}\), and the perpendicular ion pressure \(p_{2}\). Importantly, the phase velocity vanishes for \(\theta =\pi /2\), i.e., the propagation of ion acoustic excitations is not possible for this particular case. For parallel propagation (i.e., by setting \(\theta =0\)) and for cold-ion limit, we recover the earlier result of Konno et al. (1979). The effect of anisotropic ion pressure \(p_{1}\), and propagation angle \(\theta \) on the phase velocity of ion acoustic waves is shown in Fig. 1. Since the phase velocity is directly proportional to \(l_{z}\), that is why the phase speed increases with propagation angle \(\theta \), while an increase in phase speed is seen with increasing values of \(p_{1}\).

Fig. 1
figure 1

The contour plot of phase velocity \(S\) of ion acoustic excitations versus parallel ion pressure \(p_{1}\) and propagation angle \(\theta \)

Full size image

The next highest order of \(\epsilon \) gives the following set of equations;

$$\begin{aligned}& \frac{\partial n_{1}}{\partial \tau }-S\frac{\partial n_{2}}{\partial \xi }+l_{x} \frac{\partial v_{x2}}{\partial \xi }+l_{y}\frac{\partial v_{y2}}{\partial \xi }+l_{z} \frac{\partial (n_{1}v_{z1})}{\partial \xi }+l_{z}\frac{\partial v_{z2}}{\partial \xi } \\& \quad =0 \end{aligned}$$
(21)
$$\begin{aligned}& \frac{\partial v_{z1}}{\partial \tau }-S\frac{\partial v_{z2}}{\partial \xi }+l_{z}v_{z1} \frac{\partial v_{z1}}{\partial \xi } \\& \quad =-l_{z}\frac{ \partial \phi _{2}}{\partial \xi }-p_{1}l_{z} \biggl( n_{1}\frac{\partial n_{1}}{\partial \xi }+\frac{\partial n_{2}}{\partial \xi } \biggr) \end{aligned}$$
(22)
$$\begin{aligned}& \Omega v_{y2}=-S\frac{\partial v_{x1}}{\partial \xi } \end{aligned}$$
(23)
$$\begin{aligned}& \Omega v_{x2}=S\frac{\partial v_{y1}}{\partial \xi } \end{aligned}$$
(24)
$$\begin{aligned}& n_{2}=\phi _{2}+\frac{\phi _{1}^{2}}{2}- \frac{\partial ^{2}\phi _{1}}{ \partial \xi ^{2}} \end{aligned}$$
(25)

Using Eqs. (21)–(25) along with the first order results, one can eliminate second order terms (i.e., \(n_{2}\), \(v_{2}\), and \(\phi _{2}\)) resulting in the KdV equation

$$ \frac{\partial \phi }{\partial \tau }+a\phi \frac{\partial \phi }{ \partial \xi }+C_{1}l_{z} \frac{\partial \phi }{\partial \xi }+b\frac{ \partial ^{3}\phi }{\partial \xi ^{3}}=0 $$
(26)

where the nonlinear coefficient \(a\) and dispersion coefficient \(b\) have been defined as

$$\begin{aligned}& a=\frac{3S^{2}-l_{z}^{2} ( 1-p_{1} ) }{2S} \end{aligned}$$
(27)
$$\begin{aligned}& b=\frac{S}{2\Omega ^{2}} \biggl[ (1+p_{2}) \bigl( 1-l_{z}^{2} \bigr) +\frac{ \Omega ^{2}}{S^{2}}l_{z}^{2} \biggr] \end{aligned}$$
(28)

Interestingly, both the nonlinear and dispersion coefficients are functions of \(l_{z}\), \(p_{1}\), \(p_{2}\), and \(\Omega \). In Eq. (26) we have replaced \(\phi _{1}\) by \(\phi \).

4 Cnoidal wave solution

To get the steady state solution of Eq. (26), let us define a traveling wave transformation of the form \(\eta =\xi -v_{0}\tau \), where \(v_{0}\) is the velocity of the nonlinear structure in co-moving frame. Implication of this transformation transforms Eq. (26) into the following form

$$ - ( v_{0}-C_{1}l_{z} ) \frac{d}{d\eta }\phi +a\phi \frac{d}{d \eta }\phi +b\frac{d^{3}}{d\eta ^{3}} \phi =0 $$
(29)

Double integration of (29) results in the following equation

$$ \frac{1}{2} \biggl( \frac{d\phi }{d\eta } \biggr) ^{2}+W ( \phi ) =0 $$
(30)

where \(W ( \phi ) \) is the Sagdeev potential given by

$$ W ( \phi ) =\frac{a}{6b}\phi ^{3}-\frac{u}{2b}\phi ^{2}+ \rho \phi -\frac{1}{2}E^{2} $$
(31)

where \(u=v_{0}-C_{1}l_{z}\), while \(\rho \) and \(\frac{1}{2}E^{2}\) are the constants of integration. Additionally \(\rho \) and \(E\) are the charge density and electric field, respectively, when \(\phi \) vanishes. By using the initial conditions \(\phi ( 0 ) =\alpha \), and \(\frac{d\phi ( 0 ) }{d\eta }=0\), we can find

$$ E^{2}=\frac{a}{3b}\alpha ^{3}- \frac{u}{b}\alpha ^{2}+2\rho \alpha $$
(32)

Substituting Eqs. (31) and (32) in Eq. (30), and after factorization, we obtain the following equation,

$$ \biggl( \frac{d\phi }{d\eta } \biggr) ^{2}\mathbf{=} \frac{a}{3b} ( \alpha -\phi ) ( \phi -\beta ) ( \phi - \gamma ) $$
(33)

where \(\beta \) and \(\gamma \) are defined as

$$\begin{aligned}& \beta =\frac{3}{2} \biggl[ \frac{u}{a}-\frac{\alpha }{3}+ \sqrt{ \frac{1}{3} ( b_{1}-\alpha ) ( \alpha -b_{2} ) } \biggr] \end{aligned}$$
(34)
$$\begin{aligned}& \gamma =\frac{3}{2} \biggl[ \frac{u}{a}-\frac{\alpha }{3}- \sqrt{ \frac{1}{3} ( b_{1}-\alpha ) ( \alpha -b_{2} ) } \biggr] \end{aligned}$$
(35)

In above Eqs. (34) and (35), we have defined

$$ b_{1,2}=\frac{u}{a}\pm 2 \sqrt{\frac{u^{2}}{a^{2}}- \frac{2b\rho }{a}} $$
(36)

The following inequalities should be satisfied to find the nonlinear periodic (cnoidal) wave solution, \(b_{2}\leq \alpha \leq b _{1}\) or \(b_{1}\leq \alpha \leq b_{2}\). From Eqs. (30) and (33), the velocity of the cnoidal wave in terms of roots \(\alpha ,\beta \) and \(\gamma \) is

$$ u=\frac{a}{3} ( \alpha +\beta +\gamma ) $$
(37)

The cnoidal wave solution of Eq. (30) in terms of Jacobi elliptic function is given by (Yadav et al. 1994)

$$ \phi ( \eta ) =\beta + ( \alpha -\beta ) cn ^{2} ( D\eta ,m ) $$
(38)

where \(cn\) stands for the Jacobi elliptic function. The modulus \(m\) \(( 0< m\leq 1 ) \) and the parameter \(D\) in terms of the three zeros (i.e., \(\alpha \), \(\beta \) and \(\gamma \)) of the Sagdeev potential are defined as

$$\begin{aligned}& m^{2}=\frac{\alpha -\beta }{\alpha -\gamma } \end{aligned}$$
(39)
$$\begin{aligned}& D=\sqrt{\frac{a}{12b} ( \alpha -\gamma ) } \end{aligned}$$
(40)

From (30), we find the initial condition \(\phi ( 0 ) =\alpha \) for \(\eta =0\). For the plasma model under consideration, we have \(\frac{a}{b}>0\), and thus the real numbers \(\alpha \), \(\beta \) and \(\gamma \) are adjusted in such a way that \(\alpha >\beta \geq \gamma \) and \(\beta \leq \phi \leq \alpha \) must hold. The amplitude \(A\) and wavelength \(\lambda \) of the ion-acoustic cnoidal waves are defined as

$$ A=\alpha -\beta $$
(41)

and

$$ \lambda =4\sqrt{\frac{3b}{a(\alpha -\gamma )}}K(m) $$
(42)

where \(K(m)\) is the complete elliptical integral of the first kind. When \(\rho =0\) and \(E=0\), then \(\beta =\gamma =0\), so that \(m\rightarrow 1\), the cnoidal wave solution may then approach the solitary wave solution, i.e.,

$$ A=\alpha =\frac{3u}{a}=\phi _{0} $$
(43)

and

$$ D=\sqrt{\frac{a}{12b}\alpha }=\sqrt{\frac{u}{4b}}= \frac{1}{w} $$
(44)

In the limit \(m\rightarrow 1\), the Jacobi elliptical function transforms to secant hyperbolic function, that is \(cn ( D\eta ,1 ) = \sec h ( D\eta ) \), therefore, Eq. (38) becomes

$$ \phi ( \eta ) =\phi _{0}\sec h^{2} \biggl( \frac{\eta }{w} \biggr) $$
(45)

where the peak amplitude \(\phi _{0}\) and width \(w\) of ion-acoustic solitary pulses, are given by

$$ \phi _{0}=\frac{3u}{a}\quad \text{and}\quad w=\sqrt{ \frac{4b}{u}} $$

5 Numerical analysis

In order to carry out numerical study of ion acoustic cnoidal wave structures, we recall that the nonlinear coefficient \(a\) and dispersion coefficient \(b\) appearing in (26) are explicit function of various relevant plasma parameters (viz., \(p_{1}\), \(p_{2}\), and \(l_{z}\)). It is important to point out that the nonlinear and dispersion coefficients strongly affect the structural properties of the ion acoustic cnoidal wave. It is therefore tempting to investigate the effect of each of these parameters separately on the behavior of ion acoustic cnoidal wave structures.

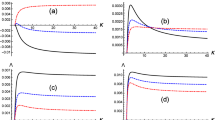
To examine the effect of anisotropic parallel pressure \(p_{1}\), we depict the variation of Sagdeev potential \(W ( \phi ) \) versus \(\phi \) for different values of \(p_{1}\), while keeping \(l_{\mathit{z}}\) and \(\Omega \) fixed. It is seen that \(W ( \phi ) \neq 0\), at \(\phi =0\), for ion acoustic cnoidal waves, shown via the dashed, dotted and dotdashed curves. We observe that increasing values of \(p_{1}\) leads to a reduction of the depth of Sagdeev potential, and, importantly, also of the amplitude of the associated cnoidal waves. However, it is also noticed from Fig. 2(a) that the Sagdeev potential \(W ( \phi ) \) (represented via the solid curve with \(\rho =0\), and \(E=0\)) corresponding to solitary pulses becomes zero at \(\phi =0\). In Fig. 2(b) we have shown the phase curves using Eqs. (30) and (31) for the same set of parameters as used in Fig. 2(a). The inner bounded curves show the ion acoustic cnoidal waves while the black solid outer curve represents the solitary pulses separatrix. We also find that the amplitude and width of the ion acoustic cnoidal waves decrease as \(p_{1}\) increases.

Fig. 2
figure 2

Variation of (a) \(W( \phi )\) versus \(\phi \) and (b) phase curves of ion acoustic cnoidal waves (dashed, dotted and dotdashed curves) for different values of \(p_{1}\). Dashed curve: \(p_{1}=0.2\), dotted curve: \(p_{1}=0.3\), dotdashed curve: \(p_{1}=0.4\) with \(u=0.3\), \(\Omega =0.3\), \(\rho =0.02\), \(l_{z}=0.96\), \(p_{2}=0.1\), and \(E=0.007\). The black (solid) curve with \(p_{1}=0.3\), \(\rho =0\) and \(E=0\) is for solitary waves

Full size image

In Fig. 3(a), we have examined the effect of obliqueness of propagation angle as manifested via \(l_{\mathit{z}} ( =\cos \theta ) \) on Sagdeev potential \(W ( \phi ) \) for given values of other plasma parameters. It is noticed that \(W ( \phi ) \neq 0\), at \(\phi =0\), for cnoidal waves, shown via the dashed, dotted and dotdashed curves. The Sagdeev potential and the corresponding cnoidal pulses are amplified with decreasing \(\theta \). Again we may remark that when \(\rho =0\), and \(E=0\), we obtain the solid curve for the Sagdeev potential \(W ( \phi ) \) corresponding to the soliton structures for which \(W ( \phi ) =0\) at \(\phi =0\). In Fig. 3(b) we display the phase curves by plotting \(\frac{d\phi }{d\eta }\) versus \(\phi \) for the varying values of \(\theta \). As the obliqueness increases, the amplitude of the cnoidal waves decreases. Here it is pointed out that the dynamical behavior of ion-acoustic cnoidal waves is different than ion-acoustic solitary waves.

Fig. 3
figure 3

Variation of \(W( \phi )\) versus \(\phi \) and (b) phase curves of ion acoustic cnoidal waves (dashed, dotted and dotdashed curves), for different values of \(l_{z}\). Dashed curve: \(l_{z}=0.94\), dotted curve: \(l_{z}=0.96\), dotdashed curve: \(l_{z}=0.98\) with \(u=0.3\), \(\Omega =0.3\), \(\rho =0.02\), \(p_{1}=0.2\), \(p_{2}=0.1\), and \(E=0.007\). The black solid curve with \(l_{z}=0.94\), \(\rho =0\) and \(E=0\) is for solitary waves

Full size image

To demonstrate the effect of anisotropic ion pressure \(p_{1}\) on ion acoustic nonlinear periodic waves, we have shown the variation of cnoidal wave solution \(\phi \) versus \(\eta \) for different values of \(p_{1} ( =0.2,0.3,0.4 ) \) (where we have considered a fixed value of all other plasma parameters). It is clearly seen that higher values of anisotropic ion pressure \(p_{1}\) leads to smaller amplitude ion acoustic cnoidal waves (see Fig. 4). To get more physical insight into the behavior of ion acoustic cnoidal wave structures in the presence of ion pressure anisotropy, we consider three different cases, namely \(p_{1}>p_{2}\), \(p_{1}< p_{2}\) and \(p_{1}=p_{2}=0\) (see Fig. 5). It is obvious that the ion parallel pressure \(p_{1}\) bears significant effect on the characteristic behavior of ion acoustic wave structures as compared to its perpendicular counterpart (\(p_{2}\)). We also see that including the ion thermal pressure (in the warm ion model) gives rise to smaller amplitude ion acoustic cnoidal waves. Finally Fig. 6 depicts the plot of \(\phi \) versus \(\eta \) for varying values of \(\theta \) (keeping all other parameters fixed). In contrast to the ion acoustic solitary waves (see Adnan et al. 2014a), it is found that lower values of \(\theta \) (i.e., increased values of \(l_{z}=\cos \theta \)) gives larger amplitude ion acoustic cnoidal wave profiles.

Fig. 4
figure 4

Variation of \(\phi \) versus \(\eta \) for different values of \(p_{1}\). Dashed curve: \(p_{1}=0.2\), dotted curve: \(p_{1}=0.3\), dotdashed curve: \(p_{1}=0.4\) with \(u=0.3\), \(\Omega =0.3\), \(\rho =0.02\), \(l_{z}=0.96\), \(p_{2}=0.1\), and \(E=0.007\)

Full size image
Fig. 5
figure 5

Variation of \(\phi \) versus \(\eta \) for \(u=0.3\), \(\Omega =0.3\), \(\rho =0.02\), \(l_{z}=0.96\), and \(E=0.007\) with \(p_{1}>p_{2}\) (dashed curve); \(p_{2}>p_{1}\) (dotted curve); and \(p_{1}=p_{2}=0 \) (dotdashed curve)

Full size image
Fig. 6
figure 6

Variation of \(\phi \) versus \(\eta \) for different values of \(l_{z}\). Dashed curve: \(l_{z}=0.94\), dotted curve: \(l_{z}=0.96\), dotdashed curve: \(l_{z}=0.98\) with \(u=0.3\), \(\Omega =0.3\), \(\rho =0.02\), \(p_{1}=0.2\), \(p_{2}=0.1\) and \(E=0.007\)

Full size image

It is instructive to note that we have used the numerical values of \(p_{1}\) and \(p_{2}\) which lies in the limits of \(T_{\Vert }\) and \(T_{\bot }\) described in Seough et al. (2013). We have used the data from reference (Denton et al. 1994) while dealing with the ion pressure anisotropy cases.

6 Conclusions

To conclude, we have studied the characteristics of ion acoustic nonlinear periodic (cnoidal) waves in a magnetized plasma consisting of warm anisotropic ions and inertialess electrons obeying Maxwellian distribution. Through the reductive perturbation technique, Korteweg-de Vries (KdV) equation is derived which admits a cnoidal wave solution. It has been found that the KdV equation admits only positive potential nonlinear periodic wave structures in the given plasma system. Through numerical analysis, it was shown that the amplitude and width of the ion acoustic cnoidal waves decreases as the parallel pressure \(p_{1}\) is increased. It has been noticed that increased values of the obliqueness (i.e., the angle between the directions of wave propagation and the external magnetic field, \(B_{0}\)) result in smaller amplitude ion acoustic cnoidal wave profiles. It was observed that the ion parallel pressure \(p_{1}\) bears significant effect on the characteristic behavior of ion acoustic cnoidal wave structures as compared to its perpendicular counterpart (\(p_{2}\)). Moreover, it has also been pointed out that the ion-acoustic cnoidal waves behave quite differently from ion-acoustic solitary waves.

It may be added, for the sake of rigor, that the present work is primarily inspired by a series of magnetosheath observations made by instruments involving two spacecraft, namely AMPET/CCF and AMPET/IRM, as mentioned in Denton et al. (1994), and somewhat by the work of Seough et al. (2013). We, therefore, anticipate that our theoretical results may provide a good qualitative description of the cnoidal wave structures observed in various space and astrophysical environments possessing strong magnetic fields with ion pressure anisotropy. In particular, such anisotropic situation can be found in the magnetosphere and in the near-Earth magnetosheath (Baumjohann and Treumann 1997; Choi et al. 2007; Denton et al. 1994).