Propagation of dust-ion-acoustic solitary waves for damped modified Kadomtsev–Petviashvili–Burgers equation in dusty plasma with a q-nonextensive nonthermal electron velocity distribution

Abstract

The nonlinear dust ion acoustic solitary waves (DIAW) in a magnetized collisional dusty plasma comprising with negatively charged dust grain, positively charged ions along with q-nonextensive nonthermal electrons and neutral particles in the presence of small damping force is studied analytically through the framework of damped modified Kadomtsev-Petviashvili-Burgers (DMKPB) equation. Reductive perturbation technique (RPT) is employed to derive the DMKPB equation. It is observed that there is a critical point for the plasma parameters where the amplitude of the solitary wave of damped KP Burgers equation diverges. The DMKPB equation is derived from there and the soliton like solutions with finite amplitude is extracted. The influence of various plasma parameters like entropic index, dust ion collisional frequency, ion kinematic viscosity, speed of the traveling wave and the parameter indicating the ratio between unperturbed dust ion density and electron are investigated on the propagation of dust ion acoustic wave (DIAW). A significant effect on the wave structures due to the variation of present plasma parameters has been observed. Finally, the temporal evolution of a solitary wave solution is depicted through a numerical standpoint.

1 Introduction

Dusty plasma is an ionized gas comprising with electrons, positive ions, neutral atoms and massive micrometer-sized solid charged dust grains. It exists in many astrophysical bodies like active galactic nuclei [27], pulsar magnetospheres [17, 26], solar atmosphere [15, 54], planetary rings, comet tails, interstellar medium, noctilucent clouds and so on [14, 20, 64]. Besides its application in astrophysical studies, nowadays investigation of the plasma becomes a promising topic because of its important role in the semiconductor processing industry, nanoparticle production, and film deposition reactors, etc., [49, 63]. During the last three decades, physicists have gained immense interest to observe DIAW in a dusty plasma system. For the first time, Tonks et al. theoretically predicted the presence of ion-acoustic waves (IAW) in ionized gas [55] whereas Rewans in the year 1933 [40] experimentally first observed IAW in gas-discharge plasma. Sazdeev [42] studied theoretically these types of wave in plasma system and Ikezi et.al. [21] observed the same experimentally. Subsequently a lot of experimental and theoretical works had been accomplished in different plasma field and it is observed that dust grain produces a number of new wave features viz. dust ion acoustic mode [50], dust acoustic mode [29, 38], dust drift mode [52], dust lattice mode [32] and Shukla–Varma mode [51], dust cyclotron mode [33], dust Berstain–Green–Krushkal mode [56] etc.

In most investigations, a solitary wave propagating in the plasma system is studied through the framework of Korteweg de Vries (KdV) equation or modified KdV equation employing the reductive perturbation technique. Kadomstev and Petviashvili were the first to make an attempt to observe solitons in two-dimensional systems and successfully developed a new model which is known as Kadomtsev–Petviashvili (KP) equations [23]. The KP equation as well as modified KP (MKP) equation in general are considered as an extension of the KdV equation into two-dimensional space. These models are extensively used in fluid mechanics [6, 18, 19, 45] and other theoretical physics [16].

Dorranian et al. [9] studied DIAW in a dusty plasma comprising with nonthermal ion species at various temperatures considering the frameworks of KP as well as MKP equations.Their observation indicates that the emergence of compressive as well as rarefactive solitary structure significantly depends on the number and the temperature of nonthermal ions. Seadawy et al. [44] employing generalized extended tanh method and F-expansion method obtained exact wave solutions for KP and MKP equations. Samanta et al. [43] considering the framework of KP equation investigates the wave quantity in a magnetized dusty plasma consisting of q-nonextensive velocity distributed electron. Finally, they found the exact solitary wave solution as well as periodic traveling wave solutions which are significantly dependent on the various physical plasma parameters. In all such observation, the system occupies nonlinear weakly dispersive waves whose wavelength is long enough. Also, the KP and MKP equation possesses a large class of wave variety. The simplest soliton type solution of the KP equation is a generalization of the solitary wave solution of the KdV equation, propagate in one direction only. But there are many other varieties other than line soliton. Further depending on the physical context a large class of investigation [7, 10,11,12, 47, 48] have been carried out through the framework of KP and MKP equation. In general, to study the behaviour of ion acoustic wave in plasma system, Maxwell distributed electron is considered. However, Maxwell distribution may not be adequate in many practical situations. For instance, in plasma systems where long-range wave interaction is considered, see, e.g., [2]. Several plasma systems contain energetic electron and ions that are not generally found in thermodynamic equilibrium. Especially, nonthermal electron-ion distributions often remain in space plasma which includes coherent nonlinear waves actively. Some remarkable observation by Bouzit et al. [4] confirmed their presence in different space environments. In such cases, kappa distribution [3, 62] and Tsallis distribution [57] may be more appropriate. In the year 1955, Renyi [39] deduced a new distribution on the basis of generalization of Boltzmann–Gibbs–Shannon entropic measure for statistical equilibrium, called q-nonextensive electron velocity distribution. Some recent investigations [13, 41] studied plasma system employing this distribution and showed significant dependency of nonextensive parameter (q) in wave propagation. Additionally it is proved by some experimental observation [1, 46] that sometime external periodic force potential together with a damping [34] may change the wave propagation significantly in a real physical situations. Recently tremendous interest begins to study plasma system considering the above physical conditions [30, 31].

Dorranian and Sabetkar [9] describe the characteristic features of dust particles in a dusty plasma with two ions at two different temperatures through the KP model. Hafeez [61] observed dust ion-acoustic solitons in pair-ion plasmas considering the KP model. Hamid [35] considered KP model and studied behaviors of IAW in a warm dusty plasma with variable dust charge, two-temperature ion and nonthermal electron. Considering Boltzmann distributed electrons and adopting KP model Sing and Honzawa [53] investigated the behaviors of ion-acoustic soliton in an unmagnetized, collisionless weakly relativistic plasma comprising hot isothermal electrons and the ions with a finite temperature. Lin and Duan [28] observed the IAW for two-ion-temperature dusty plasma considering KP model along with the extensions such as MKP model, and the coupled KP equations. Pakzad [36] considered coupled dusty plasma with variable dust charge and non-isothermal ions and studied shock and solitary waves in the framework of KP burgers as well as the Modified KP-Burger framework. Xue [66] also considered the same framework and studied dusty plasma with non-adiabatic dust charge fluctuation. In order to find dust-ion collision effect in IAW we adopt for the first time DMKPB equation.

In this present investigation, our aim is to find an analytical solitary wave solution of the DMKPB equation in a collisional magnetized dusty plasma consisting of q-nonextensive nonthermal electrons, negatively charged dust grain, positively charged ions and neutral particles incorporating with a Burger term and damping term. Furthermore, the influence of different plasma parameters such as the entropic index (q), spectral index ($\alpha$), dust ion collisional frequency ($\nu _{id0}$), the speed of the traveling wave (M) and ion kinematic viscosity ($\eta _{i0}$) are studied on the amplitude and width of the solitary waves. The rest of the manuscript is organized as follows. Following the Introduction, basic equations are provided in Sect. 2. In Sect. 3 we present the model description and derived DMKPB equation for nonlinear propagation of DIAW. Section 4 is devoted to the numerical presentation of the solution for different parameters and Sect. 5 ends with a conclusion.

2 Governing equations

We consider a magnetized collisional three component dusty plasma consisting of cold inertial ions, nonextensive nonthermal electrons and immobile negatively charged dust grains. Charges of the dust grains are believed to be a constant term. The basic governing equations are

$$\begin{aligned} \frac{\partial n_{i}}{\partial t}+\nabla \cdot ( n_{i}u_{i})= & {} 0 \end{aligned}$$

(2.1)

$$\begin{aligned} \frac{\partial u_{i}}{\partial t}+( u_{i}.\nabla ) u_{i}= & {} -\frac{e}{m_{i}}\nabla \phi +\frac{eB_{0}}{m_{i}c}u_{i}\times e_{z}+\eta _{0}\nabla ^{2}u_{i}-\nu _{0}u_{i} \end{aligned}$$

(2.2)

$$\begin{aligned} \nabla ^{2}\phi= & {} 4\pi e\left[ n_{e}-n_{i}+Z_{d}n_{d}\right] \end{aligned}$$

(2.3)

where $n_{j}$ is the density of the jth species ($j=e,i,d$ stands for electon, ion and dust grains respectively) Here $u_i$ and $m_i$ are the velocity and mass of ion where as $\phi$ denotes the plasma wave potential. Again, e represents elementary charge of electron, $T_e$ denotes the temperature of the electron and $Z_d$ is the number of charged dust particle. We consider $q_d$ as total charge of the dust particle and so $q_d=-eZ_d$. The external magnetic field is directed along z axis i.e. $B=B_{0}e_{z}$ where $e_{z}$ = unit vector along z-axis.Cairns–Tsallis distribution, first proposed by Tribeche et al. [58] is used by us in the present work. They suggested that nonthermality and non-extensivity may act simultaneously and thus may alter the propagation dynamics of ion-acoustic solitary waves. Such a hybrid distribution function, represented by two parameters, may be helpful in knowing a great variety of observed nonthermal plasma phenomena. The electrons are assumed to follow the nonextensive non-thermal velocity distribution function given by

$$\begin{aligned} f_{e}(v_{x})=C_{q\alpha }\left( 1+\alpha \frac{v_{x}^{4}}{v_{et}^{4}}\right) \left[ 1-\left( q-1\right) \frac{v_{x}^{2}}{2v_{et}^{2}}\right] ^{\frac{1}{ q-1}} \end{aligned}$$

(2.4)

where

$$\begin{aligned} v_{et}=\sqrt{\frac{T_{e}}{m_{e}}} \end{aligned}$$

represents the electron thermal velocity, $T_{e}$ represents the electron temperature, $m_{e}$ is the electron mass.$C_{q\alpha },~$the normalization constant is given by

$$\begin{aligned} C_{q\alpha }= & {} n_{e0}\left( \frac{m_{e}}{2\pi T_{e}}\right) ^{\frac{1}{2}} \frac{\varGamma \left( \frac{1}{1-q}\right) \left( 1-q\right) ^{\frac{5}{2}}}{ \varGamma \left( \frac{1}{1-q}-\frac{5}{2}\right) \left[ 3\alpha +\left( \frac{1 }{1-q}-\frac{3}{2}\right) \left( \frac{1}{1-q}-\frac{5}{2}\right) \left( 1-q\right) ^{2}\right] }\quad \text {for }-1<q<1, \\= & {} n_{e0}\left( \frac{m_{e}}{2\pi T_{e}}\right) ^{\frac{1}{2}}\frac{\varGamma \left( \frac{1}{q-1}+\frac{3}{2}\right) \left( q-1\right) ^{\frac{5}{2} }\left( \frac{1}{q-1}+\frac{3}{2}\right) \left( \frac{1}{q-1}+\frac{5}{2} \right) }{\varGamma \left( \frac{1}{q-1}+1\right) \left[ 3\alpha +\left( \frac{1 }{q-1}+\frac{3}{2}\right) \left( \frac{1}{q-1}+\frac{5}{2}\right) \left( q-1\right) ^{2}\right] }\quad \text {for }q>1. \end{aligned}$$

Here q stands for nonextensive parameter, $\alpha ~$is a parameter representing the number of nonthermal electrons present in this model, and $\varGamma ~$is the standard Gamma function. For $q>1,$the distribution function shows a thermal cut-off on the maximum value permitted for the velocity of electron, given by

$$\begin{aligned} v_{\max }=\sqrt{\frac{2T_{e}}{m_{e}\left( q-1\right) }} \end{aligned}$$

beyond which there is no existence of probable state. Now integrating (2.4) over all velocity spaces, we get the following electron density

$$\begin{aligned} n_{e}( \phi )= & {} \left\{ \begin{array}{ll} \int \limits _{-\infty }^{+\infty }f_{e}\left( v_{x}\right) dv_{x}&{}\quad \text { for } -1<q<1,\\ \int \limits _{-v_{\max }}^{+v_{\max }}f_{e}\left( v_{x}\right) dv_{x}&{}\quad \text { for }q>1 \end{array} \right. \nonumber \\= & {} n_{e0}\left[ 1+\left( q-1\right) \frac{e\phi }{T_{e}}\right] ^{\frac{q+1}{ 2\left( q-1\right) }}\times \left[ 1+L_{1}\left( \frac{e\phi }{T_{e}}\right) +L_{2}\left( \frac{e\phi }{T_{e}}\right) ^{2}\right] \end{aligned}$$

(2.5)

where

$$\begin{aligned} L_{1}= & {} -\frac{16q\alpha }{3-14q+15q^{2}+12\alpha } \\ L_{2}= & {} \frac{16q\alpha \left( 2q-1\right) }{3-14q+15q^{2}+12\alpha } \end{aligned}$$

The well known nonthermal electron density of Cairns et al. [5]

$$\begin{aligned} n_{e}\left( \phi \right) =n_{e0}\left[ 1-\frac{4\alpha }{1+3\alpha }\left( \frac{e\phi }{T_{e}}\right) +\frac{4\alpha }{1+3\alpha }\left( \frac{e\phi }{ T_{e}}\right) ^{2}\right] \times \exp \left( \frac{e\phi }{T_{e}}\right) \end{aligned}$$

is obtained from the above density in the extensive limiting case $\left( q\rightarrow 1\right) ~$and $\left( \alpha \ne 0\right) .$ On the other hand for $\left( \alpha =0\right)$ the nonextensive electron density [59]

$$\begin{aligned} n_{e}\left( \phi \right) =n_{e0}\left[ 1+\left( q-1\right) \frac{e\phi }{ T_{e}}\right] ^{\frac{q+1}{2\left( q-1\right) }} \end{aligned}$$

is obtain from the above density.

The normalized electron density $n_{e}$ is given by

$$\begin{aligned} n_{e}= & {} \left( 1+\left( q-1\right) \phi \right) ^{\frac{q+1}{2\left( q-1\right) }}\left( 1+L_{1}\phi +L_{2}\phi \right) \nonumber \\= & {} 1+P\phi +Q\phi ^{2}+R\phi ^{3}+\cdots , \end{aligned}$$

(2.6)

where

$$\begin{aligned} P= & {} L_{1}+\frac{1+q}{2} \\ Q= & {} L_{2}+L_{1}.\left( \frac{1+q}{2}\right) +\frac{\left( 1+q\right) \left( 3-q\right) }{8} \\ R= & {} L_{2}.\left( \frac{1+q}{2}\right) +L_{1}\frac{\left( 1+q\right) \left( 3-q\right) }{8}+\frac{\left( 1+q\right) \left( 3-q\right) \left( 5-3q\right) }{48} \end{aligned}$$

The effect of spectral index $\alpha$ is to make the number of particles of high energy on the shoulder of the velocity distribution curve higher. On the other hand, the entropic index q describes the effect of superthermal particles in the tail of the velocity distribution curve. Williams et al. [65] discovered the limits and influence of $\left( \alpha ,q\right) .~$They claimed that the Cairns–Tsallis hybrid distribution is highly sensitive for looking into ion-acoustic type oscillation. Another crucial condition introduced on $\left( \alpha ,q\right)$ is $\alpha =\frac{\left( 2q-1\right) }{4}$ as studied by Williams et al. This state is required for the monotonicity of the distribution. Therefore in our analysis, we go for only specific ranges, i.e. $0\le \alpha < 0.25$ and $0.6 < q \le 1$.

In order to study the nonlinear dust ion-acoustic wave in x-z plane, the normalized equations in the component form can be written as

$$\begin{aligned} \frac{\partial n}{\partial t}+\frac{\partial (nu_{x})}{\partial x}+\frac{ \partial (nu_{z})}{\partial z}= & {} 0 \end{aligned}$$

(2.7)

$$\begin{aligned} \frac{\partial u_{x}}{\partial t}+\left( u_{x}\frac{\partial }{\partial x}+u_{z} \frac{\partial }{\partial z}\right) u_{x}= & {} -\frac{\partial \phi }{\partial x} +u_{y}+\eta _{i}\left( \frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{ \partial z^{2}}\right) u_{x}-\nu _{id}u_{x} \end{aligned}$$

(2.8)

$$\begin{aligned} \frac{\partial u_{y}}{\partial t}+\left( u_{x}\frac{\partial }{\partial x}+u_{z} \frac{\partial }{\partial z}\right) u_{y}= & {} -u_{x}+\eta _{i}\left( \frac{\partial ^{2}}{ \partial x^{2}}+\frac{\partial ^{2}}{\partial z^{2}}\right) u_{y}-\nu _{id}u_{y} \end{aligned}$$

(2.9)

$$\begin{aligned} \frac{\partial u_{z}}{\partial t}+\left( u_{x}\frac{\partial }{\partial x}+u_{z} \frac{\partial }{\partial z}\right) u_{z}= & {} -\frac{\partial \phi }{\partial z} +\eta _{i}\left( \frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{ \partial z^{2}}\right) u_{z}-\nu _{id}u_{z} \end{aligned}$$

(2.10)

$$\begin{aligned} (\frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial z^{2}} )\phi= & {} \beta [ n_{e}-\mu _{1}n+\mu _{2}] \end{aligned}$$

(2.11)

Here we consider $\beta =\frac{r_g^2}{\lambda _D^2}$, $\eta _{i}=\frac{\varOmega }{C_{s}^{2}}\eta _{0}$, $\nu _{id}=\frac{1}{\varOmega }\nu _{0}$, $\mu _1 =\frac{n_{i0}}{n_{e0}}$ and $\mu _2=\frac{{n_d}{Z_d}}{n_{e0}}$ where $r_g \,(=\frac{C_s}{\varOmega })$ represents ion gyroradius, $C_s= \sqrt{T_{e}/m_i}$ is the ion acoustic velocity and $\lambda _D=\sqrt{{T_e}/{4\pi n_{e_0}e^2}}$ is taken to present electron Debye length. In this case $n_{i0}$ and $n_{e0}$ stand for representation of unperturbed ion and electron number density in equilibrium state. $\eta _i$ is the normalized ion kinematic viscosity and $\eta _0$ is the unnormalized kinematic viscocity. Ion gyrofrequency is presented as $\varOmega =eB_{0}/m_{i}c~$ where e is the charge of electron, c represents speed of light and $B_{0}$ is the magnitude of ambient magnetic field. We make normalization as $\varOmega t\rightarrow \varOmega$, $(\frac{C_s}{\varOmega })\nabla \rightarrow \nabla$, $\frac{u_i}{C_s}\rightarrow u$, $\frac{n_i}{n_{i0}}\rightarrow n$, $\frac{n_e}{n_{e0}}\rightarrow n_{e}$,$\frac{e\phi }{T_e}\rightarrow \phi$. $\nu _{id}$ is taken to present dust ion collisional frequency.

3 Nonlinear evaluation of DMKPB equation

Reductive perturbation technique (RPT) [24, 60] is employed to construct KP equation for small-amplitude ion-acoustic two dimensional solitary wave in the magnetized dusty plasma. Nowadays RPT becomes very attractive to study small amplitude ion-acoustic waves in plasma field. To investigate the DIAW through KP equation, all the standard independent variables are stretched and written as:

$$\begin{aligned} \chi= & {} \epsilon ^{2}x \nonumber \\ \xi= & {} \epsilon (z-Vt)\nonumber \\ \tau= & {} \epsilon ^{3}t \end{aligned}$$

(3.1)

Here V represents the phase velocity of DIAW and $\epsilon$ is considerd as a small parameter to measure the strength of the nonlinearity of DIAW. The dependent variables are expanded and written as bellow,

$$\begin{aligned} n= & {} 1+\epsilon ^{2}n_{1}+\epsilon ^{4}n_{2}+\cdots \nonumber \\ u_{x}= & {} \epsilon ^{3}u_{x1}+\epsilon ^{5}u_{x2}+\cdots \nonumber \\ u_{y}= & {} \epsilon ^{3}u_{y1}+\epsilon ^{\frac{9}{2}}u_{y2}+\cdots \nonumber \\ u_{z}= & {} \epsilon ^{2}u_{z1}+\epsilon ^{4}u_{z2}+\cdots \nonumber \\ \phi= & {} \epsilon ^{2}\phi _{1}+\epsilon ^{4}\phi _{2}+\cdots \nonumber \\ \nu _{id}\approx & {} \epsilon ^{3}\nu _{id0} \nonumber \\ \eta _{i}\simeq & {} \epsilon \eta _{i0} \end{aligned}$$

(3.2)

Substituting Eqs. (3.1) and (3.2) in Eqs.  (2.7)–(2.11) and collecting the coefficient of different powers of $\epsilon$, we obtain the following equations,

$$\begin{aligned} n_{1}= & {} \frac{u_{z1}}{V} \end{aligned}$$

(3.3)

$$\begin{aligned} \frac{\partial n_{1}}{\partial \tau }-V\frac{\partial n_{2}}{\partial \xi }+ \frac{\partial u_{x1}}{\partial \chi }+\frac{\partial u_{z2}}{\partial \xi }+ \frac{\partial (n_{1}u_{z1})}{\partial \xi }= & {} 0 \end{aligned}$$

(3.4)

$$\begin{aligned} V\frac{\partial u_{x1}}{\partial \xi }= & {} \frac{\partial \phi _{1}}{\partial \chi } \end{aligned}$$

(3.5)

$$\begin{aligned} u_{z1}= & {} \frac{\phi _{1}}{V} \end{aligned}$$

(3.6)

$$\begin{aligned} \frac{\partial u_{z1}}{\partial \tau }-V\frac{\partial u_{z2}}{\partial \xi } +u_{z1}\frac{\partial u_{z1}}{\partial \xi }= & {} -\frac{\partial \phi _{2}}{ \partial \xi }+\eta _{i0}\frac{\partial ^{2}u_{z1}}{\partial \xi ^{2}}-\nu _{id0}u_{z1} \end{aligned}$$

(3.7)

$$\begin{aligned} \mu _{1}-\mu _{2}= & {} 1 \end{aligned}$$

(3.8)

$$\begin{aligned} n_{1}= & {} \frac{P}{\mu _{1}}\phi _{1} \end{aligned}$$

(3.9)

$$\begin{aligned} \frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}= & {} \beta [P\phi _{2}+Q\phi _{1}^{2}-\mu _{1}n_{2}] \end{aligned}$$

(3.10)

From Eqs.  (3.3), (3.6) and (3.9), we have

$$\begin{aligned} V^{2}=\frac{\mu _{1}}{P}. \end{aligned}$$

(3.11)

Using all the results described above we finally get a relation that can be claimed as damped Kadomstev-Petviashvili Burgers equation. The result is summarized as,

$$\begin{aligned} \frac{\partial }{\partial \xi }\left[ \frac{\partial \phi _{1}}{\partial \tau } +A\phi _{1}\frac{\partial \phi _{1}}{\partial \xi }+B\frac{\partial ^{3}\phi _{1}}{\partial \xi ^{3}}+D\phi _{1}+E\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}\right] +C\frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}=0 \end{aligned}$$

(3.12)

where $A =\frac{3}{2V}-\frac{QV}{P}$, $B =\frac{V^{3}}{2\mu _{1}\beta }$, $C =\frac{V}{2}$, $D =\frac{1}{2}\nu _{id0}$, $E =-\frac{1}{2}\eta _{i0}$ For a certain values of the parameters q, $\alpha$ and $\mu _{1}$ (for example $q = 0.95$, $\alpha =0.1$ and $\mu _{1}=0.74262$), we see a critical point at which $A = 0$. Nonlinearity vanishes at the critical point and so infinite divergence of amplitude of the DIAW solution is found. Therefore, stretching of dependent variables expressed in (3.2) becomes inadequate for the present investigation. To describe the evolution of the nonlinear system at or near the critical point we consider the same set of stretched coordinates but with a new expression as follows:

$$\begin{aligned} n= & {} 1+\epsilon n_{1}+\epsilon ^{2}n_{2}++\epsilon ^{3}n_{3}\ldots \nonumber \\ u_{x}= & {} \epsilon ^{2}u_{x1}+\epsilon ^{3}u_{x2}+\ldots \nonumber \\ u_{y}= & {} \epsilon ^{2}u_{y1}+\epsilon ^{4}u_{y2}+\ldots \nonumber \\ u_{z}= & {} \epsilon u_{z1}+\epsilon ^{2}u_{z2}++\epsilon ^{3}u_{z3}\ldots \nonumber \\ \phi= & {} \epsilon \phi _{1}+\epsilon ^{2}\phi _{2}++\epsilon ^{3}\phi _{3}\ldots \nonumber \\ \nu _{id}\approx & {} \epsilon ^{3}\nu _{id0} \nonumber \\ \eta _{i}\simeq & {} \epsilon \eta _{i0} \end{aligned}$$

(3.13)

Substituting equations (3.1) and (3.13) in equations (2.7)–(2.11) and collecting the coefficient of different powers of $\epsilon$, we obtain the following equations:

$$\begin{aligned} u_{z1}= & {} Vn_{1} \end{aligned}$$

(3.14)

$$\begin{aligned}&-V\frac{\partial n_{2}}{\partial \xi }+\frac{\partial u_{z2}}{\partial \xi }+ \frac{\partial (n_{1}u_{z1})}{\partial \xi } =0 \end{aligned}$$

(3.15)

$$\begin{aligned}&\frac{\partial n_{1}}{\partial \tau }-V\frac{\partial n_{3}}{\partial \xi }+ \frac{\partial u_{x1}}{\partial \chi }+\frac{\partial u_{z3}}{\partial \xi }+ \frac{\partial (n_{1}u_{z2})}{\partial \xi }+\frac{\partial (n_{2}u_{z1})}{ \partial \xi }=0 \end{aligned}$$

(3.16)

$$\begin{aligned}&V\frac{\partial u_{x1}}{\partial \xi }=\frac{\partial \phi _{1}}{\partial \chi } \end{aligned}$$

(3.17)

$$\begin{aligned}&u_{z1} =\frac{\phi _{1}}{V} \end{aligned}$$

(3.18)

$$\begin{aligned}&-V\frac{\partial u_{z2}}{\partial \xi }+u_{z1}\frac{\partial u_{z1}}{ \partial \xi } =-\frac{\partial \phi _{2}}{\partial \xi } \end{aligned}$$

(3.19)

$$\begin{aligned}&\frac{\partial u_{z1}}{\partial \tau }-V\frac{\partial u_{z3}}{\partial \xi } +u_{z1}\frac{\partial u_{z2}}{\partial \xi }+u_{z2}\frac{\partial u_{z1}}{ \partial \xi }=-\frac{\partial \phi _{3}}{\partial \xi }+\eta _{i0}\frac{ \partial ^{2}u_{z1}}{\partial \xi ^{2}}-\nu _{id0}u_{z1} \end{aligned}$$

(3.20)

$$\begin{aligned}&\mu _{1}-\mu _{2} =1 \end{aligned}$$

(3.21)

$$\begin{aligned}&n_{1} =\frac{P}{\mu _{1}}\phi _{1} \end{aligned}$$

(3.22)

$$\begin{aligned}&P\phi _{2}+Q\phi _{1}^{2}-\mu _{1}n_{2}=0 \end{aligned}$$

(3.23)

$$\begin{aligned}&\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}=\beta [ P\phi _{3}+2Q\phi _{1}\phi _{2}+R\phi _{1}^{3}-\mu _{1}n_{3}] \end{aligned}$$

(3.24)

From Eqs. (3.14), (3.18) and (3.22), we have

$$\begin{aligned} V^{2}=\frac{\mu _{1}}{P} \end{aligned}$$

(3.25)

and from Eqs. (3.15), (3.19) and (3.23), we have

$$\begin{aligned} \mu _{1}=\frac{3P^{2}}{2Q} \end{aligned}$$

(3.26)

From Eqs. (3.16), (3.17), (3.20) and (3.24) one can obtain the following nonlinear evaluation equation as:

$$\begin{aligned} \frac{\partial }{\partial \xi }\left[ \frac{\partial \phi _{1}}{\partial \tau } +A\phi _{1}^{2}\frac{\partial \phi _{1}}{\partial \xi }+B\frac{\partial ^{3}\phi _{1}}{\partial \xi ^{3}}+D\phi _{1}+E\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}\right] +C\frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}=0 \end{aligned}$$

(3.27)

where $A =\frac{15}{4V^{3}}-\frac{3RV}{2P}$, $B =\frac{V^{3}}{2\mu _{1}\beta }$, $C =\frac{V}{2}$, $D =\frac{1}{2}\nu _{id0}$, $E =-\frac{1}{2}\eta _{i0}$

The above equation is termed as damped modified KP Burgers (DMKPB) equation. Integrating with respect to $\xi$we get

$$\begin{aligned} \frac{\partial \phi _{1}}{\partial \tau }+A\phi _{1}^{2}\frac{\partial \phi _{1}}{\partial \xi }+B\frac{\partial ^{3}\phi _{1}}{\partial \xi ^{3}} +D\phi _{1}+E\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}} +C\int \frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}d\xi =c_{1} \end{aligned}$$

(3.28)

We claim $\phi _1$ vanish as $\xi \rightarrow \pm \infty$ and thus (3.28) turns into

$$\begin{aligned} \frac{\partial \phi _{1}}{\partial \tau }+A\phi _{1}\frac{\partial \phi _{1} }{\partial \xi }+B\frac{\partial ^{3}\phi _{1}}{\partial \xi ^{3}}+D\phi _{1} +E\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}+C\int \frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}d\xi =0 \end{aligned}$$

(3.29)

In the absence of E and D i.e. for $D=0$ and $E=0$, the Eq. (3.27) takes the form of well-known MKP equation with the solitary wave solution [25]

$$\begin{aligned} \phi _{1}=\phi _{m}{sech}\left( \frac{\zeta -M\tau }{W}\right) \end{aligned}$$

(3.30)

where $\zeta =l\xi +m\chi$ and l, m are the direction cosines of the wave propagation with respect to $\xi$ and $\chi$ axes respectively.

Here $\phi _{m}=\sqrt{\frac{6(M-C)}{Al}}$ and $\text { }W=\sqrt{\frac{Bl^{3}}{M-C}}$ are the amplitude and width of the solitary waves.

During the last few decades study of plasma system in the presence of external forces together with a damping, have gained great interest. Xiao et al. [22] made an experiment to investigate nonlinear wave propagation under the influence of forcing term in a model of forced KdV equation employing Hirota’s direct test method. Then in the year 2015, Sen [46] observes the same using reductive perturbation technique. Very recently, a new trend [8, 37] arises to study plasma system comprising a damping term. Now for the MKP equation

$$\begin{aligned} I=\int _{-\infty }^{\infty }\phi _{1}^{2}d\zeta \end{aligned}$$

(3.31)

is a conserved quantity.

The classical KP equation provides the solitary wave solution with constant amplitude as well as constant width. We assume that the solitary pattern solution also exists for DMKPB equations with small burgers and damping terms. It is also considered that a small variation follows in the amplitude, width and the velocity of the wave solution due to the presence of damping and burgers terms. It leads to form a solitary type wave structure whose amplitude, width and velocity have a small dependency on $\tau$. Thus, the solution of Eq. (3.27) is approximated as

$$\begin{aligned} \phi _{1}=\phi _{m}(\tau ){sech}\left( \frac{\zeta -M(\tau )\tau }{W\left( \tau \right) }\right) \end{aligned}$$

(3.32)

where $~\phi _{m}\left( \tau \right) =\sqrt{\frac{ 6(M(\tau )-C)}{Al}}$ and $\text { }W\left( \tau \right) =\sqrt{\frac{Bl^{3}}{M(\tau )-C}}$

From equation (3.31)

$$\begin{aligned} I=12\frac{\sqrt{Bl}}{A}(M(\tau )-C)^{\frac{1}{2}} \end{aligned}$$

(3.33)

Differentiating (3.31) with respect to $\tau$ and using the equation (3.29) we get (for details see “Appendix”),

$$\begin{aligned} \frac{dI}{d\tau }+2DI=-2E\int _{-\infty }^{\infty }\phi _{1}\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}d\zeta -2C\int _{-\infty }^{\infty }\phi _{1}\left( \int \frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}d\xi \right) d\zeta \end{aligned}$$

(3.34)

Now

$$\begin{aligned} \int _{-\infty }^{\infty }\phi _{1}\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}d\zeta =-4\frac{(M(\tau )-C)^{\frac{3}{2}}}{A\sqrt{Bl}} \end{aligned}$$

and

$$\begin{aligned} \int _{-\infty }^{\infty }\phi _{1}\left( \int \frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}d\xi \right) d\zeta =\frac{{\pi }m^{2}}{l} \phi _{m}^{2}(\tau )F(\chi ,\tau ) \end{aligned}$$

where $F(\chi ,\tau )$ is an arbitrary function of $\chi$ and $\tau$. For simplicity we assume that $F(\chi ,\tau )=0$.

We obtain from Eq. (3.34)

$$\begin{aligned} \frac{dI}{d\tau }+2DI=\frac{8E}{A\sqrt{Bl}}(M(\tau )-C)^{\frac{3}{2}} \end{aligned}$$

(3.35)

Differentiation of (3.33) with respect to $\tau$ gives,

$$\begin{aligned} \frac{dI}{d\tau }=6\frac{\sqrt{Bl}}{A}(M(\tau )-C)^{-\frac{1}{2}}\frac{ dM(\tau )}{d\tau } \end{aligned}$$

(3.36)

Combining the Eqs. (3.35) and (3.36) we finally get,

$$\begin{aligned} \frac{d(M(\tau )-C)}{d\tau }+4D(M(\tau )-C) =\frac{4E}{3Bl}(M(\tau )-C)^{2} \end{aligned}$$

(3.37)

Solution of the above equation is expressed as,

$$\begin{aligned} M(\tau )=C+\frac{3lBD(M_{0}-C)}{E(M_{0}-C)(1-e^{4D\tau })+3lBDe^{4D\tau }} \end{aligned}$$

(3.38)

Here, $M(\tau )$ represents the time dependent velocity of ion acoustic wave propagating in the magnetized dusty plasma and $M_{0}$ is the initial velocity of IAW, i.e at $\tau =0$, $M(\tau )=M_{0}$. Thus, the slow time dependent wave solution for the damped modified KP burgers equation is expressed as

$$\begin{aligned} \phi _{1}=\phi _{m}(\tau ){sech}\left( \frac{\zeta -M(\tau )\tau }{W( \tau ) }\right) \end{aligned}$$

(3.39)

where $\zeta =l\xi +m\chi$ and the time dependent soliton amplitude, width of DIAW propagating in dusty plasma are given by $\phi _{m}(\tau )=\sqrt{\frac{6(M(\tau )-C)}{Al}}$, $W(\tau )=\sqrt{\frac{Bl^{3}}{M(\tau )-C}}$ and $M(\tau )$ is given by (3.38).

4 Numerical simulation and discussion

Here, the solution of DMKPB equation is illustrated through numerical standpoint. It is found that wave propagation significantly depends on dust ion collisional frequency,kinematic viscosity and parameter q and $\alpha$. The effects of the parameters like $M_0$, $\beta$, $\tau$ etc on the DIAW solution of the DMKPB Eq. (3.27) have been studied in this section.

Fig. 1

Profiles of $\phi _{1}$ is plotted against $\zeta$ for different values of $M_0$ with the parameters $q=0.65$, $\tau =2$, $\eta _{i0}=0.1$, $\alpha =0.2$,$\beta =1$ and $\nu _{id0} = 0.01$

Figure 1 expresses the variation of solitary waves of DMKPB equation for different values of the parameter $M_0$. It shows that an increase for the parameter $M_0$ increases the height of the soliton. Cause of formation of such a wave structure can be described as follows: An increase in initial wave velocity $M_0$ boosts the potential energy of the system and naturally the soliton rises.

Fig. 2

Profiles of $\phi _{1}$ is plotted against $\zeta$ for different values of q with the parameters $M_{0} = 0.75$, $\tau =2$, $\eta _{i0}=0.1$, $\alpha =0.2$, $\beta =1$ and $\nu _{id0}=0.01$

Fig. 3

Profiles of $\phi _{1}$ is plotted against $\zeta$ for different values of $\alpha$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\tau =2$, $\eta _{i0}=0.1$, $\beta =1$ and $\nu _{id0}=0.01$

Fig. 4

Profiles of $\phi _{1}$ is plotted against $\zeta$ for different values of $\beta$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\tau =2$, $\eta _{i0}=0.1$, $\alpha =0.2$, and $\nu _{id0}=0.01$

Figure 2 exhibits the variation of wave propagation due to the increase in nonextensive parameter q. This feature can be interpreted as follows: An increase in q boosts a sudden rise in the velocity of plasma particles and thus potential energy of the plasma system increases rapidly. As a result, solitary wave acquires a sharp rising diminishing its width.

Fig. 5

Profiles of $\phi _{1}$ is plotted against $\zeta$ for different values of $\nu _{id0}$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\tau =2$, $\eta _{i0}=0.1$, $\alpha =0.2$ and $\beta =1$

Figure 3 shows the variation of downswing solitary waves for increasing $\alpha$. It is one of the remarkable observation in this present context as it illustrates the significant outcome from the electron distribution function. It shows that an increase in the nonthermal parameter $\alpha$ reduces both the height and width of the soliton. Nature of such like a structure can be explained as follows: Increasing $\alpha$ causes a negative effect for total potential energy of the system. Thus velocity of the wave particle decreases and the amplitude continuously declines.

Figure 4 explores the wave characteristic of DIAW for an increase in the physical parameter $\beta$. It is noticed that enhancing $\beta$ decreases the width of the soliton keeping the amplitude of the soliton almost same.

Fig. 6

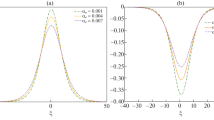
a Profiles of $W(\tau )$ is plotted against $\nu _{id0}$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\tau =2$, $\eta _{i0}=0.1$, $\alpha =0.2$ and $\beta =1$. b Profiles of $\phi _m(\tau )$ is plotted against $\nu _{id0}$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\tau =2$, $\eta _{i0}=0.1$, $\alpha =0.2$ and $\beta =1$

On the other hand Fig. 5 shows decreasing solitary wave potential for different $\nu _{id0}$. It exhibits that an increase in collisional frequency $\nu _{id0}$ intensifies damping and makes the pulses shorter. This type of wave formed as increasing $\nu _{id0}$ causes decrement in potential energy due to the loss of velocity of dust particle.

Figure 6a explores the variation of width of the soliton for DMKPB equation with respect to the dust ion collisional frequency $\nu _{id0}$. It declares that $W(\tau )$ increases as $\nu _{id0}$ increases. But it is interesting to note that amplitude of the soliton diminishes rapidly in Fig. 6b for higher collisional frequencies.

Fig. 7

Profiles of $\phi _{1}$ is plotted against $\zeta$ for different values of $\tau$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\eta _{i0}=0.1$, $\alpha =0.2$, $\beta =1$ and $\nu _{id0}=0.01$

Figure 7 depicts the structure of a decreasing soliton for a particular time interval. It is observed that as the time $\tau$ increases, the peak of the amplitude of DIAW decreases. The width of the soliton remain same. A right hand shift of the DIAW is also observed as $\tau$ increases.

Fig. 8

Profiles of $\phi _{1}$ is plotted against $\zeta$ for different values of $\eta _{i0}$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\tau =2$, $\alpha =0.2$, $\beta =1$ and $\nu _{id0}=0.01$

On the other hand Fig. 8 shows the variation of wave quantities due to the increase in $\eta _{i0}$. An increase in the normalized kinematic viscosity $\eta _{i0}$ results in the decrease of amplitude of DIAW soliton. Formation of such a wave frame can be described as follows: Enhancing kinematic viscosity diminishes wave velocity. Naturally the soliton declines.

Fig. 9

a Profiles of $W(\tau )$ is plotted against $\eta _{i0}$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\tau =2$, $\alpha =0.2$, $\beta =1$ and $\nu _{id0}=0.01$. b Profiles of $\phi _m(\tau )$ is plotted against $\eta _{i0}$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\tau =2$, $\alpha =0.2$, $\beta =1$ and $\nu _{id0}=0.01$

Variation of width of soliton against the parameter $\eta _{i0}$ is depicted in Fig. 9a. Keeping the other parameters same it is observed that width of the solitary wave increases strictly as $\eta _{i0}$ increases. On the other hand Fig. 9b shows strict decreasing of amplitude of wave soliton for higher $\eta _{i0}$.

Fig. 10

a Profiles of $W(\tau )$ is plotted against $\tau$ for different values of $\nu _{id0}$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\eta _{i0}=0.1$, $\alpha =0.2$ and $\beta =1$. b Profiles of $\phi _m(\tau )$ is plotted against $\tau$ for different values of $\nu _{id0}$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\eta _{i0}=0.1$, $\alpha =0.2$ and $\beta =1$

Fig. 11

a Profiles of $W(\tau )$ is plotted against $\tau$ for different values of $\eta _{i0}$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\tau =2$, $\alpha =0.2$, $\beta =1$ and $\nu _{id0}=0.01$. b Profiles of $\phi _m(\tau )$ is plotted against $\tau$ for different values of $\eta _{i0}$ with the parameters $q=0.65$, $M_{0} = 0.75$, $\alpha =0.2$, $\beta =1$ and $\nu _{id0}=0.01$

Variation of width and amplitude of the soliton against time for different $\nu _{id0}$ is observed through Fig. 10a, b respectively. It is observed that for an increase of collisional frequency $\nu _{id0}$, the width of the soliton increases but the amplitude of the soliton decreases. Moreover it is also noticed that for higher collisional frequency width of soliton increases rapidly. On the other hand amplitude of soliton decreases rapidly for higher collisional frequency.

Variation of width and amplitude of the soliton against time for different $\eta _{i0}$ is observed through Fig. 11a, b. For an increase of kinematic viscosity $\eta _{i0}$ width of soliton increases but the amplitude of the soliton decreases. Also it is observed that the rate of change of width of the soliton increases when kinematic viscocity increases. Similarly rate of change of amplitude of the soliton increases when kinematic viscosity increases.

In Fig. 12a, three dimensional plot of the DIAW of $\phi _1$ is drawn in the ($\xi$, $\tau$) plane for DMKPB equation with the parameters $q=0.65$, $M_{0} = 0.75$, $\tau =2$, $\alpha =0.2$, $\beta =1$ and $\nu _{id0}=0.01$, $\eta _{i0}=0.1$. In this figure, $\xi \in (-50 , 150)$, $\tau \in (0, 300)$ and a compressive soliton is observed in the presence of damping force $\nu _{id0}=0.01$. The maximum amplitude of the compressive solitary wave solution lies between 0.6 and 0.7. Figure 12b shows the contour plot of the solitary wave solution $\phi _1$ in the ($\xi$, $\tau$) plane of the DMKPB equation with other physical parameters are same as Fig. 12a. It depicts the equi-amplitude solution space of the solitary wave solution $\phi _1$ and follows a specific pattern in the ($\xi$, $\tau$) plane. It is also shown that the outermost contours sustained with a potential 0.1 at $\tau =200$. It is also observed that the value of $\phi _1$ attains its maximum at the centre of the solution space from both sides as we are characterized a solitary wave solution.

Fig. 12

a 3D plot of $\phi _1$ in ($\xi$, $\tau$) plane for DKPB equation with the parameters $q=0.65$, $M_{0} = 0.75$, $\alpha =0.2$, $\beta =1$ and $\nu _{id0}=0.01$, $\eta _{i0}=0.1$. b Contour plot of $\phi _1$ in ($\xi$, $\tau$) plane for DKPB equation with all others parameters are same as in Fig. 12a

Fig. 13

a 3D plot of $\phi _1$ in ($\xi$, $\tau$) plane for DKPB equation with the parameters $q=0.65$, $M_{0} = 0.75$, $\alpha =0.2$, $\beta =1$ and $\nu _{id0}=0.001$, $\eta _{i0}=0.1$. b Contour plot of $\phi _1$ in ($\xi$, $\tau$) plane for DKPB equation with all others parameters are same as in Fig. 13a

Again, Fig. 13a represents the three-dimensional plot of the solitary wave solution of $\phi _1$ in the presence of negligible damping force potential $\nu _{id0}=0.001$ with all other physical parameters are same as in Fig. 12a. It is observed that the soliton is propagated in the disperse media with a slow decrease in amplitude due to the impact of a negligible amount of damping effect in comparison to that of in Fig. 12a. The maximum amplitude of the compressive solitary wave lies between 0.6 and 0.7. Contour plot of $\phi _1$ in the ($\xi$, $\tau$) plane is shown in the Fig. 13b when the negligible damping force exists. It is seen from the Fig. 13b that outermost contours have the same potential 0.1 and it increases with the value of 0.1 towards the centre of the iso-potential contours. The maximum potential achieved by the contour is 0.7 and it is sustained up to the time $\tau =60$ whereas in the earlier case the highest potential contour loses its potential 0.7 at $\tau =10$. The very next level of potential of contour namely 0.6 is seen in Fig. 13b up to the time $\tau =150$ whereas this level of potential exists up to nearly $\tau =25$ in Fig. 12b. Significant effects of damping force in a dynamic system are strongly suggested by this observation.

5 Conclusions

In this present investigation, the propagating behaviors of DIAW in a magnetized collisional dusty plasma system consisting of q-nonextensive nonthermal velocity distributed electrons in the presence of inherent damping is observed. Both the damped KP Burgers and damped modified KP Burgers equations are derived for different states employing the reductive perturbation method. Significant effects of plasma parameters viz. the entropic index (q), nonthermal parameter ($\alpha$), dust ion collisional frequency ($\nu _{id0}$), speed of the traveling wave (M), ion kinematic viscosity ($\eta _{i0}$), unperturbed ion densities in the background electron on the amplitude and width of wave soliton are investigated through simulations. Finally, some three-dimensional graphs together with contours are depicted to illustrate the consequences in solitary structure due to the variation in the damping term in the system. The present analytical study could be helpful for a better understanding of nonlinear wave propagation in laboratory and space plasma environments.

Appendix

Assuming that conservation property (3.31) holds in the system we write,

$$\begin{aligned} I= & {} \int \limits _{-\infty }^{\infty }\phi _{1}^{2}d\zeta \nonumber \\= & {} \phi _{m}^{2}(\tau )\int \limits _{-\infty }^{\infty }\sec h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) d\zeta \,\, ({\text {using the result}}\, (3.32))\nonumber \\= & {} 2\phi _{m}^{2}(\tau )W\left( \tau \right) \nonumber \\= & {} 2.\frac{6\left( M\left( \tau \right) -C\right) }{Al}\sqrt{\frac{Bl^{3}}{ \left( M\left( \tau \right) -C\right) }} \nonumber \\= & {} \frac{12\sqrt{Bl}}{A}\left( M\left( \tau \right) -C\right) ^{\frac{1}{2}} \end{aligned}$$

(6.1)

where

$$\begin{aligned} \int \limits _{-\infty }^{\infty }\sec h^{2}\left( \frac{\zeta -M( \tau ) \tau }{W( \tau ) }\right) d\zeta =2W( \tau ) \end{aligned}$$

Differentiating (3.31) with respect to $\tau$ and using the Eq. (3.29) we get

$$\begin{aligned} \frac{dI}{d\tau }= & {} 2\int \limits _{-\infty }^{\infty }\phi _{1}\frac{ \partial \phi _{1}}{\partial \tau }d\zeta \nonumber \\= & {} -2A\int \limits _{-\infty }^{\infty }\phi _{1}^{3}\frac{\partial \phi _{1}}{ \partial \xi }d\zeta -2B\int \limits _{-\infty }^{\infty }\phi _{1}\frac{ \partial ^{3}\phi _{1}}{\partial \xi ^{3}}d\zeta -2E\int \limits _{-\infty }^{\infty }\phi _{1}\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}d\zeta \nonumber \\&-2D\int \limits _{-\infty }^{\infty }\phi _{1}^{2}d\zeta -2C\int \limits _{-\infty }^{\infty }\phi _{1}\left( \int \frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}d\xi \right) d\zeta \end{aligned}$$

(6.2)

From (3.32), we have

$$\begin{aligned} \phi _{1}=\phi _{m}\left( \tau \right) \sec h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \end{aligned}$$

So

$$\begin{aligned} \frac{\partial \phi _{1}}{\partial \xi }=-\frac{l\phi _{m}\left( \tau \right) }{W\left( \tau \right) }\sec h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \tan h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \end{aligned}$$

Therefore

$$\begin{aligned} \int \limits _{-\infty }^{\infty }\phi _{1}^{3}\frac{\partial \phi _{1}}{ \partial \xi }d\zeta= & {} -\frac{l\phi _{m}^{4}\left( \tau \right) }{W\left( \tau \right) }\int \limits _{-\infty }^{\infty }\sec h^{4}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \tan h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) d\zeta \nonumber \\= & {} 0 \end{aligned}$$

(6.3)

Similarly

$$\begin{aligned} \int \limits _{-\infty }^{\infty }\phi _{1}\frac{\partial ^{3}\phi _{1}}{ \partial \xi ^{3}}d\zeta =0 \end{aligned}$$

(6.4)

Using (6.3) and (6.4), we have from (6.2),

$$\begin{aligned} \frac{dI}{d\tau }= & {} -2E\int \limits _{-\infty }^{\infty }\phi _{1}\frac{ \partial ^{2}\phi _{1}}{\partial \xi ^{2}}d\zeta -2D\int \limits _{-\infty }^{\infty }\phi _{1}^{2}d\zeta -2C\int \limits _{-\infty }^{\infty }\phi _{1}\left( \int \frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}d\xi \right) d\zeta \;\, or \nonumber \\ \frac{dI}{d\tau }+ 2DI= & {} -2E\int \limits _{-\infty }^{\infty }\phi _{1}\frac{ \partial ^{2}\phi _{1}}{\partial \xi ^{2}}d\zeta -2C\int \limits _{-\infty }^{\infty }\phi _{1}\left( \int \frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}d\xi \right) d\zeta \end{aligned}$$

(6.5)

Again

$$\begin{aligned} \frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}=\frac{l^{2}\phi _{m}\left( \tau \right) }{W^{2}\left( \tau \right) }\left\{ \sec h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \tan h^{2}\left( \frac{ \zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) -\sec h^{3}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) } \right) \right\} \end{aligned}$$

and

$$\begin{aligned} \phi _{1}\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}=\frac{l^{2}\phi _{m}^{2}\left( \tau \right) }{W^{2}\left( \tau \right) }\left\{ \sec h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \tan h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) } \right) -\sec h^{4}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \right\} \end{aligned}$$

Therefore

$$\begin{aligned} \int \limits _{-\infty }^{\infty }\phi _{1}\frac{\partial ^{2}\phi _{1}}{ \partial \xi ^{2}}d\zeta= & {} \frac{l^{2}\phi _{m}^{2}\left( \tau \right) }{ W^{2}\left( \tau \right) }\int \limits _{-\infty }^{\infty }\{\sec h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \tan h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) } \right) -\sec h^{4}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \}d\zeta \nonumber \\= & {} \frac{l^{2}\phi _{m}^{2}\left( \tau \right) }{W^{2}\left( \tau \right) } \left\{ 2\int \limits _{-\infty }^{\infty }\sec h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \tan h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) d\zeta -\int \limits _{-\infty }^{\infty }\sec h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) d\zeta \right\} \nonumber \\= & {} -\frac{2l^{2}}{3}\frac{\phi _{m}^{2}\left( \tau \right) }{W\left( \tau \right) } \nonumber \\= & {} -\frac{2l^{2}}{3}\frac{6\left( M\left( \tau \right) -C\right) }{Al}\sqrt{ \frac{\left( M\left( \tau \right) -C\right) }{Bl^{3}}} \nonumber \\= & {} -\frac{4}{A\sqrt{Bl}}\left( M\left( \tau \right) -C\right) ^{\frac{3}{2}} \end{aligned}$$

(6.6)

where

$$\begin{aligned} \int \limits _{-\infty }^{\infty }\sec h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \tan h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) d\zeta =\frac{2}{3 }W\left( \tau \right) \end{aligned}$$

and

$$\begin{aligned} \int \limits _{-\infty }^{\infty }\sec h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) d\zeta =2W\left( \tau \right) \end{aligned}$$

Again

$$\begin{aligned} \frac{\partial \phi _{1}}{\partial \chi }= & {} -\frac{m\phi _{m}\left( \tau \right) }{W\left( \tau \right) }\sec h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \tan h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \\ \frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}= & {} \frac{m^{2}\phi _{m}\left( \tau \right) }{W^{2}\left( \tau \right) }\left\{ \sec h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \tan h^{2}\left( \frac{ \zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) -\sec h^{3}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) } \right) \right\} \\ \int \frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}d\xi= & {} \frac{ m^{2}\phi _{m}\left( \tau \right) }{W^{2}\left( \tau \right) }\int \left\{ \sec h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) } \right) \tan h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) -\sec h^{3}\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \right\} d\xi \\= & {} \frac{m^{2}\phi _{m}\left( \tau \right) }{lW\left( \tau \right) }\left\{ -\sec h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) } \right) \tan h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) +F\left( \chi ,\tau \right) \right\} \end{aligned}$$

Therefore

$$\begin{aligned} \int \limits _{-\infty }^{\infty }\phi _{1}\left( \int \frac{\partial ^{2}\phi _{1}}{\partial \chi ^{2}}d\xi \right) d\zeta= & {} \frac{m^{2}\phi _{m}^{2}\left( \tau \right) }{lW\left( \tau \right) }\int \limits _{-\infty }^{\infty }\left\{ -\sec h^{2}\left( \frac{\zeta -M\left( \tau \right) \tau }{ W\left( \tau \right) }\right) \tan h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) \right. \nonumber \\&\left. +F\left( \chi ,\tau \right) \sec h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) } \right) \right\} d\zeta \nonumber \\= & {} \frac{m^{2}\phi _{m}^{2}\left( \tau \right) }{lW\left( \tau \right) } F\left( \chi ,\tau \right) \int \limits _{-\infty }^{\infty }\sec h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) d\zeta \nonumber \\= & {} \frac{\pi m^{2}\phi _{m}^{2}\left( \tau \right) }{l}F\left( \chi ,\tau \right) \end{aligned}$$

(6.7)

where

$$\begin{aligned} \int \limits _{-\infty }^{\infty }\sec h\left( \frac{\zeta -M\left( \tau \right) \tau }{W\left( \tau \right) }\right) d\zeta =\pi W\left( \tau \right) \end{aligned}$$

Using (6.6) and (6.7), we have from (6.5)

$$\begin{aligned} \frac{dI}{d\tau }+2DI=\frac{8E}{A\sqrt{Bl}}\left( M\left( \tau \right) -C\right) ^{\frac{3}{2}}-\frac{2C\pi m^{2}}{l}\phi _{m}^{2}( \tau )F( \chi ,\tau ) \end{aligned}$$

Combining the equations (3.35) and (3.36) we finally get

$$\begin{aligned} \frac{6\sqrt{Bl}}{A}\left( M\left( \tau \right) -C\right) ^{-\frac{1}{2}} \frac{dM\left( \tau \right) }{d\tau }+2D\frac{12\sqrt{Bl}}{A}\left( M\left( \tau \right) -C\right) ^{\frac{1}{2}}= & {} \frac{8E}{A\sqrt{Bl}}\left( M\left( \tau \right) -C\right) ^{\frac{3}{2}}\nonumber \\ \text {or,}\,\,\frac{dM\left( \tau \right) }{d\tau }+4D\left( M\left( \tau \right) -C\right)= & {} \frac{4E}{3Bl}\left( M\left( \tau \right) -C\right) ^{2}\nonumber \\ \text {i.e.,}\,\,\frac{d\left( M\left( \tau \right) -C\right) }{d\tau }+4D\left( M\left( \tau \right) -C\right)= & {} \frac{4E}{3Bl}\left( M\left( \tau \right) -C\right) ^{2} \end{aligned}$$

(6.8)