1 Introduction

Boundary layer flow due to a stretchable surface is essential as it is beneficial in many application and engineering processes, i.e. extrusion produced materials, melt-spinning, wire drawing, manufacture of plastics, hot rolling, production of glass fibre, extrusion process, in production of polymer sheets and the association of biological fluids. BL flow in two dimensions for a viscous, laminar, as well as incompressible fluid due to a stretchable flat plate was first studied by Crane [1]. The liquid flowed at a speed that was proportional to a distance from a fixed point. Parhi and Nath [2] discussed the stability of BL flow of viscous liquid past a stretching plate. Kumaran et al. [3] examined the transition consequence of the magnetic field on the flow of VF due to a stretched wall. Yirga and Tesfay [4] numerically inspected the magnetohydrodynamic (MHD) flow of VF over an expanded wall. Hassan [5] applied the Lie group method to analyse the heat transfer on VF influenced by the magnetic field over an expanding surface. Sheikh and Abbas [6] looked into the consequence of thermophoresis on MHD flow of Newtonian liquid having chemically reactive species with heat transmission over an oscillatory stretched wall. Sigh et al. [7] explored the effects of nonlinear MHD on the flow of viscous fluid over a porous stretchable sheet with mass transpiration. Reddy and Reddy [8] dealt with heat and mass characteristics on BL flow of a VF because of an exponential inclined stretching sheet. On the other hand, Wang [9] first studied the problem in the reverse case, i.e. the flow caused by the shrinking sheet. In this article, he discussed the flow of a fluid over a shrinking sheet near stagnant point where the speed of a fluid is zero. Lok et al. [10] considered stagnant point flow of a Newtonian fluid past a contracting/expanding sheet and also discussed the existence and multiplicity of solutions of the flow. Rosila and Ishak [11] performed an analysis for SP flow in the presence of porous media past a SS sheet and obtained numerical results. By applying partial velocity slip and Joule heating, Yasin et al. [12] considered the VF flow in the vicinity of stagnant point. Nasir et al. [13] numerically examined the viscous liquid flow near SP past a quadratically SS plate. By considering viscous dissipation along with magnetic field effects, Alarifi et al. [14] studied the flow of VF past a vertical stretching sheet near SP.

Effects of thermal radiation (TR) on heat and mass transfer fluid have many significant practical applications, for example in solar power technology, electric power generator, space vehicle re-entry, radioactive waste disposal, chemical pollutants dispersal by water-saturated soil and much more. Many authors studied linear and nonlinear heat radiation effects. By using linear Rosseland approximation (RA), Magyari and Pantokratoras [15] studied heat transfer features of different BL flows. Later, Pantokratoras [16] investigated the flow along the vertical plate by considering both linear and nonlinear RA. Laxmi and Shanker [17] considered the VF flow caused by a stretching sheet with nonlinear TR and suction/injection. The effects of thermal radiation on Carreau-Yasuda nanofluid in the presence of chemical reactions were discussed by Waqas et al. [18], and it was observed that thermal radiation raises Carreau-Yasuda nanofluid temperature. Raiz et al. [19] studied the heat transfer through the rectangular channel of the Eyring–Powell fluid flow. Hashim et al. [20] presented the numerical investigation of non-Newtonian fluid flow with nonlinear TR and nanoparticles. Pattnaik et al. [21] conducted a heat transfer study of nanofluid flow and found that when nanofluid was considered, there was a rapid decline in the temperature profile. Zhang et al. [22] looked at the influence of heat transfer with generalized magnetic Reynold number on the 3D nanofluid flow and observed that with the increase in the squeeze Reynolds number, temperature drops significantly.

Chemical reactions may be categorized as heterogeneous or homogeneous. This classification is based upon the occurrence of reactions whether the reactions happen at a single-phase volume reaction or they happen at a boundary. Food processing, development and diffusion of fog, design of chemical managing equipment, moisture above agricultural fields and fruit tree groves are some areas of concern where joined mass and heat transfer occurs with a chemical reaction. Various chemical reacting structures possess both heterogeneous as well as homogeneous reactions. The interaction between both reactions happening on some catalytic surfaces is exceptionally complicated, which could be integrated at different rates in the manufacturing as well as usage of reactant species either inside the fluid or on catalytic surfaces. Chaudhary and Merkin [23, 24] originally formulated a basic HH reactions model in the BL flow near SP. The case of unequal diffusivities of homogeneous-heterogeneous reactions in viscoelastic fluid flow with magnetic field and nonlinear thermal radiation was studied by Animasaun et al. [25] and reached to the result that the change due to \( \delta \) in concentration profile is more noticeable for concentration of specie B relative to the specie A. Sheikh and Abbas [26] considered SP flow of non-Newtonian fluid with HH reactions along with slip effects. Alghamdi [27] explores the viscoelastic fluid flow with HH reactions exposed to the magnetic field.

The majority of flow and thermal transport phenomena are fundamentally nonlinear, so they are expressed by nonlinear equations. Accurate closed-form solutions to nonlinear problems are far more challenging to achieve than numerical ones. Researchers use several closed-form schemes and numerical schemes to figure out the solution to the problems of the fluid flow under consideration. See references [28,29,30,31,32,33] for information.

Furthermore, in hydrometallurgical industries and chemical technologies such as polymer manufacturing and food processing, the chemical reaction effects on heat and mass transfer with radiation through porous media are of significant importance. See references. [34,35,36,37,38,39,40,41,42,43]

A porous medium means a material composed of a solid matrix with interconnected empty spaces. These interlinked spaces permit the flow of at least one fluid through the material. Composite materials, metallic foams with high porosity and ceramics are some common examples of porous media. Due to its natural occurrence and relevance in many engineering problems such as porous rollers, porous bearings, porous layer insulation consisting of solids and pores, and in biomathematics, especially in the study of blood flow in arteries and lungs, etc., considerable interest has been shown in the study of flow past a porous medium. Role of radiative heat transmission is superficial in many engineering processes which occur at high temperatures such as in photochemical reactors, turbid water bodies, fluidized bed heat exchangers, nuclear power plants and the various propulsion devices. It is worth noting in all the above literature that little attention has been paid to investigate the movement of a viscous fluid with unequal diffusivities of chemical reactions. So, the purpose of the present study is to examine the behaviour of BL flow of VF containing two chemically reactive species through porous media. This study also includes the effects of nonlinear TR, and here diffusion coefficients of both auto-catalyst and reactant are assumed to be unequal.

2 Governing Equation

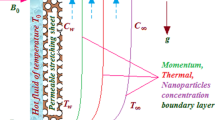
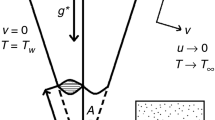
On a stretchable surface near a SP, a steady BL flow is considered in the presence of porous medium and TR. Additionally, the sheet’s temperature along with the temperature at free stream are assumed as \( \theta_{w} \) and \( \theta_{\infty}, \) respectively, with \( \theta_{w} > \theta_{\infty} \). A basic HH reactions model is also taken, which links the species \( C \) and \( D \) in a BL flow as described by [23] and [24]:

$$ C + 2D \to 3D,{\text{rate}} = k_{e} cd^{2} , $$
(1)
$$ C \to D,{\text{rate}} = k_{s} c, $$
(2)

Furthermore, both reactive processes are supposed to be isothermal and a homogeneous concentration \( c_{0} \) of reactant \( C \) is in the free stream and no auto-catalyst \( D \) is present.

The governing equations of the present flow situation, in the light of above presumptions and BL approximations, are given below [11, 25]

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 , $$
(3)
$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = - \frac{1}{\rho }\frac{\partial p}{\partial x} + \upsilon \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{\upsilon }{\varsigma }u, $$
(4)
$$ u\frac{\partial \theta }{\partial x} + v\frac{\partial \theta }{\partial y} = \frac{k}{{\rho C_{p} }}\frac{{\partial^{2} \theta }}{{\partial y^{2} }} - \frac{1}{{\rho C_{p} }}\frac{{\partial q_{r} }}{\partial y}, $$
(5)
$$ u\frac{\partial c}{\partial x} + v\frac{\partial c}{\partial y} = D_{C}^{*} \frac{{\partial^{2} c}}{{\partial y^{2} }} - k_{e} cd^{2} , $$
(6)
$$ u\frac{\partial d}{\partial x} + v\frac{\partial d}{\partial y} = D_{D}^{*} \frac{{\partial^{2} d}}{{\partial y^{2} }} + k_{e} cd^{2} . $$
(7)

The constraints at the surface of the sheet and away from it in the free stream are specified by (Fig. 1)

$$ u = u_{w} (x) = U_{w} x,v = 0,\theta = \theta_{w} ,D_{C}^{*} \frac{\partial \,c}{\partial y} = k_{s} c,D_{D}^{*} \frac{\partial d}{\partial y} = - k_{s} c\,{\text{at }}y = 0, $$
(8)
$$ u = u_{{\tilde{e}}} (x) = U_{\infty} x,\theta = \theta_{\infty} ,c \to c_{0} ,d \to 0\,{\text{as }}y \to \infty . $$
(9)

Using the condition \( u = u_{{\tilde{e}}} (x) \to U_{\infty } x\,\,\,\,\,\,\,{\text{as}}\,\,\,\,\,\,\,y \to \infty \) in Eq. (4) gives

$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = U_{\infty } \frac{{du_{\infty } }}{dx} + \upsilon \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\upsilon }{\varsigma }U_{\infty } x - \frac{\upsilon }{\varsigma }u. $$
(10)

or

$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = U_{\infty } \frac{{du_{\infty } }}{dx} + \upsilon \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\upsilon }{\varsigma }(U_{\infty } x - u). $$
(11)

With the help of RA [15], the heat flux due to radiation is given as

$$ q_{r} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial \theta^{4} }}{\partial y}, $$
(12)

Utilizing Eq. (12), Eq. (5) transforms into the form:

$$ u\frac{\partial \theta }{\partial x} + v\frac{\partial \theta }{\partial y} = \left( {\frac{k}{{\rho C_{p} }} + \frac{{16\sigma^{*} \theta_{\infty}^{3} }}{{3\rho C_{p} k^{*} }}} \right)\frac{{\partial^{2} \theta }}{{\partial y^{2} }}. $$
(13)

For the above equation, the temperature difference is supposed to be low sufficiently within the flow which leads to the linearization of \( \theta^{4} \) as

$$ \theta^{4} \cong 4\theta_{\infty}^{3} \theta - 3\theta_{\infty}^{4} $$

via Taylors series about \( \theta_{\infty} \) and neglecting higher terms. Equation (13) represents the flow equation of temperature with linear TR. But the present problem aims to explore the influence of nonlinear TR on the flow, so neglecting the above supposition, i.e. replacement of \( \theta_{\infty}^{3} \) with \( \theta^{3} \) in Eq. (12) and then putting it in Eq. (5) gives [34, 44].

$$ u\frac{\partial \theta }{\partial x} + v\frac{\partial \theta }{\partial y} = \frac{k}{{\rho C_{p} }}\frac{\partial }{\partial y}\left( {\left( {1 + \frac{{16\sigma^{*} \theta^{3} }}{{3kk^{*} }}} \right)\frac{\partial \theta }{\partial y}} \right). $$
(14)

Now, introducing the similarity transformations and non-dimensional temperature and concentrations.

$$ \psi = \left( {U_{\infty } \upsilon } \right)^{{\frac{1}{2}}} xf\left( \eta \right),\varTheta(\eta) = \frac{{\theta - \theta_{\infty} }}{{\theta_{w} - \theta_{\infty} }},\phi_{1}(\eta) = \frac{c}{{c_{o} }},\phi_{2}(\eta) = \frac{d}{{c_{o} }},\eta = \left( {\frac{{U_{\infty } }}{\upsilon }} \right)^{{\frac{1}{2}}} y $$
(15)

The following normalized form of Eqs. (11), (14), (6) and (7) is achieved after using Eq. (15):

$$ f^{\prime \prime \prime } - f^{{^{\prime } 2}} + ff^{\prime \prime } + 1 + \beta (1 - f^{\prime } ) = 0, $$
(16)
$$ \left( {\left( {1 + Rd\left( {1 + \left( {\varTheta_{w} - 1} \right)\varTheta } \right)^{3} } \right)\varTheta^{\prime}} \right)^{\prime } + \Pr f\,\varTheta^{\prime} = 0, $$
(17)
$$ \frac{1}{{Sc_{C} }}\phi_{1}^{\prime \prime } + f\phi_{1}^{\prime } - K\phi_{1} \phi_{2}^{2} = 0, $$
(18)
$$ \frac{\delta }{{Sc_{D} }}\phi_{2}^{\prime \prime } + f\,\phi_{2}^{\prime } + K\phi_{1} \phi_{2}^{2} = 0. $$
(19)

Here \( \beta = \frac{\upsilon }{{\varsigma U_{\infty } }}, \) \( \varTheta_{w} = \frac{{\theta_{w} }}{{\theta_{\infty} }},\) \( Rd = \frac{16\sigma *}{{3kk^{*} }}, \) \( Sc_{C} = \frac{\upsilon }{{D_{C}^{*} }}, \) \( Sc_{D} = \frac{\upsilon }{{D_{D}^{*} }}, \)\( K = \frac{{k_{e} c_{0}^{2} }}{{U_{\infty } }} \) and \( \Pr = \frac{\upsilon }{\alpha } \).

The surface constraints (8) and (9) become

$$ \begin{aligned} & f\left( 0 \right) = 0,f^{\prime}\left( 0 \right) = \lambda ,\varTheta \left( 0 \right) = 1, \\ & \phi_{1}^{\prime } \left( 0 \right) = K_{s} \phi_{1} \left( 0 \right),\delta \phi_{2}^{\prime } \left( 0 \right) = - K_{s} \phi_{1} \left( 0 \right), \\ \end{aligned} $$
(20)
$$ \left. \begin{aligned} & f^{\prime}\left( \eta \right) = 1,\varTheta(\eta) \to 0, \\ & \phi_{1}(\eta) \to 1,\phi_{2}(\eta) \to 0 \\ \end{aligned} \right\}{\text{ as }}\eta \to \infty . $$
(21)

Here \( \lambda = \frac{{U_{w} }}{{U_{\infty } }},K_{s} = \frac{{k_{s} }}{{\text{Re}^{1/2} D_{C}^{*} }},\delta = \frac{{D_{D}^{*} }}{{D_{C}^{*} }}. \)

3 Numerical Solution

Shooting technique with the aid of Runge–Kutta algorithm is adopted to solve the two-point boundary value problem generated by nonlinear ordinary DEs (16)–(19) along with surface constraints (20)–(21). First, the problem is transformed into an initial value problem (IVP) as

$$ \left. \begin{aligned} & f^{\prime} = \xi_{1} , \\ & f^{\prime\prime} = \xi_{2} , \\ & \xi_{2}^{\prime } = \xi_{1}^{2} - f\xi_{2} - 1 - \beta \left( {1 - \xi_{1} } \right). \\ \end{aligned} \right\} $$
(22)
$$ \left. \begin{aligned} & \varTheta = \zeta_{1} , \\ & \zeta_{1}^{\prime } = \zeta_{2} , \\ & \zeta_{2}^{\prime } = \frac{{\Pr f\zeta_{2} - 3Rd\left( {\varTheta_{w} - 1} \right)\zeta_{2}^{2} \left( {1 + \left( {\varTheta_{w} - 1} \right)\zeta_{1} } \right)^{2} }}{{1 + Rd\left( {1 + \left( {\varTheta_{w} - 1} \right)\zeta_{1} } \right)}}. \\ \end{aligned} \right\} $$
(23)
$$ \left. \begin{aligned} & \phi_{1} = \varPsi_{1} , \\ & \varPsi_{1}^{\prime } = \varPsi_{2} , \\ & \varPsi_{2}^{\prime } = Sc_{C} \left( {K\varPsi_{1} \varPhi_{1}^{2} - f\varPsi_{1} } \right). \\ \end{aligned} \right\} $$
(24)

and

$$ \left. \begin{aligned} & \phi_{2} = \varPhi_{1} , \\ & \varPhi_{1}^{\prime } = \varPhi_{2} , \\ & \varPhi_{2}^{\prime } = \frac{{Sc_{D} }}{\delta }\left( { - K\varPsi_{1} \varPhi_{1}^{2} - f\varPhi_{2} } \right), \\ \end{aligned} \right\} $$
(25)

with the constraints

$$ f\left( 0 \right) = 0,\,\,\,\,\zeta_{1} \left( 0 \right) = \lambda ,\,\,\,\,\varPsi_{1} \left( 0 \right) = \left( {1/K_{s} } \right)\varPsi_{2} \left( 0 \right),\,\,\,\varPhi_{2} \left( 0 \right) = - \left( {K_{s} /\delta } \right)\varPsi_{1} \left( 0 \right). $$
(26)

The appropriate value of the finite value of \( \eta \to \infty \) say \( \eta_{\infty } \) has a vital role in this method. To solve Eqs. (22)–(25) subject to conditions (26) as an IVP, values for \( \xi_{2} \left( 0 \right){\text{ i}} . {\text{e}} . { }f^{\prime\prime}\left( 0 \right), \) \( \zeta_{2} \left( 0 \right)\,\,{\text{i}} . {\text{e}} .\,\,\theta^{\prime}\left( 0 \right)\,,\,\,\varPsi_{2} \left( 0 \right)\,\,{\text{i}} . {\text{e}} .\,\,\phi_{1}^{\prime } \left( 0 \right)\,\,{\text{and }}\varPhi_{1} \left( 0 \right)\,\,{\text{i}} . {\text{e}} .\,\,\phi_{2} \left( 0 \right) \) are required, but the problem does not have such values. After selecting the initial guesses for \( \xi_{2} \left( 0 \right),\,\,\zeta_{2} \left( 0 \right)\,,\,\varPsi_{2} \left( 0 \right), \) \( \varPhi_{1} \left( 0 \right) \) and employing the Runge–Kutta method, the solution is obtained. The better approximation of the solution is achieved by adjusting the values for \( \xi_{2} \left( 0 \right),\,\,\zeta_{2} \left( 0 \right)\,,\,\varPsi_{2} \left( 0 \right) \) and \( \varPhi_{1} \left( 0 \right). \) For this, Newton’s approach has been used.

Fig. 1
figure 1

Schematic of the problem

Full size image

4 Results and Discussion

A numerical technique, namely shooting procedure, is opted to find the solution of the flow equations for the flow near SP in the presence of generalized TR and porous zone. The unequal diffusivities of two reactive species are also considered for the concentration profile. Graphs are presented to examine the response of velocity \( f^{\prime}\left( \eta \right), \) temperature \( \varTheta(\eta), \) and concentrations \( \phi_{1}(\eta),\phi_{2}(\eta) \) to the change in the governing parameters, i.e. \( \lambda ,\,\,\beta ,\,\,Rd,\,\Pr ,\,\,\varTheta_{w} , \)\( \,\delta ,\,\,K_{s} ,\,K,\,\,Sc_{c} \) and \( Sc_{D} \) arising in the flow equations.

Figure 2 shows the deviation in \( f^{\prime}\left( \eta \right) \) for various values of the SS parameter \( \lambda . \) \( \lambda < 0 \) means the shrinking of the surface, \( \lambda = 0 \) symbolizes the static surface while \( \lambda > 0 \) stands for stretching of the surface. From figure, it can be viewed that \( f^{\prime}\left( \eta \right) \) increases with an increase in \( \lambda . \) However, the BL thickness for the shrinking surface is more significant than static and stretched surfaces. Figure 3 is graphed to show the behavioural change in \( f^{\prime}\left( \eta \right) \) with an increment in \( \beta \) when the flow is over a shrinking wall. A decrease in the BL region is observed with a rise in the permeability of the porous zone. This reduction is related to Darcy’s resistance which enhances with the increase in \( \beta . \)

Fig. 2
figure 2

Variation in \( f^{\prime}(\eta ) \) with \( \lambda \) when \( \beta = 0.06,\Pr = 0.72,\varTheta_{w} = 1.01,Rd = 1,Sc_{C} = Sc_{D} = 0.8, \) \( \delta = 1.2,K = 1\,{\text{and }}K_{s} = 1 \)

Full size image
Fig. 3
figure 3

Variation in \( f^{\prime}(\eta ) \) with \( \beta \) when \( \lambda = - 1,\Pr = 0.72,\varTheta_{w} = 1.01,Rd = 1,Sc_{C} = Sc_{D} = 0.8, \) \( \delta = 1.2,K = 1\,{\text{and }}K_{s} = 1 \)

Full size image

Figures 4, 5, 6, and 7 are plotted to present the influence of evolving parameters on the temperature profile \( \varTheta(\eta) \). Figure 4 illustrates the effects of \( \beta \) on \( \varTheta(\eta) \) over a shrinking wall. It can be seen that \( \varTheta(\eta) \) as well as thermal BL is a decreasing function of \( \beta . \) Fig. 5 depicts the change in \( \varTheta(\eta) \) with an increase in \( \varTheta_{w} . \) It can be noticed that both thermal BL and \( \varTheta(\eta) \) enhance with a raise in \( \theta_{w} . \) The change in \( \varTheta(\eta) \) with the increasing values of \( Rd \) can be observed from Fig. 6 which depicts a rise in both \( \varTheta(\eta) \) and its BL region with raise in \( Rd. \) The decreasing effect of \( \Pr \) on \( \varTheta(\eta) \) can be noticed in Fig. 7. The decrease in thermal BL is also seen in this Figure.

Fig. 4
figure 4

Variation in \( \varTheta(\eta) \) with \( \beta \) when \( \lambda = - 1,\Pr = 1.5,\varTheta_{w} = 1.01,Rd = 1,Sc_{C} = Sc_{D} = 0.8, \) \( \delta = 1.2,K = 1\,{\text{and }}K_{s} = 1 \)

Full size image
Fig. 5
figure 5

Variation in \( \varTheta(\eta) \) with \( \varTheta_{w} \) when \( \lambda = - 1,\beta = 1,\Pr = 0.72,Rd = 1,Sc_{C} = Sc_{D} = 0.8, \)\( \delta = 1.2,K = 1\,{\text{and }}K_{s} = 1 \)

Full size image
Fig. 6
figure 6

Variation in \( \varTheta(\eta) \) with \( Rd \) when \( \lambda = - 1,\beta = 1,\Pr = 0.72,\varTheta_{w} = 1.01,Sc_{C} = Sc_{D} = 0.8, \) \( \delta = 1.2,K = 1\,{\text{and }}K_{s} = 1 \)

Full size image
Fig. 7
figure 7

Variation in \( \varTheta(\eta) \) with \( \Pr \) when \( \lambda = - 1,\,\beta = 1,\,Rd = 1,\,\,\varTheta_{w} = 1.01,\,Sc_{C} = Sc_{D} = 0.8, \) \( \delta = 1.2,K = 1\,{\text{and }}K_{s} = 1 \)

Full size image

The impacts of ruling parameters on the concentration profiles \( \phi_{1}(\eta), \phi_{2}(\eta) \) are shown in Figs. 8, 9, 10, 11, 12. Figure 8 presents the change in the behaviour of \( \phi_{1}(\eta), \phi_{2}(\eta) \) with an increment in \( \beta . \) A decrement in the regions of BL for both \( \phi_{1}(\eta) \) and \( \phi_{2}(\eta) \) is observed from this Figure with an increase in \( \beta \) due to porosity resistance. However, \( \phi_{1}(\eta) \) is showing an increment and \( \phi_{2}(\eta) \) is decreasing with a rise in \( \beta\). The response of \( \phi_{1}(\eta)\), \(\phi_{2}(\eta) \) with a hike in the values of \( K_{s} \) is portrayed in Fig. 9. The effect of \( K_{s} \) on concentration BL is reverse of \( \beta \), i.e. for both \( \phi_{1}(\eta) \) and \( \phi_{2}(\eta) \) BL increases with a raise in \( K_{s}\). Figure also shows a reduction and an increment in \( \phi_{1}(\eta) \) and \( \phi_{2}(\eta), \) respectively. The varying behaviour of \( \phi_{1}(\eta) \), \(\phi_{2}(\eta) \) with change in \( \delta \) is graphed in Fig. 10. The response of \( \phi_{1}(\eta) \) and \( \phi_{2}(\eta) \) to the increase in \( \delta \) is similar to that of \( \beta . \) However, the variance in \( \phi_{2}(\eta) \) is greater relative to \( \phi_{1}(\eta). \) Due to the rate of diffusion coefficient \( \delta \), the shift in the concentration profile is more notable in the concentration of species D relative to species C. A contraction in the BL region of both \( \phi_{1}(\eta) \) and \( \phi_{2}(\eta) \) with the increasing values of \( Sc_{C} \) and \( Sc_{D} \) is observed and can be seen in Fig. 11. The change \( Sc_{C} \) leads to an increase in \( \phi_{1}(\eta) \) while the rise in \( Sc_{D} \) reduces \( \phi_{2}(\eta). \) As a consequence of increasing Schmidt number, the mass diffusivity of the species decreases, thereby reducing the concentration BL thickness for both \( Sc_{C} \) and \( Sc_{D} \). Figure 12 shows that the variation in both \( \phi_{1}(\eta) \) and \( \phi_{2}(\eta) \) for distinct values of K. The change in the BL region for \( K \) has similar behaviour to that \( {K_{s}},\) i.e. the thickness region of concentration boundary layer increases when \( K \) and \( K_{s} \) are increased, and it is because of reactants of different reactions of species. However, \( \phi_{1}(\eta) \) reduces for larger values of \( K \) and the curve takes a S shape as \( K \) increases. An opposite trend is noticed for \( \phi_{2}(\eta). \)

Fig. 8
figure 8

Variation in \( \phi_{1}(\eta),\phi_{2}(\eta) \) with \( \beta \) when \( \,\lambda = - 1,\,\,\,\Pr = 0.72,\,\varTheta_{w} = 1.01,\,Rd = 1,\,\delta = 1.1, \)\( Sc_{C} = Sc_{D} = 0.6,K = 0.9\,{\text{and }}K_{s} = 0.9 \)

Full size image
Fig. 9
figure 9

Variation in \( \phi_{1}(\eta),\phi_{2}(\eta) \) with \( K_{s} \) when \( \lambda = - 1,\Pr = 0.72,\varTheta_{w} = 1.01,Rd = 1,\delta = 1.2, \)\( Sc_{C} = Sc_{D} = 0.8,K = 1\,{\text{and }}\beta = 1 \)

Full size image
Fig. 10
figure 10

Variation in \( \phi_{1}(\eta),\phi_{2}(\eta) \) with \( \delta \) when \( \lambda = - 1,\Pr = 0.72,\varTheta_{w} = 1.01,Rd = 1,\beta = 1, \)\( Sc_{C} = Sc_{D} = 0.8,K = 1\,{\text{and }}K_{s} = 1 \)

Full size image
Fig. 11
figure 11

Variation in \( \phi_{1}(\eta),\phi_{2}(\eta) \) with \( Sc_{C} \,{\text{and}}\,Sc_{D} \) when \( \lambda = - 1,\Pr = 0.72,\varTheta_{w} = 1.01,Rd = 1, \)\( \beta = 1,\delta = 1.2,K = 1\,{\text{and }}K_{s} = 1 \)

Full size image
Fig. 12
figure 12

Variation in \( \phi_{1}(\eta),\phi_{2}(\eta) \) with \( K \) when \( \lambda = - 1,\Pr = 0.72,\varTheta_{w} = 1.01,Rd = 1,\beta = 1, \)\( Sc_{C} = Sc_{D} = 0.8,\delta = 1.2\,{\text{and }}K_{s} = 1 \)

Full size image

The comparison of the numerical values of \( f^{\prime\prime}\left( 0 \right) \) with the findings stated by Shaw et al. [45] for the different values of \( \lambda \) are shown in Table 1 and 2 and found in excellent accordance. For \( \lambda > 0 \) (stretching sheet), a solution for all values of \( \lambda \) can be accomplished whereas the solution for \( \lambda < 0 \)(shrinking sheet) occurs only in the region \( \lambda \ge \lambda_{c} = - 1.2465, \) here \( \lambda_{c} \) denotes the critical value of \( \lambda \) so that for \( \lambda < \lambda_{c} \) no solution exist. However, for \( \lambda_{c} < \lambda < - 1, \) the solution is not unique, so there exist two solutions \( f_{1}(\eta)\,{\text{and}}\,f_{2}(\eta). \) One can see from the literature that the first solution is stable and technically feasible, although the second solution is not.

Table 1 Comparison of\( f^{\prime\prime}\left( 0 \right) \) for a stretching sheet obtained for different values of \( \lambda , \) for fixed values of \( \beta = 1 \)
Full size table
Table 2 Comparison of\( f^{\prime\prime}\left( 0 \right) \) for a shrinking sheet obtained for different values of \( \lambda , \) for fixed values of \( \beta = 1 \)
Full size table

5 Concluding Remarks

The impact of HH reactions on steady BL flow due to the SS surface close to the SP through a porous medium in the presence of nonlinear TR is investigated. By using the shooting method, a numerical solution is obtained. The following remarks have been made:

  • Porous media acts as a source of resistance in a flow; therefore, an increase in permeability parameter \( \beta \) causes a decrement in velocity, temperature and concentration BL thickness.

  • Prandtl number decreases the temperature BL thickness because the increment in Prandtl number \( \Pr \) causes decrement in the thermal diffusivity while BL thickness increases with \( Rd. \)

  • When the magnitude of \( \varTheta_{w} \) is small, the decrease in temperature distribution from the wall to the free stream is marginal compared to the maximum decreasing trend when the magnitude of \( \varTheta_{w} \) is high.

  • As a result of rising values of Schmidt number, the mass diffusivity of the species decreases consequently both \( Sc_{C} {\text{ and }}Sc_{D} \) reduce the concentration BL thickness.

  • The increase in the magnitude of the ratio of diffusion coefficient is just a growing function of the catalyst concentration within the realm of fluid

  • Both homogeneous and heterogeneous intensities increase concentration BL thickness.

  • The results will be used in studies related to food processing, fog production and diffusion, highly acidic water bodies, chemical management equipment design, photocatalytic reactors, moisture over agricultural areas and fruit tree meadows, highly acidic water bodies, heat exchangers for fluidized beds.