Framing the Activation Energy and Binary Chemical Reaction on CNT’s with Cattaneo–Christov Heat Diffusion on Maxwell Nanofluid in the Presence of Nonlinear Thermal Radiation

Abstract

A theoretical model is drafted to inspect the hydromagnetic flow of carbon nanotubes (CNT’s) suspended in a Maxwell nanofluid by means of activation energy with binary chemical reaction over a stretching sheet. Modified Arrhenius function is measured instead of the energy activation. Heat transport phenomena are explored in energy expression through a nonlinear thermal radiation and viscous dissipation, which is incorporated with a novel theory specifically Cattaneo–Christov model of heat diffusion—a sophisticated form of Fourier’s heat flux formula. The flow analysis is reported in attendance of convective slip and suction. Two different kinds of CNT’s (i.e. single and multiple walls) are consistently dispersed in the base fluid (engine oil) to illustrate the fine points of the flow. The governing system of mathematical expressions for the locally similar flow is tackled numerically by Runge–Kutta-based MATLAB bvp4c package. The procured solutions are drawn for different values of pertinent parameters of interest. The temperature of the fluid escalates with the nonlinear thermal radiation. Activation energy boosts up the concentration, and a negative trend is observed for rate of chemical reaction.

1 Introduction

Heat transfer in physical systems is nothing but transportation of thermal energy. It has bountiful applications in engineering and modern industrial process which incorporates heat conduction in tissues, cooling towers, fuel cell efficiency, and food technology, cooling of electronic devices, drug targeting and many more. 200 years ago, Fourier et al. [1] proposed a best model in heat conduction and became a yardstick to investigate the heat transport features in various practical situations, but it has an undesirable aspect, i.e. the temperature gradient impacts the system and generates a parabolic energy equation in temperature field. To overcome this inconvenience of the law, this is indicated in the literature as “Paradox of heat conduction”. Cattaneo [2] recast the Fourier Law by affixing the thermal relaxation time which permits the heat move by the use of propagation of thermal waves with fixed speed. Later Christov [3] further tailored the Cattaneo model by replacing the ordinary derivative with Oldroyd’s upper-convected derivatives in order to achieve the material-invariant mode. This enhanced model is entitled as Cattaneo–Christov heat flux model (C-CHFM). Tibulle and Zampoli [4] discovered the exclusive results of C-CHFM for incompressible flow problems. Reddy and Suneetha [5] deliberated the C-CHFM impact in the Casson fluid flow over a moveable surface and disclosed the fluid temperature is inversely proportional to the thermal relaxation time. More recently, several sleuths [6,7,8,9,10,11] studied on different C-CHFM’s.

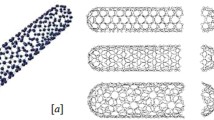
Nanotechnology is the most discussed topic of today’s epoch for its astonishing applications in innumerable engineering fields. One of the major segments of nanotechnology is nanofluid. Conductivity of the poor heat transfer liquids can be increased by hanging nanoparticles into various host fluids: water, oil, C₂H₆O₂, oxide ceramics (Al₂O₃, CuO), metals (Cu, Ag, Au), metal nitrides (AlN, SiN) and carbide ceramics (Sic, Tic) are some materials which are used for preparing nanoparticles. The term “nanofluid” was pioneered by Choi [12]. Carbon-based nanomaterials are of three types based on their shapes: tube (carbon nanotubes (CNTs)), horn (nanohorns) and spheres or ellipsoidal (fullerenes). CNTs are again of two types: single-walled CNT’s (SWCNT’s) and multi-walled CNT’s (MWCNT’s) depending on the number of concentric sheets of rolled graphene. This kind of particles has many applications in fields like medical (genomics, pharmacogenomics, drug delivery, optics, surgery, general medicine), agricultural (tissue engineering, prostheses), industrial (fabric sciences, energy) and environmental (physical sciences, health sciences), because of their massive absorption potential due to their altitude surface area was reported by Baughman et al. [13].

The thermal and chemical stability is more in MWCNT than SWCNT and can manufacture a huge production with low cost per unit. MCWNT’s has significant applications in electrostatic discharge protection in wafer processing and fabrication, plastic items for automobiles, the electrostatic spray painting for automobiles studied by Akbar et al. [14]. SWCNTs are specifically used in electronic displays, health care and composites. Maxwell was the first to disclose the conduction properties for a mixture of particles and a base medium. This model is one of the first models in nanofluids which forecast the thermal conductivity. According to Prabavathi et al. [15], the rates of heat transfer in MWCNT and SWCNT’s are inversely proportional.

Magneto hydrodynamics (MHD) is the investigation of the outcome of magnet over an electrically conducting liquid. It has massive application in earth magnetic field, cooling of fission reactors, in treatment of tumours, electrolytes, plasmas, solar wind, fusion, etc. Recently, Rizwan et al. [16, 17] considered magnetic effect on the boundary layer flow on a moveable sheet.

Electromagnetic radiation is the main cause for radiative heat transfer which depends on the components such as temperature, shape, behaviour of the surface material that emits or absorbs heat, but it does not require any medium to prorogation, while formulating a system in industry with fluid inside having minute temperature difference is troublesome. Due to this intricacy, the scientists added a spare parameter the nonlinear thermal radiation instead of thermal radiation. This additional parameter specifies the temperature differences within wall and moving fluid. At rising temperature variation, the radiation between two bodies is stronger. A brief literature survey on this subject, some of the articles are cited in Refs. [18,19,20,21,22].

Mechanochemistry, chemical engineering, oil colouring and processed food are some of the fields where mass transfer occurs that execute a chemical reaction with activation energy. Activation energy was first proposed by Svante Arrhenius in 1889. He describes it as the minimal energy to initiate the reaction. It is also being stated as the capacity to break bonds and is useful in the areas pertaining water emulsions, geothermal engineering and oil reservoir. Variations in concentration of species lead to mass transfer.

Mass transfer occurs due to difference in concentration of species in a mixture. Bestman [23] discloses the fluid flow with binary chemical reaction.

General form of Arrhenius equation is

$$K = B_{1} (T - T_{\infty } )^{m} {\text{e}}^{{\left( {\frac{{ - E_{a} }}{{k\left( {T - T_{\infty } } \right)}}} \right)}}$$

where K is the rate constant of chemical reaction, B₁ is the pre-factor (constant), E_a signifies the activation energy, fluid temperature (T), and k = 8.61 × 10 − 5 eV/K is the Boltzmann constant. In reality, when temperature increases recurrently the rate of reaction also increases.

A binary chemical reaction is a two-step reaction which is common in both (liquid and vapour) deposition processes. Varnish of metallic objects and glasses, production of electronic tools: diodes and transistors are some of the applications of chemical deposition discussed by Shafique et al. [24]. The activation energy plays a vital role in chemical reaction. In chemical deposition process, the reaction arising on the substrate surface was studied by Pedersen and Elliott [25]. Few current explorations on this topic are disclosed in Refs. [26, 27].

The above attentions evidently support that no effort has been done to reconnoitre the MHD Maxwell nanofluid flow with binary chemical reaction influenced by a stretching sheet. With these regards, an innovative mathematical formulation is being established by availing nano-carbon tubes for 2D flow of magnetic Maxwell fluid towards stretching sheet. Moreover, the nonlinear thermal radiation, viscous dissipation, activation energy, suction/injection and convective slip phenomena are also measured. Elucidations of Maxwell nanofluid are documented via Runge–Kutta-based MATLAB bvp4c package. This investigation extends the earlier explorations and is also useful for nanotubes studies.

2 Modelling and coordinate system

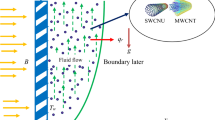
A steady two-dimensional heat and mass transfer flow with Arrhenius chemical reaction over a stretching sheet with carbon nanotubes is exposed in Fig. 1. Here, we consider engine oil as a host fluid and the carbon nanotubes are specifically: single- and multi-walled CNTs. Moreover, the impact of nonlinear thermal radiation with convective slip is also measured. The material properties of the base fluid (engine oil) and carbon nanotubes are unveiled in Table 1. In this study, Fourier’s law of conduction is restored by the C-CHFM. Here, sheet is stretched in x-axis direction which is normal to y-axis. Magnetic field B is applied perpendicular to the sheet. Reynolds number is measured as very small so the consequence of induced magnetic field is tiny. $U_{w} (x) = cx$ (where $c > 0$ is a constant) is the velocity of the stretching surface along x-axis. Based on these conventions, the governing flow of the boundary layer equations is stated as,

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

(1)

$$\begin{aligned} & u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + \lambda_{1} \left( {u^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} u}}{\partial x\partial y}} \right) \\ & \quad = \frac{1}{{\rho_{nf} }}\left( {\mu_{nf} \frac{{\partial^{2} u}}{{\partial y^{2} }} + \left( {\rho \beta } \right)_{f} g\left( {T - T_{\infty } } \right) - (\rho \beta^{*} )_{f} g(C - C_{\infty } ) - \sigma B^{2} \left( x \right)u} \right) \\ \end{aligned}$$

(2)

$$\left( {\rho C_{p} } \right)_{nf} \left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{y}} \right) = - \nabla \cdot q - \frac{1}{\upsilon }\frac{{\partial q_{r} }}{\partial y} + \mu \left( {\frac{\partial u}{\partial y}} \right)^{2}$$

(3)

$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D\frac{{\partial^{2} C}}{{\partial y^{2} }} - k_{r}^{2} \left( {\frac{T}{{T_{\infty } }}} \right)^{m} \left( {C - C_{\infty } } \right)e^{{ - \frac{{E_{a} }}{kT}}}$$

(4)

Fig. 1

Flow framework

Table 1 Thermo-physical characteristics of base fluids and CNTs [28]

In Eq. (4), the term $k_{r}^{2} \left( {\frac{T}{{T_{\infty } }}} \right)^{m} e^{{ - \frac{{E_{a} }}{kT}}}$ designates the modified Arrhenius equation, E_a represents the activation energy, k ² _r stands for the reaction rate, m be the fixed rate constants, $- 1 < m < 1$ and Boltzmann constant $k = 8.61 \times 10^{ - 5} \;{\text{eV/K}}$.

The Cattaneo–Christov heat flux (q) is expressed as

$$q + \lambda_{2} \left( {\frac{\partial q}{\partial t} + V \cdot \nabla q - q \cdot \nabla V + \left( {\nabla \cdot V} \right)q} \right) = - k_{f} \nabla \cdot T$$

(5)

$\lambda_{2}$ and V indicate relaxation time of heat flux and velocity vector, respectively; $k_{f}$ denotes the thermal conductivity of the primary fluid. For $\lambda_{2} = 0,$ Eq. (5) is converted to Fourier’s law Kundu et al. [28]. The fluid being incompressible, $\nabla .V = 0,$ and hence, Eq. (5) takes the form displayed below:

$$q + \lambda_{2} \left( {\frac{\partial q}{\partial t} + V \cdot \nabla q - q \cdot \nabla V} \right) = - k_{f} \nabla \cdot T$$

(6)

After eliminating q from Eqs. (3) and (6), the energy equation for steady flow is

$$\begin{aligned} & u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + \lambda_{2} \left( {\left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right)\frac{\partial T}{\partial x} + \left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right)\frac{\partial T}{\partial y} + \left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}} \right)^{2} } \right) \\ & = \quad \alpha_{nf} \frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{\upsilon }\frac{{\partial q_{r} }}{\partial y} + \frac{\upsilon }{{c_{p} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} \\ \end{aligned}$$

(7)

By the Rosseland approximation, the net radiation heat flux q_r [Wm⁻²] is symbolized by

$$q_{r} = - \left( {{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 {(3K*)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${(3K*)}$}}} \right){\text{grad}}(e_{b} )$$

(8)

where K* [m⁻¹] be the Rosseland mean spectral absorption coefficient, e_b [Wm⁻²] be the blackbody emission power, T be the absolute temperature, $e_{b} = \sigma^{ * } T^{4}$ be the Stefan–Boltzmann radiation law, and $\sigma^{ * } = \, 5.6697 \times 10^{ - 8} \;{\text{Wm}}^{ - 2} \;{\text{K}}^{ - 4}$ be the Stefan–Boltzmann constant.

The term $T^{4}$ can be defined as a linear function of temperature itself. Therefore, $T^{4}$ can be expanded as Taylor series in terms of $T_{\infty }$ and approximated after removing higher-order terms.

$$T^{4} = T_{\infty }^{4} \left\{ {1 + \left( {\theta_{w} - 1} \right)\theta } \right\}^{4}$$

(9)

where $\theta_{w} = \frac{{T_{w} }}{{T_{\infty } }},\quad \theta_{w} > 1$ is the wall temperature ratio parameter.

Maxwell, Jeffery, Davis, Hamilton and crosser model are some of the models that forecast the thermal conductivities of CNTs. Xue supposed that these models are specifically for spherical or elliptical particles with minor axial ratio. These models are not supported for the effect space distribution of CNT’s on thermal conductivity. So, he launched a model which is based on Maxwell theory concerning rotational elliptical nanotubes with major axial ratio and reimbursed the effect of the space distribution on CNT’s. In this paper, Xue model is used as follows:

$$\frac{{k_{nf} }}{{k_{f} }} = \frac{{1 - \chi + 2\chi \left( {\frac{{k_{\text{CNT}} }}{{k_{\text{CNT}} - k_{f} }}} \right)\ln \frac{{k_{\text{CNT}} + k_{f} }}{{2k_{f} }}}}{{1 - \chi + 2\chi \left( {\frac{{k_{f} }}{{k_{\text{CNT}} - k_{f} }}} \right)\ln \frac{{k_{\text{CNT}} + k_{f} }}{{2k_{f} }}}}$$

(10)

which are interpreted as:

$$\left. \begin{aligned} \upsilon_{nf} = \frac{{\mu_{nf} }}{{\rho_{nf} }},\quad \mu_{nf} = \frac{{\mu_{f} }}{{\left( {1 - \chi } \right)^{2.5} }},\quad \rho_{nf} = \left( {1 - \chi } \right)\rho_{f} + \chi \rho_{\text{CNT}} , \hfill \\ \alpha_{nf} = \frac{{k_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }},\quad \left( {\rho C_{p} } \right)_{nf} = \left( {1 - \chi } \right)\left( {\rho C_{p} } \right)_{f} + \chi \left( {\rho C_{p} } \right)_{\text{CNT}} \hfill \\ \end{aligned} \right\}$$

(11)

Subject to the boundary conditions:

$$\begin{aligned} u = U_{w} (x) + A\frac{\partial u}{\partial y},\quad \nu = - v_{w} ,\quad - k\frac{\partial T}{\partial y} = h_{f} (T_{w} - T),\quad C = C_{w} \quad {\text{at}}\quad y = 0 \hfill \\ u \to 0,T \to T_{\infty } ,C \to C_{\infty } \quad {\text{as}}\quad y \to \infty \hfill \\ \end{aligned}$$

(12)

Using the similarity transformations,

$$\begin{aligned} \eta = \sqrt {\frac{c}{v}} y,\quad \psi (x,y) = \sqrt {cv} xf(\eta ),\quad \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\quad \phi (\eta ) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }}, \hfill \\ u = cxf^{{\prime }} \left( \eta \right),\quad v = - \sqrt {cv} f\left( \eta \right) \hfill \\ \end{aligned}$$

(13)

Adopting Eqs. (10, 11, 13) in Eqs. (1, 2, 7, 4), we have

$$\begin{aligned} & f^{ - } + \left( {1 - \chi } \right)^{2.5} \left\{ {\left( {1 - \chi + \chi \frac{{\left( {\rho \beta } \right)_{CNT} }}{{\left( {\rho \beta } \right)_{f} }}} \right)\left( {\lambda \theta - Nr\phi } \right) - M^{2} f^{\prime } } \right\} \\ & \quad - \left( {1 - \chi } \right)^{2.5} \left( {1 - \chi + \chi \frac{{\rho_{CNT} }}{{\rho_{f} }}} \right)\left\{ {f^{\prime 2} - ff^{\prime \prime } + \alpha \left( {f^{2} f^{\prime } - 2ff^{\prime } f^{\prime \prime } } \right)} \right\} = 0 \\ \end{aligned}$$

(14)

$$\begin{aligned} & \frac{1}{pr}\left\{ {\theta^{\prime \prime } \left\{ {\frac{{k_{nf} }}{{k_{f} }} + \frac{4}{3}Rd\left[ {\left( {\theta_{w} - 1} \right)\theta + 1} \right]^{3} } \right\} + 4Rd\left[ {\left( {\theta_{w} - 1} \right)\theta + 1} \right]^{2} \left( {\theta_{w} - 1} \right)\theta^{\prime 2} } \right\} \\ & \quad + \left\{ {1 - \chi + \chi \frac{{\left( {\rho c_{p} } \right)_{CNT} }}{{\left( {\rho c_{p} } \right)_{f} }}} \right\}\left\{ {f\theta^{\prime } - \gamma \left( {ff^{\prime } \theta^{\prime } \, + f^{2} \theta^{\prime \prime } } \right)} \right\} + Ecf^{\prime \prime 2} = 0 \\ \end{aligned}$$

(15)

$$\phi^{\prime\prime} + Scf\phi^{\prime} - Sc\sigma \phi \left[ {\theta \left( {\theta_{w} - 1} \right) + 1} \right]^{m} e^{{ - \frac{E}{{\theta \left( {\theta_{w} - 1} \right) + 1}}}} = 0$$

(16)

Together with the boundary conditions

$$\begin{aligned} f\left( \eta \right) = S,f^{\prime}\left( \eta \right) = 1 + \delta f^{\prime\prime}(0),\quad \theta^{\prime}\left( \eta \right) = - Bi\left( {1 - \theta \left( \eta \right)} \right),\quad \phi (\eta ) = 1\quad {\text{at}}\quad \eta = 0 \hfill \\ f^{\prime}\left( \eta \right) = 0,\quad \theta \left( \eta \right) = 0,\quad \phi (\eta ) = 0\quad {\text{at}}\quad \eta = 0\quad {\text{at}}\quad \eta \to \infty \hfill \\ \end{aligned}$$

(17)

where

$$\begin{aligned} & Sc = \frac{\upsilon }{D},\quad \sigma = \frac{{k_{r}^{2} }}{c},\quad E = \frac{{E_{a} }}{{kT_{\infty } }},\quad \lambda = \frac{{Gr_{x} }}{{Re_{x}^{2} }},\quad Gr_{x} = \frac{{\left( {\rho \beta } \right)_{f} g\left( {T_{w} - T_{\infty } } \right)x^{3} }}{{\upsilon^{2} \rho_{f} }},Nr = \frac{{Gc_{x} }}{{\text{Re}_{x}^{2} }}, \\ & \quad Gc_{x} = \frac{{\left( {\rho \beta^{*} } \right)_{f} g\left( {C_{w} - C_{\infty } } \right)x^{3} }}{{\upsilon^{2} \rho_{f} }},\quad Re_{x}^{2} = \frac{{U_{w}^{2} x^{2} }}{{\upsilon^{2} }},\quad M = B\sqrt {\frac{\sigma }{{a\rho_{f} }}\,} x,\quad \alpha = \lambda_{1} c,\quad \gamma = \lambda_{2} c, \\ & \quad Rd = \frac{{4\sigma^{ * } T_{\infty }^{{*^{3} }} }}{{kk_{1} }},\quad Ec = {\raise0.7ex\hbox{${U_{w}^{2} }$} \!\mathord{\left/ {\vphantom {{U_{w}^{2} } {C_{p} \left( {T_{w} - T_{\infty } } \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${C_{p} \left( {T_{w} - T_{\infty } } \right)}$}},\quad pr = \frac{{\left( {\mu C_{p} } \right)_{f} }}{k},\quad S = \frac{{v_{w} }}{{a\upsilon_{f} }},\quad \delta = A\sqrt {\frac{c}{\upsilon }} ,\quad Bi = \left( {\frac{{h_{f} }}{{k_{f} }}} \right)\sqrt {{\raise0.7ex\hbox{${\upsilon_{f} }$} \!\mathord{\left/ {\vphantom {{\upsilon_{f} } c}}\right.\kern-0pt} \!\lower0.7ex\hbox{$c$}}} . \\ \end{aligned}$$

3 Quantities of interest

The quantities of interest for considering flow are surface drag force, local Nusselt number and Sherwood number and are as follows:

$$C_{{f_{x} }} = \frac{{\tau_{w} }}{{\rho_{f} U_{w}^{2} }},\quad Nu_{x} = \frac{{xq_{w} }}{{k_{f} \left( {T_{w} - T_{\infty } } \right)}}\quad {\text{and}}\quad Sh_{x} = \frac{{xq_{m} }}{{D\left( {C_{w} - C_{\infty } } \right)}}$$

(18)

where $\tau_{w}$ (wall skin friction), $q_{w}$ (wall heat flux) and $q_{m}$ (wall mass flux) are given as

$$\tau_{w} = \mu_{nf} \left( {\frac{\partial u}{\partial y}} \right)_{y = 0} ,\quad q_{w} = - xk_{nf} \left( {\frac{\partial T}{\partial y}} \right)_{y = 0} + \left( {q_{r\,\,} } \right)_{{_{y = 0} }} \quad {\text{and}}\quad q_{m} = - D\left( {\frac{\partial C}{\partial y}} \right)_{y = 0}$$

(19)

In view of Eqs. (14) and (19), the dimensionless surface drag force, local Nusselt number and local Sherwood number are given by

$$\begin{aligned} C_{f} \text{Re}_{x}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\left( {1 - \chi } \right)^{2.5} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left( {1 - \chi } \right)^{2.5} }$}}f^{\prime\prime}\left( 0 \right),\quad Nu_{x} \text{Re}_{x}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} = - \left\{ {\frac{{k_{nf} }}{{k_{f} }} + \frac{4}{3}Rd\left[ {\left( {\theta_{w} - 1} \right)\theta \left( 0 \right) + 1} \right]^{3} } \right\}\theta^{\prime}\left( 0 \right)\quad {\text{and}} \hfill \\ Sh_{x} Re_{x}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} = - \phi^{\prime}\left( 0 \right), \hfill \\ \end{aligned}$$

(20)

where $Re_{x} = \frac{{U_{w\,} x}}{\upsilon }$ represents the local Reynolds number.

4 Numerical Technique

In Runge–Kutta fourth-order technique, the nonlinear ordinary differential Eqs. (14-16) are solved with boundary condition (17) along with shooting technique. In general, in this process, we “shoot” out directions in diverse ways until we get the accurate boundary value. This technique is very fast and flexible. Here, the boundary value problem is converted into the base values, choosing finite values for $\eta_{\infty } ,$ and substituting them in the equations, the approximation of fourth order is as follows:

$$\begin{aligned} y_{n + 1} & = y_{n} + \frac{1}{6}h\left( {k_{1} + 2k_{2} + 2k_{3} + k_{4} } \right) \\ t_{n + 1} & = t_{n} + h \\ \end{aligned}$$

where y_n+1 represents the RK fourth-order approximation of y (t_n+1), and

$$\begin{aligned} k_{1} & = f(t_{n} ,y_{n} ) \\ k_{2} & = f\left( {t_{n} + \frac{1}{2}h,y_{n} + \frac{1}{2}hk_{1} } \right) \\ k_{3} & = f\left( {t_{n} + \frac{1}{2}h,y_{n} + \frac{1}{2}hk_{2} } \right) \\ k_{4} & = f\left( {t_{n} + h,y_{n} + hk_{3} } \right) \\ \end{aligned}$$

In this procedure, alter the primary differential equations into a system of first-order ODEs

$$\begin{aligned} f & = y_{1} ,f^{\prime} = y_{2} ,f^{\prime\prime} = y_{3} ,f^{\prime\prime\prime} = y_{3}^{\prime } \\ \theta & = y_{4} ,\theta^{\prime} = y_{5} ,\theta^{\prime\prime} = y_{5}^{\prime } ,\phi = y_{6} ,\phi^{\prime} = y_{7} ,\phi^{\prime\prime} = y_{7}^{\prime } \\ \end{aligned}$$

Let

$$\left. \begin{aligned} A_{1} & = \left( {1 - \chi } \right)^{2.5} \left( {1 - \chi + \chi \frac{{\rho_{\text{CNT}} }}{{\rho_{f} }}} \right), \\ A_{2} & = \left( {1 - \chi } \right)^{2.5} \left( {1 - \chi + \chi \frac{{\left( {\rho \beta } \right)_{\text{CNT}} }}{{\left( {\rho \beta } \right)_{f} }}} \right), \\ A_{3} & = \left( {1 - \chi } \right)^{2.5} , \\ A_{4} & = \left( {1 - \chi + \chi \frac{{\left( {\rho C_{p} } \right)_{\text{CNT}} }}{{\left( {\rho C_{p} } \right)_{f} }}} \right), \\ A_{5} & = \frac{{k_{nf} }}{{k_{f} }} \\ \end{aligned} \right\}$$

(21)

Then, we get first-order set-up of equations:

$$\left[ \begin{aligned} y_{1}^{\prime } \hfill \\ y_{2}^{\prime } \hfill \\ y_{3}^{\prime } \hfill \\ y_{4}^{\prime } \hfill \\ y_{5}^{\prime } \hfill \\ y_{6}^{\prime } \hfill \\ y_{7}^{\prime } \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} y_{2} \hfill \\ y_{3} \hfill \\ \frac{{\left( {M^{2} A_{3} y_{2} - A_{2} \lambda y_{4} - A_{1} \left( { - y_{1} y_{3} + y_{2}^{2} } \right) - 2\alpha y_{1} y_{2} y_{3} } \right)}}{{\left( {1 - A_{1} \alpha y_{1}^{2} } \right)}} \hfill \\ y_{5} \hfill \\ \frac{{\left( {A_{4} \left( {\gamma y_{1} y_{2} y_{5} - y_{1} y_{5} } \right) - 4Rd\left( {\left( {\theta_{w} - 1} \right)y_{4} + 1} \right)^{2} \left( {\theta_{w} - 1} \right)y_{5}^{2} - Ecy_{3}^{2} } \right)}}{{\left( {\left( {\frac{1}{pr}} \right)\left( {\left( {A_{5} + \left( {{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}} \right)Rd\left( {\left( {\theta_{w} - 1} \right)y_{4} + 1} \right)^{3} } \right) - A_{4} \left( {\gamma y_{1}^{2} } \right)} \right)} \right)}} \hfill \\ y_{7} \hfill \\ Sc\left( {\sigma y_{6} \left( {y_{4} \left( {\theta_{w} - 1} \right) + 1} \right)^{m} e^{{ - \frac{E}{{y_{4} \left( {\theta_{w} - 1} \right)}}}} - y_{1} \,y_{7} } \right) \hfill \\ \end{aligned} \right]$$

(22)

The associated initial conditions are:

$$\left[ \begin{aligned} y_{1} \hfill \\ y_{2} \hfill \\ y_{3} \hfill \\ y_{4} \hfill \\ y_{5} \hfill \\ y_{6} \hfill \\ y_{7} \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} S \hfill \\ 1 + \delta y_{3} \hfill \\ q_{1} \hfill \\ q_{2} \hfill \\ - Bi(1 - y_{4} ) \hfill \\ 1 \hfill \\ q_{3} \hfill \\ \end{aligned} \right]$$

(23)

The system of first-order ODE’s (22) with initial conditions (23) is solved using order of fourth RK integration process, and unknown initial conditions q₁, q₂ and q₃ are chosen suitably and then apply numerical integration. Here, we compare the values of $f^{\prime},$$\theta$ and $\phi$ a $\eta \to \infty ,$ through the described boundary conditions $f^{\prime}\left( \infty \right) = 0,\quad \theta \left( \infty \right) = 0\quad {\text{and }}\phi \left( \infty \right) = 0$ and adjust the estimated values of q₁, q₂ and q₃ to get an excellent agreement. The unknown initial conditions q₁, q₂ and q₃ have been approximated by Newton’s method such as the boundary conditions suitable at highest numerical values of $\eta \to \infty$, with error less than 10⁻⁸.

5 Results and Discussions

Current segment focuses on the pertinent physical parameters on fluid flow assigned over a stretching sheet. We examined the flow with two kinds of CNTs: single- and multi-walled nanofluids (blue-coloured solid line denotes SWCNT’s and green-coloured dashed line denotes MWCNT’s) for engine oil (host fluid). The numerical values of CNT’s and engine oil that depends on viscosity, density, thermal conductivity and specific heat are shown in Table 1. It is, therefore, relevant to clarify the impacts of variation of the above parameters when the others are kept constant, M = 0.5, λ = 0.1, Pr = 0.71, γ = 0.1, Sc = 0.6, Ec = 0.02, θ_w = 1.5, Bi = 20, E = 1, δ = 0.5, S = 0.5, Rd = 10.0, σ = 3, χ = 0.06 unless otherwise specified. The numerical results are thus exhibited in the velocity, temperature and concentration profiles in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18 for the different values of the governing parameters.

Fig. 2

$f^{\prime}\,\left( \eta \right)$ via M

Fig. 3

$\theta \,\left( \eta \right)$ via M

Fig. 4

a$f^{\prime}\,\,\left( \eta \right)$ via $S\left( { > 0} \right)$, b$f^{\prime}\,\,\left( \eta \right)$ via $S\left( { < 0} \right)$

Fig. 5

a$\theta \,\left( \eta \right)$ via $S\left( { > 0} \right)$, b$\theta \,\left( \eta \right)$ via $S\left( { < 0} \right)$

Fig. 6

a$\phi \left( \eta \right)$ via $S\left( { > 0} \right)$, b$\phi \left( \eta \right)$ via $S\left( { < 0} \right)$

Fig. 7

$f^{\prime}\,\,\left( \eta \right)$ via $\chi$

Fig. 8

$\theta \,\left( \eta \right)$ via Pr

Fig. 9

$\theta \,\left( \eta \right)$ via Rd

Fig. 10

$\theta \,\left( \eta \right)$ via $\theta_{w}$

Fig. 11

$\phi \left( \eta \right)$ via $\theta_{w}$

Fig. 12

$\phi \,\left( \eta \right)$ via Sc

Fig. 13

$\phi \left( \eta \right)$ via $\sigma$

Fig. 14

$\phi \left( \eta \right)$ via E

Fig. 15

Nusselt number via Rd

Fig. 16

Nusselt number via ϴ_w

Fig. 17

Sherwood Number via σ

Fig. 18

Sherwood number via E

5.1 Impacts of magnetic parameter [M] on the velocity and temperature profile for both SWCNT’s and MWCNT’s

The impact of M on velocity is shown in Fig. 2. Applying magnetic field to an electrically conducting liquid generates a dragging force called Lorentz force which is orthogonal to the velocity vector and magnetic field vector. Lorentz force enhances the colliding nature of the molecules. Collision of molecules increases in the presence of Lorentz force. This force slackens the movement of the fluid which decelerates the fluid velocity and accelerates the temperature in the thermal boundary layer as in Fig. 3; it is evident that an enhancement in magnetic field decreases the thickness of momentum boundary layer and increases the thermal boundary layer thickness.

5.2 Impacts of suction/injection parameter [S] on the velocity, temperature and concentration profiles for both SWCNT’s and MWCNT’s

The impacts of suction/injection $(S)$ on the velocity profiles are shown in Fig. 4a and b. For strong suction $(S > 0),$ the velocity profile decays away from the surface which is observed from Fig. 4a, the fact that suction stabilizes the boundary layer. It is envisaged that the velocity of SWCNT’s has decreased a little more than MWCNT’s. As for the injection $(S < 0)\,,$ from Fig. 4b, it is noticed that the velocity profile overshoots and closes to the boundary for both SWCNT’s and MWCNT’s.

The influence of suction and injection $(S)$ on the temperature profiles is shown in Fig. 5a and b. For positive values of S, the temperature profiles of MWCNT’s decrease more than the SWCNT’s; this is shown in Fig. 5a. It is noted from Fig. 5b that fluid temperature enhances for negative values of $S$.

The impact of suction and injection $(S)$ on the concentration profiles is shown in Fig. 6a and b. For increasing values of suction, the concentration profiles decrease for both SWCNT’s and MWCNT’s which are depicted in Fig. 6a. For decreasing values of injection, a reverse trend is noticed for both SWCNT’s and MWCNT’s, which are demonstrated in Fig. 6b.

5.3 Impacts of nanoparticles fraction $[\chi ]$ on the velocity profile for both SWCNT’s and MWCNT’s

By uplifting values of $\chi ,$ velocity is uplifted, and then, a rapid increase is noticed in momentum width of the boundary layer. Figure 7 elucidates that with the boosting values of $\chi ,$ the velocity increases, and hence, the width of momentum boundary layer rapidly increases. Additionally, a remarkable growth in velocity is obtained for MWCNT’s compared to SWCNT’s. The temperature of the liquid escalates as $\chi$ escalates, i.e. an expansion in the width of thermal boundary layer is noted. It is worth mentioning that the rise of temperature for MWCNT’s nanoparticles is slower than SWCNT’s nanoparticles. The reason behind is that the MWCNT’s has more thermal expansion than SWCNT’s and is shown in Table 1.

5.4 Impacts of Prandtl Number Pr on the Temperature Profiles for Both SWCNT’s and MWCNT’s

Figure 8 feeds light on the temperature for various values of Pr. It is evident that the temperature parameter $\theta$ reduces with the enhancement in Pr for both SWCNT’s and MWCNT’s. For smaller Pr, the thermal boundary layer is thicker and the rate of heat transfer is diminished. Generally, Pr is used in problems relevant to heat transfer that deduce the relative thickening of the momentum and the thermal boundary layers.

5.5 Impacts of Nonlinear Radiation Parameter (Rd) on the Temperature Profiles for Both SWCNT’s and MWCNT’s

Temperature profile $\theta (\eta )$ for radiation parameter $Rd$ is exhibited in Fig. 9. This figure revealed that greater values of thermal radiation have the rapport to increase both the fields’ temperature and thermal boundary layer thickness. This is because of hike in $Rd,$ the mean absorption coefficient pull downs. Therefore, the rate of heat transfer by radiation to the liquid rises. Physically, in the radiation process there is more heating to the working fluid which results in temperature growing.

5.6 Impacts of Temperature Ratio Parameter ($\theta_{w}$) on the Temperature and Concentration Profiles for Both SWCNT’s and MWCNT’s

Figure 10 illustrates the variations of $\theta_{w}$ of temperature $\theta .$ When $\theta_{w}$ varies, a considerable rise in temperature profile is obvious. The result is alike as in case of stretching sheet or flat plate. The increase in $\theta_{w}$ increases the wall temperature which consecutively fruitage thicker penetration depth for temperature. As mentioned in Pantokratoras [29], the thermal diffusivity of the boundary layer varies with temperature and it is expected that for large temperatures the thermal boundary layer is thicker near the wall, whereas for smaller temperatures it is thinner far from the sheet. As a result, an inflection point arises at the wall when sufficiently larger $\theta_{w}$ is accounted. It is noteworthy that the SWCNT’s has increased the temperature profile slightly more than MWCNT’s. The effect $\theta_{w}$ on concentration is portrayed in Fig. 11. It is perceived that an increase in $\theta_{w}$ signifies a poor concentration profiles, and therefore, it causes a decrease in the concentration of the boundary layer thickness.

5.7 Impacts of Schmidt number ($Sc$) on the Concentration Profiles for Both SWCNT’s and MWCNT’s

Figure 12 elucidates the concentration profile for different values of $Sc.$ It is clear that the nanoparticles concentration profile and its associated boundary layer thickness weaken by the stronger values of Sc for both SWCNT’s and MWCNT’s.

5.8 Impacts of Chemical Reaction Rate Constant ($\sigma$) on the Concentration Profiles for Both SWCNT’s and MWCNT’s

Figure 13 portrays the concentration profiles for diverse values $\sigma .$ When we gradually increase the value of $\sigma ,$ the concentration profiles become thinner. The facet $\sigma \left( {1 + \left( {\theta_{w} - 1} \right)\theta } \right)^{m} e^{{\left[ {\frac{ - E}{{1 + \left( {\theta_{w} - 1} \right)\theta }}} \right]}}$ is enhanced when we use the increment values of σ or m. A favourable destructive reaction rises which consecutively results a fall in concentration. Due to this, concentration profile falls.

5.9 Impacts of Activation Energy ($E$) on the Concentration Profiles for Both SWCNT’s and MWCNT’s

Figure 14 visualizes the activities of the activation energy $E$ against the nanoparticle concentration sketch. The Arrhenius function declines with the increasing value of the activation energy, which leads in the improvement of the productive chemical reaction generating an increase in the concentration profile. The incidence of higher activation energy and lower temperature leads to a smaller reaction rate constant which decelerates the chemical reaction. In this way, concentration of solute rises.

5.10 Impacts of Nusselt Number on Nonlinear Thermal Radiation ($Rd$) and Temperature Ratio Parameter ($\theta_{w}$) for Both SWCNT’s and MWCNT’s

Figure 15 illustrates the variation in local Nusselt number for different values of nonlinear thermal radiation. It is clear that increasing values of $Rd$ enhance the heat transfer rate for both SWCNT’s and MWCNT’s. The effect of temperature ratio parameter on local Nusselt number is demonstrated in Fig. 16. It is detected that rising values of temperature ratio parameter raise the local Nusselt number for both SWCNT’s and MWCNT’s.

5.11 Impacts of Sherwood Number on Chemical Reaction Rate Constant ($\sigma$) and Activation Energy ($E$) for Both SWCNT’s and MWCNT’s

Figures 17 and 18 exemplify the effect of Sherwood number on chemical reaction rate constant and activation energy. The outcomes show a rise in σ, and E has a fall in the Sherwood number for both SWCNT’s and MWCNT’s.

Table 2 describes the deviations of skin friction for different parameters. The magnitude of skin friction decreases with the increase in $M,$Pr, Sc and suction $(S > 0),$ a reverse trend for injection. Table 3 displays the variations in rate of heat transfer for different values of M, Pr, $S$ and $Sc.$ Heat transfer rate accelerates with Pr and suction and decelerates with M, Sc and injection $(S < 0).$ Table 4 provides the sample of values of mass transfer for several values of embedding parameters. Mass transfer declines for M, Pr and injection, whereas it inclines with $Sc$ and suction

Table 2 The values of skin friction coefficient and various dimensionless parameters

Table 3 Deviations in the rate of heat transfer and various dimensionless parameters

Table 4 Deviations in the rate of mass transfer and various dimensionless parameters

6 Final Conclusions

The current communication scrutinizes a theoretical model of Cattaneo–Christov heat diffusion with CNT’s (carbon nanotubes)—ejected in a Maxwell fluid with dissipative nanoparticles through binary chemical reaction lying on a stretching sheet by means of nonlinear thermal radiation. The numerical elucidations are established by RK4S (Runge–Kutta fourth-order through shooting) method—bvp4c codes in MATLAB.

The major points of current flow are:

• Velocity field decays for larger estimations of magnetic parameter and for $S > 0,$ and negative trend is observed for $S < 0.$

• Increasing values of radiation parameter, temperature ratio parameter, viscous dissipation and nanoparticles fraction lead to stronger temperature distribution.

• Thermal boundary layer thickness decreases by increasing the Pr.

• For positive values of $S,$ the temperature profile decreases and negative trend is observed for negative values of $S.$

• The higher value of $Sc,$ reaction rate parameter, concentration decreases.

• The fluid concentration rises with the rise in activation energy.

• Heat transfer rate is high for nonlinear thermal radiation and temperature ratio parameter.

• The Sherwood number is low for chemical reaction rate constant and activation energy.