Flexural Decoupling Analysis Method of Composite Box Girder with Corrugated Steel Webs

Abstract

The existing flexural analysis methods of corrugated steel web composite box girders are either inaccurate due to thoughtlessness of the influencing factors, or complicated due to excessive consideration of the influencing factors. In this study, a flexural displacement model of composite box girder considering both the accordion effect and shear deformation of web and the shear lag effect of flange is proposed. According to the internal force balance condition, the complex flexural models of a composite box girder are decoupled into three independent simple flexural states: Euler–Bernoulli beam flexure satisfying the quasi-plane assumption, flexure of equivalent web deformation, and flexure of shear lag of flange. Based on the flexural theory of the thin-walled beam, the generalized internal force system and beam-type finite element model was established corresponding to each flexural state. The results of numerical examples show that the proposed method has high solution accuracy and can directly obtain the displacement and internal force of each flexure deformation. The moment results show that the generalized moment has a peak value at the point of shear discontinuity, and increases or decays rapidly near it.

1 Introduction

The concrete box girder with corrugated steel webs has rapidly developed in recent years because it is lightweight and has good mechanical and seismic performance. This type of composite beam can effectively improve the buckling resistance of the web through the bending form of the steel webs (Elgaaly, 1996; Luo & Edlund, 1996). The webs hardly bear any axial bending moment or axial force owing to the accordion effect (Elgaaly et al, 1997), thus the prestressing efficiency is improved (Jiang et al, 2015). What’s more, the classical Euler–Bernoulli beam (EBB) and Timoshenko beam theory are no longer applicable to this type of structure (Machimdamrong et al, 2003). Therefore, it is of great practical significance to explore a flexural analysis theory suitable for this type of composite beam.

In the 1990s, Elgaaly (1996; 1998) argued that the influence of steel webs on the bending of composite beams was negligible, according to the bending test results of I-shaped corrugated steel webs. Subsequently, studies (Samanta & Mukhopadhyay, 1999; Sayed-Ahmed, 2001; Zhou, 2016) used the three-dimensional finite-element method (3D FEM) to analyze the flexural stress of the composite box girder and drew the similar conclusion. The 3D FEM has higher analysis accuracy while it needs to construct a complex solid model in addition constructing the numerical model for a complex composite box girder is time-consuming. Therefore, many researchers have attempted to develop a beam-type analysis method with higher accuracy and simple calculation. Kato et al., (2002; 2003) proposed a flexural analysis method similar to the sandwich beam (Khalili et al, 2010). On this basis, Chawalit et al. (2004) introduced the influence of the flange shear deformation to improve the accuracy of deflection solution. Chen et al., (2015, 2017) proposed a flexural analysis method that considers the influence of the composite box girder diaphragm. Nie et al. (2011; 2012) assumed that the deflection of the composite box girder was the synthesis of the bending of the upper and lower concrete flanges and the truss effect of the steel web. Although these analysis methods can accurately indicate the vertical deflection deformation of this composite beam, the deflection calculation is complicated due to the complex form of the deflection displacement function. To simplify the calculation, Wu et al. (2005) and Matsui et al. (2006) proposed an analysis method based on the quasi-plane assumption without considering the influence of steel web deformation. This analysis method is similar to the classical EBB and has good engineering application value, but the deflection of a composite box girder obtained by this method is quite different from the actual deflection. To solve this problem, many studies (He et al., 2009; Li et al., 2002; Liu et al., 2011) have considered the shear deformation of steel webs by introducing an another shear deflection angle. However, after testing the stress of the simply supported composite beam, Ikeda et al. (2002) found that the quasi-plane assumption is not applicable to the deformation of cross-sections near concentrated loads. Therefore, it is important to establish a simplified flexural analysis method for composite beams that can fully consider the influence of steel web deformation and can match to the classic EBB.

As a special thin-walled component, an obvious shear lag effect must exist in the flange of a composite box girder. Researchers have often used the 3D FEM (Xu et al, 2015) and energy variation method (EVM) (Cheng & Yao, 2016) to analyze the shear lag effect of composite box girders. The EVM has been widely used (Li et al, 2019) because it corresponds to the EBB meanwhile it has a clear mechanical mechanism. Nowadays, scholars analyze the shear lag effect of the composite box girder based on the quasi-plane assumption. However, this assumption cannot consider the influence of steel web deformation, which may lead to inaccurate results of flexural stress analysis. Moreover, the overall bending deformation of the composite box girder is coupled with the shear lag effect of flange and the deformation of web, which result in the flexural analysis of the composite box girder very complicated. As a steel–concrete composite structure, the fatigue degradation of materials has always been a focus of scholars' research. For example, Pipinato et al., (2009, 2010, 2021) have conducted extensive fatigue tests on steel structures and steel–concrete composite beams. Bruwhiler et al. (2010, 2013) conducted fatigue tests on composite beam shear connectors and strength tests on high-performance concrete beams. Obviously, it is of great significance to accurately obtain the flexural normal stress and shear stress, especially the detailed stress results, for the evaluation of fatigue life and bearing capacity of Bridges. To improve the analysis accuracy, a flexural displacement function of a composite box girder that both considered the deformation of web and the shear lag effect of flange is established. By introducing three generalized deflections corresponding to EBB, web deformation and shear lag effect of flange, the complex flexural state of a composite box girder is decoupled into a simple flexural state of three generalized displacements. Then, the governing differential equations of the generalized deflections are derived by using EVM and the initial parameter solutions of the flexural analysis of the composite box girder are obtained. In addition, a beam-type finite element model for the flexural analysis of a composite box girder is established. Eventually, numerical examples of composite box girders are used to verify the applicability of the proposed method.

2 Flexural Analysis of Composite Box Girder

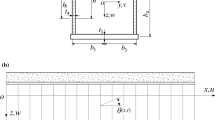
The main purpose of this part is to obtain the vertical and horizontal distribution of flexural displacement of the composite box girder. A simply supported composite box girder with trapezoidal cross-section under arbitrary load (Fig. 1) is selected as the analysis model. The variable parameters of cross-section size are shown in Fig. 1b. In Fig. 1b), b₁, b₂, and b₃ represent the width of the top slab, bottom slab and extended cantilever slab, respectively. The h_t and h_b respectively represent the vertical distance from the centroid of the cross-section to the centroids of the upper and lower flanges and h is the sum of these two distances. The a_t represents the distance from the centroid of the cross-section to the bottom of the upper flange and a_b represents the distance from the centroid of the cross-section to the top of the lower flange. The h_w is the sum of these two distances, that is, the vertical height of the corrugated steel webs.

Fig. 1

Composite box girder with corrugated steel webs: a coordinate system; b cross-section

2.1 Coordinate System and Basic Assumptions

In this paper, the Cartesian coordinate system is adopted, and the origin O of the coordinate is located at the centroid of section. The x-axis and y-axis are the centroid axes of the section, and the z-axis is the longitudinal axis of the beam. In this study, the basic assumptions used in the flexural analysis of the composite box girder are the same as those in Cheng and Yao (2016).

2.2 Vertical Distribution of Flexural Displacement

If v(z) is used represents the vertical deflection of a composite box girder, the flexural angle of upper and lower flange can be expressed as v'(z). Therefore, the side elevation of deflection angle of any beam segment flexural deformation can be shown in Fig. 2. The θ(z) denotes the angle of the line connecting centroid of upper and lower flanges around the x-axis, and α(z) denotes the angle of the line connecting the bottom of upper flange and the top of lower flange around the x-axis. Due to the combined influence of shear deformation of steel web and its accordion effect, the deflection angle v'(z) is different from θ(z). Therefore, the overall deformation of steel web can be equivalent to α(z).

Fig. 2

Schematic diagram of deflection angle relation

According to Figs. 1b and 2, the flexural longitudinal displacement u_t(y,z) and u_b(y,z) of the upper and lower flanges can be expressed as follows:

$$u_{t} (y,z) = h_{t} \theta (z) - (y + h_{t} )v^{\prime}(z){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$

(1)

$$u_{b} (y,z) = - h_{b} \theta (z) - (y - h_{b} )v^{\prime}(z){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$

(2)

From Eqs. (1) and (2) and Fig. 2, the angle α(z) can be obtained as follows,

$$\alpha (z) = \frac{{u_{t} ( - a_{t} ,z) - u_{b} (a_{b} ,z)}}{{a_{t} + a_{b} }}{\kern 1pt} = \chi \theta (z) + (1 - \chi )v^{\prime}(z)$$

(3)

where χ = h/h_w. Therefore, ignoring the bending stiffness of the corrugated steel web, the equivalent longitudinal displacement u_w(y,z) can be expressed as follows,

$$u_{w} (y,z) = - y\alpha (z)$$

(4)

2.3 Transverse Distribution of Flexural Displacement

As a special thin-walled structure, there must be a shear lag effect in the concrete flanges of the composite box girder. According to the literature (Zhang et al., 2014), the additional longitudinal displacement u_g(x,z) caused by the shear lag effect can be expressed as follows,

$$u_{g} (x,z) = \xi (x)\varphi (z)$$

(5)

where φ(z) represents the additional deflection angle function caused by the shear lag effect, and ξ(x) represents the transverse distribution function of shear lag warping deformation along the width of flange. In this study, the expression is adopted as follows (Zhou et al., 2015),

$$\xi (x) = \left\{ \begin{gathered} - h_{t} (1 - \frac{{x^{2} }}{{b_{1}^{2} }}) + d{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\text{top}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{slab}}{\kern 1pt} {\kern 1pt} \hfill \\ - h_{t} [1 - \frac{{(b_{3} + b_{1} - x)^{2} }}{{b_{3}^{2} }}](\frac{{b_{3} }}{{b_{1} }})^{2} {\kern 1pt} + d{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\text{cantilever}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{slab}} \hfill \\ h_{b} (1 - \frac{{x^{2} }}{{b_{2}^{2} }})(\frac{{b_{2} }}{{b_{1} }})^{2} + d{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\text{bottom}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{slab}} \hfill \\ \end{gathered} \right.$$

(6)

where d is the correction coefficient satisfying the self-balance of cross-section.

From Eqs. (1), (2) and (5), the flexural longitudinal displacements u_t(x,y,z) and u_b(x,y,z) of the upper and lower flange can be derived as follows:

$$u_{t} (x,y,z) = h_{t} \theta (z) - (y + h_{t} )v^{\prime}(z){\kern 1pt} + \xi (x)\varphi (z)$$

(7)

$$u_{b} (x,y,z) = - h_{b} \theta (z) - (y - h_{b} )v^{\prime}(z) + \xi (x)\varphi (z)$$

(8)

3 Deflection Analysis Based on Generalized Displacement

3.1 Define Generalized Displacements

To simplify the calculation, the deflection v(z) of the composite box girder can be divided into three types of deflection: (1) The EBB deflection w(z) satisfying quasi-plane assumption; (2) the deflection f(z) caused by equivalent flexural deformation of steel web; (3) the deflection g(z) caused by shear lag effect of flanges. The three independent flexural deformation states defined in this study are shown in Fig. 3. By synthesizing Eqs. (7) and (8), the flexural longitudinal displacement u(x,y,z) of the flange can be obtained as follows,

$$u(x,y,z) = - y[w^{\prime}(z) + f^{\prime}(z) + g^{\prime}(z)]{\kern 1pt} + \lambda \phi(y)f^{\prime}(z){\kern 1pt} {\kern 1pt} + \eta \xi (x)g^{\prime}(z) = - yw^{\prime}(z) - \beta (y)f^{\prime}(z) - \zeta (x,y)g^{\prime}(z)$$

(9)

where $\phi (y)$ denotes the vertical distribution function of longitudinal displacement caused by the equivalent flexural deformation of steel web, which is –h_t for the upper flange and h_b for the lower flange; λ and η denote the self-balance correction factors of warping displacement caused by the equivalent flexural deformation of steel web and the shear lag effect of flange respectively, and their values are obtained by the internal force balance condition of section. According to Eqs. (7) to (9), the expressions of β(y) and ζ(x,y) are respectively shown in formula (10) and formula (11), and λf'(z) = v'(z)-θ(z), ηg'(z) = φ(z).

$$\beta {(}y{)} = y - \lambda \phi(y)$$

(10)

$$\zeta {(}x,y{)} = y - \eta \xi (x)$$

(11)

Fig. 3

Decomposition of flexural deformation

From Eq. (9), the flexural normal stress σ(x, y, z) of flange can be obtained as follows,

$$\sigma {(}x,y,z{)} = E_{c} \frac{\partial u}{{\partial z}} = - E_{c} yw^{\prime\prime}(z) - {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{c} \beta (y)f^{\prime\prime}(z) - E_{c} \zeta (x,y)g^{\prime\prime}(z)$$

(12)

where E_c is the elastic modulus of concrete.

In Eq. (12), $- E_{c} yw^{\prime\prime}(z)$, $- {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{c} \beta (y)f^{\prime\prime}(z)$ and $- E_{c} \zeta (x,y)g^{\prime\prime}(z)$ are the stresses caused by the flexural deformation of EBB satisfying quasi-plane assumption, the equivalent flexural deformation of web and the shear lag effect of flanges, respectively, which can be called EBB flexural stress σ_E, web warping stress σ_β and flange warping stress σ_ζ, thus,

$$\sigma_{\beta } = - {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{c} \beta (y)f^{\prime\prime}(z)$$

(13)

$$\sigma_{\zeta } = - E_{c} \zeta (x,y)g^{\prime\prime}(z)$$

(14)

For composite box girder subjected to bending load, σ_E synthesize bending moment M with y as the moment arm, thus σ_β and σ_ζ neither synthesize axial force on the whole section nor synthesize bending moment with y as the moment arm, i.e.

$$\int_{A} {\sigma_{\beta } {\text{d}}A} = 0$$

(15)

$$\int_{A} {\sigma_{\zeta } {\text{d}}A} = 0$$

(16)

$$\int_{A} {\sigma_{\beta } y} {\text{d}}A = 0$$

(17)

$$\int_{A} {\sigma_{\zeta } y} {\text{d}}A = 0$$

(18)

where A is the area of concrete flanges. Therefore, Eqs. (15)–(18) are the internal force balance conditions of the composite box girder section. By substituting Eqs. (13) and (14) into Eqs. (15)–(18), the following expressions can be obtained:

$$\int_{A} {\xi (x){\text{d}}A} = 0$$

(19)

$$I_{x} = \lambda I_{y\phi } = \eta I_{y\xi }$$

(20)

where $I_{x} = \int_{A} {y^{2} {\text{d}}A}$; $I_{y\phi} = \int_{A} {y\phi(y){\text{d}}A}$; $I_{y\xi } = \int_{A} {y\xi (x){\text{d}}A}$. I_x and $I_{y\phi }$ denote the moment of inertia and the area moment of the flanges about the centroid x-axis respectively, and I_yξ denotes the area moment of the flange shear lag effect about the centroid x-axis. By substituting the functions $\phi (y)$ and ξ(x) into the corresponding section parameter expression above, the following expressions are obtained:

$$d = \frac{{2}}{{{3}A}}[h_{t} A_{t} + h_{t} A_{c} (\frac{{b_{3} }}{{b_{1} }})^{2} - h_{b} A_{b} (\frac{{b_{2} }}{{b_{1} }})^{2} ]$$

(21)

$$I_{y\phi } = h_{t}^{2} (A_{t} + A_{c} ) + h_{b}^{2} A_{b}$$

(22)

$$I_{y\xi } = \frac{{2h_{t}^{2} }}{3}[A_{t} + A_{c} (\frac{{b_{3} }}{{b_{1} }})^{2} + A_{b} (\frac{{b_{2} }}{{b_{1} }})^{2} (\frac{{h_{b} }}{{h_{t} }})^{2} ]$$

(23)

where A_t, A_b and A_c are the areas of the top slab, bottom slab and cantilever slab of the composite box girder respectively. What’s more, the values of the internal force balance parameters λ and η can be obtained from Eqs. (20), (22) and (23).

3.2 Define Generalized Internal Forces

To correspond to the traditional flexural analysis of EBB, the generalized internal moments M_β and M_ζ corresponding to the generalized displacements f and g are defined respectively:

$$M_{\beta } = \int_{A} {\beta (y)\sigma_{\beta } {\text{d}}A}$$

(24)

$$M_{\zeta } = \int_{A} {\zeta (x,y)\sigma_{\zeta } {\text{d}}A}$$

(25)

By substituting Eqs. (13) and (14) into Eqs. (24) and (25), respectively, the following results is obtained after simplifying:

$$M_{\beta } = - {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{c} I_{\beta } f^{\prime\prime}(z)$$

(26)

$$M_{\zeta } = - E_{c} I_{\zeta } g^{\prime\prime}(z)$$

(27)

where $I_{\beta } = \int_{A} {\beta^{2} {\text{d}}A}$ and $I_{\zeta } = \int_{A} {\zeta^{2} {\text{d}}A}$; I_β and I_ζ can be called the inertial product of generalized displacements f and g respectively. According to Eqs. (10) and (20), I_β is expressed as follows,

$$I_{\beta } = (\lambda - 1)I_{x}$$

(28)

According to Eqs. (11) and (20), I_ζ is expressed as follows,

$$I_{\zeta } = \eta^{2} I_{\xi } - I_{x}$$

(29)

where I_ξ can expressed as follows,

$$I_{\xi } = Ad^{2} + A_{t} h_{t} (\frac{8}{15}h_{t} - \frac{4}{3}d){\kern 1pt} + A_{c} h_{t} [\frac{8}{15}(\frac{{b_{3} }}{{b_{1} }})^{2} h_{t} - \frac{4}{3}d](\frac{{b_{3} }}{{b_{1} }})^{2} {\kern 1pt} + {\kern 1pt} A_{b} h_{b} [\frac{8}{15}h_{b} (\frac{{b_{2} }}{{b_{1} }})^{2} + \frac{4}{3}d](\frac{{b_{2} }}{{b_{1} }})^{2}$$

(30)

Based on Eqs. (13)-(14) and Eqs. (26)–(27), the stress σ_β and σ_ζ are expressed as follows:

$$\sigma_{\beta } = \frac{{M_{\beta } }}{{I_{\beta } }}\beta$$

(31)

$$\sigma_{\zeta } = \frac{{M_{\zeta } }}{{I_{\zeta } }}\zeta$$

(32)

Therefore, the total flexural normal stress σ of the composite box girder is expressed as follows,

$$\sigma = \frac{M}{{I_{x} }}y + \frac{{M_{\beta } }}{{I_{\beta } }}\beta + \frac{{M_{\zeta } }}{{I_{\zeta } }}\zeta$$

(33)

To show the flexural stress state of composite box girder intuitively, the longitudinal and transverse distribution of σ_E, σ_β and σ_ζ are given in Fig. 4.

Fig. 4

The distribution diagram of σ_E, σ_β and σ_ζ in different planes: a the distribution of σ_E and σ_β in the y–z plane; b the distribution of σ_ζ in the x–y plane

To analyze the relative magnitude of the warping stress, the ratios of σ_β and σ_ζ to σ_E are defined as C_β and C_ζ, respectively, and both of them can be considered as the stress increase coefficient. The following expressions can be obtained from Eq. (33),

$$C_{\beta } = \frac{{M_{\beta } }}{M} \cdot \frac{{I_{x} }}{{I_{\beta } }} \cdot \frac{\beta }{y}$$

(34)

$$C_{\zeta } = \frac{{M_{\zeta } }}{M} \cdot \frac{{I_{x} }}{{I_{\zeta } }} \cdot \frac{\zeta }{y}$$

(35)

From Eqs. (34) and (35), it is known that, if the section size of the box girder is given, the stress increase coefficient is related to the ratio of the generalized moments M_β and M_ζ to the bending moment M. Hence, the increase coefficients are positive if the sign of M_β and M_ζ are the same as the sign of M, and vice versa.

4 Establishment of Governing Differential Equation

From Eq. (9), the normal strain ε of the composite box girder can be expressed as follows,

$$\varepsilon (x,y,z) = - yw^{\prime\prime}(z) - \beta (y)f^{\prime\prime}(z) - \zeta (x)g^{\prime\prime}(z)$$

(36)

According to Eqs. (9) and (11), the shear strain γ_xz of the flange can be obtained as follows,

$$\gamma_{xz} = \eta \frac{{{\text{d}}\xi }}{{{\text{d}}x}}g^{\prime}(z)$$

(37)

According to Eqs. (3), (4), and (9), the equivalent shear strain γ_yz of the corrugated steel web can be obtained as follows,

$$\gamma_{yz} = \frac{{\partial u_{w} }}{\partial y} + \frac{\partial v}{{\partial z}} = \chi [v^{\prime}(z) - \theta (z)] = \lambda \chi f^{\prime}(z)$$

(38)

Therefore, the total flexural potential energy of the composite box girder can be obtained from Eqs. (36)-(38), as follows,

$$\begin{gathered} {\Pi }{\kern 1pt} = \frac{1}{2}\int_{l} {\int_{A} {\left( {E_{c} \varepsilon^{2} + G_{c} \gamma_{xz}^{2} + G_{w} \gamma_{yz}^{2} } \right)} {\text{d}}A{\text{d}}z} - \int_{l} {q(w + f + g){\text{d}}z} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{1}{2}\int_{0}^{l} {[E_{c} (I_{x} w^{{\prime\prime}{2}} + I_{\beta } f^{{\prime\prime}{2}} + I_{\zeta } g^{{\prime\prime}{2}} + I_{\beta } f^{\prime\prime}g^{\prime\prime}) + } \lambda^{2} \chi^{2} G_{w} A_{w} f^{{\prime}{2}} + {\kern 1pt} {\kern 1pt} {\kern 1pt} \eta^{2} G_{c} A_{x} g^{{\prime}{2}} {\kern 1pt} ]{\text{d}}z - {\kern 1pt} \int_{0}^{l} {q(w + f + g){\text{d}}z} \hfill \\ \end{gathered}$$

(39)

where q is the uniformly distributed external load; G_c is the shear modulus of the concrete; G_w is the equivalent shear modulus of the corrugated steel web (Cheng et al. 2016); A_w is the area of the steel web and A_x denotes the area of flange shear warping, which is expressed as follows,

$$A_{x} = \int_{A} {({\text{d}}\xi /{\text{d}}x)^{2} {\text{d}}A} = \frac{4}{3}[A_{t} (\frac{{h_{t} }}{{b_{1} }})^{2} + A_{c} (\frac{{b_{3} }}{{b_{1} }})^{4} (\frac{{h_{t} }}{{b_{3} }})^{2} + A_{b} (\frac{{b_{2} }}{{b_{1} }})^{4} (\frac{{h_{b} }}{{b_{2} }})^{2} ]$$

(40)

In practical projects, the coupling strain energy of shear lag deformation and equivalent deformation of web is relatively low and can be ignored. To simplify the analysis, it is assumed that f''g'' = 0 in Eq. (39); then, the first-order variation can be obtained as follows,

$$\begin{gathered} \delta \Pi {\kern 1pt} = \int_{0}^{l} {(E_{c} I_{x} } w^{\prime \prime \prime \prime } - q)\delta wdz + \int_{0}^{l} {[E_{c} I_{\beta } f^{\prime \prime \prime \prime } - \lambda^{2} \chi^{2} G_{w} A_{w} f^{\prime \prime } - q]\delta fdz + } \int_{0}^{l} {[E_{c} I_{\zeta } g^{\prime \prime \prime \prime } - \eta^{2} G_{c} A_{x} g^{\prime \prime } - q]\delta gdz + } \hfill \\ E_{c} I_{x} w^{\prime \prime } \delta w^{\prime } \left| {_{0}^{l} } \right. - E_{c} I_{x} w^{\prime \prime \prime } \delta w\left| {_{0}^{l} } \right. + E_{c} I_{\beta } f^{\prime \prime } \delta f^{\prime } \left| {_{0}^{l} } \right. + E_{c} I_{\zeta } g^{\prime\prime}\delta g^{\prime}\left| {_{0}^{l} } \right. + \left( {\lambda^{2} \chi^{2} G_{w} A_{w} f^{\prime } - E_{c} I_{\beta } f^{\prime \prime \prime } } \right)\delta f\left| {_{0}^{l} } \right. + \hfill \\ (\eta^{2} G_{c} A_{x} g^{\prime } - E_{c} I_{\zeta } g^{\prime \prime \prime } )\delta g\left| {_{0}^{l} } \right. \hfill \\ \end{gathered}$$

(41)

According to Eq. (41), the governing differential equations of the composite beam are as follows:

$$E_{c} I_{x} w^{\prime \prime \prime \prime } - q = 0$$

(42)

$$E_{c} I_{\beta } f^{\prime \prime \prime \prime } - \lambda^{2} \chi^{2} G_{w} A_{w} f^{\prime \prime } - q = 0$$

(43)

$$E_{c} I_{\zeta } g^{\prime \prime \prime \prime } - \eta^{2} G_{c} A_{x} g^{\prime \prime } - q = 0$$

(44)

As can be seen, Eq. (42) is the governing differential equation for the EBB flexure. Equations (43) and (44) are the governing differential equations for deflection f and g, respectively. By comparing Eqs. (43) and (44), it can be seen that their form is exactly the same except for the constant coefficients; therefore, the solution of these two differential equations should also be the same. In this study, Eq. (43) was considered as the object of analysis, and can be simplified as follows,

$$f^{\prime \prime \prime \prime } - k^{2} f^{\prime \prime } = \frac{q}{{E_{c} I_{\beta } }}$$

(45)

where k is the equivalent deformation constant and is expressed as follows:

$$k = \lambda \chi \sqrt {\frac{{G_{w} A_{w} }}{{E_{c} I_{\beta } }}}$$

As can be seen from Eq. (41), the moment corresponding to the deflection angles f' and g' are -E_cI_βf'' and -E_cI_ζ'g'', respectively, which are the same as the generalized internal moment Eqs. (26) and (27). The generalized shear forces corresponding to the displacement f and g are defined as Q_β and Q_ζ, respectively, and are expressed as follows:

$$Q_{\beta } = \lambda^{2} \chi^{2} G_{w} A_{w} f^{\prime} - E_{c} I_{\beta } f^{\prime\prime\prime}$$

(46)

$$Q_{\zeta } = \eta^{2} G_{c} A_{x} g^{\prime} - E_{c} I_{\zeta } g^{\prime\prime\prime}$$

(47)

5 Initial Parameter Solution and Beam-Type Finite Element Method

5.1 Initial Parameter Solution

The general solution of the homogeneous equation corresponding to differential Eq. (45) is expressed as follows,

$$f = C_{1} + C_{2} z + C_{3} \sinh kz + C_{4} \cosh kz$$

(48)

where C₁-C₄ are integral coefficients. From Eqs. (26) and (46)-(48), the expressions of the deflection angle f', generalized moment M_β, and shear force Q_β can be obtained as follows:

$$f^{\prime} = C_{2} + C_{3} k\cosh kz + C_{4} k\sinh kz$$

(49)

$$M_{\beta } = - E_{c} I_{\beta } k^{2} (C_{3} \sinh kz + C_{4} \cosh kz)$$

(50)

$$Q_{\beta } = E_{c} I_{\beta } k^{2} C_{2}$$

(51)

By substituting z = 0 into Eqs. (48)–(51), the expressions of the initial parameters about f₀, f'₀, M_β0, and Q_β0 can be obtained. These equations form a set of equations for the integral coefficients C₁-C₄. After solving C₁-C₄ and substituting them into Eqs. (48)–(51), the expressions of the initial parameter solution can be obtained as follows:

$$f = f_{0} + f^{\prime}_{0} \frac{\sinh kz}{k} + \frac{{M_{\beta 0} }}{{k^{2} E_{c} I_{\beta } }}(1 - \cosh kz) + {\kern 1pt} \frac{{Q_{\beta 0} }}{{k^{3} E_{c} I_{\beta } }}(kz - \sinh kz)$$

(52)

$$f^{\prime} = f^{\prime}_{0} \cosh kz - \frac{{M_{\beta 0} }}{{kE_{c} I_{\beta } }}\sinh kz + {\kern 1pt} \frac{{Q_{\beta 0} }}{{k^{3} E_{c} I_{\beta } }}(1 - \cosh kz)$$

(53)

$$M_{\beta } = - f^{\prime}_{0} kE_{c} I_{\beta } \sinh kz + M_{\beta 0} \cosh kz + {\kern 1pt} Q_{\beta 0} \frac{\sinh kz}{k}$$

(54)

$$Q_{\beta } = Q_{\beta 0}$$

(55)

5.2 Beam-Type Finite Element Method

For composite box girders with equal sections, the expressions of the generalized displacement and internal force can be derived using the method of initial parameter solution and structural mechanics (Zhang et al., 2014). The beam-type finite element method is an effective way to solve the continuous composite box girder with varying depth. In this study, the deflection v of the composite box girder is decoupled into three independent deflection w, f and g, so the beam element models corresponding to w, f and g can be established, respectively. A beam-type element model 3BE with two nodes and 12 degrees of freedom is established, as shown in Fig. 5.

Fig. 5

Node displacements of beam segment model

Therefore, the node displacement of the element shown in Fig. 5 can be decomposed into the following vector forms,

$$\left\{ {\delta _{w} } \right\} = \left[ {\begin{array}{*{20}c} {w_{i} } & {w^{\prime}_{i} } & {w_{j} } & {w^{\prime}_{j} } \\ \end{array} } \right]^{{\text{T}}}$$

(56)

$$\left\{ {\delta _{f} } \right\} = \left[ {\begin{array}{*{20}c} {f_{i} } & {f^{\prime}_{i} } & {f_{j} } & {f^{\prime}_{j} } \\ \end{array} } \right]^{{\text{T}}}$$

(57)

$$\left\{ {\delta _{g} } \right\} = \left[ {\begin{array}{*{20}c} {g_{i} } & {g^{\prime}_{i} } & {g_{j} } & {g^{\prime}_{j} } \\ \end{array} } \right]^{{\text{T}}}$$

(58)

where $\left\{ {\delta _{w} } \right\}$, $\left\{ {\delta _{f} } \right\}$, and $\left\{ {\delta _{g} } \right\}$ are the nodal displacement vectors corresponding to w, f and g, respectively. Superscripts i and j in the vector element denote the nodes at both ends of the element; T denotes the transpose of the matrix. The node force vector corresponding to each node displacement vector can be expressed as follows,

$$\left\{ {{\mathbf{F}}_{w} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{i} } & {M_{i} } & {Q_{j} } & {M_{j} } \\ \end{array} } \right]^{{\text{T}}}$$

(59)

$$\left\{ {{\mathbf{F}}_{f} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{\beta i} } & {M_{\beta i} } & {Q_{\beta j} } & {M_{\beta j} } \\ \end{array} } \right]^{{\text{T}}}$$

(60)

$$\{ {\mathbf{F}}_{g} \} = \left[ {\begin{array}{*{20}c} {Q_{\zeta i} } & {M_{\zeta i} } & {Q_{\zeta j} } & {M_{\zeta j} } \\ \end{array} } \right]^{{\text{T}}}$$

(61)

where $\{ {\mathbf{F}}_{w} \}$, $\left\{ {{\mathbf{F}}_{f} } \right\}$, and $\{ {\mathbf{F}}_{g} \}$ are the node force vectors corresponding to the $\left\{ {\delta _{W} } \right\}$, $\left\{ {\delta _{f} } \right\}$, and $\left\{ {\delta _{g} } \right\}$, respectively. According to the theory of finite element, it is necessary to use the element stiffness matrix to establish the relationship between the nodal force vector and the nodal displacement vector. Therefore, the element stiffness matrix corresponding to the three deformation states w, f and g can be set as $[{\mathbf{K}}_{w} ]$, $[{\mathbf{K}}_{f} ]$, and $[{\mathbf{K}}_{g} ]$, respectively.

Many studies have reported the analysis of the element stiffness matrix of the EBB, therefore, the solution to the matrix $[{\mathbf{K}}_{w} ]$ is no longer repeated here and its expression shown in Eq. (62). The elements of the stiffness matrix $[{\mathbf{K}}_{f} ]$ and $[{\mathbf{K}}_{g} ]$ can be obtained according to the initial parameter method described in this study. According to the mechanical meaning of the element stiffness matrix, when the deflection f_i = 1 at the i end of the element and the other nodal displacement components are zero (f′_i = f′_j = f_j = 0), the corresponding node force at both ends of the element is the first column elements of the $[{\mathbf{K}}_{f} ]$. Therefore, let $f_{0} = 1$, $f^{\prime}_{0} = 0$ in Eqs. (52) and (53), using of the condition that the displacement of j end of element $f_{j} = f^{\prime}_{j} = 0$, the initial parameters Q_β0 and M_β0 can be solved, thus the elements $k_{1,1}^{f}$ and $k_{2,1}^{f}$ in the first column of the $[{\mathbf{K}}_{f} ]$ can be obtained. Then, by substituting Q_β0 and M_β0 into Eqs. (54) and (55) and making z = l, the elements $k_{4,1}^{f}$ and $k_{3,1}^{f}$ are obtained. Similarly, the other column elements of the element stiffness matrix corresponding to the generalized displacement in Eq. (53) can be obtained. The lower triangular elements of the $[{\mathbf{K}}_{f} ]$ are listed as follows:

$$k_{1,1}^{f} = k_{3,3}^{f} = - k_{3,1}^{f} = \frac{{k^{3} E_{c} I_{\beta } }}{D}\sinh kl$$

$$k_{2,1}^{f} = k_{4,1}^{f} = - k_{3,2}^{f} = - k_{4,3}^{f} = - \frac{{k^{2} E_{c} I_{\beta } }}{D}(\cosh kl - 1)$$

$$k_{2,2} = k_{4,4} = \frac{{kE_{c} I_{\beta } }}{D}(kl\cosh kl - \sinh kl)$$

$$k_{4,2}^{f} = \frac{{kE_{c} I_{\beta } }}{D}(\sinh kl - kl)$$

in which D = klsinhkl + 2-2coshkl.

$$[{\varvec{K}}_{{\varvec{w}}} ] = \frac{{E_{c} I_{x} }}{{l^{3} }}\left[ {\begin{array}{*{20}c} {12} & {6l} & { - 12} & {6l} \\ {} & {4l^{2} } & { - 6l} & {2l^{2} } \\ \vdots & {} & {12} & { - 6l} \\ {{\text{Symm}}} & \ldots & {} & {4l^{2} } \\ \end{array} } \right]$$

(62)

The generalized displacement expressions (52) and (53) of the element are used to represent the generalized displacements of the nodes at both ends of the element. The matrix expression of the shape function of the generalized displacement can be obtained by solving the initial parameters simultaneously and substituting them into the displacement function formula (52). On this basis, the equivalent nodal force vector of the element can be obtained by using the principle of virtual work. Under uniform load q, the equivalent nodal force vector {P_q} of the element can be expressed as follows:

$$\{ {\varvec{P}}_{{\varvec{f}}} \} = (q/2)\left[ {\begin{array}{*{20}c} l & { - \varpi } & l & \varpi \\ \end{array} } \right]^{{\text{T}}}$$

(63)

where $\varpi = [(kl)^{2} (1 + \cosh kl) + 4(\cosh kl - kl\sinh kl - 1)]/(k^{2} D)$.

According to relevant literature (Zhou et al, 2022), the equivalent node load column vector corresponding to EBB is shown in Eq. (64).

$$\{ {\varvec{P}}_{{\varvec{w}}} \} = - (q/2)\left[ {\begin{array}{*{20}c} l & {l^{2} /6} & l & { - l^{2} /6} \\ \end{array} } \right]^{{\text{T}}}$$

(64)

6 Numerical Example

In this part, a simply supported composite box girder is selected as the analysis object, and the accuracy of the flexural displacement function proposed in this paper is verified by comparing the stress results. Then, a cantilever composite box girder is used to analyze the distribution characteristics of the generalized internal moment and bending moment. Finally, the effectiveness of beam-type element finite model is verified by an example of a continuous composite box girder with varying depth cross-section. Additionally, the 3D FEM of the presented numerical examples is established by using software ANSYS, and the analysis results are compared.

6.1 Example 1: Simply Supported Composite Box Girder

A simply supported corrugated steel web composite box girder model with a calculated span of 18 m is shown in Fig. 6. This case has also been analyzed in the study (Chawalit et al, 2004). The loading conditions are as follows: (1) concentrated load on the top of the web P = 3.40 MN; (2) uniformly distributed load q = 0.54 MN/m. Figure 6b and c shows the cross-section and the details of the steel web of the beam, respectively. The upper flange and lower flange of composite box girder bear 1.80 MN and 15.30 MN prestressing force, respectively. The elastic modulus and shear modulus of concrete and steel are E_c = 31GPa, G_c = 12.92GPa, E_s = 200GPa, G_s = 76.92GPa. The equivalent shear modulus of corrugated steel webs is G_w = 69.23GPa.

Fig. 6

Simply supported composite box girder with corrugated steel webs (m): a load cases; b cross-section; c detailed drawing of steel web

In this example, the flexure of the composite box girder is decomposed into three flexure states: EBB satisfying quasi-plane assumption, equivalent flexural deformation of web (EFW) and shear lag deformation of flanges (SLF). The 3D FEM used to verify the flexural analysis theory is shown in Fig. 7. The upper and lower flanges of the composite box girder were simulated using the solid element solid45, and the corrugated steel webs were simulated using the shell63 element. The shell and solid elements were coupled using the MPC method in ANSYS.

Fig. 7

Three-dimensional finite element model of composite box girder

Under load cases 1 and 2, the normal stresses of sections I and II are vertically distributed as shown in Figs. 8 and  9 respectively. From the figures, the analysis results considering the web equivalent flexural deformation are satisfactory agreement with the 3D FEM analysis results. Under load cases 1 and 2, the entire beam section is in compression (the stress value is negative). However, when considering the equivalent flexural deformation of web, the lower flanges of some control sections (Figs. 8a and 9b) will be in tension. Therefore, the EBB analysis method based on the quasi-plane assumption may lead to the unsafe design of structure.

Fig. 8

Vertical distribution of section normal stress under concentrated loading: a section I; b section II

Fig. 9

Vertical distribution of section normal stress under uniform loading: a section I; b section II

To quantitatively analyze the influence of the EFW and SLF on the flexural stress of the composite box girder, it is necessary to analyze the stress increase coefficients defined by Eqs. (34) and (35). Figure 10 shows the distribution of the stress increase coefficients at the top of sections I of the composite box girder under load cases 1 and 2 without the prestressing force, respectively. As shown in Fig. 10, when considering the EFW and SLF, the stress increase coefficients along the transverse distribution are in good agreement with the 3D FEM analysis results. As can be seen in Fig. 10a, the maximum stress at the top of section I increased by about 40% under the concentrated loading. The increase caused by the EFW is approximately 30% and the increase caused by the SLF is approximately 10%. As can be seen from Fig. 10b, the maximum stress at the top of section I increased by about 14% under uniform loading. The increase caused by the EFW is 10%, while the increase caused by the SLF is 4%. Therefore, the EFW has an important influence on the flexural stress of the composite box girder, especially near the concentrated load.

Fig. 10

Distribution of stress increase coefficient at top of section I: a under load case 1; b under load case 2

Figure 11 shows the deflection curves of the composite box girder under load cases 1 and 2 calculated by the method in this paper, finite segment method (FSM) (Chawalit et al, 2004) and 3D FEM. As shown in Fig. 11, when considering the EFW and SLF, the deflection curve results are in good agreement with 3D FEM results. When the influence of EFW is considered, the calculated deflection adequately corresponds to the result of FSM, but is smaller than the result obtained by the 3D FEM. The deflection f caused by the EFW is large, and resulted in a large increase in the deflection of the composite box girder. The deflection g caused by the SLF is relatively small. To quantitatively analyze the influence of EFW and SLF on the deflection of composite box girder, Table 1 lists the deflection displacement values of the mid-span cross-section under load cases 1 and 2 without the prestressing force. As presented in Table 1, the deflection caused by the EFW increased by approximately 53%, while that caused by the SLF increased by approximately 6%.

Fig. 11

Deflection curves of example: a under load case 1; b under load case 2

Table 1 Deflection of mid-span section of simply supported composite box girder

6.2 Example 2: Cantilever Composite Box Girder

The cross-section dimension and material parameters of the cantilever composite box girder are the same as those in the first example. The calculated span of the composite box girder is 7.2 m, the uniformly distributed load q is 10kN/m. According to the proposed analysis theory, the bending moment M and generalized moment M_β and M_ζ corresponding to the three flexural deformation states were calculated. The distribution form of each moment along the beam axis is shown in Fig. 12.

Fig. 12

Internal force distribution of cantilever composite box girder

As can be easily seen in Fig. 12, the bending moment M of the cantilever composite box girder is always negative along the beam axis, while the generalized moment M_β and M_ζ are either positive or negative along the beam axis. According to Eqs. (34) and (35), when the sign of moment M is the same as that of the generalized moment M_β and M_ζ, the stress increase coefficients C_β and C_ζ are positive, otherwise C_β and C_ζ are negative. Therefore, when the stress increase coefficients C_β and C_ζ are negative, the phenomenon of the negative EFW and negative SLF occurs, as shown in Fig. 12.

6.3 Example 3: Continuous Composite Box Girder With Varying Depth

To verify the effectiveness of the proposed beam-type finite element method, a two-span continuous composite box girder with varying depth is considered as a numerical example (Ji et al, 2016). The model span combination is (3000 + 3000) mm, the beam depth of the middle support is 350 mm, and the side support is 200 mm. The elastic modulus of concrete is 3.45GPa, Poisson’s ratio is 0.2, and the shear modulus of steel is 7.92GPa. The loading conditions are as follows: (1) vertical uniform loading q = 6N/mm; (2) concentrated loading P = 15kN symmetrically applied to the mid-span section. The load distribution and section form of the composite box girder are shown in Fig. 13.

Fig. 13

Continuous composite box girder with varying depth (mm): a composite box girder; b cross-section; c corrugated web

Based on the beam-type finite element model established in this paper, a beam-type finite element calculation program 3BE is developed. The continuous beam was divided into 120 beam elements along the beam axis, and the length of each beam segment was 5 cm. The deflection curves of the continuous composite box girder under uniform and concentrated loading are shown in Fig. 14. As can be seen, The deflection curve of the sum of the three deflections is very close to that obtained by 3D FEM. To quantitatively analyze the influence of the EFW and SLF on deflection of the composite box girder, the displacement values of the mid-span section under each flexural deformation state are listed in Table 2. Under uniform load, the deflection of the composite box girder caused by the EFW and SLF increased by 100% and 20%, respectively. When the mid-span was subjected to concentrated load, the deflection increased by 113% and 23%, owing to the EFW and SLF, respectively.

Fig. 14

Deflection curve of continuous composite box girder: a uniform loading; b concentrated loading

Table 2 Deflection of mid-span section of continuous composite box girder

The distribution curve of the bending moment M and generalized moment M_β and M_ζ calculated by the 3BE program is shown in Fig. 15. Under uniform loading, the generalized moment curve has a peak value at the middle support, while the curve in other parts is smooth and even. Under the action of concentrated load, the generalized moment curve has peak value at the points of the middle support and concentrated load. Therefore, the generalized moment curve has a peak at the point of shear discontinuity. Unlike the variation of bending moment distribution, the generalized moment rapidly increased or decreased near the peak point. For this continuous beam, areas I and II in Fig. 15a are the range of the negative SLF and negative EFW.

Fig. 15

Curves of internal force distribution of continuous composite box girder with varying depth: a uniform loading; b concentrated loading

Owing to the SLF and EFW, the distribution of additional stress along the cross-section is not uniform, which inevitably leads to the uneven distribution of the stress increase coefficients C_β and C_ζ along the cross-section of the beam. The maximum stress increase coefficients C_max,β and C_max,ζ at the top of the section were selected, and their distribution along the beam axis is shown in Fig. 16. According to the expression of the stress increase coefficient and Fig. 16, there is an asymptote at the beam axis reverse bending point (M = 0), and the absolute value of the stress increase coefficient near the asymptote is large. The stress increase coefficients C_max,β and C_max,ζ also have large values at the position of the peak point in the curve of the generalized moment. In this example, the influence of the EFW and SLF on the stress of the composite box girder is more than 1.5, and this should be carefully considered in practical projects.

Fig. 16

Distribution of stress increase coefficients along beam axis of continuous composite box girder with varying depth: a uniform loading; b concentrated loading

7 Conclusion

In this study, a new flexural displacement model of composite box girder considering the accordion effect and shear deformation of steel web and the shear lag effect of flange is established. By introducing generalized deflection w, f and g, the complex flexural deformation of a composite box girder is decoupled into the superposition of three independent and simple flexural deformations. Based on the simplified deflection state, a new beam-type finite element method is developed. Through the analysis of numerical examples, the following main conclusions can be drawn:

• (1) Compared with existing methods, the method proposed in this study not only has a simple analysis process, but also can obtain higher-precision flexural stress and deformation results. What’s more, this method can directly obtain the generalized moment and deformation caused by equivalent steel web deformation and flange shear lag effect.

• (2) The generalized moment curve has a peak at the point of shear discontinuity, and the generalized moment increases or decreases more rapidly near the peak point. When the generalized moment of the section is opposite to the sign of the bending moment, a negative equivalent steel web deformation and negative shear lag effect occur at the corresponding cross-section.

• (3) The numerical results show that the equivalent deformation of steel webs and the shear lag effect of flanges have great influence on the normal stress of a composite box girder near the shear discontinuity point. Moreover, the influence of equivalent deformation of steel webs on the deflection is greater than that of shear lag effect of flange.

• (4) The numerical example results show that the stress increase coefficient C_β caused by generalized shear deformation even exceeds 1.2 in the cross-sections near the concentrated loads or the middle supports. The deflection caused by generalized shear deformation reaches or even exceeds the deflection caused by the EBB, while the deflection caused by shear lag effect is about 20–30% of the deflection of the EBB.