A modified analysis method of mechanical properties of trapezoidal composite box girders

Abstract

In research on the vertical bending mechanical properties of trapezoidal box girders with corrugated steel webs, the maximum angular rotation attributable to the in-plane shear deformation of flanges is traditionally considered as the generalized displacement function. However, this analysis method is very complex and the mechanical concepts are not well-understood. To address this, the presented work adopts the additional deflection induced by the shear lag effect as the generalized displacement function. Furthermore, the accordion effect, shear lag, shear deformation, and the self-equilibrium conditions of the shear lag warping stress and bending moment are considered comprehensively. The differential equations and the corresponding natural boundary conditions of the composite box girders in the elastic range are established using the energy variational method. Further, the closed-form solutions of the generalized displacements are obtained. The results of the analysis method presented, a modification of the traditional shear lag theory algorithm, had high agreement with finite element simulation results. In comparison to the traditional analysis theories, the accuracy of this modified method was improved. Thus, the method presented provides a strong basis for understanding the mechanical properties of composite box girders.

1 Introduction

With the rapid development of transportation needs, the width and span of bridge structures are continuously increasing [1,2,3]. The trapezoidal box girder has good bending and torsion resistance, but also has a large top slab width, which effectively increases the width of the bridge deck [4,5,6]. For example, considering the Sunshine Skyway Bridge built in the United States in 1987, the Tatara Bridge completed in Japan in 1999, and the Maillau Viaduct operated in France in 2004, the main beams of such long-span bridges all used trapezoidal section beams. At present, there are more than 850,000 highway bridges in China, including many trapezoidal box girder bridges with large spans (i.e. the Changsha Xiangjiang River North Bridge and the Sutong Bridge). Hence, the trapezoidal section beams have a broad application prospect [2, 4, 6]. However, the traditional prestressed concrete (PC) trapezoidal box girder is structurally heavy, has low prestressing efficiency, and is prone to cracking of webs and flanges (as shown in Fig. 1), which leads to a variety of bridge damage issues. The main cause of bridge damage is the strong mutual restraint between the flange and the web [7,8,9,10].

Fig. 1

PC trapezoidal box girder bridge in operation or maintenance

Based on the aforementioned factors, in the early 1980s, French scholars were the first to propose replacing the traditional PC box girder bridge webs with corrugated steel webs, and eventually built the Cognac bridge in 1986 [10,11,12]. Currently, the composite box girder bridges with corrugated steel webs are very common in many countries around the world [12,13,14], such as Germany, South Korea, Spain, and Venezuela. In particular, Japan has more than 200 such girder bridges, while China has more than 100 composite girder bridges with corrugated steel webs. Since the trapezoidal composite girder bridge with corrugated steel webs is lightweight, has high prestress efficiency, and effectively eliminates any the bridge damage caused by temperature effect, shrinkage, and creep, it has good development prospects (as shown in Fig. 2) [12, 15, 16]. However, in existing research, the accordion effect, shear lag, Timoshenko shear deformation, and the self-equilibrium conditions have yet to be investigated comprehensively. Additionally, the mechanical performance analysis of trapezoidal composite box girders has certain limitations. For example, the self-equilibrium conditions of the shear lag warping stress and bending moment are not considered in traditional theory [16,17,18]. Based on this, the traditional analysis method was modified in this study and the calculation example indicates that the modified method significantly improves the calculation accuracy of this type of structure. Therefore, the theory presented will provide a more accurate theoretical basis for the design of composite box girders [19,20,21].

Fig. 2

Trapezoidal box girder bridge with corrugated steel webs

2 Governing differential equations and natural boundary conditions of composite trapezoidal box girders

2.1 Modified formula for the shear modulus of corrugated steel webs

According to previous research results in [11, 18], the modified value of the shear modulus of corrugated steel web can be expressed as

$$ G_{s} = \frac{{L_{1} + L_{3} }}{{L_{1} + L_{2} }}\frac{{E_{s} }}{{2(1 + \upsilon_{s} )}} $$

(1)

where $E_{s}$ and $\upsilon_{s}$ are the elastic modulus and Poisson’s ratio of corrugated steel web material, respectively; and $L_{1} ,L_{2} ,L_{3}$ are the length of the flat section, the length of the inclined slab section, and the projection of the inclined slab section on the horizontal plane of the corrugated steel web, respectively. In mechanical analysis, the $z_{1}$ longitudinal axis is considered to be the intersection line between the corrugated steel webs and the upper flange or lower flange (as shown in Fig. 3).

Fig. 3

Geometric shape of corrugated steel webs

2.2 Setting of the longitudinal warping displacement function of trapezoidal box girder flanges

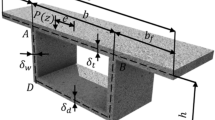
In the symmetric bending state, the composite trapezoidal box girder span is $L$(as shown in Fig. 4). $w(z),\theta (z)$ are the vertical deflection and vertical rotation angles, respectively, of the section of the composite box girders based on the elementary beam theory. $v_{1} (z),v_{2} (z),v_{3} (z)$ are the vertical deflections of composite box girder caused by the shear lag effect of the cantilever slab, upper flange, and lower flange, respectively. The longitudinal displacements $U_{1} ,U_{2} ,U_{3}$ of the cantilever slab and the upper and lower flanges are the sum of the theoretical values of the elementary beam, the longitudinal warping displacement of the box girder flanges caused by the shear lag effect, and the interaction of the shear lag effect between the flanges. This can be expressed as

Fig. 4

Cross section of trapezoidal box girders with corrugated steel webs

• (1) Cantilever slab ($b_{1}$)

  $$ U_{1} (x,y,z) = y\theta + [y - \lambda_{1} \varphi_{1} (x) - \rho_{1} ]v_{1}{\prime} + (y - \rho_{2} )v_{2}{\prime} + (y - \rho_{3} )v_{3}{\prime} $$

  (2)

  where $\varphi_{1} (x) = \cos \frac{{\pi (x - b_{2} )}}{{2b_{1} }}$ is the non-uniform distribution function of the cantilever slab of the composite trapezoidal box girder;$\lambda_{1} ,\rho_{1}$ are the modified factors when the cantilever slab meets the self-equilibrium conditions of the shear lag warping stress and bending moment; and $b_{2} \le x \le b_{1} + b_{2}$.

  Then, the shear lag warping stress of the cantilever flange can be expressed as

  $$ \sigma_{j1} = E[y - \lambda_{1} \varphi_{1} (x)]v_{1}^{\prime \prime } - E\rho_{1} v_{1}^{\prime \prime } $$

  (3)

  where $\lambda_{1} ,\rho_{1}$ are constant coefficients to meet $\int_{A} {\sigma_{j1} dA = 0}$ and $\int_{A} {\sigma_{j1} ydA = 0}$;$\lambda_{1} = \frac{\pi I}{{4h_{1} b_{1} t_{1} }},\rho_{1} = \frac{ - I}{{Ah_{1} }}$.

• (2) Upper flange ($b_{2}$)

  $$ U_{2} (x,y,z) = y\theta + [y - \lambda_{2} \varphi_{2} (x) - \rho_{2} ]v_{2}^{\prime } + (y - \rho_{1} )v_{1}^{\prime } + (y - \rho_{3} )v_{3}^{\prime } $$

  (4)

  where $\varphi_{2} (x) = \cos \frac{\pi x}{{2b_{2} }}$ is the non-uniform distribution function of the upper flange of the composite trapezoidal box girder; $\lambda_{2} ,\rho_{2}$ are the modified factors for the upper flange to meet the self-equilibrium conditions for shear lag warping stress and bending moment; and $0 \le x \le b_{2}$.

  Then, the shear lag warping stress of the upper flange can be given by

  $$ \sigma_{j2} = E[y - \lambda_{2} \varphi_{2} (x)]v_{2}^{\prime \prime } - E\rho_{2} v_{2}^{\prime \prime } $$

  (5)

  Similarly, where $\lambda_{2} ,\rho_{2}$ are constant coefficients to meet $\int_{A} {\sigma_{j2} dA = 0}$ and $\int_{A} {\sigma_{j2} ydA = 0}$. Further, $\lambda_{2} = \frac{\pi I}{{4h_{1} b_{2} t_{1} }},\rho_{2} = \frac{ - I}{{Ah_{1} }}$.

• (3) Lower flange $\left( {b_{3} } \right)$

  $$ U_{3} (x,y,z) = y\theta + [y - \lambda_{3} \varphi_{3} (x) - \rho_{3} ]v_{3}^{\prime } + (y - \rho_{1} )v_{1}^{\prime } + (y - \rho_{2} )v_{2}^{\prime } $$

  (6)

  where $\varphi_{3} (x) = \cos \frac{\pi x}{{2b_{3} }}$ is the non-uniform distribution function of the lower flange of the composite trapezoidal box girder;$\lambda_{3} ,\rho_{3}$ are the modified factors for the lower flange to meet the self-equilibrium conditions for shear lag warping stress and bending moment; and $0 \le x \le b_{3}$.

  Then, the shear lag warping stress of the lower flange is expressed as

  $$ \sigma_{j3} = E\left[ {y - \lambda_{3} \varphi_{3} (x)} \right]v_{3}^{\prime \prime } - E\rho_{3} v_{3}^{\prime \prime } $$

  (7)

  where $\lambda_{3} ,\rho_{3}$ are constant coefficients to meet $\int_{A} {\sigma_{j3} dA = 0}$ and $\int_{A} {\sigma_{j3} ydA = 0}$. Further, $\lambda_{3} = \frac{ - \pi I}{{4h_{2} b_{3} t_{3} }},\rho_{3} = \frac{I}{{Ah_{2} }}$.

  In the study, the upper, lower, and cantilever flanges were regarded as independent shear lag warping mechanical systems, which should respectively meet the self-equilibrium conditions for the shear lag warping stress and bending moment. The overall shear lag mechanical system of box girders after the superposition of the three also met the self-equilibrium condition. Further, the width of the top slab is the sum of the widths of the cantilever slab and the upper flange, while the width of the bottom slab is the width of the lower flange.

2.3 Total potential energy of composite trapezoidal box girders

• (1) Stress of the cantilever slab, upper flanges, and lower flanges of composite trapezoidal box girders.

• (1) Cantilever slab ($b_{1}$)

  $$ \sigma_{XB} = Ey\theta^{\prime } + E(y - \lambda_{1} \varphi_{1} )v_{1}^{\prime \prime } - E\rho_{1} v_{1}^{\prime \prime } + E(y - \rho_{2} )v_{2}^{\prime \prime } + E(y - \rho_{3} )v_{3}^{\prime \prime } $$

  (8)
  $$ \tau_{j1} = G\frac{{\partial U_{1} }}{\partial x} $$

  (9)

• (2) Upper flange ($b_{2}$)

  $$ \sigma_{SY} = Ey\theta^{\prime } + E(y - \lambda_{2} \varphi_{2} )v_{2}^{\prime \prime } - E\rho_{2} v_{2}^{\prime \prime } + E(y - \rho_{1} )v_{1}^{\prime \prime } + E(y - \rho_{3} )v_{3}^{\prime \prime } $$

  (10)
  $$ \tau_{j2} = G\frac{{\partial U_{2} }}{\partial x} $$

  (11)

• (3) Lower flange ($b_{3}$)

  $$ \sigma_{XY} = Ey\theta^{\prime } + E(y - \lambda_{3} \varphi_{3} )v_{3}^{\prime \prime } - E\rho_{3} v_{3}^{\prime \prime } + E(y - \rho_{1} )v_{1}^{\prime \prime } + E(y - \rho_{2} )v_{2}^{\prime \prime } $$

  (12)
  $$ \tau_{j3} = G\frac{{\partial U_{3} }}{\partial x} $$

  (13)

• (2) Deformation potential energy of composite trapezoidal box girders

  $$ \Pi_{z1} = \frac{1}{2}\iint {(\frac{{\sigma_{XB}^{2} }}{E} + \frac{{\tau_{j1}^{2} }}{G} + \frac{{\sigma_{SY}^{2} }}{E} + \frac{{\tau_{j2}^{2} }}{G}} + \frac{{\sigma_{XY}^{2} }}{E} + \frac{{\tau_{j3}^{2} }}{G})dAdz $$

  (14)
  $$ \Pi_{z1} = \frac{1}{2}\int_{0}^{l} {EI} (\theta^{\prime } )^{2} dz + \frac{E}{2}\int_{0}^{l} {I_{1} } (v_{1}^{\prime \prime } )^{2} dz + \frac{E}{2}\int_{0}^{l} {I_{3} } (v_{3}^{\prime \prime } )^{2} dz + E\int_{0}^{l} {2I_{4} } (v_{1}^{^{\prime\prime}} v_{2}^{^{\prime\prime}} )dz + E\int_{0}^{l} {2I_{5} } (v_{1}^{^{\prime\prime}} v_{3}^{^{\prime\prime}} )dz + \int_{0}^{l} {I_{2} } (v_{2}^{\prime \prime } )^{2} dz + $$
  $$ E\int_{0}^{l} {2I_{6} } (v_{2}^{\prime \prime } v_{3}^{\prime \prime } )dz + \frac{G}{2}\int_{0}^{l} {I_{G1} } (v_{1}^{\prime } )^{2} dz + \frac{G}{2}\int_{0}^{l} {I_{G2} } (v_{2}^{\prime } )^{2} dz + \frac{G}{2}\int_{0}^{l} {I_{G3} } (v_{3}^{\prime } )^{2} dz $$

  (15)

  where $I_{1} = I + \rho_{1}^{2} A + \lambda_{1}^{2} b_{1} t_{1} - \frac{8}{\pi }\lambda_{1} h_{1} b_{1} t_{1} + \frac{8}{\pi }\lambda_{1} \rho_{1} b_{1} t_{1} ;\;I_{2} = I + \rho_{2}^{2} A + \lambda_{2}^{2} b_{2} t_{2} - \frac{8}{\pi }\lambda_{2} h_{1} b_{2} t_{2} + \frac{8}{\pi }\lambda_{2} \rho_{2} b_{2} t_{2} ;$

  $I_{3} = I + \rho_{3}^{2} A + \lambda_{3}^{2} b_{3} t_{3} + \frac{8}{\pi }\lambda_{3} h_{2} b_{3} t_{3} + \frac{8}{\pi }\lambda_{3} \rho_{3} b_{3} t_{3} ;$$I_{4} = I + \rho_{1} \rho_{2} A + \frac{4}{\pi }\lambda_{1} b_{1} t_{1} (\rho_{2} - h_{1} ) + \frac{4}{\pi }\lambda_{2} b_{2} t_{2} (\rho_{1} - h_{1} );$

  $$ I_{5} = I + \rho_{1} \rho_{3} A + \frac{4}{\pi }\lambda_{1} b_{1} t_{1} (\rho_{3} - h_{1} ) + \frac{4}{\pi }\lambda_{3} b_{3} t_{3} (\rho_{1} + h_{2} );\;I_{6} = I + \rho_{2} \rho_{3} A + \frac{4}{\pi }\lambda_{2} b_{2} t_{2} (\rho_{3} - h_{1} ) + \frac{4}{\pi }\lambda_{3} b_{3} t_{3} (\rho_{2} + h_{2} ); $$

  $I_{G1} = \frac{{\lambda_{1}^{2} \pi^{2} t_{1} }}{{4b_{1} }};I_{G2} = \frac{{\lambda_{2}^{2} \pi^{2} t_{2} }}{{4b_{2} }};I_{G3} = \frac{{\lambda_{3}^{2} \pi^{2} t_{3} }}{{4b_{3} }};$$I = \int_{{A_{1} }} {y^{2} dA_{1} } + \int_{{A_{2} }} {y^{2} dA_{2} + \int_{{A_{3} }} {y^{2} dA_{3} } }$. $A_{1}$ is the area of the cantilever slab;$A_{2}$ is the area of the upper flange;$A_{3}$ is the area of the lower flange; and $A = A_{1} + A_{2} + A_{3}$.

The shear strain energy of corrugated steel webs is

$$ \Pi_{zj} = \frac{1}{2}\int_{0}^{l} {G_{s} A_{s} (w^{\prime } - \theta )^{2} dz} $$

(16)

$G_{s}$ is the modified shear modulus of corrugated steel webs; $A_{s}$ is the effective shear area of corrugated steel webs.

The external loading-induced potential energy

$$ \begin{aligned} \Pi_{p} = & - \int_{0}^{l} {q_{y} (z)[w(z) + v_{1} (z) + v_{2} (z) + v_{3} (z)]dz - } Q(z)[w(z) + v_{1} (z) + v_{2} (z) + v_{3} (z)]\left| {_{0}^{l} } \right. \\ & + [M_{1} (z)v_{1}{\prime} (z) + M_{2} (z)v_{2}{\prime} (z) + M_{3} (z)v_{3}{\prime} (z) + M_{z} (z)\theta (z)]\left| {_{0}^{l} } \right. \\ \end{aligned} $$

(17)

Then, the total potential energy of composite box girders can be obtained as follows:

$$ \Pi = \Pi_{z1} + \Pi_{zj} + \Pi_{p} $$

(18)

where $M_{1} (z),M_{2} (z),M_{3} (z)$ are the bending moments about the x-axis caused by the shear lag effect of the cantilever slab, upper flange, and lower flange of the composite box girder; $M_{z} (z)$ is the bending moment at the section end of the composite trapezoidal box girder caused by the vertical angle $\theta (z)$ about the $x$-axis; $Q_{y}$ is the vertical shear force at the end of composite box girder section; $q_{y}$ is the vertical distributed load on the composite box girder; $E$ and $G$ are the Young’s modulus and shear modulus of the top and bottom slabs, respectively; and $I$ is the moment of inertia of the composite box girder about the $x$ axis.

2.4 Governing differential equations and natural boundary conditions of composite box girders

According to the energy-variation principle $\delta \Pi = 0$, the governing differential equations and natural boundary conditions of composite trapezoidal box girders can be derived as follows.

Related shear lag warping mechanical system:

$$ EI_{1} v_{1}^{(4)} - GI_{G1} v_{1}^{\prime \prime } + EI_{4} v_{2}^{(4)} + EI_{5} v_{3}^{(4)} - q_{y} = 0 $$

(19)

$$ EI_{2} v_{2}^{(4)} - GI_{G2} v_{2}^{\prime \prime } + EI_{4} v_{1}^{(4)} + EI_{6} v_{3}^{(4)} - q_{y} = 0 $$

(20)

$$ EI_{3} v_{3}^{(4)} - GI_{G3} v_{3}^{\prime \prime } + EI_{5} v_{1}^{(4)} + EI_{6} v_{2}^{(4)} - q_{y} = 0 $$

(21)

$$ [EI_{1} v_{1}^{\prime \prime } + EI_{4} v_{2}^{\prime \prime } + EI_{5} v_{3}^{\prime \prime } - M_{1} )]\left| {_{0}^{l} \delta v_{1}^{\prime } } \right. = 0 $$

(22)

$$ [EI_{1} v_{1}^{(3)} + EI_{4} v_{2}^{(3)} + EI_{5} v_{3}^{(3)} + Q(z)]\left| {_{0}^{l} } \right.\delta v_{1} = 0 $$

(23)

$$ [EI_{2} v_{2}^{\prime \prime } + EI_{4} v_{1}^{\prime \prime } + EI_{6} v_{3}^{\prime \prime } - M_{2} )]\left| {_{0}^{l} \delta v_{2}^{\prime } } \right. = 0 $$

(24)

$$ [EI_{2} v_{2}^{(3)} + EI_{4} v_{1}^{(3)} + EI_{6} v_{3}^{(3)} + Q(z)]\left| {_{0}^{l} } \right.\delta v_{2} = 0 $$

(25)

$$ [EI_{3} v_{3}^{\prime \prime } + EI_{5} v_{1}^{\prime \prime } + EI_{6} v_{2}^{\prime \prime } - M_{3} )]\left| {_{0}^{l} \delta v_{3}^{\prime } } \right. = 0 $$

(26)

$$ [EI_{3} v_{3}^{(3)} + EI_{5} v_{1}^{(3)} + EI_{6} v_{2}^{(3)} + Q(z)]\left| {_{0}^{l} } \right.\delta v_{3} = 0 $$

(27)

Related elementary beam mechanical system:

$$ EI\theta^{\prime \prime } + G_{s} A_{s} (w^{\prime } - \theta ) = 0 $$

(28)

$$ G_{s} A_{s} (w^{\prime \prime } - \theta^{\prime } ) + q_{y} = 0 $$

(29)

$$ [EI\theta{\prime} + M_{z} )]\left| {_{0}^{l} \delta \theta } \right. = 0 $$

(30)

$$ [G_{s} A_{s} (w^{\prime } - \theta ) - Q]\left| {_{0}^{l} } \right.\delta w = 0 $$

(31)

According to the abovementioned differential equations, a complete mechanical system of composite trapezoidal box girders comprised two independent mechanical systems, primarily, the superposition of elementary beam theory and shear lag theory, where a coupling relationship between them did not exist. Further, these equations are only applicable to the mechanical analysis of the elastic range of trapezoidal composite box girders.

2.5 Solutions of the governing differential equations of composite trapezoidal box girders

From the differential Eqs. (19) and (20), Eq. (32) was obtained as follows:

$$ v_{2}^{(4)} + M_{1} v_{2}^{\prime \prime } + M_{2} v_{1}^{(4)} + M_{3} v_{1}^{\prime \prime } + M_{4} q_{y} = 0 $$

(32)

where $M_{1} = \frac{{GI_{G2} I_{5} }}{{E(I_{4} I_{6} - I_{5} I_{2} )}};M_{2} = \frac{{I_{1} I_{6} - I_{4} I_{5} }}{{I_{4} I_{6} - I_{5} I_{2} }};$$M_{3} = \frac{{ - GI_{6} I_{G1} }}{{E(I_{4} I_{6} - I_{5} I_{2} )}};M_{4} = \frac{{I_{5} - I_{6} }}{{E(I_{4} I_{6} - I_{5} I_{2} )}}.$

From the differential Eqs. (20) and (21), Eq. (33) follows

$$ v_{2}^{(6)} + N_{1} v_{2}^{(4)} + N_{2} v_{2}^{\prime \prime } + N_{3} v_{1}^{(6)} + N_{4} v_{1}^{(4)} + N_{5} q_{y} = 0 $$

(33)

where $N_{1} = \frac{{G(I_{G2} I_{3} + I_{G3} I_{2} )}}{{E(I_{6}^{2} - I_{2} I_{3} )}};N_{2} = \frac{{ - G^{2} I_{G2} I_{G3} }}{{E^{2} (I_{6}^{2} - I_{2} I_{3} )}};N_{3} = \frac{{I_{5} I_{6} - I_{3} I_{4} }}{{I_{6}^{2} - I_{2} I_{3} }};$$N_{4} = \frac{{GI_{4} I_{G3} }}{{E(I_{6}^{2} - I_{2} I_{3} )}};N_{5} = \frac{{ - GI_{G3} }}{{E^{2} (I_{6}^{2} - I_{2} I_{3} )}} \circ$.

By sorting and replacing differential Eqs. (32) and (33), Eq. (34) can be expressed as

$$ v_{1}^{(8)} + \frac{{M_{2} N_{1} - M_{1} N_{3} + (M_{3} - N_{4} )}}{{M_{2} - N_{3} }}v_{1}^{(6)} + \frac{{M_{2} N_{2} + M_{3} N_{1} - M_{1} N_{4} }}{{M_{2} - N_{3} }}v_{1}^{(4)} + \frac{{M_{3} N_{2} }}{{M_{2} - N_{3} }}v_{1}^{\prime \prime } + \frac{{M_{4} N_{2} - M_{1} N_{5} }}{{M_{2} - N_{3} }}q_{y} = 0 $$

(34)

Based on Eq. (34), the solution of its eigenvalue equation can be given as.

$r_{1,2} = \pm \eta_{1} ;$ $r_{3,4} = \pm \eta_{2} ;$ $r_{5,6} = \pm \eta_{3}$.

Then, the general solution of equation $v_{1} (z)$ was obtained as

$$ v_{1} (z) = c_{1} ch\eta_{1} z + c_{2} sh\eta_{1} z + c_{3} ch\eta_{2} z + c_{4} sh\eta_{2} z + c_{5} ch\eta_{3} z + c_{6} sh\eta_{3} z + c_{7} z + c_{8} + \frac{{ - q_{y} }}{{2GI_{G1} }}z^{2} $$

(35)

Based on the solution of equation $v_{1} (z)$, first assuming the form of the $v_{2} (z)$ and $v_{3} (z)$ solutions, substituting them into the differential Eqs. (19) to (21), and then obtaining the constant coefficients of the solutions of $v_{2} (z)$ and $v_{3} (z)$ equations,$v_{2} (z)$ and $v_{3} (z)$ equations were expressed as

$$ v_{2} (z) = c_{1} B_{1} ch\eta_{1} z + c_{2} B_{1} sh\eta_{1} z + c_{3} B_{3} ch\eta_{2} z + c_{4} B_{3} sh\eta_{2} z + c_{5} B_{5} ch\eta_{3} z + c_{6} B_{5} sh\eta_{3} z + c_{9} z + c_{10} + \frac{{ - q_{y} }}{{2GI_{G2} }}z^{2} $$

(36)

$$ v_{3} (z) = c_{1} D_{1} ch\eta_{1} z + c_{2} D_{1} sh\eta_{1} z + c_{3} D_{3} ch\eta_{2} z + c_{4} D_{3} sh\eta_{2} z + c_{5} D_{5} ch\eta_{3} z + c_{6} D_{5} sh\eta_{3} z + c_{11} z + c_{12} + \frac{{ - q_{y} }}{{2GI_{G3} }}z^{2} $$

(37)

where $B_{1} = \frac{{E(I_{4} I_{5} - I_{1} I_{6} )\eta_{1}^{2} + GI_{G1} I_{6} }}{{E(I_{4} I_{9} - I_{2} I_{8} )\eta_{1}^{2} + GI_{G2} I_{5} }};B_{3} = \frac{{E(I_{4} I_{5} - I_{1} I_{6} )\eta_{2}^{2} + GI_{G1} I_{6} }}{{E(I_{4} I_{9} - I_{2} I_{8} )\eta_{2}^{2} + GI_{G2} I_{5} }};\;B_{5} = \frac{{E(I_{4} I_{5} - I_{1} I_{6} )\eta_{3}^{2} + GI_{G1} I_{6} }}{{E(I_{4} I_{9} - I_{2} I_{8} )\eta_{3}^{2} + GI_{G2} I_{5} }};\;B_{5} = \frac{{E(I_{4} I_{5} - I_{1} I_{6} )\eta_{3}^{2} + GI_{G1} I_{6} }}{{E(I_{4} I_{9} - I_{2} I_{8} )\eta_{3}^{2} + GI_{G2} I_{5} }}.$

$$ D_{1} = \frac{{(GI_{G1} - EI_{1} \eta_{1}^{2} ) - B_{1} EI_{4} \eta_{1}^{2} }}{{EI_{5} \eta_{1}^{2} }};D_{3} = \frac{{(GI_{G1} - EI_{1} \eta_{1}^{2} ) - B_{1} EI_{4} \eta_{1}^{2} }}{{EI_{5} \eta_{1}^{2} }};D_{5} = \frac{{(GI_{G1} - EI_{1} \eta_{3}^{2} ) - B_{1} EI_{4} \eta_{3}^{2} }}{{EI_{5} \eta_{3}^{2} }}. $$

where $c_{1} ;c_{2} ;...;c_{12}$ are constant coefficients of equations $v_{1} (z),v_{2} (z)$, and $v_{3} (z)$, which can be solved according to corresponding boundary conditions.

Similarly, when differential Eqs. (28) and (29) are arranged and replaced, the solutions of $w(z)$ and $\theta (z)$ equations can be obtained as follows:

$$ w(z) = e_{1} z^{3} + e_{2} z^{2} + e_{3} z + e_{4} + \frac{{q_{y} }}{24EI}z^{4} $$

(38)

$$ \theta (z) = e_{1} (3z^{2} + \frac{6EI}{{G_{s} A_{s} }}) + e_{2} 2z + e_{3} + \frac{{q_{y} }}{{G_{s} A_{s} }}z + \frac{{q_{y} }}{6EI}z^{3} $$

(39)

where $e_{1} ,e_{2} ,e_{3} ,e_{4}$ are the constant coefficients of equation $w(z)$ and $\theta (z)$, which can be solved according to their corresponding boundary conditions.

3 Common boundary conditions of composite trapezoidal box girders

According to the boundary conditions (22) to (27) and (30) to (31), the specific boundary conditions of the composite trapezoidal box girder can be obtained. For example, the specific form can be expressed as.

• (1) The relevant $w(z)$ and $\theta (z)$ simply supported boundary conditions.

• (1) Uniformly distributed load

  $$ w(z)\left| {_{0}^{l} = 0} \right.{; }\theta^{\prime } (z)\left| {_{0}^{l} } \right. = 0 $$

  (40)

• (2) Concentrated load.

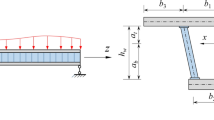
  When there is a single or several concentrated loads in the span (as shown in Fig. 5), and the adjacent distances are $L_{k1}$ and $L_{k2}$ about a load $P_{k}$, the $w(z),\theta (z)$ subscripts represent the $z_{1}$ or $z_{2}$ coordinate systems. The continuous boundary conditions of Point $k$ were expressed as

  $$ w_{1} (L_{k1} ) = w_{2} (0);w_{1}{\prime} (L) = w_{2}{\prime} (0);\theta_{1}{\prime} (L_{k1} ) = \theta_{2}{\prime} (0);\;\theta_{1} (L_{k1} ) - \theta_{2} (0) = \frac{{P_{k} }}{{G_{s} A_{s} }} $$

  (41)

  Fig. 5

  

  Coordinate and load systems of the composite box girder

• (2) Relevant $v_{1} (z)$,$v_{2} (z)$, and $v_{3} (z)$ simply supported boundary conditions.

Uniformly distributed load

$$ v_{1} (z)\left| {_{0}^{l} } \right.{ = 0 ; }v_{2} (z)\left| {_{0}^{l} } \right.{ = 0;}v_{3} (z)\left| {_{0}^{l} } \right.{ = 0;}\;v_{1}^{^{\prime\prime}} (z)\left| {_{0}^{l} } \right.{ = 0 ; }v_{2}^{^{\prime\prime}} (z)\left| {_{0}^{l} } \right.{ = 0;}v_{3}^{^{\prime\prime}} (z)\left| {_{0}^{l} } \right.{ = 0} $$

(42)

Similarly, other specific boundary conditions can be obtained based on Eqs. (22)–(27)and(30)–(31).

4 Example and analysis of composite trapezoidal box girders

For the composite trapezoidal box girder, the corrugated steel web was made of a high-quality Q235 steel, with the elastic modulus 206Gpa and Poisson's ratio 0.26; the thickness of the corrugated steel web was $t_{w}$ = 1.5 cm, and the beam height was $h$ = 3 m. The upper, lower, and cantilever flanges of the box girder were made of C50 concrete, with a thickness of $t_{1} = t_{2} = t_{3} =$ 0.25 m; the lengths of flanges were $b_{1}$ = 1.5 m,$b_{2}$ = 3 m, and $b_{3}$ = 2 m (as shown in Fig. 4). The corrugated form of the web is shown in Fig. 3, where $L_{1} = L_{2}$ = 43 cm,$L_{3}$ = 37 cm; in actual bridges, the corrugated steel web was connected with the upper and lower flanges using embedded connecting keys, and the corrugated steel webs were embedded 0.1m into the top and bottom slabs of concrete. In the mechanical analysis, the uniformly distributed load was $q_{k} (z) = 3 \times 10{\text{kN/m}}$, the concentrated load was $P_{k} (z) = 3L \times 10{\text{kN}}$, and $L$ was the span of the combined trapezoidal box girder. The finite element analysis (as shown in Fig. 6) was conducted using ANSYS software to establish the finite element calculation model. (1) The cantilever slabs, upper flange, and lower flange were simulated on solid element Solid65, and the top slab and bottom slab were divided into 7200 and 4000 elements, respectively. The corrugated steel webs were simulated on the Shell63 shell element, and divided into 3200 elements. Three diaphragms were arranged at both ends and in the middle of the box girder, and the diaphragm slabs were also simulated on solid element Solid65 and divided into 2520 elements (the diaphragm slab was 0.2m thick). (2) For the connection between the corrugated steel webs and the concrete top and bottom slabs, the MPC multi-point coupling contact method was applied. First, the grids were divided into solid and shell elements, and target elements TARGE170 and contact elements CONTA175 were added to different elements in the intersecting area. In this way, the top slab, bottom slab, and web slabs can be independently divided into grids, which ensures the accuracy of the simulation. (3) In this study, simply supported boundary conditions were used, which applied constraints in the x, y, and z directions at one end nodes of the box girder, and constraints in the z and y directions at the other end nodes. (4) In the numerical simulation, to reduce local effects, a concentrated force was symmetrically applied at the intersection of the flange and web slabs on both sides of the mid-span. Similarly, the uniformly distributed force was symmetrically applied in the form of a linear load at the intersection of the flange and web slabs on both sides. This paper adopted a 4-step loading form. Based on this, verified the linear elasticity of structural mechanical properties. But only the mechanical results of the final loading step are taken in the paper. In comparison to the theoretical analysis of the elastic range, finite element simulation could support the effectiveness of the theory proposed in this paper. The finite element calculation model example is shown in Fig. 6.

Fig. 6

Finite element model of the calculation example for a composite trapezoidal box girder ($L = 16{\text{m}}$)

Here, the traditional shear lag theory algorithm does not consider self-equilibrium for the shear lag warping stress and bending moment. Thus, the influence rates of the two algorithms are the differences between the calculated stress values of this theory and the traditional theory, and its ratio to the calculated stress value of the traditional theory. In the vertical bending state, the results are shown in Table 1, 2 and Fig. 7:

• (1) The calculated value of the theory derived in this paper was the sum of the theoretical values of the elementary beam and the influence value of shear lag. The complete mechanical system of the composite trapezoidal box girder comprised two independent mechanical systems, primarily, the superposition of the elementary beam and shear lag theories, where a coupling relationship did not exist between them. In comparison to previous results, the theoretical values obtained in this study were in good agreement with the finite element simulations.

• (2) Due to the introduction of the self-equilibrium conditions, the calculation accuracy of the theory derived in this paper was improved. For example, at the intersection of the top slab and corrugated steel web, the influence rate of the two algorithms was 20.7% under a concentrated load, and the influence rate of the two algorithms was 12.9% under uniform loading. Hence, the influence of the self-equilibrium conditions was related to the type of load distribution. In comparison to the top slab, the self-equilibrium conditions had less influence on the mechanical properties of the bottom slab. In other words, the calculated value of the traditional algorithm was evidently lower than the theoretical value presented in this study, which could be unfavourable to the durability design of this type of structure.

Table 1 Stress of the top slab for simply supported composite trapezoidal box girders [$L_{k1} = L_{k2} = 8m$] (concentrated load)

Table 2 Stress of the bottom slab for simply supported composite trapezoidal box girders [$L_{k1} = L_{k2} = 8m$] (concentrated load)

Fig. 7

Comparison between the traditional algorithm and the algorithm in this paper at the mid-span section ($L = 16m$)

Here, for box section girders, when calculated according to the elementary beam theory, the normal stress on the flange slabs is uniformly distributed along the width direction. However, in practical situations, when the composite trapezoidal box girder is vertically bent, the normal stress on the flange slabs is transmitted by shear stress. Due to the influence of shear deformation, the stress at the junction of the flange slabs and web slabs of the box girder is different from that at other positions, sometimes even significantly different. This phenomenon is called the shear lag effect, and the magnitude of the shear lag effect is reflected in the shear lag coefficients. The shear lag coefficients in this paper are the ratio of the presented theoretical value to the theoretical value of the elementary beam. Tables 1, 2 and Figs. 8, 9 and 10 indicate the following.

• (1) Due to the influence of the shear lag effect, the stress distribution of the top and bottom slabs of the trapezoidal box girder was uneven. Hence, the shear lag effect had a great impact on the mechanical properties of the composite trapezoidal box girder. The stress concentration was more severe in the concentrated load, while the stress concentration was relatively small in the uniform load. For example, at the intersection of the top slab and corrugated steel web, the shear lag coefficient was 1.58 in the concentrated load, and the shear lag coefficient was 1.16 in the uniform load. As the span increased, the influence of the shear lag effect decreased.

• (2) Due to the application of three different longitudinal displacement difference functions, the theoretical analysis of the shear lag effect presented in this study was more accurate. For example, the shear lag coefficients in this paper at the intersection of the top slab and the web and the top slab centre were 1.58 and 0.6, respectively. However, the shear lag coefficients at the intersection of the bottom slab and the web and the bottom slab centre were 1.49 and 0.75, respectively. However, according to the traditional shear lag theory, the shear lag coefficients at the intersection of the bottom slab and the web and the bottom slab centre should also be 1.58 and 0.6, respectively.

Fig. 8

Comparison of the stress on the top slab for composite trapezoidal box girders at the mid-span section (concentrated load, $L_{k1} = L_{k2} = 8m$)

Fig. 9

Comparison of the stress on the bottom slab for composite trapezoidal box girders at the mid-span section (concentrated load, $L_{k1} = L_{k2} = 8m$)

Fig. 10

Shear lag coefficients of top slab for simply supported composite trapezoidal box girder at the mid-span section

Here, due to the application of corrugated steel webs, the mutual constraint between the flange slabs and webs of composite box girders is weakened. In this type of structure, the top and bottom slabs mainly resist bending, while the corrugated steel web has a small contribution to resisting bending, and its main function is to resist shear. Therefore, the performance of corrugated steel webs is called the accordion effect. the accordion effect in the paper manifested in the stress difference between the corrugated and flat steel webs of equal thicknesses, and its ratio to the calculated stress of composite trapezoidal box girder with flat steel webs. Tables 1 and 2, along with Fig. 11, illustrate the following.

• (1) The mechanical properties of the composite trapezoidal box girder were impacted by the accordion effect. However, the accordion effect of the top slab was more impactful. At the intersection of the top slab and the web in the concentrated load, the top slab compressive stress decreased by 15.6%. On the other hand, at the intersection of the bottom slab and the web under concentrated load, the tensile stress of the bottom slab increased by 12.6%.

• (2) In comparison to the uniform load, the accordion effect of the top and bottom slabs in the concentrated load changed unevenly. At the same time, the accordion effect was related to the form of the load distribution, where the effect of the composite trapezoidal box girder in the concentrated load was more prominent. However, in bridge engineering, the dead weight of the bridge is commonly uniformly distributed load, while the vehicle load is the concentrated load.

Fig. 11

Accordion effect for simply supported composite trapezoidal box girders at the mid-span section ($L = 16m$)

The following was inferred from the results presented in Table 3 and Fig. 12.

• (1) Due to the introduction of the self-equilibrium conditions for the shear lag warping stress and bending moment, the vertical deflection of the composite box girder comprised the calculated values of the independent elementary beam and shear lag theories. However, in comparison to the traditional calculation theory, the accuracy of the modified method in this paper improved by approximately 2%; hence, the influence of self-equilibrium conditions on the vertical deflection was negligible. Therefore, the two algorithms had minimal influence on the vertical deflection values.

• (2) Under the influence of shear lag and the accordion effect, the vertical deflection of the composite box girder increased to a certain level. The accordion effect greatly influenced the vertical deflection of the composite box girder under uniform loading. In the example provided above, its influence value was approximately 10%, while the shear lag effect was affected by approximately 6%. In the concentrated force, the impact of the accordion effect was approximately 6.5%, and the effect of the shear lag was about 13.2%. That is, under the influence of shear lag and the accordion effect, the vertical stiffness of the composite box girder is greatly reduced. These results are of great importance to bridge designers.

Table 3 Deflection for simply supported composite trapezoidal box girders [$L = 16m$] (uniform load)

Fig. 12

Deflections for simply supported trapezoidal box girders (concentrated load,$L_{k1} = L_{k2} = 8m$)

5 Conclusion

Firstly, in the mechanical analysis of composite trapezoidal box girders, the additional deflections caused by the shear lag effect of the flanges were considered as generalized displacement functions. Furthermore, factors such as the accordion effect, shear deformation, self-equilibrium conditions for shear lag warping stress, and bending moment were considered comprehensively. In comparison to traditional calculation theory, the theoretical basis of this paper was stronger, and it is in good agreement with the finite element simulation; the example shows that the accuracy in this paper is improved. Thus, the method presented provides a strong basis for understanding the mechanical properties of composite box girders.

Secondly, the impact of the concentrated load on the shear lag effect of the composite trapezoidal box girder was more evident, and the stress distribution of the top and bottom slabs was uneven. For example, the shear lag coefficients in this paper at the intersection of the top slab and the web and the top slab centre are 1.58 and 0.6, respectively. The three different longitudinal displacement difference functions were employed to accurately reflect the amplitude of change of shear lag in the trapezoidal box girders with various widths of wing slabs, which also improved the calculation accuracy of the composite trapezoidal box girder’s mechanical analysis.

Finally, in comparison to the traditional PC box girder, under the influence of shear lag and the accordion effect, the vertical deflection of the composite box girder increased; therefore, the vertical stiffness of the trapezoidal composite box girder was reduced. For the simply supported box beam, although the accordion effect reduced the compressive stress of the top slab, it greatly increased the tensile stress of the bottom slab, which could certainly result in cracks at reinforced concrete (RC) bottom slabs. However, the web accordion effect effectively eliminates bridge damage caused by temperature stress, creep, and shrinkage of the PC box girder. Moreover, its structural dead weight decreased by approximately 25%. The modified method in this paper has important theoretical and practical significance for the layout of prestressed reinforcement and the durability design of such composite structures. Therefore, the computational theory in this paper will contribute to the theoretical foundation for the design of composite box girder bridges.