1 Introduction

Compared with the concrete web, when a corrugated steel web is subjected to an axial pre-pressure, it can be freely compressed because it is of a folded shape along the axial direction. So, there are less deformation constraints on the shrinkage and creep of concrete roof and cantilever plate. Hence, it is more effective in exerting an external pre-stress on the CBBCW. Further, the shear strength of a corrugated steel web is high enough to completely replace the concrete web, thereby reduces the beam’s weight significantly and eliminating cracking of the concrete webs. Compared with the ordinary steel webs, the corrugated steel webs have a strong out-of-plane stiffness, which can effectively avoid the local buckling. Therefore, the CBBCW is a new structure that is popular in application. Recently, CBBCW has been extensively used in the fields of construction, roads, railways and urban rail transit (Kim et al. 2005; Lho et al. 2014; Nguyen et al. 2013; Oh et al. 2012; Wang et al. 2013).

Since the shear stress in a CBBCW is not evenly distributed along the transverse direction of the concrete slab and the bottom plate, when the CBBCW is subjected to shear stress, the longitudinal displacements of the concrete slab and the bottom plate far away from rib plate lag behind those in the vicinity of the rib plate, resulting in a curved transverse distribution of bending normal forces on the concrete slab and the bottom plate. This is known as the shear lag effect, and cannot be ignored if the concrete slab and the bottom plate are wide. Further, since the shear stud between the steel girder and the concrete slab cannot be absolutely rigid as there is the relative slip between the steel girder and the concrete slab even when they are under the complete connection condition. Therefore, the dynamic characteristics of CBBCW are subjected to the combined effect of the shear lag and the slip (Qi and Jiang 2010; Nie et al. 2007; Zhou et al. 2012). Studies have also been reported on the method to analyze the dynamic characteristics considering the effects of several factors, such as the shear lag, interfacial slip, shear deformation and moment of inertia of CBBCW, and a series of representative study methods have emerged as well.

The analytical methods to analyze the dynamic characteristics of CBBCWs. Based on the energy variational method, Zhang et al. (2008) deduced the formula for the natural vibration frequencies of CBBCW and obtained the analytical solution according to the effects of the shear lag and shear deformation. Based on the energy variational method, Li et al. (2009) studied the shear lag effect of the CBBCW under concentrated load and uniform load and deduced the calculation formulas based on the energy variational method. Based on the energy variational method, Chen et al. (2016) built the lateral displacement distribution pattern of CBBCW considering the influence of both the shear deformation and shear lag effects. Using a theoretical analysis method to consider both the shear lag and the shear deformation effect, Qiao (2013) derived formulas which can be used to calculate the deflection of a CBBCW.

The finite element methods to analyze the dynamic characteristics of CBBCWs. Based a finite element method, Hu and Chen (2009) analyzed the shear lag effect of a curved continuous CBBCW and the factors that affect the shear lag. Based on a finite element method for a three-span continuous CBBCW, Jiang et al. (2014) carried out a comparative study on the shear lag effect under self-weight. Cheng and Yao (2016) developed a simplified analysis method for predicting the deflections of several CBBCW considering the influence of both shear deformation and shear lag, and the simplified method was validated with the results of the finite element analysis. Chen et al. (2017) proposed the sandwich beam theory to predict the flexural vibration behavior of CBBCW considering the presence of diaphragms and external prestressing tendons and the interaction between the web shear deformation and the flange local bending. Wu et al. (2003) studied the shear lag effect of a CBBCW through the loaded test and analyzed it using the 3D finite element theory.

The experimental methods to analyze the dynamic characteristics of CBBCWs. Seven steel-composite I-girders with corrugated webs to were tested to investigate the shear performance, and developed the analytical and numerical models which were verified by the experimental results (He et al. 2012a, b, c, 2014). Zhou et al. (2016a) conducted experimental and theoretical studies on the deformation of a non-prismatic scaled model with several CBBCW in order to quantitatively study the proportional relationship between the bending deformation and the shear deformation. Elamary et al. (2017) conducted an experimental program to investigate the effect of a top steel flange on the failure mechanism of a CBBCW under bending, and discussed the effects of the top steel flange on the beam stiffness, ultimate load, local buckling of the corrugated web, concrete slip, and failure mechanism of the concrete slab.

To sum up, the previous methods for studying the dynamic characteristics of CBBCW mostly suffer from complex deductions, numerous restrictions, and low calculation efficiency. The analytical calculation method that was characterized by less restrictions and higher calculation efficiency had been rarely studied. Therefore, On the basis of the Hamilton principle, this study has comprehensively considered the effects of several factors, such as the shear lag, interfacial slip, shear deformation and moment of inertia of the CBBCW. Then, an IAM for calculating the natural frequencies of the CBBCW has been developed. Using the IAM, the natural frequencies of two simply-supported (SSD) and fixed-supported (FSD) CBBCW with different spans have been calculated. To verify the correctness of the IAM developed in this study, the results calculated by the IAM have been compared with those calculated by the GBT and by the FEM. The effects of the shear lag and interfacial slip on the dynamic characteristics of the CBBCW and OCBBW have also been investigated. The IAM is a development of the earlier calculation theory for the dynamic characteristics of CBBCW. Hence, it can be used as a theoretical foundation for future studies on the dynamic characteristics of CBBCW whose conclusions are relevant to engineering design.

2 Theoretical Analyses

2.1 Geometry Shape and Characteristics of CBBCW

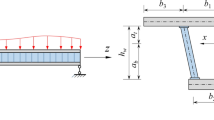
The cross-sectional dimensions and the coordinate system of a CBBCW are shown in Fig. 1. The geometrical dimensions of the corrugated steel webs is shown in Fig. 2. As can be seen from Figs. 1, 2, \(2b_{1}\), \(b_{2}\), \(2b_{3}\) and \(b_{4}^{*}\) are the widths of the concrete roof, cantilever plate, bottom plate and the width of the steel beam’s top flange; \(b_{4}\) is the height of corrugated steel web; \(t_{1}\), \(t_{2}\), \(t_{3}\), \(t_{\text{w}}\), \(t_{4}^{*}\) are the thicknesses of the concrete roof, cantilever plate, steel beam bottom plate, corrugated steel web and steel beam’s top flange, respectively; \(t_{4}\) is the width of corrugated steel web; \(h_{\text{c}}\) is the distance between the centroids of the concrete slab and interface; \(h_{\text{s}}\) is the distance between the centroids of the steel beam and interface, and \(h = h_{\text{c}} + h_{\text{s}}\); \(b_{\text{w}}\), \(b_{\text{w1}}\) and \(d_{\text{w}}\) are widths of horizontal fold, inclined fold, and horizontal projection dimension of the inclined fold; and \(\theta_{\text{w}}\) is inclination angle of the inclined fold. According to the characteristics of the CBBCW, the following assumptions are reasonable in order to simplify the calculations.

Fig. 1
figure 1

Cross-sectional dimensions and coordinate system of CBBCW

Full size image
Fig. 2
figure 2

Dimensions of corrupted steel web

Full size image
  1. (1)

    The shear modulus of the corrugated steel web is related to the geometrical shape of its corrugated web (Johnson et al. 1997, Samanta and Mukhopadhyay 1999). The shear modulus \(G_{\text{s1}}\) can be approximated as:

    $$G_{\text{s1}} = \frac{{E_{\text{s}} }}{{2(1 + v_{\text{s}} )}}\frac{{b_{\text{w}} + d_{\text{w}} }}{{b_{\text{w}} + d_{\text{w}} \sec \theta_{\text{w}} }}$$
    (1)

    where \(G_{\text{s1}}\) is the shear modulus of the corrugated steel web; \(E_{\text{s}}\) is the steel’s elastic modulus; \(v_{\text{s}}\) is the Poisson’s ratio of the steel.

  2. (2)

    The corrugated steel webs are like an accordion. Its axial stiffness is very small and the apparent elastic modulus \(E_{e}\) is only a few percent of the elastic modulus of the steel plate (He et al. 2014). So, in the calculations, the axial compression stiffness of the corrugated steel webs can be ignored, i.e. \(E_{e} = 0\).

  3. (3)

    As shown in Fig. 2, the mass of a longitudinal unit of corrugated steel web is

    $$m_{4} = 2(b_{\text{w1}} t_{\text{w}} + b_{\text{w}} t_{\text{w}} )b_{4} \rho_{\text{s}}$$
    (2)

    Based on the mass-equivalent principle, the equivalent cross-sectional area of the corrugated steel web is

    $$A_{\text{eq}} = t_{\text{weq}} b_{4} = \frac{{2(b_{\text{w1}} t_{\text{w}} + b_{\text{w}} t_{\text{w}} )}}{{l_{\text{w}} }}b_{4}$$
    (3)

2.2 GBT and IAM of CBBCW

  1. (1)

    In the GBT (Zhou et al. 2016b), as shown in Fig. 1, the longitudinal displacement of each point on the concrete slab and the steel beam are:

    $$\begin{array}{*{20}c} {u_{\text{xpi}} \left( {x,y,z,t} \right) = -\, \left( {z - z_{\text{t}} } \right)\theta \left( {x ,t} \right)\quad i = 1,2} \\ {u_{\text{xpi}} \left( {x,y,z,t} \right) = -\, \left( {z - z_{\text{s}} } \right)\theta \left( {x ,t} \right){\kern 1pt} \quad i = 3,4} \\ \end{array}$$
    (4)

    where \(\theta (x,t)\) is the cross-section rotation angle function of the CBBCW; \(z_{\text{t}}\), \(z_{\text{b}}\) and \(z_{\text{s}}\) are the z-axis coordinates of the centroids of the concrete slab, steel beam bottom plate and steel beam, respectively.

  2. (2)

    Based on the IAM developed in this study, assuming that the longitudinal displacement of each point on the cross-section of the CBBCW is superimposed by three parts: the longitudinal displacement obeying the plane-section assumption, the warping displacement caused by the shear lag and the interfacial slip displacement, the longitudinal displacement of each point on the concrete slab and the steel beam can be expressed as:

    $$u_{\text{xi}} \left( {x,y,z,t} \right) = \left\{ {\begin{array}{*{20}c} { - {{A_{\text{s}} \xi \left( {x ,t} \right)} \mathord{\left/ {\vphantom {{A_{\text{s}} \xi \left( {x ,t} \right)} {A_{0} }}} \right. \kern-0pt} {A_{0} }} - \left( {z - z_{\text{t}} } \right)\theta \left( {x ,t} \right) + \psi_{\text{i}} \left( y \right)U\left( {x ,t} \right)\quad i = 1,2} \\ {{{A_{\text{c}} \xi \left( {x ,t} \right)} \mathord{\left/ {\vphantom {{A_{\text{c}} \xi \left( {x ,t} \right)} {nA_{0} }}} \right. \kern-0pt} {nA_{0} }} - \left( {z - z_{\text{s}} } \right)\theta \left( {x ,t} \right) + \psi_{\text{i}} \left( y \right)U\left( {x ,t} \right){\kern 1pt} \quad i = 3,4} \\ \end{array} } \right.$$
    (5)

    where \(\xi \left( {x,t} \right)\) is the centroid’s longitudinal displacement difference between the concrete slab and the steel beam; \(A_{\text{c}} = A_{1} + A_{2}\) is the cross-sectional area of the concrete slab; and \(A_{\text{s}} = A_{3} + A_{4}^{ * }\) is the effective cross-sectional area of the steel beam; \(\psi_{\text{i}} \left( y \right)U\left( {x ,t} \right)\), \(\left( {i = 1,2,3,4} \right)\) are the longitudinal warping displacement function of the concrete roof, cantilever plate, bottom plate and corrugated steel web, respectively(Lai et al. 2017); \(U\left( {x ,t} \right)\) is the longitudinal warping amplitude function; \(n = {{E_{\text{s}} } \mathord{\left/ {\vphantom {{E_{\text{s}} } {E_{\text{c}} }}} \right. \kern-0pt} {E_{\text{c}} }}\), \(E_{\text{c}}\) is the elastic modulus of the concrete slab; \(\psi_{i} \left( {\text{y}} \right) = {{\alpha_{i} y^{2} } \mathord{\left/ {\vphantom {{\alpha_{i} y^{2} } {b_{i}^{2} }}} \right. \kern-0pt} {b_{i}^{2} }} - \alpha_{i} + {{2\left( {{{\alpha_{1} A_{1} } \mathord{\left/ {\vphantom {{\alpha_{1} A_{1} } n}} \right. \kern-0pt} n} + {{\alpha_{2} A_{2} } \mathord{\left/ {\vphantom {{\alpha_{2} A_{2} } n}} \right. \kern-0pt} n} + \alpha_{3} A_{3} } \right)} \mathord{\left/ {\vphantom {{2\left( {{{\alpha_{1} A_{1} } \mathord{\left/ {\vphantom {{\alpha_{1} A_{1} } n}} \right. \kern-0pt} n} + {{\alpha_{2} A_{2} } \mathord{\left/ {\vphantom {{\alpha_{2} A_{2} } n}} \right. \kern-0pt} n} + \alpha_{3} A_{3} } \right)} {3A_{0} }}} \right. \kern-0pt} {3A_{0} }}\), \({\kern 1pt} \left( {i = 1,2,3,4} \right)\); \(\alpha_{1} { = }1\), \(\alpha_{2} { = }{{{\text{b}}_{ 2}^{ 2} } \mathord{\left/ {\vphantom {{{\text{b}}_{ 2}^{ 2} } {{\text{b}}_{ 1}^{ 2} }}} \right. \kern-0pt} {{\text{b}}_{ 1}^{ 2} }}\), \(\alpha_{3} = {{{\text{b}}_{ 3}^{ 2} z_{\text{b}} } \mathord{\left/ {\vphantom {{{\text{b}}_{ 3}^{ 2} z_{\text{b}} } {{\text{b}}_{ 1}^{ 2} z_{\text{t}} }}} \right. \kern-0pt} {{\text{b}}_{ 1}^{ 2} z_{\text{t}} }}\), \(\alpha_{4} { = 0}\);\(A_{1} = 2b_{1} t_{1}\), \(A_{2} = 2b_{2} t_{2}\), \(A_{3} = 2b_{3} t_{3}\), \(A_{4} = 2b_{4} t_{\text{w}}\), \(A_{4}^{ * } = 2b_{4}^{ * } t_{4}^{ * }\), \(A_{0} = {{\left( {A_{1} + A_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {A_{1} + A_{2} } \right)} n}} \right. \kern-0pt} n} + A_{3} + A_{4}^{ * }\).

3 Governing Equation and Solving Process of CBBCW

3.1 Strain and Stress of Cross-Sectional of CBBCW

According to Eq. (5), the strain and stress at each point of the cross-section of the CBBCW can be expressed as:

$$\varepsilon_{\text{xi}} = \left\{ {\begin{array}{*{20}c} {k_{\text{c}} \frac{\partial \xi }{\partial x} - \left( {z - z_{\text{t}} } \right)\frac{\partial \theta }{\partial x} + \psi_{\text{i}} \frac{\partial U}{\partial x}\quad i = 1,2} \\ {k_{\text{s}} \frac{\partial \xi }{\partial x} - \left( {z - z_{\text{s}} } \right)\frac{\partial \theta }{\partial x} + \psi_{\text{i}} \frac{\partial U}{\partial x}\quad i = 3,4} \\ \end{array} } \right.$$
(6)
$$\sigma_{\text{xi}} = \left\{ {\begin{array}{*{20}c} {E_{\text{c}} \left[ {k_{\text{c}} \frac{\partial \xi }{\partial x} - \left( {z - z_{\text{t}} } \right)\frac{\partial \theta }{\partial x} + \psi_{\text{i}} \frac{\partial U}{\partial x}} \right]\quad i = 1,2} \\ {E_{\text{s}} \left[ {k_{\text{s}} \frac{\partial \xi }{\partial x} - \left( {z - z_{\text{s}} } \right)\frac{\partial \theta }{\partial x} + \psi_{\text{i}} \frac{\partial U}{\partial x}} \right]\quad i = 3} \\ \end{array} } \right.$$
(7)
$$\sigma_{\text{xi}} = E_{e} \left[ {k_{s} \frac{\partial \xi }{\partial x} - \left( {z{ - }z_{s} } \right)\frac{\partial \theta }{\partial x}} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 4$$
(8)
$$\gamma_{\text{xyi}} = \frac{{\partial \psi_{\text{i}} }}{\partial y}U\quad i = 1,2,3$$
(9)
$$\tau_{\text{xyi}} = G_{\text{c}} \frac{{\partial \psi_{\text{i}} }}{\partial y}U\left( x \right)\quad i = 1,2$$
(10)
$$\tau_{\text{xyi}} = G_{\text{s}} \frac{{\partial \psi_{\text{i}} }}{\partial y}U\left( x \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 3$$
(11)
$$\gamma_{\text{xz}} = \frac{\partial w}{\partial x} - \theta$$
(12)
$$\tau_{\text{xz}} = G_{\text{s1}} (\frac{\partial w}{\partial x} - \theta )$$
(13)

where \(\varepsilon_{\text{xi}} \left( {i = 1,2,3,4} \right)\) are the longitudinal normal strains of the roof, cantilever plate, bottom plate and corrugated steel web, respectively; \(\gamma_{\text{xyi}} {\kern 1pt} {\kern 1pt} (i = 1,2,3)\) are the shear strains of the roof, cantilever plate and bottom plate; \(\sigma_{\text{xi}} (i = 1,2,3,4)\) are the longitudinal normal stresses of the concrete roof, cantilever plate, bottom plate and corrugated steel web, respectively; and \(w\left( {x,t} \right)\) is the vertical deflection of the CBBCW;\(G_{\text{c}}\) is the shear modulus of the concrete slab; \(G_{\text{s}}\) is the steel’s shear modulus; \(\tau_{\text{xyi}} (i = 1,2)\) are the shear stress of the concrete roof and the cantilever plate, respectively; \(\tau_{\text{xyi}} (i = 3)\) is the shear stress of the bottom plate; \(\gamma_{\text{xz}}\) is the shear strain of the corrugated steel web; \(\tau_{\text{xz}}\) is the shear stress of the corrugated steel web.

Since the vertical compression of the concrete slab and the steel beam, and the transverse strains of the plates are very small, they can be ignored (Chen and Wang 2012; Kashefi et al. 2017; Ng and Ronagh 2004), and the relative interfacial longitudinal displacement \(\zeta \left( {x,t} \right)\) can be expressed as:

$$\zeta \left( {x,t} \right) = \xi + h_{\text{c}} \theta + h_{\text{s}} \theta = \xi + h\theta$$
(14)

According to Eq. (14), the interfacial shear stress can be expressed as (Nie et al. 2005, 2007):

$$\varsigma \left( {x,t} \right) = k_{\text{sl}} \zeta \left( {x,t} \right) = k_{\text{sl}} \left( {\xi + h\theta } \right)$$
(15)
$$k_{\text{sl}} = {{k_{1} n_{\text{s}} } \mathord{\left/ {\vphantom {{k_{1} n_{\text{s}} } {l_{\text{s}} }}} \right. \kern-0pt} {l_{\text{s}} }},\quad k_{1} = 0.66\,V_{\text{u}}$$
(16)

where \(k_{\text{sl}}\) is the interfacial slip stiffness; \(k_{1}\) is the slip stiffness of a single stud; \(V_{\text{u}} = {{A_{\text{s}} f_{\text{s}} rl_{\text{s}} } \mathord{\left/ {\vphantom {{A_{\text{s}} f_{\text{s}} rl_{\text{s}} } {\left( {Ln_{\text{s}} } \right)}}} \right. \kern-0pt} {\left( {Ln_{\text{s}} } \right)}}\) is the shear capacity of a single stud; \(n_{s}\) is the number of studs for each row; \(L\) is the calculated span of the CBBCW; \(r\) is the shear connection degree; \(f_{\text{s}}\) is the stud’s yield strength; and \(l_{\text{s}}\) is the stud’s longitudinal spacing.

3.2 Strain Energy and Kinetic Energy of CBBCW

  1. (1)

    The strain energy of the CBBCW can be expressed as

$$V = \frac{1}{2}\int_{L} {\left[ {\sum\limits_{i = 1}^{4} {\int_{{A_{\text{i}} }} {\left( {\sigma_{\text{xi}} \varepsilon_{\text{xi}} + \tau_{\text{xyi}} r_{\text{xyi}} + \tau_{\text{xzi}} r_{\text{xzi}} } \right){\text{d}}A} } + \varsigma \zeta } \right]{\text{d}}x}$$
(17)

Substituting Eqs. (6)–(15) into Eq. (17) gives:

$$\begin{aligned} V = &\, \frac{1}{2}\int_{L} {\left\{ {\left( {E_{\text{c}} k_{\text{c}}^{ 2} A_{\text{c}} + E_{\text{s}} k_{\text{s}}^{ 2} A_{4*} + E_{\text{s}} k_{\text{s}}^{ 2} A_{3} } \right)\xi^{\prime 2} - 2\left[ {\int_{{A_{\text{c}} }} {k_{\text{c}} E_{\text{c}} \left( {z - z_{\text{t}} } \right)} dA + \int_{{A_{\text{s}} }} {k_{\text{s}} E_{\text{s}} \left( {z - z_{\text{s}} } \right)} dA} \right]\xi^{\prime } \theta^{\prime } } \right.} \\ & \quad + \left[ {\int_{{A_{\text{c}} }} {E_{\text{c}} \left( {z - z_{\text{t}} } \right)}^{2} dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \left( {z - z_{\text{s}} } \right)}^{2} dA} \right]\theta^{\prime 2} + \left( {\int_{{A_{\text{c}} }} {E_{\text{c}} \psi_{\text{i}}^{ 2} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \psi_{\text{i}}^{ 2} } dA} \right)U^{\prime 2} \\ & \quad - 2\left[ {\int_{{A_{\text{c}} }} {E_{\text{c}} \left( {z - z_{\text{t}} } \right)\psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi_{\text{i}} } dA} \right]\theta^{\prime } U\prime + 2\left( {\int_{{A_{\text{c}} }} {E_{\text{c}} k_{\text{c}} \psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} k_{\text{s}} \psi_{\text{i}} } dA} \right)\xi^{\prime } U^{\prime } \\ & \quad \left. {{\kern 1pt} + \left( {\int_{{A_{\text{c}} }} {G_{\text{c}} \psi_{\text{i}}^{\prime 2} dA + \int_{{A_{3} }} {G_{\text{s}} \psi_{\text{i}}^{\prime 2} dA} } } \right)U^{2} + k_{\text{sl}} \zeta^{2} + G_{\text{s1}} A_{4} \left( {w^{\prime } - \theta } \right)^{2} } \right\}{\text{d}}x \\ \end{aligned}$$
(18)
  1. (2)

    The kinetic energy of the CBBCW can be expressed as

$$T = \frac{1}{2}\int_{L} {\left( {m\dot{w}^{2} + \sum\limits_{i = 1}^{4} {\int_{{A_{i} }} {\rho_{i} \dot{u}_{i}^{2} {\text{d}}A} } } \right){\text{d}}x}$$
(19)

where \(m = \rho_{\text{c}} A_{\text{c}} + \rho_{\text{s}} (A_{\text{s}} + A_{\text{eq}} )\); \(\rho_{1} = \rho_{2} = \rho_{\text{c}}\); \(\rho_{3} = \rho_{4} = \rho_{4}^{*} = \rho_{\text{s}}\); \(\rho_{\text{c}}\) is the density of concrete; and \(\rho_{\text{s}}\) is the density of steel.

Substituting Eq. (5) into Eq. (19) gives

$$\begin{aligned} T & = \frac{1}{2}\int_{L} {\left\{ {m\dot{w}^{2} + \left( {\rho_{\text{c}} k_{\text{c}}^{ 2} A_{\text{c}} + \rho_{\text{s}} k_{\text{s}}^{ 2} A_{\text{s}} + \rho_{\text{s}} k_{\text{s}}^{ 2} A_{\text{eq}} } \right)\dot{\xi }^{2} + \left[ {\int_{{A_{\text{c}} }} {\rho_{\text{c}} } \left( {z - z_{\text{t}} } \right)^{2} {\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} \left( {z - z_{\text{s}} } \right)^{2} {\text{d}}A} } \right]\dot{\theta }^{2} } \right.} \\ & \quad + \left( {\int_{{A_{\text{c}} }} {\rho_{\text{c}} \psi^{2} } {\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} \psi^{2} } {\text{d}}A{\kern 1pt} } \right)\dot{U}^{2} - 2\left[ {\int_{{A_{\text{c}} }} {\rho_{\text{c}} } k_{\text{c}} \left( {z - z_{\text{t}} } \right){\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} k_{\text{s}} \left( {z - z_{\text{s}} } \right)} {\text{d}}A} \right]\dot{\xi }\dot{\theta } \\ & \left. {\quad - 2\left[ {\int_{{A_{\text{c}} }} {\rho_{\text{c}} \left( {z - z_{t} } \right)\psi } {\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi } {\text{d}}A{\kern 1pt} } \right]\dot{\theta }\dot{U} + 2\left( {\int_{{A_{\text{c}} }} {\rho_{\text{c}} k_{\text{c}} \psi dA} + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} k_{\text{s}} \psi } dA} \right)\dot{\xi }\dot{U}} \right\}{\text{d}}x \\ \end{aligned}$$
(20)

3.3 Solving the Equations of CBBCW

According to the Hamilton principle,

$$\delta \int_{{t_{0} }}^{{t_{1} }} {\left( {T - V} \right)dt} = 0$$
(21)

The governing differential equations and the boundary conditions for the bending vibration of a CBBCW are as follows:

$$\begin{aligned} & \left( {\int_{{A_{\text{c}} }} {E_{\text{c}} \psi_{\text{i}}^{ 2} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \psi_{\text{i}}^{ 2} } dA} \right)U^{\prime \prime } - \left[ {\int_{{A_{\text{c}} }} {E_{\text{c}} \left( {z - z_{\text{t}} } \right)\psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi_{\text{i}} } dA} \right]\theta^{\prime \prime } + \left[ {\int_{{A_{\text{c}} }} {E_{\text{c}} k_{\text{c}} \psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} k_{\text{s}} \psi_{\text{i}} } dA} \right]\xi^{\prime \prime } \\ {\kern 1pt} & \quad {\kern 1pt} - \left( {\int_{{A_{\text{c}} }} {G_{\text{c}} \psi_{\text{i}}^{\prime 2} dA + \int_{{A_{3} }} {G_{\text{s}} \psi_{\text{i}}^{\prime 2} dA} } } \right)U - \left( {\int_{{A_{\text{c}} }} {\rho_{\text{c}} \psi^{2} } {\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} \psi^{2} } {\text{d}}A{\kern 1pt} } \right)\ddot{U} - \left( {\int_{{A_{\text{c}} }} {\rho_{\text{c}} k_{\text{c}} \psi dA} + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} k_{\text{s}} \psi } dA_{1} } \right)\ddot{\xi } \\ & \quad {\kern 1pt} + \left( {\int_{{A_{\text{c}} }} {\rho_{\text{c}} \left( {z - z_{t} } \right)\psi } {\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi } {\text{d}}A{\kern 1pt} } \right)\ddot{\theta } = 0 \\ \end{aligned}$$
(22)
$$\begin{aligned} & \left( {E_{\text{c}} k_{\text{c}}^{ 2} A_{\text{c}} + E_{\text{s}} k_{\text{s}}^{ 2} A_{4*} + E_{\text{s}} k_{\text{s}}^{ 2} A_{3} } \right)\xi^{\prime \prime } - \left[ {\int_{{A_{\text{c}} }} {k_{\text{c}} E_{\text{c}} \left( {z - z_{\text{t}} } \right)} dA + \int_{{A_{\text{s}} }} {k_{\text{s}} E_{\text{s}} \left( {z - z_{\text{s}} } \right)} dA} \right]\theta^{\prime \prime } + \left( {\int_{{A_{\text{c}} }} {E_{\text{c}} k_{\text{c}} \psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} k_{\text{s}} \psi_{\text{i}} } dA} \right)U^{\prime \prime } \\ {\kern 1pt} & \quad - k_{\text{sl}} \zeta - \left( {\rho_{\text{c}} k_{\text{c}}^{ 2} A_{\text{c}} + \rho_{\text{s}} k_{\text{s}}^{ 2} A_{\text{s}} + \rho_{\text{s}} k_{\text{s}}^{ 2} A_{\text{eq}} } \right)\ddot{\xi } + \left[ {\int_{{A_{\text{c}} }} {\rho_{\text{c}} } k_{\text{c}} \left( {z - z_{\text{t}} } \right){\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} k_{\text{s}} \left( {z - z_{\text{s}} } \right)} {\text{d}}A} \right]\ddot{\theta } \\ & \quad - \left( {\int_{{A_{\text{c}} }} {\rho_{\text{c}} k_{\text{c}} \psi dA} + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} k_{\text{s}} \psi } dA} \right)\ddot{U} = 0 \\ \end{aligned}$$
(23)
$$\begin{aligned} & G_{\text{s1}} A_{4} \left( {w^{\prime } - \theta } \right) - \left[ {\int_{{A_{\text{c}} }} {k_{\text{c}} E_{\text{c}} \left( {z - z_{\text{t}} } \right)} dA + \int_{{A_{\text{s}} }} {k_{\text{s}} E_{\text{s}} \left( {z - z_{\text{s}} } \right)} dA} \right]\xi^{\prime \prime } + \left[ {\int_{{A_{\text{c}} }} {E_{\text{c}} \left( {z - z_{\text{t}} } \right)}^{2} dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \left( {z - z_{\text{s}} } \right)}^{2} dA} \right]\theta^{\prime \prime } \\ {\kern 1pt} & \quad - \left[ {\int_{{A_{\text{c}} }} {E_{\text{c}} \left( {z - z_{\text{t}} } \right)\psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi_{\text{i}} } dA} \right]U^{\prime \prime } - k_{\text{sl}} \zeta h - \left[ {\int_{{A_{\text{c}} }} {\rho_{\text{c}} } \left( {z - z_{\text{t}} } \right)^{2} {\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} \left( {z - z_{\text{s}} } \right)^{2} {\text{d}}A} } \right]\ddot{\theta } \\ & \quad + \left[ {\int_{{A_{\text{c}} }} {\rho_{\text{c}} } k_{\text{c}} \left( {z - z_{\text{t}} } \right){\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} k_{\text{s}} \left( {z - z_{\text{s}} } \right)} {\text{d}}A} \right]\ddot{\xi } + \left[ {\int_{{A_{\text{c}} }} {\rho_{\text{c}} \left( {z - z_{t} } \right)\psi } {\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi } {\text{d}}A{\kern 1pt} } \right]\ddot{U} = 0 \\ \end{aligned}$$
(24)
$$G_{\text{s1}} A_{4} \left( {w^{\prime\prime} - \theta^{\prime}} \right) - m\ddot{w} = 0$$
(25)
$$\left\{ \begin{aligned} &\left( {\int_{{A_{\text{c}} }} {E_{\text{c}} \psi_{\text{i}}^{ 2} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \psi_{\text{i}}^{ 2} } dA} \right)U^{\prime } \delta U - \left[ {\int_{{A_{\text{c}} }} {E_{\text{c}} \left( {z - z_{\text{t}} } \right)\psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi_{\text{i}} } dA} \right]\theta^{\prime } \delta U \hfill \\ &\quad + \left( {\int_{{A_{\text{c}} }} {E_{\text{c}} k_{\text{c}} \psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} k_{\text{s}} \psi_{\text{i}} } dA} \right)\xi^{\prime } \hfill \\ \end{aligned} \right\}\delta U\left| {_{0}^{L} = 0} \right.$$
(26)
$${\kern 1pt} \left\{ \begin{aligned} {\kern 1pt} &\left( {E_{\text{c}} k_{\text{c}}^{ 2} A_{\text{c}} + E_{\text{s}} k_{\text{s}}^{ 2} A_{4*} + E_{\text{s}} k_{\text{s}}^{ 2} A_{3} } \right)\xi^{\prime } - \left[ {\int_{{A_{\text{c}} }} {k_{\text{c}} E_{\text{c}} \left( {z - z_{\text{t}} } \right)} dA + \int_{{A_{\text{s}} }} {k_{\text{s}} E_{\text{s}} \left( {z - z_{\text{s}} } \right)} dA} \right]\theta^{\prime } \hfill \\ &\quad + \left( {\int_{{A_{\text{c}} }} {E_{\text{c}} k_{\text{c}} \psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} k_{\text{s}} \psi_{\text{i}} } dA} \right)U^{\prime } \hfill \\ \end{aligned} \right\}\delta \xi \left| {_{0}^{L} = 0} \right.$$
(27)
$$\left\{ \begin{aligned} & \left[ {\int_{{A_{\text{c}} }} {E_{\text{c}} \left( {z - z_{\text{t}} } \right)}^{2} dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \left( {z - z_{\text{s}} } \right)}^{2} dA} \right]\theta^{\prime } {\kern 1pt} - \left[ {\int_{{A_{\text{c}} }} {k_{\text{c}} E_{\text{c}} \left( {z - z_{\text{t}} } \right)} dA + \int_{{A_{\text{s}} }} {k_{\text{s}} E_{\text{s}} \left( {z - z_{\text{s}} } \right)} dA} \right]\xi^{\prime } \hfill \\ & \quad- \left[ {\int_{{A_{\text{c}} }} {E_{\text{c}} \left( {z - z_{\text{t}} } \right)\psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi_{\text{i}} } dA} \right]U^{\prime } \hfill \\ \end{aligned} \right\}\delta \theta \left| {_{0}^{L} = 0} \right.$$
(28)
$$G_{\text{s1}} A_{4} \left( {w^{\prime } - \theta } \right)\delta w\left| {_{0}^{L} = 0} \right.$$
(29)

Let:

$$U\left( {x,t} \right) = U_{1} \left( x \right)\varGamma \left( t \right),\quad \xi \left( {x,t} \right) = \xi_{1} \left( x \right)\varGamma \left( t \right),\quad w\left( {x,t} \right) = w_{1} \left( x \right)\varGamma \left( t \right),\quad \theta \left( {x,t} \right) = \theta_{1} \left( x \right)\varGamma \left( t \right)$$
(30)

where \(\varGamma \left( t \right) = \sin \left( {\omega t + \varphi } \right)\).

$$\lambda^{k} = {{\partial^{k} } \mathord{\left/ {\vphantom {{\partial^{k} } {\partial x^{k} }}} \right. \kern-0pt} {\partial x^{k} }}$$
(31)

Substituting Eqs. (30)–(31) into Eqs. (22)–(25) gives

$$F_{11} U_{1} + F_{12} \xi_{1} + F_{13} w_{1} + F_{14} \theta_{1} = 0$$
(32)
$$F_{21} U_{1} + F_{22} \xi_{1} + F_{23} + F_{24} \theta_{1} = 0$$
(33)
$$F_{31} U_{1} + F_{32} \xi_{1} + F_{33} w_{1} - F_{34} \theta_{1} = 0$$
(34)
$$F_{41} U_{1} + F_{42} \xi_{1} + F_{43} w_{1} + F_{44} \theta_{1} = 0$$
(35)
$$F_{11} = \left( {\int_{{A_{\text{c}} }} {E_{\text{c}} \psi_{\text{i}}^{ 2} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \psi_{\text{i}}^{ 2} } dA} \right)\lambda^{2} - \int_{{A_{\text{c}} }} {G_{\text{c}} \psi_{\text{i}}^{\prime 2} dA + \int_{{A_{3} }} {G_{\text{s}} \psi_{\text{i}}^{\prime 2} dA} } + \left( {\int_{{A_{\text{c}} }} {\rho_{\text{c}} \psi^{2} } {\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} \psi^{2} } {\text{d}}A{\kern 1pt} } \right)\omega^{2}$$
(36)
$$F_{21} = \left( {\int_{{A_{c} }} {E_{c} k_{c} \psi_{i} } dA + \int_{{A_{s} }} {E_{s} k_{s} \psi_{i} } dA} \right)\lambda^{2} + \left( {\int_{{A_{c} }} {\rho_{c} k_{c} \psi dA} + \int_{{A_{s} + A_{eq} }} {\rho_{s} k_{s} \psi } dA} \right)\omega^{2}$$
(37)
$$F_{41} = -\, \left( {\int_{{A_{\text{c}} }} {E_{\text{c}} \left( {z - z_{\text{t}} } \right)\psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi_{\text{i}} } dA} \right)\lambda^{2} - \left( {\int_{{A_{\text{c}} }} {\rho_{\text{c}} \left( {z - z_{t} } \right)\psi } {\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi } {\text{d}}A{\kern 1pt} } \right)\omega^{2}$$
(38)
$$F_{12} = \left( {\int_{{A_{\text{c}} }} {E_{\text{c}} k_{\text{c}} \psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} k_{\text{s}} \psi_{\text{i}} } dA} \right)\lambda^{2} + \left( {\int_{{A_{\text{c}} }} {\rho_{\text{c}} k_{\text{c}} \psi dA} + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} k_{\text{s}} \psi } dA} \right)\omega^{2}$$
(39)
$$F_{22} = \left( {E_{\text{c}} k_{\text{c}}^{ 2} A_{\text{c}} + E_{\text{s}} k_{\text{s}}^{ 2} A_{4*} + E_{\text{s}} k_{\text{s}}^{ 2} A_{3} } \right)\lambda^{2} - k_{\text{sl}} + \left( {\rho_{\text{c}} k_{\text{c}}^{ 2} A_{\text{c}} + \rho_{\text{s}} k_{\text{s}}^{ 2} A_{\text{s}} + \rho_{\text{s}} k_{\text{s}}^{ 2} A_{\text{eq}} } \right)\omega^{2}$$
(40)
$$F_{42} = -\, \left[ {\int_{{A_{\text{c}} }} {k_{\text{c}} E_{\text{c}} \left( {z - z_{\text{t}} } \right)} dA + \int_{{A_{\text{s}} }} {k_{\text{s}} E_{\text{s}} \left( {z - z_{\text{s}} } \right)} dA} \right]\lambda^{2} - k_{\text{sl}} h - \left[ {\int_{{A_{\text{c}} }} {\rho_{\text{c}} } k_{\text{c}} \left( {z - z_{\text{t}} } \right){\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} k_{\text{s}} \left( {z - z_{\text{s}} } \right)} {\text{d}}A} \right]\omega^{2}$$
(41)
$$F_{33} = G_{\text{s1}} A_{4} \lambda^{2} + m\omega^{2} ,\quad F_{43} = G_{\text{s1}} A_{4} \lambda ,\quad F_{34} = -\, G_{\text{s1}} A_{4} \lambda ,\quad F_{13} = F_{23} = F_{31} = F_{32} = 0$$
(42)
$$F_{14} = -\, \left( {\int_{{A_{\text{c}} }} {\rho_{\text{c}} \left( {z - z_{t} } \right)\psi } {\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi } {\text{d}}A{\kern 1pt} } \right)\omega^{2} - \left( {\int_{{A_{\text{c}} }} {E_{\text{c}} \left( {z - z_{\text{t}} } \right)\psi_{\text{i}} } dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \left( {z - z_{\text{s}} } \right)\psi_{\text{i}} } dA} \right)\lambda^{2}$$
(43)
$$F_{24} = -\, k_{\text{sl}} h - \left( {\int_{{A_{\text{c}} }} {\rho_{\text{c}} } k_{\text{c}} \left( {z - z_{\text{t}} } \right){\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} k_{\text{s}} \left( {z - z_{\text{s}} } \right)} {\text{d}}A} \right)\omega^{2} - \left( {\int_{{A_{\text{c}} }} {k_{\text{c}} E_{\text{c}} \left( {z - z_{\text{t}} } \right)} dA + \int_{{A_{\text{s}} }} {k_{\text{s}} E_{\text{s}} \left( {z - z_{\text{s}} } \right)} dA} \right)\lambda^{2}$$
(44)
$$F_{44} = -\, G_{\text{s1}} A_{4} + \left[ {\int_{{A_{\text{c}} }} {E_{\text{c}} \left( {z - z_{\text{t}} } \right)}^{2} dA + \int_{{A_{\text{s}} }} {E_{\text{s}} \left( {z - z_{\text{s}} } \right)}^{2} dA} \right]\lambda^{2} - k_{\text{sl}} h^{2} + \left[ {\int_{{A_{\text{c}} }} {\rho_{\text{c}} } \left( {z - z_{\text{t}} } \right)^{2} {\text{d}}A + \int_{{A_{\text{s}} + A_{\text{eq}} }} {\rho_{\text{s}} \left( {z - z_{\text{s}} } \right)^{2} {\text{d}}A} } \right]\omega^{2}$$
(45)

The characteristic Eqs. (32)–(35) corresponding to the set of differential equations is

$$\left| {\begin{array}{*{20}c} {F_{11} } & {F_{12} } & {F_{13} } & {F_{14} } \\ {F_{21} } & {F_{22} } & {F_{23} } & {F_{24} } \\ {F_{31} } & {F_{32} } & {F_{33} } & {F_{34} } \\ {F_{41} } & {F_{42} } & {F_{43} } & {F_{44} } \\ \end{array} } \right| = 0$$
(46)

Letting \(\lambda_{i} \left( {i = 1,2, \ldots ,8} \right)\) be the characteristic root of the characteristic Eq. (46), the solutions to the set of differential Eqs. (32)–(35) can be expressed as:

$$U_{1} = \sum\limits_{i = 1}^{8} {a_{i} C_{1i} \exp \left( {\lambda_{i} x} \right)} ,\quad \xi_{1} = \sum\limits_{i = 1}^{8} {a_{i} C_{2i} \exp \left( {\lambda_{i} x} \right)} ,\quad w_{1} = \sum\limits_{i = 1}^{8} {a_{i} C_{3i} \exp \left( {\lambda_{i} x} \right)} ,\quad \theta_{1} = \sum\limits_{i = 1}^{8} {a_{i} C_{4i} \exp \left( {\lambda_{i} x} \right)}$$
(47)

where \(a_{i}\) is the integral constant; \(C_{i} = \left\{ {C_{1i} ,C_{2i} ,C_{3i} ,C_{4i} } \right\}^{\text{T}}\) are the characteristic vector corresponding to the characteristic root \(\lambda_{i}\).

According to Eqs. (26)–(29), the usual boundary conditions of a CBBCW can be expressed as: The natural boundary conditions of the CBBCW with SSD are \(U_{1}^{\prime } = 0\), \(\theta_{1}^{\prime } = 0\), \(\xi_{1}^{\prime } = 0\), \(w_{1} = 0\); The natural boundary conditions of the CBBCW with FSD are \(U_{1} = 0\), \(\theta_{1} = 0\), \(\xi_{1} = 0\), \(w_{1} = 0\). According to the boundary conditions of the SSD and FFD CBBCW, each of the two ends of the CBBCW has four boundary conditions. Substituting Eq. (30) into the boundary conditions and giving the eight equations with integral constants, the matrix expressions of the eight equations can be expressed as (Xiang et al. 2017) \(\left[ {B\left( \omega \right)} \right]\left\{ a \right\} = 0\), \(\left\{ a \right\} = \left\{ {a_{1} ,a_{2} , \ldots ,a_{8} } \right\}^{\text{T}}\), \(\left[ {B\left( \omega \right)} \right]\left\{ a \right\} = 0\) is non-zero only if \(\left| {B\left( \omega \right)} \right| = 0\). Solving \(\left| {B\left( \omega \right)} \right| = 0\) can obtain the natural vibration frequency of a CBBCW.

4 Verification of IAM

In order to verify the effectiveness of the IAM developed in the study, two simple-supported CBBCW and two fixed-supported CBBCW with different spans have been used as cases for analyses. The natural frequencies calculated by the GBT, IAM and FEM. The calculation results are shown in Tables 1, 2.

Table 1 Calculation result comparison for the natural frequencies of CBBCW (L = 10 m)
Full size table
Table 2 Calculation result comparison for the natural frequencies of CBBCW (L = 12 m)
Full size table

The finite element software ANSYS has been used to simulate the CBBCW cases, in which the concrete slab has been modeled by SOLID65 element, the steel beam has been modeled by SHELL43 element, and the stud has been modeled by COMBIN14 element, where the stud’s longitudinal slip stiffness, namely the spring stiffness of COMBIN14, has been calculated according to Eq. (16). The vertical interface interactions between the concrete slab and the steel beam were simulated by coupling the free degrees of the nodes in the vertical direction at the same position, i.e., the vertical separation between the concrete slab and the steel beam was ignored (Deng et al. 2017; Jiang et al. 2018; Xiang et al. 2017). The boundary conditions at the ends of the FE models were simulated by constraining the free degrees in both the vertical and transverse directions for the simply supported end, and by constraining the free degrees in the vertical, transverse and longitudinal directions for the fixed supported end (Zhou et al. 2016c).

The mechanical parameters and geometric parameters of the CBBCW cases are as follows: \(r = 0.25,\)\(r = 2.00,\)\(\rho_{\text{s}} = 7.87 \times 10^{ - 9} \,{\text{t}}\,{\text{mm}}^{ - 3},\)\(\rho_{\text{c}} = 2.570 \times 10^{ - 9} \,{\text{t}}\,{\text{mm}}^{ - 3},\)\(\mu_{\text{s}} = 0.30,\)\(\mu_{\text{c}} = 0.18,\)\(b_{1} = 800\,{\text{mm}},\)\(b_{3} = 900\,{\text{mm}},\)\(b_{2} = 400\,{\text{mm}},\)\(b_{4} = 400\,{\text{mm}},\)\(b_{5} = 200\,{\text{mm}},\)\(t_{1} = 120\,{\text{mm}},\)\(t_{2} = 120\,{\text{mm}},\)\(t_{3} = 25\,{\text{mm}},\)\(t_{5} = 25\,{\text{mm}},\)\(t_{4} = 12{\text{mm}},\)\(E_{\text{s}} = 2.0 \times 10^{5} \,{\text{MPa}},\)\(E_{\text{c}} = 4.5 \times 10^{4} \,{\text{MPa}}.\)\({\text{E}}_{\text{a}}\) denotes the error between the calculation results of the IAM and FEM for natural frequencies of CBBCW.

From Tables 1 and 2, it can be seen that, the IAM and FEM have been used to calculate the first five-order natural vibration frequencies of the four CBBCW cases. The calculation errors between the two methods are less than 4%. This is an indication that with the comprehensive consideration of the shear deformation, interfacial slip and shear lag, the results by IAM developed in this study are in good agreement with those by the FEM. Therefore, the correctness and reasonability of the IAM are validated. However, in the low natural frequency, the results by GBT are basically the same as those by the FEM and IAM, the calculation errors by GBT are significantly larger in the high natural frequency. The accuracy of IAM is further verified.

5 Analysis of Effect Factors

5.1 The Effect of Interface Slip on Natural Frequencies of CBBCW

Table 3 shows the effect of interface slip on natural frequencies of the CBBCW of SSD and FSD with the \(r = 0.25\) and \(r = 2.00\), respectively. Where, \({\text{C}}_{\text{s}}\) denotes the effect of interface slip.

Table 3 The effect of interface slip on natural frequencies of CBBCW (L = 10 m)
Full size table

As shown in Table 3, in the first-order and second-order vibration modes of the CBBCW cases, the maximum interface slip of the CBBCW is 28.42%. This is an indication that the interface slip corresponding to the low-order vibration mode of the CBBCW is significant and the increase in the shear connection degree can significantly increase the CBBCW’s low-order natural frequency. The interface slip corresponding to the high-order vibration mode of the CBBCW decreases significantly with the increasing order of the vibration mode. This is an indication that the effect of the shear connection degree on the high-order vibration mode of the CBBCW has been reduced and the proportion of deflection caused by the shear deformation is larger on the high-order vibration curve of the CBBCW.

5.2 The Effect of Shear Lag on Natural Frequencies of CBBCW

Figure 3 shows the effect of shear lag on natural frequencies of the CBBCW of SSD and FSD with \(r = 0.25\) and \(r = 2.00\) considered shear lag and not considered shear lag, respectively. \({\text{C}}_{\text{l}}\) denotes the effect of shear lag.

Fig. 3
figure 3

Relationship between the effect of shear lag and the mode orders of natural frequencies

Full size image

As shown in Fig. 3, under the condition with different shear connection degrees, the shear lag effect of the CBBCW is significant. The shear lag effect of the CBBCW increases with increasing shear connection degree. This is an indication that the longitudinal nonlinear deformation effect of the concrete slab and bottom plate of the CBBCW increase significantly with increasing shear connection degree. The shear lag effect of the CBBCW increases with the order of the vibration mode. For the four CBBCW cases, the shear lag effect of the CBBCW is up to 6.2% in the first five orders of the vibration modes. So, the shear lag effect has a certain effect on the high-order vibration mode of the CBBCW.

5.3 Comparison of CBBCW and OCBBW with Equal Web Thickness in Terms of Shear Lag

Figure 4 shows the comparison of CBBCW and OCBBW with equal web thickness in terms of shear lag under \(r = 0.25\) and \(r = 2.00\), respectively. \({\text{C}}_{\text{O}}\) denotes the effect of shear lag.

Fig. 4
figure 4

Comparison of CBBCW and OCBBW in terms of shear lag

Full size image

From Fig. 4, it can be seen that, except the first order natural vibration mode, the shear lag effect of the OCBBW are larger than those of the CBBCW, and the relative differences in the shear lag effect between the CBBCW and the OCBBW increases significantly with rising natural vibration mode order.

6 Discussion

Compared with the FEM, the IAM can incarnate the key influence factors and their influence laws affecting the dynamic characteristics of CBBCW more intuitively, saves a lot of time in modeling, model debugging and operating, and provide a theoretical basis for deriving a practical formula for engineering calculation and make up the deficiency of numerical simulation analysis.

In order to study the calculation efficiency of IAM, take the cases with spans of 10 m and 12 m (FSD, \(r = 0.25\)) as examples. The calculation efficiency is expressed by \(E_{c} {{ = \left( {t_{FEM} - t_{IAM} } \right)} \mathord{\left/ {\vphantom {{ = \left( {t_{FEM} - t_{IAM} } \right)} {t_{IAM} }}} \right. \kern-0pt} {t_{IAM} }} \times 100\%\). When the calculated span of CBBCW is 10 m, FEM takes 199 s to calculate the dynamic characteristics, IAM takes 159 s, and the calculation efficiency is improved by 25.2%; When the calculated span of CBBCW is 12 m, FEM takes 284 s to calculate the dynamic characteristics, while IAM only takes 160 s, the computational efficiency was improved by 78.6%. It can be found that IAM has a higher calculation efficiency, and with the increase of geometric size of CBBCW, the advantages are more significant.

7 Conclusions

With the comprehensive consideration of the characteristics of the CBBCW and factors such as shear lag, interfacial slip, shear deformation and moment of inertia, based on the Hamilton principle, an IAM for calculating the natural frequencies of a CBBCW has been developed. Using the IAM, the natural frequencies of multiple CBBCW cases with different spans, shear connection degrees and boundary conditions have been calculated. The results calculated by the IAM have been compared with those calculated by GBT and by FEM. The conclusions are as follows:

  1. (1)

    The results calculated by the IAM are in good agreements with those by the FEM, which validates the correctness of the IAM. The IAM provides a theoretical basis for the further study and application of CBBCW dynamic characteristics.

  2. (2)

    The interface slip for low-order vibration mode of CBBCW is significant, and the increase in the shear connection degree can significantly increase the low-order natural frequency of CBBCW.

  3. (3)

    The shear connection degree has little effect on the high-order natural vibration frequencies of CBBCW.

  4. (4)

    The shear lag effect of CBBCW increases with increasing shear connection degree, and increases with rising natural vibration mode order.

  5. (5)

    The relative differences in the shear lag effect between the CBBCW and the OCBBW increases significantly with rising natural vibration mode order.