Keywords

1 Introduction

In modern times, laminated composite beams, plates, and shells are extensively used in high-speed aircraft, rocket, launch vehicle, aerospace, or civil structures due to their high specific strength and stiffness, excellent fatigue and corrosion resistance. In engineering application, many structures are required stiffness-to-weight ratio, thus the structure made of laminated composite materials represents efficient constructive solutions. To analyze the mechanical behavior of such type of structures are extremely complex process. Although a considerable number of analytical and numerical methods have been proposed over the years. To analyze the structural behavior of this type of structure, the beam theories are extensively used. In the case of modeling of weight-sensitive structures, the one-dimensional (1D) approach is more significant due to its simplicity and low computational cost and more efficient than two-dimensional (2D) (plate and shell) and three-dimensional (3D) (solid) elements. The classical theories that are most employed are proposed by Euler–Bernoulli [1] and Timoshenko [2], which are also known as first-order shear deformation theories (FSDTs).

For modeling the composite structure these theories are inadequate. Several higher order shear deformation theories (HSDTs) are purposed for the composite structure, which can be classified into two main categories: equivalent single layer (ESL) and layer-wise (LW) theories. The ESL enables to produce piecewise continuous displacement and transverse stress in the thickness direction of the laminate structures [3, 4]. In this approach, the number of unknowns is independent of the number of layers, for example, first-and second-order shear deformation theories [5, 6]. Third-order shear deformation theories were purposed for the analysis of beams [7] and plates [8]. Arya et al. [9] presented a HSDT for the static analysis of laminated composite beams. Later, Li et al. [10] extended this refined model to study the free vibration of angle-ply laminated beams. And recently, Sahoo and Singh [11] studied new inverse zig-zag shear deformation theories for the static analysis of sandwich laminated plates. Carrera [12] compared different 2D theories to investigate the effects of the curvature and shear deformation on the buckling and vibrations of cross-ply laminated shells. Although ESL exhibits many applications in static and dynamic analysis of composite beams, it results in efficient theories for laminate structures. The main drawback of the ESL approach is that the continuity of transverse shear and normal stresses is not always assured. In the domain of LW, a continuous displacement assumption is considered in each separate layer. In LW approach, the number of degrees of freedom (DOFs) depends directly on the number of layers. In the LW approach the required computational cost is more than the ESL approach. Robin and Reddy [13] used LW theory to develop modeling of thick composites. Shimpi and Ainapure [14] presented a trigonometric shear deformation theory to develop modeling of two-layered cross-ply beams. Later, the same theory extended and utilized [15] for free vibration analysis of cross-ply laminated beams.

The present work has focused on refined theories with generalized displacement variables for the free vibration and stress analysis of the laminated box beam. For preliminaries model, the Carrera unified formulations (CUF) are used. CUF formulation has been developed over the last decade for plate/shell models [12, 16,17,18] and it has recently been extended for beam modeling [19]. In this study the cross section of laminated box beam made of orthotropic material with discretized with 16 nine-node elements (16L9). Two types of cross-sectional distribution 16L9 (a) and 16L9 (b) are used for the analysis as shown in Fig. 2. A combination of orthotropic fiber composite layers is used to be a construction of walls. The objective of this study is to develop a laminated box beam model with cut-off and without cut-off and this model is used for analysis in the form of free vibrations, displacements, and stresses with the help of refined one-dimensional beam theories. For finite element formulation, CUF framework is used to prepare a model, which is a hierarchical formulation leading to very accurate and computationally efficient finite element (FE) models. The laminated box made of two orthotropic layers with same thickness. In order to demonstrate the effectiveness of the proposed refined elements, the results in terms of natural frequencies, and displacements, are computed and compared with the available research literature.

Fig. 1
figure 1

Coordinate frame work of the beam model

Full size image

2 The Structural Model: Carrera Unified Formulation

According to the Carrera Unified Formulation the displacement fields \( u^{T} \left( {x, y, z,t} \right) = \left\{ {u_{x} u_{y} u_{z} } \right\}^{T} \), for the displacement vector, \( u_{\tau } (y) \) with expansion of generic functions, \( F_{\tau } (x,z) \)

$$ u(x, y, z, t) = F_{\tau } (x,z) u_{\tau } (y)\quad \tau = 1,2, \ldots ,T $$
(1)

where T stands for the terms in expansion, in Einstein’s generalized notation it stands for summation, \( u_{\tau } \) is the displacement vector, and \( F_{\tau } \) represents expansion function to approximate the behavior of the cross section of box beam.

In this work Eq. (1) consists of Lagrange polynomials, which are used to build the 1D higher order models. In this paper, the nine points (L9) cross-sectional polynomial (Fig. 2) set was adopted and the interpolation functions are given as:

Fig. 2
figure 2

Cross-sectional distribution of L9 elements of laminated box beam

Full size image
$$ \begin{aligned} F_{\tau } & = \frac{1}{4}\left( {r^{2} + r r_{\tau } } \right)\left( {s^{2} + s s_{\tau } } \right),\quad \tau = 1,3,5,7 \\ F_{\tau } & = \frac{1}{2}s_{\tau }^{2} \left( {s^{2} - s s_{\tau } } \right)\left( {1 - r^{2} } \right) + \frac{1}{2}r_{\tau }^{2} \left( {r^{2} + rr_{\tau } } \right)\left( {1 - s^{2} } \right),\quad \tau = 2,4,6,8 \\ F_{\tau } & = \left( {1 - r^{2} } \right)\left( {1 - s^{2} } \right),\quad \tau = 9 \\ \end{aligned} $$
(2)

where r and s vary from −1 to +1, whereas \( r_{\tau } \) and \( s_{\tau } \) are the coordinates of the nine points whose locations in the natural coordinate frame. The displacement of a L9 element therefore

$$ \begin{aligned} u_{x} & = F_{1} u_{{x_{1} }} + F_{2} u_{{x_{2} }} + F_{3} u_{{x_{3} }} + \cdots + F_{9} u_{{x_{9} }} \\ u_{y} & = F_{1} u_{{y_{1} }} + F_{2} u_{{y_{2} }} + F_{3} u_{{y_{3} }} + \cdots + F_{9} u_{{y_{9} }} \\ u_{z} & = F_{1} u_{{z_{1} }} + F_{2} u_{{z_{2} }} + F_{3} u_{{z_{3} }} + \cdots + F_{9} u_{{z_{9} }} \\ \end{aligned} $$
(3)

where \( u_{{x_{1} }} \ldots u_{{x_{9} }} \) represents the displacement field of the components x of the L9 element.

The stress and strains are

$$ \begin{aligned} \sigma_{p} & = \left\{ {\sigma_{zz} \sigma_{xx} \sigma_{xz} } \right\}^{T} ,\varepsilon_{p} = \left\{ {\varepsilon_{zz} \varepsilon_{xx} \varepsilon_{xz} } \right\}^{T} \\ \sigma_{n} & = \left\{ {\sigma_{zy} \sigma_{xy} \sigma_{yy} } \right\}^{T} ,\varepsilon_{n} = \left\{ {\varepsilon_{zy} \varepsilon_{xy} \varepsilon_{yy} } \right\}^{T} \\ \end{aligned} $$
(4)

where the subscripts p and n stands for the terms lying cross section and planes, respectively.

Hooke’s law and strain–displacement relations are, respectively,

$$ \begin{aligned} \sigma_{p} & = \widetilde{C}_{pp} \varepsilon_{p} + \widetilde{C}_{np} \varepsilon_{n} \\ \sigma_{n} & = \widetilde{C}_{np} \varepsilon_{p} + \widetilde{C}_{nn} \varepsilon_{n} \\ \varepsilon_{p} & = D_{p} u \\ \varepsilon_{n} & = \left( {D_{ny} + D_{np} } \right) \\ \end{aligned} $$
(5)

where

$$ D_{p} = \left[ {\begin{array}{*{20}c} 0 & 0 & {\frac{\partial }{\partial z}} \\ {\frac{\partial }{\partial x}} & 0 & 0 \\ {\frac{\partial }{\partial z}} & 0 & {\frac{\partial }{\partial x}} \\ \end{array} } \right],\quad D_{nA} = \left[ {\begin{array}{*{20}c} 0 & {\frac{\partial }{\partial z}} & 0 \\ 0 & {\frac{\partial }{\partial x}} & 0 \\ 0 & 0 & 0 \\ \end{array} } \right],\;\;D_{ny} = \left[ {\begin{array}{*{20}c} 0 & 0 & {\frac{\partial }{\partial y}} \\ {\frac{\partial }{\partial y}} & 0 & 0 \\ 0 & {\frac{\partial }{\partial y}} & 0 \\ \end{array} } \right] $$
(6)

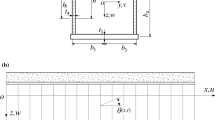
Box beam is a complex laminated structure, for such type of structure can be considered constituted by a certain number of straight orthotropic layers, material coordinate system (1; 2; 3) generally do not coincide with the physical coordinate system (x; y; z) as shown in Fig. 1. The matrices of the material coefficient of the generic material k based on the above approach are

$$ \widetilde{C}_{pp}^{k} = \left[ {\begin{array}{*{20}c} {\widetilde{C}_{11}^{k} } & {\widetilde{C}_{12}^{k} } & {\widetilde{C}_{14}^{k} } \\ {\widetilde{C}_{12}^{k} } & {\widetilde{C}_{22}^{k} } & {\widetilde{C}_{24}^{k} } \\ {\widetilde{C}_{14}^{k} } & {\widetilde{C}_{24}^{k} } & {\widetilde{C}_{44}^{k} } \\ \end{array} } \right],\quad \widetilde{C}_{pn}^{k} = \left[ {\begin{array}{*{20}c} {\widetilde{C}_{15}^{k} } & {\widetilde{C}_{16}^{k} } & {\widetilde{C}_{13}^{k} } \\ {\widetilde{C}_{25}^{k} } & {\widetilde{C}_{26}^{k} } & {\widetilde{C}_{23}^{k} } \\ {\widetilde{C}_{45}^{k} } & {\widetilde{C}_{46}^{k} } & {\widetilde{C}_{43}^{k} } \\ \end{array} } \right],\;\;\widetilde{C}_{nn}^{k} = \left[ {\begin{array}{*{20}c} {\widetilde{C}_{55}^{k} } & {\widetilde{C}_{56}^{k} } & {\widetilde{C}_{35}^{k} } \\ {\widetilde{C}_{56}^{k} } & {\widetilde{C}_{66}^{k} } & {\widetilde{C}_{36}^{k} } \\ {\widetilde{C}_{35}^{k} } & {\widetilde{C}_{36}^{k} } & {\widetilde{C}_{33}^{k} } \\ \end{array} } \right] $$
(7)

For the sake of brevity, shape function and explicit form of the coefficients are shown in [12]. To handle for arbitrary shaped cross section, classical finite element technique is adopted here and generalized displacement vector becomes

$$ u_{\tau } (y) = N_{i} (y) q_{\tau i} $$
(8)

where \( N_{i} (y) \) is the shape function and \( q_{\tau i} \) is the nodal displacement vector:

$$ q_{\tau i} = \left\{ {q_{{u_{{x_{\tau i} }} }} q_{{u_{{y_{\tau i} }} }} q_{{u_{{z_{\tau i} }} }} } \right\}^{T} $$
(9)

3 The Equation of Motion in the CUF Framework

The equation of motion can be directly derived from the Principle of Virtual Displacement (PVD), which states

$$ \delta L_{\text{int}} = \delta L_{\text{ext}} + \delta L_{\text{ine}} $$
(10)

where \( \delta L_{\text{int}} \), \( \delta L_{\text{ext}} \), \( \delta L_{\text{ine}} \), and \( \delta \) stands for internal work, external work, inertial work, and virtual variation, respectively.

With the help of Eqs. (1), (3), (4), and (5), the virtual variation can be written as

$$ \delta L_{\text{int}} = \delta q_{\tau i}^{T} K^{ij\tau s} q_{si} $$
(11)

where \( K^{ij\tau s} \) is in the form of a fundamental nucleus for the stiffness matrix and can be written as follows:

$$ \begin{aligned} K^{ij\tau s} & = I_{l}^{ij} \int {\left\{ {D_{np}^{T} \left( {F_{\tau } I} \right)\left[ {\widetilde{C}_{np}^{k} D_{p} \left( {F_{s} I} \right) + \widetilde{C}_{nn}^{k} D_{np} \left( {F_{s} I} \right)} \right]} \right.} \\ & \quad \left. { + D_{p}^{T} \left( {F_{\tau } I} \right)\left[ {\widetilde{C}_{pp}^{k} D_{p} \left( {F_{s} I} \right) + \widetilde{C}_{pn}^{k} D_{np} \left( {F_{s} I} \right)} \right]} \right\}{\text{d}}A \\ & \quad + + I_{l}^{ij,y} \int {\left[ {D_{np}^{T} \left( {F_{\tau } I} \right) + D_{p}^{T} \left( {F_{\tau } I} \right)\widetilde{C}_{pn}^{k} } \right]} F_{s} {\text{d}}A + I_{Ay} \\ & \quad + I_{l}^{i,yj} I_{Ay}^{T} \int {F_{\tau } \left[ {\widetilde{C}_{np}^{k} D_{p} \left( {F_{s} I} \right) + \widetilde{C}_{nn}^{k} D_{np} \left( {F_{s} I} \right)} \right]} {\text{d}}A \\ & \quad + I_{l}^{i,yj,y} I_{Ay}^{T} I_{Ay} \int {F_{\tau } \widetilde{C}_{nn}^{k} F_{s} } {\text{d}}A \\ \end{aligned} $$
(12)

where apex k denotes the layer and

$$ I_{Ay} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] $$
(13)
$$ \left( {I_{l}^{ij} , I_{l}^{ij,y} ,I_{l}^{i,yj} ,I_{l}^{i,yj,y} } \right) = \int\limits_{l} {\left( {N_{i} N_{j} , N_{i} N_{j,y} , N_{i,y} N_{j} , N_{i,y} N_{j,y} } \right) {\text{d}}y} $$
(14)

Similarly for the inertial loads

$$ \delta L_{\text{ine}} = \delta q_{\tau i}^{T} M^{ij\tau s} \ddot{q}_{sj} {\text{d}}y $$
(15)

where \( \ddot{q} \) stands for nodal acceleration and \( M^{ij\tau s} \) stands for mass matrix in the form of fundamental nucleus:

$$ M^{ij\tau s} = I_{l}^{ij} \int {\left( {F_{\tau } \rho^{k} I F_{\tau } } \right) {\text{d}}A} $$
(16)

Similarly for the external loads

$$ \delta L_{\text{ext}} = P \delta u^{T} $$
(17)
$$ \delta L_{\text{ext}} = F_{\tau } N_{i} P \delta q_{\tau i}^{T} $$
(18)
$$ P = \left\{ {P_{{u_{x} }} \;P_{{u_{y} }} \;P_{{u_{z} }} } \right\}^{T} $$
(19)

After assembly of global FE matrices, the undamped dynamic problem as follows:

$$ M\ddot{q} + Kq = 0 $$
(20)

Introducing harmonic solution, it is possible to compute the natural frequencies, \( \omega_{k} \) by solving a classical eigenvalue problem,

$$ \left( { - \omega_{k}^{2} M + K} \right)q_{k} = 0 $$
(21)

4 Analysis of Composite Box Beam

4.1 Free Vibration Analysis

In this section, the free vibration analysis of composite box beam is discussed. The cantilever box beam is prismatic with length L = 762 mm, width b = 24:21 mm, and height h = 13:46 mm. Each wall of the box beam has a total thickness equal to t = 0.762 mm was consider in the first numerical example. The length to height ratio, L/h is assumed equal to 10 and each layer of the structure is made of an orthotropic material, whose density and mechanical properties along the fiber (L) and transverse (T) directions are ρ = 1601 kg/m3, EL = 142 GPa, ET = 9.8 GPa, GLT = 6 GPa, GTT = 4.83 GPa, ν = 0.5. The box beam made of single and double layers and lamination schemes are reported in Table 1. The Lagrange Element (LE) consists of 9 four-noded (9B4) beam elements along the longitudinal axis and various approximations of the cross-sectional kinematics are assumed shows in Fig. 2 where each rectangle represents one L9 (Fig. 3) polynomial set. The two 16L9 models are considered for the free vibration analysis. Natural frequencies of the box beam reported in Table 2 and the computed results were compared with the finite element solution provided by [16]. The compared results have good agreement with references. The natural frequencies related to the mode number for the various aspect ratio and stacking sequences of 16L9(a) and 16L9(b) models were shown in Fig. 4 and Fig. 5 respectively. From the results given, it should be clear that aspect ratio and stacking sequences can significantly influence the natural frequencies of the model.

Table 1 The different lamination sequences of the layered box beam
Full size table
Fig. 3
figure 3

L9 element in the natural coordinate system

Full size image
Table 2 Comparison of natural frequencies for Case 1 and 3 with θ = 45°
Full size table
Fig. 4
figure 4

Natural frequencies for 16L9(a) model of box beam

Full size image
Fig. 5
figure 5

Natural frequencies for 16L9(b) model of box beam

Full size image

4.2 Static Analysis

In this section the static analysis of a composite box beam has been discussed, the box beam was clamped at the one end while a point load applied at the other end. The magnitude of the applied load was F = −5000 N. The geometrical data of the structure were as the previous and length to height ratio was equal to the 10. 9B4 elements were used to describe the box beam and the number of beam elements was derived from the convergence analysis. The vertical displacement reported in Table 3 for the various cases and computed results were compared with shell element of the commercial software. The vertical displacement was computed at two points ‘a’ and ‘b’ those projected on the middle of top and bottom surface at the free end of the beam. The computed results were compared with commercial software and have a good agreement. The study shows that the different stacking sequence can influence the vertical displacement of the box beam.

Table 3 Vertical displacement of box beam with and without cut-off model
Full size table

4.3 Effects of Cut-Offs

In this section, the static and free vibration analysis of a composite box beam with cut-off has been discussed. The cut-off located on the center of the bottom surface of the box beam, the dimension of the cut-off was width (bc) = 11:343 and length (lc) = 44:866 mm. The vertical displacement and natural frequencies of box beam (L/h = 10) without and with cut-off have been reported in Table 3 and Table 4 respectively. The computed results are in good agreement with shell elements model of commercial software. For the static analysis, the magnitude of the applied force was F = −5000 N. Vertical displacement and natural frequencies have been analyzed for various cases. The computed results show that the cut-off model was more displaced than the without cut-off model for static analysis and natural frequencies of cut-off model were lower than the without cut-off model for free vibration analysis. The natural frequencies related to the mode number for case 1 and case 3 of 16L9(b) models have been shown in Figs. 6 and 7. The graph shows that the low variation trends of frequencies at lower modes and higher modes but more variation in between lower and higher modes.

Table 4 Natural frequencies (Hz) of box beam with and without cut-off model
Full size table
Fig. 6
figure 6

Natural frequencies for 16L9(b) model of box beam for case 1

Full size image
Fig. 7
figure 7

Natural frequencies for 16L9(b) model of box beam for case 3

Full size image

5 Conclusion

In this present work, free vibration and static analyses of composite box beam have been carried out. The analyses were performed by means of a refined beam model based on the Lagrange Expansion (LE). The principle of virtual displacement has been used along with CUF to formulate the finite element arrays in the terms of fundamental nuclei, which neither depend on the expansion order nor the class of the beam model. The present methodology can deal with full material anisotropy and the cut-off also can be easily implemented in the box structure. Various composite box beams have been analyzed and in the domain to focus on the parametric studies have been performed to see the effects of cut-off versus free vibration and static analysis. The computed results show that the different stacking sequence and aspect ratio can influence the results of both free vibration and static analysis. The results were compared with published literature obtained in LE expansion of CUF models. The provided comparison shows that with lower computation cost, the 1D-CUF approach yields eventually the same results of the 3D solid element solution.