Transient thin-film spin-coating flow of chemically reactive and radiative Maxwell nanofluid over a rotating disk

Abstract

In recent years, the investigation on nanofluids has developed a hot topic among researchers, because in the presence of the nanoparticles in the fluids enhances appreciably the thermal conductivity of the fluid and thus improves the heat transfer characteristics. The current work aims to study the unsteady finite thin-film flow of upper convected Maxwell fluid due to horizontal rotating disk in the presence of nanoparticles. The development of a thin conducting liquid film on the surface of a rotating disk is investigated under the impacts of nonlinear thermal radiations, variable magnetic field, and Joule heating. A significant perspective of this attempt is to incorporate the features of exothermic chemical reaction with activation energy for Buongiorno’s model of nanofluid owing to their improved heat transfer. The leading equations of the governing problem are modeled by utilizing the notion of Boussinesq approximation. The non-dimensional analysis is performed to acquire the ordinary differential equations. A finite-difference-based numerical scheme, namely, bv4c is implemented for the numerical simulation of the nonlinear problem. The physical consequence of the active parameters, that influenced the model, are argued through graphs on nanofluid velocity, temperature, solute concentration, local Nusselt number, and Sherwood number. The obtained results intimate that nanofluid film thickness decay with the growing values of unsteadiness parameter, magnetic parameter, and Deborah number. It is noted that the nanoparticles’ volume fraction increases with incremented values of activation energy parameter. Moreover, the nanofluid temperature shows a remarkable increase with the thermophoresis parameter.

1 Introduction

The process of developing a uniform thin liquid film over a horizontal rotating disk is known as spin coating. This procedure is widely applicable in spin-coating industry and has a lot of applications in various industry and technology sectors. To name few; magnetic disk coatings, head lubricants, photoresist for defining patterns in microcircuit fabrication, flat screen display coatings, anti reflection coatings, etc. The innovative idea on thin-film flow over a rotating disk was first reported by Emslie et al. [1]. By considering the balance between viscous and centrifugal force during the disk rotation process allow them to simplify the governing equations and concluded that the film uniformity retains as it thin more and more continuously. In electronic industry, the applicability of the spin-coating process was explored through experimental interpretations and theoretical investigations by Washo [2]. Jenekhe [3] and Flack et al. [4] extended the work of Emslie et al. [1] by incorporating the mass transfer and non-Newtonian fluid models. The resulted lubrication equations were tackled with finite-difference scheme. Wang et al. [5] studied numerically the problem of liquid thin-film developed over an accelerating rotating disk. The asymptotic solution in the case of values of accelerating, thin and thick parameters was also obtained. Andersson et al. [6] acquired the both the numerical as well as asymptotic solution of liquid thin-film flow due to a rotating disk with magnetic field effects. Kumari and Nath [7] discussed the unsteady magnetohydrodynamic liquid thin-film flow spread due to a rotating disk. The Navier–Stokes together with energy equations were transformed and the solution was obtained numerically and asymptotically. Their results showed that the film thickness and the surface shear stresses in the radial and tangential directions increase with accelerating disk for a fixed value of magnetic field. The phenomenon of non-uniform disk rotation with planar disk interface in two layers thin-film flow with uniform transverse magnetic field was attempted by Dandapat and Singh [8].

Fig. 1

Schematic of the physical system

Fig. 2

Variation of S on a $F^{\prime }(\eta )$ b $G(\eta )$ c $F(\eta )$ and d $\theta (\eta )$

Fig. 3

Variation of $\omega$ on a $F^{\prime }(\eta )$ b $G(\eta )$ c $F(\eta )$ and d $\theta (\eta )$

Fig. 4

Variation of M on a $F^{\prime }(\eta )$ b $G(\eta )$ c $F(\eta )$ and d $\theta (\eta )$

Fig. 5

Variation of $\beta _{1}$ on a $F^{\prime }(\eta )$ b $G(\eta )$ c $F(\eta )$ and d $\theta (\eta )$

Fig. 6

Variation of a Ec and b Pr on $\theta (\eta )$

Fig. 7

Variation of a Rd and b $\theta _{\text {w}}$ on $\theta (\eta )$

Nanoscience and nanotechnologies are widely seen as having huge potential to bring benefits to many areas of research and applications such as nanofluids and nanocomposites [9,10,11]. Nowadays, investigation on nanofluids has been a subject of widespread research in view of its improved thermal conductivity [12]. Nanofluids comprise of nanoparticles such as silver Ag, copper Cu, copper oxide CuO, alumina oxide $\hbox {Al}_{2}\hbox {O}_{3}$, iron oxide $\hbox {Fe}_{3}\hbox {O}_{4}$, carbon nanotube CNT, and titanium oxide $\hbox {TiO}_{2}$ having sizes of 1–100 nm suspended in the base fluids such as water, alcohol, carboxymethyl cellulose CMC, etc. Some applications of nanoparticles were comprehensively reported by the authors [13,14,15,16]. It has been shown through experiments that the addition of these ultrafine solid metal particles in base fluids brings out a significant improvement in the thermal conductivity. A large amount of research has been conducted to explore the nanofluids physical properties and has assisted to better enlighten the basic mechanism of nanofluids. For instance, the nanometer-size particles’ suspension and their scattering and adhesion characteristics on the solid surfaces can give the materials having required optical and structural properties [17]. Nanofluids play a vital role in cooling process of inkjets and equipment [18, 19]. The usages of nanofluids are very wide in applications to the various fields such as nuclear reactor cooling, electronics, aerospace, vehicles, cancer therapy, power generation, etc.

Fig. 8

Variation of a $N_{\text {t}}$ and b $N_{\text {b}}$ on $\theta (\eta )$

Fig. 9

Variation of a, b $Ec$ when $T_{0}=0.1$ and c, d Ec when $T_{0}=0.0$ on isotherms

Fig. 10

Variation of a, b $N_{\text {t}}$ when $T_{0}=0.1$ on isotherms

Fig. 11

Variation of a $N_{\text {b}}$ and b Nt on $\phi (\eta )$

Fig. 12

Variation of a $\sigma^{**}$ and b $n$ on $\phi (\eta )$

Fig. 13

Variation of a E and b $\delta$ on $\phi (\eta )$

The term “nanofluids” was first used by the Choi [20] in 1995, who revealed that nanofluids possess enhanced thermal conductivity and thermal transport features of common liquids can be improved with the suspension of nanoparticles. Buongiorno [21] built up a significant two phase investigation regarding the heat transfer mechanism in nanofluids flow by proposing two-slip mechanisms, namely, Brownian diffusion and thermophoresis. A single-phase model that characterize the impacts of particle size, viscosity, volume fraction, and thermal conductivity on heat transfer enhancement was proposed by Tiwari and Das [22]. A large number of problems related to nanofluids flow were studied utilizing these two models. Kuznetsov and Nield [23] solved the problem of two-dimensional natural convection nanofluid flow past a vertical plate. Oztop and Nada [24] deliberated the nanoparticles fluid motion inside a rectangular enclosure along with heat transfer analysis. Lin and Jiang [25] explored numerically the effectiveness of thermophoresis and Brownian motion mechanisms due to nanofluids in a circular rotating groove.

The role of Arrhenius activation energy and chemical reaction in mass transfer analysis is noteworthy owing to its countless uses in technology and industrial processes including, retrieval of thermal lubricant, geothermal artificial lake, simmer down of atomic reacting, and compounds invention. Activation energy is the minimum amount of energy that must be required to begin chemical reaction for reacting species. The activation energy for a reaction can be described with the Arrhenius equation:

$$\begin{aligned} K_{\text {r}}=B\left( \frac{T}{T_{\infty }}\right) ^{n}\exp \left( -\frac{E_{\text {a}}}{ k_{1}T}\right) , \end{aligned}$$

(1)

where $K_{\text {r}},\ B,\ T,\ T_{\infty },\ n,\ E_{\text {a}},$ and $\ k_{1}$, respectively, denote the rate constant, pre-exponential factor or simply a constant, temperature, ambient temperature, fitted rate constant lying in range $-1$ to 1, activation energy, and Boltzmann constant $(k_{1}=8.6\times 10^{-5}\hbox {eV/K})$. This equation defines how the rate constant is related to the temperature. Chemical reaction is described as a process of chemical change in which one or more substances are produced which differed in properties from the reactants. Many chemically reacting systems involve the species chemical reactions with finite Arrhenius activation energy, with examples occurring in geothermal and oil reservoir engineering. The interactions between mass transport and chemical reactions are generally very complex, and can be observed in the production and consumption of reactant species at different rates both within the fluid and the mass transfer. Bestman [26] studied the chemically reactive and radiative flow with heat transport in a vertical pipe under the impact of activation energy. Maleque [27] reported a detail discussion regarding the impact of binary chemical reaction and activation energy in dissipative boundary layer flow. The outcomes revealed that the impact of activation energy parameter is to enhance the temperature and concentration distributions. Zhang et al. [28] discussed the effectiveness of chemical reaction and thermal radiations in the MHD flow of nanofluid caused by flat surface by solving the problem with differential transformation method (DTM) for an approximate solution. The chemical reactive stagnation-point flow with nanoparticles and viscous dissipation impact were considered with numerical approach by Mabood et al. [29]. They concluded that the influence of chemical reaction parameter plays a critical role in reducing the nanoparticle concentration. Afify and Elgazery [30] studied numerically the MHD Maxwell fluid flow caused by stretching sheet with the consideration on chemical reaction. Their results indicated that nanoparticles’ concentration reduces with higher chemical reaction parameter, whereas a reverse pattern is noted for temperature. Chemical reaction and activation energy aspects in nanofluid past a vertical plate in the presence buoyancy effects are considered by Mustafa et al. [31]. Their results showed that nanoparticles’ concentration is higher when activation energy for chemical reaction is higher.

The flow behaviors of frequently occurring fluids in nature and industry such as motor oils, biological fluids, polymeric liquids and many other complex mixtures, etc. can be described with the non-Newtonian fluid models. A non-Newtonian fluids type in which applied shear stress is a memory function of the deformation rate is known as viscoelastic fluids. In such a type of fluids, when the shear stress is removed, the rate of deformation slowly diminishes. This is called stress relaxation property. Furthermore, the time required by the fluid for partial elastic recovery upon the removal of stress is relaxation time. The first and the simplest viscoelastic model which is used widely to account for fluid rheological effects is called the Maxwell model [32,33,34,35].

A careful observation of the existing literature reveals that the study of thin-film flow of Maxwell fluid in the regimes horizontal rotating disk have not been explored. The main concern of present research is to study this problem thoroughly. The novel contributions of the current study can be summarized in the following main points:

• Maxwell thin nanoliquid film constitutive law modelling over a stretchable rotating disk with magnetic field properties.

• The features of Brownian diffusion and thermophoresis on temperature and concentration fields due to nanofluid are studied using Buongiorno’s model.

• The mechanism of heat transfer analysis is considered with nonlinear radiative heat flux and Joule heating.

• The distinctive resulting properties of Arrhenius chemical reaction with activation energy are studied on solute concentration.

• The resulting nonlinear system of ordinary differential equations corresponding to momentum, thermal energy and nanoparticles concentration for Maxwell fluid are numerically solved with the finite-difference-based scheme called bvp4c in Matlab.

In the end, the active physical parameters that influence the physical model are analyzed for radial, axial, and azimuthal velocities, temperature, and concentration distributions, local Nusselt and Sherwood numbers.

2 Problem formulation

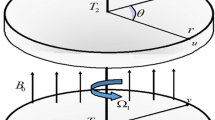
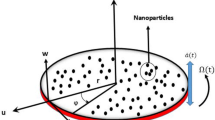
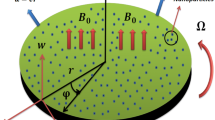
Consider the magnetohydrodynamic (MHD) time-dependent electrically conducting thin-film flow of upper convected Maxwell nanofluid over a stretchable rotating disk. The motion of fluid is due to stretching as well as rotating phenomena. The thin elastic disk emerges radially from a narrow slit at the origin of the cylindrical coordinate system $(r,\varphi ,z)$, as shown in Fig. 1.

A uniform liquid film of thickness $h(r,t)$ is formed horizontally on the surface of rotating disk. The disk stretching, rotating velocities, temperature, and concentration vary with space and time. For the simplification of physical problem, we made the following assumptions.

The disk is rotating with uniform velocity in the azimuthal direction as

$$\begin{aligned} v=\frac{r\Omega }{1-at}, \end{aligned}$$

(2)

where $\Omega$ is the disk rotating rate. In addition, the disk is stretching with velocity:

$$\begin{aligned} u=\frac{cr}{1-at}, \end{aligned}$$

(3)

where $c$ is denoting the stretching rate and a positive constant. The surface temperature $T_{\text {s}}$ and concentration $C_{\text {s}}$ of the stretchable rotating disk are expressed as

$$\begin{aligned} T_{\text {s}}& = T_{0}-T_{\text {ref}}\frac{\Omega r^{2}}{\nu \left( 1-at\right) ^{3/2}}, \end{aligned}$$

(4)

$$\begin{aligned} C_{\text {s}}& = C_{0}-C_{\text {ref}}\frac{\Omega r^{2}}{\nu \left( 1-at\right) ^{3/2}}, \end{aligned}$$

(5)

where $\left( T_{0},C_{0}\right)$ denote the temperature and concentration at the origin, respectively, and $\left( T_{\text {ref}},C_{\text {ref}}\right)$ the constant reference temperature and concentration. A time-dependent magnetic field $B(t)=B_{0}/\sqrt{1-at}$ is applied in the z-direction on liquid thin-film motion. The process of heat transfer is carried in the presence of nonlinear thermal radiations and Joule heating. The Buongiorno model is used to study the features of nanoparticles described by Brownian motion and thermophoresis quantities. The above assumptions together with species chemical reaction with Arrhenius activation energy lead the following system of governing equations [35]:

$$\begin{aligned}&\frac{\partial u}{\partial r}+\frac{u}{{r}}+\frac{\partial w}{\partial z}=0, \end{aligned}$$

(6)

$$\begin{aligned}&\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial r}+w\frac{ \partial u}{\partial z}-\frac{v^{2}}{r}+\lambda _{1}\left( \frac{\partial ^{2}u}{\partial t^{2}}+u^{2}\frac{\partial ^{2}u}{\partial r^{2}}\right. \nonumber \\&\qquad \left. +2u\frac{ \partial ^{2}u}{\partial r\partial t}-2\frac{v}{r}\frac{\partial v}{\partial t}+2w\frac{\partial ^{2}u}{\partial z\partial t}-\frac{2uv}{r}\frac{\partial v}{\partial r}+\frac{uv^{2}}{r^{2}}\right. \nonumber \\&\qquad \left. +2uw\frac{\partial ^{2}u}{\partial r\partial z}-\frac{2vw}{r}\frac{ \partial v}{\partial z}+w^{2}\frac{\partial ^{2}u}{\partial z^{2}}+\frac{ v^{2}}{r}\frac{\partial u}{\partial r}\right) \nonumber \\&\quad =\nu \left( \frac{\partial ^{2}u}{\partial z^{2}}\right) -\frac{\sigma B\left( t\right) ^{2}}{\rho } \left( u+\lambda _{1}\left( \frac{\partial u}{\partial t}+w\frac{\partial u}{ \partial z}\right) \right) , \end{aligned}$$

(7)

$$\begin{aligned}&\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial r}+w\frac{ \partial v}{\partial z}+\frac{uv}{r}+\lambda _{1}\left( \frac{\partial ^{2}v }{\partial t^{2}}\right. \nonumber \\&\left. \qquad + \, 2u\frac{\partial ^{2}v}{\partial r\partial t}+2\frac{v}{r} \frac{\partial u}{\partial t}+2w\frac{\partial ^{2}v}{\partial z\partial t} +u^{2}\frac{\partial ^{2}v}{\partial r^{2}}-\frac{2u^{2}v}{r^{2}}+\frac{2uv}{ r}\frac{\partial u}{\partial r}\right. \nonumber \\&\qquad \left. +\, 2uw\frac{\partial ^{2}v}{\partial r\partial z}-\frac{v^{3}}{r^{2}}+ \frac{2vw}{r}\frac{\partial u}{\partial z}+\frac{v^{2}}{r}\frac{\partial v}{ \partial r}+w^{2}\frac{\partial ^{2}v}{\partial z^{2}}\right) \nonumber \\&\quad =\nu \left( \frac{\partial ^{2}v}{\partial z^{2}}\right) -\frac{\sigma B\left( t\right) ^{2}}{\rho }\left( v+\lambda _{1}\left( \frac{\partial v}{\partial t}+w\frac{ \partial v}{\partial z}\right) \right) , \end{aligned}$$

(8)

$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}\nonumber \\&\quad =\alpha \frac{\partial ^{2}T}{\partial z^{2}}+\tau \left[ D_{\text {B}} \frac{\partial T}{\partial z}\frac{\partial C}{\partial z}+\frac{D_{\text {T}}}{T_{0} }\left( \frac{\partial T}{\partial z}\right) ^{2}\right] \nonumber \\&\qquad +\frac{\sigma B\left( t\right) ^{2}}{\rho }\left( u^{2}+v^{2}\right) -\frac{1}{\rho c_{\text {p}}} \frac{\partial q_{\text {rad}}}{\partial z}, \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial r}+w\frac{\partial C}{\partial z}\nonumber \\&\quad =D_{\text {B}}\frac{\partial ^{2}C}{\partial z^{2}}+\frac{D_{\text {T}}}{T_{0}} \frac{\partial ^{2}T}{\partial z^{2}}-k_{\text {r}}^{2}\left( C-C_{0}\right) \left( \frac{T}{T_{0}}\right) ^{n}\exp \left( -\frac{E_{\text {a}}}{k_{1}T}\right) , \end{aligned}$$

(10)

where ν is the kinematic viscosity, $\lambda _{1}$ the relaxation time, $\tau$ the heat capacities ratio$,\ D_{\text {B}}$ is the Brownian diffusion coefficient ${\small ,}\ D_{\text {T}}$ the thermophoresis diffusion coefficient, $k_{\text {r}}$the reaction rate. Radiative heat flux $q_{\text {rad}}$ in Eq. (9) can be simplified using Rosseland approximation as

$$\begin{aligned} q_{\text {rad}}=-\frac{4\sigma ^{*}}{3k^{*}}\frac{\partial T^{4}}{ \partial z}, \end{aligned}$$

(11)

where the Stephan–Boltzmann constant is denoted by $\sigma ^{*}$ and the mean absorption coefficient by $k^{*}$. Assume that the temperature difference is sufficiently small within the flow. Therefore, $T^{4}$ can be expanded in Taylor series about $T_{\infty }$ and omitting the higher terms to obtain

$$\begin{aligned} q_{\text {rad}}=-\frac{16\sigma ^{*}T^{3}}{3k^{*}}\frac{\partial T}{ \partial z}. \end{aligned}$$

(12)

Making use of expression (12), Eq. (9) simplified as

$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial r}+w\frac{ \partial T}{\partial z}=\alpha \frac{\partial ^{2}T}{\partial z^{2}}+\tau \left[ D_{\text {B}}\frac{\partial T}{\partial z}\frac{\partial C}{\partial z}+\frac{ D_{\text {T}}}{T_{0}}\left( \frac{\partial T}{\partial z}\right) ^{2}\right] \nonumber \\&\quad +\frac{\sigma B\left( t\right) ^{2}}{\rho }\left( u^{2}+v^{2}\right) +\frac{ 16\sigma ^{*}}{3\rho c_{\text {p}}k^{*}}\frac{\partial }{\partial z}\left( T^{3}\frac{\partial T}{\partial z}\right) . \end{aligned}$$

(13)

The physical problem is modeled in the form of the following boundary conditions:

$$\begin{aligned}&\left( u,v,w,T,C\right) =\left( \frac{cr}{1-at},\ \frac{r\Omega }{1-at},\ 0,\ T_{\text {s}},\ C_{\text {s}}\right) \ \text {at}\ z=0, \nonumber \\&\frac{\partial u}{\partial z}=\frac{\partial v}{\partial z}=0,\ w=\frac{ \partial h}{\partial t}+u\frac{\partial h}{\partial r},\ \frac{\partial T}{ \partial z}=\frac{\partial C}{\partial z}=0\ \text {at}\ z=h. \end{aligned}$$

(14)

Taking into account the following similarity variables:

$$\begin{aligned} \eta& = \sqrt{\frac{\Omega }{\nu \left( 1-at\right) }}z,\ \left[ u,v,w\right] \nonumber \\& = \left[ \frac{r\Omega }{1-at}F^{\ \prime }\left( \eta \right) ,\ \frac{ r\Omega }{1-at}G\left( \eta \right) ,\ -2\left( \frac{\nu \Omega }{1-at} \right) ^{1/2}F\left( \eta \right) \right] , \end{aligned}$$

(15)

$$\begin{aligned} h(t)& = \sqrt{\frac{\nu \left( 1-at\right) }{\Omega }}\beta , \end{aligned}$$

(16)

$$\begin{aligned} T& = T_{0}-T_{\text {ref}}\frac{\Omega r^{2}}{\nu \left( 1-at\right) ^{3/2}}\theta \left( \eta \right) , \end{aligned}$$

(17)

$$\begin{aligned} C& = C_{0}-C_{\text {ref}}\frac{\Omega r^{2}}{\nu \left( 1-at\right) ^{3/2}}\phi \left( \eta \right) , \end{aligned}$$

(18)

where the dimensionless radial, azimuthal, and axial velocities are symbolized by $F^{\prime} (\eta),\, G (\eta)\, \text{and}\, F(\eta)$, respectively. Substituting Eqs. (15)–(18) in Eqs. (6)–(8), (10), (13), and (14), the following system of ordinary differential equations is obtained:

$$\begin{aligned}&F^{\prime \prime \prime }-S\left( F^{\prime }+\frac{\eta }{2}F^{\prime \prime }\right) -\left( F^{\prime ^{2}}-G^{2}-2FF^{\prime \prime }\right) \nonumber \\&\qquad -\beta _{1}\left[ S^{2}\left( 2F^{\prime }+\frac{7}{4}\eta F^{\prime \prime }+\frac{1}{4}\eta ^{2}F^{\prime \prime \prime }\right) \right. \nonumber \\&\qquad \left. +S\left( 2F^{\prime ^{2}}-2G^{2}-6FF^{\prime \prime }\right) +\eta S\left( F^{\prime }F^{\prime \prime }-GG^{\prime }-2FF^{\prime \prime \prime }\right) \right. \nonumber \\&\qquad \left. -4FF^{\prime }F^{\prime \prime }+4F^{2}F^{\prime \prime \prime } -4FGG^{\prime }\right] \nonumber \\&\qquad -M\left[ F^{\prime }+\beta _{1}\left( SF^{\prime }+\frac{1}{2}\eta SF^{\prime \prime }-2FF^{\prime \prime }\right) \right] =0, \end{aligned}$$

(19)

$$\begin{aligned}&G^{\prime \prime }-S\left( G+\frac{\eta }{2}G^{\prime }\right) -2\left( F^{\prime }G-FG^{\prime }\right) \nonumber \\&\qquad -\beta _{1}\left[ S^{2}\left( 2G+\frac{7}{4} \eta G^{\prime }+\frac{1}{4}\eta ^{2}G^{\prime \prime }\right) \right. \nonumber \\&\qquad \left. + S\left( 4F^{\prime }G-6FG^{\prime }\right) +\eta S\left( F^{\prime }G^{\prime }+F^{\prime \prime }G-2FG^{\prime \prime }\right) \right. \nonumber \\&\qquad \left. -4FF^{\prime }G^{\prime }-4FF^{\prime \prime }G+4F^{2}G^{\prime \prime }\right] \nonumber \\&\qquad -M\left[ G+\beta _{1}\left( SG+\frac{1}{2}S\eta G^{\prime }-2FG^{\prime }\right) \right] =0, \end{aligned}$$

(20)

$$\begin{aligned}&\left( 1+\frac{4}{3}Rd\right) \theta ^{\prime \prime }+\frac{4}{3}Rd\left[ \left( \theta _{\text {w}}-1\right) ^{3}\left( 3\theta ^{2}\theta ^{\prime ^{2}}\right. \right. \nonumber \\&\qquad \left. \left. +\theta ^{3}\theta ^{\prime \prime }\right) +3\left( \theta _{\text {w}}-1\right) ^{2}\left( 2\theta \theta ^{\prime ^{2}}+\theta ^{2}\theta ^{\prime \prime }\right) \right. \nonumber \\&\qquad \left. +3\left( \theta _{\text {w}}-1\right) \left( \theta ^{\prime ^{2}}+\theta \theta ^{\prime \prime }\right) \right] +2\Pr \left( F\theta ^{\prime }-F^{\prime }\theta \right) \nonumber \\&\qquad -\frac{1}{2}\Pr S\left( \eta \theta ^{\prime }+3\theta \right) +\Pr \left( Nt\ \theta ^{\prime ^{2}}+Nb\theta ^{\prime }\phi ^{\prime }\right) \nonumber \\&\qquad +\Pr MEc\left( F^{\prime ^{2}}+G^{2}\right) =0, \end{aligned}$$

(21)

$$\begin{aligned}&\phi ^{\prime \prime }+2Sc\left( F\phi ^{\prime }-F^{\prime }\phi \right) - \frac{1}{2}Sc\left( 3\phi +\eta \phi ^{\prime }\right) S\nonumber \\&\qquad +\frac{Nt}{Nb}\theta ^{\prime \prime }-Sc\sigma ^{**}\left( 1+\delta \theta \right) ^{n}\phi \exp \left( -\frac{E}{1+\delta \theta }\right) =0, \end{aligned}$$

(22)

with transformed boundary conditions:

$$\begin{aligned} F\left( 0\right)& = 0,\text { }F^{\prime }(0)=\omega \text {, }G(0)=1,\ \theta (0)=1,\ \phi (0)=1, \nonumber \\ F\left( \beta \right)& = \frac{S\beta }{4},\text { }F^{\prime \prime }(\beta )=0\text {, }G^{\prime }(\beta )=0,\ \theta ^{\prime }(\beta )=0,\ \phi ^{\prime }(\beta )=0, \end{aligned}$$

(23)

where the dimensionless parameters $S,\ M,\ \beta _{1},\ \Pr ,\ \theta _{\text {w}},\ Ec,\ Rd,\ N_{\text {t}},\ N_{\text {b}},\ Sc,\ \omega ,\ \sigma ^{**},\ \delta ,\ E$ are the measure of unsteadiness, magnetic parameter, Deborah number, Prandtl number, temperature ratio parameter, Eckert number, radiation parameter, thermophoresis parameter, Brownian motion parameter, Schmidt number, rotation parameter, reaction rate, temperature difference parameter and activation energy parameter. In dimensionless forms, we can write these parameters as

$$\begin{aligned} S& = \frac{a}{\Omega },\ M=\frac{\sigma B_{0}^{2}}{\rho \Omega },\ \beta _{1}=\frac{\lambda _{1}\Omega }{1-at},\nonumber \\ \Pr& = \frac{v}{\alpha },\ \theta _{\text {w}}= \frac{Ts}{T_{0}},\ \nonumber \\ Ec& = \frac{v^{2}}{c_{\text {p}}\left( T_{\text {s}}-T_{0}\right) },\ Rd=\frac{4\sigma ^{*}T_{0}^{3}}{kk^{*}},\nonumber \\ N_{\text {t}}& = \frac{\tau D_{\text {T}}\left( T_{s}-T_{\text {0}}\right) }{T_{0}v},\ N_{\text {b}}=\frac{\tau D_{\text {B}}\left( C_{s}-C_{\text {0}}\right) }{v}, \nonumber \\ \ Sc& = \frac{\nu }{D_{\text {B}}},\ \omega =\frac{c}{\Omega },\ \sigma ^{**}=\frac{k_{\text {r}}^{2}\left( 1-at\right) }{\Omega },\nonumber \\ \delta& = \frac{\left( T_{\text {s}}-T_{0}\right) }{T_{0}},E=\frac{E_{\text {a}}}{k_{1}T_{0}}. \end{aligned}$$

(24)

Furthermore, $\beta$ denotes the value of the similarity variable $\eta$ at the free surface. Thus, Eq. (16) gives

$$\begin{aligned} \beta =\sqrt{\frac{\Omega }{\nu \left( 1-at\right) }}h. \end{aligned}$$

(25)

The local Nusselt number $Nu_{\text {r}}$ and Sherwood number $Sh_{\text {r}}$are defined as

$$\begin{aligned} Nu_{\text {r}}=\frac{rq_{w}}{k\left( T_{\text {s}}-T_{0}\right) },Sh_{\text {r}}=\frac{r\ j_{w}}{ k\left( C_{\text {s}}-C_{0}\right) }, \end{aligned}$$

(26)

where

$$\begin{aligned} q_{w}=-k\left[ 1+\frac{16\sigma ^{*}T^{3}}{3kk^{*}}\right] \left( \frac{\partial T}{\partial z}\right) \mid _{z=0},\ j_{w}=-k\left( \frac{ \partial C}{\partial z}\right) \mid _{z=0}, \end{aligned}$$

(27)

and dimensionless expressions of these quantities are

$$\begin{aligned} \hbox {Re}^{-1/2}\ Nu_{\text {r}}& = -\left( 1+\frac{4}{3}Rd\left\{ 1+\left( \theta _{w}-1\right) \theta (0)\right\} ^{3}\right) \theta ^{\prime }(0), \end{aligned}$$

(28)

$$\begin{aligned} \hbox {Re}^{-1/2}\ Sh_{\text {r}}& = -\phi ^{\prime }(0), \end{aligned}$$

(29)

where $\hbox {Re}^{1/2}=r\sqrt{\frac{\Omega }{v\left( 1-at\right) }}$ is the local Reynolds number.

3 Solution approach

The dimensionless nonlinear momentum, temperature, and concentration Eqs. (19–22) with conditions (23) are considered for the numerical computations. However, the numerical scheme bvp4c is followed to characterize the flow, temperature, and concentration profiles in the form of graphs. Bvp4c is one of the collocation method which uses Lobatto IIIA formula. To approximate solution of Eqs. (19–22) together with conditions (23), it will need the initial guesses which satisfy the boundary conditions. Once a user provides initial guesses, then another builtin method, namely, finite difference which modify the initial guesses for further iteration. To implement this numerical builtin method, the higher order system of ordinary differential equations is converted into a system of first-order ordinary differential equations by introducing some new variables. The steps for the conversion are given below. Let

$$\begin{aligned} F& = z_{1},\ F^{\prime }=z_{2},\ F^{\prime \prime }=z_{3},\ G=z_{4},\ G^{\prime }=z_{5},\ \theta =z_{6},\ \theta ^{\prime }=z_{7},\ \phi =z_{8},\ \phi ^{\prime }=z_{9}, \end{aligned}$$

(30)

$$\begin{aligned} z_{1}^{\prime }& = z_{2},\ z_{2}^{\prime }=z_{3}, \end{aligned}$$

(31)

$$\begin{aligned} z_{3}^{\prime }& = \frac{ \begin{array}{c} S\left( z_{2}+\frac{\eta }{2}z_{3}\right) +z_{2}^{2}-z_{4}^{2}-2z_{1}z_{3}+M\left[ z_{2}+\beta _{1}\left( Sz_{2}+\frac{ \eta }{2}Sz_{3}-2z_{1}z_{3}\right) \right] \\ +\beta _{1}\left[ S^{2}\left( 2z_{2}+\frac{7}{4}\eta z_{3}\right) +S\left( 2z_{2}^{2}-2z_{4}^{2}-6z_{1}z_{3}\right) +S\eta \left( z_{2}z_{3}-z_{4}z_{5}\right) -4z_{1}z_{2}z_{3}-4z_{1}z_{4}z_{5}\right] \end{array} }{\left( 1-\beta _{1}S^{2}\frac{\eta ^{2}}{4}+2\beta _{1}S\eta z_{1}-4\beta _{1}z_{1}^{2}\right) }, \end{aligned}$$

(32)

$$\begin{aligned} z_{4}^{^{\prime }}& = z_{5}, \end{aligned}$$

(33)

$$\begin{aligned} z_{5}^{^{\prime }}& = \frac{ \begin{array}{c} S\left( z_{4}+\frac{\eta }{2}z_{5}\right) -2z_{1}z_{5}+2z_{2}z_{4}+M\left[ z_{4}+\beta _{1}\left( Sz_{4}+\frac{\eta }{2}Sz_{5}-2z_{1}z_{5}\right) \right] \\ +\beta _{1}\left[ S^{2}\left( 2z_{4}+\frac{7}{4}\eta z_{5}\right) +S\left( 4z_{2}z_{4}-6z_{1}z_{5}\right) +S\eta \left( z_{2}z_{5}+z_{3}z_{4}\right) -4z_{1}z_{2}z_{5}-4z_{1}z_{3}z_{4}\right] \end{array} }{\left( 1-\beta _{1}S^{2}\frac{\eta ^{2}}{4}+2\beta _{1}S\eta z_{1}-4\beta _{1}z_{1}^{2}\right) }, \end{aligned}$$

(34)

$$\begin{aligned} z_{6}^{^{\prime }}& = z_{7}, \end{aligned}$$

(35)

$$\begin{aligned} z_{7}^{^{\prime }}& = \frac{ \begin{array}{c} -\frac{4}{3}Rd\left[ 3\left( \theta _{\text {w}}-1\right) ^{3}z_{6}^{^{2}}z_{7}^{^{2}}+6\left( \theta _{\text {w}}-1\right) ^{2}z_{6}z_{7}^{^{2}}+3\left( \theta _{\text {w}}-1\right) z_{7}^{^{2}}\right] -2\Pr \left( z_{1}z_{7}-z_{2}z_{6}\right) \\ +\frac{1}{2}\Pr S\left( \eta z_{7}+3z_{6}\right) -\Pr \left( N_{\text {b}}z_{7}z_{9}+N_{\text {t}}z_{7}^{2}\right) -\Pr MEc\left( F^{\prime ^{2}}+G^{2}\right) , \end{array} }{1+\frac{4}{3}Rd\left( 1+\left( \theta _{\text {w}}-1\right) ^{3}z_{6}^{^{3}}+3\left( \theta _{\text {w}}-1\right) ^{2}z_{6}^{^{2}}+3\left( \theta _{\text {w}}-1\right) z_{6}\right) } \end{aligned}$$

(36)

$$\begin{aligned} z_{8}^{^{\prime }}& = z_{9}, \end{aligned}$$

(37)

$$\begin{aligned} z_{9}^{^{\prime }}& = \frac{1}{2}Sc\left( 3z_{8}+\eta z_{9}\right) S+2Sc\left( z_{2}z_{8}-z_{1}z_{9}\right) -\frac{N_{\text {t}}}{N_{\text {b}}}z_{7}^{^{\prime }}+Sc\sigma ^{**}\left( 1+\delta \theta \right) ^{n}\phi e^{-\frac{E}{1+\delta \theta }}, \end{aligned}$$

(38)

with corresponding boundary conditions then become

$$\begin{aligned} z_{1}(0)& = 0,\ z_{2}(0)=\omega ,\ z_{4}(0)=1,\ z_{6}(0)=1,\ z_{8}(0)=1, \nonumber \\ z_{1}(\beta )& = \frac{S}{4}\beta ,\ z_{3}(\beta )=0,\ z_{5}(\beta )=0,\ z_{7}(\beta )=0,\ z_{9}(\beta )=0. \end{aligned}$$

(39)

Here, ten boundary conditions are reduced into nine by finding the relationship between film thickness $\beta$ and unsteadiness parameter S. This relationship can be obtained by solving first Eqs. (30)–(39) and the initial guess for the film thickness $\beta$ is provided to the bvp4c numerical scheme. The value of the guess for $\beta$ is settled in such a manner so that the condition $z_{1}(\beta )=\frac{S}{4}\beta$ holds. This procedure is based on trial and error basis. Then, Eqs. (30)–(39) are solved numerically with bvp4c method for known estimation of $\beta$ and S.

4 Results and discussion

The current work focuses on the transient heat and mass transfer properties in liquid thin-film flow over a horizontal rotating disk with the impact magnetic field, nonlinear thermal radiation, Joule heating, and Arrhenius chemical reaction with activation energy. Numerical computations have been accomplished for various values of emerging quantities in appropriate ranges such as unsteadiness parameter $S\ (1.0-1.9)$, magnetic field parameter $M\ (1.0-2.5)$, rotation parameter $\omega$ $(1.0-1.6)$, Deborah number $\beta _{1}$ $(0.0-0.2)$, Prandtl number $Pr\ (1.0-2.5)$, temperature ratio parameter $\theta _{\text {w}}$ $(1.0-2.2)$, radiation parameter $Rd\ (1.0-2.2)$, Eckert number $Ec\ (0.0-1.5)$, thermophoresis parameter $N_{\text {t}}$ $(0.5-2.0)$, Brownian motion parameter $N_{\text {b}}$ $(0.4-1.6)$, reaction rate parameter $\sigma ^{**}$ $(0.0-3.0)$, temperature difference parameter $\delta$ $(0.0-3.0)$, activation energy parameter E $(0.0-1.5)$, and fitted rate constant n $(0.0-3.0)$. Throughout the analysis of velocity, temperature, concentration fields, Nusselt number, and Sherwood number, the values of $S=1.0,\ \beta _{1}=0.1,\ M=1.0,\ \omega =1.0,\ Pr=1.7,$ $\theta _{\text {w}}=1.5,\ Rd=1.0,\ Ec=0.5,\ Sc=1.5$, $N_{\text {t}}=0.6$, $N_{\text {b}}=0.9$, $\sigma ^{**}=1.0,\ n=0.5$, $\delta =1.0,$ and $E=1.0$ are fixed. The obtained numerical results are plotted through Figs. 2a–d, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, and 13a, b.

Figure 2a–c describes the consequences of unsteadiness parameter S on the velocity components represented by $F^{\prime }\left( \eta \right)$, $G\left( \eta \right)$, and $F\left( \eta \right)$ in radial, azimuthal and axial directions, respectively. A significant increase is noted with the intensifying variation in the unsteadiness parameter S. These figures also exhibit that the increasing unsteadiness parameter S $(1.0-1.9)$ results in a reduction the film thickness $\beta$ from 2.213683 to 1.094566. Figure 2d illustrates the temperature field $\theta (\eta )$ with the growing values of unsteadiness parameter. It is observed from these curves that fluid temperature increases with the unsteadiness parameter at the expense of reduction in the non-dimensional film thickness of nanofluid. When the unsteady stretching rate S on the surface rises, friction and the flow velocity also rise. When friction increases, the area of the stretching surface in contact with the flow increases, therefore, generated heat from the friction on the surface is transferred to the flow. This leads to a decline in wall heat flux $\theta ^{\prime }(0)$, while the flow is heated. The fundamental parameter of the physical problem specified by the rotation parameter $\omega$ affects the velocity and temperature field which is sketched in Fig. 3a–d. It can be seen from Fig. 3a that radial velocity component increases with boosting the rotation parameter. Actually, when the rotation parameter is enhanced, the stretching effects become dominant as compared to rotation effects. In addition, in view of this argument, the azimuthal velocity component decreases with increasing rotation parameter, as observed in Fig. 3b. An increasing movement is shown by the axial velocity with increasing rotation parameter as depicted in Fig. 3c. Figure 3d portrays that without Joule heating and dissipation, the fluid temperature drops with growing rotation parameter which leads to heat loss.

The magnetic field parameter M properties on velocities and temperature field are demonstrated in Fig. 4a–d. We observe a noteworthy reduction in the velocity components curves in r-, $\varphi$- and z-directions, as shown in Fig. 4a–c. The fluid temperature is seen in an increasing manner which is displayed in Fig. 4d. It is also prominent that these graphs that the film thickness $\beta$ decreases with the magnetic field parameter M. When an electrically conducting fluid flows through a transverse magnetic field, the viscous action of the fluid is opposed by the magnetic force. As magnetic field parameter M enlarges, that is, the parameter inversely related to the rotation rate $\Omega$ decreases, magnetic force becomes dominant compared to the inertial force. This reduces convection and eventually drops the heat transfer coefficient at the disk. The effect of Deborah number $\beta _{1}$, which is associated with the fluid relaxation time characteristics, on the radial, azimuthal, and axial velocity components and temperature field is depicted in Fig. 5a–d. By fixing the values of other parameters, it is revealed that the fluid velocity is a decreasing function of Deborah number, while an enhancement occurs in the temperature field. The value $\beta _{1}=0$ corresponds to the viscous fluid model, while the curves for $\beta _{1}\ne 0$ are shown for the Maxwell fluid model. The Deborah number is the ratio of fluid relaxation time to observation time. The lesser values of Deborah number correspond to the smaller recovery interval and the material behave like a purely viscous fluid. On the other hand, material depicts a solid-like response for the larger value of Deborah number. Thus, an enhancement in Deborah number leads to increase the fluid relaxation time, and therefore, the fluid velocity decreases. As a result, the temperature field $\theta (\eta )$ increases with the Deborah number, as depicted in Fig. 5d. It is also perceived that the liquid thickness $\beta$ decreases the increasing value of Deborah number. Furthermore, the nanoliquid film thickness decreases from 2.4565061 to 2.033285 as the Deborah number increases from 0.0 to 2.0.

The temperature field $\theta (\eta )$ variation with Eckert number Ec is shown in Fig. 6a. It is remarked that temperature field increases with the enhancement of Eckert number Ec. In addition, note that the thin-film thickness of Maxwell nanofluid remains constant with the increasing value of Eckert number Ec. When the Eckert number Ec is augmented from 0.0 to 1.5, then due to molecules internal friction, the fluid mechanical energy is transformed to thermal energy. Therefore, the fluid temperature increases. The Prandtl number Pr impact on temperature field is described in Fig. 6b. A significant decline in fluid temperature occurs with higher value of Prandtl number. Physically, Prandtl number has an inverse relation with thermal diffusivity. Therefore, the fluid having higher Prandtl number Pr slowly diffuses as compared to fluid having lower values of Prandtl number. This argument results in a reduction in the fluid temperature within the thin-film flow.

Figure 7a shows the characteristics of radiation parameter Rd on temperature field $\theta (\eta )$. It is obvious from the curves that with the rising values of radiation parameter Rd, a significant development happens in fluid temperature. This observation is seen for linear as well as for nonlinear thermal radiations. Physically, more heat is provided to the liquid by flourishing the thermal radiation effects which as a result increases the temperature field. The role of temperature ratio parameter $\theta _{\text {w}}$ on fluid temperature $\theta (\eta )$ is shown in Fig. 7b. The value $\theta _{\text {w}}=1$ corresponds to linear thermal radiation phenomenon. The temperature field is directly proportional to the temperature ratio parameter $\theta _{w}$. It is due to the reason that improving temperature ratio parameter, the wall temperature value will be greater than the ambient fluid temperature.

The impact of nanofluid parameters, represented by, thermophoresis parameters $N_{\text {t}}$ and Brownian motion $N_{\text {b}}$ on temperature field $\theta (\eta )$ is elucidated in Fig. 8a, b. As shown by these plots, the temperature field magnifies and the film thickness $\beta$ decreases with rising values of thermophoresis and Brownian motion parameters. Physically, the Brownian motion signify the disorderly motion of the fluid particles and increase in Brownian motion indicates the improvement in particles disorder motion which formed much heat. The temperature profile rises with increasing thermophoretic effects. The force that diffuses nanoparticles into the ambient fluid due to temperature gradient is known as thermophoresis force. The role of thermophoretic force is such that the nanoparticles near the hot boundary are being pushed towards the cold fluid at the ambient.

Figure 9a, b represents the isotherms with variations in Eckert number $Ec=0.5$ and $Ec=1.5$, respectively, when $T_{0}=0.1.$ By moving in the radial and axial directions, the temperature values increase in both cases. The same behavior is depicted in Fig. 9c, d for $Ec=0.5$ and $Ec=1.5$, respectively, when $T_{0}=0.0.$ However, the difference between Fig. 9a, b and c, d is that hotter region is little bit greater in the case when $T_{0}=0.1.$ Furthermore, on the surface of the disk when $z=0$, the temperature value 0.3 is achieved around the radial distance $r=0.8$ in the case $T_{0}=0.1$, while in case of $T_{0}=0.0$, it is achieved at $r=1.0$. The behavior of thermophoresis parameter $N_{\text {t}}=0.0$and $N_{\text {t}}=0.6$ on the isotherms is displayed in Fig. 10a, b, respectively, when $T_{0}=0.0$. Here, temperature increases in the increasing r- and z-directions. In addition, we observe that moving along the disk surface, value of the temperature 0.3 is achieved at the radial distance after $r=0.8$ in case of $N_{\text {t}}=0.0$, while it is meet before $r=0.8$ in case of $N_{\text {t}}=0.6.$

In Fig. 11a, it is revealed that the nanoparticles’ volume fraction $\phi (\eta )$ show a decreasing behavior with the increasing value of Brownian motion parameter $N_{\text {b}}$. The thermophoresis parameter $N_{\text {t}}$ action on nanoparticles concentration is explained in Fig. 11b. The cumulative action of thermophoresis parameter has shown an increasing trend in nanoparticles fluid concentration. This is because the thermophoresis larger impact acts to transport the nanoparticles near to the hot disk on the way to cold fluid at the ambient, and hence, larger penetration depth is delivered. Figure 12a, b are sketched to show the influence of reaction rate $\sigma ^{**}$and fitted rate n constant on solute concentration $\phi (\eta )$. It can be detected that an enhancement in either reaction rate or fitted rate constant implies an increment in the factor $Sc\sigma ^{**}\left( 1+\delta \theta \right) ^{n}\phi \exp \left( -\frac{E}{1+\delta \theta }\right)$. This ultimately favors the destructive chemical reaction and thus reduces the concentration field $\phi (\eta )$. The non-dimensional activation energy E parameter as a function of concentration profile $\phi (\eta )$ is plotted in Fig. 13a. The pattern of the curves indicates the thickening of the concentration boundary layer with increasing value of activation energy parameter E. This occurs, because the low temperature and high activation energy results in a smaller rate constant and thus slows down the chemical reaction. Therefore, the solutal concentration increases. The temperature difference parameter $\delta$ impact on concentration field is shown in Fig.  13b. A decreasing trend in solute concentration is noted with the variation in fitted rate constant. This indicates that when the wall and ambient temperature difference enlarges, the concentration boundary layer thickness increases.

The variation of dimensionless thin fluid thickness $\beta$ against the parameters S, M, $\beta _{1}$ and $\omega$ is computed in Table 1. It can be observed that the effect of S, M, and $\beta _{1}$ is to reduce the nanofluid film thickness, whereas it is raised with the increasing impact of $\omega .$ Table 2 is organized to see the impact of parameters S,  $\beta _{1},M,\ \omega ,\ \theta _{w},\ Rd,\ Ec,\ N_{\text {t}}$ and $N_{\text {b}}$ on heat transfer rate $\hbox {Re}^{-1/2}Nu_{\text {r}}$ at the surface of disk. It is revealed from the table that heat transfer rate intensified with $S,\ \omega ,\ \theta _{\text {w}},$ and Rd, whereas it decreases with $\beta _{1}$, $M,\ Ec,\ N_{\text {t}}$ and $N_{\text {b}}.$ The rate of mass transfer $\hbox {Re}^{-1/2}Sh_{\text {r}}$ against the parameters $N_{\text {t}}$, $N_{\text {b}},\ Sc,\ E, \sigma ^{**},$ and $\delta$ is shown in Table 3. The mass transfer rate for the parameters $N_{\text {b}},\ Sc,\ \sigma ^{**},$ and $\delta$ have the increasing tendency, while the conflicting trend is observed for the parameters $N_{\text {t}}$ and E.

Table 1 Variations of film thickness $\beta$ for different values of $S,\ M,\ \beta _{1},$when $\omega =1.0.$

Table 2 The Nusselt number $Nu_{\text {r}}\hbox {Re}^{-1/2}$values when $\Pr =1.7,\ Sc=2.0$, $n=2.0$, $E=1.0$, $\sigma ^{**}=1.0,\ \delta =1.0.$

Table 3 The Sherwood number $Sh_{\text {r}}\hbox {Re}^{-1/2}$values when $S=1.3$ , $\beta _{1}=0.1,M=1.0,\ \Pr =1.7$, $\omega =1.0,$ $\theta _{\text {w}}=1.5,$ $Rd=1.0\ Ec=1.0,$ and $n=2.0$

5 Conclusions

Unsteady thin conducting film of Maxwell nanofluid flow over a rotating disk has been analyzed using Buongiorno’s mathematical model in the presence of nonlinear thermal radiation, variable magnetic field and Joule heating. The mass transfer analysis is studied with the impact of chemical reaction and activation energy. The system of partial differential equations is modeled with the assistance of Boussinesq approximation. The non-dimensional ordinary differential equations are obtained by adopting similarity approach. The numerical simulations for the unknown velocity, temperature and concentration fields have been done by applying a finite-difference-based numerical scheme called bvp4c. The present study can be summarized with the following main concluding points:

• The effect of rotation parameter is to increase the radial and axial velocities while diminishing the azimuthal velocity and temperature profile.

• A rise in the values of radiation, temperature ratio, thermophoresis and Brownian motion parameters leads to an increase in the temperature field of the Maxwell nanofluid flow.

• The rotation parameter play a significant role in enhancing the film thickness.

• More heat is transferred at the disk surface by reducing the thermophoresis diffusion and the Brownian motion parameters.

• The Sherwood number is raised considerably with the Schmidt number and temperature difference parameter.

• The impact of the activation energy parameter is to enhance the concentration of the fluid, while an opposite trend is noted in case of temperature difference parameter.