Stoneley wave propagation in transversely isotropic thermoelastic medium with two temperature and rotation

Abstract

In the present paper we studied Stoneley wave propagation at the interface of two dissimilar homogeneous transversely isotropic thermoelastic media with two temperatures and rotation. The secular equations of Stoneley waves are derived in the form of the determinant by using appropriate boundary conditions. The wave characteristics such as phase velocity and attenuation coefficients are computed and depicted graphically. Effect of rotation and two temperature has been depicted on the phase velocity, attenuation coefficient, displacement component, stress component, and Temperature distribution change. Some particular cases are also deduced from the present investigation.

1 Introduction

A Stoneley wave is an interface wave that usually travels along with the interface of two solids. Moreover, when initiates at the interface of liquid and solid, this wave is known as Scholte wave. This wave has maximum intensity at the boundary and decreases exponentially away from it. The wave generated by the sonic tool in a bore well is the example of these types of waves. Stoneley wave’s analysis provides information about the positions of fractures and permeability of the formation. These waves not only deliver better information about the internal structure of the earth but are also helpful in the assessment of valuable materials under the earth’s surface. Stoneley waves are a major source of noise in vertical seismic profiles. These waves help in the study of geophysics, seismological processes, ocean acoustics, SAW devices, and non-destructive evaluation.

Stoneley (1924) firstly studied the existence of these waves propagating at the interface of two solid, solid–liquid medium and derived the Stoneley wave’s dispersion equation. Tajuddin (1995) studied the presence of Stoneley waves at the boundary of two micropolar elastic half-spaces. Ting (2004) explored a surface wave propagation in an anisotropic rotating medium. Othman and Song (2006, 2008) presented different hypotheses about magneto-thermo-elastic waves in a homogeneous and isotropic medium. Abo-Dahab (2013, 2015) studied the different forms of surface waves. Kumar et al. (2013) investigated the Stoneley waves propagation at the boundary of two couple stress thermoelastic medium with LS and GL theories. Mahmoud (2014) studied the effect of the magnetic field, gravity field, and rotation on the propagation of Rayleigh waves in an initially stressed non-homogeneous orthotropic medium. Lata et al. (2016) investigated plane waves in an anisotropic thermoelastic. Abd-Alla et al. (2017) explored the propagation of surface waves in fiber-reinforced anisotropic media of nth order with rotation and magnetic field. Singh and Tochhawng (2019) studied the propagation of surface waves at the bonded and unbonded interfaces with voids. Despite of this numerous investigators worked on diverse thermoelasticity theories as Marin (1999), Marin et al. (2016), Kumar et al. (2016), Marin and Craciun (2017), Ezzat et al. (2017), Hassan et al. (2018), Othman and Marin (2017), Lata and Kaur (2019a, b, c) and Lata and Kaur (2019d, e).

In this paper, we have studied the Stoneley wave propagation at the interface of two dissimilar transversely isotropic thermoelastic homogeneous media with two temperature and rotation. Keeping in view of this, dispersion equation for Stoneley waves at the interface of two different TIT mediums with two temperature and rotation have been derived. Numerical methods are used to study the variation of displacement component, stress component, Temperature, phase velocity, and attenuation coefficient w.r.t. wave number.

2 Basic equations

The basic governing equations for homogeneous, anisotropic, generalized thermoelastic solids in the absence of body forces, heat sources following Chandrasekharaiah (1998), Youssef (2011) and Green and Naghdi (1992) are

$$ t_{ij} = C_{ijkl} e_{kl} - \beta_{ij} T, $$

(1)

$$ K_{ij}^{*} \varphi_{ij} = \beta_{ij} T_{0} \ddot{e}_{ij} + \rho C_{E} \ddot{T} $$

(2)

where

$$ \beta_{ij} = C_{ijkl} \alpha_{ij} , $$

$$ e_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right),\quad i,j = 1,2,3. $$

$$ T = \varphi - a_{ij} \varphi_{,ij} , $$

$$ \beta_{ij} = \beta_{i} \delta_{ij} ,\;K_{ij}^{*} = K_{i}^{*} \delta_{ij} \; {{i}}\;{\text{is}}\;{\text{not}}\;{\text{summed}}. $$

Here, $c_{ijkl} \left( {c_{ijkl} = c_{klij} = c_{jikl} = c_{ijlk} } \right)$ are elastic parameters and having symmetries due to

• 1. The stress tensor is symmetric, which is only possible if $\left( {C_{ijkl} = C_{jikl} } \right)$

• 2. If a strain energy density exists for the material, the elastic stiffness tensor must satisfy $C_{ijkl} = C_{klij}$

• 3. From stress tensor and elastic stiffness tensor symmetries infer $\left( {C_{ijkl} = C_{ijlk} } \right)$ and $C_{ijkl} = C_{klij} = C_{jikl} = C_{ijlk}$

Equation of motion as described by Schoenberg and Censor (1973) for an homogeneous transversely isotropic (HTI) medium rotating uniformly with an angular velocity ${{\Omega }}$

$$ t_{ij,j} = \rho \left\{ {\ddot{u}_{i} + \left( {{{\Omega }} \times ({{\Omega }} \times {\text{u}}} \right)_{i} + (2{{\Omega }} \times \dot{u}_{i } )} \right\}, $$

(3)

The terms ${{\Omega }} \times \left( {{{\Omega }} \times {\text{u}}} \right)$ and $2{{\Omega }} \times \dot{u}$ are the centripetal acceleration and Coriolis acceleration due to the time-varying motion respectively.

3 Formulation of the problem

We consider a perfectly conducting homogeneous TIT half-pace $M_{1 }$ with rotation overlying another homogeneous, transversely isotropic thermoelastic half-space $M_{2 }$ with rotation connecting at the interface $z = 0$. We take the origin of the coordinate system ($x, y, z)$ on $\left( {z = 0} \right)$. We choose x-axis in the direction of wave propagation in such a way that all the particles on a line parallel to the y-axis are equally displaced, so that $v = 0$ and $u,w,\varphi$ are independent of y. Medium $M_{2 }$ occupies the region $- \infty < z \le 0$ and the medium $M_{1 }$ occupies the region $0 \le z < \infty$. The plane signifies the boundary among the two medium $M_{1 }$ and $M_{2 }$. The quantities represented for the medium $M_{1 } \;{\text{are}}\;{\text{without}}\;{\text{bar }}$ and with bar for medium $M_{2 }$. For the 2D problem in xz-plane, we take (Fig. 1)

$$ \varvec{u} = \left( {u,0,w} \right). $$

Fig. 1

Geometry of the problem

Now using the transformation on Eqs. (1)–(2) following Slaughter (2002) is as under:

$$ C_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + C_{13} \frac{{\partial^{2} w}}{\partial x\partial z} + C_{44 } \left( {\frac{{\partial^{2} u}}{{\partial z^{2} }} + \frac{{\partial^{2} w}}{\partial x\partial z}} \right) - \beta_{1 } \frac{\partial }{\partial x}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} = \rho \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }} - \Omega^{2} u + 2\Omega \frac{\partial w}{\partial t}} \right), $$

(4)

$$ \left( {C_{13} + C_{44 } } \right)\frac{{\partial^{2} u}}{\partial x\partial z} + C_{44} \frac{{\partial^{2} w}}{{\partial x^{2} }} + C_{33 } \frac{{\partial^{2} w}}{{\partial z^{2} }} - \beta_{3 } \frac{\partial }{\partial z}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} = \rho \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} - \Omega^{2} w - 2\Omega \frac{\partial u}{\partial t}} \right), $$

(5)

$$ K_{1}^{*} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + K_{3}^{*} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }} = \left[ {\rho C_{E} \frac{{\partial^{2} }}{{\partial t^{2} }}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} + T_{0} \left\{ {\beta_{1} \frac{{\partial \ddot{u}}}{\partial x} + \beta_{3} \frac{{\partial \ddot{w}}}{\partial z}} \right\}} \right] . $$

(6)

and

$$ t_{xx} = C_{11} e_{xx} + C_{13} e_{xz} - \beta_{1 } T, $$

(7)

$$ t_{zz} = C_{13} e_{xx} + C_{33} e_{zz} - \beta_{3 } T, $$

(8)

$$ t_{xz} = 2C_{44} e_{xz} , $$

(9)

where

$$ \beta_{1 } = \left( {C_{11} + C_{12} } \right)\alpha_{1} + C_{13} \alpha_{3,} $$

(10)

$$ \beta_{3 } = 2C_{13} \alpha_{1} + C_{33} \alpha_{3} , $$

(11)

Using dimensionless quantities:

$$ \begin{aligned} \left( {x^{\prime},z^{\prime}} \right) & = \frac{1}{L}\left( {x,z,} \right), \left( {u^{\prime}, w^{{\prime }} } \right) = \frac{{\rho C_{1}^{2} }}{{L\beta_{1} T_{0} }}\left( {u,w} \right),\;\rho C_{1}^{2} = C_{11} ,\;\left( {T^{\prime},\varphi^{\prime}} \right) = \frac{1}{{T_{0} }} \left( {T,\varphi } \right), \\ t^{\prime} & = \frac{{C_{1} }}{L}t,\;\left( {t_{xx}^{{\prime }} ,t_{zx}^{{\prime }} t_{zz}^{{\prime }} } \right) = \frac{1}{{\beta_{1} T_{0} }}\left( {t_{xx} ,t_{zx} ,t_{zz} } \right), \left( {a_{1}^{{\prime }} ,a_{3}^{{\prime }} } \right) = \frac{1}{{L^{2} }}\left( {a_{1} ,a_{3} } \right), {{\Omega }}^{{\prime }} = \frac{\text{L}}{{C_{1} }}{{\Omega }}. \\ \end{aligned} $$

(12)

With the use of (12) in Eqs. (4)–(6), and suppressing the primes, we get

$$ \frac{{\partial^{2} u}}{{\partial x^{2} }} + \delta_{2} \frac{{\partial^{2} w}}{\partial x\partial z} + \delta_{1} \frac{{\partial^{2} u}}{{\partial z^{2} }} - \frac{\partial }{\partial x}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} = \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }} - \Omega^{2} u + 2\Omega \frac{\partial w}{\partial t}} \right), $$

(13)

$$ \delta_{2} \frac{{\partial^{2} u}}{\partial x\partial z} + \delta_{1} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \delta_{3} \frac{{\partial^{2} w}}{{\partial z^{2} }} - \delta_{5} \frac{\partial }{\partial z}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} = \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} - \Omega^{2} w - 2\Omega \frac{\partial u}{\partial t}} \right), $$

(14)

$$ \left( {\frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + \delta_{6} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right) = \left[ {\delta_{8} \frac{{\partial^{2} }}{{\partial t^{2} }}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} + \delta_{7} \left\{ {\frac{\partial u}{\partial x} + \delta_{5} \frac{\partial w}{\partial z}} \right\} + } \right], $$

(15)

where

$$ \delta_{1} = \frac{{c_{44} }}{{c_{11} }},\quad \delta_{2} = \frac{{c_{13} + c_{44} }}{{c_{11} }},\quad \delta_{3} = \frac{{c_{33} }}{{c_{11} }},\quad \delta_{5} = \frac{{\beta_{3} }}{{\beta_{1} }},\quad \delta_{6} = \frac{{K_{3}^{*} }}{{K_{1}^{*} }},\quad \delta_{7} = \frac{{T_{0} \beta_{1}^{2} }}{{K_{1}^{*} \rho }},\quad \delta_{8} = \frac{{C_{E} C_{11} }}{{K_{1}^{*} }}. $$

We consider the solution of the form

$$ \left( {u,w,\varphi } \right) = \left( {u^{*} ,w^{*} ,\varphi^{*} } \right)\left( z \right)e^{{i\xi \left( {x - ct} \right)}} , $$

(16)

where $c = {{\omega }}/{{\xi }}$ is the dimensionless phase velocity.

Upon using Eq. (16) in Eqs. (13)–(15) we get

$$ u^{*} \left[ {l_{1} + \delta_{2} D^{2} } \right] + w^{*} \left[ {l_{2} + l_{3} D} \right] + \varphi^{*} \left[ {l_{4} + l_{5} D^{2} } \right] = 0, $$

(17)

$$ u^{*} \left[ { - l_{2} + l_{3} D} \right] + w^{*} \left[ {l_{6} + \delta_{3} D^{2} } \right] + \varphi^{*} \left[ {l_{7} D + l_{8} D^{3} } \right] = 0, $$

(18)

$$ u^{*} \left[ {l_{9} } \right] + w^{*} \left[ {l_{10} D} \right] + \varphi^{*} \left[ {l_{11} + l_{12} D^{2} } \right] = 0, $$

(19)

where

$$ l_{1} = \xi^{2} \left( {c^{2} - 1} \right),\quad l_{2} = 2i\xi c,\quad l_{3} = \delta_{2} i\xi ,\quad l_{4} = - i\xi \left( {1 + a_{1} \xi^{2} } \right),\quad l_{5} = a_{3} i\xi , $$

$$ l_{6} = \left( {c^{2} - \delta_{1} } \right)\xi^{2} + 1, \quad l_{7} = - \delta_{5} \left( {1 + a_{1} \xi^{2} } \right),\quad l_{8} = \delta_{5} a_{3} ,\quad l_{9} = \delta_{7 } i\xi^{3} c^{2} ,\quad l_{10} = \delta_{7} \delta_{5} \xi^{2} c^{2} , $$

$$ l_{11} = \delta_{8} \xi^{2} c^{2} \left( {1 + a_{1} \xi^{2} } \right) - \xi^{2} , \quad l_{12} = - \delta_{8} \xi^{2} c^{2} a_{3} + \delta_{6} . $$

and characteristic equation is a biquadratic equation in $D^{2}$ given by

$$ D^{6} + \frac{B}{A}D^{4} + \frac{C}{A}D^{2} + \frac{E}{A} = 0, $$

(20)

where

$$ {\text{A}} = {{\delta }}_{2} {{\delta }}_{3} l_{12} - l_{10} {{\delta }}_{2} l_{8} , $$

$$ {\text{B}} = {{\delta }}_{3} {{\delta }}_{2} l_{11} + \delta_{2} {\text{l}}_{6} {\text{l}}_{12} + {\text{l}}_{1} {{\delta }}_{3} {\text{l}}_{12} - {{\delta }}_{2} {\text{l}}_{10} {\text{l}}_{7} - {\text{l}}_{1} {\text{l}}_{10} l_{8} - l_{1}^{2} {\text{l}}_{12} + {\text{l}}_{8} {\text{l}}_{9} l_{3} + l_{3} {\text{l}}_{5} l_{10} - l_{5} {{\delta }}_{3} {\text{l}}_{9} , $$

$$ {\text{C}} = {{\delta }}_{2} {\text{l}}_{11} {\text{l}}_{6} + {\text{l}}_{11} {{\delta }}_{3} {\text{l}}_{1} + {\text{l}}_{1} {\text{l}}_{6} {\text{l}}_{12} - l_{1} {\text{l}}_{10} {\text{l}}_{7} + l_{1}^{2} {\text{l}}_{11} + l_{2}^{2} {\text{l}}_{12} - l_{3}^{2} {\text{l}}_{11} + {\text{l}}_{3} l_{9} {\text{l}}_{7} + {\text{l}}_{3} {\text{l}}_{4} l_{10} - l_{5} {\text{l}}_{9} {\text{l}}_{6} - {\text{l}}_{4} {{\delta }}_{3} {\text{l}}_{9} , $$

$$ E = {\text{l}}_{11} {\text{l}}_{1} {\text{l}}_{6} - {\text{l}}_{9} {\text{l}}_{4} l_{6} , $$

For medium $M_{1} {(z > 0)}$

$$ \left( {u,w,\varphi } \right) = \mathop \sum \limits_{j = 1}^{3} A_{j} \left( {1,d_{j} ,k_{j} } \right)e^{{ - m_{j} z}} e^{{i\xi \left( {x - ct} \right)}} , $$

(21)

Thus from Eq. (16) and (21)

$$ u^{*} = \mathop \sum \limits_{j = 1}^{3} A_{j} e^{{ - m_{j} z}} , $$

$$ w^{*} = \mathop \sum \limits_{j = 1}^{3} d_{j} A_{j} e^{{ - m_{j} z}} , $$

$$ \varphi^{*} = \mathop \sum \limits_{j = 1}^{3} k_{j} A_{j} e^{{ - m_{j} z}} , $$

where

$$ d_{j} = \frac{{l_{1} l_{11} - l_{9} {\text{l}}_{4} + \left( {l_{11} \delta_{2} + l_{1} {\text{l}}_{12} - l_{9} {\text{l}}_{5} } \right)m_{j}^{2} + \left( {\delta_{2} l_{12} } \right)m_{j}^{4} }}{{l_{6} l_{11} + \left( {l_{11} \delta_{3} + l_{6} {\text{l}}_{12} - l_{10} {\text{l}}_{7} } \right)m_{j}^{2} + \left( {\delta_{3} l_{12} - l_{10} {\text{l}}_{8} } \right)m_{j}^{4} }}, $$

(22)

$$ k_{j} = \frac{{l_{1} l_{6} + l_{2}^{2} + \left( {l_{6} \delta_{2} + l_{1} {{\delta }}_{3} - l_{3}^{2} } \right)m_{j}^{2} + \left( {\delta_{2} \delta_{3} } \right)m_{j}^{4} }}{{l_{6} l_{11} + \left( {l_{11} \delta_{3} + l_{6} {\text{l}}_{12} - l_{10} {\text{l}}_{7} } \right)m_{j}^{2} + \left( {\delta_{3} l_{12} - l_{10} {\text{l}}_{8} } \right)m_{j}^{4} }}. $$

(23)

For medium $M_{2}$ (z > 0)we will attach a bar

$$ \left( {\bar{u},\bar{w},\bar{\varphi }} \right) = \left( {1,\bar{d}_{j} ,\bar{k}_{j} } \right)e^{{\bar{m}_{j} z}} \bar{A}_{j} e^{{i\xi \left( {x - ct} \right)}} , $$

where quantities $\bar{u},\bar{w},\bar{\varphi }$, $\bar{d}_{j} ,\bar{k}_{j}$, $\bar{A}_{j}$, $\bar{m}_{j}$ are obtained by attaching bars in the above expressions.

4 Boundary conditions

We consider that both half-spaces are in perfect contact. Thus, there is the stability of components of the displacement vector, stress vector, and temperature change at the interface.

The boundary conditions at z = 0 are given by

$$ t_{zz} = \bar{t}_{zz} ,\quad t_{zx} = \bar{t}_{zx} ,\quad \varphi = \bar{\varphi },\quad u = \bar{u},\quad w = \bar{w},\quad K_{3}^{*} \frac{\partial \varphi }{\partial z} = \bar{K}_{3}^{*} \frac{{\partial \bar{\varphi }}}{\partial z}. $$

(24)

5 Derivations of the secular equations

By using the values of $u,w, \varphi , \bar{u},\bar{w},\bar{\varphi }$ in (24), we get six linear equations as:

$$ \mathop \sum \limits_{j = 1}^{3} Q_{pj} A_{j} + \mathop \sum \limits_{j = 1}^{3} Q_{{p\left( {j + 3} \right)}} \bar{A}_{j} = 0, p = 1,2,3,4.5.6. $$

where

$$ Q_{1j} = i\xi - \delta_{9} d_{j} m_{j} - \left( {1 + a_{1} \xi^{2} - a_{3} m_{j}^{2} } \right)k_{j} , Q_{{1\left( {j + 3} \right)}} = - i\xi - \delta_{9} \bar{d}_{j} \bar{m}_{j} + \left( {1 + a_{1} \xi^{2} - a_{3} \bar{m}_{j}^{2} } \right)\bar{k}_{j} , $$

$$ Q_{2j} = - m_{j} + d_{j} i\xi ,Q_{{2\left( {j + 3} \right)}} = - m_{j} - d_{j} i\xi , $$

$$ Q_{3j} = k_{j} ,Q_{{3\left( {j + 3} \right)}} = - \bar{k}_{j} , $$

$$ Q_{4j} = \delta_{1} m_{j}^{2} + \left( {2i\xi c - \delta_{2} i\xi m_{j} } \right)d_{j} + \left( { - i\xi \left( {1 + a_{1} \xi^{2} } \right) + a_{3} i\xi m_{j}^{2} } \right)k_{j} , $$

$$ Q_{{4\left( {j + 3} \right)}} = - \delta_{1} \bar{m}_{j}^{2} - \left( {2i\xi c - \delta_{2} i\xi \bar{m}_{j} } \right)d_{j} - \left( { - i\xi \left( {1 + a_{1} \xi^{2} } \right) + a_{3} i\xi \bar{m}_{j}^{2} } \right)\bar{k}_{j} , $$

$$ Q_{5j} = - 2\delta_{4} i\xi c - \delta_{2} i\xi m_{j} + \delta_{3} m_{j}^{2} d_{j} - \delta_{5} \left( { - \left( {1 + a_{1} \xi^{2} } \right)m_{j} + a_{3} m_{j}^{3} } \right)k_{j} , $$

$$ Q_{{5\left( {j + 3} \right)}} = 2\delta_{4} i\xi c - \delta_{2} i\xi \bar{m}_{j} + \delta_{3} \bar{m}_{j}^{2} \bar{d}_{j} + \delta_{5} \left( { - \left( {1 + a_{1} \xi^{2} } \right)\bar{m}_{j} + a_{3} \bar{m}_{j}^{3} } \right)\bar{k}_{j} , $$

$$ Q_{6j} = - K_{3}^{*} \bar{k}_{j} \bar{m}_{j} . $$

(25)

The system of Eqs. (25) has a non-trivial solution if the determinant of unknowns $A_{j} , \bar{A}_{j} , {\text{j}} = 123$ vanishes i.e.

$$ \left| {Q_{ij} } \right|_{6 \times 6} = 0. $$

These secular equations have entire information regarding the wavenumber, phase velocity, and attenuation coefficient of Stoneley waves in the TIT medium.

6 Particular cases

If $C_{11} = C_{33} = \lambda + 2\mu , C_{12} = C_{13} = \lambda ,C_{44} = \mu , \alpha_{1} = \alpha_{3} = \alpha^{\prime}, \beta_{1} = \beta_{3} = \beta , K_{1}^{*} = K_{3}^{*} = K^{*}$ we obtain expressions for Stoneley wave propagation in isotropic materials with rotation.

7 Numerical results and discussion

To demonstrate the theoretical results and effect of rotation and two temperatures, we now present some numerical results. Following Kumar et al. (2017), copper material has been taken for TIT material as medium 1,

Quantity	Value	Unit
$c_{11}$	$18.78 \times 10^{10}$	${\text{Kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2}$
$c_{12}$	$8.76 \times 10^{10}$	${\text{Kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2}$
$c_{33}$	$17.2 \times 10^{10}$	${\text{Kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2}$
$c_{13}$	$8.0 \times 10^{10}$	${\text{Kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2}$
$c_{44}$	$5.06 \times 10^{10}$	${\text{Kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2}$
$\beta_{1}$	$7.543 \times 10^{6}$	${\text{N}}\,{\text{m}}^{ - 2} \,{ \deg }^{ - 1}$
$\beta_{3}$	$9.208 \times 10^{6}$	${\text{N}}\,{\text{m}}^{ - 2} \,{ \deg }^{ - 1}$
$\rho$	$8.954 \times 10^{3}$	${\text{kg}}\,{\text{m}}^{ - 3}$
$C_{E}$	$4.27 \times 10^{2}$	${\text{jKg}}^{ - 1} \,{ \deg }^{ - 1}$
$K_{1}^{*}$	$0.04 \times 10^{2}$	${\text{N}}\,{\text{s}}^{ - 2} \,{ \deg }^{ - 1}$
$K_{3}^{*}$	$0.02 \times 10^{2}$	${\text{N}}\,{\text{s}}^{ - 2} \,{ \deg }^{ - 1}$
${\text{T}}_{0}$	$293$	$\deg$
$\alpha_{1}$	$2.98 \times 10^{ - 5}$	${\text{K}}^{ - 1}$
$\alpha_{3}$	$2.4 \times 10^{ - 5}$	${\text{K}}^{ - 1}$

Following Kumar et al. (2017), magnesium material has been taken for thermoelastic material as medium 2:

Quantity	Value	Unit
$\bar{c}_{11}$	$5.974 \times 10^{10}$	${\text{Kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2}$
$\bar{c}_{12}$	$2.624 \times 10^{10}$	${\text{Kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2}$
$\bar{c}_{33}$	$6.17 \times 10^{10}$	${\text{Kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2}$
$\bar{c}_{13}$	$2.17 \times 10^{10}$	${\text{Kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2}$
$\bar{c}_{44}$	$3.278 \times 10^{10}$	${\text{Kg}}\,{\text{m}}^{ - 1} \,{\text{s}}^{ - 2}$
$\bar{\beta }_{1}$	$2.68 \times 10^{6}$	${\text{N}}\,{\text{m}}^{ - 2} \,{ \deg }^{ - 1}$
$\bar{\beta }_{3}$	$2.68 \times 10^{6}$	${\text{N}}\,{\text{m}}^{ - 2} \,{ \deg }^{ - 1}$
$\bar{\rho }$	$1.74 \times 10^{3}$	${\text{kg}}\,{\text{m}}^{ - 3}$
$\bar{C}_{E}$	$1.04 \times 10^{3}$	${\text{jKg}}^{ - 1} \,{ \deg }^{ - 1}$
$\bar{K}_{1}^{*}$	$0.02 \times 10^{2}$	${\text{N}}\,{\text{s}}^{ - 2} \,{ \deg }^{ - 1}$
$\bar{K}_{3}^{*}$	$0.02 \times 10^{2}$	${\text{N}}\,{\text{s}}^{ - 2} \,{ \deg }^{ - 1}$
${\bar{\text{T}}}_{0}$	$293$	${ \deg }$
$\bar{\alpha }_{1}$	$2.98 \times 10^{ - 5}$	${\text{K}}^{ - 1}$
$\bar{\alpha }_{3}$	$2.4 \times 10^{ - 5}$	${\text{K}}^{ - 1}$

Using the above values, the graphical representations of stress components, temperature change, wave velocity, attenuation coefficient depth of Stoneley wave in TIT medium have been investigated with two temperature and rotation and demonstrated graphically as:

Case-I: Effect of rotation

• 1. The solid line relates to ${{\Omega }} = 0$,

• 2. The dashed line relates to ${{\Omega }} = 0.5$,

• 3. The dotted line relates to ${{\Omega }} = 1.0$.

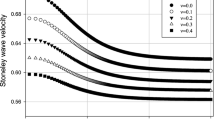
Figure 2 demonstrates the Stoneley wave’s attenuation coefficient w.r.t. $\xi$ for different values of rotation. It is clear from the graph, as we increase the rotation, the attenuation coefficient is declined. Near the interface of the two material, the attenuation coefficient is very high and below the boundary surface, it declines to zero for all the cases of rotation. Figure 3 shows the Stoneley wave’s phase velocity w.r.t. $\xi$ for different values of rotation. It is clear from the graph, as we increase the rotation, the phase velocity is increased. Near the interface of the two material, the phase velocity is very high when ${{\Omega }} = 1.0$ and below the boundary surface, it comes to steady-state. Moreover, near the interface of the two material, the phase velocity is increased when ${{\Omega }} = 0.0 {\text{ and }} 0.5$ and below boundary surface it comes to steady-state for both the cases of rotation.

Fig. 2

Variation of Stoneley waves attenuation coefficient w.r.t. $\xi$

Fig. 3

Variation of Stoneley waves velocity w.r.t. $\xi$

Figure 4 shows the magnitude values of Temperature distribution w.r.t. $\xi$ for different values of rotation. It is clear from the graph, as we increase the rotation, the magnitude values of the Temperature Distribution of the Stoneley wave is increased. Near the interface of the two material, the magnitude values of the temperature of the Stoneley wave are very high when ${{\Omega }} = 1.0$ and below the boundary surface, it comes to steady-state. Moreover, near the interface of the two material the magnitude values of the temperature of Stoneley wave show the opposite behavior when ${{\Omega }} = 0.0\;{\text{and}}\;0.5$ and below boundary surface it comes to steady-state for both the cases of rotation. Figure 5 demonstrates the Stoneley wave’s displacement component w w.r.t. $\xi$ for different values of rotation. It is clear from the graph, as we increase the rotation, the displacement component w of Stoneley wave declines. Near the interface of the two material the displacement component w of Stoneley wave is very high and below boundary surface, it declines to zero for all the cases of rotation.

Fig. 4

Variation of Temperature distribution w.r.t. $\xi$

Fig. 5

Variation of Stoneley waves displacement component w w.r.t. $\xi$

Figure 6 illustrates the stress component t_zz w.r.t. $\xi$ for different values of rotation. It is clear from the graph, as we increase the rotation, the stress component t_zz of the Stoneley wave is varied. Near the interface of the two material, the t_zz of Stoneley wave is very high when ${{\Omega }} = 1.0$ and below boundary surface, it comes to steady-state. Moreover, near the interface of the two material, the t_zz of Stoneley wave shows the opposite behavior when ${{\Omega }} = 0.0\;{\text{and}}\;0.5$ and below boundary surface it comes to steady-state for both the cases of rotation.

Fig. 6

Variation of Stoneley waves stress component T_zz w.r.t. $\xi$

Case-II: Effect of two temperature

• 1. The solid line relates to $a_{1} = a_{3} = 0$,

• 2. The dashed line relates to $a_{1} = 0.2,a_{3} = 0.4.$

Figure 7 demonstrates the Stoneley wave’s attenuation coefficient w.r.t. $\xi$ with and without two temperatures. It is clear from the graph, with two temperatures, the attenuation coefficient is declined. Near the interface of the two material, the attenuation coefficient is very high and below the boundary surface, it declines to zero in absence and presence of two temperatures. Figure 8 shows the Stoneley wave’s phase velocity w.r.t. $\xi$ with and without two temperatures. It is clear from the graph, with two temperatures, the phase velocity of the Stoneley wave is increased.

Fig. 7

Variation of Stoneley waves attenuation coefficient w.r.t. $\xi$

Fig. 8

Variation of Stoneley waves velocity w.r.t. $\xi$

Figure 9 shows the magnitude values of Temperature distribution w.r.t. $\xi$ with and without two temperatures. It is clear from the graph, with two temperatures., the magnitude values of the Temperature Distribution of the Stoneley wave is increases. Near the interface of the two material, the magnitude values of the temperature of the Stoneley wave are very high with two temperature and below the boundary surface, it comes to steady-state. Moreover, near the interface of the two material, the magnitude values of the temperature of the Stoneley wave show the opposite behavior without two temperature and below the boundary surface, it comes to steady-state.

Fig. 9

Variation of temperature distribution T w.r.t. $\xi$

Figure 10 demonstrates the Stoneley wave’s displacement component w w.r.t. $\xi$ with and without two temperatures. It is clear from the graph, with two temperatures, the displacement component w of Stoneley wave declines. Near the interface of the two material the displacement component w of Stoneley wave is very high and below boundary surface, it declines to zero. Figure 11 illustrates the stress component t_zz w.r.t. $\xi$ with and without two temperatures. It is clear from the graph, with two temperatures, the stress component t_zz of the Stoneley wave is increased. Near the interface of the two material, the t_zz of Stoneley wave is very high with two temperature and below boundary surface, it comes to steady-state.

Fig. 10

Variation of Stoneley waves displacement component w w.r.t. $\xi$

Fig. 11

Variation of Stoneley waves stress component T_zz w.r.t. $\xi$

8 Conclusion

From the analysis of graphs, some concluding interpretations are:

• The Stoneley waves in a homogeneous TIT solid media with the rotation, with and without two temperatures are investigated.

• The figures clearly indicate that at the interface of the two mediums, there is a considerable influence of two temperatures and rotation on the Stoneley wave phase velocity, attenuation coefficient, displacement component, and stress component, as well as on Temperature distribution. It is also observed that the velocity of surface (Stoneley) waves not only influenced by the direction of wave propagation but as well as on the elastic properties and density of materials. The characteristics of waves change drastically in diverse mediums and also at different depth.

• From the wave velocity equation, we find that there is a dispersion of waves due to rotation and two temperatures. The dispersive nature of the Stoneley waves is defined through the resulting Secular equation. Various special cases are also considered to approve the formulation and numerical results with the existing solutions.

• Stoneley wave’s analysis provides information about the positions of fractures and permeability of the formation. These waves not only deliver better information about the internal structure of the earth but are also helpful in the assessment of valuable materials under the earth’s surface. Stoneley waves are a major source of noise in vertical seismic profiles. These waves help in the study of geophysics, seismological processes, ocean acoustics, SAW devices, and non-destructive evaluation.