Stoneley wave propagation in transversely isotropic thermoelastic rotating medium with memory-dependent derivative and two temperature

Abstract

In the present paper, we bring forth the study of the propagation of the Stoneley wave with modified GN theory of type II thermoelasticity without energy dissipation, including memory-dependent derivative (MDD) and two temperatures and with rotation. Secular equations of Stoneley waves at the interface of two separate homogeneous transversely isotropic (HTI) thermoelastic mediums are determined in the form of determinants after constructing the formal solution based on the necessary boundary conditions. The wave characteristics have been obtained for different Kernel functions of the MDD from the secular equations and are depicted graphically. The effect of Kernel functions and two temperature has been depicted on the displacement component, Temperature distribution, stress component, phase velocity, and attenuation coefficient.

1 Introduction

A Stoneley wave is an interface wave that often moves along the boundary between two solids. Due to the existence of homogeneities in the crust of the earth and the fact that the earth is made up of several layers, the propagation of surface waves in a homogeneous elastic media is of significant importance in the fields of earthquake engineering and seismology. Furthermore, this wave is called a Scholte wave if it originates at the interface between such a liquid and a solid. The intensity of the Stoneley wave is maximum at the boundary and exponentially diminishes away from it. One example of these waves is the wave produced by a sonic tool in a bore well. The Stoneley wave study reveals details regarding the locations of fractures and formation permeability. These waves assist appraise valuable resources beneath the surface of the earth and provide better knowledge of the interior structure of the planet. In vertical seismic profiles, Stoneley waves are a prominent source of background noise.

In 1924, it was Stoneley who developed the theory of surface waves. Stoneley [1] developed the Stoneley wave's dispersion equation after initially examining the occurrence of these waves propagating at the interface of two solid, solid–liquid media. Scholte [2] investigated a wave similar to the Stoneley wave known as the Scholte wave that originates at the fluid–solid interfaces. Stoneley waves were investigated by Tajuddin [3] at the intersection of two micropolar elastic half-spaces. In the context of different theories of thermoelasticity, Kumar et al. [4] examined the Stoneley waves at the interface of isotropic modified coupling stress thermoelastic with mass diffusion media.

In the following years, several researchers have discussed problems regarding Stoneley waves propagating along solid–solid and fluid–solid boundaries, such as Ting [5], Abo-Dahab [6, 7], Kumar et al. [8], Abd-Alla et al. [9], Singh and Tochhawng [10], Kaur and Lata [11], Lata and Himanshi [12], Kaur et al. [13, 14], Kaur and Singh [15] and Lata et al. [16].

In addition, A common derivative and kernel function is used to define the MDD in integral form. In many models that explain physical terms with the memory effect, the kernels in physical laws are crucial. The idea of an MDD was first presented by Wang and Li [17] in 2011. When calculating the heat flux rate in the Lord–Shulman (LS) generalized thermoelasticity theory, Yu et al. [18] developed the MDD as an alternative to fractional calculus to reflect memory dependence and be recognized as a memory-dependent LS model. The following reasons suggest that this novel model may be advantageous to fractional models. First, the shape of the new model is distinct from that of the fractional-order models, which have different modifications. The substance of the MDD definition also makes the physical significance of the new model more obvious. Third, the new model is more practical for numerical calculation than fractional models since it is represented by differentials and integrals of integer order. As a result, the model is more adaptable in applications than fractional models, in which the significant variable is the fractional-order parameter. The kernel function and time delay of the MDD can also be changed arbitrarily. Ezzat et al. [19,20,21,22] discussed the MDD LS model of generalized thermoelasticity was used to solve a few one-dimensional problems. Although this is true, different researchers have developed varying theories of thermoelasticity, such as Kaur et al. [23,24,25,26], Marin [27], and [28], Marin et al. [29, 30], Kaur et al. [31], Golewski [32, 33], Trivedi et al. [34], Zhang et al. [35], Sur and Kanoria [36], Golewski [37, 38], Gupta et al. [39]. Chandrasekharaiah [40], and Green and Naghdi [41].

In this paper, Stoneley wave propagation with the memory-dependent derivative (MDD) has been studied. Secular equations of Stoneley waves at the interface of two separate homogeneous transversely isotropic (HTI) thermoelastic media are determined in the form of determinants after constructing the formal solution based on the necessary boundary conditions. The wave characteristics have been obtained for different Kernel functions of the MDD and are depicted graphically.

2 Basic equations

The fundamental governing equations for homogeneous, anisotropic, generalized thermoelastic and without body forces are.

• Equation of motion with rotation

Following Schoenberg and Censor [42] for rotating solids with a uniform angular velocity $\Omega$ we have,

$${t}_{ij,j}= \rho \left\{{\ddot{{\varvec{u}}}}_{i}+{\left({\varvec{\Omega}}\times \left({\varvec{\Omega}}\times \mathbf{u}\right)\right)}_{i}+{\left(2{\varvec{\Omega}}\times \dot{{\varvec{u}}}\right)}_{i}\right\},$$

(1)

The terms ${\varvec{\Omega}}\times ({\varvec{\Omega}}\times \mathbf{u})$ represent the centripetal acceleration due to the time-varying motion.

• Constitutive equations

Following Youssef [43], the constitutive equations for anisotropic solids with two temperature theory are

$$ t_{ij} = C_{ijkl} e_{kl} - \beta_{ij} T, $$

(2)

$$ e_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right),\quad i,j = 1,2,3, $$

(3)

$$ T = \varphi - a_{ij} \varphi_{,ij} , $$

(4)

$$ \beta_{ij} = C_{ijkl} \alpha_{kl} , $$

(5)

Here ${C}_{ijkl}= {C}_{klij}= {C}_{jikl}= {C}_{ijlk}.$

• Heat conduction equation

Following Youssef [43], Bachher [44] the heat conduction equation without energy dissipation, two temperature theory and with memory-dependent derivatives is

$$ K_{ij}^{*} \varphi_{,ij} = \left( {1 + \chi D_{\chi } } \right)\left( {\beta_{ij} T_{0} \ddot{e}_{ij} + \rho C_{E} \ddot{T}} \right), $$

(6)

Following Wang and Li [17], for a first-order MDD for a differentiable function $f(t)$ with delay $\chi$ > 0 for a fixed time $t$ is:

$$ D_{\chi } f\left( t \right) = \frac{1}{\chi }\int_{t - \chi }^{t} K\left( {t - \xi } \right)f^{\prime}\left( \xi \right)\,{\text{d}}\xi , $$

(7)

The choice of the kernel function, $K(t-\xi )$ and time delay parameter, $\chi$ are determined by the material properties. Following Ezzat et al. [19,20,21] the kernel function $K(t - \xi )$ is taken here in the form

$$ K\left( {t - \xi } \right) = 1 - \frac{{2\beta }}{\chi }\left( {t - \xi } \right) + \frac{{\alpha ^{2} }}{{\chi ^{2} }}\left( {t - \xi } \right)^{2} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad \alpha = 0,\beta = 0,} \hfill \\ {1 + \left( {\xi - t} \right)/\chi } \hfill & {\quad \alpha = 0,\beta = 1/2,} \hfill \\ {\xi - t + 1} \hfill & {\quad \alpha = 0,\beta = \chi /2,} \hfill \\ {\left[ {1 + \left( {\xi - t} \right)/\chi } \right]^{2} } \hfill & {\quad \alpha = 1,\beta = 1.} \hfill \\ \end{array} } \right.$$

(8)

where $\alpha$ and $\beta$ are constants. Additionally, the comma indicates the derivative w.r.t. the space variable and the dot superimposed on it signifies the time derivative.

3 Formulation of the problem

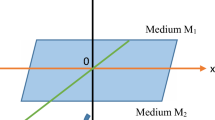
We take into account two homogeneous, transversely isotropic thermoelastic rotating half-spaces M₁ and M₂, both of which are perfectly conducting. These half-spaces are connected at the interface $z=0$. The coordinate system's $(x,y,z)$ origin is taken to be at $(z=0)$. Displacement vector $\overrightarrow{u}$ has the components $u, v, w$ along x, y, z-axis, respectively. We select the x-axis in the wave propagation direction such that all particles on a line parallel to the y-axis are equally displaced, ensuring that $v=0 \mathrm{and} u,w$, are independent of $y$. The regions $-\infty <x\le 0$ and $0\le x<\infty$ are occupied by the media M₁ and M₂, respectively. The plane represents the separation between the two mediums, M₁ and M₂. The quantities symbolized are without a bar for the media ${M}_{1}$ and with a bar for media ${M}_{2}$. For the 2D problem in xz-plane, we consider (Fig. 1)

$${\varvec{u}}=\left(u,0,w\right).$$

(9)

Following Slaughter [45], Eqs. (1) and (6) can now be transformed as follows:

$$ C_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + C_{13} \frac{{\partial^{2} w}}{\partial x\partial z} + C_{44 } \left( {\frac{{\partial^{2} u}}{{\partial z^{2} }} + \frac{{\partial^{2} w}}{\partial x\partial z}} \right) - \beta_{1 } \frac{\partial }{\partial x}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} = \rho \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }} - \Omega^{2} u + 2\Omega \frac{\partial w}{{\partial t}}} \right), $$

(10)

$$ \left( {C_{13} + C_{44 } } \right)\frac{{\partial^{2} u}}{\partial x\partial z} + C_{44} \frac{{\partial^{2} w}}{{\partial x^{2} }} + C_{33 } \frac{{\partial^{2} w}}{{\partial z^{2} }} - \beta_{3 } \frac{\partial }{\partial z}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} = \rho \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} - \Omega^{2} w - 2\Omega \frac{\partial u}{{\partial t}}} \right), $$

(11)

$$ K_{1}^{*} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + K_{3}^{*} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }} = \left( {1 + \chi D_{\chi } } \right)\left[ {\rho C_{E} \frac{{\partial^{2} }}{{\partial t^{2} }}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} + T_{0} \left\{ {\beta_{1} \frac{{\partial \ddot{u}}}{\partial x} + \beta_{3} \frac{{\partial \ddot{w}}}{\partial z}} \right\}} \right] $$

(12)

and

$${t}_{xx}={C}_{11}{e}_{xx} + {C}_{13}{e}_{xz}-{\beta }_{1 }\left\{\varphi -\left({a}_{1}\frac{{\partial }^{2}\varphi }{\partial {x}^{2}}+{a}_{3}\frac{{\partial }^{2}\varphi }{\partial {z}^{2}}\right)\right\},$$

(13)

$${t}_{zz}={C}_{13}{e}_{xx} + {C}_{33}{e}_{zz}-{\beta }_{3 }\left\{\varphi -\left({a}_{1}\frac{{\partial }^{2}\varphi }{\partial {x}^{2}}+{a}_{3}\frac{{\partial }^{2}\varphi }{\partial {z}^{2}}\right)\right\},$$

(14)

$${t}_{xz}={2C}_{44}{e}_{xz},$$

(15)

where

$${\beta }_{1 }=\left({C}_{11}+{C}_{12}\right){\alpha }_{1}+{C}_{13}{\alpha }_{3,}$$

(16)

$${\beta }_{3 }={2C}_{13}{\alpha }_{1}+{C}_{33}{\alpha }_{3},$$

(17)

${a}_{1}\& {a}_{3}$ are two temperature parameters. In the above equations, we use the contracting subscript notations (1 → 11, 2 → 22, 3 → 33, 5 → 23, 4 → 13, 6 → 12) to relate ${C }_{ijkl}$ to ${C}_{mn}$.

Fig. 1

Geometry of the problem

Using dimensionless quantities:

$$\left({x}^{{\prime}},{z}^{{\prime}}\right)= \frac{1}{L}\left(x,z,\right), \left({u}^{{\prime}},{ w}^{{\prime}}\right)= \frac{\rho {C}_{1}^{2}}{L{\beta }_{1}{T}_{0}}\left(u,w\right), \rho {C}_{1}^{2}={C}_{11}, \left({T}^{{\prime}},{\varphi }^{{\prime}}\right)= \frac{1}{{T}_{0}} \left(T,\varphi \right),$$

(18)

$${t}^{{\prime}}=\frac{{C}_{1}}{L}t, \left({t}_{xx}^{{\prime}},{t}_{zx}^{{\prime}}{t}_{zz}^{{\prime}}\right)=\frac{1}{{\beta }_{1}{T}_{0}}\left({t}_{xx},{t}_{zx},{t}_{zz}\right), \left({a}_{1}^{{\prime}},{a}_{3}^{{\prime}}\right)= \frac{1}{{L}^{2}}\left({a}_{1},{a}_{3}\right){,\Omega }^{{\prime}}=\frac{\mathrm{L}}{{C}_{1}}\Omega .$$

Suppressing the primes and utilizing (18) in Eqs. (10)–(12), we obtain

$$ \frac{{\partial^{2} u}}{{\partial x^{2} }} + \delta_{2} \frac{{\partial^{2} w}}{\partial x\partial z} + \delta_{1} \frac{{\partial^{2} u}}{{\partial z^{2} }} - \frac{\partial }{\partial x}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} = \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }} - \Omega^{2} u + 2\Omega \frac{\partial w}{{\partial t}}} \right), $$

(19)

$$ \delta_{2} \frac{{\partial^{2} u}}{\partial x\partial z} + \delta_{1} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \delta_{3} \frac{{\partial^{2} w}}{{\partial z^{2} }} - \delta_{5} \frac{\partial }{\partial z}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} = \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} - \Omega^{2} w - 2\Omega \frac{\partial u}{{\partial t}}} \right), $$

(20)

$$ \left( {\frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + \delta_{6} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right) = \left( {1 + \chi D_{\chi } } \right)\left[ {\delta_{8} \frac{{\partial^{2} }}{{\partial t^{2} }}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} + \delta_{7} \left\{ {\frac{\partial u}{{\partial x}} + \delta_{5} \frac{\partial w}{{\partial z}}} \right\}} \right], $$

(21)

where

$${\delta }_{1}= \frac{{c}_{44}}{{c}_{11}},{\delta }_{2}= \frac{{c}_{13}+{c}_{44}}{{c}_{11}}, {\delta }_{3}= \frac{{c}_{33}}{{c}_{11}}, {\delta }_{5}=\frac{{\beta }_{3}}{{\beta }_{1}},{\delta }_{6}=\frac{{K}_{3}^{*}}{{K}_{1}^{*}},{\delta }_{7}=\frac{{T}_{0}{\beta }_{1}^{2}}{{K}_{1}^{*}\rho },{\delta }_{8}=\frac{{C}_{E}{C}_{11}}{{K}_{1}^{*}} .$$

We consider the solution of the form

$$\left(u,w,\varphi \right)=\left({u}^{*},{w}^{*},{\varphi }^{*}\right){\left(z\right)e}^{i\xi \left(x-ct\right)},$$

(22)

where $c=\upomega /\upxi$ represents the dimensionless phase velocity.

After applying (22) in Eqs. (19)–(21) yields

$$ u^{*} \left[ {l_{1} + \delta_{2} D^{2} } \right] + w^{*} \left[ {l_{2} + l_{3} D} \right] + \varphi^{*} \left[ {l_{4} + l_{5} D^{2} } \right] = 0, $$

(23)

$$ u^{*} \left[ { - l_{2} + l_{3} D} \right] + w^{*} \left[ {l_{6} + \delta_{3} D^{2} } \right] + \varphi^{*} \left[ {l_{7} D + l_{8} D^{3} } \right] = 0, $$

(24)

$$ u^{*} \left[ {l_{9} } \right] + w^{*} \left[ {l_{10} D} \right] + \varphi^{*} \left[ {l_{11} + l_{12} D^{2} } \right] = 0, $$

(25)

where

$${l}_{1}= {\xi }^{2}\left({c}^{2}-1\right), { l}_{2}=2i\xi c, { l}_{3}={\delta }_{2}i\xi , {l}_{4}=-i\xi \left(1+{a}_{1}{\xi }^{2}\right), {l}_{5}={a}_{3}i\xi ,$$

$${{l}_{6}=\left({c}^{2}-{\delta }_{1}\right){\xi }^{2}+1, l}_{7}={{-\delta }_{5}\left(1+{a}_{1}{\xi }^{2}\right) , l}_{8}={\delta }_{5}{a}_{3}, {l}_{9}=\left(1+G\right){\delta }_{7 }i{\xi }^{3}{c}^{2},{ l}_{10}=\left(1+G\right){\delta }_{7}{\delta }_{5}{\xi }^{2}{c}^{2},$$

$${l}_{11}={\delta }_{8}{\xi }^{2}{c}^{2}\left(1+{a}_{1}{\xi }^{2}\right){-\xi }^{2}, {l}_{12}=-{\delta }_{8}{\xi }^{2}{c}^{2}{a}_{3}+{\delta }_{6}.$$

$$ G = \frac{1}{\chi }\left[ {\left( {1 - e^{i\xi c\chi } } \right)\left( {1 + \frac{2\beta }{{\chi i\xi c}} - \frac{{2\alpha^{2} }}{{\chi^{2} \xi^{2} c^{2} }}} \right) - \left( {\alpha^{2} - 2\beta - \frac{{2\alpha^{2} }}{\chi i\xi c}} \right)e^{i\xi c\chi } } \right] $$

and characteristic equation in the form of a biquadratic equation represented in ${D}^{2}$ given by

$${D}^{6}+\frac{B}{A}{D}^{4}+\frac{C}{A}{D}^{2}+\frac{E}{A}=0,$$

(26)

where

$$ \begin{aligned} A & = \delta_{2} \delta_{3} l_{12} - l_{10} \delta_{2} l_{8} , \\ B & = \delta_{3} \delta_{2} l_{11} + \delta_{2} l_{6} l_{12} + l_{1} \delta_{3} l_{12} - \delta_{2} l_{10} l_{7} - l_{1} l_{10} l_{8} \\ & \quad - l_{1}^{2} l_{12} + l_{8} l_{9} l_{3} + l_{3} l_{5} l_{10} - l_{5} \delta_{3} l_{9} , \\ C & = \delta_{2} l_{11} l_{6} + l_{11} \delta_{3} l_{1} + l_{1} l_{6} l_{12} - l_{1} l_{10} l_{7} + l_{1}^{2} l_{11} + l_{2}^{2} l_{12} - l_{3}^{2} l_{11} \\ & \quad + l_{3} l_{9} l_{7} + l_{3} l_{4} l_{10} - l_{5} l_{9} l_{6} - l_{4} \delta_{3} l_{9} , \\ E & = l_{11} l_{1} l_{6} - l_{9} l_{4} l_{6} . \\ \end{aligned} $$

For medium ${M}_{1}$

$$ \left( {u,w,\varphi } \right) = \mathop \sum \limits_{j = 1}^{3} A_{j} \left( {1,d_{j} ,k_{j} } \right)e^{{ - m_{j} z}} e^{{i\xi \left( {x - ct} \right)}} , $$

(27)

Thus from Eqs. (22) and (27)

$$ \begin{aligned} u^{*} & = \mathop \sum \limits_{j = 1}^{3} A_{j} e^{{ - m_{j} z}} , \\ w^{*} & = \mathop \sum \limits_{j = 1}^{3} d_{j} A_{j} e^{{ - m_{j} z}} , \\ \varphi^{*} & = \mathop \sum \limits_{j = 1}^{3} k_{j} A_{j} e^{{ - m_{j} z}} , \\ \end{aligned} $$

where

$$ d_{j} = \frac{{l_{1} l_{11} - l_{9} {\text{l}}_{4} + \left( {l_{11} \delta_{2} + l_{1} {\text{l}}_{12} - l_{9} {\text{l}}_{5} } \right)m_{j}^{2} + \left( {\delta_{2} l_{12} } \right)m_{j}^{4} }}{{l_{6} l_{11} + \left( {l_{11} \delta_{3} + l_{6} {\text{l}}_{12} - l_{10} {\text{l}}_{7} } \right)m_{j}^{2} + \left( {\delta_{3} l_{12} - l_{10} {\text{l}}_{8} } \right)m_{j}^{4} }}, $$

(28)

$$ k_{j} = \frac{{l_{1} l_{6} + l_{2}^{2} + \left( {l_{6} \delta_{2} + l_{1} {\updelta }_{3} - l_{3}^{2} } \right)m_{j}^{2} + \left( {\delta_{2} \delta_{3} } \right)m_{j}^{4} }}{{l_{6} l_{11} + \left( {l_{11} \delta_{3} + l_{6} {\text{l}}_{12} - l_{10} {\text{l}}_{7} } \right)m_{j}^{2} + \left( {\delta_{3} l_{12} - l_{10} {\text{l}}_{8} } \right)m_{j}^{4} }}. $$

(29)

For medium ${M}_{2}$ (z > 0) we will attach a bar

$$ \left( {\overline{u},\overline{w},\overline{\varphi }} \right) = \left( {1,\overline{{d_{j} }} ,\overline{{k_{j} }} } \right)e^{{\overline{{m_{j} }} z}} \overline{{A_{j} }} e^{{i\xi \left( {x - ct} \right)}} , $$

(30)

where quantities $\overline{u },\overline{w },\overline{\varphi }$,$\overline{{d }_{j}},\overline{{k }_{j}}$,$\overline{{A }_{j}}$,$\overline{{m }_{j}}$ are obtained by attaching bars in the above expressions.

4 Boundary conditions

We assume that there is perfect contact between the two half-spaces. As a result, the Stoneley wave characteristics are stable at the interface.

Following are the boundary conditions at z = 0:

$$ t_{zz} = \overline{t}_{zz} ,t_{zx} = \overline{t}_{zx} ,\varphi = \overline{\varphi },u = \overline{u},w = \overline{w},K_{3}^{*} \frac{\partial \varphi }{{\partial z}} = \overline{{K_{3}^{*} }} \frac{{\partial \overline{\varphi }}}{\partial z}. $$

(31)

5 Derivations of the secular equations

With the values of $u,w, \varphi , \overline{u },\overline{w },\overline{\varphi }$ in (31), it yields six linear equations:

$$ \mathop \sum \limits_{j = 1}^{3} Q_{pj} A_{j} + \mathop \sum \limits_{j = 1}^{3} Q_{{p\left( {j + 3} \right)}} \overline{A}_{j} = 0,\quad p = 1,2,3,4,5,6. $$

(32)

where

$$ \begin{aligned} Q_{1j} & = i\xi - \delta_{9} d_{j} m_{j} - \left( {1 + a_{1} \xi^{2} - a_{3} m_{j}^{2} } \right)k_{j} , \\ Q_{{1\left( {j + 3} \right)}} & = - i\xi - \delta_{9} \overline{{d_{j} }} \overline{{m_{j} }} + \left( {1 + a_{1} \xi^{2} - a_{3} \overline{{m_{j}^{2} }} } \right)\overline{{k_{j} }} , \\ Q_{2j} & = - m_{j} + d_{j} i\xi ,Q_{{2\left( {j + 3} \right)}} = - m_{j} - d_{j} i\xi , \\ Q_{3j} & = k_{j} ,Q_{{3\left( {j + 3} \right)}} = - \overline{{k_{j} }} , \\ Q_{4j} & = \delta_{1} m_{j}^{2} + \left( {2i\xi c - \delta_{2} i\xi m_{j} } \right)d_{j} + \left( { - i\xi \left( {1 + a_{1} \xi^{2} } \right) + a_{3} i\xi m_{j}^{2} } \right)k_{j} , \\ Q_{{4\left( {j + 3} \right)}} & = - \delta_{1} \overline{{m_{j}^{2} }} - \left( {2i\xi c - \delta_{2} i\xi \overline{m}_{j} } \right)d_{j} - \left( { - i\xi \left( {1 + a_{1} \xi^{2} } \right) + a_{3} i\xi \overline{{m_{j}^{2} }} } \right)\overline{{k_{j} }} , \\ Q_{5j} & = - 2\delta_{4} i\xi c - \delta_{2} i\xi m_{j} + \delta_{3} m_{j}^{2} d_{j} - \delta_{5} \left( { - \left( {1 + a_{1} \xi^{2} } \right)m_{j} + a_{3} m_{j}^{3} } \right)k_{j} , \\ Q_{{5\left( {j + 3} \right)}} & = 2\delta_{4} i\xi c - \delta_{2} i\xi \overline{{m_{j} }} + \delta_{3} \overline{{m_{j}^{2} }} \overline{{d_{j} }} + \delta_{5} \left( { - \left( {1 + a_{1} \xi^{2} } \right)\overline{{m_{j} }} + a_{3} \overline{{m_{j}^{3} }} } \right)\overline{{k_{j} ,}} \\ Q_{6j} & = - K_{3}^{*} \overline{{k_{j} }} \overline{{m_{j} .}} \\ \end{aligned} $$

(33)

The system of Eq. (33) has a non-trivial solution if the determinant of unknowns ${A}_{j}, {\overline{A} }_{j}, j=1,2,3$ vanishes, i.e.,

$$ \left| {Q_{ij} } \right|_{6 \times 6} = 0. $$

(34)

The attenuation coefficient, wavenumber, and phase velocity of Stoneley waves in the TIT medium are completely described by these secular Eq. (34).

6 Particular cases

If ${ C}_{11}={C}_{33}=\lambda +2\mu , {C}_{12}={C}_{13}=\lambda ,{C}_{44}=\mu , {\alpha }_{1}={\alpha }_{3}={\alpha }^{{\prime}}, {\beta }_{1}={\beta }_{3}=\beta ,{ K}_{1}^{*}={K}_{3}^{*}={K}^{*}$ we get Stoneley wave propagation equations for isotropic materials with MDD with two temperature and rotation.

7 Numerical results and discussion

This section presents numerical results that illustrate the theoretical results and the effects of MDD. Copper material was chosen as medium 1 according to Kumar et al. [46].

Quantity	Value	Unit
${c}_{11}$	$18.78\times {10}^{10}$	${\mathrm{Kgm}}^{-1}{\mathrm{s}}^{-2}$
${c}_{12}$	$8.76\times {10}^{10}$	${\mathrm{Kgm}}^{-1}{\mathrm{s}}^{-2}$
${c}_{33}$	$17.2\times {10}^{10}$	${\mathrm{Kgm}}^{-1}{\mathrm{s}}^{-2}$
${c}_{13}$	$8.0\times {10}^{10}$	${\mathrm{Kgm}}^{-1}{\mathrm{s}}^{-2}$
${c}_{44}$	$5.06\times {10}^{10}$	${\mathrm{Kgm}}^{-1}{\mathrm{s}}^{-2}$
${\beta }_{1}$	$7.543\times {10}^{6}$	${\mathrm{Nm}}^{-2}{\mathrm{deg}}^{-1}$
${\beta }_{3}$	$9.208\times {10}^{6}$	${\mathrm{Nm}}^{-2}{\mathrm{deg}}^{-1}$
$\rho$	$8.954\times {10}^{3}$	${\mathrm{Kgm}}^{-3}$
${C}_{E}$	$4.27\times {10}^{2}$	${\mathrm{jKg}}^{-1}{\mathrm{deg}}^{-1}$
${{K}_{1}}^{*}$	$0.04\times {10}^{2}$	${\mathrm{Ns}}^{-2}{\mathrm{deg}}^{-1}$
${{K}_{3}}^{*}$	$0.02\times {10}^{2}$	${\mathrm{Ns}}^{-2}{\mathrm{deg}}^{-1}$
${T}_{0}$	$293$	$\mathrm{deg}$
${\alpha }_{1}$	$2.98\times {10}^{-5}$	${\mathrm{K}}^{-1}$
${\alpha }_{3}$	$2.4\times {10}^{-5}$	${\mathrm{K}}^{-1}$

Magnesium material [46], has been taken for medium 2, thermoelastic material as

Quantity	Value	Unit
${\overline{c} }_{11}$	$5.974\times {10}^{10}$	${\mathrm{Kgm}}^{-1}{\mathrm{s}}^{-2}$
${\overline{c} }_{12}$	$2.624\times {10}^{10}$	${\mathrm{Kgm}}^{-1}{\mathrm{s}}^{-2}$
${\overline{c} }_{33}$	$6.17\times {10}^{10}$	${\mathrm{Kgm}}^{-1}{\mathrm{s}}^{-2}$
${\overline{c} }_{13}$	$2.17\times {10}^{10}$	${\mathrm{Kgm}}^{-1}{\mathrm{s}}^{-2}$
${\overline{c} }_{44}$	$3.278\times {10}^{10}$	${\mathrm{Kgm}}^{-1}{\mathrm{s}}^{-2}$
${\overline{\beta }}_{1}$	$2.68\times {10}^{6}$	${\mathrm{Nm}}^{-2}{\mathrm{deg}}^{-1}$
${\overline{\beta }}_{3}$	$2.68\times {10}^{6}$	${\mathrm{Nm}}^{-2}{\mathrm{deg}}^{-1}$
$\overline{\rho }$	$1.74\times {10}^{3}$	${\mathrm{Kgm}}^{-3}$
${\overline{C} }_{E}$	$1.04\times {10}^{3}$	${\mathrm{jKg}}^{-1}{\mathrm{deg}}^{-1}$
${{\overline{K} }_{1}}^{*}$	$0.02\times {10}^{2}$	${\mathrm{Ns}}^{-2}{\mathrm{deg}}^{-1}$
${{\overline{K} }_{3}}^{*}$	$0.02\times {10}^{2}$	${\mathrm{Ns}}^{-2}{\mathrm{deg}}^{-1}$
${\overline{T} }_{0}$	$293$	$\mathrm{deg}$
${\overline{\alpha }}_{1}$	$2.98\times {10}^{-5}$	${\mathrm{K}}^{-1}$
${\overline{\alpha }}_{3}$	$2.4\times {10}^{-5}$	${\mathrm{K}}^{-1}$

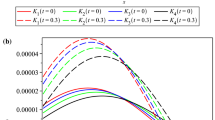
The graphical representations of stress components, temperature change, wave velocity, and attenuation coefficient have been explored with MDD and two temperature (2T) using the aforementioned data and are illustrated graphically as:

7.1 Effect of MDD and 2T

• 1. The solid line corresponds to $K\left(t-\xi \right)=1$ when $\alpha =0,\beta =0$ and with 2T.

• 2. The dashed line corresponds to $K\left(t-\xi \right)=1+\frac{\left(\xi -t\right)}{\chi }$ when $\alpha =0,\beta =\frac{1}{2}$ and with 2T.

• 3. The dotted line corresponds to $K\left(t-\xi \right)=\xi -t+1$ when $\alpha =0,\beta =\frac{\chi }{2}$ and with 2T.

• 4. The dash-dotted line corresponds to $K\left(t-\xi \right)={\left[1+\frac{\left(\xi -t\right)}{\chi }\right]}^{2}$ when $\alpha =1,\beta =1$ and with 2T.

• 5. The red dash-dot-dot line corresponds to without MDD.

• 6. The purple dash-dot line corresponds to without 2T.

Figure 2 exhibits the displacement component w of the Stoneley wave w.r.t. $\xi$ for various values of the kernel function of MDD. The variation in the displacement component near the interface of the two mediums changes with the change in the kernel function. The kernel function $K\left(t-\xi \right)=1$ when $\alpha =0,\beta =0$ shows the higher variation near the interface and starts vanishing as moving away from the interface. However kernel function $K\left(t-\xi \right)={\left[1+\frac{\left(\xi -t\right)}{\chi }\right]}^{2}$ when $\alpha =1,\beta =1$ reduces the variation in the displacement component. So lower the value of the kernel function higher the variation in the displacement component at small values of $\xi$, as the value of $\xi$ increases, the displacement becomes zero. Moreover, the displacement component shows the opposite behavior without MDD. In addition, as $\xi$ increases, the effect of MDD also decreases.

Fig. 2

Deviation of displacement component w of Stoneley waves with MDD

Figure 3 illustrates the magnitude values of conductive temperature $\varphi$ w.r.t. $\xi$ for various values of the kernel function of MDD. The variation in the $\varphi$ near the interface of the two mediums changes with the change of the kernel function. The kernel function $K\left(t-\xi \right)={\left[1+\frac{\left(\xi -t\right)}{\chi }\right]}^{2}$ when $\alpha =1,\beta =1$ shows a higher variation near the interface and starts vanishing as moving away from the interface. So higher the value of the kernel function higher the variation in the conductive temperature at small values of $\xi$, as the value of $\xi$ increases, the $\varphi$ becomes zero. Moreover, the $\varphi$ shows the opposite behavior without MDD. In addition, as $\xi$ increases, the effect of MDD also decreases. However, without two temperature, the $\varphi$ shows the opposite behavior and decreases sharply near the interface and then become zero. Figure 4 demonstrates the stress component ${t}_{zz}$ w.r.t. $\xi$ for various values of kernel function of MDD. The variation in the ${t}_{zz}$ near the interface of the two mediums changes with the change of the kernel function. The kernel function $K\left(t-\xi \right)=1$ when $\alpha =0,\beta =0$ shows the higher variation near the interface and starts vanishing as moving away from the interface. However kernel function $K\left(t-\xi \right)={\left[1+\frac{\left(\xi -t\right)}{\chi }\right]}^{2}$ when $\alpha =1,\beta =1$ reduces the variation in the ${t}_{zz}$. Moreover, the ${t}_{zz}$ shows the same behavior with high magnitude without MDD. In addition, as $\xi$ increases, the effect of MDD also decreases. So lower the value of the kernel function higher the variation in the ${t}_{zz}$ at small values of $\xi$, as the value of $\xi$ increases, the ${t}_{zz}$ becomes zero.

Fig. 3

Deviation of conductive temperature with MDD

Fig. 4

Deviation of stress component ${t}_{zz}$ with MDD

Figure 5 illustrates the attenuation coefficient w.r.t. $\xi$ for various values of the kernel function of MDD. The variation in the attenuation coefficient near the interface of the two mediums changes with the change in the kernel function. The kernel function $K\left(t-\xi \right)={\left[1+\frac{\left(\xi -t\right)}{\chi }\right]}^{2}$ when $\alpha =1,\beta =1$ shows a higher variation near the interface and starts vanishing as moving away from the interface. So higher the value of the kernel function higher the variation in the attenuation coefficient at small values of $\xi$, as the value of $\xi$ increases, the attenuation coefficient becomes zero. Moreover, the attenuation coefficient shows the opposite behavior without MDD. In addition, as $\xi$ increases, the effect of MDD also decreases. However, without two temperature, the attenuation coefficient shows the opposite behavior and decreases sharply near the interface and then become zero. Figure 6 illustrates the phase velocity w.r.t. $\xi$ for various values of the kernel function of MDD. The variation in the phase velocity sharply increases near the interface of the two mediums with the change of the kernel function. The kernel function $K\left(t-\xi \right)={\left[1+\frac{\left(\xi -t\right)}{\chi }\right]}^{2}$ when $\alpha =1,\beta =1$ shows a higher variation near the interface and approximately remains the same as moving away from the interface. So higher the value of the kernel function higher the variation in the phase velocity. Moreover, the phase velocity shows the opposite behavior without MDD. However, without two temperature, the phase velocity shows the different behavior and increases sharply near the interface.

Fig. 5

Deviation of attenuation coefficient of Stoneley waves with MDD

Fig. 6

Deviation of Stoneley waves phase velocity with MDD

8 Conclusion

We bring forth the study of the propagation of the Stoneley wave at the interface of two separate homogeneous transversely isotropic (HTI) thermoelastic mediums with modified GN theory of type II thermoelasticity without energy dissipation, including memory-dependent derivative (MDD) and two temperatures and with rotation. The wave characteristics have been obtained for different Kernel functions of the MDD from the secular equations and are depicted graphically.

Analyzing the graphs revealed the following findings:

• It is also noticed that all the component except the phase velocity of Stoneley waves vanishes away from the interface of the two mediums. In different mediums and at different depths, the characteristics of waves also differ dramatically. MDD and two temperature exhibits a significant influence on the Stoneley wave displacement component, phase velocity, stress component, attenuation coefficient, and temperature distribution at the interface of the two mediums as shown in the figures

• Based on the wave velocity equation, we notice that the change in the kernel function's values causes the dispersion of waves. The resulting Secular equation defines the dispersive property of the Stoneley waves. The problem formulation and numerical results are also approved based on diverse special cases.

• Studying these waves can help us understand geophysics, seismology, ocean physics, SAW devices, and the non-destructive evaluation of structures. Seismological profiles with vertical sections are frequently disturbed by Stoneley waves.