Concept reduction in formal concept analysis based on representative concept matrix

Abstract

Reduction theory is an important topic in formal concept analysis, and the research of reduction theory generally focuses on attribute reduction. Attribute reduction deletes redundant attributes and simplifies formal context. Nevertheless, it may lose part of original information of formal context. As a new direction of knowledge reduction, concept reduction avoids the defects of information loss caused by attribute reduction and enriches reduction theory. Concept reduction not only preserves the binary relation of a formal context, but also reduces the number of formal concepts. Furthermore, the information of formal context can be expressed simply and completely, and the complexity of solving problems with formal concept analysis can be reduced. In this paper, the definition of representative concept matrix is given to visualize the connection between concepts and binary relation. Then, the method for calculating concept reducts by representative concept matrix is obtained, and two simplified representative concept matrices named the clarified representative concept matrix and the minimal representative concept matrix are proposed. In addition, an algorithm for obtaining the minimal representative concept matrix is presented and compared with the previous algorithm. Finally, from the perspective of concept consistent set and minimal representative concept matrix respectively, the characteristics of three types of concepts, i.e., core concepts, relatively necessary concepts and absolutely unnecessary concepts, are discussed.

1 Introduction

Formal concept analysis (FCA), an efficient tool for data analysis and knowledge discovery, was proposed by Wille in 1982 [1] and further improved by Ganter and Wille [2]. In FCA, data are represented in formal contexts, from which concept lattices can be constructed as the basic and important structure in FCA.

A formal context is a triple (G, M, I) consisting of a set of objects G, a set of attributes M, and a binary relation $I\subseteq G\times M$ indicating that each object in G has what attributes in M. A formal context can be regarded as a Boolean matrix in form. Let X denote an object subset and B an attribute subset. If each object in X possesses all attributes in B and each attribute in B is exactly shared by all objects in X, then X and B constitute a formal concept (X, B), where X is called an extent and B is called an intent. Concept lattice can be formed after proper partial order and supremum and infimum are defined between formal concepts.

Actually, extents and intents in formal concept are formal representation of denotation and connotation in philosophy respectively. Therefore, FCA gives a kind of mathematical representation for basic notions in philosophy, and has outstanding contribution for cognition and knowledge discovery.

Concept lattice simplification [3,4,5], concept lattice construction [5,6,7,8], attribute reduction [5, 9,10,11,12,13,14,15,16] and rule acquisition [5, 17, 18] are research hotspots in FCA for many years. Recently, the combinations of FCA with other theories, such as rough set [5, 19], granular computing [5, 12, 20, 21], fuzzy set [3, 5, 22,23,24], three-way decision [5, 7, 8, 11, 18, 21, 23, 25, 26], Boolean factor analysis [27,28,29,30], have become new and influential research directions and produced a large number of achievements.

Since the structure of concept lattice is the research basis of FCA, there are multi-perspective researches with respect to concept lattice, and attribute reduction preserving lattice structure is an important one. In general, not all attributes are necessary for keeping the structure of a concept lattice. On this basis, Zhang and Wei proposed and studied attribute reduction to preserve the concept lattice structure [9, 10]. This kind of attribute reduction can not only completely determine the formal concepts and hierarchy among these concepts of the original formal context, but also simplify the original data in formal context by removing redundant attributes. Subsequently, a variety of attribute reductions based on different semantics were proposed. For instance, Wu et al. proposed the granular reduction from the viewpoint of granular computing [12]. Wang et al. defined the meet-irreducible attribute reduction to preserve the extents of meet-irreducible elements in the original formal concept lattice [13]. Li et al. discussed the join-irreducible attribute reduction from the perspective of join-irreducible elements [14]. Shao et al. presented the attribute reduction with threshold $\delta$ and lattice-keep-based attribute reduction in formal fuzzy contexts and generalized one-sided formal contexts respectively [15, 16]. Attribute reduction makes the processing of problem more succinct by simplifying formal contexts, so it can be used as the preprocessing of data.

Although attribute reduction with specific semantics can simplify formal context on account of deleting some attributes and related data, it also loses part of original information of formal context. Thus, it will be an interesting topic to investigate how to preserve original information in a formal context. As a reflection of knowledge, formal concepts are connected with the purpose of knowledge discovery. In fact, not all formal concepts are necessary in preserving original information of a formal context. In other words, we can dig out a subset of concept lattice to store all the information of a formal context when we use FCA, which will greatly reduce the complexity of problem solving. Therefore, it is worth studying the idea and the methods of how to delete redundant concepts while preserving original information in a formal context.

Boolean factor analysis (BFA) is a powerful method to reveal and reduce information redundancy in high-dimensional binary data [31, 32]. Boolean matrix factorization (BMF) is a model which can decompose a higher-dimensional Boolean matrix into two lower-dimensional matrices approximately, i.e., $I_{n\times m} \approx A_{n\times k}\circ B_{k\times m}$, where $k<m$, $k<n$ [33,34,35]. Since the binary relation I in a formal context (G, M, I) can be regarded as a Boolean matrix $I_{\vert G \vert \times \vert M \vert }$, Keprt et al. firstly used FCA as a tool to deal with the issues in BFA. Specifically, they treated the matrix $I_{n \times m}$ that needs to be decomposed in BFA as the binary relation I of a formal context (G, M, I), where $\vert G \vert =n$, $\vert M \vert =m$, and used the formal concepts of the formal context as the factors to decompose Boolean matrix $I_{n\times m}$ [27]. On this basis, Bělohlávek et al. provided the corresponding theoretical support [28, 29]. They found that concepts are suitable for decomposing $I_{n\times m}$ into $A_{n\times k}$ and $B_{k\times m}$, where columns of matrix $A_{n\times k}$ are composed of extents of the concepts as factors and rows of matrix $B_{k\times m}$ are composed of intents of the concepts as factors. That is, Bělohlávek proposed a theoretical method of BMF using FCA as a tool from the perspective of BFA.

However, if we understand and explain the above idea and method from the perspective of FCA, then we can conclude the following fact: the concepts as factors in BMF are a subset of concept lattice, but they can restore the binary relation I of formal context (G, M, I). In other words, the number of concepts can be reduced without changing the original information in a formal context. Based on this idea, Wei et al. proposed the topic of concept reduction and conducted a preliminary study [36, 37]. Concept reduction not only avoids the defects of information loss caused by attribute reduction, but also digs out a subset of concept lattice to preserve the binary relation and reduces the complexity of problem solving in FCA. At present, concept reduction has attracted the attention of scholars in related fields. For instance, Wang et al. defined the concept discernibility matrix to find all concept reducts. Each element of the matrix is a set of object-attribute pairs which belongs to a formal concept in the corresponding row but not belongs to another in the corresponding column [38]. Li et al. proposed the triadic concept reduction which preserves all triadic relations in triadic context [39]. Xie et al. studied the concept characteristics and concept reduction by Boolean matrix operation [40]. Focusing on the infrastructure of concept reduction, this paper further extends the content of concept reduction, and defines the representative concept matrix to visualize the correspondence between concepts and binary relation I. Then it gives the representative-concept-matrix method to calculate all concept reducts.

The rest of the paper is organized as follows. In Sect. 2, the basic notions in FCA and concept reduction are reviewed. In Sect. 3, the representative concept matrix is defined and the corresponding judgment theorem of concept consistent set is proposed. In Sect. 4, the simplified methods of representative concept matrix are presented, and an algorithm for obtaining minimal representative concept matrix is given. In Sect. 5, the characteristics of three types of concepts are discussed. Finally, Sect. 6 concludes the paper and suggests some potential interesting topics in concept reduction.

2 Preliminaries

This section reviews some basic notions in FCA and concept reduction.

Definition 1

[1] A formal context (G, M, I) consists of two sets G and M and a relation I between G and M. The elements of G are called the objects and the elements of M are called the attributes of the formal context. In order to express that an object g is in a relation I with an attribute m, we write gIm or $(g, m) \in I$ and read it as “the object g has the attribute m”.

A pair of derivation operators are defined on a set of objects $X \subseteq G$ and a set of attributes $B \subseteq M$, respectively [1]:

$$\begin{aligned} ^*:{\mathcal {P}}(G)\rightarrow {\mathcal {P}}(M),X^*= & {} \{m \in M \mid \forall g \in X, gIm \}, \\ ^*:{\mathcal {P}}(M)\rightarrow {\mathcal {P}}(G),B^*= & {} \{g \in G \mid \forall m \in B, gIm\}. \end{aligned}$$

The above formulas tell us $X^*$ is the set of attributes shared by all the objects in X, and $B^*$ is the set of objects possessing all attributes in B.

The properties of this pair of derivation operators are shown in [1]. Here we only list some of the properties relevant to this paper. For any $X_1, X_2, X \subseteq G$ and $B_1, B_2, B \subseteq M$, the pair of derivation operators satisfies the following properties:

• 1. $X \subseteq X^{**}$ and $B \subseteq B^{**}$,

• 2. $X_1 \subseteq X_2 \Longrightarrow X_2^* \subseteq X_1^*$ and $B_1 \subseteq B_2 \Longrightarrow B_2^* \subseteq B_1^*$.

For simplicity, we denote $\{g\}^*$ as $g^*$ and $\{m\}^*$ as $m^*$ in this paper. If for any $g \in G, g^*\ne M$ and $g^*\ne \emptyset$ hold, and for any $m \in M, m^*\ne G$ and $m^*\ne \emptyset$ hold, then (G, M, I) is called a canonical formal context. A canonical formal context is the context without empty rows (columns) and full rows (columns).

Definition 2

[1] A formal context (G, M, I) is called clarified, if for any objects $g_1$, $g_2\in G$, from $g_1^*=g_2^*$ it always follows that $g_1=g_2$, and correspondingly, $m_1^*=m_2^*$ implies $m_1=m_2$ for all $m_1$, $m_2 \in M$.

For a formal context (G, M, I), the clarified context of (G, M, I) is the context formed by deleting the redundant rows and columns from (G, M, I).

Example 1

[28] Table 1 shows a formal context (G, M, I) with the object set $G=\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}$ and the attribute set $M=\{a, b, c, d, e, f, g, h\}$. In Table 1, the number “1” in position (i, j) means that the i-th object has the j-th attribute, and the number “0” in position (i, j) means the opposite. Table 2 shows the clarified context of (G, M, I). For $d^*= \emptyset$, neither the formal context in Table 1 nor the clarified context in Table 2 is canonical.

Table 1 The formal context (G, M, I) in Example 1

Table 2 The clarified context of (G, M, I) in Example 1

Based on the pair of derivation operators, a formal concept is obtained.

Definition 3

[1] A formal concept of the formal context (G, M, I), for short, a concept is a pair (X, B) with $X \subseteq G$, $B \subseteq M$, $X^*=B$ and $B^*=X$. We call X the extent and B the intent of the formal concept (X, B).

The definition tells us the following fact: if (X, B) is a formal concept, then $X=X^{**}, B=B^{**}$.

Let L(G, M, I) denote the set of all concepts of (G, M, I). The concepts $(X_1, B_1),(X_2, B_2)\in L(G, M, I)$ can be ordered by [1]:

$$\begin{aligned} (X_1, B_1) \le (X_2, B_2)&\Longleftrightarrow X_1 \subseteq X_2(\Longleftrightarrow B_1 \supseteq B_2). \end{aligned}$$

Then “$\le$” is a partial order on L(G, M, I), and L(G, M, I) is called the concept lattice of (G, M, I). The concept lattice is a complete lattice in which infimum and supremum are given as follows [1]:

$$\begin{aligned} (X_1, B_1) \wedge (X_2, B_2)&= (X_1 \cap X_2, (B_1 \cup B_2)^{**}),\\ (X_1, B_1) \vee (X_2, B_2)&= ((X_1 \cup X_2)^{**}, B_1 \cap B_2). \end{aligned}$$

Example 2

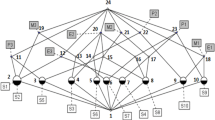
(Continued with Example 1) Fig. 1 shows the concept lattice of the formal context (G, M, I) in Table 1, where $c_1=(G,\emptyset )$, $c_2=(\{3, 6, 7, 8, 10\}, \{g\})$, $c_3=(\{1, 2, 3, 4, 5, 6, 7, 9, 11, 12\}, \{b\})$, $c_4=(\{1, 3, 5, 6, 7, 9, 11\}, \{b, e\})$, $c_5=(\{1, 2, 4, 5, 9, 11, 12\}, \{a, b\})$, $c_6=(\{3, 6, 7\}, \{b, e, g\})$, $c_7=(\{1, 5, 9, 11\}, \{a, b, c, e\})$, $c_8=(\{2, 4, 12\}, \{a, b, f, h\})$, $c_9=(\emptyset , M)$.

The concept lattice of the clarified context in Table 2 is isomorphic to that of the formal context in Table 1. We use $c_i'$ to represent the corresponding formal concept $c_i$ in the same position of the concept lattice. Then $c_1'=(\{1, 2, 3, 8\},\emptyset )$, $c_2'=(\{3, 8\}, \{g\})$, $c_3'=(\{1, 2, 3\}, \{b\})$, $c_4'=(\{1, 3\}, \{b, e\})$, $c_5'=(\{1, 2\}, \{a, b\})$, $c_6'=(\{3\}, \{b, e, g\})$, $c_7'=(\{1\}, \{a, b, c, e\})$, $c_8'=(\{2\}, \{a, b, f\})$, $c_9'=(\emptyset , \{a, b, c, d, e, f, g\})$.

Fig. 1

The concept lattice L(G, M, I) in Example 1

Given a formal context (G, M, I), the binary relation I can be reconstructed by all concepts in L(G, M, I), which is formally described in the following lemma.

Lemma 1

[2] Let (G, M, I) be a formal context and L(G, M, I) be its corresponding concept lattice. Then $I=\bigcup \{X\times B \vert (X,B)\in L(G,M,I)\}$.

However, not every concept is necessary to reconstruct the formal context and preserve the binary relation I. The topic of concept reduction proposed by Wei et al. solves this issue properly. Concept reduction reconstructs the original formal context with fewer concepts (subsets of the concept lattice) and preserves the binary relation [36, 37]. Firstly, Wei et al. gave the definition of concept consistent set. A concept consistent set is a subset of concept lattice that preserves the binary relation I in formal context, and a minimum concept consistent set is a concept reduct.

Definition 4

[36, 37] Let (G, M, I) be a formal context and L(G, M, I) be its corresponding concept lattice. For ${\mathcal {F}} \subseteq L(G, M, I)$, if

$$\begin{aligned} I=\bigcup _{(X,B)\in {\mathcal {F}}}(X\times B), \end{aligned}$$

we call ${\mathcal {F}}$ a binary relation-preserving concept consistent set, for short, a concept consistent set. And further, if for any $(X_i,B_i)\in {\mathcal {F}}$,

$$\begin{aligned} I\ne \bigcup _{(X,B)\in {\mathcal {F}}\backslash \{(X_i,B_i)\}}(X\times B), \end{aligned}$$

we call ${\mathcal {F}}$ a binary relation-preserving concept reduct, for short, a concept reduct.

Example 3

(Continued with Example 1) Suppose we consider two subsets ${\mathcal {F}}_1=\{c_2,c_4,c_7,c_8\}$ and ${\mathcal {F}}_2=\{c_3,c_4,c_5\}$ of L(G, M, I).

For ${\mathcal {F}}_1=\{c_2,c_4,c_7,c_8\}$, the sets of binary relations reflected respectively in concepts $c_2,c_4,c_7,c_8$ are as follows.

$c_2:\{(3,g),(6,g),(7,g),(8,g),(10,g)\};$

$c_4:\{(1,b),(3,b),(5,b),(6,b),(7,b),(9,b),(11,b),(1,e),(3,e),(5,e),(6,e),(7,e),$

$(9,e),(11,e)\};$

$c_7:\{(1,a),(5,a),(9,a),(11,a),(1,b),(5,b),(9,b),(11,b),(1,c),(5,c),(9,c),(11,c),$

$(1,e),(5,e),(9,e),(11,e)\};$

$c_8:\{(2,a),(4,a),(12,a),(2,b),(4,b),(12,b),(2,f),(4,f),(12,f),(2,h),(4,h),$

$(12,h)\}.$

The union of above four sets is equal to the binary relation I, that is, $I=\bigcup _{(X,B)\in {\mathcal {F}}_1}(X\times B)$. Thus ${\mathcal {F}}_1=\{c_2,c_4,c_7,$ $c_8\}$ is a concept consistent set. Further, for any $c_i\in {\mathcal {F}}_1(i=2,4,7,8)$, $I\ne \bigcup _{(X,B)\in {\mathcal {F}}_1\backslash \{c_i\}}(X\times B)$ holds. Therefore, ${\mathcal {F}}_1=\{c_2,c_4,c_7,c_8\}$ is a concept reduct.

For ${\mathcal {F}}_2=\{c_3,c_4,c_5\}$, the sets of binary relations reflected respectively in concepts $c_3,c_4,c_5$ are as follows.

$c_3:\{(1,b),(2,b),(3,b),(4,b),(5,b),(6,b),(7,b),(9,b),(11,b),(12,b)\};$

$c_4:\{(1,b),(3,b),(5,b),(6,b),(7,b),(9,b),(11,b),(1,e),(3,e),(5,e),(6,e),(7,e),$ $(9,e),(11,e)\};$

$c_5:\{(1,a),(2,a),(4,a),(5,a),(9,a),(11,a),(12,a),(1,b),(2,b),(4,b),(5,b),(9,b),$ $(11,b),(12,b)\}.$

The union of above three sets is $\{(1,a),(2,a),(4,a),(5,a),(9,a),(11,a),(12,a),$ (1, b), (2, b), (3, b), (4, b), (5, b), (6, b), (7, b), (9, b), (11, b), (12, b), (1, e), (3, e), (5, e),  $(6,e),(7,e),(9,e),(11,e)\}\ne I$. Thus ${\mathcal {F}}_2=\{c_3,c_4,c_5\}$ is not a concept consistent set. Apparently, it is not a concept reduct.

It is worth noting that Yao [41] gave a conceptual definition of reducts that unifies different kinds of reducts in rough sets (RS), which is proposed by Pawlak [42] in 1982 and is widely used in data analysis [43, 44].

Definition 5

[41] Suppose S is a finite set and ${\mathbb {P}}$ is a unary predicate on subsets of S, that is, for $A\subseteq S$, ${\mathbb {P}}(A)$ stands for the statement that “subset A has property ${\mathbb {P}}$”. Given an evaluation e of ${\mathbb {P}}$, if a subset $A\subseteq S$ satisfies the following conditions:

• 1. existence: ${\mathbb {P}}_e(S)$,

• 2. sufficiency: ${\mathbb {P}}_e(A)$,

• 3. minimization: $\forall B \subset A, \lnot {\mathbb {P}}_e(B)$,

we call A a reduct of S.

Actually, this definition can be regard as the uniform of reducts in RS and FCA. Let (G, M, I) be a formal context, $T=(OB, AT, \{V_a\mid a \in AT\}, \{I_a\mid a \in AT\})$ be an information table and $E_A$ be an equivalence relation which is defined as follows, $xE_Ay \Leftrightarrow I_a(x)=I_a(y), \forall a\in A$. Here we list a few examples:

• 1. for the attribute reduct in RS [42, 45], S is AT, ${\mathbb {P}}_e(A)$ is $E_A=E_{AT}, A\subseteq AT$;

• 2. for the attribute reduct in FCA [9, 10], S is M, ${\mathbb {P}}_e(A)$ is $L(G,M,I)\cong L(G,A,I\cap G\times A), A\subseteq M$;

• 3. for the concept reduct in FCA [36, 37], S is L(G, M, I), ${\mathbb {P}}_e(A)$ is $\bigcup _{(X,B)\in L(G,M,I)}(X\times B)=\bigcup _{(X,B)\in A}(X\times B), A \subseteq L(G,M,I)$.

According to the role of concepts in concept reducts, all concepts in L(G, M, I) can be classified into three types.

Definition 6

[36] Let (G, M, I) be a formal context and L(G, M, I) be its corresponding concept lattice. {${\mathcal {F}}_i \mid i\in \tau ,\tau$ is an index set} denotes the set of all the concept reducts. Then L(G, M, I) can be divided into three parts:

• 1. absolutely necessary concept (core concept) set ${\mathcal {C}}=\bigcap _{i\in \tau }{\mathcal {F}}_i$;

• 2. relatively necessary concept set ${\mathcal {K}}=\bigcup _{i\in \tau }{\mathcal {F}}_i \setminus \bigcap _{i\in \tau }{\mathcal {F}}_i$;

• 3. absolutely unnecessary concept set ${\mathcal {U}}=L(G,M,I)\setminus \bigcup _{i\in \tau }{\mathcal {F}}_i$.

Example 4

(Continued with Example 1). There are two concept reducts in (G, M, I) shown in Table 1, ${\mathcal {F}}_1=\{c_2,c_4,c_7,c_8\}$ and ${\mathcal {F}}_2=\{c_2,c_6,c_7,c_8\}$. We know from Definition 6 that the core concept set is ${\mathcal {C}}=\{c_2, c_7, c_8\}$, the relatively necessary concept set is ${\mathcal {K}}=\{c_4, c_6\}$, and the absolutely unnecessary concept set is ${\mathcal {U}}=\{c_1, c_3, c_5, c_9\}$.

In fact, dividing the family of all concepts into three parts, as shown in Definition 6, fits well with the “trisecting” of three-way decision (3WD) proposed by Yao [46,47,48].

With respect to the number of concepts in a concept reduct, the following fact needs to be noticed. For a formal context (G, M, I), the cardinality of concept reduct may be different, i.e., the numbers of concepts in different concept reducts may be different.

Example 5

Table 3 shows a formal context (G, M, I) with $G=\{1, 2, 3\}$ and $M=\{a, b, c, d\}$. $L(G, M, I)=\{(G, \emptyset ), (\{1,2\}, \{a,d\}), (\{1,3\}, \{b\}), (\{2,3\}, \{c\}), (\{1\}, \{a,b,$ $d\}), (\{2\}, \{a,c,d\}), (\{3\}, \{b,c\}), (\emptyset , M)\}$.

By Definition 4, we know that both ${\mathcal {F}}_1=\{(\{1,2\}, \{a,d\}), (\{1,3\}, \{b\}),$ $(\{2,3\}, \{c\})\}$ and ${\mathcal {F}}_2=\{(\{1,3\}, \{b\}),(\{2,3\}, \{c\}), (\{1\}, \{a,b,$ $d\}), (\{2\}, \{a,c,d\})\}$ are concept reducts of (G, M, I). We can see that $\vert {\mathcal {F}}_1\vert =3$ and $\vert {\mathcal {F}}_2\vert =4$, which shows the numbers of concepts in different concept reducts are different.

Table 3 The formal context in Example 5

Figure 2 shows the Venn diagram of three kinds of concepts in L(G, M, I). Suppose a formal context (G, M, I) has two concept reducts. In Fig. 2, the rectangle represents the set of all concepts L(G, M, I), the ellipses represent the two concept reducts (the ellipses with different sizes represent the concept reducts with different numbers of concept), the slash area represents the core concept set ${\mathcal {C}}$, the dot area represents the absolutely unnecessary concept set ${\mathcal {U}}$, and the blank area represents the relatively unnecessary concept set ${\mathcal {K}}$.

Fig. 2

The Venn diagram of three kinds of concepts in L(G, M, I)

3 Representative concept matrix and the judgment theorem of concept consistent sets

According to the definitions of formal contexts and concepts, we know that a concept possesses a set of relations between objects and attributes. Meanwhile, a relation between an object and an attribute is possessed by a set of concepts. This section defines the representative concepts of an object-attribute pair (g, m) to identify the concepts which possess the relation between g and m. Then, the representative concept matrix is proposed. In a representative concept matrix, the set of representative concepts in position (i, j) includes all concepts which possess the relation between i-th object and j-th attribute.

Definition 7

Let (G, M, I) be a formal context, $g \in G, m \in M$, $(X, B) \in L(G, M, I)$. If $(g, m)\in X\times B$, then (X, B) is called a representative concept of the pair (g, m). Further,

$$\begin{aligned} { REP}((g,m))=\{(X, B)\in L(G, M, I) \mid (g, m)\in X\times B\} \end{aligned}$$

is called the set of representative concepts of (g, m), and

$$\begin{aligned} \mathbf {\Lambda }=({ REP}((g,m)), g\in G, m\in M)_{\vert G\vert \times \vert M\vert } \end{aligned}$$

is called the representative concept matrix of (G, M, I).

Remark 1

For a canonical formal context, $(G,\emptyset )$ and $(\emptyset ,M)$ must be the greatest and least elements of the corresponding concept lattice respectively, but we notice that neither $(G,\emptyset )$ nor $(\emptyset ,M)$ is in any set of representative concepts. Therefore, both $(G,\emptyset )$ and $(\emptyset ,M)$ are absolutely unnecessary concepts.

Example 6

(Continued with Example 1) For $1 \in G$, $a \in M$, considering all concepts in L(G, M, I), we have $(1, a)\in \{1,2,4,5,9,11,12\}\times \{a,b\}$, $(1, a)\in \{1,5,9,11\}\times \{a,b,c,e\}$. Then ${ REP}((1,a))=\{(\{1,2,4,5,9,11,12\},\{a,b\}),(\{1,$ $5,9,11\},\{a,b,c,e\})\}=\{c_5,c_7\}$. For any $g \in G$, $m \in M$, REP((g, m)) can be calculated in a similar way. Thus, the representative concept matrix $\mathbf {\Lambda }$ of (G, M, I) can be obtained as follows, where the representation of rows and columns in representative concept matrix are conform to the formal context, respectively.

$$\begin{aligned} \mathbf {\Lambda } = \left( \begin{array}{cccccccc} \{c_5,c_7\} &{} \{c_3,c_4,c_5,c_7\} &{} \{c_7\} &{} \emptyset &{} \{c_4,c_7\} &{} \emptyset &{} \emptyset &{} \emptyset \\ \{c_5,c_8\} &{} \{c_3,c_5,c_8\} &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_8\} &{} \emptyset &{} \{c_8\}\\ \emptyset &{} \{c_3,c_4,c_6\} &{} \emptyset &{} \emptyset &{} \{c_4,c_6\} &{} \emptyset &{} \{c_2,c_6\} &{} \emptyset \\ \{c_5,c_8\} &{} \{c_3,c_5,c_8\} &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_8\} &{} \emptyset &{} \{c_8\}\\ \{c_5,c_7\} &{} \{c_3,c_4,c_5,c_7\} &{} \{c_7\} &{} \emptyset &{} \{c_4,c_7\} &{} \emptyset &{} \emptyset &{} \emptyset \\ \emptyset &{} \{c_3,c_4,c_6\} &{} \emptyset &{} \emptyset &{} \{c_4,c_6\} &{} \emptyset &{} \{c_2,c_6\} &{} \emptyset \\ \emptyset &{} \{c_3,c_4,c_6\} &{} \emptyset &{} \emptyset &{} \{c_4,c_6\} &{} \emptyset &{} \{c_2,c_6\} &{} \emptyset \\ \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_2\} &{} \emptyset \\ \{c_5,c_7\} &{} \{c_3,c_4,c_5,c_7\} &{} \{c_7\} &{} \emptyset &{} \{c_4,c_7\} &{} \emptyset &{} \emptyset &{} \emptyset \\ \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_2\} &{} \emptyset \\ \{c_5,c_7\} &{} \{c_3,c_4,c_5,c_7\} &{} \{c_7\} &{} \emptyset &{} \{c_4,c_7\} &{} \emptyset &{} \emptyset &{} \emptyset \\ \{c_5,c_8\} &{} \{c_3,c_5,c_8\} &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_8\} &{} \emptyset &{} \{c_8\}\\ \end{array} \right) _{12\times 8} \end{aligned}$$

Property 1 shows that if an object g possesses an attribute m, then the corresponding set of representative concepts is non-empty; otherwise, the set of representative concepts is empty.

Property 1

Let (G, M, I) be a formal context, $g\in G$, $m\in M$, and REP((g, m)) be the set of representative concepts of (g, m). Then,

• 1. $(g,m)\in I \Leftrightarrow { REP}((g,m)) \ne \emptyset$,

• 2. $(g,m)\notin I \Leftrightarrow { REP}((g,m)) = \emptyset$.

Proof

1. Necessity. Suppose $(g, m)\in I$. From Lemma 1, we know that $I=\bigcup \{X\times B \mid (X, B)\in L(G, M, I)\}$, which means that there exists $(X, B)\in L(G, M, I)$ such that $(g, m)\in X\times B$, i.e., $(X, B)\in { REP}((g,m))$. Thus ${ REP}((g,m))\ne \emptyset$.

Sufficiency. If ${ REP}((g,m))\ne \emptyset$, then there exists $(X, B)\in L(G, M, I)$ such shat $(g, m)\in X\times B$. Because of $I=\bigcup \{X\times B \mid (X, B)\in L(G, M, I)\}$ from Lemma 1, we have $(g, m)\in I$. So, the first proposition is proved.

2. The proposition is consequently proved for it is equivalent to the first one. $\square$

In addition, Property 1 implies that if an object g is in a relation I with an attribute m, then there must be a concept embodying the pair (g, m), and vice versa.

According to the definition of the set of representative concepts, REP((g, m)) identifies the concepts which possess the relation between g and m. That is, REP((g, m)) reflects which concept can embody the pair (g, m), and which cannot. In order to preserve the binary relation I, we only need to find such concepts that the intersection between them and each non-empty set of representative concepts are non-empty. The set of such concepts are therefore the concept consistent set. Hence, the judgment theorem of concept consistent set is obtained.

Since only non-empty set in representative concept matrix is worth studying, we also denote the matrix of all non-empty sets of representative concepts as $\mathbf {\Lambda }$. That is, $\mathbf {\Lambda }=({ REP}((g, m)), (g, m)\in I)_{\vert G\vert \times \vert M\vert }$. For the sake of presentation, we sometimes regard $\mathbf {\Lambda }$ as a set of all its elements.

Theorem 1

(The judgment theorem of concept consistent set) Let (G, M, I) be a formal context and L(G, M, I) be its corresponding concept lattice. For ${\mathcal {F}} \subseteq L(G, M, I)$, ${\mathcal {F}} \ne \emptyset$, the following propositions are equivalent:

• 1. ${\mathcal {F}}$ is a concept consistent set;

• 2. for any $(g,m)\in I$, ${\mathcal {F}} \cap { REP}((g,m)) \ne \emptyset$;

• 3. for any ${\mathcal {D}}\subseteq L(G, M, I)$, if ${\mathcal {F}}\cap {\mathcal {D}}=\emptyset$, then ${\mathcal {D}} \notin \mathbf {\Lambda }$.

Proof

1 $\Rightarrow$ 2. Suppose ${\mathcal {F}}$ is a concept consistent set, which means $I=\bigcup _{(X,B)\in {\mathcal {F}}} (X\times B)$. Then for any $(g, m)\in I$, there exists $(X, B)\in {\mathcal {F}}$ such that $(g, m)\in X\times B$, i.e., $(X, B) \in { REP}((g,m))$. Thus ${\mathcal {F}} \cap { REP}((g,m)) \ne \emptyset$;

2 $\Rightarrow$ 1. For any $(g, m)\in I$, ${\mathcal {F}} \cap { REP}((g,m)) \ne \emptyset$, there exists $(X,B)\in {\mathcal {F}}$ satisfying $(X, B) \in { REP}((g,m))$. Then $(X,B)\in {\mathcal {F}}$ and $(g, m)\in X\times B$ hold. Therefore, $\bigcup _{(X,B)\in {\mathcal {F}}} (X\times B)=\bigcup _{(g, m)\in X\times B,(X,B)\in {\mathcal {F}}} \{(g, m)\}=I$, i.e., ${\mathcal {F}}$ is a concept consistent set;

2 $\Rightarrow$ 3. We assume that ${\mathcal {F}} \cap { REP}((g,m)) \ne \emptyset$ and ${\mathcal {F}}\cap {\mathcal {D}}=\emptyset$ hold for any $(g, m)\in I$ and ${\mathcal {D}}\subseteq L(G, M, I)$. Suppose ${\mathcal {D}} \in \mathbf {\Lambda }$. Then there exists $(g_0,m_0)\in I$ such that ${ REP}((g_0,m_0))={\mathcal {D}}$. Furthermore, ${\mathcal {F}}\cap {\mathcal {D}}={\mathcal {F}}\cap { REP}((g_0,m_0)) \ne \emptyset$, which is in contradiction to the known condition. Therefore, we have ${\mathcal {D}} \notin \mathbf {\Lambda }$.

3 $\Rightarrow$ 2. For any ${\mathcal {D}}\subseteq L(G, M, I)$, because ${\mathcal {F}}\cap {\mathcal {D}}=\emptyset$ implies ${\mathcal {D}} \notin \mathbf {\Lambda }$, we know that ${\mathcal {D}} \in \mathbf {\Lambda }$ implies ${\mathcal {F}}\cap {\mathcal {D}} \ne \emptyset$. In addition, because for any $(g, m)\in I$, ${ REP}((g,m)) \in \mathbf {\Lambda }$. Thus ${\mathcal {F}} \cap { REP}((g,m)) \ne \emptyset$ holds for any $(g, m)\in I$. $\square$

Combining Definition 4 with Theorem 1, the judgment theorem of concept reduct can be obtained.

Theorem 2

Let (G, M, I) be a formal context and L(G, M, I) be its corresponding concept lattice. For ${\mathcal {F}} \subseteq L(G, M, I)$, if the following conditions hold:

• 1. for any $(g,m)\in I$, ${\mathcal {F}} \cap { REP}((g,m)) \ne \emptyset$;

• 2. for any $(X_i,B_i)\in {\mathcal {F}}$, there exists $(g_0,m_0)\in I$ such that $({\mathcal {F}}\backslash \{(X_i,B_i)\})\cap { REP}((g_0,m_0))= \emptyset$.

then ${\mathcal {F}}$ is a concept reduct.

Theorem 2 indicates that finding a concept reduct of a formal context is actually finding the minimum concept set ${\mathcal {F}}$ that satisfies ${\mathcal {F}} \cap { REP}((g,m)) \ne \emptyset$ for all $(g,m)\in I$.

Example 7

(Continued with Example 1) Let ${\mathcal {F}}_1=\{c_2,c_4,c_7,c_8,c_9\}$. It’s easy to see that ${\mathcal {F}}_1 \cap { REP}((g,m)) \ne \emptyset$ for any $(g,m)\in I$, which means that ${\mathcal {F}}_1$ is a concept consistent set. However, for ${\mathcal {F}}_1\backslash \{c_9\}=\{c_2,c_4,c_7,c_8\}$, we know that ${\mathcal {F}}_1\backslash \{c_9\} \cap { REP}((g,m)) \ne \emptyset$ holds for all $(g,m)\in I$. Therefore, ${\mathcal {F}}_1$ is not a concept reduct.

Let ${\mathcal {F}}_2=\{c_2,c_4,c_7,c_8\}$. We can get ${\mathcal {F}}_2 \cap { REP}((g,m)) \ne \emptyset$ for any $(g,m)\in I$, that is, ${\mathcal {F}}_2$ is a concept consistent set. Further, for ${\mathcal {F}}_2\backslash \{c_2\}=\{c_4,c_7,c_8\}$, there exsits $\{c_2\} \in \mathbf {\Lambda }$ such that $\{c_4,c_7,c_8\} \cap \{c_2\}=\emptyset$; for ${\mathcal {F}}_2\backslash \{c_4\}=\{c_2,c_7,c_8\}$, there exsits $\{c_4,c_6\} \in \mathbf {\Lambda }$ such that $\{c_2,c_7,c_8\} \cap \{c_4,c_6\}=\emptyset$; for ${\mathcal {F}}_2\backslash \{c_7\}=\{c_2,c_4,c_8\}$, there exsits $\{c_7\} \in \mathbf {\Lambda }$ such that $\{c_2,c_4,c_8\} \cap \{c_7\}=\emptyset$; for ${\mathcal {F}}_2\backslash \{c_8\}=\{c_2,c_4,c_7\}$, there exsits $\{c_8\} \in \mathbf {\Lambda }$ such that $\{c_2,c_4,c_7\} \cap \{c_8\}=\emptyset$. Thus ${\mathcal {F}}_2=\{c_2,c_4,c_7,c_8\}$ is a concept reduct.

With respect to the approach for acquiring all the concept reducts, Wei et al. proposed a method on the basis of the representative concept function [36].

Theorem 3

[36] Let (G, M, I) be a formal context and L(G, M, I) be its corresponding concept lattice. For any $(g_i, m_j)\in I$, $CS_{ij}=\{(X, B) \in L(G,M,I) \mid (g_i, m_j) \in X\times B\}, DC=\{CS_{ij} \mid (g_i, m_j)\in I\}$. Denote a function

$$\begin{aligned} g(DC)=\bigwedge _{CS_{ij}\in DC}\left(\bigvee _{(X,B)\in CS_{ij}}(X,B)\right), \end{aligned}$$

then all conjunctions in the minimal disjunctive normal form corresponding to g(DC) are exactly the whole concept reducts corresponding to the formal context.

Actually, Theorem 2 and Theorem 3 provide two methods for obtaining all concept reducts from the perspective of the representative concept matrix and representative concept function, respectively. In fact, if $(g_i,m_j) \in I$, then $CS_{ij}={ REP}((g_i,m_j))$. Therefore, the representative concept matrix $\mathbf {\Lambda }$ is the matrix representation of DC. On this basis, the method in this paper is actually consistent with [36]. However, since the representation of matrix can intuitively exhibit the connections between concepts and binary relation, the calculation method in this paper is simpler and more acceptable to readers.

The following conclusion is about core concept set.

Theorem 4

Core concept set ${\mathcal {C}}$ is a concept reduct if and only if there is only one concept reduct.

Proof

Necessity. We assume that there are more than one concept reduct. Without generality, we suppose that there are two concept reducts: ${\mathcal {F}}$ and ${\mathcal {C}}$, ${\mathcal {F}}\ne {\mathcal {C}}$, and ${\mathcal {C}}$ is also the core concept set. Since ${\mathcal {C}}$ is the core concept set and ${\mathcal {C}}\ne {\mathcal {F}}$, we know that ${\mathcal {C}}\subset {\mathcal {F}}$, which means there exists a concept $c\in {\mathcal {F}}$ but $c\notin {\mathcal {C}}$ such that ${\mathcal {C}}\subseteq {\mathcal {F}} \backslash \{c\}$. In addition, because ${\mathcal {C}}$ is a concept reduct, ${\mathcal {F}} \backslash \{c\}$ is a consistent set. Thus ${\mathcal {F}}$ is not a concept reduct, which is in contradiction to the known condition.

Sufficiency. Suppose that there is only one concept reduct and denoted by ${\mathcal {F}}$. From the definition of core concept set, we know ${\mathcal {C}}={\mathcal {F}}$, and then ${\mathcal {C}}$ is a concept reduct. $\square$

4 Simplification of representative concept matrix

For a formal context (G, M, I), the number of the set of representative concepts is $\vert I \vert$. When $\vert I \vert$ is large, the calculation of concept reduction is complicatied. In order to facilitate the calculation of concept reduction, this section proposes the simplified methods of the representative concept matrix defined in Sect. 3 and provides theoretical supports for the algorithm of concept reduction.

We know that a formal context can be clarified to make the information representation simpler and clearer. By doing this, the representative concept matrix with same rows or columns can also be dealt to be simpler.

Property 2

Let (G, M, I) be a formal context. For any $g_1, g_2\in G$, $m_1, m_2\in M$, the following properties hold:

• 1. If $g_1^*=g_2^*$, then for any $m \in M$, ${ REP}((g_1,m))={ REP}((g_2,m))$;

• 2. If $m_1^*=m_2^*$, then for any $g \in G$, ${ REP}((g,m_1))={ REP}((g,m_2))$.

Proof

1. For any $(X,B)\in { REP}((g_1,m))$, we have $g_1\in X$, $m\in B$, so $g_1^*\supseteq X^*$. In addition, we obtain $g_2^*\supseteq X^*$ for $g_1^*=g_2^*$, and further, $g_2^{**}\subseteq X^{**}$. Since $g_2 \in g_2^{**}$, we have $g_2\in X^{**}=X$, then $(X,B)\in { REP}((g_2,m))$, i.e., ${ REP}((g_1,m))\subseteq { REP}((g_2,m))$. Similarly, ${ REP}((g_2,m))\subseteq { REP}((g_1,m))$ also holds. Thus, ${ REP}((g_1,m))={ REP}((g_2,m))$. So, the first proposition is proved.

2. The proposition can be proved in a similar way. $\square$

According to Property 2, if some rows (or columns) in a formal context are same, then the corresponding rows (or columns) of the representative concept matrix are same. Furthermore, because a concept consistent set is a non-empty concept set which has non-empty intersections with all non-empty sets of representative concepts, only one row (or column) needs to be retained. Then the representative concept matrix can be simplified, or clarified. Example 8 gives the clarified representative concept matrix for Example 6.

Example 8

(Continued with Example 6) Deleting rows 4-7, 9-12 and column 8 in the representative concept matrix $\mathbf {\Lambda }$, we obtain the clarified representative concept matrix $\mathbf {\Lambda }_{cla}$ as follows.

$$\begin{aligned} \mathbf {\Lambda }_{cla} = \left( \begin{array}{ccccccc} \{c_5,c_7\} &{} \{c_3,c_4,c_5,c_7\} &{} \{c_7\} &{} \emptyset &{} \{c_4,c_7\} &{} \emptyset &{} \emptyset \\ \{c_5,c_8\} &{} \{c_3,c_5,c_8\} &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_8\} &{} \emptyset \\ \emptyset &{} \{c_3,c_4,c_6\} &{} \emptyset &{} \emptyset &{} \{c_4,c_6\} &{} \emptyset &{} \{c_2,c_6\} \\ \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_2\} \\ \end{array} \right) _{4\times 7} \end{aligned}$$

We find that the clarified representative concept matrix of original context is consistent with the representative concept matrix of clarified context, and the difference between the two matrices is just composition of different elements of concepts. In fact, for the clarified representative concept matrix of the original context, if we remove the redundant objects and attributes in every representative concept, then we obtain the representative concept matrix of the clarified context, and vice versa.

Example 9

(Continued with Example 1) The representative concept matrix of the clarified context in Table 2 is as follows:

$$\begin{aligned} \mathbf {\Lambda }'= \left( \begin{array}{ccccccc} \{c_5',c_7'\} &{} \{c_3',c_4',c_5',c_7'\} &{} \{c_7'\} &{} \emptyset &{} \{c_4',c_7'\} &{} \emptyset &{} \emptyset \\ \{c_5',c_8'\} &{} \{c_3',c_5',c_8'\} &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_8'\} &{} \emptyset \\ \emptyset &{} \{c_3',c_4',c_6'\} &{} \emptyset &{} \emptyset &{} \{c_4',c_6'\} &{} \emptyset &{} \{c_2',c_6'\} \\ \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_2'\} \\ \end{array} \right) _{4\times 7} \end{aligned}$$

Accordingly, the relationship of concept reducts between original context and clarified context is described in Theorem 5, where $(X,A)\cap (Y,B)= (X\cap Y,A\cap B)$ for any $X,Y\subseteq G,A,B\subseteq M$.

Theorem 5

Let (G, M, I) be a formal context and $(G', M', I')$ be its corresponding clarified context. {${\mathcal {F}}_i \mid i\in \tau ,\tau$ is an index set} is the set of all concept reducts in (G, M, I), and {${\mathcal {F}}_j' \mid j\in \tau ',\tau '$ is an index set} is the set of the concept reducts in $(G', M', I')$. Then there exists a bijection $\varphi$ from {${\mathcal {F}}_i \mid i\in \tau ,\tau$ is an index set} to {${\mathcal {F}}_j' \mid j\in \tau ',\tau '$ is an index set}, such that $\varphi ({\mathcal {F}}_i)={\mathcal {F}}_j'$, and $\varphi ^{-1}({\mathcal {F}}_j')={\mathcal {F}}_i$, where ${\mathcal {F}}_i=\{c_{i_1},c_{i_2},\dots ,c_{i_n}\}, {\mathcal {F}}_j'=\{c_{i_1}\cap (G', M'),c_{i_2}\cap (G', M'),\dots ,c_{i_n}\cap (G', M')\}$.

Therefore, for any formal context (G, M, I), we can directly calculate the concept reducts of its corresponding clarified context $(G',M',I')$, and then get the concept reducts of (G, M, I).

Although the clarified representative concept matrix simplifies the original matrix, there still exists repeated information when calculating concept reducts using Theorem 2. Thus the speed of calculation is affected. Definition 8 defines the minimal representative concept matrix $\mathbf {\Lambda }_{min}$ to further simplify the clarified representative concept matrix. Then, all concept reducts can be easily acquired by Theorem 2 on the basis of the minimal representative concept matrix.

Definition 8

Let (G, M, I) be a formal context. $\mathbf {\Lambda }_{min}$ is the matrix consisting of all minimum sets of representative concepts under inclusion relation. We call $\mathbf {\Lambda }_{min}$ the minimal representative concept matrix of (G, M, I).

Example 10

(Continued with Example 8) We consider the clarified representative concept matrix $\mathbf {\Lambda }_{cla}$. It is easy to see that $\{c_7\}$ is a subset of $\{c_5,c_7\}$, $\{c_4,c_7\}$ and $\{c_3,c_4,c_5,c_7\}$; $\{c_8\}$ is a subset of $\{c_5,c_8\}$ and $\{c_3,c_5,c_8\}$; $\{c_4,c_6\}$ is a subset of $\{c_3,c_4,c_6\}$; $\{c_2\}$ is a subset of $\{c_2,c_6\}$. Thus, the minimal representative concept matrix $\mathbf {\Lambda }_{min}$ is:

$$\begin{aligned} \mathbf {\Lambda }_{min} = \left( \begin{array}{ccccccc} \emptyset &{} \emptyset &{} \{c_7\} &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset \\ \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_8\} &{} \emptyset \\ \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_4,c_6\} &{} \emptyset &{} \emptyset \\ \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \emptyset &{} \{c_2\} \\ \end{array} \right) _{4\times 7} \end{aligned}$$

With respect to the approach for simplifying the calculation of concept reduction, Wei et al. proposed a method based on the representative concept function using the minimum interval sets [36].

In the Boolean algebra of the power set of a set, an interval set is the family of all subsets falling within the lower and upper bounds [49, 50]. For the concept lattice, the interval sets are defined as $[(X_1,B_1),(X_2,B_2)]=\{(Y,A)\in L(G,M,I)\mid (X_1,B_1)\le (Y,A)\le (X_2,B_2)\}$ and also of the form ${\mathcal {I}}_{ij}=[(g_i^{**},g_i^{*}),(m_j^{*},m_j^{**})]$ [35]. In fact, ${\mathcal {I}}_{ij}$ covers all concepts whose extents are in $[g_i^{**},m_j^{*}]$ and intents are in $[m_j^{**},g_i^{*}]$.

Theorem 6

[36] For any $(g_i, m_j)\in I$, ${\mathcal {I}}_{ij}=[(g_i^{**},g_i^{*}),(m_j^{*},m_j^{**})]$. ${\mathcal {I}}_{min}$ is the set of minimum intervals under inclusion relation, ${\mathcal {I}}_{min_m}$ is the m-th element of ${\mathcal {I}}_{min}$, and $f(l_{min})=\bigwedge _{m=1}^{\vert {\mathcal {I}}_{min}\vert }(\bigvee _{(X,B)\in {\mathcal {I}}_{min_m}}(X,B))$. Then all conjunctions in the minimal disjunctive normal form corresponding to $f(l_{min})$ are exactly the whole concept reducts corresponding to the formal context.

The essence of interval set ${\mathcal {I}}_{ij}=[(g_i^{**},g_i^{*}),(m_j^{*},m_j^{**})]$ is a set of concepts commonly reflecting the relation between $g_i$ and $m_j$, which is consistent with the meaning of the set of representative concepts of $(g_i, m_j)$ defined in this paper. Thus, we obtain the following theorem.

Theorem 7

For any $(g_i, m_j) \in I$, ${\mathcal {I}}_{ij}={ REP}((g_i,m_j))$.

Proof

For any $(X,B) \in { REP}((g_i,m_j))$, we have $g_i \in X$, $m_j \in B$. Then $g_i^* \supseteq X^*$, $g_i^{**} \subseteq X^{**}$ and $m_j^* \supseteq B^*$, $m_j^{**} \subseteq B^{**}$. From $g_i^{**} \subseteq X^{**}$ and $m_j^* \supseteq B^*$, it follows that $g_i^{**} \subseteq X^{**}=X=B^* \subseteq m_j^*$. From $g_i^* \supseteq X^*$ and $m_j^{**} \subseteq B^{**}$, it follows that $m_j^{**} \subseteq B^{**}=B=X^* \subseteq g_i^*$. Thus, $(X,B) \in {\mathcal {I}}_{ij}$, then ${ REP}((g_i,m_j))\subseteq {\mathcal {I}}_{ij}$. For any $(X,B) \in {\mathcal {I}}_{ij}$, we have $g_i^{**} \subseteq X=B^*\subseteq m_j^*$ and $m_j^{**} \subseteq B=X^*\subseteq g_i^*$. From $B^*\subseteq m_j^*$ we know that $m_j^{**} \subseteq B^{**}=B$. Since $m_j \in m_j^{**}$, $m_j \in B$. From $X^*\subseteq g_i^*$ we know that $g_i^{**} \subseteq X^{**}=X$. Since $g_i \in g_i^{**}$, $g_i \in X$. Thus $(X,B) \in { REP}((g_i,m_j))$, then ${\mathcal {I}}_{ij}\subseteq { REP}((g_i,m_j))$. Therefore, ${\mathcal {I}}_{ij}={ REP}((g_i,m_j))$ holds. $\square$

Example 11

(Continued with Example 1) From the definition of interval set, we know that ${\mathcal {I}}_{11}=[(1^{**},1^{*}),(a^{*},a^{**})]=[(\{1, 5, 9, 11\}, \{a, b, c, e\}),(\{1, 2, 4, 5, 9, 11, 12\},$ $\{a, b\})]=\{c_5, c_7\}$. Also from ${ REP}((1,a))=\{c_5, c_7\}$, we obtain ${\mathcal {I}}_{11}={ REP}((1,a))$.

Hence, the minimal representative concept matrix $\mathbf {\Lambda }_{min}$ in this paper is the matrix representation of the set of minimum interval sets ${\mathcal {I}}_{min}$ in [36]. $\mathbf {\Lambda }_{min}$ can clearly show the minimal sets of representative concepts of arbitrary object-attribute pair.

It can be seen from Examples 6, 8 and 10 that the representative concept matrix becomes more intuitive and clearer after the previous simplified methods given in this section. When the minimal representative concept matrix is obtained, the concept reducts can be obtained by the disjunction and conjunction operations directly. Therefore, this paper gives the algorithm for obtaining the minimal representative concept matrix, which is shown in Algorithm 1.

Since the method of generating all formal concepts does not affect the construction of the minimal representative concept matrix, Algorithm 1 omits the corresponding step of generating L(G, M, I). In fact, we can use any existing concept lattice construction algorithm as a prerequisite for this algorithm. In addition, the relationship between the clarified representative concept matrix of a formal context and the representative concept matrix of the clarified context has been discussed in this section. Therefore, for simplicity, Algorithm 1 is applied directly to the clarified context. The step related to the calculation of the clarified representative concept matrix is no longer displayed in Algorithm 1.

Algorithm 1 consists of the following two parts:

Steps 1-24: constructing the representative concept matrix $\Lambda$.

Steps 25-44: constructing the minimal representative concept matrix $\Lambda _{min}$.

We carry out experiments to compare our proposed algorithm with the algorithm proposed by Wei [36] (only the part of obtaining the minimal discernable concept matrix). The results are presented in Table 4, where seven datasets (iris, sonar.all, balance-scale, zoo, car-evaluation, lung-cancer, ionosphere) are from UCI (http://archive.ics.uci.edu/ml/datasets.php) and bold values indicate items with shorter running times. In addition,  we clarify each formal context before the algorithm is executed.

Table 4 Comparison of running time between Wei [36] and Algorithm 1

5 Concept characteristics

According to the role of each concept in concept reducts, all formal concepts of a formal context can be classified into three parts, i.e., core concept set ${\mathcal {C}}$, relatively necessary concept set ${\mathcal {K}}$, and absolutely unnecessary concept set ${\mathcal {U}}$. It’s worth noting that, concept reducts are closely related to concept consistent sets and minimal representative concept matrix. This section studies the concept characteristics of three types of concepts from the perspective of concept consistent sets and minimal representative concept matrix respectively.

5.1 Concept characteristics from the perspective of concept consistent set

Using the definitions of concept consistent set and core concept, we investigate the judgment theorem of core concept. The opposite is a relatively necessary concept or an absolutely unnecessary concept.

Theorem 8

Let (G, M, I) be a formal context and L(G, M, I) be its corresponding concept lattice. We have the following statements.

• 1. $c\in L(G, M, I)$ is a core concept if and only if $L(G, M, I)-\{c\}$ is not a concept consistent set;

• 2. $c\in L(G, M, I)$ is a relatively necessary concept or an absolutely unnecessary concept if and only if $L(G, M, I)-\{c\}$ is a concept consistent set.

Proof

Let {${\mathcal {F}}_i \mid i\in \tau ,\tau$ is an index set} denote the set of all the concept reducts.

1. Necessity. Let $c\in L(G, M, I)$ be a core concept, which means $c\in \bigcap _{i\in \tau }{\mathcal {F}}_i$. Suppose that $L(G, M, I)-\{c\}$ is a concept consistent set . Then $\bigcap _{i\in \tau }{\mathcal {F}}_i \subseteq L(G, M, I)-\{c\}$ holds. Because of $c\in \bigcap _{i\in \tau }{\mathcal {F}}_i$ and $\bigcap _{i\in \tau }{\mathcal {F}}_i \subseteq L(G, M, I)-\{c\}$, we get that $c\in L(G, M, I)-\{c\}$, which is a contradiction.

Sufficiency. We prove it from the contrapositive, i.e., if c is a non-core concept, then $L(G,M,I) -\{c\}$ is a concept consistent set. Let $c\in L(G, M, I)$ be a non-core concept, which means $c\in {\mathcal {K}}$ or $c\in {\mathcal {U}}$. If $c\in {\mathcal {K}}=\bigcup _{i\in \tau }{\mathcal {F}}_i \setminus \bigcap _{i\in \tau }{\mathcal {F}}_i$, then there exists a concept reduct ${\mathcal {F}}_{i_0}$, $c\notin {\mathcal {F}}_{i_0}$. Then $L(G, M, I)-\{c\} \supseteq {\mathcal {F}}_{i_0}$. Therefore, $L(G, M, I)-\{c\}$ is a concept consistent set. If $c\in {\mathcal {U}}$, which means $c \in L(G,M,I)\setminus \bigcup _{i\in \tau }{\mathcal {F}}_i$. Then $c \notin \bigcup _{i\in \tau }{\mathcal {F}}_i$, namely, $\forall i\in \tau$, $c\notin {\mathcal {F}}_i$. Further, $L(G,M,I)-\{c\} \supseteq {\mathcal {F}}_i$. Thus, $L(G, M, I)-\{c\}$ is a concept consistent set.

2. The proposition can be proved directly by the first one. $\square$

Example 12

(Continued with Example 1) . We consider a concept $c_2\in L(G,M,I)$. From $\{c_2\} \in \mathbf {\Lambda }$ and $(L(G,M,I)-\{c_2\}) \cap \{c_2\}=\emptyset$, it follows that $L(G,M,I)-\{c_2\}$ is not a concept consistent set by Theorem 1. Therefore, $c_2$ is a core concept by Theorem 8.

We consider a concept $c_4\in L(G,M,I)$. For any ${ REP}((g,m)) \in \mathbf {\Lambda }$, from $(L(G,M,I)-\{c_4\}) \cap { REP}((g,m)) \ne \emptyset$ we know that $L(G,M,I)-\{c_4\}$ is a concept consistent set by Theorem 1. Therefore, $c_4$ is a relatively necessary concept or an absolutely unnecessary concept by Theorem 8.

5.2 Concept characteristics from the perspective of minimal representative concept matrix

A concept reduct is a minimum concept set which can be formed by taking any one concept from each non-empty set in minimal representative matrix. On this basis, we study the characteristics of three types of concepts. Firstly, a core concept is the concept that is contained in every concept reduct, and therefore it should be represented in a representative concept matrix as a single-point set.

Theorem 9

Let (G, M, I) be a formal context and L(G, M, I) be its corresponding concept lattice. $c\in L(G, M, I)$ is a core concept if and only if there exists $(g_0, m_0)\in I$ such that ${ REP}((g_0, m_0))=\{c\}$.

Proof

c is a core concept.

$\Leftrightarrow$ $L(G, M, I)-\{c\}$ is not a concept consistent set.

$\Leftrightarrow$ $\exists (g_0, m_0)\in I$, s.t. $(L(G, M, I)-\{c\})\cap { REP}((g_0,m_0))=\emptyset$.

$\Leftrightarrow$ ${ REP}((g_0, m_0))=\{c\}$. $\square$

An absolutely unnecessary concept is the concept that is not contained in any concept reduct. According to the definition of minimal representative concept matrix, we obtain the concept characteristic of absolutely unnecessary concepts as described later in Theorem 10. Before that, we give a related lemma.

Lemma 2

Let (G, M, I) be a formal context, {${\mathcal {F}}_i \mid i\in \tau ,\tau$ is an index set} is the set of all concept reducts, and $\mathbf {\Lambda }_{min}$ is the minimal representative concept matrix. Then $\bigcup _{i\in \tau }{\mathcal {F}}_{i}=\bigcup _{{ REP}((g,m))\in \mathbf {\Lambda }_{min}}{ REP}((g,m))$.

Proof

For any $c\in \bigcup _{i\in \tau }{\mathcal {F}}_{i}$, there exists $i_0\in \tau$ such that $c\in {\mathcal {F}}_{i_0}$. Since ${\mathcal {F}}_{i_0}$ is a concept reduct, then for any ${ REP}((g,m)) \in \mathbf {\Lambda }_{min}$, we have ${ REP}((g,m)) \cap {\mathcal {F}}_{i_0}\ne \emptyset$. Suppose that $c\notin \bigcup _{{ REP}((g,m))\in \mathbf {\Lambda }_{min}}{ REP}((g,m))$, which means for any ${ REP}((g,m))\in \mathbf {\Lambda }_{min}$, $c\notin { REP}((g,m))$ holds. Then ${ REP}((g,m)) \cap ({\mathcal {F}}_{i_0}\setminus \{c\})\ne \emptyset$, thus ${\mathcal {F}}_{i_0}\setminus \{c\}$ is a concept consistent set. Furthermore, ${\mathcal {F}}_{i_0}$ is not a concept reduct, which is in contradiction to the known condition. Hence $c\in \bigcup _{{ REP}((g,m))\in \mathbf {\Lambda }_{min}}{ REP}((g,m))$, and we have $\bigcup _{i\in \tau }{\mathcal {F}}_{i} \subseteq \bigcup _{{ REP}((g,m))\in \mathbf {\Lambda }_{min}}{ REP}((g,m))$.

For any $c\in \bigcup _{{ REP}((g,m))\in \mathbf {\Lambda }_{min}}{ REP}((g,m))$, there exists ${ REP}((g_0, m _0))\in \mathbf {\Lambda }_{min}$ such that $c\in { REP}((g_0, m _0))$. It means that there exists $i_0\in \tau$ such that $c\in {\mathcal {F}}_{i_0}$, i.e., $c\in \bigcup _{i\in \tau }{\mathcal {F}}_{i}$. Hence $\bigcup _{i\in \tau }{\mathcal {F}}_{i} \supseteq \bigcup _{{ REP}((g,m))\in \mathbf {\Lambda }_{min}}{ REP}((g,m))$. $\square$

Theorem 10

Let (G, M, I) be a formal context and L(G, M, I) be its corresponding concept lattice. $c\in L(G, M, I)$ is an absolutely unnecessary concept if and only if for any ${ REP}((g,m)) \in \mathbf {\Lambda }_{min}$, $c\notin { REP}((g,m))$ holds.

Proof

c is an absolutely unnecessary concept.

$\Leftrightarrow$ $c \notin \bigcup _{i\in \tau }{\mathcal {F}}_i$.

$\Leftrightarrow$ $c \notin \bigcup _{{ REP}((g,m))\in \mathbf {\Lambda }_{min}}{ REP}((g,m))$.

$\Leftrightarrow$ For any ${ REP}((g,m))\in \mathbf {\Lambda }_{min}$, $c \notin { REP}((g,m))$. $\square$

A relatively necessary concept is the concept that is neither a core concept nor an absolutely unnecessary concept. Therefore, we can use the negative of Theorem 9 and Theorem 10 to judge whether a concept is a relatively necessary concept, and give the following comprehensive result.

Corollary 1

Let (G, M, I) be a formal context and L(G, M, I) be its corresponding concept lattice. We have following statements.

• 1. $c\in L(G, M, I)$ is a core concept if and only if there exists $(g_0, m _0)\in I$ such that ${ REP}((g_0, m_0))=\{c\}$;

• 2. $c\in L(G, M, I)$ is an absolutely unnecessary concept if and only if for any ${ REP}((g,m)) \in \mathbf {\Lambda }_{min}$, $c\notin { REP}((g,m))$ holds;

• 3. $c\in L(G, M, I)$ is a relatively necessary concept if and only if there exists ${ REP}((g_0,m_0)) \in \mathbf {\Lambda }_{min}$, such that $c\in { REP}((g_0,m_0))$ and for any $(g, m)\in I$, ${ REP}((g, m)) \ne \{c\}$ holds.

Example 13

(Continued with Example 1) Because of ${ REP}((1, c))=\{c_7\}$, we know that $c_7$ is a core concept by Theorem 9. Because for any ${ REP}((g,m)) \in \mathbf {\Lambda }_{min}$, $c_3\notin { REP}((g,m))$ holds, we know that $c_3$ is an absolutely unnecessary concept by Theorem 10. Because for any $(g, m)\in I$, ${ REP}((g, m)) \ne \{c_4\}$ holds, and there exists ${ REP}((3,e)) \in \mathbf {\Lambda }_{min}$ such that $c_4\in { REP}((3,e))$, we know that $c_4$ is a relatively necessary concept by Corollary 1.

6 Conclusion

Concept reduction is a new reduction theory. It can avoid information loss caused by attribute reduction, and reduce the number of concepts to simplify the complexity of solving problems with FCA. Considering the fact that concepts are created from the binary relation, this paper proposed the representative concept matrix to visualize the strong connection between concepts and the binary relation, and gave a simple and intuitive calculation method of acquiring concept reduction. To simplify the calculation furtherly, this paper clarified and simplified the representative concept matrix, and then gave an algorithm for obtaining the minimal representative concept matrix in Section 4. Compared with the algorithm in [36], the running time of our proposed algorithm is greatly reduced. Finally, we discussed the characteristics of three kinds of concepts from the perspective of concept consistent set and minimal representative concept matrix, respectively.

The results of this paper suggest several future research topics, here are some examples.

1. We know that the number of concepts in different concept reducts may be different. So, what are the conditions that the concept number of different reducts are equal? How to explain the meaning of this situation? In addition, since different concept reducts have different significance, can we use it to discuss the ordering of all concept reducts so as to obtain the optimal concept reduct?

2. Attribute reduction and concept reduction are two different reduction theories in FCA. Attribute reduction reduces the number of attributes while preserving the specific information, and concept reduction reduces the number of concepts while preserving the binary relation. Are there any connection between these two different reduction theories? In addition, what’s the relationship between the concept reducts of a formal context before and after attribute reduction?

3. Section 2 explains the concept reduction in terms of the “trisecting” of TAO model integrating trisecting, acting and outcome. On this basis, what are the “acting” and “outcome” corresponding to this “trisecting”? Can we make a complete and reasonable explanation of concept reduction by using the ideology of 3WD?

Generally, the concept reduction theory is proposed and studied based on formal context. In fact, we can also extend the concept reduction theory to other context or from other perspectives. For example, we can extend the concept reduction to incomplete formal context, interval-valued formal context, fuzzy formal context, and so on. Moreover, from the perspective of data storage, concept reduction can store all information of formal context with fewer concepts and retain the core part of concept lattice. From the perspective of compression and simplification of concept lattice, concept reduction can also be regarded as a simplification method of concept lattice. So we can use concept reduction to further study the related issues of data analysis or concept lattice simplification.

Now the research on concept reduction theory is in the initial stage. The above topics are just a few of interesting topics related to concept reduction, and more research are worth investigating.